1 Introduction

Usually, after translating of algebraic properties of rings into graph-theoretic language, some problems in ring theory might be more easily solved. When one assigns a graph to a ring, numerous interesting algebraic problems arise from the translation of some graph-theoretic parameters such as clique number, chromatic number, diameter, and radius. There are many extensive studies of this topic; for instance, see [1, 3–5, 8, 13]. Throughout this paper, all rings are assumed to be non-domain commutative rings with identity. By \({\mathbb {I}}(R)\) (\({\mathbb {I}}(R)^*\)), \(\mathrm{Min}(R)\) and Z(R), we mean the set of all proper (nontrivial) ideals of R, the set of minimal prime ideals of R, and the set of zero-divisors of R, respectively. Moreover, the set of all nilpotent elements of R is denoted by \(\mathrm{Nil}(R)\). The ring R is said to be reduced, if \(\mathrm{Nil}(R)=(0)\).

Let G be a graph with the vertex set V(G) and the edge set E(G). The degree of a vertex x of G is denoted by d(x), and the maximum degree of vertices of G is denoted by \(\Delta (G)\). Recall that a k -edge coloring of a graph G is an assignment of k colors \(\{1,\ldots ,k\}\) to the edges of G such that no two adjacent edges have the same color. For a graph G, let \(\chi (G)\) (\(\chi '(G)\)) denote the vertex (edge ) chromatic number of the graph G, i.e., the minimal number of colors which can be assigned to the vertices (edges) of G in such a way that every two adjacent vertices (edges) have different colors. To see the coloring of some special graphs, we refer the reader to [1, 14–16]. A clique of a graph G is a complete subgraph of G and the number of vertices in the largest clique of graph G, denoted by \(\omega (G)\), is called the clique number of G. The complete graph of order n is denoted by \(K_n\). Also, the girth of G and the diameter of G are denoted by girth(G) and diam(G), respectively. The distance between two vertices x and y of a graph is denoted by d(x, y). For any vertex x of G, the eccentricity of x, denoted by e(x), is the maximum of the distances to the other vertices of G. The set of vertices with minimal eccentricity is called the center of the graph G, and this minimum eccentricity value is the radius of G which is denoted by r(G). For every vertex x of a connected graph G, the status of x, denoted by s(x), is the sum of the distances from x to the other vertices of G. The set of vertices with minimal status is called the median of the graph.

We call an ideal I of R, an annihilating-ideal if there exists a nonzero ideal J of R such that \(IJ =(0)\). We use the notation \({\mathbb {A}}(R)\) for the set of all annihilating-ideals of R. By the annihilating-ideal graph of R, \({\mathbb {AG}}(R)\), we mean the graph with the vertex set \({\mathbb {A}}(R)^{*}= {\mathbb {A}}(R)\setminus \{0\}\) and two distinct vertices I and J are adjacent if and only if \(IJ=0\). Some properties of this graph have been studied in [1, 2, 8]. For a ring R, we define another kind of undirected graph \({\mathbb {AG}}_N(R)\) with the vertex set \(\{I:\ (0)\ne I\lhd R\), and there exists a nonzero ideal J such that \(IJ\subseteq \mathrm{Nil}(R)\}\) and two distinct vertices are adjacent if and only if \(IJ\subseteq \mathrm{Nil}(R)\). Obviously, our definition is different from the one defined by Behboodi and Rakeei in [8], and it is easy to see that the usual annihilating-ideal graph \({\mathbb {AG}}(R)\) is a subgraph of \({\mathbb {AG}}_N(R)\).

2 Diameter, Radius, and Center

We start this section by the main definition of this paper.

Definition 1

Let R be a ring. The nil-graph of ideals of R, denoted by \({\mathbb {AG}}_N(R)\), is an undirected graph whose vertex set is the set of all nontrivial ideals I of R such that \(IJ\subseteq \mathrm{Nil}(R)\) for some nontrivial ideal J of R and two distinct vertices I and J are adjacent if and only if \(IJ\subseteq \mathrm{Nil}(R)\).

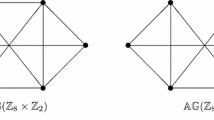
Example 2

The following figures show the nil-graph of ideals of some rings:

figure a

In this section, some upper bounds for the diameter, girth, and radius of the nil-graph of ideals are given. Then the central vertices of \({\mathbb {AG}}_N(R)\) are studied when R is an Artinian ring. Finally, it is shown that the center and median of \({\mathbb {AG}}_N(R)\) coincide, for every ring R with finitely many ideals.

Remark 3

Let R be a ring. Then every nontrivial ideal of R which is contained in \(\mathrm{Nil}(R)\) is adjacent to every other vertex of \({\mathbb {AG}}_N(R)\). In particular, if R is an Artinian local ring, then \({\mathbb {AG}}_N(R)\) is a complete graph. It is worthy to mention that if \(\mathrm{Nil}(R)\ne 0\), then every ideal of R is a vertex of \({\mathbb {AG}}_N(R)\). However, the converse is not true in general. For example, if \(F_1\) and \(F_2\) are fields and \(R\cong F_1\times F_2\), then every ideal of R is a vertex of \({\mathbb {AG}}_N(R)\) (Indeed \({\mathbb {AG}}_N(R)=K_2\)), whereas \(\mathrm{Nil}(R)=0\).

In the first theorem of this paper, we study the connectedness, diameter, and girth of \({\mathbb {AG}}_N(R)\).

Theorem 4

For every ring R, \({\mathbb {AG}}_N(R)\) is connected and \(\mathrm{diam}({\mathbb {AG}}_N(R))\le 3\). Moreover, if \({\mathbb {AG}}_N(R)\) contains a cycle, then \(\mathrm{girth}({\mathbb {AG}}_N(R))\le 4\).

Proof

If R is reduced, then the assertion follows from [8, Theorem 2.1]. So, suppose that \(\mathrm{Nil}(R)\ne (0)\). In this case, Remark 3 implies that \({\mathbb {AG}}_N(R)\) is connected and \(\mathrm{diam}({\mathbb {AG}}_N(R))\le 2\). Now, suppose that \({\mathbb {AG}}_N(R)\) contains a cycle. Then by Remark 3, \(\mathrm{Nil}(R)\) is adjacent to every other vertex of \({\mathbb {AG}}_N(R)\) and so \(\mathrm{girth}({\mathbb {AG}}_N(R))=3\). \(\square \)

The next theorem characterizes all rings whose nil-graphs of ideals are complete.

Theorem 5

Let R be a ring. Then \({\mathbb {AG}}_N(R)\) is complete if and only if one of the following holds:

  1. (i)

    (\(R, \mathrm{Nil}(R)\mathrm{)}\) is a local ring.

  2. (ii)

    \(R\cong F_1\times F_2\), where \(F_1\) and \(F_2\) are two fields.

Proof

One side is clear. To prove the other side, suppose that \({\mathbb {AG}}_N(R)\) is complete. Hence we infer two cases:

Case 1. Every vertex of \({\mathbb {AG}}_N(R)\) is contained in \(\mathrm{Nil}(R)\). Thus one may assume that \(\mathrm{Nil}(R)\ne 0\). By Remark 3, every (maximal) ideal of R is a vertex of \({\mathbb {AG}}_N(R)\). It is well known that \(\mathrm{Nil}(R)\) is the intersection of all minimal prime ideals of R and so \(\mathrm{Nil}(R)\) is the unique maximal ideal of R.

Case 2. There exists a vertex \(I\in V({\mathbb {AG}}_N(R))\) such that \(I\nsubseteq \mathrm{Nil}(R)\). Let \(x\in I\setminus \mathrm{Nil}(R)\) and consider two ideals Rx and \(Rx^2\). It is easily seen that Rx and \(Rx^2\) are vertices of \({\mathbb {AG}}_N(R)\). Since \({\mathbb {AG}}_N(R)\) is complete, we deduce that \(Rx=Rx^2\). Thus \(x=tx^2\), for some \(t\in R\). It is not hard to see that \(1-tx\ne 1\) is a nonzero idempotent. By [6, Proposition 5.10], \(R\cong R_1\times R_2\), for some rings \(R_1\) and \(R_2\). Now, we show that \(R_1\) and \(R_2\) are two fields. Assume to the contrary, \(R_1\) is not field. If \(R_1\) is not an integral domain, then \(R_1\) contains a nontrivial annihilating-ideal, say J. Then the vertices \(J\times R_2\) and \((0)\times R_2\) are not adjacent, which is impossible. If \(R_1\) is an integral domain, then consider two arbitrary ideals I and J of \(R_1\). So, the vertices \(I\times (0)\) and \(J\times (0)\) are not adjacent, a contradiction. Thus \(R_1\) is a field. By a similar argument, one can show that \(R_2\) is a field, and this completes the proof. \(\square \)

Now, we study the radius of the nil-graph of ideals of a Noetherian ring R.

Theorem 6

If R is a Noetherian non-domain ring, then the radius of \({\mathbb {AG}}_N(R)\) is at most 2.

Proof

If R is nonreduced, then \(\mathrm{Nil}(R)\) is adjacent to every other vertex of \({\mathbb {AG}}_N(R)\) and so \(r({\mathbb {AG}}_N(R))=1\). Now, suppose that R is reduced. By [11, Corollary 2.4], \(Z(R)=\bigcup _{i=1}^n {{\mathfrak {p}}}_i\), where each \({\mathfrak {p}}_i\) is a minimal prime ideal of R. We claim that Z(R) is not an ideal of R. Suppose to the contrary, Z(R) is an ideal of R. By the Prime Avoidance Theorem (see [7, Proposition 1.11]), there exists \(1\le k\le n\) such that \(Z(R)={\mathfrak {p}}_k\). Since R is reduced, we conclude that R is an integral domain, a contradiction. So, the claim is proved. Since Z(R) is not an ideal, we deduce that \(n\ge 2\). For every \(1\le j\le n\), define \(\widehat{{\mathfrak {p}}}_j=\bigcap _{i\ne j}{\mathfrak {p}}_i\). To complete the proof, we show that \(e(\widehat{{\mathfrak {p}}}_j)\le 2\). Choose a vertex I. Then there exists \(1\le m\le n\) such that \(I\subseteq {\mathfrak {p}}_m\). If \(m=j\), then \(I\widehat{{\mathfrak {p}}}_j=(0)\). Thus we can assume that \(m\ne j\) and so is a path in \({\mathbb {AG}}_N(R)\) and so \(d(I,\widehat{{\mathfrak {p}}}_j)\le 2\), as desired. \(\square \)

In the next theorem, we determine all rings R for which \(r({\mathbb {AG}}_N(R))=1\).

Theorem 7

For every ring R, \(r({\mathbb {AG}}_N(R))=1\) if and only if either R is nonreduced or \(R\cong F\times D\), where F is a field and D is an integral domain.

Proof

The proof of the previous theorem shows that for every nonreduced ring R, \(r({\mathbb {AG}}_N(R))=1\). Also, if \(R\cong F\times D\), where F is a field and D is an integral domain, then \(F\times (0)\) is adjacent to every other vertex of \({\mathbb {AG}}_N(R)\). Hence \(r({\mathbb {AG}}_N(R))=1\). Conversely, suppose that \(r({\mathbb {AG}}_N(R))=1\). Then there exists a vertex, say I, which is adjacent to every other vertex of \({\mathbb {AG}}_N(R)\). Now, let R be reduced. We show that \(R\cong F\times D\), where F is a field and D is an integral domain. To see this, we choose \(0\ne e\in I\). Clearly, Re is adjacent to every other vertex of \({\mathbb {AG}}_N(R)\). Since R is reduced, Re is a minimal ideal of R, otherwise there exists a nonzero ideal J such that \(J\subsetneqq Re\) and so \(J^2\subseteq JRe=(0)\), a contradiction. Thus by Brauer’s Lemma (see [12, 10.22]), e is idempotent and so \(R\cong Re\times R(1-e)\). Since Re is a minimal ideal, we deduce that Re is a field. To complete the proof, it is enough to show that \(R(1-e)\) is an integral domain. Suppose to the contrary, \(0\ne y\) is a zero-divisor in \(R(1-e)\). Then \(Re\times (y)\) is a vertex of \({\mathbb {AG}}_N(R)\). On the other hand, we know that \(Re\times (0)\) is adjacent to every other vertex of \({\mathbb {AG}}_N(R)\). Thus \((Re\times (0))(Re\times (y))=Re\times (0)=(0)\), a contradiction.  \(\square \)

In the next theorem, the center of \({\mathbb {AG}}_N(R)\) is determined, for every Artinian ring R. Before this, we need the following notation.

Notation Let R be an Artinian ring. Using [7, Theorem 8.7], with no loss of generality, one can deduce that there exists a positive integer n such that \(R=R_1\times \cdots \times R_n\), where each \((R_i,{\mathfrak {m}}_i)\), \(1\le i\le n\), is an Artinian local ring. It is clear that \(\mathrm{Nil}(R)={\mathfrak {m}}_1\times \cdots \times {\mathfrak {m}}_n\). We denote by \({\mathcal {N}}(R)\) and \({\mathcal {F}}(R)\), the set of nontrivial ideals of R, contained in \(\mathrm{Nil}(R)\) and the set of ideals of the form \(I_j=(0)\times \cdots \times (0)\times R_j\times (0)\times \cdots \times (0)\), where \(1\le j\le n\), respectively.

Theorem 8

Let R be an Artinian ring such that \(R\ncong F\times S\), for every field F and every Artinian local ring S. Then the center of \({\mathbb {AG}}_N(R)\) is \({\mathcal {F}}(R)\) if R is reduced and it is \({\mathcal {N}}(R)\) if R is nonreduced.

Proof

First suppose that R is reduced. From Theorem 6, we know that \(r({\mathbb {AG}}_N(R))\le 2\). If \(r({\mathbb {AG}}_N(R))=1\), then Theorem 7 implies that \(R\cong F_1\times F_2\) (since R is Artinian). Hence \({\mathbb {AG}}_N(R)\cong K_2\) and so the center of \({\mathbb {AG}}_N(R)\) equals \({\mathcal {F}}(R)\). Thus we can assume that \(R\cong F_1\times \cdots \times F_n\), where each \(F_i\) is a field and \(n\ge 3\). In this case, Theorem 6 implies that \(r({\mathbb {AG}}_N(R))=2\). Now, we show that the center of \({\mathbb {AG}}_N(R)\) is \({\mathcal {F}}(R)\). To see this, let \(I_j\in {\mathcal {F}}(R)\) and \(J=J_1\times \cdots \times J_n\) be a vertex of \({\mathbb {AG}}_N(R)\). Assume that \(\Delta _J=\{1\le i\le n:\ J_i=F_i\}\). If \(j\notin \Delta _J\), then \(I_j\) and J are adjacent. So, suppose that \(j\in \Delta _J\). Then it is clear that there exists \(t\ne j\) such that \(J_t=(0)\). Thus \(I_t\) is adjacent to both \(I_j\) and J. Therefore, the distance between \(I_j\) and J is at most \(r({\mathbb {AG}}_N(R))=2\) and so \({\mathcal {F}}(R)\) is contained in the center of \({\mathbb {AG}}_N(R)\). Now, assume that \(J=J_1\times \cdots \times J_n\) is a vertex of \({\mathbb {AG}}_N(R)\) with \(J\notin {\mathcal {F}}(R)\). Then there exist the indices i and j such that \(J_i=F_i\) and \(J_j=F_j\). In this case, we claim that the distance between J and \(K=F_1\times \cdots \times F_{i-1}\times (0)\times F_{i+1}\times \cdots \times F_n\) is more than 2. It is clear that J and K are not adjacent. Suppose to the contrary, there is a vertex such as \(I=I_1\times \cdots \times I_n\), which is adjacent to both J and K. Since I is adjacent to J, we have \(I_i=I_j=(0)\). On the other hand, the adjacency of I and K implies that \(I_t=(0)\), for every \(t\ne i\). Thus \(I=(0)\), a contradiction. So, the claim is proved and hence the center of \({\mathbb {AG}}_N(R)\) is \({\mathcal {F}}(R)\). Now, suppose that R is nonreduced. It follows from Theorem 7 that \(r({\mathbb {AG}}_N(R))=1\). By Remark 3, \({\mathcal {N}}(R)\) is contained in the center of \({\mathbb {AG}}_N(R)\) and we can assume that R is not local. So, [7, Theorem 8.7] implies that \(R\cong T\times S\), where T is an Artinian local ring. By hypothesis, we can suppose that S is not a field. To complete the proof, we show that the center of \({\mathbb {AG}}_N(R)\) is contained in \({\mathcal {N}}(R)\). Suppose to the contrary, \(I\times J\) is a vertex in the center of \({\mathbb {AG}}_N(R)\) and \(I\times J\notin {\mathcal {N}}(R)\). Then either \(I\nsubseteq \mathrm{Nil}(T)\) or \(J\nsubseteq \mathrm{Nil}(S)\). If \(I\nsubseteq \mathrm{Nil}(T)\), then \(I=T\). Since S is not a field, we deduce that there exists a proper ideal of S, say K, such that \(K\ne J\). It is easy to check that \(I\times J\) and \(I\times K\) are not adjacent and so \(I\times J\) does not belong to the center of \({\mathbb {AG}}_N(R)\), a contradiction. Also, if \(J\nsubseteq \mathrm{Nil}(S)\), then \(J^2\nsubseteq \mathrm{Nil}(S)\) and so \(I\times J\) is not adjacent to \(L\times J\), for every ideal L of T with \(L\ne I\), a contradiction. So, the proof is complete. \(\square \)

Remark 9

If \(R\cong F\times S\), where F is a field and S is an Artinian local ring, then the center of \({\mathbb {AG}}_N(R)\) is \({\mathcal {N}}(R)\cup \{(0)\times S\}\).

We are interested here in finite graphs. Hence, in the following theorem, we suppose that all rings have finitely many ideals. Although both the center and the median relate to the topic of centrality in a graph, they need not coincide. In general, finding the median of a graph is more involved than finding the center. However, in the case of nil-graphs of ideals of rings, the following theorem shows that the center and median coincide. It is trivial to see that in any connected graph of radius one, the center and median coincide.

Theorem 10

Let R be a ring with finitely many ideals. Then the center and median of \({\mathbb {AG}}_N(R)\) are equal.

Proof

First suppose that R is nonreduced. In this case, Theorem 7 implies that \(r({\mathbb {AG}}_N(R))=1\). Thus the center and median coincide. Now, assume that R is reduced. Since R is Artinian, we deduce that \(R\cong F_1\times \cdots \times F_n\), where n is a positive integer and every \(F_i\) is a field. If \(n=2\), then \({\mathbb {AG}}_N(R)\cong K_2\) and so the center and median of \({\mathbb {AG}}_N(R)\) are equal. Now, suppose that \(n\ge 3\). We claim that for every \(I\in {\mathcal {F}}(R)\), \(s(I)=3(2^{n-1}-1)-2\). With no loss of generality, we can assume that \(I=F_1\times (0)\times \cdots \times (0)\). By Theorems 6 and 7, \(r({\mathbb {AG}}_N(R))=2\) and hence the distance between I and every other vertex of \({\mathbb {AG}}_N(R)\) is either 1 or 2. Clearly, I is adjacent to exactly \(2^{n-1}-1\) vertices. Since \({\mathbb {AG}}_N(R)\) has \(2^{n}-2\) vertices, we deduce that \(s(I)=2^{n-1}-1+2(2^{n-1}-2)=3(2^{n-1}-1)-2\) and so the claim is proved. Now, we show that \(s(J)>3(2^{n-1}-1)-2\), for every \(J_1\times \cdots \times J_n=J\notin {\mathcal {F}}(R)\). Let t be the number of indices in which \(J_i=F_i\). Then J is adjacent to exactly \(2^{n-t}-1\) vertices. Since \(t>1\) and \({\mathbb {AG}}_N(R)\) has \(2^{n}-2\) vertices, we deduce that \(s(J)> 2^{n-1}-1+2(2^{n-1}-2)=3(2^{n-1}-1)-2\). Therefore, Theorem 8 implies that both the center and median of \({\mathbb {AG}}_N(R)\) are equal to \({\mathcal {F}}(R)\). \(\square \)

3 The Edge and Vertex Chromatic Number

In this section, first we determine conditions under which the edge chromatic number of \({\mathbb {AG}}_N(R)\) equals the maximum degree. Then we show that for every ring R, the vertex chromatic number and the clique number of \({\mathbb {AG}}_N(R)\) are equal.

Vizing’s Theorem (see [17, p. 16]) states that if G is a simple graph, then either \(\chi '(G)=\Delta (G)\) or \(\chi '(G)=\Delta (G)+1\). If \(G\cong K_n\), for some odd number n, then \(\chi '(G)=\Delta (G)+1\). We guess that unless in this case, \(\chi '({\mathbb {AG}}_N(R))=\Delta ({\mathbb {AG}}_N(R))\), for every ring R. The next theorem provides some sufficient conditions under which \(\chi '({\mathbb {AG}}_N(R))=\Delta ({\mathbb {AG}}_N(R))\). First of all, we recall the following lemma.

Lemma 11

([9, Corollary 5.4]) Let G be a simple graph. Suppose that for every vertex u of maximum degree, there exists an edge \(\{u,v\}\) such that \(\Delta (G)-d(v)+2\) is more than the number of vertices with maximum degree in G. Then \(\chi '(G)=\Delta (G)\).

Theorem 12

Let R be an Artinian ring which is not a field.

  1. (i)

    If R is reduced, then \(\chi '({\mathbb {AG}}_N(R))=\Delta ({\mathbb {AG}}_N(R))\).

  2. (ii)

    Let \(R\cong R_1\times \cdots \times R_n\), where every \(R_i\) is an Artinian local ring and \(t=\mathrm{max}\{|{\mathbb {I}}(R_i)|\,:\,1\le i\le n\}\). If \(n \log _{3}((t+1)/t)\ge 1\), then \(\chi '({\mathbb {AG}}_N(R))=\Delta ({\mathbb {AG}}_N(R))\) unless R is a local ring such that \(|{\mathbb {I}}(R)^*|\) is an odd number.

Proof

Let R be an Artinian ring. Then by [7, Theorem 8.7], there exists a positive integer n such that \(R\cong R_1\times \cdots \times R_n\), where every \(R_i\) is an Artinian local ring. If R contains infinitely many ideals, then with no loss of generality, we can assume that \({\mathbb {I}}(R_1)\) is an infinite set. Thus by Remark 3, \(\chi '({\mathbb {AG}}_N(R_1))=\Delta ({\mathbb {AG}}_N(R_1))=\infty \) and so there is nothing to prove. Therefore, we can suppose that \(|{\mathbb {I}}(R)^*|<\infty \). If R is a local ring, then by Remark 3, we can suppose that \({\mathbb {AG}}_N(R)\cong K_{|{\mathbb {I}}(R)^*|}\). By [17, Theorem 1.2], we have \(\chi '({\mathbb {AG}}_N(R))=\Delta ({\mathbb {AG}}_N(R))\) if \(|{\mathbb {I}}(R)^*|\) is even and \(\chi '({\mathbb {AG}}_N(R))=\Delta ({\mathbb {AG}}_N(R))+1\) if \(|{\mathbb {I}}(R)^*|\) is odd. For the nonlocal case, we follow the proof in the following two cases:

Case 1. R is a reduced ring. Since R is Artinian, we conclude that \(R\cong F_1\times \cdots \times F_n\), where every \(F_i\) is a field. If \(n=2\), then it is clear that \(\chi '({\mathbb {AG}}_N(R))=\Delta ({\mathbb {AG}}_N(R))=1\). So, let \(n>2\). Then \(\Omega =\{(0)\times \cdots \times (0)\times F_i\times (0)\times \cdots \times (0)\,|\,1\le i\le n\}\) is the set of all vertices with maximum degree and \(|\Omega |=n\). Also, one can easily check that \(\Delta ({\mathbb {AG}}_N(R))=2^{n-1}-1\). Now, let u be a vertex with maximum degree in \({\mathbb {AG}}_N(R)\). With no loss of generality, one can suppose that \(u=F_1\times (0)\times \cdots \times (0)\). In this case, we choose the vertex \(v=(0)\times F_2\times \cdots \times F_n\). Then \(\Delta ({\mathbb {AG}}_N(R))-d(v)+2=2^{n-1}>n\) and so by Lemma 11, \(\chi '({\mathbb {AG}}_N(R))=\Delta ({\mathbb {AG}}_N(R))\). This proves (i).

Case 2. R is a nonreduced ring. For every \(1\le i\le n\), let \(t_i=|{\mathbb {I}}(R_i)|\). It is clear that \(\mathrm{Nil}(R)\) is adjacent to every other vertex of \({\mathbb {AG}}_N(R)\) and so \(\Delta ({\mathbb {AG}}_N(R))=\prod _{i=1}^n(t_i+1)-3\). On the other hand, a vertex \(J_1\times \cdots \times J_n\) is adjacent to every other vertex of \({\mathbb {AG}}_N(R)\) if and only if \(J_i\subseteq \mathrm{Nil}(R_i)\), for every i. So the number of vertices with maximum degree is \(\prod _{i=1}^nt_i-1\). For every vertex u of \({\mathbb {AG}}_N(R)\) with maximum degree, choose \(v=R_1\times \cdots \times R_{n-1}\times (0)\). Then by an easy calculation, one can see that

$$\begin{aligned} d(v)=(t_n+1)\prod _{i=1}^{n-1}t_i-1=\prod _{i=1}^nt_i+\prod _{i=1}^{n-1}t_i-1< 2\prod _{i=1}^nt_i. \end{aligned}$$

Thus we have

$$\begin{aligned} \Delta ({\mathbb {AG}}_N(R))-d(v)+2>\prod _{i=1}^n(t_i+1)-2\prod _{i=1}^{n}t_i-1. \end{aligned}$$

Now, one can easily show that the condition \(n \log _{3}((t+1)/t)\ge 1\) implies that

$$\begin{aligned} \prod _{i=1}^n(t_i+1)>3\prod _{i=1}^{n}t_i. \end{aligned}$$

So Lemma 11 completes the proof. \(\square \)

The following example shows that the condition \(n\log _{3}((t+1)/t)\ge 1\) in Theorem 12(ii) is necessary.

Example 13

Let \(R={\mathbb {Z}}_{p^2}\times {\mathbb {Z}}_{q^2}\), for some prime numbers p and q. Clearly, \(t=2\). Thus the above condition does not hold. On the other hand, we have \(|E({\mathbb {AG}}_N(R))|=19\), \(|V({\mathbb {AG}}_N(R))|=7\) and \(|\Delta ({\mathbb {AG}}_N(R))|=6\). Therefore, by [10, Exercise 17.2.1], \(\chi '({\mathbb {AG}}_N(R))=\Delta ({\mathbb {AG}}_N(R))+1\).

In the sequel, we study the vertex chromatic number of \({\mathbb {AG}}_N(R)\). The following lemma is needed.

Lemma 14

(See [1, Theorem 6]) Let R be a ring and \(\{{{\mathfrak {p}}}_1,\ldots , {{\mathfrak {p}}}_n\}\) be a finite set of distinct minimal prime ideals of R. Then there exists a clique of \({\mathbb {AG}}(R)\) of size n.

We close this paper with the following result.

Theorem 15

For every ring R, \(\chi ({\mathbb {AG}}_N(R))=\omega ({\mathbb {AG}}_N(R))=|\mathrm{Min}(R)|+t\), where t is the number of nonzero ideals of R contained in \(\mathrm{Nil}(R)\).

Proof

If \(\mathrm{Nil}(R)\) contains infinitely many ideals, then Remark 3 implies that \(\chi ({\mathbb {AG}}_N(R))=\omega ({\mathbb {AG}}_N(R))=\infty \). Thus we can assume that \(\mathrm{Nil}(R)\) contains t nonzero ideals, say \(I_1,\ldots ,I_t\). If R has infinitely many minimal prime ideals, then the assertion follows from Lemma 14. Thus we can assume that R has finitely many minimal prime ideals, say \({\mathfrak {p}}_1,\cdots ,{\mathfrak {p}}_n\). In this case, we define \(c:V({\mathbb {AG}}_N(R))\longrightarrow \{1,\ldots ,n+t\}\) by

$$\begin{aligned} c(I)= {\left\{ \begin{array}{ll} \min \{1\le i\le n|\, I\nsubseteq {\mathfrak {p}}_i\} ; &{} I\nsubseteq \mathrm{Nil}(R)\,\,\, \\ n+j; &{} I=I_j,\, \mathrm{for\, some} \,1\le j\le t.\,\,\, \,\, \end{array}\right. } \end{aligned}$$

We show that c is a proper vertex coloring of \({\mathbb {AG}}_N(R)\). Suppose to the contrary, I and J are two distinct adjacent vertices in \({\mathbb {AG}}_N(R)\) and \(c(I)=c(J)=k\). Then it is clear that neither \(I\subseteq \mathrm{Nil}(R)\) nor \(J\subseteq \mathrm{Nil}(R)\) and so \(1\le k\le n\). Since I and J are adjacent, \(IJ\subseteq \mathrm{Nil}(R)\subseteq {\mathfrak {p}}_k\). Thus either \(I\subseteq {\mathfrak {p}}_k\) or \(J\subseteq {\mathfrak {p}}_k\), a contradiction. Therefore, \(\chi ({\mathbb {AG}}_N(R))\le n+t\). Now, let \(C=\{I_1,\ldots ,I_t\}\cup \{\bigcap _{i=1, i\ne r}^n {\mathfrak {p}}_i|\, 1\le r\le n\}\). Then C is a clique of size \(n+t\) in \({\mathbb {AG}}_N(R)\). Thus \(\chi ({\mathbb {AG}}_N(R))=\omega ({\mathbb {AG}}_N(R))=n+t\). \(\square \)