The Largest Normalized Laplacian Spectral Radius of Non-Bipartite Graphs

Abstract

In this paper, we firstly consider how the normalized Laplacian spectral radius of a non-bipartite graph behaves by several graph operations. As applications of the result, the largest normalized Laplacian spectral radius of non-bipartite unicyclic graphs with fixed order and girth is determined. Moreover, the largest normalized Laplacian spectral radius among non-bipartite unicyclic graphs with fixed girth and order is also determined. The maximizer is the tadpole graph with the same (odd) girth.

1 Introduction

Let $G=(V,E)$ be a simple graph with vertex set $V=\{v_1, \dots , v_n\}$ and edge set E. Let $d_G(v_i)$ (or simply $d(v_i)$) denote the degree of the vertex $v_i\in V$ $(i=1, 2, \dots , n)$, and $D=D(G)=diag(d(v_1), d(v_2), \dots , d(v_n))$ be the diagonal matrix of vertex degrees. The Laplacian matrix of G is defined by $L(G)=D(G)-A(G)$, and the normalized Laplacian matrix of G is defined by $\mathcal {L}(G)=D(G)^{-1/2}L(G)D(G)^{-1/2}$ (with the convention that if the degree of v is 0, then $d(v)^{ -1/2}=0$). It is easy to see that $\mathcal {L}(G)$ is a symmetric positive semidefinite matrix and $D(G)^{1/2}\varvec{j}_n$ is an eigenvector of $\mathcal {L}(G)$ with eigenvalue 0, where $\varvec{j}_n$ is the vector in $\mathbb R^n$ whose entries are 1’s. Denote the eigenvalues of $\mathcal {L}(G)$ by

$$\begin{aligned} 0=\lambda _1(G)\le \lambda _2(G)\le \cdots \le \lambda _{n-1}(G)\le \lambda _n(G), \end{aligned}$$

which are always enumerated in non-decreasing order and repeated according to their multiplicity.

The largest eigenvalue $\lambda _n(G)$ of $\mathcal {L}(G)$ is called the normalized Laplacian spectral radius of the graph G, denoted by $\lambda (G)$. Chung [4] proved that for a connected graph G with $n\ge 2$ vertices, $\frac{n}{n-1}\le \lambda (G)\le 2$, the left equality holds if and only if G is a complete graph, and the right equality holds if and only if G is a bipartite graph.

The normalized Laplacian is a rather new but important tool popularized by Chung in the mid 1990s. As pointed out by Chung [4], the eigenvalues of the normalized Laplacians are in a normalized form, and the spectra of the normalized Laplacians relate well to other graph invariants for general graphs in a way that the other two definitions (such as the eigenvalues of adjacency matrix) fail to do. The advantages of this definition are perhaps due to the fact that it is consistent with the eigenvalues in spectral geometry and in stochastic processes. For more details, see [1, 2, 4, 5]. For a fixed list $\{v_1, \dots , v_n\}$ of vertices of G. Let $X=(x_1, \dots , x_n)^T$ be a real vector. It can be viewed as a labeling of G in which vertex $v_i$ is labeled by $x_{i}$ (or $X(v_i)$). Such labeling is sometimes called a valuation [8] of G. If X is a unit eigenvector of G corresponding to $\lambda (G)$, then we have

$$\begin{aligned} \lambda (G)=\max _{{\begin{matrix} Y\in \mathbb R^n\\ \ \Vert Y\Vert =1\end{matrix}}}Y^T\mathcal {L}(G)Y=X^T\mathcal {L}(G)X=\sum _{ {\begin{matrix}v_iv_j\in E\\ 1\le i<j\le n\end{matrix}}}\left( \frac{1}{\sqrt{d_i}}x_i-\frac{1}{\sqrt{d_j}}x_j\right) ^2. \end{aligned}$$

(1.1)

Let $P_n$ and $C_n$ denote the path and the cycle with n vertices, respectively. It is a well-known fact [4] that if g is odd, then we have

$$\begin{aligned} \lambda (C_g)=\lambda _{g}(P_{g+1})=1-\cos \frac{(g-1)\pi }{g}. \end{aligned}$$

(1.2)

A unicyclic graph is a connected graph in which the number of vertices equals the number of edges. So, if G is a unicyclic graph with girth g, then G consists of the unique cycle (say $C_g$) of length g and a certain number of trees attached at vertices of $C_g$ having in total $n-g$ edges.

In this paper, we firstly consider how the normalized Laplacian spectral radius of a non-bipartite graph behaves by several graph operations. As applications, the largest normalized Laplacian spectral radius of non-bipartite unicyclic graphs with fixed order and girth is determined. Moreover, the largest normalized Laplacian spectral radius among non-bipartite unicyclic graphs with fixed order is also determined.

2 The Normalized Laplacian Spectral Radius of a Graph Under Perturbation

Lemma 2.1

Let X be an eigenvector of $\mathcal {L}(G)$ corresponding to $\lambda (G)$. Then for any $v \in V(G)$, we have

$$\begin{aligned} \sum _{uv\in E(G)}\frac{X(u)}{\sqrt{d(u)}}=\sqrt{d(v)}(1-\lambda (G))X(v). \end{aligned}$$

Proof

The result follows from $D(G)^{-1/2}(D(G)-A(G))D(G)^{-1/2}X=\lambda (G)X$. $\square$

In the following, we consider how the normalized Laplacian spectral radius of a graph behaves by moving pendant edges from one vertex to another.

Theorem 2.2

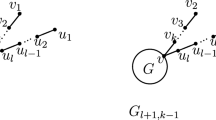
Suppose that u, v are two distinct vertices of a connected non-bipartite graph G, and $vv_1, \dots , vv_s$ are $s\ (s\ge 1)$ pendant edges of G. Let X be a unit eigenvector of G corresponding to $\lambda =\lambda (G)$. Let

$$\begin{aligned} G_u=G-vv_{1}-vv_{2}-\cdots -vv_{s}+uv_{1}+uv_{2}+\cdots +uv_{s}. \end{aligned}$$

If $\frac{|X(u)|}{\sqrt{d(u)}}\ge \frac{|X(v)|}{\sqrt{d(v)}}$, then $\lambda (G_u)\ge \lambda .$ Furthermore, if $\lambda (G_u)= \lambda$, then $X(u)=X(v)= 0$.

Proof

Let Y be a valuation of $G_u$ defined by

$$\begin{aligned} {\left\{ \begin{array}{ll} Y(u)=\sqrt{\frac{d(u)+s}{d(u)}}X(u);\\ Y(v)=\sqrt{\frac{d(v)-s}{d(v)}}X(v);\\ Y(v_i)=\frac{X(u)}{(1-\lambda )\sqrt{d(u)}}, \quad \ i=1, \dots , s;\\ Y(w)=X(w), \quad \ w\ne u, v, v_1, \dots , v_s. \end{array}\right. } \end{aligned}$$

From Lemma 2.1, we have

$$\begin{aligned} (1-\lambda )X(v_i)=\frac{1}{\sqrt{d(v)}}X(v),\quad \ i=1, \dots , s. \end{aligned}$$

(2.1)

Then, we have

$$\begin{aligned} \lambda (G_u)=\max _{Z\ne \varvec{0}}\frac{Z^T\mathcal {L}(G_u)Z}{Z^TZ}\ge \frac{Y^T\mathcal {L}(G_u)Y}{Y^TY} . \end{aligned}$$

Note that

$$\begin{aligned} Y^TY-1&=Y^TY-X^TX\\&=\frac{(d(u)+s)X(u)^2}{d(u)} + \frac{(d(v)-s)X(v)^2}{d(v)} + \frac{sX(u)^2}{d(u)(1-\lambda )^2}\\&\qquad -\frac{sX(v)^2}{d(v)(1-\lambda )^2} -X(u)^2-X(v)^2\\&= \frac{sX(u)^2}{d(u)} -\frac{sX(v)^2}{d(v)}+\frac{sX(u)^2}{d(u)(1-\lambda )^2}- \frac{sX(v)^2}{d(v)(1-\lambda )^2}\\&= s\left[ 1+\frac{1}{(1-\lambda )^2}\right] \left[ \frac{X(u)^2}{d(u)}-\frac{X(v)^2}{d(v)}\right] . \end{aligned}$$

So $Y^TY= 1+s\left[ 1+\frac{1}{(1-\lambda )^2}\right] \left[ \frac{X(u)^2}{d(u)}-\frac{X(v)^2}{d(v)}\right]$.

For easy to illustrate, we rearrange the order of vertices as u, v, $v_1,\dots , v_s$ and others are arranged after $v_s$ arbitrary. We partition $X^TD(G)^{-1/2}$ into three parts $(X_1, X_2, X_3)$, where $X_1^T\in \mathbb R^2$, $X_2^T\in \mathbb R^s$ and $X_3^T\in \mathbb R^{n-s-2}$. Namely, $X_1=(\frac{X(u)}{\sqrt{d(u)}}, \frac{X(v)}{\sqrt{d(v)}})$ and $X_2=\frac{X(v)}{(1-\lambda )\sqrt{d(v)}}\varvec{j}_s^T$. We also partition $Y^TD(G_u)^{-1/2}$ into three parts $(Y_1, Y_2, Y_3)$ accordingly. Then $Y_1=X_1$, $Y_3=X_3$ and $Y_2= \frac{X(u)}{(1-\lambda )\sqrt{d(u)}}\varvec{j}_s^T$.

Write $L(G)=\begin{pmatrix}A_{11} &{} A_{21}^T &{} A_{31}^T\\ A_{21} &{} I_s &{} O^T\\ A_{31} &{} O &{} A_{33}\end{pmatrix}$, where $A_{11}=\begin{pmatrix} d(u) &{} a\\ a &{} d(v)\end{pmatrix}$, $a=0$ or $-1$ dependent on $uv\in E(G)$ or not; $A_{21}=\begin{pmatrix}\varvec{0}_s&-\varvec{j}_s\end{pmatrix}$; $\varvec{0}_s$ is a zero column vector of length s; O is a zero matrix of certain size, $A_{31}$ and $A_{33}$ are some matrices of certain sizes. Accordingly, $L(G_u)=\begin{pmatrix}B_{11} &{} B_{21}^T &{} A_{31}^T\\ B_{21} &{} I_s &{} O^T\\ A_{31} &{} O &{} A_{33}\end{pmatrix}$, where $B_{11}=\begin{pmatrix} d(u)+s &{} a\\ a &{} d(v)-s\end{pmatrix}$ and $B_{21}=\begin{pmatrix} -\varvec{j}_s&\varvec{0}_s\end{pmatrix}$.

Next

$$\begin{aligned} Y^T\mathcal {L}(G_u)Y&= Y_1B_{11}Y_1^T+ 2Y_2B_{21}Y_1^T+ Y_2Y_2^T + 2Y_3A_{31}Y_1^T + Y_3A_{33}Y_3^T\\&= (X_1B_{11}X_1^T+ 2Y_2B_{21}X_1^T+ Y_2Y_2^T) + 2X_3A_{31}X_1^T + X_3A_{33}X_3^T\\&= (X_1B_{11}X_1^T + 2Y_2B_{21}X_1^T+Y_2Y_2^T)+\lambda - 2X_2A_{21}X_1^T -X_2X_2^T -X_1A_{11}X_1^T\\&= \left( X_1(B_{11}-A_{11})X_1^T-\frac{2sX(u)^2}{d(u)(1-\lambda )} +\frac{sX(u)^2}{d(u)(1-\lambda )^2}\right) +\lambda \\&\quad +\frac{2sX(v)^2}{d(v)(1-\lambda )} -\frac{sX(v)^2}{d(v)(1-\lambda )^2}\\&= \left( \frac{sX(u)^2}{d(u)}-\frac{sX(v)^2}{d(v)} -\frac{2sX(u)^2}{d(u)(1-\lambda )}+ \frac{sX(u)^2}{d(u)(1-\lambda )^2}\right) +\lambda \\&\quad +\frac{2sX(v)^2}{d(v)(1-\lambda )} -\frac{sX(v)^2}{d(v)(1-\lambda )^2}\\&= \lambda + s\left[ \frac{X(u)}{\sqrt{d(u)}}- \frac{X(u)}{(1-\lambda )\sqrt{d(u)}}\right] ^2 -s\left[ \frac{X(v)}{\sqrt{d(v)}}- \frac{X(v)}{(1-\lambda )\sqrt{d(v)}}\right] ^2\\&= \lambda + \frac{s\lambda ^2}{(1-\lambda )^2} \left( \frac{X(u)^2}{d(u)}-\frac{X(v)^2}{d(v)}\right) . \end{aligned}$$

So

$$\begin{aligned} \lambda (G_u)-\lambda \ge \frac{Y^T\mathcal {L}(G_u)Y}{Y^TY}-\lambda = \frac{\frac{s\lambda (2-\lambda )}{\lambda -1} \left( \frac{X(u)^2}{d(u)}-\frac{X(v)^2}{d(v)}\right) }{Y^TY}. \end{aligned}$$

(2.2)

Since G is a connected non-bipartite graph and $G\ne K_n$, we have $1<\lambda (G)<2$ [4]. Therefore, we have $\lambda (G_u)\ge \lambda$ when $\frac{|X(u)|}{\sqrt{d(u)}}\ge \frac{|X(v)|}{\sqrt{d(v)}}$.

If $\lambda (G_u)= \lambda$, then the equality in Eq. (2.2) holds. So $\lambda (G_u)=\frac{Y^T\mathcal {L}(G_u)Y}{Y^TY}$. We have $\mathcal {L}(G_u)Y=\lambda (G_u)Y$ (see [6]). Thus, from Lemma 2.1 we have

$$\begin{aligned}&\sqrt{d(v)-s}(1-\lambda (G_u))Y(v)=\sum _{w\in V(G_u),wv\in E(G_u)}\frac{1}{\sqrt{d(w)}}X(w); \end{aligned}$$

(2.3)

$$\begin{aligned}&\sqrt{d(v)}(1-\lambda )X(v)=\sum _{w\in V(G_u),wv\in E(G_u)}\frac{1}{\sqrt{d(w)}}X(w)+\sum _{i=1}^sX(v_i). \end{aligned}$$

(2.4)

Note that $Y(v)=\sqrt{\frac{d(v)-s}{d(v)}}X(v)$. Thus, from Eqs. (2.1), (2.3) and (2.4), we have

$$\begin{aligned} \frac{d(v)-s}{\sqrt{d(v)}}(1-\lambda )X(v) =\sqrt{d(v)}(1-\lambda )X(v) -\frac{s}{\sqrt{d(v)}(1-\lambda )}X(v). \end{aligned}$$

Simplifying the above equation, we have $\lambda (\lambda -2)X(v)=0$. Since $\lambda \ne 2$, we have $X(v)=0$. From Eq. (2.2) we get $X(u)=0$. So we have the last result. $\square$

From Theorem 2.2, we immediately have the following result.

Corollary 2.3

Suppose that u, v are two distinct vertices of a connected non-bipartite graph G, $uu_1, \dots , uu_t$ and $vv_1, \dots , vv_s$ are $t\ (t\ge 1)$ and $s\ (s\ge 1)$ pendant edges of G at vertices u and v, respectively. Let X be a unit eigenvector of G corresponding to $\lambda (G)$. Let

$$\begin{aligned}&G_u=G-vv_{1}-vv_{2}-\cdots -vv_{s}+uv_{1}+uv_{2}+\cdots +uv_{s};\\&G_v=G-uu_{1}-uu_{2}-\cdots -uu_{t}+vu_{1}+vu_{2}+\cdots +vu_{t}. \end{aligned}$$

Then either $\lambda (G_u)\ge \lambda (G)$ or $\lambda (G_v)\ge \lambda (G)$ holds. Furthermore, if $X(u)\ne 0$ or $X(v)\ne 0$, then either $\lambda (G_u)> \lambda (G)$ or $\lambda (G_v)> \lambda (G)$.

Corollary 2.4

Suppose that v is a vertex of a connected non-bipartite graph G, and $vv_1$, $vv_2$, $\dots , vv_s$ are $s\ (s\ge 2)$ pendant edges of G at vertex v. Let X be a unit eigenvector of G corresponding to $\lambda (G)$. Let

$$\begin{aligned} G'=G-vv_{2}-\cdots -vv_{s}+v_{1}v_{2}+\cdots +v_{1}v_{s} \end{aligned}$$

Then we have $\lambda (G')\ge \lambda (G)$. Furthermore, if $X(v)\ne 0$, then we have $\lambda (G')> \lambda (G)$.

Proof

From Lemma 2.1, we have $(1-\lambda (G))X(v_1)=\frac{1}{\sqrt{d(v)}}X(v)$. Since $1<\lambda (G)<2$, we have $|X(v_1)|\ge \frac{1}{\sqrt{d(v)}}|X(v)|$. Note that if $X(v)\ne 0$, then $X(v_1)\ne 0$. The result follows from Theorem 2.2. $\square$

In [3, 7], the authors considered how the normalized Laplacian eigenvalues of a graph behave by deleting an edge.

Lemma 2.5

Let G be a simple graph and $H=G-e$ be the graph obtained from G by removing an edge e. Then $\lambda _{i-1}(G)\le \lambda _{i}(H)\le \lambda _{i+1}(G)$ for $i=1, \ldots , n$, where $\lambda _{0}(G)=0$ and $\lambda _{n+1}(G)=2$.

For the normalized Laplacian spectral radius of a non-bipartite graph, we have the following further result.

Theorem 2.6

Suppose that u is a vertex of a non-bipartite graph G. Let $G_v$ be the graph obtained from G by attaching a pendant edge uv at u of G. Let X be a unit eigenvector of G corresponding to $\lambda (G)$. Then we have $\lambda (G_v)\ge \lambda (G)$, the inequality is strict if $X(u)\ne 0$.

Proof

Let Y be a valuation of $G_v$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} Y(u)=\sqrt{\frac{d(u)+1}{d(u)}}X(u);&{}\\ Y(v)=-\frac{X(u)}{\sqrt{d(u)}};&{}\\ Y(w)=X(w), \quad w\ne u, v.&{} \end{array}\right. } \end{aligned}$$

Then, we have

$$\begin{aligned} \lambda (G_v)-\lambda (G)&=\max _{Z\ne \varvec{0}}\frac{Z^T\mathcal {L}(G_v)Z}{Z^TZ}-\lambda (G)\ge \frac{Y^T\mathcal {L}(G_v)Y}{Y^TY}-\lambda (G)\\&=\frac{\lambda (G)+\big (\frac{2X(u)}{\sqrt{d(u)}}\big )^2}{1+\frac{2X(u)^2}{d(u)}} -\lambda (G)=\frac{\frac{2(2-\lambda (G))X(u)^2}{d(u)}}{1+\frac{2X(u)^2}{d(u)}}. \end{aligned}$$

Since G is a connected non-bipartite graph, we have $1<\lambda (G)<2$ [4]. From the above equation, the result follows. $\square$

3 The Largest Normalized Laplacian Spectral Radius of Non-Bipartite Unicyclic Graphs

A pendant is a vertex with degree 1. A pendant neighbor (which is also called support in some articles) is a vertex adjacent to a pendant. Suppose that $v_1,\dots , v_q$ are all the pendant neighbors of G. Let $t(v_i)$ be the number of pendants adjacent to $v_i$ $(i=1, \dots , q)$, and $t(G)=\max \{t(v_1), \dots , t(v_q)\}$. As an application of Corollary 2.3, in the following, we give the largest normalized Laplacian spectral radius of non-bipartite unicyclic graphs with fixed girth and order.

A tadpole graph $C_{n,g}$, shown in Fig. 1, is the graph obtained by appending a g-cycle $C_g$ to a pendant of a path on $n-g$ vertices.

Fig. 1

Tadpole graph $C_{n,g}$

Theorem 3.1

Let G be a non-bipartite unicyclic graph on n vertices with girth $g\ge 3$. Then $\lambda (G)\le \lambda (C_{n,g})$. The equality holds if and only if G is isomorphic to $C_{n,g}$.

Proof

Let q(G) be the number of pendant neighbors of G. We consider the following three cases:

Case 1. Suppose $q(G)=0$. Then $G=C_n$. The result is obvious.

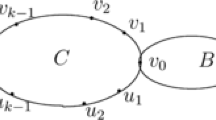
Case 2. Suppose $q(G)=1$. Then $G=C_{n, g}(s)$, where $C_{n, g}(s)$ is the graph of order n obtained from $C_g$ and $K_{1, s}$ by joining a vertex w in $C_g$ and the center u of $K_{1, s}$ by a path $ww_1\cdots w_{n-g-s-1}u$. If $s=1$, then $C_{n, g}(s)=C_{n, g}$, and the result is obvious. Suppose $s\ge 2$. Let $v_1, \dots , v_s$ be all the pendant vertices of $C_{n, g}(s)$. Let X be the unit eigenvector of $C_{n, g}(s)$ corresponding to $\lambda (C_{n, g}(s))$. Applying Corollary 2.4 repeatedly, we have $\lambda (C_{n, g}(s))\le \lambda (C_{n, g})$.

Suppose $\lambda (C_{n, g}(s))= \lambda (C_{n, g})$. From Corollary 2.4 we have $X(v_1)=0$. Applying Lemma 2.1 repeatedly, we have

$$\begin{aligned} X(v_1)=\cdots =X(v_s)=X(u)=X(w_{n-g-s-1})=\cdots =X(w_1)=X(w)=0. \end{aligned}$$

(3.1)

Then X is an eigenvector of $C_{n, g}$ corresponding to $\lambda (C_{n, g})$. According Eq. (3.1) we see that $\lambda (C_{n, g})$ is also a normalized Laplacian eigenvalue of the graph $C_{n-k, g}$ $(1\le k\le n-g)$. From Theorem 2.6, we have $\lambda (C_{n, g})=\lambda (C_{g+2, g})=\lambda (C_g)$. From Lemma 2.5 and Eq. (1.2), we have $\lambda (C_{g+2, g})\ge \lambda _{g+1}(P_{g+2})=1-\cos \frac{g\pi }{g+1} >1-\cos \frac{(g-1)\pi }{g}= \lambda (C_g)$, which yields a contradiction.

Case 3. Suppose $q(G)\ge 2$. Let $u_1$ and $u_2$ be two of pendant neighbors of G such that $1\le t(u_2)\le t(u_1)=t(G)$. Let $G_1$ (resp. $G_2$) be the graph obtained from G by removing $t(u_1)$ (resp. $t(u_2)$) pendant edges from vertex $u_1$ (resp. $u_2$) to vertex $u_2$ (resp. $u_1$). Then we have $t(G_1)=t(G_2) >t(G)$ and from Corollary 2.3, we have either $\lambda (G_1)\ge \lambda (G)$ or $\lambda (G_2)\ge \lambda (G)$. Note that the number of pendant neighbors may not decrease. We continue the above process until there remains only one pendant neighbor. Since the t value of graph is strictly increasing and the number of vertices outside the cycle $C_g$ is finite, the process will stop. Then the last constructed graph is $C_{n, g}(s)$, for some s $(s\ge 2)$. Moreover, $\lambda (G)\le \lambda (C_{n, g}(s))$. It refers to Case 2. $\square$

For the largest normalized Laplacian spectral radius among all non-bipartite unicyclic graphs, we have the following result.

Theorem 3.2

Let G be a non-bipartite unicyclic graph on n vertices. Then $\lambda (G)\le \lambda (C_{n, 3})$, the equality holds if and only if $G=C_{n, 3}$.

Proof

If G is a unicyclic graph with girth 3, then the result follows from Theorem 3.1. Now suppose that G is a non-bipartite unicyclic graph with girth $g\ge 5$. Then from Theorem 3.1, we only need to prove that for $g\ge 5$, $\lambda =\lambda (C_{n,g})<\lambda (C_{n,3})$. Suppose that the unique cycle of $C_{n,g}$ is $C_g=u_1 u_2 \cdots u_g u_1$ with $d(u_1)=3$. Let X be a unit eigenvector of $C_{n,g}$ corresponding to $\lambda$. Since g is odd, there exist two vertices, say $u_i$ and $u_{i+1}$, such that $X(u_i)X(u_{i+1})\ge 0$ (if $i=g$, then $i+1=1$). We consider the following two cases.

Case 1. If $d(u_i)=d(u_{i+1})=2$, then after rearranging the indices of the vertices in $C_g$, we may suppose that

$$\begin{aligned} X(u_i)\ge 0, \quad \ X(u_{i+1})\ge 0, \quad \frac{X(u_{i-1})}{\sqrt{d(u_{i-1})}} -\frac{X(u_{i+2})}{\sqrt{d(u_{i+2})}}\le 0. \end{aligned}$$

(3.2)

From Lemma 2.1, we have

$$\begin{aligned} \sqrt{d(u_i)}(1-\lambda )X(u_i)&= \frac{X(u_{i-1})}{\sqrt{d(u_{i-1})}} +\frac{X(u_{i+1})}{\sqrt{d(u_{i+1})}};\\ \sqrt{d(u_{i+1})}(1-\lambda )X(u_{i+1})&= \frac{X(u_{i})}{\sqrt{d(u_{i})}} +\frac{X(u_{i+2})}{\sqrt{d(u_{i+2})}}. \end{aligned}$$

From the above two equations, we have

$$\begin{aligned} \frac{X(u_{i-1})}{\sqrt{d(u_{i-1})}} +\frac{X(u_{i+2})}{\sqrt{d(u_{i+2})}}&= \left[ \sqrt{d(u_i)}(1-\lambda )-\frac{1}{\sqrt{d(u_i)}}\right] X(u_i)\nonumber \\&\quad +\,\left[ \sqrt{d(u_{i+1})}(1-\lambda ) -\frac{1}{\sqrt{d(u_{i+1})}}\right] X(u_{i+1}). \end{aligned}$$

(3.3)

Let $H=C_{n,g}-u_iu_{i-1}+u_iu_{i+2}$. It is obvious that H is a unicyclic graph with girth 3. Note that $\lambda (H)\le \lambda (C_{n,3})$ by Theorem 3.1. Let Y be a valuation of H such that

$$\begin{aligned} {\left\{ \begin{array}{ll} Y(u_{i-1})=\sqrt{\frac{d(u_{i-1})-1}{d(u_{i-1})}}X(u_{i-1});\\ Y(u_{i+2})=\sqrt{\frac{d(u_{i+2})+1}{d(u_{i+2})}}X(u_{i+2});\\ Y(w)=X(w), \quad w\ne u_{i-1}, u_{i+2}. \end{array}\right. } \end{aligned}$$

Similar to the proof of Theorem 2.2, we rearrange the order of vertices as $u_{i-1}, u_{i+2}, u_i, u_{i+1}$ and the others are arranged after $u_{i+1}$ arbitrary and partition $X^T D(C_{n,g})^{-1/2}$ into three parts $(X_1,X_2,X_3)$, where $X_1^T, X_2^T \in \mathbb {R}^2$ and $X_3^T\in \mathbb {R}^{n-4}$. Namely, $X_1=(\frac{X(u_{i-1})}{\sqrt{d(u_{i-1})}}, \frac{X(u_{i+2})}{\sqrt{d(u_{i+2})}})$ and $X_2=(\frac{X(u_{i})}{\sqrt{d(u_{i})}}, \frac{X(u_{i+1})}{\sqrt{d(u_{i+1})}})$. We also partition $Y^TD(G_u)^{-1/2}$ into three parts $(Y_1, Y_2, Y_3)$ accordingly. We have $(Y_1, Y_2, Y_3)=(X_1,X_2,X_3)$.

Write $L(G)=\begin{pmatrix}A_{11} &{} A_{12} &{} A_{13}\\ A_{12}^T &{} A_{22} &{} A_{23}\\ A_{13}^T &{} A_{23}^T &{} A_{33}\end{pmatrix}$, where $A_{11}=\begin{pmatrix} d(u_{i-1}) &{} 0\\ 0 &{} d(u_{i+1})\end{pmatrix}$ and $A_{12}=\begin{pmatrix} -1 &{} 0\\ 0 &{} -1\end{pmatrix}$. Accordingly, $L(H)=\begin{pmatrix}B_{11} &{} B_{12} &{} A_{13}\\ B_{12}^T &{} A_{22} &{} A_{23}\\ A_{13}^T &{} A_{23}^T &{} A_{33}\end{pmatrix}$, where $B_{11}=\begin{pmatrix} d(u_{i-1})-1 &{} 0\\ 0 &{} d(u_{i+1})+1\end{pmatrix}$ and $B_{12}= \begin{pmatrix} 0 &{} 0\\ -1 &{} -1 \end{pmatrix}$.

Similarly we have

$$\begin{aligned} Y^T\mathcal {L}(H)Y&= X^T\mathcal L(C_{n,g})X+X_1(B_{11}-A_{11})X_1^T+ 2X_1(B_{12}-A_{12})X_2^T\\&= \lambda -\left( \frac{X(u_{i-1})}{\sqrt{d(u_{i-1})}}\right) ^2 +\left( \frac{X(u_{i+2})}{\sqrt{d(u_{i+1})}}\right) ^2\\ {}&\quad +2\left( \frac{X(u_{i-1})}{\sqrt{d(u_{i-1})}}\right) \left( \frac{X(u_{i})}{\sqrt{d(u_{i})}}\right) -2\left( \frac{X(u_{i+2})}{\sqrt{d(u_{i+2})}}\right) \left( \frac{X(u_{i})}{\sqrt{d(u_{i})}}\right) \\&= \lambda +\left[ \frac{X(u_i)}{\sqrt{d(u_i)}} -\frac{X(u_{i+2})}{\sqrt{d(u_{i+2})}}\right] ^2 -\left[ \frac{X(u_i)}{\sqrt{d(u_i)}} -\frac{X(u_{i-1})}{\sqrt{d(u_{i-1})}}\right] ^2\\ \lambda (H)-\lambda&=\max _{Z\ne 0}\frac{Z^T\mathcal {L}(H)Z}{Z^TZ}-\lambda \ge \frac{Y^T\mathcal {L}(H)Y}{Y^TY}-\lambda \\&=\frac{\lambda +\left[ \frac{X(u_i)}{\sqrt{d(u_i)}} -\frac{X(u_{i+2})}{\sqrt{d(u_{i+2})}}\right] ^2 -\left[ \frac{X(u_i)}{\sqrt{d(u_i)}} -\frac{X(u_{i-1})}{\sqrt{d(u_{i-1})}}\right] ^2}{1+\frac{X(u_{i+2})^2}{d(u_{i+2})} -\frac{X(u_{i-1})^2}{d(u_{i-1})}} -\lambda \\&=\frac{(\lambda -1)\left[ \frac{X(u_{i-1})^2}{d(u_{i-1})} -\frac{X(u_{i+2})^2}{d(u_{i+2})}\right] +\frac{2X(u_{i})}{\sqrt{d(u_i)}} \left[ \frac{X(u_{i-1})}{\sqrt{d(u_{i-1})}} -\frac{X(u_{i+2})}{\sqrt{d(u_{i+2})}}\right] }{1+\frac{X(u_{i+2})^2}{d(u_{i+2})} -\frac{X(u_{i-1})^2}{d(u_{i-1})}}\\&=\frac{\left[ \frac{X(u_{i-1})}{\sqrt{d(u_{i-1})}} -\frac{X(u_{i+2})}{\sqrt{d(u_{i+2})}}\right] \left[ (\lambda -1)\left( \frac{X(u_{i-1})}{\sqrt{d(u_{i-1})}}+ \frac{X(u_{i+2})}{\sqrt{d(u_{i+2})}}\right) +\frac{2X(u_{i})}{\sqrt{d(u_i)}}\right] }{1+\frac{X(u_{i+2})^2}{d(u_{i+2})} -\frac{X(u_{i-1})^2}{d(u_{i-1})}}. \end{aligned}$$

From Eq. (3.3), we have

$$\begin{aligned}&(\lambda -1)\left( \frac{X(u_{i-1})}{\sqrt{d(u_{i-1})}}+ \frac{X(u_{i+2})}{\sqrt{d(u_{i+2})}}\right) +\frac{2X(u_{i})}{\sqrt{d(u_i)}}\nonumber \\&\quad = \left[ (\lambda -1)\left( \sqrt{d(u_i)}(1-\lambda ) -\frac{1}{\sqrt{d(u_i)}}\right) +\frac{2}{\sqrt{d(u_i)}}\right] X(u_i)\\&\qquad +(\lambda -1)\left[ \sqrt{d(u_{i+1})}(1-\lambda ) -\frac{1}{\sqrt{d(u_{i+1})}}\right] X(u_{i+1}). \end{aligned}$$

Since $1<\lambda <2$, we have $(\lambda -1)\left[ \sqrt{d(u_{i+1})}(1-\lambda ) -\frac{1}{\sqrt{d(u_{i+1})}}\right] <0$.

$$\begin{aligned}&(\lambda -1)\left( \sqrt{d(u_i)}(1-\lambda ) -\frac{1}{\sqrt{d(u_i)}}\right) +\frac{2}{\sqrt{d(u_i)}}\\&\quad = (\lambda -1)\left( \sqrt{2}(1-\lambda ) -\frac{1}{\sqrt{2}}\right) +\frac{2}{\sqrt{2}}\\&\quad = -\frac{1}{\sqrt{2}}[2\lambda ^2 -3\lambda -1]< 0 \text{ if } \lambda > \frac{3+\sqrt{17}}{4}. \end{aligned}$$

Thus, $\lambda \le \lambda (H)\le \lambda (C_{n,3})$ when $\lambda >\frac{3+\sqrt{17}}{4}$.

If $\lambda \le \frac{3+\sqrt{17}}{4}$, then by direct calculation $\lambda <\lambda (C_{5,3})\approx 1.85657$.¹ Hence, $\lambda <\lambda (C_{n,3})$ from Theorem 2.6.

Suppose $\lambda =\lambda (C_{n,3})$. Then $\lambda =\lambda (H)=\lambda (C_{n,3})$. It implies that $\frac{X(u_{i-1})}{\sqrt{d(u_{i-1})}} = \frac{X(u_{i+2})}{\sqrt{d(u_{i+2})}}$. Moreover, by Theorem 3.1, $H\cong C_{n,3}$, and hence, $i=2$. Let $H^*=C_{n,g}-u_{3}u_{4}+u_{3}u_{1}$. Then $H\not \cong C_{n,3}$. By a similar argument, we have $\lambda <\lambda (H^*)< \lambda (C_{n,3})$.

Case 2. If $d(u_i)=3$, that is $i=1$, then suppose that $u_1v_{n-g}\cdots v_2v_1$ are the pendant path of $C_{n,g}$ and $d(v_1)=1$ (see Fig. 1). Let Y be another valuation of $C_{n,g}$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} Y(u_i)=X(u_{g-i+2}), &{} i=1, \dots , g;\\ Y(v_i)=X(v_i), &{} i=1, \dots , n-g. \end{array}\right. } \end{aligned}$$

If we swap the order of $u_i$ with $u_{g-i+2}$ for $i=1,\dots , g$ (i.e., reverse the order of vertices in $C_g$), then the matrix $\mathcal L(C_{n,g})$ does not change. So Y is still a unit eigenvector of $\mathcal L(C_{n,g})$. Since $X-Y$ is a vector belonging to the eigenspace corresponding to $\lambda$ and $X(v_1)=Y(v_1)$, by the same proof of Case 2 of Theorem 3.1, we know that $X-Y$ is not an eigenvector of $\mathcal L(C_{n,g})$. That means $X-Y=\varvec{0}_n$. So $X(u_2)=Y(u_2)=X(u_g)$, and hence, we have $X(u_1)X(u_2)\ge 0$ and $X(u_1)X(u_g)\ge 0$. Since g is odd, there exist two vertices, say $u_j$ and $u_{j+1}$, such that $X(u_j)X(u_{j+1})\ge 0$ and $d(u_j)=d(u_{j+1})=2$. It refers to Case 1.

The proof is complete. $\square$