Diameter of Neighborhood Graphs

Abstract

The neighborhood graph $G'$ of a graph G has the same vertex set as G and two vertices are adjacent in $G'$ if and only if they have a common neighbor in G. We study the diameter $\mathrm{diam}(G')$ of the neighborhood graph $G'$ in terms of the diameter of G. We show that if G is a connected non-bipartite graph of diameter d, then $\lceil d/2 \rceil \le \mathrm{diam}(G') \le d$ and the bounds are best possible for every $d \ge 1$. If G is a connected bipartite graph, then $G'$ has 2 components. We also present results on the diameter of components of $G'$, if $G'$ is the neighborhood graph of a connected bipartite graph.

1 Introduction

One interesting problem of a discrete mathematics model used in biology is a food web. Each organism depends for food on one or more other organisms. In an ecosystem the vertices of a graph represent the species in the community and there is a directed edge from a vertex w to a vertex v if and only if w is a prey of v. Predator–prey relationships are often modeled by undirected graphs called competition graphs, where we have an edge between the species u and v if and only if u and v have a common prey. Food webs and competition graphs were studied for example in the recent work of Cozzens [6]. In this paper we consider competition graphs, which arise from undirected base graphs; and they are called neighborhood graphs.

Let G be an undirected graph with the vertex set V(G) and with the edge set E(G). The neighborhood graph $G'$ of a graph G has the same vertex set as G, so we have $V(G) = V(G')$, and two vertices u, v are adjacent in $G'$ if and only if they have at least one common neighbor in G (if and only if there exists a path of length 2 between u and v in G).

A path of length n is a sequence of n edges which connects a sequence of $n+1$ distinct vertices. The distance $d_G (u,v)$ between two vertices u and v in a graph G is the number of edges in a shortest path connecting them. The eccentricity $ec_G (v)$ of a vertex v in G is the greatest distance between v and any other vertex of G. The diameter $\mathrm{diam}(G)$ of G is the maximum eccentricity among the vertices of G. If G consists of components $G_1, G_2, \ldots , G_p$, then the diameter of the component $G_i$, $i = 1, 2, \ldots , p$, is defined as the greatest distance between all pairs of vertices in $G_i$. The i-th neighborhood $N_i (v)$ of a vertex v in G is the set of vertices at distance i from v. $N_0 (v) = \{ v \}$ and $N_1 (v)$ is often denoted by N(v). A graph is bipartite if its vertices can be divided into 2 disjoint sets, such that no 2 vertices in the same set are adjacent. A tree is a graph which contains no cycles.

Let us mention a few works, which consider neighborhood graphs. Boland, Brigham, and Dutton [4, 5] studied the connection between neighborhood graphs and the embedding number. Brigham and Dutton [7] studied graphs G such that the neighborhood graph of G is isomorphic to the complement of G. Schiermeyer, Sonntag, and Teichert [9] considered the Hamiltonicity of neighborhood graphs. Two recent papers [2, 3] present results on the energy of neighborhood graphs. The diameter of a graph is the most common of the classical distance parameters. In this paper we consider the diameter of connected neighborhood graphs and the diameter of the components of disconnected neighborhood graphs.

2 Results

It is known that if G is a connected graph, then the neighborhood graph $G'$ of G has at most 2 components (see [2, 9]). Moreover, $G'$ is connected if and only if G is a connected non-bipartite graph. Thus the neighborhood graph of a connected bipartite graph has exactly 2 components. Evidently, neighborhood graphs of disconnected graphs are also disconnected.

We first consider connected non-bipartite graphs G. The neighborhood graph of the complete graph is the same graph, hence if $\mathrm{diam}(G) = 1$, then $\mathrm{diam}(G') = 1$ too. We present a lower bound on the diameter of the neighborhood graph of G if $\mathrm{diam}(G) \ge 2$.

Theorem 2.1

Let G be a connected non-bipartite graph of diameter d where $d \ge 2$. Then $\mathrm{diam}(G') \ge \lceil d/2 \rceil$.

Proof

Let G be a connected non-bipartite graph of diameter $d \ge 2$, and let $v, v'$ be two vertices of G, such that $d_G (v,v') = d$. Let $N_i(v)$ be the i-th neighborhood of v in G, $i=0, 1, \ldots , d$. No vertex of $N_i (v)$ can be adjacent to a vertex of $N_j (v)$ in $G'$ for $|i-j|>2$, since such vertices do not have a common neighbor in G. On the other hand, every vertex in $N_i(v)$ is of distance 2 to some vertex of $N_{i-2}(v)$ in G, $i=2, 3, \ldots , d$, therefore any vertex in $N_i(v)$ is adjacent to some vertex of $N_{i-2}(v)$ in $G'$. Thus for any vertex $u \in N_i (v)$, where i is even, we have $d_{G'} (v,u) = i/2$. If $w \in N_i (v)$, where i is odd, say $i=2p+1$, then $d_{G'} (v,w) > p$, hence $d_{G'} (v,w) \ge p+1 = (i+1)/2$. Then for $v' \in N_d (v)$ we obtain $d_{G'} (v,v') \ge \lceil d/2 \rceil$, which implies $diam(G') \ge \lceil d/2 \rceil$. $\square$

We give a construction, which shows that the bound given in Theorem 2.1 is best possible for every $d \ge 2$.

Construction 2.1

Let P be the path of length $d \ge 2$. We can write $P = u_0 u_1 \ldots u_d$. The graph G is constructed from the path P by adding p new vertices $v_1, v_2, \ldots , v_p$, $p \ge 1$, where $v_i$, $i = 1, 2, \ldots , p$, is adjacent to the vertices $u_{ \lceil d/2 \rceil - 1}, u_{ \lceil d/2 \rceil }, u_{ \lceil d/2 \rceil + 1}$. Thus we have

It is easy to see that $diam(G) = d$. The graph $G'$ has the following edge set:

$$\begin{aligned} E(G')= & {} \{ u_0u_2, u_1u_3 \ldots , u_{d-2}u_d \} \ \cup \ \left\{ u_{ \lceil d/2 \rceil - 1} u_{ \lceil d/2 \rceil }, u_{ \lceil d/2 \rceil } u_{ \lceil d/2 \rceil + 1} \right\} \\&\cup \, \{ v_i v_j \ | \ i,j = 1, 2, \ldots , p; i \ne j \} \\&\cup \left\{ v_i u_j \ | \ i = 1, 2, \ldots , p; j = \lceil d/2 \rceil - 2, \lceil d/2 \rceil - 1, \ldots , \lceil d/2 \rceil + 2\quad \hbox {if}\; d \ge 4; \right. \\&\left. j = 0, 1, 2, 3\quad \hbox {if}\quad d=3; \ j = 0, 1, 2\quad \hbox {if} \quad d = 2\right\} . \end{aligned}$$

It can be checked that the diameter of $G'$ is $\lceil d/2 \rceil$ and the diametral path is $u_0 u_2 \ldots u_{ \lceil d/2 \rceil - 1 } u_{ \lceil d/2 \rceil } u_{ \lceil d/2 \rceil - 2 } \ldots u_1$ if $\lceil d/2 \rceil$ is odd, and it is $u_0 u_2 \ldots u_{ \lceil d/2 \rceil } u_{ \lceil d/2 \rceil - 1 }$ $u_{ \lceil d/2 \rceil - 3 } \ldots u_1$ if $\lceil d/2 \rceil$ is even.

Now we show that if G is not bipartite, then the diameter of the neighborhood graph of G cannot exceed the diameter of G.

Theorem 2.2

Let G be a connected non-bipartite graph. Then $\mathrm{diam}(G') \le \mathrm{diam}(G)$.

Proof

Let G be a connected non-bipartite graph of diameter d where $d \ge 1$. We prove that $\mathrm{diam}(G') \le d$. Let v be any vertex of G and let $ec_G(v) = p$. Clearly $p \le d$. We show that $ec_{G'}(v) \le d$.

Let $N_i(v)$ be the i-th neighborhood of v in G, $i=0, 1, \dots , p$. Any vertex in $N_i(v)$ is adjacent to some vertices of $N_{i-2}(v)$ in $G'$, $i=2, 3, \dots , p$, therefore we have $d_{G'}(v,v') = i/2$ for any vertex $v' \in N_i (v)$, where i is even and $i \le p$. Since $i/2 < d$, we get $d_{G'}(v,v') < d$.

It can be checked that since G is not bipartite, it contains an odd cycle, and there exists at least 2 vertices in the same neighborhood $N_i (v)$, $i \in \{ 1, 2, \ldots , p \}$, which are adjacent in G. Let U be the set of vertices, where $u \in U$ if u is adjacent to at least one vertex in the same neighborhood.

Let $v_i$ be any vertex in $N_i (v)$, where i is odd. We show that $d_{G'}(v,v_i) \le d$. Let $u'$ be a vertex of U such that $d_G (v_i, u') \le d_G (v_i, u)$ for every $u \in U$, so the vertex $u'$ is the closest to $v_i$ in G among the vertices of U. Let $u_0u_1 \ldots u_k$ be the shortest path between $v_i=u_0$ and $u' = u_k$ in G. Clearly, for the length k of the path, we have $0 \le k \le d$. Note that, for $k \ge 1$, if $u_l \in N_j (v)$, $l = 0, 1, \ldots k-1$, then $u_{l+1}$ is in $N_{j-1} (v)$ or $N_{j+1} (v)$, since $u_l \notin U$. Hence for $u_l \in N_j (v)$, if l is even, $0 \le l \le k$, then j is odd; and if l is odd, then j is even. We distinguish 2 cases:

• (i) k is odd. Then $u_0 u_2 \ldots u_{k-1}$ is the path of length $(k-1)/2$ in $G'$. If d is even, then $k \le d-1$ and $d_{G'} (v_i, u_{k-1}) \le d/2 - 1$. If d is odd, then $k \le d$ and $d_{G'} (v_i, u_{k-1}) \le (d-1)/2$. We know that $u_k \in N_j (v)$, where j is even, and $u_k$ is in G adjacent to a vertex, say $w \in N_j (v)$. Thus $d_{G'} (u_{k-1}, w) = 1$ and $w \in N_j (v)$ is of distance j / 2 from v in $G'$. If d is even, then $j \le d$ and $d_{G'} (w,v) \le d/2$; and if d is odd, then $j \le d-1$ and $d_{G'} (w,v) \le (d-1)/2$. Consequently $d_{G'} (v_i,v) \le d_{G'} (v_i,u_{k-1}) + d_{G'} (u_{k-1},w) + d_{G'} (w,v) \le d$.

• (ii) k is even. Then $u_0 u_2 \ldots u_{k}$ is the path of length k / 2 in $G'$. If d is even, then $k \le d$ and $d_{G'} (v_i, u_{k}) \le d/2$. If d is odd, then $k \le d-1$ and $d_{G'} (v_i, u_{k}) \le (d-1)/2$. We know that $u' = u_k \in N_j (v)$, where j is odd, and $u_k$ is in G adjacent to a vertex, say $w \in N_j (v)$. There must be a vertex in $N_{j-1} (v)$, say $w'$, which is adjacent to w in G. Since $u_k$ and $w'$ have a common neighbor in G, we obtain $d_{G'} (u_{k}, w') = 1$. Every vertex in $N_{j-1} (v)$ is of distance $(j-1)/2$ from v in $G'$. If d is even, then $j \le d-1$ and $d_{G'} (w',v) \le d/2 - 1$; and if d is odd, then $j \le d$ and $d_{G'} (w',v) \le (d-1)/2$. Thus $d_{G'} (v_i,v) \le d_{G'} (v_i,u_{k}) + d_{G'} (u_{k},w') + d_{G'} (w',v) \le d$.

Since $d_{G'} (v,v') \le d$ for every vertex $v' \in V(G')$, we obtain $ec_{G'}(v) \le d$. This inequality holds for every vertex v, hence $\mathrm{diam}(G') \le d$. $\square$

Construction 2.2 shows that the bound presented in the previous theorem is sharp.

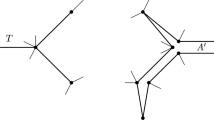
Construction 2.2

Let T be a tree, such that every leaf of T is of distance d ($d \ge 1$) from the central vertex of T. We form G from T by connecting any two leaves.

We show that $\mathrm{diam}(G) = \mathrm{diam}(G') = d$. Let v be the central vertex of T and let $N_i(v)$ be the i-th neighborhood of v in T (and in G), $i=0, 1, \ldots , d$. Since any two vertices of $N_d (v)$ are adjacent in G, any pair of vertices of G, say u and $u'$, is contained in a cycle of length at most $2d+1$ in G. Hence $d_G (u, u') \le d$. We also know that for any vertex, say w, in $N_d (v)$, we have $d_G (v, w) = d$. Thus the diameter of G is d. By Theorem 2.2, $\mathrm{diam}(G') \le d$. It can be checked, that the distance between v and any vertex in N(v) is d in $G'$, hence $\mathrm{diam}(G') = d$.

Note that one simple example of a graph G, for which $\mathrm{diam}(G) = \mathrm{diam}(G')$, is the cycle $C_{2d+1}$.

In the next theorem we consider the case when G is bipartite. It is known that if G is bipartite, then $G'$ has exactly 2 components. We present a result about the diameter of the components of $G'$ in terms of the diameter of G.

Theorem 2.3

Let G be a connected bipartite graph of diameter d where $d \ge 2$, and let $G_1$, $G_2$ be the components of $G'$ such that $\mathrm{diam}(G_1) \le \mathrm{diam}(G_2)$.

• (i) If d is odd, then $\mathrm{diam}(G_1) = \mathrm{diam}(G_2) = (d-1)/2$.

• (ii) If d is even, then $d/2 -1 \le \mathrm{diam}(G_1) \le d/2$ and $\mathrm{diam}(G_2) = d/2$.

Proof

Let G be a bipartite graph of diameter $d \ge 2$. Let $v_0, v_d$ be any two vertices of distance d in G, and let $v_0 v_1 \ldots v_d$ be a shortest path between $v_0$ and $v_d$ in G. Note that, if u, w are 2 vertices of G such that $d_G (u,w) = p$, then $d_{G'} (u,w) = p/2$ if p is even. If p is odd, then there is no walk (or path) of even length between u and w in G (because bipartite graphs do not contain odd cycles), therefore u and w are in different components in $G'$. Let $H_1$ be the component of $G'$ containing $v_1$, and let $H_2$ be the component of $G'$ containing $v_0$. We distinguish 2 cases:

• (i) d is odd. From the previous part of this proof it follows that any 2 vertices u, w of G are either in different components in $G'$ or of even distance p in G. Then $p \le d-1$ and u, w are of distance at most $(d-1)/2$ in $G'$. It follows that $\mathrm{diam}(H_1)$ and $\mathrm{diam}(H_2)$ are at most $(d-1)/2$. We also know that each component of $G'$ contains a pair of vertices of distance $(d-1)/2$, $d_{H_1} (v_1,v_d) = (d-1)/2$ and $d_{H_2} (v_0,v_{d-1}) = (d-1)/2$, hence the diameter of both components of $G'$ is exactly $(d-1)/2$.

• (ii) d is even. Any 2 vertices, which are in the same component in $G'$ must be of even distance $p \le d$ in G, thus they are of distance at most d / 2 in $G'$. Thus $\mathrm{diam}(H_1) \le d/2$ and $\mathrm{diam}(H_2) \le d/2$. Since there is a pair of vertices of distance $d/2 -1$ in $H_1$ ($d_{H_1} (v_1,v_{d-1}) = d/2 -1$), we have $d/2 -1 \le \mathrm{diam}(H_1) \le d/2$. In $H_2$ there exists a pair of vertices of distance d / 2 ($d_{H_2} (v_0,v_d) = d/2$), hence $\mathrm{diam}(H_2) = d/2$. The proof is complete. $\square$

From Theorem 2.3 we know that if the diameter of a bipartite graph G is d, where d is even, then one component of $G'$ has diameter d / 2, and the diameter of the other component of $G'$ is either $d/2 -1$ or d / 2. For example, if G is a tree of an even diameter $d \ge 2$, one component of $G'$ has diameter d / 2 and the other component has diameter $d/2 -1$. On the other hand, if G is the cycle of length 2d, then $\mathrm{diam}(G) = d$ and the diameter of both components of $G'$ is d / 2.

Finally, let us mention that one interesting open problem is to bound the diameter of the derived graph of G in terms of the diameter of G. This problem seems to be a very complicated one. Note that the derived graph of a graph G has the same vertex set as G and two vertices are adjacent in the derived graph if and only if they are of distance 2 in G. Derived graphs were studied for example in [1] and [8].