Neighbor Sum Distinguishing Edge Colorings of Graphs with Small Maximum Average Degree

Abstract

A proper edge-k-coloring of a graph G is an assignment of k colors $1,2,\ldots ,k$ to the edges of G such that no two adjacent edges receive the same color. A neighbor sum distinguishing edge-k-coloring of G is a proper edge-k-coloring of G such that for each edge $uv\in E(G)$, the sum of colors taken on the edges incident with u is different from the sum of colors taken on the edges incident with v. By ${ {ndi}}_{\sum }(G)$, we denote the smallest value k in such a coloring of G. The maximum average degree of G is ${ {mad}}(G)=\max \{2|E(H)|/|V(H)|\}$, where the maximum is taken over all the non-empty subgraphs H of G. In this paper, we obtain that if G is a graph without isolated edges and ${ {mad}}(G)<8/3$, then ${ {ndi}}_{\sum }(G)\le k$ where $k=\max \{\Delta (G)+1,6\}$. It partially confirms the conjecture proposed by Flandrin et al. (Graphs Comb 29:1329–1336, 2013).

1 Introduction

In this paper, all graphs considered are finite, simple, and undirected. The terminology and notation used but undefined in this paper can be found in [1]. Let $G=(V,E)$ be a graph. We use $V(G), E(G),\Delta (G)$, and $\delta (G)$ to denote the vertex set, edge set, maximum degree, and minimum degree of G, respectively. Let $d_G(v)$ or simply d(v) denote the degree of a vertex v in G. A vertex v is called a k-vertex (resp. $k^{-}$-vertex, or $k^{+}$-vertex) if $d(v)=k$ [resp. $d(v)\le k$, or $d(v)\ge k$]. A vertex is called a leaf of G if $d(v)=1$. A 2-vertex is called bad if it is adjacent to a 2-vertex, otherwise we call it good. A 5-vertex is called bad if it is adjacent to four bad 2-vertices, otherwise we call it good. The girth of a graph G is the length of a smallest cycle in G, and we denote it by g(G). The maximum average degree of G is ${ {mad}}(G)=\max \{2|E(H)|/|V(H)|\}$, where the maximum is taken over all the non-empty subgraphs H of G.

A proper edge-k-coloring of a graph G is an assignment of k colors $1,2,\ldots ,k$ to the edges of G such that no two adjacent edges receive the same color. Let c be a proper edge-k-coloring of G. By w(v) [resp. S(v)], we denote the sum (resp. set) of colors taken on the edges incident with v, i.e., $w(v) =\sum _{uv\in E(G)}c(uv)$ [resp. $S(v)=\{c(uv){\mid } uv\in E(G)\}$]. We call the coloring c such that $w(u)\ne w(v)$ [resp. $S(u)\ne S(v)$] for each edge $uv\in E(G)$ a neighbor sum distinguishing (resp. neighbor distinguishing) edge-k-coloring of G. For simplicity, we use ${ {nsd}}$-k-coloring (resp. nd-k-coloring) to denote the neighbor sum distinguishing (resp. neighbor distinguishing) edge-k-coloring of G. By ${ {ndi}}_{\sum }(G)$ [resp. ${ {ndi}}(G)$], we denote the smallest value k such that G has an ${ {nsd}}$-k-coloring (resp. nd-k-coloring) of G.

Obviously, a graph G has a neighbor sum distinguishing (neighbor distinguishing) coloring if and only if G has no isolated edges (we call it normal). Apparently, for any normal graph G, ${ {ndi}}(G)\le { {ndi}}_{\sum }(G)$. In 2002, Zhang et al. [2] proposed the following conjecture.

Conjecture 1.1

[2] If G is a normal graph with at least six vertices, then ${ {ndi}}(G)\le \Delta (G)+2$.

Balister et al. [3] proved Conjecture 1.1 for bipartite graphs and for graphs G with $\Delta (G)=3$. If G is bipartite planar with maximum degree $\Delta (G)\ge 12$, Conjecture 1.1 was confirmed by Edwards et al. [4]. Hatami [5] showed that if G is a normal graph and $\Delta (G)>10^{20}$, then ${ {ndi}}(G)\le \Delta (G)+300$. Akbari et al. [6] proved that ${ {ndi}}(G)\le 3 \Delta (G)$ for any normal graph. Wang et al. [7, 8] confirmed Conjecture 1.1 for sparse graphs and $K_4$-minor free graphs. More precisely, in [7] they showed that if G is a normal graph and ${ {mad}}(G) <5/2$, then ${ {ndi}}(G)\le \Delta (G)+1$. Furthermore, ${ {ndi}}(G) = \Delta (G)+1$ if and only if G has two adjacent maximum degree vertices. Recently, Hocquard et al. [9] proved that for every normal graph with $\Delta (G)\ge 5$ and ${ {mad}}(G)<13/5$, we have ${ {ndi}}(G)\le \Delta (G)+1$. Later, in [10] they proved that if G is a normal graph with $\Delta (G)\ge 5$ and ${ {mad}}(G) <3-2/\Delta (G)$, then ${ {ndi}}(G)\le \Delta (G)+1$.

Recently, Flandrin et al. [11] studied the neighbor sum distinguishing colorings of cycles, trees, complete graphs, and complete bipartite graphs. Based on these examples, they proposed the following conjecture.

Conjecture 1.2

[11] If G is a connected graph on at least three vertices and $G\ne C_5$, then ${ {ndi}}_{\sum }(G)\le \Delta (G)+2$.

Flandrin et al. [11] also proved that for each connected graph G with maximum degree $\Delta \ge 2$, we have ${ {ndi}}_{\sum }(G)\le \lceil (7\Delta -4)/2\rceil$. Dong et al. [12] considered the neighbor sum distinguishing colorings of planar graphs and showed that if G is a normal planar graph, then ${ {ndi}}_{\sum }(G)\le \max \{2\Delta (G)+1,25\}$. In [13], Dong et al. proved that if G is a normal graph and ${ {mad}}(G)\le 5/2$, then ${ {ndi}}_{\sum }(G)\le k$ where $k=\max \{\Delta (G)+1,6\}$. Other results on graph coloring problems are referred to [14–16].

In this paper, we will prove the following results.

Theorem 1.3

Let G be a normal graph. If ${ {mad}}(G)<\frac{8}{3}$, then ${ {ndi}}_{\sum }(G)\le k$ where $k=\max \{\Delta (G)+1,6\}$.

Corollary 1.4

Let G be a normal graph. If ${ {mad}}(G)<\frac{8}{3},\Delta (G)\ge 5$, then ${ {ndi}}_{\sum }(G)\le \Delta (G)+1$.

In [17], the authors obtained that ${ {mad}}(G)<2g/(g-2)$ if G is a planar graph with girth g. The following corollary is obvious.

Corollary 1.5

Let G be a normal planar graph. If $g(G)\ge 8$ and $\Delta (G)\ge 5$, then ${ {ndi}}_{\sum }(G)\le \Delta (G)+1$.

We note that if G contains two adjacent vertices of maximum degree, then ${ {ndi}}_{\sum }(G)\ge \Delta (G)+1$. So the bound $\Delta (G)+1$ in Corollary 1.4 is sharp. Furthermore, Corollary 1.4 implies a result of Hocquard et al. [9] about the neighbor distinguishing coloring of sparse graphs.

2 Proof of Theorem 1.3

Firstly, we give two lemmas obtained by Dong et al. in [13], all the elements in each set are integers.

Lemma 2.1

[13] Let $S_1,S_2$ be two sets and $S_3=\{\alpha +\beta {\mid }\alpha \in S_1,\beta \in S_2,\alpha \ne \beta \}$.

• (i) If $|S_1|=2$ and $|S_2|=3$, then $|S_3|\ge 3$.

• (ii) If $|S_1|=2$ and $|S_2|=4$, then $|S_3|\ge 4$.

• (iii) If $|S_1|=|S_2|=2$ and $S_1\ne S_2$, then $|S_3|\ge 3$.

Lemma 2.2

[13] Let S be a set of size $k+1$. If $S_1=\bigg \{\sum \limits _{i=1}^{k}x_i{\mid }x_i\in S,x_i\ne x_j\ \text{ if }\ 1\le i<j\le k\bigg \}$, then $|S_1|\ge k+1$.

Let $k=\max \{\Delta (G)+1,6\}$ and $[k]=\{1,2,\ldots ,k\}$. Suppose to the contrary that G is a counterexample to Theorem 1.3, such that |E(G)| is minimum. By the choice of G, it is clear that G is connected and any normal subgraph $G'$ has an ${ {nsd}}$-k-coloring c. We use w(v) and S(v) to denote the sum and the set of colors taken on the edges incident with v in the coloring c of $G'$, i.e., $w(v) =\sum _{v\in e,e\in E(G')}c(e)$ and $S(v) =\{c(e)\mid v\in e,e\in E(G')\}$. In the following, we will extend c to the whole graph G.

Let H be the graph obtained by removing all the leaves of G. Obviously, H is a connected graph and ${ {mad}}(H)<8/3$. In the following, we give some properties of H.

Claim 2.3

H has the following properties:

• (i) [13] $\delta (H)\ge 2$, where $\delta (H)$ is the minimum degree of H.

• (ii) [13] Let $v\in V(H)$ such that $d_H(v) = 2$, then $d_G(v) = 2$.

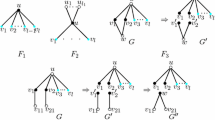
• (iii) Let uvxy be a path in H such that $d_H(v) = d_H(x) = 2$, then $d_G(u) = d_H(u)$ and $d_G(y)=d_H(y)$ (Fig. 1).

  Fig. 1

  

  Illustration of Claim 2.3 (iii)

Proof

(iii) Let uvxy be a path in H such that $d_{H}(v)=d_{H}(x)=2$. By Claim 2.3 (ii), $d_{G}(v)=d_{G}(x)=2$. By contradiction suppose $d_{G}(u)\ne d_{H}(u)$ [it follows from Claim 2.3 (i) and construction of H that $d_{G}(u)\ge 3$]. Hence there exists at least one 1-vertex adjacent to u in G, say $u_1$. Consider $G'=G\backslash \{vx\}$. By the minimality of G, $G'$ admits an ${ {nsd}}$-k-coloring c. If $c(uv)\ne c(xy)$, then we color vx with a color distinct from $c(uv),c(xy),w(u)-w(v),w(y)-w(x)$, then we obtain an ${ {nsd}}$-k-coloring of G. Otherwise, we permute the colors assigned to $uu_1$ and uv. The obtained coloring is still an ${ {nsd}}$-k-coloring of $G'$. We then extend this coloring to G as previously. This is a contradiction. $\square$

Claim 2.4

Let $u\in V(H),d_H(u)=l,uu_i\in E(H),i=1,2,\ldots ,l$.

• (i) [13] If $l=2$, then u is adjacent to at most one 2-vertex.

• (ii) (a) [13] If $l=3$ and $d_H(u)<d_G(u)$, then u is adjacent to at most one 2-vertex.

• (b) If $l=3$, then u is not adjacent to any bad 2-vertex. Furthermore, u is adjacent to at most one good 2-vertex.

• (iii) If $l=4$, then u is adjacent to at most one bad 2-vertex. Furthermore, if u is adjacent to one bad 2-vertex, then u is adjacent to at most two good 2-vertices.

• (iv) If $l\ge 5$ and u is adjacent to $(l-1)$ bad 2-vertices, then u is adjacent to at most $(l-1)$ 2-vertices (Fig. 2).

Fig. 2

Illustration of Claim 2.4

Proof

(ii) (b) Firstly, we prove that u is not adjacent to any bad 2-vertex. Suppose to the contrary that $u_1$ is a bad 2-vertex. Let x be the other neighbor of $u_1$ with $d_H(x)=2$, and $xy\in E(H)$, $y\ne u_1$. By Claim 2.3 (iii), $d_G(u)=d_H(u)=3$. Consider the graph $G'=G\backslash \{uu_1\}$, then $G'$ admits an ${ {nsd}}$-k-coloring c. Color $uu_1$ with a color $\alpha$ in $S=[k]\backslash \left( \{c(xy)\}\bigcup \{c(uu_2),c(uu_3)\}\bigcup \{w(u_2)-w(u)\}\bigcup \{w(u_3)-w(u)\}\right)$. Recolor $u_1x$ with a color distinct from $\alpha ,c(xy),w(y)-c(xy),c(uu_2)+c(uu_3)$ and we obtain an ${ {nsd}}$-k-coloring of G, a contradiction.

In the following, we prove that u is adjacent to at most one good 2-vertex. Suppose to the contrary that $d_H(u_1)=d_H(u_2)=2$, $v_iu_i\in E(H),v_i\ne u,i=1,2$.

Case 1 $d_G(u)>d_H(u)=3$. By Claim 2.4 (ii) (a), this Claim holds.

Case 2 $d_G(u)=d_H(u)=3$.

Subcase 2.1 $k\ge 7$. Consider the graph $G'=G\backslash \{uu_1,uu_2\}$, then $G'$ has an ${ {nsd}}$-k-coloring c. Let $S_i=[k]\backslash \left( \{c(u_iv_i)\}\bigcup \{c(uu_3)\}\bigcup \{w(v_i)-w(u_i)\}\bigcup \{w(u_{3-i})\right. \left. -c(uu_3)\}\right) , i=1,2$, then $|S_i|\ge 3,i=1,2$. By Lemma 2.1 (ii), we can choose $\alpha _i\in S_i,i=1,2$ such that $\alpha _1\ne \alpha _2$, $\alpha _1+\alpha _2+c(uu_3)\ne w(u_3)$. We obtain an ${ {nsd}}$-k-coloring of G, which is a contradiction.

Subcase 2.2 $k=6$. From the above discussion, $d_G(v_i)\ge 3,i=1,2$. If $d_G(v_1)=5$, then $u_1$ can be distinguished from $v_1$ under an arbitrary proper edge coloring of G. Consider $G'=G\backslash \{uu_1,uu_2\}$, then $G'$ has an ${ {nsd}}$-6-coloring c. The colors in $\left\{ c(u_1v_1)\}\bigcup \{c(uu_3)\}\bigcup \{c(u_2v_2)-c(uu_3)\right\}$ are forbidden for $uu_1$. Let $S_1=[6]\backslash \left( \{c(u_1v_1)\}\bigcup \{c(uu_3)\}\bigcup \{c(u_2v_2)-c(uu_3)\}\right)$, $S_2=[6]\backslash \left( \{c(u_2v_2)\}\bigcup \{c(uu_3)\}\bigcup \{w(v_2)-w(u_2)\}\bigcup \{c(u_1v_1)-c(uu_3)\}\right)$, then $|S_1|\ge 3,|S_2|\ge 2$. By Lemma 2.1 (ii), we can choose $\alpha _i\in S_i,i=1,2$ such that $\alpha _1\ne \alpha _2$, $\alpha _1+\alpha _2+c(uu_3)\ne w(u_3)$. We obtain an ${ {nsd}}$-6-coloring of G, which is a contradiction. Therefore, $d_G(v_1)\ne 5$. Similarly, $d_G(v_2)\ne 5$.

If $d_G(v_1)=3$ and $x_1,y_1$ are the other two neighbors of $v_1$. Consider $G'=G\backslash \{uu_1,uu_2,u_1v_1\}$, then $G'$ has an ${ {nsd}}$-6-coloring c. Let $S_1=[6]\backslash \left( \{c(v_1x_1)\right. \left. +c(v_1y_1)\}\bigcup \{c(uu_3)\}\right)$, $S_2=[6]\backslash \left( \{c(uu_3)\}\bigcup \{c(u_2v_2)\}\bigcup \{w(v_2)-w(u_2)\}\right)$, $S_3=[6]\backslash \left( \{c(v_1x_1),c(v_1y_1)\}\bigcup \{w(x_1)-w(v_1)\}\bigcup \{w(y_1)-w(v_1)\}\right)$, then $|S_1|\ge 4$, $|S_2|\ge 3$, $|S_3|\ge 2$. We can choose $\alpha _i\in S_i,i=1,2,3$ such that $\alpha _1\ne \alpha _2, \alpha _1\ne \alpha _3$, u can be distinguished from $u_1,u_2,u_3$, and $v_1$ can be distinguished from $x_1,y_1$. We obtain an ${ {nsd}}$-6-coloring of G, a contradiction. Therefore, $d_G(v_1)\ne 3$. Similarly, $d_G(v_2)\ne 3$.

Now we assume that $d_G(v_1)=d_G(v_2)=4$, $x_i,y_i,z_i$ are the other three neighbors of $v_i$, $i=1,2$. Consider $G'=G\backslash \{uu_1,uu_2\}$, then $G'$ has an ${ {nsd}}$-6-coloring c. If $c(v_1x_1)+c(v_1y_1)+c(v_1z_1)>6$, then $u_1$ and $v_1$ can be distinguished. Let $S_1=[6]\backslash \left( \{c(uu_3)\}\bigcup \{c(u_1v_1)\}\bigcup \{w(u_2)-c(uu_3)\}\right)$, $S_2=[6]\backslash \left( \{c(uu_3)\}\bigcup \{c(u_2v_2)\}\bigcup \{w(v_2)-w(u_2)\}\bigcup \{w(u_1)-c(uu_3)\}\right)$, then $|S_1|\ge 3,|S_2|\ge 2$. We can choose $\alpha _i\in S_i,i=1,2$ such that $\alpha _1\ne \alpha _2$, $\alpha _1+\alpha _2+c(uu_3)\ne w(u_3)$. We obtain an ${ {nsd}}$-6-coloring of G, which is a contradiction. Therefore, $c(v_1x_1)+c(v_1y_1)+c(v_1z_1)=6$. Similarly, $c(v_2x_2)+c(v_2y_2)+c(v_2z_2)=6$. Without loss of generality we assume that $c(v_ix_i)=1,c(v_iy_i)=2,c(v_iz_i)=3,i=1,2$. Suppose that $c(u_1v_1)\ne c(u_2v_2)$ or $c(uu_3)=6$, then we can obtain an ${ {nsd}}$-6-coloring of G as previously. Hence, $c(u_1v_1)=c(u_2v_2)$, $c(uu_3)\ne 6$. From the above discussion, $d_G(u_3)\ge 3$. If $d_G(u_3)=3$, let $x_3,y_3$ be the neighbors of $u_3$ distinct from u. Consider the graph $G'=G\backslash \{uu_1,uu_2,uu_3\}$, then $G'$ has an ${ {nsd}}$-6-coloring c. Let $S_1=[5]\backslash \{c(u_1v_1)\}$, $S_2=[5]\backslash \{c(u_2v_2)\}$, $S_3=[6]\backslash \left( \{c(v_3x_3),c(v_3y_3)\}\bigcup \{w(x_3)-w(u_3)\}\bigcup \{w(y_3)-w(u_3)\}\right)$, then $|S_1|\ge 4$, $|S_2|\ge 4$, $|S_3|\ge 2$. From the above discussion, we know that $S_1=S_2=\{1,2,3,4\}$ or $\{1,2,3,5\}$, so we can choose $\alpha _i\in S_i,i=1,2,3$ such that $\alpha _1,\alpha _2,\alpha _3$ are pairwise distinct and u can be distinguished from $u_1,u_2,u_3$. We obtain an ${ {nsd}}$-6-coloring of G, which is a contradiction. Therefore, $d_G(u_3)\ge 4$. If $c(uu_3)\in \{1,2,3\}$, color $uu_1,uu_2$ properly with $\{1,2,3\}\backslash \{c(uu_3)\}$. Otherwise, properly color $uu_1,uu_2$ with colors in $\{1,2,3\}$. In both cases, we obtain an ${ {nsd}}$-6-coloring of G, a contradiction.

(iii) Suppose to the contrary that $d_H(u_1)=d_H(u_2)=2$, $u_iv_i\in E(H),d_H(v_i)=2,i=1,2$, $x_i$ is the other neighbor of $v_i,i=1,2$. By Claim 2.3 (iii), $d_G(u)=d_H(u)=4$. Consider the graph $G'=G\backslash \{uu_1,uu_2\}$, then $G'$ has an ${ {nsd}}$-k-coloring c. Let $S_i=[k]\backslash \left( \{c(uu_3),c(uu_4)\} \bigcup \{c(v_ix_i)\}\right) ,i=1,2$, then $|S_i|\ge 3$. By Lemma 2.1 (i), we can choose $\alpha _i\in S_i,i=1,2$ such that $\alpha _1\ne \alpha _2$ and u can be distinguished from $u_3,u_4$. Recolor $u_iv_i$ with a color distinct from $\alpha _i,c(v_ix_i),w(x_i)-c(v_ix_i),\alpha _1+\alpha _2+c(uu_3)+c(uu_4)-\alpha _i$, $i=1,2$, then u can be distinguished from $u_1,u_2$. We obtain an ${ {nsd}}$-k-coloring of G, a contradiction.

Now assume that u is adjacent to a bad 2-vertex $u_1$ with $u_1v_1\in E(H),d_H(v_1)=2,v_1x_1\in E(H),x_1\ne v_1$. Suppose to the contrary that $d_H(u_i)=2,u_iv_i\in E(H),v_i\ne u,i=2,3,4$. By Claim 2.3 (iii), $d_G(u)=d_H(u)=4$. Consider $G'=G\setminus \{uu_1\}$, then $G'$ has an ${ {nsd}}$-k-coloring c. Let $S=[k]\setminus (\{c(uu_2),c(uu_3),c(uu_4)\}\bigcup \{c(v_1x_1)\})$. When $k\le 7$, if $1\in S$, then color $uu_1$ with $\alpha \in S\setminus \{1\}$, otherwise color $uu_1$ with $\alpha \in S\setminus \{2\}$. In both cases $w(u)+\alpha >w(u_i),i=2,3,4$. Then recolor $u_1v_1$ with a color distinct from $\alpha ,c(v_1x_1),w(u),w(x_1)-c(v_1x_1)$. We obtain an ${ {nsd}}$-k-coloring of G, a contradiction. When $k\ge 8$, $|S|\ge 4$, we can choose $\alpha \in S$ such that $\alpha +w(u)\ne w(u_i),i=2,3,4$. Then recolor $u_1v_1$ with a color distinct from $\alpha ,c(v_1x_1),w(u),w(x_1)-c(v_1x_1)$. We obtain an ${ {nsd}}$-k-coloring of G, a contradiction.

(iv) Suppose to the contrary that $d_H(u_i)=2,i=1,2,\ldots ,l$, $u_iv_i\in E(H),v_i\ne u,i=1,2,\ldots ,l$ and $d_H(v_j)=2,v_jx_j\in E(H),x_j\ne v_j,j=1,2,\ldots ,l-1$. By Claim 2.3 (iii), $d_G(u)=d_H(u)=l$. Let $G'=G\backslash \{uu_1\}$, then $G'$ has an ${ {nsd}}$-k-coloring c. If $l<\Delta =k-1$, color $uu_1$ with $\alpha \in [k]\setminus \left( \{c(uu_2),\ldots ,c(uu_l)\}\bigcup \{c(v_1x_1)\}\bigcup \left\{ \alpha +\sum \limits _{i=2}^{l-1}c(uu_i)\right\} \right)$. Otherwise color $uu_1$ with $\alpha \in [k]\setminus \left( \{c(uu_2),\ldots ,c(uu_l)\}\bigcup \{c(v_1x_1)\}\right)$. In both cases, u can be distinguished from $u_l$. Properly recolor $u_iv_i$ such that u can be distinguished from $u_i$ and $v_i$ can be distinguished from $x_i,i=1,2,\ldots ,l-1$. We obtain an ${ {nsd}}$-k-coloring of G, a contradiction. $\square$

Claim 2.5

Let $u\in V(H), d_H(u)=5,uu_i\in E(H),i=1,2,3,4,5$.

• (i) If $\Delta (G)\ge 6$, then u is adjacent to at most two bad 2-vertices. If $\Delta (G)=5$ and u is adjacent to three bad 2-vertices, then u is adjacent to at most one good 2-vertex.

  Furthermore, if $\Delta (G)=5$ and u is a bad 5-vertex, then by Claim 2.3 (iii), $d_G(u)=d_H(u)=5$. Let $d_H(u_i)=2,u_iv_i\in E(H)$, $d_H(v_i)=2$, $x_i$ be the other neighbor of $v_i,i=1,2,3,4$, we have

• (ii) $d_H(u_5)\ge 4$.

• (iii) If $d_H(u_5)=4$, then $u_5$ is adjacent to no bad 2-vertex.

• (iv) If $d_H(u_5)=5$, then $u_5$ is adjacent to at most two bad 2-vertices (Fig. 3).

Fig. 3

Illustration of Claim 2.5

Proof

(i) Assume $\Delta (G)\ge 6$. Suppose to the contrary that $d_H(u_1)=d_H(u_2)=d_H(u_3)=2$, $v_i$ is the other neighbor of $u_i$ with $d_H(v_i)=2$, $x_i$ is the other neighbor of $v_i,i=1,2,3$. By Claim 2.3 (iii), $d_G(u)=d_H(u)=5$. Consider the graph $G'=G\backslash \{uu_1,uu_2,uu_3\}$, then $G'$ has an ${ {nsd}}$-k-coloring c. Let $S_i=[k]\backslash \left( \{c(uu_4),c(uu_5)\}\bigcup \{c(v_ix_i)\}\right) ,i=1,2,3$, then $|S_i|\ge 4,i=1,2,3$. We can choose $\alpha _i\in S_i,i=1,2,3$ such that $\alpha _1,\alpha _2,\alpha _3$ are pairwise distinct and u can be distinguished by $u_4,u_5$. Recolor $u_iv_i$ with a color distinct from $\alpha _i,c(v_ix_i),w(x_i)-c(v_ix_i),\sum \limits _{i=1}^{3}\alpha _i+w(u)-\alpha _i,i=1,2,3$, then u can be distinguished from $u_1,u_2,u_3$. We obtain an ${ {nsd}}$-k-coloring of G, a contradiction.

Assume that $\Delta (G)=5$. Suppose to the contrary that $d_H(u_i)=2$, $u_iv_i\in E(H),v_i\ne u,i=1,2,\ldots ,5$ and $d_H(v_j)=2,v_jx_j\in E(H),j=1,2,3$. By Claim 2.3 (iii), $d_G(u)=d_H(u)=5$. Consider the graph $G'=G\backslash \{uu_1\}$, then $G'$ has an ${ {nsd}}$-6-coloring c. Color $uu_1$ with $\alpha \in [6]\backslash \left( \{c(uu_2),\ldots ,c(uu_5)\}\bigcup \{c(v_1x_1)\}\right)$. Then recolor $u_1v_1$ with a color distinct from $\alpha ,c(v_1x_1),w(x_i)-c(v_1x_1),\sum \limits _{i=2}^{5}c(uu_i)$. It can be seen that $w(u)+\alpha >w(u_i),i=2,\ldots ,5$, so we obtain an ${ {nsd}}$-6-coloring of G, a contradiction.

(ii) By Claim 2.4 (iv), $d_H(u_5)\ge 3$. Suppose to the contrary that $d_H(u_5)=3$, $v_{51},v_{52}$ are the other two neighbors of $u_5$. Consider the graph $G'=G\backslash \{uu_1,uu_2,uu_3,uu_4,uu_5\}$, then $G'$ has an ${ {nsd}}$-6-coloring c. Let $S_i=[6]\backslash \{c(v_ix_i)\},i=1,2,3,4$, $S_5=[6]\backslash \left( \{c(u_5v_{51}),c(u_5v_{52})\} \bigcup \{w(v_{51})-w(u_5)\}\bigcup \{w(v_{52})-w(u_5)\}\right)$, then $|S_i|\ge 5,i=1,2,3,4$, $|S_5|\ge 2$. We can choose $\alpha _i\in S_i,i=1,2,3,4,5$ such that $\alpha _1,\alpha _2,\alpha _3,\alpha _4,\alpha _5$ are pairwise distinct and u can be distinguished by $u_5$. Obviously, u can be distinguished by $u_1,u_2,u_3,u_4$. Recolor $u_iv_i$ with a color distinct from $\alpha _i,c(v_ix_i),w(x_i)-c(v_ix_i),i=1,2,3,4$ and we obtain an ${ {nsd}}$-6-coloring of G, a contradiction.

(iii) Let $v_{51},v_{52},v_{53}$ be the other three neighbors of $u_5$. Suppose to the contrary that $d_H(v_{51})=d_H(x_{51})=2,v_{51}x_{51}\in E(H)$, $x_{51}y_{51}\in E(H),y_{51}\ne v_{51}$. By Claim 2.3 (iii), $d_G(u_5)=d_H(u_5)=4$. Consider the graph $G'=G\backslash \{uu_1,uu_2,uu_3,uu_4\}$, then $G'$ has an ${ {nsd}}$-6-coloring c. Assume that $c(uu_5)=\alpha _5$, $c(u_5v_{5j})=\beta _j,j=1,2,3$, $c(v_ix_i)=\gamma _i,i=1,2,3,4$, $c(x_{51}y_{51})=\eta$. Let $S_i=[6]\backslash (\{\gamma _i\}\bigcup \{\alpha _5\}),i=1,2,3,4$, then $|S_i|\ge 4,i=1,2,3,4$.

If there exists some $\gamma _i=\alpha _5$ ($i\in \{1,2,3,4\}$) or $\gamma _i\ne \gamma _j$ ($i\ne j,i,j\in \{1,2,3,4\}$), then we can choose $\alpha _i\in S_i,i=1,2,3,4$ such that u can be distinguished by $u_5$. Recolor $u_iv_i$ with a color distinct from $\gamma _i,\alpha _i,w(x_i)-c(v_ix_i),i=1,2,3,4$, we can obtain an ${ {nsd}}$-6-coloring of G, a contradiction. Therefore, we assume that $\gamma _1=\gamma _2=\gamma _3=\gamma _4=\gamma ,\alpha _5\ne \gamma$. Then $S_1=S_2=S_3=S_4=[6]\backslash \{\alpha _5,\gamma \}$. Assume that $S_i=\{\alpha _1,\alpha _2,\alpha _3,\alpha _4\},i=1,2,3,4$. Color $uu_i$ with $\alpha _i,i=1,2,3,4$.

If $|\{\alpha _1,\alpha _2,\alpha _3,\alpha _4\}\bigcap \{\beta _1,\beta _2,\beta _3\}|=3$, then u can be distinguished by $u_5$, recolor $u_iv_i,i=1,2,3,4$ as previously and we obtain an ${ {nsd}}$-6-coloring of G, a contradiction. Furthermore, $\left| \{\alpha _1,\alpha _2,\alpha _3,\alpha _4\}\bigcap \{\beta _1,\beta _2,\beta _3\}\right| \ge 2$ because there are six colors in total. Therefore, $\left| \{\alpha _1,\alpha _2,\alpha _3,\alpha _4\} \bigcap \{\beta _1,\beta _2,\beta _3\}\right| =2$. Without loss of generality we assume that $\{\alpha _1,\alpha _2\}\subseteq \{\beta _1,\beta _2,\beta _3\}$.

If $\beta _1=\gamma$, then $\{\alpha _1,\alpha _2\}=\{\beta _2,\beta _3\}$. If $\alpha _5\ne \eta$, suppose u can not be distinguished by $u_5$, then $\gamma =\alpha _3+\alpha _4$. Recolor $uu_5$ with $\gamma$ and recolor $u_5v_{51}$ with $\alpha _5$, we obtain an ${ {nsd}}$-6-coloring of G, a contradiction. Therefore, $\alpha _5=\eta$. Recolor $u_5v_{51}$ with one of $\alpha _3,\alpha _4$, or exchange the colors of $uu_3$ and $uu_5$, or exchange the colors of $uu_4$ and $uu_5$ such that $u_5$ can be distinguished by $u,v_{52},v_{53}$. It is easy to see that u can be distinguished by $u_1,u_2,u_3,u_4$. Recolor $u_iv_i,i=1,2,3,4$, and $v_{51}x_{51}$ as previously and we can obtain an ${ {nsd}}$-6-coloring of G, a contradiction.

If $\beta _1\ne \gamma$. Without loss of generality we assume that $\beta _1=\alpha _1,\beta _2=\alpha _2$. Recolor $u_5v_{51}$ with one of $\alpha _3,\alpha _4$, or exchange the colors of $uu_3$ and $uu_5$, or exchange the colors of $uu_4$ and $uu_5$ such that $u_5$ can be distinguished by $u,v_{52},v_{53}$. It is easy to see that u can be distinguished by $u_1,u_2,u_3,u_4$. Recolor $u_iv_i,i=1,2,3,4$, and $v_{51}x_{51}$ as previously and we can obtain an ${ {nsd}}$-6-coloring of G, a contradiction.

(iv) Let $v_{51},v_{52},v_{53},v_{54}$ be the other four neighbors of $u_5$. Suppose to the contrary that $d_H(v_{5i})=d_H(x_{5i})=2,v_{5i}x_{5i}\in E(H)$, $x_{5i}y_{5i}\in E(H),y_{5i}\ne v_{5i},i=1,2,3$. By Claim 2.3 (iii), $d_G(u_5)=d_H(u_5)=5$. Consider the graph $G'=G\backslash \{uu_1,uu_2,uu_3,uu_4\}$, then $G'$ has an ${ {nsd}}$-6-coloring c. Assume that $c(uu_5)=\alpha _5$, $c(u_5v_{5j})=\beta _j,j=1,2,3,4$, $c(v_ix_i)=\gamma _i,i=1,2,3,4$. Let $S_i=[6]\backslash \left( \{\gamma _i\}\bigcup \{\alpha _5\}\right) ,i=1,2,3,4$, then $|S_i|\ge 4,i=1,2,3,4$.

If there exists some $\gamma _i=\alpha _5$ ($i\in \{1,2,3,4\}$) or $\gamma _i\ne \gamma _j$ ($i\ne j,i,j\in \{1,2,3,4\}$), then we can choose $\alpha _i\in S_i,i=1,2,3,4$ such that u can be distinguished by $u_5$. Recolor $u_iv_i$ with a color distinct from $\alpha _i,\gamma _i,w(x_i)-c(v_ix_i),i=1,2,3,4$. We obtain an ${ {nsd}}$-6-coloring of G, a contradiction. Therefore, we assume that $\gamma _1=\gamma _2=\gamma _3=\gamma _4=\gamma ,\alpha _5\ne \gamma$. Then $S_1=S_2=S_3=S_4=[6]\backslash \{\alpha _5,\gamma \}$. Assume that $S_i=\{\alpha _1,\alpha _2,\alpha _3,\alpha _4\}$. Color $uu_i$ with $\alpha _i$ and recolor $u_iv_i$ with a color distinct from $\gamma ,\alpha _i,w(x_i)-c_(v_ix_i),i=1,2,3,4$.

If $\{\alpha _1,\alpha _2,\alpha _3,\alpha _4\}\ne \{\beta _1,\beta _2,\beta _3,\beta _4\}$, then u can be distinguished by $u_5$, it is easy to see that u can be distinguished from $u_1,u_2,u_3,u_4$. We obtain an ${ {nsd}}$-6-coloring of G, a contradiction. Therefore, $\{\alpha _1,\alpha _2,\alpha _3,\alpha _4\}= \{\beta _1,\beta _2,\beta _3,\beta _4\}$. Without loss of generality we assume that $\alpha _i=\beta _i,i=1,2,3,4$. If $c(x_{51}y_{51})\ne \gamma$, then recolor $u_5v_{51}$ with $\gamma$. We can see that u can be distinguished from $u_5$. If $u_5$ can not be distinguished from $v_{54}$, then exchange the colors of $uu_1$ and $uu_5$. Recolor $v_{51}x_{51}$ with a color distinct from $\gamma _1,c(x_{51}y_{51}),w(y_{51})-c(x_{51}y_{51})$. We obtain an ${ {nsd}}$-6-coloring of G, a contradiction. Similarly, $c(x_{52}y_{52})=c(x_{53}y_{53})=\gamma$. Recolor $uu_5$ with $\gamma$. Then recolor $u_5v_{51}$ or recolor $u_5u_{52}$ with $\alpha _5$ such that $u_5$ can be distinguished by $v_{54}$. Recolor $v_{5i}x_{5i}$ with a color distinct from $\gamma ,\alpha _5,\alpha _i,w(y_{5i})-c(x_{5i}y_{5i}),i=1,2$. We obtain an ${ {nsd}}$-6-coloring of G, a contradiction. $\square$

In order to complete the proof, we use a discharging procedure. For every $v\in V(H)$, we define the original charge of v to be $ch(v)=d_H(v)=l$. We then redistribute the charges according to the rules R1, R2, and R3 (below). To complete the proof, our aim is to prove that, for every vertex v, the new charge ${ {ch}}^{*}(v)$ is at least 8/3.

The discharging rules are defined as follows:

• (R1) Every $4^{+}$-vertex gives $\frac{2}{3}$ to each adjacent bad 2-vertex.

• (R2) Every $3^{+}$-vertex gives $\frac{1}{3}$ to each adjacent good 2-vertex.

• (R3) If u is a bad 5-vertex, $u_i,i=1,2,3,4,5$, are the neighbors of u, and if $u_1,u_2,u_3,u_4$ are bad 2-vertices, then $u_5$ gives $\frac{1}{3}$ to u.

Case $l=2$. Observe that $ch(v)=2$. Suppose v is a good 2-vertex. Hence, by (R2), ${ {ch}}^{*}(v)\ge 2+2\times \frac{1}{3}=\frac{8}{3}$. Suppose v is bad, By Claim 2.4 (i) and Claim 2.4 (ii), v is adjacent to at most one 2-vertex and is adjacent to a $4^{+}$-vertex. Hence, by (R1), ${ {ch}}^{*}(v)= 2+1\times \frac{2}{3}=\frac{8}{3}$.

Case $l=3$. Observe that $ch(v)=3$. By Claim 2.4 (ii), v is adjacent to no bad 2-vertex and is adjacent to at most one good 2-vertex. By Claim 2.5 (ii), v is adjacent to no bad 5-vertex. By (R2) and (R3), ${ {ch}}^{*}(v)\ge 3-1\times \frac{1}{3}=\frac{8}{3}$.

Case $l=4$. Observe that $ch(v)=4$. Suppose v is not adjacent to a bad 2-vertex. Then, by (R2) and (R3), ${ {ch}}^{*}(v)\ge 4-4\times \frac{1}{3}=\frac{8}{3}$. Assume now, v is adjacent to a bad 2-vertex. By Claim 2.4 (iii), v is adjacent to at most two good 2-vertices. By Claim 2.5 (iii), v is adjacent to no bad 5-vertex. Hence by (R1), (R2), and (R3), ${ {ch}}^{*}(v)\ge 4-1\times \frac{2}{3}-2\times \frac{1}{3}=\frac{8}{3}$.

Case $l=5$. Observe that $ch(v)=5$. Suppose v is adjacent to at most two bad 2-vertices, then by (R1), (R2), and (R3), ${ {ch}}^{*}(v)\ge 5-2\times \frac{2}{3}-3\times \frac{1}{3}=\frac{8}{3}$. If v is adjacent to three bad 2-vertices, then by Claim 2.5 (i) and (iv), v is adjacent to at most one good 2-vertex and v is adjacent to no bad 5-vertex. Hence by (R1), (R2), and (R3), ${ {ch}}^{*}(v)\ge 5-3\times \frac{2}{3}-1\times \frac{1}{3}=\frac{8}{3}$. Assume now, v is a bad 5-vertex. By (R1), (R2), and (R3), ${ {ch}}^{*}(v)\ge 5-4\times \frac{2}{3}+1\times \frac{1}{3}=\frac{8}{3}$.

Case $l\ge 6$. Observe that $ch(v)=l$. By Claim 2.5 (i), any 5-vertex in H is good. By Claim 2.4 (iv), v is adjacent to at most $(l-1)$ bad 2-vertices. Moreover if v is adjacent to $(l-1)$ bad 2-vertices, then its last neighbor has degree at least 3. It follows by (R1), ${ {ch}}^{*}(v)\ge l-(l-1)\times \frac{2}{3}\ge \frac{8}{3}$.

This completes the proof of Theorem 1.3.