1 Introduction

In recent years, scientists and engineers have devoted an increasing interest to the analytical asymptotic techniques for solving nonlinear problems. Many new numerical techniques have been widely applied to nonlinear problems. Nonlinear phenomena play a crucial role in various fields of science and engineering. Similarly, the corresponding nonlinear equations and their analytical or numerical solutions are fundamentally important. Many physical phenomena are modeled by nonlinear differential equations in order to have more opportunities to handle the real objects in our real world. Therefore, solving these equations is in the circle of most scientists’ and engineers’ priority and requirements. Nonlinear differential equations are generally difficult to solve and their exact solutions are difficult to obtain; therefore, various approximate methods have recently been developed to solve these types of equations.

The Duffing equation is a well-known nonlinear equation of applied science which is used as a powerful tool to discuss some important practical phenomena such as orbit extraction, nonuniformity caused by an infinite domain, nonlinear mechanical oscillators, etc. Besides, the Duffing equation is applied in the field of disease prediction . In this paper, we consider the nonlinear Duffing equation of the form

$$\begin{aligned}&y^{\prime \prime }(x)+\alpha y^{\prime }(x)+\beta y(x)+\gamma y^3(x)=f(x), \end{aligned}$$
(1.1)
$$\begin{aligned}&y(0)=a, \quad y'(0)=b, \end{aligned}$$
(1.2)

where \(\alpha \), \(\beta \), \(\gamma \), a, and b are real constants. This equation was first introduced by Duffing to explain forced vibrations of industrial machinery with linear damping [38]. Duffing’s equation has many catastrophic, diverging, and oscillative behaviors by several stable and unstable states due to the value of its coefficients. The solutions of some versions of Duffing’s equation can be seen in [29, 33, 36, 37]. Yusufoglu in [41] applied the Laplace transform decomposition algorithm to solve Duffing’s equation. Vahidi et al. in [40] used the restarted Adomian’s decomposition method to solve Duffing’s equation. Cveticanin [14] applied the HPM to solve nonlinear differential equations by a cubic nonlinear term, as in Duffing’s equation, and showed that the method worked extremely well.

Perturbation techniques are widely used in science and engineering to handle nonlinear problems [34]. The HPM was first proposed by He in [20] and further developed and improved by him in [21–24]. This method is based on the use of traditional perturbation method and the homotopy technique. By using this method, a rapid convergent series solution can be obtained in most cases. Usually, a small number of terms of the series solution can be used for numerical purposes with a high degree of accuracy. The applications of the HPM in nonlinear problems have been demonstrated by many researchers, cf. [3, 13, 16, 17, 28]. Recently, the HPM was employed for solving singular second-order differential equations [10] and nonlinear population dynamics models [11]. Very recently, the standard HPM was successfully applied to the Klein–Gordon and sine-Gordon equations [12]. The applicability of the HPM has also been extended to fractional equations [8, 31, 32, 35]. In general, this method has been successfully applied to solve many types of linear and nonlinear problems in science and engineering by many authors [1, 4, 9, 15, 39]. Also, correction for the HPM based on the initial solution is done by Hesameddini [26]. However, development of the HPM can be found in [5, 25, 30]. Accordingly, it can be said that He’s homotopy perturbation method is a universal one, and is able to solve various kinds of nonlinear functional equations.

In this paper, we apply the NHPM to solve nonlinear Duffing’s equation (1.1). This method was presented in [4] for the Riccati equation and we extend it in order to solve nonlinear Duffing’s equation (1.1). By this method, we get a truncated series solution that often coincides with the Maclaurin expansion of the true solution. In order to improve the accuracy of the series solutions, we apply the Laplace transformation and then the Padé approximant [6, 7] yielding the analytic approximate solution with fast convergence rate and high accuracy, and finally adopt the inverse Laplace transformation to get an analytic solution.

2 HPM for Nonlinear Differential Equations

In this section, the HPM is described for the solution of nonlinear differential equations. Toward this end, suppose that

$$\begin{aligned} A(u(x))=f(r(x)), \quad r(x) \in \Omega , \end{aligned}$$
(2.1)

with boundary conditions

$$\begin{aligned} B\big (u(x),\partial u(x)/ \partial n\big )=0, \quad r(x)\in \Gamma , \end{aligned}$$
(2.2)

where A is a general differential operator, B is a boundary operator, f(r(x)) is a known analytic function, and \(\Gamma \) is the boundary of the domain \(\Omega \). The operator A can be divided into two parts L and N, where L is a linear operator and N is a nonlinear one. Therefore, Eq. (2.1) may be expressed as

$$\begin{aligned} L(u(x))+N(u(x))=f(r(x)). \end{aligned}$$
(2.3)

By the homotopy technique, we construct a homotopy \(v(r(x),p):\Omega \times [0,1]\rightarrow R\), which satisfies

$$\begin{aligned} \begin{aligned} H(U(x),p)&=(1-p)\big [L(U(x))-u_0(x)\big ] \\&\,\,\quad +p\big [A(U(x))-f(r(x))\big ]=0,\quad p \in [0,1],\quad r(x)\in \Omega , \end{aligned} \end{aligned}$$
(2.4)

where \(p\in [0,1]\) is an embedding parameter and \(u_0(x)\) is an initial approximation of the solution of Eq. (2.1). Clearly, from Eq. (2.4) we have

$$\begin{aligned} H(U(x),0)&=L(U(x))-u_0(x)=0, \end{aligned}$$
(2.5)
$$\begin{aligned} H(U(x),1)&=A(U(x))-f(r(x))=0, \end{aligned}$$
(2.6)

and the changing process of p from zero to one is just that of H(U(x), p) from \(L(U(x))-u_0(x)\) to \(A(U(x))-f(r(x))\). If the embedding parameter \(p\in [0,1]\) is considered as a “small parameter,” applying the classical perturbation technique, we can naturally assume that the solution of Eqs. (2.5) and (2.6) can be given as a power series in p, i.e.,

$$\begin{aligned} U(x)=U_{0}(x)+p U_{1}(x)+p^{2} U_{2}(x)+\cdots \end{aligned}$$
(2.7)

setting \(p=1\) results in the approximate solution of Eq. (2.1) as

$$\begin{aligned} u(x)=\lim _{p\longrightarrow 1}U(x)=U_{0}(x)+U_{1}(x)+U_{2}(x)+\cdots . \end{aligned}$$
(2.8)

The series in (2.8) converges in most cases and the rate of convergence depends on \(A(u(x))-f(r(x))\) [19].

Note that in the HPM in order to obtain an approximate solution, the components \(U_i(x)\) for \(i=0,1,\ldots \) must be calculated. Specially for \(i \ge 3\), it needs large and sometimes complicated computations and, in the case of nonlinearity, the use of He’s polynomials [18]. To obviate this problem, the NHPM is introduced, in which \(U_0(x)\) is calculated in such a way that \(U_i(x)=0\) for \(i\ge 1\). So, the number of computations decreases in comparison with that in the HPM. The NHPM will be discussed in detail in the following section.

3 Basic Idea of the NHPM

In order to illuminate the solution procedure of the NHPM, we consider the equivalence convex homotopy (2.4) as

$$\begin{aligned} H(U(x),p)=L(U(x))-u_0(x)+pu_0(x)+p\big [N(U(x))-f(r(x))\big ]=0, \end{aligned}$$
(3.1)

which can be written in the following form

$$\begin{aligned} L(U(x))=u_0(x)+p\big [f(r(x))-u_0(x)-N(U(x))\big ]. \end{aligned}$$
(3.2)

Denoting \(d^2/dx^2\) by G, we have \(G^{-1}\) as a two-fold integration from 0 to x. By applying \(G^{-1}\) to both sides of Eq. (3.2), we have

$$\begin{aligned} U(x)= T(x)+G^{-1}(u_0(x))+p\big [G^{-1}(f(r(x)))-G^{-1}(u_0(x))-G^{-1}(N(U(x)))\big ], \end{aligned}$$
(3.3)

where T incorporates the constants of integration and satisfies \(GT=0\). In order to apply the NHPM, suppose that the initial approximation of Eq. (2.1) has the form

$$\begin{aligned} u_{0}(x)=\sum _{n=0}^{\infty }a_{n}F_{n}(x), \end{aligned}$$
(3.4)

where \(a_{0},a_{1},a_{2},\ldots \) are unknown coefficients and \(F_{0}(x),F_{1}(x),F_{2}(x),\ldots \) are specific functions depending on the problem. By substituting Eqs. (2.7) and (3.4) into Eq. (3.3), we obtain

$$\begin{aligned}&\sum _{n=0}^{\infty }p^{n}U_{n}(x)=T(x)+G^{-1}\Bigg (\sum _{n=0}^{\infty }a_{n}F_{n}(x)\Bigg ) \nonumber \\&\quad +p\Bigg [G^{-1}(f(r(x)))-G^{-1}\Bigg (\sum _{n=0}^{\infty }a_{n}F_{n}(x)\Bigg )-G^{-1}N\Bigg (\sum _{n=0}^{\infty }p^{n}U_{n}(x)\Bigg )\Bigg ].\qquad \quad \end{aligned}$$
(3.5)

Comparing coefficients of terms with identical powers of p leads to

$$\begin{aligned} \begin{aligned} p^{0}:U_0(x)&= T(x)+G^{-1}\left( \sum _{n=0}^{\infty }a_{n}F_{n}(x)\right) , \\ p^{1}:U_{1}(x)&=G^{-1}(f(r(x)))-G^{-1}\left( \sum _{n=0}^{\infty }a_{n}F_{n}(x))-G^{-1}N(U_{0}(x)\right) , \\ p^{2}:U_{2}(x)&=-G^{-1}N(U_{0}(x),U_{1}(x)), \\ \vdots \quad&\ \\ p^{j}:U_{j}(x)&=-G^{-1}N\big (U_{0}(x),U_{1}(x),U_{2}(x),\ldots ,U_{j-1}(x)\big ), \\ \vdots \quad&\ \end{aligned} \end{aligned}$$
(3.6)

Now, we solve these equations in such a way that \(U_1(x)=0\), then Eq. (3.6) results in \(U_{2}(x)=U_{3}(x)=\cdots =0\). Therefore, the exact solution may be obtained as follows:

$$\begin{aligned} u(x)=U_{0}(x)=T(x)+G^{-1}\left( \sum _{n=0}^{\infty }a_{n}F_{n}(x)\right) . \end{aligned}$$
(3.7)

4 NHPM for Duffing’s Equation

In this section, we consider Duffing’s equation (1.1) and apply the NHPM to solve it. To this end, by considering the convex homotopy defined in Eq. (2.4), we have

$$\begin{aligned} \begin{aligned} H(Y(x),p)&=(1-p)\big (Y''(x)-y_{0}(x)\big ) \\&\quad {}+p\big (Y''(x)+\alpha Y'(x)+\beta Y(x)+\gamma Y^{3}(x)-f(x)\big )=0, \end{aligned} \end{aligned}$$
(4.1)

or equivalently

$$\begin{aligned} Y''(x)=y_{0}(x)-p\big [y_{0}(x)+\alpha Y'(x)+\beta Y(x)+\gamma Y^{3}(x)-f(x)\big ]. \end{aligned}$$
(4.2)

Denoting \(d^2/\mathrm{d}x^2\) by G, we have \(G^{-1}\) as a two-fold integration. Using the operator G, Eq. (4.2) becomes

$$\begin{aligned} G Y(x)=y_{0}(x)-p\big [y_{0}(x)+\alpha Y'(x)+\beta Y(x)+\gamma Y^{3}(x)-f(x)\big ]. \end{aligned}$$
(4.3)

Applying the inverse operator \(G^{-1}\) to both sides of Eq. (4.3), we obtain

$$\begin{aligned} Y(x)= & {} Y(0)+xY'(0)+\int _{0}^{x}\int _{0}^{x}y_{0}(x)\mathrm{d}x \mathrm{d}x \nonumber \\&-p\int _{0}^{x}\int _{0}^{x}\big [y_{0}(x)+\alpha Y'(x)+\beta Y(x)+\gamma Y^{3}(x)-f(x)\big ]\mathrm{d}x \mathrm{d}x. \nonumber \\ \end{aligned}$$
(4.4)

By considering \(y_{0}(x)=\sum _{n=0}^{\infty }a_{n}F_{n}(x)\), where \(F_{n}(x)=x^{n}\), \(Y(0)=a\) and \(Y'(0)=b\), Eq. (4.4) is as follows:

$$\begin{aligned}&Y(x)=a+bx+\int _{0}^{x}\int _{0}^{x}\left( \sum _{n=0}^{\infty }a_{n}F_{n}(x)\right) \mathrm{d}x\mathrm{d}x \nonumber \\&\quad -p\int _{0}^{x}\int _{0}^{x}\Bigg [\left( \sum _{n=0}^{\infty }a_{n}F_{n}(x)\right) +\alpha Y'(x)+\beta Y(x)+\gamma Y^{3}(x)-f(x)\Bigg ]\mathrm{d}x \mathrm{d}x.\nonumber \\ \end{aligned}$$
(4.5)

By substituting \(Y(x)=\sum _{i=0}^{\infty }p^{i}Y_{i}(x)\) into the above equation, we have

$$\begin{aligned} \sum _{i=0}^{\infty }p^{i}Y_{i}(x)=&\,\,a+bx+\int _{0}^{x}\int _{0}^{x}\left( \sum _{n=0}^{\infty }a_{n}F_{n}(x)\right) \mathrm{d}x\mathrm{d}x -p\int _{0}^{x}\int _{0}^{x}\Bigg [\left( \sum _{n=0}^{\infty }a_{n}F_{n}(x)\right) \nonumber \\&+\alpha \frac{d}{d x}\left( \sum _{i=0}^{\infty }p^{i}Y_{i}(x)\right) +\beta \left( \sum _{i=0}^{\infty }p^{i} Y_{i}(x)\right) \nonumber \\&+\gamma \left( \sum _{i=0}^{\infty }p^{i} Y_{i}(x)\right) ^{3}-f(x)\Bigg ]\mathrm{d}x\mathrm{d}x, \end{aligned}$$
(4.6)

where \(Y_{i}(x)\) for \(i=1,2,\ldots \) are unknown functions which should be determined. By equating the terms with identical powers of p, we obtain

$$\begin{aligned} p^{0}:Y_0(x)= & {} a+bx+\int _{0}^{x}\int _{0}^{x}\left( \sum _{n=0}^{\infty }a_{n}x^n\right) \mathrm{d}x\mathrm{d}x, \nonumber \\ p^{1}:Y_1(x)= & {} -\int _{0}^{x}\int _{0}^{x}\left[ \left( \sum _{n=0}^{\infty }a_{n}x^n\right) +\alpha Y_{0}'(x)+\beta Y_{0}(x)+\gamma Y_{0}^3(x)-f(x)\right] \mathrm{d}x\mathrm{d}x, \nonumber \\ p^{2}:Y_2(x)= & {} -\int _{0}^{x}\int _{0}^{x}\big [\alpha Y'_{1}(x)+\beta Y_{1}(x)+3\gamma Y_{0}^2(x) Y_{1}(x)\big ]\mathrm{d}x\mathrm{d}x, \nonumber \\ p^{3}: Y_3(x)= & {} -\int _{0}^{x}\int _{0}^{x}\big [\alpha Y'_{2}(x)+\beta Y_{2}(x)+3\gamma (Y_{0}(x)Y_{1}^2(x)+Y_{0}^2(x)Y_{2}(x))\big ]\mathrm{d}x\mathrm{d}x, \nonumber \\&\vdots \quad \end{aligned}$$
(4.7)

Since the complicated excitation term f(x) can cause difficult integrations and proliferation of terms, we can express f(x) in the Taylor series at \(x_{0}=0\), which is truncated for simplification. By replacing \(\widetilde{f}(x)=\sum _{i=0}^{k}b_{i}x^{i}\), where \(b_{i}=f^{i}(0)/i!\), instead of f(x) into \(Y_{1}(x)\), one gets

$$\begin{aligned} Y_{1}(x)&=1/2(-a_{0}-\alpha b-\beta a-\gamma a^{3}+b_{0})x^{2}+1/6(-a_{1}-\alpha a_{0}-\beta b-3\gamma a^{2}b+b_{1})x^{3} \nonumber \\&\quad +1/12(-a_{2}-1/2\alpha a_{1}-1/2\beta a_{0}-3/2\gamma a^{2}a_{0}-3\gamma ab^{2}+b_{2})x^{4} \nonumber \\&\quad +1/20(-a_{3}-1/3\alpha a_{2}-1/6\beta a_{1}-1/2\gamma a^{2}a_{1}-3\gamma aa_{0}b-\gamma b^{3}+b_{3})x^{5}+\cdots . \nonumber \\ \end{aligned}$$
(4.8)

Eliminating \(Y_{1}(x)\) lets the coefficients \(a_{n}\) for \(n=1,2,\cdots \) take the following values:

$$\begin{aligned} \begin{aligned} a_0&=-\alpha b-\beta a-\gamma a^{3}+b_{0}, \\ a_{1}&=-\alpha a_{0}-\beta b-3\gamma a^{2}b+b_{1}, \\ a_{2}&=-1/2\alpha a_{1}-1/2\beta a_{0}-3/2\gamma a^{2}a_{0}-3\gamma ab^{2}+b_{2}, \\ a_{3}&=-1/3\alpha a_{2}-1/6\beta a_{1}-1/2\gamma a^{2}a_{1}-3\gamma aa_{0}b-\gamma b^{3}+b_{3}, \\ \vdots&\ \end{aligned} \end{aligned}$$
(4.9)

Therefore, we gain the solution of Eq. (1.1) as

$$\begin{aligned} y(x)&=Y_{0}(x)=a+bx+1/2a_{0}x^{2}+1/6a_{1}x^{3}+1/12a_{2} x^{4}+1/20a_{3}x^{5}+\cdots \nonumber \\&=a+bx+1/2(-\alpha b-\beta a-\gamma a^{3}+b_{0})x^{2}+1/6(-\alpha a_{0}-\beta b-3\gamma a^{2}b+b_{1})x^{3} \nonumber \\&\quad +1/12(-1/2\alpha a_{1}-1/2\beta a_{0}-3/2\gamma a^{2}a_{0}-3\gamma ab^{2}+b_{2})x^{4} \nonumber \\&\quad +1/20(-1/3\alpha a_{2}-1/6\beta a_{1}-1/2\gamma a^{2}a_{1}-3\gamma aa_{0}b-\gamma b^{3}+b_{3})x^{5}+\cdots \nonumber \\ \end{aligned}$$
(4.10)

and this, in the limit of infinitely many terms, yields the exact solution of Eq. (1.1).

5 Numerical Implementation

In this section, to give a clear overview of the analysis method presented above, we choose two test problems.

Example 5.1

Consider Duffing’s equation [27]

$$\begin{aligned} y^{\prime \prime }(x)+3y(x)-2y^{3}(x)= \cos x\sin 2x \end{aligned}$$
(5.1)

with the initial condition \(y(0)=0\) and \(y'(0)=1\) and the exact solution \(y(x)=\sin x\). In order to apply the NHPM to Eq. (5.1), consider the convex homotopy (2.4) as

$$\begin{aligned} (1-p)\big [Y^{\prime \prime }(x)-y_{0}(x)\big ]+p\big [Y''(x)+3Y(x)-2Y^{3}(x)-\cos x\sin 2x\big ]=0 \quad \end{aligned}$$
(5.2)

or

$$\begin{aligned} Y^{\prime \prime }(x)=y_{0}(x)-p\big [y_{0}(x)+3Y(x)-2Y^{3}(x)-\cos x\sin 2x\big ]. \end{aligned}$$
(5.3)

Denoting \(d^2/\mathrm{d}x^2\) by G, we have \(G^{-1}\) as a two-fold integration. Using the operator G, Eq. (5.3) becomes

$$\begin{aligned} G Y(x)=y_{0}(x)-p\big [y_{0}(x)+3Y(x)-2Y^{3}(x)-\cos x\sin 2x\big ]. \end{aligned}$$
(5.4)

Applying the inverse operator \(G^{-1}\) to both sides of Eq. (5.4) and using the initial conditions, we obtain

$$\begin{aligned} Y(x)=x+G^{-1}(y_{0}(x))-pG^{-1}[(y_{0}(x)+3Y(x)-2Y^{3}(x)-\cos x\sin 2x)]. \end{aligned}$$
(5.5)

By replacing \(y_{0}(x)=\sum _{n=0}^{\infty }a_{n}x^{n}\) in the above equation, one gets

$$\begin{aligned} Y(x)=&\,\,x+G^{-1}\left( \sum _{n=0}^{\infty }a_{n}x^{n}\right) \nonumber \\&-pG^{-1}\left[ \left( \sum _{n=0}^{\infty }a_{n}x^{n}+3Y(x)-2Y^{3}(x)- \cos x\sin 2x\right) \right] . \end{aligned}$$
(5.6)

Substituting \(Y(x)=\sum _{i=0}^{\infty }p^{i}Y_{i}(x)\) into Eq. (5.6), considering the Maclaurin series of the excitation term

$$\begin{aligned} \cos x\sin 2x\simeq 2x-7/3x^{3}+61/60x^{5}-547/2520x^{7}, \end{aligned}$$
(5.7)

and equating the terms with identical powers of p give

$$\begin{aligned} \begin{aligned} p^{0}:Y_{0}(x)&=x+G^{-1}\left( \sum _{n=0}^{\infty }a_{n}x^{n}\right) , \\ p^{1}:Y_{1}(x)&=-G^{-1}\left[ \left( \sum _{n=0}^{\infty }a_{n}x^{n}+3Y_0(x)-2Y_0^{3}(x) \right. \right. \\&\left. \left. \quad {}-(2x-7/3x^{3}+61/60x^{5}-547/2520x^{7})\right) \right] , \\ p^{2}:Y_{2}(x)&=-G^{-1}\big [3Y_1(x)-6Y_0^{2}(x)Y_1(x)\big ], \\ \vdots \quad&\ \end{aligned} \end{aligned}$$
(5.8)

Solving the above equation for \(Y_{1}(x)\) leads to the result

$$\begin{aligned} \begin{aligned} Y_{1}(x)=&-1/2a_{0}x^{2}-1/6(1+a_{1})x^{3}-1/12(a_{2}+3/2a_{0})x^{4} \\&-1/60(1+3/2a_{1}+3 a_{3})x^{5}+\cdots . \end{aligned} \end{aligned}$$
(5.9)

Eliminating \(Y_{1}(x)\) lets the coefficients \(a_{n}\) for \(n=0,1,2,\cdots \) take the following values:

$$\begin{aligned} a_{0}=0, \quad a_{1}=-1, \quad a_{2}=0, \quad a_{3}=1/6, \quad a_{4}=0, \quad \cdots \end{aligned}$$
(5.10)

By substituting the above values into \(Y_0(x)\), we obtain

$$\begin{aligned} \begin{aligned} y(x)=Y_{0}(x)&=x-1/6x^{3}+1/120x^{5}+\cdots \\&=x-x^{3}/3!+x^{5}/5!+\cdots +(-1)^{n}x^{2n+1}/(2n+1)!,\quad n\ge 0, \end{aligned} \end{aligned}$$
(5.11)

which is the partial sum of the Taylor series of the exact solution at \(x = 0\). In order to obtain a more accurate solution, we use the truncated series of Eq. (5.11). Consider five terms in y(x) as

$$\begin{aligned} \varphi (x)=x-x^{3}/3!+x^{5}/5!-x^{7}/7!+x^{9}/9!, \end{aligned}$$
(5.12)

By applying the Laplace transformation to both sides of Eq. (5.12), we have

$$\begin{aligned} L[\varphi (x)]=1/s^{2}-1/s^{4}+1/s^{6}-1/s^{8}+1/s^{10}. \end{aligned}$$
(5.13)

If \(s=1/t\), then

$$\begin{aligned} L[\varphi (x)]=t^{2}-t^{4}+t^{6}-t^{8}+t^{10}. \end{aligned}$$
(5.14)

All of the [L / M] Pade approximants of Eq. (5.14) with \(L\ge 2\), \(M\ge 2\) and \(L+M\le 10\) yield

$$\begin{aligned}{}[L/M]=t^{2}/(1+t^{2}). \end{aligned}$$
(5.15)

Replacing \(t=1/s\), we obtain [L / M] in terms of s as

$$\begin{aligned}{}[L/M]=1/(1+s^{2}). \end{aligned}$$
(5.16)

By using the inverse Laplace transformation in Eq. (5.16), we obtain the exact solution sin(x).

Example 5.2

Consider Duffing’s equation [2]

$$\begin{aligned} y^{\prime \prime }(x)+y^{\prime }(x)+y(x)+y^{3}(x)= \cos ^{3}x-\sin x \end{aligned}$$
(5.17)

with the initial conditions \(y(0)=1\) and \(y'(0)=0 \) and the exact solution \(y(x)=\cos x\). In order to apply the NHPM to Eq. (5.17), consider the convex homotopy (2.4) as

$$\begin{aligned} (1-p)\big [Y^{\prime \prime }(x)-y_{0}(x)\big ]+p\big [Y^{\prime \prime }(x)+Y^{\prime }(x)+Y(x)+Y^{3}(x)-\cos ^{3}x+\sin x\big ]=0, \end{aligned}$$
(5.18)

which is equivalent to

$$\begin{aligned} Y^{\prime \prime }(x)=y_{0}(x)-p\big [y_{0}(x)+Y'(x)+Y(x)+Y^{3}(x)-\cos ^{3}x+\sin x\big ]. \end{aligned}$$
(5.19)

Denoting \(d^2/\mathrm{d}x^2\) by G, we have \(G^{-1}\) as a two-fold integration. Using the operator G, Eq. (5.19) becomes

$$\begin{aligned} G Y(x)=y_{0}(x)-p\big [y_{0}(x)+Y^{\prime }(x)+Y(x)+Y^{3}(x)-\cos ^{3}x+\sin x\big ]. \end{aligned}$$
(5.20)

Applying the inverse operator \(G^{-1}\) to both sides of Eq. (5.20) and using the initial conditions, we obtain

$$\begin{aligned} Y(x)=1+G^{-1}(y_{0}(x))-pG^{-1}\big [(y_{0}(x)+Y'(x)+Y(x)+Y^{3}(x)-\cos ^{3}x+\sin x)\big ]. \end{aligned}$$
(5.21)

By replacing \(y_{0}(x)=\sum _{n=0}^{\infty }a_{n}x^{n}\) in the above equation, we have

$$\begin{aligned} Y(x)=1+ & {} G^{-1}\left( \sum _{n=0}^{\infty }a_{n}x^{n}\right) \nonumber \\&-pG^{-1}\left[ \left( \sum _{n=0}^{\infty }a_{n}x^{n}+Y'(x)+Y(x)+Y^{3}(x)-\cos ^{3}x+\sin x\right) \right] . \nonumber \\ \end{aligned}$$
(5.22)

Substituting \(Y(x)=\sum _{i=0}^{\infty }p^{i}Y_{i}(x)\) into Eq. (5.21), considering the Maclaurin series of the excitation term

$$\begin{aligned} \cos ^{3}x-sinx\simeq 1-x-3/2x^{2}+1/6x^{3}+7/8x^{4}-1/120x^{5}, \end{aligned}$$
(5.23)

and equating the terms with identical powers of p give

$$\begin{aligned} \begin{aligned} p^{0}:Y_{0}(x)&=1+G^{-1}\Bigg (\sum _{n=0}^{\infty }a_{n}x^{n}\Bigg ), \\ p^{1}:Y_{1}(x)&=-G^{-1}\Bigg [\sum _{n=0}^{\infty }a_{n}x^{n}+Y'_{0}(x)+Y_{0}(x)+Y_{0}^{3}(x) \\&\;\;\quad -(1-x-3/2x^{2}+1/6x^{3}+7/8x^{4}-1/120x^{5})\Bigg ], \\ p^{2}:Y_{2}(x)&=-G^{-1}\big [-Y'_{1}(x)+Y_{1}(x)+3Y_0^{2}(x)Y_1(x)\big ], \\ \vdots \quad&\end{aligned} \end{aligned}$$
(5.24)

Solving the above equation for \(Y_{1}(x)\) leads to the result

$$\begin{aligned} Y_{1}(x)= & {} -1/2(1+a_{0})x^{2}-1/6(1+a_{0}+a_{1})x^{3}-1/24(3+4a_{0}+a_{1}+2a_{2})x^{4} \nonumber \\&+\,\,1/120(1-4a_{1}-2a_{2}-6a_{3})x^{5}+\cdots . \end{aligned}$$
(5.25)

Eliminating \(Y_{1}(x)\) lets the coefficients \(a_{n}\) for \(n=0,1,2,\cdots \) take the following values:

$$\begin{aligned} a_{0}=-1, \quad a_{1}=0, \quad a_{2}=1/2, \quad a_{3}=0, \quad a_{4}=-1/24, \quad \cdots \end{aligned}$$
(5.26)

This implies that

$$\begin{aligned} y(x)=Y_{0}(x) =1-x^{2}/2!+x^{4}/4!+\cdots +(-1)^{n}x^{2n}/(2n)!,\quad n\ge 0, \end{aligned}$$
(5.27)

which is the partial sum of the Taylor series of the exact solution at \(x = 0\). In order to obtain a more accurate solution, we use the truncated series of Eq. (5.27). Consider four terms in y(x) as

$$\begin{aligned} \varphi (x)=1-x^{2}/2!+x^{4}/4!-x^{6}/6!, \end{aligned}$$
(5.28)

which represents the partial sum of the Taylor series of the solution y(x) at \(x=0\). By applying the Laplace transformation to both sides of Eq. (5.28), we have

$$\begin{aligned} L[\varphi (x)]= 1/s-1/s^{3}+1/s^{5}-1/s^{7}. \end{aligned}$$
(5.29)

If \(s=1/t\), then

$$\begin{aligned} L[\varphi (x)]=t-t^{3}+t^{5}-t^{7}. \end{aligned}$$
(5.30)

All of the [L / M] Pade approximants of Eq. (5.30) with \(L\ge 2\), \(M\ge 2\) and \(L+M\le 10\) yield

$$\begin{aligned}{}[L/M]=t/(1+t^{2}). \end{aligned}$$
(5.31)

Replacing \(t=1/s\), we obtain [L / M] in terms of s as

$$\begin{aligned}{}[L/M]=s/(1+s^{2}). \end{aligned}$$
(5.32)

By applying the inverse Laplace transformation to Eq. (5.32), we obtain the exact solution cos(x).

6 Conclusion

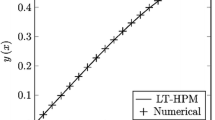
In this paper, we presented the NHPM to solve nonlinear Duffing’s equations, which yielded the Maclaurin series of the true solution. In order to obtain a more accurate solution, we applied the Laplace transformation to the truncated Maclaurin series and then the Padé approximation, as shown in the examples. In this method, there was no need to calculate He’s polynomials. Therefore, the number of computations in the NHPM was less than that in the HMP. The obtained results indicated that the method was very efficient and simple and led to the exact solution of nonlinear Duffing’s equations.