An Efficient Method for Solving Systems of Linear Ordinary and Fractional Differential Equations

Abstract

This paper presents a reliable approach for solving linear systems of ordinary and fractional differential equations. First, the FDEs or ODEs of a system with initial conditions to be solved are transformed to Volterra integral equations. Then Taylor expansion for the unknown function and integration method are employed to reduce the resulting integral equations to a new system of linear equations for the unknown and its derivatives. The fractional derivatives are considered in the Riemann–Liouville sense. Some numerical illustrations are given to demonstrate the effectiveness of the proposed method in this paper.

1 Introduction

Fractional differential equations have gained considerable importance due to their varied applications as well as many problems in Physics, Chemistry, Biology, Applied Sciences and Engineering are modelled mathematically by systems of ordinary and fractional differential equations, e.g. series circuits, mechanical systems with several springs attached in series lead to a system of differential equations. On the other hand, motion of an elastic column fixed at one end and loaded at the other can be formulated in terms of a system of fractional differential equations [1, 2, 4, 8, 10, 11, 16–22, 24–26, 29]. Most realistic systems of fractional differential equations do not have exact analytic solutions, so approximation and numerical techniques must be used. Recently, Atanackovic and Stankovic [1] introduced the system of fractional differential equations into the analysis of lateral motion of an elastic column fixed at one end and loaded at the other. Daftardar-Gejji and Babakhani [5] studied the system of linear fractional differential equations with constant coefficients using methods of linear algebra and proved existence and uniqueness theorems for the initial value problem. Furthermore, a large amount of literatures were developed concerning the application of fractional systems of differential equations in nonlinear dynamics [7, 9, 13, 14].

Xian-Fang Li [12] has proposed an approximate method for solving linear ordinary differential equations which can also be considered for linear fractional differential equations in view of Riemann–Liouville fractional derivatives. In this paper, based on the proposed method in [12], we propose a novel approach for solving a system of ordinary and fractional differential equations. In this method, the FDEs or ODEs of a system are transformed to Volterra integral equations and then Taylor expansion for the unknown function and integration method are employed to reduce the resulting integral equations to a new system of linear equations for the unknown and its derivatives. In this method, the accuracy of approximate solutions depends on the order of the Taylor expansion. Clearly, for small orders of Taylor expansion, high accuracy is not expected for approximate solutions and conversely, when taking a larger order of Taylor expansion, more accuracy is expected for the approximate results.

This paper is arranged as follows. In Sect. 2, we first recall some necessary definitions and mathematical preliminaries of the fractional calculus theory used throughout the paper. This is particularly important with fractional derivatives because there are several definitions available and they have some fundamental differences. Section 3 deals with the analysis of system of linear ordinary differential equations. In Sect. 4, we analyse system of linear fractional differential equations. In Sect. 5, we discuss convergence of the method. In Sect. 6, we investigate several numerical examples, which demonstrate the effectiveness of our new approach. In Sect. 7, we summarize our findings.

2 Preliminaries and Basic Definitions

We give some basic definitions and properties of the fractional calculus theory, which are used further in this paper.

Definition 2.1

A real function $f(x),\ \ x>0$, is said to be in the space $C_{\mu },\ \ \mu \in {R}$ if there exists a real number $p(>\mu )$, such that $f(x)=x^{p}f_{1}(x)$, where $f_{1}(x)\in {C[0,\infty )}$, and it is said to be in the space $C_{\mu }^{m}$ iff $f^{(m)}\in {C_{\mu }}, \ \ m\in {N}$.

Definition 2.2

The Riemann–Liouville fractional integral operator of order $\alpha \ge 0$, of a function $f\in {C_{\mu }}, \ \ \mu \ge -1$, is defined as

$$\begin{aligned} \displaystyle&J^{\alpha }f(x)=\frac{1}{\Gamma (\alpha )} \int _{0}^{x}(x-t)^{\alpha -1}f(t)dt, \ \ \alpha >0, \ \ x>0 , \end{aligned}$$

(1)

$$\begin{aligned} \displaystyle&J^{0}f(x)=f(x). \end{aligned}$$

(2)

Properties of the operator $J^\alpha$ can be found in [15, 22, 23], we mention only the following:

For $f\in {C_{\mu }}, \ \ \mu \ge -1$, $\alpha$, $\beta \ge 0$ and $\gamma >-1$:

$$\begin{aligned} J^{\alpha }J^{\beta }f(x)= & {} J^{\alpha +\beta }f(x), \end{aligned}$$

(3)

$$\begin{aligned} J^{\alpha }J^{\beta }f(x)= & {} J^{\beta }J^{\alpha }f(x), \end{aligned}$$

(4)

$$\begin{aligned} J^{\alpha }x^{\gamma }= & {} \frac{\Gamma (\gamma +1)}{\Gamma (\alpha +\gamma +1)}x^{\alpha +\gamma }. \end{aligned}$$

(5)

Definition 2.3

The fractional derivative of f(x) in the Caputo sense is defined as

$$\begin{aligned} D_{*}^{\alpha }f(x)=J^{m-\alpha }\left( \frac{d^{m}}{dx^{m}}f(x)\right) =\frac{1}{\Gamma (m-\alpha )}\int _{0}^{x}(x-t)^{m-\alpha -1}f^{(m)}(t)dt, \end{aligned}$$

(6)

for $m-1<\alpha \le m, \ \ m\in {N}, \ \ x>0, \ \ f\in {C_{-1}^{m}}$.

Definition 2.4

The fractional derivative of f(x) in the Riemann–Liouville sense is defined as

$$\begin{aligned} D^{\alpha }f(x)=\frac{d^{m}}{dx^{m}}\left( J^{m-\alpha }f(x)\right) , \end{aligned}$$

(7)

for $m-1<\alpha \le m, \ \ m\in {N}, \ \ x>0, \ \ f\in {C_{-1}^{m}}$.

3 System of Linear Ordinary Differential Equations

Consider the following system of ordinary differential equations:

$$\begin{aligned} y_{i}'(x)+\sum _{j=1}^{n}{b_{ij}(x)y_{j}(x)}=f_{i}(x), \ \ y_{i}(0)=c_{i}, \ \ i=1,\ldots ,n , \end{aligned}$$

(8)

where $b_{ij}(x)$ and $f_{i}(x)$ are known functions, satisfying $b_{ij}(x), \ f_{i}(x)\in {C(I)}$, I is the interval of interest. We focus our attention to first-order linear ODEs, and for higher-order linear ODEs, the method is completely similar and omitted here.

Integrating both side of Eq. (8) from 0 to x and using the initial conditions, we obtain

$$\begin{aligned} y_{i}(x)+\int _{0}^{x}\sum _{j=1}^{n}{b_{ij}(t)y_{j}(t)}dt =c_{i}+\int _{0}^{x}f_{i}(t)dt, \ \ i=1,\ldots ,n . \end{aligned}$$

(9)

Hence, we transformed system of ODEs (8) under initial conditions to a system of Volterra integral equations with continuous kernels. To approximately solve the system of Volterra integral equations, we reduce the resulting Volterra integral equations to a new system of linear equations in the unknown function and its derivatives.

To achieve this end, we employ the Taylor expansion for the unknown function $y_{j}(t)$ at x

$$\begin{aligned} y_{j}(t)=y_{j}(x)+y_{j}'(x)(t-x)+\cdots +\frac{1}{m!} y_{j}^{(m)}(x)(t-x)^{m}+R_{j,m}(t,x), \end{aligned}$$

(10)

where $R_{j,m}(t,x)$ denotes the Lagrange remainder

$$\begin{aligned} R_{j,m}(t,x)=\frac{y_{j}^{(m+1)}(\delta _{j})}{(m+1)!}(t-x)^{m+1}, \end{aligned}$$

(11)

for some point $\delta _{j}$ between x and t. In general, the Lagrange remainder $R_{j,m}(t,x)$ becomes sufficiently small when m is large enough. In particular, if the desired solution $y_{j}(t)$ is a polynomial of the degree equal to or less than m, then $R_{j,m}(t,x)=0$. In other words, the obtained approximate solution of Eq. (9) is just the desired exact solution.

Substituting (10) for $y_{j}(t)$ in the integrand into (9) leads to

$$\begin{aligned} y_{i}(x)+\sum _{j=1}^{n}\sum _{k=0}^{m}\frac{(-1)^k}{k!}y_{j}^{(k)}(x)\int _{0}^{x}{b_{ij}(t)(x-t)^{k}}dt=g_{i}(x), \ \ i=1,\ldots ,n . \end{aligned}$$

(12)

where

$$\begin{aligned} g_{i}(x)=c_{i}+\int _{0}^{x}f_{i}(t)dt, \end{aligned}$$

(13)

and in the above derivation, the Lagrange remainder has been dropped due to a sufficiently small truncated error. Moreover, the notation $y_{j}^{(0)}=y_{j}(x)$ is adopted. In Eq. (12) $y_{j}^{(k)}(x)$, for $k=0,\ldots ,m$ are unknown functions. In order to obtain these unknown functions, we understand the above equation as a linear equation for $y_{j}(x)$ and its derivatives up to m. Consequently, other m independent linear equations for $y_{j}(x)$ and its derivatives up to m are needed. These equations can be obtained by integration of both sides of Eq. (9) m times as follows:

$$\begin{aligned} \int _{0}^{x}{\frac{(x-t)^{l-1}}{(l-1)!}y_{i}(t)}dt +\sum _{j=1}^{n}\int _{0}^{x} \frac{(x-t)^l}{l!}{b_{ij}(t)y_{j}(t)}dt=g_{i}^{(l)}(x) , \ \ l=1,\ldots ,m ,\nonumber \\ \end{aligned}$$

(14)

where

$$\begin{aligned} g_{i}^{(l)}(x)=\int _{0}^{x}\frac{(x-t)^{l-1}}{(l-1)!}c_{i}dt +\int _{0}^{x}\frac{(x-t)^l}{l!}f_{i}(t)dt . \end{aligned}$$

(15)

Substituting (10) for $y_{j}(t)$ in the integrand into (14), we have

$$\begin{aligned}&\sum _{k=0}^{m}\frac{(-1)^k}{k!}y_{i}^{(k)}(x) \int _{0}^{x}{\frac{(x-t)^{k+l-1}}{(l-1)!}}dt\nonumber \\&\quad +\sum _{j=1}^{n}\sum _{k=0}^{m}\frac{(-1)^k}{k!}y_{j}^{(k)}(x) \int _{0}^{x}\frac{(x-t)^{k+l}}{l!}{b_{ij}(t)}dt=g_{i}^{(l)}(x) , \end{aligned}$$

(16)

for $l=1,\ldots ,m .$

Hence, Eqs. (12) and (16) form a system of linear equations for the unknowns $y_{j}(x)$ and its derivatives up to m. The above system composed of Eqs. (12) and (16) can be written in compact form as

$$\begin{aligned} C(x)Y(x)=G(x), \end{aligned}$$

(17)

where

$$\begin{aligned} C(x)= & {} \left[ \begin{array}{ccccccccccc} c_{10}^{10}(x)&{}\cdots &{}c_{n0}^{10}(x)&{}\cdots &{}c_{1k}^{10}(x)&{}\cdots &{}c_{nk}^{10}(x)&{}\cdots &{}c_{1m}^{10}(x)&{}\cdots &{}c_{nm}^{10}(x)\\ \vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots \\ c_{10}^{n0}(x)&{}\cdots &{}c_{n0}^{n0}(x)&{}\cdots &{}c_{1k}^{n0}(x)&{}\cdots &{}c_{nk}^{n0}(x)&{}\cdots &{}c_{1m}^{n0}(x)&{}\cdots &{}c_{nm}^{n0}(x)\\ \vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots \\ c_{10}^{1l}(x)&{}\cdots &{}c_{n0}^{1l}(x)&{}\cdots &{}c_{1k}^{1l}(x)&{}\cdots &{}c_{nk}^{1l}(x)&{}\cdots &{}c_{1m}^{1l}(x)&{}\cdots &{}c_{nm}^{1l}(x)\\ \vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots \\ c_{10}^{1m}(x)&{}\cdots &{}c_{n0}^{1m}(x)&{}\cdots &{}c_{1k}^{1m}(x)&{}\cdots &{}c_{nk}^{1m}(x)&{}\cdots &{}c_{1m}^{1m}(x)&{}\cdots &{}c_{nm}^{1m}(x)\\ \vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots \\ c_{10}^{nm}(x)&{}\cdots &{}c_{n0}^{nm}(x)&{}\cdots &{}c_{1k}^{nm}(x)&{}\cdots &{}c_{nk}^{nm}(x)&{}\cdots &{}c_{1m}^{nm}(x)&{}\cdots &{}c_{nm}^{nm}(x)\\ \end{array} \right] , \end{aligned}$$

(18)

$$\begin{aligned} G(x)= & {} \left[ \begin{array}{ccccccccccc} g_{1}(x),\ldots ,g_{n}(x),\ldots ,g_{1}^{(l)}(x),\ldots ,g_{n}^{(l)}(x),\ldots ,g_{1}^{(m)}(x),\ldots ,g_{n}^{(m)}(x) \end{array} \right] ^{T} ,\nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned} Y(x)= & {} \left[ \begin{array}{ccccccccccc} y_{1}(x),\ldots ,y_{n}(x),\ldots ,y_{1}^{(k)}(x),\ldots ,y_{n}^{(k)}(x),\ldots ,y_{1}^{(m)}(x),\ldots ,y_{n}^{(m)}(x) \end{array} \right] ^{T} ,\nonumber \\ \end{aligned}$$

(20)

where in (18), the first n rows refer to coefficients of $y_{j}^{(k)}(x)$ in Eq. (12) for $j=1,\ldots ,n$, $k=0,\ldots ,m$ and the other rows refer to coefficients of $y_{j}^{(k)}(x)$ in Eq. (16) for $j=1,\ldots ,n$, $k=0,\ldots ,m$. Application of Cramer’s rule to the resulting new system yields an approximate solution of Eq. (8). We note that not only $y_{j}(x)$ but also $y_{j}^{(k)}(x)$, for $j=1,\ldots ,n$, $k=0,\ldots ,m$, are determined by solving the resulting new system but in effect, it is $y_{j}(x)$ that we want to look for.

4 System of Fractional Differential Equations

Consider the following system of fractional differential equations:

$$\begin{aligned} y_{i}^{(\alpha _{i})}(x)+\sum _{j=1}^{n}{b_{ij}(x)y_{j}(x)}=f_{i}(x), \ \ y_{i}(0)=c_{i}, \ \ i=1,\ldots ,n , \end{aligned}$$

(21)

where $b_{ij}(x)$ and $f_{i}(x)$ are known functions, satisfying $b_{ij}(x), \ f_{i}(x)\in {C(I)}$, and I is the interval of interest. In Eq. (21), $y_{i}^{(\alpha _{i})}(x)=D^{\alpha _{i}}y_{i}(x)$ denotes Riemann–Liouville fractional derivative of order $\alpha _{i}$ and here we assume $0<\alpha _{i}\le 1$, $i=1,\ldots ,n$.

Based on definition (2.4), Eq. (21) can be rewritten as

$$\begin{aligned} \frac{d}{dx}\left( J^{1-\alpha _{i}}y_{i}(x)\right) +\sum _{j=1}^{n}{b_{ij}(x)y_{j}(x)}=f_{i}(x), \ \ i=1,\ldots ,n , \end{aligned}$$

(22)

or equivalently using definition (2.2), we have

$$\begin{aligned} \frac{d}{dx}\left( \frac{1}{\Gamma (1-\alpha _{i})}\int _{0}^{x}(x-t)^{-\alpha _{i}}y_{i}(t)dt\right) +\sum _{j=1}^{n}{b_{ij}(x)y_{j}(x)}=f_{i}(x), \ \ i=1,\ldots ,n .\nonumber \\ \end{aligned}$$

(23)

By integrating both sides of Eq. (23) from 0 to x, we obtain

$$\begin{aligned} \frac{1}{\Gamma (1-\alpha _{i})}\int _{0}^{x}(x-t)^{-\alpha _{i}}y_{i}(t)dt+\int _{0}^{x}\sum _{j=1}^{n}{b_{ij}(t)y_{j}(t)}dt=\int _{0}^{x}f_{i}(t)dt, \ i=1,\ldots ,n .\nonumber \\ \end{aligned}$$

(24)

To solve the above equation similar proposed method in Sect. 3, substituting (10) for $y_{i}(t)$ in the integrand into (24) leads to

$$\begin{aligned}&\frac{1}{\Gamma (1-\alpha _{i})}\sum _{k=0}^{m}\frac{(-1)^k}{k!}y_{i}^{(k)}(x)\int _{0}^{x}(x-t)^{k-\alpha _{i}}dt\nonumber \\&\quad +\sum _{j=1}^{n}\sum _{k=0}^{m} \frac{(-1)^k}{k!}y_{j}^{(k)}(x)\int _{0}^{x}{b_{ij}(t)}(x-t)^{k}dt= g_{(i)}(x), \end{aligned}$$

(25)

where

$$\begin{aligned} g_{(i)}(x)=\int _{0}^{x}f_{i}(t)dt, \end{aligned}$$

(26)

for $i=1,\ldots ,n$.

In Eq. (25), $y_{i}^{(k)}(x)$, for $k=0,\ldots ,m$ are unknown functions. In order to obtain these unknown functions, we understand the above equation as a linear equation for $y_{i}(x)$ and its derivatives up to m. Consequently, other m independent linear equations for $y_{i}(x)$ and its derivatives up to m are needed.

To achieve this end, we continue to integrate both sides of Eq. (24) m times from 0 to x, and get

$$\begin{aligned}&\frac{1}{\Gamma (1-\alpha _{i})}\int _{0}^{x}\int _{t}^{x}\frac{(x-s)^{l-1}}{(l-1)!}\frac{y_{i}(t)}{(s-t)^{\alpha _{i}}}dsdt\nonumber \\&\quad +\sum _{j=1}^{n}\int _{0}^{x}\frac{(x-t)^{l}}{(l)!}{b_{ij}(t)y_{j}(t)}dt=g_{(i)}^{(l)}(x), \end{aligned}$$

(27)

where

$$\begin{aligned} g_{(i)}^{(l)}(x)=\int _{0}^{x}\frac{(x-t)^{l}}{(l)!}f_{i}(t)dt, \end{aligned}$$

(28)

for $i=1,\ldots ,n$, $l=1,\ldots ,m$.

Substituting (10) for $y_{i}(t)$ in the integrand into (27), we obtain

$$\begin{aligned}&\frac{1}{\Gamma (1-\alpha _{i})}\sum _{k=0}^{m}\frac{(-1)^k}{k!}y_{i}^{(k)}(x)\int _{0}^{x}\int _{t}^{x}\frac{(x-s)^{l-1}}{(l-1)!}(x-t)^{k}(s-t)^{-\alpha _{i}}dsdt\nonumber \\&\quad +\sum _{j=1}^{n}\sum _{k=0}^{m}\frac{(-1)^k}{k!}y_{i}^{(k)}(x)\int _{0}^{x}\frac{(x-t)^{k+l}}{(l)!}{b_{ij}(t)}dt=g_{(i)}^{(l)}(x), \end{aligned}$$

(29)

for $i=1,\ldots ,n$, $l=1,\ldots ,m$.

Hence, Eqs. (25) and (29) form a system of linear equations for the unknowns $y_{i}(x)$ and its derivatives up to m. The above system composed of Eqs. (25) and (29) can be written in compact form as

$$\begin{aligned} C(x)Y(x)=G(x), \end{aligned}$$

(30)

where

$$\begin{aligned} C(x)= & {} \left[ \begin{array}{ccccccccccc} c_{10}^{10}(x)&{}\cdots &{}c_{n0}^{10}(x)&{}\cdots &{}c_{1k}^{10}(x)&{}\cdots &{}c_{nk}^{10}(x)&{}\cdots &{}c_{1m}^{10}(x)&{}\cdots &{}c_{nm}^{10}(x)\\ \vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots \\ c_{10}^{n0}(x)&{}\cdots &{}c_{n0}^{n0}(x)&{}\cdots &{}c_{1k}^{n0}(x)&{}\cdots &{}c_{nk}^{n0}(x)&{}\cdots &{}c_{1m}^{n0}(x)&{}\cdots &{}c_{nm}^{n0}(x)\\ \vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots \\ c_{10}^{1l}(x)&{}\cdots &{}c_{n0}^{1l}(x)&{}\cdots &{}c_{1k}^{1l}(x)&{}\cdots &{}c_{nk}^{1l}(x)&{}\cdots &{}c_{1m}^{1l}(x)&{}\cdots &{}c_{nm}^{1l}(x)\\ \vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots \\ c_{10}^{1m}(x)&{}\cdots &{}c_{n0}^{1m}(x)&{}\cdots &{}c_{1k}^{1m}(x)&{}\cdots &{}c_{nk}^{1m}(x)&{}\cdots &{}c_{1m}^{1m}(x)&{}\cdots &{}c_{nm}^{1m}(x)\\ \vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots &{}\ddots &{}\vdots \\ c_{10}^{nm}(x)&{}\cdots &{}c_{n0}^{nm}(x)&{}\cdots &{}c_{1k}^{nm}(x)&{}\cdots &{}c_{nk}^{nm}(x)&{}\cdots &{}c_{1m}^{nm}(x)&{}\cdots &{}c_{nm}^{nm}(x)\\ \end{array} \right] , \end{aligned}$$

(31)

$$\begin{aligned} G(x)= & {} \left[ \begin{array}{ccccccccccc} g_{1}(x),\ldots ,g_{n}(x),\ldots ,g_{1}^{(l)}(x),\ldots ,g_{n}^{(l)}(x),\ldots ,g_{1}^{(m)}(x),\ldots ,g_{n}^{(m)}(x) \end{array} \right] ^{T},\nonumber \\ \end{aligned}$$

(32)

$$\begin{aligned} Y(x)= & {} \left[ \begin{array}{ccccccccccc} y_{1}(x),\ldots ,y_{n}(x),\ldots ,y_{1}^{(k)}(x),\ldots ,y_{n}^{(k)}(x),\ldots ,y_{1}^{(m)}(x),\ldots ,y_{n}^{(m)}(x) \end{array} \right] ^{T} ,\nonumber \\ \end{aligned}$$

(33)

where in (31), the first n rows refer to coefficients of $y_{i}^{(k)}(x)$ in Eq. (25) for $i=1,\ldots ,n$, $k=0,\ldots ,m$ and the other rows refer to coefficients of $y_{i}^{(k)}(x)$ in Eq. (29) for $i=1,\ldots ,n$, $k=0,\ldots ,m$. Application of Cramer’s rule to the resulting new system under the solvability condition of this system yields an approximate solution of Eq. (21). We note that not only $y_{i}(x)$ but also $y_{i}^{(k)}(x)$, for $i=1,\ldots ,n$, $k=0,\ldots ,m$, are determined by solving the resulting new system but in effect, it is $y_{i}(x)$ that we want to look for.

5 Error Analysis

Since in our proposed method in this paper for solving systems of both linear ordinary and fractional differential equations, finally we achieve integral equations, hence the error analysis of the convergence of approximate solutions derived from the integration method here is completely similar and applicable with the proposed error analysis in [27].

6 Numerical Examples

Several authors in their papers such as Daftardar-Gejji and Babakhani [5], Bonilla et al. [3], Duan et al. [6] and Wang et al. [28] have investigated various approaches for solving systems of linear fractional differential equations and mentioned some of their applications which show the importance of these kinds of problems. Also, the differential equations involving the Riemann-Liouville differential operators of fractional order $0<\alpha <1$ appear to be more important in modelling several physical phenomena [28]. Therefore, in this work, we studied a method for solving systems of linear ordinary and fractional differential equations of order $0<\alpha <1$. Since our purpose is to demonstrate the effectiveness of the proposed method in this paper for both systems of ODEs and FDEs, in this section, we have chosen three specific examples of order $0<\alpha <1$ where the exact solution is known for $\alpha =1$. All calculations were performed using the MATHEMATICA software package.

Example 1

Consider the following linear fractional system

$$\begin{aligned} \left\{ \begin{array}{c} {\displaystyle y_{1}^{(\alpha _{1})}(x)+y_{2}(x)=1, \ \ 0<\alpha _{1}\le 1}\\ {\displaystyle y_{2}^{(\alpha _{2})}(x)-y_{1}(x)=4, \ \ 0<\alpha _{2}\le 1} \end{array} \right. \end{aligned}$$

(34)

subject to the initial conditions

$$\begin{aligned} y_{1}(0)=1, \ \ y_{2}(0)=-3 . \end{aligned}$$

(35)

The exact solution, when $\alpha _{1}=\alpha _{2}=1$, is

$$\begin{aligned} y_{1}(x)= & {} 5 \cos x + 4 \sin x - 4, \end{aligned}$$

(36)

$$\begin{aligned} y_{2}(x)= & {} -4 \cos x + 5 \sin x +1. \end{aligned}$$

(37)

The values of $\alpha _{1}=\alpha _{2}=1$ are the only case for which we know the exact solution, and using our proposed method in Sect. 3, we can evaluate the approximate solutions of $y_{1}(x)$ and $y_{2}(x)$ when $\alpha _{1}=\alpha _{2}=1$. Figures 1, 2 and 3 show the approximate solutions of $y_{1}(x)$ and $y_{2}(x)$ when $\alpha _{1}=\alpha _{2}=1$ for $m=1$, 2 and 3, respectively, in Taylor expansion in comparison with the exact solutions. Our approximate solutions are in good agreement with the exact values. Of course, the accuracy can be improved as m is raised in Taylor expansion.

Fig. 1

The exact solutions (solid) versus the approximate solutions (dashed) for $m=1$

Fig. 2

The exact solutions (solid) versus the approximate solutions (dashed) for $m=2$

Fig. 3

The exact solutions (solid) versus the approximate solutions (dashed) for $m=3$

Also, we calculated the approximate solutions for $m=4$ and 5 in Taylor expansion which due to the graphs of the approximate solutions, which coincide with the graph of the exact solution, we cannot use the graphs for comparing the approximate solutions with the exact solution. Consequently, we have to employ tables for comparing errors when m is increased. The absolute errors at thirty equidistant points in the interval [0, 3] are shown in Tables 1 and 2, taking $m=4, 5$, respectively. In Tables 1 and 2, E1 and E2 show the absolute errors of $y_{1}$ and $y_{2}$, respectively.

Table 1 Absolute errors of Example 1 for $m=4$

Table 2 Absolute errors of Example 1 for $m=5$

A considerable point is that the accuracy of the approximate solutions is improved remarkably when we take larger values of m as well as the runtime computations are mutually increased. In this test case the calculation times for $m=1,\ldots ,5$ measured in seconds are 1, 4, 14, 32 and 48, respectively in a computer with hardware configuration: Intel Core i5 CPU 1.33 GHz, 4 GB of RAM and 64-bit Operating System (Windows 7).

Setting $\alpha _{1}=\alpha _{2}=\frac{1}{2}$ and applying our proposed method in Sect. 4, we can evaluate the solutions of $y_{1}(x)$ and $y_{2}(x)$. Figure 4 shows the solutions of $y_{1}(x)$ and $y_{2}(x)$ when $\alpha _{1}=\alpha _{2}=\frac{1}{2}$ for $m=2$ in Taylor expansion.

Fig. 4

$\alpha _1=\alpha _2=0.5$

Example 2

Consider the following linear fractional system

$$\begin{aligned} \left\{ \begin{array}{c} {\displaystyle y_{1}^{(\alpha _{1})}(x)-y_{1}(x)-3y_{2}(x)=1, \ \ 0<\alpha _{1}\le 1} \\ {\displaystyle y_{2}^{(\alpha _{2})}(x)-3y_{1}(x)-y_{2}(x)=4, \ \ 0<\alpha _{2}\le 1} \end{array} \right. \end{aligned}$$

(38)

subject to the initial conditions

$$\begin{aligned} y_{1}(0)=1, \ \ y_{2}(0)=-3 . \end{aligned}$$

(39)

The exact solution, when $\alpha _{1}=\alpha _{2}=1$, is

$$\begin{aligned} y_{1}(x)= & {} \frac{1}{8}e^{-2x}(22-11e^{2x}-3e^{6x}), \end{aligned}$$

(40)

$$\begin{aligned} y_{2}(x)= & {} \frac{1}{8}e^{-2x}(-22+e^{2x}-3e^{6x}). \end{aligned}$$

(41)

Using our proposed method in Sect. 3, we can evaluate the approximate solutions of $y_{1}(x)$ and $y_{2}(x)$ when $\alpha _{1}=\alpha _{2}=1$. Figures 5 and 6 show the approximate solutions of $y_{1}(x)$ and $y_{2}(x)$ when $\alpha _{1}=\alpha _{2}=1$ for $m=3$ and $m=4$, respectively, in Taylor expansion in comparison with the exact solutions. Our approximate solutions are in good agreement with the exact values. Of course it is clear that the accuracy can be improved as m is raised in Taylor expansion and in this test case for $m=4,\ldots$ the graphs of the approximate solutions coincide with the graphs of the exact solutions and there is no deviation to exact solution.

Fig. 5

The exact solutions (solid) versus the approximate solutions (dashed) for $m=3$

Fig. 6

The exact solutions (solid) versus the approximate solutions (dashed) for $m=4$

Fig. 7

Variations of the errors between several approximations of $y_{1}(x)$ and the corresponding exact values

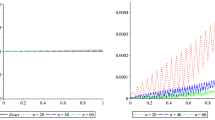
In order to show the variation of the accuracy of approximations, the errors, between several approximate solutions and the exact values are plotted in Figs. 7 and 8 for $y_{1}(x)$ and $y_{2}(x)$, respectively.

Fig. 8

Variations of the errors between several approximations of $y_{2}(x)$ and the corresponding exact values

Setting $\alpha _{1}=\alpha _{2}=\frac{1}{2}$ and applying our proposed method in Sect. 4, we can evaluate the solutions of $y_{1}(x)$ and $y_{2}(x)$. Figure 9 shows the solutions of $y_{1}(x)$ and $y_{2}(x)$ when $\alpha _{1}=\alpha _{2}=\frac{1}{2}$ for $m=3$ in Taylor expansion.

Fig. 9

$\alpha _1=\alpha _2=0.5$

Example 3

Consider the following linear fractional system

$$\begin{aligned} \left\{ \begin{array}{c} {\displaystyle y_{1}^{(\alpha _{1})}(x)+2y_{1}(x)=\frac{3}{2}, \ \ 0<\alpha _{1}\le 1} \\ {\displaystyle y_{2}^{(\alpha _{2})}(x)-4y_{2}(x)=\frac{5}{2}, \ \ 0<\alpha _{2}\le 1} \end{array} \right. \end{aligned}$$

(42)

subject to the initial conditions

$$\begin{aligned} y_{1}(0)=-2, \ \ y_{2}(0)=-1 . \end{aligned}$$

(43)

The exact solution, when $\alpha _{1}=\alpha _{2}=1$, is

$$\begin{aligned} y_{1}(x)= & {} \frac{1}{4}e^{-2x}(-11+3e^{2x}), \end{aligned}$$

(44)

$$\begin{aligned} y_{2}(x)= & {} \frac{1}{8}(-5-3e^{4x}). \end{aligned}$$

(45)

Using our proposed method in Sect. 3, we can evaluate the approximate solutions of $y_{1}(x)$ and $y_{2}(x)$ when $\alpha _{1}=\alpha _{2}=1$. Figures 10 and 11 show the approximate solutions of $y_{1}(x)$ and $y_{2}(x)$ when $\alpha _{1}=\alpha _{2}=1$ for $m=3$ and $m=4$, respectively, in Taylor expansion in comparison with the exact solutions. Our approximate solutions are in good agreement with the exact values. Of course the accuracy can be improved as m is raised in Taylor expansion which in this example for $m=4,\ldots$ the graphs of the approximate solutions coincide with the graphs of the exact solutions.

Fig. 10

The exact solutions (solid) versus the approximate solutions (dashed) for $m=3$

Fig. 11

The exact solutions (solid) versus the approximate solutions (dashed) for m = 4

In order to show the variation of the accuracy of approximations, the errors, between several approximate solutions and the exact values are plotted in Figs. 12 and 13 for $y_{1}(x)$ and $y_{2}(x)$, respectively.

Fig. 12

Variations of the errors between several approximations of $y_{1}(x)$ and the corresponding exact values

Fig. 13

Variations of the errors between several approximations of $y_{2}(x)$ and the corresponding exact values

Setting $\alpha _{1}=\alpha _{2}=\frac{1}{2}$ and applying our proposed method in Sect. 4, we can evaluate the solutions of $y_{1}(x)$ and $y_{2}(x)$. Figure 14 shows the solutions of $y_{1}(x)$ and $y_{2}(x)$ when $\alpha _{1}=\alpha _{2}=\frac{1}{2}$ for $m=3$ in Taylor expansion.

Fig. 14

$\alpha _1=\alpha _2=0.5$

7 Conclusion

In this paper, we have proposed an approximate method suitable for both systems of linear ordinary and fractional differential equations. In the method, first, the FDEs or ODEs of a system with initial conditions to be solved have transformed to Volterra integral equations. Then Taylor expansion for the unknown function and integration method have employed to reduce the resulting integral equations to a new system of linear equations for the unknown and its derivatives. Application of Cramer’s rule the resulting new system has been solved. We must emphasize that the method can only be used to solve linear systems of ODEs or FDEs.