1 Introduction

Let \(\mathbb {D}=\left\{ z:\left| z\right| <1\right\} \) denote the unit disc. Let \(\mathcal {A}\) be the class of all analytic functions \(f\) in the open unit disc \(\mathbb {D}\) with normalization \(f(0)=0\), \(f^{\prime }(0)=1\) and let \(\mathcal {S}\) denote the subset of \(\mathcal {A}\) which is composed of univalent functions. We say that \(f\) is subordinate to \(F\) in \(\mathbb {D}\), written as \(f\prec F\), if and only if \(f(z)=F(\omega (z))\) for some analytic function \(\omega \), \(\omega (0)=0\), \(\left| \omega (z)\right| <1\), \(z\in \mathbb {D}\). The idea of subordination was used for defining many classes of functions studied in geometric function theory. Let us recall

$$\begin{aligned} {\mathcal {S}}^{*}[\varphi ]&:= \left\{ f\in {\mathcal {A}}:\ \frac{ zf^{\prime }(z)}{f(z)}\prec \varphi (z),\ z\in \mathbb {D}\right\} ,\end{aligned}$$
(1.1)
$$\begin{aligned} {\mathcal {K}}[\varphi ]&:= \left\{ f\in {\mathcal {A}}:\ \left[ 1+\frac{ zf^{\prime \prime }(z)}{f^{\prime }(z)}\right] \prec \varphi (z),\ z\in \mathbb {D}\right\} , \end{aligned}$$
(1.2)

where \(\varphi \) is analytic in \(\mathbb {D}\) with \(\varphi (0)=1\). For \( \varphi (z)=(1+z)/(1-z)\) we obtain the well-known classes \({\mathcal {S}} ^{*}\), \({\mathcal {K}}\) of starlike and convex functions, respectively. A lot of classes of functions have been defined by exchanging the function \( \varphi \) in (1.1) or in (1.2) by other functions giving very often an interesting image of the unit circle. If \(\varphi (z)=(1+(1-2\alpha )z)/(1-z)\), \(\alpha <1\), then \(\varphi (\mathbb {D})\) is the half plane \( \mathfrak {Re}(w)>\alpha \), and the sets (1.1), (1.2) become the classes \({\mathcal {S}}^{*}(\alpha )\) of starlike or \({\mathcal {K}} (\alpha )\) of convex functions of order \(\alpha \), respectively, introduced in [14]. If \(\varphi (z)=(1+Az)(1+Bz)\), \(-1<B<A\le 1\), then \( \varphi (\mathbb {D})\) is a disc, and the classes (1.1), (1.2) become the classes considered in [6, 7]. The class of strongly starlike functions of order \(\beta \), \(0<\beta \le 1\), see [20] is obtained from (1.1) with \(\varphi (z)=\left( (1+z)/(1-z)\right) ^{\beta }\). Then \(\varphi (\mathbb {D})\) is an angle. If

$$\begin{aligned} \varphi (z)=1+\frac{2}{\pi ^{2}}\left( \log \frac{1+\sqrt{z}}{1-\sqrt{z}} \right) ^{2}, \end{aligned}$$

then \(\varphi (\mathbb {D})\) is a parabolic region, and the set (1.2) is a class of the so-called uniformly convex function introduced in [5, 11, 15]. Close related classes, connected with a hyperbola or with an ellipse were considered in [8–10]. If \( \varphi (z)=\sqrt{1+z}\), where the branch of the square root is chosen in order that \(\sqrt{1}=1\), then \(\varphi (\mathbb {D})\) is interior of the right loop of the Lemniscate of Bernoulli and the class (1.1) becomes a class considered in [17, 19]. The function

$$\begin{aligned} \varphi (z)=\left( \frac{1+z}{1+(1-b)/bz}\right) ^{1/\alpha } \end{aligned}$$

in (1.1) forms a class considered in [13]. In the above and in other not cited here cases the function \(\varphi \) is a convex univalent function. In [12] Ma and Minda proved some general results for classes (1.1) and (1.2), where \(\varphi \) is assumed to be univalent, \(\varphi (\mathbb {D})\) is assumed to be symmetric with respect to real axis and starlike with respect to \(\varphi (0)=1\). The problems in the classes defined by (1.1) and by (1.2) become much more difficult if the function \(\varphi \) is not univalent. In [18] the second author defined the class \(\mathcal {SL}\) of shell-like functions as the set of functions \(f\in \mathcal {A}\) satisfying the condition that

$$\begin{aligned} \frac{zf^{\prime }(z)}{f(z)}\prec \widetilde{p}(z),\quad z\in \mathbb {D}, \end{aligned}$$

where

$$\begin{aligned} \widetilde{p}(z)=\frac{1+\tau ^{2}z^{2}}{1-\tau z-\tau ^{2}z^{2}},\ \tau = \frac{1-\sqrt{5}}{2}\approx -0.618,\ z\in \mathbb {D}. \end{aligned}$$

The class \(\mathcal {SL}\) is a subclass of the class of starlike functions \( \mathcal {S}^{\star }\). The name attributed to the class \(\mathcal {SL}\) is motivated by the shape of the curve

$$\begin{aligned} \mathcal {C=}\left\{ \widetilde{p}(e^{it}):t\in \left[ 0,2\pi \right) \backslash \left\{ \pi \right\} \right\} , \end{aligned}$$

which is a shell-like curve. Furthermore, the coefficients of shell-like functions are connected with well-known Fibonacci numbers \(F_{n}\) defined as

$$\begin{aligned} F_{0}=0,F_{1}=1\,\quad \text {and}\quad \,F_{n+1}=F_{n}+F_{n-1}\quad \,\text {for}\quad \,n\ge 1. \end{aligned}$$
(1.3)

More recently, a lot of new studies have been done about several classes of functions related to shell-like curves connected with Fibonacci numbers (see [1, 2] and [16]).

Motivated by the above studies, we define new subclasses \(\mathcal {SL}^{k}\) of the class \(\mathcal {S}^{\star }\), where \(k\) is any positive real number. The coefficients of such functions are connected with \(k\)-Fibonacci numbers. For \(k=1\), we obtain the class \(\mathcal {SL}\) of shell-like functions.

For any positive real number \(k\), the \(k\)-Fibonacci numbers \(F_{k,n}\) are defined recurrently by

$$\begin{aligned} F_{k,0}=0,F_{k,1}=1\quad \text { and }\quad F_{k+1,n}=kF_{k,n}+F_{k,n-1} \quad \text { for } \quad n\ge 1. \end{aligned}$$
(1.4)

The Fibonacci numbers defined in (1.3) are obtained from (1.4) for \(k=1\). It is known that the n\(^{th}\) \(k\)-Fibonacci number is given by

$$\begin{aligned} F_{k,n}=\frac{\left( k-\tau _{k}\right) ^{n}-\tau _{k}^{n}}{\sqrt{k^{2}+4}}, \end{aligned}$$
(1.5)

where \(\tau _{k}=\frac{k-\sqrt{k^{2}+4}}{2}\) (see [3] and [4] for more details about \(k\)-Fibonacci numbers).

2 The Class \(\mathcal {SL}^{k}\)

Definition 2.1

Let \(k\) be any positive real number. The function \(f\in \mathcal {S}\) belongs to the class \(\mathcal {SL}^{k}\) if satisfies the condition that

$$\begin{aligned} \frac{zf^{\prime }(z)}{f(z)}\prec \widetilde{p}_{k}(z)\text {, }z\in \mathbb {D }, \end{aligned}$$

where

$$\begin{aligned} \widetilde{p}_{k}(z)=\frac{1+\tau _{k}^{2}z^{2}}{1-k\tau _{k}z-\tau _{k}^{2}z^{2}}=\frac{1+\tau _{k}^{2}z^{2}}{1-(\tau _{k}^{2}-1)z-\tau _{k}^{2}z^{2}}\text {, }\tau _{k}=\frac{k-\sqrt{k^{2}+4}}{2}\text {, }z\in \mathbb {D}.\nonumber \\ \end{aligned}$$
(2.1)

Theorem 2.1

The image of the unit circle of the function \(\widetilde{p} _{k}(z)\) defined in (2.1) is the curve \(\mathcal {C}_{k}\) with equation

$$\begin{aligned} x=\frac{k\sqrt{k^{2}+4}}{2\left[ k^{2}+2-2\cos \theta \right] }\text {, } \quad y= \frac{\left( 4\cos \theta -k^{2}\right) \sin \theta }{2\left[ k^{2}+2-2\cos \theta \right] \left[ 1+\cos \theta \right] }\text {, } \quad \theta \in [0,2\pi )\backslash \left\{ \pi \right\} .\nonumber \\ \end{aligned}$$
(2.2)

Proof

The proof follows by some straightforward calculations.\(\square \)

Recall that the curve which is called conchoid of Sluze has the following equation

$$\begin{aligned} a(x-a)\left( x^{2}+y^{2}\right) +\lambda ^{2}x^{2}=0, \end{aligned}$$
(2.3)

where \(a>0\) and \(\lambda >0\). For \(\lambda =2a/k\), the conchoid of Sluze (2.3) becomes the curve

$$\begin{aligned} x^{3}+(x-a)y^{2}+\left( \frac{4-k^{2}}{k^{2}}\right) ax^{2}=0. \end{aligned}$$
(2.4)

For \(k=1\), this curve is the trisectrix of Maclaurin.

We can find the corresponding Cartesian equation of the curve \(\mathcal {C} _{k}\) with Eq. (2.2) as

$$\begin{aligned} \left[ (8+2k^{2})x-k\sqrt{k^{2}+4}\right] y^{2}=\left( \frac{\sqrt{k^{2}+4}}{ k}-2x\right) \left( \sqrt{k^{2}+4}x-k\right) ^{2}. \end{aligned}$$
(2.5)

If we rewrite (2.5) in the following form

$$\begin{aligned}&\left( \frac{k\sqrt{k^{2}+4}}{k^{2}+4}-x\right) ^{3}+\frac{4-k^{2}}{k^{2}}. \frac{k\sqrt{k^{2}+4}}{2(k^{2}+4)}\left( \frac{k\sqrt{k^{2}+4}}{k^{2}+4} -x\right) ^{2}\\&\quad +\left[ \left( \frac{k\sqrt{k^{2}+4}}{k^{2}+4}-x\right) -\frac{k\sqrt{k^{2}+4 }}{2(k^{2}+4)}\right] y^{2}=0, \end{aligned}$$

then the image of the unit circle under the function \(\widetilde{p}_{k}\) is translated into a curve with Eq.  (2.4), where

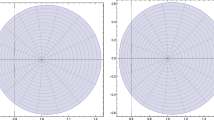
$$\begin{aligned} a=\frac{k\sqrt{k^{2}+4}}{2(k^{2}+4)}=\frac{1-\frac{2\tau _{k}\left( 1-k\sqrt{ k^{2}+4}\right) }{k-\sqrt{k^{2}+4}}}{2(k^{2}+4)}. \end{aligned}$$

Therefore, the curve \(\mathcal {C}_{k}\) has a shell-like shape and symmetric with respect to the real axis, see Fig. 1.

Fig. 1
figure 1

The curve \(\mathcal {C}_{k}\) for \(k=\frac{1}{2}\)

Full size image

For \(k<2\), note that we have

$$\begin{aligned} \widetilde{p}\left( e^{\pm i\arccos \left( \frac{k^{2}}{4}\right) }\right) = \frac{k\sqrt{k^{2}+4}}{k^{2}+4}, \end{aligned}$$

and so the curve \(\mathcal {C}_{k}\) intersects itself on the real axis at the point \(\frac{k\sqrt{k^{2}+4}}{k^{2}+4}\). Thus, \(\mathcal {C}_{k}\) has a loop intersecting the real axis at the points \(e=\frac{k\sqrt{k^{2}+4}}{k^{2}+4}\) and \(f=\frac{\sqrt{k^{2}+4}}{2k}\). For \(k\ge 2\), the curve \(\mathcal {C}_{k}\) has no loops and it is like a conchoid.

Corollary 2.1

For each \(k>0\), \(\mathcal {SL}^{k}\subset \mathcal {S}^{*}(\alpha _{k})\), where \(\alpha _{k}=\frac{k\sqrt{k^{2}+4}}{2\left( k^{2}+4\right) }=\frac{ k\left( k-2\tau _{k}\right) }{2\left( k^{2}+4\right) }\), that is, \(f\in \mathcal {SL}^{k}\) is starlike of order \(\alpha _{k}\).

The function \(\widetilde{p}_{k}\) defined in (2.1) is not univalent in \(\mathbb {D}\). For example, we have \(\widetilde{p}_{k}(0)=\widetilde{p}( \frac{-k}{2\tau _{k}})=1\) and \(\widetilde{p}(1)=\widetilde{p}(\tau _{k}^{4})= \frac{\sqrt{k^{2}+4}}{2k}\). We can give the following theorem.

Theorem 2.2

For each \(k>0\), the function \(\widetilde{p}_{k}\) is univalent in the disc \( \mathbb {D}_{r_{k}}=\left\{ z:\left| z\right| <r_{k}\right\} \), where

$$\begin{aligned} r_{k}=\frac{2-\sqrt{k^{2}+4}}{k\tau _{k}}=\frac{k^{2}-2k+4+(k-2)\sqrt{k^{2}+4 }}{2k} \end{aligned}$$
(2.6)

and it is not univalent in the disc \(\mathbb {D}_{r_{k}}\) for each \(r\ge r_{k}\).

Proof

Suppose that \(\widetilde{p}_{k}(z)=\widetilde{p}_{k}(w)\) for some \(z,w\in \mathbb {D}\) . After some calculations we have

$$\begin{aligned} \tau _{k}\left( z-w\right) \left( w-\frac{2\tau _{k}z+k}{k\tau _{k}^{2}z-2\tau _{k}}\right) =0\text {. } \end{aligned}$$
(2.7)

We see that the function

$$\begin{aligned} g_{k}(z)=\frac{2\tau _{k}z+k}{k\tau _{k}^{2}z-2\tau _{k}} \end{aligned}$$

maps a circle \(\left| z\right| =r<2/(k\tau _{k})\) onto a circle centred at \(m=-\frac{2k(1+\tau _{k}^{2}r^{2})}{\tau _{k}\left( 4-k^{2}\tau _{k}^{2}r^{2}\right) }\) and of radius \(\rho =\frac{r(k^{2}+4)}{4-k^{2}\tau _{k}^{2}r^{2}}\) with the diameter from \(g_{k}(-r)\) to \(g_{k}(r)\). Therefore, \( g_{\begin{array}{c} k \\ \end{array}}\) maps the circle \(\left| z\right| =r_{k}\) onto a circle with the diameter from the point \(g_{k}(r_{k})=r_{k}\) to the point \(g_{k}(-r_{k})\). We have \(g_{k}(-r_{k})>g_{k}(r_{k})=r_{k}\) for all \(k\) because the function \(g_{k}(x)\), \(x\in \mathbb {R}\) has negative derivative for all real \(x\). Therefore, if \(|w|\le r_{k}\) and \(|z|\le r_{k}\), then the third factor in (2.7) is equal to \(0\) for \(w=z-r_{k}\) only. Consequently, we see that (2.7) is not satisfied when \(|w|<r_{k}\) and \(|z|<r_{k}\), which proves that in the disc (2.6) the function \( \widetilde{p}_{k}(z)\) is univalent.

On the other hand, the derivative of the function \(\widetilde{p}_{k}(z)\) is

$$\begin{aligned} \widetilde{p}_{k}^{\prime }(z)=\frac{\left( z-r_{k}\right) \left( z-\frac{2+ \sqrt{k^{2}+4}}{k\tau _{k}}\right) }{\left( 1-k\tau _{k}z-\tau _{k}^{2}z^{2}\right) ^{2}}. \end{aligned}$$

The function \(\widetilde{p}_{k}^{\prime }(z)\) vanishes at the point \(z=r_{k}\) and hence we see that the function \(\widetilde{p}_{k}(z)\) fails to be univalent for \(\left| z\right| \ge r_{k}\).\(\square \)

Theorem 2.3

Let \(\left( F_{k,n}\right) \) be the sequence of \(k\)-Fibonacci numbers defined in (1.4). If

$$\begin{aligned} \widetilde{p}_{k}(z)=\frac{1+\tau _{k}^{2}z^{2}}{1-k\tau _{k}z-\tau _{k}^{2}z^{2}}=1+\overset{\infty }{\underset{n=1}{\sum }}p_{n}z^{n}, \end{aligned}$$

then we have

$$\begin{aligned} p_{n}=(F_{k,n-1}+F_{k,n+1})\tau _{k}^{n}\text {, } \quad n=1,2,3,\ldots \text { .} \end{aligned}$$
(2.8)

Proof

Let us denote \(u=\tau _{k}z\), \(\left| u\right| <\left| \tau _{k}\right| \). Using the equations \(\tau _{k}\left( k-\tau _{k}\right) =-1\) and \(2\tau _{k}-k=-\sqrt{k^{2}+4}\), we have

$$\begin{aligned} \widetilde{p}_{k}(z)&= \frac{1+\tau _{k}^{2}z^{2}}{1-k\tau _{k}z-\tau _{k}^{2}z^{2}}=\frac{1+u^{2}}{1-ku-u^{2}}=\left( u+\frac{1}{u}\right) \frac{u }{1-ku-u^{2}} \\&= \left( u+\frac{1}{u}\right) \frac{1}{\sqrt{k^{2}+4}}\left( \frac{1}{1+ \frac{u}{\tau _{k}}}-\frac{1}{1+\frac{u}{k-\tau _{k}}}\right) \\&= \left( u+\frac{1}{u}\right) \frac{1}{\sqrt{k^{2}+4}}\overset{\infty }{ \underset{n=1}{\sum }}(-1)^{n}\left[ \left( \frac{u}{\tau _{k}}\right) ^{n}-\left( \frac{u}{k-\tau _{k}}\right) ^{n}\right] \\&= \left( u+\frac{1}{u}\right) \overset{\infty }{\underset{n=1}{\sum }}\frac{ \left( k-\tau _{k}\right) ^{n}-\tau _{k}^{n}}{\sqrt{k^{2}+4}}u^{n}. \end{aligned}$$

Now by the Eq. (1.5), we find

$$\begin{aligned} \widetilde{p}_{k}(z)&= \left( u+\frac{1}{u}\right) \overset{\infty }{ \underset{n=1}{\sum }}F_{k,n}u^{n} \\&= 1+\overset{\infty }{\underset{n=1}{\sum }}\left( F_{k,n-1}+F_{k,n+1}\right) u^{n} \\&= 1+\overset{\infty }{\underset{n=1}{\sum }}\left( F_{k,n-1}+F_{k,n+1}\right) \tau _{k}^{n}z^{n}, \end{aligned}$$

and hence we obtain (2.8).\(\square \)

Theorem 2.4

A function \(f\in \mathcal {S}\) belongs to the class \(\mathcal {SL}^{k}\) if and only if there exists a function \(q,\) \(q\prec \widetilde{p}_{k}(z)= \frac{ 1+\tau _{k}^{2}z^{2}}{1-k\tau _{k}z-\tau _{k}^{2}z^{2}}\) such that

$$\begin{aligned} f(z)=z\exp \underset{0}{\overset{z}{\int }}\frac{q(\zeta )-1}{\zeta }{\text {d}}\zeta \text {, } \quad z\in \mathbb {D}. \end{aligned}$$
(2.9)

Proof

Let \(f\in \mathcal {SL}^{k}\). Then by definition

$$\begin{aligned} \frac{zf^{\prime }(z)}{f(z)}=\widetilde{p}_{k}(\omega (z))\text {, } \left| \omega (z)\right| <1\text {, } \quad z\in \mathbb {D}\text {. } \end{aligned}$$
(2.10)

If we take \(q(z)=\widetilde{p}(\omega (z))\), we see that the Eq.  (2.10) is equivalent to (2.9).\(\square \)

For \(\widetilde{p}_{k}(z)=\frac{1+\tau _{k}^{2}z^{2}}{1-k\tau _{k}z-\tau _{k}^{2}z^{2}}\), the formula (2.9) gives \(f_{0}(z)=\frac{z}{1-k\tau _{k}z-\tau _{k}^{2}z^{2}}\). Hence the function \(f_{0}\) belongs to the class \( \mathcal {SL}^{k}\) and it is extremal function for several problems in this class.

Theorem 2.5

If \(f(z)=z+\overset{\infty }{\underset{n=2}{\sum }}a_{n}z^{n}\) belongs to the class \(\mathcal {SL}^{k}\), then we have

$$\begin{aligned} \left| a_{n}\right| \le |\tau _{k}|^{n-1}F_{k,n}, \end{aligned}$$
(2.11)

where \(\left( F_{k,n}\right) \) is the sequence of \(k\)-Fibonacci numbers and \( \tau _{k}=\frac{k-\sqrt{k^{2}+4}}{2}\). Equality holds in (2.11) for the function \(f_{0}(z)=\frac{z}{1-k\tau _{k}z-\tau _{k}^{2}z^{2}}\).

Proof

Let \(f\in \mathcal {SL}^{k}\), \(f(z)=\overset{\infty }{\underset{m=0}{\sum }} a_{m}z^{m}\), \(a_{0}=0\), \(a_{1}=1\). By the definition of the class \(\mathcal { SL}^{k}\), there exists a function \(\omega \), \(\left| \omega (z)\right| <1\) for \(z\in \mathbb {D}\) such that

$$\begin{aligned} \frac{zf^{\prime }(z)}{f(z)}=\frac{1+\tau _{k}^{2}\omega ^{2}(z)}{1-k\tau _{k}\omega (z)-\tau _{k}^{2}\omega ^{2}(z)}. \end{aligned}$$

We get

$$\begin{aligned} zf^{\prime }(z)-f(z)&= k\tau _{k}\omega (z)zf^{\prime }(z)+\tau _{k}^{2}\omega ^{2}(z)\left[ zf^{\prime }(z)+f(z)\right] ,\\ \overset{\infty }{\underset{m=1}{\sum }}(m-1)a_{m}z^{m}&= k\tau _{k}\omega (z) \overset{\infty }{\underset{m=1}{\sum }}ma_{m}z^{m}+\tau _{k}^{2}\omega ^{2}(z)\overset{\infty }{\underset{m=1}{\sum }}(m+1)a_{m}z^{m} \end{aligned}$$

and so

$$\begin{aligned} \overset{n}{\underset{m=1}{\sum }}(m-1)a_{m}z^{m}\!+\!\overset{\infty }{\underset{m=n+1}{\sum }}c_{m}z^{m}=k\tau _{k}\omega (z)\overset{n-1}{\underset{m=1}{ \sum }}ma_{m}z^{m}+\tau _{k}^{2}\omega ^{2}(z)\overset{n-2}{\underset{m=1}{ \sum }}(m+1)a_{m}z^{m}. \end{aligned}$$

For \(n\ge 2\), we find

$$\begin{aligned}&\left| \overset{n}{\underset{m=1}{\sum }}(m-1)a_{m}z^{m}+\overset{ \infty }{\underset{m=n+1}{\sum }}c_{m}z^{m}\right| ^{2} \\&= \left| k\tau _{k}\omega (z)\overset{n-1}{\underset{m=1}{\sum }} ma_{m}z^{m}+\tau _{k}^{2}\omega ^{2}(z)\overset{n-2}{\underset{m=1}{\sum }} (m+1)a_{m}z^{m}\right| ^{2} \\&\le \left| k\tau _{k}\overset{n-1}{\underset{m=1}{\sum }} ma_{m}z^{m}+\tau _{k}^{2}\omega (z)\overset{n-1}{\underset{m=1}{\sum }} ma_{m-1}z^{m-1}\right| ^{2} \\&\le \overset{n-1}{\underset{m=1}{\sum }}\left| k\tau _{k}ma_{m}z^{m}+\tau _{k}^{2}\omega (z)ma_{m-1}z^{m-1}\right| ^{2} \\&\le \sum _{m=1}^{n-1}\left( \left| k\tau _{k}ma_{m}z^{m}\right| ^{2}+\left| \tau _{k}^{2}ma_{m-1}z^{m-1}\right| ^{2}+2\left| k\tau _{k}^{3}m^{2}a_{m}a_{m-1}z^{2m-1}\right| \right) . \end{aligned}$$

Integrating the both sides of this inequality around \(z=re^{im\varphi }\) and taking limit \(r\rightarrow 1^{-}\) we obtain

$$\begin{aligned} \overset{n}{\underset{m=1}{\sum }}(m-1)^{2}\left| a_{m}\right| ^{2}+\overset{\infty }{\underset{m=n+1}{\sum }}\left| c_{m}\right| ^{2}&\le k^{2}\tau _{k}^{2}\overset{n-1}{\underset{m=1}{\sum }}m^{2}\left| a_{m}\right| ^{2}+\tau _{k}^{4}\underset{m=1}{\overset{n-1}{\sum }} m^{2}\left| a_{m-1}\right| ^{2}\\&+\,2k\left| \tau _{k}\right| ^{3}\overset{n-1}{\underset{m=1}{\sum }}m^{2}\left| a_{m}\right| \left| a_{m-1}\right| \end{aligned}$$

and hence we find

$$\begin{aligned} (n-1)^{2}\left| a_{n}\right| ^{2}&\le \overset{n-1}{\underset{m=1}{\sum }}\left\{ k^{2}\tau _{k}^{2}m^{2}-(m-1)^{2}\right\} \left| a_{m}\right| ^{2}+\underset{ m=1}{\overset{n-1}{\sum }}\tau _{k}^{4}m^{2}\left| a_{m-1}\right| ^{2} \nonumber \\&+\,\overset{n-1}{\underset{m=1}{\sum }}2k|\tau _{k}|^{3}m^{2}\left| a_{m}\right| \left| a_{m-1}\right| \nonumber \\ \end{aligned}$$
(2.12)

The inequality (2.11) holds for \(n=1\). Assume that the estimation (2.11) holds for all natural numbers less or equal to \(n\). Then from (2.12) and from (2.11) we have

$$\begin{aligned}&n^{2}\left| a_{n+1}\right| ^{2} \nonumber \\&\le \overset{n}{\underset{m=1}{\sum }}\left\{ k^{2}\tau _{k}^{2}m^{2}\!-\!(m\!-\!1)^{2}\right\} \left| a_{m}\right| ^{2}\!+\!\tau _{k}^{4}\underset{m=1}{\overset{n}{\sum }}m^{2}\left| a_{m-1}\right| ^{2}\!+\!2k\left| \tau _{k}\right| ^{3}\overset{n}{\underset{m=1}{\sum }} m^{2}\left| a_{m}\right| \left| a_{m-1}\right| \nonumber \\&\le \overset{n}{\underset{m=1}{\sum }}\left\{ k^{2}\tau _{k}^{2}m^{2}-(m-1)^{2}\right\} \left\{ |\tau _{k}|^{m-1}F_{k,m}\right\} ^{2}+\tau _{k}^{4}\underset{m=1}{\overset{n}{\sum }}m^{2}\left\{ |\tau _{k}|^{m-2}F_{k,m-1}\right\} ^{2} \nonumber \\&+2k\left| \tau _{k}\right| ^{3}\overset{n}{\underset{m=1}{\sum }} m^{2}\left\{ |\tau _{k}|^{m-1}F_{k,m}\right\} \left\{ |\tau _{k}|^{m-2}F_{k,m-1}\right\} \nonumber \\&= \overset{n}{\underset{m=1}{\sum }}\left[ \left\{ m\tau _{k}^{m}\left( kF_{k,m}+F_{k,m-1}\right) \right\} ^{2}-(m-1)^{2}\left\{ |\tau _{k}|^{m-1}F_{k,m}\right\} ^{2}\right] \nonumber \\&= \overset{n}{\underset{m=1}{\sum }}\left[ \left\{ m\tau _{k}^{m}F_{k,m+1}\right\} ^{2}-(m-1)^{2}\left\{ |\tau _{k}|^{m-1}F_{k,m}\right\} ^{2}\right] \nonumber \\&= n^{2}|\tau _{k}|^{2n}\left\{ F_{k,n+1}\right\} ^{2}. \end{aligned}$$
(2.13)

In this way we have proved by induction the inequality (2.11) for all \( n\in \mathbb {N}\).\(\square \)