Solutions and Periodicity of a Rational Recursive Sequences of Order Five

Abstract

In this paper, the solutions of the recursive sequences

$$\begin{aligned} x_{n+1}=\dfrac{x_{n}x_{n-2}x_{n-4}}{x_{n-1}x_{n-3}(\pm 1\pm x_{n}x_{n-2}x_{n-4})},\;\;\;n=0,1,..., \end{aligned}$$

where the initial conditions $x_{-4},\ x_{-3},\ x_{-2},\ x_{-1}$ and $x_{0}$ are arbitrary nonzero real numbers are obtained. The stability and periodicity of the solutions are studied as well.

1 Introduction

In this paper, we obtain the solutions of the following difference equations of order five.

$$\begin{aligned} x_{n+1}=\dfrac{x_{n}x_{n-2}x_{n-4}}{x_{n-1}x_{n-3}(\pm 1\pm x_{n}x_{n-2}x_{n-4})},\;\;\;n=0,1,..., \end{aligned}$$

(1)

where the initial conditions $x_{-4},\ x_{-3},\ x_{-2},\ x_{-1}\$and $x_{0}$ are arbitrary real numbers.

Recently, there has been a great interest in studying the qualitative properties of rational difference equations. For the systematical studies of rational and nonrational difference equations, one can refer to the papers [1–40] and references therein.

The study of rational difference equations of order greater than one is quite challenging and rewarding because some prototypes for the development of the basic theory of the global behavior of nonlinear difference equations of order greater than one come from the results for rational difference equations. However, there have not been any effective general methods to deal with the global behavior of rational difference equations of order greater than one so far. Therefore, the study of rational difference equations of order greater than one is worth further consideration.

Agarwal and Elsayed [2] investigated the global stability and periodicity character and gave the solution of some special cases of the difference equation

$$\begin{aligned} x_{n+1}=a+\dfrac{dx_{n-l}x_{n-k}}{b-cx_{n-s}}. \end{aligned}$$

Aloqeili [4] has obtained the solutions of the difference equation

$$\begin{aligned} x_{n+1}=\dfrac{x_{n-1}}{a-x_{n}x_{n-1}}. \end{aligned}$$

Cinar [7–9] investigated the solutions of the following difference equations:

$$\begin{aligned} x_{n+1}=\dfrac{x_{n-1}}{1+ax_{n}x_{n-1}},\ \ x_{n+1}=\dfrac{x_{n-1}}{ -1+ax_{n}x_{n-1}},\ \ x_{n+1}=\dfrac{ax_{n-1}}{1+bx_{n}x_{n-1}}. \end{aligned}$$

Elabbasy et al. [10, 12] investigated the global stability and periodicity character and gave the solution of special case of the following recursive sequences:

$$\begin{aligned} x_{n+1}=ax_{n}-\dfrac{bx_{n}}{cx_{n}-dx_{n-1}},\ \ \ x_{n+1}=\dfrac{\alpha x_{n-k}}{\beta +\gamma \prod _{i=0}^{k}x_{n-i}}. \end{aligned}$$

Elsayed in [18] studied the behavior of the solutions of the third-order rational difference equation

$$\begin{aligned} x_{n+1}=ax_{n-1}+\dfrac{bx_{n}x_{n-1}}{cx_{n}+dx_{n-2}}. \end{aligned}$$

Also, he obtained the expressions of the solutions of four special cases of this equation.

Ibrahim [24] got the solutions of the rational difference equation

$$\begin{aligned} x_{n+1}=\dfrac{x_{n}x_{n-2}}{x_{n-1}(a+bx_{n}x_{n-2})}. \end{aligned}$$

Karatas et al. [25] got the form of the solution of the difference equation

$$\begin{aligned} x_{n+1}=\dfrac{x_{n-5}}{1+x_{n-2}x_{n-5}}. \end{aligned}$$

Simsek et al. [31, 32] obtained the solutions of the following difference equations:

$$\begin{aligned} x_{n+1}=\dfrac{x_{n-3}}{1+x_{n-1}},\ \ \ \ \ \ x_{n+1}=\dfrac{x_{n-5}}{ 1+x_{n-1}x_{n-3}}. \end{aligned}$$

In [39, 40] Zayed and El-Moneam dealt with the dynamics of the following rational recursive sequences:

$$\begin{aligned} x_{n+1}&= ax_{n}-\dfrac{bx_{n}}{cx_{n}-dx_{n-k}}, \\ x_{n+1}&= \dfrac{\alpha x_{n}+\beta x_{n-1}+\gamma x_{n-2}+\delta x_{n-3}}{ Ax_{n}+Bx_{n-1}+Cx_{n-2}+Dx_{n-3}}. \end{aligned}$$

Here, we recall some notations and results which will be useful in our investigation.

Let $I$ be some interval of real numbers and let

$$\begin{aligned} f:I^{k+1}\rightarrow I \end{aligned}$$

be a continuously differentiable function. Then for every set of initial conditions $x_{-k},x_{-k+1},...,x_{0}\in I,$ the difference equation

$$\begin{aligned} x_{n+1}=f(x_{n},x_{n-1},...,x_{n-k}),\ \ n=0,1,..., \end{aligned}$$

(2)

has a unique solution $\{x_{n}\}_{n=-k}^{\infty }$ [27].

Definition 1

(Equilibrium Point)

A point $\overline{x}\in I$ is called an equilibrium point of Eq. (2), if

$$\begin{aligned} \overline{x}=f(\overline{x},\overline{x},...,\overline{x}). \end{aligned}$$

That is, $x_{n}=\overline{x}$ for $n\ge 0\;$is a solution of Eq. (2), or equivalently, $\overline{x}$ is a fixed point of $f$.

Definition 2

(Stability)

• (i) The equilibrium point $\overline{x}\;$of Eq. (2) is locally stable if for every $\epsilon >0,\;$ there exists $\delta >0\;\;$such that for all $x_{-k},x_{-k+1},...,x_{-1},x_{0}\in I\;$with

  $$\begin{aligned} \left| x_{-k}-\overline{x}\right| +\left| x_{-k+1}-\overline{x} \right| + \cdots +\left| x_{0}-\overline{x}\right| <\delta , \end{aligned}$$

  we have

  $$\begin{aligned} \left| x_{n}-\overline{x}\right| <\epsilon \quad \text {for all} \quad n\ge -k. \end{aligned}$$

• (ii) The equilibrium point $\overline{x}\;$of Eq. (2) is locally asymptotically stable if $\;\overline{x}\;$is locally stable solution of Eq. (2) and there exists $\gamma >0,$ such that for all $x_{-k},x_{-k+1},...,x_{-1},x_{0}\in I\;$with

  $$\begin{aligned} \left| x_{-k}-\overline{x}\right| +\left| x_{-k+1}-\overline{x} \right| +\cdots +\left| x_{0}-\overline{x}\right| <\gamma , \end{aligned}$$

  we have

  $$\begin{aligned} \lim _{n\rightarrow \infty }\;x_{n}=\overline{x}. \end{aligned}$$

• (iii) The equilibrium point $\overline{x}\;$of Eq. (2) is global attractor if for all $x_{-k},x_{-k+1},...,x_{-1},x_{0}\in I,\;$we have

  $$\begin{aligned} \lim _{n\rightarrow \infty }\;x_{n}=\overline{x}. \end{aligned}$$

• (iv) The equilibrium point $\overline{x}\;$of Eq. (2) is globally asymptotically stable if $\overline{x}\;$is locally stable, and $\overline{x }\;$is also a global attractor of Eq. (2).

• (v) The equilibrium point $\overline{x}\;$of Eq. (2) is unstable if $\overline{x}\;$is not locally stable.

Definition 3

(Periodicity)

A solution $\{x_{n}\}_{n=-k}^{\infty }$ of Eq. (2) is called periodic with period $p$, if there exists an integer $p\ge 1$ such that

$$\begin{aligned} x_{n+p}=x_{n},\; \text {for all}\; n\ge -k. \end{aligned}$$

A solution is called periodic with prime period $p$, if $p$ is the smallest positive integer for which the previous equation holds.

The linearized equation of Eq. (2) about the equilibrium point $\overline{x} \;$is the linear difference equation

$$\begin{aligned} y_{n+1}=\sum \limits _{i=0}^{k}\frac{\partial f(\overline{x},\overline{x},..., \overline{x})}{\partial x_{n-i}}y_{n-i}, \end{aligned}$$

(3)

and the equation

$$\begin{aligned} \lambda ^{k+1}-q_{0}\lambda ^{k}-q_{1}\lambda ^{k-1}-\cdots -q_{k-1}\lambda -q_{k}=0, \end{aligned}$$

(4)

where $q_{i}=\frac{\partial f(\overline{x},\overline{x},...,\overline{x})}{ \partial x_{n-i}},\$for$\ i=0,1,...,k,$ is called the characteristic equation of Eq. (3) about $\overline{x}.$

The following result, known as the Linearized Stability Theorem, is very useful in determining the local stability character of the equilibrium point $\overline{x}$ of Eq. (2).

Theorem A

[6] (The Linearized Stability Theorem)

Assume that the function $f$ is a continuously differentiable function defined on some open neighborhood of an equilibrium point $\overline{x}$. Then the following statements are true:

• (1) When all the roots of Eq. (4) have absolute value less than one, then the equilibrium point $\overline{x}$ of Eq. (2) is locally asymptotically stable.

• (2) If at least one root of Eq. (4) has absolute value greater than one, then the equilibrium point $\overline{x}$ of Eq. (2) is unstable.

Definition 4

(Hyperbolic) The equilibrium point $\overline{x}$ of Eq. (2) is called hyperbolic if no root of Eq. (4) has absolute value equal to one. If there exists a root of Eq. (4) with absolute value equal to one, then the equilibrium $\overline{x}$ is called nonhyperbolic.

2 The First Equation $x_{n+1}=\frac{x_{n}x_{n-2}x_{n-4}}{x_{n-1}x_{n-3}(1+x_{n}x_{n-2}x_{n-4})}$

In this section, we give a specific form of the solution of the first equation in the form

$$\begin{aligned} x_{n+1}=\dfrac{x_{n}x_{n-2}x_{n-4}}{x_{n-1}x_{n-3}(1+x_{n}x_{n-2}x_{n-4})} ,\;\;\;n=0,1,..., \end{aligned}$$

(5)

where the initial values are arbitrary nonzero real numbers.

Theorem 1

Let $\{x_{n}\}_{n=-4}^{\infty }$ be a solution of Eq. (5). Then for $n=0,1,...$

$$\begin{aligned}&x_{6n-4} =e\mathop {\displaystyle \prod }\limits _{i=0}^{n-1}\left( \frac{1+6iace}{1+\left( 6i+2\right) ace}\right) ,\quad x_{6n-3}=d\mathop {\displaystyle \prod }\limits _{i=0}^{n-1}\left( \frac{1+(6i+1)ace}{1+\left( 6i+3\right) ace}\right) , \\&x_{6n-2} =c\mathop {\displaystyle \prod }\limits _{i=0}^{n-1}\left( \frac{1+(6i+2)ace}{1+\left( 6i+4\right) ace}\right) ,\quad x_{6n-1}=b\mathop {\displaystyle \prod }\limits _{i=0}^{n-1}\left( \frac{1+(6i+3)ace}{1+\left( 6i+5\right) ace}\right) , \\&x_{6n} =a\mathop {\displaystyle \prod }\limits _{i=0}^{n-1}\left( \frac{1+(6i+4)ace}{1+\left( 6i+6\right) ace}\right) ,\quad x_{6n+1}=\frac{ace}{bd(1+ace)} \mathop {\displaystyle \prod }\limits _{i=0}^{n-1}\left( \frac{1+(6i+5)ace}{1+\left( 6i+7\right) ace} \right) , \end{aligned}$$

where$\;x_{-4}=e,\ x_{-3}=d,\ x_{-2}=c,\ x_{-1}=b,\ x_{0}=a.$

Proof

For $n=0$, the result holds. Now suppose that $n>0$ and that our assumption holds for $n-1$. That is,

$$\begin{aligned} x_{6n-10}&= e\mathop {\displaystyle \prod }\limits _{i=0}^{n-2}\left( \frac{1+6iace}{1+\left( 6i+2\right) ace}\right) ,\quad x_{6n-9}=d\mathop {\displaystyle \prod }\limits _{i=0}^{n-2}\left( \frac{1+(6i+1)ace}{1+\left( 6i+3\right) ace}\right) , \\ x_{6n-8}&= c\mathop {\displaystyle \prod }\limits _{i=0}^{n-2}\left( \frac{1+(6i+2)ace}{1+\left( 6i+4\right) ace}\right) ,\quad x_{6n-7}=b\mathop {\displaystyle \prod }\limits _{i=0}^{n-2}\left( \frac{1+(6i+3)ace}{1+\left( 6i+5\right) ace}\right) , \\ x_{6n-6}&= a\mathop {\displaystyle \prod }\limits _{i=0}^{n-2}\left( \frac{1+(6i+4)ace}{1+\left( 6i+6\right) ace}\right) ,\quad x_{6n-5}=\frac{ace}{bd(1+ace)} \mathop {\displaystyle \prod }\limits _{i=0}^{n-2}\left( \frac{1+(6i+5)ace}{1+\left( 6i+7\right) ace} \right) . \end{aligned}$$

Now, it follows from Eq. (5) that

$$\begin{aligned}&x_{6n-4}=\displaystyle \dfrac{x_{6n-5}x_{6n-7}x_{6n-9}}{ x_{6n-6}x_{6n-8}(1+x_{6n-5}x_{6n-7}x_{6n-9})}\\&\quad =\dfrac{\dfrac{ace}{bd(1+ace)}\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{1+(6i+5)ace }{1+\left( 6i+7\right) ace}\right) b\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{ 1+(6i+3)ace}{1+\left( 6i+5\right) ace}\right) d\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{1+(6i+1)ace}{1+\left( 6i+3\right) ace} \right) }{ \begin{array}{c} \left( a\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{1+(6i+4)ace}{1+\left( 6i+6\right) ace}\right) c\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{1+(6i+2)ace}{ 1+\left( 6i+4\right) ace}\right) \right) \\ \left( 1+\dfrac{ace}{bd(1+ace)}\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{ 1+(6i+5)ace}{1+\left( 6i+7\right) ace}\right) b\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{1+(6i+3)ace}{1+\left( 6i+5\right) ace} \right) d\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{1+(6i+1)ace}{1+\left( 6i+3\right) ace}\right) \right) \end{array}}\\&\quad =\dfrac{\dfrac{ace}{(1+ace)}\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{1+(6i+1)ace }{1+\left( 6i+7\right) ace}\right) }{\left( ac\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{1+(6i+2)ace}{1+\left( 6i+6\right) ace}\right) \right) \left( 1+\dfrac{ace}{(1+ace)}\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2} \left( \dfrac{1+(6i+1)ace}{1+\left( 6i+7\right) ace}\right) \right) }\\&\quad =\dfrac{\left( \dfrac{e}{1+(6n-5)ace}\right) }{\left( \mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{1+(6i+2)ace}{1+\left( 6i+6\right) ace} \right) \right) \left( 1+\dfrac{ace}{1+(6n-5)ace}\right) } \\&\quad =\dfrac{e}{\left( \mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{1+(6i+2)ace}{ 1+\left( 6i+6\right) ace}\right) \right) \left( 1+(6n-5)ace+ace\right) } \\&\quad =e\mathop {\displaystyle \prod }\limits _{i=0}^{n-2}\left( \dfrac{1+\left( 6i+6\right) ace}{ 1+(6i+2)ace}\right) \left( \dfrac{1}{1+(6n-4)ace}\right) . \end{aligned}$$

Hence, we have

$$\begin{aligned} x_{6n-4}=e\mathop {\displaystyle \prod }\limits _{i=0}^{n-1}\left( \dfrac{1+6iace}{1+(6i+2)ace} \right) . \end{aligned}$$

Similarly,

$$\begin{aligned}&x_{6n-3}=\dfrac{x_{6n-4}x_{6n-6}x_{6n-8}}{ x_{6n-5}x_{6n-7}(1+x_{6n-4}x_{6n-6}x_{6n-8})}\\&\quad =\dfrac{e\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-1}\left( \dfrac{1\!+\!6iace}{1\!+\!\left( 6i\!+\!2\right) ace}\right) a\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{1\!+\!(6i+4)ace}{1+\left( 6i+6\right) ace}\right) c\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{1+(6i+2)ace}{ 1+\left( 6i+4\right) ace}\right) }{ \begin{array}{c} \left( \dfrac{ace}{bd(1+ace)}\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{1+(6i+5)ace }{1+\left( 6i+7\right) ace}\right) b\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{ 1+(6i+3)ace}{1+\left( 6i+5\right) ace}\right) \right) \\ \left( 1+e\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-1}\left( \dfrac{1+6iace}{1+\left( 6i+2\right) ace}\right) a\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{1+(6i+4)ace}{ 1+\left( 6i+6\right) ace}\right) c\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{ 1+(6i+2)ace}{1+\left( 6i+4\right) ace}\right) \right) \end{array}}\\&\quad =\dfrac{ace\left( \dfrac{1}{1+\left( 6n-4\right) ace}\right) }{\left( \dfrac{ ace}{d(1+ace)}\mathop {\displaystyle \prod }\nolimits _{i=0}^{n-2}\left( \dfrac{1+(6i+3)ace}{1+\left( 6i+7\right) ace}\right) \right) \left( 1+ace\left( \dfrac{1}{1+\left( 6n-4\right) ace}\right) \right) }\\&\quad =d\mathop {\displaystyle \prod }\limits _{i=0}^{n-2}\left( \dfrac{1+\left( 6i+7\right) ace}{ 1+(6i+3)ace}\right) \dfrac{(1+ace)}{\left( 1+\left( 6n-3\right) ace\right) }. \end{aligned}$$

Hence, we have

$$\begin{aligned} x_{6n-3}=d\mathop {\displaystyle \prod }\limits _{i=0}^{n-1}\left( \dfrac{1+\left( 6i+1\right) ace}{ 1+(6i+3)ace}\right) . \end{aligned}$$

Similarly, one can easily obtain the other relations. Thus, the proof is completed.

Theorem 2

Eq. (5) has a unique equilibrium point which is the number zero, and this equilibrium point is nonhyperbolic.

Proof

For the equilibrium points of Eq. (5), we can write

$$\begin{aligned} \overline{x}=\dfrac{\overline{x}^{3}}{\overline{x}^{2}\left( 1+\overline{x} ^{3}\right) }. \end{aligned}$$

Then we have

$$\begin{aligned} \overline{x}^{3}\left( 1+\overline{x}^{3}\right)&= \overline{x}^{3}, \\ \overline{x}^{3}\left( 1+\overline{x}^{3}-1\right)&= 0, \end{aligned}$$

or,

$$\begin{aligned} \overline{x}^{6}=0. \end{aligned}$$

Thus, the equilibrium point of Eq. (5) is $\overline{x}=0.$

Let $\ f:(0,\infty )^{5}\longrightarrow (0,\infty )$ be a function defined by

$$\begin{aligned} f(u,v,w,t,p)=\frac{uwp}{vt\left( 1+uwp\right) }. \end{aligned}$$

Therefore, it follows that

$$\begin{aligned} f_{u}(u,v,w,t,p)&= \frac{wp}{vt\left( 1+uwp\right) ^{2}},\ \ f_{v}(u,v,w,t,p)=-\frac{uwp}{v^{2}t\left( 1+uwp\right) }, \\ f_{w}(u,v,w,t,p)&= \frac{up}{vt\left( 1+uwp\right) ^{2}},\ \ \ f_{t}(u,v,w,t,p)=-\frac{uwp}{vt^{2}\left( 1+uwp\right) }, \\ f_{p}(u,v,w,t,p)&= \frac{uw}{vt\left( 1+uwp\right) ^{2}}. \end{aligned}$$

We see that

$$\begin{aligned} f_{u}(\overline{x},\overline{x},\overline{x},\overline{x},\overline{x})&= 1,\quad f_{v}(\overline{x},\overline{x},\overline{x},\overline{x}, \overline{x})=-1,\quad f_{w}(\overline{x},\overline{x},\overline{x}, \overline{x},\overline{x})=1, \\ f_{t}(\overline{x},\overline{x},\overline{x},\overline{x},\overline{x})&= -1,\quad f_{p}(\overline{x},\overline{x},\overline{x},\overline{x}, \overline{x})=1, \end{aligned}$$

and the characteristic equation about the equilibrium point $\overline{x}=0$ is given by

$$\begin{aligned} \lambda ^{5}-\lambda ^{4}+\lambda ^{3}-\lambda ^{2}+\lambda -1=0, \end{aligned}$$

then we obtain that $\lambda =1,$ is one of the roots of the previous equation, then the equilibrium point $\overline{x}=0$ is nonhyperbolic.

Numerical examples

For confirming the results of this section, we consider numerical examples which represent different types of solutions to Eq. (5).

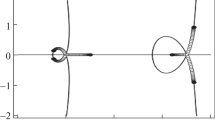
Example 1

We assume the initial condition as follows: $x_{-4}=5,$ $x_{-3}=13,\ x_{-2}=7,\ x_{-1}=3,\ x_{0}=9.$ See Fig. 1.

Example 2

See Fig. 2, since $x_{-4}=11,\ x_{-3}=3,\ x_{-2}=9,\ x_{-1}=3,\ x_{0}=2$.

Fig. 1

This figure shows the stability behavior of the solution of the difference equation $x_{n+1}=\dfrac{x_{n}x_{n-2}x_{n-4}}{x_{n-1}x_{n-3}(1+x_{n}x_{n-2}x_{n-4})}$, with the initial conditions $x_{-4}=5, x_{-3}\!=\!13,\ x_{-2}=7,\ x_{-1}\!=\!3,\ x_{0}=9$

Fig. 2

This figure shows the solutions of Eq. (5) when we put the initial conditions as follows: $x_{-4}=11,\ x_{-3}=3,\ x_{-2}=9,\ x_{-1}=3,\ x_{0}=2$

3 The Second Equation $x_{n+1}=\frac{x_{n}x_{n-2}x_{n-4}}{x_{n-1}x_{n-3}(-1+x_{n}x_{n-2}x_{n-4})}$

In this section, we obtain the solution of the second equation in the form

$$\begin{aligned} x_{n+1}=\dfrac{x_{n}x_{n-2}x_{n-4}}{x_{n-1}x_{n-3}(-1+x_{n}x_{n-2}x_{n-4})} ,\;\;\;n=0,1,..., \end{aligned}$$

(6)

where the initial values are arbitrary nonzero real numbers with $x_{0}x_{-2}x_{-4}\ne 1.$

Theorem 3

Let $\{x_{n}\}_{n=-4}^{\infty }$ be a solution of Eq. (6). Then every solution of Eq. (6) is periodic with period 6 and for $n=0,1,...$

$$\begin{aligned} x_{6n-4}&= e,\quad x_{6n-3}=d,\quad x_{6n-2}=c, \\ x_{6n-1}&= b,\quad x_{6n}=a,\quad x_{6n+1}=\frac{ace}{ bd(-1+ace)}, \end{aligned}$$

where$\;x_{-4}=e,\ x_{-3}=d,\ x_{-2}=c,\ x_{-1}=b,\ x_{0}=a.$

Proof

For $n=0$ the result holds. Now suppose that $n>0$ and that our assumption holds for $n-1$. That is,

$$\begin{aligned} x_{6n-10}&= e,\quad x_{6n-9}=d,\quad x_{6n-8}=c, \\ x_{6n-7}&= b,\quad x_{6n-6}=a,\quad x_{6n-5}=\frac{ace}{ bd(-1+ace)}. \end{aligned}$$

Now, it follows from Eq. (6) that

$$\begin{aligned} x_{6n-4}&= \dfrac{x_{6n-5}x_{6n-7}x_{6n-9}}{ x_{6n-6}x_{6n-8}(-1+x_{6n-5}x_{6n-7}x_{6n-9})}\\&= \frac{acebd}{ bd(-1+ace)ac\left( -1+\dfrac{acebd}{bd(-1+ace)}\right) } \\&= \frac{e}{(-1+ace)\left( -1+\dfrac{ace}{(-1+ace)}\right) }=\frac{e}{\left( 1-ace+ace\right) }=e, \end{aligned}$$

$$\begin{aligned} x_{6n-3}&= \dfrac{x_{6n-4}x_{6n-6}x_{6n-8}}{ x_{6n-5}x_{6n-7}(-1+x_{6n-4}x_{6n-6}x_{6n-8})}=\dfrac{eac}{\left( \dfrac{ace }{bd(-1+ace)}\right) b(-1+ace)}=d, \\ x_{6n-2}&= \dfrac{x_{6n-3}x_{6n-5}x_{6n-7}}{ x_{6n-4}x_{6n-6}(-1+x_{6n-3}x_{6n-5}x_{6n-7})}=\dfrac{d\left( \dfrac{ace}{ bd(-1+ace)}\right) b}{ea\left( -1+d\left( \dfrac{ace}{bd(-1+ace)}\right) b\right) }=c, \\ x_{6n-1}&= \dfrac{x_{6n-2}x_{6n-4}x_{6n-6}}{ x_{6n-3}x_{6n-5}(-1+x_{6n-2}x_{6n-4}x_{6n-6})}=\dfrac{cea}{d\left( \dfrac{ace }{bd(-1+ace)}\right) \left( -1+cea\right) }=b,\\ x_{6n}&= \dfrac{x_{6n-1}x_{6n-3}x_{6n-5}}{ x_{6n-2}x_{6n-4}(-1+x_{6n-1}x_{6n-3}x_{6n-5})}=\dfrac{bd\left( \dfrac{ace}{ bd(-1+ace)}\right) }{ce\left( -1+bd\left( \dfrac{ace}{bd(-1+ace)}\right) \right) }=a. \end{aligned}$$

Finally,

$$\begin{aligned} x_{6n+1}=\dfrac{x_{6n}x_{6n-2}x_{6n-4}}{ x_{6n-1}x_{6n-3}(-1+x_{6n}x_{6n-2}x_{6n-4})}=\dfrac{ace}{db\left( -1+ace\right) }. \end{aligned}$$

Thus, the proof is completed.$\square$

Theorem 4

Equation (6) has a periodic solution of period three iff $e=b,\ d=a,$ $ace=2\$ and it will be taken the following form $\{x_{n}\}=\left\{ b,a,c,b,a,...\right\} .$

Proof

First, suppose that there exists a prime period three solution $\{x_{n}\}=\{ b,a,c,b,a,...\}$ of Eq. (6), we see from the form of the solution of Eq. (6) that

$$\begin{aligned} x_{6n-4}&= e=b,\quad x_{6n-3}=d=a,\quad x_{6n-2}=c, \\ x_{6n-1}&= b,\quad x_{6n}=a,\quad x_{6n+1}=\frac{ace}{bd(-1+ace)}=c, \end{aligned}$$

Then we get

$$\begin{aligned} e=b,\ \ d=a,\ \ ace=2. \end{aligned}$$

Second, assume that $e=b,\ \ d=a,\ \ ace=2.$ Then we see that

$$\begin{aligned} x_{6n-4}&= b,\quad x_{6n-3}=a,\quad x_{6n-2}=c, \\ x_{6n-1}&= b,\quad x_{6n}=a,\quad x_{6n+1}=c. \end{aligned}$$

Thus, we have a periodic solution of period three, and the proof is completed.

Theorem 5

Equation (6) has two equilibrium points which are $0,\root 3 \of {2}$ and the equilibrium point $\overline{x}=\root 3 \of {2}$ is nonhyperbolic.

Proof

For the equilibrium points of Eq. (6), we can write

$$\begin{aligned} \overline{x}=\dfrac{\overline{x}^{3}}{\overline{x}^{2}\left( -1+\overline{x} ^{3}\right) }. \end{aligned}$$

Then we have

$$\begin{aligned} \overline{x}^{3}\left( -1+\overline{x}^{3}\right) =\overline{x}^{3}, \end{aligned}$$

or

$$\begin{aligned} \overline{x}^{3}\left( \overline{x}^{3}-2\right) =0. \end{aligned}$$

Thus, the equilibrium points of Eq. (6) are $0,\root 3 \of {2}.$

Let $\ f:(0,\infty )^{5}\longrightarrow (0,\infty )$ be a function defined by

$$\begin{aligned} f(u,v,w,t,p)=\frac{uwp}{vt\left( -1+uwp\right) }. \end{aligned}$$

Therefore, it follows that

$$\begin{aligned} f_{u}(u,v,w,t,p)&= -\frac{wp}{vt\left( -1+uwp\right) ^{2}},\ \ f_{v}(u,v,w,t,p)=-\frac{uwp}{v^{2}t\left( -1+uwp\right) }, \\ f_{w}(u,v,w,t,p)&= -\frac{up}{vt\left( -1+uwp\right) ^{2}},\ \ \ f_{t}(u,v,w,t,p)=-\frac{uwp}{vt^{2}\left( -1+uwp\right) }, \\ f_{p}(u,v,w,t,p)&= -\frac{uw}{vt\left( -1+uwp\right) ^{2}}. \end{aligned}$$

We see that ( at $\overline{x}=\root 3 \of {2}$ )

$$\begin{aligned} f_{u}(\overline{x},\overline{x},\overline{x},\overline{x},\overline{x})&= -1,\quad f_{v}(\overline{x},\overline{x},\overline{x},\overline{x}, \overline{x})=-1,\quad f_{w}(\overline{x},\overline{x},\overline{x}, \overline{x},\overline{x})=-1, \\ f_{t}(\overline{x},\overline{x},\overline{x},\overline{x},\overline{x})&= -1,\quad f_{p}(\overline{x},\overline{x},\overline{x},\overline{x}, \overline{x})=-1. \end{aligned}$$

Thus, the characteristic equation about the equilibrium point $\overline{x}= \root 3 \of {2}$ is given by

$$\begin{aligned} \lambda ^{5}+\lambda ^{4}+\lambda ^{3}+\lambda ^{2}+\lambda +1=0. \end{aligned}$$

Also, we see that $\lambda =-1,$ one of the roots of this equation; then the equilibrium point $\overline{x}=\root 3 \of {2}$ is nonhyperbolic.$\square$

Numerical examples

Here, we will represent different types of solutions of Eq. (6).

Example 3

We consider Eq. (6) with $x_{-4}=11,\ x_{-3}=3,\ x_{-2}=9,\ x_{-1}=3,\ x_{0}=2$ (see Fig. 3).

Fig. 3

This figure shows the periodicity of the solution of the equation $x_{n+1}=\dfrac{x_{n}x_{n-2}x_{n-4}}{x_{n-1}x_{n-3}(-1+x_{n}x_{n-2}x_{n-4})},$ when the initial conditions $x_{-4}=11,\ x_{-3}=3,\ x_{-2}=9,\ x_{-1}=3,\ x_{0}=2$

Example 4

Figure 4 shows the behavior of the solutions of Eq.(6) with the initial conditions: $x_{-4}=5,\ x_{-3}=-3,\ x_{-2}=-2/15,\ x_{-1}=5,\ x_{0}=-3$.

Fig. 4

This figure shows the periodic behavior of the solution of Eq. (6) with the initial conditions $x_{-4}=5,\ x_{-3}=-3,\ x_{-2}=-2/15,\ x_{-1}=5,\ x_{0}=-3$

The following cases can be proved similarly.

4 The Third Equation $x_{n+1}=\frac{x_{n}x_{n-2}x_{n-4}}{x_{n-1}x_{n-3}(1-x_{n}x_{n-2}x_{n-4})}$

In this section, we get the expressions of the solution of the third equation in the following form:

$$\begin{aligned} x_{n+1}=\dfrac{x_{n}x_{n-2}x_{n-4}}{x_{n-1}x_{n-3}(1-x_{n}x_{n-2}x_{n-4})} ,\;\;\;n=0,1,..., \end{aligned}$$

(7)

where the initial values are arbitrary nonzero real numbers.

Theorem 6

Let $\{x_{n}\}_{n=-4}^{\infty }$ be a solution of Eq. (7). Then the solutions of Eq. (7) take the following form for $n=0,1,...$

$$\begin{aligned} x_{6n-4}&= e\mathop {\displaystyle \prod }\limits _{i=0}^{n-1}\left( \frac{1-6iace}{1-\left( 6i+2\right) ace}\right) ,\ \ \ \ \ \ \ \ x_{6n-3}=d\mathop {\displaystyle \prod }\limits _{i=0}^{n-1}\left( \frac{1-(6i+1)ace}{1-\left( 6i+3\right) ace}\right) , \\ x_{6n-2}&= c\mathop {\displaystyle \prod }\limits _{i=0}^{n-1}\left( \frac{1-(6i+2)ace}{1-\left( 6i+4\right) ace}\right) ,\ \ \ \ \ \ \ \ x_{6n-1}=b\mathop {\displaystyle \prod }\limits _{i=0}^{n-1}\left( \frac{1-(6i+3)ace}{1-\left( 6i+5\right) ace}\right) , \\ x_{6n}&= a\mathop {\displaystyle \prod }\limits _{i=0}^{n-1}\left( \frac{1-(6i+4)ace}{1-\left( 6i+6\right) ace}\right) ,\ \ \ \ x_{6n+1}=\frac{ace}{bd(1-ace)} \mathop {\displaystyle \prod }\limits _{i=0}^{n-1}\left( \frac{1-(6i+5)ace}{1-\left( 6i+7\right) ace} \right) , \end{aligned}$$

where $x_{-4}=e,\ x_{-3}=d,\ x_{-2}=c,\ x_{-1}=b,\ x_{0}=a.$

Theorem 7

Equation (7) has a unique equilibrium point which is the number zero, and this equilibrium point is nonhyperbolic.

Example 5

Assume that the initial values for Eq. (7) $x_{-4}=10,\ x_{-3}=4,\ x_{-2}=9,\ x_{-1}=6,\ x_{0}=2\$(see Fig. 5).

Example 6

See Fig. 6 since $x_{-4}=2,\ x_{-3}=7,\ x_{-2}=5,\ x_{-1}=8,\ x_{0}=12$.

Fig. 5

This figure shows the solution of Eq. (7) when $x_{-4}=10,\ x_{-3}=4,\ x_{-2}=9,\ x_{-1}=6,\ x_{0}=2$

Fig. 6

This figure shows the behavior of the solutions of the difference equation (7) with initial conditions $x_{-4}=2,\ x_{-3}=7,\ x_{-2}=5,\ x_{-1}=8,\ x_{0}=12$

5 The Fourth Equation $x_{n+1}=\frac{x_{n}x_{n-2}x_{n-4}}{x_{n-1}x_{n-3}(-1-x_{n}x_{n-2}x_{n-4})}$

Here, we obtain a form of the solutions of the equation

$$\begin{aligned} x_{n+1}=\dfrac{x_{n}x_{n-2}x_{n-4}}{x_{n-1}x_{n-3}(-1-x_{n}x_{n-2}x_{n-4})} ,\;\;\;n=0,1,..., \end{aligned}$$

(8)

where the initial values are arbitrary nonzero real numbers with $x_{-4}x_{-2}x_{0}\ne -1.$

Theorem 8

Let $\{x_{n}\}_{n=-4}^{\infty }$ be a solution of Eq. (8). Then every solution of Eq. (8) is periodic with period 6 and for $n=0,1,...$

$$\begin{aligned} x_{6n-4}&= e,\quad x_{6n-3}=d,\quad x_{6n-2}=c, \\ x_{6n-1}&= b,\quad x_{6n}=a,\quad x_{6n+1}=\frac{ace}{ bd(-1-ace)}, \end{aligned}$$

where$\;x_{-4}=e,\ x_{-3}=d,\ x_{-2}=c,\ x_{-1}=b,\ x_{0}=a.$

Theorem 9

Equation (8) has a periodic solution of period three iff $e=b,\ d=a,$ $ace=-2\$, and it will be taken the following form $\{x_{n}\}=\left\{ b,a,c,b,a,...\right\} .$

Theorem 10

Equation (8) has two equilibrium points which are $0,\root 3 \of {-2}$, and the equilibrium point $\overline{x}=\root 3 \of {-2}$ is nonhyperbolic.

Example 7

Consider $x_{-4}=-2,\ x_{-3}=7,\ x_{-2}=1/7,\ x_{-1}=-2,\ x_{0}=7\$(see Fig. 7).

Example 8

Figure 8 shows the solution of Eq. (8) with the initial conditions $x_{-4}=11,\ x_{-3}=-7,\ x_{-2}=13,\ x_{-1}=8,\ x_{0}=-3$.

Fig. 7

This figure shows the periodicity of the solution of Eq. (8) where the initial conditions equals $x_{-4}=-2,\ x_{-3}=7,\ x_{-2}=1/7,\ x_{-1}=-2,\ x_{0}=7$

Fig. 8

This figure shows the periodic nature of the solution of Eq. (8) where the initial conditions $x_{-4}=11,\ x_{-3}=-7,\ x_{-2}=13,\ x_{-1}=8,\ x_{0}=-3$