Inverse Hybrid Linear Multistep Methods for Solving the Second Order Initial Value Problems in Ordinary Differential Equations

Abstract

Inverse linear multistep methods (ILMMs) for first and second order differential equations have been proved to be suitable numerical methods for the solution of inverse initial value problems (IVPs). This paper presents the hybrid version of the ILMMs for the numerical solution of second order inverse IVPs. The stability of the proposed methods is represented in the boundary locus graph. The applicability of the schemes is demonstrated herein for the solution of linear and nonlinear problems. Computational results on the problems are compared with those from the existing method and ode45 (the explicit Runge–Kutta method).

Introduction

The modelling of real-life phenomenon may result in second order differential equations of the form

$$\begin{aligned} F \left( x,y, y', y'' \right) = 0, \quad y(a)=y_{0}, \quad y'(a)=y'_{0}, \quad a \le x \le b, \quad F \in {\mathbb {R}}^{m}. \end{aligned}$$

(1)

In this regard, we consider the two special classes of (1) which are:

$$\begin{aligned} y'' = f \left( x,y\right) , \quad y(a)=y_{0}, \quad y'(a)=y'_{0}, \quad a \le x \le b, \quad f \in {\mathbb {R}}^{m} \end{aligned}$$

(2)

and

$$\begin{aligned} y = \eta \left( x,y'' \right) , \quad y(a)=y_{0}, \quad y'(a)=y'_{0}, \quad a \le x \le b, \quad \eta \in {\mathbb {R}}^{m}. \end{aligned}$$

(3)

The initial value problem (IVP) (2) often occur in physical phenomenon such as mechanical systems without dissipation, satalite tracking and celestial mechanics [1]. Several numerical techniques have been used to solve the special class of the IVP (2). See for example, the works presented in [1, 7, 8, 19, 21, 22, 24] and other references herein. An example of a realistic problem emanating naturally from the theory of viscoelasticity that gives rise to an IVP of the form (3) is described in [2, 3]. However, the IVP (2) sometimes may be converted easily into the IVP (3). For instance, the situation when

$$\begin{aligned} f \left( x,y \right) = \omega y, \quad \omega \ne 0, \quad \omega \in {\mathbb {R}}. \end{aligned}$$

The equivalent IVP (3) is expressed as

$$\begin{aligned} \eta \left( x,y'' \right) = \omega ^{-1} f(x,y). \end{aligned}$$

That is,

$$\begin{aligned} y = \omega ^{-1} y''. \end{aligned}$$

The IVP (2) of the form

$$\begin{aligned} f \left( x,y'' \right) = \phi f(x,y) \end{aligned}$$

with function $\phi$ sometimes may be converted into the integration problem (3). As in [4,5,6], the LMM for solving the second order IVP (2) is given by

$$\begin{aligned} \sum _{j=0}^{k} {\bar{\alpha }}_{j} y_{n+j} = h^{2} \sum _{j=0}^{k} {\bar{\beta }}_{j} f_{n+j}, \quad k \ge 2. \end{aligned}$$

(4)

There is a vast literature on the development of efficient numerical methods from the LMM (4) for the solution of special second order IVP (for which $y'$ is explicitly missing) (2). See the works in [1, 7,8,9,10,11,12, 19, 22]. The direct application of the LMM (4) on IVP (2) has been found to be more advantageous than the application of the conventional LMM (4) on IVP (1) [1]. Alfeld [2] was the first to introduce the idea of ILMM for the first order IVPs. However, Krishnaiah [13] later extended the ILMM to the second order IVP of (3). To be precised further, we write the ILMM for IVP (3) as

$$\begin{aligned} h^{-2} \sum _{j=0}^{k} \alpha _{j} y_{n+j} = \sum _{j=0}^{k} \beta _{j} f_{n+j} \end{aligned}$$

(5)

where $\beta _{k}=1$, $y_{n+j} = \eta (x_{n+j},f_{n+j})$. The ILMM (5) is usually explicit when applied to the problem of the form (3) [13]. To be precise, we give an example of the ILMMs presented in [13] for $k = 4$ as

$$\begin{aligned} \begin{aligned} f_{n+4}&= -\beta _{3}f_{n+3}-\beta _{2}f_{n+2} -\beta _{1}f_{n+1}-\beta _{0}f_{n} +h^{-2} \Big ( (3+ 2 \beta _{3} + \beta _{2}-\beta _{0})y_{n+3} \\&\quad + (-8- 5 \beta _{3} -2 \beta _{2}+\beta _{1} +4\beta _{0})y_{n+2} + ( 7+ 4 \beta _{3} + \beta _{2} \\&\quad -2 \beta _{1}- 5 \beta _{0})y_{n+1} + ( -2- \beta _{3} + \beta _{1}+2\beta _{0})y_{n} \Big ). \end{aligned} \end{aligned}$$

The order of the method is $p = 1$ with non-vanishing error constant given in terms of $\beta _{j=0,1,2,3}$ as

$$\begin{aligned} C_{4} = \frac{1}{12} (-35-11 \beta _{3}+\beta _{2}+\beta _{1}-11 \beta _{0}). \end{aligned}$$

All the methods proposed in [13] are inspired by the introduction of the ILMM for the first order IVPs presented in [2]. The ILMM (5) has an associated local truncation error (LTE) difference operator

$$\begin{aligned} L [y(x_{n});h]=\sum _{j=0}^{k} \left[ h^{-2} \alpha _{j} y(x_{n+j})-\beta _{j} y''(x_{n+j}) \right] \end{aligned}$$

(6)

with $\alpha _{k} = 0$ and the arbitrarily often differentiable test function is $y(x_{n})$. On expanding $L [y(x_{n});h]$, we obtain

$$\begin{aligned} L [y(x_{n});h] = h^{-2} \left[ C_{0} y(x_{n})+C_{1} h y(x_{n}) + \cdots \right] \end{aligned}$$

(7)

where

$$\begin{aligned} C_{0}&= \alpha _{0} + \alpha _{1}+\cdots +\alpha _{k} \\ C_{1}&= \alpha _{1} + 2 \alpha _{2}+\cdots +k \alpha _{k} \\&\vdots \\ C_{q}&= \frac{1}{q!} \left( \alpha _{1} + 2^{q} \alpha _{2}+\cdots +k^{q} \alpha _{k} \right) - \frac{1}{(q-2)!} \left( \beta _{1} + 2^{q-2} \beta _{2}+\cdots +k^{q-2} \beta _{k} \right) ; \; \text {for} \; q \ge 2. \end{aligned}$$

Definition 1.1

[13] The ILMM (5) is of error order p if in (7), $C_{0} = C_{1} = \cdots = C_{p+2} = 0$, and the non-vanishing error constant in (7) is $C_{p+3} \ne 0$.

Lemma 1.2

[13] The ILMM (5) is consistent if it is of error order $p \ge 1$.

Remark 1.3

The corresponding definition of consistency for the second order LMM (4) is given in [4, 5, 9].

This paper is coordinated as following: In section two, the theory of the stability property of the family of ILMM(s) is considered. Section three presents the construction of the new hybrid version of the formula in (5). The stability graphs are considered in section four. Implementation process of the methods and the numerical results are presented and discussed in section five, and the concluding part of the paper followings.

Stability Properties of ILMMs

The stability of the ILMM (5) is examined via the application on the scalar test problem for second order IVPs (2,3)

$$\begin{aligned} y'' = - \lambda ^{2} y, \quad Re(\lambda ) >0 \end{aligned}$$

(8)

to obtain the stability polynomial

$$\begin{aligned} \prod (\xi , H) = \rho (\xi ) + H^{2} \sigma (\xi ), \quad H^{2} = \lambda ^{2} h^{2}. \end{aligned}$$

(9)

In this regard, the first and second characteristics polynomial of (5) are

$$\begin{aligned} {\rho }(\xi ) = \sum _{j=0}^{k-1} \alpha _{j} \xi ^{j} \quad \text {and} \quad \sigma (\xi ) = \sum _{j=0}^{k} \beta _{j} \xi ^{j}. \end{aligned}$$

The following are definitions, lemmas, and theorem based on the theory of ILMMs (5) in [13].

Definition 2.1

[13] The ILMM (5) is said to be absolutely stable for a given $H^{2} \in {\mathbb {C}}$, if for that $H^{2}$, all the roots $\xi _{m}$ of the stability polynomial (9) satisfy $\mid \xi _{m} \mid < 1$ for $m=1(1)k$.

Lemma 2.2

[13] The set $R = \lbrace H^{2} \in {\mathbb {C}} / absolutely\;stable for H^{2} \rbrace$ is called the interval of absolute stability.

It follows from the stability polynomial (9), the degree $d_1$ of the first characteristic polynomial $\rho (\xi )$ satisfies $d_1 \le k-1 < k$ whereas the degree $d_2$ of the second characteristic polynomial $\sigma (\xi )$ satisfies $d_2 = k$. Trivially, one of the zeros of the stability polynomial (9) approaches infinity as $H \rightarrow 0$ [13]. The implication is that the ILMM (5) is unstable for small values of H. It is of great importance to seek for ILMM (5) whose polynomial $\sigma (\xi )$ posses only roots of modulus less than unity, i.e., the Schur polynomial [13].

Definition 2.3

[13] The ILMM (5) is said to be infinite-stable if the second characteristics polynomial $\sigma (\xi )$ is a Schur polynomial.

Remark 2.4

The concept of infinite-stable is in a way dual to the concept of zero-stability. In the case of zero-stability, $H \rightarrow 0$ while the infinite-stability deals with the case where $H \rightarrow \infty$.

Definition 2.5

[13] The ILMM (5) is said to be strong infinite-stable if the first characteristics polynomial is $\rho (\xi ) = \xi ^{k}$, i.e., the roots are located on the origin, with the result that such formula are highly stable.

As in Krishnaiah [13], the strong infinite-stable ILMM is given by

$$\begin{aligned} f_{n+k} = h^{-2} \sum _{j=0}^{k-1} \alpha _{j} y_{n+j}. \end{aligned}$$

(10)

The coefficient $\alpha _{j}; j=0(1)k-1$ are expected to attain an order $k-3$ for a strong infinite-stable ILMM (5).

Lemma 2.6

[13] A consistent strongly infinite-stable ILMM (5) has step number $k \ge 4$.

The maximum attainable order of infinite-stability or strong infinite-stability of the ILMMs is stated in the following theorem.

Theorem 2.7

[13]

Case 1: Let $\sigma (\xi )$ be a polynomial of degree k (with $\beta _{k}=1)$. Then there exists a unique polynomial of degree $k-1$, such that the ILMM (5) defined by $\rho (\xi )$ and $\sigma (\xi )$ have order at least $k-3$.

Case 2: The maximum attainable order of infinite-stable ILMMs is $k-3$. For each $k \ge 4$, there exists a strong infinite-stable ILMM of order $k-3$.

The proof of the first order ILMMs version of theorem (2.7) can be found in [2]. However, we omit the proof for the second order ILMMs as it follows closely the lines of Alfeld’s proof in [2] for the first order. As far as the authors know, the ILMM developed in [13] is the only type of LMM (4) that has been applied to solve the second order IVPs. Hence, this paper is aimed at proposing a new class of ILMM (5) for solving the second order IVP (3). In the following section, our interest is to extend the ILMM (5) in [2] by adding an hybrid extension which gives room for hybrid predictors. The motivation behind this is based on the general role that a hybrid LMM plays in improving the stability and the order of the traditional LMM (4), see [1, 7, 9,10,11, 14, 15, 19, 22]. In fact, Felix and Okuonghae [19]; Ibrahim and Ikhile [22] have recently proposed hybrid methods with orders as high as four and sixteen respectively for IVP (2). Thus, the effect of relevant parameters in the extension will be discussed as follows.

Construction of the Generalized Hybrid Extension of ILMM

The class of method under investigation is the inverse hybrid linear multistep methods (IHLMMs)

$$\begin{aligned} \sum _{l=1}^{s} h^{(-2l)} \sum _{j=0}^{k-1} \alpha ^{(l)}_{j} y^{(2l-2)}_{n+j} = \sum _{l=1}^{s} \sum _{j=0}^{k} \beta ^{(l)}_{j} f\left( x^{(2l-2)}_{n+j},y^{(2l-2)}_{n+j}\right) +\sum _{l=1}^{s} Q^{(l)}_{v} f\left( x^{(2l-2)}_{n+v},y^{(2l-2)}_{n+v}\right) \end{aligned}$$

(11)

with the hybrid predictor

$$\begin{aligned} y_{n+v} =\sum _{l=1}^{s} h^{(-2l)} \sum _{j=0}^{k-1} \gamma ^{(l)}_{j} y^{(2l-2)}_{n+j} + \sum _{l=1}^{s} \psi ^{(l)}_{j} f\left( x^{(2l-2)}_{n+j},y^{(2l-2)}_{n+j}\right) . \end{aligned}$$

(12)

However, such method can be referred to as an Obreckoff type of method (see [10]). Here, $s = 1(1)k$, $\beta _{k} = 1$, k is the step number, h is the step length expressed as $h = x_{n+j}-x_{n}$, $v_{j}$ are the off-step points to be chosen as $v_{j} = k - \frac{1}{2}$ for an increasing k, $y''(x_{n+j},y_{n+j}) = f_{n+j}$,  $y''(x_{n+v},y_{n+v}) = f_{n+v}$. The IHLMM (11) has Runge-Kutta’s flavour which is called a $k-$stage general linear methods (GLMs), if $v \ne v_{k}$. Otherwise, it is called a single stage GLM [15]. The procedure for the development of this implicit linear multistep methods is identical to that of the explicit linear multistep methods; the basic difference being the range of integration [5]. In particular, the IHLMM of interest is given by

$$\begin{aligned} h^{-2} \sum _{j=0}^{k-1} \alpha _{j} y_{n+j} = \sum _{j=0}^{k} \beta _{j} f_{n+j} + Q_{v} f_{n+v} \end{aligned}$$

(13)

where $s=1$. The hybrid predictor is given by

$$\begin{aligned} y_{n+v} = h^{-2} \sum _{j=0}^{k-1} \gamma _{j} y_{n+j} + \sum _{j=0}^{k} \psi _{j} f_{n+j}. \end{aligned}$$

(14)

The method (13) approximates the hybrid quantities $y_{n+v}$ by an expression involving the quantities $\{y_{n+j}; f_{n+j}\}$ only. The introduction of the hybrid predictor is to improve the stability and the order of the ILMMs. More importantly, the off-step points is carefully chosen to ensure an improve stability features and LTE order. The crucial role hybrid predictor play in this regard is evident in the literature such as [7, 14, 19, 22] and other references herein. For $k = 4$ in (13), we have

$$\begin{aligned} \begin{aligned}&h^{-2} \Big (\alpha _{3} y_{n+3} + \alpha _{2} y_{n+2} + \alpha _{1} y_{n+1} + \alpha _{0} y_{n}\Big ) \\&\quad = f_{n+4}+ \beta _{3}f_{n+3}+\beta _{2}f_{n+2} +\beta _{1}f_{n+1}+\beta _{0}f_{n} + Q_{v}f_{n+v}. \end{aligned} \end{aligned}$$

(15)

We expand (15) using the Taylor’s series approach on Mathematica v11 to obtain the consistent equations in terms of $\beta _{j=0,1,2,3}$ and the off-step point v

$$\begin{aligned}&h^{-0}: \left( \alpha _0+\alpha _1+\alpha _2+\alpha _3\right) =0 \\&h^{-1}: \left( \alpha _1+2 \alpha _2+3 \alpha _3\right) =0\\&h^{-2}: \frac{1}{2} \left( -2 Q_v+\alpha _1+4 \alpha _2+9 \alpha _3-2 \left( 1+\beta _0+\beta _1+\beta _2+\beta _3\right) \right) =0 \\&h^{-3}:\frac{1}{6} \left( -6 v Q_v+\alpha _1+8 \alpha _2+27 \alpha _3-6 \left( 4+\beta _1+2 \beta _2+3 \beta _3\right) \right) =0\\&h^{-4}: \frac{1}{24} \left( -12 v^2 Q_v+\alpha _1+16 \alpha _2+81 \alpha _3-12 \left( 16+\beta _1+4 \beta _2+9 \beta _3\right) \right) . \end{aligned}$$

On solving the system of equations simultaneously, we obtain

$$\begin{aligned} \alpha _0= & {} -\frac{92-71 v+12 v^2+25 v \beta _0-12 v^2 \beta _0-13 \beta _1+19 v \beta _1-6 v^2 \beta _1-2 \beta _2+v \beta _2+33 \beta _3-29 v \beta _3+6 v^2 \beta _3}{11-18 v+6 v^2}\\ \alpha _1= & {} -\frac{3 \left( -84+77 v-14 v^2-19 v \beta _0+10 v^2 \beta _0+9 \beta _1-13 v \beta _1+4 v^2 \beta _1-2 \beta _2+5 v \beta _2-2 v^2 \beta _2-33 \beta _3+35 v \beta _3-8 v^2 \beta _3\right) }{11-18 v+6 v^2}\\ \alpha _2= & {} \frac{3\left( -76+83 v-16 v^2-13 v \beta _0+8 v^2 \beta _0+5 \beta _1-7 v \beta _1+2 v^2 \beta _1-6 \beta _2+11 v \beta _2-4 v^2 \beta _2-33 \beta _3+41 v \beta _3-10 v^2 \beta _3\right) }{11-18 v+6 v^2}\\ \alpha _3= & {} -\frac{-68+89 v-18 v^2-7 v \beta _0+6 v^2 \beta _0+\beta _1-v \beta _1-10 \beta _2+17 v \beta _2-6 v^2 \beta _2-33 \beta _3+47 v \beta _3-12 v^2 \beta _3}{11-18 v+6 v^2} \\ Q_v= & {} -\frac{35+11 \beta _0-\beta _1-\beta _2+11 \beta _3}{11-18 v+6 v^2} . \end{aligned}$$

The IHLMM for $k = 4$ is given by

$$\begin{aligned} f_{n+4}= & {} -\left( f_n \beta _0+f_{n+1} \beta _1+f_{n+2} \beta _2+f_{n+3} \beta _3-f_{n+v} \frac{ \left( 35+11 \beta _0-\beta _1-\beta _2+11 \beta _3\right) }{11-18 v+6 v^2} \right) \\&+ h^{-2}\Big (- y_{n+3}\frac{ \left( -68+89 v-18 v^2-7 v \beta _0+6 v^2 \beta _0+\beta _1-v \beta _1-10 \beta _2+17 v \beta _2-6 v^2 \beta _2-33 \beta _3+47 v \beta _3-12 v^2 \beta _3\right) }{11-18 v+6 v^2}\\&+y_{n+2} \frac{3 \left( -76+83 v-16 v^2-13 v \beta _0+8 v^2 \beta _0+5 \beta _1-7 v \beta _1+2 v^2 \beta _1-6 \beta _2+11 v \beta _2-4 v^2 \beta _2-33 \beta _3+41 v \beta _3-10 v^2 \beta _3\right) }{11-18 v+6 v^2} \\&-y_{n+1}\frac{3 \left( -84+77 v-14 v^2-19 v \beta _0+10 v^2 \beta _0+9 \beta _1-13 v \beta _1+4 v^2 \beta _1-2 \beta _2+5 v \beta _2-2 v^2 \beta _2-33 \beta _3+35 v \beta _3-8 v^2 \beta _3\right) }{11-18 v+6 v^2}\\&-y_n\frac{ \left( 92-71 v+12 v^2+25 v \beta _0-12 v^2 \beta _0-13 \beta _1+19 v \beta _1-6 v^2 \beta _1-2 \beta _2+v \beta _2+33 \beta _3-29 v \beta _3+6 v^2 \beta _3\right) }{11-18 v+6 v^2}\Big ) . \end{aligned}$$

The new IHLMM is of error order $p = 2$ with non-vanishing error constant given in terms of $\beta _{j=0,1,2,3}$ and v as

$$\begin{aligned} LTE_1= & {} \frac{1}{132+72 (-3+v) v}\Big (5 (-4+v) (23+2 v (-20+7 v))+v \left( 51-72 v+22 v^2\right) \beta _0 \\&-(1+v (3+2 (-3+v) v)) \beta _1- (-2+v) (5+2 (-4+v) v) \beta _2-99 \beta _3 \\&+v (213+2 v (-63+11 v)) \beta _3\Big ) y ^5 (x) h^5 . \end{aligned}$$

Similarly for the hybrid predator (14), at $k=4$, we have

$$\begin{aligned} \begin{aligned} y_{n+v}&= h^{-2}\left( \gamma _0y_n +\gamma _1y_{n+1}+\gamma _2y_{n+2}+\gamma _3y_{n+3} \right) +\psi _0f_n +\psi _1f_{n+1} \\&\quad +\psi _2f_{n+2}+\psi _3f_{n+3}+\psi _4f_{n+4}. \end{aligned} \end{aligned}$$

(16)

We employ the Taylor’s series approach to obtain the consistent equations

$$\begin{aligned}&h ^-0: -\left( -1+\gamma _0+\gamma _1+\gamma _2+\gamma _3\right) =0\\&h^-1:\left( v-\gamma _1-2 \gamma _2-3 \gamma _3\right) =0\\&h^-2: \frac{1}{2} \left( v^2-\gamma _1-4 \gamma _2-9 \gamma _3-2 \psi _0-2 \psi _1-2 \psi _2-2 \psi _3-2 \psi _4\right) =0 \\&h^-3: \frac{1}{6} \left( v^3-\gamma _1-8 \gamma _2-27 \gamma _3-6 \psi _1-12 \psi _2-18 \psi _3-24 \psi _4\right) =0 . \end{aligned}$$

On solving the system, we obtain

$$\begin{aligned} \ \gamma _0= & {} \frac{1}{6} \left( 6-11 v+6 v^2-v^3-12 \psi _0-6 \psi _1+6 \psi _3+12 \psi _4\right) \\ \gamma _1= & {} \frac{1}{2} \left( 6 v-5 v^2+v^3+10 \psi _0+4 \psi _1-2 \psi _2-8 \psi _3-14 \psi _4\right) \\ \gamma _2= & {} \frac{1}{2} \left( -3 v+4 v^2-v^3-8 \psi _0-2 \psi _1+4 \psi _2+10 \psi _3+16 \psi _4\right) \\ \gamma _3= & {} \frac{1}{6} \left( 2 v-3 v^2+v^3+6 \psi _0-6 \psi _2-12 \psi _3-18 \psi _4\right) . \end{aligned}$$

The hybrid predictor for $k=4$ is given by

$$\begin{aligned} y_{n+v}= & {} h^ {-2} \Big (\frac{1}{6} y_{n+3} \Big (2 v-3 v^2+v^3+6 \psi _0-6 \psi _2-12 \psi _3-18 \psi _4\Big ) \\&+\frac{1}{2} y_{n+1} \Big (6 v-5 v^2+v^3+10 \psi _0+4 \psi _1-2 \psi _2-8 \psi _3-14 \psi _4\Big ) \\&+\frac{1}{6} y_n \Big (6-11 v+6 v^2-v^3-12 \psi _0-6 \psi _1+6 \psi _3+12 \psi _4\Big ) \\&+\frac{1}{2} y_{n+2} \Big (-3 v+4 v^2-v^3-8 \psi _0-2 \psi _1+4 \psi _2+10 \psi _3+16 \psi _4\Big )\Big ) \\&+f_n \psi _0+f_{n+1} \psi _1+f_{n+2} \psi _2+f_{n+3} \psi _3+f_{n+4} \psi _4. \end{aligned}$$

The error order $p = 1$ and the LTE is given by

$$\begin{aligned} LTE_2 = \frac{1}{24} \left( (-3+v) (-2+v) (-1+v) v-22 \psi _0+2 \psi _1+2 \psi _2-22 \psi _3-70 \psi _4\right) y^4(x) h^4. \end{aligned}$$

For $k = 5$, see the appendix.

Stability of the Inverse Hybrid Linear Multistep Methods

We present the k-step IHLMM (13) for $k = 4$ with free parameters that does not only allow total control over the coefficients but also, ensure that the stability criteria described in Sect. 2 holds. The off-step point is given by $k-\frac{1}{2}$. For $k = 4, v= \frac{7}{2}$, we have the new IHLMM of error order $p = 2$ as

$$\begin{aligned} \begin{aligned} f_{4+n}&= -\left( f_n \beta _0+f_{n+1} \beta _1+f_{n+2} \beta _2+f_{n+3} \beta _3-\frac{2}{43} f_{n+\frac{7}{2}} \left( 35+11 \beta _0-\beta _1-\beta _2+11 \beta _3\right) \right) \\&\quad + h^ {-2} \Big (-\frac{2}{43} y_{n+3} \left( 23+49 \beta _0-\frac{5 \beta _1}{2}-24 \beta _2-\frac{31 \beta _3}{2}\right) \\&\quad +\frac{6}{43} y_{n+2} \left( \frac{37}{2}+\frac{105 \beta _0}{2}+5 \beta _1-\frac{33 \beta _2}{2}-12 \beta _3\right) \\&\quad -\frac{6}{43} y_{1+n} \left( 14+56 \beta _0+\frac{25 \beta _1}{2}-9 \beta _2-\frac{17 \beta _3}{2}\right) \\&\quad -\frac{2}{43} y_n \left( -\frac{19}{2}-\frac{119 \beta _0}{2}-20 \beta _1+\frac{3 \beta _2}{2}+5 \beta _3\right) \Big ). \end{aligned} \end{aligned}$$

(17)

The corresponding IHLMM predictor for (17) is given by

$$\begin{aligned} \begin{aligned} y_{\frac{7}{2}+n}&=h^ {-2}\Big ( \frac{1}{6} y_{n+3} \left( \frac{105}{8}+6 \psi _0-6 \psi _2-12 \psi _3-18 \psi _4\right) \\&\quad +\frac{1}{2} y_{n+1} \left( \frac{21}{8}+10 \psi _0+4 \psi _1-2 \psi _2-8 \psi _3-14 \psi _4\right) \\&\quad +\frac{1}{6} y_n \left( -\frac{15}{8}-12 \psi _0-6 \psi _1+6 \psi _3+12 \psi _4\right) \\&\quad +\frac{1}{2} y_{n+2} \left( -\frac{35}{8}-8 \psi _0-2 \psi _1+4 \psi _2+10 \psi _3+16 \psi _4\right) \Big )\\&\quad +f_n \psi _0+f_{n+1} \psi _1+f_{n+2} \psi _2+f_{n+3} \psi _3+f_{n+4} \psi _4. \end{aligned} \end{aligned}$$

(18)

The stability polynomial is obtained by substituting the hybrid predictor (18) into the main method (17), and then apply it on the scalar test problem (8). Where $v= \frac{7}{2}$, $\beta _{j=0,1,2,3} = 1$, $\psi _{j=0,1,2,3,4} = 0,$ have been incorporated to satisfy the stability polynomial

$$\begin{aligned} \prod (\xi ,H)= & {} \frac{165}{43}-\frac{390 e^{i \xi }}{43}+\frac{285}{43} e^{2 i \xi }-\frac{60}{43} e^{3 i \xi } \\&+ \Big (1+e^{i \xi }+e^{2 i \xi }+e^{3 i \xi }+e^{4 i \xi }-\frac{110}{43} \Big (-\frac{5}{16}\\&+\frac{21 e^{i \xi }}{16} -\frac{35}{16} e^{2 i \xi }+\frac{35}{16} e^{3 i \xi }\Big )\Big ) H. \end{aligned}$$

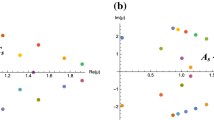
Figure 1 presents three stability graphs for $\beta _{j=0,1,2,3} = 0,1,10$, by keeping $v= \frac{7}{2}$ and $\psi _{j=0,1,2,3,4} = 0$ fixed.

Fig. 1

The stability graphs of IHLMM for k = 4 with $\beta _{j=0,1,2,3}=0$ (left), $\beta _{j=0,1,2,3}=1$ (middle), $\beta _{j=0,1,2,3}=10$ (right)

Furthermore, we present the summary of the interval of absolute stability of the IHLMM (11) for $k = 4,5,6$ in Table 1.

Table 1 Summary of the stability intervals of the IHLMM (11) for $k= 4,5,6$

The advantages of the proposed IHLMM (11) over the ILMM (5) in [13] are:

• 1. The IHLMM (11) can easily be extended to other forms of methods for an increasing k and s. The new formula (11) of ours generalises the work presented in [2] and [13].

• 2. Also, the LTE order p of the proposed IHLMM (11) is higher than the LTE order of the ILMM (5) in [13] for the same step number.

• 3. The methods IHLMM (11) and ILMM (5) allow the $\beta _{j}$ variation to attain strong-infinity stability criteria in Sect. 2 but the proposed IHLMM (11) has an additional hybrid predictor coefficients $\psi _{j}$ that could be varied for desired stability.

The Table 2 presents the order of ILMM (5) in [13] as compared to the order of IHLMM (11).

Table 2 Comparison of the order p of ILMM (5) in [13] and IHLMM (11)

In respect of the above advantages, we claim that the order of IHLMM (11) is higher than that of the ILMM (5) for thesame step number because of the introduction of hybrid parameter. We have also observed that choice of the hybrid parameter can be manipulated to guarantee a better stability. Furthermore, we established the following.

Lemma 4.1

Case 1: The minimum order of a consistent IHLMM (11) is $p \ge 2$.

Case 2: The minimum order of a consistent hybrid predictor (12) of the IHLMM (11) is $p \ge 1$.

However, we conjecture that for an increasing value of k with s fixed at one, the proposed IHLMM (11), will continue to satisfy the stability conditions presented in Sect. 2. Further comparison is the methods is given in Table 3.

Table 3 Comparison of ILMM (5) [13], IHLMM (11), and predictor (pre.) IHLMM (12)

Implementation of Methods and Numerical Results

This section presents the numerical experiment of the developed scheme using the GNU Octave v3 software. A class of IVPs to which the method (11) can be adopted is

$$\begin{aligned} y = \dfrac{z'' - \phi (x,y)}{-\lambda ^2} + z(x) \end{aligned}$$

where $\lambda$ is large and z(x) is the theoretical solution and $\phi$ could be linear or nonlinear. However, we shall consider implementing method (17) following the idea in [1, 7, 10, 11]. The approach of Newton-Raphson iterative method will be used to implement the method (17), unlike the method of Picard iterative techniques employed in [13]. In the method (17), we set $\beta _{j}$ to one (as in [13]), $\psi _{j}$ to zero, and then carefully choose the off-step point $v = \frac{7}{2}$ to ensure desirable stability. The method (17) can be expressed as

$$\begin{aligned}&f_n+f_{n+1}+f_{2+n}+f_{3+n}-\frac{110}{43} f_{n+\frac{7}{2}}+f_{n+4} \\&\quad = h^{-2} \Big (\frac{165 y_n}{43}-\frac{390 y_{1+n}}{43}+\frac{285 y_{n+2}}{43}-\frac{60 y_{n+3}}{43} \Big ) \end{aligned}$$

with the hybrid predictor given by

$$\begin{aligned} y_ {n+{\frac{7}{2}}}=-\frac{5 y_n}{16}+\frac{21 y_{n+1}}{16}-\frac{35 y_{n+2}}{16}+\frac{35 y_{n+3}}{16}. \end{aligned}$$

However, we adopt the use of the exact solution for the $\lbrace y_{n+j} \rbrace _{j=0,1,2,3}$ while the functions $\lbrace f_{n+j} \rbrace _{j=0,1,2,3}$ are obtained from the respective IVPs in Examples 1 and 2 for the case of IHLMM (17). Thus the Newton-Raphson iteration becomes

$$\begin{aligned} y_{n+1}^{[u+1]}=y_{n+1}^{[u]}-\Big (\ J(y_{n+1}^{[u]}) \Big )^{-1} F(y_{n+1}^{[u]}), \quad u=0,1,2,...,\tau , \end{aligned}$$

(19)

with the Jacobian,

$$\begin{aligned} J(y)= \dfrac{\partial F(y)}{\partial y}. \end{aligned}$$

(20)

The numerical method (17) is applied to solve the Examples 1 and 2. In the case of the IHLMM in (17),

$$\begin{aligned} F(y_{n+3}^{[u+1]})= & {} \frac{165 y_n}{43}-\frac{390 y_{n+1}}{43}+\frac{285 y_{n+2}}{43}-\frac{60 y^{[u]}_{n+3}}{43}\\&+h^2 \Big (f_n+f_{n+1}+f_{n+2} +f^{[u]}_{n+3} +f_{n+4}\\&-\frac{110}{43} \Big ( -\frac{5 y_n}{16}+\frac{21 y_{n+1}}{16}-\frac{35 y_{n+2}}{16}+\frac{35 y^{[u]}_{n+3}}{16}\Big )\Big ). \end{aligned}$$

Fig. 2

The schematic diagram of exact, IHLMM (17), and ode45 solutions for Example 1a ($x_n = 25$)

Fig. 3

The schematic diagram of exact and IHLMM (17) solutions for Example 1b ($h= 0.1, \Lambda = 0.1, x_n = 25$)

Fig. 4

The schematic diagram of exact and IHLMM (17) solutions for Example 2 ($h= 0.1, x_n = 20$)

Furthermore, the numerical results of the method (17) are compared with the results obtained from the work in [13], ode45 (based on the explicit Runge–Kutta method).

Example 1

Consider the linear inverse problem in [13]

$$\begin{aligned} y(x) = \dfrac{ y''(x) + \cos x }{- \lambda ^2} + \cos x \end{aligned}$$

(21)

where $\lambda ^2 = 10.$ The initial conditions are given by

$$\begin{aligned} (a): \quad y(0) = 1, \quad y'(0) = 0 \end{aligned}$$

and

$$\begin{aligned} (b): \quad y(0) = 1 + \Lambda , \quad y'(0) =0, \quad \Lambda = 0.0001. \end{aligned}$$

The exact solution is given by

$$\begin{aligned} y(x) = \left( y(0) - 1 \right) \cos 100x + y'(0) \sin 100 x + \cos x, \end{aligned}$$

where $x_0 = 0$ is the initial point while the absolute error will be taken at $x_n = 25$ (that is, the output point is taken at $x_n = 25$).

Example 2

Consider the nonlinear inverse problem in [13]

$$\begin{aligned} y = \dfrac{ y'' - \exp (2y)}{- \lambda ^2} - \log (1+x) \end{aligned}$$

(22)

where $\lambda ^2 = 100.$ The initial conditions are given by

$$\begin{aligned} y(0) = 0, \quad y'(0) = -1. \end{aligned}$$

The exact solution is given by

$$\begin{aligned} y(x) = -\log (1+x). \end{aligned}$$

Table 4 Comparison of the absolute error $\mid y_{n}-y(x_{n})\mid$ of the IHLMM (17), ILMM (5) in [13] and ode45 for Example 1a

Table 5 Comparison of the absolute error $\mid y_{n}-y(x_{n})\mid$ of the IHLMM (17) and ILMM (5) in [13] for Example 1b ($\Lambda = 0.0001, x_n = 25$)

Table 6 Comparison of the absolute error $\mid y_{n}-y(x_{n})\mid$ of the IHLMM (17) solution with the exact solution for Example 1b ($\Lambda = 0.1, x_n = 25$)

Table 7 Comparison of the absolute error $\mid y_{n}-y(x_{n})\mid$ of the IHLMM (17) and ILMM (5) in [13] for Example 2 with $h = 0.1$

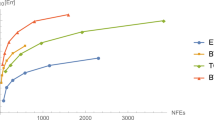
With respect to Sect. 4 and applying the Newton-Raphson iterative method to the Problems 1 and 2; it is seen that the numerical results from IHLMM (17) yielded better accuracy than that of the results in [13] and ode45 as shown in the graphical and numerical solutions (see Figures 2, 3, 4 and Tables 4, 5, 6, 7 respectively). This confirms the earlier discussion on the effect of introducing hybrid parameter in Sect. 3.

Furthermore, the order of the proposed IHLMMs (11) increases as the step number increases more than the order of a RKM for a comparable number of stages. The introduction of the hybrid improves the order and the stability of the method (11) as evident in Tables 1,  2,  3. In particular, the IHLMM of order $p = 4$ possess an interval of absolute stability that is larger than the order $p = 4$ of the RKM.

It is also important to note that the choice of step size is limited in the Runge–Kutta method likewise the order and region of absolute stability.

Conclusion

We have successfully developed the new IHLMMs (11) through the modification of the ILMMs (5) in [13]. The IHLMMs (11) attain higher order than that of ILMMs (5) for the same step number. We have also shown the pictorial representation of the interval of absolute stability by employing the boundary locus approach. The strength of the new method is shown by the encouraging numerical results when compared with the existing results in the literature and that of the explicit Runge–Kutta method (See Tables 4, 5, 6, 7) and (Figs. 2, 3, 4). More importantly, the numerical accuracy is as a result of larger interval of absolute stability which the IHLMMs (11) (with order $p = 4$ on Table 1) attain as compared to that of the ode45 (based on Runge-Kutta method of order $p = 4$ with stability interval of $(-2.8, 0)$) [6]. Hence, the results herein outperform the ones presented in [13], ode45 and could further compete with other emerging numerical methods proposed in [16, 19, 20, 22, 23] for solving IVPs.

Appendix

We go further for $k = 5$ in (13) to obtain

$$\begin{aligned} \begin{aligned}&h^{-2} \Big (\alpha _{4} y_{n+4} +\alpha _{3} y_{n+3} + \alpha _{2} y_{n+2} + \alpha _{1} y_{n+1} + \alpha _{0} y_{n}\Big ) \\&\quad = f_{n+5}\beta _{4}f_{n+4}+ \beta _{3}f_{n+3}+\beta _{2}f_{n+2} +\beta _{1}f_{n+1}+\beta _{0}f_{n} + Q_{v}f_{n+v}. \end{aligned} \end{aligned}$$

(23)

We expand (23) using the Taylor’s series approach on Mathematica v11 to obtain the consistent equations in terms of $\beta _{j=0,1,2,3,4}$ and the off-step point v

$$\begin{aligned}&h ^-0: \alpha _0+\alpha _1+\alpha _2+\alpha _3+\alpha _4 =0\\&h ^-1: \left( \alpha _1+2 \alpha _2+3 \alpha _3+4 \alpha _4\right) =0\\&h ^-2:\frac{1}{2} \left( -2 Q_v+\alpha _1+4 \alpha _2+9 \alpha _3+16 \alpha _4-2 \left( 1+\beta _0+\beta _1+\beta _2+\beta _3+\beta _4\right) \right) =0 \\&h ^-3:\frac{1}{6} \left( -6 v Q_v+\alpha _1+8 \alpha _2+27 \alpha _3+64 \alpha _4-6 \left( 5+\beta _1+2 \beta _2+3 \beta _3+4 \beta _4\right) \right) =0 \\&h ^-4: \frac{1}{24} \left( -12 v^2 Q_v+\alpha _1+16 \alpha _2+81 \alpha _3 +256 \alpha _4-12 \left( 25+\beta _1+4 \beta _2 \right. \right. \\&\left. \left. \quad +9 \beta _3+16 \beta _4\right) \right) =0 \\&h ^-5: \frac{1}{120} \left( -20 v^3 Q_v+\alpha _1+32 \alpha _2+243 \alpha _3+1024 \alpha _4-20 \left( 125+\beta _1 \right. \right. \\&\left. \left. \quad +8 \beta _2+27 \beta _3+64 \beta _4\right) \right) =0 . \end{aligned}$$

On solving the system of equations simultaneously, we obtain

$$\begin{aligned} \alpha _0= & {} -\frac{1}{12 A}\Big (1925-2085 v+690 v^2-70 v^3-435 v \beta _0+360 v^2 \beta _0-70 v^3 \beta _0 \\&+145 \beta _1-261 v \beta _1+138 v^2 \beta _1-22 v^3 \beta _1-10 \beta _2 \\&+ 21 v \beta _2-12 v^2 \beta _2+2 v^3 \beta _2-45 \beta _3+51 v \beta _3-18 v^2 \beta _3+2 v^3 \beta _3 \\&+460 \beta _4-531 v \beta _4+192 v^2 \beta _4-22 v^3 \beta _4\Big )\\ \alpha _1= & {} -\frac{1}{3 A}2 \Big (-790+1038 v-381 v^2+41 v^3+138 v \beta _0-126 v^2 \beta _0+26 v^3 \beta _0-38 \beta _1 \\&+66 v \beta _1-33 v^2 \beta _1+5 v^3 \beta _1+20 \beta _2-42 v \beta _2+24 v^2 \beta _2 \\&-4 v^3 \beta _2+18 \beta _3-24 v \beta _3+9 v^2 \beta _3 -v^3 \beta _3 \\&-200 \beta _4+282 v \beta _4-114 v^2 \beta _4+14 v^3 \beta _4\Big )\\ \alpha _2= & {} -\frac{1}{2 A}\Big (1345-2109 v+858 v^2-98 v^3-159 v \beta _0 \\&+168 v^2 \beta _0-38 v^3 \beta _0+29 \beta _1-45 v \beta _1+18 v^2 \beta _1 \\&-2 v^3 \beta _1-50 \beta _2+105 v \beta _2-60 v^2 \beta _2+10 v^3 \beta _2-9 \beta _3+3 v \beta _3 \\&+6 v^2 \beta _3-2 v^3 \beta _3+380 \beta _4-639 v \beta _4+288 v^2 \beta _4-38 v^3 \beta _4 Big)\\ \alpha _3= & {} \frac{1}{3 A}2 \Big (610-1092 v+489 v^2-59 v^3-42 v \beta _0+54 v^2 \beta _0 \\&-14 v^3 \beta _0+2 \beta _1-3 v^2 \beta _1+v^3 \beta _1-20 \beta _2+42 v \beta _2 -24 v^2 \beta _2+4 v^3 \beta _2 \\&+18 \beta _3-42 v \beta _3+27 v^2 \beta _3-5 v^3 \beta _3+200 \beta _4-378 v \beta _4+186 v^2 \beta _4-26 v^3 \beta _4\Big )\\ \alpha _4= & {} -\frac{1}{12 A}\Big (1205-2301 v+1122 v^2-142 v^3-51 v \beta _0+72 v^2 \beta _0 \\&-22 v^3 \beta _0+\beta _1 +3 v \beta _1-6 v^2 \beta _1+2 v^3 \beta _1-10 \beta _2+21 v \beta _2-12 v^2 \beta _2\\&+2 v^3 \beta _2+99 \beta _3-213 v \beta _3+126 v^2 \beta _3 -22 v^3 \beta _3+460 \beta _4\\&-915 v \beta _4+480 v^2 \beta _4-70 v^3 \beta _4\Big )\\ Q_v= & {} -\frac{45-10 \beta _0+\beta _1-\beta _3+10 \beta _4}{A} \end{aligned}$$

where $A = \left( -10+21 v-12 v^2+2 v^3\right)$. The IHLMM for $k = 5$ is given by

$$\begin{aligned}&-\frac{1}{12 A}y_{n+4} \Big (1205-2301 v+1122 v^2-142 v^3-51 v \beta _0+72 v^2 \beta _0-22 v^3 \beta _0 \\&\quad +\beta _1+3 v \beta _1-6 v^2 \beta _1+2 v^3 \beta _1-10 \beta _2+21 v \beta _2-12 v^2 \beta _2+2 v^3 \beta _2+99 \beta _3-213 v \beta _3 \\&\quad +126 v^2 \beta _3-22 v^3 \beta _3+460 \beta _4-915 v \beta _4+480 v^2 \beta _4-70 v^3 \beta _4\Big )\\&-\frac{1}{2 A}y_{n+2} \Big (1345-2109 v+858 v^2-98 v^3-159 v \beta _0+168 v^2 \beta _0 \\&\quad -38 v^3 \beta _0+29 \beta _1-45 v \beta _1+18 v^2 \beta _1-2 v^3 \beta _1-50 \beta _2 \\&\quad +105 v \beta _2-60 v^2 \beta _2+10 v^3 \beta _2-9 \beta _3+3 v \beta _3+6 v^2 \beta _3 \\&\quad -2 v^3 \beta _3+380 \beta _4-639 v \beta _4+288 v^2 \beta _4-38 v^3 \beta _4\Big )\\&+\frac{1}{3 A}2 y_{n+3} \Big (610-1092 v+489 v^2-59 v^3-42 v \beta _0+54 v^2 \beta _0-14 v^3 \beta _0 \\&\quad +2 \beta _1-3 v^2 \beta _1+v^3 \beta _1-20 \beta _2+42 v \beta _2-24 v^2 \beta _2+4 v^3 \beta _2+18 \beta _3 \\&\quad -42 v \beta _3+27 v^2 \beta _3-5 v^3 \beta _3+200 \beta _4-378 v \beta _4+186 v^2 \beta _4-26 v^3 \beta _4\Big )\\&-\frac{1}{12 A}y_n \Big (1925-2085 v+690 v^2-70 v^3-435 v \beta _0+360 v^2 \beta _0 \\&\quad -70 v^3 \beta _0+145 \beta _1-261 v \beta _1 +138 v^2 \beta _1-22 v^3 \beta _1 -10 \beta _2+21 v \beta _2-12 v^2 \beta _2 \\&\quad +2 v^3 \beta _2-45 \beta _3+51 v \beta _3 -18 v^2 \beta _3+2 v^3 \beta _3+460 \beta _4-531 v \beta _4 \\&\quad +192 v^2 \beta _4-22 v^3 \beta _4\Big )-\frac{1}{3 A}2 y_{n+1} \Big (-790+1038 v-381 v^2 +41 v^3 \\&\quad +138 v \beta _0-126 v^2 \beta _0+26 v^3 \beta _0-38 \beta _1 \\&\quad +66 v \beta _1-33 v^2 \beta _1+5 v^3 \beta _1 +20 \beta _2-42 v \beta _2+24 v^2 \beta _2-4 v^3 \beta _2+18 \beta _3\\&\quad -24 v \beta _3+9 v^2 \beta _3-v^3 \beta _3-200 \beta _4+282 v \beta _4-114 v^2 \beta _4 +14 v^3 \beta _4\Big )=h^2 \Big (f_{n+5}+f_n \beta _0\\&\quad +f_{n+1} \beta _1+f_{n+2} \beta _2+f_{n+3} \beta _3+f_{n+4} \beta _4 \\&\quad -f_{n+v}\frac{ \left( 45-10 \beta _0+\beta _1-\beta _3+10 \beta _4\right) }{A}\Big ). \end{aligned}$$

The new IHLMM for $k = 5$ is of error order $p = 3$ with non vanishing LTE given in terms of $\beta _{j=0,1,2,3,4}$, v, A as

$$\begin{aligned} LTE_1= & {} -\frac{1}{360 A}\Big (78680+9375 A-v (160746+v (-86262+v (11452+675 v))) \\&+(136+15 A) \beta _1+40 (59+6 A) \beta _2 +9 (1376+135 A) \beta _3+35920 \beta _4+3840 A \beta _4 \\&-v \Big (2 (498+v (-906+(476-75 v) v)) \beta _0+(186+v (18+v (-68+15 v))) \beta _1 \\&+6 \left( 826 \beta _2 +4351 \beta _3 +12406 \beta _4\right) +v \Big (472 (-6+v) \beta _2 \\&+(-15042+(2572-15 v) v) \beta _3 +2 (-20646+v (3116+75 v)) \beta _4\Big )\Big )\Big ). \end{aligned}$$

Similarly for $k=5$ in the hybrid predictor (14), we have

$$\begin{aligned} y_{n+v}= & {} h^{-2}\left( \gamma _0y_n +\gamma _1y_{n+1}+\gamma _2y_{n+2}+\gamma _3y_{n+3}+\gamma _4y_{n+4} \right) \\&+\psi _0f_n +\psi _1f_{n+1}+\psi _2f_{n+2}+\psi _3f_{n+3}+\psi _4f_{n+4} +\psi _5f_{n+5}. \end{aligned}$$

The consistent equations obtained using the Taylor’s series approach are given by

$$\begin{aligned}&h^-0: -\left( -1+\gamma _0+\gamma _1+\gamma _2+\gamma _3+\gamma _4\right) =0\\&h^-1: \left( v-\gamma _1-2 \gamma _2-3 \gamma _3-4 \gamma _4\right) =0\\&h^-2: \frac{1}{2} \left( v^2-\gamma _1-4 \gamma _2-9 \gamma _3-16 \gamma _4-2 \psi _0-2 \psi _1-2 \psi _2-2 \psi _3-2 \psi _4-2 \psi _5\right) =0\\&h^-3: \frac{1}{6} \left( v^3-\gamma _1-8 \gamma _2-27 \gamma _3-64 \gamma _4-6 \psi _1-12 \psi _2-18 \psi _3-24 \psi _4-30 \psi _5\right) =0\\&h^-4: \frac{1}{24} \left( v^4-\gamma _1-16 \gamma _2-81 \gamma _3-256 \gamma _4-12 \psi _1-48 \psi _2-108 \psi _3-192 \psi _4-300 \psi _5\right) =0. \end{aligned}$$

The coefficients after solving the system is given by

$$\begin{aligned} \gamma _0= & {} \frac{1}{24} \left( 24-50 v+35 v^2-10 v^3+v^4-70 \psi _0-22 \psi _1+2 \psi _2+2 \psi _3-22 \psi _4-70 \psi _5\right) \\ \gamma _1= & {} \frac{1}{6} \left( 24 v-26 v^2+9 v^3-v^4+52 \psi _0+10 \psi _1-8 \psi _2-2 \psi _3+28 \psi _4+82 \psi _5\right) \\ \gamma _2= & {} \frac{1}{4} \left( -12 v+19 v^2-8 v^3+v^4-38 \psi _0-2 \psi _1+10 \psi _2-2 \psi _3-38 \psi _4-98 \psi _5\right) \\ \gamma _3= & {} \frac{1}{6} \left( 8 v-14 v^2+7 v^3-v^4+28 \psi _0-2 \psi _1-8 \psi _2+10 \psi _3+52 \psi _4+118 \psi _5\right) \\ \gamma _4= & {} \frac{1}{24} \left( -6 v+11 v^2-6 v^3+v^4-22 \psi _0+2 \psi _1+2 \psi _2-22 \psi _3-70 \psi _4-142 \psi _5\right) . \end{aligned}$$

The hybrid predictor is then given by

$$\begin{aligned} y_{n+v}= & {} h^{-2}\Big (\frac{1}{24} y_{n+4} \Big (-6 v+11 v^2-6 v^3+v^4-22 \psi _0+2 \psi _1+2 \psi _2-22 \psi _3-70 \psi _4-142 \psi _5\Big ) \\&+\frac{1}{4} y_{n+2} \Big (-12 v+19 v^2-8 v^3 +v^4-38 \psi _0-2 \psi _1+10 \psi _2-2 \psi _3-38 \psi _4-98 \psi _5\Big ) \\&+\frac{1}{24} y_n\Big (24-50 v+35 v^2-10 v^3+v^4-70 \psi _0-22 \psi _1+2 \psi _2+2 \psi _3-22 \psi _4-70 \psi _5\Big ) \\&+\frac{1}{6} y_{n+1} \Big (24 v-26 v^2+9 v^3-v^4+52 \psi _0+10 \psi _1-8 \psi _2-2 \psi _3+28 \psi _4+82 \psi _5\Big ) \\&+\frac{1}{6} y_{n+3} \Big (8 v-14 v^2+7 v^3-v^4+28 \psi _0-2 \psi _1-8 \psi _2+10 \psi _3+52 \psi _4+118 \psi _5\Big )\Big ) \\&+\Big (f_n \psi _0+f_{n+1} \psi _1+f_{n+2} \psi _2+f_{n+3} \psi _3+f_{n+4} \psi _4+f_{n+5} \psi _5\Big ). \end{aligned}$$

Thus, the LTE is given by

$$\begin{aligned} LTE_2= & {} \frac{1}{120} \left( (-4+v) (-3+v) (-2+v) (-1+v) v+100 \psi _0 \right. \\&\left. -10 \psi _1+10 \psi _3-100 \psi _4-450 \psi _5\right) \end{aligned}$$

with the error order $p =2$.