Introduction

There are a lot of methods to solve differential equations. Spectral methods are the most important of these methods. They have many applications in the field of applied mathematics and scientific computing. For some of these applications, see [1,2,3]. The main idea of spectral methods is to approximate the solution of a differential equation by a finite sum of certain basis functions and then to determine the expansion coefficients in the sum in order to satisfy the differential equation and its conditions. In addition, we have some versions which are used to determine the expansion coefficients. They are the collocation, Galerkin and tau methods. In the first method, collocation, it enforce the residual of the given differential equation vanishes at given set of points. For example, Doha et al. [4] used the collocation method to solve nonlinear FDEs subject to initial/boundary conditions. For the second method, Galerkin, which requires choosing orthogonal polynomials as basis functions which satisfy the initial/boundary conditions of the given differential equation, and then enforcing the residual to be orthogonal with the basis functions. For example, Youssri and Abd-Elhameed [5] used the Galerkin method for solving time fractional telegraph equation. For the last method, tau, it is based on minimizing the residual and then, applying the initial/boundary conditions of the differential equation. For example, Abd-Elhameed and Youssri [6] used the tau method to solve coupled system of FDEs and also, in [7] they used the modified tau to solve some types of linear and nonlinear FDEs.

As known that second-order recurrence relations may generate many polynomial sequences. One of the most important of these sequences is the Fibonacci polynomials. The Fibonacci polynomial is a polynomial sequence which can be considered as a generalization circular for the Fibonacci numbers. It used in many applications like biology, statistics, physics, and computer science [8]. There are several studies that discussed practically Fibonacci polynomials and GFPs. For example, see [6, 9].

Fractional calculus is a generalization for ordinary differentiation and integration to an arbitrary (non-integer) order. It is a branch of the mathematical analysis which focus on studying the possibility of defining real/even complex number, powers of the differential operator and the integration operator. The fractional calculus is recently used in many fields of engineering, science, finance, applied mathematics, and engineering [10,11,12]. It is definitely hard to obtain analytical solutions for FDEs. Therefore, it is important approach to use numerical methods to obtain efficient and appropriate solutions to these equations. Many researches dealt with FDEs using many different methods. For example, the finite difference method [13], the Adomian decomposition method [14] and the ultraspherical wavelets method [15].

In accordance with the previous aspects, this paper focuses on the following two aspects:

  1. (i)

    Deriving operational matrices for integer and fractional derivatives of the GFPs.

  2. (ii)

    Presenting an algorithm for solving multi-term FDE by using collocation spectral method.

This paper is organized as follows: in “Preliminaries and Essential Relations” section, some necessary definitions and mathematical preliminaries of the fractional calculus is introduced. In “Generalized Fibonacci Operational Matrix of Fractional Derivatives” section, a new operational matrix of fractional derivatives of GFPs is presented. Section “A New Matrix Algorithm for Solving Multi-term FDE” is interested in solving one-dimensional multi-term FDE. In “Illustrative Examples” section, we apply the suggested method to several examples. Finally a conclusion is presented in “Concluding Remarks” section.

Preliminaries and Essential Relations

This section is devoted to presenting some important definitions of the fractional calculus.

Some Definition and Properties of the Fractional Calculus

Definition 1

As shown in Podlubny [16], the Riemann–Liouville fractional integral operator \(I^{\rho }\) of order \(\rho \) on the usual Lebesgue space \(L_1[0,1]\) is defined as

$$\begin{aligned} I^{\rho }h(y)= {\left\{ \begin{array}{ll} \frac{1}{\Gamma (\rho )}\displaystyle \int _{0}^{y}(y-t)^{\rho -1}h(t)dt,&{}\quad \rho >0, \\ h(y),&{}\quad \rho =0. \end{array}\right. } \end{aligned}$$
(1)

Definition 2

As shown in Podlubny [16], the Caputo definition of the fractional-order derivative is defined as:

$$\begin{aligned} D^{\rho }h(y)=\frac{1}{\Gamma (m-\rho )}\displaystyle \int _{0}^{y}(y-t)^{m-\rho -1}h^{(m)}(t)dt,\quad \rho>0 ,\quad y>0, \end{aligned}$$
(2)

where \(m-1\leqslant \rho <m,\; m\in {\mathbb {N}}\).

The operator \(D^{\rho }\) satisfies the following properties for \(\,m-1\leqslant \rho <m,\; m\in {\mathbb {N}},\)

$$\begin{aligned}&(i)\,(D^{\rho }\,I^{\rho }h)(y)=h(y),\\&(ii)\,(I^{\rho }\,D^{\rho }h)(y)=h(y)-\sum _{k=0}^{m-1}{\frac{h^{(k)}(0^+)}{\Gamma (k+1)}}(y-a)^k,\quad y>0,\\&(iii)D^{\rho }\,y^k=\frac{\Gamma (k+1)}{\Gamma (k+1-\rho )}\,y^{k-\rho },\quad k\in {\mathbb {N}},\quad k\ge \lceil \rho \rceil , \end{aligned}$$

where \(\lceil \rho \rceil \) denotes the smallest integer greater than or equal to \(\rho \).

Some Properties and Relations of the GFPs

The following recurrence relation

$$\begin{aligned} F_j(y)=y\,F_{j-1}(y)+F_{j-2}(y),\quad j\ge 2, \end{aligned}$$
(3)

generates the sequence of Fibonacci polynomials with the initial values: \(F_0(y)=0\) and \(F_1(y)=1\).

Let a and b be any two real constants, we define GFPs which may be generated with the aid of the following recurrence relation:

$$\begin{aligned} {\varphi _{j}^{a,b}}(y)=a\,y\,{\varphi _{j-1}^{a,b}}(y)+b\,{\varphi _{j-2}^{a,b}}(y),\quad j\ge 2, \end{aligned}$$
(4)

with the initial values: \({\varphi _{0}^{a,b}}(y)=0\) and \({\varphi _{1}^{a,b}}(y)=1\). The analytic form of \({\varphi _{j}^{a,b}}(y)\) is

$$\begin{aligned} {\varphi _{j}^{a,b}}(y)=\sum _{m=0}^{\left\lfloor \frac{j-1}{2}\right\rfloor } \left( {\begin{array}{c}j-m-1\\ m\end{array}}\right) (ay)^{j-2m-1}(b)^m, \end{aligned}$$
(5)

where \(\lfloor {j}\rfloor \) denotes the largest integer that less than or equal to j. Note that \({\varphi _{j}^{a,b}}(y)\) is a polynomial of degree \((j-1)\).

Now, let \({P_{j}^{a,b}}(y)\) of degree j which can be obtained by the following formula:

$$\begin{aligned} {P_{j}^{a,b}}(y)={\varphi _{j+1}^{a,b}}(y),\quad j\ge 0. \end{aligned}$$
(6)

This means that the sequence of polynomials \(\{{P_{j}^{a,b}}(y)\}\) is generated by the following recurrence relation:

$$\begin{aligned} {P_{j}^{a,b}}(y)=a\,y\,{P_{j-1}^{a,b}}(y)+b\,{P_{j-2}^{a,b}}(y),\quad j\ge 2, \end{aligned}$$
(7)

with the initial values: \({P_{0}^{a,b}}(y)=1\) and \({P_{1}^{a,b}}(y)=a\,y\).

The analytic form of \({P_{j}^{a,b}}(y)\) is

$$\begin{aligned} {P_{j}^{a,b}}(y)=\sum _{r=0}^{\left\lfloor \frac{j}{2}\right\rfloor } \left( {\begin{array}{c}j-r\\ r\end{array}}\right) (a\,y)^{j-2r}(b)^r, \end{aligned}$$
(8)

which can be expressed alternatively as:

$$\begin{aligned} {P_{j}^{a,b}}(y)=\sum _{k=0}^{j}{a^k}b^{\frac{j-k}{2}}\delta _{j+k} \left( {\begin{array}{c}\frac{j+k}{2}\\ \frac{j-k}{2}\end{array}}\right) y^k, \end{aligned}$$
(9)

where

$$\begin{aligned} \delta _r={\left\{ \begin{array}{ll} 1, &{}\quad \text{ if }\,\, r\,\text {even}, \\ 0, &{}\quad \text{ if }\,\, r\,\text {odd}. \end{array}\right. } \end{aligned}$$
(10)

For more properties about GFPs, see [17, 18].

Theorem 1

As shown by Abd-Elhameed and Youssri [6], for every nonnegative integer m, the following inversion formula holds:

$$\begin{aligned} y^m={a^{-m}}\sum _{i=0}^{\left\lfloor \frac{m}{2}\right\rfloor }\frac{(-1)^i \left( {\begin{array}{c}m\\ i\end{array}}\right) (m-2i+1)b^i}{m-i+1}{P_{m-2i}^{a,b}}(y). \end{aligned}$$
(11)

Remark 1

The inversion formula (11) can be written alternatively as:

$$\begin{aligned} y^m=2{a^{-m}}\sum _{\begin{array}{c} r=0 \\ {r+m\, \text {even}} \end{array}}^{m}\frac{(-b)^\frac{m-r}{2}\left( {\begin{array}{c}m\\ \frac{m-r}{2}\end{array}}\right) (r+1)}{m+r+1}{P_{r}^{a,b}}(y). \end{aligned}$$
(12)

Generalized Fibonacci Operational Matrix of Fractional Derivatives

This section is devoted to establish an operational matrix of fractional derivatives of the GFPs.

Operational Matrix of Integer Derivatives

Let u(y) be a square Lebesgue integrable function on (0,1) satisfies the following homogenous initial conditions:

$$\begin{aligned} u(0)=u^{(1)}(0)=u^{(2)}(0)=\cdots =u^{(n-1)}(0)=0. \end{aligned}$$

Assume that it can be written as a combination of a linearly independent GFPs:

$$\begin{aligned} u(y)=\sum _{j=0}^{\infty }{e_j}{\psi _{j}^{a,b}}(y), \end{aligned}$$
(13)

where

$$\begin{aligned} {\psi _{j}^{a,b}}(y)=y^n{P_{j}^{a,b}}(y). \end{aligned}$$
(14)

Suppose that u(y) can be approximated as:

$$\begin{aligned} u(y)\approx u_M(y)=\sum _{k=0}^{M}{e_k}{\psi _{k}^{a,b}}(y)=\varvec{E^T}\,\varvec{\psi (y)}, \end{aligned}$$
(15)

where

$$\begin{aligned} \varvec{E^T}=[e_0,e_1,\ldots ,e_M] \end{aligned}$$
(16)

and

$$\begin{aligned} \varvec{\psi (y)}=[y^n{P_{0}^{a,b}}(y),y^n{P_{1}^{a,b}}(y),\ldots , y^n{P_{M}^{a,b}}(y)]^T. \end{aligned}$$
(17)

At this end, the first derivative of the vector \(\varvec{\psi (y)}\) can be expressed in a matrix form as

$$\begin{aligned} \frac{d\varvec{\psi (y)}}{dy}=L\varvec{\psi (y)}+\varvec{\lambda }, \end{aligned}$$
(18)

where

$$\begin{aligned}&\displaystyle \varvec{\lambda }=(\lambda _0(y),\lambda _1(y),\ldots ,\lambda _M(y))^T, \end{aligned}$$
(19)
$$\begin{aligned}&\displaystyle \lambda _i(y)={\left\{ \begin{array}{ll} 0, &{}\quad \text{ if } i\, \text {odd},\\ n\,b^\frac{i}{2}y^{n-1}, &{}\quad \text{ if } i\, \text {even} , \end{array}\right. } \end{aligned}$$
(20)

and \(L=(l_{ij})_{0\le i,j\le M}\) is the \((M+1)\times (M+1)\) operational matrix of derivative given by:

$$\begin{aligned} l_{ij}={\left\{ \begin{array}{ll} a\,b^{\left\lfloor \frac{i-j}{2}\right\rfloor }(n+j+1), &{}\quad \text{ if } i>j,(i+j)\,\text {odd},{\left\lfloor \frac{i-j}{2}\right\rfloor }\,\text {even}, \\ a\,b^{\left\lfloor \frac{i-j}{2}\right\rfloor }(n-j-1), &{}\quad \text{ if } i>j,(i+j)\,\text {odd},{\left\lfloor \frac{i-j}{2}\right\rfloor }\,\text {odd}, \\ 0, &{}\quad \text{ otherwise }. \end{array}\right. } \end{aligned}$$
(21)

For example, for \(M=5\), one gets

$$\begin{aligned} L=\begin{bmatrix} 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \\ a(n+1)&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \\ 0&\quad a(n+2)&\quad 0&\quad 0&\quad 0&\quad 0 \\ a\,b(n-1)&\quad 0&\quad a(n+3)&\quad 0&\quad 0&\quad 0 \\ 0&\quad a\,b(n-2)&\quad 0&\quad a(n+4)&\quad 0&\quad 0 \\ a\,b^2(n+1)&\quad 0&\quad a\,b(n-3)&\quad 0&\quad a(n+5)&\quad 0 \end{bmatrix} \end{aligned}$$
(22)

Operational Matrix of Fractional Derivatives

Now, we will state and prove an important theorem. The following theorem displays the fractional derivatives of the vector \(\varvec{\psi (y)}\).

Theorem 2

Let \(\varvec{\psi (y)}\) be the GFP vector defined in Eq. (17). Then for all \(\alpha >0\) the following formula holds:

$$\begin{aligned} D^{\alpha }\varvec{\psi (y)}=\frac{d^{\alpha }\varvec{\psi (y)}}{dy^\alpha }=y^{-\alpha }L^{(\alpha )}\varvec{\psi (y)}, \end{aligned}$$
(23)

where \(L^{(\alpha )}=(l_{ij}^\alpha )_{0\le i,j\le M}\) is an \((M+1)\times (M+1)\) matrix and the elements can be written explicitly in the form

$$\begin{aligned} l_{ij}^\alpha ={\left\{ \begin{array}{ll} \beta _\alpha (i,j), &{}\quad \text{ if } i\ge j ,(i+j)\, \text {even}, \\ 0, &{}\quad \text{ otherwise }, \end{array}\right. } \end{aligned}$$
(24)

where

$$\begin{aligned} \beta _\alpha (i,j)=\sum _{k=\lceil \alpha \rceil }^{i+\lceil \alpha \rceil } \frac{(j+1)\,\delta _{i+k-\lceil \alpha \rceil }\,\delta _{j+k-\lceil \alpha \rceil }\,b^{\frac{i-j}{2}}\,\left( \frac{i+k-\lceil \alpha \rceil }{2}\right) !\, (-1)^{\frac{k-j-\lceil \alpha \rceil }{2}}\,(k+n-\lceil \alpha \rceil )!}{\left( \frac{i-k+\lceil \alpha \rceil }{2}\right) !\,\left( \frac{k-j-\lceil \alpha \rceil }{2}\right) !\,\left( \frac{j+k-\lceil \alpha \rceil }{2}\right) !\,\left( \frac{j+k+2-\lceil \alpha \rceil }{2}\right) \,\Gamma [1+n+k-\alpha -\lceil \alpha \rceil ]},\nonumber \\ \end{aligned}$$
(25)

\(\delta _r\) is defined in (10). The operational matrix \(L^{(\alpha )}\) can expressed explicitly as:

$$\begin{aligned} L^{(\alpha )}= \begin{bmatrix} \beta _\alpha (0,0)&\quad 0&\quad \dots&\quad 0 \\ 0&\quad \beta _\alpha (1,1)&\quad \dots&\quad 0 \\ \vdots&\quad \vdots&\quad \ddots&\quad \vdots \\ \beta _\alpha (M,0)&\quad \beta _\alpha (M,1)&\quad \vdots&\quad \beta _\alpha (M,M) \end{bmatrix} \end{aligned}$$
(26)

Proof

Equation (9) enables us to write Eq. (14) as

$$\begin{aligned} {\psi _{i}^{a,b}}(y)=\sum _{k=0}^{i}{a^k}b^{\frac{i-k}{2}}\delta _{i+k} \left( {\begin{array}{c}\frac{i+k}{2}\\ \frac{i-k}{2}\end{array}}\right) y^{k+n}. \end{aligned}$$
(27)

The application of the fractional differential operator \(D^\alpha \) to Eq. (27) yields

$$\begin{aligned} D^\alpha {\psi _{i}^{a,b}}(y)=\sum _{k=0}^{i}{\frac{\delta _{i+k}{a^k} b^{\frac{i-k}{2}}\left( \frac{i+k}{2}\right) !(n+k)!}{\left( \frac{i-k}{2}\right) !(k)!(k+n-\alpha )!}} y^{k+n-\alpha }, \end{aligned}$$
(28)

by using the formula given in (12) and performing some algebraic calculations we have

$$\begin{aligned} D^\alpha {\psi _{i}^{a,b}}(y)=y^{-\alpha }\sum _{j=0}^{i}\beta _\alpha (i,j) {\psi _{j}^{a,b}}(y), \end{aligned}$$
(29)

where \(\beta _\alpha (i,j)\) is given in (25). \(\square \)

A New Matrix Algorithm for Solving Multi-term FDE

In this section, we are interested in solving one-dimensional multi-term (FDE)

$$\begin{aligned} {D^{\alpha _1}}v(y)+\sum _{i=2}^{N}{\varepsilon _i}(y){D^{\alpha _i}}v(y)=f(y,v(y)),\quad y\in [0,1], \end{aligned}$$
(30)

which governed by the nonhomogeneous initial conditions:

$$\begin{aligned} v^{(i)}(0)=a_i,\quad i=0,1,\ldots ,n_1-1, \end{aligned}$$
(31)

where

$$\begin{aligned} {n_i-1}<{\alpha _i}\le n_i,\quad n_1\ge n_2\ge \cdots \ge n_N, \quad n_1,n_2,\ldots ,n_N\in {\mathbb {N}}, \quad a_i\in {\mathbb {R}}, \end{aligned}$$

and \(\epsilon _i:[0,1]\rightarrow {\mathbb {R}},\quad i=2,3,\ldots ,N,\quad f:[0,1]\times {\mathbb {R}}\rightarrow {\mathbb {R}}\)   is a given continuous function.

Nonhomogenous Initial Conditions

In the following, our aim is to illustrate how problems with nonhomogeneous initial conditions convert to problems with homogeneous initial conditions.

Let

$$\begin{aligned} v(y)=u(y)+\sum _{j=0}^{n_1-1}{c_j}\,{y^j}, \end{aligned}$$
(32)

then Eq. (30) becomes

$$\begin{aligned}&{D^{\alpha _1}}u(y)+\sum _{i=2}^{N}{\varepsilon _i}(y){D^{\alpha _i}} \left( u(y)+\sum _{j=0}^{n_1-1}{c_j}\,{y^j}\right) =f\left( y,u(y)+ \sum _{j=0}^{n_1-1}{c_j}\,{y^j}\right) , \nonumber \\&\quad y\in [0,1], \end{aligned}$$
(33)

where

$$\begin{aligned} c_j=\frac{1}{j!}\,a_j ,\quad j=0,1,\ldots ,n_1-1. \end{aligned}$$

The transformation (32) converts the nonhomogeneous initial conditions (31) to homogeneous initial conditions

$$\begin{aligned} u^{(i)}(0)=0,\quad i=0,1,\ldots ,n_1-1. \end{aligned}$$
(34)

With the aid of the approximations in Eqs. (15), (23). The residual of Eq. (33) takes the form

$$\begin{aligned} \begin{aligned} R(y)&=y^{-\alpha _1}\,{E^T} \,L^{(\alpha _1)}\,{\varvec{\psi (y)}}+\sum _{i=2}^{N}{\varepsilon _i}(y)\,y^{-\alpha _i}\,{E^T} L^{(\alpha _i)}\,{\varvec{\psi (y)}} \\&\quad +{\sum _{i=2}^{N}}{\sum _{j=0}^{n_1-1}}{\varepsilon _i} (y)\,{c_j}\,{\frac{\Gamma (j+1)}{\Gamma (j+1-\alpha _i)}\,y^{j-\alpha _i}}\\&\quad -f\left( y,E^T\, \varvec{\psi (y)}+{\sum _{j=0}^{n_1-1}{c_j}\,{y^j}}\right) . \end{aligned} \end{aligned}$$
(35)

We choose the equidistant collocation points    \(y_i=\frac{i}{M+2} ,\quad i=1,2,\ldots ,M+1\). As a result of collocation method, the following system of equations can be obtained as

$$\begin{aligned} R(y_i)=0,\quad i=1,2,\ldots ,M+1. \end{aligned}$$
(36)

Equation should be Eq. (36) form a nonlinear equations in the expansion coefficients \(e_i\). They may be solved with the aid of the well-known Newton’s iterative method by using the initial guess   \(\{e_i=10^{-i},\quad i=0,1,\ldots ,M\}.\)

Illustrative Examples

In this section, we apply the generalized Fibonacci collocation method (GFCM) which is presented in “A New Matrix Algorithm for Solving Multi-term FDE” section. Numerical results show that GFCM is applicable and effective.

Example 1

As given by Abd-Elhameed and Youssri [7], consider the nonlinear fractional initial value problem:

$$\begin{aligned} D^{0.5}u(y)+e^{u(y)}=9+y+\frac{2\,\cosh ^{-1}\left( \frac{3}{\sqrt{y}}\right) }{\sqrt{\pi }\,\sqrt{9+y}}, \quad u(0)=ln{(9)}, \quad y\in [0,1], \end{aligned}$$
(37)

where the exact solution of Eq. (37) is \(u(y)=ln(9+y)\).

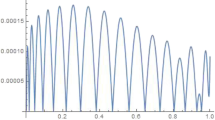
By applying GFCM to Eq. (37). The maximum absolute error (MAE) for different values of M are shown in Table 1. Also, Table 2 compares our results with this obtained in [7]. Moreover, Fig. 1 shows the absolute error for the case \(M=6\) and \(a=b=1\).

Table 1 MAE of Example 1
Full size table
Table 2 Comparison between best errors of Example 1
Full size table
Fig. 1
figure 1

The error of Example 1 when M=6

Full size image

Example 2

As given by Doha et al. [19], consider the initial value problem:

$$\begin{aligned} D^{\frac{5}{2}}u(y)-3D^{\frac{2}{3}}u(y)=f(y), \quad u(0)=1,\quad u'(0)=\gamma ,\quad u''(0)=\gamma ^2, \quad y\in [0,1],\qquad \end{aligned}$$
(38)

whose exact solution is given by \(u(y)=e^{\gamma {y}}\) and \(f(y)=\frac{e^{\gamma \,y}\,\gamma ^{\frac{2}{3}} \left[ \left( -3+\gamma ^{\frac{11}{6}}\,erf(\sqrt{\gamma \,y})\right) \,\Gamma (\frac{1}{3})+3\,\Gamma (\frac{1}{3},\gamma \,y)\right] }{\Gamma (\frac{1}{3})}\).

\(\Gamma (.)\) and \(\Gamma (.,.)\) are called gamma and incomplete gamma functions respectively [20] and \(\text {erf(y)}\) is defined as:

$$\begin{aligned} \text {erf(y)}=\frac{2}{\sqrt{\pi }}\int _{0}^{y}e^{-x^2}dx. \end{aligned}$$
(39)

We apply GFCM. In Table 3 we list the MAE of Eq. (38) for the case \(a=b=1\). Table 4 compares our results with those obtained in [19]. Figure 2 shows the absolute error for the case \(M=20\) at \(\gamma =1\) and \(a=b=1\).

Table 3 MAE of Example 2
Full size table
Table 4 Comparison between best errors of Example 2
Full size table
Fig. 2
figure 2

The error of Example 2 when \(M=20\) at \(\gamma =1\)

Full size image

Example 3

As given by Doha et al. [4], consider the initial value problem:

$$\begin{aligned} D^{\frac{3}{2}}u(y)+7D^{\frac{1}{4}}u(y)=g(y), \quad u(0)=1,\quad u'(0)=0 \quad y\in [0,1], \end{aligned}$$
(40)

where g(y) is chosen such that the exact solution is \(u(y)=\cos (\alpha y)\).

In Table 5, we introduce the MAE resulted from the application of GFCM for the case \(a=b=1\) and \(M=4,8,12\).

Table 5 MAE of Example 3
Full size table

Example 4

As given by Keshavarz et al. [21], in this example we consider the following Riccati fractional differential equation:

$$\begin{aligned} D^{\beta }u(y)+(u(y))^2=1, \quad u(0)=0, \quad y\in [0,1]. \end{aligned}$$
(41)

For \(\beta =1\), the exact solution is \(u(y)=\frac{e^{2y}-1}{e^{2y}+1}\).

In Table 6 we compare our results with those obtained in [21]. Figure 3 shows that the approximate solutions have smaller variations for values of \(\beta \) near the value 1.

Table 6 Comparison between different errors of Example 4 for the case \(M=5\)
Full size table
Fig. 3
figure 3

Different solutions of Example 4

Full size image

Concluding Remarks

The current work derived a general operational matrix of fractional derivatives of the GFPs together with the appropriate recruitment spectral collocation method. The results given in “Illustrative Examples” section demonstrated a good accuracy of this algorithm. The proposed algorithm can be applied to treat different kinds of FDEs. Therefore, the algorithm is powerful and propitious.