Wave Interactions in Non-ideal Isentropic Magnetogasdynamics

Abstract

In this paper, we consider the Riemann problem and wave interactions for a quasi-linear hyperbolic system of partial differential equations governing the one dimensional unsteady simple wave flow of an isentropic, non-ideal, inviscid and perfectly conducting compressible fluid, subject to a transverse magnetic field. This class of equations includes, as a special case of ideal isentropic magnetogasdynamics. We study the shock and rarefaction waves and their properties, and show the existence and uniqueness of the solution to the Riemann problem for arbitrary initial data under certain conditions and then we discuss the vacuum state in non-ideal isentropic magnetogasdynamics. We discuss numerical tests and study the solution influenced by the van der Waals excluded volume for different initial data along with all possible interactions of elementary waves.

Introduction

In the recent past, analysis of magnetogasdynamics has been the subject of great interest both from mathematical and physical point of view due to its applications in the variety of fields such as astrophysics, nuclear science, engineering physics and plasma physics, etc (see, [1–6] and the references cited therein). Lax [7] solved the Riemann problem for the case when the initial data consisting of constant states $U_l$ and $U_r$ are such that $U_l$ and $U_r$ are sufficiently small; here U is the vector of conserved variable with $U_l$ to the left of $x= 0$ and $U_r$ to the right of $x= 0$ separated by a discontinuity at $x= 0.$ Smoller [8] solved the Riemann problem by considering $U_l$ and $U_r$ to be arbitrary constant vectors; for details and methodologies, the reader is referred to the book by Smoller [9]. Smoller and Temple [10] demonstrated the existence of solutions with shocks for equations describing a perfect fluid in special relativity; this work was generalized by Chen [11] for the general isentropic relativistic gases. The striking features of wave interactions as well as the variety of engineering and physical situations where this phenomenon has to be faced gave rise over the years to a great and growing interest on this subject. For interaction of elementary waves in unsteady one-dimensional Euler equations, we refer to Smoller [9], and Chang and Hsiao [12]. Liu [13] is concerned with the interactions of the elementary waves for the nonlinear degenerate wave equations. Curro and Usco [14] investigated the nonlinear wave interactions for quasilinear hyperbolic $2\times 2$ systems. Ji and Zheng [15] are concerned with classical solutions for the interaction of two arbitrary planar rarefaction waves for the self-similar Euler equations in two space dimensions. The interaction of steady rarefaction waves, and the interaction of a rarefaction wave in a supersonic jet stream out of an orifice into the atmosphere is presented by Chen and Qu [16]. Liu and Sun [17] discussed the existence and uniqueness of the solutions for the Riemann problem in magnetogasdynamics and investigated the interactions of the elementary waves. Kuila and Raja Sekhar [18] investigated the elementary waves of the Riemann problem in magnetogasdynamics and construct the exact solution for it in different approach and compare exact solutions with numerical solutions. Solution of the Riemann problem in magnetogasdynamics have been obtained by Singh and Singh [19]. Radha and Sharma [20] studied the interaction of a weak discontinuity wave with the elementary waves of the Riemann problem for the one-dimensional Euler equations. Interactions of forward and backward centered rarefaction waves for pressure-gradient equations are presented by Zhang et al. [21]. Using the theory of progressive waves and some related procedures, waves of finite and moderately small amplitudes, influenced by the effects of non-linear convection, attenuation and geometrical spreading are studied by Ambika et al. [22] in an imperfect gas modeled by the van der Waals equation of state. Chadha and Jena [23] used the Lie group of transformations and obtained the whole range of self-similar solutions to the problem of propagation of shock waves through a non-ideal dusty gas.

Recently, Raja Sekhar and Sharma [24] studied the Riemann problem and elementary wave interactions for the one-dimensional unsteady simple flow of an isentropic, inviscid and perfectly conducting compressible fluid, subject to a transverse magnetic field

$$\begin{aligned}&\rho _{t} + (\rho u)_{x} = 0,\nonumber \\&(\rho u)_{t} + (p + \rho u^{2} + B^{2}/2\mu )_{x} = 0, \end{aligned}$$

(1)

where $\rho , u, p, B$ and $\mu$ denotes the density, velocity, pressure, transverse magnetic field and magnetic permeability respectively; $p = A\rho ^{\gamma }$ for ideal polytropic gas, A is positive constant and $\gamma$ is the adiabatic constant lies $1< \gamma < 2$ for most gases and $B = k_{2}\rho$ where $k_{2}$ is a positive constant.

In this paper, we consider a van der Waals gas obeying the equation of state [25, 26]:

$$\begin{aligned} p = k_{1}\left( \frac{\rho }{1 - a\rho }\right) ^{\gamma }, \end{aligned}$$

(2)

where $k_1$ is the constant and a the van der Waals excluded volume, which lies in the range $0\le a \le 0.05$ [25] and satisfying $1\gg a\rho \ge 0$ [26]. It may be noticed that the case $a = 0$ corresponds to the ideal gas. Our main purpose is to discuss all possible interactions of the elementary waves obtained in solving the Riemann problem for (3). By analyzing the explicit expressions of the shock waves and the rarefaction waves of the left state $U_l$ and the right state $U_r$ in the $(\rho , u)$ plane, we discuss the interactions of shock waves and rarefaction waves from the different family and the same family.

This paper is organized as follows. In Sect. 2, we study the elementary wave solutions and their properties of the Riemann problem, i.e., shock waves and rarefaction waves. In Sect. 3, we consider the Riemann problem for arbitrary initial data and show the existence and uniqueness of the solution under certain conditions and then we discuss the vacuum state in isentropic non ideal magnetogasdynamics. In Sect. 4, we present numerical examples for different initial data and discuss the solutions under the effect of van der Waals excluded volume a. We study all possible interaction of elementary waves in Sect. 5. Section 6 is devoted to some concluding remarks and ideas for further future work.

Elementary Waves and Their Properties

We consider the Riemann problem for the system (1), with piecewise constant initial data, separated by a discontinuity at $x = x_{0},$ in conservation form

$$\begin{aligned} \frac{\partial U}{\partial t} + \frac{\partial F(U)}{\partial x} = 0, \end{aligned}$$

(3)

where $U=(\rho , \rho u)^{tr}, F(U)=(\rho u, p + \rho u^{2} + B^{2}/2\mu )^{tr}$, tr denote the transformation and

$$\begin{aligned} U(x,t_{0})= {\left\{ \begin{array}{ll} U_{l}, &{} x < x_{0},\\ U_{r}, &{} x > x_{0}. \end{array}\right. } \end{aligned}$$

(4)

To carry out the characteristic analysis of (3), it is convenient to use the primitive variables $V = (\rho , u)^{tr}$. Then for smooth solution, system (3) is equivalent to

$$\begin{aligned} \frac{\partial V}{\partial t} + M(V)\frac{\partial V}{\partial x} = 0, \end{aligned}$$

(5)

where M(V) is a 2 $\times$ 2 matrix having components $M_{ij}$ with nonzero entries $M_{11} = M_{22} = u, M_{12} = \rho , M_{21} = \frac{w^{2}}{\rho },$ where $w = \sqrt{b^{2} + c^{2}}; b^{2} = k_{2}^{2}\rho /\mu$ and $c^{2} = k_{1}\gamma \rho ^{\gamma - 1}/(1 - a\rho )^{\gamma + 1}$. The eigenvalues of the system (5) are $\lambda _{1} = u - w$ and $\lambda _{2} = u + w.$ As the eigenvalues of M are real and distinct when $w > 0$; so it is strictly hyperbolic. Let r$^{(1)} = (- \rho , w)^{tr}$, r$^{(2)} = (\rho , w)^{tr}$, be the right eigenvectors corresponding to eigenvalues $\lambda _{1}$ and $\lambda _{2}$, respectively. Since $\nabla \lambda _{i}$.r$^{(i)} \ne 0$ for $i = 1, 2,$ so both the characteristic fields are genuinely nonlinear. Thus the elementary wave solutions of the system (3) consists of shocks or centred rarefaction waves.

Shock Waves

Suppose U is a weak solution of (3) such that $U_{l}$ and U are $C^{1}$ and extend continuously to the shock $x = x(t).$ Let $[U] = U_{l} - U$ be the jump discontinuity across the shock and $s = dx/dt$ the shock speed. Then, the following Rankine–Hugoniot (RH) jump conditions hold across the shock

$$\begin{aligned}&s[\rho ] = [\rho u], \end{aligned}$$

(6)

$$\begin{aligned}&s[\rho u] = [p + \rho u^{2} + B^{2}/2\mu ]. \end{aligned}$$

(7)

We have the following lemma.

Lemma 1

Let the states $U_{l}$ and U satisfy the Rankine–Hugoniot jump conditions (6) and (7). Let $S_{1} = S_{1}(U_{l})$ and $S_{2} = S_{2}(U_{l})$ respectively denote 1-shock and 2-shock curves associated with $\lambda _{1}$ and $\lambda _{2}$ characteristic fields. Then the shock curves satisfy

$$\begin{aligned} u = u_{l} - h(\rho _{l}, \rho ), \end{aligned}$$

(8)

where $h(\rho _{l}, \rho ) = \sqrt{\left( p + \frac{B^{2}}{2\mu } - p_{l} - \frac{B_{l}^{2}}{2\mu }\right) \left( \frac{\rho - \rho _{l}}{\rho \rho _{l}}\right) }$ such that for $1< \gamma < 2,$ we have for $\rho > \rho _{l}, u' < 0$ and $u'' > 0$ on $S_{1}$, whilst for $\rho < \rho _{l}$ we have $u' > 0$ and $u'' < 0$ on $S_{2}.$

Proof

Using (6) and (7), we get (8). Let $\phi (\rho ) = h^{2}(\rho _{l}, \rho )$; then differentiating (8) with respect to $\rho$ we obtain $u' = - \frac{\phi '(\rho )}{2\sqrt{\phi (\rho )}}.$ Since $\phi$ and $\phi '$ are positive for $\rho > \rho _{l}$ and therefore, $u' < 0.$ Let $\psi (\rho ) = (\phi '(\rho ))^{2} - 2\phi (\rho )\phi ''(\rho )$ and so $\psi '(\rho ) = - 2\phi (\rho )\phi '''(\rho )$. Further, for $1< \gamma < 2, \phi ''(\rho ) > 0,$ whilst $\phi '''(\rho ) < 0$ and hence $\psi '(\rho ) > 0.$ Thus $\psi (\rho ) > \psi (\rho _{l})$ for $\rho > \rho _{l}$ and $\psi (\rho _{l}) = 0.$ For $1< \gamma < 2$, we have $u'' = \frac{(\phi '(\rho ))^{2} - 2\phi (\rho )\phi ''(\rho )}{4\phi (\rho )^{3/2}} > 0$ on $S_{1}.$ In a similar manner, it follows that for $\rho < \rho _{l}$ and $1< \gamma < 2$, we have $u' > 0$ and $u'' < 0$ on $S_{2}.$

Here we are going to prove that the shock curves satisfy the Lax entropy conditions.

Theorem 2

Across 1-shock (respectively, 2-shock), $\rho _{l} < \rho$ and $u_{l} > u$ (respectively, $\rho _{l} > \rho$ and $u_{l} > u$) if, and only if, the Lax conditions hold, i.e.,

$$\begin{aligned} s_{1}< \lambda _{1}(U_{l}),\quad \lambda _{1}(U)< s_{1} < \lambda _{2}(U), \end{aligned}$$

(9)

and

$$\begin{aligned} \lambda _{1}(U_{l})< s_{2}< \lambda _{2}(U_{l}),\quad \lambda _{2}(U) < s_{2}. \end{aligned}$$

(10)

Proof

First, let us consider 1-shocks and prove $\lambda _{1}(U_{l}) > s_{1}$. Since $p' > 0$ and $p'' > 0$, by Lagrange’s mean value theorem, there exists a $\xi \in (\rho _{l},\rho )$ such that $p'(\xi ) = (p - p_{l})/(\rho - \rho _{l}).$ Furthermore, since $p'' > 0$, we have $p'(\xi ) > p'_{l} = c^{2}_{l}$ and thus $c^{2}_{l} < p'(\xi )\rho /\rho _{l},$ which implies that

$$\begin{aligned} c^{2}_{l} < \frac{(p - p_{l})\rho }{\rho _{l}(\rho - \rho _{l})}. \end{aligned}$$

(11)

Since $(\rho + \rho _{l})/2 > \rho _{l},$ we have $k_{2}^{2}(\rho + \rho _{l})/2\mu > k_{2}^{2}\rho _{l}/\mu$ thereby implies that $(B^{2} - B^{2}_{l})\rho /2\mu \rho _{l}(\rho - \rho _{l})> (B^{2} - B^{2}_{l})/2\mu (\rho - \rho _{l}) > B^{2}/\mu \rho _{l},$ and therefore

$$\begin{aligned} b^{2}_{l} < \frac{(B^{2} - B^{2}_{l})\rho }{2\mu \rho _{l}(\rho - \rho _{l})}. \end{aligned}$$

(12)

From (11) and (12), we obtain

$$\begin{aligned} w^{2}_{l} < \frac{\rho }{\rho _{l}(\rho - \rho _{l})} \left( p - p_{l} + \frac{B^{2} - B^{2}_{l}}{2\mu }\right) , \end{aligned}$$

(13)

this implies

$$\begin{aligned} \frac{-\rho \sqrt{(p - p_{l} + (B^{2} - B^{2}_{l})/2\mu )((1/\rho _{l}) - (1/\rho ))}}{\rho - \rho _{l}} < - w_{l}. \end{aligned}$$

(14)

In view of (9), the above inequality yields $\rho (u - u_{l})/ (\rho - \rho _{l}) < - w_{l}$, and hence $s_{1} < \lambda _{1}(U_{l}) = u_{l} - w_{l}.$

Next, since $p'' > 0$ and $\rho _{l} < \rho$ for 1-shock wave, we have $p'(\eta ) = (p - p_{l})/(\rho - \rho _{l}) < p'$ for some $\eta \in (\rho _{l}, \rho ),$ and hence

$$\begin{aligned} c^{2}_{l} > \frac{(p - p_{l})\rho _{l}}{\rho (\rho - \rho _{l})}. \end{aligned}$$

(15)

Furthermore, since $(\rho + \rho _{l})/2 < \rho ,$ it follows that

$$\begin{aligned} b^{2}_{l} > \frac{(B^{2} - B^{2}_{l})\rho _{l}}{2\mu \rho (\rho - \rho _{l})}, \end{aligned}$$

(16)

and hence from (15) and (16), we obtain

$$\begin{aligned} b^{2}_{l} + c^{2}_{l} > \frac{(B^{2} - B^{2}_{l})\rho _{l}}{2\mu \rho (\rho - \rho _{l})} + \frac{(p - p_{l})\rho _{l}}{\rho (\rho - \rho _{l})}, \end{aligned}$$

(17)

thereby implying that

$$\begin{aligned} \frac{\rho _{l} \sqrt{(p - p_{l} + (B^{2} - B^{2}_{l})/2\mu )((1/\rho _{l}) - (1/\rho ))}}{\rho - \rho _{l}} > - w. \end{aligned}$$

(18)

Also, from (6)–(9) imply that $u - w < (\rho u - \rho _{l} u_{l})/(\rho - \rho _{l}) = s_{1},$ and hence $\lambda _{1}(U) < s_{1}$.

Lastly, we show that $s_{1} < \lambda _{2}(U)$. From (19), we have

$$\begin{aligned} \sqrt{\frac{(B^{2} - B^{2}_{l})\rho _{l}}{2\mu \rho (\rho - \rho _{l})} + \frac{(p - p_{l})\rho _{l}}{\rho (\rho - \rho _{l})}} < w. \end{aligned}$$

For 1-shock curve, using (8) we obtain $\frac{(u - u_{l})\rho _{l}}{\rho - \rho _{l}} < w,$ which implies that $s_{1} < \lambda _{2}(U).$ Therefore 1-shock satisfies Lax conditions; proof for 2-shocks follows on similar lines.

Conversely, we want to prove that for 1-shock Lax conditions hold. It follows from (11) that for 1-shock waves, we have $s_{1} < u_{l} - w_{l}$, where $s_{1}$ is the speed of the one-shock wave, which implies that $w_{l} < \tilde{u_{l}}$ and $u - w< s_{1} < u + w$, and hence $|\tilde{u}| < w$. From (6), we have $\rho \tilde{u} = \rho _{l} \tilde{u_{l}}.$ Since $\rho$ and $\rho _{l}$ are positive, so both $\tilde{u}$ and $\tilde{u_{l}}$ must have the same sign. Therefore, $\tilde{u} > 0$ and $\tilde{u_{l}} > 0,$ the gas speed on both sides of the shock is greater than the shock speed, so particles cross the shock from the left to the right for one-shock waves. In the case of 2-shock waves, the shock inequalities give $|\tilde{u_{l}}| < w_{l}$ and $\tilde{u}< - w < 0,$ which imply that the shock speed is greater than the gas speed on both sides of the shock, and so the particles cross 2-shocks from the right to the left.

For both the shock families, $\tilde{u_{l}}$ and $\tilde{u}$ are non-zero so that $L = \rho \tilde{u} = \rho _{l} \tilde{u_{l}} \ne 0.$ Thus, for 1-shock waves, we have ${\tilde{u}^{2}_{l}} > w^{2}_{l}$ and $w^{2} > {\tilde{u}^{2}}$. From (7), yields

$$\begin{aligned} p + \rho \tilde{u}^{2} + B^{2}/2\mu = p_{l} + \rho _{l}\tilde{u_{l}}^{2} + B_{l}^{2}/2\mu , \end{aligned}$$

(19)

which, by virtue of the fact that ${\tilde{u}^{2}_{l}} > w^{2}_{l}$ and $w^{2} > {\tilde{u}^{2}}$, yields

$$\begin{aligned} p + \rho w^{2} + B^{2}/2\mu > p_{l} + \rho _{l}w^{2}_{l} + B_{l}^{2}/2\mu \end{aligned}$$

that is,

$$\begin{aligned} \left( 1 + \frac{\gamma }{1 - a\rho }\right) p + \frac{3k_{2}^{2}}{2\mu } \rho ^{2} > \left( 1 + \frac{\gamma }{1 - a\rho _{l}}\right) p_{l} + \frac{3k_{2}^{2}}{2\mu } \rho _{l}^{2}, \end{aligned}$$

which implies that $p > p_{l}$ and $\rho > \rho _{l}$, hence $B > B_{l}$, $u < u_{l}$. Since for one-shock waves, $\tilde{u}$ and ${\tilde{u}_{l}}$ are positive. In similar way, for 2-shock waves, we can prove that $p < p_{l}$ and $B < B_{l},$ hence $\rho < \rho _{l}$, $u < u_{l}$. Therefore, both the shock waves are compressive.

Now we show that the shock curves are starlike with respect to $(\rho _{l}, u_{l})$.

Theorem 3

The 1-shock and 2-shock curves are starlike with respect to $(\rho _{l}, u_{l})$ when $p = k_{1}\left( \frac{\rho }{1 - a\rho }\right) ^{\gamma }$ and $B = k_{2}\rho$ for values of $\gamma$ lying in the range $1< \gamma < 2.$

Proof

We shall show that any ray through the point $(\rho _{l}, u_{l})$ intersects 1-shock curve in at most one point; for this, it is sufficient to show that for any two rays through $(\rho _{l}, u_{l})$ and two different points $(\rho _{1}, u_{1})$, $(\rho _{2}, u_{2})$ on the 1-shock curve, their slopes are different.

The slope of the lines joining $(\rho _{l}, u_{l})$ with $(\rho _{1}, u_{1})$ and $(\rho _{2}, u_{2})$ are respectively $\frac{u_{1} - u_{l}}{\rho _{1} - \rho _{l}}$ and $\frac{u_{2} - u_{l}}{\rho _{2} - \rho _{l}}$. For the 1-shock curve, (8) implies that $\left( \frac{u - u_{l}}{\rho - \rho _{l}}\right) ^{2} = f_{1}(\rho ) + f_{2}(\rho ),$ where $f_{1}(\rho ) = \frac{p - p_{l}}{\rho _{l}\rho (\rho - \rho _{l})}$ and $f_{2}(\rho ) = \frac{B^{2} - B_{l}^{2}}{2\mu \rho _{l}\rho (\rho - \rho _{l})}.$

Now we show that $f'_{1}(\rho ) < 0$ and $f'_{2}(\rho ) < 0.$ Differentiate $f_{1}(\rho )$ with respect to $\rho ,$ we get

$$\begin{aligned} f'_{1}(\rho ) = \frac{\rho _{l}\rho (\rho - \rho _{l})p' - \rho _{l}(p - p_{l})(2\rho - \rho _{l})}{\rho _{l}^{2}\rho ^{2}(\rho - \rho _{l})^{2}}. \end{aligned}$$

Let $g_{1}(\rho ) = \rho _{l}\rho (\rho - \rho _{l})p' - \rho _{l}(p - p_{l})(2\rho - \rho _{l})$, so that $g_{1}(\rho _{l}) = 0.$ Now $g'_{1}(\rho ) = \rho _{l}\rho (\rho - \rho _{l})p'' - 2\rho _{l}(p - p_{l})$ and $g'_{1}(\rho _{l}) = 0.$ Further, using $p = k_{1}\left( \frac{\rho }{1 - a\rho }\right) ^{\gamma }$, we get $g''_{1}(\rho ) = -\frac{ k_{1}\gamma \rho _{l}\rho ^{\gamma - 2}}{(1- a\rho )^{\gamma + 3}}[ ((2- \gamma (\gamma - 1))\rho + (5\gamma - 3)a\rho _{l}\rho + (\gamma - 1)^{2}\rho _{l} + 4a^{2}\rho _{l}\rho ^{2}) - 4(\gamma + 1)a\rho ^{2}]$. Therefore, $g''_{1}(\rho ) < 0$ for $1< \gamma < 2, 0\le a \le 0.05$ and $1\gg a\rho \ge 0$. Across 1-shock wave, we have $\rho _{l} < \rho$ and $g'_{1}(\rho ) < g'_{1}(\rho _{l}) = 0,$ implying thereby that $g_{1}(\rho )$ is a decreasing function of $\rho .$ Thus, $g_{1}(\rho ) < g_{1}(\rho _{l})$, and $f'_{1}(\rho ) < 0.$ Again, we substitute $B = k_{2}\rho$ in $f_{2}(\rho )$ and differentiate with respect to $\rho$ obtain $f'_{2}(\rho ) = - \frac{k^2_2}{2\mu \rho ^2} < 0.$ Therefore, $\left( \frac{u - u_{l}}{\rho - \rho _{l}}\right)$ is an increasing function of $\rho ,$ since $\rho >\rho _{l}$ and $u < u_{l}$ for 1-shock wave, and hence 1-shock curve is starlike with respect to $(\rho _{l}, u_{l})$. Similarly, we can show that 2-shock curve is also starlike with respect to $(\rho _{l}, u_{l})$.

Rarefaction Waves

Here we construct the rarefaction wave curves. For an i rarefaction wave $(i = 1, 2)$, the two constant states $V_{l}$ and V are connected through a smooth transition in i-th genuinely nonlinear characteristic field, is a solution to (5) of the form

$$\begin{aligned} V(x,t)= {\left\{ \begin{array}{ll} V_{l}, &{} \frac{x}{t} \le \lambda _{i}(V_{l})\\ V(\frac{x}{t}), &{} \lambda _{i}(V_{l}) \le \frac{x}{t} \le \lambda _{i}(V)\\ V_{r}, &{} \frac{x}{t} \ge \lambda _{i}(V), \end{array}\right. } \end{aligned}$$

(20)

with $\lambda _{i}(V_{l}) \le \lambda _{i}(V).$ If we set $\varrho = \frac{x}{t}$, then the system (5) becomes $(M - \varrho I)(\dot{\rho }, \dot{u})^{tr} = 0,$ where I is a 2 $\times$ 2 identity matrix and an overhead dot denotes differentiation with respect to the variable $\varrho .$ If $(\dot{\rho }, \dot{u})^{tr} = (0, 0)$ then $\rho$ and u are constant; but as we are interested in non-constant solutions, we consider $(\dot{\rho }, \dot{u})^{tr} \ne (0, 0)$ and then it follows that $(\dot{\rho }, \dot{u})^{tr}$ is an eigenvector of the matrix M corresponding to the eigenvalue $\varrho .$ Since the matrix M has two real and distinct eigenvalues, $\lambda _{1} < \lambda _{2}$, there are two families of rarefaction waves, $R_{1}$ and $R_{2}$ which denote, respectively, 1-rarefaction waves and 2-rarefaction waves.

First we consider 1-rarefaction waves. Since $(M - \lambda _{1} I)(\dot{\rho }, \dot{u})^{tr} = 0$ with $\lambda _{1} = u - w,$ we have, $w \dot{\rho } + \rho \dot{u} = 0,$ implying thereby that

$$\begin{aligned} {\varvec{\Gamma }}_{1} = u + \int ^{\rho } \frac{w(\theta )}{\theta }d\theta = constant, \end{aligned}$$

(21)

which represents $R_{1}$ curves with ${\varvec{\Gamma }}_{1}$ as the 1-Riemann invariant. Similarly, 2-rarefaction wave curves are given by

$$\begin{aligned} {\varvec{\Gamma }}_{2} = u - \int ^{\rho } \frac{w(\theta )}{\theta }d\theta = constant, \end{aligned}$$

(22)

and ${\varvec{\Gamma }}_{2}$ is the 2-Riemann invariant.

Theorem 4

The $R_{1}$ curve is convex and monotonic decreasing while $R_{2}$ curve is concave and monotonic increasing.

Proof

The 1-rarefaction wave is given by

$$\begin{aligned} u = u_{l} + \int ^{\rho _{l}}_{\rho } \frac{w(\theta )}{\theta }d\theta ,\quad \mathrm{if} \;{\rho \le \rho _{l}} \end{aligned}$$

(23)

which on differentiating with respect to $\rho$, yields $\frac{du}{d\rho } = - \frac{w}{\rho } < 0,$ and subsequently,

$$\begin{aligned} \frac{d^{2}u}{d\rho ^{2}} = \frac{w}{\rho ^2} - \frac{w'}{\rho }. \end{aligned}$$

(24)

From (24), for $1< \gamma < 2$ yields $\frac{d^{2}u}{d\rho ^{2}} = \frac{\frac{k_{1}\gamma \rho ^{\gamma - 1}}{(1 - a\rho )^{\gamma + 2}}[2 - (\gamma - 1) - 4a\rho ] + \frac{k_{2}^{2}\rho }{\mu }}{2\rho ^{2}w} > 0$ and, therefore, u is convex with respect to $\rho$ for 1-rarefaction waves. In similar way, we can prove for 2-rarefaction waves.

Lemma 5

Across 1-rarefaction waves (respectively, 2-rarefaction waves), $\rho < \rho _{l}$ and $u > u_{l}$ (respectively, $\rho > \rho _{l}$, and $u > u_{l}$) if and only if, the characteristic speed increases from left hand to right hand state, i.e.,

$$\begin{aligned} \lambda _{i}(V_{l}) < \lambda _{i}(V), i = 1,2. \end{aligned}$$

(25)

Proof

Let the characteristic speed increases from left hand to right hand state. Therefore from the inequality (25) implies that

$$\begin{aligned} w - w_{l} < u - u_{l}, \end{aligned}$$

(26)

Further, since in 1-rarefaction wave region ${\varvec{\Gamma }}_{1}$ is constant, we have $u + \int ^{\rho } \frac{w(\theta )}{\theta }d\theta = u_{l} + \int ^{\rho _{l}} \frac{w(\theta )}{\theta }d\theta$, which by virtue of (26) yields $u + \int ^{\rho } \frac{w(\theta )}{\theta }d\theta < u_{l} + \int ^{\rho _{l}} \frac{w(\theta )}{\theta }d\theta$; which implies $\rho _{l} > \rho$ and $u_{l} < u.$ Similarly, for 2-rarefaction waves, we can prove that $\rho > \rho _{l}$ and $u > u_{l}$.

Conversely, for one-rarefaction wave, we assume that $\rho _{l} > \rho$ and $u_{l} < u.$ Then prove that the characteristic speed increases from the left to the right, that is, $\lambda _{1}(V_{l}) \le \lambda _{1}(V).$ Since $dw/d\rho = (p'' + (B')^{2}/\mu )/2w > 0, w$ is an increasing function of $\rho ;$ this implies that for one-rarefaction waves, $w(\rho ) \le w(\rho _{l})$ or equivalently $-w_{l} \le -w$. From $u_{l} \le u$ and $-w_{l} \le - w$ imply that $\lambda _{1}(V_{l}) \le \lambda _{1}(V).$ In similar way, we can prove this for the 2-rarefaction waves.

The Riemann Problem

We solve the Riemann problem (3) and (4) in the class of functions consisting of constant states, separated by either shocks or rarefaction waves. The solution of the Riemann problem consists of at most three constant states (including $U_{l}$ and $U_{r}$), which are separated either by a shock or a rarefaction wave. The Riemann invariant coordinates are

$$\begin{aligned} \nonumber {\varvec{\Gamma }}_{1} = u + \int ^{\rho } \frac{w(\theta )}{\theta }d\theta ,\\ {\varvec{\Gamma }}_{2} = u - \int ^{\rho } \frac{w(\theta )}{\theta }d\theta . \end{aligned}$$

(27)

Lemma 6

The mapping $(\rho , u) \longrightarrow ({\varvec{\Gamma }}_{1}, {\varvec{\Gamma }}_{2})$ is one to one and the Jacobian of this mapping is nonzero when $\rho > 0.$

Proof

From (27), we have $\frac{\partial {\varvec{\Gamma }}_{1}}{\partial \rho } = \frac{w}{\rho }, \frac{\partial {\varvec{\Gamma }}_{1}}{\partial u} = 1, \frac{\partial {\varvec{\Gamma }}_{2}}{\partial \rho } = - \frac{w}{\rho }$ and $\frac{\partial {\varvec{\Gamma }}_{2}}{\partial u} = 1.$ Thus, the Jacobian of the mapping $(\rho , u) \longrightarrow ({\varvec{\Gamma }}_{1}, {\varvec{\Gamma }}_{2})$ is $2w(\rho )/\rho ,$ which is one to one and onto when $\rho > 0.$

When $U_{r}$ is sufficiently close to $U_{l}$, the existence and uniqueness of the solution of Riemann problem for system (3) in the class of elementary waves follow from the general theorem of Lax, which applies to any system of conservation laws that is strictly hyperbolic and genuinely nonlinear in each characteristic field (see [6, 7]). For arbitrary data we discuss the existence of the solution of the Riemann problem for the system (3).

Fig. 1

Wave curves in $\rho -u$ plane for $a=0.0$ and $a=0.03$ as dotted and solid line respectively

Fig. 2

$U_r$ is in region I

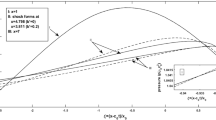
We consider the physical variables as coordinate system. We divide the $(\rho , u)$-plane into four disjoint open regions namely I, II, III and IV; separated by the curves $S_{1}, S_{2}, R_{1}, R_{2}$ as well as $S^{*}_{1}, S^{*}_{2}, R^{*}_{1}, R^{*}_{2}$ for $a = 0.03$ and $a = 0.0$ respectively; these curves are drawn in Fig. 1 for a given left state $U_{l}$. Indeed, we fix $U_{l}$ and allow $U_{r}$ to vary; if $U_{r}$ lies on any of the above four curves, then we have seen how to solve the problem. We thus assume that $U_{r}$ belongs to one of the four open regions I, II, III and IV as shown in Fig. 1.

As in [9], we define, for $\overline{U} \in {\mathbb {R}}^{+} \times {\mathbb {R}},$

$$\begin{aligned} S_{i}(\overline{U}) = \{(\rho , u): (\rho , u) \in S_{i}(\overline{U})\},\\ R_{i}(\overline{U}) = \{(\rho , u): (\rho , u) \in R_{i}(\overline{U})\}, \end{aligned}$$

and

$$\begin{aligned} T_{i}(\overline{U}) = S_{i}(\overline{U}) \cup R_{i}(\overline{U}), i = 1, 2. \end{aligned}$$

For fixed $U_{l} \in {\mathbb {R}}^{+} \times {\mathbb {R}},$ we consider the family of curves $S = \{T_{2}(\overline{U}): \overline{U} \in T_{1}(U_{l})\}.$ As the $(\rho , u)$ plane is covered univalently by the family of curves S,  i.e., through each point $U_{r}$, there passes exactly one curve $T_{2}(\overline{U})$ of S, the solution to the Riemann problem is given as follows; we connect $\overline{U}$ to $U_{l}$ on the right by a 1-wave (either shock or rarefaction wave), and then we connect $U_{r}$ to $\overline{U}$ on the right by a 2-wave (either $S_{2}$ or $R_{2}$). Indeed, depending on the position of $U_{r}$ we have different wave configurations.

Theorem 7

Let $U_{l}, U_{r} \in {\mathbb {R}}^{+} \times {\mathbb {R}}$ with $U_{l}$ fixed, and $U_{r}$ is allowed to vary then the Riemann problem is solvable.

Proof

Suppose first that $U_{r}$ lies in region I. Let the vertical line $\rho = \rho _{r}$ meet $R_{2}(U_{l})$ at B, and let it meet $S_{1}(U_{l})$ at A,  as shown in Fig 2. We observe that the subfamily of curves in S,  consisting of the set $\{T_{2}(\overline{U}) \equiv T_{2}(\overline{\rho }, \overline{u}): \rho _{l} \le \overline{\rho } \le \rho _{r}\},$ induces a continuous mapping $g \longrightarrow \varphi (g)$ from the arc $U_{l}A$ to the line segment AB, see Smoller [9]; indeed, the region I is covered by curves in S. So, let us suppose that $(\rho _{m}, u_{m})$ is the point which is mapped to $U_{r}$. Then

$$\begin{aligned} u = u_{l} + \int ^{\rho _{r}}_{\rho } \frac{w(\theta )}{\theta }d\theta - \sqrt{(p - p_{l} + (B^{2} - B^{2}_{l})/2\mu )((1/\rho _{l}) - (1/\rho ))} \end{aligned}$$

(28)

which on differentiation yields $\frac{du}{d\rho }|_{\rho = \rho _{m}} < 0,$ implying thereby that $(\rho _{m}, u_{m})$ is unique. Similarly, we can prove that uniqueness if $U_{r}$ is in region II, III and IV.

Thus if $U_{r} \in I$, then the solution to Riemann problem consists of 1-shock and a 2-rarefaction wave connecting $U_{l}$ to $U_{r}$. Suppose $U_{r}$ is in region II,  then the solution consists of shocks $S_{1}$ and $S_{2}$ joining $U_{l}$ to $U_{r}$. If $U_{r} \in III,$ then the solution of Riemann problem is obtained by connecting $U_{l}$ to $U_{r}$ by $R_{1}$, followed by $S_{2}.$ If $U_{r}$ is in region IV,  then the solution consists of 1-rarefaction wave and 2-rarefaction wave. Thus the set $\{T_{2}(\overline{U}): \overline{U} \in T_{1}(U_{l})\}$ covers the region I, II, III and IV in a 1-1 fashion. Therefore, the solution to the Riemann problem is solvable for arbitrary $U_{r}$ lying in any of the regions I, II, III and IV.

However the vacuum state $(\rho = 0)$ does occur in some cases and we have the following result:

Lemma 8

If ${\varvec{\Gamma }}_{1}(\rho _{l}, u_{l}) - {\varvec{\Gamma }}_{2}(\rho _{r}, u_{r}) \le 0,$ then the vaccum occurs.

Proof

Across 1-rarefaction wave, 1-Riemann invariant is constant, i.e., ${\varvec{\Gamma }}_{1}(\rho _{l}, u_{l}) = {\varvec{\Gamma }}_{1}(\rho _{m}, u_{m})$ and similarly across 2-rarefaction wave, 2-Riemann invariant is constant, i.e., ${\varvec{\Gamma }}_{2}(\rho _{m}, u_{m}) = {\varvec{\Gamma }}_{2}(\rho _{r}, u_{r}).$ So ${\varvec{\Gamma }}_{1}(\rho _{m}, u_{m}) - {\varvec{\Gamma }}_{2}(\rho _{m}, u_{m}) = {\varvec{\Gamma }}_{1}(\rho _{l}, u_{l}) - {\varvec{\Gamma }}_{2}(\rho _{r}, u_{r}) \le 0.$ But, ${\varvec{\Gamma }}_{1}(\rho _{m}, u_{m}) - {\varvec{\Gamma }}_{2}(\rho _{m}, u_{m}) = 2\int ^{\rho _{m}} \frac{w(\theta )}{\theta }d\theta$, which implies that $\rho _{m} = 0.$ Hence the proof.

Numerical Results and Discussions

For a given left state $U_{l}$ and a right state $U_{r}$, we give numerical algorithm to find the unknown state $U_{m}$ (see table 2) in (x, t) plane.

Case a For $\rho _{l} < \rho _{m}$ and $\rho _{r} \ge \rho _{m}$, we eliminating $u_{m}$ from (8) and (22) to obtain

$$\begin{aligned} u_{r} - u_{l} + h(\rho _{l}, \rho _{m}) + \int ^{\rho _{m}}_{\rho _{r}} \frac{w(\theta )}{\theta }d\theta = 0. \end{aligned}$$

(29)

Case b For $\rho _{l} \ge \rho _{m}$ and $\rho _{r} \ge \rho _{m}$, we obtain from (21) and (22), that

$$\begin{aligned} u_{r} - u_{l} + \int ^{\rho _{m}}_{\rho _{l}} \frac{w(\theta )}{\theta }d\theta + \int ^{\rho _{m}}_{\rho _{r}} \frac{w(\theta )}{\theta }d\theta = 0. \end{aligned}$$

(30)

Case c For $\rho _{l} \ge \rho _{m}$ and $\rho _{r} < \rho _{m}$, we eliminating $u_{m}$ from (21) and (8), we get

$$\begin{aligned} u_{r} - u_{l} + \int ^{\rho _{m}}_{\rho _{r}} \frac{w(\theta )}{\theta }d\theta + h(\rho _{m}, \rho _{r}) = 0. \end{aligned}$$

(31)

Case d For $\rho _{l} < \rho _{m}$ and $\rho _{r} < \rho _{m}$, we eliminating $u_{m}$ from (8),we get

$$\begin{aligned} u_{r} - u_{l} + h(\rho _{l}, \rho _{m}) + h(\rho _{m}, \rho _{r}) = 0. \end{aligned}$$

(32)

Thus, for all the four possible wave patterns (29)–(32), we obtain a single nonlinear equation

$$\begin{aligned} f_{r}(\rho _{m}, U_{r}) + f_{l}(\rho _{m}, U_{l}) + u_{r} - u_{l} = 0, \end{aligned}$$

(33)

where

$$\begin{aligned} f_{l}(\rho _{m}, U_{l}) = \left\{ \begin{array}{l l} h(\rho _{l}, \rho _{m}) &{} \quad \mathrm{if}\;{\rho _{m} > \rho _{l},}\\ \int ^{\rho _{m}}_{\rho _{l}} \frac{w(\theta )}{\theta }d\theta &{} \quad \mathrm{if}\;{\rho _{l} \ge \rho _{m},} \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} f_{r}(\rho _{m}, U_{r}) = \left\{ \begin{array}{l l} h(\rho _{m}, \rho _{r}) &{} \quad \mathrm{if}\; {\rho _{m} > \rho _{r},}\\ \int ^{\rho _{m}}_{\rho _{r}} \frac{w(\theta )}{\theta }d\theta &{} \quad \mathrm{if}\;{\rho _{r} \ge \rho _{m}.} \end{array} \right. \end{aligned}$$

We solve (33) for $\rho _{m}$ by using Newton–Raphson iterative procedure with a stop criterion when the relative error is less than $10^{-8}$; the initial guess for $\rho _{m}$ is taken to be the average value of $\rho _{l}$ and $\rho _{r}$. Once $\rho _{m}$ is known, the solution for the particle velocity $u_{m}$ can be obtained from (8) or (21) (respectively, from (8) or (22) depending on whether the 1-wave (respectively, 2-wave) is a shock or a rarefaction wave, the slope of the characteristic from (0, 0) to (x, t) is

$$\begin{aligned} \frac{dx}{dt} = \frac{x}{t} = u - w, \end{aligned}$$

(34)

where the particle velocity u and the magneto-acoustic speed w are functions of the unknown $\rho$. Since ${\varvec{\Gamma }}_{1}$ is constant in 1-rarefaction wave region we have

$$\begin{aligned} u = u_{l} + \int ^{\rho _{l}}_{\rho } \frac{w(\theta )}{\theta }d\theta , \end{aligned}$$

(35)

which in view of (34) yields

$$\begin{aligned} u_{l} + \int ^{\rho _{l}}_{\rho } \frac{w(\theta )}{\theta }d\theta - \frac{x}{t} - w = 0. \end{aligned}$$

(36)

Equation (36) is solved for $\rho$ using Newton–Raphson method and then u is found from (35). In a similar way, we find the solution inside the 2-rarefaction wave.

Four Riemann problems are selected to test the performance of numerical scheme highlighting the influence of van der Waals excluded volume, which enters into calculation through the parameter a. From the solution of the Riemann problem, we illustrate some typical wave patterns using MATLAB. Table 1 presents the data for all the four tests in terms of primitive variables. In all these cases, we consider the ratio of specific heat as $\gamma = 1.4$. The solutions of the Riemann problem with the given data (Table 1) for $k_1 = 1.0, k_2 = 1.0, \mu = 1.0$ and $a = 0.0, a = 0.015, a = 0.03$ are respectively given in Table 2.

Table 1 Initial data for Riemann problem

Table 2 Solution of the Riemann problem for $a = 0.0, a = 0.015$ and $a = 0.03$ with the initial data from Table 1

Fig. 3

Test 1: The solution for density and velocity at time $t=0.085$ for different values of a

Let us now focus on the influence of the van der Waals excluded volume through the parameter a. The main differences are related to the velocity, wave speed, position and the values of the intermediate states (region of unknown solutions) of each structure.

In test 1, the solution of the Riemann problem consists of a left and right shock waves; the solution profiles at time $t=0.085$ are shown in Fig. 3. Consequently, as it can be observed looking at density $(\rho )$ that the left shock wave is located at $x = 0.39832, x = 0.36179$ and $x = 0.25299,$ and the right wave is located at $x = 0.74142, x = 0.77794$ and $x = 0.88671$ for $a=0.0, a=0.015$ and $a=0.03$, respectively (see Fig. 3). It is observed that the left shock speed decreases and right shock speed increases when the van der Waals excluded volume a increases.

Fig. 4

Test 2: The solution for density and velocity at time $t=0.16$ for different values of a

In test 2, the solution consists of a left shock wave and right rarefaction wave; the solution profiles at time $t=0.16$ are shown in Fig. 4. In this case, the velocity decreases when the van der Waals excluded volume a increases. In particular, the intermediate states for density and velocity are higher when a is higher.

Fig. 5

Test 3: The solution for density and velocity at time $t=0.20$ for different values of a

In test 3, the solution consists of a left rarefaction wave and a right shock wave; the solution profiles at time $t=0.20$ are shown in Fig. 5. Let us focus on the position of head of the left rarefaction wave and the right shock wave for density profile. The head of the left rarefaction wave is located at $x = -0.73529, x = -0.77959$ and $x = -0.85504$, and the right shock wave is located at $x = 0.83247, x = 0.85841$ and $x = 0.89256$ for $a=0.0, a=0.015$ and $a=0.03$. The velocity increases for the van der Waals excluded volume a increases.

Fig. 6

Test 4: The solution for density and velocity at time $t=0.15$ for different values of a

In test 4, the solution consists of a left rarefaction wave and right rarefaction wave; the solution profiles at time $t=0.15$ are shown in Fig. 6. From this test case, we noticed that the intermediate states and velocity increases for the increases of a. For the density profile, the wave speed for right rarefaction wave increases when a increases but decreases for left rarefaction wave.

Interaction of Elementary Waves

The interaction of elementary waves, obtained from the Riemann problem (4), gives rise to new emerging elementary waves. We define the initial function, with two jump discontinuities at $x_{1}$ and $x_{2}$, as follows:

$$\begin{aligned} U(x,t_{0})= {\left\{ \begin{array}{ll} U_{l}, &{} -\infty< x \le x_{1}\\ U_{*}, &{} x_{1}< x \le x_{2}\\ U_{r}, &{} x_{2}< x < \infty , \end{array}\right. } \end{aligned}$$

(37)

with an appropriate choice of $U_{*}$ and $U_{r}$ in terms of $U_{l}$ and arbitrary $x_{1}$ and $x_{2} \in {\mathbb {R}}$. With the above initial data, we have two Riemann problems locally. An elementary wave of the first Riemann problem may interact with an elementary wave of the second Riemann problem, and a new Riemann problem is formed at the time of interaction.

Here, we use the notation $S_{2}R_{1} \rightarrow R_{1}S_{2}$, which means that a 2-shock wave, $S_{2}$, of first Riemann problem (connecting $U_{l}$ to $U_{*}$) interacts with 1-rarefaction, $R_{1}$, of second Riemann problem (connecting $U_{*}$ to $U_{r}$ ), and the interaction leads to a new Riemann problem (connecting $U_{l}$ to $U_{r}$ via $U_{m}$), the solution of which consists of 1-rarefaction, $R_{1}$, and 2-shock wave $S_{2}$ (i.e., $R_{1}S_{2}$). The possible interactions of elementary waves belonging to different families are $R_{2}R_{1}, R_{2}S_{1}, S_{2}R_{1}$ and $S_{2}S_{1}$ while the elementary waves belonging to same families are $R_{2}S_{2}, S_{2}R_{2}, S_{1}R_{1}, R_{1}S_{1}, S_{1}S_{1}$ and $S_{2}S_{2}.$

Interaction of Elementary Waves from Different Families

(i) Collision of two shocks $(S_{2}S_{1})$: We consider that $U_{l}$ is connected to $U_{*}$ by 2-shock, $S_{2}$, of first Riemann problem and $U_{*}$ is connected to $U_{r}$ by a 1-shock, $S_{1}$, of second Riemann problem. In other words, for a given $U_{l}$, we choose $U_{*}$ and $U_{r}$ in such a way that $\rho _{*} < \rho _{l}, u_{*} = u_{l} - h(\rho _{l}, \rho _{*})$ and $\rho _{*} < \rho _{r}, u_{r} = u_{*} - h(\rho _{*}, \rho _{r}).$ Since speed of 2-shock of the first Riemann problem is positive and speed of 1-shock of the second Riemann problem is negative, $S_{2}$ overtakes $S_{1}$. In order to show that for any arbitrary state $U_{l}$, the state $U_{r}$ lies in the region II (see Fig. 7), it is sufficient to prove that $h(\rho _{*}, \rho ) - h(\rho _{l}, \rho ) + h(\rho _{l}, \rho _{*}) > 0$ for $\rho _{*} < \rho _{l}$ and $\rho _{*} < \rho .$ Suppose $h(\rho _{*}, \rho ) - h(\rho _{l}, \rho ) + h(\rho _{l}, \rho _{*}) \le 0$. Then $h^{2}(\rho _{l}, \rho _{*}) + h^{2}(\rho _{*}, \rho ) + 2h(\rho _{l}, \rho _{*})h(\rho _{*}, \rho ) \le h^{2}(\rho _{l}, \rho )$, which implies that

$$\begin{aligned}&\nonumber \left( p_{*} + \frac{B_{*}^{2}}{2\mu } - p - \frac{B^{2}}{2\mu }\right) \left( \frac{1}{\rho _{l}} - \frac{1}{\rho _{*}}\right) + \left( p_{*} + \frac{B_{*}^{2}}{2\mu } - p_{l} - \frac{B_{l}^{2}}{2\mu }\right) \left( \frac{1}{\rho } - \frac{1}{\rho _{*}}\right) \\&\qquad +\, 2h(\rho _{l}, \rho _{*})h(\rho _{*}, \rho ) \le 0. \end{aligned}$$

(38)

But the left hand side of (38) is strictly positive, which leaves us with a contradiction. Hence $h(\rho _{*}, \rho ) - h(\rho _{l}, \rho ) + h(\rho _{l}, \rho _{*}) > 0$, i.e., the curve $S_{1}(U_{*})$ lies below the curve $S_{1}(U_{l}),$ and therefore $U_{r}$ lies in the region II. Thus, in view of the result presented in a preceding section, it follows that the interaction result is $S_{2}S_{1}\rightarrow S_{1}S_{2};$ the computed results illustrate this case in Fig. 7.

Fig. 7

Collision of $S_{2}S_{1}$

(ii) Collision of a shock and a rarefaction $(S_{2}R_{1})$: Here $U_{*} \in S_{2}(U_{l})$ and $U_{r} \in R_{1}(U_{*}).$ That is, for a given $U_{l}$, we choose $U_{*}$ and $U_{r}$ such that $\rho _{*} < \rho _{l}, u_{*} = u_{l} - h(\rho _{l}, \rho _{*})$ and $\rho _{r} \le \rho _{*}, u_{r} = u_{*} + \int ^{\rho _{*}}_{\rho _{r}} \frac{w(\theta )}{\theta }d\theta .$ Since 2-shock has positive velocity and 1-rarefaction wave has negative velocity, it follows that $S_{2}$ overtakes $R_{1}$. Moreover, since for any given $U_{l}, \int ^{\rho _{l}}_{\rho } \frac{w(\theta )}{\theta }d\theta - \int ^{\rho _{*}}_{\rho } \frac{w(\theta )}{\theta }d\theta + h(\rho _{l}, \rho _{*}) > 0$ for $\rho< \rho _{*} < \rho _{l},$ it follows that the curve $R_{1}(U_{*})$ lies below the curve $R_{1}(U_{l});$ hence $U_{r}$ lies in the region III,  and subsequently $S_{2}R_{1} \rightarrow R_{1}S_{2}$. The computed results illustrate this case in Fig. 8.

(iii) Collision of two rarefaction waves $(R_{2}R_{1})$: We consider $U_{*} \in R_{2}(U_{l})$ and $U_{r} \in R_{1}(U_{*})$. In other words, for a given $U_{l}$, we choose $U_{*}$ and $U_{r}$ such that $\rho _{l} \le \rho _{*}, u_{*} = u_{l} + \int ^{\rho _{*}}_{\rho _{l}} \frac{w(\theta )}{\theta }d\theta$ and $\rho _{r} \le \rho _{*}, u_{r} = u_{*} + \int ^{\rho _{*}}_{\rho _{r}} \frac{w(\theta )}{\theta }d\theta .$ Since the trailing end of 2-rarefaction wave has a positive velocity (bounded above) in (x, t)-plane and that 1-rarefaction wave has a negative velocity (bounded above), interaction will take place. Since $\rho _{l} < \rho _{*}$ and $\int ^{\rho _{*}}_{\rho } \frac{w(\theta )}{\theta }d\theta - \int ^{\rho _{l}}_{\rho } \frac{w(\theta )}{\theta }d\theta + \int ^{\rho _{*}}_{\rho _{l}} \frac{w(\theta )}{\theta }d\theta > 0,$ it follows that the curve $R_{1}(U_{*})$ lies above the curve $R_{1}(U_{l});$ hence $U_{r}$ lies in the region IV and the interaction result is $R_{2}R_{1} \rightarrow R_{1}R_{2}.$ The computed results illustrate this case in Fig. 9.

Fig. 8

Collision of $S_{2}R_{1}$

Fig. 9

Collision of $R_{2}R_{1}$

(iv) Collision of a rarefaction wave and a shock $(R_{2}S_{1})$: Here $U_{*} \in R_{2}(U_{l})$ and $U_{r} \in S_{1}(U_{*})$, i.e., for a given $U_{l}$, we choose $U_{*}$ and $U_{r}$ such that $\rho _{l} \le \rho _{*}, u_{*} = u_{l} + \int ^{\rho _{*}}_{\rho _{l}} \frac{w(\theta )}{\theta }d\theta$ and $\rho _{*} < \rho _{r}, u_{r} = u_{*} - h(\rho _{*}, \rho _{r})$. Since 1-shock speed of second Riemann problem is less than the speed of trailing end of 2-rarefaction wave of first Riemann problem in (x, t)-plane, and therefore $S_{1}$ penetrates $R_{2}$. For any given $U_{l}$, we show that $U_{r}$ lies in the region I;  for this, it is enough to show that

$$\begin{aligned} \int ^{\rho _{*}}_{\rho _{l}} \frac{w(\theta )}{\theta }d\theta + h(\rho _{l}, \rho ) - h(\rho _{*}, \rho ) > 0. \end{aligned}$$

(39)

Since $h(\rho _{l}, \rho )$ is a decreasing function with respect to the first variable $\rho _{l}$, we have $h(\rho _{l}, \rho ) > h(\rho _{*}, \rho )$ for $\rho _{l} < \rho _{*}$; hence, the inequality (39) follows that the curve $S_{1}(U_{*})$ lies above the curve $S_{1}(U_{l})$, and $U_{r}$ lies in the region I. Thus the interaction result is $R_{2}S_{1} \rightarrow S_{1}R_{2}$; the computed results illustrate this case in Fig. 10.

Fig. 10

Collision of $R_{2}S_{1}$

Interaction of Elementary Waves from Same Families

(i) 1-shock wave overtakes another 1-shock wave $(S_{1}S_{1})$: We consider the situation in which $U_{l}$ is connected to $U_{*}$ by a 1-shock of first Riemann problem and $U_{*}$ is connected to $U_{r}$ by a 1-shock of second Riemann problem. In other words, for a given left state $U_{l}$, the intermediate state $U_{*}$, and the right state $U_{r}$ are chosen such that $\rho _{l} < \rho _{*}$ and $u_{*} = u_{l} - h(\rho _{l}, \rho _{*})$ with Lax stability conditions

$$\begin{aligned} s_{1}(U_{l},U_{*})< \lambda _{1}(U_{l}),\quad \lambda _{1}(U_{*})< s_{1}(U_{l},U_{*}) < \lambda _{2}(U_{*}), \end{aligned}$$

(40)

and $\rho _{*} < \rho _{r}$ and $u_{r} = u_{*} - h(\rho _{*}, \rho _{r})$ with Lax stability conditions

$$\begin{aligned} s_{1}(U_{*},U_{r})< \lambda _{1}(U_{*}),\quad \lambda _{1}(U_{r})< s_{1}(U_{*},U_{r}) < \lambda _{2}(U_{r}), \end{aligned}$$

(41)

where $s_{1}(U_{l},U_{*})$ is the speed of shock connecting $U_{l}$ to $U_{*}$, and similarly $s_{1}(U_{*},U_{r})$ is the speed of shock connecting $U_{*}$ to $U_{r}$. From (40) and (41) we obtain $s_{1}(U_{*},U_{r}) < s_{1}(U_{l},U_{*}),$ i.e., the 1-shock of second Riemann problem overtakes 1-shock of the first Riemann problem at a finite time, and gives rise to a new Riemann problem with data $U_{l}$ and $U_{r}$. In order to solve this problem, we must determine the region in which $U_{r}$ lies with respect to $U_{l}$. We claim that $U_{r}$ lies in region I so that the solution of the new Riemann problem consists of $S_{1}$ and $R_{1}$. In other words, to prove our claim, we need to show that $S_{1}(U_{r})$ lies entirely in the region I; to show this we are required to prove that for $\rho _{l}< \rho _{*} < \rho ,$ $h(\rho _{l}, \rho ) - h(\rho _{*}, \rho ) - h(\rho _{l}, \rho _{*}) > 0.$ Let us assume on the contrary that $h(\rho _{l}, \rho ) - h(\rho _{*}, \rho ) - h(\rho _{l}, \rho _{*}) \le 0$ for $\rho _{l}< \rho _{*} < \rho .$ Then, it follows that $h^{2}(\rho _{l}, \rho ) + h^{2}\rho _{l}, \rho _{*}) - 2h(\rho _{l}, \rho )h(\rho _{l}, \rho _{*}) \le h^{2}(\rho _{*}, \rho ),$ which showing thereby that

$$\begin{aligned} \left[ \left( p + \frac{B^{2}}{2\mu } - p_{l} - \frac{B_{l}^{2}}{2\mu }\right) \left( \frac{1}{\rho _{l}} - \frac{1}{\rho _{*}}\right) - \left( p_{*} + \frac{B_{*}^{2}}{2\mu } - p_{l} - \frac{B_{l}^{2}}{2\mu }\right) \left( \frac{1}{\rho _{l}} - \frac{1}{\rho }\right) \right] ^{2} \le 0, \end{aligned}$$

(42)

which is a contradiction as the left hand side of inequality (42) is positive. Hence, $S_{1}S_{1} \rightarrow S_{1}R_{2}$; the computed results illustrate this situation in Fig. 11.

(ii) 2-shock wave overtakes another 2-shock wave $(S_{2}S_{2})$: The analytical proof that $U_{r}$ lies in the region III, so that $S_{2}S_{2} \rightarrow R_{1}S_{2},$ is similar to the previous case (see Fig. 12).

Fig. 11

$S_1$ overtakes $S_1$

Fig. 12

$S_2$ overtakes $S_2$

(iii) 1-rarefaction wave overtakes 1-shock wave $(R_1S_1)$: In this case, $U_{l}$ is connected to $U_{*}$ by 1-rarefaction wave of the first Riemann problem and $U_{*}$ is connected to $U_{r}$ by a 1-shock of second Riemann problem. That is, for a given $U_{l}$, we choose $U_{*}$ and $U_{r}$ in such a way that $\rho _{*} \le \rho _{l}, u_{*} = u_{l} + \int ^{\rho _{l}}_{\rho _{*}} \frac{w(\theta )}{\theta }d\theta$ and $\rho _{*} < \rho _{r}, u_{r} = u_{*} - h(\rho _{*}, \rho _{r})$. First we show that $S_{1}(U_{*})$ lies below the curve $R_{1}(U_{l})$ for $\rho _{*} < \rho \le \rho _{l}$; in other words, for $\rho _{*} < \rho \le \rho _{l}$

$$\begin{aligned} h(\rho _{*}, \rho ) + \int ^{\rho _{l}}_{\rho } \frac{w(\theta )}{\theta }d\theta - \int ^{\rho _{l}}_{\rho _{*}} \frac{w(\theta )}{\theta }d\theta > 0. \end{aligned}$$

Let us define $F_{1}(\rho ) = h(\rho _{*}, \rho ) + \int ^{\rho _{l}}_{\rho } \frac{w(\theta )}{\theta }d\theta - \int ^{\rho _{l}}_{\rho _{*}} \frac{w(\theta )}{\theta }d\theta$, so that $F_{1}(\rho _{*}) = 0$. Differentiating $F_{1}(\rho )$ with respect to $\rho$, we obtain $F'_{1}(\rho ) > 0$, implying thereby that $F_{1}(\rho _{*}) < F_{1}(\rho )$ i.e., $F_{1}(\rho ) > 0$; hence $S_{1}(U_{*})$ lies below the curve $R_{1}(U_{l})$ for $\rho _{*} < \rho \le \rho _{l}$.

Fig. 13

$R_1$ overtakes $S_1$

Next we prove that $S_{1}(U_{l})$ lies above the curve $S_{1}(U_{*})$ for $\rho _{l} \le \rho$; for this it is sufficient to prove that

$$\begin{aligned} h(\rho _{*}, \rho ) - h(\rho _{l}, \rho ) - \int ^{\rho _{l}}_{\rho _{*}} \frac{w(\theta )}{\theta }d\theta > 0, \end{aligned}$$

for $\rho _{l} \le \rho$. Let us define $F_{2}(\rho ) = h(\rho _{*}, \rho ) - h(\rho _{l}, \rho ) - \int ^{\rho _{l}}_{\rho _{*}} \frac{w(\theta )}{\theta }d\theta .$ Let us assume that $h(\rho _{*}, \rho ) - h(\rho _{*}, \rho _{l}) \le h(\rho _{l}, \rho )$ for $\rho _{*}< \rho _{l} < \rho$, which implies that $h^{2}(\rho _{*}, \rho ) +h^{2}(\rho _{*}, \rho _{l}) - 2h(\rho _{*}, \rho )h(\rho _{*}, \rho _{l}) \le h^{2}(\rho _{l}, \rho ),$ implying thereby that $\bigl (p_l-p_*+\frac{B_l^2-B_*^2}{2\mu }\bigr )\bigl (\frac{1}{\rho _*}-\frac{1}{\rho }\bigr )+\bigl (p-p_*+\frac{B^2-B_*^2}{2\mu }\bigr )\bigl (\frac{1}{\rho _*}-\frac{1}{\rho _l }\bigr )\le 2h(\rho _*,\rho )h(\rho _*,\rho _l);$ or equivalently

$$\begin{aligned} \left[ \left( p_l-p_*+\frac{B_l^2-B_*^2}{2\mu }\right) \left( \frac{1}{\rho _*}-\frac{1}{\rho }\right) -\left( p-p_*+\frac{B^2-B_*^2}{2\mu }\right) \left( \frac{1}{\rho _*}-\frac{1}{\rho _l}\right) \right] ^2\le 0. \end{aligned}$$

(43)

But the left hand side of inequality (43) is positive, which leaves us with a contradiction. Hence, $h(\rho _*,\rho )-h(\rho _l,\rho )>h(\rho _*,\rho _l)$ for $\rho _*<\rho _l<\rho ,$ which implies that $h(\rho _*,\rho )-h(\rho _l,\rho )-\int _{\rho _*}^{\rho _l} \frac{w(\theta )}{\theta }d\theta>h(\rho _*,\rho _l)-\int _{\rho _*}^{\rho _l} \frac{w(\theta )}{\theta }d\theta =F_2(\rho _l)>0.$

Lastly, we show that $S_2(U_l)$ and $S_1(U_*)$ intersect at some point $(\tilde{\rho _1},\tilde{u_1}),$ where $\rho _*<\tilde{\rho _1}<\rho _l.$ To prove this, we define a new function $F_3(\rho )=h(\rho _*,\rho )-h(\rho _l,\rho )-\int _{\rho _*}^{\rho _l} \frac{w(\theta )}{\theta }d\theta$ for $\rho _*\le \rho \le \rho _l.$ Since $F_3(\rho _*)<0,$ by virtue of monotonicity and intermediate value property, there exists a $\tilde{\rho _1}$ between $\rho _*$ and $\rho _l,$ such that $F_3(\tilde{\rho _1})=0.$ Thus, the intersection of $S_2(U_l)$ and $S_1(U_*)$ is uniquely determined; the computed results are shown in Fig. 13. Depending on the value of $\rho _r$ we distinguish three cases.

• (a) When $\rho _r<\tilde{\rho _1}, U_r\in III$ and the interaction result is $R_1S_1\rightarrow R_1S_2;$ indeed, 1-shock is weak compared to 1-rarefaction wave.

• (b) When $\rho _r=\tilde{\rho _1}, U_r$ lies on $S_2(U_l)$ and the interaction result is $R_1S_1\rightarrow S_2;$ indeed, when two waves of first family interact, they annihilate each other, and give rise to a wave of second family.

• (c) When $\rho _r>\tilde{\rho _1}, U_r\in II$ and the interaction result is $R_1S_1\rightarrow S_1S_2;$ indeed, the 1-shock of second Riemann problem, which is strong compared to the 1-rarefaction of first Riemann problem, overtakes the trailing end of 1-rarefaction wave, and a reflected shock $S_2(U_m,U_r),$ connecting a new constant state $U_m$ on the left to $U_r$ on the right, is produced. The transmitted wave, after interaction, is the 1-shock that joins $U_l$ on the left and $U_m$ on the right.

(IV) 1-shock wave overtakes 1-rarefaction wave $(S_{1}R_{1})$: Here $U_* \in S_1(U_l)$ and $U_r \in R_1(U_*).$ That is, for a given $U_l,$ we choose $U_*$ and $U_r$ in such a way that $\rho _l<\rho _*, u_{*} = u_{l} - h(\rho _{l}, \rho _{*})$ and $\rho _{r} \le \rho _{*}, u_{r} = u_{*} + \int ^{\rho _{*}}_{\rho _{r}} \frac{w(\theta )}{\theta }d\theta$. In the (x, t) plane the speed of trailing end of 1-rarefaction wave, $\lambda _1(U_*),$ is less than 1-shock speed $s_1(U_l,U_*)$ and therefore 1-shock from left overtakes 1-rarefaction wave from right after a finite time. First we show that $R_1(U_*)$ lies below the curve $S_1(U_l)$ for $\rho _l\le \rho \le \rho _*;$ for this we need to show $h(\rho _{l}, \rho _{*})-h(\rho _{l}, \rho )-\int ^{\rho _*}_{\rho } \frac{w(\theta )}{\theta }d\theta >0$ for $\rho _l\le \rho <\rho _*.$ To prove this, we define a new function $G_1(\rho )=h(\rho _{l}, \rho _{*})-h(\rho _{l}, \rho )-\int ^{\rho _*}_{\rho } \frac{w(\theta )}{\theta }d\theta >0$ for $\rho _l\le \rho <\rho _*.$ This, in view of the expression for $\psi (\theta )$ and $h(\rho _{l}, \rho )$, yields

$$\begin{aligned} G'_1(\rho )=-\frac{\left[ \left( p-p_l+\frac{B^2-B_l^2}{2\mu }\right) \frac{1}{\rho ^2}-\left( p'+\frac{BB'}{\mu }\right) \left( \frac{1}{\rho _l}- \frac{1}{\rho }\right) \right] ^2}{2h(\rho _{l}, \rho )}<0, \end{aligned}$$

which implies that $G_1(\rho )>G_1(\rho _*);$ but since $G_1(\rho _*) = 0,$ we have $G_1(\rho )>0.$

Next we show that $R_1(U_l)$ lies above the curve $R_1(U_*)$ for $\rho \le \rho _l<\rho _*,$ i.e., $g(\rho _{l}, \rho _{*})+\int ^{\rho _l}_{\rho } \frac{w(\theta )}{\theta }d\theta -\int ^{\rho _*}_{\rho } \frac{w(\theta )}{\theta }d\theta >0$ for $\rho _l\le \rho <\rho _*.$

Since the left hand side of this inequality, $\rho \le \rho _l<\rho _*,$ turns out to be $G_1(\rho _l)$, which has already been shown to be positive, the conclusion follows.

Lastly, we show that $R_1(U_*)$ and $S_2(U_l)$ intersect uniquely at some point, say, $(\tilde{\rho _2},\tilde{u_2});$ for this, it is enough to show that the equation $h(\rho _{l}, \rho _{*})-h(\rho _{l}, \rho )-\int ^{\rho _*}_{\rho } \frac{w(\theta )}{\theta }d\theta =0$ has unique root $\tilde{\rho _2}$ such that $\tilde{\rho _2}<\rho _l$. To establish this, we define a new function $G_2(\rho )=h(\rho _{l}, \rho _{*})-h(\rho _{l}, \rho )-\int ^{\rho _*}_{\rho } \frac{w(\theta )}{\theta }d\theta$; since $G_2(\rho _l) > 0$, and $G_2(\rho )$ takes negative value as $\rho$ is close to zero, in view of monotonicity and intermediate value property, it follows that the curves $R_1(U_*)$ and $S_2(U_l)$ intersect uniquely; here again we distinguish three cases depending on the value of $\rho _r$.

• (a) When $\rho _r>\tilde{\rho _2}, U_r\in II$ and the interaction result is $S_1R_1\rightarrow S_1S_2;$ indeed, the 1-shock is sufficiently strong compared to 1-rarefaction wave which, after interaction, produces a new elementary wave.

• (b) When $\rho _r=\tilde{\rho _2}, U_r\in S_2(U_l)$ and the interaction result is $S_1R_1\rightarrow S_2.$ The interaction of elementary waves of first family gives rise to a new elementary wave of second family.

• (c) When $\rho _r<\tilde{\rho _2}, U_r\in III$ and the interaction result is $S_1R_1\rightarrow R_1S_2.$ The computed results shown in Fig. 14.

(V) 2-shock wave overtakes 2-rarefaction wave $(S_{2}R_{2})$: The $S_{2}R_{2}$ interaction takes place when $U_*\in S_2(U_l)$ and $U_r \in R_2(U_*).$ In other words, for a given $U_l,$ we choose $U_*$ and $U_r$ in such a way that $\rho _*<\rho _l, u_{*} = u_{l} - h(\rho _{l}, \rho _{*})$ and $\rho _{*} \le \rho _{r}, u_{r} = u_{*} + \int ^{\rho _{r}}_{\rho _{*}} \frac{w(\theta )}{\theta }d\theta$.

First we show that for $\rho _*<\rho \le \rho _l,S_2(U_l)$ lies above $R_2(U_*)$, i.e.,

$$\begin{aligned} h(\rho _{l}, \rho _{*})-h(\rho _{l}, \rho )-\int ^{\rho }_{\rho _{*}} \frac{w(\theta )}{\theta }d\theta >0, \end{aligned}$$

for $\rho _{*} \le \rho _l$. To prove this we define a new function $M_1(\rho )=h(\rho _{l}, \rho _{*})-h(\rho _{l}, \rho )-\int ^{\rho }_{\rho _{*}} \frac{w(\theta )}{\theta }d\theta >0.$ Since $M'_1(\rho ) > 0,$ we have $M_1(\rho )>M_1(\rho _*);$ further since $M_1(\rho _*)=0,$ it follows that $M_1(\rho )>0,$ implies thereby that $S_2(U_l)$ lies above $R_2(U_*)$ for $\rho _*<\rho \le \rho _l.$

Next we show that the curve $R_2(U_l)$ lies above the curve $R_2(U_*)$ for $\rho _*<\rho _l\le \rho ;$ for this it is enough to prove $h(\rho _{l}, \rho _{*})-\int ^{\rho }_{\rho _{*}} \frac{w(\theta )}{\theta }d\theta +\int ^{\rho }_{\rho _{l}} \frac{w(\theta )}{\theta }d\theta >0$ for $\rho _*<\rho _l\le \rho .$ We notice that the left hand side of this inequality is $M_1(\rho _l)$ which has already been shown to be positive, and hence the curve $R_2(U_l)$ lies above $R_2(U_*)$ for $\rho _*<\rho _l\le \rho .$

Lastly, we show that $R_2(U_*)$ and $S_1(U_l)$ intersect uniquely, say, at $(\tilde{\rho _3},\tilde{u_3})$ for $\rho _*<\rho _l<\tilde{\rho _3}.$

Fig. 14

$S_1$ overtakes $R_1$

Fig. 15

$S_2$ overtakes $R_2$

Now we define $M_2(\rho )=h(\rho _{l}, \rho )-h(\rho _{l}, \rho _*)+\int ^{\rho }_{\rho _{*}} \frac{w(\theta )}{\theta }d\theta$ for $\rho _*<\rho _l\le \rho$ so that $M_2(\rho _l)<0$, and we can choose a constant $k>0$ such that $M_2(\rho )>0$ for all $\rho >k.$ Then, there exits a $\tilde{\rho _3}$ such that $M_2(\tilde{\rho _3}) =0$. Thus $R_2(U_*)$ and $S_1(U_l)$ intersect uniquely at $(\tilde{\rho _3},\tilde{u_3})$ as $R_2(U_*)$ and $S_1(U_l)$ are monotone; the computed results are shown in Fig. 15. Here again the following cases arise.

• (a) When $\rho _r<\tilde{\rho _3}, U_r\in II$ and the interaction result is $S_2R_2\rightarrow S_1S_2;$ indeed, the strength of $R_2$ is small computed to the elementary wave $S_2$, and $S_2$ annihilates $R_2$ in a finite time. The strength of reflected $S_1$ wave is small compared to the incident waves $S_2$ and $R_2$.

• (b) When $\rho _r=\tilde{\rho _3}, U_r$ lies on $S_1(U_l)$ and the interaction result is $S_2R_2\rightarrow S_1.$ The reflected shock $S_1$ is weak computed to incident waves $S_2$ and $R_2$.

• (c) When $\rho _r>\tilde{\rho _3}, U_r\in I$ and the interaction result is $S_2R_2\rightarrow S_1R_2;$ indeed, $R_2$ is stronger than $S_2.$

(vi) 2-rarefaction wave overtakes 2-shock wave $(R_2S_2)$: Here $U_*\in R_2(U_l)$ and $U_r \in S_2(U_*).$ That is, for a given $U_l$, we choose $U_*$ and $U_r$ such that $\rho _l\le \rho _*, u_{*} = u_{l} + \int ^{\rho _{*}}_{\rho _{l}} \frac{w(\theta )}{\theta }d\theta$ and $\rho _{r} < \rho _{*}, u_r=u_{*} - h(\rho _{*}, \rho _{r})$. Now we show that $R_2(U_l)$ lies above $S_2(U_*)$ for $\rho _l\le \rho <\rho _*$, i.e.,

Fig. 16

$R_2$ overtakes $S_2$

$$\begin{aligned} h(\rho _{*}, \rho ) + \int ^{\rho }_{\rho _l} \frac{w(\theta )}{\theta }d\theta - \int ^{\rho _{*}}_{\rho _{l}} \frac{w(\theta )}{\theta }d\theta > 0, \end{aligned}$$

for $\rho _{l} \le \rho <\rho _*$. To prove this we define a new function $N_1(\rho )=h(\rho _{*}, \rho ) + \int ^{\rho }_{\rho _l} \frac{w(\theta )}{\theta }d\theta - \int ^{\rho _{*}}_{\rho _{l}} \frac{w(\theta )}{\theta }d\theta$ for $\rho _{l} \le \rho \le \rho _*$ so that $N_1(\rho _*) = 0.$ This, in view of the expressions for $w(\theta )$ and $h(\rho _{*}, \rho )$, yields

$$\begin{aligned} N'_1(\rho )=-\frac{\left[ \left( p'+\frac{BB'}{\mu }\right) \left( \frac{1}{\rho }- \frac{1}{\rho _*}\right) -\left( p_*-p+\frac{B_*^2-B^2}{2\mu }\right) \frac{1}{\rho ^2}\right] ^2}{2h(\rho _{*}, \rho )}<0, \end{aligned}$$

implying thereby that $N_1(\rho ) > N_1(\rho _*) = 0.$ Hence, the result.

Next we show that $S_2(U_*)$ lies below the curve $S_2(U_l)$ for $\rho \le \rho _l<\rho _*$; for this it is sufficient to prove $h(\rho _{*}, \rho )-h(\rho _{l}, \rho )-\int ^{\rho _*}_{\rho _l} \frac{w(\theta )}{\theta }d\theta >0$ for $\rho \le \rho _l<\rho _*$. If $h(\rho _{*}, \rho )-h(\rho _{l}, \rho )>h(\rho _{*}, \rho _l)$ then $h(\rho _{*}, \rho )-h(\rho _{l}, \rho )-\int ^{\rho _*}_{\rho _l} \frac{w(\theta )}{\theta }d\theta>h(\rho _{*}, \rho _l)-\int ^{\rho _*}_{\rho _l} \frac{w(\theta )}{\theta }d\theta =N_1(\rho _l)>0.$

Let us assume on the contrary that $h(\rho _{*}, \rho )-h(\rho _{l}, \rho )\le h(\rho _{*}, \rho _l)$. Then, it follows that $h(\rho _{*}, \rho )-h(\rho _{*}, \rho _l)\le h(\rho _{l}, \rho )$, implying thereby that $h^2(\rho _{*}, \rho )+h^2(\rho _{*}, \rho _l) -2h(\rho _{*}, \rho )h(\rho _{*}, \rho _l) \le h^2(\rho _{l}, \rho )$; this, in view of the expressions for $h(\rho _{*}, \rho ), h(\rho _{*}, \rho _l)$ and $h(\rho _{l}, \rho )$ yields $\bigl (p_l-p_*+\frac{B_1^2-B_*^2}{2\mu }\bigr )\bigl (\frac{1}{\rho _*}-\frac{1}{\rho }\bigr )+\bigl (p-p_*+\frac{B^2-B_*^2}{2\mu }\bigr )\bigl (\frac{1}{\rho _*}-\frac{1}{\rho _l }\bigr )\le 2h(\rho _*,\rho )h(\rho _*,\rho _l),$ or equivalently

$$\begin{aligned} \left[ \left( p_l-p_*+\frac{B_l^2-B_*^2}{2\mu }\right) \left( \frac{1}{\rho _*}-\frac{1}{\rho }\right) -\left( p-p_*+\frac{B^2-B_*^2}{2\mu }\right) \left( \frac{1}{\rho _*}-\frac{1}{\rho _l}\right) \right] ^2\le 0. \end{aligned}$$

(44)

But the left hand side of (44) is positive for $\rho \le \rho _l<\rho _*,$ which leaves us with a contradiction. Hence, $h(\rho _{*}, \rho )-h(\rho _{l}, \rho )>h(\rho _{*}, \rho _l)$ for $\rho \le \rho _l<\rho _*$.

Lastly, we show that $S_2(U_*)$ and $S_1(U_l)$ intersect uniquely at a point, $(\tilde{\rho _4},\tilde{u_4})$ for $\rho _l<\tilde{\rho _4}<\rho _*.$ The proof for this follows on similar lines as discussed earlier; here also we encounter three possibilities.

• (a) When $\rho _r>\tilde{\rho _4}, U_r\in I$ and the interaction result is $R_2S_2\rightarrow S_1R_2;$ indeed, $R_2$ is strong compared to the elementary wave $S_2,$ and the strength of reflected $S_1$ is small compared to the incident waves $S_2$ and $R_2.$

• (b) When $\rho _r=\tilde{\rho _4}, U_r \in S_1(U_l)$ and the interaction result is $R_2S_2 \rightarrow S_1.$

• (c) When $\rho _r<\tilde{\rho _4}, U_r\in II$ and the interaction result is $R_2S_2 \rightarrow S_1S_2;$ indeed,the elementary wave $S_2$ is strong compared to $R_2.$ The computed results illustrate this case in Fig. 16.

Conclusion

The Riemann problem for the one-dimensional unsteady simple flow of an isentropic, inviscid and perfectly conducting compressible fluid, subject to a transverse magnetic field, is solved, at any point (x, t) in the relevant domain of interest $x_l< x <x_r; t > 0,$ with $x_l < 0$ and $x_r > 0$ under the influence of van der Waals excluded volume through the parameter a. It has been observed that the position, velocity, shock speed and the values of the intermediate states of each structure in the flow, i.e., rarefaction wave and shock wave, is strongly influenced by the van der Waals excluded volume a. It is observed that the left shock speed decreases and right shock speed increases when the van der Waals excluded volume a increases in test 1. In test 2, the velocity decreases when the van der Waals excluded volume a increases and but the velocity increases for test 3. It is noticed that for the density profile of test 4, the wave speed for right rarefaction wave increases when a increases but decreases for left rarefaction wave. We have discussed all possible wave interactions of the Riemann problem. We will extend this analytical procedure to construct the exact solution and wave interactions to the case of non-isentropic flows in future.