EOQ Model for Time Dependent Demand and Exponentially Increasing Holding Cost Under Permissible Delay in Payment with Complete Backlogging

Abstract

In this study, economic order quantity model is considered in which demand rate is assumed to be continuous function of time and holding cost is exponentially increasing function under the condition of permissible delay in payment. The scheduling period is assumed to be a variable. Shortages are allowed which are completely backlogged. The objective of this study is to obtain the retailer’s optimal replenishment policy that maximizes the total profit. Numerical examples are provided to illustrate the proposed model. Sensitivity analysis has been provided and managerial implications are discussed.

Introduction

Many of the Economic Order Quantity (EOQ) models were developed under the assumption that the retailer should pay for products as soon as it is received from the supplier. However, the existing practice is that the supplier may offer a stipulated period to the retailer to settle the account. Within this stipulated period, the retailer need not have to settle the account is generally termed as permissible delay in payment.

To manage the inventory level successfully, the retailer needs to find a balance between the costs and benefits of holding stock. The costs of holding stock include the money has been spent buying the stock as well as storage. The benefits include having enough stock on hand to meet the demand of customers. Having too much stock equals extra expense for the retailer as it can lead to a shortfall in cash flow and incur excess storage costs. And having too little stock equals lost income in the form of lost sales, while also undermining customer confidence in retailer’s ability to supply the products the retailer claims to sell. Hence keeping the right stock and being able to sell it can lead to—increased sales, new customers, increased customer confidence, improved cash flow.

The first attempt was made to describe the optimal ordering policies by Ghare and Shrader [12] in which they discussed EOQ model for an exponentially decaying inventory. Philip [42] developed an inventory model with a three-parameter Weibull distribution rate without considering shortages. In the literature referring to models with permissible delay in payments, Goyal [13] developed an EOQ model in which he ignored the difference between the selling price and the purchase cost. But Dave [10] corrected Goyal’s model in which selling price exceeds the purchasing cost. Deb and Chaudhuri [11] derived inventory model with time-dependent deterioration rate. Shah [14] assumed a stochastic inventory model when delays in payments are permissible. Datta and Pal [9] considered inventory model with a linear time-dependent demand with shortages. Jamal et al. [15] generalized Aggarwal and Jaggi’s [2] model to allow shortages. Under the condition of permissible delay in payments Hwang and Shinn [16] added pricing strategy to the model. Chung [17] developed an alternative approach to find EOQ under trade credit being granted. Teng [18] implemented Goyal’s model by considering the difference between unit price and unit cost. Chang et al. [19] developed an EOQ model for deteriorating items under supplier credits linked to ordering quantity. Chung and Huang [20] developed an EPQ for a retailer where the supplier offers a permissible delay in payments. Huang [22] extended Goyal’s model to develop an EOQ model in which the supplier offers the retailer permissible delay period. Teng and Goyal [23] addressed the shortcoming of Huang’s model. Many related articles can be found in Chang and Teng [24], Chung [25], Chung and Liao [26], Goyal et al. [28], Huang [30, 31], Huang and Hsu [32], Liao et al. [36], Ouyang et al. [38, 39], Shinn and Hwang [46], Teng et al.[47–49], and their references. Also researchers established their inventory model under trade credit financing by assuming that the demand rate is constant. However, it is observed that the demand rate of new brand of consumer goods comes to the market, increases at the beginning of the season up to a certain moment and then remains to be constant for the rest of the time. However, they assumed that both the first derivative and second derivative of the demand rate must be greater than zero, which excluded not only a constant demand but also a linearly increasing demand which is not covered by Hsieh et al. [29]. Teng et al. [33] considered a deter inventory model when delay in payments are permissible. Musa and Sani [1] developed inventory model for deteriorating items under permissible delay in payments. Khanra et al. [34] inventory model with quadratic demand under trade credit with shortages. Chung and Cardenas-Barron [27] developed EOQ model for deteriorating items under stock-dependent demand with two-level credit policy. Ouyang et al. [40] addressed EOQ model for two-levels of trade credit policy. Cardenas-Barron [4] developed EOQ model with different back-ordering rates. Chen et al. [6] developed retailer’s economic order quantity model when the supplier offers conditionally permissible delay in payments link to order quantity. Chung [7] developed EOQ model for deteriorating items under two-level trade credit policy. Wu et al. [50] developed an EOQ model with for exponentially increasing function of retailers down stream credit period. Nita et al. [37] Retailer’s decision for ordering and credit policies for deteriorating items when a supplier offers order-linked credit period. Saren and Cardenas-Barron [44] developed inventory model with trade-credit policy and variable deterioration for fixed lifetime products. Chowdhury et al. [45] developed an inventory model in which demand is influenced by the selling price and the inventory level over finite planning horizon. Khanra et al. [35] analyzed comparison between inventory followed by shortages model and shortages followed by inventory model with variable demand rate.

Battini et al. [8] explored the integration of factors affecting the environmental impact within the traditional EOQ model. San-Jose et al. [43] developed EOQ model where the unit holding cost has two significant components: a fixed cost which represents the cost of accommodating the item in the warehouse and a variable cost given by a potential function of the length of time over which the item is held in stock in which shortages are partially backlogged. Jaggi et al. [5] developed EOQ model with allowable shortage under trade credit . Pentico et al. [21] approximated an the EOQ with partial backordering at an exponential or rational rate by a constant or linearly changing rate. Guchhait et al. [41] studied an inventory model for a deteriorating item with time dependent deterioration in imprecise environment. Taleizadeh et al. [3] developed EOQ models with incremental discounts and either full or partial backordering.

Hence in this paper, the constant demand is extended to linear non-decreasing demand function of time and holding cost is assumed to be exponentially increasing function of time containing two parameters f and d. And if d $=$ 0 indicates that holding cost is constant. Shortages are allowed to occur which are completely backlogged. Also the necessary and sufficient conditions of the existence and uniqueness of the optimal solutions are provided. Numerical examples are presented to demonstrate the developed model and the solution procedure. Sensitivity analysis of the optimal solution with respect to major parameters of the system is carried out and their results are discussed. The paper is organized as follows: The notations and assumptions used are given in “Notations and Assumptions” section. In “Mathematical Model” section the mathematical model is developed. “Numerical Examples” section is devoted to numerical examples. Sensitivity analysis is presented in “Sensitivity Analysis” section. The paper closes with concluding remarks in “Conclusion” section.

Notations and Assumptions

The following notations and assumptions are used in this paper.

Notations

k:

ordering cost per order

c:

unit purchasing cost

s:

unit selling price (with s$>$c)

$\delta$ :

the backlogging parameter which is a positive constant

$c_2$ :

shortage cost per unit per order

$I_e$ :

interest earned per $ per unit of time by the retailer

$I_c$ :

interest payable per $ in stocks per unit of time by the supplier

$I_m$ :

the maximum inventory level for each replenishment cycle

$I_b$ :

the maximum amount of demand backlogged per cycle

M:

the retailer’s trade credit period offered by supplier in years

T:

inventory cycle length (decision variable)

$t_{1}$ :

the time at which the inventory level falls to zero (decision variable)

Q :

the retailer’s order quantity

$\Pi (t_{1},T)$ :

the retailer’s total profit function per unit of time

Assumptions

• 1. The demand rate D(t) is given by

  $$\begin{aligned} D(t)=\left\{ \begin{array}{lll} &{}a+bt &{} 0 < t \le t_1 \\ &{}-\delta (a+bt) &{} t_1 < t \le T \end{array} \right. \end{aligned}$$

  (1)

  where a and b are non-negative constants.

• 2. The holding cost is time dependent and h(t) $=$ f exp(dt) where f and d are positive constants.

• 3. The replenishment rate is infinite.

• 4. The time horizon of the inventory model is infinite.

• 5. The lead time is negligible.

• 6. The inventory model deals with single item.

• 7. There is no replacement or repair of deteriorating items during the period under consideration.

• 8. Shortages are allowed to occur which are completely backlogged.

Mathematical Model

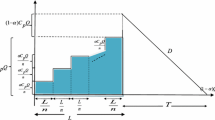
The model begins without shortages and ends with shortages which is depicted graphically in Fig. 1. Based on the above assumptions, the retailer orders and receives Q units of a single product from the supplier at the beginning of time t $=$ 0. The reduction of the inventory is due to the effect of demand only in the interval [0,$t_{1}$) and the demand is backlogged in the interval [$t_{1}$,T). At time $t=t_{1}$ the inventory level reaches zero. Hence the change in the inventory level I(t) with respect to time can be written as follows:

$$\begin{aligned} \frac{{ dI}(t)}{dt}= & {} -(a+bt)\;\quad 0 < t \le t_1 \end{aligned}$$

(2)

$$\begin{aligned} \frac{{ dI}(t)}{dt}= & {} -\delta (a+bt)\;\quad t_1 < t \le T \end{aligned}$$

(3)

with boundary condition $I(t_1)=0$.

Fig. 1

Graphical representation of inventory model

Fig. 2

Graphical representation of inventory model for various cases of M

The solutions to the above differential equations are

$$\begin{aligned} I(t)= & {} a(t_1-t)+\frac{b}{2}(t_1^2-t^2)\;\quad 0 < t \le t_1 \end{aligned}$$

(4)

$$\begin{aligned} I(t)= & {} \delta \Big [a(t_1-t)+\frac{b}{2}(t_1^2-T^2)\Big ]\;\quad t_1 < t \le T \end{aligned}$$

(5)

The maximum inventory level $I_m$ is given by

$$\begin{aligned} I_m = I(t=0) = at_1 + \frac{b}{2}t_1^2 \end{aligned}$$

(6)

The maximum amount of demand backlogged $I_b$ is given by

$$\begin{aligned} I_b = -I(T) = \delta \Big [a(T-t_1)+\frac{b}{2}(T^2-t_1^2)\Big ] \end{aligned}$$

(7)

The retailer’s order quantity Q is

$$\begin{aligned} Q = I_m+I_b = at_1+\frac{b}{2}t_1^2+\delta \Big [a(T-t_1)+\frac{b}{2}(T^2-t_1^2)\Big ] \end{aligned}$$

(8)

The various costs associated with the retailer’s profit function per cycle are listed below with interest earned and payable for $0 < M \le t_1$ and $t_1 < M \le T$ which is depicted in Fig. 2

a) :

ordering cost $=$ k

b) :

holding cost (excluding interest charges)

$$\begin{aligned} C_H= & {} \int \limits _{0}^{t_1}h(t)~I(t)~dt \\= & {} \int \limits _{0}^{t_1} f~exp(dt)\Big [a(t_1-t)+\frac{b}{2}(t_1^2-T^2)\Big ]~dt\\= & {} f\Bigg [\frac{exp(dt_1)}{d^2}\left( a+bt_1-\frac{b}{d}\right) +\frac{b}{d^3}-\frac{a}{d^2}-\frac{at_1}{d}-\frac{bt_1^2}{2d}\Bigg ] \end{aligned}$$

c) :

purchase cost $=$ cQ $=$ c$\Bigg [at_1+\frac{b}{2}t_1^2+\delta \Big [a(T-t_1)+\frac{b}{2}(T^2-t_1^2)\Big ] \Bigg ]$

d) :

sales revenue $=$ sQ $=$ s$\Bigg [at_1+\frac{b}{2}t_1^2+\delta \Big [a(T-t_1)+\frac{b}{2}(T^2-t_1^2)\Big ] \Bigg ]$

e) :

shortage cost

$$\begin{aligned} c_s= & {} c_2\int \limits _{t_1}^{T}~-I(t)~dt \\= & {} \int \limits _{t_1}^{T}~\delta \Big [a(T-t_1)+\frac{b}{2}(T^2-t_1^2)\Big ]~dt\\= & {} \delta c_2\left[ \bigg (\frac{aT^2}{2}+\frac{bT^3}{6}\bigg ) \right] \end{aligned}$$

f) :

Case 1: $0 < M \le t_1$

$$\begin{aligned} \hbox {Interest earned }= & {} sI_e~\int \limits _{0}^{M}D(t)~(M-t)~dt\\= & {} sI_e\Big [\frac{aM^2}{2}+\frac{bM^3}{6}\Big ]\\ \hbox {Interest payable }= & {} cI_c~\int \limits _{M}^{t_1}I(t)~dt\\= & {} cI_c~\int \limits _{M}^{t_1}\Big [a(t_1-t)+\frac{b}{2}\Big (t_1^2-T^2\Big )\Big ]~dt\\= & {} cI_c\Bigg [\frac{a(t_1-M)^2}{2}+\frac{b\left( t_1^2-Mt_1^2 \right) }{2}-\frac{b(t_1^3-M^3)}{6}\Bigg ] \end{aligned}$$

g) :

Case 2: $t_1 < M \le T$ From 0 to $t_1$, the retailer sells goods and continues accumulate sales revenue to earn interest $I_e$.

$$\begin{aligned} sI_e\int \limits _{0}^{t_1}(a+bt)~(t_1-t)~dt =sI_e\Big [\frac{at_1^2}{2}+\frac{bt_1^3}{6}\Big ] \end{aligned}$$

From $t_1$ to M, the retailer can use the sales revenue generated in [0, $t_1$] to earn interest. Thus the interest earned from 0 to M is

$$\begin{aligned} sI_e\Bigg [\frac{at_1^2}{2}+\frac{bt_1^3}{6}+(M-t_1)\Big [at_1+\frac{bt_1^2}{2}\Big ]\Bigg ] \end{aligned}$$

Interest payable in this case is zero.

From the above results, the total profit per unit time can be expressed as $\Pi (t_1,T)=\big \{\hbox {sales revenue} - \hbox {ordering cost} - \hbox {purchase cost} - \hbox {holding cost} - \hbox {interest payable} + \hbox {interest earned} - \hbox {shortage cost}\big \}/\hbox {T}$.

$$\begin{aligned} \Pi (t_1,T)=\left\{ \begin{array}{ll} \Pi _1(t_1,T) &{}\quad 0 < M \le t_1 \\ \Pi _2(t_1,T) &{}\quad t_1 < M \le T\\ \end{array} \right. \end{aligned}$$

(9)

where

$$\begin{aligned} \Pi _1(t_1,T)= & {} \frac{1}{T}\Bigg \{(s-c)(1-\delta ) \left( at_1+\frac{b}{2}t_1^2\right) -k-f\Big [\frac{exp(dt_1)}{d^2} \left( a-\frac{b}{d}\right) \nonumber \\&+\,exp(dt_1)\frac{bt_1}{d^2}+\frac{b}{d^3}-\frac{a}{d^2}-\frac{at_1}{d}-\frac{bt_1^2}{2d}\Big ] +sI_e\Bigg [\frac{aM^2}{2}+\frac{bM^3}{6}\Bigg ]\nonumber \\&-\,cI_c\Bigg [\frac{a(t_1-M)^2}{2}+\frac{b(t_1^3-t_1^2M)}{2}-\frac{b(t_1^3-M^3)}{6}\Bigg ]\nonumber \\&-\,c_2\Bigg [\frac{a\delta t_1^2}{2}+\frac{b\delta t_1^3}{3}\Bigg ]\Bigg \} -c_2\Bigg [\frac{a\delta T}{2}+\frac{b\delta T^2}{6}-a\delta t_1-\frac{b\delta t_1^2}{2}\Bigg ] \end{aligned}$$

(10)

$$\begin{aligned} \Pi _2(t_1,T)= & {} \frac{1}{T}\Bigg \{(s-c)(1-\delta )\left( at_1+\frac{b}{2}t_1^2\right) -k-f\Big [\frac{exp(dt_1)}{d^2}\left( a-\frac{b}{d}\right) \nonumber \\&+\,exp(dt_1)\frac{bt_1}{d^2}+\frac{b}{d^3}-\frac{a}{d^2}-\frac{at_1}{d}-\frac{bt_1^2}{2d}\Big ] -c_2\Bigg [\frac{a\delta t_1^2}{2}+\frac{b\delta t_1^3}{3}\Bigg ]\nonumber \\&+\,sIe\Bigg [\frac{at_1^2}{2}+\frac{bt_1^3}{6} +(m-t_1)\left( at_1+\frac{bt_1^2}{2}\right) \Bigg ]+(s-c)\Big [a\delta T+\frac{b\delta }{2}\Big ]\nonumber \\&-\,c_2\Bigg [\frac{a\delta }{2}+\frac{b\delta T}{6}\Bigg ]\Bigg \} +c_2\bigg [a\delta t_1 +\frac{b\delta t_1^2}{2}\bigg ] \end{aligned}$$

(11)

Theoretical Results and Optimal Solutions

The necessary conditions for the total profit per unit time in Eq. (10) to be maximum at $t_1=t_1^*, T=T^*$ are $\frac{\delta \Pi _1(t_1,T)}{\delta t_1}=0$ and $\frac{\delta \Pi _2(t_1,T)}{\delta T}=0$, provided all principle minors are $\left| \begin{array}{cc} \frac{\delta ^2 \Pi _1(t_1,T)}{\delta t_1^2} &{} \frac{\delta ^2 \Pi _1(t_1,T)}{\delta t_1 \delta T}\\ \frac{\delta ^2 \Pi _1(t_1,T)}{\delta t_1 \delta T} &{} \frac{\delta ^2 \Pi _1(t_1,T)}{\delta T^2} \end{array} \right| >0$ and $\frac{\delta ^2\Pi _1(t_1,T)}{\delta t_1^2} < 0$ , $\frac{\delta ^2\Pi _1(t_1,T)}{\delta T^2} < 0$

$$\begin{aligned} \frac{\delta \Pi _1(t_1,T)}{\delta t_1}= & {} \frac{1}{T}\Bigg \{(s-c)(1-\delta )(a+bt_1) -f\Bigg [\frac{exp(dt_1)}{d}\left( a-\frac{b}{d}\right) \nonumber \\&+\,exp(dt_1)\frac{b}{d^2}+exp(dt_1)\frac{bt_1}{d}-\frac{a}{d}-\frac{bt_1}{d}\Bigg ]\nonumber \\&-\,cIc\Bigg [a(t_1-M)+\frac{b}{2}(3t_1^2-2Mt_1)-\frac{bt_1^2}{2}\Bigg ]\nonumber \\&-\,c_2\Bigg [a\delta t_1+b\delta t_1^2\Bigg ]\Bigg \}+c_2\Big [a\delta +b\delta t_1\Big ]=0 \end{aligned}$$

(12)

$$\begin{aligned} \frac{\delta \Pi _1(t_1,T)}{\delta T}= & {} \frac{-1}{T^2}\Bigg \{(s-c)(1-\delta )(at_1+\frac{b}{2}t_1^2)-k-f\Big [\frac{exp(dt_1)}{d^2}\left( a-\frac{b}{d}\right) \nonumber \\&+\,exp(dt_1)\frac{bt_1}{d^2}+\frac{b}{d^3}-\frac{a}{d^2}-\frac{at_1}{d}-\frac{bt_1^2}{2d}\Big ] +sI_e\Big [\frac{aM^2}{2}+\frac{bM^3}{6}\Big ]\nonumber \\&-\,c_2\Big [\frac{a\delta t_1^2}{2}+\frac{b\delta t_1^3}{3}\Big ]\Bigg \} -c_2\Big [\frac{a\delta }{2}+\frac{b\delta T}{3}\Big ]+(s-c)\frac{b\delta }{2}=0 \end{aligned}$$

(13)

$$\begin{aligned} \frac{\delta ^2\Pi (t_1,T)}{\delta t_1^2}= & {} \frac{1}{T}\Bigg \{(s-c)b(1-\delta )-f\Big [a~exp(dt_1)+bt_1exp(dt_1)\Big ]\nonumber \\&+\,\frac{bf}{d}\Bigg [1-exp(dt_1)\Bigg ]-cIc\big [a+2bt_1-Mb\big ]-c_2\big [a\delta +2b\delta t_1\big ]\nonumber \\&+\,c_2b\delta T\Bigg \} < 0 \end{aligned}$$

(14)

$$\begin{aligned} \frac{\delta ^2\Pi _1(t_1,T)}{\delta T\delta t_1}= & {} \frac{a\delta + b\delta t_1}{T} \end{aligned}$$

(15)

$$\begin{aligned} \frac{\delta ^2\Pi _1(t_1,T)}{\delta T^2}= & {} -\Bigg [\frac{c_2a\delta }{T}+c_2b\delta +\frac{cb\delta }{T}\Bigg ] +\,\frac{sb\delta }{T} < 0 \end{aligned}$$

(16)

Clearly

$$\begin{aligned} \left| \begin{array}{cc} \frac{\delta ^2 \Pi _1(t_1,T)}{\delta t_1^2} &{} \frac{\delta ^2 \Pi _1(t_1,T)}{\delta t_1 \delta T}\\ \frac{\delta ^2 \Pi _1(t_1,T)}{\delta t_1 \delta T} &{} \frac{\delta ^2 \Pi _1(t_1,T)}{\delta T^2} \end{array} \right|= & {} \Bigg \{\frac{sb\delta }{T}-\Bigg [\frac{c_2a\delta }{T}+c_2b\delta +\frac{cb\delta }{T}\Bigg ]\Bigg \}\nonumber \\&\times \frac{1}{T}\Bigg \{(s-c)b(1-\delta )-f\Big [a~exp(dt_1)+bt_1exp(dt_1)\Big ]\nonumber \\&+\,\frac{bf}{d}\Big [1-exp(dt_1)\Big ]-cIc\big [a+2bt_1-Mb\big ]\nonumber \\&-\,c_2\big [a\delta +2b\delta t_1\big ]+c_2b\delta T\Bigg \} -\Bigg \{\frac{a\delta +b\delta t_1}{T}\Bigg \}^2\nonumber \\&>0 \end{aligned}$$

(17)

Hence $\Pi _1(t_1,T)$ is convex.

$$\begin{aligned} \frac{\delta \Pi _2(t_1,T)}{\delta t_1}= & {} \frac{1}{T}\Bigg \{(s-c)(1-\delta )(a+bt_1)-f\Big [\frac{exp(dt_1)}{d} \left( a-\frac{b}{d}\right) \nonumber \\&+\,\frac{exp(dt_1)b}{d^2}+\frac{exp(dt_1)bt_1}{d}-\frac{a}{d}-\frac{bt_1}{d}\Big ]+sIe\Big [at_1+\frac{bt_1^2}{2}\nonumber \\&-\,\Big (at_1+\frac{bt_1^2}{2}\Big )+(M-t_1)(a+bt_1)\Big ]-c_2\Big [a\delta t_1+b\delta t_1^2\Big ]\Bigg \}\nonumber \\&+\,c_2\Big [a\delta +b\delta t_1\Big ]=0 \end{aligned}$$

(18)

$$\begin{aligned} \frac{\delta \Pi _2(t_1,T)}{\delta t_1}= & {} \frac{-1}{T^2}\Bigg \{(s-c)(1-\delta ) \left( at_1+\frac{b}{2}t_1^2\right) -k-f\Bigg [\frac{exp(dt_1)}{d^2} \left( a-\frac{b}{d}\right) \nonumber \\&+\,exp(dt_1)\frac{bt_1}{d^2}+\frac{b}{d^3} -\,\frac{a}{d^2}-\frac{at_1}{d}-\frac{bt_1^2}{2d}\Bigg ] -c_2\Bigg [\frac{a\delta t_1^2}{2}+\frac{b\delta t_1^3}{3}\Bigg ]\nonumber \\&+\,sIe\Bigg [\frac{at_1^2}{2}+\frac{bt_1^3}{6}+(m-t_1) \left( at_1+\frac{bt_1^2}{2}\right) \Bigg ]\Bigg \}\nonumber \\&+\,(s-c)\frac{b\delta }{2}-c_2\Big [\frac{a\delta }{2}+\frac{b\delta T}{3}\Big ]=0 \end{aligned}$$

(19)

Similarly it can be shown that $\Pi _2(t_1,T)$ is convex.

Fig. 3

Graph of T versus total profit $\Pi$

Fig. 4

Graph of $t_1$ versus total profit $\Pi$

Fig. 5

Graph of M versus total profit $\Pi$

Fig. 6

Graph of $c_2$ versus total profit $\Pi$

Fig. 7

Graph of $c_2$ versus cost functions

By solving Eqs. (12–13), the value of $t_1$, T can be obtained and with the use of this value, Eq.  (10) provides the maximum total profit per unit time of the inventory model. Similarly solving Eqs.  (14, 15), we can find $t_1$, T and Eq.  (11) provides the maximum total profit per unit time.Hence, our aim is to find the optimal value of $t_1$ and T which maximizes the total profit $\Pi (t_1,T)$ (Figs. 3, 4, 5, 6, 7).

Numerical Examples

Numerical examples are carried out using SCILAB(5.5.0).

In each table, the column TC that corresponds to the total cost when permissible delay period M $=$ 0.

Example 1

 a $=$ 10, b $=$ 50, f $=$ 15, d $=$ 8, k $=$ 200, c $=$ 50, s $=$ 60, $i_e=0.11$, $i_c=0.04$, M $=$ 35/365, $\delta =8$, $c_2=30$ with suitable units. The results are tabulated below.

$t_1$	T	$\Pi _1$	$t_1$	T	$\Pi _2$	$Q^*$	TC	Q
0.2746	0.6227	581.2332	0.3089	0.6663	516.3449	94.9492	472.8069	103.6823

Example 2

a $=$ 10, b $=$ 50, f $=$ 15, d $=$ 8, k = 140, c $=$ 50, s $=$ 60, $i_e$ $=$ 0.12, $i_c$ $=$ 0.13, M $=$ 48/365, $\delta$ $=$ 8, $c_2$ $=$ 30 with suitable units. The results are tabulated below.

$t_1$	T	$\Pi _1$	$t_1$	T	$\Pi _2$	$Q^*$	TC	Q
0.2624	0.6136	620.978	0.2618	0.6130	609.8865	93.9553	566.6639	94.8394

Example 3

a $=$ 10, b $=$ 50, f $=$ 15, d $=$ 8, k $=$ 450, c $=$ 40, s $=$ 50, $i_e$ $=$ 0.11, $i_c$ $=$ 0.04, M $=$ 14/365, $\delta$ $=$ 8, $c_2$ $=$ 30 with suitable units. The results are tabulated below.

$t_1$	T	$\Pi _1$	$t_1$	T	$\Pi _2$	$Q^*$	TC	Q
0.3426	0.7431	201.9775	0.3567	0.7613	159.9815	125.3839	121.77	130.3446

Example 4

a $=$ 10, b $=$ 50, f $=$ 15, d $=$ 8, k = 60, c $=$ 45, s $=$ 50, $i_e$ $=$ 0.11, $i_c$ $=$ 0.13, M $=$ 14/365, $\delta$ $=$ 8, $c_2$ $=$ 30 with suitable units. The results are tabulated below.

$t_1$	T	$\Pi _1$	$t_1$	T	$\Pi _2$	$Q^*$	TC	Q
0.2083	0.3918	116.0514	0.2398	0.4136	128.7446	40.4518	86.3469	40.4443

Example 5

a $=$ 10, b $=$ 50, f $=$ 15, d $=$ 8, k = 200, c $=$ 50, s $=$ 60, $i_e$ $=$ 0.11, $i_c$ $=$ 0.04, $\delta$ $=$ 8, $c_2$ $=$ 30 with suitable units. To study the effects of change in the parametric values of M, $\delta$ and $c_2$, we use the data of Example 1 and the results are presented in the following Tables 1, 2 and 3 respectively.

Table 1 Effects of changes in parameter M of the model

Table 2 Effects of changes in parameter $\delta$ of the model

Table 3 Effects of changes in parameter $c_2$ of the model

From the above example, the following observations are made:

• 1. If the permissible delay period M increases, the optimal total cost decreases first and then increases for a fixed value of $\delta$. When M is greater than 15 days, the total profit increases. Thus the retailer should place optimum order quantity accordingly and carefully in order to gain maximum profit. If the permissible delay period set by the supplier is too short, the retailer may decide to order a quantity so as to gain profit. The managerial insight is as follows: Hence the retailer can maximize the total profit if the retailer gets shorter permissible delay period from the supplier.

• 2. If the values of the backlogging parameter $\delta$ increase, the optimum total profit and optimum order quantity $Q^*$ increases but the optimum order cycle $T^*$ decreases. Thus we see that the optimum total profit increases to a greater extent for large values of $\delta$. The managerial insight is as follows: In order to gain maximum total profit the retailer ought to improve the backlogging rate.

• 3. If shortage cost $c_2$ increases for a fixed value of $\delta$, the optimum total profit, optimum order quantity and the optimum order cycle all decreases. Thus, changes in $c_2$ result negative change in the total cost, order quantity and order cycle. The managerial insight is as follows: The retailer has to adopt for planned back order level strategically so as to gain maximum profit.

Sensitivity Analysis

To study the effects of change in the parametric values a, b, d, s, c, k, $i_e$, $i_c$, $\delta$, M, $c_2$ on the optimal total cost, we use the data of Example 1. The sensitive analysis is performed by changing each of the parameter by $-50$, $-25$, 25 and 50 %, taking one parameter at a time and keeping the remaining parameters unchanged. Based on the computational results we obtained the numerical results which is presented in the Table 4.

Table 4 Effects of changes in parameter of the model

Based on the computational results, we obtained the following managerial phenomena:

• 1. If the values of a and b of the model increase, the optimal order quantity $Q^*$ increases. Hence, the optimal total profit of the model increases.

• 2. The optimal total profit alternatively decreases and increases with the increase in the values of the small variation in the values of f. But the optimal order quantity $Q^*$ gradually decreases with the increasing values of f.

• 3. If we increase the value of d, then the optimal total profit and the optimal order quantity $Q^*$ decreases. Thus the retailer must set up the holding cost strategically so as to gain maximum total profit.

• 4. The optimal total profit decreases with the increase in the value of ordering cost K. Also the optimal order quantity $Q^*$ increases with the increase in the value of k. The economic interpretation is that the higher the ordering cost k is, the larger the replenishment cycle becomes. Hence, it turns out a smaller profit.

• 5. If the value of purchase cost c increases then both the optimal total profit and the optimal order quantity $Q^*$ decreases.

• 6. Both optimal total profit and optimal order quantity $Q^*$ increases for the increasing values of selling price c. Thus, changes in the optimal total profit indicate that the model is highly sensitive to the changes on s.

• 7. The changes in the optimal total profit indicate that the model is moderately sensitive to the changes on ie while it is low sensitive to the optimal order quantity $Q^*$.

• 8. The optimal total profit and $Q^*$ decreases with the increase in the value of ic.

• 9. The changes of permissible delay M by a small amount have no impact on the optimal order quantity $Q^*$. Also the optimal total profit of the model is low sensitive to small variation in M.

• 10. If the values of the backlogging parameter $\delta$ increase, the optimum total profit and optimum order quantity $Q^*$ increases. Thus we see that the optimum total profit increases to a greater extent for large values of $\delta$. In order to gain maximum total profit the retailer ought to improve the backlogging rate.

• 11. If shortage cost $c_2$ increases for a fixed value of $\delta$, the optimum total profit, optimum order quantity and the optimum order cycle all decreases. Thus, changes in $c_2$ result negative change in the total cost, order quantity and order cycle. Hence, the retailer has to adopt for planned back order level strategically so as to gain maximum profit.

Conclusion

In this paper EOQ model for time varying demand and variable holding cost under permissible delay with shortages is studied. In this model shortages are allowed which are completely backlogged. We have considered two different cases to obtain optimal total profit, optimal order quantity and optimal replenishment policy. Based on sensitive analysis, this paper revealed the following observations: (1) The optimal total profit of the model is low sensitive to small variation in M. Hence, the retailer can maximize the total profit if the retailer gets shorter permissible delay period from the supplier. (2) The changes in the optimal total profit indicate that the model is highly sensitive to the changes on s. (3) In order to gain maximum total profit the retailer ought to improve the backlogging rate. (4) The retailer has to adopt for planned back order level strategically so as to gain maximum profit. (5) The optimal total profit is highly sensitive on the parameters c, s and $c_2$ of this model. Some numerical examples are given to illustrate the proposed model. Graphical representation is provided to establish the total profit function attains it’s optimum value. The sensitivity of the solution to changes in the values of the parameters between the range $-50$ to +50 % has also been discussed. To author’s best knowledge, such type of EOQ model with variable holding cost inventory model has not yet been discussed.