Introduction

Free and forced convection flow and heat transfer around cylinders has received much attention in recent years due to its many important practical applications such as thermal design of buildings, electronics cooling, solar collectors, drilling operations, commercial refrigeration, geothermal power generation and float glass production etc., Sparrow and Gregg [1] provided the first approximate solution for the mixed convection boundary layer flow over a vertical cylinder with prescribed surface heat flux, by applying the similarity method and power series expansion. The steady mixed convection boundary layer flow along a vertical cylinder with prescribed surface heat flux was made by Ishak [2]. By considering partial slip at the boundary, Mukhopadhyay [3] presented an analysis for the axi-symmetric laminar boundary layer flow of a viscous incompressible fluid and heat transfer towards a stretching cylinder under the influence of a uniform magnetic field. Mishra and Singh [4] studied the effect of second order momentum slip and the first order thermal slip on the flow of viscous fluid over a permeable shrinking cylinder.

Mixed convection boundary-layer flow and heat transfer of thermally driven flows in porous media have several engineering applications such as geothermal energy recovery, crude oil extraction, ground water pollution, thermal energy storage and flow through filtering media.

Minkowycz [5] presented an analysis for the problem of free convection about a vertical cylinder embedded in a porous medium with a variable wall temperature. Bassom and Rees [6] investigated the variable wall temperature case on free convection from an isothermal vertical cylinder embedded in a saturated porous medium. Mixed convection boundary layer flow past a vertical cylinder in a porous medium saturated with a nanofluid was treated numerically by Gorla and Hossain [7]. Temperature-dependent viscosity on non-Darcy natural convection flow over a vertical cylinder in a saturated porous medium was analyzed by Hakiem and Rashad [8]. Chamkha et al. [9] studied the effect of temperature-dependent viscosity on the combined heat and mass transfer by non-Darcy natural convection flow over an isothermal vertical cylinder embedded in a fluid-saturated porous medium. Recently Rashad et al. [10] investigated steady mixed convection boundary-layer flow past a horizontal circular cylinder in a stream flowing vertically upwards embedded in porous medium filled with a nanofluid.

In the context of space technology and in the processes involving high temperatures, the effect of radiation plays a vital role. Ganesan and Loganathan [11] investigated the radiation and mass transfer effects on flow of an incompressible viscous fluid past a moving vertical cylinder. Suneetha and Bhaskar Reddy [12] discussed the radiation and mass transfer effects on MHD free convection flow past a moving vertical cylinder embedded in a porous medium. Hakiem [13] studied the radiation effects on hydromagnetic free convective and mass transfer flow of a gas past a circular cylinder with uniform heat and mass flux. Abbas et al. [14] analyzed laminar MHD flow and heat transfer of an electrically conducting viscous fluid over a stretching cylinder in the presence of thermal radiation through a porous medium. Akbar et al. [15] obtained numerical solutions of the steady MHD two dimensional stagnation point flow of an incompressible nano fluid towards a stretching cylinder in the presence of thermal radiation and convective heat exchange at the surface. EL-Kabeir et al. [16] have developed a theoretical model to analyze the effects of thermal radiation and the nonlinear Forchheimer terms on boundary-layer flow and heat transfer by non-Darcy natural convection from a vertical cylinder embedded in a porous medium saturated with nanofluids.

Applications involving two-phase flows in which solid spherical particles are distributed in a fluid are quite broad, and include such areas as sedimentation, environmental pollution, centrifugal separation of particles and blood rheology. There are several investigations on this topic. Saffman [17] has formulated the basic equations for the flow of dusty fluid. Since then several different numerical and analytical investigations of dusty fluid flow process have been performed in recent years, see, for example, Chamkha [18], Attia [19], Damseh [20], Ezzat et al. [21], Datta and Mishra [22], Kulandaivel [24]. Ganesan and Palani [23] studied numerical solution of heat transfer effects on dusty gas flow past a semi-infinite inclined plate using an implicit finite difference method. Palani and Kim [25] presented the approximate solution for the free convection of a dusty-gas flow along a semi-infinite isothermal vertical cylinder. Recently Gireesha et al. [26–28] obtained interesting results on dusty fluid flow due to linear and exponential stretching of porous and non porous plate with various effects like source/sink parameter, radiation, viscous decapitation etc., Nandkeolyar and Sibanda [?] studied steady two dimensional boundary layer flow of a viscous, incompressible and electrically conducting dusty fluid past a vertical permeable stretching sheet under the influence of a transverse magnetic field with the viscous and Joule dissipations.

The above investigators restricted their analysis to flows of a dusty fluid over stretching sheet. However, recently, boundary layer flow of a dusty fluid over stretching cylinder has gained considerable importance due to its applications. In this paper, we restrict our consideration to the regime of porous media and focus on effects induced by stretching parameter on flow and heat transfer phenomena in presence of magnetic field and radiation effect. The governing coupled nonlinear partial differential equations are reduced to ordinary differential equations and then solved numerically using RKF45 method. Numerical results are presented as graphs. The effect of external uniform magnetic field, Prandtal number, thermal conductivity on the velocity and temperature distributions for both fluid and dust particle phase is discussed. Finally, numerical results for the local skin-friction coefficient and local Nusselt number are also presented.

Flow Analysis of the Problem

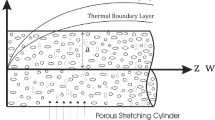
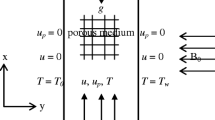
Let us consider a steady laminar flow of an incompressible viscous conducting dusty fluid caused by a stretching cylinder of radius a in the axial direction in a fluid at rest as shown in Fig. 1, where the z-axis is measured along the axis of the cylinder and the r-axis is measured in the radial direction. Two phases to be considered here are a continuous fluid phase interspersed with a discrete solid particulate phase. The particles are taken to be small enough and of sufficient number to be treated as a continuum and allow concepts such as density and velocity to have physical meaning. The dust particles are assumed to be spherical in shape, uniform in size and mass, and are undeformable. Here both phases behave as viscous fluids and the volume fraction of suspended particles is finite and constant. A uniform magnetic field of strength \(B_0 \) is applied in the radial direction. The magnetic Reynolds number is assumed to be small so that the induced magnetic field is neglected in comparison with the applied magnetic field. The class of flows that we emphasize is the boundary layer induced above the stretching cylinder. Taking into account these and the previously mentioned assumptions, the governing equations in cylindrical coordinates can be written as

$$\begin{aligned} \frac{\partial \left( {rw} \right) }{\partial z}+\frac{\partial \left( {ru} \right) }{\partial r}= & {} 0,\quad \end{aligned}$$
(1)
$$\begin{aligned} w\frac{\partial w }{\partial z}+u\frac{\partial w }{\partial r}= & {} \nu \left[ {\frac{\partial ^{2}w }{\partial r^{2}}+\frac{1 }{r}\frac{\partial w }{\partial r}} \right] +\frac{KN }{\rho }\left( {w_p -w} \right) +\frac{\sigma B_0^2 }{\rho }w-\frac{\nu }{K_p }w,\end{aligned}$$
(2)
$$\begin{aligned} w_p\frac{\partial {w_p } }{\partial z}+u_p \frac{\partial {w_p } }{\partial r}= & {} \frac{K }{m}\left( {w-w_p } \right) , \end{aligned}$$
(3)
$$\begin{aligned} \frac{\partial \left( {rw_p } \right) }{\partial z}+\frac{\partial \left( {ru_p } \right) }{\partial r}= & {} 0. \end{aligned}$$
(4)

where \(\left( {w,u} \right) \) and \(\left( {w_p , u_p } \right) \) are the velocity components of the fluid and dust particle phase \(\nu ,\rho ,N,K, B_0 ,k_{0 } \) and m are the kinematic viscosity of the fluid, density of the fluid, number density of the particle phase, Stoke’s resistance (drag co-efficient), magnetic filed, permeability of the porous medium and mass of the dust particle respectively. In deriving these equations, the drag force is considered for the interaction between the fluid and particle phases where (w, u) and \((w_p ,u_p )\) are the velocity components of the fluid and dust particle phases and are the co-efficient of viscosity of the fluid, density of the fluid, number density of the particle phase, is the stokes’ resistance (drag co-efficient), is the mass of the dust particle respectively. In deriving these equations, the drag force is considered for the interaction between the fluid and particle phases.

Fig. 1
figure 1

Schematic diagram of the flow problem

Full size image

The physical boundary conditions for the flow problem are given by

$$\begin{aligned}&w=u_w \left( z \right) , u=0, \quad at\, r=a,\nonumber \\&\quad w\rightarrow 0, w_p \rightarrow 0, u_p \rightarrow u \quad as\, r\rightarrow \infty . \end{aligned}$$
(5)

where a is the radius of the cylinder, \(u_w \left( z \right) =b\left( {\frac{z }{l} } \right) \) is the stretching velocity, \(b>0,\)    is stretching rate and l is the reference length. The following similarity transformations are used in order to reduce the governing equations into the corresponding ordinary differential equations:

$$\begin{aligned} u= & {} - \frac{a}{r}\sqrt{\frac{{\nu b}}{l}} f(\eta ), w = {u_w}\left( z \right) f'(\eta ), \quad \eta = \frac{{{r^2} - {a^2}}}{{2a}}\sqrt{\frac{{\nu b}}{l}}\nonumber \\ {u_p}= & {} - \frac{a}{r}\sqrt{\frac{{\nu b}}{l}} f(\eta ), {w_p} = {u_w}\left( z \right) f'(\eta ). \end{aligned}$$
(6)

It can be verified that the Eqs. (1) and (4) are identically satisfied and substituting (6) in to (2) and (3), we obtain the following non-linear ordinary differential equations:

$$\begin{aligned}&\left( {1 + 2\eta \gamma } \right) f'''(\eta ) + 2\gamma f''(\eta ) - {\left[ {f'(\eta )} \right] ^2} + f(\eta )f''(\eta )\nonumber \\&\quad - \left[ {Q + S} \right] f'(\eta ) + {\beta _\nu }\left[ {F'(\eta ) - f'(\eta )} \right] = 0,\end{aligned}$$
(7)
$$\begin{aligned}&F(\eta )F''(\eta ) - {\left[ {F'(\eta )} \right] ^2} + {\beta _\nu }\left( {f'(\eta ) - F'(\eta )} \right) = 0. \end{aligned}$$
(8)

where a prime denotes differentiation with respect to \(\eta \) and \(\gamma =\sqrt{\frac{l \nu }{b a^{2}}}\) curvature parameter, \(Q=\frac{\sigma B_0^2 l}{\rho b}\) is the magnetic parameter, \(S=\frac{\nu l}{bk_p }\) is the permeability parameter, \(\tau =\frac{m}{K}\) is the relaxation time of the particle phase, \(\beta _\nu =\frac{l}{b\tau _\nu }\) is the fluid particle interaction parameter for velocity.

The transformed dimensionless boundary conditions become,

$$\begin{aligned} f( \eta )= & {} 0, f'(\eta ) = 1, \quad at\, \eta = 0,\nonumber \\ F'(\eta )= & {} 0, {f'}(\eta ) = 0, F(\eta ) = f(\eta ), \quad as\, \eta \rightarrow \infty . \end{aligned}$$
(9)

Heat Transfer Analysis

The governing boundary layer energy equation for the two dimensional dusty fluid flow in the presence of internal heat generation/absorption for axisymmetric flow is given by Schlichting [30]:

$$\begin{aligned} \rho c_p \left( {w\frac{\partial T}{\partial z}+u\frac{\partial T}{\partial r}} \right)= & {} \frac{k}{r}\frac{\partial }{\partial r}\left[ r\frac{\partial T}{\partial r}+\frac{Nc_p }{\tau _T }\left( {T_p -T} \right) \right. \nonumber \\&\left. +\frac{N}{\tau _\nu }\left( {w_p -w} \right) ^{2}+Q_{0} \left( {T-T_\infty } \right) -\frac{\partial q_r }{\partial r} \right] ,\end{aligned}$$
(10)
$$\begin{aligned} w_p \frac{\partial T_p }{\partial z}+u_p \frac{\partial T_p }{\partial r}= & {} -\frac{c_p }{c_m \tau _T }\left( {T_p -T} \right) , \end{aligned}$$
(11)

where T and \(T_p \) are the temperatures of the fluid and dust particle phase respectively, \(c_p \) and \(c_m \) are the specific heat of fluid and dust particles, \(Q_{0} \) is the heat generation or absorption coefficient, \(\tau _T \) is the thermal equilibrium time and is time required by a dust cloud to adjust its temperature to the fluid, \(\tau _\nu \) is the relaxation time of the dust particle, i.e., the time required by the dust particle to adjust its velocity relative to the fluid, k is the thermal conductivity, \(q_r \) is the radiative heat flux.

The fluid is considered to be radiation absorbing-emitting but non-scattering medium and the Roseland approximation is used to describe the radiative heat flux in the energy equation. Using the Rosseland approximation for radiation (Bassom [6]), radiation heat flux is simplified as

$$\begin{aligned} q_r =-\frac{4\sigma ^{*}}{3k^{*}}\frac{\partial T^{4}}{\partial y}, \end{aligned}$$
(12)

where \(\sigma ^{*}\) and \(k^{*}\) are the Stefan–Boltzman constant and mean absorption co-efficient, respectively. Assuming that the temperature differences within the flow such that the term \(T^{4}\) may be expressed as a linear function of the temperature, we expand \(T^{4}\) in a Taylor series about \(T_\infty \) and neglecting the higher order terms beyond the first degree in \(\left( {T-T_\infty } \right) \) we get,

$$\begin{aligned} T^{4}\cong 4T_\infty ^3 T-3T_\infty ^4 . \end{aligned}$$
(13)

Substituting Eqs. (12) and (13) in Eq. (10) reduces to

$$\begin{aligned} \rho c_p \left( {w\frac{\partial T}{\partial z}+u\frac{\partial T}{\partial r}} \right)= & {} k^{*}\frac{\partial ^{2}T}{\partial y^{2}}+\frac{Nc_p }{\tau _T }\left( {T_p -T} \right) +\frac{N}{\tau _\nu }\left( {w_p -w} \right) ^{2}\nonumber \\&+\,Q_0 \left( {T-T_\infty } \right) -\frac{16\sigma ^{*}T_\infty ^3 }{3k^{*}}\frac{\partial ^{2}T}{\partial y^{2}}, \end{aligned}$$
(14)

In this paper we have discussed two types of heating process namely prescribed surface temperature (PST) and prescribed heat flux (PHF). Here the prescribed surface temperature is defined as quadratic function of x, while i the case of PHF is the power law of heat flux.

We have adopted the following boundary conditions to solve Eqs. (11) and (14) in both the cases;

$$\begin{aligned}&T=T_w =T_\infty +A\left( {\frac{z}{l}} \right) ^{2}\hbox { at } r=a, \quad \hbox {(PST)}\nonumber \\&\quad -k^{*}\frac{\partial T}{\partial r}=q_w =D\left( {\frac{z}{l}} \right) ^{2}\hbox { at }r=a, \quad \hbox {(PHF)}\nonumber \\&\quad T\rightarrow T_\infty , T_p \rightarrow T_\infty \hbox { as } r \rightarrow \infty . \end{aligned}$$
(15)

where \( T_w \) and \(T_\infty \) denote the temperature at the wall and at large distance from the wall respectively. A and D are positive constant, \(l=\sqrt{\frac{\nu }{c}}\) is a characteristic length.

We now introduce the following dimensionless fluid phase temperature \(\theta (\eta )\) and dust phase temperature \(\theta _p (\eta )\) as

$$\begin{aligned} \theta (\eta )=\frac{T-T_\infty }{T_w -T_\infty }, \quad \theta _p (\eta )=\frac{T_p -T_\infty }{T_w -T_\infty }, \end{aligned}$$
(16)

where \(T-T_\infty =A\left( {\frac{z}{l}} \right) ^{2}\theta (\eta )\) (PST-Case) and \(T_w -T_\infty =\frac{D}{k^{*}}\left( {\frac{z}{l}} \right) ^{2}\sqrt{\frac{\nu }{c}}\) (PHF-Case).

The boundary layer Eqs. (11) and (14) on using (6) and (16) take the following form,

$$\begin{aligned}&\left( {1 + 2\eta \gamma } \right) \left( {1 + \frac{{4R}}{3}} \right) \theta ''(\eta ) + \Pr \left[ {f(\eta )\theta '(\eta ) - 2f'(\eta )\theta (\eta )} \right] + \gamma \theta '(\eta )\nonumber \\&\quad +\, N{P_r}{\beta _T}\left( {{\theta _p} - \theta } \right) + N{P_r}{E_c}{\beta _T}\left( {F'(\eta - f'(\eta )} \right) + {P_r}\delta \theta (\eta ) = 0,\end{aligned}$$
(17)
$$\begin{aligned}&2F'(\eta ){\theta _p}(\eta ) - F(\eta ){\theta _p}(\eta ) + {\beta _T}\delta \left( {{\theta _p} - \theta } \right) = 0, \end{aligned}$$
(18)

where \(P_r =\frac{\mu c_p }{k^{*}}\) is the Prandtl number, \(E_c =\frac{bl^{2}}{Ac_p }\) (PST-Case), \(E_c =\frac{k^{*}l^{2}b^{3/2}}{D c_p v^{1/2}}\) (PHF-Case) is the Eckert number, \(B_T =\frac{1}{b\tau _T }\) is the fluid-particle interaction parameter for temperature, \(\delta =\frac{c_p }{c_m }\) is the specific ratio and \(\Gamma =\frac{Q_0 }{\rho c_p b}\) is the heat generation or absorption parameter.

Now the boundary conditions for \(\theta (\eta )\) and \(\theta _p (\eta )\) follows from (15) and (16) as

$$\begin{aligned}&\theta (\eta ) = 1, \quad at\, \eta = 0 \,\left( {{\hbox {PST - Case}}} \right) {\hbox { and }}\theta '(\eta ) = - 1 at\, \eta = 0 \left( {{\hbox {PHF - Case}}} \right) \nonumber \\&\quad \theta (\eta ) \rightarrow 0, {\theta _p}(\eta ) \rightarrow 0 as\, \eta \rightarrow \infty . \end{aligned}$$
(19)

Numerical Technique

The heat transfer problem for linearly stretching cylinder represented by Eqs. (7), (8), (17) and (18) are highly nonlinear and coupled and therefore solved numerically means of efficient Runge–Kutta Felhberg-45 method, which gives accurate result for boundary layer equations. For numerical solution it is necessary to assign some numerical values to all values of the parameters considered in the problem. For the computation work the default values of the parameters are taken as \(P_r =5, R=1, \beta _\nu =\beta _T =\gamma =\Gamma =0.5, E_c =0.1, S=2, N=2, \delta =1.\) The boundary condition for \(\eta \) at \(\infty \) is replaced by a sufficiently large value of \(\eta \) where the velocity and temperature approach far field boundary conditions asymptotically for all values of the parameters considered. In order to test the validity and accuracy of the numerical results obtained in the present analysis, the case when the curvature parameter is absent \(({\gamma =0, { flat\, plate}})\) has also been considered and compared with previously published results available in the literature. Table 1 presents a comparison of dimensionless temperature gradient \(-{\theta }''\) for different values of \(P_r \) with Grubka and Bobba [31], Abel et al. [32], Ali [33], Ishak et al. [34] and the present numerical results. It can be observed that the present numerical results are found to be in excellent agreement with those reported by previous investigators. A comprehensive numerical parametric computations have been carried out for various values of curvature parameter \((\gamma )\), fluid particle interaction parameter for velocity \(\left( {\beta _\nu } \right) \), Prandtl number \(\left( {P_r } \right) ,\) fluid-particle interaction parameter for temperature \((\beta _T )\), radiation parameter \(\left( R \right) \),heat generation or absorption parameter \((\Gamma )\), magnetic parameter (Q), permeability parameter (S) in both PST and PHF cases.

Table 1 Comparison of the results for the dimensionless temperature gradient \(-\theta '(0)\) various values of \(P_r \) in the case of \(\beta _\nu =\beta _\tau =\gamma =Q=N=0\, and\, S=0\)
Full size table

Results and Discussion

Equations (7) and (17) contain the transverse curvature parameter term which can significantly influence the fluid as well as dust phase velocity and the temperature profiles, and the corresponding skin friction and heat transfer rate as the ratio of the radius of the cylinder to the boundary-layer thickness becomes small. The velocity and temperature profiles for the fluid and dust phases for increasing values of curvature parameter \(\gamma \) are shown in Figs. 2 and 3a, b. It is evident from the plots that increasing in \(\gamma \) results in the enhancement of both fluid and dust phase velocity and also temperature of both fluid and dust phases. Here \(\gamma =0\), corresponds to flat plate and velocity as well as temperature are minimum for this case. So both velocity and temperature within the boundary layer in the case of cylinder is larger than the flat surface.

Fig. 2
figure 2

Effect of curvature parameter \((\gamma )\) on velocity profiles

Full size image
Fig. 3
figure 3

a Effect of curvature parameter \((\gamma )\) on temperature profiles in PST case, b effect of curvature parameter \((\gamma )\) on temperature profiles in PHF case

Full size image

Figure 4a, b presents typical profile for temperature for various values of the radiation parameter. An increase in R modifies the quantity \(\theta (\eta )\) and \(\theta _p (\eta )\) as expected, it decreases the thermal boundary layer thicknesses in both PST and PHF cases.

Fig. 4
figure 4

a Effect of radiation parameter (R) on temperature profile in PST case, b effect of radiation parameter \(\left( R \right) \) on temperature profile in PHF case

Full size image

Figures 5a and 6a, b demonstrate the effects of permeability parameter on velocity and temperature profiles. It is obvious that the presence of a porous medium causes higher restriction to the fluid flow which, in turn, slows its motion. Therefore, with increasing permeability parameter, the resistance to the fluid motion also increases. This causes the fluid velocity to decrease and due to which there is rise in the temperature in the boundary layer. It can thus be concluded that an increase in S decreases the boundary layer thickness and consequently brings about an increase in the heat transfer rate. The influence of magnetic field on the velocity and temperature within the boundary layer are shown in Figs. 7 and 8a, b. It is observed that the increase in magnetic field decreases the velocity but increasing the temperature of the fluid.

Fig. 5
figure 5

a Effect of permeability parameter (S) on velocity profile in PST case

Full size image
Fig. 6
figure 6

a Effect of permeability parameter (S) on temperature profile in PST case, b effect of permeability parameter (S) on temperature profile in PHF case

Full size image
Fig. 7
figure 7

Effect of magnetic parameter (Q) on velocity profiles

Full size image
Fig. 8
figure 8

a Effect of magnetic parameter (Q) on temperature profile in PST case, b effect of magnetic parameter (Q) on temperature profile in PHF case

Full size image

The variations in fluid and dust phase velocity profiles for various values of the Prandtl number, in PST and PHF cases are illustrated through the Fig. 9a, b. From the figure, we found that the temperature of both phases decreases with increase of Prandtl number.

Fig. 9
figure 9

a Effect of Prandtl number \(\left( {P_r } \right) \) on temperature profile in PST case, b effect of Prandtl number \(\left( {P_r } \right) \) on temperature profile in PHF case

Full size image

Figure 10a, b illustrates the influence of the heat generation or absorption parameter \(\Gamma \) on the temperature profile. The source term represents the heat generation that is distributed everywhere when \(\Gamma \) is positive, the heat absorption when \(\Gamma \)is negative and \(\Gamma \) is zero in the case of no heat source. It can be seen that the thermal boundary layer generates the energy, and this causes the temperature of both fluid and dust phases increases with increase in the value of \(\left( {\Gamma >0} \right) \) (heat source), where as for \(\left( {\Gamma <0} \right) \) the temperature is minimum. From Fig. 11 we observe that both \({f}''\) and \({F}''\) increases with increasing value of \(\beta _\nu .\) Figure 12a, b represents the variations of \(\theta (\eta )\) and \(\theta _p (\eta )\) with fluid particle interaction parameter for temperature and it is found that temperature of both phases decreases as \(\beta _T \) increases.

Fig. 10
figure 10

a Effect of heat generation or absorption parameter \((\Gamma )\) on temperature profile in PST case, b effect of heat generation or absorption parameter \((\Gamma )\) on temperature profile in PST case

Full size image
Fig. 11
figure 11

Effect of fluid-particle interaction parameter for velocity \(({\beta _\nu })\) on velocity profile

Full size image
Fig. 12
figure 12

a effect of is the fluid-particle interaction parameter for temperature \(({\beta _\tau })\) on temperature profile in PST case, b effect of is the fluid-particle interaction parameter for temperature \(({\beta _\tau })\) on temperature profile in PHF case

Full size image

Skin friction coefficient \({f}''\) wall temperature gradient \({\theta }'(0)\) in case of PST and in \(\theta (0)\) case of PHF for various values of governing parameters are tabulated in Table 2. The value of \({f}'' (0)\) is decreased by increasing the curvature parameter suggests that, to minimize the skin friction value which we usually look for in an industrial application, one needs to decrease the radius of the stretching cylinder. Numerical results also indicate that the values of \({f}''(0)\) decreases with increasing permeability parameter, magnetic field, fluid-particle interaction parameter for velocity and fluid-particle interaction parameter for temperature. The value of local Nusselt number \(\theta ^{{\prime }}(0)\) is increased by increasing the curvature parameter, which means that the skin friction as well as the heat transfer rate at the surface are larger for a cylinder compared to the flat plate. Also we observe that \(\theta ^{{\prime }}(0)\) is increased by increasing Prandtl number and fluid particle interaction parameter where as it decreases with increase of radiation parameter, magnetic field and blowing parameter.

Table 2 The values \(f''(0), - \theta '(0)\, and\, \theta (0)\) for various values of \(\Gamma , \gamma , S, R, Q, P_r , \delta , \beta _\nu , \beta _\tau , E_c\,and\, N\)
Full size table

Conclusions

A numerical analysis has been developed for the flow and velocity characteristics of an electrically conducting dusty fluid over a stretching cylinder embedded in a porous medium in the presence of a transverse magnetic field and thermal radiation. The governing boundary-layer equations for the problem are reduced to dimensionless ordinary differential equations using suitable similarity transformations. Numerical computations for the effects of controlling parameters on velocity and temperature fields have been carried out and physical quantities such as the skin-friction coefficient and the heat transfer coefficient are determined for different values of the Prandtl number, radiation parameter and curvature parameter, Magnetic parameter, permeability parameter, fluid particle interaction parameter, heat generation or absorption parameter. A comparison between the present numerical solutions and previously published results has been included, and the results are found to be in excellent agreement. The study concludes with the following results:

  • The results of the present study indicate that dusty fluid may be preferable to clean fluids in applications where control of heat transfer is important.

  • PHF boundary conditions are best suitable for cooling and PST for heating of the stretching cylinder.

  • Both the magnitude of the skin friction coefficient and the heat transfer rate at the surface are higher for cylinder when compared to that of flat plate.

  • The velocity of both fluid and dust phase decreases with increase of permeability and magnetic parameter.

  • The temperature within the boundary layer increases with increase of curvature parameter, radiation parameter, heat generation or absorption parameter permeability parameter, magnetic parameter and decrease with increase of fluid particle interaction parameter for temperature and Prandtl number.

  • The coefficient of skin friction decreases with increasing permeability parameter, Magnetic field, fluid particle interaction parameter and suction parameter

  • The value of local Nusselt number \({\theta }''\)s increased by increasing the curvature parameter, which means that the skin friction as well as the heat transfer rate at the surface are larger for a cylinder compared to the flat plate.