1 Introduction

Dusty fluid flows has its importance in many applications like wastewater treatment, power plant piping, combustion and petroleum transport. Fluid flow under the influence of magnetic field and heat transfer occurs in magneto-hydrodynamics accelerators, pumps and generators. This type of fluid has uses in nuclear reactors, plasma studies, geothermal energy extraction, and the boundary layer control in the field of aerodynamics. The flow of fluids through porous media has become an important topic because of recovery of crude oil from pores of reservoir rocks. Several authors have examined this type of problem theoretically in various ways. Saffman (1962) proposed equations of motion for binary mixture of fluid and dust particles. Kulshretha & Puri (1981) studied wave structure in oscillatory Couette flow of a dusty gas. Han et al (1991) analyzed the heat transfer in a pipe carrying two-phase gas-particle suspension.

Meanwhile, thermal radiation is a characteristic of any flow system at temperatures above the absolute zero and can strongly interact with convection in many situations of engineering interest. The differential approximation for radiative transfer in a non-grey gas near equilibrium was analyzed by Cogley et al (1968). Bestman & Adjepong (1988) studied the unsteady hydromagnetic free-convection flow with radiative heat transfer in a rotating fluid. Forced convection-radiation interaction with heat transfer in boundary layer flow over a flat plate submerged in a porous medium was studied by Mansour (1997). Raptis (1998) examined the effect of radiation on free convection flow through a porous medium. The effect of radiative heat transfer on arbitrary shaped axisymmetric enclosures with gases media was studied by Nune et al (1998). El-Hakiem (2000) investigated MHD oscillatory flow on free convection-radiation through a porous medium with constant suction velocity. Non-gray thermal radiation effects on the sound wave propagation in gas-particle two-phase medium have been analyzed by Park & Baek (2002). Raptis et al (2004) investigated the effect of thermal radiation on MHD flow. Unsteady MHD free convection flow of a compressible fluid past a moving vertical plate in the presence of radiative heat transfer was discussed by Mbeledogu et al (2007). Makinde & Ogulu (2008) studied the effect of thermal radiation on heat and mass transfer flow of a variable viscosity fluid past a vertical porous plate permeated by a transverse magnetic field. Unsteady oscillatory flow and heat transfer in a horizontal composite porous medium was investigated by Umavathi et al (2009). Cookey et al (2010) contributed to MHD oscillatory Couette flow of a radiating viscous fluid in a porous medium with periodic wall temperature. Makinde & Chinyoka (2010a) discussed MHD transient flows and heat transfer of dusty fluid in a channel with variable physical properties and Navier slip condition. A numerical investigation of transient heat transfer to hydromagnetic channel flow with radiative heat and convective cooling has been carried out by Makinde & Chinyoka (2010b). Gireesha et al (2010) analyzed unsteady flow and heat transfer of a dusty fluid through a rectangular channel under the influence of pulsatile pressure gradient and uniform magnetic field. Prakash et al (2011) investigated MHD free convective flow of a viscoelastic (Kuvshinski type) dusty gas through a porous medium induced by the motion of a semi-infinite flat plate under the influence of radiative heat transfer.

In this present paper, we extend the study of Makinde & Mhone (2005) on heat transfer characteristics of MHD oscillatory flow in a channel filled with porous medium by introducing the fluid as binary mixture of fluid and suspended particles. In the following sections, the problem is formulated, analyzed and solved. Pertinent results are presented graphically and discussed quantitatively.

2 Mathematical formulation

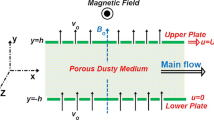
Consider the dusty fluid flow of a conducting optically thin fluid in a channel filled with saturated porous medium under the influence of an externally applied homogeneous magnetic field and radiative heat transfer as shown in figure 1. It is assumed that the fluid has small electrical conductivity. Take a Cartesian coordinate system (x, y) where x lies along the centre of the channel, y is the distance measured in the normal direction.

Figure 1
figure 1

Schematic diagram of the problem.

Full size image

The dust particles are solid, spherical, non-conducting equal in size and uniformly distributed in the flow region and their number density N 0 is constant throughout the motion. The temperature between the particles is uniform throughout the motion. The interactions between the particles and chemical reaction have not been considered. The magnetic Reynolds number is taken to be very small so that induced magnetic field is negligible and the Hall effects have been neglected. This means that the flow region has uniform temperature, uniform applied magnetic field. The dust particles are uniformly distributed and transported within the fluid such that the continuity equation is satisfied. Then, assuming a Boussinesq incompressible fluid model, the equations governing the motion and energy balance are as follows:

$$ \frac{\partial u}{\partial t}=-\frac{1}{\rho} \frac{\partial P}{\partial x}+\upsilon \frac{\partial^{2}u}{\partial y^{2}}-\frac{\upsilon} {K}u+\frac{N_{0} K_{0}} {\rho} (u_{p} -u)-\frac{\sigma_{e} {B_{0}^{2}}} {\rho} u+g\beta (T-T_{0} ), $$
(1)
$$ \frac{\partial u_{p}} {\partial t}=K_{0} (u-u_{p} ), $$
(2)
$$ \frac{\partial T}{\partial t}=\frac{k}{\rho c_{p}} \frac{\partial^{2}T}{\partial y^{2}}-\frac{1}{\rho c_{p}} \frac{\partial q}{\partial y}, $$
(3)

with initial and boundary conditions,

$$ u(y,0)=u_{p} (y,0)=0, T(y,0)=T_{f} , $$
(4)
$$ u(a,t)=u_{p} (a,t)=0, T(a,t)=T_{w} =T_{0} +(T_{f} -T_{0} )e^{i\omega t}, $$
(5)
$$ u(0,t)=u_{p} (0,t)=0, T(0,t)=T_{0} , $$
(6)

where u, u p are the velocities of fluid and dust particles in the x- direction, t is time, ω is the frequency of oscillation, T is the fluid temperature, T f is the fluid initial temperature, T 0 is the left wall temperature, T w is the right wall temperature, P is the fluid pressure, g is the gravitational force, q is the radiative heat flux, β is the coefficient of volume expansion due to temperature, K 0 (=6π ρ υ D) is the Stokes constant, D is the average radius of dust particles, c p is the specific heat at constant pressure, k is the thermal conductivity, K is the porous medium permeability coefficient, σ e is the conductivity of the fluid, ρ is the fluid density, υ is the kinematic viscosity, B 0 is the electromagnetic induction \(\left ({\mu _{e} H_{0}} \right )\), μ e is the magnetic permeability and H 0 is the intensity of magnetic field.

The fluid is assumed to be optically thin with a relatively low density and the radiative heat flux is given by Cogley et al (1968),

$$ \frac{\partial q}{\partial y}=4\alpha^{2}(T_{0} -T), $$
(7)

where α is the mean radiation absorption coefficient. The following dimensionless variables and parameters are introduced:

$$\overline x =\frac{x}{a}, \overline y =\frac{y}{a}, \overline u =\frac{u}{U}, \theta =\frac{T-T_{0}} {T_{f} -T_{0}} , \overline t =\frac{tU}{a}, Da=\frac{K}{a^{2}}, M=\frac{\upsilon} {K_{0} a^{2}}, $$
$$l=\frac{N_{0} K_{0} a^{2}}{\rho \upsilon} , Re=\frac{Ua}{\upsilon} ,\Pr =\frac{\upsilon \rho c_{p}} {k}, N^{2}=\frac{4\alpha^{2}a^{2}}{k}, \bar{{u}}_{p} =\frac{u_{p}} {U}, $$
$$ Gr=\frac{g\beta (T_{f} -T_{0} )a^{2}}{\upsilon U},\bar{{P}}=\frac{aP}{\upsilon \rho U},H^{2}=\frac{a^{2}\sigma_{e} {B_{0}^{2}}} {\upsilon \rho} ,s^{2}=\frac{1}{Da}, $$
(8)

where U is the flow mean velocity.

The dimensionless governing equations together with the appropriate boundary conditions (omitting the bars) can be written as

$$ Re\frac{\partial u}{\partial t}=-\frac{\partial P}{\partial x}+\frac{\partial^{2}u}{\partial y^{2}}-(s^{2}+H^{2}+l)u+lu_{p} +Gr\theta , $$
(9)
$$ ReM\frac{\partial u_{p}} {\partial t}=(u-u_{p} ), $$
(10)
$$ Re\Pr \frac{\partial \theta} {\partial t}=\frac{\partial^{2}\theta} {\partial y^{2}}+N^{2}\theta , $$
(11)

with initial and boundary conditions given as

$$ u(y,0)=u_{p} (y,0)=0,\theta (y,0)=1, $$
(12)
$$ u(1,t)=u_{p} (1,t)=0,\theta (1,t)=e^{i\omega t}, $$
(13)
$$ u(0,t)=u_{p} (0,t)=0,\theta (0,t)=0, $$
(14)

where s is porous medium shape factor parameter, Da is the Darcy number, Gr is the Grashof number, H is the Hartmann number, l is the particle concentration parameter, M is the particle mass parameter, N is the radiation parameter, Re is the flow Reynolds number and Pr is the Prandtl number.

3 Method of solution

In order to solve the Eqs. (9), (10) and (11) for pure oscillatory flow, let

$$ -\frac{\partial P}{\partial x}=\lambda e^{i\omega t}, u(y,t)=u_{0} (y)e^{i\omega t}, u_{p} (y,t)=u_{p0} (y)e^{i\omega t}, \theta (y,t)=\,\theta_{0} (y)e^{i\omega t}, $$
(15)

where λ is constant oscillation amplitude for pressure gradient. Substituting the values from Eq. (15) into Eqs. (9)–(14), we obtain

$$ \frac{d^{2}u_{0}} {dy^{2}}-{m_{2}^{2}} u_{0} =-\lambda -Gr\theta_{0} $$
(16)
$$ u_{p0} =\frac{u_{0}} {(1+i\omega ReM)}, $$
(17)
$$ \frac{d^{2}\theta_{0}} {dy^{2}}+{m_{1}^{2}} \theta_{0} =0 , $$
(18)

with

$$ u_{0} =u_{p0} =0,\theta_{0} =1,\, \text{on}\, y=1, $$
(19)
$$ u_{0} =u_{p0} =0,\theta_{0} =0,\, \text{on}\, y=0, $$
(20)

where \(m_{1} =\sqrt {N^{2}-i\omega Re\Pr } \) and \({m_{2}^{2}} =\left [ {s^{2}+H^{2}+i\omega Re+\frac {l}{(1+i\omega ReM)}} \right ]\).

On solving Eq. (18) with boundary condition (19) and (20), we obtain the temperature for fluid as

$$ \theta (y,t)=\frac{\sin (m_{1} y)}{\sin (m_{1} )}e^{i\omega t} . $$
(21)

Using Eq. (16) together with (19)–(20), we obtain the solution for the dusty fluid velocity as

$$\begin{array}{@{}rcl@{}} u(y,t)&=&\left\{ \frac{Gr}{{m_{1}^{2}} +{m_{2}^{2}}} \left[ {\frac{\sin (m_{1} y)}{\sin m_{1}} -\frac{\sinh (m_{2} y)}{\sinh m_{2}} } \right]+\frac{\lambda \sinh (m_{2} y)}{{m_{2}^{2}} \sinh m_{2}} \left( {\cosh m_{2} -1} \right)\right.\\ &&\quad\left.+\frac{\lambda} {{m_{2}^{2}}} \left( {1-\cosh m_{2} y} \right) \right\}e^{i\omega t}. \end{array} $$
(22)

From Eq. (17), dust particles velocity is obtained as

$$\begin{array}{@{}rcl@{}} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!u_{p} (y,t)\!\!\!&=&\!\!\!\frac{e^{i\omega t}}{(1+i\omega ReM)}\left\{ \frac{Gr}{{m_{1}^{2}} +{m_{2}^{2}}} \left[ {\frac{\sin (m_{1} y)}{\sin (m_{1} )}\,-\,\frac{\sinh (m_{2} y)}{\sinh (m_{2} )}} \right]\,+\,\frac{\lambda \sinh (m_{2} y)}{{m_{2}^{2}} \sinh (m_{2} )}\left( {\cosh (m_{2} )\,-\,1} \right)\right.\\ &&\qquad\qquad\qquad\quad\left.+\frac{\lambda} {{m_{2}^{2}}} (1-\cosh (m_{2} y)) \right\}. \end{array} $$
(23)

Other quantities of interest in the study are the skin friction C f and the Nusselt number Nu at channel walls. For dusty fluid the skin friction is given as

$$\begin{array}{@{}rcl@{}} &&C_{f} =\frac{a\tau_{f}} {\rho \upsilon U}=\left. {\frac{\partial u}{\partial y}} \right|_{y=1} =\left\{ \frac{Gr}{{m_{1}^{2}} +{m_{2}^{2}}} \left[ {m_{1} \cot (m_{1} )-m_{2} \coth (m_{2} )} \right]\right.\\ &&\qquad\qquad\qquad\qquad\quad~\left.+\frac{\lambda \coth (m_{2} )}{m_{2}} \left( {\cosh (m_{2} )-1} \right)-\frac{\lambda} {m_{2}} \sinh (m_{2} ){\vphantom{\frac{Gr}{{m_{1}^{2}} +{m_{2}^{2}}}}}\right\}e^{i\omega t} , \end{array} $$
(24)

where τ f = ρ υ ∂ u/∂ y at y = a is the fluid shear stress at the right wall. For dusty particles the skin friction is given as

$$\begin{array}{@{}rcl@{}} &&C_{f} =\frac{a\tau_{fp}} {\rho \upsilon U}=\left. {\frac{\partial u_{p}} {\partial y}} \right|_{y=1} =\frac{e^{i\omega t}}{(1+i\omega ReM)}\left\{ \frac{Gr}{{m_{1}^{2}} +{m_{2}^{2}}} \left[ {m_{1} \cot (m_{1} )-m_{2} \coth (m_{2} )} \right]\right.\\ &&\qquad\qquad\qquad\qquad\qquad\quad\left.{\vphantom{\frac{Gr}{{m_{1}^{2}} +{m_{2}^{2}}}}}+\frac{\lambda \coth (m_{2} )}{m_{2}} \left( {\cosh (m_{2} )-1} \right)-\frac{\lambda} {m_{2}} \sinh (m_{2}) \right\} , \end{array} $$
(25)

where τ f p = ρ υ ∂ u p /∂ y at y = a is the dusty particles and the shear stress at the right wall. The Nusselt number across the channel’s wall is given by

$$ Nu=\frac{aq_{w}} {k(T_{f} -T_{0} )}=-\left. {\frac{\partial \theta} {\partial y}} \right|_{y=1} =-m_{1} \cot (m_{1} )e^{i\omega t}, $$
(26)

where q w = −k ∂ T/∂ y at y = a is the heat flux at the right wall.

4 Results and discussion

The problem of heat transfer to MHD oscillatory dusty fluid flow in a vertical channel filled with porous medium has been studied. In order to understand the physical situation of the problem and the manifestations of the various material parameters entering in the problem, we have presented graphically in figures 2–6 the numerical values of the velocity profiles, temperature profiles, skin friction coefficient and Nusselt number for dusty fluid as well as dust particles using the software “MATLAB 7.0”. The plots for the temperature and velocity profiles are in dimensionless form; hence, the units are not attached. However, it is noteworthy that dimensional unit for the velocity is m/s while that of temperature is °C. For the purposes of our numerical computation, we have used the following parameter values Re = 1, 3, 4, 5; N = 0, 0.5, 1, 1.5, 2, 3; Gr = 0, 1, 2, 3; H = 0, 1, 2, 3; s = 0, 1, 2, 3; M = 0.5; λ = 0.5; ω = 1. The Prandtl number is taken as Pr = 0.71 which physically corresponds to the atmospheric environment (air) at 20 °C fixed for the velocity and temperature profiles. Figure 2a depicts the effect of radiation parameter on temperature field. It is clear that the dusty fluid temperature increases with increasing values of radiation parameter. This rise in temperature may be attributed to internal radiative heat generation within the flow system. Moreover, maximum dusty fluid temperature seems to occur within the centerline region of the channel (i.e. y = 0.5). This may be attributed to the combined effects of thermal buoyancy, thermal radiation and minimum velocity gradient experienced in this region. In figure 2b, it is observed that an increase in radiation parameter decreases the Nusselt number due to a decrease in the temperature gradient at the channel walls.

Figure 2
figure 2

(a) Temperature profiles with increasing N. (b) Nusselt number with increasing N.

Full size image

Figures 3 and 4 illustrate the dusty fluid and dust particles velocity profiles across the channel. It is noteworthy that the velocity profiles are parabolic in nature with zero values at the walls satisfying the prescribed boundary condition. Generally, maximum fluid and particles velocities are observed within the centerline region of the channel. This may be attributed to the combined effects of thermal buoyancy and minimum velocity gradient experienced in this region. An increase in the radiation parameter causes a general increase in the dusty fluid velocity as shown in figure 3a. This may be attributed to the fact that the fluid becomes lighter and flow faster with high temperature due to radiative heat generation. Similar trend of an increase in dusty fluid velocity is observed in figure 3b with increasing values of Grashof number due to buoyancy force. In figure 3c, it is observed that the fluid velocity profiles decrease with an increase in Hartmann number due to a rise in magnetic field intensity. This observation is in agreement with the earlier results of Makinde & Chinyoka (2010a, b). The transversely imposed magnetic field on the conducting dusty fluid produced a Lorentz force which acts as a resistance to the flow, consequently, the velocity decreases. Figure 3d also shows a decrease in the dusty fluid velocity profiles with an increase in porous medium shape factor parameter. This is expected, since as the parameter s increases, the porous medium permeability decreases, consequently, the velocity profiles decrease. Figure 4a and 4b shows that the dust particles velocity increases with increasing values of radiation parameter and Grashof number while the trend is opposite in figure 4c and 4d with a decrease in the dust particles velocity profiles as both Hartmann number and porous medium shape factor parameters increases. This can be explained based on the fact that the dust particles are transported within the fluid and a rise in the fluid velocity will invariably cause a rise in the particles velocity while a decrease in the fluid velocity will decrease the particle velocity as well. Moreover, it is interesting to note that the velocity of the dusty fluid seems to be a bit higher generally than that of the dust particles.

Figure 3
figure 3

(a) Velocity profiles with increasing N. (b) Velocity profiles with increasing Gr. (c) Velocity profiles with increasing H. (d) Velocity profiles with increasing s.

Full size image
Figure 4
figure 4

(a) Particles velocity profiles with increasing N. (b) Particles velocity profiles with increasing Gr. (c) Particles velocity profiles with increasing H. (d) Particles velocity profiles with increasing s.

Full size image

The effects of parameter variation of the skin friction coefficient are demonstrated in figures 5 and 6. The skin friction coefficient at the right wall increases with an increase in the radiation parameter N as shown in figure 5a. This can be attributed to a rise in the velocity gradient of the dusty fluid at the channel walls. In figure 5b, it is observed that the skin friction coefficient produced by the dusty fluid decreases with increasing Reynolds number and Hartmann number due to a fall in the velocity gradient at the channel walls. Similar trend of a decrease in skin friction coefficient is noticed in figure 5c with increasing porous medium shape factor resulting from a combined decrease in porous medium permeability and velocity gradient. Moreover, an increase in buoyancy force represented by Grashof number increases the skin friction coefficient. Figure 6a–6c describes the effects on parameter increase on dust particles skin friction coefficient. It is observed that the dust particles skin friction increases with an increase in radiation parameter and Grashof number but decreases with an increase in Reynolds number, Hartmann number and porous medium shape factor parameter.

Figure 5
figure 5

(a) Fluid skin friction with increasing N. (b) Fluid skin friction with increasing Re and H. (c) Fluid skin friction with increasing s and Gr.

Full size image
Figure 6
figure 6

(a) Particles skin friction with increasing N. (b) Particles skin friction with increasing Re and H. (c) Particles skin friction with increasing Gr and s.

Full size image

5 Conclusion

The combined effects of buoyancy force, magnetic field and thermal radiation on heat transfer to hydromagnetic oscillatory flow of dusty fluid in a vertical channel filled with porous medium are analytically investigated. Variable separable method is employed to tackle the model problem. Our results can be summarized as follows:

  • The dusty fluid temperature increases while the Nusselt number decreases with increasing values of N.

  • The dusty fluid and dust particles velocities increase with N and Gr but decrease with H and s.

  • The skin friction coefficient increases with N and Gr but decreases with H, s and Re for both dusty fluid and dust particles.

The results obtained in this paper will be useful in recovery of crude oil from pores of reservoir rocks, waste water treatment, in juice purification in sugar industry, etc.