On Global Dynamics of Three Dimensional Magnetohydrodynamics: Nonlinear Stability of Alfvén Waves

Abstract

Magnetohydrodynamics (MHD) studies the dynamics of magnetic fields in electrically conducting fluids. In addition to the sound wave and electromagnetic wave behaviors, magneto-fluids also exhibit an interesting phenomenon: They can produce the Alfvén waves, which were first described in a physics paper by Hannes Alfvén in 1942. Subsequently, Alfvén was awarded the Nobel prize for his fundamental work on MHD with fruitful applications in plasma physics, in particular the discovery of Alfvén waves. This work studies (and constructs) global solutions for the three dimensional incompressible MHD systems (with or without viscosity) in strong magnetic backgrounds. We present a complete and self-contained mathematical proof of the global nonlinear stability of Alfvén waves. Specifically, our results are as follows:

• We obtain asymptotics for global solutions of the ideal system (i.e.,viscosity $\mu =0$) along characteristics; in particular, we have a scattering theory for the system.

• We construct the global solutions (for small viscosity $\mu$) and we show that as $\mu \rightarrow 0$, the viscous solutions converge in the classical sense to the zero-viscosity solution. Furthermore, we have estimates on the rate of the convergence in terms of $\mu$.

• We explain a linear-driving decay mechanism for viscous Alfvén waves with arbitrarily small diffusion. More precisely, for a given solution, we exhibit a time $T_{n_0}$ (depending on the profile of the datum rather than its energy norm) so that at time $T_{n_0}$ the $H^2$-norm of the solution is small compared to $\mu$ (therefore the standard perturbation approach can be applied to obtain the convergence to the steady state afterwards).

The results and proofs have the following main features and innovations:

• We do not assume any symmetry condition on initial data. The size of initial data (and the a priori estimates) does not depend on viscosity $\mu$. The entire proof is built upon the basic energy identity.

• The Alfvén waves do not decay in time: the stable mechanism is the separation (geometrically in space) of left- and right-traveling Alfvén waves. The analysis of the nonlinear terms are analogous to the null conditions for non-linear wave equations.

• We use the (hyperbolic) energy method. In particular, in addition to the use of usual energies, the proof relies heavily on the energy flux through characteristic hypersurfaces.

• The viscous terms are the most difficult terms since they are not compatible with the hyperbolic approach. We obtain a new class of space-time weighted energy estimates for (weighted) viscous terms. The design of weights is one of the main innovations and it unifies the hyperbolic energy method and the parabolic estimates.

• The approach is ‘quasi-linear’ in nature rather than a linear perturbation approach: the choices of the coordinate systems, characteristic hypersurfaces, weights and multiplier vector fields depend on the solution itself. Our approach is inspired by Christodoulou–Klainerman’s proof of the nonlinear stability of Minkowski space-time in general relativity.

Introduction

Magnetohydrodynamics (MHD) studies the dynamics of magnetic fields in electrically conducting fluids. It has wide and profound applications to plasma physics, geophysics, astrophysics, cosmology and engineering. In most interesting physical applications, one uses low frequency/velocity approximations so that one may focus on the mutual interaction of magnetic fields and the fluid (or plasma) velocity field. As the name indicates, MHD is in the scope of fluid theories so that it has many similar wave phenomena as usual fluids do. Roughly speaking, the most common restoring forces for perturbations in fluid theory is the gradient of the fluid pressure and the sound waves are the corresponding wave phenomena. In addition to the fluid pressure, the magnetic field in MHD provides two forces: the magnetic tension force and the magnetic pressure force. The magnetic pressure plays a similar role as the fluid pressure and it generates (fast and slow) magnetoacoustic waves (similar to sound waves). The magnetic tension force is a restoring force that acts to straighten bent magnetic field lines and it leads to a new wave phenomenon, to which there is no analogue in the ordinary fluid theory. The new waves are called Alfvén waves, named after the Swedish plasma physist Hannes Olof Gösta Alfvén. On 1970, H. Alfvén was awarded the Nobel prize for his ‘fundamental work and discoveries in magnetohydrodynamics with fruitful applications in different parts of plasma physics’, in particular his discovery of Alfvén waves [1] in 1942.

We discuss briefly the physical origin of Alfvén waves. For detailed descriptions, the reader may consult the original paper [1] or text books on MHD, e.g., [4]. One can think of Alfvén waves as vibrating strings or more precisely transverse inertial waves. In a electrically conducting fluid, if the conductivity is sufficiently high, one will observe that the magnetic field lines tend to be frozen into the fluid. In other words, the fluid particles tend to move along the magnetic field lines. Therefore, we may suppose that the fluid lies along a steady constant magnetic field $B_0$ and we perturb the fluid by a small velocity field v which is perpendicular to $B_0$. The magnetic field line will be swept along with the fluid and the resulting curvature of the lines provides a restoring force (magnetic tension force) on the fluid. The fluid will eventually go back to the rest state and then the Faraday tensions will reverse the flow. The waves developed by the oscillations are precisely the Alfvén waves. According to this description, Alfvén wave is different from sound waves and electromagnetic waves. It is driven by the Lorentz force.

We now give a heuristic description for Alfvén waves. Let $B_0=(0,0,1)$ be a constant magnetic field along the $x_3$-axis. We assume that the fluids are frozen along the magnetic lines. Let $v=(0,\Delta v,0)$ be an infinitesimal velocity perturbation (perpendicular to $B_0$) for a fluid particle. Therefore, the Lorentz force on the particle is proportional to $v\times B = (\Delta v, 0, 0)$. After a small time $\Delta t$, the Lorentz force leads to a velocity change proportional to $v_1=(v\times B)\Delta t = (\Delta v\Delta t, 0, 0)$ in $x_1$ direction. Likewise, the velocity component $v_1$ provides the Lorentz force $v_1\times B =(0,-\Delta v\Delta t,0)$, which is opposite to the initial velocity perturbation. Thus, it acts as a restoring force to push the particle back to the original position; hence, waves develop.

An Alfvén wave is a transverse wave. It propagates anisotropically in the direction of the magnetic field. In other words, the motion of the fluid particles (such as ions) and the perturbation of the magnetic field are in the same direction and transverse to the direction of propagation. It also propagates the incompressibility, involving no changes in plasma density or pressure. We remark that, in contrast, the magnetoacoustic waves reflect the compressibility of the plasma.

The theory of Alfvén waves supports the existing explanations for the origin of the earth’s magnetic field. The magnetic fields have an ability to support two inertial waves, the Alfvén waves and the magnetostropic waves (involving the Coriolis force). Both of the inertial waves are of considerable importance in the geodynamo-theory and they are useful in explaining the maintenance of the earth’s magnetic fields in terms of a self-excited fluid dynamo. Alfvén waves are also fundamental in the astrophysics, particularly topics such as star formation, magnetic field oscillation of the sun, sunspots, solar flares and so on.

In [1], when Alfvén first discovered the waves named after him, he also provided a formal linear analysis. He considered the following situation: the conductivity is set to be infinite, the permeability is 1 and the background constant magnetic field $B_0$ is homogenous and parallel to the $x_3$-axis of the space. He then took the plane waves ansatz by assuming all the physical quantities depending only on the time t and the variable $x_3$. The MHD equations (see also (1.1) below) become

$$\begin{aligned} -\frac{4\pi \rho }{B_0^2}\frac{\partial ^2b}{\partial t^2}+\frac{\partial ^2b}{\partial x_3^2}=0, \end{aligned}$$

where b is the magnetic field and $\rho$ is the plasma density. This is a $1+1$ dimensional wave equation and it implies immediately that the Alfvén waves move along the $x_3$-axis (in both directions) with the velocity (so called the Alfvén velocity) $V_A=\frac{B_0}{\sqrt{4\pi \rho }}$. The linear analysis also indicates that the Alfvén waves are dispersionless. In the real world, the MHD waves obey the nonlinear dynamics and many of them detected sofar seem to be stable, such as the solar wind and waves generated by a solar flare rapidly propagating out across the solar disk. It is surprising that Alfvén’s linear analysis provides a rather good approximation for nonlinear evolutions. The nonlinear terms may pose serious difficulties in the mathematical studies of the propagation of the Alfvén waves in the MHD system, especially in the dispersionless situation. One of the main objects of the paper is to analyze the relationship between the genuine nonlinear evolution and the linearized analysis.

The phenomena for the Alfvén waves are ubiquitous and complex. The existing mathematical theories on Alfvén waves are mostly concerning the linearized equations and are far from being complete. In the present work, we study the incompressible fluids and consider the nonlinear stability of the Alfvén waves. The word ‘stability’ roughly means the following two things: 1) the asymptotics of the waves as $t\rightarrow \infty$ for the ideal case (no viscosity); 2) the asymptotics for the viscous waves as the viscosity $\mu \rightarrow 0$ and as $t\rightarrow \infty$. In particular, our work will provide a way to justify why the linearized Alfvén waves provide a good approximation for the nonlinear evolution and how the viscosity damps the Alfvén waves–two interesting phenomena commonly described in text books on MHD, e.g., [4], but there is no rigorous mathematical explanation for the phenomena.

Next, we write down the incompressible MHD equations. For simplification, we assume that both the fluid (plasma) density and the permeability equal 1. Then the incompressible MHD equations read

$$\begin{aligned} \begin{aligned} \partial _t v+ v\cdot \nabla v&= -\nabla p + (\nabla \times b)\times b+ {\mu \triangle v}, \\ \partial _t b+ v\cdot \nabla b&= b\cdot \nabla v+ {\mu \triangle b},\\ \text {div}\,v&=0,\\ \text {div}\,b&=0, \end{aligned} \end{aligned}$$

(1.1)

where $b$ is the magnetic field, $v,\ p$ are the velocity and scalar pressure of the fluid respectively, $\mu$ is the viscosity coefficient or equivalently the dissipation coefficient.

We can write the Lorentz force term $(\nabla \times b)\times b$ in the momentum equation in a more convenient form. Indeed, we have

$$\begin{aligned} (\nabla \times b)\times b=-\nabla \left( \frac{1}{2}|b|^2\right) +b\cdot \nabla b. \end{aligned}$$

The first term $\nabla (\frac{1}{2}|b|^2)$ is called the magnetic pressure force since it is in the gradient form just as the fluid pressure does. The second term $b\cdot \nabla b=\nabla \cdot (b\otimes b)$ is the magnetic tension force, which produces Alfvén waves. Therefore, we can use p again in the place of $p+\frac{1}{2}|b|^2$. The momentum equation then reads

$$\begin{aligned} \partial _t v+ v\cdot \nabla v= -\nabla p + b\cdot \nabla b+ {\mu \Delta v}. \end{aligned}$$

We study the most interesting situation when a strong back ground magnetic field $B_0$ presents (to generate Alfvén waves). Heuristically, if $\mu$ is large, the influence of $v$ on $b$ is negligible, the magnetic field is dissipative in nature (so that the magnetic disturbance $b-B_0$ tends to decay very fast). If $\mu$ is small, the velocity $v$ will strongly influence $b$ so that the situation is similar to ideal Alfvén waves and the damping from the dissipations is so weak that it takes a long time to see the effect. We will rigorously justify these facts later on. The heuristics can be depicted as follows:

We now give a formal (or linear analysis) discussion about the properties showed in the above figures. Let $B_0=|B_0| \,\varvec{e}_3$ be a uniform constant (non-vanishing) background magnetic field. The vector $\varvec{e}_3$ is the unit vector parallel to $x_3$-axis. We remark that the pair $(0,B_0)$ solves the incompressible MHD system. We consider an infinitesimal perturbation $(v,b-B_0)$ of $(0,B_0)$. We take v to be perpendicular to $B_0$. The leading order terms of the MHD system satisfy the following system of equations:

$$\begin{aligned} \begin{aligned}&\partial _tv-B_0\cdot \nabla b=-\nabla p+\mu \Delta v,\\&\partial _tb-B_0\cdot \nabla v= \mu \Delta b. \end{aligned} \end{aligned}$$

We remark that for convenience we do not distinguish b from $b-B_0$ because they have the same derivatives. Taking the $\text {curl}\,$ of the above equations, we obtain the vorticity equations, namely, for $\omega =\text {curl}\,v$ and $j=\text {curl}\,b$, we have

$$\begin{aligned} \begin{aligned}&\partial _t\omega -B_0\cdot \nabla j=\mu \Delta \omega ,\\&\partial _tj-B_0\cdot \nabla \omega =\mu \Delta j. \end{aligned} \end{aligned}$$

(1.2)

Alternatively, since $\nabla p$ is a quadratic term, we can ignore it for linear analysis.

We study the dispersion relation $f(\xi )$ of the above linearized equations (1.2). Considering the plane wave solutions

$$\begin{aligned} \omega =\omega _0\exp {[i(\xi \cdot x-f(\xi )t)]},\quad j=j_0\exp {[i(\xi \cdot x-f(\xi )t)]}, \end{aligned}$$

we obtain

$$\begin{aligned} f(\xi )^2+2i\mu |\xi |^2f(\xi )-(|B_0|^2 \xi _3^2+\mu ^2|\xi |^4)=0, \end{aligned}$$

or equivalently,

$$\begin{aligned} f(\xi )=-i \mu |\xi |^2 \pm |B_0|\xi _3. \end{aligned}$$

(1.3)

We remark that according to the physics literatures, the plane waves with dispersive relation

$$\begin{aligned} f^2(\xi )-|B_0|^2 \xi ^2_3=0 \end{aligned}$$

are called Alfvén waves, i.e., $\mu =0$. We study the following three cases for (1.3) and this analysis can also be found in [4].

• Case-1 The ideal case $\mu =0$. We have

  $$\begin{aligned} f(\xi )=\pm |B_0|\xi _3. \end{aligned}$$

  Both the phase velocity $\frac{f(\xi )}{|\xi |}$ and group velocity $\nabla _\xi f(\xi )$ are $v_A=|B_0|$, i.e., the Alfvén velocity. It represents two families of plane waves propagating in the direction (or the opposite direction) of the magnetic field with velocity $v_A$. There is no dispersion. This corresponds to the first situation in the previous figure.

• Case-2 The case when $1>>\mu >0$ is small. We have a closed form for $f(\xi )$. In fact, we have

  $$\begin{aligned} f(\xi )=-i\mu |\xi |^2\pm v_A \xi _3. \end{aligned}$$

  It represents plane waves propagating in the direction (or the opposite direction) of the magnetic field with velocity $v_A$ and damped by a weak dissipation ($\mu<<1$).

• Case-3 The case $\mu>> 1$. We have

  $$\begin{aligned} f(\xi )\sim -i\mu |\xi |^2. \end{aligned}$$

  It represents the situation that the disturbance damped rapidly by the dissipations. This corresponds to the third drawing in the previous figure.

The third case corresponds to systems with strong diffusion. The mathematical analysis of such systems is analogous to the small data problem for the classical Navier–Stokes equations in three dimensional space. Since the theory is rather classical and well-understood, we will not consider the case in the paper. In the first two cases, the plane waves can travel across a vast distance before we see a significant effect of damping caused by the dissipation. The wave patterns can survive for a long time, which is approximately at least of time scale $O(\frac{1}{\mu })$. We will provide a rigorous justification for Case-1 and Case-2 in the nonlinear setting.

Main Theorem (First Version) and Previous Works

We recall that, by incorporating the magnetic pressure into the fluid pressure, we can rewrite the incompressible MHD equations as

$$\begin{aligned} \begin{aligned} \partial _t v+ v\cdot \nabla v&= -\nabla p + b\cdot \nabla b+ {\mu \triangle v}, \\ \partial _t b+ v\cdot \nabla b&= b\cdot \nabla v+ {\mu \triangle b},\\ \text {div}\,v&=0,\\ \text {div}\,b&=0, \end{aligned} \end{aligned}$$

(1.4)

where the viscosity $\mu$ is either 0 or a small positive number. We introduce the Elsässer variables:

$$\begin{aligned} {Z}_+= v+b, \ \ {Z}_-= v-b. \end{aligned}$$

Then the MHD equations (1.4) read

$$\begin{aligned} \begin{aligned} \partial _t {Z}_++{Z}_-\cdot \nabla {Z}_+- {\mu \triangle {Z}_+}&= -\nabla p, \\ \partial _t {Z}_-+{Z}_+\cdot \nabla {Z}_-- {\mu \triangle {Z}_-}&= -\nabla p,\\ \text {div}\,{Z}_+&=0,\\ \text {div}\,{Z}_-&=0. \end{aligned} \end{aligned}$$

(1.5)

We use $B_0 =|B_0|(0,0,1)$ to denote a uniform background magnetic field and we define

$$\begin{aligned} {z}_+= {Z}_+-B_0, \ \ {z}_-= {Z}_-+ B_0. \end{aligned}$$

The MHD equations can then be reformulated as

$$\begin{aligned} \begin{aligned} \partial _t {z}_++{Z}_-\cdot \nabla {z}_+- {\mu \triangle {z}_+}&= -\nabla p, \\ \partial _t {z}_-+{Z}_+\cdot \nabla {z}_-- {\mu \triangle {z}_-}&= -\nabla p,\\ \text {div}\,{z}_+&=0,\\ \text {div}\,{z}_-&=0. \end{aligned} \end{aligned}$$

(1.6)

For a vector field X on $\mathbb {R}^3$, its curl is defined by $\text {curl}\,X=(\partial _2X^3-\partial _3X^2,\partial _3X^1-\partial _1X^3,\partial _1X^2-\partial _2X^1)$ or $\text {curl}\,X = \varepsilon _{ijk}\partial _iX^j \partial _k$. We use the Einstein’s convention: if an index appears once up and once down, it is understood to be summing over $\{1,2,3\}$.

By taking curl of (1.6), we derive the following system of equations for $(j_+, j_{-})$:

$$\begin{aligned} \begin{aligned} \partial _t j_++{Z}_-\cdot \nabla j_+- {\mu \triangle {z}_+}&= -\nabla {z}_-\wedge \nabla {z}_+, \\ \partial _t j_{-}+{Z}_+\cdot \nabla j_{-}- {\mu \triangle {z}_-}&= -\nabla {z}_+\wedge \nabla {z}_-, \end{aligned} \end{aligned}$$

(1.7)

where

$$\begin{aligned} j_+= \text {curl}\,{z}_+, \ \ j_{-}= \text {curl}\,{z}_-. \end{aligned}$$

We remark both $j_+$ and $j_{-}$ are divergence free vector fields. The explicit expressions of the nonlinearities on the righthand side are

$$\begin{aligned} \nabla {z}_-\wedge \nabla {z}_+=\varepsilon _{ijk}\partial _i {z}_-^l\partial _l {z}_+^j\partial _k, \ \ \nabla {z}_+\wedge \nabla {z}_-=\varepsilon _{ijk}\partial _i {z}_+^l\partial _l {z}_-^j\partial _k. \end{aligned}$$

(1.8)

Before introducing more notations, we now provide a first version of our main theorem. It is a rough version in the sense that it only states the global existence part of the result. We will give more precise versions of the main theorem later on. The main result can be stated as follows:

Theorem 1.1

(First version) Let $B_0 =(0,0,1)$ be a given background magnetic field. Given constants $R\ge 100$ and $N_* \in \mathbb {Z}_{\ge 5}$, there exists a constant $\varepsilon _0$ so that for all given smooth vector fields $(v_0(x),\widetilde{b}_0)(x)$ on $\mathbb {R}^3$ with the following bound

$$\begin{aligned}&\big \Vert \big (\log (R^2+|x|^2)^{\frac{1}{2}}\big )^2(v_0,\widetilde{b}_0)\big \Vert _{L^2(\mathbb {R}^3)}^2\\&\quad +\sum _{k=0}^{N_*}\big \Vert (R^2+|x|^2)^{\frac{1}{2}}\left( \log (R^2+|x|^2)^{\frac{1}{2}}\right) ^2\nabla ^{k+1} (v_0,\widetilde{b}_0)\big \Vert _{L^2(\mathbb {R}^3)}^2\\&\quad +\mu \big \Vert (R^2+|x|^2)^{\frac{1}{2}}\left( \log (R^2+|x|^2)^{\frac{1}{2}}\right) ^2\nabla ^{N_*+2} (v_0,\widetilde{b}_0)\big \Vert _{L^2(\mathbb {R}^3)}^2 \le \varepsilon _0^2, \end{aligned}$$

for the initial data (to the MHD system (1.4)) of the form

$$\begin{aligned} v(0,x)=v_0(x), \ \ b(0,x)= B_0 + \widetilde{b_0}(x), \end{aligned}$$

the MHD system (1.4) admits a unique global smooth solution. In particular, the constant $\varepsilon _0$ is independent of the viscosity coefficient $\mu$.

Remark 1.1

The proof for the viscous case when $\mu >0$ is in fact considerably harder than the ideal case $\mu =0$. This seems to contradict the intuition that diffusions help the system to stabilize (This intuition will be proved and justified towards the end of the paper). In the statement of the theorem, the weight functions for (v, b) are different from those for the higher order terms. If $\mu =0$, we can choose the weights in a uniform way and in a much simpler form. However, if $\mu >0$, the choice of different weights plays an essential role in the proof and it unifies the hyperbolic estimates (for waves) and the parabolic estimates (for diffusive systems). This is one of the main innovations of the paper and we will explain this point when we discuss the ideas of the proof.

Remark 1.2

From now on, we will only consider the case where $|B_0|=1$. We can also use $B_0=|B_0|(0,0,1)$ to model the constant background magnetic field. The choice of the constant $\varepsilon _0$ will depend on $|B_0|$ but not on the viscosity $\mu$.

We end this subsection by a quick review of the results on three dimensional incompressible MHD systems with strong magnetic backgrounds. Bardos, Sulem and Sulem [2] first obtained the global existence in the Hölder space $C^{1,\alpha }$ (not in the energy space) for the ideal case $(\mu =0)$. They do not treat the case with small diffusion, which we believe is fundamentally different from the ideal case. For the case with strong fluid viscosity but without Ohmic dissipation, [9] (see also [5]) studies the small-data-global-existence with very special choice of data. We remark that the smallness of the data depends on the viscosity, while the data in the current work are independent of the viscosity coefficient $\mu$. Technically speaking, the work [2] treats the system as one dimensional wave equations and it relies on the convolution with fundamental solutions; the work [9] observes that the system can be roughly regarded as a damped wave equation in Lagrangian coordinates $\partial _t^2Y-\mu \Delta \partial _tY-\partial _3^2Y\approx 0$ and the proof is based on Fourier analysis (more precisely on Littlewood-Paley decomposition).

The proof, which will be presented in the sequel, is different from the aforementioned approaches. We will regard the MHD system as a system of $1+1$ dimensional wave equations and the proof makes essential use of the fact that the system is defined on three dimensional space. We derive energy estimates purely in physical space. The characteristic geometry (see next subsection) defined by two families of characteristic hypersurfaces of nonlinear solutions underlies the entire proof. The approach is in nature quasi-linear and is similar in spirit to the proof of the nonlinear stability of Minkowski spacetime [3]. In order to make this remark transparent, we first introduce the underlying geometric structure defined by a solution of (1.5).

The Characteristic Geometries

We study the spacetime $[0,t^*] \times \mathbb {R}^3_{x_1,x_2,x_3}$ associated to a solution $(v,b)$ of the MHD equations or equivalently (1.5). More precisely, we assume a smooth solution $(v,b)$ exists on $[0,t^*] \times \mathbb {R}^3$ and we study the foliation of the characteristic hypersurfaces associated to $(v,b)$. We recall that $[0,t^*] \times \mathbb {R}^3$ admits a natural time foliation $\bigcup _{0\le t \le t^*} \Sigma _t$, where $\Sigma _t$ is the constant time slice (in particular, $\Sigma _0$ is the initial time slice where the initial data are given).

We first define two characteristic (spacetime) vector fields ${L}_+$ and ${L}_-$ as follows

$$\begin{aligned} {L}_+= T + {Z}_+, \ \ {L}_-= T + {Z}_-, \end{aligned}$$

(1.9)

where the time vector field T is the usual $\partial _t$ defined in the Cartesian coordinates (we also use the same notations to denote the partial differential operators ${L}_+=\partial _t+{Z}_+\cdot \nabla$ and ${L}_-=\partial _t+{Z}_-\cdot \nabla$).

Given a constant c, we use $S_{0,c}$ to denote the 2-plane $x_3 = c$ in $\Sigma _0$. Therefore, $\bigcup _{ x_3 \in \mathbb {R}} S_{0,x_3}$ is a foliation of the initial hypersurface $\Sigma _0$. We define the characteristic hypersurfaces ${C}^+_{x_3}$ and ${C}^-_{x_3}$ to be the hypersurfaces emanated from $S_{0,x_3}$ along the vector fields ${L}_+$ and ${L}_-$ respectively. A better way to define ${C}^\pm$ is to understand the hypersurface as the level set of a certain function. We define the optical function $u_+=u_+(t,x)$ as follows

$$\begin{aligned} \begin{aligned} {L}_+u_+= 0,\ \ \ \ u_+\big |_{\Sigma _0} = x_3. \end{aligned} \end{aligned}$$

(1.10)

Similarly, we define the optical function $u_{-}$ by

$$\begin{aligned} \begin{aligned} {L}_-u_{-}= 0,\ \ \ \ u_{-}\big |_{\Sigma _0} = x_3. \end{aligned} \end{aligned}$$

(1.11)

Therefore, the characteristic hypersurfaces ${C}^+_{x_3}$ and ${C}^-_{x_3}$ are the level sets $\{u_+= x_3\}$ and $\{u_{-}= x_3\}$ respectively. We will use the notations ${C}^+_{u_+}$ and ${C}^-_{u_{-}}$ to denote them. By construction, ${L}_+$ is tangential to ${C}^+_{u_+}$ and ${L}_-$ is tangential to ${C}^-_{u_{-}}$.

We remark that the spacetime $[0,t^*] \times \mathbb {R}^3$ admits two characteristic foliations: $\bigcup _{u_+\in \mathbb {R}}{C}^+_{u_+}$ and $\bigcup _{u_{-}\in \mathbb {R}}{C}^-_{u_{-}}$. The intersection ${C}^+_{u_+} \bigcap \Sigma _t$ is a two-plane, denoted by ${S}^+_{t,u_+}$. Similarly, we denote ${C}^-_{u_{-}} \bigcap \Sigma _t$ by ${S}^-_{t,u_{-}}$. Therefore, for each t, we obtain two foliations $\bigcup _{u_+\in \mathbb {R}}{S}^+_{t,u_+}$ and $\bigcup _{u_{-}\in \mathbb {R}}{S}^-_{t,u_{-}}$ of $\Sigma _t$. In general, they may differ from each other.

Similar to the definitions of $u_\pm$, we also define $x_1^{\pm }=x_1^{\pm }(t,x)$ and $x_2^{\pm }=x_2^\pm (t,x)$. For $i=1$ or 2, we require

$$\begin{aligned} {L}_+x_i^+= & {} 0,\ \ \ {L}_-x_i^- = 0\nonumber \\ x_i^+\big |_{\Sigma _0}= & {} x_i, \ \ \ x_i^-\big |_{\Sigma _0} = x_i. \end{aligned}$$

(1.12)

We remark that if we let $i=3$ in the above defining formulas, we obtain $x_3^\pm =u^\pm$.

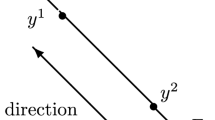
We use the following pictures to illustrate the above geometric constructions:

The right-traveling hypersurfaces ${C}^+_{u_+}$ are painted grey; the left-traveling hypersurfaces ${C}^-_{u_{-}}$ are tiled with grey lines. The dashed lines are integral curves of either ${L}_+$ or ${L}_-$.

In order to specify the region where the energy estimates are taken place, for t, $u_+^1$, $u_+^2$, $u_{-}^1$ and $u_{-}^2$ given with $u_+^1 < u_+^2$ and $u_{-}^1 < u_{-}^2$, we define the following hypersurfaces / regions:

$$\begin{aligned} \begin{aligned} \Sigma _{t}^{\left[ u_+^1,u_+^2\right] } = \bigcup _{u_+\in \left[ u_+^1,u_+^2\right] }{S}^+_{t,u_+}, \ \ W_{t}^{\left[ u_+^1,u_+^2\right] } = \bigcup _{\tau \in [0,t]}\Sigma _{\tau }^{\left[ u_+^1,u_+^2\right] },\\ \Sigma _{t}^{\left[ u_{-}^1,u_{-}^2\right] } = \bigcup _{u_{-}\in \left[ u_{-}^1,u_{-}^2\right] }{S}^-_{t,u_{-}}, \ \ W_{t}^{\left[ u_{-}^1,u_{-}^2\right] } = \bigcup _{\tau \in [0,t]}\Sigma _{\tau }^{\left[ u_{-}^1,u_{-}^2\right] }. \end{aligned} \end{aligned}$$

Roughly speaking, $W_{t}^{[u_+^1,u_+^2]} = \bigcup _{\tau \in [0,t]}\Sigma _{\tau }^{[u_+^1,u_+^2]}$ is the spacetime region bounded by the two grey hypersurfaces in the above picture.

As a subset of $\mathbb {R}^4$, the domain $W_{t}^{[u_+^1,u_+^2]}$ or $W_{t}^{[u_{-}^1,u_{-}^2]}$ admits a standard Euclidean metric. By forgetting the $x_1$ and $x_2$ axes, the outwards normals of the boundaries of the above domains are depicted schematically as follows:

The outward unit normal of $\Sigma _{0}$ and $\Sigma _{t}$ are $-T$ and T respectively. We use $\nu ^+_1$ to denote the outward unit normal of ${C}^+_{u_+^1}$. Since ${C}^+_{u_+^1}$ is the level set of $u_+$, we have

$$\begin{aligned} \nu ^+_1 = -\frac{(\partial _t u_+,\nabla u_+)}{\sqrt{(\partial _t u_+)^2+ |\nabla u_+|^2}} \end{aligned}$$

Similarly, for the outward unit normals $\nu ^+_2$, $\nu ^{-}_1$ and $\nu ^{-}_2$ of ${C}^+_{u_+^2}$,${C}^-_{u_{-}^1}$ and ${C}^-_{u_{-}^2}$ respectively, we have

$$\begin{aligned} \nu ^+_2 = \frac{(\partial _t u_+,\nabla u_+)}{\sqrt{(\partial _t u_+)^2+ |\nabla u_+|^2}}, \ \ \nu ^{-}_1= & {} -\frac{(\partial _t u_{-},\nabla u_{-})}{\sqrt{(\partial _t u_{-})^2+ |\nabla u_{-}|^2}}, \\ \nu ^{-}_2= & {} \frac{(\partial _t u_{-},\nabla u_{-})}{\sqrt{(\partial _t u_{-})^2+ |\nabla u_{-}|^2}}. \end{aligned}$$

Main Theorems (Second Version)

The notation $a\lesssim b$ means that there exists a universal constant C such that $a\le Cb$. We use the notation $C_{\omega _1,\omega _2, \cdots }$ to represent the constant that depends on the parameters $\omega _1, \omega _2, \cdots$.

For a multi-index $\alpha =(\alpha _1,\alpha _2,\alpha _3)$ with $\alpha _i\in \mathbb {Z}_{\ge 0}$, we define ${z}_{\pm }^{(\alpha )}=\big (\frac{\partial {}}{\partial {x_1}}\big )^{\alpha _1}\big (\frac{\partial {}}{\partial {x_2}}\big )^{\alpha _2}\big (\frac{\partial {}}{\partial {x_3}}\big )^{\alpha _3}{z}_{\pm }$; for a positive integer k, we define $|{z}_{\pm }^{(k)}|=(\sum _{|\alpha |=k}|{z}_{\pm }^{(\alpha )}|^2)^{\frac{1}{2}}$. One can also define ${j}_{\pm }^{(\alpha )}$ and $|{j}_{\pm }^{(k)}|$ in a similar way. Let R and $\varepsilon _0$ be two positive numbers. They will be determined later on. In principle, R is large and $\varepsilon _0$ is small.

We introduce two weight functions $\langle w_+\rangle$ and $\langle w_{-} \rangle$ as follows

$$\begin{aligned} \langle w_+\rangle =\big (R^2 + |x_1^+|^2+|x_2^+|^2+|u_+|^2\big )^\frac{1}{2}, \ \ \ \langle w_{-} \rangle =\big (R^2 + |x_1^-|^2+|x_2^-|^2+|u_{-}|^2\big )^\frac{1}{2}. \end{aligned}$$

We remark that $L_+ \langle w_+\rangle =0$ and $L_- \langle w_{-} \rangle =0$.

For a given multi-index $\alpha$, we define the energy $E_{\mp }^{(\alpha )}$ and flux $F_{\mp }^{(\alpha )}$ (associated to characteristic hypersurfaces) of the solution ${z}_{\pm }$ as follows:

$$\begin{aligned} E_{\mp }^{(\alpha )}(t)&= \int _{\Sigma _t} \langle w_{\pm } \rangle ^2 \big (\log \langle w_{\pm } \rangle \big )^4 |\nabla z_{\mp }^{(\alpha )}|^2 dx, \ \ \ |\alpha |\ge 0,\\ F_{\mp }^{(0)}(\nabla z_{\mp })&=\int _{C_{u_{\mp }}^{\mp }} \langle w_{\pm } \rangle ^2 \big (\log \langle w_{\pm } \rangle \big )^4 |\nabla z_{\mp }|^2d\sigma _{\mp },\\ F_{\mp }^{(\alpha )}(j_{\mp })&=\int _{C_{u_{\mp }}^{\mp }} \langle w_{\pm } \rangle ^2 \big (\log \langle w_{\pm } \rangle \big )^4 |j_{\mp }^{(\alpha )}|^2d\sigma _{\mp },\ \ \ |\alpha |\ge 1, \end{aligned}$$

where $d\sigma _{\pm }$ is the surface measure of the characteristic hypersurface $C_{u_{\pm }}^\pm$. We define the diffusion $D_{\mp }^{(\alpha )}$ as follows

$$\begin{aligned} D_{\mp }^{(\alpha )}(t)=\mu \int _0^t\int _{\Sigma _\tau }\langle w_{\pm } \rangle ^2 \big (\log \langle w_{\pm } \rangle \big )^4 |\nabla ^2 z_{\mp }^{(\alpha )}|^2 dxd\tau , \ \ \ |\alpha |\ge 0. \end{aligned}$$

We remark that, for $|\alpha |\ge 1$, the flux parts contain only the vorticity component rather than the full derivatives of $\nabla z_\pm ^{(\alpha )}$. This is a technical choice that makes it easier to deal with the nonlinear contribution from the pressure term. If we consider the energy identities (2.24)–(2.28) (see below), the corresponding weight functions ${\lambda }_+$ and ${\lambda }_-$ will be $\langle w_{-} \rangle ^2 \big (\log \langle w_{-} \rangle \big )^4$ and $\langle w_+\rangle ^2 \big (\log \langle w_+\rangle \big )^4$. In particular, we have ${L}_+{\lambda }_-=0$ and ${L}_-{\lambda }_+=0$.

The lowest order energy and flux are defined as

$$\begin{aligned} E_{\mp }(t) = \int _{\Sigma _t} \big (\log \langle w_{\pm } \rangle \big )^4 | z_{\mp }|^2 dx, \ \ \ F_{\mp }(z_{\mp })=\int _{C_{u_{\mp }}^{\mp }}\big (\log \langle w_{\pm } \rangle \big )^4 |z_{\mp }|^2d\sigma _{\mp }. \end{aligned}$$

The lowest order diffusion is defined as

$$\begin{aligned} D_{\mp }(t)=\mu \int _0^t\int _{\Sigma _\tau }(\log \langle w_{\pm } \rangle )^4 |\nabla z_{\mp }|^2 dxd\tau . \end{aligned}$$

In view of the energy identities (2.24)–(2.28), the corresponding weight functions ${\lambda }_+$ and ${\lambda }_-$ will be $\big (\log \langle w_{-} \rangle \big )^4$ and $\big (\log \langle w_+\rangle \big )^4$. The constraints ${L}_+{\lambda }_-=0$ and ${L}_-{\lambda }_+=0$ still hold.

Remark 1.3

Unlike the usual choice, the weight functions $\langle w_{\pm } \rangle$ indeed depend on the solutions $z_\pm$. This reflects the quasilinear nature of the problem.

Remark 1.4

The weight functions for the lowest order energy and flux are different from those for higher order energy and flux. The difference is exactly $\langle w_{\pm } \rangle ^2$. These special weights are designed to control the diffusion terms $\mu \triangle {z}_{\pm }$. Indeed, for the ideal MHD system ($\mu =0$), we can choose the weight functions in a much simpler and uniform manner, say $\langle w_{\pm } \rangle = (R^2+|u_{\pm }|^2)^{\frac{1+\delta }{2}}$ for some small $\delta >0$. The choice of different weights is essential to the proof and it incorporates the hyperbolic and parabolic estimates at the same time. Since we use different weights and consider a hyperbolic-parabolic mixed situation, we also say the energy estimates are hybrid.

To make the statement of the energy estimates simpler, we introduce the total energy norms, total flux norms and total diffusions as follows:

$$\begin{aligned} E_{\mp }&= \sup _{0\le t\le t^*} E_{\mp }(t),\ \ E_{\mp }^k = \sup _{0\le t\le t^*} \sum _{|\alpha |=k}E_{\mp }^{(\alpha )}(t), \\ F_{\mp }&= \sup _{u_{\mp } \in \mathbb {R}} F_{\mp }(z_{\mp }), \ \ F_{\mp }^{0}= \sup _{u_{\mp } \in \mathbb {R}} F_{\mp }^{0}(\nabla z_{\mp }),\\ F_{\mp }^{k}&= \sup _{u_{\mp } \in \mathbb {R}} \sum _{|\alpha |=k} F_{\mp }^{(\alpha )}(j_{\mp }),\ \ D_{\mp }^k=\sum _{|\alpha |=k}D_{\mp }^{(\alpha )}(t^*). \end{aligned}$$

The first theorem is about the global existence to the MHD system (1.5) with small $\mu \ge 0$.

Theorem 1.2

(Second version with a priori estimates) Let $B_0 =(0,0,1)$, $R= 100$ and $N^* \in \mathbb {Z}_{\ge 5}$. There exists a constant $\varepsilon _0$, which is independent of the viscosity coefficient $\mu$, such that if the initial data of (1.4) or equivalently (1.5) satisfy

$$\begin{aligned} \mathcal {E}^\mu (0)=&\sum _{+,-}\Bigl (\big \Vert \big (\log (R^2+|x|^2)^{\frac{1}{2}}\big )^2{z}_{\pm }(0,x) \big \Vert _{L_x^2}^2\\&+\sum _{k=0}^{N_*}\big \Vert (R^2+|x|^2)^{\frac{1}{2}}\big (\log (R^2+|x|^2)^{\frac{1}{2}}\big )^2\nabla ^{k+1} {z}_{\pm }(0,x)\big \Vert _{L_x^2 }^2\\&+\mu \big \Vert (R^2+|x|^2)^{\frac{1}{2}}\big (\log (R^2+|x|^2)^{\frac{1}{2}}\big )^2\nabla ^{N_*+2} {z}_{\pm }(0,x)\big \Vert _{L^2_x}^2\Bigr )\le \varepsilon _0^2, \end{aligned}$$

then (1.5) admits a unique global solution ${z}_{\pm }(t,x)$. Moreover, there exists a constant C independent of $\mathcal {E}^\mu (0)$ and $\mu$, such that the solution ${z}_{\pm }(t,x)$ enjoys the following energy estimate:

$$\begin{aligned} \begin{aligned}&\sup _{t\ge 0}\bigl (E_{\pm }(t)+\sum _{k=0}^{N_*}E_{\pm }^k(t)+\mu E_{\pm }^{N_*+1}(t)\bigr )+\sup _{u_{\pm }\in \mathbb {R}}\bigl (F_{\pm }({z}_{\pm })+F_{\pm }^0(\nabla {z}_{\pm }) +\sum _{k=1}^{N_*}F_{\pm }^k(j_{\pm })\bigr )\\&\quad +\bigl (D_{\pm }+\sum _{k=0}^{N^*}D_{\mp }^k+\mu D_{\mp }^{N^*+1}\bigr )\big |_{t^*=\infty } \le C \mathcal {E}^\mu (0). \end{aligned} \end{aligned}$$

(1.13)

As a direct consequence of the above theorem, we obtain the global existence result for ideal MHD for the data with the following bound

$$\begin{aligned}&\sum _{+,-}\Bigl (\big \Vert \big (\log (R^2+|x|^2)^{\frac{1}{2}}\big )^2{z}_{\pm }(0,x)\big \Vert _{L^2(\mathbb {R}^3)}^2\\&\quad +\sum _{k=0}^{N_*}\big \Vert (R^2+|x|^2)^{\frac{1}{2}}\big (\log (R^2+|x|^2)^{\frac{1}{2}}\big )^2 \nabla ^{k+1}{z}_{\pm }(0,x)\big \Vert _{L^2(\mathbb {R}^3)}^2\Bigr )\le \varepsilon _0^2. \end{aligned}$$

Due to the absence of the viscous terms, we can actually do much better. As we mentioned above, the different weights on ${z}_{\pm }$ and higher derivatives of ${z}_{\pm }$ are designed to deal with the small diffusions. Roughly speaking, when we derive the usual (hyperbolic or wave) energy estimates, the procedure of integrations by parts acting on the viscosity term will generate a linear term. This term is extremely difficult to control. It mirrors the fact that the hyperbolic type of energy estimates is not entirely compatible with the small diffusions. This is one of the main difficulties of the problem. When $\mu =0$, we are free of the above contraint and we can use much simpler choices of weights, such as $(R^2+|u_\pm |^2)^{\frac{1+\delta }{2}}$ or $(R^2+|x_1^\pm |^2+|x_2^\pm |^2+|u_\pm |^2)^{\frac{1+\delta }{2}}$. This leads to the following theorem:

Theorem 1.3

(Global existence for ideal MHD) Let $\mu =0$, $B_0 =(0,0,1)$, $\delta \in (0,1)$, $R= 100$ and $N^* \in \mathbb {Z}_{\ge 5}$. There exists a constant $\varepsilon _0$, such that if the initial data of (1.4) or equivalently (1.5) satisfy

$$\begin{aligned} \mathcal {E}^{\mu =0}(0) = \sum _{+,-}\sum _{k=0}^{N_*+1}\big \Vert (R^2+|x_3|^2)^{\frac{1+\delta }{2}} \nabla ^{k}{z}_{\pm }(0,x)\big \Vert _{L^2(\mathbb {R}^3)}^2\le \varepsilon _0^2, \end{aligned}$$

the ideal MHD system (1.5) ($\mu =0$) admits a unique global solution ${z}_{\pm }(t,x)$. Moreover, there is a universal constant C, so that, for all $k\le N_*$, we have

$$\begin{aligned}&\sup _{t\ge 0}\big \Vert (R^2+|u_\mp |^2)^{\frac{1+\delta }{2}}\nabla ^{k+1}{z}_{\pm }(t,x)\big \Vert _{L^2(\mathbb {R}^3)}^2 +\sup _{u_{\pm }}\int _{C_{u_\pm }^\pm }(R^2+|u_\mp |^2)^{1+\delta }|{z}_{\pm }|^2d\sigma _\pm \\&\quad +\sup _{u_{\pm }} \int _{C_{u_\pm }^\pm }(R^2+|u_\mp |^2)^{1+\delta }|j_{\pm }^{(k)}|^2d\sigma _\pm \le C \mathcal {E}^{\mu =0}(0). \end{aligned}$$

Remark 1.5

For the ideal MHD system, we could prove more stronger existence results in the sense that the weighted $L^2$ condition on ${z}_{\pm }$ can be removed in Theorem 1.2 and Theorem 1.3. The key point lies in the proof to Theorem 1.2 and Theorem 1.3. In fact, the lowest order energy estimates of ${z}_{\pm }$ are not needed for the ideal MHD under the assumption $\Vert {z}_{\pm }(t,\cdot )\Vert _{L^\infty }\le \frac{1}{2}$. Thanks to the Gagliardo-Nirenberg interpolation inequality, $\Vert {z}_{\pm }(t,\cdot )\Vert _{L^\infty }$ can be bounded by $C\Vert \nabla {z}_{\pm }(t,\cdot )\Vert _{L^2}^{\frac{1}{2}}\Vert \nabla ^2{z}_{\pm }(t,\cdot )\Vert _{L^2}^{\frac{1}{2}}(\lesssim \varepsilon )$ which is enough to close the argument by the continuity method. This is merely a technical improvement and we will not pursue this direction in the paper.

As applications of the above theorems, we are now ready to study the nonlinear asymptotic stability of Alfvén waves.

Nonlinear Stability of Ideal Alfvén Waves: A Scattering Picture

We now focus on the ideal incompressible MHD system. The goal is to understand the global dynamics of the Alfvén waves, or equivalently the asymptotics of ${z}_{\pm }$ for $t\rightarrow \infty$. For this purpose, we introduce a so-called scattering diagram for the Alfvén waves. The idea is to capture the behavior of waves along each characteristic curves. It is similar to the Penrose diagram in general relativity (which keeps record of the null/characteristic geometry of the spacetime).

Given a point $(x_1,x_2,x_3) \in \Sigma _0$, it determines uniquely a left-traveling characteristic line: it is parameterized by $(x_1,x_2,u_-,t)$, where $u_-= x_3$ and $t \in [0,+\infty )$. This line is denoted by $l_-(x_1,x_2,u_-)$ (with $u_-=x_3$) or simply $l_-$. We use $\mathcal {C}_+$ to denote the collection of all the characteristic lines and we call it the left future characteristic infinity. We use $(x_1,x_2,u_-)$ as a global coordinate system on $\mathcal {C}_+$ so that $\mathcal {C}_+$ can be regarded as a differentiable manifold. In the picture, $\mathcal {C}_+$ is depicted as the double-dotted dashed line on the left hand side. The picture shows that $l_-$ starts from $(x_1,x_2,x_3) \in \Sigma _0$ and hits $\mathcal {C}_+$ at $(x_1,x_2,u_-)$ with $u_- = x_3$. The tangent vector field of the line $l_-$ is exactly $L_-$. We remark that a line $l_-(x_1,x_2,u_-)$ lies on the characteristic hypersurface $C_{u_-}^-$. The intersection of $C_{u_-}^-$ with $\mathcal {C}_+$ should be understood as the collection of all the $l_-(x_1,x_2,u_-)$’s, where $u_- \in \mathbb {R}$.

Similarly, we can also define the right future characteristic infinity $\mathcal {C}_-$ as the collection of all the right-traveling characteristic lines.

We use $\mathcal {T}_+$ to denote the virtual intersection of $\mathcal {C}_+$ and $\mathcal {C}_-$ in the picture. We call it the future time infinity since it represents morally $t\rightarrow +\infty$. Besides $\mathcal {T}_+$, $\mathcal {C}_{+}$ has another endpoint $\mathcal {S}_+$ in the picture. It represents the left space infinity, i.e., $x_3 \rightarrow -\infty$. Similarly, we can define the right space infinity $\mathcal {S}_-$. For an arbitrary time slice $\Sigma _t$, it is depicted by the horizontal dotted line in the picture. We remark that each $\Sigma _t$ ends at $\mathcal {S}_-$ and $\mathcal {S}_+$.

We can now define the scattering fields $z_+^{\text {(scatter)}}(x_1,x_2,u_-)$ on $\mathcal {C}_+$ and $z_-^{\text {(scatter)}}(x_1,x_2,u_+)$ on $\mathcal {C}_-$:

Definition 1.6

Given points $l_\mp \in \mathcal {C}_\pm$ with coordinates $(x_1,x_2, u_\mp )$, the corresponding scattering field of the ideal Alfvén waves for the solutions $z_\pm$ are defined by the following formulas

$$\begin{aligned} \begin{aligned} z_+^{\text {(scatter)}}(x_1,x_2,u_-)&= \lim _{t\rightarrow \infty } z_+(x_1,x_2,u_-, t),\\ z_-^{\text {(scatter)}}(x_1,x_2,u_+)&= \lim _{t\rightarrow \infty } z_-(x_1,x_2,u_+, t). \end{aligned} \end{aligned}$$

(1.14)

Similarly, we also introduce the scattering vorticities (and their derivatives) as limits of the corresponding objects along the characteristics:

$$\begin{aligned} \begin{aligned} \left( \text {curl}\,z_+^{\text {(scatter)}}\right) (x_1,x_2,u_-)&= \lim _{t\rightarrow \infty } (\text {curl}\,z_+)(x_1,x_2,u_-, t),\\ \left( \text {curl}\,z_-^{\text {(scatter)}}\right) (x_1,x_2,u_+)&= \lim _{t\rightarrow \infty }(\text {curl}\,z_-)(x_1,x_2,u_+, t). \end{aligned} \end{aligned}$$

(1.15)

Remark 1.7

(Notation Convention) We would like to avoid confusions when we switch between coordinates. Given a vector field f on $\mathbb {R}_t\times \mathbb {R}^3$, $\nabla f$, $\text {div}\,f$ or $\text {curl}\,f$ are defined on each time slice with respect to the standard coordinates $(x_1,x_2,x_3)$. Geometrically, they are defined with respect to the standard Euclidean metric on $\Sigma _t$. It is in this sense that they are globally defined, in particular, are independent of the choices of coordinates. On the other hand, for the quantities defined as scattering limit (e.g. $\text {curl}\,z_+^{\text {(scatter)}}$), the corresponding $\nabla$, $\text {div}\,$ and $\text {curl}\,$ are merely symbols rather than having any geometric meanings.

To better illustrate the idea, we consider some examples.

• 1) $\nabla p$ are understood as vector field in $\mathbb {R}^4$ and it is coordinate independent. More precisely, we can write $(\nabla p)(t, x_1^+, x_2^+, x_3^+)$. It simply means the vector field $\nabla p$ evaluated at the point $(t, x_1^+, x_2^+, x_3^+)$ rather than $(\partial _t p, \partial _{x_1^+}p, \partial _{x_2^+}p, \partial _{x_3^+}p)$.

• 2) ${z}_+$ are obviously global defined as the real physical objects. If we change coordinates according to $\Phi :\, (y_0,y_1,y_2,y_3)\mapsto (t,x_1,x_2,x_3)$, then ${z}_+(y_0,y_1,y_2,y_3)={z}_+|_{(t,x_1,x_2,x_3)=\Phi (y_0,y_1,y_2,y_3)}$ represents the same vector field on the same space-time point.

In physics, the scattering fields have more pratical/physical meaning than the original fields. They are the fields received and measured by a far-away observer. Based on Theorem 1.3, we will prove that the scattering fields are well-defined. In fact, we will prove that $\nabla p$ is integrable over each $l_\pm$ and the scattering fields are given by the following explicit formulas:

$$\begin{aligned} z_+^{\text {(scatter)}}(x_1,x_2, u_-) = z_+(x_1,x_2, u_-, 0) -\int _{0}^\infty (\nabla p) (x_1,x_2, u_-,\tau ) d\tau , \end{aligned}$$

(1.16)

and

$$\begin{aligned} z_-^{\text {(scatter)}}(x_1,x_2, u_+) = z_-(x_1,x_2, u_+, 0) -\int _{0}^\infty (\nabla p) (x_1,x_2, u_+,\tau ) d\tau . \end{aligned}$$

(1.17)

The vorticities of the scattering fields can be written down explicitly:

$$\begin{aligned}&\left( \text {curl}\,z_+^{(\text {scatter})}\right) (x_1,x_2, u_-)=(\text {curl}\,z_+)(x_1,x_2, u_-,0)\nonumber \\&\quad -\int _{0}^\infty (\nabla z_-\wedge \nabla z_+) (x_1,x_2, u_-,\tau ) d\tau . \end{aligned}$$

(1.18)

and

$$\begin{aligned}&\left( \text {curl}\,z_-^{(\text {scatter})}\right) (x_1,x_2, u_+)=(\text {curl}\,z_+)(x_1,x_2, u_+,0)\nonumber \\&\quad -\int _{0}^\infty (\nabla z_+\wedge \nabla z_-) (x_1,x_2, u_+,\tau ) d\tau . \end{aligned}$$

(1.19)

The above analysis also provides a framework, via the scattering fields, to compare the nonlinear Alfvén waves with the linearized theory of Alfvén waves (à la Alfvén). For the linearized theory, one assumes that $v\cdot \nabla v\sim 0$, $\nabla p \sim 0$ and $b\cdot \nabla \sim B_0\cdot \nabla$ (they are of order $O(\varepsilon _0^2)$ in the nonlinear evolution). The linearized ideal MHD system reduces to

$$\begin{aligned} \begin{aligned} \partial _t v-&B_0 \cdot \nabla b= 0, \ \ \partial _t b-B_0 \cdot \nabla v= 0, \end{aligned} \end{aligned}$$

or equivalently,

$$\begin{aligned} \begin{aligned} \partial _t {z}_+-&B_0 \cdot \nabla {z}_+= 0, \ \ \partial _t {z}_-+B_0 \cdot \nabla {z}_-= 0. \end{aligned} \end{aligned}$$

Given initial data $z_\pm (x_1,x_2,x_3,0)$, the linearized system can be solved directly by the method of characteristics. Therefore, the solutions of the linearized system can also define a similar scattering diagram as above. To give a precise description, we first fix a measure $d\tilde{\sigma }_\pm$ on $\mathcal {C}_\pm$. By virtue of the coordinates $(x_1,x_2,u_\mp )$ on $\mathcal {C}_\pm$, we require that $d\tilde{\sigma }_\pm = dx_1\wedge dx_2 \wedge d u_\mp$. Intuitively, if we regard $\mathcal {C}_\pm$ as the limits of $C^\pm _{u_\pm }$, we would like to define the measure as limiting objects of $d\sigma _\pm$ on $C^\pm _{u_\pm }$ as $u_\pm \rightarrow \mp \infty$. Our definition may be different from the limiting measures by universal constants (thanks to the proof to Theorem 1.3) and this will not effect any statement in this subsection. Then we introduce the following weighted Sobolev spaces:

$$\begin{aligned}&H^{N_*+1,\delta }(\Sigma _0) = \ \text {the completion of compactly supported smooth vector fields on }\ \mathbb {R}^3 \ \\&\quad \text {with respect to the norm} \sum _{k=0}^{N_*+1}\Vert (R^2+|x_3|^2)^{\frac{1+\delta }{2}}\nabla ^{k} f(x)\Vert _{L^2(\mathbb {R}^3)}^2,\\&\quad H^{N_*+1,\delta }(\mathcal {C}_{\pm }) = \ \text {the completion of compactly supported smooth vector fields }f \text { on }\ \mathbb {R}^3 \\&\quad \text {with respect to the norm} \int _{\mathcal {C}_{\pm }}(R^2+|u_\mp |^2)^{1+\delta }|f|^2d\tilde{\sigma }_\pm \\&\quad +\sum _{k=0}^{N_*}\int _{\mathcal {C}_{\pm }}(R^2+|u_\mp |^2)^{1+\delta }|\nabla ^k (\text {curl}\,f)|^2d\tilde{\sigma }_\pm . \end{aligned}$$

We now define the following linear solution operator or linear scattering operator:

$$\begin{aligned} \begin{aligned}&\mathbf {S}^{\text {linear}}:H^{N_*+1,\delta }(\Sigma _0)\times H^{N_*+1,\delta }(\Sigma _0)\rightarrow H^{N_*+1,\delta }(\mathcal {C}_-) \times H^{N_*+1,\delta }(\mathcal {C}_+),\\&\quad \left( z^{(0)}_-,z^{(0)}_+\right) \mapsto \big (z^{(0)}_-,z^{(0)}_+\big ), \end{aligned} \end{aligned}$$

(1.20)

where we identify $\Sigma _0$ with $\mathcal {C}_\pm$ by the coordinates $(x_1,x_2,x_3)\mapsto (x_1,x_2,u_\mp )(u_\mp =x_3)$.

For the nonlinear scattering theory, we can similarly define the nonlinear scattering operator as follows:

$$\begin{aligned} \begin{aligned} \mathbf {S}:H^{N_*+1,\delta }(\Sigma _0)\times H^{N_*+1,\delta }(\Sigma _0)&\rightarrow H^{N_*+1,\delta }(\mathcal {C}_-) \times H^{N_*+1,\delta }(\mathcal {C}_+),\\ \left( z^{(0)}_-,z^{(0)}_+\right)&\mapsto \big (z_-^{\text {(scatter)}},z_+^{\text {(scatter)}}\big ), \end{aligned} \end{aligned}$$

(1.21)

where $(z_-^{\text {(scatter)}}, z_+^{\text {(scatter)}})$ are the scattering fields associated to the initial data $(z^{(0)}_-,z^{(0)}_+)$. By the a priori estimates in Theorem 1.3, $\mathbf {S}$ is an continuous operator.

We compare the linear (scattering) theory and the nonlinear scattering theory. In the linear theory, we use $z_\pm ^{\text {(linear)}}$ to denote the scattering fields. In the above pictures, the characteristic curves of the linearized equations are straight lines; the characteristic curves of the nonlinear equations are curved lines. Since in both theories we can use $(x_1,x_2,u_\mp )$ as common coordinate systems for $\mathcal {C}_\pm$, we can compute the differences $z_\pm ^{\text {(scatter)}}-z_\pm ^{\text {(linear)}}$ to quantify the difference between the linear theory and the nonlinear theory:

$$\begin{aligned} \begin{aligned} \big (z_\pm ^{\text {(scatter)}}-z_\pm ^{\text {(linear)}}\big )(x_1,x_2, u_\mp ,\tau )&= -\int _{0}^\infty (\nabla p) (x_1,x_2, u_\mp ,\tau ) d\tau \\&= \int _{0}^\infty \big (\nabla \triangle ^{-1}\partial _i\partial _j\big (z_-^iz_+^j\big )\big )(x_1,x_2, u_\mp ,\tau ) d\tau . \end{aligned} \end{aligned}$$

Therefore, the deviation of the nonlinear theory from the linearized theory reflects the nonlinear interactions between the nonlinear left-traveling wave $z_+$ and the nonlinear right-traveling wave $z_-$. Based on this formula, we show that the linearization of the nonlinear scattering operator is the linear scattering operator:

Theorem 1.4

Assume the initial data of the ideal MHD system satisfy $\Vert {z}_{\pm }\Vert _{H^{N_*+1,\delta }(\Sigma _0)} \le \varepsilon _0$ with $N_*\ge 5$ and $\varepsilon _0$ being determined in Theorem 1.3. Therefore, the scattering fields given in (1.14) is well defined. Similarly, the scattering vorticities fields given in (1.15) is also well-defined. Moreover, regarded as operators between Hilbert spaces:

$$\begin{aligned} H^{N_*+1,\delta }(\Sigma _0)\times H^{N_*+1,\delta }(\Sigma _0) \rightarrow H^{0,\delta }(\mathcal {C}_-) \times H^{0,\delta }(\mathcal {C}_+), \end{aligned}$$

the differential of $\mathbf {S}$ at $\mathbf 0 \in H^{N_*+1,\omega }(\Sigma _0)\times H^{N_*+1,\omega }(\Sigma _0)$ is equal to $\mathbf {S}^{\text {linear}}$, i.e.,

$$\begin{aligned} d \,\mathbf {S} \big |_\mathbf{0 }=\mathbf {S}^{\text {linear}}. \end{aligned}$$

(1.22)

Remark 1.8

The map $\mathbf {S}: H^{N_*+1,\delta }(\Sigma _0)\times H^{N_*+1,\delta }(\Sigma _0) \rightarrow H^{0,\delta }(\mathcal {C}_-) \times H^{0,\delta }(\mathcal {C}_+)$ considered in the theorem only addresses the $L^2$ norm of the scattering fields. Indeed, to recover all the derivatives at infinity, this motivates the study of the inverse scattering problem for the ideal Alfvén waves. Since the problem is of great independent interests and difficulties (in particular because this would be a quasi-linear type inverse scattering theory), we will discuss this issue in a forthcoming paper.

Nonlinear Stability of Viscous Alfvén Waves

The main application of the estimates given in Theorem 1.2 is the study of global dynamics of viscous Alfvén waves. The analysis of the Alfvén waves in the previous subsection is subject to the constraint that the MHD system is ideal. In reality, all the physical systems have diffusion phenomena and the corresponding wave phenomena will be damped by the diffusion.

For the presentation of our main result, for a fixed $\mu$, we first introduce the so called the classical $\mu$ -small-data parabolic regime for (1.6). Once the viscosity $\mu$ is given, as one usually does for the Navier–Stokes equations, one can regard (1.6) as semi-linear heat equations rather than a quasi-linear system. Therefore, the classical approach for the Navier–Stokes equations shows that, there exists a constant $\varepsilon _\mu$, such that if the $H^2$-norm of the initial data are bounded above by $\varepsilon _\mu$, then we can construct global solutions of (1.6) by regarding the system as a small perturbation of the linearized equation. We remark that usually $\varepsilon _\mu =O(\mu )$. Intuitively, in the small-data parabolic regime, the diffusion is so strong (compared to the convection) so that the solution will stay in this regime and converge to the steady state of the system.

In Theorem 1.2, the size of initial data is of order $\varepsilon$. We emphasize that $\varepsilon$ is independent of $\mu$. Since $\mu$ can be arbitrarily small, we can think of the size of the data as being very large compared to $\varepsilon _\mu$. It is in this sense that the initial data given in Theorem 1.2 is far away from the classical $\mu$-small-data parabolic regime. Now the problem on global dynamics of viscous Alfvén waves can be formulated that, given a $\mu$, how and when the solution of the MHD system from a far away position will enter the small-data parabolic regime.

To understand the mechanism of the small dissipation for the energy, we begin with two families of special data to see the dissipative properties of the corresponding viscous solutions. Their behaviors are very different near the time $T_c=O(\frac{1}{\mu })$. This on one hand shows the rich dynamical phenomena of the viscous Alfvén waves; on the other hand, this shows that it is more natural to consider the small diffusion problem via the hyperbolic method rather than the parabolic method, since the dissipative property of a solution is sensitive to the initial data. In the following discussion, we assume that $\mu$ is given.

Example 1

The first family of data is so-called the low frequency data or data with very small oscillations. We may take

$$\begin{aligned} (v(0,x),b(0,x))=(\varepsilon ^{5/2} f_1(\varepsilon ^{} x),\varepsilon ^{5/2} f_2(\varepsilon ^{} x)), \end{aligned}$$

where $f_1(x)$ and $f_2(x)$ are two compactly supported smooth divergence-free vector fields and $\varepsilon \le \varepsilon _0$ measures the smallness of the data. According to the energy estimates in Theorem 1.2, one can show that

$$\begin{aligned} \int _{\mathbb {R}^3}(|\nabla v|^2+|\nabla b|^2)dx \lesssim \varepsilon ^3. \end{aligned}$$

Roughly speaking, the main reason of having $\varepsilon ^3$ instead of $\varepsilon ^2$ in the energy is that the initial data on one derivative of (v, b) is one-order-in-$\varepsilon$ smaller than (v, b) itself. According to the basic energy identity, we have

$$\begin{aligned}&\int _{\mathbb {R}^3}\bigl (|v(T_1,x)|^2+|(b-B_0)(T_1,x)|^2\bigr ) dx = \int _{\mathbb {R}^3}\bigl (|v(0,x)|^2+|(b-B_0)(0,x)|^2\bigr ) dx\\&\qquad -2\mu \int _{0}^{T_1}\int _{\mathbb {R}^3}\bigl (|\nabla v(\tau ,x)|^2+|\nabla b(\tau ,x)|^2\bigr )dx d\tau \\&\qquad \ge \int _{\mathbb {R}^3}\bigl (|v(0,x)|^2+|(b-B_0)(0,x)|^2\bigr ) dx-\mu T_1 \varepsilon ^3. \end{aligned}$$

Since the initial energy is proportional to $\varepsilon ^2$, for the time $T_1= \frac{1}{\mu }$, the dissipation of energy is approximately $\varepsilon ^3$. Therefore, almost no energy has been consumed due to viscosity all the way up to the time $T_1$. In other words, for the data with very small oscillations, the dissipation on the waves is very weak within the time $T_1$ and the viscous waves resemble the ideal Alfvén waves.

Example 2

The second family of data contains considerable oscillations. We measure the oscillations by looking at the energies. Let $E_k (t)= \int _{\mathbb {R}^3}|\nabla ^k v(t,x)|^2+|\nabla ^k (b(t,x)-B_0)|^2 dx$. We assume that

$$\begin{aligned} E_0(0) \sim E_1 (0) \sim E_2(0). \end{aligned}$$

We recall that for the low frequency data, we have $E_0(0)>> E_1 (0)>>E_2(0)$. To avoid dealing with too many constants, we further assume that $E_0(0) = E_1 (0) = E_2(0)=\varepsilon ^2$ and the analysis for the general case is the same. Similar to the analysis in the low frequency data case, since $E_2(t)\le C\varepsilon ^2$, we have

$$\begin{aligned} E_1(t)&= E_1(0) -2\mu \int _{0}^{t}E_2(\tau ) d\tau \ge \varepsilon ^2 -2C\mu \varepsilon ^2 t. \end{aligned}$$

In fact, we have neglected the contribution of the nonlinear terms since they are all of order $\varepsilon ^3$. Therefore, we have

$$\begin{aligned} E_1(t) \ge \frac{1}{2}\varepsilon ^2,\ \ \ \text { for } t\le \frac{1}{4C\mu }. \end{aligned}$$

This implies that, for $T_2=\frac{1}{4C\mu }$, we have

$$\begin{aligned} E_0(T_2)&= E_0(0) -2\mu \int _{0}^{T_2}E_1(\tau ) d\tau \le \varepsilon ^2 -2\mu \frac{1}{2}\varepsilon ^2 T_2=\left( 1-\frac{1}{4C}\right) \varepsilon ^2. \end{aligned}$$

We remark that C is the universal constant in the energy estimates in Theorem 1.2. This analysis shows that for oscillating data, within the time $T_2$, a considerable amount of energy has been dissipated. Indeed, by suffering a loss of derivatives (since the viscous terms require one more derivative), we can further iterate the above analysis to amplify the dissipation. This shows that the highly oscillating solutions damp much faster than the low frequency data.

These two examples show that on one hand, the viscous Alfvén waves (for small $\mu$) preserve the wave profile for a long time (approximately $\frac{1}{\mu }$) and the behavior of the waves in this regime is very similar to that of the ideal Alfvén waves; on the other hand, after a sufficiently long time ($> \frac{1}{\mu }$), the dissipation accumulates and the wave amplitude begins to dissipate and will eventually vanish. The time scale $T_c =O( \frac{1}{\mu })$ is called the characteristic time for the system which is also suggested by the physics (see [4]). It is roughly the time for the transition from non-dissipative wave like solutions to solutions of the heat equation (with fast decay in time). It also indicates on when solutions decay to the $\mu$-small-data parabolic regime.

The main theorem of the subsection is as follows:

Theorem 1.5

(Nonlinear stability of viscous Alfvén waves) Let $B_0 =(0,0,1)$, $\mu _0>0$, $R\ge 100$ and $N_* \in \mathbb {Z}_{\ge 5}$. For all $\mu \le \mu _0$, there exists a constant $\varepsilon _0$, which is independent of the viscosity coefficient $\mu$, so that if the initial data of (1.4) or equivalently (1.5) satisfy

(1.23)

then (1.5) admits a unique global solution ${z}_{\pm }^\mu (t,x)$ or $(v^\mu ,b^\mu )$. We remark that the solutions ${z}_{\pm }^\mu (t,x)$ have the same initial data and we use ${z}_{\pm }(t,x)$ or (v, b)to denote the solution corresponding to the ideal system. The solutions ${z}_{\pm }^\mu (t,x)$ satisfy the following properties:

• 1) (Convergence to the ideal solution) For any given $T>0$, we have

  $$\begin{aligned} \Vert {z}_{\pm }^\mu (t,x)-{z}_{\pm }(t,x)\Vert ^2_{L_t^\infty L^2_x\big ([0,T]\times \mathbb {R}^3\big )} \lesssim \mu \varepsilon e^{\varepsilon T}. \end{aligned}$$

  (1.24)

• 2) (Decay to the small-data parabolic regime) We fix $\varepsilon _0$ (determined by Theorem 1.2) and fix the initial data $(z_+(x,0),z_-(x,0))$ so that it satisfies (1.23). We define the total energy $\mathcal {E}^\mu (t)$ as

  $$\begin{aligned} \mathcal {E}^\mu (t) = \sum _{+,-}\Bigl (E_\pm (t)+\sum _{|\alpha |\le N^*}E_{\pm }^{(\alpha )}(t) +\mu \sum _{|\alpha |=N^*+1}E_{\pm }^{(\alpha )}(t)\Bigr ), \end{aligned}$$

  For arbitrary small $\mu >0$, there exist a universal constant C and a sequence of time $T_1<T_2<\cdots <T_{n_0}$ in such way that, for any $k\le n_0$, we have

  $$\begin{aligned} \mathcal {E}^\mu (T_k) \le (C\mathcal {E}(0))^{\frac{k}{2}+1}. \end{aligned}$$

  Moreover,

  $$\begin{aligned} \mathcal {E}^\mu (T_{n_0}) \le \varepsilon _\mu . \end{aligned}$$

  In other words, at time $T_{n_0}$ the solution enters the $\mu$-small-data parabolic regime.

The next figure shows the intuitive idea of the decay:

The gray region is the classical $\mu$-small-data parabolic regime in the energy space (roughly $H^2(\mathbb {R}^3)$) and the curve is the evolution curve of the solution. The solution initially is far-way from the grey region. In the course of the evolution, the viscosity damps the total energy. The total energy may decay very slowly (the rate depends on the profile of the data) before the solution enters the parabolic regime. Once it enters the grey region at time $T_{n_0}$, the diffusion takes over and we see that the solution converges to the steady state (denoted by a circle in the figure) very fast.

Remark 1.9

It is routine to repeat the proof of (1.24) to show that, for $k\le 4$, we have

$$\begin{aligned} \Vert {z}_{\pm }^\mu (t,x)-{z}_{\pm }(t,x)\Vert ^2_{L_t^\infty H^k_x\big ([0,T]\times \mathbb {R}^3\big )} \lesssim \mu \varepsilon e^{\varepsilon T}. \end{aligned}$$

In particular, for any fixed time interval [0, T], in the classical sense (with respect to the topology of ${L^\infty _t C_x^2([0,T]\times \mathbb {R}^3)}$), we have

$$\begin{aligned} \lim _{\mu \rightarrow 0} (v^\mu ,b^\mu ){\longrightarrow }(v,b). \end{aligned}$$

Moreover, for fixed $\mu$, it shows that viscous Alfvén waves are very close to the ideal Alfvén waves at least for $t\le |\log \mu -2\log \varepsilon |/\varepsilon$.

Remark 1.10

(Choice of $T_k$) We emphasize that the choice of $T_k$ depends not only on the size of energy norms of the initial data but also on the profile of the data.

In the course of the proof of the above theorem (which will be at the end of the paper), we have to iterate the following decay estimates:

$$\begin{aligned} \mathcal {E}^\mu (t)\lesssim \mathcal {I}^\mu (t;0)+\frac{\log \bigl (\log (\mu t+e)+e\bigr )}{\log (\mu t+e)}\mathcal {E}^\mu (0) +\bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{3}{2}}. \end{aligned}$$

(1.25)

The function $\mathcal {I}^\mu (t;0)$ is completely and explicitly determined by the initial data in a straightforward manner. It has the property that $\mathcal {I}^\mu (t;0)\rightarrow 0$ for $t\rightarrow \infty$. Roughly speaking, it measures the distribution of the data in the low frequency (in Fourier space) region. The exact form of the function is not enlightening so that we only give the expression in the proof.

Remark 1.11

(Comparison to known decay estimates which are based on the parabolic method) If we assume the initial data are in $L^1(\mathbb {R}^3)$, classical results such as [7] or [8] suggest that the energy of the system should have the following decay estimates:

$$\begin{aligned} \Vert z_+(t)\Vert _{L^2}^2+\Vert z_-(t)\Vert _{L^2}^2\lesssim & {} (1+\mu t)^{-\frac{3}{2}}\bigl ( \Vert z_+(0)\Vert _{L^1\cap L^2}^2+\Vert z_-(0)\Vert _{L^1\cap L^2}^2\bigr )\\&+\,\frac{\big (\Vert z_+(0)\Vert _{L^2}^2+\Vert z_-(0)\Vert _{L^2}^2\big )^2}{\mu ^2} (1+\mu t)^{-\frac{1}{2}}. \end{aligned}$$

In the case where $E_0(0)=\varepsilon ^2\gg \mu ^2$, for $t\ll \varepsilon ^4/\mu ^3$, we see that the upper bound of the energy from the above inequality is extremely large compared to $\varepsilon ^2$. This cannot help to justify the characteristic time $T_c=O(\frac{1}{\mu })$ as the physics suggested. Therefore, in a large time scale (up to time $\varepsilon ^4/\mu ^3$) the classical estimates do not capture the decay mechanism for the small diffusion.

In our approach, with the additional assumption that the datum is in $L^1(\mathbb {R}^3)$, we can improve (1.25) to

$$\begin{aligned} \mathcal {E}^\mu (t)\lesssim \frac{\log \bigl (\log (\mu t+e)+e\bigr )}{\log (\mu t+e)}\mathcal {E}^\mu (0) +\bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{3}{2}}. \end{aligned}$$

It is straightforward to see that, if $t\gg T_c=O(\frac{1}{\mu })$, the total energy becomes $o(\varepsilon ^2)$. Therefore, much energy has been dissipated at $T_c$. This provides a theoretical support to the characteristic time and it is also consistent with the previous two examples.

We also want to point out that, in the classical estimates, the factor $\mu ^{-2}$ makes the estimates rougher. It comes from the estimates for convection terms in the equations since they are treated as nonlinear terms. Our approach is quasi-linear hyperbolic energy method and the convection terms do not contribute extra negative power of $\mu$.

Remark 1.12

Once the solution enters the classical $\mu$-small-data regime, classical approach yields immediately the final decay rate for $t\rightarrow \infty$:

$$\begin{aligned} \Vert (v^\mu ,b^\mu -B_0)\Vert _{L^\infty (\mathbb {R}^3)}\lesssim \frac{\mu }{(1+\mu t)^\frac{3}{4}}. \end{aligned}$$

In particular, due to the diffusion, $(v^\mu ,b^\mu )$ converges to the steady state $(0,B_0)$.

Comments on the Proof

We would like to address the motivations for difficulties in the proof.

• Separation of Alfvén waves and null structures

A main difficulty in understanding the three dimensional Euler equations is the accumulation of the vorticity. In fact, the vorticity $\omega$ for incompressible Euler equations satisfies the following equation:

$$\begin{aligned} \partial _t \omega + v \cdot \nabla \omega = \nabla v \wedge \nabla v. \end{aligned}$$

This is a transport type of equation and in general we do not expect decay in time for $\omega$. The righthand side can be roughly regarded as $|\omega |^2$ and this nonlinearity of Ricatti type is hard to control.

In the current work, the strong magnetic background provides a cancellation structure for the nonlinear terms. It resembles the null structure (à la Klainerman) in many nonlinear wave equations. First of all, it is crucial to realize that the solutions are indeed waves (Alfvén waves) and we have two families of waves $z_+$ and $z_-$. The vorticity equations now read as (up to a sign)

$$\begin{aligned} \partial _t j_\pm + Z_\mp \cdot \nabla j_\pm =-\nabla z_\pm \wedge \nabla z_\mp . \end{aligned}$$

Here, $z_+$ and $z_-$ are $1+1$ dimensional waves and we do not expect any decay in time for each of them (just as for Euler equations!). The remarkable fact is that $z_+$ and $z_-$ travel in opposite directions. Therefore, after a long time, $z_+$ and $z_-$ are far apart from each other and their distance can be measured by the time t. Therefore, the quadratic nonlinearity $\nabla z_+ \wedge \nabla z_-$ must be small (in sharp contrast to the Euler equations!) since $z_+$ and $z_-$ are basically supported in different regions. This observation provides the decay mechanism to control the nonlinear terms. We remark that, in the context of the standard null structure for wave equations, $z_+$ and $z_-$ can be regarded as incoming and outgoing waves and the null structure says that incoming waves can only couple with outgoing waves.

More precisely, we have the following schematic equations:

$$\begin{aligned} \partial _t {z}_++{Z}_-\cdot \nabla {z}_+= \cdots , \ \ \partial _t {z}_-+{Z}_+\cdot \nabla {z}_-= \cdots ,\ \ {Z}_-\sim -B_0, \ \ {Z}_+\sim B_0. \end{aligned}$$

Therefore, we can roughly think of the waves ${z}_+$ and ${z}_-$ as follows:

• a) ${z}_+$ travels along the $-B_0$ direction (we say that it is left-traveling) with speed approximately 1. It is centered around $(0,0,-t)$.

• b) ${z}_-$ travels along the $B_0$ direction (we say that it is right-traveling) with speed approximately 1. It is centered around (0, 0, t).

The centers of ${z}_+$ and ${z}_-$ are moving away from each other. We will later on say that ${z}_{\pm }$ separate from each other to refer to this phenomenon. This picture indeed underlies each step in the proof. For instance, although $\nabla z_+$ and $\nabla z_-$ are not decaying in $L^\infty$ norm, but their product satisfies the following decay estimate:

$$\begin{aligned} |\nabla {z}_+(t,x) \nabla {z}_-(t,x)|\lesssim \frac{1}{1+t}\big (\frac{1}{\log (2+t)}\big )^2. \end{aligned}$$

Moreover, the decay is fast enough so that righthand side is integrable in t.

• Weighted estimates and $(1+1)-$ dimension wave equations

As we have noted before, at least on the linearization level, the Alfvén waves $z_\pm$ satisfy $1+1$ dimensional wave equations. It is well-known that $(1+1)$-dimension waves are conformally invariant (the energy-momentum tensor of a linear wave is trace-free!). We briefly recall the conformal structure of $(1+1)$-dimensional Minkowski space $(\mathbb {R}^{1+1}, m=-dt\otimes dt+dx\otimes dx)$. If we let $u=-t+x$ and $\underline{u}=t+x$, we have $m=\frac{1}{2}(du\otimes d\underline{u}+d\underline{u}\otimes d {u})$. The optical functions u and ${\underline{u}}$ are analogues of the Riemann invariants for the $2\times 2$ conservation laws and the defining functions for the characteristic surfaces $u_+$ and $u_-$ in the current paper are also similar. We define $L =\partial _t + \partial _x$ and $\underline{L} =\partial _t -\partial _x$ (analogues of $L_\pm$ in this paper). Therefore, all the conformal Killing vector fields on $\mathbb {R}^{1+1}$ are linear combinations of f(u)L and $g(\underline{u})\underline{L}$. The associated energy current will provide conservation quantities (energies) for $(1+1)$-waves. In a more analytical way, the above analysis shows that, if one wants to define a good conserved energy, we can systematically multiply the equations by $f(u)\varphi$ or $g(\underline{u})\varphi$ ($\varphi$ is a solution of the wave equations) and then integrate by parts.

This idea underlies all the energy estimates in the sequel. We will multiply the MHD equations by $f(u_-)z_+$ or $g(u_+)z_-$ to derive energy estimates. This leaves another important issue: the choices of the weights $f(u_-)$ and $g(u_+)$. This question is far from being trivial since we also have to take the viscosity terms into account. This term indeed prevents (via damping) the solution from behaving like $(1+1)$-waves (dispersionless). We will discuss this issue later on.

• Energy flux through characteristic hypersurface

In the study of fluid problems, it is common to use energy associated to each slice $\Sigma _t$, e.g., the standard energy such as $\int _{\mathbb {R}^3}|v(t,x)|^2dx$. However, given the facts that the solutions are waves (Alfvén wave), there are other more natural energy type quantities, called the energy flux. In our work, the flux comes into play merely as auxiliary (except for the scattering picture for ideal Alfvén waves) quantities, but it is indeed indispensable for each step of the proof. The use of the flux is indeed one of the main innovations in our approach.

To make the meaning of flux more transparent, we consider the left-traveling characteristic hypersurface $C^-_{u_-}$. The associated energy flux for $z_-$ is defined as

$$\begin{aligned} F(z_-)=\int _{C^-_{u_-}} |z_-|^2 d\sigma _-, \end{aligned}$$

where $d\sigma _-$ is the surface measure for $C^-_{u_-}$. Since $z_-$ is right-traveling and is transversal to $C^-_{u_-}$, the flux $F(z_-)$ measures exactly the amount of energy carried by $z_-$ through $C^-_{u_-}$.

Besides its clear physical meaning, the flux is a robust technical tool to explore the “decay” of $(1+1)$-waves. Indeed, the weighted fluxes provide decays such as $(1+|u_-|^2)^{-\frac{1+\delta }{2}}$. We may think of $|u_-|$ as $|x_3+t|$. This factor is not integrable in t but is integrable in $u_-$! This on one hand indicates that the usual quantities associated to $\Sigma _t$ may be inadequate in the proof and on the other hand shows the importance of the quantities (such as flux!) associated to $u_-$ or $C^-_{u_-}$. This will be clear in the course of the proof.

• The quasi-linear approach versus linear perturbation

One of the main innovations of the current work is to use the ‘quasi-linear’ approach to attack the problem. It consists of two main ingredients: first of all, we use the characteristic surfaces defined by the solution itself rather than the ‘linear’ solution (or equivalently the background solution $(0,B_0)$); secondly, the multiplier vector fields and the weight functions that we use to derive energy estimates are also constructed from the solutions. Roughly speaking, each step in the course of obtaining the main estimates depends completely on the solution and we believe that a less ‘non-linear’ approach may not work.

As we mentioned, this shares many main features with the proof of nonlinear stability of Minkowski spacetime [3] in general relativity. In fact, in [3], the authors use the solution ($\approx$ spacetime) itself to construct the outgoing and incoming light cones and they are defined as the level sets of two optical functions u and $\underline{u}$. In the current paper, we have constructed the functions $u_+$ and $u_-$ as analogues of optical functions and the left-traveling and right-traveling characteristic hypersurfaces $C^{\pm }_{u_\pm }$ play a similar role as light cones. In [3], the authors also use the solution to construct the multiplier vector fields, such as $\partial _t$ and Morawetz vector field K. We point out that in the situation of relativity the time function t is not a priori defined (since the spacetime is not defined yet and it is the solution that one is looking for) and one has to define it by knowing the solution. In our approach, the weight functions $\langle w_{\pm } \rangle$ or the multiplier vector fields $L_\pm$ are also defined by the solutions.

We would like to point out that, if one uses a more ‘linear’ approach, it may not work (even for the global existence part of the main theorems). This is in contrast to the proof of stability of Minkowski spacetime. Indeed, Lindblad and Rodnianski in [6] proved a weaker version of the stability of Minkowski spacetime based on the multiplier vector fields and light cones of the Minkowski spacetime (near infinity, the spacetime should be more like a Schwarzschild solution rather than a flat solution). The main reason is that free waves in three dimensions decay fast (of order $\frac{1}{t}$ while $z_\pm$ behave more like a 1-dimension waves which have no decay!) and the decoupling structure of Einstein equations in harmonic coordinates still allows one to use the null structure. In the current work, if we use the linear characteristic hypersufaces defined by $u^{(\text {linear})}_\pm =x_3\mp t$ and the corresponding $w^{(\text {linear})}_\pm$, when we derive the energy estimates, since $L_ \pm (u^{(\text {linear})}_\pm )\ne 0$, we obtain linear terms like

$$\begin{aligned} \int _0^t\int _{\Sigma _\tau } L_\pm \left( \log ^2 \left< w^{(\text {linear})}_\pm \right>\right) |z_\mp |^2dxd\tau . \end{aligned}$$

We can show that $L_\pm \left( \log ^2 \left< w^{(\text {linear})}_\pm \right>\right) \ge \frac{\varepsilon }{1+|x_3\mp t|}$ and the decay is too weak to close the energy estimates. We remark that using the characteristic hypersurfaces of a real solution one can avoid this linear term.

• The hybrid energy estimates

The most difficult part of the proof is to deal with the viscosity terms (small diffusion) since one seeks for estimates independent of the viscosity $\mu$. To make this clear, we first consider the ideal MHD system which is free of diffusion. As we mentioned before, we can use weight functions $(1+|u_\mp |^2)^\frac{1+\delta }{2}=\langle u_\mp \rangle ^{1+\delta }$ for $z_\pm$ and the derivatives of $z_\pm$. The uniform choice of the weights reflects the fact that the solution $z_\pm$ behaves in all the scale like waves. When viscosity presents, we may also attempt to use the same weight. In the course of deriving energy estimates, we use integration by parts for the viscous term and the derivative will hit the weights to generate linear terms such as

$$\begin{aligned} \mu \int _{0}^t\int _{\Sigma _\tau }\nabla ^2\big (\langle u_\mp \rangle ^{1+\delta }\big )|{z}_{\pm }|^2dxd\tau , \ \mu \int _{0}^t\int _{\Sigma _\tau }\nabla ^2\big (\langle u_\mp \rangle ^{1+\delta }\big )|\nabla {z}_{\pm }|^2dxd\tau ,\ \cdots . \end{aligned}$$

(1.26)

Since we do not have decay estimates for terms like $\int _{\Sigma _\tau }\nabla ^2\big (\langle u_\mp \rangle ^{1+\delta }\big )|{z}_{\pm }|^2 dx$, we can not use usual energy type estimates for wave equations to close the argument. This difficulty is indeed natural since the diffusion terms are not a wave phenomenon one does not expect to bound those terms by usual energy estimates (unless there is a new idea).

One possible approach is to lower the weight to $\langle u_\mp \rangle$ instead of $\langle u_\mp \rangle ^{1+\delta }$. We can show that $|\nabla \bigl (\langle u_\mp \rangle \bigr )| \lesssim 1$ and the second term $\mu \int _{0}^t\int _{\Sigma _\tau }\nabla ^2\bigl (\langle u_\mp \rangle \bigr )|\nabla {z}_{\pm }|^2dxd\tau$ in (1.26) can be bounded by $\mu \int _{0}^t\int _{\Sigma _\tau } |\nabla {z}_{\pm }|^2dxd\tau$. Hence, it is bounded by the basic energy estimates. It implies that $\mu \int _{0}^t\int _{\Sigma _\tau } |\nabla {z}_{\pm }|^2dxd\tau$ is bounded by the initial energy. However, the first term in (1.26) cannot be bounded in this way since there is no estimates at the moment to control terms like $\mu \int _{0}^t\int _{\Sigma _\tau } |{z}_{\pm }|^2dxd\tau$. We remark that, although this approach does not work, we can actually use this idea to show that the lifespan of the solution is at least $\min (\frac{1}{\mu }, e^{\frac{1}{\varepsilon }})$. Combined with the iteration method mentioned at the end of the last subsection, we can show that for $\mu \approx \varepsilon$, the solution is global. This is in fact much better than most of the small-global-existence results in three dimensional fluids whose smallness on energy is relative to the size of $\mu$.

The new idea in our approach is to use hybrid weights to combine the hyperbolic and parabolic estimates at the same time. In fact, by lowering the weights of $z_\pm$ to $\log$-level, the first term in (1.26) will be bounded by a term that looks like

$$\begin{aligned} \mu \int _{0}^t\int _{\Sigma _\tau }\frac{\big (\log \langle w_{\pm } \rangle \big )^4}{\langle w_{\pm } \rangle ^2}|z_\mp |^2dxd\tau . \end{aligned}$$

By Hardy inequalities with respect to a right coordinates system defined by the solutions, the above terms will be bounded by

$$\begin{aligned} \mu \int _0^t\int _{\Sigma _\tau }\big (\log \langle w_{\mp } \rangle \big )^4 |\nabla z_\pm |^2dxd\tau . \end{aligned}$$

This quantity will be bounded in (2.54) and we believe that this is a new estimate to deal with small diffusion terms. This new estimate plays a central role in the proof and makes use of the full strength of the basic energy identity for the viscous MHD system.

Finally, we emphasize again that the estimate on

$$\begin{aligned} \mu \int _{0}^t\int _{\Sigma _\tau }\frac{\big (\log \langle w_{\pm } \rangle \big )^4}{\langle w_{\pm } \rangle ^2}|z_\mp |^2dxd\tau \end{aligned}$$

will make an essential use of the basic energy identity. In some sense, the basic energy identity is cornerstone of the entire proof.

• Three dimensional feature of the problem

Although the viscous Alfvén waves $z_\pm$ behave very similar to $(1+1)$-dimension waves on a large time scale ($\approx \frac{1}{\mu }$), the analysis indeed relies heavily on the fact that the problem is over the three dimensional space. This is another indication why the viscous case is more difficult than the ideal case (where we can only use weights function in $u_\pm$ so that it is very similar to 1-dimension theory). A key step in the proof is to bound the weighted spacetime viscous energy $\mu \int _0^t\int _{\Sigma _\tau }\big (\log \langle w_{\mp } \rangle \big )^4 |\nabla z_\pm |^2dxd\tau$ by the initial energy. We use 3-dimensional Hardy’s inequality in the moving coordinate systems $(x_1^\pm ,x_2^\pm ,x_3^\pm )$ for $\Sigma _t$ to obtain desired estimates. It forces the weight functions involving the three dimensional radius functions $r^\pm =\sqrt{(x_1^\pm )^2 + (x_2^\pm )^2+(x_3^\pm )^2}$ (rather than $x_3^\pm = u_\pm$ as in the ideal case).

The physical picture is clear: the weight functions defined by $\langle w_{\pm } \rangle$ indicate that the Alfvén waves can be thought of as localized in all the directions in a small region of space with support moving along the characteristics.

• Linear-driving decay mechanism for Alfvén waves with very small viscosity

We would like to discuss the intuition for the decay (second statement) in Theorem 1.5. We treat the MHD system as $(1+1)$-dimensional wave equations and regard the small diffusion term more or less as an error term, therefore the estimates obtained do not provide any information on the decay, just like the usual $(1+1)$-dimensional waves. In order to explore the possible decay mechanism, the new idea is now to treat the system as heat equations (with small diffusion). In a schematic manner, we can simplify the system to the following model equation:

$$\begin{aligned} \partial _t f - \mu \triangle f = \underbrace{\cdots }_{\text {error terms}}. \end{aligned}$$

By the a priori energy estimates, we can show that the error terms are of order $\varepsilon ^2$ (say, according to $L^\infty$ norm). Therefore, by inverting the heat operator, we can think of f as

$$\begin{aligned} f(t)=e^{t\mu \triangle } f(0)+\underbrace{\cdots }_{\text {error terms of order }\varepsilon ^2}. \end{aligned}$$

We remark that the best estimate for the error terms at the moment is a bound of order $\varepsilon ^2$ and there is no decay so far for the errors.

We make the following key observation: the linear part $e^{t\mu \triangle } f(0)$ decays! Therefore, after a long time $T_1$, although initially $f(0) \sim \varepsilon$, the linear decay forces $f(T_1)$ to be of order $\varepsilon ^2$. We then use the a priori energy estimates again but set $T_1$ as the initial time for the system, this shows that after $T_1$, the solution is already of order $\varepsilon ^2$ so that we have

$$\begin{aligned} f(t)=e^{(t-T_1)\mu \triangle } f(T_1)+\underbrace{\cdots }_{\text {error terms of order } \varepsilon ^3}. \end{aligned}$$

It is clear how to repeat the above linear-driving decay mechanism to improve the order of $\varepsilon$ by 1 each time. This eventually pushes the solution into the $\mu$-small-data parabolic regime.

In reality, we explore the decay of $L^2$-norms of the semi-group $e^{t\mu \triangle }$. The reason is that we can only prove $L^2$-type estimates are propagated (via the hyperbolic method) and the iteration requires the estimates must be propagated in evolution. It is well-know that $\lim _{t\rightarrow \infty }\Vert e^{t\mu \triangle }f(0)\Vert _{L^2}=0$ without an explicit decay rate. Indeed, the decay behavior of $\Vert e^{t\mu \triangle }f(0)\Vert _{L^2}$ depends on the distribution of $\widehat{f}(\xi )$ around zero frequency. This is exactly the reason why the decay behavior in Theorem 1.5 depends not only on the energy norm but also on the profile of the initial data.

The rest of the paper consists of two sections. The next section is the technical heart of the paper and it proves the main a priori energy estimates (and Theorem 1.2). The last section proves Theorem 1.3, Theorem 1.4 and Theorem 1.5.

Main A Priori Estimates

Ansatz for the Method of Continuity

To use the method of continuity, we have three sets of assumptions concerning the underlying geometry and the energy of the waves.

The first set describes the geometry defined by the solution. Recall that, $(x_1^+, x_2^+, x_3^+(=u_+))$ are the $L_+$-transported functions which coincide with the Cartesian coordinates $(x_1,x_2,x_3)$ on $\Sigma _0$. For a given time $t\in [0,t^*]$, the restrictions of $(x_1^+,x_2^+,x_3^+)$ on $\Sigma _t$ yield a new coordinate system. We consider the change of coordinates $(x_1,x_2,x_3) \rightarrow (x_1^+,x_2^+,x_3^+)$ on $\Sigma _t$ and we use $\big ({\partial x_i^+} / {\partial x_j}\big )_{1\le i,j \le 3}$ to denote the corresponding Jacobian matrix. Similarly, we have another change of coordinates $(x_1,x_2,x_3) \rightarrow (x_1^-,x_2^-,x_3^-)$ on $\Sigma _t$ and the corresponding Jacobian matrix $\big ({\partial x_i^-} / {\partial x_j}\big )_{1\le i,j \le 3}$.

We make the following ansatz on the underlying geometry:

(2.1)

where ${{\mathrm{I}}}$ is the $3\times 3$ identity matrix and $C_0$ is a universal constant which will be determined towards the end of the proof.

The second ansatz is about the amplitude of ${z}_{\pm }$. We assume that

(2.2)

The third set of ansatz is designed for the energy and flux. We fix a positive integer $N_* \ge 5$. For all $k\le N_*$, we assume that

(2.3)

Here $C_1$ will be determined by the energy estimate.

We will use the standard continuity argument: since (2.1) and (2.3) hold for the initial data, they remain correct for a short time, say $[0,t_{\max }]$ where $t_{\max }$ is the maximal possible time so that the three sets of ansatz remain valid. Without loss of generality, we can assume $t_{\max }=t^*$. We need two steps to close the continuity argument:

Step 1 :

There exists a $\varepsilon _0$, for all $\varepsilon <\varepsilon _0$, we can improve the constant 2 in (2.3) to 1, i.e.,

$$\begin{aligned} E_{\pm } \le C_1 \varepsilon ^2,\ \ F_{\pm } \le C_1 \varepsilon ^2,\ \ \mu E^{N^*+1}_{\pm }+E^k_{\pm } \le C_1\varepsilon ^2,\ \ F^k_{\pm } \le C_1 \varepsilon ^2, \ \ k \le N_*. \end{aligned}$$

Step 2 :

There exists a $\varepsilon _0$, for all $\varepsilon <\varepsilon _0$, we can improve the constant $2C_0$ to $C_0$ in (2.1), i.e., we have

$$\begin{aligned} \big |\big (\frac{\partial x_i^\pm }{\partial x_j}\big )-{{\mathrm{I}}}\big |\le C_0 \varepsilon ,\ \big |\nabla \big (\frac{\partial x_i^\pm }{\partial x_j}\big )\big |\le C_0 \varepsilon , \ \ \text {for all } (t,x)\in [0,t^*]\times \mathbb {R}^3, \end{aligned}$$

Once we complete the above two steps, the method of continuity implies global solutions for the MHD system. We emphasize that the smallness of $\varepsilon _0$ in the above two steps does not depend on the size of viscosity $\mu$ and does not depend on the lifespan $[0,t^*]$. It indeed depends only on the background stationary magnetic field $B_0$.

Preliminary Estimates

In this subsection, we assume that the geometric ansatz (2.1) and the amplitude ansatz (2.2) hold.

Let $\psi _{\pm }(t,y)=(\psi ^1_{\pm }(t,y), \psi ^2_{\pm }(t,y), \psi ^3_{\pm }(t,y))$ (the mapping from $\Sigma _0$ to $\Sigma _t$) be the flow generated by $Z_{\pm }$, i.e.,

$$\begin{aligned} \frac{d}{dt}\psi _{\pm }(t,y)=Z_{\pm }(t,\psi _{\pm }(t,y)), \ \ \psi _{\pm }(0,y)=y, \end{aligned}$$

(2.4)

where $y\in \mathbb {R}^3$. Here and in what follows, if we use the flow map, we use y as the initial label(or the Lagrangian coordinates), and x as the present label (or the Eulerian coordinates). Since ${z}_{\pm }= {Z}_{\pm }\mp B_0$ (recall that $B_0=(0,0,1)$), after integration, we obtain

$$\begin{aligned} \psi _{\pm }(t,y)=y+\int _0^tZ_{\pm }(\tau ,\psi _{\pm }(\tau ,y))d\tau =y \pm t B_0+\int _0^tz_{\pm }(\tau ,\psi _{\pm }(\tau ,y))d\tau . \end{aligned}$$

(2.5)

We remark that the flows $\psi _{\pm }$ are the analogues of the Lagrangian coordinates in the ordinary fluid theory.

Let $\frac{\partial \psi _{\pm }(t,y)}{\partial y}$ be the differential of $\psi (t,y)$ at y. Thanks to the privileged Cartesian coordinates on $\mathbb {R}^3$, we regard $\frac{\partial \psi _{\pm }(t,y)}{\partial y}$ as a $3\times 3$ matrix. By definition, we know that $\psi _{\pm }(t,\cdot )^* x^\pm _i = x_i$, i.e., $x^\pm (t,\psi _\pm (t,y))=y$. Therefore, we indeed have

$$\begin{aligned} \frac{\partial x^\pm }{\partial x}|_{x=\psi _\pm (t,y)}= & {} \Bigl (\frac{\partial \psi _{\pm }(t,y)}{\partial y}\Bigr )^{-1}, \ \ \nabla _x\big (\frac{\partial x^\pm }{\partial x}\big )|_{x=\psi _\pm (t,y)} \\= & {} \nabla _y\bigr \{\Bigl (\frac{\partial \psi _{\pm }(t,y)}{\partial y}\Bigr )^{-1}\bigr \}\Bigl (\frac{\partial \psi _{\pm }(t,y)}{\partial y}\Bigr )^{-1}. \end{aligned}$$

Therefore, we can rephrase the geometric ansatz (2.1) as

(2.6)

This ansatz gives the following bounds on the weight functions:

Lemma 2.1

(Differentiate Weights) We have

$$\begin{aligned} |\nabla ^i \langle w_{\pm } \rangle | \le 2, \quad \text {for}\quad i=1,2. \end{aligned}$$

(2.7)

In particular, for all $\omega _1,\omega _2 \in \mathbb {R}$, we have for $i=1,2$

$$\begin{aligned} \begin{aligned}&\big |\nabla ^i \langle w_+\rangle ^{\omega _1} \big | \le C_{\omega _1}\langle w_+\rangle ^{\omega _1-1}, \ \ \big |\nabla ^i \langle w_{-} \rangle ^{\omega _2} \big |\le C_{\omega _2}\langle w_{-} \rangle ^{\omega _2-1},\ \ \big |\nabla ^i\big (\langle w_+\rangle ^{\omega _1}\langle w_{-} \rangle ^{\omega _2}\big )\big |\\&\quad \le C_{\omega _{1},\omega _2}\frac{\langle w_+\rangle ^{\omega _1}\langle w_{-} \rangle ^{\omega _2}}{R},\\&\quad \big |\nabla ^i \big (\log \langle w_{\pm } \rangle \big )^{\omega _1} \big | \le C_{\omega _1} \frac{\big (\log \langle w_{\pm } \rangle \big )^{\omega _1-1}}{\langle w_{\pm } \rangle }, \ \ \big |\nabla ^i \Big (\langle w_{\pm } \rangle ^{\omega _1}\big (\log \langle w_{\pm } \rangle \big )^{\omega _2}\Big ) \big |\\&\quad \le C_{\omega _{1},\omega _2}\langle w_{\pm } \rangle ^{\omega _1-1}\big (\log \langle w_{\pm } \rangle \big )^{\omega _2}. \end{aligned} \end{aligned}$$

Proof

It suffices to show (2.7) and the rest inequalities are immediate consequences of this inequality. It suffices to bound $\nabla ^i\langle w_+\rangle$ for $i=1,2$. The inequalities for $\langle w_{-} \rangle$ will be similar to derive.

In view of the the definition of $\langle w_+\rangle$ and the chain rule for differentiation, letting $k \in \{1,2,3\}$, we have

$$\begin{aligned} \partial _k \langle w_+\rangle = \frac{x_1^+\frac{\partial x_1^+}{\partial x_k} + x_2^+\frac{\partial x_2^+}{\partial x_k}+u_+\frac{\partial u_+}{\partial x_k} }{\big (R^2 + |x_1^+|^2+|x_2^+|^2+|u_+|^2\big )^\frac{1}{2}}. \end{aligned}$$

By the geometric ansatz (2.1), we have $\big |\frac{\partial x_l^+}{\partial x_k}\big | \le 2$ for all l (recall that $x_3^+ = u_+$). Then we obtain $|\nabla \langle w_+\rangle |\le 2$. Similarly, by the chain rule and the ansatz (2.1), we could obtain that $|\nabla ^2\langle w_+\rangle |\le 2$. Therefore, (2.7) is proved. This completes the proof of lemma. $\square$

As an application of this lemma, we claim the following weighted Sobolev inequalities hold:

Lemma 2.2

(Sobolev inequalities) For all $k \le N_*-2$ and multi-indices $\alpha$ with $|\alpha |=k$, we have

$$\begin{aligned} \begin{aligned} |z_{\mp }|&\lesssim \frac{1}{\big (\log \langle w_{\pm } \rangle \big )^2}\big (E_{\mp } + E^0_{\mp }+E^1_{\mp }\big )^\frac{1}{2},\\ |\nabla z_{\mp }^{(\alpha )}|&\lesssim \frac{1}{\langle w_{\pm } \rangle \big (\log \langle w_{\pm } \rangle \big )^2} \big (E_{\mp }^{k}+E_{\mp }^{k+1}+E_{\mp }^{k+2}\big )^\frac{1}{2}. \end{aligned} \end{aligned}$$

(2.8)

Proof

We only give the proof concerning the right-traveling Alfvén wave $z_-$. The estimates for $z_+$ can be derived in the same manner.

By the standard Sobolev inequality, we have

$$\begin{aligned} \big | \big (\log \langle w_+\rangle \big )^2 z_- \big |^2&\lesssim \Vert \big (\log \langle w_+\rangle \big )^2 z_- \Vert _{H^2(\mathbb {R}^3)}^2= \sum _{|\beta |\le 2}\big \Vert \partial ^\beta \Big (\big (\log \langle w_+\rangle \big )^2 z_-\Big )\big \Vert ^2_{L^2}. \end{aligned}$$

According to Lemma 2.1, we have

$$\begin{aligned} \Big |\partial ^\beta \Big (\big (\log \langle w_+\rangle \big )^2 z_-\Big )\Big |&\le \sum _{\gamma \le \beta }\Big |\nabla ^{\gamma } \big (\log \langle w_+\rangle \big )^2 z_-^{(\beta -\gamma )}\Big |\\&\lesssim \sum _{\gamma \le \beta }\Big | \big (\log \langle w_+\rangle \big )^2 z_-^{(\beta -\gamma )}\Big |. \end{aligned}$$

Hence,

$$\begin{aligned} \big | \big (\log \langle w_+\rangle \big )^2 z_- \big |^2&\lesssim \sum _{|\beta |\le 2}\big \Vert \big (\log \langle w_+\rangle \big )^2 z^{(\beta )}_-\big \Vert ^2_{L^2}\\&\lesssim E_{-} + E^0_{-}+E^1_{-}. \end{aligned}$$

This gives the $L^\infty$ bound on $z_-$.

For higher order derivatives, we have

$$\begin{aligned} \big | \langle w_+\rangle \big (\log \langle w_+\rangle \big )^2 \nabla z_-^{(\alpha )}\big |^2&\lesssim \sum _{|\beta |\le 2}\big \Vert \partial ^\beta \Big (\langle w_+\rangle \big (\log \langle w_+\rangle \big )^2 \nabla z_-^{(\alpha )}\Big )\big \Vert ^2_{L^2}\\&{\mathop {\lesssim }\limits ^{Lemma\, 2.1}}\sum _{k\le |\beta |\le k+2}\big \Vert \langle w_+\rangle \big (\log \langle w_+\rangle \big )^2 \nabla z_-^{(\beta )}\big \Vert ^2_{L^2}. \end{aligned}$$

The last line is obviously bounded by $E_{-}^{k}+E_{-}^{k+1}+E_{-}^{k+2}$. This completes the proof of the lemma. $\square$

We present the lemma about the separation property of the left- and right-traveling waves.

Lemma 2.3

Assume that $\Vert {z}_{\pm }\Vert _{L^\infty }\le \frac{1}{2}$, $R>10$, we have

$$\begin{aligned} t\le |u_+-u_-|\le 3t. \end{aligned}$$

(2.9)

Moreover, there hold

$$\begin{aligned} \begin{aligned}&\langle w_+\rangle \langle w_{-} \rangle \ge (R^2+|u_+|^2)^{\frac{1}{2}}(R^2+|u_-|^2)^{\frac{1}{2}}\ge \frac{R}{2}(R^2+t^2)^{\frac{1}{2}},\\&\quad \log \langle w_+\rangle \log \langle w_{-} \rangle \ge \log (R^2+|u_+|^2)^{\frac{1}{2}}\log (R^2+|u_-|^2)^{\frac{1}{2}}\ge \frac{\log R}{2}\log (R^2+t^2)^{\frac{1}{2}}. \end{aligned} \end{aligned}$$

(2.10)

Proof

By virtue of $\psi _\pm (t,y)$, we solve $u_\pm$ from $L_\pm u_\pm =0$ as follows

$$\begin{aligned} u_\pm (t,\psi _\pm (t,y))=y_3. \end{aligned}$$

Thanks to (2.5), we have

$$\begin{aligned} u_\pm (t,\psi _\pm (t,y))=\psi _{\pm }^3(t,y)\mp t-\int _0^tz_{\pm }^3(\tau ,\psi _{\pm }(\tau ,y))d\tau . \end{aligned}$$

Then

$$\begin{aligned} u_\pm (t,x)=x_3\mp t-\int _0^tz_{\pm }^3(\tau ,\psi _{\pm }(\tau ,\psi ^{-1}_{\pm }(t,x)))d\tau , \end{aligned}$$

which gives rise to

$$\begin{aligned} |(u_--u_+)-2t|\le \int _0^t(\Vert {z}_+^3\Vert _{L^\infty }+\Vert {z}_-^3\Vert _{L^\infty })dt\le t, \end{aligned}$$

where we used the assumption $\Vert {z}_{\pm }^3\Vert _{L^\infty }\le \frac{1}{2}$. This yields the estimate (2.9). And (2.9) gives rise to $|u_+|+|u_-|\ge t$ which shows that either $|u_+|\ge \frac{t}{2}$ or $|u_-|\ge \frac{t}{2}$. Then there holds (2.10). The lemma is proved. $\square$

Remark 2.4

The estimate (2.9) shows that if $\Vert {z}_{\pm }^3\Vert _{L^\infty }$ is small than the background magnetic field, the left-traveling hypersurface $C_{u_+}^+$ and the right-traveling hypersurface $C_{u_-}^-$ will separate from each other after the initial time. And at time t, the distance between them is of order O(t).

We now state a lemma to control the normal derivatives of the characteristic hypersurfaces in $[0,t^*]\times \mathbb {R}^3$:

Lemma 2.5

Assume that $\Vert {z}_{\pm }\Vert _{L^\infty }\le \frac{1}{2}$. Then for all $u_+$ and $u_-$, we have

$$\begin{aligned} \frac{7}{16}\le \langle L_-,\nu _+\rangle |_{C_{u_+}^+}\le 4, \ \ \frac{7}{16}\le \langle L_+,\nu _-\rangle |_{C_{u_-}^-}\le 4, \end{aligned}$$

(2.11)

where $\nu _{\pm }$ is the normal vector field of $C_{u_\pm }^\pm$.

Proof

We prove the first inequality and the second can be derived exactly in the same manner.

Since $L_-=(1,Z_-^1,Z_-^2,Z_-^3)$ and $\nu _+=-\frac{\widetilde{\nabla }_{t,x}u_+}{|\widetilde{\nabla }_{t,x}u_+|}=-\frac{(\partial _tu_+,\nabla u_+)}{\sqrt{|\partial _tu_+|^2+|\nabla u_+|^2}}$, we have

$$\begin{aligned} \langle L_-,\nu _+\rangle =\frac{1}{|\widetilde{\nabla }_{t,x}u_+|}\bigl (-\partial _tu_+-Z_-\cdot \nabla u_+\bigr ). \end{aligned}$$

(2.12)

Let $\varvec{e}_3 =(0,0,1)$. Since $\partial _tu_++Z_+\cdot \nabla u_+=0$, we have

$$\begin{aligned} \langle L_-,\nu _+\rangle&=\frac{1}{|\widetilde{\nabla }_{t,x}u_+|}(Z_+-Z_-)\cdot \nabla u_+\\&=\frac{1}{|\widetilde{\nabla }_{t,x}u_+|}\bigl (2\varvec{e}_3\cdot \nabla u_++(z_+-z_-)\cdot \nabla u_+\bigr ) \end{aligned}$$

and

$$\begin{aligned} |\widetilde{\nabla }_{t,x}u_+|&=\sqrt{|Z_+\cdot \nabla u_+|^2+|\nabla u_+|^2}\\&=\sqrt{|\partial _3 u_+|^2+|z_+\cdot \nabla u_+|^2+|\nabla u_+|^2+2\partial _3 u_+(z_+\cdot \nabla u_+)}. \end{aligned}$$

In view of (2.1), we obtain

$$\begin{aligned} |\nabla u_+-\varvec{e}_3|\le \sqrt{2C_0}\varepsilon . \end{aligned}$$

By virtue of (2.2) i.e., $\Vert {z}_{\pm }\Vert _{L^\infty }\le \frac{1}{2}$, we have

$$\begin{aligned} |z_\pm \cdot \nabla u_+|\le \frac{1}{2}+ \sqrt{2C_0}\varepsilon . \end{aligned}$$

It is straightforward to see that the numerator in (2.12) is in $[\frac{7}{8},\frac{25}{8}]$; the denominator in (2.12) is in $[\frac{7}{8},2]$, provided $\varepsilon$ is sufficiently small. This completes the proof. $\square$

We will also need a weighted version of div-curl lemma:

Lemma 2.6

(div-curl lemma) Let $\lambda (x)$ be a smooth positive function on $\mathbb {R}^3$. For all smooth vector field $\varvec{v}(x)\in H^1(\mathbb {R}^3)$ with the following properties

$$\begin{aligned} \text{ div }\,\varvec{v}=0,\ \ \ \sqrt{\lambda }\nabla \varvec{v}\in L^2(\mathbb {R}^3), \ \ \ \frac{|\nabla \lambda |}{\sqrt{\lambda }}\varvec{v}\in L^2(\mathbb {R}^3), \end{aligned}$$

we have

$$\begin{aligned} \Vert \sqrt{\lambda }\nabla \varvec{v}\Vert _{L^2}^2\lesssim \Vert \sqrt{\lambda }\text {curl}\,\varvec{v}\Vert _{L^2}^2+\big \Vert \frac{|\nabla \lambda |}{\sqrt{\lambda }}\varvec{v}\big \Vert _{L^2}^2. \end{aligned}$$

(2.13)

Proof

Since $\text{ div }\,\varvec{v}=0$, we have $-\Delta \varvec{v}=\text {curl}\,\text {curl}\,\,\varvec{v}$. We now multiply this identity by $\lambda \varvec{v}$ and then integrate over $\mathbb {R}^3$. We obtain

$$\begin{aligned} \int _{\mathbb {R}^3}\lambda |\nabla \varvec{v}|^2dx&=-\int _{\mathbb {R}^3}\sum _{i=1}^3\partial _i\lambda \partial _i\varvec{v}\cdot \varvec{v}dx+\int _{\mathbb {R}^3}\text {curl}\,\,\varvec{v}\cdot \text {curl}\,(\lambda \varvec{v})dx\\&\le \int _{\mathbb {R}^3}\lambda |\text {curl}\,\,\varvec{v}|^2dx+2\int _{\mathbb {R}^3}|\nabla \lambda ||\varvec{v}||\nabla \varvec{v}|dx\\&\le \int _{\mathbb {R}^3}\lambda |\text {curl}\,\,\varvec{v}|^2dx+2\int _{\mathbb {R}^3}\frac{|\nabla \lambda |^2}{\lambda }|\varvec{v}|^2dx+\frac{1}{2}\int _{\mathbb {R}^3}\lambda |\nabla \varvec{v}|^2dx. \end{aligned}$$

To complete the proof, it suffices to move the last term to the left hand side. $\square$

Remark 2.7

Because of $\text {div}\,z_\pm =0$, this lemma allows us to switch the term $\nabla z_{\pm }^{(\gamma )}$ in energy to the vorticity term $j_\pm ^{(\gamma )}$. This enables us to use the vorticity formulation (1.7) of the MHD system. And we will show that it is difficult for us to avoid investigating the vorticity formulation (1.7), especially for the highest order energy estimates.

Remark 2.8

In applications, we will take weight function $\lambda$ satisfying the following property:

$$\begin{aligned} |\nabla \lambda |\lesssim \lambda . \end{aligned}$$

(2.14)

Therefore, (2.13) becomes

$$\begin{aligned} \Vert \sqrt{\lambda }\nabla \varvec{v}\Vert _{L^2(\mathbb {R}^3)}^2 \lesssim \Vert \sqrt{\lambda }\text {curl}\,\varvec{v}\Vert _{L^2(\mathbb {R}^3)}^2+ \Vert \sqrt{\lambda }\varvec{v}\Vert _{L^2(\mathbb {R}^3)}^2. \end{aligned}$$

In particular, for $v=\nabla z_+^{(\gamma )}$ which is divergence free, we have

$$\begin{aligned} \big \Vert \sqrt{\lambda }\nabla z_+^{(\gamma )}\big \Vert _{L^2(\Sigma _\tau )}^2\lesssim \big \Vert \sqrt{\lambda }j_+^{(\gamma |)}\big \Vert _{L^2(\Sigma _\tau )}^2+\big \Vert \sqrt{\lambda }\nabla z_+^{(|\gamma |-1)}\big \Vert _{L^2(\Sigma _\tau )}^2. \end{aligned}$$

(2.15)

For $1\le |\gamma | \le N_*$, we can iterate (2.15) to derive

$$\begin{aligned} \big \Vert \sqrt{\lambda }\nabla z_+^{(\gamma )}\big \Vert _{L^2(\Sigma _\tau )}^2 \lesssim \big \Vert \sqrt{\lambda }\nabla z_+\big \Vert _{L^2(\Sigma _\tau )}^2+\sum _{k=1}^{|\gamma |} \big \Vert \sqrt{\lambda }j_+^{( k)}\big \Vert _{L^2(\Sigma _\tau )}^2. \end{aligned}$$

(2.16)

We remark that in (2.16), we do not iterate $\Vert \sqrt{\lambda }\nabla z_+\Vert _{L^2(\Sigma _\tau )}^2$ by $\Vert \sqrt{\lambda }j_+\Vert _{L^2(\Sigma _\tau )}^2+\Vert \frac{|\nabla \lambda |}{\sqrt{\lambda }} z_+\Vert _{L^2(\Sigma _\tau )}^2$. We will see that it is difficult to control $\Vert \frac{|\nabla \lambda |}{\sqrt{\lambda }} z_+\Vert _{L^2(\Sigma _\tau )}^2$ by taking $\lambda =\lambda (u_+,u_-)$.

The geometric ansatz (2.1) also provides a trace theorem for restrictions of functions to the characteristic hypersurfaces $C_{u_\pm }^\pm$:

Lemma 2.9

(Trace) For all $f(t,x)\in L^2([0,t^*];H^1(\mathbb {R}^3))$, the restriction of f to $C_{u_\pm }^\pm$ belongs to $L^2(C_{u_\pm }^\pm )$. In fact, we have

$$\begin{aligned} \Vert f\Vert _{L^2(C_{u_\pm }^\pm )}\lesssim \Vert f\Vert _{L^2([0,t^*];H^1(\mathbb {R}^3))}. \end{aligned}$$

Proof

Let $a_+$ be a fixed real number and we will prove the trace estimates for $C^+_{a_+}$. By definition, we have $S_{t,u_+}^+ =\partial \,\Sigma _t^{[u_+,+\infty )}$ and $C_{u_+}^+=\bigcup _{0\le \tau \le t^*}S_{\tau ,u_+}^+$. On each $\Sigma _t$, we will write $S_{t,a_+}^+$ as a graph over $(x_1,x_2)$ plane. We emphasize that $(x_1,x_2,x_3)$ is the standard Cartesian coordinates system on $\Sigma _t$.

We claim that $S_{t,a_+}^+ \subset \Sigma _t$ is the following graph

$$\begin{aligned} S_{t,a_+}^+=\{(x_1,x_2,x_3)\,|\,x_3=\eta _+(t,x_h),\ x_h=(x_1,x_2)\} \end{aligned}$$

(2.17)

where $\eta _+$ is defined by $\partial _t\eta _++z_+^h\cdot \nabla _{x_h}\eta _+=1+z_+^3$ with $\eta _+|_{t=0}=a_+$ and $z_+^h=(z_+^1,z_+^2)$. In fact, the equation for $\eta _+$ is equivalent to $\partial _t(x_3-\eta _+)+Z_+\cdot \nabla (x_3-\eta _+)=0$. Therefore, it is easy to see that $u_+(t,x)=x_3-\eta _+(t,x_h)+a_+$ and

$$\begin{aligned} C_{a_+}^+=\{(t,x)\,|\,x_3=\eta _+(t,x_h),\,\,\text {with}\,\,\eta _+(0,x_h)=a_+\}. \end{aligned}$$

To prove the lemma, we will first of all control the hypersurface measure on $C_{a_+}^+$:

$$\begin{aligned} d\sigma _+&=\sqrt{1+|\nabla _{t,x_h}\eta _+|^2}dx_1dx_2dt =\sqrt{1+|\nabla _{t,x_h}u_+|^2}dx_1dx_2dt. \end{aligned}$$

Since $\partial _tu_+ + Z_+\cdot \nabla u_+=0$, we have

$$\begin{aligned} d\sigma _+=\sqrt{1+|Z_+\cdot \nabla u_+|^2+|\nabla _{x_h}u_+|^2}dx_1dx_2dt. \end{aligned}$$

(2.18)

By (2.2), for sufficiently small $\varepsilon$, we have $|z_+| \le C\varepsilon$. By (2.1), we have $|\nabla u_+-\varvec{e}_3| \le C\varepsilon$. Therefore, we obtain that

$$\begin{aligned} \sqrt{2}-C\varepsilon \le \sqrt{1+|Z_+\cdot \nabla u_+|^2+|\nabla _{x_h}u_+|^2}\le \sqrt{2}+C\varepsilon . \end{aligned}$$

As a consequence, we have

$$\begin{aligned} \int _{C_{u_+}^+}|f|^2 d\sigma _+ \le 4 \int _0^t\int _{\mathbb {R}^2}\Big (f(\tau ,x)\big |_{x_3=\eta _+(\tau ,x_h)}\Big )^2dx_1dx_2d\tau . \end{aligned}$$

(2.19)

We consider a change of coordinates on $\Sigma _t$:

$$\begin{aligned} (x_1,x_2,x_3)\rightarrow (\tilde{x}_1,\tilde{x}_2,\tilde{x}_3) \end{aligned}$$

where the new coordinate $\tilde{x}_1 =x_1$, $\tilde{x}_2 = x_2$ and $\tilde{x}_3=x_3-\eta _+(t,x_h)$. We define

$$\begin{aligned} \tilde{f}(t,\tilde{x})= f(t,\tilde{x}_1,\tilde{x}_2,\tilde{x}_3+\eta _+(t,\tilde{x}_1,\tilde{x}_2)). \end{aligned}$$

Hence,

$$\begin{aligned} f(t,x)|_{x_3=\eta _+(t,x_h)}=\tilde{f}(t,\tilde{x}_h,\tilde{x}_3)|_{\tilde{x}_3=0}. \end{aligned}$$

By the standard trace theorem, we have

$$\begin{aligned} \Vert \tilde{f}(t,\tilde{x}_h,0)\Vert _{L^2(\mathbb {R}^2)} \lesssim \Vert \tilde{f}(t,\tilde{x})\Vert _{H^1(\mathbb {R}^3)}. \end{aligned}$$

In view of (2.19), we have

$$\begin{aligned} \int _{C_{u_+}^+}|f|^2 d\sigma _+\lesssim \int _0^t\big (\Vert \tilde{f}(\tau ,\tilde{x})\Vert _{L^2(\mathbb {R}^3)}^2+\Vert \nabla _{\tilde{x}}\tilde{f}(\tau ,\tilde{x})\Vert _{L^2(\mathbb {R}^3)}^2\big )d\tau . \end{aligned}$$

(2.20)

We now change the $(\tilde{x}_1,\tilde{x}_2,\tilde{x}_3)$ coordinates back to $(x_1,x_2,x_3)$. Since $\frac{\partial \tilde{x}(x)}{\partial x}=\begin{pmatrix}1&{}0&{}0\\ 0&{}1&{}0\\ -\partial _1\eta _+&{}-\partial _2\eta _+&{}1\end{pmatrix}$, the inverse Jacobian matrix reads as $\bigl (\frac{\partial \tilde{x}(x)}{\partial x}\bigr )^{-1}=\begin{pmatrix}1&{}0&{}0\\ 0&{}1&{}0\\ \partial _1\eta _+&{}\partial _2\eta _+&{}1\end{pmatrix}.$ As a result, we have $\det \bigl (\frac{\partial \tilde{x}(x)}{\partial x}\bigr )=1$. We also remark that $\nabla _{\tilde{x}}=\bigl (\frac{\partial \tilde{x}(x)}{\partial x}\bigr )^{-T}\nabla _x$.

Because $\det \bigl (\frac{\partial \tilde{x}(x)}{\partial x}\bigr )=1$, we have

$$\begin{aligned} \Vert \tilde{f}(\tau ,\tilde{x})\Vert _{L^2(\mathbb {R}^3)}^2=\Vert f(\tau ,x)\Vert _{L^2(\mathbb {R}^3)}^2. \end{aligned}$$

Furthermore, we have

$$\begin{aligned} \Vert \nabla _{\tilde{x}}\tilde{f}(\tau ,\tilde{x})\Vert _{L^2(\mathbb {R}^3)}^2&=\big \Vert \bigl (\frac{\partial \tilde{x}(x)}{\partial x}\bigr )^{-T}\nabla _xf(\tau ,x)\big \Vert _{L^2(\mathbb {R}^3)}^2 \\&\le \Vert \nabla _xf(\tau ,x)\Vert _{L^2(\mathbb {R}^3)}^2+\big \Vert \bigl (\bigl (\frac{\partial \tilde{x}(x)}{\partial x}\bigr )^{-T}-{{\mathrm{I}}}\bigr )\nabla _xf(\tau ,x)\big \Vert _{L^2(\mathbb {R}^3)}^2\\&\le \big (1+\Vert \nabla _h\eta _+\Vert _{L^\infty (\mathbb {R}^2)}^2\big )\Vert \nabla _xf(\tau ,x)\Vert _{L^2(\mathbb {R}^3)}^2\\&=\big (1+\Vert \nabla _hu_+\Vert _{L^\infty (\mathbb {R}^2)}^2\big )\Vert \nabla _xf(\tau ,x)\Vert _{L^2(\mathbb {R}^3)}^2. \end{aligned}$$

By (2.1), we have

$$\begin{aligned} \Vert \nabla _{\tilde{x}}\tilde{f}(\tau ,\tilde{x})\Vert _{L^2(\mathbb {R}^3)}^2\lesssim \Vert \nabla _xf(\tau ,x)\Vert _{L^2(\mathbb {R}^3)}^2. \end{aligned}$$

Combining all the estimates with (2.20), this completes the proof of lemma. $\square$

Energy Estimates for Linear Equations

We start by deriving energy identities for the following linear system of equations:

$$\begin{aligned} \begin{aligned} \partial _t {f}_++{Z}_-\cdot \nabla {f}_+&= {\rho }_+, \\ \partial _t {f}_-+{Z}_+\cdot \nabla {f}_-&= {\rho }_-. \end{aligned} \end{aligned}$$

(2.21)

We emphasize that ${Z}_+$ and ${Z}_-$ are divergence-free vector fields.

We consider two weight functions ${\lambda }_+$ and ${\lambda }_-$ defined on $[0,t^*]\times \mathbb {R}^3$. They will be determined later on in the paper. We require that

$$\begin{aligned} {L}_+{\lambda }_-=0, \ \ {L}_-{\lambda }_+=0. \end{aligned}$$

We start with the estimates on ${f}_-$ which corresponds to the right-traveling Alfvén waves. By multiplying (or taking inner product with) ${\lambda }_-{f}_-$ to the second equation in (2.21), we have

$$\begin{aligned} \frac{1}{2}{\lambda }_-\partial _t \big ( |{f}_-|^2\big ) +\frac{1}{2}{\lambda }_-({Z}_+\cdot \nabla ) \big (|{f}_-|^2\big ) = {\lambda }_-{f}_-\cdot {\rho }_-. \end{aligned}$$

(2.22)

By the definition of ${L}_+$, the left hand side can be rewritten as $\frac{1}{2}{\lambda }_-{L}_+\big (|{f}_-|^2\big )$. In view of the fact that ${L}_+{\lambda }_-=0$, it again can be reformulated as $\frac{1}{2}{L}_+\big ( {\lambda }_-|{f}_-|^2\big )$.

We use $\widetilde{\text {div}\,}$ to denote the divergence of $\mathbb {R}^4$ with respect to the standard Euclidean metric. Since $\text {div}\,{Z}_+=0$, therefore, $\widetilde{\text {div}\,}{L}_+=0$. We integrate equation (2.22) on $W_{t}^{[u_+^1,u_+^2]}$. According to the Stokes formula, the left hand side of the resulting equation yields

$$\begin{aligned} \begin{aligned}&\frac{1}{2}{\int \!\!\!\!\int }_{W_{t}^{\big [u_+^1,u_+^2\big ]}} {L}_+\big ( {\lambda }_-|{f}_-|^2\big ) dxd\tau \\&\quad =\frac{1}{2}{\int \!\!\!\!\int }_{W_{t}^{\big [u_+^1,u_+^2\big ]}} \widetilde{\text {div}\,} \big ({\lambda }_-|{f}_-|^2 {L}_+\big ) dxd\tau -\underbrace{\frac{1}{2}{\int \!\!\!\!\int }_{W_{t}^{[u_+^1,u_+^2]}} {\lambda }_-|{f}_-|^2 \widetilde{\text {div}\,} {L}_+dxd\tau }_{\widetilde{\text {div}\,}{L}_+=0 \ \Rightarrow \ \text {This term is } 0.}\\&\quad \overset{\text {Stokes}}{=} \frac{1}{2}\int _{\Sigma _{t}^{\big [u_+^1,u_+^2\big ]}}{\lambda }_-|{f}_-|^2 \langle {L}_+, T \rangle dx -\frac{1}{2}\int _{\Sigma _{0}^{\big [u_+^1,u_+^2\big ]}}{\lambda }_-|{f}_-|^2 \langle {L}_+, T \rangle dx\\&\quad \qquad +\frac{1}{2}\sum _{k=1,2}\int _{{C}^+_{u_+^k}}{\lambda }_-|{f}_-|^2 \underbrace{\langle {L}_+,\nu ^+_k \rangle }_{\ \ \ \ \ \ {L}_+\ \text {is tangential to}\ {C}^+_{u_+^k} \Rightarrow \text {This term is} \ 0}d\sigma _+. \end{aligned} \end{aligned}$$

(2.23)

Finally, we obtain by using $\langle {L}_+, T \rangle =1$ that

$$\begin{aligned} { \int _{\Sigma _{t}^{\big [u_+^1,u_+^2\big ]}}{\lambda }_-|{f}_-|^2 dx= \int _{\Sigma _{0}^{\big [u_+^1,u_+^2\big ]}}{\lambda }_-|{f}_-|^2dx + 2\int _{0}^t \int _{\Sigma _\tau ^{\big [u_+^1,u_+^2\big ]}} {\lambda }_-{f}_-\cdot {\rho }_-\ dx d\tau . } \end{aligned}$$

(2.24)

We now derive the estimates for ${f}_+$ in $W_t^{[u_+^1,u_+^2]}$. In view of the facts that ${L}_-= T + {Z}_-$ and ${L}_-{\lambda }_+=0$, by taking inner product with ${\lambda }_+{f}_+$ for the first equation in (2.21), we obtain

$$\begin{aligned} \frac{1}{2} {L}_-\big ( {\lambda }_+|{f}_+|^2\big )= {\lambda }_+{f}_+\cdot {\rho }_+. \end{aligned}$$

(2.25)

We integrate equation (2.25) on $W_{t}^{[u_+^1,u_+^2]}$. Similar to the previous calculation, by virtue of Stokes formula and the fact that $\text {div}\,{Z}_-=0$, the left hand side of (2.25) gives

$$\begin{aligned}&\ \frac{1}{2}{\int \!\!\!\!\int }_{W_{t}^{\big [u_+^1,u_+^2\big ]}} {L}_-\big ( {\lambda }_+|{f}_+|^2\big ) dxd\tau \\&\quad =\frac{1}{2}{\int \!\!\!\!\int }_{W_{t}^{\big [u_+^1,u_+^2\big ]}} \widetilde{\text {div}\,} \big ({\lambda }_+|{f}_+|^2 {L}_-\big ) dxd\tau -\underbrace{\frac{1}{2}{\int \!\!\!\!\int }_{W_{t}^{\big [u_+^1,u_+^2\big ]}} {\lambda }_+|{f}_+|^2 \widetilde{\text {div}\,} {L}_-\ dxd\tau }_{\widetilde{\text {div}\,}{L}_-=0 \ \Rightarrow \ \text {This term is } 0.}\\&\quad \overset{\text {Stokes}}{=} \frac{1}{2}\int _{\Sigma _{t}^{\big [u_+^1,u_+^2\big ]}}{\lambda }_+|{f}_+|^2 dx-\frac{1}{2}\int _{\Sigma _{0}^{\big [u_+^1,u_+^2\big ]}}{\lambda }_+|{f}_+|^2 dx\\&\qquad +\frac{1}{2}\sum _{k=1,2}\int _{{C}^+_{u_+^k}}{\lambda }_+|{f}_+|^2 \langle {L}_-,\nu ^+_k \rangle d\sigma _+. \end{aligned}$$

Finally, we obtain

$$\begin{aligned} {\begin{aligned}&\int _{\Sigma _{t}^{\big [u_+^1,u_+^2\big ]}}{\lambda }_+|{f}_+|^2dx + \int _{{C}^+_{u_+^1}}{\lambda }_+|{f}_+|^2 \langle {L}_-,\nu ^+_1 \rangle d\sigma _+\\&\quad = \int _{\Sigma _{0}^{\big [u_+^1,u_+^2\big ]}}{\lambda }_+|{f}_+|^2dx + \int _{{C}^+_{u_+^2}}{\lambda }_+|{f}_+|^2 \langle {L}_-,-\nu ^+_2 \rangle d\sigma _+\\&\quad \quad + 2\int _{0}^t \int _{\Sigma _\tau ^{\big [u_+^1,u_+^2\big ]}} {\lambda }_+{f}_+\cdot {\rho }_+\ dx d\tau . \end{aligned}} \end{aligned}$$

(2.26)

Similarly, on $W_{t}^{[u_{-}^1,u_{-}^2]}$, we have

$$\begin{aligned} { \int _{\Sigma _{t}^{\big [u_{-}^1,u_{-}^2\big ]}}{\lambda }_+|{f}_+|^2dx= \int _{\Sigma _{0}^{\big [u_{-}^1,u_{-}^2\big ]}}{\lambda }_+|{f}_+|^2dx + 2\int _{0}^t \int _{\Sigma _\tau ^{\big [u_{-}^1,u_{-}^2\big ]}} {\lambda }_+{f}_+\cdot {\rho }_+\ dx d\tau . } \end{aligned}$$

(2.27)

and

$$\begin{aligned} \begin{aligned}&\int _{\Sigma _{t}^{\big [u_{-}^1,u_{-}^2\big ]}}{\lambda }_-|{f}_-|^2dx + \int _{{C}^-_{u_{-}^2}}{\lambda }_-|{f}_-|^2 \langle {L}_+,\nu ^{-}_2 \rangle d\sigma _-\\&\quad = \int _{\Sigma _{0}^{\big [u_{-}^1,u_{-}^2\big ]}}{\lambda }_-|{f}_-|^2dx + \int _{{C}^-_{u_{-}^1}}{\lambda }_-|{f}_-|^2 \langle {L}_+,-\nu ^{-}_1 \rangle d\sigma _-\\&\quad \quad + 2\int _{0}^t \int _{\Sigma _\tau ^{\big [u_{-}^1,u_{-}^2\big ]}} {\lambda }_-{f}_-\cdot {\rho }_-\ dx d\tau . \end{aligned} \end{aligned}$$

(2.28)

Under the bootstrap ansatz (2.1) and (2.2), we study the energy estimates for the following viscous linear system:

$$\begin{aligned} \begin{aligned} \partial _tf_++Z_-\cdot \nabla f_+-\mu \Delta f_+&=\rho _+,\\ \partial _tf_-+Z_+\cdot \nabla f_--\mu \Delta f_-&=\rho _-, \end{aligned} \end{aligned}$$

(2.29)

where $Z_+$ and $Z_-$ are divergence free.

Proposition 2.1

For all weight functions $\lambda _{\pm }$ with the properties $L_{\pm }\lambda _{\mp }=0$, we have

$$\begin{aligned}&\sup _{0\le \tau \le t}\int _{\Sigma _\tau }\lambda _\pm |f_\pm |^2dx + \frac{1}{2}\sup _{u_\pm }\int _{C_{u_\pm }^\pm }\lambda _\pm |f_\pm |^2d\sigma _\pm +\mu \int _0^t\int _{\Sigma _\tau }\lambda _\pm |\nabla f_\pm |^2dxd\tau \nonumber \\&\quad \le 2\int _{\Sigma _0}\lambda _\pm |f_\pm |^2dx + 4\int _0^t\int _{\Sigma _\tau }\lambda _\pm |f_\pm ||\rho _\pm |dxd\tau +{\mu }\int _0^t\int _{\Sigma _\tau }\frac{|\nabla \lambda _\pm |^2}{\lambda _\pm }|f_\pm |^2dxd\tau \nonumber \\&\quad \quad +\,2\mu ^2\sup _{u_\pm }\int _{C_{u_\pm }^\pm }\lambda _\pm |\nabla f_\pm |^2d\sigma _\pm . \end{aligned}$$

(2.30)

We remark that except for the coefficients of the first terms in the first and second line of (2.30), the exactly numerical constants are irrelevant to the rest of the proof.

Proof

We only give the estimates for $f_+$. The estimates on $f_-$ can be derived in the same manner.

By setting $u_-^1=-\infty$ and $u_-^2=\infty$ in (2.27), we have

$$\begin{aligned}&\frac{1}{2}\int _{\Sigma _t}\lambda _+|f_+|^2dx\underbrace{-\mu \int _0^t\int _{\Sigma _\tau }\Delta f_+\cdot \lambda _+f_+dxd\tau }_{\text {the viscosity term}}\\&\quad =\frac{1}{2}\int _{\Sigma _0}\lambda _+|f_+|^2dx + \int _0^t\int _{\Sigma _\tau }\lambda _+f_+\cdot \rho _+dxd\tau . \end{aligned}$$

Integrating by parts, we can deal with the viscosity term as follows:

$$\begin{aligned} \text {Viscosity term}=\,&\mu \int _0^t\int _{\Sigma _\tau }\lambda _+ |\nabla f_+|^2dxd\tau +\underbrace{\mu \int _0^t\int _{\Sigma _\tau }\partial _i\lambda _+ f_+\cdot \partial _i f_+dxd\tau }_{\text {Cauchy-Schwarz}}\\ \ge&\, \mu \int _0^t\int _{\Sigma _\tau }\lambda _+ |\nabla f_+|^2dxd\tau -\big (\frac{1}{2}\mu \int _0^t\int _{\Sigma _\tau }\lambda _+ |\nabla f_+|^2dxd\tau \\&+\,\frac{1}{2}\mu \int _0^t\int _{\Sigma _\tau } \frac{|\nabla \lambda _+|^2}{\lambda _+} |f_+|^2dxd\tau \big )\\ =&\,\frac{1}{2} \mu \int _0^t\int _{\Sigma _\tau }\lambda _+ |\nabla f_+|^2dxd\tau -\frac{1}{2}\mu \int _0^t\int _{\Sigma _\tau } \frac{|\nabla \lambda _+|^2}{\lambda _+} |f_+|^2dxd\tau . \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} \begin{aligned}&\int _{\Sigma _t}\lambda _+|f_+|^2dx+\mu \int _0^t\int _{\Sigma _\tau }\lambda _+|\nabla f_+|^2dxd\tau \\&\quad \le \int _{\Sigma _0}\lambda _+|f_+|^2dx+2\int _0^t\int _{\Sigma _\tau }\lambda _+f_+\cdot \rho _+ dxd\tau +\mu \int _0^t\int _{\Sigma _\tau }\frac{|\nabla \lambda _+|^2}{\lambda _+}|f_+|^2dxd\tau . \end{aligned} \end{aligned}$$

(2.31)

By setting $u_+^1=u_+$ and $u_+^2=\infty$ in (2.28), we have

$$\begin{aligned}&\int _{\Sigma _t^{[u_+,+\infty )}}\lambda _+|f_+|^2dx +\underbrace{\int _{C_{u_+}^+}\lambda _+|f_+|^2\langle L_-,\nu _+\rangle d\sigma _+}_{II} \underbrace{-2\mu {\int \!\!\!\!\int }_{W_t^{[u_+,+\infty )}}\Delta f_+\cdot \lambda _+f_+dxd\tau }_{I} \nonumber \\&\quad = \int _{\Sigma _0^{[u_+,+\infty )}}\lambda _+|f_+|^2dx+2{\int \!\!\!\!\int }_{W_t^{[u_+,+\infty )}}\lambda _+f_+\cdot \rho _+dxd\tau , \end{aligned}$$

(2.32)

where $L_-=(1,Z_-^1,Z_-^2,Z_-^3)$ and $\nu _+=-\frac{(\partial _tu_+,\nabla u_+)}{\sqrt{|\partial _tu_+|^2+|\nabla u_+|^2}}$. After an integration by parts, the viscosity term I can be written as

$$\begin{aligned} I= & {} \underbrace{2\mu {\int \!\!\!\!\int }_{W_t^{\ge u_+}}\lambda _+ |\nabla f_+|^2dxd\tau }_{I_1}\\&+ \underbrace{2\mu {\int \!\!\!\!\int }_{W_t^{\ge u_+}}\partial _i\lambda _+ f_+\cdot \partial _i f_+dxd\tau }_{I_2}\underbrace{-2\mu \int _{C_{u_+}^+}\lambda _+ f_+\cdot \sum _{i=1}^3\nu _+^i\partial _i f_+d\sigma _+}_{I_3}, \end{aligned}$$

where $\nu _+=(\nu _+^0,\nu _+^1,\nu _+^2,\nu _+^3)$.

We can bound $I_2$ and $I_3$ by Cauchy-Schwarz inequality:

$$\begin{aligned} \begin{aligned} |I_2|&\le \mu {\int \!\!\!\!\int }_{W_t^{[u_+,+\infty )}}\lambda _+|\nabla f_+|^2dxd\tau +\mu {\int \!\!\!\!\int }_{W_t^{[u_+,+\infty )}} \frac{|\nabla \lambda _+|^2}{\lambda _+}|f_+|^2dxd\tau ,\\ |I_3|&\le \frac{1}{2}\int _{C_{u_+}^+}\lambda _+|f_+|^2d\sigma _+ +2\mu ^2\int _{C_{u_+}^+}\lambda _+|\nabla f_+|^2d\sigma _+. \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} I&\ge \mu {\int \!\!\!\!\int }_{W_t^{[u_+,\infty )}}\lambda _+|\nabla f_+|^2dxd\tau - \frac{1}{2}\int _{C_{u_+}^+}\lambda _+|f_+|^2d\sigma _+ \\&\quad -\mu {\int \!\!\!\!\int }_{W_t^{[u_+,\infty )}}\frac{|\nabla \lambda _+|^2}{\lambda _+}|f_+|^2dxd\tau -2\mu ^2\int _{C_{u_+}^+}\lambda _+|\nabla f_+|^2d\sigma _+. \end{aligned} \end{aligned}$$

(2.33)

To bound the term II in (2.32), we use Lemma 2.5. Indeed, since $\langle L_-,\nu _+\rangle \sim 1$, we have

$$\begin{aligned} II=\int _{C_{u_+}^+}\lambda _+|f_+|^2\langle L_-,\nu _+\rangle d\sigma _+ \sim \int _{C_{u_+}^+}\lambda _+|f_+|^2d\sigma _+, \end{aligned}$$

Together with (2.31), (2.32) and (2.33), this completes the proof of the proposition. $\square$

A byproduct of the proof is the energy inequality (2.31). Since it will be used many times to control the viscosity terms, we restate the estimates in the following lemma:

Corollary 2.10

For all weight functions $\lambda _{\pm }$ with the properties $L_{\pm }\lambda _{\mp }=0$, we have

$$\begin{aligned} \begin{aligned}&\int _{\Sigma _t}\lambda _\pm |f_\pm |^2dx+\mu \int _0^t\int _{\Sigma _\tau }\lambda _\pm |\nabla f_\pm |^2dxd\tau \\&\quad \le \int _{\Sigma _0}\lambda _\pm |f_\pm |^2dx +2\int _0^t\int _{\Sigma _\tau }\lambda _\pm f_\pm \cdot \rho _\pm dxd\tau +\mu \int _0^t\int _{\Sigma _\tau }\frac{|\nabla \lambda _\pm |^2}{\lambda _\pm }|f_\pm |^2dxd\tau . \end{aligned} \end{aligned}$$

(2.34)

By the trace estimates in Lemma 2.9, we can indeed remove the last flux term in (2.30):

Corollary 2.11

We make an extra assumption that $\mu<<1$. For all weight functions $\lambda _{\pm }$ with the properties $L_{\pm }\lambda _{\mp }=0$, $|\nabla \lambda _{\pm }| \le |\lambda _{\pm }|$ and $|\nabla ^2\lambda _{\pm }|\le |\lambda _{\pm }|$, we have

$$\begin{aligned} \begin{aligned}&\sup _{0\le \tau \le t}\int _{\Sigma _\tau }\lambda _\pm |f_\pm |^2dx + \frac{1}{2}\sup _{u_\pm }\int _{C_{u_\pm }^\pm }\lambda _\pm |f_\pm |^2d\sigma _\pm +\frac{1}{2}\mu \int _0^t\int _{\Sigma _\tau }\lambda _\pm |\nabla f_\pm |^2dxd\tau \\&\quad \le 2\int _{\Sigma _0}\lambda _\pm |f_\pm |^2dx + 4\int _0^t\int _{\Sigma _\tau }\lambda _\pm |f_\pm ||\rho _\pm | dxd\tau \\&\quad +2{\mu }\int _0^t\int _{\Sigma _\tau }\frac{|\nabla \lambda _\pm |^2}{\lambda _\pm }|f_\pm |^2dxd\tau +2{\mu ^2}\int _0^t\int _{\Sigma _\tau }\lambda _\pm |\nabla ^2 f_\pm |^2dxd\tau . \end{aligned} \end{aligned}$$

(2.35)

Proof

According to Lemma 2.9, we have

$$\begin{aligned}&\mu ^2\int _{C_{u_+}^+}\lambda _+|\nabla f_+|^2d\sigma _+ \lesssim \mu ^2\int _0^t\Vert \sqrt{\lambda _+}\nabla f_+\Vert _{H^1(\Sigma _\tau )}^2d\tau \\&\qquad = \underbrace{\mu ^2\int _0^t\int _{\Sigma _\tau }\lambda _+ |\nabla f_+|^2dxd\tau }_{I} +\mu ^2\int _0^t \underbrace{\Vert \nabla \bigl (\sqrt{\lambda _+}\nabla f_+\bigr )\Vert _{L^2(\Sigma _\tau )}^2}_{II}d\tau . \end{aligned}$$

We can ignore the term I. The reason is as follows: Since $\mu<<1$, the term I will be absorbed by the viscosity term on the left hand side of (2.30).

We bound the term II as follows:

$$\begin{aligned} II&\le \Vert \sqrt{\lambda _+}\nabla ^2 f_+\Vert _{L^2(\Sigma _\tau )}^2 +\underbrace{\Vert (\nabla \sqrt{\lambda _+})\nabla f_+\Vert _{L^2(\Sigma _\tau )}^2}_{II_1}. \end{aligned}$$

We can ignore the term $II_1$. The reason is as follows: since $|\nabla \sqrt{\lambda _+}|^2=\frac{|\nabla {\lambda }_+|^2}{{\lambda }_+}$ and $\mu<<1$, the contribution of the $II_1$ term can be absorbed by the viscosity term on the left hand side of (2.30).

Then, the corollary follows immediately from the above analysis. $\square$

Energy Estimates on the Lowest Order Terms

In this section, we will apply Proposition 2.1 to the system

$$\begin{aligned} \begin{aligned} \partial _t {z}_++{Z}_-\cdot \nabla {z}_+- {\mu \triangle {z}_+}&= -\nabla p, \\ \partial _t {z}_-+{Z}_+\cdot \nabla {z}_-- {\mu \triangle {z}_-}&= -\nabla p. \end{aligned} \end{aligned}$$

(2.36)

The weight functions $\lambda _\pm$ will be chosen as $\big (\log \langle w_{\mp } \rangle \big )^4$. We remark that by choosing the constant weights $\lambda _\pm =1$, we have the energy identities:

$$\begin{aligned} \begin{aligned} \int _{\Sigma _t} |z_\pm |^2dx+2\mu \int _0^t\int _{\Sigma _\tau }|\nabla z_\pm |^2dxd\tau = \int _{\Sigma _0} |z_\pm |^2dx. \end{aligned} \end{aligned}$$

(2.37)

In particular, it implies that

$$\begin{aligned} \mu \int _0^t\int _{\Sigma _\tau }|\nabla z_\pm |^2dxd\tau \le \frac{1}{2} \int _{\Sigma _0} |z_\pm |^2dx. \end{aligned}$$

This is the cornerstone of all the estimates in this work.

In this section, our task is to prove the following proposition concerning the lowest order energy estimate.

Proposition 2.12

Under the bootstrap ansatz (2.1) (or (2.6)) and

$$\begin{aligned} \sup _{0\le l\le 2}E_\mp ^l\le 2C_1\varepsilon ^2, \end{aligned}$$

for $\varepsilon$ sufficiently small, there holds

$$\begin{aligned} E_\pm (t) + \frac{1}{4}\sup _{u_\pm }F_\pm (z_\pm ) +\frac{1}{2}D_\pm (t) \lesssim E_\pm (0)+\sup _{0\le l\le 2}\bigl (E_\mp ^l\bigr )^{\frac{1}{2}}\sup _{u_\pm }F_\pm ^0(\nabla {z}_{\pm })+2\mu D_\pm ^0(t). \end{aligned}$$

(2.38)

Estimates on the Pressure

The current subsection is devoted to derive the following estimates concerning the pressure term $\nabla p$:

Proposition 2.13

Under the ansatz (2.1), for all $t\in [0,t^*]$, we have

$$\begin{aligned} \Big |\int _0^t\int _{\Sigma _\tau }\big (\log \langle w_{\mp } \rangle \big )^4 |z_\pm ||\nabla p|dxd\tau \Big | \lesssim \sum _{k=0}^2\bigl (E_\mp ^k\bigr )^{\frac{1}{2}} \bigl (\sup _{u_\pm }F_\pm (z_\pm )+\sup _{u_\pm } F_\pm ^0(\nabla z_\pm )\bigr ). \end{aligned}$$

(2.39)

Proof

We only derive bound on $I=\big |\int _0^t\int _{\Sigma _\tau }\big (\log \langle w_{-} \rangle \big )^4 |z_+||\nabla p|dxd\tau \big |$. To do this, we start with a decomposition on $\nabla p$. Since $\text {div}\,z_{\pm }=0$, by taking the divergence of the first equation of (2.36), we obtain

$$\begin{aligned} -\Delta p=\partial _i\big (z_+^j \partial _jz_-^i\big ). \end{aligned}$$

Therefore, on each time slice $\Sigma _\tau$, we have

$$\begin{aligned} \nabla p(\tau ,x)=-\frac{1}{4\pi }\nabla \int _{\mathbb {R}^3}\frac{1}{|x-y|}\partial _i(z_+^j \partial _jz_-^i)(\tau ,y)dy. \end{aligned}$$

We choose a smooth cut-off function $\theta (r)$ so that

$$\begin{aligned} \theta (r)=\left\{ \begin{aligned}&1,\quad \text {for}\quad |r|\le 1,\\&0,\quad \text {for}\quad |r|\ge 2. \end{aligned}\right. \end{aligned}$$

After a possible integration by parts, we can split $\nabla p$ as

$$\begin{aligned} \begin{aligned} \nabla p(\tau ,x)=&\underbrace{-\frac{1}{4\pi }\int _{\mathbb {R}^3}\nabla \frac{1}{|x-y|} \cdot \theta (|x-y|) \cdot \big (\partial _iz_-^j\partial _jz_+^i\big )(\tau ,y)dy}_{A_1(\tau ,x)}\\&+\underbrace{\frac{1}{4\pi }\int _{\mathbb {R}^3}\partial _i \Bigl (\nabla \frac{1}{|x-y|}\cdot \bigl (1-\theta (|x-y|)\bigr )\Bigr )\cdot \big (z_+^j \partial _jz_-^i\big )(\tau ,y)dy}_{A_2(\tau ,x)}. \end{aligned} \end{aligned}$$

(2.40)

According to this decomposition, we split I into two parts:

$$\begin{aligned} I=\underbrace{\int _0^t\int _{\Sigma _\tau }\big (\log \langle w_{-} \rangle \big )^4 |z_+||A_1|dxd\tau }_{I_{1}}+\underbrace{\int _0^t\int _{\Sigma _\tau }\big (\log \langle w_{-} \rangle \big )^4 |z_+||A_2|dxd\tau }_{I_{2}}. \end{aligned}$$

We deal with $I_1$ first. In fact, we have

$$\begin{aligned} I_{1}&=\int _0^t\int _{\Sigma _\tau }\frac{\big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2}\big (\log \langle w_+\rangle \big )}|z_+| \cdot {\big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2}\big (\log \langle w_+\rangle \big )}|A_1|dxd\tau \\&\le \int _0^t\big \Vert \frac{\big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2}\big (\log \langle w_+\rangle \big )}z_+\big \Vert _{L^2(\Sigma _\tau )} \big \Vert {\big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2}\big (\log \langle w_+\rangle \big )}A_1\big \Vert _{L^2(\Sigma _\tau )}d\tau . \end{aligned}$$

By the definition of $A_1$, we have

$$\begin{aligned}&{\big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2}\log \langle w_+\rangle }|A_1(\tau ,x)|\nonumber \\&\quad \le \int _{|y-x|\le 2}\frac{\overbrace{\big \{\big (\log \langle w_{-} \rangle \big )^2\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle \big \} (t,x)}^{\text {weight functions with } x \text { as variables}}|\nabla z_-(\tau ,y)||\nabla z_+(\tau ,y)|}{|x-y|^2}dy.\qquad \end{aligned}$$

(2.41)

The following auxiliary lemma allows us to switch the x variables in the above functions to y variables. $\square$

Lemma 2.14

For $|x-y|\le 2$, $R\ge 100$, we have

$$\begin{aligned} \langle w_{\pm } \rangle (\tau ,x)\le \sqrt{2} \langle w_{\pm } \rangle (\tau ,y), \ \ \log \langle w_{\pm } \rangle (\tau ,x)\le 2\log \langle w_{\pm } \rangle (\tau ,y). \end{aligned}$$

(2.42)

Proof

In fact, by the geometric ansatz (2.1) and the mean value theorem, we have

$$\begin{aligned} |x_i^\pm (\tau ,x)|&\le |x_i^\pm (\tau ,y)|+|x_i^\pm (\tau ,x)-x_i^\pm (\tau ,y)|\\&\le |x_i^\pm (\tau ,y)|+|x-y|\sup |\nabla x_i^\pm |\\&\le |x_i^\pm (\tau ,y)|+4, \end{aligned}$$

where $i=1,2,3$ and $x_3^\pm = u_\pm$. Thus, for $R\ge 100$, we have

$$\begin{aligned} \langle w_{\pm } \rangle (\tau ,x)=\big (R^2 + |x^\pm |^2\big )^\frac{1}{2}(\tau ,x)\le {\sqrt{2}}\big (R^2 + |x^\pm |^2\big )^\frac{1}{2}(\tau ,y) ={\sqrt{2}}\langle w_{\pm } \rangle (\tau ,y) \end{aligned}$$

This proves the first inequality in (2.42). For the second one, we have

$$\begin{aligned} \log \langle w_{\pm } \rangle (\tau ,x)\le \log (\sqrt{2})+\log \langle w_{\pm } \rangle (\tau ,y)\le 2\log \langle w_{\pm } \rangle (\tau ,y). \end{aligned}$$

This ends the proof of the lemma. $\square$

We return to (2.41) and we now have

$$\begin{aligned}&{\big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2}\log \langle w_+\rangle }|A_1(\tau ,x)|\nonumber \\&\quad \le 8\int _{|y-x|\le 2}\frac{{\big (\log \langle w_{-} \rangle \big )^2\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle (t,y)}|\nabla z_-(\tau ,y)||\nabla z_+(\tau ,y)|}{|x-y|^2}dy\nonumber \\&\quad \le 8\Vert \langle w_+\rangle (\log \langle w_+\rangle )^2 \nabla z_-\Vert _{L^\infty }\int _{|x-y|\le 2}\frac{1}{|x-y|^2}\frac{\big ( \log \langle w_{-} \rangle \big )^2|\nabla z_+(\tau ,y)|}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }dy\nonumber \\&\quad {\mathop {\lesssim }\limits ^{(2.8)}}\sum _{k=0}^2\bigl (E_-^k(\tau )\bigr )^{\frac{1}{2}}\int _{|x-y|\le 2}\frac{1}{|x-y|^2}\frac{\big ( \log \langle w_{-} \rangle \big )^2|\nabla z_+(\tau ,y)|}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }dy. \end{aligned}$$

(2.43)

By Young’s inequality, we obtain

$$\begin{aligned} \begin{aligned}&\big \Vert {\big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2}\log \langle w_+\rangle }A_1(\tau ,x)\big \Vert _{L^2(\Sigma _\tau )}\\&\quad \lesssim \sum _{k=0}^2\bigl (E_-^k(\tau )\bigr )^{\frac{1}{2}}\big \Vert \frac{1}{|x|^2}\big \Vert _{L^1(|x|\le 2)} \bigg \Vert \frac{\big ( \log \langle w_{-} \rangle \big )^2\nabla z_+}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }\bigg \Vert _{L^2(\Sigma _\tau )}\\&\quad \lesssim \sum _{k=0}^2\bigl (E_-^k(\tau )\bigr )^{\frac{1}{2}} \bigg \Vert \frac{\big ( \log \langle w_{-} \rangle \big )^2\nabla z_+}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }\bigg \Vert _{L^2(\Sigma _\tau )}. \end{aligned} \end{aligned}$$

(2.44)

Therefore, we can bound $I_{1}$ as follows:

$$\begin{aligned} I_1\lesssim & {} \sum _{k=0}^2\bigl (E_-^k(\tau )\bigr )^{\frac{1}{2}}\int _0^t\bigg \Vert \frac{\big ( \log \langle w_{-} \rangle \big )^2 z_+}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }\bigg \Vert _{L^2(\Sigma _\tau )}\bigg \Vert \frac{\big ( \log \langle w_{-} \rangle \big )^2\nabla z_+}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }\bigg \Vert _{L^2(\Sigma _\tau )}d\tau \nonumber \\\lesssim & {} \sum _{k=0}^2\bigl (E_-^k(\tau )\bigr )^{\frac{1}{2}}\Bigl (\underbrace{\int _0^t\int _{\Sigma _\tau }\frac{\big ( \log \langle w_{-} \rangle \big )^4 |z_+(\tau ,x)|^2}{\langle w_+\rangle \big ( \log \langle w_+\rangle \big )^2}dxd\tau }_{I_{11}}\nonumber \\&\quad + \underbrace{\int _0^t \int _{\Sigma _\tau }\frac{\big ( \log \langle w_{-} \rangle \big )^4 |\nabla z_+(\tau ,x)|^2}{\langle w_+\rangle \big ( \log \langle w_+\rangle \big )^2}dxd\tau }_{I_{12}}\Bigr ). \end{aligned}$$

(2.45)

We will use the flux to bound $I_{11}$ and $I_{12}$. For this purpose, we consider the following change of coordinates on $\mathbb {R}^3\times [0,t^*)$:

$$\begin{aligned} \Phi _+:\mathbb {R}^3\times [0,t^*)&\rightarrow \mathbb {R}^3\times [0,t^*), \\ (x_1,x_2,x_3,\tau )&\mapsto (x_1,x_2,u_+,t)=(x_1,x_2,u_+(\tau ,x),t). \end{aligned}$$

In view of the geometric ansatz (2.1), it is straightforward to see that the Jacobian $d\Phi _+$ of $\Phi _+$ satisfies

$$\begin{aligned} \det (d\Phi _+)=\partial _3u_+=1+O(\varepsilon ). \end{aligned}$$

(2.46)

Therefore, to compute the integral $I_{11}$, up to the Jacobian factor coming from the change of coordinates, we use $(x_1,x_2,u_+,t)$ as reference coordinates. As a result, by using the obtained result (2.18) that $d\sigma _+=(\sqrt{2}+O(\varepsilon ))d{x_1}d{x_2}dt$, we have

$$\begin{aligned} \begin{aligned} I_{11}&\lesssim \int _{u_+}\left( \int _{C_{u_+}^+}\frac{\big ( \log \langle w_{-} \rangle \big )^4 |z_+(\tau ,x)|^2}{\langle w_+\rangle \big ( \log \langle w_+\rangle \big )^2}d\sigma _+\right) du_+\\&\le \int _{u_+}\left( \int _{C_{u_+}^+}\frac{\big ( \log \langle w_{-} \rangle \big )^4 |z_+(\tau ,x)|^2}{(R^2+|u_+|^2)^\frac{1}{2}\big ( \log ((R^2+|u_+|^2)^\frac{1}{2})\big )^2}d\sigma _+\right) du_+. \end{aligned} \end{aligned}$$

(2.47)

Since $u_+$ is constant along $C_{u_+}^+$, we then have

$$\begin{aligned} I_{11}\le & {} \sup _{u_+}\Big [\int _{C_{u_+}^+}\big ( \log \langle w_{-} \rangle \big )^4 |z_+|^2d\sigma _+\Big ] \int _{\mathbb {R}} \underbrace{\frac{1}{(R^2+|u_+|^2)^\frac{1}{2}\big ( \log ((R^2+|u_+|^2)^\frac{1}{2})\big )^2}}_{\text {integrable!}}du_+\nonumber \\\lesssim & {} \sup _{u_+}F_+(z_+) \end{aligned}$$

(2.48)

For $I_{12}$, proceeding exactly in the same manner as for (2.47) and (2.48), we obtain

$$\begin{aligned} I_{12}\lesssim \sup _{u_+}\Big [\int _{C_{u_+}^+}\big ( \log \langle w_{-} \rangle \big )^4 |\nabla z_+|^2d\sigma _+\Big ]=\sup _{u_+} F_+^0(\nabla z_+). \end{aligned}$$

We then conclude that

$$\begin{aligned} I_{1}\lesssim \sum _{k=0}^2\bigl (E_-^k\bigr )^{\frac{1}{2}} \bigl (\sup _{u_+}F_+(z_+)+\sup _{u_+} F_+^0(\nabla z_+)\bigr ) \end{aligned}$$

(2.49)

We turn to the estimate on $I_{2}$. We first split $A_{2}(t,x)$ as

$$\begin{aligned} \begin{aligned} |A_2(\tau ,y)|&\lesssim \underbrace{\int _{\mathbb {R}^3}\frac{1-\theta (|x-y|)}{|x-y|^3}|z_+(\tau ,y)||\nabla z_-(\tau ,y)|dy}_{A_{21}(t,x)}\\&\quad +\underbrace{\int _{\mathbb {R}^3} \frac{\theta '(|x-y|)}{|x-y|^2}|z_+(\tau ,y)||\nabla z_-(\tau ,y)|dy}_{A_{22}(t,x)}. \end{aligned} \end{aligned}$$

(2.50)

Since the support of $\theta '$ is in [1, 2], the contribution of the $A_{22}(t,x)$ term to $I_2$ is essentially the same as the contribution of $A_1(t,x)$ to $I_{1}$, i.e.,

$$\begin{aligned} \int _0^t\int _{\Sigma _\tau }(\log \langle w_{-} \rangle )^4|z_+||A_{22}|dxd\tau \lesssim \sum _{k=0}^2\bigl (E_-^k\bigr )^{\frac{1}{2}}\sup _{u_+}F_+(z_+). \end{aligned}$$

Therefore,

$$\begin{aligned} I_{2}\lesssim \sum _{k=0}^2\bigl (E_-^k\bigr )^{\frac{1}{2}}\sup _{u_+}F_+(z_+) + \underbrace{\int _0^t\int _{\Sigma _\tau } \big (\log \langle w_{-} \rangle \big )^4 |z_+||A_{21}|dxd\tau }_{I_{21}}. \end{aligned}$$

To bound $I_{21}$, we first prove the following lemma concerning the weights:

Lemma 2.15

For $|y-x|\ge 1$, $R\ge 100$, we have

$$\begin{aligned} \langle w_{\pm } \rangle (\tau ,x) \le 2|x-y|\langle w_{\pm } \rangle (\tau ,y), \ \ \ \log \langle w_{\pm } \rangle (\tau ,x) \le 4\log \langle w_{\pm } \rangle (\tau ,y)\log \big (2|y-x|\big ). \end{aligned}$$

(2.51)

Proof

By (2.7) and mean value theorem, we have

$$\begin{aligned} \langle w_{\pm } \rangle (\tau ,x)&\le \langle w_{\pm } \rangle (\tau ,y)+2|x-y|\\&\le 2|x-y|\langle w_{\pm } \rangle (\tau ,y). \end{aligned}$$

Therefore,

$$\begin{aligned} \log \langle w_{\pm } \rangle (\tau ,x)\le \log \big (2|x-y|)+\log \langle w_{\pm } \rangle (\tau ,y)\le 4\log \big (2|x-y|)\log \langle w_{\pm } \rangle (\tau ,y). \end{aligned}$$

This completes the proof of the lemma. $\square$

By the above Lemma 2.15, we have

$$\begin{aligned}&I_{21}=\int _0^t\int _{\Sigma _\tau } \big (\log \langle w_{-} \rangle (\tau ,x) \big )^2 |z_+(\tau ,x)|\Big [\big (\log \langle w_{-} \rangle (\tau ,x) \big )^2 |A_{21}(\tau ,x)|\Big ]dxd\tau \\&\quad \lesssim \int _0^t\int _{\Sigma _\tau } \big (\log \langle w_{-} \rangle \big )^2 |z_+|\\&\qquad \underbrace{\Big [\int _{|y-x|\ge 1}\frac{\big (\log (2|x-y|)\big )^2}{|x-y|^3}\big (\log \langle w_{-} \rangle (\tau ,y) \big )^2 |z_+(\tau ,y)||\nabla z_-(\tau ,y)|dy\Big ]}_{A_3(\tau ,x)}dxd\tau . \end{aligned}$$

We now rewrite $A_3(\tau ,x)$, i.e., the term in the bracket in last line, as follows

$$\begin{aligned}&\int _{|y-x|\ge 1}\frac{\big (\log (2|x-y|)\big )^2}{|x-y|^3}\frac{\big (\log \langle w_{-} \rangle (\tau ,y) \big )^2}{\langle w_+\rangle (\tau ,y)^\frac{1}{2}\log \langle w_+\rangle (\tau ,y)} |z_+(\tau ,y)|\\&\quad \frac{\langle w_+\rangle (\tau ,y)\big (\log \langle w_+\rangle (\tau ,y) \big )^2}{\underbrace{\langle w_+\rangle (\tau ,y)^\frac{1}{2}\log \langle w_+\rangle (\tau ,y)}_{D}}|\nabla z_-(\tau ,y)|dy \end{aligned}$$

We will change the denominator D, which is a function in y, to a function in x so that we can move it to the outside of the integral. In fact, according to (2.51), we have

$$\begin{aligned} \frac{1}{\langle w_+\rangle (\tau ,y)^\frac{1}{2}\log \langle w_+\rangle (\tau ,y)}\lesssim \frac{|x-y|^\frac{1}{2}\log (2|x-y|)}{\langle w_+\rangle (\tau ,x)^\frac{1}{2}\log \langle w_+\rangle (\tau ,x)}. \end{aligned}$$

Therefore,

$$\begin{aligned}&I_{21}\lesssim \int _0^t\int _{\Sigma _\tau } \frac{\big (\log \langle w_{-} \rangle \big )^2|z_+|}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }\cdot \\&\quad \qquad \cdot \underbrace{\int _{|y-x|\ge 1}\frac{\big (\log (2|x-y|)\big )^3}{|x-y|^{\frac{5}{2}}}\Bigl (\frac{\big (\log \langle w_{-} \rangle \big )^2|z_+|}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle } \cdot \langle w_+\rangle \big (\log \langle w_+\rangle \big )^2|\nabla z_-|dy\Bigr )(\tau ,y)}_{A_4(t,x)}dxd\tau \\&\quad \lesssim \int _0^t\bigg \Vert \frac{\big (\log \langle w_{-} \rangle \big )^2|z_+|}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }\bigg \Vert _{L^2(\Sigma _\tau )}\Vert A_4(t,x)\Vert _{L^2(\Sigma _\tau )}d\tau . \end{aligned}$$

For $A_4(t,x)$, according to the Young’s inequality, we have

$$\begin{aligned} \begin{aligned} \Vert A_4(t,x)\Vert _{L^2(\Sigma _\tau )}&=\bigg \Vert \frac{(\log (2|x|))^3}{|x|^\frac{5}{2}}\chi _{|x|\ge 1}\\&\qquad *\left( \frac{\big (\log \langle w_{-} \rangle \big )^2|z_+|}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle } \cdot \langle w_+\rangle \big (\log \langle w_+\rangle \big )^2|\nabla z_-|\right) \bigg \Vert _{L^2(\Sigma _\tau )}\\&\le \bigg \Vert \frac{(\log (2|x|))^3}{|x|^\frac{5}{2}}\chi _{|x|\ge 1}\bigg \Vert _{L^2(\Sigma _\tau )}\bigg \Vert \frac{\big (\log \langle w_{-} \rangle \big )^2|z_+|}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }\\&\qquad \cdot \langle w_+\rangle \big (\log \langle w_+\rangle \big )^2|\nabla z_-|\bigg \Vert _{L^1(\Sigma _\tau )}\\&\lesssim \bigg \Vert \frac{\big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle } z_+\bigg \Vert _{L^2(\Sigma _\tau )}\big \Vert \langle w_+\rangle \big (\log \langle w_+\rangle \big )^2\nabla z_-\big \Vert _{L^2 (\Sigma _\tau )}\\&\lesssim \bigl (E_-^0(\tau )\bigr )^{\frac{1}{2}}\bigg \Vert \frac{\big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }z_+ \bigg \Vert _{L^2(\Sigma _\tau )}. \end{aligned} \end{aligned}$$

(2.52)

Hence,

$$\begin{aligned} I_{21}&\lesssim \bigl (E_-^0\bigr )^{\frac{1}{2}} \int _0^t\bigg \Vert \frac{\big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }z_+ \bigg \Vert ^2_{L^2(\Sigma _\tau )}d\tau . \end{aligned}$$

The righthand side is exactly the same as for $I_{11}$, so it is bounded by $\bigl (E_-^0\bigr )^{\frac{1}{2}}\sup _{u_+} F_+(z_+)$. As a result, we also have

$$\begin{aligned} I_{2} \lesssim \sum _{k=0}^2\bigl (E_-^k\bigr )^{\frac{1}{2}}\sup _{u_+}F_+(z_+). \end{aligned}$$

(2.53)

Two inequalities (2.49) and (2.53) complete the proof of the proposition. $\square$

Estimates on the Viscosity Terms

The current subsection is devoted to derive the following estimates on the viscosity term:

Proposition 2.16

Under the ansatz (2.1), for all $t\in [0,t^*]$ and $R\ge 100$, we have

$$\begin{aligned} \mu \int _0^t\int _{\Sigma _\tau }\big (\log \langle w_{\mp } \rangle \big )^4 |\nabla z_\pm |^2dxd\tau \le 1000\bigl (E_\pm (0)+\sum _{l=0}^2\bigl (E_\mp ^l\bigr )^{\frac{1}{2}}\big (F_\pm +F_\pm ^0\big )\bigr ). \end{aligned}$$

(2.54)

Proof

We will use (2.34) twice by induction. Indeed, for the $k^{\text {th}}$-time, we will choose the weight function $\lambda _\pm = (\log \langle w_{\mp } \rangle )^{2k}$, where $k=1,2$. In this situation, (2.34) shows that

$$\begin{aligned}&\int _{\Sigma _t}(\log \langle w_{\mp } \rangle )^{2k}|z_\pm |^2dx + \mu \int _0^t\int _{\Sigma _\tau }(\log \langle w_{\mp } \rangle )^{2k}|\nabla z_\pm |^2dxd\tau \\&\quad \le \int _{\Sigma _0}(\log \langle w_{\mp } \rangle )^{2k}|z_\pm |^2dx +2\int _0^t\int _{\Sigma _\tau }\big |(\log \langle w_{\mp } \rangle )^{2k} z_\pm \big |\big |\nabla p\big |dxd\tau \\&\quad \quad +\mu \int _0^t\int _{\Sigma _\tau } \frac{|\nabla \big (\log \langle w_{\mp } \rangle \big )^{2k}|^2}{(\log \langle w_{\mp } \rangle )^{2k}}|z_\pm |^2dxd\tau . \end{aligned}$$

We only treat $z_+$ and the estimates on $z_-$ can be derived in the same manner. Since $k\le 2$, the first term on the righthand side are bounded by the initial data and the second term can be bounded thanks to Proposition 2.13 from last subsection. Therefore, we have

$$\begin{aligned}&\mu \int _0^t\int _{\Sigma _\tau }(\log \langle w_{-} \rangle )^{2k}|\nabla z_+|^2dxd\tau \le E_+(0)+\sum _{l=0}^2\bigl (E_-^l\bigr )^{\frac{1}{2}}\big (F_++F_+^0\big )\\&\quad +\mu \int _0^t\int _{\Sigma _\tau }\frac{|\nabla \big (\log \langle w_{-} \rangle \big )^{2k}|^2}{(\log \langle w_{-} \rangle )^{2k}}|z_+|^2dxd\tau . \end{aligned}$$

According to (2.7) (and its immediate consequences in the Lemma), we see that

$$\begin{aligned} \frac{|\nabla \big (\log \langle w_{-} \rangle \big )^{2k}|^2}{(\log \langle w_{-} \rangle )^{2k}} \le 16k^2\frac{\big (\log \langle w_{-} \rangle \big )^{2(k-1)}}{\langle w_{-} \rangle ^2}. \end{aligned}$$

Therefore, we have

$$\begin{aligned}&\mu \int _0^t\int _{\Sigma _\tau }(\log \langle w_{-} \rangle )^{2k}|\nabla z_+|^2dxd\tau \le E_+(0)+\sum _{l=0}^2\bigl (E_-^l\bigr )^{\frac{1}{2}}\big (F_++F_+^0\big )\nonumber \\&\quad +16k^2\mu \int _0^t\int _{\Sigma _\tau }\frac{\big (\log \langle w_{-} \rangle \big )^{2(k-1)}}{\langle w_{-} \rangle ^2}|z_+|^2dxd\tau . \end{aligned}$$

(2.55)

Step 1. $k=1$. It suffices to estimate $\int _0^t\int _{\Sigma _\tau }\frac{|z_+|^2}{\langle w_{-} \rangle ^2}dxd\tau$ in (2.55). Noticing that $\langle w_{-} \rangle =(R^2+|x^-|^2)^2$ and $x^-(t,\psi _-(t,y))=y$, we will use Lagrangian coordinates y. Therefore, since $\det \bigl (\frac{\partial \psi _-(t,y)}{\partial y}\bigr )=1$, we have

$$\begin{aligned} \int _0^t\int _{\Sigma _\tau }\frac{|z_+|^2}{\langle w_{-} \rangle ^2} dxd\tau&= \int _0^t\int _{\Sigma _0}\frac{|z_+(\tau , \psi _-(t,y))|^2}{R^2+|y|^2}dyd\tau . \end{aligned}$$

Now by using the Hardy’s inequality¹ on each $\Sigma _0$, we obtain

$$\begin{aligned} \int _0^t\int _{\Sigma _\tau }\frac{|z_+|^2}{\langle w_{-} \rangle ^2} dxd\tau \le 4\int _0^t\int _{\Sigma _0} |\nabla _y z_+(\tau ,\psi _-(t,y))|^2 dyd\tau . \end{aligned}$$

On the other side, we have

$$\begin{aligned} \nabla _y z_+(\tau , \psi _-(t,y)) = (\nabla _x z_+)|_{x=\psi _-(t,y)}\frac{\partial \psi _-(t,y)}{\partial y}. \end{aligned}$$

Then changing back to the Eulerian coordinates on $\Sigma _\tau$ and using (2.6) with small $\epsilon$, we obtain

$$\begin{aligned}&\mu \int _0^t\int _{\Sigma _\tau }\frac{|z_+|^2}{\langle w_{-} \rangle ^2} dxd\tau \le 5\mu \int _0^t\int _{\Sigma _\tau } |\nabla z_+(\tau , x)|^2 dxd\tau \\&\quad {\mathop {\le }\limits ^{(2.37)}} 5\int _{\Sigma _0}|z_+|^2d\tau \le \frac{5E_+(0)}{2(\log R)^4}. \end{aligned}$$

Here we used the most basic energy identity (2.37).

Finally, going back to (2.55), taking $R\ge 100$, we obtain

$$\begin{aligned} \mu \int _0^t\int _{\Sigma _\tau }(\log \langle w_{-} \rangle )^2|\nabla z_+|^2 \le \frac{7}{6}E_+(0)+\sum _{l=0}^2\bigl (E_-^l\bigr )^{\frac{1}{2}}\big (F_++F_+^0\big ). \end{aligned}$$

(2.56)

Step 2. $k=2$. It suffices to estimate $\int _0^t\int _{\Sigma _\tau }\frac{(\log \langle w_{-} \rangle )^2 |z_+|^2}{\langle w_{-} \rangle ^2}dxd\tau$ in (2.55). As we have observed in Step 1, we can freely switch the Eulerian coordinates x to Lagrangian coordinates y. We have

$$\begin{aligned} \begin{aligned}&\mu \int _0^t\int _{\Sigma _\tau }\frac{(\log \langle w_{-} \rangle )^2 |z_+|^2}{\langle w_{-} \rangle ^2} dxd\tau {\mathop {=}\limits ^{\det \big (\frac{\partial \psi _-}{\partial y}\big )=1}}\\&\quad \mu \int _0^t\int _{\Sigma _0}\frac{(\log (R^2+|y|^2)^{\frac{1}{2}})^2|z_+ (\tau ,\psi _-(\tau ,y))|^2}{R^2+|y|^2}dyd\tau \\&\quad {\mathop {\le }\limits ^{\text {Hardy}}} 4\mu \int _0^t \int _{\Sigma _0} \Big | \nabla _y \Big [\log (R^2+|y|^2)^{\frac{1}{2}} z_+(\tau , \psi _-(\tau ,y))\Big ]\Big |^2 dy d\tau \\&\quad \le 8\mu \int _0^t \int _{\Sigma _0} \Bigl (\frac{ \big |z_+(\tau , \psi _-(\tau ,y))\big |^2}{R^2+|y|^2}\\&\quad \quad +\big (\log (R^2+|y|^2)^\frac{1}{2}\big )^2\big |\nabla _yz_+(\tau , \psi _-(\tau ,y))\big |^2\Bigr ) dyd\tau \\&\quad \le 8\mu \int _0^t \int _{\Sigma _\tau }\Bigl (\frac{ |z_+|^2}{\langle w_{-} \rangle ^2} +\frac{5}{4}(\log \langle w_{-} \rangle )^2 |\nabla z_+|^2\Bigr )dx d\tau . \end{aligned} \end{aligned}$$

Since both terms in the last line have been estimated in Step 1, we obtain that

$$\begin{aligned} \mu \int _0^t\int _{\Sigma _\tau }\frac{(\log \langle w_{-} \rangle )^2 |z_+|^2}{\langle w_{-} \rangle ^2} dxd\tau \le 13E_+(0)+10\sum _{l=0}^2\bigl (E_-^l\bigr )^{\frac{1}{2}}\big (F_++F_+^0\big ). \end{aligned}$$

(2.57)

In view of (2.55) and (2.57), we obtain

$$\begin{aligned} \mu \int _0^t\int _{\Sigma _\tau }(\log \langle w_{-} \rangle )^4 |\nabla z_+|^2 dxd\tau \le 1000\bigl (E_+(0)+\sum _{l=0}^2\bigl (E_-^l\bigr )^{\frac{1}{2}}\big (F_++F_+^0\big )\bigr ).\quad \end{aligned}$$

(2.58)

This completes the proof. $\square$

Completion of the Estimates on Lowest Order Terms

In this subsection, we will end the proof of Proposition 2.12.

Proof of Proposition 2.12

We specialize (2.35) to the current situation: $f_\pm = z_\pm$, $\rho _\pm =\nabla p$ and $\lambda _\pm =\big (\log \langle w_{\mp } \rangle \big )^4$. Hence,

$$\begin{aligned} \begin{aligned}&\int _{\Sigma _t}\big (\log \langle w_{\mp } \rangle \big )^4 |z_\pm |^2dx + \frac{1}{2}\sup _{u_\pm }\int _{C_{u_\pm }^\pm }\big (\log \langle w_{\mp } \rangle \big )^4|z_\pm |^2d\sigma _\pm \\&\quad +\frac{1}{2}\mu \int _0^t\int _{\Sigma _\tau }\big (\log \langle w_{\mp } \rangle \big )^4|\nabla z_\pm |^2 dxd\tau \le 2\int _{\Sigma _0}\big (\log \langle w_{\mp } \rangle \big )^4|z_\pm |^2dx\\&\quad + 4\int _0^t\int _{\Sigma _\tau }\big (\log \langle w_{\mp } \rangle \big )^4|z_\pm ||\nabla p|dxd\tau +128{\mu }\int _0^t\int _{\Sigma _\tau }\frac{(\log \langle w_{\mp } \rangle )^2}{\langle w_{\mp } \rangle ^2}|z_\pm |^2dxd\tau \\&\quad +2{\mu ^2}\int _0^t\int _{\Sigma _\tau }\big (\log \langle w_{\mp } \rangle \big )^4|\nabla ^2 z_\pm |^2dxd\tau . \end{aligned} \end{aligned}$$

The second and third terms have been controlled by (2.39) and (2.57) in the previous two subsections (notice that for $\lambda _\pm =\big (\log \langle w_{\mp } \rangle \big )^4$ we have $\frac{|\nabla \lambda _\pm |^2}{\lambda _\pm } \le 64 \frac{(\log \langle w_{\mp } \rangle )^2}{\langle w_{\mp } \rangle ^2}$). While the last term is controlled by $2\mu D_\pm ^0(t)$. We then have

$$\begin{aligned} \begin{aligned}&\int _{\Sigma _t}\big (\log \langle w_{\mp } \rangle \big )^4 |z_\pm |^2dx + \frac{1}{2}\sup _{u_\pm }\int _{C_{u_\pm }^\pm }\big (\log \langle w_{\mp } \rangle \big )^4|z_\pm |^2d\sigma _\pm \\&\quad +\frac{1}{2}\mu \int _0^t\int _{\Sigma _\tau }\big (\log \langle w_{\mp } \rangle \big )^4|\nabla z_\pm |^2 dxd\tau \\&\quad \lesssim E_\pm (0)+\sum _{l=0}^2\bigl (E_\mp ^l\bigr )^{\frac{1}{2}}\big (F_\pm +F_\pm ^0\big )+2\mu D_\pm ^0(t). \end{aligned} \end{aligned}$$

In other words, if $\sum _{l=0}^2E_\mp ^l\le 2C_1\varepsilon ^2$ with $\varepsilon$ sufficiently small, we have

$$\begin{aligned} E_\pm (t) + \frac{1}{4}\sup _{u_\pm }F_\pm (z_\pm ) +\frac{1}{2}D_\pm (t) \lesssim E_\pm (0)+\sum _{l=0}^2\bigl (E_\mp ^l\bigr )^{\frac{1}{2}} F_\pm ^0+2\mu D_\pm ^0(t). \end{aligned}$$

This proves the proposition. $\square$

Energy Estimates for the First Order Terms

This section is devoted to derive energy estimates on $\nabla z_\pm$. For this purpose, we first commute one derivative with (1.5) and we obtain

$$\begin{aligned} \begin{aligned} \partial _t \partial {z}_++{Z}_-\cdot \nabla \partial {z}_+- \mu \triangle \partial {z}_+&= -\partial \nabla p-\partial {z}_-\cdot \nabla {z}_+, \\ \partial _t \partial {z}_-+{Z}_+\cdot \nabla \partial {z}_-- \mu \triangle \partial {z}_+&= -\partial \nabla p-\partial {z}_+\cdot \nabla {z}_-, \end{aligned} \end{aligned}$$

where $\partial {z}_{\pm }$ denotes for some $\partial _i {z}_{\pm }$ with $i=1,2,3$. The main result of this section is stated as follows:

Proposition 2.17

Assume that $\Vert z_\pm \Vert _{L^\infty }\le \frac{1}{2}$, $R\ge 100$ and

$$\begin{aligned} \sup _{0\le l\le 3} E_{\mp }^l\le 2C_1\varepsilon ^2, \end{aligned}$$

for $\varepsilon$ sufficiently small. Then under the ansatz (2.1) (or (2.6)), for all $t\in [0,t^*]$, we have

$$\begin{aligned} \begin{aligned}&E^0_\pm (t) +\sup _{u_\pm }F^0_\pm (\nabla z_\pm ) +D^0_\pm (t) \lesssim E_\pm ^0(0)+\sup _{0\le l\le 3}\bigl (E_\mp ^l\bigr )^{\frac{1}{2}}\sup _{u_\pm }F_\pm ^1(j_\pm )\\&\quad +\mu \int _0^t\int _{\Sigma _\tau }\big (\log \langle w_{\mp } \rangle \big )^4|\nabla z_\pm |^2dxd\tau + 2\mu D_\pm ^1(t). \end{aligned} \end{aligned}$$

(2.59)

Remark 2.18

Thanks to (2.54), we can bounded the third term in the righthand side of (2.59) by $E_\pm (0)+\sum _{l=0}^2\bigl (E_\mp ^l\bigr )^{\frac{1}{2}}(F_\pm +F_\pm ^0)$. Then we obtain

$$\begin{aligned}&E^0_\pm (t) +\sup _{u_\pm }F^0_\pm (\nabla z_\pm ) +D^0_\pm (t) \lesssim E_\pm (0)+E_\pm ^0(0)\nonumber \\&\quad +\sum _{l=0}^3\bigl (E_\mp ^l\bigr )^{\frac{1}{2}} \sup _{u_\pm }(F_\pm ({z}_{\pm })+F_\pm ^1(j_\pm ))+ 2\mu D_\pm ^1(t). \end{aligned}$$

(2.60)

Estimates on the Pressure

The subsection is devoted to derive the following estimates concerning the pressure p:

Proposition 2.19

Under the assumptions of Proposition 2.17, for all $t\in [0,t^*]$, we have

$$\begin{aligned}&\Big |\int _0^t\int _{\Sigma _\tau }\langle w_{\mp } \rangle ^2 \big (\log \langle w_{\mp } \rangle \big )^4 |\nabla z_\pm ||\nabla ^2 p|dxd\tau \Big |\nonumber \\&\quad \lesssim \sum _{k=0}^3\bigl (E_\mp ^k\bigr )^{\frac{1}{2}} \bigl (E_\pm ^0+\sup _{u_\pm }\big (F_\pm ^0(\nabla {z}_{\pm })+F_\pm ^1(j_\pm )\big )\bigr ). \end{aligned}$$

(2.61)

Proof

We only derive bound on $I=\int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2 \big (\log \langle w_{-} \rangle \big )^4 |\nabla z_+||\nabla ^2 p|dxd\tau$. Similar to the proof of Proposition 2.13, we choose the same cut-off function $\theta (r)$ and we have

$$\begin{aligned} \partial \nabla p(\tau ,x)=-\frac{1}{4\pi }\int _{\mathbb {R}^3}\big (\partial \nabla \frac{1}{|x-y|}\big )\cdot \big (\partial _iz_+^j \partial _jz_-^i\big )(\tau ,y)dy. \end{aligned}$$

We split $\partial \nabla p$ as

$$\begin{aligned} \begin{aligned} \partial \nabla p(\tau ,x)=&\underbrace{-\frac{1}{4\pi }\int _{\mathbb {R}^3}\partial \nabla \frac{1}{|x-y|} \cdot \theta (|x-y|) \cdot \big (\partial _iz_-^j\partial _jz_+^i\big )(\tau ,y)dy}_{A_1(\tau ,x)}\\&-\underbrace{\frac{1}{4\pi }\int _{\mathbb {R}^3} \Bigl (\partial \nabla \frac{1}{|x-y|}\cdot \bigl (1-\theta (|x-y|)\bigr )\Bigr )\cdot \big (\partial _iz_+^j \partial _jz_-^i\big )(\tau ,y)dy}_{A_2(\tau ,x)}. \end{aligned} \end{aligned}$$

(2.62)

This gives the following decomposition for I:

$$\begin{aligned} I= & {} \underbrace{\int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^4 |\nabla z_+||A_1|dxd\tau }_{I_{1}}\\&+\underbrace{\int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^4 |\nabla z_+||A_2|dxd\tau }_{I_{2}}. \end{aligned}$$

For $I_1$, after an integration by parts, we first rewrite $A_1$ as (to avoid the non-integrable singularity $\frac{1}{|x-y|}$)

$$\begin{aligned} \begin{aligned} A_1&=\underbrace{\frac{1}{4\pi }\int _{\mathbb {R}^3}\nabla \frac{1}{|x-y|} \cdot \partial \theta (|x-y|) \cdot \big (\partial _iz_+^j \partial _jz_-^i\big )(\tau ,y)dy}_{A_{11}}\\&\quad +\underbrace{\frac{1}{4\pi }\int _{\mathbb {R}^3}\nabla \frac{1}{|x-y|} \cdot \theta (|x-y|) \cdot \big (\partial \partial _iz_+^j \partial _jz_-^i\big )(\tau ,y)dy}_{A_{12}}\\&\quad + \underbrace{\frac{1}{4\pi }\int _{\mathbb {R}^3}\nabla \frac{1}{|x-y|} \cdot \theta (|x-y|) \cdot \big (\partial _iz_+^j \partial \partial _jz_-^i\big )(\tau ,y)dy}_{A_{13}}. \end{aligned} \end{aligned}$$

(2.63)

We have

$$\begin{aligned} I_{1}&=\int _0^t\int _{\Sigma _\tau }\frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2}\log \langle w_+\rangle }|\nabla z_+| \cdot \langle w_{-} \rangle {\big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }|A_{1}|dxd\tau \\&\le \sum _{k=1}^3\int _0^t\bigg \Vert \frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2}\log \langle w_+\rangle }\nabla z_+\bigg \Vert _{L^2(\Sigma _\tau )} \big \Vert \langle w_{-} \rangle {\big (\log \langle w_{-} \rangle \big )^2}\langle w_+\rangle ^\frac{1}{2}\\&\quad \log \langle w_+\rangle A_{1k}\big \Vert _{L^2(\Sigma _\tau )}d\tau . \end{aligned}$$

For $A_{1k}$, since the integration is taken place for $|y-x|\le 2$, by (2.42), we have

$$\begin{aligned} \langle w_{\pm } \rangle (\tau ,x) \big (\log \langle w_{\pm } \rangle (\tau ,x)\big )^2 \lesssim \langle w_{\pm } \rangle (\tau ,y)\big (\log \langle w_{\pm } \rangle (\tau ,y)\big )^2. \end{aligned}$$

In particular, it implies that

$$\begin{aligned}&\langle w_{-} \rangle {\big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2}\log \langle w_+\rangle }|A_1(\tau ,x)|\\&\quad \le \sum _{l_1,l_2=1}^2\int _{|y-x|\le 2}\frac{\langle w_{-} \rangle (\tau ,y)\big (\log \langle w_{-} \rangle (\tau ,y) \big )^2\langle w_+\rangle (\tau ,y)^\frac{1}{2} \log \langle w_+\rangle (t,y)|\nabla ^{l_1} z_-(\tau ,y)||\nabla ^{l_2} z_+(\tau ,y)|}{|x-y|^2}dy\\&\quad \le \sum _{l_1,l_2=1}^2\Vert \langle w_+\rangle (\log \langle w_+\rangle )^2 \nabla ^{l_1} z_-\Vert _{L^\infty }\int _{|x-y|\le 2}\frac{1}{|x-y|^2}\Bigl (\frac{\langle w_{-} \rangle \big ( \log \langle w_{-} \rangle \big )^2|\nabla ^{l_2} z_+|}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }\Bigr )(\tau ,y)dy\\&\quad {\mathop {\lesssim }\limits ^{(2.8)}}\sum _{l=0}^3\bigl (E_-^l\bigr )^{\frac{1}{2}}\sum _{l_2=1}^2\int _{|x-y|\le 2}\frac{1}{|x-y|^2}\Bigl (\frac{\langle w_{-} \rangle \big ( \log \langle w_{-} \rangle \big )^2|\nabla ^{l_2} z_+|}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }\Bigr )(\tau ,y)dy, \end{aligned}$$

where $(l_1,l_2) = (1,1), (1,2)$ or (2, 1). By Young’s inequality, we have

$$\begin{aligned} \begin{aligned}&\big \Vert \langle w_{-} \rangle {\big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2}\log \langle w_+\rangle }A_1(\tau ,x)\big \Vert _{L^2(\Sigma _\tau )}\\&\quad \lesssim \sum _{l=0}^3\bigl (E_-^l\bigr )^{\frac{1}{2}}\big \Vert \frac{1}{|x|^2} \big \Vert _{L^1(|x|\le 2)} \sum _{l_2=1}^2\bigg \Vert \frac{\langle w_{-} \rangle \big ( \log \langle w_{-} \rangle \big )^2\nabla ^{l_2} z_+}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }\bigg \Vert _{L^2(\Sigma _\tau )}\\&\quad \lesssim \sum _{l=0}^3\bigl (E_-^l\bigr )^{\frac{1}{2}} \sum _{l_2=1}^2\bigg \Vert \frac{\langle w_{-} \rangle \big ( \log \langle w_{-} \rangle \big )^2\nabla ^{l_2} z_+}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }\bigg \Vert _{L^2(\Sigma _\tau )}. \end{aligned} \end{aligned}$$

Therefore, thanks to Hölder inequality and div-curl lemma, we can bound $I_{1}$ as follows:

(2.64)

This is exactly the same situation as for (2.45) in the proof of Proposition 2.13. We repeat the procedure to obtain

$$\begin{aligned} I_{1} \lesssim \sum _{l=0}^3\bigl (E_-^l\bigr )^{\frac{1}{2}}\sup _{u_+}\bigl (F_+^0(\nabla z_+)+F_+^1(j_+)\bigr ). \end{aligned}$$

(2.65)

We move to the bound on $I_{2}$. We first make the following observation: $\square$

Lemma 2.20

For $|x-y|\ge 1$, $R\ge 100$, we have

$$\begin{aligned} \langle w_{\pm } \rangle (\tau ,x)\big (\log \langle w_{\pm } \rangle (\tau ,x))^2\le & {} 8\langle w_{\pm } \rangle (\tau ,y)\big (\log \langle w_{\pm } \rangle (\tau ,y)\big )^2\nonumber \\&+\,4|x-y|\big (\log (4|x-y|)\big )^2. \end{aligned}$$

(2.66)

Proof

To see this, we recall that by (2.7) and mean value theorem, we have

$$\begin{aligned} \langle w_{\pm } \rangle (\tau ,x) \le \langle w_{\pm } \rangle (\tau ,y)+2|x-y|. \end{aligned}$$

Therefore, we either have $\frac{1}{2}\langle w_{\pm } \rangle (\tau ,x) \le \langle w_{\pm } \rangle (\tau ,y)$ or $\frac{1}{2}\langle w_{\pm } \rangle (\tau ,x) \le 2|x-y|$.

If $\frac{1}{2}\langle w_{\pm } \rangle (\tau ,x) \le \langle w_{\pm } \rangle (\tau ,y)$, we have

$$\begin{aligned} \langle w_{\pm } \rangle (\tau ,x)\big (\log \langle w_{\pm } \rangle (\tau ,x)\big )^2&\le 2\langle w_{\pm } \rangle (\tau ,y)\big (\log \big (2\langle w_{\pm } \rangle (\tau ,y))\big )^2\\&\le 4\langle w_{\pm } \rangle (\tau ,y)\Big (\big (\log 2\big )^2+ \big (\log \langle w_{\pm } \rangle (\tau ,y)\big )^2\Big )\\&\le 8\langle w_{\pm } \rangle (\tau ,y)\log \big (\langle w_{\pm } \rangle (\tau ,y)). \end{aligned}$$

If $\frac{1}{2}\langle w_{\pm } \rangle (\tau ,x) \le 2|x-y|$, we have

$$\begin{aligned} \langle w_{\pm } \rangle (\tau ,x)\big (\log \langle w_{\pm } \rangle (\tau ,x)\big )^2&\le 4|x-y|\big (\log \big (4|x-y|)\big )^2. \end{aligned}$$

This completes the proof of the lemma. $\square$

According to the lemma, we have

$$\begin{aligned} I_{2}&=\int _0^t\int _{\Sigma _\tau } \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2 |\nabla z_+ |\cdot \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2 |A_{2}|dxd\tau \\&\lesssim \underbrace{\int _0^t\int _{\Sigma _\tau } \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2 |\nabla z_+ | \underbrace{\int _{|x-y|\ge 1} \frac{1}{|x-y|^3}\cdot \bigl (\langle w_{-} \rangle (\log \langle w_{-} \rangle )^2|\nabla z_+| |\nabla z_-|\bigr )(\tau ,y)dy}_{B_1(\tau ,x)}dxd\tau }_{I_{21}}\\&\quad + \underbrace{\int _0^t\int _{\Sigma _\tau } \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2 |\nabla z_+|\underbrace{\int _{|x-y|\ge 1} \frac{\big (\log (4|x-y|)\big )^2}{|x-y|^2}\cdot \bigl (|\nabla z_+| |\nabla z_-|\bigr )(\tau ,y)dy}_{B_2(\tau ,x)}}_{I_{22}}. \end{aligned}$$

To deal with $I_{21}$, we bound $B_{1}(\tau ,x)$ by

$$\begin{aligned} \int _{|y-x|\ge 1}\frac{1}{|x-y|^3}\frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2}\log \langle w_+\rangle } |\nabla z_+ |\cdot \frac{\langle w_+\rangle \big (\log \langle w_+\rangle \big )^2}{\underbrace{\langle w_+\rangle ^\frac{1}{2}\log \langle w_+\rangle }_{D}}|\nabla z_- |dy \end{aligned}$$

According to (2.51), we have

$$\begin{aligned} \frac{1}{\langle w_+\rangle (\tau ,y)^\frac{1}{2}\log \langle w_+\rangle (\tau ,y)}\lesssim \frac{|x-y|^\frac{1}{2}\log (2|x-y|)}{\langle w_+\rangle (\tau ,x)^\frac{1}{2}\log \langle w_+\rangle (\tau ,x)}. \end{aligned}$$

(2.67)

Therefore,

$$\begin{aligned} I_{21}&\lesssim \int _0^t\int _{\Sigma _\tau } \frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2|\nabla z_+|}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }\\&\quad \underbrace{\int _{|y-x|\ge 1}\frac{\log (2|x-y|)}{|x-y|^{\frac{5}{2}}}\frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2|\nabla z_+|}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle } \cdot \langle w_+\rangle \big (\log \langle w_+\rangle \big )^2|\nabla z_-|dy}_{B_1'(t,x)}dxd\tau \\&\lesssim \int _0^t\bigg \Vert \frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2|\nabla z_+|}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }\bigg \Vert _{L^2(\Sigma _\tau )}\Vert B_1'(t,x)\Vert _{L^2(\Sigma _\tau )}d\tau . \end{aligned}$$

Since $\frac{\log (2|x|)}{|x|^\frac{5}{2}}\chi _{|x|\ge 1} \in L^2(\mathbb {R}^3)$, we can repeat the proof of (2.52) to obtain

$$\begin{aligned} \Vert B_1'(\tau ,x)\Vert _{L^2(\Sigma _\tau )}\lesssim \bigl (E_-^0\bigr )^{\frac{1}{2}}\bigg \Vert \frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }\nabla z_+ \bigg \Vert _{L^2(\Sigma _\tau )}. \end{aligned}$$

Hence,

$$\begin{aligned} I_{21}&\lesssim \bigl (E_-^0\bigr )^{\frac{1}{2}}\int _0^t\Vert \frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^\frac{1}{2} \log \langle w_+\rangle }\nabla z_+ \Vert ^2_{L^2(\Sigma _\tau )}d\tau \lesssim \bigl (E_-^0\bigr )^{\frac{1}{2}}\sup _{u_+}F_+^0(\nabla z_+). \end{aligned}$$

To deal with $I_{22}$, we have

$$\begin{aligned} I_{22}\le \int _0^t\Vert \langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2\nabla z_+\Vert _{L^2(\Sigma _\tau )}\Vert B_2\Vert _{L^2(\Sigma _\tau )}d\tau \lesssim \bigl (E_+^0\bigr )^{\frac{1}{2}}\int _0^t\Vert B_2\Vert _{L^2(\Sigma _\tau )}d\tau . \end{aligned}$$

Then we only need to bound $\Vert B_2\Vert _{L^2(\Sigma _\tau )}$. We rewrite $B_2$ as follows

$$\begin{aligned} B_2\le & {} \int _{|x-y|\ge 1} \frac{\big (\log (4|x-y|)\big )^2}{|x-y|^2}\\&\cdot \frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2|\nabla z_+|(\tau ,y)\cdot \langle w_+\rangle \big (\log \langle w_+\rangle \big )^2|\nabla z_-|(\tau ,y)}{ \langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2\langle w_+\rangle \big (\log \langle w_+\rangle \big )^2(\tau ,y)}dy. \end{aligned}$$

Since $\Vert {z}_{\pm }\Vert _{L^\infty }\le \frac{1}{2}$, by virtue of the separation property (2.10), we have

$$\begin{aligned} \frac{1}{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2\langle w_+\rangle \big (\log \langle w_+\rangle \big )^2(\tau ,y)}\lesssim \frac{1}{(R^2+\tau ^2)^{\frac{1}{2}} \big (\log (R^2+\tau ^2)^{\frac{1}{2}}\big )^2}. \end{aligned}$$

(2.68)

Notice that $\frac{\big (\log (4|x|)\big )^2}{|x|^2}\chi _{|x|\ge 1}\in L^2(\mathbb {R}^3)$. Then we obtain

$$\begin{aligned} \begin{aligned}&\Vert B_2\Vert _{L^2(\Sigma _\tau )}{\mathop {\lesssim }\limits ^{(2.68),\text {Young's}}}\frac{1}{(R^2+\tau ^2)^{\frac{1}{2}}\big (\log (R^2+\tau ^2)^{\frac{1}{2}}\big )^2} \bigg \Vert \frac{\big (\log (4|x|)\big )^2}{|x|^2}\chi _{|x|\ge 1} \bigg \Vert _{L^2(\mathbb {R}^3)}\\&\quad \cdot \big \Vert \langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2\nabla z_+\big \Vert _{L^2(\Sigma _\tau )}\big \Vert \langle w_+\rangle \big (\log \langle w_+\rangle \big )^2\nabla z_-\big \Vert _{L^2(\Sigma _\tau )}\\&\quad \lesssim \frac{\bigl (E_+^0\bigr )^{\frac{1}{2}}\bigl (E_-^0\bigr )^{\frac{1}{2}}}{(R^2+\tau ^2)^{\frac{1}{2}}\big (\log (R^2+\tau ^2\big )^{\frac{1}{2}})^2}, \end{aligned} \end{aligned}$$

which gives rise to

$$\begin{aligned} I_{22}\lesssim \varepsilon ^3\int _0^t\frac{1}{(R^2+\tau ^2)^{\frac{1}{2}} \big (\log (R^2+\tau ^2)^{\frac{1}{2}}\big )^2} d\tau \lesssim \bigl (E_-^0\bigr )^{\frac{1}{2}}E_+^0. \end{aligned}$$

Combining all the estimates, we complete the proof of the proposition. $\square$

Completion of the Estimates on the First Order Terms

Proof of Proposition 2.17

We specialize (2.35) to the current situation: $f_\pm = \partial z_\mp$, $\rho _\pm =\partial \nabla p + \partial z_\pm \cdot \nabla z_\mp$ and $\lambda _\pm =\langle w_{\mp } \rangle ^2\big (\log \langle w_{\mp } \rangle \big )^4$, with $\partial =\partial _1,\partial _2,\partial _3$. Hence,

$$\begin{aligned} \begin{aligned}&\int _{\Sigma _t}\langle w_{\mp } \rangle ^2\big (\log \langle w_{\mp } \rangle \big )^4 |\nabla z_\pm |^2dx + \frac{1}{2}\sup _{u_\pm }\int _{C_{u_\pm }^\pm }\langle w_{\mp } \rangle ^2\big (\log \langle w_{\mp } \rangle \big )^4|\nabla z_\pm |^2d\sigma _\pm \\&\quad \quad +\frac{1}{2}\mu \int _0^t\int _{\Sigma _\tau }\langle w_{\mp } \rangle ^2\big (\log \langle w_{\mp } \rangle \big )^4|\nabla ^2 z_\pm |^2 dxd\tau \\&\quad \le 2\int _{\Sigma _0}\langle w_{-} \rangle ^2\big (\log \langle w_{\mp } \rangle \big )^4|\nabla z_\pm |^2dx \\&\quad \quad + 4\int _0^t\int _{\Sigma _\tau }\langle w_{\mp } \rangle ^2\big (\log \langle w_{\mp } \rangle \big )^4|\nabla z_\pm |\big (|\nabla ^2 p| +|\nabla z_+| |\nabla z_-|\big )dxd\tau \\&\quad \quad +2{\mu }\int _0^t\int _{\Sigma _\tau }\frac{|\nabla \lambda _\pm |^2}{\lambda _\pm }|\nabla z_\pm |^2dxd\tau + 2{\mu ^2}\int _0^t\int _{\Sigma _\tau }\langle w_{\mp } \rangle ^2\big (\log \langle w_{\mp } \rangle \big )^4|\nabla ^3 z_\pm |^2dxd\tau . \end{aligned} \end{aligned}$$

Notice that the first part involving $\nabla ^2p$ of the second term on the righthand side can be estimated by (2.61) while the last term can be bounded by $2\mu D_\pm ^1$. For $\lambda _\pm =\langle w_{\mp } \rangle ^2\big (\log \langle w_{\mp } \rangle \big )^4$, we have

$$\begin{aligned} \frac{|\nabla \lambda _\pm |^2}{\lambda _\pm } \lesssim \big (\log \langle w_{\mp } \rangle \big )^4. \end{aligned}$$

We then have

$$\begin{aligned} \begin{aligned}&E^0_\pm (t) + \sup _{u_\pm }F^0_\pm (\nabla z_\pm ) +D_\pm ^{0}(t) \\&\quad \lesssim E_\pm ^0(0)+\sum _{k=0}^3\bigl (E_\mp ^k\bigr )^{\frac{1}{2}} \bigl (E_\pm ^0+\sup _{u_\pm }(F_\pm ^0(\nabla {z}_{\pm })+F_\pm ^1(j_\pm ))\bigr )\\&\quad +\mu \int _0^t\int _{\Sigma _\tau }\big (\log \langle w_{\mp } \rangle \big )^4|\nabla z_\pm |^2dxd\tau \\&\quad + 2\mu D_\pm ^1+ \underbrace{\int _0^t\int _{\Sigma _\tau }\langle w_{\mp } \rangle ^2\big (\log \langle w_{\mp } \rangle \big )^4|\nabla z_\pm ||\nabla z_+||\nabla z_-|dxd\tau }_{\text {nonlinear interaction} I_\pm }. \end{aligned} \end{aligned}$$

It remains to bound the nonlinear interaction term $I_\pm$. We only handle $I_+$.

$$\begin{aligned} \begin{aligned} I_+&=\int _0^t\int _{\Sigma _\tau } \frac{\langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^4 |\nabla z_+|^2 }{\langle w_+\rangle \big (\log \langle w_+\rangle \big )^2}\underbrace{\langle w_+\rangle \big (\log \langle w_+\rangle \big )^2|\nabla z_-|}_{L^\infty }dxd\tau \\&{\mathop {\lesssim }\limits ^{(2.8)}} \sum _{l=0}^2\bigl (E_-^l\bigr )^{\frac{1}{2}}\int _0^t\int _{\Sigma _\tau } \frac{\langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^4 |\nabla z_+|^2 }{\langle w_+\rangle \big (\log \langle w_+\rangle \big )^2}dxd\tau . \end{aligned} \end{aligned}$$

Similar to (2.47) and (2.48), we obtain

$$\begin{aligned} I_+\lesssim \sum _{l=0}^2\bigl (E_-^l\bigr )^{\frac{1}{2}} \sup _{u_+}\int _{C_{u^+}^+}\langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^4 |\nabla z_+|^2d\sigma _+ \lesssim \sum _{l=0}^2\bigl (E_-^l\bigr )^{\frac{1}{2}} F_+^0. \end{aligned}$$

Then we have

$$\begin{aligned} \begin{aligned}&E^0_\pm (t) + \sup _{u_\pm }F_\pm ^0(\nabla {z}_{\pm }) +D_\pm ^{0}(t) \\&\quad \lesssim E_\pm ^0(0)+\sum _{k=0}^3\bigl (E_\mp ^k\bigr )^{\frac{1}{2}} \bigl (E_\pm ^0+F_\pm ^0+F_\pm ^1\bigr )\\&\quad +\mu \int _0^t\int _{\Sigma _\tau } \big (\log \langle w_{\mp } \rangle \big )^4|\nabla z_\pm |^2dxd\tau + 2\mu D_\pm ^1(t). \end{aligned} \end{aligned}$$

(2.69)

Since $\sup _{0\le l\le 3}E_\mp ^l\le 2C_1\varepsilon ^2$ for sufficiently small $\varepsilon$, we obtain

$$\begin{aligned} \begin{aligned}&\frac{1}{2}E^0_\pm (t) +\frac{1}{2}\sup _{u_\pm }F^0_\pm (\nabla z_\pm ) +D^0_\pm (t) \lesssim E_\pm (0)+E_\pm ^0(0)+\sup _{0\le l\le 3}\bigl (E_\mp ^l\bigr )^{\frac{1}{2}}F_\pm ^1\\&\quad +\mu \int _0^t\int _{\Sigma _\tau }\big (\log \langle w_{\mp } \rangle \big )^4|\nabla z_\pm |^2dxd\tau + 2\mu D_\pm ^1(t). \end{aligned} \end{aligned}$$

This ends the proof of the proposition. $\square$

Remark 2.21

Estimate (2.59) in Proposition 2.17 is not good in the sense that we use one more derivative of flux term, i.e. $F_\pm ^1$, in the righthand side which is caused by the nonlocal and nonlinear term $\nabla p$. It will bring the trouble to close the energy estimates. This is the main reason that we turn to the investigation of the system of $j_{\pm }=\text {curl}\,z_{\pm }$.

Energy Estimates on Higher Order Terms

To derive higher order energy estimates, we first commute derivatives with the vorticity equations. For a given multi-index $\beta$ with $1\le |\beta |\le N_*$, we apply $\partial ^\beta$ to the system (1.7) and we obtain

$$\begin{aligned} \left\{ \begin{aligned}&\partial _tj_+^{(\beta )}+Z_-\cdot \nabla j_+^{(\beta )}-\mu \Delta j_+^{(\beta )}=\rho _+^{(\beta )},\\&\partial _tj_-^{(\beta )}+Z_+\cdot \nabla j_-^{(\beta )}-\mu \Delta j_-^{(\beta )}=\rho _-^{(\beta )}, \end{aligned}\right. \end{aligned}$$

(2.70)

where source terms $\rho _\pm ^{(\beta )}$ are defined as

$$\begin{aligned} \rho _+^{(\beta )}&=-\partial ^\beta (\nabla z_-\wedge \nabla z_+)-[\partial ^\beta ,z_-\cdot \nabla ] j_+,\\ \rho _-^{(\beta )}&=-\partial ^{\beta }(\nabla z_+\wedge \nabla z_-)-[\partial ^\beta ,z_+\cdot \nabla ] j_-. \end{aligned}$$

Then we could obtain the following proposition concerning the energy estimates to (2.70).

Proposition 2.22

Assume that $R\ge 100$, $\mu$ is very small and

$$\begin{aligned} E_\pm ^k\le 2C_1\varepsilon ^2, \ \ \text {for}\ \ 0\le k\le N_* \end{aligned}$$

for $\varepsilon$ sufficiently small. Then under the assumption (2.1) (or (2.6)), we obtain

$$\begin{aligned} \begin{aligned}&\sum _{k=1}^{N_*}\bigl (E_\pm ^k(t) + \sup _{u_\pm }F_\pm ^{k}(j_\pm ) +D^{k}_+(t)\bigr ) \\&\quad \lesssim \sum _{k=1}^{N_*} E_\pm ^{k}(0) +\sup _{k\le N_*}\bigl (E_\pm ^k\bigr )^{\frac{1}{2}}\sup _{u_\pm }F_\pm ^0(\nabla {z}_{\pm }) +\frac{1}{R^2} E_\pm ^{0}(t)+\frac{2}{R^2} D_\pm ^{0}(t)\\&\quad +{\mu ^2}\int _0^t\int _{\Sigma _\tau }\langle w_{\mp } \rangle ^2\big (\log \langle w_{\mp } \rangle \big )^4|\nabla j_\pm ^{(N_*+1)}|^2dxd\tau . \end{aligned} \end{aligned}$$

(2.71)

Proof

We divide the proof into several steps:

Step 1. Energy estimate for the linear system. Applying (2.35) to (2.70) and choosing the weight functions $\lambda _\pm$ to be $\langle w_{\mp } \rangle ^2 \big (\log \langle w_{\mp } \rangle \big )^4$ yield (we only deal with the left-traveling waves)

$$\begin{aligned} \begin{aligned}&\int _{\Sigma _t}\langle w_{-} \rangle ^2 \big (\log \langle w_{-} \rangle \big )^4 |j_+^{(\beta )}|^2dx + \sup _{u_+}F_+^{(\beta )}(j_+)\\&\quad +\frac{1}{2}\mu \int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2 \big (\log \langle w_{-} \rangle \big )^4|\nabla j_+^{(\beta )}|^2 dxd\tau \\&\quad \le 2\int _{\Sigma _0}\langle w_{-} \rangle ^2 \big (\log \langle w_{-} \rangle \big )^4 |j_+^{(\beta )}|^2dx + 4\underbrace{\int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^4 |j_+^{(\beta )}||\rho ^{(\beta )}_+|dxd\tau }_{\text {nonlinear interaction } I} \\&\quad +2\underbrace{{\mu }\int _0^t\int _{\Sigma _\tau }(\log \langle w_{-} \rangle )^4|j_+^{(\beta )}|^2dxd\tau }_{\text {diffusion term } II} +2\underbrace{{\mu ^2}\int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^4|\nabla ^2 j_+^{(\beta )}|^2dxd\tau }_{\text {parabolic term } III}, \end{aligned} \end{aligned}$$

(2.72)

where we have used the fact that $\Big |\frac{|\nabla \lambda _+|^2}{\lambda _+}\Big | \lesssim \big (\log \langle w_{-} \rangle \big )^4$ for the diffusion term II ($\lambda _+ = \langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^4$).

Step 2. Estimates on the nonlinear interactions. This step is devoted to the study of the nonlinear interaction term I in (2.72). The source term $\rho _+^{(\beta )}$ in (2.70) can be bounded by

$$\begin{aligned} \begin{aligned} |\rho _+^{(\beta )}|&\le \sum _{\gamma \le \beta } C_\beta ^\gamma |\nabla z_-^{(\gamma )}||\nabla z_+^{(\beta -\gamma )}| +\sum _{0\ne \gamma \le \beta } C_\beta ^\gamma |z_-^{(\gamma )}||\nabla j_+^{(\beta -\gamma )}|\\&\quad {\mathop {\lesssim }\limits ^{|\nabla j_+^{(\beta -\gamma )}|\le |\nabla z_+^{(|\beta |-(|\gamma |-1))}|}}\sum _{k\le |\beta |} |\nabla z_-^{(k)}||\nabla z_+^{(|\beta |-k)}|. \end{aligned} \end{aligned}$$

(2.73)

As a consequence, we obtain

$$\begin{aligned} \begin{aligned} I&\lesssim \sum _{k\le |\beta |} \int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^4|j_+^{(\beta )}||\nabla z_-^{(k)}||\nabla z_+^{(|\beta |-k)}|dxd\tau . \end{aligned} \end{aligned}$$

(2.74)

According to the size of $|\beta |$, we have two cases:

Case 1. $1\le |\beta | \le N_*-2$.

In this case, we can use Sobolev inequality on $\nabla z_-^{(k)}$ because $k+2\le N_*$. Therefore, we have

$$\begin{aligned} \begin{aligned} I&\lesssim \sum _{k\le |\beta |} \int _0^t\int _{\Sigma _\tau } \frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2 j_+^{(\beta )}\cdot \langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2|\nabla z_+^{(|\beta |-k)}|}{\langle w_+\rangle \big (\log \langle w_+\rangle \big )^2}\\&\quad \underbrace{\langle w_+\rangle \big (\log \langle w_+\rangle \big )^2|\nabla z_-^{(k)}|}_{L^\infty }dxd\tau \\&{\mathop {\lesssim }\limits ^{(2.8)}}\sum _{k\le |\beta |}\sum _{l=k}^{k+2}\bigl (E_-^l\bigr )^{\frac{1}{2}}\underbrace{\int _0^t\int _{\Sigma _\tau }\frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2 j_+^{(\beta )}\cdot \langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2|\nabla z_+^{(|\beta |-k)}|}{\langle w_+\rangle \big (\log \langle w_+\rangle \big )^2}dxd\tau }_{I_{1}}. \end{aligned} \end{aligned}$$

To bound $I_{1}$, we will make use of (2.16). In fact, we have

$$\begin{aligned} \begin{aligned} I_{1}&\lesssim \int _0^t\int _{\Sigma _\tau } \frac{\langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^4|j_+^{(\beta )}|^2}{\langle w_+\rangle \big (\log \langle w_+\rangle \big )^2}dxd\tau \\&\quad +\sum _{k\le |\beta |} \underbrace{\int _0^t\int _{\Sigma _\tau } \frac{\langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^4|\nabla z_+^{(k)}|^2}{\langle w_+\rangle \big (\log \langle w_+\rangle \big )^2}dxd\tau }_{\text {apply } (2.16)}\\&\lesssim \sum _{1\le k\le |\beta |}\int _0^t\int _{\Sigma _\tau } \frac{\langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^4|j_+^{(k)}|^2}{\langle w_+\rangle \big (\log \langle w_+\rangle \big )^2}dxd\tau \\&\quad +\int _0^t\int _{\Sigma _\tau } \frac{\langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^4|\nabla z_+|^2}{\langle w_+\rangle \big (\log \langle w_+\rangle \big )^2}dxd\tau . \end{aligned} \end{aligned}$$

(2.75)

Remark 2.23

We remark that, when one applies (2.16), one has to stop at $\nabla z_+$ instead of descending one more step to $z_+$. The main obstacle is that the weight functions for the lowest order terms are different from those for higher order terms. In fact, in the course of using (2.16), the weight functions for lowest order term takes the form $\frac{|\nabla \lambda |^2}{\lambda }$. Since in (2.75) the weight function is a mixture of $w_+$ and $w_-$, the differentiation on $\lambda$ cannot lower the weights in $w_-$.

From (2.75), we can repeat the proof for (2.47) and (2.48). This allows us to use the flux terms to control $I_{1}$. Finally we are led to

$$\begin{aligned} I\lesssim \sup _{l\le N_*}\bigl (E_-^l\bigr )^{\frac{1}{2}}\bigl (F_+^0+\sum _{1\le k\le |\beta |} F_+^k\bigr ). \end{aligned}$$

Case 2. $|\beta | = N_*-1$ or $N_*$.

We rewrite I as

$$\begin{aligned} \begin{aligned} I&\lesssim \Big (\underbrace{\sum _{k\le N_*-2}}_{I_1} +\underbrace{\sum _{N_*-1 \le k\le |\beta |}}_{I_2}\Big ) \int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^2|j_+^{(\beta )}||\nabla z_-^{(k)}||\nabla z_+^{(|\beta |-k)}|dxd\tau . \end{aligned} \end{aligned}$$

The first sum $I_1$ can be controlled in the same manner as in Case 1 so that

$$\begin{aligned} I_1\lesssim \sup _{l\le N_*}\bigl (E_-^l\bigr )^{\frac{1}{2}}\bigl (F_+^0+\sum _{1\le k\le |\beta |} F_+^k\bigr ). \end{aligned}$$

For $k\ge N_*-1$, one can not use $L^\infty$ estimates directly on $\nabla z_-^{(k)}$ since one can not afford more than $N_*$ derivatives (via Sobolev inequality). Instead, we will use $L^\infty$ estimates on $\nabla z_+^{(|\beta |-k)}$ in a different way:

$$\begin{aligned} \begin{aligned} I_2&\lesssim \sum _{k =N_*-1}^{|\beta |} \int _0^t \int _{\Sigma _\tau }\underbrace{\frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^{\frac{1}{2}}\log \langle w_+\rangle }|j_+^{(\beta )}|}_{L^2_\tau L^2_x} \cdot \underbrace{\langle w_+\rangle \big (\log \langle w_+\rangle \big )^2 |\nabla z_-^{(k)}|}_{L^\infty _\tau L^2_x}\\&\quad \cdot \underbrace{\frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^{\frac{1}{2}}\log \langle w_+\rangle }|\nabla z_+^{(|\beta |-k)}|}_{L^2_\tau L^\infty _x}dxd\tau \\&\lesssim \sum _{k =N_*-1}^{|\beta |}\,\, \underbrace{\bigg \Vert \frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^{\frac{1}{2}}\log \langle w_+\rangle }j_+^{(\beta )} \bigg \Vert _{L^2_\tau L^2_x}}_{\lesssim \bigl (\sup _{u_+}F_+^{\beta }(j_+)\bigr )^{\frac{1}{2}}} \ \underbrace{\Vert \langle w_+\rangle \big (\log \langle w_+\rangle \big )^2 \nabla z_-^{(k)}\Vert _{L^\infty _\tau L^2_x}}_{\le \bigl (E_-^k\bigr )^{\frac{1}{2}}} \\&\quad \underbrace{\bigg \Vert \frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^{\frac{1}{2}}\log \langle w_+\rangle } \nabla z_+^{(|\beta |-k)}\bigg \Vert _{L^2_\tau L^\infty _x}}_{I_{2}'}, \end{aligned} \end{aligned}$$

where we bounded the first term in the righthand side in the same manner as (2.47) and (2.48). Therefore, we obtain

$$\begin{aligned} \begin{aligned} I_2\lesssim \sup _{N_*-1\le k\le |\beta |}\bigl (E_-^k\bigr )^{\frac{1}{2}}\bigl (F_+^{|\beta |}\bigr )^{\frac{1}{2}}\sum _{k =0}^{|\beta |+1-N_*}\underbrace{\bigg \Vert \frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^{\frac{1}{2}}\log \langle w_+\rangle } \nabla z_+^{(k)}\bigg \Vert _{L^2_\tau L^\infty _x}}_{I_2'}. \end{aligned} \end{aligned}$$

(2.76)

For the most difficult term $I_2'$, we use Sobolev inequality with weight function $\frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^{\frac{1}{2}}\log \langle w_+\rangle }$. In fact, we have

$$\begin{aligned}&|I_2'|^2\lesssim \bigg \Vert \frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^{\frac{1}{2}}\log \langle w_+\rangle }\nabla z_+^{(k)}\bigg \Vert _{L^2_\tau (L^2(\Sigma _\tau ))}^2 +\bigg \Vert \nabla ^2\big (\frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^{\frac{1}{2}}\log \langle w_+\rangle }\nabla z_+^{(k)}\big )\bigg \Vert _{L^2_\tau (L^2(\Sigma _\tau ))}^2. \end{aligned}$$

Since $\nabla ^l\big (\frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^{\frac{1}{2}}\log \langle w_+\rangle }\big ) \lesssim \frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^{\frac{1}{2}}\log \langle w_+\rangle }$ for $l=1,2$, we have

$$\begin{aligned} |I_2'|^2&\lesssim \sum _{l=k}^{k+2}\bigg \Vert \frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^{\frac{1}{2}}\log \langle w_+\rangle }\nabla z_+^{(l)}\bigg \Vert _{L^2_\tau L^2_x}^2\\&{\mathop {\lesssim }\limits ^{(2.16)}} \bigg \Vert \frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^{\frac{1}{2}}\log \langle w_+\rangle }\nabla z_+\bigg \Vert _{L^2_\tau L^2_x}^2+\sum _{1\le l\le k+2}\bigg \Vert \frac{\langle w_{-} \rangle \big (\log \langle w_{-} \rangle \big )^2}{\langle w_+\rangle ^{\frac{1}{2}}\log \langle w_+\rangle } j_+^{(l)}\bigg \Vert _{L^2_\tau L^2_x}^2.\\&\lesssim F_+^0+\sum _{1\le l\le k+2} F_+^l, \end{aligned}$$

where we bound $I_2'$ by the flux terms in a similar manner as for (2.47) and (2.48). Then we have

Finally, we can bound the nonlinear interaction term I by

$$\begin{aligned} I \lesssim \sup _{k\le N_*}\bigl (E_-^k\bigr )^{\frac{1}{2}}\bigl (F_+^0+\sum _{1\le k\le |\beta |} F_+^k\bigr ). \end{aligned}$$

(2.77)

Step 3 Completion of the higher order energy estimates. For the diffusion term II, we have for $1\le |\beta |\le N_*$,

$$\begin{aligned} II\le \frac{2\mu }{R^2}\int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2(\log \langle w_{-} \rangle )^4|\nabla z_+^{(|\beta |)}|^2dxd\tau =\frac{2}{R^2} D_+^{|\beta |-1}(t). \end{aligned}$$

Thanks to the div-curl lemma (Lemma 2.6), we have

$$\begin{aligned}&\int _{\Sigma _t}\langle w_{-} \rangle ^2 \big (\log \langle w_{-} \rangle \big )^4 |\nabla z_+^{(|\beta |)}|^2dx\le \int _{\Sigma _t}\langle w_{-} \rangle ^2 \big (\log \langle w_{-} \rangle \big )^4 |j_+^{(|\beta |)}|^2dx\\&\quad +\frac{1}{R^2}\int _{\Sigma _t}\langle w_{-} \rangle ^2 \big (\log \langle w_{-} \rangle \big )^4 |z_+^{(|\beta |)}|^2dx \end{aligned}$$

and

$$\begin{aligned}&\mu \int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2 \big (\log \langle w_{-} \rangle \big )^4|\nabla z_+^{(|\beta |+1)}|^2dxd\tau \\&\quad \le \mu \int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2 \big (\log \langle w_{-} \rangle \big )^4|\nabla j_+^{(|\beta |)}|^2dxd\tau \\&\quad +\frac{\mu }{R^2}\int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2 \big (\log \langle w_{-} \rangle \big )^4|\nabla z_+^{(|\beta |)}|^2dxd\tau . \end{aligned}$$

These estimates enable us to replace the first and the third term in the left hand side of (2.72) by the terms in the left hand side of the above two estimates respectively. Then with the estimates on I and II, we obtain that

$$\begin{aligned} \begin{aligned}&E_+^{|\beta |}(t) + \sup _{u_+}F_+^{|\beta |}(j_+) +D^{|\beta |}_+(t) \\&\quad \lesssim E_+^{|\beta |}(0)+\sup _{k\le N_*}\bigl (E_-^k\bigr )^{\frac{1}{2}} F_+^0+\sup _{k\le N_*}\bigl (E_-^k\bigr )^{\frac{1}{2}}\sum _{1\le k\le |\beta |} F_+^k+\frac{1}{R^2} E_+^{|\beta |-1}(t)\\&\quad +\frac{2}{R^2} D_+^{|\beta |-1}(t) +\underbrace{{\mu ^2}\int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^4|\nabla ^2 j_+^{(|\beta |)}|^2dxd\tau }_{\text {parabolic term } III\ \lesssim \ \mu D^{|\beta |+1}_+(t)}. \end{aligned} \end{aligned}$$

(2.78)

Then we sum up (2.78) for all $1\le |\beta |\le N_*$: each flux term $\sup _{k\le N_*}\bigl (E_-^k\bigr )^{\frac{1}{2}}\sum _{1\le k\le |\beta |} F_+^k$ from the righthand side of (2.78), by virtue of assumption $\sup _{k\le N_*} E_-^k\le 2C_1\varepsilon ^2$ with sufficiently small $\varepsilon$, they are absorbed by the sum of the lower flux for $1\le k\le |\beta |$ on the lefthand side; each energy term $\frac{1}{R^2} E_+^{|\beta |-1}(t)$ and each diffusion term $\frac{2}{R^2} D_+^{|\beta |-1}(t)$ except for $|\beta |=1$ can be controlled from the estimates for lower order terms, by taking R large, they are absorbed by lower order energy and diffusion terms on the lefthand side; all parabolic terms III except for $|\beta |=N_*$ can also be controlled from the viscosity terms on the lefthand side for higher order terms($\mu<<1$). Therefore, we finally obtain that

$$\begin{aligned} \begin{aligned}&\sum _{k=1}^{N_*}\bigl (E_+^k(t) + \sup _{u_+}F_+^{k}(j_+) +D^{k}_+(t)\bigr ) \\&\quad \lesssim \sum _{k=1}^{N_*} E_+^{k}(0)+\sup _{k\le N_*}\bigl (E_-^k\bigr )^{\frac{1}{2}}F_+^0+\frac{1}{R^2} E_+^{0}(t)+\frac{2}{R^2} D_+^{0}(t)\\&\qquad +{\mu ^2}\int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^4|\nabla j_+^{(N_*+1)}|^2dxd\tau . \end{aligned} \end{aligned}$$

(2.79)

This ends the proof. $\square$

Combining (2.38), (2.60) and (2.71), we could obtain the following proposition.

Proposition 2.24

Assume that R is very large, $\mu$ is very small, $\Vert {z}_{\pm }\Vert _{L^\infty }\le \frac{1}{2}$ and

$$\begin{aligned} E_\pm ^k\le 2C_1\varepsilon ^2, \ \ \text {for}\ \ 0\le k\le N_* \end{aligned}$$

for $\varepsilon$ sufficiently small. Then under the assumption (2.1) (or (2.6)), we obtain

$$\begin{aligned} \begin{aligned}&E_\pm +\sum _{0\le k\le N_*}E_\pm ^{k}+ \sup _{u_\pm }F_\pm (z_\pm ) +\sup _{u_\pm }F_\pm ^{0}(\nabla z_\pm )\\&\quad +\sum _{1\le k\le N_*} \sup _{u_\pm }F_\pm ^{k}(j_\pm ) +D_\pm +\sum _{0\le k\le N_*}D_{\pm }^{k}\\&\quad \lesssim E_\pm (0)+\sum _{0\le k\le N_*} E_\pm ^{k}(0) + \underbrace{{\mu ^2}\int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2\big (\log \langle w_{-} \rangle \big )^4|\nabla j_+^{(N_*+1)}|^2dxd\tau }_{\text {top order parabolic term}}. \end{aligned} \end{aligned}$$

(2.80)

Top Order Parabolic Estimates

This section is devoted to a typical parabolic type estimate designed to control the highest order terms due to the presence of non-zero viscosity. We only study the estimates for the left-traveling Alfvén wave $z_+$. The estimates for the right-traveling waves can be derived exactly in the same manner.

For $|\beta |= N_*+1$, we work with the following system of equations

$$\begin{aligned} \left\{ \begin{aligned}&\partial _tj_+^{(\beta )}+Z_-\cdot \nabla j_+^{(\beta )}-\mu \Delta j_+^{(\beta )}=\rho _+^{(\beta )},\\&\partial _tj_-^{(\beta )}+Z_+\cdot \nabla j_-^{(\beta )}-\mu \Delta j_-^{(\beta )}=\rho _-^{(\beta )}. \end{aligned}\right. \end{aligned}$$

(2.81)

Then we shall prove the following proposition.

Proposition 2.25

Assume that $R\ge 100$ and $\mu$ is sufficiently small. Then under the ansatz (2.1), we have

$$\begin{aligned} \begin{aligned}&\mu E_+^{N_*+1}(t)+\mu D_+^{N_*+1}(t)\\&\quad \lesssim \mu E_+^{N_*+1}(0) +\mu E_+^{N_*}(t)+\mu D_+^{N_*}(t)+\left( \sup _{l\le N_*} \bigl (E_-^l\bigr )^{\frac{1}{2}}\right. \\&\quad + \left. \left( \sum _{k=1}^{N_*} D_-^k(t)\right) ^{\frac{1}{2}}\right) \left( \sup _{l\le N_*}E_+^l+\sum _{k=1}^{N_*} D_+^k(t)\right) . \end{aligned} \end{aligned}$$

(2.82)

Proof

Applying (2.34) to (2.81) and choosing the weight functions $\lambda _\pm =\mu \langle w_{\mp } \rangle ^2 \big (\log \langle w_{\mp } \rangle \big )^4$ (we only deal with the left-traveling waves) yield

$$\begin{aligned}&\mu \int _{\Sigma _t}\langle w_{-} \rangle ^2 \big (\log \langle w_{-} \rangle \big )^4|j_+^{(\beta )}|^2dxd\tau +\mu ^2\int _{0}^t\int _{\Sigma _\tau } \langle w_{-} \rangle ^2 \big (\log \langle w_{-} \rangle \big )^4 |\nabla j_+^{(\beta )}|^2dxd\tau \nonumber \\&\quad \lesssim \mu E_+^{|\beta |+1}(0) +\underbrace{ \mu \int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2 \big (\log \langle w_{-} \rangle \big )^4|\rho _+^{(\beta )}|\cdot |j_+^{(\beta )}|dxd\tau }_{\text {nonlinear interaction } I}\nonumber \\&\quad +\underbrace{ \mu ^2 \int _0^t\int _{\Sigma _\tau }\big (\log \langle w_{-} \rangle \big )^4|j_+^{(\beta )}|^2dxd\tau }_{\text {diffusion term } II\lesssim \mu D_+^{|\beta |-1}(t)} \end{aligned}$$

(2.83)

It remains to control the nonlinear term I. We recall (2.73) ($|\beta |=N_*+1$)

$$\begin{aligned} |\rho _+^{(\beta )}|\lesssim \sum _{k \le N_*+1}|\nabla z_-^{(k)}||\nabla z_+^{(N_*+1-k)}|. \end{aligned}$$

We rewrite I as

$$\begin{aligned}&I\lesssim \mu \left( \underbrace{\sum _{k \le N_*-2}}_{I_{1}}+\underbrace{\sum _{N_*-1\le k\le N_*+1}}_{I_{2}}\right) \int _0^t\int _{\Sigma _\tau }\langle w_{-} \rangle ^2 \big (\log \langle w_{-} \rangle \big )^4\\&\qquad \quad |\nabla z_-^{(k)}||\nabla z_+^{(N_*+1-k)}||j_+^{(\beta )}|dxd\tau . \end{aligned}$$

For $I_{1}$, since $k\le N_*-2$, we bound $\langle w_+\rangle \big (\log \langle w_+\rangle \big )^2 \nabla z_-^{(k)}$ in $L^\infty$. Hence,

For $I_{2}$, we proceed as follows:

Finally, we have

$$\begin{aligned} I\lesssim \big (\sup _{l\le N_*} \bigl (E_-^l\bigr )^{\frac{1}{2}} + \bigl (\sum _{k=1}^{N_*} D_-^k(t)\bigr )^{\frac{1}{2}}\big )\big (\sup _{l\le N_*} E_+^l+\sum _{k=1}^{N_*} D_+^k(t)\big ). \end{aligned}$$

(2.84)

Going back to (2.83), by virtue of div-curl lemma (Lemma 2.6), we can replace the first term and the second term in the lefthand side of (2.83) by $\mu E_+^{N_*+1}(t)-\mu E_+^{N_*}(t)$ and $\mu D_+^{N_*+1}(t)-\mu D_+^{N_*}(t)$. Then thanks to (2.84), we obtain the top order parabolic estimates (2.82). This ends the proof of the proposition. $\square$

Combining (2.80) and (2.82), we obtain the total energy estimates and then close the energy estimates.

Proposition 2.26

Assume that $R\ge 100$, $\mu$ is very small, $\Vert {z}_{\pm }\Vert _{L^\infty }\le \frac{1}{2}$ and

$$\begin{aligned} E_\pm ^k+D_\pm ^k\le 2C_1\varepsilon ^2, \ \ \text {for}\ \ 0\le k\le N_* \end{aligned}$$

for $\varepsilon$ sufficiently small. Then under the assumption (2.1) (or (2.6)), we obtain

$$\begin{aligned} \begin{aligned}&E_\pm +\sum _{0\le k\le N_*}E_\pm ^{k}+\mu E_\pm ^{N_*+1}+ \sup _{u_\pm }F_\pm (z_\pm )+\sup _{u_\pm }F_\pm ^{0}(\nabla z_\pm )+\sum _{1\le k\le N_*} \sup _{u_\pm }F_\pm ^{k}(j_\pm ) \\&\quad +D_\pm +\sum _{0\le k\le N_*}D_{\pm }^{k}+\mu D_{\pm }^{N_*+1} \lesssim E_\pm (0)+\sum _{k=0}^{N_*} E_\pm ^{k}(0)+ \mu E_\pm ^{N_*+1}(0). \end{aligned} \end{aligned}$$

(2.85)

Proof of the Main A Priori Estimates and Theorem 1.2

We now complete the continuity argument (from Sect. 2.1) and hence the proof of Theorem 1.2. It consists of four steps.

Step 1 Improving ansatz (2.3). Under the ansatz (2.1), (2.2) and (2.3) by virtue of Proposition 2.26, taking $\varepsilon$ sufficiently small, we can find such $C_1>0$ such that

$$\begin{aligned} \begin{aligned}&E_\pm +\sum _{0\le k\le N_*}E_\pm ^{k}+\mu E_\pm ^{N_*+1}+ \sup _{u_\pm }F_\pm (z_\pm )+\sup _{u_\pm }F_\pm ^{0}(\nabla z_\pm )+\sum _{1\le k\le N_*} \sup _{u_\pm }F_\pm ^{k}(j_\pm )\\&\quad +D_\pm +\sum _{0\le k\le N_*}D_{\pm }^{k}+\mu D_{\pm }^{N_*+1} \le C_1\mathcal {E}_0^\mu \le C_1\varepsilon ^2. \end{aligned} \end{aligned}$$

This improves the Ansatz 2.3.

Step 2 Improving ansatz (2.1) (or equivalently (2.6)). We just improve the ansatz (2.6).

We recall that $\psi _{\pm }(t,y)$ be the flow generated by $Z_{\pm }$ and they are given by

$$\begin{aligned} \psi _{\pm }(t,y)=y+\int _0^tZ_{\pm }(\tau ,\psi _{\pm }(\tau ,y))d\tau =y \pm t B_0+\int _0^tz_{\pm }(\tau ,\psi _{\pm }(\tau ,y))d\tau . \end{aligned}$$

We only give the proof for $\psi _+$. According to (2.5), we have

$$\begin{aligned} \frac{\partial \psi _+(t,y)}{\partial y}={{\mathrm{I}}}+\int _0^t(\nabla z_+)(\tau ,\psi _+(\tau ,y))\frac{\partial \psi _+(\tau ,y)}{\partial y}d\tau . \end{aligned}$$

(2.86)

Therefore, we have

$$\begin{aligned} \big |\frac{\partial \psi _+(t,y)}{\partial y}-{{\mathrm{I}}}\big |\le & {} \int _0^t|(\nabla z_+)(\tau ,\psi _+(\tau ,y))|\big |\frac{\partial \psi _+(\tau ,y)}{\partial y}-{{\mathrm{I}}}\big |d\tau \\&+\int _0^t|(\nabla z_+)(\tau ,\psi _+(\tau ,y))|d\tau . \end{aligned}$$

It suffices to bound the righthand side of the above equation, which is denoted by G(t, y). We deduce from (2.86) that

$$\begin{aligned} \frac{d}{dt}G(t,y)&=|(\nabla z_+)(t,\psi _+(t,y))|\big |\frac{\partial \psi _+(t,y)}{\partial y}-I\big |+|(\nabla z_+)(t,\psi _+(t,y))|\\&\le |(\nabla z_+)(t,\psi _+(t,y))|G(t,y)+|(\nabla z_+)(t,\psi _+(t,y))|. \end{aligned}$$

By virtue of Gronwall’s inequality, we obtain

$$\begin{aligned} G(t,y)&\le \int _0^t\exp \Bigl (\int _s^t|(\nabla z_+)(\tau ,\psi _+(\tau ,y))|d\tau \Bigr )|(\nabla z_+)(s,\psi _+(s,y))|ds\\&\le \exp \Bigl (\int _0^t|(\nabla z_+)(\tau ,\psi _+(\tau ,y))|d\tau \Bigr )\underbrace{\int _0^t|(\nabla z_+)(\tau ,\psi _+(\tau ,y))|d\tau }_{A}. \end{aligned}$$

Then, to get the bound of G(t, y), we have to bound the integration A. Firstly, by (2.8) and ansatz (2.3), we have

$$\begin{aligned} |\nabla z_+(\tau ,\psi _+(\tau ,y))|&\lesssim \frac{\varepsilon }{\langle w_{-} \rangle (\log \langle w_{-} \rangle )^2}\\&\lesssim \frac{\varepsilon }{(R^2+|u_-|^2)^{\frac{1}{2}}\big (\log (R^2+|u_-|^2)^{\frac{1}{2}}\big )^2 \big |_{x=\psi _+(\tau ,y)}}. \end{aligned}$$

Then we will switch the variable $\tau$ to $u_-$ in the integration A. To do this, we have to calculate the Jacobian as follows

$$\begin{aligned} \frac{d}{d\tau }u_-(\tau ,\psi _+(\tau ,y))=(\partial _t u_-)(\tau ,\psi _+(\tau ,y))+\partial _t\psi _+(\tau ,y)\cdot (\nabla u_-)(\tau ,\psi _+(\tau ,y)) \end{aligned}$$

Notice that $L_-u_-=0$ and $\partial _t\psi _+(\tau ,y)=Z_+(\tau ,\psi _+(\tau ,y))$, we have

$$\begin{aligned} \begin{aligned} \frac{d}{d\tau }u_-(\tau ,\psi _+(\tau ,y))&=(Z_+-Z_-)(\tau ,\psi _+(\tau ,y))\cdot (\nabla u_-)(\tau ,\psi _+(\tau ,y))\\&=2(\partial _3 u_-)\big |_{x=\psi _+(\tau ,y)}+\bigl ((z_+-z_-)\cdot (\nabla u_-)\bigr )\big |_{x=\psi _+(\tau ,y)}\\&{\mathop {\ge }\limits ^{(2.1), (2.2)}}1-4\sqrt{2C_0}\varepsilon . \end{aligned} \end{aligned}$$

By taking $\varepsilon$ small, we obtain

$$\begin{aligned} \frac{d}{d\tau }u_-(\tau ,\psi _+(\tau ,y))\ge \frac{1}{2}. \end{aligned}$$

(2.87)

With the above inequality, by changing variables, we have

$$\begin{aligned} A&\lesssim \int _0^t\frac{\varepsilon }{(R^2+|u_-|^2)^{\frac{1}{2}} \big (\log (R^2+|u_-|^2)^{\frac{1}{2}}\big )^2\big |_{x=\psi _+(t,y)}}d\tau \\&\lesssim \int _0^\infty \frac{\varepsilon }{(R^2+|u_-|^2)^{\frac{1}{2}}(\log (R^2+|u_-|^2)^{\frac{1}{2}})^2} du_-\sup _{\tau }\frac{1}{\frac{d}{d\tau }u_-(\tau ,\psi _+(\tau ,y))}\\&{\mathop {\lesssim }\limits ^{(2.87)}}\varepsilon . \end{aligned}$$

This implies

$$\begin{aligned} \Big |\frac{\partial \psi _{\pm }(t,y)}{\partial y}-{{\mathrm{I}}}\Big |\le e^AA\le C_0' \varepsilon . \end{aligned}$$

(2.88)

This improves the first part of ansatz (2.6).

To improve the second part, applying $\partial _k$ (with $k=1,2,3$) to (2.86), one gets by the chain rule that

$$\begin{aligned} \begin{aligned} \partial _k\Bigl (\frac{\partial \psi _+(t,y)}{\partial x}\Bigr )=&\int _0^t(\nabla z_+)(\tau ,\psi _+(\tau ,y))\partial _k\Bigl (\frac{\partial \psi _+(\tau ,y)}{\partial y}\Bigr )d\tau \\&+\int _0^t\partial _k\Bigl ((\nabla z_+)(\tau ,\psi _+(\tau ,y))\Bigl )\Bigl (\frac{\partial \psi _+(\tau ,y)}{\partial y}\Bigr )d\tau , \end{aligned} \end{aligned}$$

from which and Gronwall’s inequality, we obtain that

$$\begin{aligned} \begin{aligned}&\big |\partial _k\Bigl (\frac{\partial \psi _+(t,y)}{\partial y}\Bigr )\big |\le \exp \Bigl (\int _0^t|(\nabla z_+)(\tau ,\psi _+(\tau ,y))|d\tau \Bigr )\\&\quad \int _0^t|(\partial ^2 z_+)(\tau ,\psi _+(\tau ,y))|\big |\frac{\partial \psi _+(\tau ,y)}{\partial y}\big |^2d\tau . \end{aligned} \end{aligned}$$

Thanks to (2.88), we then obtain that

$$\begin{aligned} \big |\partial _k\Bigl (\frac{\partial \psi _+(t,y)}{\partial y}\Bigr )\big |\le 2 \exp \Bigl (\underbrace{\int _0^t|(\nabla z_+)(\tau ,\psi _+(\tau ,y))|d\tau }_{A}\Bigr )\underbrace{\int _0^t|(\partial ^2 z_+)(\tau ,\psi _+(\tau ,y))|d\tau }_{B}. \end{aligned}$$

The previous proof shows that $A\lesssim \varepsilon$. By virtue of (2.8), we also have

$$\begin{aligned}&|\nabla ^2 z_+(\tau ,\psi _+(\tau ,y))|\lesssim \frac{\varepsilon }{\langle w_{-} \rangle (\log \langle w_{-} \rangle )^2} \\&\quad \lesssim \frac{\varepsilon }{(R^2+|u_-|^2)^{\frac{1}{2}}(\log (R^2+|u_-|^2)^{\frac{1}{2}})^2\big |_{x=\psi _+(\tau ,y)}}. \end{aligned}$$

The same argument as A, we obtain that

$$\begin{aligned} B\lesssim \varepsilon . \end{aligned}$$

Therefore, by taking $\varepsilon$ sufficiently small, we could obtain that

$$\begin{aligned} \Big |\nabla _y\frac{\partial \psi _{\pm }(t,y)}{\partial y}\Big |\le 2e^AB\le C_0'' \varepsilon . \end{aligned}$$

(2.89)

This improves the second part of ansatz (2.6). Notice that one may take $C_0\ge \max \{C_0',C_0''\}$ by taking $\varepsilon$ small enough.

Step 3 Improving ansatz (2.2). The Sobolev inequality (2.8) shows that

$$\begin{aligned} \Vert {z}_{\pm }\Vert _{L^\infty }{\mathop {\le }\limits ^{(2.8)}}\frac{C}{(\log R)^2}\bigl (E_\pm +E_\pm ^0+E_\pm ^1\bigr )^{\frac{1}{2}}{\mathop {\le }\limits ^{(2.3)}} \frac{C\sqrt{6C_1}}{(\log R)^2}\varepsilon {\mathop {\le }\limits ^{\varepsilon \ll 1}}\frac{1}{4}. \end{aligned}$$

This improves ansatz (2.2).

Step 4 Existence and uniqueness. The local existence for smooth data is well-known. The global existence and uniqueness of the solution is a direct consequence of the a priori energy estimate (1.13).

The above four steps complete the proof of Theorem 1.2.

Proof of Main Theorems

Proof of Theorem 1.3

The proof is indeed very similar to and much easier than that of Theorem 1.2: first of all, we do not have diffusion terms; secondly, we can deal with the first order energy estimates and higher order energy estimates in the same way. The treatment of the pressure estimates will be different due to the choice of different weight functions. We only sketch the necessary modifications.

We fix a small number $\delta >0$ and let $\omega =1+\delta$. Let $\langle u_+\rangle = (R^2+|u_+|^2)^\frac{1}{2}$ and $\langle u_{-} \rangle = (R^2+|u_{-}|^2)^\frac{1}{2}$. We define the energy and flux norms as follows:

$$\begin{aligned}&E_{\mp }^{(\alpha )}(t) = \int _{\Sigma _t} \langle u_{\pm } \rangle ^{2\omega } |\nabla z_{\mp }^{(\alpha )}|^2 dx, \ \ F_{\mp }^{(\alpha )}(j_{\mp })=\int _{C_{u_{\mp }}^{\mp }}\langle u_{\pm } \rangle ^{2\omega } |j_{\mp }^{(\alpha )}|^2d\sigma _{\mp }, \ \ |\alpha |\ge 0. \end{aligned}$$

The lowest order energy and flux are defined as

$$\begin{aligned} E_{\mp }(t) = \int _{\Sigma _t} \langle u_{\pm } \rangle ^{2\omega } | z_{\mp }|^2 dx, \ \ \ F_{\mp }(z_{\mp })=\int _{C_{u_{\mp }}^{\mp }}\langle u_{\pm } \rangle ^{2\omega }|z_{\mp }|^2d\sigma _{\mp }. \end{aligned}$$

The total energy norms and total flux norms as defined as before, e.g.,

$$\begin{aligned}&E_{\mp } = \sup _{0\le t\le t^*} E_{\mp }(t),\ \ E_{\mp }^k = \sup _{0\le t\le t^*} \sum _{|\alpha |=k}E_{\mp }^{(\alpha )}(t). \end{aligned}$$

The three sets of ansatz for continuity method remain the same. Since the energy and flux norms are stronger than the original norms, all the estimates in the Sect. 2.2 still hold. We can improve the Sobolev inequalities to

$$\begin{aligned} \begin{aligned} |z_{\mp }|&\lesssim \frac{1}{\langle u_{\pm } \rangle ^{\omega }}\big (E_{\mp } + E^0_{\mp }+E^1_{\mp }\big )^\frac{1}{2},\ \ |\nabla z_{\mp }^{(\alpha )}|\\&\lesssim \frac{1}{\langle u_{\pm } \rangle ^{\omega }} \big (E_{\mp }^{k}+E_{\mp }^{k+1}+E_{\mp }^{k+2}\big )^\frac{1}{2}\ \ \text {for}\ \ |\alpha |=k. \end{aligned} \end{aligned}$$

(3.1)

A Better Control on the Underlying Geometry

The essential improvement in the ideal case is that we can obtain a much more precise picture for the characteristic hypersurfaces.

We recall and repeat some definition and argument from last section. The defining equation for the flow $\psi _{\pm }(t,x)$ generated by $Z_{\pm }$ is $\frac{d}{dt}\psi _{\pm }(t,x)=Z_{\pm }(t,\psi _{\pm }(t,x))$. where $x\in \mathbb {R}^3$. Since ${z}_+= {Z}_+\mp B_0$, we obtain $\psi _{\pm }(t,x)=x \pm t B_0+\int _0^tz_{\pm }(\tau ,\psi _{\pm }(\tau ,x))d\tau$. This is exactly (2.5).

Let $\frac{\partial \psi _{\pm }(t,x)}{\partial x}$ be the differential of $\psi (t,x)$. Repeat the proof for (2.88) and (2.89), we obtain for $k=0,1$

$$\begin{aligned} \big |\partial ^k \Bigl (\frac{\partial \psi _{\pm }(t,x)}{\partial x}-{{\mathrm{I}}}\Bigr )\big |\lesssim \varepsilon . \end{aligned}$$

(3.2)

Similarly, it follows that

$$\begin{aligned} |\nabla u_{\pm }|\le 2, \ \ |\nabla ^2u_{\pm }|\lesssim \varepsilon . \end{aligned}$$

The key improvement can be stated in the following lemma:

Lemma 3.1

For sufficiently small $\varepsilon$, we have

$$\begin{aligned} |u_\pm (t,x)-(x_3\mp t)|\le \frac{C_0 \varepsilon }{\delta R^{\delta }}. \end{aligned}$$

(3.3)

In particular, we can measure the separation of $u_\pm$:

$$\begin{aligned} \Big |\big (u_+-u_-\big )-2t\Big |\lesssim \varepsilon . \end{aligned}$$

Proof

By the definition of $\psi _\pm$, we have

$$\begin{aligned} \psi _{\pm }^3(t,y)=y_3\pm t+\int _0^tz_{\pm }^3(\tau ,\psi _{\pm }(\tau ,x))d\tau , \end{aligned}$$

where $\psi _{\pm }^3$ and $z_{\pm }^3$ are the $x_3$-coordinate component of $\psi _{\pm }$ and $z_{\pm }$ respectively. Since $u_\pm (t,\psi _\pm (t,y))=y_3$, we have

$$\begin{aligned} u_\pm (t,\psi _\pm (t,y))=\psi _{\pm }^3(t,y)\mp t-\int _0^tz_{\pm }^3(\tau ,\psi _{\pm }(\tau ,x))d\tau . \end{aligned}$$

We can repeat the proof (2.88) to derive

$$\begin{aligned} \int _0^t|z_\pm (\tau ,\psi _\pm (\tau ,x))|d\tau \le \frac{C_0\varepsilon }{\delta R^{\delta }}. \end{aligned}$$

This completes the proof of the lemma. $\square$

Remark 3.2

In the viscous case, the decay of $z_\pm$ in the ansatz is roughly $\big (\log (1+|u_\pm |)\big )^{-2}$; in the current situation, the decay of $z_\pm$ in the ansatz is roughly $(1+|u_\pm |)^{-(1+\delta )}$ which is integrable. The faster decay in the ideal case allows us to integrate the equation $z_\pm$. This is why we can control $u_\pm$ in a great precision.

As a corollary, we can measure the separation of $z_\pm$ in terms of decay in t:

Lemma 3.3

(Separation Estimates) For all $\alpha$ and $\beta$ with $|\alpha |,|\beta |\le 2$, we have

$$\begin{aligned} \big |{z}_+^{(\alpha )}(t,x) {z}_-^{(\beta )}(t,x)\big |\lesssim \frac{\varepsilon ^2}{(1+t)^{\omega }}. \end{aligned}$$

(3.4)

Proof

The bootstrap assumptions and the previous lemma immediately imply

$$\begin{aligned} \big |{z}_+^{(\alpha )}(t,x) {z}_-^{(\beta )}(t,x)\big | \le \frac{4\varepsilon ^2}{( 1+|x_3 + t|)^{\omega }(1+|x_3- t|)^{\omega }}. \end{aligned}$$

Since for all $x_3$, at least one of the inequalities $|x_3 + t|\ge \frac{t}{2}$ and $|x_3 - t|\ge \frac{t}{2}$ holds. The above inequality yields the lemma. $\square$

On the contrary, for the self-intersections such as ${z}_+^{(\alpha )}(t,x) {z}_+^{(\beta )}(t,x)$, we can not obtain a decay factor in t. Since near the center of ${z}_+$, the wave is approximately of size $\varepsilon$. The best pointwise estimate one can hope is

$$\begin{aligned} \big |{z}_+^{(\alpha )}(t,x) {z}_+^{(\beta )}(t,x)\big |\lesssim \varepsilon ^2. \end{aligned}$$

The A Priori Energy Estimates in the Ideal Case

We now prove the energy estimates on the lowest order terms. This part corresponds to the estimates derived in Sect. 2.4. We first prove the following pressure estimates: for all $t\in [0,t^*]$, we have

$$\begin{aligned} \Big |\int _0^t\int _{\Sigma _\tau }\langle u_{\mp } \rangle ^{2\omega } |z_\pm ||\nabla p|dxd\tau \Big | \lesssim \varepsilon ^3. \end{aligned}$$

(3.5)

Firstly, by Hölder inequality, we have

$$\begin{aligned}&\Big |\int _0^t\int _{\Sigma _\tau }\langle u_{\mp } \rangle ^{2\omega } |z_\pm ||\nabla p|dxd\tau \Big |\\&\quad \lesssim \Bigl (\int _0^t\int _{\Sigma _\tau }\frac{\langle u_{\mp } \rangle ^{2\omega }}{\langle u_{\pm } \rangle ^{\omega }} |z_\pm |^2dxd\tau \Bigr )^{\frac{1}{2}} \Bigl (\int _0^t\int _{\Sigma _\tau }\langle u_{\mp } \rangle ^{2\omega }\langle u_{\pm } \rangle ^{\omega }|\nabla p|^2dxd\tau \Bigr )^{\frac{1}{2}}. \end{aligned}$$

Changing the variables from $(x_1,x_2,x_3,t)$ to $(x_1,x_2,u_+,u_-)$ (see in Sect. 2.4) and noticing that the denominator $\langle u_{\pm } \rangle ^{\omega }$ is integral in $\langle u_{\pm } \rangle$, we have

$$\begin{aligned} \int _0^t\int _{\Sigma _\tau }\frac{\langle u_{\mp } \rangle ^{2\omega }}{\langle u_{\pm } \rangle ^{\omega }} |z_\pm |^2dxd\tau \lesssim F(z_\pm )\lesssim \varepsilon ^2. \end{aligned}$$

Thus, to prove (3.5), we only need to verify the following inequality:

$$\begin{aligned} \int _0^t\int _{\Sigma _\tau }\langle u_{\mp } \rangle ^{2\omega }\langle u_{\pm } \rangle ^{\omega }|\nabla p|^2dxd\tau \lesssim \varepsilon ^4. \end{aligned}$$

(3.6)

To derive the above estimates, we first decompose $\nabla p$ as

$$\begin{aligned} \begin{aligned} \nabla p(t,x)=&\underbrace{-\frac{1}{4\pi }\int _{\mathbb {R}^3}\nabla \frac{1}{|x-y|}\theta (|x-y|)(\partial _iz_-^j\partial _jz_+^i)(t,y)dy}_{A_1(t,x)}\\&\underbrace{-\frac{1}{4\pi }\int _{\mathbb {R}^3}\partial _i\partial _j\Bigl (\nabla \frac{1}{|x-y|}\bigl (1-\theta (|x-y|)\bigr )\Bigr )(z_-^iz_+^j)(t,y)dy}_{A_2(t,x)}. \end{aligned} \end{aligned}$$

(3.7)

where the smooth cut-off function $\theta (r)$ is chosen in such way that $\theta (r)\equiv 1$ for $r\le 1$ and $\theta (r)\equiv 0$ for $r\ge 2$. Therefore, it suffices to bound the following two terms:

$$\begin{aligned} \underbrace{\int _0^t\int _{\Sigma _\tau }\langle u_{-} \rangle ^{2\omega }\langle u_+\rangle ^{\omega }|A_1|^2dxd\tau }_{I_{1}} +\underbrace{\int _0^t\int _{\Sigma _\tau }\langle u_{-} \rangle ^{2\omega }\langle u_+\rangle ^{\omega }|A_2|^2dxd\tau }_{I_{2}}. \end{aligned}$$

By definition, we have

$$\begin{aligned} \langle u_{-} \rangle ^{\omega }\langle u_+\rangle ^{\frac{\omega }{2}}|A_1| \le \int _{|x-y|\le 2}\frac{|\nabla z_-(\tau ,y)||\nabla z_+(\tau ,y)|\langle u_{-} \rangle ^{\omega }(\tau ,x)\langle u_+\rangle ^{\frac{\omega }{2}}(\tau ,x)}{|x-y|^2}dy. \end{aligned}$$

For $|x-y|\le 2$, it is straightforward to check that $\langle u_{\pm } \rangle (\tau ,x) \lesssim \langle u_{\pm } \rangle (\tau ,y)$. Hence,

$$\begin{aligned} \begin{aligned} \langle u_{-} \rangle ^{\omega }\langle u_+\rangle ^{\frac{\omega }{2}}|A_1|&\lesssim \int _{|x-y|\le 2}\frac{|\nabla z_-(\tau ,y)||\nabla z_+(\tau ,y)|\langle u_{-} \rangle ^{\omega }(\tau ,y)\langle u_+\rangle ^{\frac{\omega }{2}}(\tau ,y)}{|x-y|^2}dy\\&\le \Vert \langle u_+\rangle ^{\omega }\nabla z_-\Vert _{L^\infty }\int _{|x-y|\le 2}\frac{\langle u_{-} \rangle ^{{\omega }}(\tau ,y)|\nabla z_+(\tau ,y)|}{\langle u_+\rangle ^{\frac{\omega }{2}}(\tau ,y)|x-y|^2}dy\\&{\mathop {\le }\limits ^{(3.1)}} \varepsilon \int _{|x-y|\le 2}\frac{1}{|x-y|^2}\frac{\langle u_{-} \rangle ^{\omega } (\tau ,y)}{\langle u_+\rangle ^{\frac{\omega }{2}}(\tau ,y)} |\nabla z_+(\tau ,y)|dy. \end{aligned} \end{aligned}$$

(3.8)

By Young’s inequality, similar to (2.44), we obtain

$$\begin{aligned} \begin{aligned} \Vert \langle u_{-} \rangle ^{\omega }\langle u_+\rangle ^{\frac{\omega }{2}}A_1\Vert _{L^2(\Sigma _\tau )}&\lesssim \varepsilon \big \Vert \frac{\langle u_{-} \rangle ^{\omega }}{\langle u_+\rangle ^{\frac{\omega }{2}}}\nabla z_+\big \Vert _{L^2(\Sigma _\tau )}. \end{aligned} \end{aligned}$$

(3.9)

Therefore, by the virtue of div-curl lemma (Lemma 2.6), we can bound $I_{1}$ as

$$\begin{aligned} I_{1}\lesssim \varepsilon ^2\int _0^t \int _{\Sigma _\tau }\frac{\langle u_{-} \rangle ^{2\omega }}{\langle u_+\rangle ^{\omega }}|\nabla z_+|^2 dx d\tau \lesssim \varepsilon ^4. \end{aligned}$$

(3.10)

To bound $I_{2}$, we split $A_{2}(t,x)$ as

$$\begin{aligned} \begin{aligned} |A_2(t,x)|&\lesssim \underbrace{\int _{\mathbb {R}^3}\frac{1-\theta (|x-y|)}{|x-y|^4}|\big (z_-^iz_+^j\big ) (t,y)|dy}_{A_{21}(t,x)}\\&\quad +\underbrace{\int _{\mathbb {R}^3}\bigl (\frac{\theta ''(|x-y|)}{|x-y|^2} +\frac{\theta '(|x-y|)}{|x-y|^3}\bigr )|\big (z_-^iz_+^j\big )(t,y)|dy}_{A_{22}(t,x)}. \end{aligned} \end{aligned}$$

(3.11)

We then split $I_2$ as

$$\begin{aligned} I_{2}\le \underbrace{\int _0^t\int _{\Sigma _\tau }\langle u_{-} \rangle ^{2\omega }\langle u_+\rangle ^{\omega }|A_{21}|^2dxd\tau }_{I_{21}} +\underbrace{\int _0^t\int _{\Sigma _\tau }\langle u_{-} \rangle ^{2\omega }\langle u_+\rangle ^{\omega }|A_{22}|^2dxd\tau }_{I_{22}}. \end{aligned}$$

In view of the property of the cut-off function $\theta (r)$, we can bound $A_{22}$ as

$$\begin{aligned} A_{22}(t,x) \lesssim \int _{|x-y|\le 2}\frac{1}{|x-y|^2}|z_-^i(t,y)||z_+^j(t,y)|dy. \end{aligned}$$

Therefore, $I_{22}$ can be bounded similarly as $I_1$. This leads to

$$\begin{aligned} I_{22} \lesssim \varepsilon ^4. \end{aligned}$$

(3.12)

We turn to $I_{21}$. Since $|u_\pm (\tau ,x)|\le |u_\pm (\tau ,y)|+2|x-y|$, we conclude that

$$\begin{aligned}&\langle u_{-} \rangle ^{\omega }(\tau ,x)\lesssim \langle u_{-} \rangle ^{\omega }(\tau ,y)+|x-y|^{\omega },\\&\quad \text {and}\ \ \bigl (\langle u_{-} \rangle ^{\omega }\langle u_+\rangle ^{\frac{\omega }{2}}\bigr )(\tau ,x) \lesssim \bigl (\langle u_{-} \rangle ^{\omega }\langle u_+\rangle ^{\frac{\omega }{2}}\bigr )(\tau ,y)+|x-y|^{\frac{3\omega }{2}}. \end{aligned}$$

Therefore, we can bound $I_{21}$ by

$$\begin{aligned} I_{21}&\lesssim \underbrace{\int _0^t \int _{\Sigma _{\tau }}\Big (\int _{|x-y|\ge 1}\frac{|z_-(\tau ,y)||z_+(\tau ,y)|}{|x-y|^{4-\frac{3\omega }{2}}}dy\Big )^2dxd\tau }_{I_{211}}\\&\quad +\underbrace{\int _0^t \int _{\Sigma _\tau }\Big (\underbrace{\int _{|x-y|\ge 1}\frac{|z_-(\tau ,y)||z_+(\tau ,y)|}{|x-y|^4}\langle u_{-} \rangle ^{\omega }\langle u_+\rangle ^{\frac{\omega }{2}}(\tau ,y)dy}_{A_3(\tau ,x)}\Big )^2dxd\tau }_{I_{212}}. \end{aligned}$$

We use Hölder and Young inequalities to bound $I_{211}$:

$$\begin{aligned} \begin{aligned} I_{211}&\lesssim \int _0^t\Big \Vert \big (\frac{1}{|x|^{4-\frac{3\omega }{2}}}\chi _{|x|\ge 1}\big )*(z_-z_+)\Big \Vert _{L^2(\Sigma _\tau )}^2d\tau \\&\lesssim \int _0^t\Big \Vert \frac{1}{|x|^{4-\frac{3\omega }{2}}}\Big \Vert _{L^2(|x|\ge 1)}^2 \Vert z_-z_+\Vert _{L^1(\Sigma _\tau )}^2d\tau \\&\quad {\mathop {\lesssim }\limits ^{\omega \in \big (1,\frac{5}{3}\big )}} \int _0^t\Vert z_-z_+\Vert _{L^1(\Sigma _\tau )}^2d\tau . \end{aligned} \end{aligned}$$

(3.13)

Since $\frac{1}{\langle u_{-} \rangle ^{\omega }\langle u_+\rangle ^{\omega }}\lesssim \frac{1}{(R+\tau )^{\omega }}$, we have

$$\begin{aligned} \begin{aligned} I_{211}&\lesssim \int _0^t\Big \Vert \frac{1}{\langle u_+\rangle ^{\omega }\langle u_{-} \rangle ^{\omega }}\langle u_+\rangle ^{\omega }z_- \langle u_{-} \rangle ^{\omega }z_+\Big \Vert _{L^1(\Sigma _\tau )}^2d\tau \\&\lesssim \int _0^t\frac{1}{(R+\tau )^{2\omega }}\Vert \langle u_{-} \rangle ^{\omega }z_+\Vert _{L^2(\Sigma _\tau )}^2\Vert \langle u_+\rangle ^{\omega }z_-\Vert _{L^2(\Sigma _\tau )}^2d\tau \\&\lesssim \varepsilon ^4\int _0^t\frac{1}{(R+\tau )^{2\omega }}d\tau \lesssim \varepsilon ^4. \end{aligned} \end{aligned}$$

(3.14)

For $I_{212}$, we first bound $A_{3}(\tau ,x)$ as follows:

$$\begin{aligned} \Vert A_{3}\Vert _{L^2(\Sigma _\tau )}&\lesssim \Big \Vert \frac{\chi _{|x|\ge 1}}{|x|^4}*\big (\frac{\langle u_{-} \rangle ^{\omega }}{\langle u_+\rangle ^{\frac{\omega }{2}}}|z_+| \cdot \langle u_+\rangle ^{\omega }|z_-|\big )\Big \Vert _{L^2(\Sigma _\tau )}\\&\lesssim \Big \Vert \frac{\chi _{|x|\ge 1}}{|x|^4}\Big \Vert _{L^1(\Sigma _\tau )}\Big \Vert \frac{\langle u_{-} \rangle ^{\omega }}{\langle u_+\rangle ^{\frac{\omega }{2}}}|z_+ |\cdot \langle u_+\rangle ^{\omega }|z_-|\Big \Vert _{L^2(\Sigma _\tau )}\\&\lesssim \Vert \langle u_+\rangle ^{\omega }z_-\Vert _{L^\infty (\Sigma _\tau )}\Big \Vert \frac{\langle u_{-} \rangle ^{\omega }}{\langle u_+\rangle ^{\frac{\omega }{2}}}z_+\Big \Vert _{L^2(\Sigma _\tau )} \lesssim \varepsilon \Big \Vert \frac{\langle u_{-} \rangle ^{\omega }}{\langle u_+\rangle ^{\frac{\omega }{2}}}z_+\Big \Vert _{L^2(\Sigma _\tau )}. \end{aligned}$$

This implies

$$\begin{aligned} I_{212}&\lesssim \varepsilon ^2\int _0^t\int _{\mathbb {R}^3}\frac{\langle u_{-} \rangle ^{2\omega }}{\langle u_+\rangle ^{\omega }}|z_+|^2dxd\tau \lesssim \varepsilon ^4. \end{aligned}$$

Combined with (3.10), (3.12) and (3.14), we obtain (3.6). Then we finally have (3.5).

We then turn to the first and higher order terms. The proof goes exactly as in Sect. 2.6. Indeed, in Sect. 2.6, by virtue of the flux, the only essential use of the weight is the fact that $\frac{1}{\langle w_{\pm } \rangle \big (\log (\langle w_{\pm } \rangle )\big )^2}$ is integrable in $u_{\pm }$. In the current situation, the factor is replaced by $\frac{1}{\langle u_{\pm } \rangle ^{\omega }}$ which is still integrable.

According to the above discussion, we can control all the nonlinear terms in the a priori energy estimates. This completes the proof of Theorem 1.3.

Proof of Theorem 1.4

We divide the proof into three steps.

Step 1 Explicit formulas for scattering fields.

We only prove this for $z_+$. We integrate $\partial _t {z}_++Z_{-} \cdot \nabla {z}_+= -\nabla p$ along $L_-$: for any given point $q=(y_1,y_2,y_3,0)$ on the initial hypersurface $\Sigma _0$, along the $L_-$ direction, the characteristic line emanated from this point hits $\Sigma _t$ at the point $(y_1,y_2, u_-,t)$. We then integrate the equation over the characteristic line segment between $(y_1,y_2, u_-,0)$ and $(y_1,y_2, u_-,t)$. Therefore,

$$\begin{aligned} z_+(y_1,y_2, u_-,t) = z_+(y_1,y_2,u_-,0) -\int _{0}^t (\nabla p) (y_1,y_2, u_-,\tau ) d\tau . \end{aligned}$$

(3.15)

In order to understand (3.15), we now derive (3.15) by characteristics method. Indeed, we first introduce the coordinate transformations on $\mathbb {R}^3\times [0,\infty )$ as follows:

$$\begin{aligned} \begin{aligned}&\Phi _-:\ \mathbb {R}^3\times [0,\infty ) \rightarrow \mathbb {R}^3\times [0,\infty )\\&\quad (x_1,x_2,x_3,t)\mapsto (x_1,x_2,u_-,t)=(x_1,x_2,u_-(x_1,x_2,x_3,t),t), \end{aligned} \end{aligned}$$

where $u_-$ is defined by (1.11) with $u_-(x,0)=y_3$ at point q. Thanks to Theorem 1.3, we have $\det (d\Phi _-)=\partial _3u_-=1+O(\varepsilon )$ (see also (2.46)). Denoting by , we deduce that $\widetilde{z_+}$ satisfies

$$\begin{aligned} \partial _t\widetilde{z_+}+\widetilde{z_-}^h\cdot \nabla _h\widetilde{z_+} =-(\nabla _xp)|_{(x,t)=\Phi _-^{-1}(x_1,x_2,u_-,t)}, \end{aligned}$$

where $\Phi _-^{-1}$ is the inverse of the mapping $\Phi _-$, and $\widetilde{z_-}^h=(\widetilde{z_-}^1,\widetilde{z_-}^2)$, $\nabla _h=(\partial _1,\partial _2)$. Notice that on $C_{u_-}^-$, $u_-$ is a constant. Then for fixed $u_-$, we define the flow $\phi ^-_{(u_-)}(y_1, y_2,t)$ (the mapping from $S_{0,u_-}$ to $S_{t,u_-}$) associated to $\widetilde{z_-}^h$ as follows:

$$\begin{aligned} \frac{d}{dt}\phi ^-_{(u_-)}(y_1, y_2,t)=\widetilde{z_-}^h(x_1,x_2,u_-,t)|_{(x_1,x_2)=\phi ^-_{(u_-)}(y_1, y_2,t)},\quad \phi ^-_{(u_-)}(y_1, y_2,0)=(y_1,y_2). \end{aligned}$$

Thanks to Theorem 1.3, the Jacobian $d\phi ^-_{(u_-)}$ satisfies $\det (d\phi ^-_{(u_-)})=1+O(\varepsilon )$. Then denoting by $\overline{z_+}(y_1, y_2,u_-,t)=\widetilde{z_+}(x_1,x_2,u_-,t)|_{(x_1,x_2)=\phi ^-_{(u_-)}(y_1, y_2,t)}$, we have

$$\begin{aligned} \frac{d\overline{z_+}}{dt}=-(\nabla _xp)|_{(x,t)=\Phi _-^{-1}(\phi ^-_{(u_-)}(y_1, y_2,t),u_-,t)}, \end{aligned}$$

which implies that

$$\begin{aligned} \overline{z_+}(y_1, y_2,u_-,t)=\overline{z_+}(y_1, y_2,u_-,0)-\int _0^t(\nabla _xp)|_{(x,\tau )=\Phi _-^{-1}(\phi ^-_{(u_-)}(y_1, y_2,\tau ),u_-,\tau )}d\tau . \end{aligned}$$

Notice that

$$\begin{aligned} \overline{z_+}(y_1, y_2,u_-,0)=\widetilde{z_+}(y_1, y_2,u_-,0)=z_+(y_1,y_2,y_3,0). \end{aligned}$$

Without confusion, we use notation $z_+(y_1,y_2, u_-,t)$ to present $\overline{z_+}(y_1, y_2, u_-,t)$ which is the expression for $z_+$ in terms of the coordinates $(y_1, y_2,u_-,t)$. So does $(\nabla p) (y_1,y_2, u_-,\tau )$. Then we obtain (3.15).

Similarly, we integrate $\partial _t j_+ +Z_{-} \cdot \nabla j_+ = -\nabla z_-\wedge \nabla z_+$ to derive

$$\begin{aligned} (\text {curl}\,z_+)(y_1,y_2, u_-,t) =j_+(y_1,y_2,u_-,0) -\int _{0}^t (\nabla z_-\wedge \nabla z_+) (y_1,y_2, u_-,\tau ) d\tau . \end{aligned}$$

(3.16)

Step 2 The scattering fields are well-defined.

To show that $z_+^{(\text {scatter})}$ is well defined, in view of (3.15), it suffices to prove that $\nabla p$ is integrable (in time) along any left-traveling characteristic line.

In view of (3.7), we have $(\nabla p)(t,x) =A_1(t,x)+A_2(t,x)$, where

$$\begin{aligned} \begin{aligned} A_1&=-\frac{1}{4\pi }\int _{\mathbb {R}^3}\nabla \frac{1}{|x-x'|}\theta (|x-x'|) \big (\partial _iz_-^j\partial _jz_+^i\big )(t,x')dx',\\ A_2&=-\frac{1}{4\pi } \int _{\mathbb {R}^3}\partial _i\partial _j\Bigl (\nabla \frac{1}{|x-x'|} \bigl (1-\theta (|x-x'|)\bigr )\Bigr )\big (z_-^iz_+^j\big )(t,x')dx'. \end{aligned} \end{aligned}$$

Similar to (3.8), setting $\omega =1+\delta$, we have

$$\begin{aligned} \begin{aligned} \langle u_{-} \rangle ^{\omega }\langle u_+\rangle ^{{\omega }}|A_1|&{\lesssim }\, \varepsilon \int _{|x-x'|\le 2}\frac{1}{|x-x'|^2}\langle u_{-} \rangle ^{{\omega }}(t,x')|\nabla z_+(t,x')|dx'\\&\lesssim \varepsilon \big \Vert \frac{1}{|x|^2}\big \Vert _{L^1(|x|\le 2)} \Vert \langle u_{-} \rangle ^{\omega }\nabla z_+\Vert _{L^\infty (\Sigma _t)}\\&\lesssim \varepsilon ^2. \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \big |A_1\big | \lesssim \frac{\varepsilon ^2}{\langle u_{-} \rangle ^\omega \langle u_+\rangle ^\omega }. \end{aligned}$$

(3.17)

According to (3.11), we further split $A_2(t,x)$ as $A_{21}(t,x)+A_{22}(t,x)$. Since

$$\begin{aligned} A_{22}(t,x) \lesssim \int _{|x-x'|\le 2}\frac{1}{|x-x'|^2}|z_-^i(t,x')||z_+^j(t,x')|dx', \end{aligned}$$

it can be estimated in the same manner as for $A_{1}(t,x)$. Therefore, we can ignore this term.

It remains to bound $A_{21}(t,x) =\int _{\mathbb {R}^3}\frac{1-\theta (|x-x'|)}{|x-x'|^4}(z_-^iz_+^j)(t,x')dx'$. Since $(1+t)\lesssim \langle u_+\rangle \langle u_{-} \rangle$, we have

$$\begin{aligned} \begin{aligned} (1+t)^{{\omega }}|A_{21}(t,x)|&\lesssim \int _{|x-x'|\ge 1}\frac{1}{|x-x'|^4}|\langle u_+\rangle ^{{\omega }}(t,x') z_-^i(t,x')||\langle u_{-} \rangle ^{{\omega }}(t,x')z_+^j(t,x')|dx'\\&{\mathop {\lesssim }\limits ^{Young}}\big \Vert \frac{1}{|x|^4}\big \Vert _{L^1(|x|\ge 1)} \Vert \langle u_{-} \rangle ^{\omega }) z_+\Vert _{L^\infty (\Sigma _t)}\Vert \langle u_+\rangle ^{\omega }) z_-\Vert _{L^\infty (\Sigma _t)}. \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \big |A_{21}\big | \lesssim \frac{\varepsilon ^2}{(1+t)^{\omega }}. \end{aligned}$$

Combined with (3.17), we obtain that

$$\begin{aligned} \big |(\nabla p )(y_1,y_2, u_-,\tau )\big | \le \frac{\varepsilon ^2}{(1+\tau )^{\omega }}. \end{aligned}$$

This implies that $\lim _{t\rightarrow \infty }\int _{0}^t (\nabla p) (y_1,y_2, u_-,\tau ) d\tau$ is well-defined.

To show that $(\text {curl}\,z)_+^{(\text {scatter})}$ is well defined, in view of (3.16), it suffices to bound $\nabla z_-\wedge \nabla z_+$. According to Lemma 3.3, we have

$$\begin{aligned} |\nabla z_-\wedge \nabla z_+|\lesssim \frac{\varepsilon ^2}{(1+\tau )^{\omega }}, \end{aligned}$$

which is integrable in t. Therefore $(\text {curl}\,z)_+^{(\text {scatter})}$ is well defined.

Similarly, the higher derivatives of the scattering fields are well-defined and we omit the routine details.

Step 3 Calculate the differential of  $\mathbf {S}:H^{N_*+1,\delta }(\Sigma _0)\times H^{N_*+1,\delta }(\Sigma _0) \rightarrow H^{0,\delta }(\mathcal {C}_-) \times H^{0,\delta }(\mathcal {C}_+)$.

We first clarify the relation of the measure $d\tilde{\sigma }_\pm$ on $\mathcal {C}_\pm$ and the measure $d\sigma _\pm$ on $C_{u_\pm }^\pm$. Recall that in the proof of Lemma 2.9, $d\sigma _+$ on $C_{u_+}^+$ was calculated as follows:

$$\begin{aligned} d\sigma _+=\sqrt{1+|Z_+\cdot \nabla u_+|^2+|\nabla _{x_h}u_+|^2}dx_1dx_2dt{\mathop {=}\limits ^{(2.1)}}(\sqrt{2}+O(\varepsilon ))d{x_1}d{x_2}dt. \end{aligned}$$

Similar to the definitions of $\Phi _-$ and $\phi ^-_{(u_-)}$, we introduce the coordinates transformation $\Phi _+:\ (x_1,x_2,x_3,t)\mapsto (x_1,x_2,u_+,t)=(x_1,x_2,u_+(x_1,x_2,x_3,t),t)$ (the mapping from $\mathbb {R}^3\times [0,\infty )$ to $\mathbb {R}^3\times [0,\infty )$) and the flow $\phi ^+_{(u_+)}(y_1, y_2,t)$ (the mapping from $S_{0,u_+}$ to $S_{t,u_+}$) which is generated by $z_+^h(x_1,x_2,u_+,t)$ for fixed $u_+$. Since $u_+$ is a constant on $C_{u_+}^+$, then by the fact that $\det (d\phi ^+_{(u_+)})=1+O(\varepsilon )$, we have

$$\begin{aligned} d\sigma _+=(\sqrt{2}+O(\varepsilon ))d{y_1}d{y_2}dt. \end{aligned}$$

Observe that for fixed $u_+$,

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}u_-(y_1, y_2,u_+,t) =\frac{d}{dt}u_-\big (\Phi _+^{-1}(\phi ^+_{(u_+)}(y_1, y_2,t),u_+,t)\big )\\&\quad =(\nabla _{x,t}u_-)(y_1, y_2,u_+,t)\cdot \frac{d}{dt}\Phi _+^{-1} \big (\phi ^+_{(u_+)}(y_1,y_2,t),u_+,t\big )\\&\quad =\Bigl (\partial _tu_-+Z_+\cdot \nabla u_-\Bigr )(y_1,y_2,u_+,t)\\&\quad {\mathop {=}\limits ^{L_-u_-=0}}\Bigl (\bigl (Z_+-Z_-\bigr )\cdot \nabla u_-\Bigr )(y_1, y_2,u_+,t){\mathop {=}\limits ^{(2.1)}} 2+O(\varepsilon ). \end{aligned} \end{aligned}$$

(3.18)

Since $u_+$ is a constant on $C_{u_+}^+$, by changing the variable t to $u_-$ via $u_-=u_-(y_1, y_2,u_+,t)$, we obtain

$$\begin{aligned} d\sigma _+=(2\sqrt{2}+O(\varepsilon ))d{y_1}d{y_2}du_-. \end{aligned}$$

Finally, to compare the measure $d\tilde{\sigma }_+$ (on $\mathcal {C}_+$) with $d\sigma _+$ (on $C_{u_+}^+$), we use the common coordinates $(y_1,y_2,u_-)$. Since by definition we take $d\tilde{\sigma }_+ = d{y_1}d{y_2}du_-$, we finally claim that

$$\begin{aligned} d\tilde{\sigma }_+ \sim d\sigma _+, \end{aligned}$$

where the difference is a universal constant which will not effect any estimate thereafter.

We remark that the continuity of $\mathbf {S}$ at 0 is an immediate consequence of the a priori estimates for the ideal MHD system. For the differential of $\mathbf {S}$, we derive weighted $L^2$-estimates for $z_+^{(\text {scatter})}-z_+^{(\text {linear})}$.

According to (3.15) (or (1.16)), we have

$$\begin{aligned} \left( z_+^{(\text {scatter})}-z_+^{(\text {linear})}\right) (y_1,y_2, u_-)=-\int _{0}^\infty (\nabla p) (y_1,y_2, u_-,\tau ) d\tau \end{aligned}$$

We will switch the $\tau$-variable to $u_+$ by $\tau \mapsto u_+(y_1,y_2, u_-,\tau )$ in the integral. Indeed, similar to (3.18), we have

$$\begin{aligned} \frac{d}{d\tau }u_+(y_1,y_2, u_-,\tau )=-2+O(\varepsilon ). \end{aligned}$$

(3.19)

Therefore,

$$\begin{aligned} \begin{aligned}&\int _{0}^\infty |(\nabla p) (y_1,y_2, u_-,\tau )|d\tau \lesssim \int _{\mathbb {R}}|(\nabla p) (y_1,y_2, u_-,u_+)|du_+\\&\quad \lesssim \Bigl (\int _{\mathbb {R}}\frac{1}{\langle u_+\rangle ^\omega }du_+\Bigr )^{\frac{1}{2}} \Bigl (\int _{\mathbb {R}}\langle u_+\rangle ^\omega |(\nabla p) (y_1,y_2, u_-,u_+)|^2du_+\Bigr )^{\frac{1}{2}}\\&\quad \lesssim \Bigl (\int _{\mathbb {R}}\langle u_+\rangle ^\omega |(\nabla p) (y_1,y_2, u_-,u_+)|^2du_+\Bigr )^{\frac{1}{2}}. \end{aligned} \end{aligned}$$

Thus, we have

$$\begin{aligned} \begin{aligned}&\int _{\mathcal {C_+}}\langle u_{-} \rangle ^{2\omega } \big |z_+^{(\text {scatter})}-z_+^{(\text {linear})}\big |^2d\tilde{\sigma }_+\\&\quad \lesssim \int _{\mathcal {C_+}}\langle u_{-} \rangle ^{2\omega }\Bigl (\int _{\mathbb {R}} |(\nabla p) (y_1,y_2, u_-,u_+)|du_+\Bigr )^2d\sigma _+\\&\quad \lesssim \int _{\mathbb {R}^3}\int _{\mathbb {R}}\langle u_{-} \rangle ^{2\omega }\langle u_+\rangle ^\omega |(\nabla p) (y_1,y_2, u_-,u_+)|^2du_+d{y_1}d{y_2}du_-. \end{aligned} \end{aligned}$$

(3.20)

We then use the coordinate $(x_1,x_2,x_3,\tau )$ instead of $(y_1,y_2,u_-,u_+)$. Since

$$\begin{aligned} \begin{aligned}&d{y_1}d{y_2}du_-du_+=\big |\frac{d}{d\tau }u_+(y_1,y_2,u_-,\tau )\big |d{y_1}d{y_2}du_-d\tau \\&\quad =\det \big (d\phi ^-_{(u_-)}\big )^{-1}\big |\frac{d}{d\tau }u_+(y_1,y_2,u_-,\tau ) \big |d{x_1}d{x_2}du_-d\tau \\&\quad =\det (d\Phi _+)\det \big (d\phi ^-_{(u_-)}\big )^{-1}|\frac{d}{d\tau }u_+ (y_1,y_2,u_-,\tau )|d{x_1}d{x_2}d{x_3}d\tau \end{aligned} \end{aligned}$$

in view of (3.19) and the facts that $\det (d\Phi _+)=1+O(\varepsilon )$ and $\det (d\phi ^-_{(u_-)})=1+O(\varepsilon )$, we have

$$\begin{aligned} d{y_1}d{y_2}du_-du_+=(2+O(\varepsilon ))d{x_1}d{x_2}d{x_3}d\tau . \end{aligned}$$

Therefore, (3.20) yields the following estimate:

$$\begin{aligned} \int _{\mathcal {C_+}}\langle u_{-} \rangle ^{2\omega } \big |z_+^{(\text {scatter})}-z_+^{(\text {linear})}\big |^2d\tilde{\sigma }_+ \lesssim \int _0^t\int _{\mathbb {R}^3}\langle u_{-} \rangle ^{2\omega }\langle u_+\rangle ^\omega |\nabla p(x,\tau )|^2dxd\tau . \end{aligned}$$

(3.21)

Thanks to (3.6), we obtain that

$$\begin{aligned} \int _{\mathcal {C_+}}\langle u_{-} \rangle ^{2\omega }\big |z_+^{(\text {scatter})}-z_+^{(\text {linear})} \big |^2d\tilde{\sigma }_+\lesssim \varepsilon ^4. \end{aligned}$$

(3.22)

In other words, we obtain

$$\begin{aligned} \big \Vert z_+^{(\text {scatter})}-z_+^{(\text {linear})}\big \Vert _{H^{0,\delta }(\mathcal {C}_+)}\lesssim \varepsilon ^2. \end{aligned}$$

(3.23)

The similar estimate also holds for $z_-$. Since $\Vert (z^{(0)}_-,z^{(0)}_+)\Vert _{H^{N_*+1,\delta }(\Sigma _0)\times H^{N_*+1,\delta }(\Sigma _0) } \sim \varepsilon$, for $\varepsilon \rightarrow 0$, this implies

$$\begin{aligned} d \,\mathbf {S} \big |_\mathbf{0 }=\mathbf {S}^{\text {linear}}. \end{aligned}$$

Proof of Theorem 1.5

There are two statements in the theorem and we will prove them one by one.

Proof of the First Statement

We fix $\mu$ and T. Let $\mathfrak {Z}_\pm = z_\pm ^\mu -z_\pm$. By (1.5), we have

$$\begin{aligned} \begin{aligned} \partial _t \mathfrak {Z}_\pm +Z_\mp \cdot \nabla \mathfrak {Z}_\pm&=-\mathfrak {Z}_\mp \cdot \nabla z^\mu _\pm -\nabla (p^\mu -p)+ {\mu \triangle z_\pm ^\mu }. \end{aligned} \end{aligned}$$

(3.24)

We remark that $\text {div}\,\mathfrak {Z}_\pm =0$ and $\mathfrak {Z}_\pm \big |_{t=0}\equiv 0$. We multiply both sides of (3.24) by $\mathfrak {Z}_\pm$ and we integrate over $\Sigma _t$. By virtue of the divergence-free property of $\mathfrak {Z}_\pm$, this yields

$$\begin{aligned} \begin{aligned}&\frac{1}{2}\frac{d}{dt}\big (\Vert \mathfrak {Z}_+\Vert ^2_{L^2(\Sigma _t)} +\Vert \mathfrak {Z}_-\Vert ^2_{L^2(\Sigma _t)}\big )\\&\quad =\underbrace{-\int _{\Sigma _t}\big (\mathfrak {Z}_-\cdot \nabla z^\mu _+\big )\cdot \mathfrak {Z}_+dx}_{I_1} -\int _{\Sigma _t}\big (\mathfrak {Z}_+\cdot \nabla z^\mu _-\big )\cdot \mathfrak {Z}_- dx\\&\quad -\underbrace{\mu \int _{\Sigma _t}\nabla z_+^\mu \cdot \nabla \mathfrak {Z}_+dx}_{I_2}- \mu \int _{\Sigma _t}\nabla z_-^\mu \cdot \nabla \mathfrak {Z}_-dx \end{aligned} \end{aligned}$$

According to the $\mu$-independent a priori estimates derived in Theorem 1.2, we have

$$\begin{aligned} |I_1|&\lesssim \Vert \nabla z_+^\mu \Vert _{L^\infty } \Vert \mathfrak {Z}_+\Vert _{L^2(\Sigma _t)} \Vert \mathfrak {Z}_-\Vert _{L^2(\Sigma _t)}\\&\lesssim \varepsilon \big ( \Vert \mathfrak {Z}_+\Vert ^2_{L^2(\Sigma _t)}+ \Vert \mathfrak {Z}_-\Vert ^2_{L^2(\Sigma _t)}\big ), \end{aligned}$$

and

$$\begin{aligned} |I_2|&\lesssim \mu \Vert \nabla z_+^\mu \Vert _{L^2(\Sigma _t)} \Vert \nabla \mathfrak {Z}_+\Vert _{L^2(\Sigma _t)} \lesssim \mu \varepsilon ^2. \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} \begin{aligned}&\ \ \ \frac{d}{dt}\big (\Vert \mathfrak {Z}_+\Vert ^2_{L^2(\Sigma _t)}+\Vert \mathfrak {Z}_-\Vert ^2_{L^2(\Sigma _t)}\big )\lesssim \varepsilon \big (\Vert \mathfrak {Z}_+\Vert ^2_{L^2(\Sigma _t)}+\Vert \mathfrak {Z}_-\Vert ^2_{L^2(\Sigma _t)}\big ) + \mu \varepsilon ^2. \end{aligned} \end{aligned}$$

For all $\tau \in [0,T]$, we integrate this equation over $[0,\tau ]$ and we use Gronwall’s inequality to obtain

$$\begin{aligned} \begin{aligned} \Vert \mathfrak {Z}_+\Vert ^2_{L^2(\Sigma _\tau )}+\Vert \mathfrak {Z}_-\Vert ^2_{L^2(\Sigma _\tau )}\lesssim \mu \varepsilon (e^{\varepsilon \tau }-1). \end{aligned} \end{aligned}$$

This completes the proof for the first statement.

Proof of the Second Statement

Since we have many coordinate systems in the proof, to make the notations simpler, we define the so-called Lagrangian forms $\widetilde{v_\pm }(t,y)$ of $v_\pm (t,x)$ as

$$\begin{aligned} \widetilde{ v_\pm }(t,y)=v_\pm (t,x)|_{x=\psi _\mp (t,y)}, \end{aligned}$$

where $\psi _\mp (t,y)$ is the flow generated by $Z_\mp$ and $y \in \Sigma _0$. In other words, $\widetilde{v_\pm }(t,y)$ is the expression of the vector field v in the $(t,y_1,y_2,y_3)$ coordinates.

We divide the proof into several steps.

Step 1 The linear and nonlinear decomposition of solutions.

For the given solution $(z_+,z_-)$, we decompose it as where the linear part ${z}_{\pm }^{(\text {lin})}$ and nonlinear part ${z}_{\pm }^{(\text {non})}$ satisfy

$$\begin{aligned} \begin{aligned}&\partial _t{z}_{\pm }^{(\text {lin})}+Z_\mp \cdot \nabla {z}_{\pm }^{(\text {lin})} -\mu \Delta {z}_{\pm }^{(\text {lin})}=0,\\&\quad {z}_{\pm }^{(\text {lin})}|_{t=0}={z}_{\pm }(0,x), \end{aligned} \end{aligned}$$

(3.25)

and

$$\begin{aligned} \begin{aligned}&\partial _t{z}_{\pm }^{(\text {non})}+Z_\mp \cdot \nabla {z}_{\pm }^{(\text {non})} -\mu \Delta {z}_{\pm }^{(\text {non})}=-\nabla p,\\&\quad \text{ div }{z}_{\pm }^{(\text {non})}=- \text{ div }{z}_{\pm }^{(\text {lin})},\\&\quad {z}_{\pm }^{(\text {non})}|_{t=0}=0. \end{aligned} \end{aligned}$$

(3.26)

We shall use $E_{\pm ,(\text {lin})}^{(\alpha )}(t)$ to denote the energies for $z_\pm ^{(\text {lin})}$ while we use $E_{\pm ,(\text {non})}^{(\alpha )}(t)$ to denote the energies for $z_\pm ^{(\text {non})}$. We shall also use $D_\pm ^{(\text {lin})}$, $D_\pm ^{(\text {lin}),k}$ to denote the diffusions for $z_\pm ^{(\text {lin})}$ while we use $D_\pm ^{(\text {non})}$, $D_\pm ^{(\text {non}),k}$ to denote the diffusions for $z_\pm ^{(\text {non})}$. All the above notations are defined in the same manner as that for $z_\pm$. We define the following total energy for the linear part:

Similarly, we can define $\mathcal {E}^\mu _{(\text {non}),\pm }(t)$.

For linear system (3.25), we regard $Z_\pm$ as given divergence-free vectore fields, similar to (1.13), for all $t\ge 0$, $u_\pm \in \mathbb {R}$ we have

$$\begin{aligned} \begin{aligned}&\mathcal {E}^\mu _{(\text {lin}),\pm }(t)+ F_{\pm }\big ({z}_{\pm }^{(\text {lin})}\big )+\sum _{k=0}^{N_*}F_{\pm }^k\big (\nabla {z}_{\pm }^{(\text {lin})}\big )\\&\quad +\bigl (D_{\pm }^{(\text {lin})}+\sum _{k=0}^{N_*}D_{\mp }^{(\text {lin}),k}+\mu D_{\mp }^{(\text {lin}),N_*+1}\bigr )|_{t^*=\infty } \lesssim \mathcal {E}^\mu (0). \end{aligned} \end{aligned}$$

(3.27)

To derive energy estimates for (3.26), we first point out a modification of Lemma 2.6 for general vector field $\varvec{v}$:

$$\begin{aligned} \Vert \sqrt{\lambda }\nabla \varvec{v}\Vert _{L^2}^2\lesssim \Vert \sqrt{\lambda }\text{ div }\varvec{v}\Vert _{L^2}^2+\Vert \sqrt{\lambda }\text {curl}\,\varvec{v}\Vert _{L^2}^2+\big \Vert \frac{|\nabla \lambda |}{\sqrt{\lambda }}\varvec{v}\big \Vert _{L^2}^2. \end{aligned}$$

(3.28)

Since the initial data ${z}_{\pm }^{(\text {non})}|_{t=0}$ are zero, in view of (1.13) and (3.27), for all $t\ge 0$, $u_\pm \in \mathbb {R}$, we have

$$\begin{aligned} \begin{aligned}&\mathcal {E}^\mu _{(\text {non}),\pm }(t)+F_{\pm }\big ({z}_{\pm }^{(\text {non})}\big ) +F_{\pm }^0\big (\nabla {z}_{\pm }^{(\text {non})}\big )+\sum _{k=1}^{N_*}F_{\pm }^k\big (\text {curl}\,{z}_{\pm }^{(\text {non})}\big )\\&\quad +\bigl (D_{\pm }^{(\text {non})}+\sum _{k=0}^{N^*}D_{\mp }^{(\text {non}),k}+\mu D_{\mp }^{(\text {non}),N^*+1}\bigr )\big |_{t^*=\infty } \lesssim \bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{3}{2}}. \end{aligned} \end{aligned}$$

(3.29)

As a consequence, we have

$$\begin{aligned} \mathcal {E}^\mu (t)\lesssim \sum _{+,-}\big (\mathcal {E}^\mu _{(\text {lin}),\pm }(t) +\mathcal {E}^\mu _{(\text {non}),\pm }(t)\big )\lesssim \sum _{+,-}\mathcal {E}^\mu _{(\text {lin}),\pm }(t) +\bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{3}{2}}. \end{aligned}$$

(3.30)

Step 2 Estimate on the total linear energy $\mathcal {E}^\mu _{(\text {lin}),\pm }$.

By symmetry, it suffices to bound $\mathcal {E}^\mu _{(\text {lin}),+}$. For simplicity, we set $z = {z}_+^{(\text {lin})}$. Therefore, we have

$$\begin{aligned} \partial _tz+Z_-\cdot \nabla z-\mu \Delta z=0, \end{aligned}$$

(3.31)

and $z|_{t=0}=z_+(0,x)$. By taking $L^2$ inner product of (3.31) with z, $(\log \langle w_{-} \rangle )^2 z$ and $(\log \langle w_{-} \rangle )^4 z$ respectively, we have

$$\begin{aligned}&\frac{1}{2}\frac{d}{dt}\Vert z\Vert _{L^2}^2+\mu \Vert \nabla z\Vert _{L^2}^2=0,\\&\frac{1}{2}\frac{d}{dt}\Vert \log \langle w_{-} \rangle z\Vert _{L^2}^2+\mu \Vert \log \langle w_{-} \rangle \nabla z\Vert _{L^2}^2\le 4\mu \Vert \log \langle w_{-} \rangle \nabla z\Vert _{L^2}\big \Vert \frac{z}{\langle w_{-} \rangle }\big \Vert _{L^2},\\&\frac{1}{2}\frac{d}{dt}\Vert (\log \langle w_{-} \rangle )^2z\Vert _{L^2}^2+\mu \Vert (\log \langle w_{-} \rangle )^2\nabla z\Vert _{L^2}^2\le 8\mu \Vert (\log \langle w_{-} \rangle )^2\nabla z\Vert _{L^2}\big \Vert \frac{\log \langle w_{-} \rangle }{\langle w_{-} \rangle }z\big \Vert _{L^2}. \end{aligned}$$

We remark that we have already proved that $\Vert \frac{z}{\langle w_{-} \rangle }\Vert _{L^2}\lesssim \Vert \nabla z\Vert _{L^2}$ and $\Vert \frac{\log \langle w_{-} \rangle }{\langle w_{-} \rangle }z\Vert _{L^2}\lesssim \Vert \nabla z\Vert _{L^2}+\Vert \log \langle w_{-} \rangle \nabla z\Vert _{L^2}^2$ by Hardy’s inequality.

For higher order energy estimates, we apply $\partial ^\alpha$ with $|\alpha |\ge 1$ to (3.31) to derive

$$\begin{aligned} \partial _t(\partial ^\alpha z)+Z_-\cdot \nabla (\partial ^\alpha z)-\mu \Delta (\partial ^\alpha z)=-[\partial ^\alpha , z_-]\cdot \nabla z, \end{aligned}$$

(3.32)

where $\partial ^\alpha z|_{t=0}=(\partial ^\alpha z_+)(0,x)$. By taking $L^2$ product with $\langle w_{-} \rangle ^2(\log \langle w_{-} \rangle )^4 \partial ^\alpha z$, we obtain

$$\begin{aligned} \begin{aligned}&\frac{1}{2}\frac{d}{dt}\Vert \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\partial ^\alpha z\Vert _{L^2}^2+\mu \Vert \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\nabla (\partial ^\alpha z)\Vert _{L^2}^2\\&\quad \le 12\mu \Vert \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\nabla (\partial ^\alpha z)\Vert _{L^2}\Vert (\log \langle w_{-} \rangle )^2(\partial ^\alpha z)\Vert _{L^2}+f_\alpha (t), \end{aligned} \end{aligned}$$

The nonlinear terms $f_\alpha$ is defined as follows:

$$\begin{aligned} \begin{aligned} f_\alpha (t)&=\bigg |\int _{\Sigma _t}\bigl ([\partial ^\alpha , z_-]\cdot \nabla z\bigr )\cdot (\partial ^\alpha z)\langle w_{-} \rangle ^2(\log \langle w_{-} \rangle )^4dx\bigg |.\\ \end{aligned} \end{aligned}$$

It is straightforward to see that $\int _{t\ge 0}f_\alpha (t)$ (for $1\le |\alpha |\le N_*+1$) can be controlled by the flux terms in (3.27) while $\mu \int _{t\ge 0}f_{\alpha }(t)$ (for $|\alpha |=N_*+2$) can be bounded by the diffusion terms. Therefore, thanks to (3.27) and (1.13), we have

$$\begin{aligned} \left( \sum _{1\le |\alpha |\le N_*+1}+\mu \sum _{|\alpha |=N_*+2}\right) \int _0^\infty f_\alpha (t)dt\lesssim \bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{3}{2}}, \end{aligned}$$

(3.33)

where we use the notation

Putting the above differential inequalities together, we obtain there exist constants c, $c_{00}$, $c_{01}$, $c_{02}$ and $\{c_\alpha \}_{1\le |\alpha |\le N_*+2}$ such that

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}\Bigl (c_{00}\Vert z\Vert _{L^2}^2+ c_{01}\Vert \log \langle w_{-} \rangle z\Vert _{L^2}^2+ c_{02}\Vert (\log \langle w_{-} \rangle )^2z\Vert _{L^2}^2\\&\quad +\sum _{1\le |\alpha |\le N_*+1} c_\alpha \Vert \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\partial ^\alpha z\Vert _{L^2}^2+\mu \sum _{|\alpha |=N_*+2} c_\alpha \Vert \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\partial ^\alpha z\Vert _{L^2}^2\Bigr ) \\&\quad +c\mu \Bigl (\Vert \nabla z\Vert _{L^2}^2+\Vert \log \langle w_{-} \rangle \nabla z\Vert _{L^2}^2+\Vert (\log \langle w_{-} \rangle )^2\nabla z\Vert _{L^2}^2\\&\quad +\sum _{1\le |\alpha |\le N_*+1}\Vert \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\nabla (\partial ^\alpha z)\Vert _{L^2}^2\Bigr )\\&\quad +c\mu ^2\sum _{|\alpha |=N_*+2}\Vert \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\nabla (\partial ^\alpha z)\Vert _{L^2}^2 \le \left( \sum _{1\le |\alpha |\le N_*+1}+\mu \sum _{|\alpha |=N_*+2}\right) f_\alpha (t). \end{aligned} \end{aligned}$$

(3.34)

To further simplify the notations, we introduce

$$\begin{aligned} z_{00}= z,\ \ z_{01}=\log \langle w_{-} \rangle z,\ \ z_{02}=(\log \langle w_{-} \rangle )^2 z,\ \ z_\alpha =\langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\partial ^\alpha z. \end{aligned}$$

Using the new notations, we have

$$\begin{aligned} \mathcal {E}^\mu _{(\text {lin}),+}(t)\sim \sum _{k=0}^2\Vert z_{0k}(t)\Vert _{L^2}^2 +\sum _{1\le |\alpha |\le N_*+1}\Vert z_\alpha (t)\Vert _{L^2}^2+\mu \sum _{|\alpha |=N_*+1}\Vert \nabla z_\alpha (t)\Vert _{L^2}^2. \end{aligned}$$

(3.35)

By virtue of (3.33), for all $t\ge 0$, we have

$$\begin{aligned} \begin{aligned}&\sum _{k\le 2}\Vert z_{0k}\Vert _{L^2}^2 +\sum _{1\le |\alpha |\le N_*+1}\Vert z_\alpha \Vert _{L^2}^2\\&\quad +\mu \sum _{|\alpha |=N_*+2}\Vert z_\alpha \Vert _{L^2}^2 +\mu \int _0^\infty \left( \sum _{k\le 2} \Vert \nabla z_{0k}\Vert _{L^2}^2 +\sum _{1\le |\alpha |\le N_*+1}\Vert \nabla z_\alpha \Vert _{L^2}^2\right) dt\\&\quad +\mu ^2\sum _{|\alpha |=N_*+2}\int _0^\infty \Vert \nabla z_\alpha \Vert _{L^2}^2dt\lesssim \mathcal {E}^\mu (0), \end{aligned} \end{aligned}$$

(3.36)

where $L^2$ should be understood as $L^2(\Sigma _t)$.

Step 3 Decomposition of $z_\alpha$ and the refined energy for  (3.31).

By definition, $z_{0k}$ and $z_\alpha$ satisfy the following equations:

$$\begin{aligned} \begin{aligned} \partial _tz_{00}+Z_-\cdot \nabla z_{00}-\mu \Delta z_{00}&=0,\\ \partial _tz_{01}+Z_-\cdot \nabla z_{01}-\mu \Delta z_{01}&=-2\mu \bigl (\nabla (\log \langle w_{-} \rangle )\cdot \nabla \bigr )z-\mu z\Delta (\log \langle w_{-} \rangle ),\\ \partial _tz_{02}+Z_-\cdot \nabla z_{02}-\mu \Delta z_{02}&=-2\mu \bigl (\nabla \bigl ((\log \langle w_{-} \rangle )^2\bigr )\cdot \nabla \bigr )z-\mu z\Delta \bigl ((\log \langle w_{-} \rangle )^2\bigr ),\\ \partial _tz_\alpha +Z_-\cdot \nabla z_\alpha -\mu \Delta z_\alpha&=-2\mu \bigl (\nabla \bigl (\langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\bigr )\cdot \nabla \bigr )\partial ^\alpha z\\&\quad -\mu \partial ^\alpha z\Delta \bigl (\langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\bigr )\\&\quad -[\partial ^\alpha , z_-]\cdot \nabla z \cdot \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2. \end{aligned} \end{aligned}$$

(3.37)

Step 3.1 Decomposition of $z_\alpha$. We split $z_\alpha$ into two parts $z_\alpha =Y_\alpha +R_\alpha$. The vector fields $Y_\alpha$ and $R_\alpha$ satisfy

$$\begin{aligned} \begin{aligned}&\partial _tY_\alpha +Z_-\cdot \nabla Y_\alpha -\mu \Delta Y_\alpha =-2\mu \bigl (\nabla \bigl (\langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\bigr )\cdot \nabla \bigr )\partial ^\alpha z\\&\quad -\mu \partial ^\alpha z\Delta \bigl (\langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\bigr ),\\&\quad Y_\alpha |_{t=0}=z_\alpha |_{t=0}\big (=(\langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\partial ^\alpha z_+)(0,x)\big ), \end{aligned} \end{aligned}$$

(3.38)

and

$$\begin{aligned} \begin{aligned} \partial _tR_\alpha +Z_-\cdot \nabla R_\alpha -\mu \Delta R_\alpha&=-[\partial ^\alpha , z_-]\cdot \nabla z \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2,\\ R_\alpha |_{t=0}&=0. \end{aligned} \end{aligned}$$

(3.39)

Step 3.2 Energy estimates for (3.38). By taking $L^2(\Sigma _t)$-product with $Y_\alpha$, (3.38) yields

$$\begin{aligned} \begin{aligned}&\frac{1}{2}\frac{d}{dt}\Vert Y_\alpha \Vert _{L^2}^2+\mu \Vert \nabla Y_\alpha \Vert _{L^2}^2= -\mu \int _{\Sigma _t}[2\bigl (\nabla \bigl (\langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\bigr )\cdot \nabla \bigr )\partial ^\alpha z\cdot Y_\alpha \\&\quad +\partial ^\alpha z\Delta \bigl (\langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\bigr )\cdot Y_\alpha ] dx. \end{aligned} \end{aligned}$$

Since $|\nabla \bigl (\langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\bigr )|\lesssim (\log \langle w_{-} \rangle )^2$ and $\Vert \frac{Y_\alpha }{\langle w_{-} \rangle }\Vert _{L^2} {\lesssim }\Vert \nabla Y_\alpha \Vert _{L^2}$, integrating the second term in the righthand side by parts will lead to the following upper bound for the righthand side:

$$\begin{aligned} \mu \Vert \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\nabla (\partial ^\alpha z)\Vert _{L^2}\Vert \nabla Y_\alpha \Vert _{L^2}+\mu \Vert (\log \langle w_{-} \rangle )^2\partial ^\alpha z\Vert _{L^2}\Vert \nabla Y_\alpha \Vert _{L^2}. \end{aligned}$$

Hence,

$$\begin{aligned} \frac{d}{dt}\Vert Y_\alpha \Vert _{L^2}^2+\mu \Vert \nabla Y_\alpha \Vert _{L^2}^2\lesssim \mu \Vert \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\nabla (\partial ^\alpha z)\Vert _{L^2}^2+\mu \Vert (\log \langle w_{-} \rangle )^2\partial ^\alpha z\Vert _{L^2}^2. \end{aligned}$$

Since $\Vert \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\nabla (\partial ^\alpha z)\Vert _{L^2}$ can be bounded by

$$\begin{aligned} \begin{aligned}&\sum _{1\le |\beta |\le |\alpha |}\Vert \nabla \bigl (\langle w_{-} \rangle (\log \langle w_{-} \rangle )^2(\partial ^\beta z)\bigr )\Vert _{L^2} +\Vert \nabla \bigl ((\log \langle w_{-} \rangle )^2 z\bigr )\Vert _{L^2} +\Vert \nabla \bigl (\log \langle w_{-} \rangle z\bigr )\Vert _{L^2}, \end{aligned} \end{aligned}$$

Then we have

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}\left( \sum _{1\le |\alpha |\le N_*+1}\Vert Y_\alpha \Vert _{L^2}^2+\mu \sum _{|\alpha |=N_*+2} \Vert Y_\alpha \Vert _{L^2}^2\right) \\&\quad +\mu \sum _{1\le |\alpha |\le N_*+1}\Vert \nabla Y_\alpha \Vert _{L^2}^2 +\mu ^2\sum _{|\alpha |=N_*+2}\Vert \nabla Y_\alpha \Vert _{L^2}^2\\&\quad \lesssim \mu \sum _{k=0}^2\Vert \nabla z_{0k}\Vert _{L^2}^2+\mu \sum _{1\le |\alpha |\le N_*+1}\Vert \nabla z_\alpha \Vert _{L^2}^2+\mu ^2\sum _{|\alpha |=N_*+2}\Vert \nabla z_\alpha \Vert _{L^2}^2. \end{aligned} \end{aligned}$$

(3.40)

Integrating over t, (3.40) together with (3.36) gives the following bound on $Y_\alpha$:

$$\begin{aligned} \begin{aligned}&\sup _{t\ge 0}\left( \sum _{1\le |\alpha |\le N_*+1}\Vert Y_\alpha \Vert _{L^2}^2+\mu \sum _{|\alpha |=N_*+2}\Vert Y_\alpha \Vert _{L^2}^2\right) \\&\quad +\mu \sum _{1\le |\alpha |\le N_*+1}\int _0^\infty \Vert \nabla Y_\alpha \Vert _{L^2}^2dt +\mu ^2\sum _{|\alpha |=N_*+2}\int _0^\infty \Vert \nabla Y_\alpha \Vert _{L^2}^2dt\lesssim \mathcal {E}^\mu (0). \end{aligned} \end{aligned}$$

(3.41)

Step 3.3 Energy estimate for (3.39). Once again, similar to the derivation of (1.13), for all $t\ge 0$ and $u_+ \in \mathbb {R}$, we have

$$\begin{aligned} \begin{aligned}&\sum _{1\le |\alpha |\le N_*+1}\Vert R_\alpha (t)\Vert _{L^2}^2+\mu \sum _{|\alpha |=N_*+2}\Vert R_\alpha (t)\Vert _{L^2}^2+ \sum _{1\le |\alpha |\le N_*+1}\int _{C_{u_+}}|R_\alpha |^2 d\sigma _+ \\&\quad +\mu \sum _{1\le |\alpha |\le N_*+1}\int _0^t\Vert \nabla R_\alpha (\tau )\Vert _{L^2}^2 d\tau +\mu ^2\sum _{|\alpha |=N_*+2}\int _0^t\Vert \nabla R_\alpha (\tau )\Vert _{L^2}^2 d \tau \\&\quad \lesssim \left( \sum _{1\le |\alpha |\le N_*+1}+\mu \sum _{|\alpha |=N_*+2}\right) \underbrace{\bigg |\int _0^t\int _{\mathbb {R}^3} \biggl (\big ([\partial ^\alpha , z_-]\cdot \nabla z\big ) \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\biggr )\cdot R_\alpha dxd\tau \bigg | }_{I_\alpha } \end{aligned} \end{aligned}$$

Since $z=z_+^{(\text {lin})}$, in view of (1.13) and (3.27), we have for $1\le |\alpha |\le N_*+1$

$$\begin{aligned} \begin{aligned} I_\alpha \lesssim \mathcal {E}^\mu (0)\Bigl (\sup _{u_+}\int _{C_{u_+}} |R_\alpha |^2d\sigma _+\Bigr )^{\frac{1}{2}}. \end{aligned} \end{aligned}$$

Whereas for $|\alpha |=N_*+2$, we have

$$\begin{aligned} \begin{aligned} \mu I_\alpha&\lesssim \sqrt{\mu }\int _0^t\Vert \big ([\partial ^\alpha , z_-]\cdot \nabla z\big ) \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\Vert _{L^2}d\tau \cdot \Bigl (\sup _{0\le \tau \le t}\mu \Vert R_\alpha (\tau )\Vert _{L^2}^2\Bigr )^{\frac{1}{2}}\\&\lesssim \left( \underbrace{\sum _{0\le k\le N_*-2}}_{A_1}+\underbrace{\sum _{N_*-1\le k\le N_*+1}}_{A_2}\right) \sqrt{\mu }\int _0^t\Vert (\partial ^{N_*+2-k}z_-)\\&\quad \cdot (\partial ^k\nabla z)\langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\Vert _{L^2}d\tau \cdot \Bigl (\sup _{0\le \tau \le t}\mu \Vert R_\alpha (\tau )\Vert _{L^2}^2\Bigr )^{\frac{1}{2}}. \end{aligned} \end{aligned}$$

For $A_1$, we have

$$\begin{aligned} \begin{aligned} A_1&\lesssim \sum _{0\le k\le N_*-2}\sqrt{\mu }\big \Vert \langle w_+\rangle \bigl (\log \langle w_+\rangle \bigr )^2\partial ^{N_*+2-k}z_-\big \Vert _{L^2_\tau L^2_x}\\&\quad \cdot \Big \Vert \frac{\langle w_{-} \rangle (\log \langle w_{-} \rangle )^2}{\langle w_+\rangle \bigl (\log \langle w_+\rangle \bigr )^2}\partial ^k\nabla z\Big \Vert _{L^2_\tau L^\infty _x}\\&\lesssim \sum _{k\le N_*}\bigl (D_-^k\bigr )^{\frac{1}{2}}\sum _{k\le N_*}\bigl (F_+^k(\nabla z)\bigr )^{\frac{1}{2}}. \end{aligned} \end{aligned}$$

For $A_2$, we have

$$\begin{aligned} \begin{aligned} A_2&\lesssim \sum _{N_*-1\le k\le N_*+1}\sqrt{\mu }\big \Vert \langle w_+\rangle \bigl (\log \langle w_+\rangle \bigr )^2\partial ^{N_*+2-k}z_-\big \Vert _{L^2_\tau L^\infty _x}\\&\quad \cdot \Big \Vert \frac{\langle w_{-} \rangle (\log \langle w_{-} \rangle )^2}{\langle w_+\rangle \bigl (\log \langle w_+\rangle \bigr )^2}\partial ^k\nabla z\Big \Vert _{L^2_\tau L^2_x}\\&\lesssim \sum _{k\le N_*}\bigl (D_-+D_-^k\bigr )^{\frac{1}{2}}\sum _{k\le N_*}\bigl (F_+^k(\nabla z)\bigr )^{\frac{1}{2}}, \end{aligned} \end{aligned}$$

where we used the Gagliardo–Nirenberg interpolation inequality $\Vert u\Vert _{L^\infty }\lesssim \Vert \nabla u\Vert _{L^2}^{\frac{1}{2}}\Vert \nabla ^2u\Vert _{L^2}^{\frac{1}{2}}$. Then by virtue of (1.13) and (3.27), we have

$$\begin{aligned} \mu I_\alpha \lesssim \mathcal {E}^\mu (0)\Bigl (\sup _{0\le \tau \le t}\mu \Vert R_\alpha (\tau )\Vert _{L^2}^2\Bigr )^{\frac{1}{2}}. \end{aligned}$$

Thus, by the smallness of $\mathcal {E}^\mu (0)$, for all $t\ge 0$, $u_+\in \mathbb {R}$, we finally obtain

$$\begin{aligned} \begin{aligned}&\sum _{1\le |\alpha |\le N_*+1}\Vert R_\alpha (t)\Vert _{L^2}^2+\mu \sum _{|\alpha |=N_*+2}\Vert R_\alpha (t)\Vert _{L^2}^2+ \sum _{1\le |\alpha |\le N_*+1}\int _{C_{u_+}}|R_\alpha |^2 d\sigma _+ \\&\quad +\mu \sum _{1\le |\alpha |\le N_*+1}\int _0^t\Vert \nabla R_\alpha (\tau )\Vert _{L^2}^2 d\tau +\mu ^2\sum _{|\alpha |=N_*+2}\int _0^t\Vert \nabla R_\alpha (\tau ) \Vert _{L^2}^2 d \tau \lesssim \bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{3}{2}}. \end{aligned} \end{aligned}$$

(3.42)

Step 3.4 Energy estimates for the Lagrangian forms. We recall that $\widetilde{v}(t,y)=v(t,\psi _-(t,y))$ is a Lagrangian form of v, i.e., in the Lagrangian coordinates system. Since $\det \bigl (\frac{\partial \psi _-}{\partial y}\bigr )=1$, we have $\Vert v\Vert _{L^2}=\Vert \widetilde{v}\Vert _{L^2}$. When we write $\nabla \widetilde{v}(t,y)$, the derivative $\nabla$ is always understood as taken with respect to y. Therefore, (3.34) and (3.40) together give the following estimates (the $L^2$ norms are taken on $\Sigma _0$):

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}\left( \sum _{k=0}^2 c_{0k}\Vert \widetilde{z_{0k}}\Vert _{L^2}^2 +\sum _{1\le |\alpha |\le N_*+1} c_\alpha \Vert \widetilde{z_\alpha }\Vert _{L^2}^2+\mu \sum _{|\alpha |=N_*+2} c_\alpha \Vert \widetilde{z_\alpha }\Vert _{L^2}^2\right. \\&\left. \quad +\sum _{1\le |\alpha |\le N_*+1} c'_\alpha \Vert \widetilde{Y_\alpha }\Vert _{L^2}^2 +\mu \sum _{|\alpha |=N_*+2}c'_\alpha \Vert \widetilde{ Y_\alpha }\Vert _{L^2}^2\right) \\&\quad +c\mu \sum _{k=0}^2\Vert \nabla \widetilde{z_{0k}}\Vert _{L^2}^2 +\mu \sum _{1\le |\alpha |\le N_*+1}\big (c\Vert \nabla \widetilde{z_\alpha }\Vert _{L^2}^2+c' \Vert \nabla \widetilde{Y_\alpha }\Vert _{L^2}^2\big )\\&\quad +\mu ^2\sum _{|\alpha |=N_*+2} \big (c\Vert \nabla \widetilde{z_\alpha }\Vert _{L^2}^2+c'\Vert \nabla \widetilde{ Y_\alpha }\Vert _{L^2}^2\big )\\&\quad \le \left( \sum _{1\le |\alpha |\le N_*+1}+\mu \sum _{|\alpha |=N_*+2}\right) f_\alpha (t). \end{aligned} \end{aligned}$$

(3.43)

Step 3.5 The refined energy X(t). Let

$$\begin{aligned} X(t)=\sum _{k=0}^2 c_{0k} \Vert \widetilde{z_{0k}}\Vert _{L^2}^2 +\sum _{1\le |\alpha |\le N_*+1}(c_\alpha +c'_\alpha ) \Vert \widetilde{Y_\alpha }\Vert _{L^2}^2 +\mu \sum _{|\alpha |=N_*+2}(c_\alpha + c'_\alpha )\Vert \widetilde{Y_\alpha }\Vert _{L^2}^2. \end{aligned}$$

(3.44)

In view of the fact that $z_\alpha =Y_\alpha +R_\alpha$ and estimates (3.35), (3.41) and (3.42), we have

$$\begin{aligned} \mathcal {E}^\mu _{(\text {lin}),+}+\bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{3}{2}}\sim X(t)+\bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{3}{2}}. \end{aligned}$$

(3.45)

We rewrite (3.43) as

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}X(t)+c\mu \left( \sum _{k=0}^2\Vert \nabla \widetilde{z_{0k}}\Vert _{L^2}^2 +\sum _{1\le |\alpha |\le N_*+1}\Vert \nabla \widetilde{Y_\alpha }\Vert _{L^2}^2+\mu \sum _{|\alpha |=N_*+2}\Vert \nabla \widetilde{Y_\alpha }\Vert _{L^2}^2\right) \le F(t), \end{aligned} \end{aligned}$$

(3.46)

where

$$\begin{aligned} F(t)= & {} \left( \sum _{1\le |\alpha |\le N_*+1}+\mu \sum _{|\alpha |=N_*+2}\right) \left( f_\alpha (t) -2c_\alpha \frac{d}{dt}\int _{\Sigma _t}\widetilde{Y_\alpha }\cdot \widetilde{R_\alpha }dy -c_\alpha \frac{d}{dt}\Vert \widetilde{R_\alpha }\Vert _{L^2}^2\right) .\nonumber \\ \end{aligned}$$

(3.47)

To further refine the estimates, we quickly introduce a dyadic decomposition. Let $\psi$ and $\phi$ be non-negative smooth functions so that $\text {supp}\,\psi \subset B_{\frac{4}{3}}=\{y\,|\, |y|\le \frac{4}{3}\}$, $\text {supp}\,\phi \subset \mathcal {C}=\{y\,|\, \frac{3}{4}\le |y|\le \frac{8}{3}\}$ and

$$\begin{aligned} \psi (y)+\sum _{j\ge 0}\phi (2^{-j}y)=1. \end{aligned}$$

Let $p_{-1}(y)= \psi (y)$. For $j\ge 0$, we define $p_j(y) = \phi (2^{-j}y)$. We use $\widehat{f}$ to denote the Fourier transform of a function or a vector field f on $\mathbb {R}^3$.

By Hardy inequality, we have

$$\begin{aligned} 2^{-j}\Vert p_j\widetilde{z}\Vert _{L^2} \lesssim \big \Vert \frac{p_j\widetilde{z}}{\langle y\rangle }\big \Vert _{L^2} \lesssim \Vert \nabla (p_j\widetilde{z})\Vert _{L^2}^2. \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} \Vert \nabla \widetilde{z}\Vert _{L^2}^2 \sim \sum _{j=-1}^\infty \big (\Vert p_j\nabla \widetilde{z}\Vert _{L^2}^2 +2^{-2j}\Vert p_j\widetilde{z}\Vert _{L^2}^2\big )\sim \sum _{j=-1}^\infty \big (\Vert \nabla (p_j\widetilde{z})\Vert _{L^2}^2+ 2^{-2j}\Vert p_j\widetilde{z}\Vert _{L^2}^2\big ). \end{aligned} \end{aligned}$$

(3.48)

We now pick up a function $h(t)\ge 0$ and it will be determined later on. By Plancherel theorem, we have

$$\begin{aligned} \Vert \nabla \widetilde{z}\Vert _{L^2}^2\simeq \int _{\mathbb {R}^3}|\xi |^2|\widehat{\widetilde{z}}(\xi )|^2d\xi \ge h(t)^2\Vert \widetilde{z}\Vert _{L^2}^2-{h(t)^2}\int _{|\xi |\le h(t)} |\widehat{\widetilde{z}}(\xi )|^2d\xi . \end{aligned}$$

(3.49)

By (3.48) and (3.49), we deduce that

$$\begin{aligned}&\sum _{k=0}^2\Vert \nabla \widetilde{z_{0k}}\Vert _{L^2}^2 +\sum _{1\le |\alpha |\le N_*+1} \Vert \nabla \widetilde{Y_\alpha }\Vert _{L^2}^2 +\mu \sum _{|\alpha |=N_*+2}\Vert \nabla \widetilde{Y_\alpha }\Vert _{L^2}^2\\&\quad \gtrsim \mathop {\sum }_{\begin{array}{c} k\le 2 \\ j\ge -1 \end{array}} \Vert \nabla (p_j\widetilde{z_{0k}})\Vert _{L^2}^2 +\mathop {\sum }\limits _{\begin{array}{c} 1\le |\alpha |\le N_*+1 \\ j\ge -1 \end{array}} \Vert \nabla (p_j\widetilde{Y_\alpha })\Vert _{L^2}^2 +\mu \mathop {\sum }\limits _{\begin{array}{c} |\alpha |=N_*+2 \\ j\ge -1 \end{array}} \Vert \nabla (p_j\widetilde{Y_\alpha })\Vert _{L^2}^2\\&\quad \gtrsim h(t)^2X(t)-{h(t)^2}\int _{|\xi |\le h(t)}\left( \mathop {\sum }\limits _{\begin{array}{c} k\le 2 \\ j\ge -1 \end{array}} |\widehat{p_j\widetilde{z_{0k}}}(\xi )|^2 +\mathop {\sum }\limits _{\begin{array}{c} 1\le |\alpha |\le N_*+1 \\ j\ge -1 \end{array}} |\widehat{p_j\widetilde{Y_\alpha }}(\xi )|^2\right. \\&\left. \qquad +\mu \mathop {\sum }\limits _{\begin{array}{c} |\alpha |=N_*+2 \\ j\ge -1 \end{array}} |\widehat{p_j\widetilde{Y_\alpha }}(\xi )|^2 \right) d\xi . \end{aligned}$$

We then deduce from (3.46) that

$$\begin{aligned} \begin{aligned}&\frac{d}{dt} X(t)+c\mu h(t)^2 X(t)\\&\quad \le F(t) +c\mu h(t)^2\int _{|\xi |\le h(t)}\left( \mathop {\sum }\limits _{\begin{array}{c} k\le 2 \\ j\ge -1 \end{array}} |\widehat{p_j\widetilde{z_{0k}}}(\xi )|^2 +\mathop {\sum }\limits _{\begin{array}{c} 1\le |\alpha |\le N_*+1 \\ j\ge -1 \end{array}} |\widehat{p_j\widetilde{Y_\alpha }}(\xi )|^2\right. \\&\left. \qquad +\mu \mathop {\sum }\limits _{\begin{array}{c} |\alpha |=N_*+2 \\ j\ge -1 \end{array}} |\widehat{p_j\widetilde{Y_\alpha }}(\xi )|^2 \right) d\xi . \end{aligned} \end{aligned}$$

(3.50)

The integral terms on the right-side will be called low frequency terms.

Step 4 Estimates on the low frequency terms in (3.50).

Step 4.1 Estimates on $\int _{|\xi |\le h(t)}|\widehat{p_j\widetilde{Y_\alpha }}|^2d\xi$. Since $\psi _-(t,y)$ is the flow generated by $Z_-$ which defines the coordinates $(t, y_1,y_2,y_3)$, we have

$$\begin{aligned} (\partial _t+Z_{-}\cdot \nabla )f|_{x=\psi _-(t,y)}=\partial _t\widetilde{f}(t,y),\quad \nabla f|_{x=\psi _-(t,y)}=\bigl (\frac{\partial \psi _-(t,y)}{\partial y}\bigr )^{-T}\nabla _y\widetilde{f}(t,y). \end{aligned}$$

Let $A_{-}=\bigl (\frac{\partial \psi _-(t,y)}{\partial y}\bigr )^{-1}\bigl (\frac{\partial \psi _-(t,y)}{\partial y}\bigr )^{-T}$. By the divergence free property of $Z_-$, we have $\det \bigl (\frac{\partial \psi _-(t,y)}{\partial y}\bigr )=1$ so that $\bigl (\frac{\partial \psi _-(t,y)}{\partial y}\bigr )^{-1}$ is the adjoint matrix of $\frac{\partial \psi _-(t,y)}{\partial y}$. Then we have $\text{ div }\bigl (\frac{\partial \psi _-(t,y)}{\partial y}\bigr )^{-1}=0$ and

$$\begin{aligned} \Delta f|_{x=\psi _-(t,y)} =\nabla _y\cdot \Bigl (A_{-}\nabla _y \widetilde{f}(t,y)\Bigr ), \end{aligned}$$

Thus, (3.38) can be written as

$$\begin{aligned} \begin{aligned} \partial _t\widetilde{Y_\alpha }-\mu \Delta \widetilde{Y_\alpha }&=\mu \text{ div }\bigl ((A_{-}-I)\nabla \widetilde{Y_\alpha }\bigr )-2\mu \bigl (\frac{\partial \psi _-}{\partial y}\bigr )^{-T}\nabla \bigl (\langle y\rangle (\log \langle y\rangle )^2\bigr )\cdot \widetilde{\nabla \partial ^\alpha z}\\&\quad -\mu \widetilde{\partial ^{\alpha } z}\text{ div }\bigl (A_-\nabla [\langle y\rangle (\log \langle y\rangle )^2]\bigr ), \end{aligned} \end{aligned}$$

(3.51)

In the above expression, we used the fact that $\langle w_{\pm } \rangle |_{x=\psi _\pm (t,y)}=\langle y\rangle$.

We decompose (3.51) by multiplying $p_j$ for each $j\ge -1$:

$$\begin{aligned} \begin{aligned}&\partial _t(p_j\widetilde{Y_\alpha })-\mu \Delta (p_j\widetilde{Y_\alpha })=\underbrace{-2\mu \nabla p_j\cdot \nabla \widetilde{Y_\alpha }-\mu \Delta p_j \widetilde{Y_\alpha }}_{L_\alpha ^1}+\underbrace{\mu p_j \text{ div }\bigl ((A_--I)\nabla \widetilde{Y_\alpha }\bigr )}_{L_\alpha ^2}\\&\quad \underbrace{-\,2\mu \bigl (\frac{\partial \psi _-}{\partial y}\bigr )^{-T}\nabla \bigl (\langle y\rangle (\log \langle y\rangle )^2\bigr )\cdot (p_j\widetilde{\nabla \partial ^\alpha z})}_{L_\alpha ^3}-\underbrace{\mu (p_j\widetilde{\partial ^\alpha z})\text{ div }\bigl (A_-\nabla [\langle y\rangle (\log \langle y\rangle )^2]\bigr )}_{L_\alpha ^4}. \end{aligned} \end{aligned}$$

(3.52)

We use $L_\alpha$ to denote the righthand side of (3.52). In frequency space, we have

$$\begin{aligned} \frac{d}{dt}\big |\widehat{p_j\widetilde{Y_\alpha }}\big |^2+2\mu |\xi |^2\big |\widehat{p_j\widetilde{Y_\alpha }}\big |^2 =2\mathcal {R}e \big ( \widehat{L}_\alpha \cdot \overline{\widehat{p_j\widetilde{Y_\alpha }}}\big ), \end{aligned}$$

which implies

$$\begin{aligned} \big |\widehat{p_j\widetilde{Y_\alpha }}\big |^2(t,\xi )=e^{-2\mu t|\xi |^2}\big |\widehat{p_j\widetilde{Y_\alpha }}(0,\xi )\big |^2+2\int _0^te^{-2\mu (t-s)|\xi |^2} \mathcal {R}e \bigl (\widehat{L}_\alpha \cdot \overline{\widehat{p_j\widetilde{Y_\alpha }}}\bigr )(s,\xi )ds, \end{aligned}$$

Therefore,

$$\begin{aligned}&\int _{|\xi |\le h(t)}\big |\widehat{p_j\widetilde{Y_\alpha }}\big |^2(t,\xi )d\xi \le \int _{\mathbb {R}^3}e^{-2\mu t|\xi |^2}\big |\widehat{p_j\widetilde{Y_\alpha }}\big |_{t=0}\big |^2\psi \big (\frac{3|\xi |}{4h(t)}\big ) d\xi \nonumber \\&\quad +\underbrace{2\mathcal {R}e\int _0^t\int _{\mathbb {R}^3}e^{-2\mu (t-s)|\xi |^2} \psi \big (\frac{3|\xi |}{4h(t)}\big ) \bigl (\widehat{L}_\alpha \cdot \overline{\widehat{p_j\widetilde{Y_\alpha }}}\bigr )(s,\xi ) d\xi ds}_{T_j^{\alpha }}. \end{aligned}$$

(3.53)

By Plancherel theorem, we have

$$\begin{aligned} |T_j^{\alpha }|\lesssim \big |\int _0^t\int _{\mathbb {R}^3}L_\alpha \cdot a_1*a_2*\bigl (p_j\widetilde{Y_\alpha }\bigr )dy ds\big |. \end{aligned}$$

where we take the following $a_1,\ a_2\in \mathcal {S}(\mathbb {R}^3)$:

$$\begin{aligned} a_1&=\left( 2\sqrt{\mu (t-s)}\right) ^{-3}e^{-\frac{|x|^2}{8\mu (t-s)}} \Leftrightarrow \hat{a}_1=e^{-2\mu (t-s)|\xi |^2},\\ a_2&=\left( \frac{4}{3}h(t)\right) ^3\breve{\psi }\left( \frac{4}{3}h(t)x\right) \Leftrightarrow \hat{a}_2=\psi \left( \frac{3|\xi |}{4h(t)}\right) . \end{aligned}$$

There exists a universal constant C independent of $t,s,\mu$, such that

$$\begin{aligned} \Vert a_1\Vert _{L^1}+\Vert a_2\Vert _{L^1}\le C. \end{aligned}$$

To proceed, we first make the following observation

$$\begin{aligned} \nabla p_j=\nabla p_j\left( \sum _{|j-k|\le 2}p_k\right) =\nabla p_j p'_j,\quad p_j\langle y\rangle ^{-1}\le 2^{-j} p_j,\quad |\partial ^k p_j|\lesssim 2^{-kj}p'_{j}, \end{aligned}$$

(3.54)

where $p'_j=\sum _{|j-k|\le 2}p_k$.

We first bound , i.e., the contribution from $L^1_\alpha$ in $T_j^\alpha$. By integration by parts, we have

$$\begin{aligned} \begin{aligned} T_{j1}^\alpha&=\mu \int _0^t\int _{\mathbb {R}^3}(\Delta p_j) \widetilde{Y_\alpha }\cdot a_1*a_2*\bigl (p_j\widetilde{Y_\alpha }\bigr )dyds\\&\quad +2\mu \int _0^t\int _{\mathbb {R}^3}(\partial p_j) \widetilde{Y_\alpha }\cdot \partial \bigl (a_1*a_2*(p_j\widetilde{Y_\alpha })\bigr )dyds. \end{aligned} \end{aligned}$$

According to (3.54), we have

$$\begin{aligned} \begin{aligned} \big |T_{j1}^\alpha \big |&\lesssim \mu \int _0^t\int _{\mathbb {R}^3}\big |p'_j\widetilde{Y_\alpha }\big |\cdot \bigl ( 2^{-2j}|a_1*a_2*\big (p_j\widetilde{Y_\alpha }\big )|\\&\quad +2^{-j}\big |\partial \bigl ((a_1*a_2*(p_j\widetilde{Y_\alpha })\bigr )\big |\bigr )dy ds\\&{\mathop {\lesssim }\limits ^{|y|\sim 2^j}}\mu \int _0^t\Vert p'_j\widetilde{Y_\alpha }\Vert _{L^2}\bigl (2^{-j} \big \Vert \frac{1}{|y|}a_1*a_2*\bigl (p_j\widetilde{Y_\alpha }\bigr )\big \Vert _{L^2}\\&\quad +2^{-j}\big \Vert \nabla \bigl (a_1*a_2*(p_j\widetilde{Y_\alpha })\bigr )\big \Vert _{L^2}\bigr )ds. \end{aligned} \end{aligned}$$

In view of the fact that $supp\,\hat{a}_2\subset \{|\xi |\le h(t)\}$, by Young’s and Hardy’s inequalities and Plancherel theorem, we have

$$\begin{aligned} \begin{aligned}&\big \Vert \frac{1}{|y|}a_1*a_2*\bigl (p_j\widetilde{Y_\alpha }\bigr )\big \Vert _{L^2}\\&\quad \lesssim \Vert \nabla \bigl (a_1*a_2*(p_j\widetilde{Y_\alpha })\bigr )\Vert _{L^2} \lesssim \Vert a_1*(|\nabla |\nabla a_2)*\bigl (|\nabla |^{-1}(p_j\widetilde{Y_\alpha })\bigr )\Vert _{L^2}\\&\quad \lesssim h(t)^2 \Vert a_1\Vert _{L^1}\Vert a_2\Vert _{L^1}\Vert |\nabla |^{-1}(p_j\widetilde{Y_\alpha })\bigr )\Vert _{L^2} \lesssim h(t)^2\big \Vert \frac{1}{|\xi |}\widehat{p_j\widetilde{Y_\alpha }}\big \Vert _{L^2}\\&\quad {\mathop {\lesssim }\limits ^{Hardy}} h(t)^2\Vert \nabla _\xi \widehat{p_j\widetilde{Y_\alpha }}\Vert _{L^2}\lesssim h(t)^2\Vert \widehat{yp_j\widetilde{Y_\alpha }}\Vert _{L^2} {\mathop {\lesssim }\limits ^{|y|\lesssim 2^j}}2^j h(t)^2\Vert p_j\widetilde{Y_\alpha }\Vert _{L^2}. \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} 2^{-j}\big \Vert \frac{1}{|y|}a_1*a_2*\bigl (p_j\widetilde{Y_\alpha }\bigr ) \big \Vert _{L^2}\lesssim 2^{-j}\Vert \nabla \bigl (a_1*a_2*(p_j\widetilde{Y_\alpha })\bigr )\Vert _{L^2} \lesssim h(t)^2\Vert p_j\widetilde{Y_\alpha }\Vert _{L^2}. \end{aligned}$$

(3.55)

Thus, we obtain

$$\begin{aligned} |T_{j1}^\alpha |\lesssim \mu h(t)^2\int _0^t\Vert p_j\widetilde{Y_\alpha }\Vert _{L^2}\Vert p_j'\widetilde{Y_\alpha }\Vert _{L^2}ds\lesssim \mu h(t)^2\int _0^t\Vert p_j'\widetilde{Y_\alpha }\Vert _{L^2}^2ds. \end{aligned}$$

(3.56)

We then bound $T_{j2}^\alpha =\int _0^t\int _{\mathbb {R}^3}L_\alpha ^2\cdot a_1*a_2*\bigl (p_j\widetilde{Y_\alpha }\bigr )dyds$, i.e., the contribution from $L^2_\alpha$ in $T_j^\alpha$. By integration by parts, we have

$$\begin{aligned} T_{j2}^\alpha= & {} -\,\mu \int _0^t\int _{\mathbb {R}^3}\bigl (\nabla p_j\cdot (A_--I)\nabla \widetilde{Y_\alpha }\bigr )\cdot a_1*a_2*\bigl (p_j\widetilde{Y_\alpha }\bigr )dyds\\&-\,\mu \int _0^t\int _{\mathbb {R}^3}p_j(A_--I)\nabla \widetilde{Y_\alpha }\cdot \nabla \bigl (a_1*a_2*(p_j\widetilde{Y_\alpha })\bigr )dyds. \end{aligned}$$

Similar to the argument used to bound $T_{j1}^\alpha$, we have

$$\begin{aligned} \begin{aligned} T_{j2}^\alpha&\lesssim \mu \int _0^t \Vert A_--I\Vert _{L^\infty _y} \bigl (\Vert p_j'\nabla \widetilde{Y_\alpha }\Vert _{L^2}+\Vert p_j\nabla \widetilde{Y_\alpha }\Vert _{L^2}\bigr ) \Vert a_1*a_2*\nabla (p_j\widetilde{Y_\alpha })\Vert _{L^2}ds. \end{aligned} \end{aligned}$$

By Young’s inequality, we have $\Vert a_1*a_2*\nabla (p_j\widetilde{Y_\alpha })\Vert _{L^2} \lesssim \Vert \nabla (p_j\widetilde{Y_\alpha })\Vert _{L^2}$. We then conclude that

$$\begin{aligned} |T_{j2}^\alpha | \lesssim \mu \Vert A_--I\Vert _{L^\infty _{t,y}} \int _0^t\Vert p_j'\nabla \widetilde{Y_\alpha }\Vert _{L^2}\Vert \nabla (p_j\widetilde{Y_\alpha })\Vert _{L^2}ds. \end{aligned}$$

(3.57)

We move to the bound on $T_{j3}^\alpha =\int _0^t\int _{\mathbb {R}^3}L_\alpha ^3\cdot a_1*a_2*\bigl (p_j\widetilde{Y_\alpha }\bigr )dyds$. First of all, since $\widetilde{\nabla \partial ^\alpha z}=\bigl (\frac{\partial \psi _-}{\partial y}\bigr )^{-T}\nabla \widetilde{\partial ^\alpha z}$, we rewrite $L_\alpha ^3$ as

$$\begin{aligned} \begin{aligned} L_\alpha ^3&=\underbrace{-\,2\mu \nabla \bigl (\langle y\rangle (\log \langle y\rangle )^2\bigr )\cdot (p_j\nabla \widetilde{\partial ^\alpha z})}_{L_\alpha ^{31}}\\&\quad \underbrace{-\,2\mu \nabla \bigl (\langle y\rangle (\log \langle y\rangle )^2\bigr )\cdot \Bigl (\bigl (\frac{\partial \psi _-}{\partial y}\bigr )^{-T}-I\Bigr )(p_j\nabla \widetilde{\partial ^\alpha z})} _{L_\alpha ^{32}}\\&\quad \underbrace{-\,2\mu \Bigl (\bigl (\frac{\partial \psi _-}{\partial y}\bigr )^{-T}-I\Bigr )\nabla \bigl (\langle y\rangle (\log \langle y\rangle )^2\bigr )\cdot (p_j\widetilde{\nabla \partial ^\alpha z})} _{L_\alpha ^{33}}. \end{aligned} \end{aligned}$$

For $i\le 3$, let $T_{j3i}^\alpha$ be the contribution of $L_\alpha ^{3i}$ in $T_{j3}^\alpha$. For $T_{j31}^\alpha$, by integration by parts and (3.54), we have

$$\begin{aligned} \begin{aligned} |T_{j31}^\alpha |&\lesssim \mu \int _0^t\int _{\mathbb {R}^3}\bigl (|p_j\bigl (\langle y\rangle (\log \langle y\rangle )^2\widetilde{\partial ^\alpha z}\bigr )|\big |\frac{a_1*a_2*\bigl (p_j\widetilde{Y_\alpha }\bigr )}{\langle y\rangle ^2} \big |\\&\quad +|p'_j\bigl (\langle y\rangle (\log \langle y\rangle )^2\widetilde{\partial ^\alpha z}\bigr )| 2^{-j} \big |\frac{a_1*a_2*\bigl (p_j\widetilde{Y_\alpha }\bigr )}{\langle y\rangle } \big |\bigr )dyds \\&\quad +\mu \int _0^t\int _{\mathbb {R}^3}|p_j\bigl (\langle y\rangle (\log \langle y\rangle )^2\widetilde{\partial ^\alpha z}\bigr )|\cdot \big |\frac{\nabla \bigl (a_1*a_2*(p_j\widetilde{Y_\alpha })\bigr )}{\langle y\rangle }\big |dyds. \end{aligned} \end{aligned}$$

We observe that $p_j\frac{1}{{\langle y\rangle }}\lesssim p_j2^{-j}$ and $\langle y\rangle (\log \langle y\rangle )^2\widetilde{\partial ^\alpha z}=\widetilde{z_\alpha }$. Thanks to (3.55), we have

$$\begin{aligned} |T_{j31}^\alpha | \lesssim \mu h(t)^2\int _0^t\Vert p'_j\widetilde{z_\alpha }\Vert _{L^2}\Vert p_j\widetilde{Y_\alpha }\Vert _{L^2}ds. \end{aligned}$$

To bound $T_{j32}^\alpha$ and $T_{j33}^\alpha$, we have

$$\begin{aligned} \begin{aligned} \big |T_{j32}^\alpha +T_{j33}^\alpha \big |&\lesssim \mu \left\| \left( \frac{\partial \psi _-}{\partial y}\right) ^{-T}-I\right\| _{L^\infty _{t,y}}\int _0^t\bigl (\Vert p_j\bigl (\langle y\rangle (\log \langle y\rangle )^2\nabla \widetilde{\partial ^\alpha z}\bigr )\Vert _{L^2}\\&\quad +\Vert p_j\bigl (\langle y\rangle (\log \langle y\rangle )^2\widetilde{\nabla \partial ^\alpha z}\bigr )\Vert _{L^2}\bigr )\big \Vert \frac{a_1*a_2*\bigl (p_j\widetilde{Y_\alpha }\bigr )}{\langle y\rangle } \big \Vert _{L^2}ds\\&\quad {\mathop {\lesssim }\limits ^{Hardy}}\mu \left\| \left( \frac{\partial \psi _-}{\partial y}\right) ^{-T}-I\right\| _{L^\infty _{t,y}}\int _0^t\big \Vert p_j\bigl (\langle y\rangle (\log \langle y\rangle )^2\widetilde{\nabla \partial ^\alpha z}\bigr )\big \Vert _{L^2}\\&\quad \Vert a_1*a_2*\nabla (p_j\widetilde{Y_\alpha })\Vert _{L^2}ds\\&\quad \lesssim \mu \left\| \left( \frac{\partial \psi _-}{\partial y}\right) ^{-T}-I\right\| _{L^\infty _{t,y}}\int _0^t\Vert p_j\bigl (\langle y\rangle (\log \langle y\rangle )^2\widetilde{\nabla \partial ^\alpha z}\bigr )\Vert _{L^2}\\&\qquad \Vert \nabla (p_j\widetilde{Y_\alpha })\Vert _{L^2}ds. \end{aligned} \end{aligned}$$

As a result, we finally have

$$\begin{aligned} \begin{aligned}&\big |T_{j3}^\alpha \big | \lesssim \mu h(t)^2\int _0^t\Vert p'_j\widetilde{z_\alpha }\Vert _{L^2}\Vert p_j\widetilde{Y_\alpha }\Vert _{L^2}ds\\&\quad +\mu \left\| \left( \frac{\partial \psi _-}{\partial y}\right) ^{-T}-I\right\| _{L^\infty _{t,y}}\int _0^t\big \Vert p_j\bigl (\langle y\rangle (\log \langle y\rangle )^2\widetilde{\nabla \partial ^\alpha z}\bigr )\big \Vert _{L^2}\Vert \nabla (p_j\widetilde{Y_\alpha })\Vert _{L^2}ds. \end{aligned} \end{aligned}$$

(3.58)

It remains to bound $T_{j4}^\alpha =\int _0^t\int _{\mathbb {R}^3}L_\alpha ^4\cdot a_1*a_2*\bigl (p_j\widetilde{Y_\alpha }\bigr )dyds$. Since $L^4_\alpha$ can be written as

$$\begin{aligned} L_\alpha ^4=-\mu (p_j\widetilde{\partial ^\alpha z})\Delta [\langle y\rangle (\log \langle y\rangle )^2]\bigr )-\mu (p_j\widetilde{\partial ^\alpha z})\text{ div }\bigl ((A_--I)\nabla [\langle y\rangle (\log \langle y\rangle )^2]\bigr ), \end{aligned}$$

we can proceed exactly in the same manner as for $T_{j3}^\alpha$ and we obtain

$$\begin{aligned} \begin{aligned} |T_{j4}^\alpha |&\lesssim \mu h(t)^2\int _0^t\Vert p'_j\widetilde{z_\alpha } \Vert _{L^2}\Vert p_j\widetilde{Y_\alpha }\Vert _{L^2}ds +\mu \Vert A_-\\&\quad -I\Vert _{L^\infty _{t,y}} \int _0^t\Vert p_j\bigl (\langle y\rangle (\log \langle y\rangle )^2\widetilde{\nabla \partial ^\alpha z}\bigr )\Vert _{L^2}\Vert \nabla (p_j\widetilde{Y_\alpha })\Vert _{L^2}ds. \end{aligned} \end{aligned}$$

(3.59)

Finally, in view of (3.48), when we sum over j, (3.56)–(3.59) together yield

$$\begin{aligned} \sum _{j=-1}^\infty |T_j^\alpha |\lesssim & {} \mu h(t)^2\int _0^t \bigl (\Vert \widetilde{z_\alpha }\Vert _{L^2}^2+\Vert \widetilde{Y_\alpha }\Vert _{L^2}^2\bigr )ds\\&+\,\mu \big (\Vert A_--I\Vert _{L^\infty _{t,y}}+\big \Vert \bigl (\frac{\partial \psi _-}{\partial y}\bigr )^{-T}-I\big \Vert _{L^\infty _{t,y}}\big )\\&\times \int _0^t\bigl (\Vert \langle y\rangle (\log \langle y\rangle )^2\widetilde{\nabla \partial ^\alpha z}\Vert _{L^2}^2+\Vert \nabla \widetilde{Y_\alpha }\Vert _{L^2}^2\bigr )ds\\\lesssim & {} \mu t h(t)^2\sup _{t\ge 0}\bigl (\Vert z_\alpha \Vert _{L^2}^2+\Vert Y_\alpha \Vert _{L^2}^2\bigr )\\&+\,\mu \big (\Vert A_--I\Vert _{L^\infty _{t,y}}+\big \Vert \bigl (\frac{\partial \psi _-}{\partial y}\bigr )^{-T}-I\big \Vert _{L^\infty _{t,y}}\big )\\&\times \int _0^t\bigl (\Vert \langle w_{-} \rangle (\log \langle w_{-} \rangle )^2\nabla \partial ^\alpha z\Vert _{L^2}^2+\Vert \nabla Y_\alpha \Vert _{L^2}^2\bigr )ds. \end{aligned}$$

By (3.36) and (3.41), we obtain

$$\begin{aligned}&\left( \sum _{1\le |\alpha |\le N_*+1}+\mu \sum _{|\alpha |=N_*+2}\right) \sum _{j=-1}^\infty |T_j^\alpha |\nonumber \\&\quad \lesssim \mu th(t)^2\mathcal {E}^\mu (0)+\left( \Vert A_--I\Vert _{L^\infty _{t,y}}+\left\| \left( \frac{\partial \psi _-}{\partial y}\right) ^{-T}-I\right\| _{L^\infty _{t,y}}\right) \mathcal {E}^\mu (0).\qquad \quad \end{aligned}$$

(3.60)

As a consequence, (3.53) yields

$$\begin{aligned} \begin{aligned}&\mathop {\sum }\limits _{\begin{array}{c} 1\le |\alpha |\le N_*+1 \\ j\ge -1 \end{array}}\int _{|\xi |\le h(t)}|\widehat{p_j\widetilde{Y_\alpha }}(\xi )|^2d\xi +\mu \mathop {\sum }\limits _{\begin{array}{c} |\alpha |=N_*+2 \\ j\ge -1 \end{array}}\int _{|\xi |\le h(t)}|\widehat{p_j\widetilde{Y_\alpha }}(\xi )|^2d\xi \\&\quad \lesssim \mu th(t)^2\mathcal {E}^\mu (0)+\big (\Vert A_--I\Vert _{L^\infty _{t,y}}+\Vert \bigl (\frac{\partial \psi _-}{\partial y}\bigr )^{-T}-I\Vert _{L^\infty _{t,y}}\big )\mathcal {E}^\mu (0)\\&\quad +\left( \sum _{1\le |\alpha |\le N_*+1}+\mu \sum _{|\alpha |=N_*+2}\right) \sum _{j\ge -1}\int _{\mathbb {R}^3}e^{-2\mu t|\xi |^2}|\widehat{p_j\widetilde{Y_\alpha }}(0,\xi )|^2\psi \big (\frac{3|\xi |}{4h(t)}\big )d\xi . \end{aligned} \end{aligned}$$

(3.61)

Step 4.2 Estimates on  $\int _{|\xi |\le h(t)}|\widehat{p_j\widetilde{z_{0k}}}|^2d\xi$ for $k=0,1,2$.

From (3.37), we deduce that

$$\begin{aligned}&\partial _t\widetilde{z_{0k}}-\mu \Delta \widetilde{z_{0k}}=\mu \text{ div }\bigl ((A_--I)\nabla \widetilde{z_{0k}}\bigr )-2\mu \bigl (\frac{\partial \psi _-}{\partial y}\bigr )^{-T}\nabla \bigl ((\log \langle y\rangle )^k\bigr )\cdot \widetilde{\nabla z}\nonumber \\&\quad -\,\mu \widetilde{z}\text{ div }\bigl (A_-\nabla [(\log \langle y\rangle )^k]\bigr ). \end{aligned}$$

(3.62)

We can compared with this equation with (3.51) by replacing $\partial ^\alpha z$, $Y_\alpha$ and $\langle y\rangle (\log \langle y\rangle )^2$ by z, $z_{0k}$ and $(\log \langle y\rangle )^k$ respectively. Therefore, following the simialr derivation, we also have similar estimates (compared to (3.61)):

$$\begin{aligned} \begin{aligned}&\sum _{j\ge -1} \int _{|\xi |\le h(t)}\big |\widehat{p_j\widetilde{z_{0k}}}\big |^2(t,\xi )d\xi \lesssim \mu th(t)^2\mathcal {E}^\mu (0)\\&\quad + \big (\Vert A_--I\Vert _{L^\infty _{t,y}}+\big \Vert \bigl (\frac{\partial \psi _-}{\partial y}\bigr )^{-T}-I\big \Vert _{L^\infty _{t,y}}\big )\mathcal {E}^\mu (0)\\&\quad +\sum _{j\ge -1}\int _{\mathbb {R}^3}e^{-2\mu t|\xi |^2}\big |\widehat{p_j\widetilde{z_{0k}}}(0,\xi )\big |^2\psi \big (\frac{3|\xi |}{4h(t)}\big )d\xi . \end{aligned} \end{aligned}$$

(3.63)

Step 5 The decay of X(t).

By virtue of (3.50), (3.61) and (3.63), we conclude that there exists universal constant c and C (independent of $\mu$) such that

$$\begin{aligned} \begin{aligned} \frac{d}{dt} X(t)+c\mu h(t)^2 X(t)&\le F(t) +C\mu h(t)^2I^\mu (t)+C\mu ^2 th(t)^4\mathcal {E}^\mu (0)\\&\quad +C\mu h(t)^2 \big (\Vert A_--I\Vert _{L^\infty _{t,y}}+\big \Vert \bigl (\frac{\partial \psi _-}{\partial y}\bigr )^{-T}-I\big \Vert _{L^\infty _{t,y}}\big )\mathcal {E}^\mu (0), \end{aligned} \end{aligned}$$

(3.64)

where the new function $I^\mu (t)$ are determined by the initial data as follows:

$$\begin{aligned} \begin{aligned} I^\mu (t)&= \int _{\mathbb {R}^3} \sum _{j=-1}^\infty e^{-2\mu t|\xi |^2}\psi \left( \frac{3|\xi |}{4h(t)}\right) \left( \sum _{k=0}^2\big |\widehat{p_j\widetilde{z_{0k}}}(0,\xi )\big |^2\right. \\&\left. \quad +\sum _{1\le |\alpha |\le N_*+1}\big |\widehat{p_j\widetilde{Y_\alpha }}(0,\xi )\big |^2 +\mu \sum _{|\alpha |=N_*+2}\big |\widehat{p_j\widetilde{ Y_\alpha }}(0,\xi )\big |^2\right) d\xi . \end{aligned} \end{aligned}$$

(3.65)

We also notice that $|I^\mu (t)|\lesssim \mathcal {E}^\mu (0)$.

Multiplying both sides of (3.64) by the factor $e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau }$, we obtain

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}\Bigl (e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau } X(t)\Bigr )+\frac{c}{2}\mu h(t)^2 e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau }X(t)\\&\quad \le e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau } \underbrace{\Big (F(t)+\cdots \Big )}_{\text {Righthand side of} (3.64)}. \end{aligned} \end{aligned}$$

(3.66)

We first give the bound of F(t). In view of its definition in (3.47), we obtain that

$$\begin{aligned} \begin{aligned} e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau }F(t)&=\left( \sum _{1\le |\alpha |\le N_*+1}+\mu \sum _{|\alpha |=N_*+2}\right) e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau }f_\alpha (t)\\&\quad -\frac{d}{dt}G(t)+\frac{c}{2}\mu h(t)^2 G(t), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} G(t)&=e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau }\left( \sum _{1\le |\alpha |\le N_*+1}+\mu \sum _{|\alpha |= N_*+2}\right) \left( 2c_\alpha \int _{\mathbb {R}^3}\widetilde{Y_\alpha }\cdot \widetilde{R_\alpha } dy+c_\alpha \Vert \widetilde{R_\alpha }\Vert _{L^2}^2\right) . \end{aligned} \end{aligned}$$

We can bound G(t) as

$$\begin{aligned} \begin{aligned} |G(t)|\le&e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau }\left( \sum _{1\le |\alpha |\le N_*+1}+\mu \sum _{|\alpha |= N_*+2}\right) \left( c_\alpha \Vert {Y_\alpha }\Vert _{L^2}^2+2c_\alpha \Vert R_\alpha \Vert _{L^2}^2\right) . \end{aligned} \end{aligned}$$

Thanks to (3.42) and the expression of X(t) in (3.44), we obtain that

$$\begin{aligned} e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau } X(t)+G(t)\gtrsim e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau } X(t)-Ce^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau }\bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{3}{2}}, \end{aligned}$$

(3.67)

and

$$\begin{aligned} \frac{c}{2}\mu h(t)^2G(t)\le \frac{c}{2}\mu h(t)^2 e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau } X(t)+C \frac{c}{2}\mu h(t)^2e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau }\bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{3}{2}}. \end{aligned}$$

Thus, (3.66) implies that

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}\Bigl (e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau } X(t)+G(t)\Bigr )\\&\quad \le \left( \sum _{1\le |\alpha |\le N_*+1}+\mu \sum _{|\alpha |= N_*+2}\right) e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau }f_\alpha (t)+C\mu h(t)^2e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau }\bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{3}{2}}\\&\quad \quad +C\mu h(t)^2e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau }I^\mu (t)+C\mu ^2 th(t)^4e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau }\mathcal {E}^\mu (0)\\&\quad \quad +C\mu h(t)^2e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau } \left( \Vert A_--I\Vert _{L^\infty _{t,y}}+\left\| \left( \frac{\partial \psi _-}{\partial y}\right) ^{-T}-I\right\| _{L^\infty _{t,y}}\right) \mathcal {E}^\mu (0). \end{aligned} \end{aligned}$$

(3.68)

We set from now on that

$$\begin{aligned} \frac{c}{2}h(t)^2=(\mu t+e)^{-1}\bigl (\log (\mu t+e)\bigr )^{-1}. \end{aligned}$$

Thus, we have $e^{\frac{c}{2}\mu \int _0^th(\tau )^2d\tau }=\log (\mu t+e)$. By integrating (3.68) on [0, t] and by the estimate (3.33) on $f_\alpha$ and the estimate (3.67), we obtain

$$\begin{aligned} \begin{aligned}&\log (\mu t+e) X(t)\le 2X(0) +C\mu \int _0^t\frac{I^\mu (s)}{\mu s +e}ds+C\log \bigl (\log (\mu t+e)\bigr )\mathcal {E}^\mu (0)\\&\quad +C\log (\mu t+e)\big [\bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{3}{2}} +\big (\Vert A_--I\Vert _{L^\infty _{t,y}}+\big \Vert \bigl (\frac{\partial \psi _-}{\partial y}\bigr )^{-T}-I\big \Vert _{L^\infty _{t,y}}\big )\mathcal {E}^\mu (0)\big ]. \end{aligned} \end{aligned}$$

Since $X(0)\lesssim \mathcal {E}^\mu (0)$, we get

$$\begin{aligned} X(t)\lesssim & {} \frac{\log \bigl (\log (\mu t+e)+e\bigr )}{\log (\mu t+e)}\mathcal {E}^\mu (0)+\frac{\mu \int _0^t\frac{I^\mu (s)}{\mu s+e}ds}{\log (\mu t+e)}\\&+\,\bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{3}{2}} +\big (\Vert A_--I\Vert _{L^\infty _{t,y}}+\big \Vert \bigl (\frac{\partial \psi _-}{\partial y}\bigr )^{-T}-I\big \Vert _{L^\infty _{t,y}}\big )\mathcal {E}^\mu (0). \end{aligned}$$

We bound the second term on the righthand side as follows:

For $s\le \frac{1}{\mu } \log (\mu t+e)$, we use $I^\mu (t)\lesssim \mathcal {E}^\mu (0)$ and we obtain

$$\begin{aligned} \frac{\mu \int _0^{\frac{1}{\mu } \log (\mu t+e)}\frac{I^\mu (s)}{ \mu s+e }ds}{\log (\mu t+e)} \lesssim \frac{\log \bigl (\log (\mu t+e)+e\bigr )}{\log (\mu t+e)}\mathcal {E}^\mu (0). \end{aligned}$$

For $s\ge \frac{1}{\mu } \log (\mu t+e)$, we use $|h(s)|^2\le \frac{2}{c} (\log (\mu t+e)+e)^{-1}\bigl [\log \bigl (\log (\mu t+e)+e\bigr )\bigr ]^{-1}$ and the definition of $I^\mu (t)$ to obtain

$$\begin{aligned}&\frac{\mu \int _{\frac{1}{\mu } \log (\mu t+e)}^t\frac{I^\mu (s)}{\mu s+e}ds}{\log (\mu t+e)}\\&\quad \lesssim \underbrace{\sum _{j=-1}^\infty \int _{|\xi |^2\le \frac{8}{c}(\log (\mu t+e)+e)^{-1}} \left( \sum _{k=0}^2\big |\widehat{p_j\widetilde{z_{0k}}}(0,\xi )\big |^2 +\sum _{1\le |\alpha |\le N_*+1}\big |\widehat{p_j\widetilde{Y_\alpha }}(0,\xi )\big |^2 +\mu \sum _{|\alpha |=N_*+2} \big |\widehat{p_j\widetilde{Y_\alpha }}(0,\xi )\big |^2\right) d\xi }_{I^\mu (t;0)}. \end{aligned}$$

We remark that $I^\mu (t;0)$ is determined by the initial data and $\lim _{t\rightarrow \infty } I^\mu (t;0)=0$.

Finally, we obtain that the decay estimate on X(t):

$$\begin{aligned} \begin{aligned} X(t)&\lesssim \frac{\log \bigl (\log (\mu t+e)+e\bigr )}{\log (\mu t+e)}\mathcal {E}^\mu (0) + I^\mu (t;0)\\&\quad +\bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{3}{2}}+\big (\Vert A_- -I\Vert _{L^\infty _{t,y}}+\big \Vert \bigl (\frac{\partial \psi _-}{\partial y}\bigr )^{-T}-I\big \Vert _{L^\infty _{t,y}}\big )\mathcal {E}^\mu (0). \end{aligned} \end{aligned}$$

(3.69)

Step 6 Decay mechanism on energy and convergence to the parabolic regime.

By virtue of (3.30), (3.45) and (3.69), we have the following decay estimates for the total energy:

$$\begin{aligned} \begin{aligned} \mathcal {E}^\mu (t)&\lesssim \frac{\log \bigl (\log (\mu t+e)+e\bigr )}{\log (\mu t+e)}\mathcal {E}^\mu (0) + I^\mu (t;0)\\&+\underbrace{\bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{3}{2}}}_{H_1} +\underbrace{\sum _{+,-}\left( \Vert A_\pm -I\Vert _{L^\infty _{t,y}}+\big \Vert \bigl (\frac{\partial \psi _\pm }{\partial y}\bigr )^{-T}-I\big \Vert _{L^\infty _{t,y}}\right) \mathcal {E}^\mu (0)}_{H_2}. \end{aligned} \end{aligned}$$

(3.70)

We remark that the higher order term $H_1$ comes from the non-linear structure of the system while the term $H_2$ comes from the change of the coordinates from $(x_1, x_2, x_3)$ to $(y_1, y_2, y_3)$ (the label of $\Sigma _0$). And we also emphasize that the estimates of $\Vert A_\pm -I\Vert _{L^\infty _{t,y}}$ and $\Vert \bigl (\frac{\partial \psi _\pm }{\partial y}\bigr )^{-T}-I\Vert _{L^\infty _{t,y}}$ depend only on the total energy at the time $t=0$ since at the beginning $t=0$, it holds $(x_1^\pm , x_2^\pm , x_3^\pm )|_{t=0}=(x_1, x_2, x_3)$.

For $t\ge s$, we define

$$\begin{aligned} \begin{aligned} \mathcal {I}^\mu (t;s)&=\mathop {\sum }\limits _{\begin{array}{c} +,- \\ j\ge -1 \end{array}}\int _{|\xi |^2 \le \frac{8}{c}(\log (\mu (t-s)+e)+e)^{-1}} \left( \sum _{k=0}^2\big |\widehat{p_j\widetilde{z_{\pm ,0k}}}(s,\xi )\big |^2\right. \\&\left. \quad +\sum _{1\le |\alpha |\le N_*+1}\big |\widehat{p_j\widetilde{z_{\pm ,\alpha }}}(s,\xi )\big |^2 +\mu \sum _{|\alpha |=N_*+2}\big | \widehat{p_j\widetilde{z_{\pm ,\alpha }}}(s,\xi )\big |^2\right) d\xi , \end{aligned} \end{aligned}$$

where

$$\begin{aligned} z_{\pm , 00}:= & {} z_{\pm },\ \ z_{\pm ,01}:=\log \langle w_{\mp } \rangle z_{\pm },\ \ z_{\pm ,02}:=(\log \langle w_{\mp } \rangle )^2 z_{\pm },\\ z_{\alpha ,\pm }:= & {} \langle w_{\mp } \rangle (\log \langle w_{\mp } \rangle )^2\partial ^\alpha z_{\pm }. \end{aligned}$$

Then it is easy to generalize (3.70) to

$$\begin{aligned} \begin{aligned} \mathcal {E}^\mu (t)&\lesssim \frac{\log \bigl (\log (\mu (t-s)+e)+e\bigr )}{\log (\mu (t-s)+e)}\mathcal {E}^\mu (s) + I^\mu (t;s)\\&\quad +\bigl (\mathcal {E}^\mu (s)\bigr )^{\frac{3}{2}}+\sum _{+,-} \left( \Vert A_\pm -I\Vert _{L^\infty _{t,y}}+\left\| \left( \frac{\partial \psi _\pm }{\partial y}\right) ^{-T}-I\right\| _{L^\infty _{t,y}}\right) \mathcal {E}^\mu (s), \end{aligned} \end{aligned}$$

(3.71)

where we use the global energy estimate (1.13).

An easy but useful observation on $\mathcal {I}^\mu (t;s)$ is that, for a fixed s, we have $\mathcal {I}^\mu (t;s)\rightarrow 0$ as $t\rightarrow \infty$. Since $\mathcal {E}^\mu (0) \sim \varepsilon ^2$ and

$$\begin{aligned} \Vert A_\pm -I\Vert _{L^\infty _{t,y}}+\big \Vert \bigl (\frac{\partial \psi _\pm }{\partial y}\bigr )^{-T}-I\big \Vert _{L^\infty _{t,y}}\lesssim \bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{1}{2}}, \end{aligned}$$

there exists $T_1>0$ and a universal constant C such that

$$\begin{aligned} \mathcal {E}^\mu (T_1)\le \bigl (C\mathcal {E}^\mu (0)\bigr )^{\frac{3}{2}}. \end{aligned}$$

Therefore, at time $T_1$, the total energy drops for an order of $\varepsilon$. It is obvious that the time $T_1$ depends on the profile of the initial data and there is no uniform (with respect to the energy norms) control on $T_1$.

We can now iterate the above decay process: we treat $T_1$ as an initial time and by (3.71), for $t\ge T_1$, we obtain that

$$\begin{aligned} \mathcal {E}^\mu (t)\lesssim \mathcal {I}^\mu (t;T_1)+\frac{\log \bigl (\log (\mu (t-T_1)+e)+e\bigr )}{\log (\mu (t-T_1)+e)}\mathcal {E}^\mu (T_1) + \bigl (\mathcal {E}^\mu (0)\bigr )^{\frac{1}{2}}\mathcal {E}^\mu (T_1). \end{aligned}$$

Since $\lim _{t\rightarrow \infty }\mathcal {I}^\mu (t;T_1)= 0$, there also exists $T_2>T_1$ in such a way that

$$\begin{aligned} \mathcal {E}^\mu (T_2)\le \bigl (C\mathcal {E}^\mu (0)\bigr )^{\frac{1}{2}}\mathcal {E}^\mu (T_1)\le \bigl (C\mathcal {E}^\mu (0)\bigr )^{2}. \end{aligned}$$

By repeating the process, we can find time $T_1$, $T_2$, $\cdots$, $T_{n_0}$ such that

$$\begin{aligned} \mathcal {E}^\mu (T_{n_0})\le \bigl (C\mathcal {E}^\mu (0)\bigr )^{\frac{n_0}{2}+1}. \end{aligned}$$

We take $n_0 = 2\lfloor \frac{\log \varepsilon _{\mu }}{\log (\sqrt{C}\varepsilon )}\rfloor +1$ where $\lfloor m\rfloor$ denotes the maximum integer which does not exceed m. Therefore it holds

$$\begin{aligned} \mathcal {E}^\mu (T_{n_0})\le \varepsilon _\mu ^2. \end{aligned}$$

In particular, the $H^2$-norm of the system at $T_{n_0}$ are bounded above by $\varepsilon _\mu$. Therefore, the solutions are in the classical small-data parabolic regime. This completes the proof of the theorem.