The Multi-objective Solid Transportation Problem with Preservation Technology Using Pythagorean Fuzzy Sets

Abstract

This study’s motive is to vindicate the result of the preservation of a transportation system for transporting perishable items. We introduce a certain preservation technology (PT) with preservation cost to reduce the rate of deterioration, and then simultaneously to increase the lifetime of such items. Here we initiate a multi-objective solid transportation problem with a connection of PT. To make the problem realistic, we consider various criteria, such as transportation cost, preservation cost, time, and deterioration under a Pythagorean fuzzy environment. Pythagorean fuzzy sets are the extension of intuitionistic fuzzy sets and more flexible than the fuzzy sets, intuitionistic fuzzy sets, or other uncertainty. We introduce two numerical examples to elaborate the appropriateness of our approach, which is then solved in three ways: by the $\varepsilon$-constraint method, by neutrosophic linear programming, and by the fuzzy TOPSIS approach.

1 Introduction

We consider a transportation problem (TP) where the transported items deteriorate during the time of transportation. These goods include various foods, fruits, vegetables, flowers, blood, medicines, or fish. The lifetime of such items may expire during long time transportation. If the items are valuable or cannot be replaced easily (e.g., blood or medicines), this leads to huge losses. There exist certain PT, such as managing the temperature, keeping items in air tight packages, ice packeting, deep-freezing system, or by adding a cold storage within the transportation vehicle, that help to remain the items good so that they survive a longer time. However, the PT measures further costs, such as freezing cost, which is an extra investment for the transportation system. It increases the transportation cost, but reduces the rate of deterioration of these items.

In our model formulation below we attempt to find an optimal strategy that will keep a balance among transportation cost, preservation cost, and deterioration over time. To reduce the preservation cost, we endeavor to connect the freezing system of the related vehicles, so that the necessary energy can be supplied by the engine of that vehicles. When it comes to deterioration, the disposed items generate an economic loss, affect the environment, and consume natural resources. The benefit of PT during the transport is that it reduces the rate of deterioration of transported perishable items by preventing or reducing chemical reactions which are the cause of deterioration. By this, the profit can be increased by getting short lifetime items into a longer lifetime, so that more items can be sold at a higher price. This in turn recovers the economic loss and helps to reduce the burden for the environment.

1.1 Survey of the Literature

The TP is a special type of a linear programming problem introduced by Hitchcock [18]. It is also known as the Hitchcock–Koopmans TP. When it comes to the inclusion of PT, Pervin et al. [28] introduced an inventory model for the deterioration of items in the presence of PT with sensitive demand, including prices and stocks. Hsu et al. [19] formulated an inventory model with deterioration and considering PT. He and Huang [17] applied PT on an inventory model with seasonal deterioration and analyzed it with respect to a pricing policy.

For transporting items from one source to several destinations through many incidents, different types of conveyances, such as trucks, goods train, ships, cargo flights, etc., are utilized. Apart from source constraints and demand constraints, additional constraints named as conveyance constraints are included in classical TP, and the new type of TP is defined as solid transportation problem (STP), which was first established by Haley [14]. A group of researchers considered various research analyses on STP with different circumstances which are comprehended here. Ghosh et al. [13] proposed STP within a fully intuitionistic fuzzy (IF) environment with fixed charge and multiple objectives. Roy et al. [31] provided an STP with fixed charges in the presence of a two-fold uncertain situation. Das et al. [8] formulated an STP using heuristic method based on the p-facility location problem.

For an economic policy of TP, transportation cost, preservation cost, deterioration and transporting time, etc., are annexed at the time of transportation of items from a source to different destinations, but a single objective function is not enough to describe the entire situation. Hence the system balances the economic condition by introducing a multi-objective optimization problem, and then the traditional single objective TP turns into a multi-objective transportation problem (MOTP). Whenever an STP contains multiple objectives, then the problem is called an MOSTP. From literature we find some research studies on MOTP and MOSTP. A few of them is surveyed here. Roy and Midya [30] solved the MOSTP in an IF environment with fixed charges and a product blending concept. Das and Roy [9] studied the effect of carbon emissions on a multi-objective problem and treated the variables as a neutrosophic field within a p-facility location TP. Dalman et al. [7] discussed the MOSTP in uncertain situation including multi-item and then solved by fuzzy programming. Midya and Roy [26] presented rough programming for solving the MOTP with fixed charges. Maity et al. [23] briefly defined a TP with multiple objectives and solved it within an uncertain situation. Allah et al. [2] defined an MOTP in a neutrosophic environment. Roy et al. [29] analyzed the MOTP in a random-rough environment by considering fixed charges. An MOTP with transfer station was discussed by Ghosh and Roy [12] by considering product blending in fuzzy rough environment. They analyzed fixed charge for the presence of truck load constraints. A multi-objective model was introduced by Tirkolaee et al. [35] for perishable product on intermediate depot that related with two-echelon green routing problem.

Traditional MOTP and MOSTP are tackled by decision maker (DM) by choosing the parameters as an imprecise nature, because of the existence of restricted information, a lack of evidence, competitive economic condition, or the instability of financial market. For such realistic background there exist various uncertainties provided by the literature, such as fuzzy, interval, stochastic, randomness, roughness, IF, or neutrosophic. Zadeh [41] first defined fuzzy set (FS) where uncertainty was defined by a membership grade $\in [0,1]$. Thereafter Zimmermann [44] introduced fuzzy programming for different objective functions. Wang et al. [37] formulated logistic transportation by introducing polygonal fuzzy set and solved by TOPSIS (technique for order of preference by similarity to ideal solution) approach with ordered representation. Maity et al. [25] defined a TP in a dual-hesitant fuzzy environment with some restrictions. Zamzamzadeh and Yaghoobi [42] formulated a bi-objective TP by including fuzzy objective function. After a generalization of FS, Atanassov [3] introduced intuitionistic fuzzy set (IFS) in which the uncertainty was defined by both a membership grade and a non-membership grade, and their sum value has to be in the interval [0, 1]. If a critical situation arises, such that the sum of membership and non-membership value is greater than 1, then FS and IFS cannot tackle this situation. In this situation, Yager [38, 39] initiated the concept of a Pythagorean fuzzy set (PFS) by a generalization of IFS, and Peng [27] further refined it. A PFS is characterized by a membership and a non-membership degree, and the additional criteria are that the sum of the squares of its membership and non-membership values is less or equal to 1, and that the sum of membership and non-membership is greater than or less than l. PFS is capable of modeling a wider range of applications with uncertain information. It can be applied for multi-criteria decision making, information measures, or aggregation operators due to its flexibility to cope more complex uncertainty and inexactness. Our formulated model on MOSTP is mainly developed within a Pythagorean fuzzy environment named Pythagorean fuzzy number (PFN), and we consider all the parameters as triangular Pythagorean fuzzy number (TPFN).

We now discuss some research studies on PFS in different directions. Abbas et al. [1] defined cubic PFS and applied its concept to multi-attribute decision making by considering unknown weight information. Chen [6] modeled PFS with an interval for a multiple criteria decision analysis that depends on a bridge construction method. Ejegwa [10] applied PFS in career placements based on a max-min-max composition. Fei and Deng [11] introduced a Pythagorean fuzzy system for multi-criteria decision making. Han et al. [16] gave an interval-valued Pythagorean system and applied it in a multi-criteria decision-making problem with a prioritized operator-based game theoretical framework. Khan et al. [22] solved a multi-criteria decision-making problems with the help of Pythagorean cubic fuzzy aggregation operators. A list of some recent remarkable articles on TP in different environments is shown in Table 1.

Table 1 Survey of research works of TP under various environments

1.2 Our Contribution

From the literature survey, we observe that every MOTP or MOSTP is considered with objective functions as transportation cost, time, carbon emission, deterioration, and all of these functions are optimized. But to the best of our knowledge, no one did so far introduce any process to reduce the rate of deterioration. Here we include the PT to the MOTP in a Pythagorean fuzzy environment for the first time. Many transportation systems are considered with general items, but without considering perishable items in a MOTP or MOSTP with crisp or uncertain nature. They assumed that the uncertainty is defined by a membership value, or by both a membership and a non-membership value, and that each of these values lies in the interval [0, 1]. Also the sum of membership and non-membership value lies in [0, 1]. But no study has considered the case when the sum of membership and non-membership value is greater than 1, which we include here.

In summary, the main focuses of this study are the following:

• To formulate a model of MOSTP with three objective functions as transportation cost, time and deterioration with source, demand, and conveyance constraints.

• To introduce preservation cost and PT into MOSTP for reducing the rate of deterioration.

• To consider a Pythagorean fuzzy environment for tackling the uncertainty and to control the particular contradictory situation of an IF environment.

• To display a new ranking function that transforms PFN into crisp number.

• To utilize three progressive methods, namely the $\varepsilon$-constraint, neutrosophic linear programming (NLP), and fuzzy TOPSIS.

• To include a comparative study and finding conclusions from the discussion to justify the effectiveness of the proposed model.

1.3 Outline of the Paper

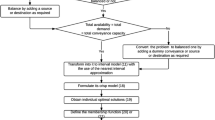
The remainder of this paper is organized as follows. A motivation of this study is described in Sect. 2. The basic preliminaries for FS, IFS, neutrosophic sets, and PFS with some basic properties are defined in Sect. 3. Section 4 presents notations and assumptions for the mathematical model of MOSTP in a Pythagorean fuzzy environment in connection with PT. The three methods, namely $\varepsilon$-constraint, NLP and fuzzy TOPSIS, with related models are illustrated in Sect. 5. Benefits including limitations of the proposed study are depicted in Sect. 6. Two numerical examples are described in Sect. 7. Section 8 contains the computational results and their discussion. Conclusions together with opportunities for future research are given in Sect. 9.

2 Motivation for this Study

Transporting systems are designed for different transport scenarios, such as long distance, long time, bad weather, sudden strike, sudden accident, road block due to unnatural situation, or bad road conditions. These situations are in particular making the transport of perishable items more challenging, since the suppliers or production companies cannot supply their items properly as these items deteriorate after expiring their lifetime. Some particular perishable items are very costly or cannot be easily manufactured. In such critical conditions, these items remain good or extend their lifetime by introducing PT. But an investment in PT leads to preservation cost which depends on amount of transported items, time and the preservation mode, and in turn reduces the deterioration by some fraction. Whenever cost increases then deterioration decreases due to adding a PT and vice versa. Therefore cost and deterioration are conflicting objectives, and the overall aim is to minimize both of these functions by introducing an optimal strategy. The scope is to reduce the transportation cost for supplying the energy of freezing system (one of the modes of PT) from the vehicle’s engine. For low deterioration rates, the consumption of energy is also reduced, and a preservation can be obtained in an environmentally sustainable way for the perishable items.

Even when PT is in use, there is no full guarantee that the perishable goods arrive at their destinations. The outcome of the transport is subject to uncertainty. To model this, we introduce a membership grade about the question whether the arriving items are still merchantable. For example, if the support for a “yes” is 0.8, and the non-membership grade against the support to “no” criteria is 0.5, then the sum of 0.8 and 0.5 does not lie in [0, 1]. Therefore the general criteria of IFS fails to express the uncertainty with membership and non-membership grades, but $(0.8)^2+(0.5)^2 \le 1$ holds. This situation is handled by introducing PFS and decision makers take decisions without modifying the provided information to meet the constraints of IFS. It can be seen that PFS can express more uncertain information and gave more advantages than IFSs in fuzzy and imprecise modeling. Also PFS can provide a better alternative whenever FSs or IFSs have some limitations on vagueness and uncertainty. Hence our motivation is to introduce a multi-objective solid transportation model under PT in a Pythagorean fuzzy environment, and after solving the model to obtain a compromise solution.

3 Basic Fundamental Definitions

Fuzzy sets (FSs) were introduced by Zadeh [41], and thereafter FS theory evolved as an important tool to tackle uncertainty and vagueness for decision-making problem. Atanassov [3, 4] introduced intuitionistic fuzzy sets (IFSs) by extending the FS theory. Yager [38, 39] introduced Pythagorean fuzzy sets (PFSs) by extending the IFS. For convenience, we introduce to definitions and fundamental elementary operations based on FS, IFS, intuitionistic fuzzy numbers (IFNs), neutrosophic sets, PFS and PFN.

Definition 1

[41] A FS ${{\tilde{A}}}$ in a universal set X is characterized by a membership function $\mu _{{\tilde{A}}}(x)$ which associates with each element x in X to a real number $\in [0,1]$. For a triangular fuzzy number ${\tilde{A}}=(a_1,a_2,a_3)$, where $a_1\le a_2\le a_3$, the membership function $\mu _{{\tilde{A}}}(x)$ is defined as:

$$ \mu _{\tilde{A}}(x)=\left\{\begin{array}{ll} {\frac{x-{a_1}}{a_2}-{a_1}},&\quad{\text{if}} \; {a_1}\le {x}\le {a_2}\\ {\frac{{a_3}-x}{a_3}-{a_2}},&\quad{\text{if}}\; {a_2}<{x}\le {a_3}\\ 0 ,&\quad{\text{Otherwise}}. \end{array} \right. $$

Definition 2

[3] Let X be a universal set, then an IFS ${\tilde{A}}^I$ in X is described as: ${\tilde{A}}^I=\{(x,\mu _{{\tilde{A}}^I}(x),\gamma _{{\tilde{A}}^I}(x)): x\in X\}$, where $\mu _{{\tilde{A}}^I}(x),\gamma _{{\tilde{A}}^I}(x):X \rightarrow [0,1]$ are the degrees of membership and of non-membership with satisfying $0\le \mu _{{\tilde{A}}^I}(x)+\gamma _{{\tilde{A}}^I}(x)\le 1$ for all $x\in X$. The degree of hesitation of an element x in the set ${\tilde{A}}^I$ is defined as function $\pi _{{\tilde{A}}^I}(x)=1-\mu _{{\tilde{A}}^I}(x)-\gamma _{{\tilde{A}}^I}(x)$. Note that when $\pi _{{\tilde{A}}^I}(x)=0,~x\in X$ then an IFS reduces to a FS.

Definition 3

A triangular IFN is of the form ${\tilde{A}}^I=(a_1,a_2,a_3;{{\overline{a}}}_1,a_2,{{\overline{a}}}_3)$ where ${{\overline{a}}}_1\le a_1\le a_2\le a_3\le {{\overline{a}}}_3$, with a membership and a non-membership functions of ${\tilde{A}}^I$ defined as:

$$\begin{aligned} \mu _{{\tilde{A}}^{I}} (x) = \left\{ {\begin{array}{ll} {\frac{{x - a_{1} }}{{a_{2} - a_{1} }},} & {{\text{if}}\;a_{1} \le x \le a_{2} ,} \\ {\frac{{a_{3} - x}}{{a_{3} - a_{2} }},} & {{\text{if}}\;a_{2} \le x \le a_{3} ,} \\ {0,} & {{\text{otherwise}},} \\ \end{array} } \right. \\ {\text{and}}\;\mu _{{\tilde{A}}^{I}} (x) = \left\{ {\begin{array}{ll} {\frac{{a_{2} - x}}{{a_{2} - a_{1} }},} & {{\text{if}}\;\bar{a}_{1} \le x \le a_{2} ,} \\ {\frac{{x - a_{2} }}{{a_{3} - a_{2} }},} & {{\text{if}}\;a_{2} \le x \le \bar{a}_{3} ,} \\ {1,} & {{\text{otherwise}},} \\ \end{array} } \right. \end{aligned} $$

Definition 4

[38, 40, 43] Let X be a universal set, then a PFS ${\tilde{A}}^p$ in X is defined as ${\tilde{A}}^p=\{(x,\mu _{{\tilde{A}}^p}(x),\gamma _{{\tilde{A}}^p}(x)): x\in X\}$, where $\mu _{{\tilde{A}}^p}(x), \gamma _{{\tilde{A}}^p}(x):X \rightarrow [0,1]$ are the membership and non-membership functions, respectively, which satisfy $0\le \mu _{{\tilde{A}}^p}^2(x)+ \gamma _{{\tilde{A}}^p}^2(x)\le 1$ for all $x\in X$. The degree of indeterminacy of an element x in the set ${\tilde{A}}^p$ is defined as the function

$\pi _{{\tilde{A}}^p}(x)=\sqrt{1-\mu _{{\tilde{A}}^p}^2(x) -\gamma _{{\tilde{A}}^p}^2(x)}$.

We remark that both $\mu _{{\tilde{A}}^p}(x)+\gamma _{{\tilde{A}}^p}(x)\ge 1$ or $\mu _{{\tilde{A}}^p}(x)+\gamma _{{\tilde{A}}^p}(x)\le 1$ can occur, which is the main difference between IFS and PFS. For this reason every IFS is a PFS, but the converse does not hold.

A comparison between IFN and PFN is shown in Fig. 1, and a comparison between IFS and PFS is given in Table 2.

Fig. 1

Graph of IFN and PFN

Table 2 Difference between IFS and PFS

Definition 5

[27] Considering two PFSs ${\tilde{A}}^p$ and ${\tilde{B}}^p$ in the universal set X, where ${\tilde{A}}^p$ and ${\tilde{B}}^p$ are defined as ${\tilde{A}}^p=\{(x,\mu _{{\tilde{A}}^p}(x), \gamma _{{\tilde{A}}^p}(x)): x\in X\}$ and ${\tilde{B}}^p=\{(x, \mu _{{\tilde{B}}^p}(x), \gamma _{{\tilde{B}}^p}(x)): x\in X\}$, respectively. Let $r \ge 0$. Then the following arithmetic operations are defined:

• 1. Sum: ${\tilde{A}}^p \oplus {\tilde{B}}^p=$ $\{(x, \sqrt{\mu _{{\tilde{A}}^p}^2(x)+ \mu _{{\tilde{B}}^p}^2(x) -\mu _{{\tilde{A}}^p}^2(x)\mu _{{\tilde{B}}^p}^2(x)},$ $\gamma _{{\tilde{A}}^p}(x)\gamma _{{\tilde{B}}^p}(x)):x\in X\}$.

• 2. Inner product: ${\tilde{A}}^p \odot {\tilde{B}}^p= \{(x, \mu _{{\tilde{A}}^p}(x)\mu _{{\tilde{B}}^p}(x)$, $\sqrt{\gamma _{{\tilde{A}}^p}^2(x)+\gamma _{{\tilde{B}}^p}^2(x)-\gamma _{{\tilde{A}}^p}^2(x) \gamma _{{\tilde{B}}^p}^2(x)}): x\in X\}$.

• 3. Scalar product: $r.{\tilde{A}}^p=\{(x,\sqrt{1-(1-\mu _{{\tilde{A}}^p}^2(x))^r}$, $(\gamma _{{\tilde{A}}^p}(x))^r): x\in X\}$.

• 4. Power: $({\tilde{A}}^p)^r=\{(x,(\mu _{{\tilde{A}}^p}(x))^r,\sqrt{1-(1-{\gamma _{{\tilde{A}}^p}^2(x)})^r}): x\in X\}$.

• 5. Complement: $({\tilde{A}}^p)^c=\{(x,\gamma _{{\tilde{A}}^p}(x),\mu _{{\tilde{A}}^p}(x)): x\in X\}$.

Definition 6

The TPFN on the real axis is defined as ${\tilde{A}}^p= \{((a,b,c); \mu _{{\tilde{A}}^p}(x),\gamma _{{\tilde{A}}^p}(x)): x\in X\}$, where $\mu _{{\tilde{A}}^p}(x)\ge 0; \gamma _{{\tilde{A}}^p}(x)\ge 0$, $\mu _{{\tilde{A}}^p}^2(x)+\gamma _{{\tilde{A}}^p}^2(x)\le 1$, $0\le a\le b\le c$ and (a, b, c) is a triangular fuzzy number. The membership and non-membership functions are defined as:

$$ \mu _{{\tilde{A}}^p}(x)=\left\{ \begin{array}{ll} \frac{x-{a}}{{b}-{a}},&{}\text{ if } \quad {a}\le {x}\le {b},\\ \frac{c-x}{c-b},&{}\text{ if }\quad {b}<{x}\le {c},\\ 0, &{} \quad \text{ Otherwise},\\ \end{array} \right. $$

and

$$ \gamma _{{\tilde{A}}^p}(x)=\left\{ \begin{array}{ll} \sqrt{1-(\frac{x-{a}}{{b}-{a}})^2},&{}\text{ if } \quad {{a}}\le {x}\le {b},\\ \sqrt{1-(\frac{c-x}{{c}-{b}})^2},&{}\text{ if } \quad {b}<{x}\le {c}\\ 1, &{} \quad \text{ Otherwise}.\\ \end{array} \right. $$

Definition 7

[33] Considering two TPFNs ${\tilde{A}}^p$ and ${\tilde{B}}^p$ in the universal set X, where ${\tilde{A}}^p$ and ${\tilde{B}}^p$ are given as ${\tilde{A}}^p= \{((a_1,b_1,c_1);\mu _{{\tilde{A}}^p}(x),\gamma _{{\tilde{A}}^p}(x)): x\in X\}$ and ${\tilde{B}}^p= \{((a_2,b_2,c_2); \mu _{{\tilde{B}}^p}(x),\gamma _{{\tilde{B}}^p}(x)): x\in X\}$. Let $r \ge 0$. The following arithmetic operations are defined for TPFNs:

• 1. Sum: ${\tilde{A}}^p \oplus {\tilde{B}}^p=\{((a_1+a_2,b_1+b_2,c_1+c_2);$ $\sqrt{\mu _{{\tilde{A}}^p}^2(x)+ \mu _{{\tilde{B}}^p}^2(x) -\mu _{{\tilde{A}}^p}^2(x)\mu _{{\tilde{B}}^p}^2(x)}, \gamma _{{\tilde{A}}^p}(x)\gamma _{{\tilde{B}}^p}(x))$ $: x\in X\}$.

• 2. Inner product: ${\tilde{A}}^p \odot {\tilde{B}}^p= \{(({a_1}{a_2},{b_1}{b_2},{c_1}{c_2});$ $\mu _{{\tilde{A}}^p}(x)\mu _{{\tilde{B}}^p}(x), \sqrt{\gamma _{{\tilde{A}}^p}^2(x)+\gamma _{{\tilde{B}}^p}^2(x) -\gamma _{{\tilde{A}}^p}^2(x) \gamma _{{\tilde{B}}^p}^2(x)})$ $: x\in X\}$.

• 3. Scalar product: $r.{\tilde{A}}^p=\{((ra,rb,rc);$ $\sqrt{1-(1-{\mu _{{\tilde{A}}^p}^2(x)})^r},(\gamma _{{\tilde{A}}^p}(x))^r): x\in X\}$.

• 4. Power: $({\tilde{A}}^p)^r=\{((a^r,b^r,c^r);(\mu _{{\tilde{A}}^p}(x))^r,$ $\sqrt{1-(1-{\gamma _{{\tilde{A}}^p}^2(x)})^r})): x\in X\}$.

Definition 8

[32] Let ${\tilde{A}}^p= \{((a,b,c);\mu _{{\tilde{A}}^p}(x),\gamma _{{\tilde{A}}^p}(x)): x\in X\}$ be a TPFN. Then the score function $S({\tilde{A}}^p)$ and the accuracy function $M({\tilde{A}}^p)$ of ${\tilde{A}}^p$ are defined as:

$$ S({\tilde{A}}^p)= \frac{a+b+c}{3}\cdot (\mu _{{\tilde{A}}^p}^2-\gamma _{{\tilde{A}}^p}^2), M({\tilde{A}}^p)= \frac{a+b+c}{3}\cdot (\mu _{{\tilde{A}}^p}^2+\gamma _{{\tilde{A}}^p}^2). $$

We remark that $S({\tilde{A}}^p)\in ~[-1,1]$ and $M({\tilde{A}}^p)\in ~[0,1]$.

Next we define the defuzzified value or the ranking index of a TPFN. Although the score function and the accuracy function are potential types of defuzzified values, both of them are not satisfied for any linear operation. Consequently, we newly define a ranking function in terms of the TPFN.

Definition 9

Let ${\tilde{A}}^p= \{((a,b,c);\mu _{{\tilde{A}}^p}(x),\gamma _{{\tilde{A}}^p}(x)):x\in X\}$ be a TPFN. Let $\lambda \in ~(0,1)$ be a fixed parameter. Then the ranking index is defined as:

$${\mathfrak{R}}({\tilde{A}}^p)=\frac{\lambda \int _a^c x{\mu _{{\tilde{A}}^p}^2} {\text {d}}x+ (1-\lambda )\int _a^c x{\gamma _{{\tilde{A}}^p}^2} {\text {d}}x}{\lambda \int _a^c {\mu _{{\tilde{A}}^p}^2} {\text {d}}x+ (1-\lambda )\int _a^c {\gamma _{{\tilde{A}}^p}^2} {\text {d}}x}=\frac{1}{4}\frac{\lambda (a+2b+c)+(1-\lambda )(5a-2b+5c)}{(2-\lambda )}. $$

Theorem 1

Let ${\tilde{A}}^p= \{((a,b,c);\mu _{{\tilde{A}}^p}(x),\gamma _{{\tilde{A}}^p}(x)): x\in X\}$ be a TPFN, and $\alpha \ge 0$. Then ${\mathfrak{R}}(\alpha .{\tilde{A}}^p)=\alpha {\mathfrak{R}}({\tilde{A}}^p)$.

Proof

From Definition 9 we have the ranking index as

$$\begin{aligned} {\mathfrak{R}}({\tilde{A}}^p)=\frac{1}{4}\frac{\lambda (a+2b+c) +(1-\lambda )(5a-2b+5c)}{(2-\lambda )}. \end{aligned}$$

Now it follows that

$${\mathfrak{R}}(\alpha \cdot {\tilde{A}}^p)=\frac{1}{4}\frac{\lambda (\alpha a+2\alpha b+\alpha c)+(1-\lambda )(5\alpha a-2\alpha b+5\alpha c)}{(2-\lambda )}=\alpha \cdot \frac{1}{4}\frac{\lambda (a+2b+c)+(1-\lambda )(5a-2b+5c)}{(2-\lambda )}=\alpha \cdot {\mathfrak{R}}({\tilde{A}}^p). $$

$\square$

Theorem 2

Let ${\tilde{A}}^p= \{((a_1,b_1,c_1);\mu _{{\tilde{A}}^p}(x),\gamma _{{\tilde{A}}^p}(x)):x \in X\}, {\tilde{B}}^p= \{((a_2,b_2,c_2);\mu _{{\tilde{B}}^p}(x),\gamma _{{\tilde{B}}^p}(x)): x \in X\}$ are two TPFNs. Let $\alpha ,\beta \ge 0$. Then ${\mathfrak{R}}(\alpha .{\tilde{A}}^p+\beta .{\tilde{B}}^p)=\alpha . {\mathfrak{R}}({\tilde{A}}^p)+\beta . {\mathfrak{R}}({\tilde{B}}^p)$.

Proof

From the definition of the ranking index in Definition 9 we have that

$${\mathfrak{R}}(\alpha \cdot {\tilde{A}}^p+\beta \cdot {\tilde{B}}^p) =\frac{1}{4}\left[\frac{\lambda (\alpha a_1+\beta a_2+2\alpha b_1+2\beta b_2+\alpha c_1+\beta c_2)}{(2-\lambda )}+\frac{(1-\lambda )(5\alpha a_1+5\beta a_2-2\alpha b_1-2\beta b_2+5\alpha c_1+5\beta c_2)}{(2-\lambda )}\right]=\alpha \cdot \frac{1}{4}\left[\frac{\lambda ( a_1+2 b_1+c_1)+(1-\lambda )(5 a_1-2 b_1+5 c_1)}{(2-\lambda )}\right]+\beta \cdot \frac{1}{4}\left[\frac{\lambda ( a_2+2 b_2+ c_2)+(1-\lambda )(5 a_2-2 b_2+5 c_2)}{(2-\lambda )}\right]=\alpha \cdot {\mathfrak{R}}({\tilde{A}}^p)+\beta \cdot {\mathfrak{R}}({\tilde{B}}^p). \quad \square$$

The concept of a neutrosophic set is an analytical sight to represent the indeterminate and inconsistent information. It can be applied in scientific and engineering applications.

Definition 10

[34] Let X be the universal set. A single valued neutrosophic set ${\tilde{A}}^n$ over X is of the form $\tilde{A}^n=\{(x,\mu _{{\tilde{A}}^n}(x),\sigma _{\tilde{A}^n}(x),\gamma _{{\tilde{A}}^n}(x)): x\in X\}$, where $\mu _{\tilde{A}^n}(x):X\rightarrow [0,1],~ \sigma _{\tilde{A}^n}(x):X\rightarrow [0,1],~\gamma _{{\tilde{A}}^n}(x):X\rightarrow [0,1]$ with $0\le \sup \{\mu _{{\tilde{A}}^n}(x)\}+\sup \{\sigma _{\tilde{A}^n}(x)\}+\sup \{\gamma _{{\tilde{A}}^n}(x)\}\le 3$ for all $x\in X$. Here $\mu _{{\tilde{A}}^n}(x)$, $\sigma _{{\tilde{A}}^n}(x)$ and $\gamma _{{\tilde{A}}^n}(x)$ are the degrees of truth membership, indeterminacy membership and falsity membership of x in $\tilde{A}^n$, respectively.

4 Problem Background

In this section, we specify a list of notations with their intended meaning and some assumptions made in our model of an MOSTP in a Pythagorean fuzzy environment. Thereafter we introduce the model formulation itself in two cases: one is a Pythagorean fuzzy MOSTP with PT, and the other is Pythagorean fuzzy MOSTP without PT.

4.1 Notations and Assumptions of the Proposed Study

The following notations and assumptions are considered in the formulation of the proposed mathematical model:

i::

index for sources $(i=1,2,\ldots , m)$,

j::

index for destinations $(j=1,2,\ldots , n)$,

k::

index for conveyances $(k=1,2,\ldots , r)$,

${x}_{ijk}$::

amount of items that to be transported from the ith source to the jth destination through kth conveyance,

$\tilde{{c}}$ ^p_ijk ::

Pythagorean fuzzy transportation cost for a unit quantity of the items transported from the ith source to the jth destination through kth conveyance,

$\tilde{{p}}$ ^p_ijk ::

Pythagorean fuzzy preservation charge of the items transported from the ith source to the jth destination through kth conveyance,

${\alpha }_z$::

freezing function $\in [0,1]$ acts to reduce a certain percentage of deterioration, i.e, new deterioration rate is equivalent to $\alpha _z$ % of old deterioration rate,

$\tilde{{t}}$ ^p_ijk ::

Pythagorean fuzzy time of transportation of the items from the ith source to the jth destination through kth conveyance,

$\tilde{{d}}$ ^p_ijk ::

Pythagorean fuzzy rate of deterioration of the transported items from the ith source to the jth destination through kth conveyance,

${{\eta }_{ijk}}$::

binary variable taking the value 1 if $x_{ijk}>0$, and 0 otherwise,

$\tilde{{a}}$ ^p_i ::

Pythagorean fuzzy amount of items available at the ith source,

$\tilde{{b}}$ ^p_j ::

Pythagorean fuzzy demand of items at the jth destination,

$\tilde{{e}}$ ^p_k ::

Pythagorean fuzzy kth conveyance capacity,

$\tilde{{Z}}$ ^p_l ::

the objective function is a PFN for $l=1,2,3$,

${Z}_{l}$::

the crisp value of objective function ${\tilde{{Z}}_{l}}^p$ for $l=1,2,3$, where ${Z}_{l}={\mathfrak{R}}[{\tilde{{Z}}_{l}}^p]$ and ${\mathfrak{R}}$ denotes the ranking operator.

We further make the assumptions that all transported items are perishable, and that ${{\tilde{a}}_{i}}^p>0, {{\tilde{b}}_{j}}^p>0, {{\tilde{e}}_{k}}^p>0$ for all i, j, k.

4.2 Model Formulation

We construct a mathematical model for the MOSTP under PT to describe an optimal transportation scheme for perishable items that tries to prevent their deterioration. We consider $x_{ijk}$ as continuous decision variables which denote the amount of items transported from the ith source to the jth destination through the kth conveyance. This transport comes with transportation cost ${{\tilde{c}}_{ijk}}^p$. Here we define two types of models, one is “Model PT” in which PT is applied, and the first objective function (1a) is defined as the total transportation cost including preservation cost. After incorporating PT, the rate deterioration becomes ${{\tilde{d}}_{ijk}}^p.\alpha _z$ and the total deterioration is described in the third objective function (1c) which shows the effectiveness of PT on deterioration. The second objective function (1b) is chosen to model the total transportation time. “Model w/oPT” is the other case, in which we present a general MOSTP without any PT. The aim of both models is to minimize total transportation cost (with or without freezing cost), time and deterioration (with or without preservation) while satisfying source, demand, and conveyance constraints. Due to some exceptional uncertain situations rather than fuzzy or IF in realistic background, we consider all the data in both models as TPFN to represent more uncertainty. Henceforth the formulated models of MOSTP with PT and without PT are defined in Pythagorean fuzzy environment.

Model PT

$$\text{ minimize }\;\tilde{Z_1^p}(x)=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^r {{\tilde{c}}_{ijk}}^p{{x}_{ijk}}+ \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^r \alpha _{z}{{\tilde{t}}_{ijk}}^p {{\tilde{p}}_{ijk}}^p{{x}_{ijk}} $$

(1a)

$$\text{ minimize }\;\tilde{Z_2^p}(x)=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^r{{\tilde{t}}_{ijk}}^p{{\eta }_{ijk}} $$

(1b)

$$\text{ minimize }\;\tilde{Z_3^p}(x)=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^r{\alpha }_z{{\tilde{d}}_{ijk}}^p{{x}_{ijk}} $$

(1c)

$$ \text{ subject } \text{ to }\;\sum _{i=1}^m\sum _{k=1}^r(1- {\alpha }_z{{\tilde{d}}_{ijk}}^p){{x}_{ijk}}\ge {\tilde{b}}_{j}^p (j=1,2,\ldots ,n), $$

(1d)

$$\sum _{j=1}^n\sum _{k=1}^r{{x}_{ijk}} \le {\tilde{a}}_{i}^p ~~(i=1,2,\ldots ,m), $$

(1e)

$$\sum _{i=1}^m\sum _{j=1}^n{{x}_{ijk}}\le {\tilde{e}}_{k}^p ~~(k=1,2,\ldots ,r), $$

(1f)

$${{x}_{ijk}}\ge 0, \forall ~i,~j,~k. $$

(1g)

$${{\eta }_{ijk}}=\left\{ \begin{array}{ll} 1 ,&{}\text{ if } \quad x_{ijk}>0, \\ 0,&{} \quad \text{ Otherwise. }\end{array} \right. $$

(1h)

The feasibility conditions of this TP are set as:

$$ \sum _{i=1}^m {\tilde{a}}_{i}^p\ge \sum _{j=1}^n {\tilde{b}}_{j}^p, \text {and}$$

$$ \sum _{k=1}^r {\tilde{e}}_{k}^p\ge \sum _{j=1}^n {\tilde{b}}_{j}^p. $$

Model w/oPT

$$\text{ minimize }\tilde{Z_1^p}(x)=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^r {{\tilde{c}}_{ijk}}^p{{x}_{ijk}} $$

(2a)

$$\text{ minimize }\tilde{Z_2^p}(x)=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^r {{\tilde{t}}_{ijk}}^p{{\eta }_{ijk}} $$

(2b)

$$\text{ minimize }\tilde{Z_3^p}(x)=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^r{{\tilde{d}}_{ijk}}^p{{x}_{ijk}} $$

(2c)

$$\text{ subject } \text{ to } \sum _{i=1}^m\sum _{k=1}^r(1-d_{ijk}){{x}_{ijk}}\ge {\tilde{b}}_{j}^p (j=1,2,\ldots ,n), {\text{ constraints }}~(1e) - (1h). $$

(2d)

The feasibility conditions of this TP are same as in Model PT.

In Model PT, the first and second term of objective function (1a) for $\tilde{Z_1^p}(x)$ represent the transportation cost and preservation charge for transporting items from the ith source to the jth destination using the kth conveyance, respectively. Hence a preservation charge is considered for investment of PT on the perishable items that to be transported and the charge depends on the time ${{\tilde{t}}_{ijk}}^p$, the preservation function $\alpha _z$, and amount of transported items ${x}_{ijk}$. The second objective function (1b) for $\tilde{Z_2^p}(x)$ indicates the transportation time from the ith source to the jth destination using the kth conveyance. The third objective function (1c) for $\tilde{Z_3^p}(x)$ represents the total deterioration after applying PT on the transported items from the ith source to the jth destination using the kth conveyance. Constraints (1d) are the demand conditions after applying PT. The remaining constraints (1e), (1f) represent the source and conveyance capacity, respectively.

In Model w/oPT, the first (2a), the second (2b), and the third (2c) objective functions exist for transportation cost, time, and deterioration, respectively, subject to source (1e), demand (2d), and conveyance constraints (1f).

4.3 Equivalent Deterministic Model

Since all the data in the Models PT and w/oPT are TPFN, we cannot directly obtain a solution of the MOSTP. So, we employ a ranking operator (c.f. Definition 9) and use Theorems 1 and 2 to transform the Pythagorean fuzzy Models PT and w/oPT into their crisp forms Model crPT and Model crw/oPT:

Model crPT

$$\text{ minimize }{\mathfrak{R}}[\tilde{Z_1^p}(x)]=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^r {\mathfrak{R}}[{{\tilde{c}}_{ijk}}^p]{{x}_{ijk}}+ \sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^r \alpha _{z}R[{{\tilde{t}}_{ijk}}^p {{\tilde{p}}_{ijk}}^p]{{x}_{ijk}} $$

(3a)

$${\text{minimize}} {\mathfrak{R}}[\tilde{Z_2^p}(x)]=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^r {\mathfrak{R}}[{{\tilde{t}}_{ijk}}^p]{{\eta }_{ijk}} $$

(3b)

$${\text{ minimize}} {\mathfrak{R}}[\tilde{Z_3^p}(x)]=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^r {\alpha }_z {\mathfrak{R}}[{{\tilde{d}}_{ijk}}^p]{{x}_{ijk}} $$

(3c)

$${\text{ subject}} \text{ to } \sum _{i=1}^m\sum _{k=1}^r \big (1- {\alpha }_z {\mathfrak{R}}[{{\tilde{d}}_{ijk}}^p]\big ){{x}_{ijk}} \ge {\mathfrak{R}}[\tilde{b}_{j}^p] (j=1,2,\ldots ,n), $$

(3d)

$$\sum _{j=1}^n\sum _{k=1}^r{{x}_{ijk}} \le {\mathfrak{R}}[{\tilde{a}}_{i}^p] (i=1,2,\ldots ,m), $$

(3e)

$$ \sum _{i=1}^m\sum _{j=1}^n{{x}_{ijk}}\le {\mathfrak{R}}[{\tilde{e}}_{k}^p] ~~(k=1,2,\ldots ,r), {\text{ constraints }}~(1g)-(1h). $$

(3f)

The feasibility conditions of this TP are:

$$ \sum _{i=1}^m {\mathfrak{R}}[{\tilde{a}}_{i}^p]\ge \sum _{j=1}^n {\mathfrak{R}}[{\tilde{b}}_{j}^p], \text{and}$$

$$ \sum _{k=1}^r {\mathfrak{R}}[{\tilde{e}}_{k}^p]\ge \sum _{j=1}^n {\mathfrak{R}}[{\tilde{b}}_{j}^p]. $$

Model crw/oPT

$${\text{ minimize}}{\mathfrak{R}}[\tilde{Z_1^p}(x)]=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^r {\mathfrak{R}}[{{\tilde{c}}_{ijk}}^p]{{x}_{ijk}} $$

(4a)

$$ {\text{ minimize}} {\mathfrak{R}}[\tilde{Z_2^p}(x)]=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^r {\mathfrak{R}}[{{\tilde{t}}_{ijk}}^p]{{\eta }_{ijk}} $$

(4b)

$$ {\text{ minimize}} {\mathfrak{R}}[\tilde{Z_3^p}(x)]=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^r {\mathfrak{R}}[{{\tilde{d}}_{ijk}}^p]{{x}_{ijk}} $$

(4c)

$$ {\text{ subject}} \text{ to } \sum _{i=1}^m\sum _{k=1}^r \big (1- {\mathfrak{R}}[{{\tilde{d}}_{ijk}}^p]\big ){{x}_{ijk}} \ge {\mathfrak{R}}[\tilde{b}_{j}^p] (j=1,2,\ldots ,n), {\text{ constraints }}~(3e)-(3f), ~ {\text{ constraints }}~(1g)-(1h). $$

(4d)

The feasibility conditions of this TP are same as in Model crPT.

5 Solution Methodology

A multi-objective optimization problem appears practically in many real-world applications. It is recommended for DMs not to focus on a single objective alone, but instead to optimize all the objective functions at once and try to explore the best optimal compromise solution. However, due to the potentially contradictory nature of these objective functions, there exists no single solution that simultaneously optimizes all the objective functions. That is, the solution will be the best for one objective function and that may be worst with respect to another objective function. In this case, DMs select a “most favorable” solution instead of an optimal solution. Therefore, the view of optimality is replaced by Pareto-optimality.

Definition 11

A Pareto-optimal solution of Model crPT or crw/oPT is a feasible solution $x^{\ast}=\{{x}^{\ast}_{ijk}:~i= 1,2,\ldots ,m;~j=1,2,\ldots ,n;~ k=1,2,\ldots ,r\}$ such that there exists no other feasible solution $x=\{{x}_{ijk}:~ i= 1,2,\ldots ,m;~ j=1,2,\ldots ,n;~ k=1,2,\ldots ,r\}$ with ${Z_l}(x)\le {Z_l}(x^{\ast}),~l= 1, 2, 3$ and ${Z_l}(x)< {Z_l}(x^{\ast})$ for at least one l.

In other words, Pareto-optimal solutions are the ones that cannot be upgraded in one objective function without dominating the performances in at least one remaining objective function. Several methods are convenient for solving the MOSTP. To obtain a Pareto-optimal solution we discuss the following three methods and apply them to the proposed model:

• the $\varepsilon$-constraint method,

• the Neutrosophic linear programming (NLP), and

• the Fuzzy TOPSIS approach.

5.1 The $\varepsilon$-Constraint Method

The $\varepsilon$-constraint method is a useful method introduced by Haimes et al. [15]. This method finds the Pareto-optimal solution by varying the value of $\varepsilon$ along the Pareto-optimal front to each objective function. Therefore for each value of $\varepsilon$, there exists a new optimization problem. Whenever we solve the crisp problem that is to minimize the ranking function, then the MOSTP transforms into single objective STP by choosing one objective at that time, and the remaining objective functions are treated as constraints by defining their aspiration levels. The necessary steps for solving the problem are given below:

• Step 1: Transform the Pythagorean fuzzy MOSTP into a crisp MOSTP with the help of a ranking function.

• Step 2: Compute the solution of each crisp single objective function at a time by omitting the other objective functions and subject to the given constraints.

• Step 3: Find the best value and the worst value of every objective function.

• Step 4: Select any one objective function $Z_{l}$ among $Z_{l^{\prime }}$, $(l,~l^{\prime }=1,2,3:l \ne l^{\prime })$.

• Step 5: Turn the other objective functions into constraints and set up a single objective deterministic model is as follows:

Model 5

$$ {\text{ minimize}} \, Z_{l^{\prime }} $$

(5a)

$$ {\text{ subject}} \text{ to } Z_l\le \varepsilon _l~~(l, l^{\prime }=1,2,3, l\ne l^{\prime }), $$

(5b)

$${\text{ constraints } \text{ either }}~(3d)-(3f) \text{ or }~ (3e)-(3f),(4d),$$

(5c)

$$ {\text{ constraints }}~(1g)-(1h). $$

(5d)

Here the range of $\varepsilon _l$ is defined by the DM who represents the maximum entrance values of the objective functions. The DM can also vary the value of $\varepsilon _l$ along the Pareto-optimal front for each objective function to find a suitable Pareto-optimal solution. Constraints (3d) to (3f) are used for Model crPT, and constraints (3e) to (3f), (4d) are chosen for Model crw/oPT.

• Step 6: Compute the value of the objective function for each case (using a solver such as LINGO), and then find the Pareto-optimal solution of Model crPT and Model crw/oPT.

5.2 The Neutrosophic Linear Programming (NLP)

Solving Model crPT and Model crw/oPT, we may obtain solutions which are not overall compromise solution. So we utilize NLP to derive a Pareto-optimal solution of a multi-objective decision-making problem. NLP is a modified and improved programming method that finds a Pareto-optimal solution of multi-objective problems. The notion of the neutrosophic set was defined by Smarandache [34]. Khalil et al. [21] worked on neutrosophic sets and their application to multi-objective decision-making problems. In this program, a truth membership function, an indeterminacy membership function and a falsity membership function are formulated for every objective function. Whenever the NLP maximizes the truth and the indeterminacy membership function and minimizes the falsity membership function, then it is said to define the best Pareto-optimal solution. To solve the proposed model as a NLP, we carry out the following steps:

• Step 1: Find a crisp MOSTP from the Pythagorean fuzzy MOSTP by a ranking operator.

• Step 2: Evaluate the solution of each objective function individually, subject to all constraints.

• Step 3: Determine the lower bound and upper bound, i.e., positive ideal solution (PIS) and negative ideal solution (NIS) for each objective function from a pay-off matrix defined in Table 3. Denoting PIS = ${Z_l^{\ast}} = \min \{{Z_l}({X_1^{\ast}}),~{Z_l}({X_2^{\ast}}),~{Z_l}({X_3^{\ast}}): l=1,2,3\}$ and NIS = ${Z_l}^{\prime } = \max \{{Z_l}({X_1^{\ast}}),~{Z_l}({X_2^{\ast}}),~{Z_l}({X_3^{\ast}}):l=1,2,3\}$ respectively.

Table 3 Pay-off matrix

• Step 4: Formulate the truth membership function and indeterminacy membership function with the highest degree and the falsity membership function with the lowest degree.

• Step 5: Set the tolerance and then construct the truth membership function $T_{{l}}(Z_l(x))$, the indeterminacy membership function $I_{{l}}(Z_l(x))$, and the falsity membership function $F_{{l}}(Z_l(x))$ of each objective function $Z_l(x)$ according to the bounds as:

  $$ T_{l}(Z_l(x))=\left\{ \begin{array}{ll} 1,& \text{ if } \quad {Z_l(x)}\le L_{l}^{T}, \\ 1- \frac{{Z_l(x)}-L_{l}^{T}}{U_{l}^{T}-{L_{l}^{T}}},& \text{ if }\quad L_{l}^{T} \le {Z_l(x)}\le U_{l}^{T},\\ 0 ,& \text{ if } \quad {Z_l(x)}\ge U_{l}^{T}, \end{array} \right. I_{l}(Z_l(x))=\left\{ \begin{array}{ll} 1,& \text{ if } \quad {Z_l(x)}\le L_{l}^{I},\\ 1-\frac{{Z_l(x)}-L_{l}^{I}}{U_{l}^{I}-L_{l}^{I}},& \text{ if }\quad L_{l}^{I}\le {Z_{l}(x)}\le U_{l}^{I}, \\ 0 , & \text{ if } \quad {Z_{l}(x)}\ge U_{l}^{I}, \end{array} \right. F_{l}(Z_{l}(x))=\left\{ \begin{array}{ll} 0,& \text{ if } \quad {Z_{l}(x)}\le L_{l}^{F},\\ 1-\frac{U_{l}^{F}-Z_{l}(x)}{U_{l}^{F}-L_{l}^{F}},& \text{ if }\quad L_{l}^{F}\le {Z_{l}(x)}\le U_{l}^{F}, \\ 1 ,& \text{ if } \quad {Z_{l}(x)}\ge U_{l}^{F}. \end{array} \right. $$

  Here $U_{l}^T= U_l$ = PIS for $Z_l$, and $L_{l}^T = L_l$ = NIS for $Z_l$; $U_{l}^F = U_{l}^T$, $L_{l}^F = L_{l}^T+t_l(U_{l}^T-L_{l}^T)$; $L_{l}^I = L_{l}^T$, $U_{l}^I = L_{l}^T+s_l(U_{l}^T-L_{l}^T)$; $t_l, s_l \in (0,1)$ are predetermined real numbers.

• Step 6: Choose the values of $\mu , \nu , \gamma$ in [0, 1] for each neutrosophic number as the truth, indeterminacy, and falsity degrees, respectively.

• Step 7: Constitute the following NLP:

  
  

  Model 6

  $$ {\text{ Maximize}}\; T_{{l}}(Z_l(x))~(l=1,2,3) $$

  (6a)
  $$ {\text{ Maximize}}\; I_{{l}}(Z_l(x))~(l=1,2,3) $$

  (6b)
  $$ {\text{ Minimize}}\; F_{{l}}(Z_l(x))~(l=1,2,3) $$

  (6c)
  $${\text{ Subject}} \text{ to }\; {\text{ constraints } \text{ either }}~(3d)-(3f)\text{ or }~ (3e)-(3f), (4d), {\text{ Constraints }}~(1g)-(1h). $$

  (6d)

  Model (6) can be reduced to:

  Model 7

  $${\text{ Maximize}} \,\mu $$

  (7a)
  $${\text{ Maximize}}\, \nu $$

  (7b)
  $$ {\text{ Minimize}}\, \gamma $$

  (7c)
  $$ {\text{ Subject}} \text{ to } T_{{l}}(Z_l(x))\ge \mu , $$

  (7d)
  $$ I_{{l}}(Z_l(x))\ge \nu , $$

  (7e)
  $$ F_{{l}}(Z_l(x))\le \gamma ,$$

  (7f)
  $$ \mu +\nu +\gamma \le 3,$$

  (7g)
  $$\mu \ge \gamma ,$$

  (7h)
  $$\mu \ge \nu ,$$

  (7i)
  $$\mu , \nu , \gamma \in [0,1],(l=1,2,3), $$

  (7j)
  $${\text{ Constraints } \text{ either }}~(3d)-(3f) \text{ or }~ (3e)-(3f), (4d),$$

  (7k)
  $${\text{ Constraints }}~(1g)-(1h).$$

  (7l)

  The NLP Model (7) that derives the Pareto-optimal solution of the MOTP is defined as follows:

  Model 8

  $$\text{ Maximize }\,\mu +\nu -\gamma $$

  (8a)
  $${\text{ Subject}} \text{ to }\, {Z_l}(x)+(U_{l}^T-L_{l}^T)\mu \le U_{l}^T, $$

  (8b)
  $${Z_l}(x)+(U_{l}^I-L_{l}^I)\nu \le U_{l}^I, $$

  (8c)
  $${Z_l}(x)-(U_{l}^F-L_{l}^F)\gamma \le L_{l}^F,$$

  (8d)
  $$\mu +\nu +\gamma \le 3, $$

  (8e)
  $$\mu \ge \gamma , $$

  (8f)
  $$\mu \ge \nu ,$$

  (8g)
  $$\mu , \nu , \gamma \in [0,1],(l=1,2,3), $$

  (8h)
  $${\text{ Constraints } \text{ either }}~(3d)-(3f) \text{ or }~ (3e)-(3f), (4d), $$

  (8i)
  $${\text{ Constraints }}~(1g)-(1h). $$

  (8j)

• Step 8: Solve Model (8) (for instance, by a numerical solver such as LINGO), and obtain a Pareto-optimal solution of Model crPT and Model crw/oPT, respectively.

Theorem 3

If $x^{\ast}=\{x_{ijk}:~i=1,2,\ldots ,m; ~j=1,2,\ldots ,n;~k=1,2,\ldots ,r\}$ is an optimal solution of Model (8) then it is also Pareto-optimal (non-dominated) solution of Model crPT or Model crw/oPT, respectively.

Proof

Let $x^{\ast}$ be a non-Pareto-optimal (non-dominated) solution of Model crPT or Model crw/oPT. From Definition 11, we obtain that there exists at least one x such that $Z_l(x)\le Z_l(x^{\ast})$ for $l=1,2,3$, and $Z_l(x)< Z_l(x^{\ast})$ for at least one l. The truth and the indeterminacy membership functions $\mu _{{l}}(Z_l(\cdot ))$ and $\nu _{{l}}(Z_l(\cdot ))$ are strictly decreasing with respect to the corresponding objective function $Z_l$ in [0,1], respectively, whereas the falsity membership function $\gamma _{{l}}(Z_l(\cdot ))$ is strictly increasing with respect to the objective function $Z_l$ in [0,1]. Hence $\mu _{{l}}(Z_l(x)) \ge \mu _{{l}}(Z_l(x^{\ast}))$ for all l, and $\mu _{{l}}(Z_l(x)) > \mu _{{l}}(Z_l(x^{\ast}))$ for at least one l. Similarly $\nu _{{l}}(Z_l(x)) \ge \nu _{{l}}(Z_l(x^{\ast}))$ for all l, and $\nu _{{l}}(Z_l(x)) > \nu _{{l}}(Z_l(x^{\ast}))$ for at least one l. Also $\gamma _{{l}}(Z_l(x)) \le \gamma _{{l}}(Z_l(x^{\ast}))$ for all l, and $\gamma _{{l}}(Z_l(x)) < \gamma _{{l}}(Z_l(x^{\ast}))$ for at least one l. Denote by $\mu ^{\ast},\nu ^{\ast}$, and $\gamma ^{\ast}$ the values of $\mu ,\nu$ and $\gamma$ at $x^{\ast}$, respectively. Then $(\mu +\nu -\gamma )$ = $\min \{\mu _{{l}}(Z_l(x)),\nu _{{l}}(Z_l(x))$,

$\gamma _{{l}}(Z_l(x))\} \ge \min \{\mu _{{l}}(Z_l(x^{\ast})),\nu _{{l}}(Z_l(x^{\ast})),\gamma _{{l}}(Z_l(x^{\ast}))\} = (\mu ^{\ast}+\nu ^{\ast}-\gamma ^{\ast})$, which contradicts the fact that $x^{\ast}$ is an optimal solution of Model (8). This completes the proof of the theorem. $\square$

5.3 The Fuzzy TOPSIS Approach

TOPSIS stands for technique for order preference by similarity to ideal solution. This approach was initiated by Hwang and Yoon [20]. TOPSIS is based on the idea of choosing an alternative closest to PIS and the farthest to NIS for finding a Pareto-optimal solution to a multi-attribute decision-making problem. Classical TOPSIS is often used for solving selection and ranking problems. At first, all the alternatives from the best to worst are ranked, and then the best alternative is selected. The extended fuzzy TOPSIS approach generates a better Pareto-optimal solution by transforming the multi-objective problem into a bi-objective problem. This approach can accommodate the large number of variables included in the MOSTP. When a multi-objective optimization problem is reduced to a bi-objective problem by a fuzzy TOPSIS approach, then the new problem is called a fuzzy TOPSIS-based bi-objective optimization problem. The steps of this approach are defined as follows:

• Step 1: Transform the Pythagorean fuzzy MOSTP into an equivalent crisp problem by a ranking operator.

• Step 2: Solve each objective function individually, and find the maximum and the minimum value of each objective function with subject to all constraints.

• Step 3: Obtain the PIS ($Z^+$) and the NIS ($Z^-$), which are defined in Step 3 of Sect. 5.2. Hence $Z_{l}^+ < Z_{l}^-$, and the range is defined as ${Z_{l}^-}-{Z_{l}^+}$.

• Step 4: Calculate the distance function $d_{r}^{\text {PIS}}(x)$ and $d_{r}^{\text {NIS}}(x)$ from PIS and NIS, respectively, which are defined as:

  $$ d_{r}^{\text {PIS}}(x)= \left[\sum _{l=1}^3\left[W_l{\frac{Z_l(x)-{Z_l}^+}{Z_{l}^--Z_{l}^+}}\right]^r\right]^{\frac{1}{r}} d_{r}^{\text {NIS}}(x)= \left[\sum _{l=1}^3\left[W_l{\frac{{Z_l}^--Z_l(x)}{Z_{l}^--Z_{l}^+}}\right]^r\right]^{\frac{1}{r}} \sum _{l=1}^3 W_l= 1, W_l\ge , \quad \forall \,l. $$

  Here the parameters $W_l$ for $l = 1,2,3$ denote the weights of objective functions. For r any real positive number or positive infinity can be used. Most typical choices are $r=1, r=2$, or $r=+\infty$: For $r=1$, the distance is known as Manhattan distance; for $r=2$, the distance is the Euclidean distance; for $r=+\infty$ it defines the Tchebycheff distance.

• Step 5: Transform the crisp model into a bi-objective problem by taking $r=2$:

  Model 9

  $${\text{ Minimize}}\; d_{2}^{\text {PIS}}(x) $$

  (9a)
  $${\text{ Maximize}}\; d_{2}^{\text {NIS}}(x) $$

  (9b)
  $${\text{ Subject}}\; {\text{ to }}\; {\text{ constraints }}\; {\text{ either }} (3d)-(3f) {\text{ Constraints }} (1g)-(1h). $$

  (9c)

  (Note that (3d) is left out and (4d) is added for Model crw/oPT.)

• Step 6: Solve Model (9) and construct a pay-off Table 4.

Table 4 Pay-off matrix for PIS and NIS

• Step 7: Formulate the membership functions for two objective functions of Model (9) using the pay-off Table 4. The functions are defined as follows:

  $$ \mu _1(x)=\left\{ \begin{array}{ll} 1,&{}\text{ if } \quad d_{2}^{\text {PIS}}(x)\le (d_{2}^{\text {PIS}})^{\ast},\\ 1-\frac{d_{2}^{\text {PIS}}(x)-(d_{2}^{\text {PIS}})^{\ast}}{(d_{2}^{\text {PIS}})^{\prime }- (d_{2}^{\text {PIS}})^{\ast}},&{}\text{ if }\quad (d_{2}^{\text {PIS}})^{\ast}< d_{2}^{\text {PIS}}(x) \\ &{} \le (d_{2}^{\text {PIS}})^{\prime } ,\\ 0 ,&{}\text{ if } \quad (d_{2}^{\text {PIS}})^{\prime }< d_{2}^{\text {PIS}}(x), \end{array} \right. \mu _2(x)=\left\{ \begin{array}{ll} 1,&{}\text{ if } \quad (d_{2}^{\text {NIS}})^{\ast}\le d_{2}^{\text {NIS}}(x),\\ 1-\frac{(d_{2}^{\text {NIS}})^{\ast}-d_{2}^{\text {NIS}}(x)}{(d_{2}^{\text {NIS}})^{\ast}- (d_{2}^{\text {NIS}})^{\prime }},&{}\text{ if }\quad (d_{2}^{\text {NIS}})^{\prime }< d_{2}^{\text {NIS}}(x) \\ &{} \le (d_{2}^{\text {NIS}})^{\ast} ,\\ 0 ,&{}\text{ if } \quad d_{2}^{\text {NIS}}(x) < (d_{2}^{\text {NIS}})^{\prime }. \end{array} \right. $$

• Step 8: Using max–min operator (introduced by Bellman and Zadeh [5] and further extended by Zimmermann [44]) and the above membership functions, we solve a general fuzzy programming problem and find a Pareto-optimal solution of Model crPT and Model crw/oPT, respectively:

  Model 10

  $$\begin{aligned}&\text{ Maximize } \lambda \end{aligned}$$

  (10a)
  $$\begin{aligned}&\text{ Subject } \text{ to } \mu _1(x)\ge \lambda , \mu _2(x)\ge \lambda , \end{aligned}$$

  (10b)
  $$\begin{aligned}&0 \le \lambda \le 1, \end{aligned}$$

  (10c)
  $$\begin{aligned}&{\text{ Constraints }}~(3d)-(3f), \end{aligned}$$

  (10d)
  $$\begin{aligned}&{\text{ Constraints }}~(1g)-(1g). \end{aligned}$$

  (10e)

  Here $\lambda =\min \{\mu _1(x), \mu _2(x)\}$ is the satisfactory level for both the criteria of the minimum distance from the PIS and the maximum distance from the NIS of Model crPT and Model crw/oPT, respectively. (Note that (3d) is left out and (4d) is added for Model crw/oPT.)

• Step 9: Finally we obtain a Pareto-optimal solution of Model crPT and Model crw/oPT, respectively, by numerically solving the model (for example, using LINGO as solver).

6 Benefits from and Limitations of the Proposed Approach

In this section we discuss the main contributions and limitations of our proposed model.

• We design the model for the MOSTP under PT to reduce the rate of deterioration of perishable items which will be transported. In order to decrease the deterioration at the same time, the preservation cost is included in the transportation cost. As a result, the total cost is increased. To reduce the preservation cost, we attempt to use the energy from the engine of running vehicles for the preservation system. The main contribution of this study is to tackle such situation by introducing an optimal strategy for finding a Pareto-optimal solution.

• We consider three objective functions. The first one is the combination of the transportation cost and the preservation cost. The second and the third objective functions are transportation time and deterioration, respectively. In the formulated model, we minimize the deterioration after applying PT.

• We introduce a restriction as in constraints (1d) to satisfy the demand of the destinations after applying PT. Also we formulate two models which are with PT and without PT to explicate the significance of PT.

• In the proposed model, we include a Pythagorean fuzzy environment and consider all data as TPFN to label strong fuzziness and ambiguity than fuzzy or intuitionistic fuzzy or other uncertainty which explicitly defined in Fig. 1.

• We introduce a ranking operator using membership and non-membership functions to convert the Pythagorean fuzzy system into a crisp system and this operator obeys the linearity property.

• For finding a Pareto-optimal solution of the suggested MOSTP, we include three preferable methods, which are the $\varepsilon$-constraint method, NLP and a fuzzy TOPSIS approach.

• We incorporate a numerical example with a real-world background with PT and without PT. A comparative study is depicted to justify the appropriateness of the proposed model. We select a method among the three proposed methods which provides better result.

• The main limitations of the proposed MOSTP are that we only consider for highly important perishable items, not for any breakable items. We also do not consider any fixed charge in the suggested model.

• Another limitation is not fix the transportation time, which is an important part for transporting such perishable items. Whenever the vehicles are at rest due to some critical situations, such as a strike, bad weather, or a road accident, then the vehicle engines must be stopped for some durations. Then PT, such as freezing system, will not work. Thus the rate of deterioration will be increased, even to the point that the items may be fully deteriorated. We do not include such situations, and we do not consider how these situations will be tackled.

Table 5 Supply, demand and conveyance in pythagorean fuzzy

Table 6 Transportation cost ${\tilde{{c}}_{ijk}}^p$ ($) in Pythagorean fuzzy

Table 7 Transportation time ${\tilde{{t}}_{ijk}}^p$ (hour) in Pythagorean fuzzy

7 Numerical Results

Example 1

In this section, we illustrate the applicability of the described model using a suitable real-life based example. Consider a reputed company which supplies various types of sea fishes (such as Elisha, Prawn, or Pomfret). There are two source points, which are situated at West Bengal and Odisha in India from where these fishes are supplied to two different demand points that are situated at Punjab and Himachal Pradesh in India. The company supplies these items by introducing PT (refrigeration) to reduce the deterioration rate. The DM wants to minimize the transportation cost, the preservation cost, the transportation time and the deterioration after applying PT. Here the transportation cost is considered in Dollar per ton, the deterioration rate in % and the time in hour. The preservation cost in Dollar depends on the transportation time, the amount of transported items and the preservation method. The supply, demand and conveyance capacity are measured in ton. The preservation is measured in %. Source, demand, conveyance, transportation cost, preservation cost, transportation time, deterioration and all the data are taken in TPFNs and presented in Tables 5, 6, 7, 8, and  9. The DM wishes to transport an amount of items from the ith source to the jth destination using the kth type of conveyance as to satisfy the total requirement. By the ranking operator we transform all TPFNs into crisp numbers and thereafter formulate two models. We consider $\lambda = \frac{1}{2};~\alpha =5\%;$ $m=2; n=2;$ and $r=2$. To show the applicability of PT we introduce Model A and Model B obtained from Model crPT and Model crw/oPT, respectively, using the tabulated data.

Table 8 Preservation cost ${\tilde{{p}}_{ijk}}^p$ ($) in Pythagorean fuzzy

Table 9 Deterioration rate ${\tilde{{d}}_{ijk}}^p$ (%) in Pythagorean fuzzy

Model A (with PT)

$$\text{ minimize } {Z_1}=21.1x_{111}+26.8x_{112}+29.4x_{121}+24x_{122}+33.35x_{211}+28.75x_{212}+31.1x_{221}+27.2x_{222}\text{ minimize } {Z}_2=26{{\eta }_{111}}+24{{\eta }_{112}}+28{{\eta }_{121}}+20{{\eta }_{122}}+19{{\eta }_{211}}+21{{\eta }_{212}}+22{{\eta }_{221}}+23{{\eta }_{222}}\text{ minimize } {Z_3}=0.0005(8x_{111}+7x_{112}+10x_{121}+5x_{122}+ 4x_{211}+6x_{212}+8x_{221}+10x_{222}) \text{ subject } \text{ to }{x}_{111}+{x}_{112}+{x}_{121}+{x}_{122} \le 250,{x}_{211}+{x}_{212}+{x}_{221}+{x}_{222} \le 275,{x}_{111}+{x}_{211}+{x}_{121}+{x}_{221} \le 250, {x}_{112}+{x}_{122}+{x}_{212}+{x}_{222} \le 265, 0.996{x}_{111}+0.9965{x}_{112}+0.998{x}_{211}+0.997{x}_{212} \ge 200, 0.995{x}_{121}+0.9975{x}_{122}+0.996{x}_{221}+0.995{x}_{222} \ge 225,{{x}_{ijk}}\ge 0, \forall ~i,~j,~k. $$

Model B (without PT)

$$\begin{aligned} \text{ minimize }&{Z_1}=12x_{111}+16x_{112}+14x_{121}+16x_{122}+\\&21x_{211}+13x_{212}+19x_{221}+18x_{222}\\ \text{ minimize }&{Z}_2=26{{\eta }_{111}}+24{{\eta }_{112}}+28{{\eta }_{121}}+20{{\eta }_{122}}+\\&19{{\eta }_{211}}+21{{\eta }_{212}}+22{{\eta }_{221}}+23{{\eta }_{222}}\\ \text{ minimize }&{Z_3}=0.01(8x_{111}+7x_{112}+10x_{121}+5x_{122}\\&+ 4x_{211}+6x_{212}+8x_{221}+10x_{222})\\ \text{ subject } \text{ to }&{x}_{111}+{x}_{112}+{x}_{121}+{x}_{122} \le 250,\\&{x}_{211}+{x}_{212}+{x}_{221}+{x}_{222} \le 275,\\&0.92{x}_{111}+0.93{x}_{112}+0.96{x}_{211}\\&+0.94{x}_{212} \ge 200,\\&0.90{x}_{121}+0.95{x}_{122}+0.92{x}_{221}\\&+ 0.90{x}_{222} \ge 225, \\&{x}_{111}+{x}_{211}+{x}_{121}+{x}_{221} \le 250,\\&{x}_{112}+{x}_{122}+{x}_{212}+{x}_{222} \le 265,\\&{{x}_{ijk}}\ge 0, \forall ~i,~j,~k. \end{aligned}$$

Table 10 Supply, demand and conveyance in Pythagorean fuzzy

Table 11 Transportation cost ${\tilde{{c}}_{ijk}}^p$ ($) in Pythagorean fuzzy

Table 12 Transportation time ${\tilde{{t}}_{ijk}}^p$ (hour) in Pythagorean fuzzy

Example 2

We consider another example with $\lambda = \frac{1}{4};~\alpha =2\%$; $m=2; n=2$ and $r=2$.

To show the applicability of PT we solve two models as similar to Model A and Model B obtained from Model crPT and Model crw/oPT, respectively, using the tabulated data presented in Tables 10, 11, 12, 13, and 14.

Table 13 Preservation cost ${\tilde{{p}}_{ijk}}^p$ ($) in Pythagorean fuzzy

Table 14 Deterioration rate ${\tilde{{d}}_{ijk}}^p$ (%) in Pythagorean fuzzy

8 Computational Results and Discussion

Here we present Pareto-optimal solutions of the numerical example defined in previous section and solve the models using the three methods: the $\varepsilon$-constraint, the NLP and the fuzzy TOPSIS approach. We compare the performance of the methods by evaluating the obtained results. We also discuss the applicability of PT by observing the objective values of two models corresponding to two examples. Here we use the notations w and wt to define the problems with PT and without PT respectively.

8.1 The $\varepsilon$-Constraint Method (Example 1)

We find the Pareto-optimal solution of Model A and Model B using Model (5) by varying the value of $\varepsilon$ along Pareto-optimal front to each objective function. The objective values are defined in Tables 15 and 16 for two cases. Thereafter we find the final Pareto-optimal solution for two cases and give the objective values in Table 17. The achieved solutions are as: $x_{122}=225.5639$, $x_{211}=200.4008$ and other variables are zero for Model A. $x_{111}=83.1468$, $x_{122}=166.8532$, $x_{211}=32.5489$, $x_{212}=98.1468$, $x_{221}=72.2712$ and other variables are zero for Model B.

Table 15 Pareto-optimal solution in $\varepsilon$-constraint method (with PT)

Table 16 Pareto-optimal solution in $\varepsilon$-constraint method (without PT)

Table 17 Solutions from the $\varepsilon$-constraint, the NLP and the Fuzzy TOPSIS method (Example 1)

8.2 The NLP (Example 1)

In the NLP approach, we solve Model A and Model B, respectively, by a LINGO solver. We obtain solutions with PT and without PT using the following parameters: $\mu ^{w}=0.59929$, $\nu ^{w}=0.59929$, $\gamma ^{w}=0$; $x_{111}=77.0373$, $x_{122}=172.9627$, $x_{211}=84.2533$, $x_{212}=39.3039$, $x_{222}=52.7334$ and other variables are zero for Model A, and $\mu ^{wt}=0.58293$, $\nu ^{wt}=0.58293$, $\gamma ^{wt}=0$; $x_{111}=78.3602$, $x_{122}=171.6398$, $x_{211}=41.8229$, $x_{212}=93.3602$, $x_{221}=67.3285$ and other variables are zero for Model B. See Table 17 for the results.

8.3 The Fuzzy TOPSIS Approach (Example 1)

We consider the crisp problems Model A and Model B, respectively, and use the fuzzy TOPSIS solution procedure. We set the weights to $W_1=0.25, W_2=0.25, W_3=0.5$, and $r=2$. We then get $\lambda ^{w}=0.5845$; $x_{111}=21.043$, $x_{122}=225.564$, $x_{211}=179.4003$ and all other variables are zero for Model A, and $\lambda ^{wt}=0.6951$; $x_{111}=8.2399$, $x_{122}=236.842$, $x_{211}=172.8655$, $x_{212}=28.1579$ and other variables are zero for Model B. The objective function values are again given in Table 17.

8.4 The $\varepsilon$-Constraint Method (Example 2)

The objective values are defined in Tables 18 and 19 for two cases and we find the final Pareto-optimal solution of $\varepsilon$-constraint method for two cases in Table 20. The illustrated solutions are as: $x_{122}=145.1451$, $x_{211}=160.0961$ and other variables are zero for Model A. $x_{122}=152.6316$, $x_{211}=164.9485$ and other variables are zero for Model B.

Table 18 Pareto-optimal solution in $\varepsilon$-constraint method (with PT)

Table 19 Pareto-optimal solution in $\varepsilon$-constraint method (without PT)

8.5 The NLP (Example 2)

In the NLP, we obtain solutions for example 2 with PT and without PT using the following parameters: $\mu ^{w} =0.52705$, $\nu ^{w}=0.52705$, $\gamma ^{w}=0$; $x_{121}=50.6911$, $x_{122}=94.4642$, $x_{211}=84.5754$, $x_{212}=75.5358$ and other variables are zero (similar for Model A), and $\mu ^{wt}=0.517135$, $\nu ^{wt}=0.517135$, $\gamma ^{wt}=0$; $x_{121}=64.1055$, $x_{122}=89.2009$, $x_{211}=84.9823$, $x_{212}=80.7991$ and other variables are zero (similar for Model B). See Table 20 for the results.

Table 20 Solutions from the $\varepsilon$-constraint, the NLP and the Fuzzy TOPSIS method (Example 2)

8.6 The Fuzzy TOPSIS Approach (Example 2)

Using the Fuzzy TOPSIS solution procedure and set the weights to $W_1=0.3, W_2=0.3, W_3=0.4$, and $r=2$, we then find $\lambda ^{w}=0.64742$; $x_{122}=145.1451$, $x_{211}=141.3181$, $x_{212}=18.7816$ and all other variables are zero (similar for Model A), and $\lambda ^{wt}=0.65077$; $x_{121}=2.602$, $x_{122}=150.0569$, $x_{211}=145.211$, $x_{212}=19.9431$ and other variables are zero (similar for Model B). The objective function values are again given in Table 20.

8.7 Comparison and Discussion of the Obtained Results

A comparison of the results from the three approaches is shown in Tables 17 and 20.

From Tables 17 and 20 we conclude that the values of the objective functions $Z_2$ and $Z_3$ from the $\varepsilon$-constraint method are better than NLP and from the fuzzy TOPSIS approach. This method gives most minimum value of $Z_2$ and $Z_3$, though $Z_1$ is better in NLP. As our target is to minimize deterioration and time with cost, therefore according to the priority of second and third objective values from these two numerical results we select $\varepsilon$-constraint method as better than other two methods. This method is defined the final results of two numerical examples.

The novelty of this approach is as: $\varepsilon$-constraint method is non-fuzzy technique that has less computational burden than two fuzzy techniques, NLP and fuzzy TOPSIS approach. This method is confirmed to supply Pareto-optimal solution in its intellectual way by varying the value of $\varepsilon _l$ along with Pareto-optimal front corresponding to each objective value. Here DM has a flexibility to choose a better Pareto-optimal solution among with several optimal solutions. This method gives priority one objective at a time for each case, but DM selects the most preferable case which gives important on most objective values. Also this method converts a multi-objective problem into a single objective problem without violating the constraints and without neglecting all objective functions.

The main achievements of this study are highlighted from the numerical results. We observe that the total investment cost $Z_1$ increases, while the deterioration $Z_3$ decreases due to the inclusion of PT. Some valuable items are transported where the quality and quantity are more important than money, then application of PT is a great opportunity. For economically weaker supply or demand company where the quality or quantity is not a vital matter, then they select this MOTP without investing any PT. For this reason the transportation systems make more profit by choosing a suitable choice as of their economical condition. Furthermore, PT is highly applicable and suitable for the transport of perishable items to reduce the problem of deterioration.

9 Conclusion and Outlook to Future Research

In this manuscript, we investigated the MOSTP with a new practical modification: the transport of perishable items. We targeted to minimize the deterioration with PT or without PT including time and cost. For the first time in the course of research, we introduced the concept of PT within MOSTP based on a Pythagorean fuzzy environment. The practical relevance of PT in TP lies in the fact that it is very sizeable, as the total transportation cost varies, if the effect of PT increases or decreases, and there exists a trade-off between the increased cost and decreased rate of deterioration. For this reason the items can be sold at a higher price, and so the profit becomes higher, which recovers the economic loss. All the data have been chosen as TPFNs that were transformed into their crisp counterpart by utilizing a ranking operator. A Pythagorean fuzzy systems break the limitation of a fuzzy or an IFS, and provides the use of extensive uncertain information. Pareto-optimal solutions have been obtained by computation of the $\varepsilon$-constraint method, the NLP and the fuzzy TOPSIS approach using the LINGO optimization software package. A comparative study has been drawn among the Pareto-optimal solutions of a real-life based numerical problem for these three approaches. We found out that the $\varepsilon$-constraint method has produced a better result of a Pareto-optimal solution than the fuzzy TOPSIS and the NLP method. We used a PT that prevents the deterioration at the price of preservation cost. Finally, from the applied viewpoint, we conclude that our model is highly significant in real-life situations and this gives a new prototype to the decision makers.

In future studies, the content of this paper can open a new dimension to make a separate investigation for the MOSTP in a Pythagorean fuzzy environment. One may consider different safety factors with limited time for transporting breakable items in our model. Another option is to consider a deterioration with sustainability ([24, 36]) under different uncertain environments [29], such as cubic/interval Pythagorean fuzzy, Gaussian type-2 fuzzy, or neutrosophic systems, to be included in the proposed model. Also distance measures for different value indexes r in the fuzzy TOPSIS or the intuitionistic fuzzy TOPSIS approach can be a subject of further studies in the area of the MOSTP with PT.