Recurrent Interval Type-2 Fuzzy Wavelet Neural Network with Stable Learning Algorithm: Application to Model-Based Predictive Control

Abstract

Fuzzy neural networks, with suitable learning strategy, have been demonstrated as an effective tool for online data modeling. However, it is a challenging task to construct a model to ensure its quality and stability for non-stationary dynamic systems with some uncertainties. To solve this problem, this paper presents a novel identification model based on recurrent interval type-2 fuzzy wavelet neural network (RIT2FWNN) with new learning algorithm. The model benefits from both advantages of recurrent and wavelet neural networks such as use of temporal data and fast convergence properties. The proposed antecedent and consequent parameters update rules are derived using sliding-mode-control-theory. To evaluate the proposed fuzzy model, it is utilized to design a nonlinear model-based predictive controller and is applied for the synchronization of fractional-order time-delay chaotic systems. Using Lyapunov stability analysis, it is shown that all update rules of the parameters are uniformly ultimately bounded. The adaptation laws obtained in this method are very simple and have closed forms. Some stability conditions are derived to prove learning dynamics and asymptotic stability of the network by using an appropriate Lyapunov function. The efficacy and performance of the proposed method is verified by simulation examples.

1 Introduction

In the study of nonlinear dynamical system identification, conventional modeling approaches may not be suitable to be used due to the lack of precise, formal knowledge about the system, strongly nonlinear behavior, a high degree of uncertainty, and time-varying characteristics. Most of problems require methods that can handle qualitative and quantitative information with varying precision and complexity. These considerations impose extra demands on the effectiveness of process modeling techniques [30]. Model-free methods like fuzzy logic and neural network are universal estimators that can be applied to approximate the behavior of the nonlinear dynamical systems [20]. Fusion of these techniques into a system enhances the capability of them like fuzzy neural network [8, 18].

Since the output of dynamic systems is a function of time-delayed input and time-delayed output, recurrent neural network (RNN) is suitable choice for identifying their behavior. These networks have recurrent loops in their topologies that make it possible to temporarily store information, capture dynamic response of the system and enhance the approximation accuracy of the network [15, 18]. In addition, combination of RNN and type-2 fuzzy sets is applied to various practical applications [11, 17, 18] to enhance noise tolerance of the system; different methods for their parameter tuning are discussed. The recurrent fuzzy structure that is used in [17] formed an external loop and internal feedback by feeding the rule firing strength of each rule to other rules and itself. The structure benefits from variable-dimensional Kalman filter and gradient descent (GD) algorithm for tuning its parameters. The recurrent Takagi–Sugeno–Kang (TSK) fuzzy structure in [10] obtains from locally feeding the firing strength of each fuzzy rule back to itself. An iterative linear support vector regression algorithm is applied to tune all parameters. In addition interval type-2 fuzzy system applied to represent the complex nonlinear plant in practical industrial systems [25, 26]. For example on fault detection problem, the author in [25] utilized it to design an event-triggered fault detection filter for nonlinear networked systems which the parameter uncertainty is captured by type-2 fuzzy membership functions.

Due to the number of possible nonlinear interactions in nonlinear dynamical system is theoretically infinite, a nonlinear function should be chosen which is rich enough to describe a nonlinear process with good accuracy. Moreover, certain types of functions can efficiently approximate only certain nonlinear relationships [30]. Some basis functions have important general properties to deal with nonlinearity and uncertainties like wavelet representation.

Wavelet function as the activation function can enhance the advantages of neural networks for faster learning ability and wavelet decomposition for identification purposes. In literature, wavelet neural network (WNN) and its integration with fuzzy logic to determine an optimal definition of premise and consequent part of fuzzy rules, are applied in identification and control of nonlinear dynamical systems [5, 19, 20]. Discrete wavelet transform and WNN which is trained by back propagation and GD algorithms has also been used to improve the pattern recognition effects of sEMG signals [6].

Stability and convergence are fundamental in numerical analysis for online modeling, identification and control tasks. One of the foremost stability analysis techniques is the direct implementation of Lyapunov’s stability theory. Another way of designing a robust and stable system is to use the variable structure systems (VSS) theory, which constructs the parameter adaptation mechanism and a rigorous stability analysis [9, 29].

Sliding mode control (SMC) approach as a class of VSS has high performance in dealing with uncertainties and imprecision. Since robustness and invariance properties to matched uncertainties are the most significant properties of an SMC, the use of it in artificial neural networks (ANN) or fuzzy neural networks (FNN) can ensure convergence and stability of the learning algorithm [32]. As the result has shown in [29], SMC improves the performance of systems based on soft-computing techniques which utilize the gradient-based training strategies.

In literature, several research works use the diffusion of SMC approach into ANNs. In [12] a sliding mode incremental learning algorithm is used for tuning the parameters of interval type-2 FNN (IT2FNN) where an adaptive learning rate with an adaptation law is derived. An adaptive controller for speed control of induction motor which utilizes IT2FNN and SMC-based learning algorithm is proposed in [21]. In another study, a new learning algorithm for radial basis function neural networks is demonstrated that is based on applying fast terminal sliding mode [13]. In [33], a novel identification and control scheme using multi-time scale recurrent high-order neural networks is presented. The scheme uses modified optimal bounded ellipsoid based weight’s updating laws to identify a nonlinear systems.

Recently, the synchronization of the fractional-order chaotic systems have been studied for many applications in science and technology. It has been observed that many applications arising in various fields of science and engineering are described more accurately by fractional-order differential equations. Fractional calculus is a mathematical topic which deals with derivatives and integrations with non-integer order and applied to model nonlinear biological systems with complex behavior and long-term memory [2].

Chaos is a nonlinear and deterministic phenomenon which characterized by a subset of features comprising having an unusual sensitivity to initial states, not being periodic, having fractal structures, and being governed by one or more control parameters [7]. On the other hands, the chaotic dynamics of fractional-order differential systems has gained attraction in the investigation of dynamical systems, such as the fractional order of Chua’s circuit, Duffing system [1], Lu system, Chen system [27].

In [4], a direct adaptive fuzzy controller is designed to obtain a generalized projective synchronization of two different incommensurate fractional-order chaotic systems in the presence of both uncertain dynamics and external disturbances. Lin and Lee developed an adaptive fuzzy-control scheme incorporating with SMC approach to synchronize two nonlinear fractional-order Duffing-Holmes chaotic systems [16]. They investigated the effect of delay on the chaotic behavior of the fractional-order system for the first time. Mohammadzadeh et.al formulated a robust nonlinear model-based predictive control for synchronization of the fractional-order chaotic systems [23]. By considering a fractional-order Lyapunov function, Mohadeszadeh and Delavari designed an adaptive finite time sliding mode control for chaos synchronization between two identical and nonidentical fractional-order hyper-chaotic systems [22]. The robust adaptive interval type-2 fuzzy-control strategy incorporating Lyapunov stability criterion and $H_\infty$ synchronization performance is studied in [14].

The models of real-world systems are not known completely and/or their accuracy are affected by nonlinear and time-varying behavior which can be originated from actual high degrees of uncertainties about the plant or from the plant dynamics, external disturbances and time-varying parameters. Identification performance of such applications is influenced by these factors. This study presents a new robust nonlinear and stable identification model RIT2FWNN to address these issues. In order to show the capabilities of the proposed model in such conditions, it is used to identify a second-order nonlinear time-varying plant and as a model in MPC to estimate the tracking error online. The controller is applied for the synchronization of uncertain fractional-order chaotic systems and the robustness of its synchronization in the presence of external disturbances, and approximation errors are investigated. The model performance in handling the uncertainties and imprecision can be achieved by utilization of recurrent IT2FNN and wavelet activation function. For the parameter adaptation of the RIT2FWNN, sliding mode theory-based supervised online training algorithm is elaborated. This learning algorithm is shown to be stable in the sense of Lyapunov stability theory which derives mathematical stability proofs to ensure finite time stability in RIT2FWNN. Moreover, fast convergence learning speed and the robustness of recurrent proposed structure is guaranteed. The main contributions of this manuscript are as follows:

• The proposed structure of RIT2FWNN includes wavelet activation function with its parameters being tuned by a novel sliding-mode-control-theory learning algorithm.

• Utilizing the Lyapunov stability theorem which is applied to obtain the parameter tuning algorithms. As it is expected, it is shown that the error value will be smaller in cases where the number of rules and input variables are more.

• Since the performance of MPC highly depends on the accuracy of the model, a robust model-based predictive controller scheme is developed with the aid of the proposed model.

• The robustness of the developed model-based predictive controller is examined in the case there exist uncertain dynamics and time delays in the dynamic system.

Different symbols defined in this paper are listed in Table 1.

The organization of this paper is as follows. In Sect. 2, problem statement and preliminaries are given. The structure of RIT2FWNN and the novel SMC-theory-based learning rules are introduced in Sect. 3. The enhanced model-based predictive controller is presented in Sect. 4. To demonstrate the validation of the proposed method, synchronization of two fractional-order time-delay chaotic systems and identification of a nonlinear dynamic system are investigated in Sect. 5. Finally, the conclusions are given in Sect. 6.

Table 1 Symbols defined in this paper

2 Problem Statement and Preliminaries for Fractional-Order Systems

The commonly used definitions in literature for Fractional-Order operator are Grunwald–Letnikov, Riemann–Liouville, and Caputo definitions. The last one is introduced for engineering applications because its Laplace transform requires integer-order derivatives for the initial conditions. The Caputo’s fractional derivative of a function x(t) with respect to time is defined as follows [28]:

$$\begin{aligned} D^\alpha _t=\frac{1}{\varGamma (m-\alpha )}\int _0^t (t-\tau )^{-\alpha +m-1} x^{(m)}(\tau )\text{d}\tau \end{aligned}$$

(1)

where $m=[\alpha ]+1$, $[\alpha ]$ is the integer part of $\alpha$, $D_t^\alpha$ is called the $\alpha$-order Caputo differential operator, and $\varGamma (.)$ is the well-known Euler’s gamma function:

$$\begin{aligned} \varGamma (P)=\int _0^\infty t^{P-1}e^{-t}\text{d}t; \ \ \text{with} \ \varGamma (P+1)=P\varGamma (P) \end{aligned}$$

(2)

This function can be considered as an extension of the factorial to real number arguments. The mathematical model of the fractional-order chaotic nonlinear systems to be discussed in this paper can be described as:

$${\left\{ \begin{array}{ll} D^{(\alpha _1)}_t x_1=x_2\\ \vdots \\ D^{(\alpha _{n-1})}_t x_{n-1}=x_n \\ D^{(\alpha _{n})}_t x_{n}=f(X,t)+u+\omega (t) \\ y=x_1 \end{array}\right. } $$

(3)

where $X=[x_1,x_2,\ldots ,x_n]^T= [x,x^{(\alpha )},x^{(2\alpha )},\ldots ,x^{(n-1)\alpha }]$ is the system’s states vector, $y\in R$ outputs, $u\in R$ is the control input with the initial conditions, $u(0)=0$ and $y(0)=0$. If $\alpha _1=\alpha _2=\cdots =\alpha _n=\alpha$ the above system is called a commensurate order system. Then equivalent form of the above system is specified as:

$$\begin{aligned} x^{n\alpha }&=f(X,t)+u+\omega (t) \nonumber \\ y&=x_1 \end{aligned}$$

(4)

The unknown function f(X, t) is a bounded smooth nonlinear function which specifies system dynamics and $\omega (t)$ is the external bounded disturbance. The main objective is to force the system output y to follow a given bounded reference signal $y_d$ while assuring under certain constraint, all involved signals are bounded. To quantify this objective, the reference signal vector $y_d$ and the tracking error vector e are defined as,

$$\begin{aligned}&y_d=[y_d,y_d^{(\alpha )},\ldots ,y_d^{(n-1)\alpha }]^T \end{aligned}$$

(5)

$$\begin{aligned}e&=y_d-y=[e,e^{(\alpha )},\ldots ,e^{(n-1)\alpha }]^T \nonumber \\ e^{(i\alpha )}&=y_d^{(i\alpha )} - y^{(i\alpha )} \end{aligned}$$

(6)

By substituting (6) into (4), the control system in the state space domain is obtained as follows:

$$\begin{aligned} x^{n\alpha }&=Ax+B[f(X)+u] \nonumber \\ y&=C^T x \end{aligned}$$

(7)

where

$$\begin{aligned} A = \begin{bmatrix} 0&1&0&0&\ldots&0 \\ 0&0&1&0&\ldots&0 \\ \ldots&\ldots&\ldots&\ldots&\ddots&\ldots \\ 0&0&0&0&\ldots&1 \\ -k_1&-k_2&-k_3&-k_4&\ldots&-k_n \end{bmatrix} \quad B = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \\ 1 \end{bmatrix} \quad C = \begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \\ 0 \end{bmatrix}. \end{aligned}$$

(8)

The equivalent control effort can be considered as follows:

$$\begin{aligned} u=-K^Te+D^\alpha _t y_d+u_s \end{aligned}$$

(9)

where $u_s$ is predictive control signal in previous sample times which is designed based on model predictive control. $K=(k_1,k_2,\ldots ,k_n)^T \in R$ is chosen such that the stability condition $|\text{arg}(\text{eig}(A))|>q\pi /2$, $0<q<1$ is satisfied, eig(A) is the eigenvalues of the system state matrix given in (7).

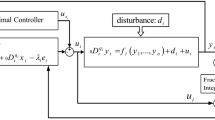
To design $u_s$, dynamic of the tracking error is modeled by the proposed RIT2FWNN with its premise and consequent part as well adaptive learning rate are updated using the proposed online learning algorithm based on SMC. Fig.1 shows a conceptual diagram of the control scheme.

Fig. 1

The designed control block diagram

3 Proposed Recurrent Interval Type-2 Fuzzy Wavelet Neural Network Structure

The structure of RIT2FWNN implements a recurrent wavelet fuzzy model is organized into layers whose consequent part is nonlinear function of the input variables. Each rule in RIT2FWNN has the following form:

$R_{r}:$ If $x_1$ is $\tilde{A}_{1j}\cdots \ x_i$ is $\tilde{A}_{ih}$ and $\cdots$ and $x_I$ is $\tilde{A}_{Il}$ then:

$$\begin{aligned} f_r = \sum _{i=1}^{I} \rho _{ri} |a_{ri}|^{-\frac{1}{2}} (1-z_{ri}^2) e^{-\frac{z_{ri}^2}{2}} \end{aligned}$$

(10)

where I is the number of input variables, h is the number of membership function and $f_r$ is the output of rth rule $(r=\{1,2,\ldots , N\})$. $\tilde{A}_{ik}$ is the kth type-2 fuzzy membership function (MF) related to ith input variable. $\rho$ is the weight coefficient between the input and the hidden layer. Consequent part of above rule involved a wavelet function of input variables. Wavelets are defined by a family of functions a and b $(a>0, b \ \in \ R )$ as follows:

$$\begin{aligned} \varPsi _{r}(x)= |a_r|^{-\frac{1}{2}} \psi \left( \frac{X-b_r}{a_r}\right) , \ \ a_r\ne 0 \end{aligned}$$

(11)

where $\varPsi _{r}(x)$ demonstrates the family of wavelets obtained from the single $\psi (x)$ function, called as a mother wavelet and localized in both time and frequency space, by dilation and translation, $a_r=\{a_{r1}, a_{r2}, \ldots , \ a_{rI}\}$ and $b_r=\{b_{r1}, b_{r2}, \ldots , \ b_{rI}\}$, respectively and $x_r=\{x_{1}, x_{2}, \ldots , \ x_{I}\}$ are input variables. In this manuscript, among several families of wavelets, Mexican Hat is considered as mother wavelet function. It is derived from a function that is proportional to the second derivative function of the Gaussian probability density function.

$$\begin{aligned} \varPsi _r(z)= \sum _{i=1}^{I}|a_{ri}|^{-\frac{1}{2}} \left (1-z_{ri}^2\right) e^{-\frac{z_{ri}^2}{2}} \end{aligned}$$

(12)

where, $z_{ri}=\frac{x_i-b_{ri}}{a_{ri}}$.

RIT2FWNN consists of seven layers. In the first layer, nodes representing input linguistic variables are fed into the network. In the second layer, each node corresponds to one linguistic term. For each entering input variable, type-2 MFs are used which have uncertain standard deviation and fixed center. The membership degree $\overline{\mu }_{ik}(x_i)$ and $\underline{\mu }_{ik}(x_i)$ are calculated according to (13):

$$\begin{aligned} \overline{\mu }_{ik}(x_i)&=\exp \left( -\frac{1}{2} \frac{{(x_i+\xi _{ik}-c_{ik})}^2}{{\overline{\sigma }_{ik}}^2}\right) \nonumber \\ \underline{\mu }_{ik}(x_i)&=\exp \left( -\frac{1}{2} \frac{{(x_i+\xi _{ik}-c_{ik})}^2}{{ \underline{\sigma }_{ik}}^2}\right) \end{aligned}$$

(13)

where $c_{ik}$ is center of type-2 MF, $\overline{\sigma }_{ik}$ and $\underline{\sigma }_{ik}$ are the upper and lower standard deviation of the kth type-2 MF of ith input. Moreover, $\xi _{ik}$ is the recurrent parameter defined as (14) which store the past information of the network. It is to be noted that the feedback weights of nodes in layer 2 are interval values.

$$\begin{aligned} \xi _{ik}=\frac{\underline{\theta }_{ik} \underline{\mu }_{ik}(t-1) + \overline{\theta }_{ik}\overline{\mu }_{ik}(t-1)}{\underline{\theta }_{ik} +\overline{\theta }_{ik}} \end{aligned}$$

(14)

where $\underline{\theta }_{ik}$ and $\overline{\theta }_{ik}$ are considered as feedback weights of the nodes. Nodes in the third layer correspond to one fuzzy rule and perform a fuzzy meet operation on inputs from layer 2 to obtain upper and lower firing strength as follows:

$$\begin{aligned} \overline{w}_{r}&=\overline{\mu }_{\tilde{A}1}(x_1)*\overline{\mu }_{\tilde{A}2}(x_2)* \ \cdots \ * \overline{\mu }_{\tilde{A}I}(x_I) \nonumber \\ \underline{w}_{r}&=\underline{\mu }_{\tilde{A}1}(x_1)*\underline{\mu }_{\tilde{A}2}(x_2)* \ \cdots \ * \underline{\mu }_{\tilde{A}I}(x_I) \end{aligned}$$

(15)

Layer 4 determines the normalized values of the lower and the upper firing strength corresponding to each node in layer 3:

$$\begin{aligned} \tilde{\underline{w}}_{r}=\frac{\underline{w}_{r}}{\sum _{r=1}^{N}\underline{w}_{r}} \ \ \ \text{and} \ \ \ \tilde{\overline{w}}_{r}=\frac{\overline{w}_{r}}{\sum _{r=1}^{N}\overline{w}_{r}} \end{aligned}$$

(16)

Layer 5 is consequent layer. In this layer, Nodes compute the product of normalized firing strength $\tilde{\underline{w}}_{r}$, $\tilde{\overline{w}}_{r}$ and wavelet function of input variables. Layer 6 involves two summation blocks, one of them is for upper and the other is for lower outputs of the previous layer. Layer 7 calculates the output of the network using (17):

$$\begin{aligned} y_N &= q \sum _{r=1}^{N} f_{r}\underline{\tilde{w}}_{r}+(1-q)\sum _{r=1}^{N} f_{r}\tilde{\overline{w}}_{r} \nonumber \\ &= q \sum _{r=1}^{N} \rho _r |a_r|^{-\frac{1}{2}} \psi \left( \frac{X-b_r}{a_r}\right) \underline{\tilde{w}}_{r} \nonumber \\ & \quad + (1-q)\sum _{r=1}^{N} \rho _r |a_r|^{-\frac{1}{2}} \psi \left( \frac{X-b_r}{a_r}\right) \tilde{\overline{w}}_{r} \end{aligned}$$

(17)

where q is the design parameter which enables to adjust the contribution of the lower or the upper values of rules depending on identification requirements for the system [3]. In literature, q has either been considered to be a constant or a time-varying parameter [12]. In this paper, the adaptation laws for the parameters and the proof of the stability of the learning process are given using a time-varying q.

Remark 1

Main improvement made in the proposed approach with respect to existing approaches in literature [25, 26] are use of wavelet functions which makes it possible to benefit from a local nonlinear general function approximator. This in turn will improve function approximation property of the system and provides means for a tight control system. On the other hand, the existence of recurrent term in type-2 fuzzy membership functions allows the use of a short term memory which captures the dynamics of the system and improves the performance of controller.

3.1 Sliding Mode Online Learning Algorithm

Based on the principles of the SMC theory, the zero value of the learning error coordinate can be defined as a time-varying sliding surface, i.e.

$$\begin{aligned} S(e(t))=e(t)=y_N(t)-y(t)=0 \end{aligned}$$

(18)

which is the condition that guarantees when the system is on the sliding surface S the RIT2FWNN output $y_N(t)$ will track the desired output signal y(t) for all time $t>t_h$ where $t_h$ is the hitting time of $e(t)=0$.

Definition 1

A sliding motion will have place on a sliding manifold $S(e(t))=e(t)=0$, after time $t_h$ if the condition $S(t)\dot{S}(t)<0$ is true for all t in some nontrivial semi open subinterval of time of the form $[t,t_h)\subset (0,t_h)$.

The online learning algorithm for the adaptation of the parameters of RIT2FWNN should be derived in such a way that the sliding mode condition of the above definition will be enforced.

Theorem 1

If the learning algorithm for the parameters of upper and lower Gaussian MFs and weights of feedback loops are chosen as follows:

$$\begin{aligned} \dot{c}_{ik}= & {} \dot{x}_i+\left( x_i-c_{ik} + \xi _{ik}\right) \alpha \ \text{sgn}(e) \end{aligned}$$

(19)

$$\begin{aligned} \dot{\underline{\sigma }}_{ik}= & {} -\left( \underline{\sigma }_{ik}+\frac{\underline{\sigma }_{ik}^3}{\left( x_i-c_{ik} + \xi _{ik}\right) ^2} \right) \alpha \ \text{sgn}(e) \end{aligned}$$

(20)

$$\begin{aligned} \dot{\overline{\sigma }}_{ik}= & {} -\left( \overline{\sigma }_{ik}+\frac{\overline{\sigma }_{ik}^3}{\left( x_i-c_{ik} + \xi _{ik}\right) ^2} \right) \alpha \ \text{sgn}(e) \end{aligned}$$

(21)

$$\begin{aligned} \dot{\underline{\theta }}_{ik}= & {} - (x_i-c_{ik} + \xi _{ik})^{-1} \left( \frac{2}{\overline{\sigma }_{ik}+\underline{\sigma }_{ik}}\right) ^{-2} \nonumber \\&\left( \frac{\underline{\mu }_{ik}(t-1)-\xi _{ik}}{\underline{\theta }_{ik} +\overline{\theta }_{ik}}\right) ^{-1} \alpha \ \text{sgn}(e) \end{aligned}$$

(22)

$$\begin{aligned} \dot{\overline{\theta }}_{ik}= & {} - (x_i-c_{ik} + \xi _{ik} )^{-1} \left( \frac{2}{\overline{\sigma }_{ik}+\underline{\sigma }_{ik}}\right) ^{-2} \nonumber \\&\left( \frac{\overline{\mu }_{ik}(t-1)-\xi _{ik}}{\underline{\theta }_{ik} +\overline{\theta }_{ik}}\right) ^{-1} \alpha \ \text{sgn}(e) \end{aligned}$$

(23)

and the adaptation of the parameters of wavelet functions and coefficient in the consequents part of fuzzy rules are chosen as follows:

$$\begin{aligned} \dot{a}_{ri}&=-\frac{1}{\varPsi _{ri}(z)\rho _{ri}} \left( -\frac{1}{2} a_{ri}^{-1} +\frac{z_{ri}^2}{a_{ri}} \frac{3-z_{ri}^2}{1-z_{ri}^2} \right) ^{-1} \nonumber \\&\quad \frac{q\tilde{\underline{w}}_{r}+ (1-q)\tilde{\overline{w}}_{r}}{(q\tilde{\underline{w}}_{r}+ (1-q)\tilde{\overline{w}}_{r})^T(q\tilde{\underline{w}}_{r}+ (1-q)\tilde{\overline{w}}_{r})} \alpha \text{sgn}(e) \end{aligned}$$

(24)

$$\begin{aligned} \dot{b}_{ri}&=-\frac{1}{\varPsi _{ri}(z) \rho _{ri}} \left( \frac{ z_{ri} }{a_{ri}} \frac{3-z_{ri}^2}{1-z_{ri}^2} \right) ^{-1} \nonumber \\&\quad \frac{q\tilde{\underline{w}}_{r}+ (1-q)\tilde{\overline{w}}_{r}}{(q\tilde{\underline{w}}_{r}+ (1-q)\tilde{\overline{w}}_{r})^T(q\tilde{\underline{w}}_{r}+ (1-q)\tilde{\overline{w}}_{r})} \alpha \text{sgn}(e) \end{aligned}$$

(25)

$$\begin{aligned} \dot{\rho }_{ri}&= -\frac{1}{ \varPsi _{ri}(z)} \frac{q\tilde{\underline{w}}_{r}+ (1-q)\tilde{\overline{w}}_{r}}{(q\tilde{\underline{w}}_{r}+ (1-q)\tilde{\overline{w}}_{r})^T(q\tilde{\underline{w}}_{r}+ (1-q)\tilde{\overline{w}}_{r})} \alpha \text{sgn}(e) \end{aligned}$$

(26)

and the parameter q is updated as follows:

$$\begin{aligned} \dot{q}= -\frac{1}{F(\tilde{\underline{W}}-\tilde{\overline{W}})^T} \alpha \text{sgn}(e) \end{aligned}$$

(27)

and the adaptive learning rate $(\alpha )$ changes as follows:

$$\begin{aligned} \dot{\alpha } = (2NI+N+1)\gamma |e|-\nu \gamma \alpha \ \ \ \ \ \nu , \gamma >0 \end{aligned}$$

(28)

The parameter $\gamma$ is considered as the learning rate for the adaptive learning rate $\alpha$ which has a small positive real value. The parameter $\nu$ should be very small not to interrupt the adaptation mechanism. Then, given an arbitrary initial condition e(0), the learning error e(t) will converge to zero within a finite time $t_h$.

Proof

The reader is referred to Appendix. According to the following equation which obtained from the proof, the error value will be smaller in cases where the number of rules and input variables are more.

$$\begin{aligned} |e| \le \frac{\alpha ^* \nu }{2(3IN+1)} \end{aligned}$$

(29)

$\square$

In Eq. (28) the parameter $\gamma$ is the learning rate for the adaptive learning rate $\alpha$. Since the first term of this equation is positive, the second term is considered to avoid bursting in parameter $\alpha$. The value of the parameter $\nu$ should be adjusted in such a way that the adaptation mechanism not to be disturbed.

Despite aforementioned advantages of simplicity and robustness of SMC, it suffers from a technical problem, called chattering. Sensitivity to noise is another phenomena caused by the presence of signum function in the structure of SMC. In this manuscript, in order to alleviate the problem associated with the chattering and sensitivity to noise, a continuous approximation method is used which smooths the discontinuity caused by the signum function as follows:

$$\begin{aligned} \text{sign}(e(t)) \approx \frac{e(t)}{|e(t)|+\delta } \end{aligned}$$

(30)

where $\delta$ is a small positive number [32].

4 Model Predictive Control Design

The target of the following Eq. (31) as the cost function is to solve an enhanced model-based predictive control:

$$\begin{aligned}&\min _{u_s(k),\ldots ,u_s(k+N_c)} J= \sum _{k-t}^{t+N_p} {\hat{e}(k)^T Q \hat{e}(k) + \varDelta u_s(k)^T R \varDelta u_s(k)} \nonumber \\&\quad \hat{e}(t) = \text{RIT2FWNN}[e(t-k_1), \ldots ,e(t-k_l),u_s(t-1)] \end{aligned}$$

(31)

where $u_s$ is predictive control signal, $e(t-k_l),l=1,\ldots ,r$ are the tracking errors, $\varDelta u_s(t)=u_s(t)-u_s(t-1)$, R and Q are positive definite weighting matrices. $N_c$ and $N_p$ are control and prediction horizon. In order to minimize the cost function (31), the output predictions over the horizon must be computed. RIT2FWNN is used to estimate the tracking error e(t). The consequent parameters of RIT2FWNN are tuned based on the updating rule proposed in previous section. By considering the Diophantine equation corresponding to the prediction for $\hat{e}(t+k+1|t)$:

$$\begin{aligned} \hat{e}(t+k|t)&= G_k(z^{-1}) \varDelta u_s(t+k-1) \nonumber \\ & \quad +G_{kp}(z^{-1}) \varDelta u_s(t-1)+ F_k(z^{-1})e(t) \end{aligned}$$

(32)

The last two terms of Eq. (32) depend on past values of the process output and input variables. That is, they correspond to the free response $e_r$ of the process considered if the control signals are kept constant and are computed as follows:

$$\begin{aligned}&e_r(t+k|t)=\text{RIT2FWNN} [e(t+k-1), \ldots , \nonumber \\&\quad e(t+k-r),u_s(t-1)] \end{aligned}$$

(33)

The first term of Eq. (32) depends only on future values of the control signal and can be interpreted as the forced response which is obtained by (34). That is, the response obtained when the initial conditions are zero $e(t-k)=0$, $\varDelta u_s(t-k)=0$.

$$\begin{aligned} e_o(t+k|t)=\sum _{i=0}^{k-1} {\vartheta _i \varDelta u_s(t+k-i+1|t)} \end{aligned}$$

(34)

where $\vartheta _i$, $i=0,\ldots ,k-1$ are the step response coefficients that are obtained using unit step on RIT2FWNN model. Step response can be estimated as follows [24]:

$$\begin{aligned} g(t-1)= \frac{\hat{e}_{\text{step}}(t+k|t) -\hat{e}_{r}(t+k|t)}{du_s(t)} \end{aligned}$$

(35)

where $du_s(t)$ is the step size and $\hat{e}_{\text{step}}(t+k|t)$ is calculated by RIT2FWNN like as $e_r$. Equation (32) can be rewritten as follows:

$$\begin{aligned} \hat{e}(t+k|t)=G_k(z^{-1}) \varDelta u(t+k-1)+f_k \end{aligned}$$

(36)

such that $f_k= G_{kp}(z^{-1}) \varDelta u_s(t-1)+ F_k(z^{-1})e(t)$. Then the step ahead prediction of the system output on data up to time $N_p$ in matrix form described as follows:

$$\begin{aligned} \begin{bmatrix} \hat{e}(t+1|t) \\ \hat{e}(t+2|t) \\ \vdots \\ \hat{e}(t+N_p|t) \\ \end{bmatrix}&= \begin{bmatrix} G_0&0&\cdots&0 \\ G_1&G_1&\cdots&0 \\ \vdots&\vdots&\ddots&\vdots \\ G_{N_p-1}&G_{N_p-2}&\cdots&G_0 \end{bmatrix}\\&\quad \begin{bmatrix} \varDelta u(t) \\ \varDelta u(t+1) \\ \vdots \\ \varDelta u(t+N_p-1) \end{bmatrix} + \begin{bmatrix} f_1 \\ f_2 \\ \vdots \\ f_{N_p} \end{bmatrix} \end{aligned}$$

The predictions can be expressed in condensed form as follows:

$$\begin{aligned} E=G \varDelta u_s + e_r \end{aligned}$$

(37)

The optimization problem (31) can be written as follows:

$$\begin{aligned} J&= E^TQE+\varDelta U_s^TR\varDelta U_s \nonumber \\&=(G\varDelta U_s+e_r )^T Q (G\varDelta U_s+e_r) +\varDelta U_s^TR\varDelta U_s \end{aligned}$$

(38)

By making the gradient of J in (38) equal to zero:

$$\begin{aligned} \frac{\partial J}{\partial \varDelta U_s}= 2G^TQf_r+2(G^TQG+R)\varDelta U_s \end{aligned}$$

(39)

Then the optimum is:

$$\begin{aligned} \varDelta U_s=(G^TQG+R)^{-1} G^TQe_r \end{aligned}$$

(40)

5 Simulation Studies and Discussions

In this section, two illustrative examples are presented to demonstrate the applicability and feasibility of the proposed method and to confirm the theoretical results. In these examples, the designed controller is applied to synchronize two identical and nonidentical uncertain fractional-order chaotic systems in the presence of external disturbances. Besides, to analyze how the proposed structure measures the mathematical model of a system from measurements of the system inputs and outputs, an example of nonlinear system identification is considered.

Example 1

As the first example, the proposed identification model, is applied to identify a second-order nonlinear time-varying plant [12] described as:

$$\begin{aligned} y(k)= \frac{x_1x_2+x_3}{x_4} \end{aligned}$$

(41)

where $x(1)=y(k-1)y(k-2)y(k-3)u(k-1)$, $x(2)=y(k-3)-b(k)$, $x(3)=c(k)u(k)$ and $x(4)=a(k)+y(k-2)^2 +y(k-3)^2$. The time-varying parameters a, b and c are defined as:

$$\begin{aligned} a(k)&= 1.2 - 0.2 \cos(2 \pi k/T) \nonumber \\ b(k)&= 1 - 0.4 \sin(2 \pi k/T) \nonumber \\ c(k)&= 1 + 0.4 \sin(2 \pi k/T) \end{aligned}$$

(42)

where $T=1000$ is the time span of the test. This example has been implemented with three inputs which are fuzzified with three Gaussian type-2 MFs with a fixed center and uncertain standard deviation. The inputs are the delayed signal from the plant output- $y(t-T_0), y(t-2T_0)$ and input signal u(t), with the period of discretization selected as $T_0=1$ ms. The incoming network signals have been normalized to be in the range $[-1, 1]$. The input signal u(k) is as follows:

$$ u(k) = \left\{ {\begin{array}{*{20}c} {\sin (\pi k/25),} & {k < 250.} \\ {1.0,} & {250 \le k < 500.} \\ { - 1.0,} & {500 \le k < 750.} \\ 0.3\sin (\pi k/25) + 0.1\sin (\pi k/32) \hfill \\ + 0.6\sin (\pi k/10), \hfill \\ & {750 \le k < 1000.} \\ \end{array} } \right. $$

(43)

Figure 2a compares the plant output with the output yielded by RIT2FWNN. Figure 2b shows the root mean square error (RMSE) values versus each epoch number which illustrates the proposed SMC-based learning algorithm is stable. Figure 2c, d show the adaptation of parameter $\alpha$ and q, respectively. Figure 2c shows the learning rate $\alpha$ will be stable at infinity. Table 2 compares the performance of RIT2FWNN with two different approaches and [12]. These results reveal the benefit of using recurrent structure and SMC-based learning algorithm of RIT2FWNN by achieving smaller RMSE values. It is to be noted that by increasing the nonlinearity of the RIT2FWNN by using wavelet functions in the consequents part of fuzzy rules and feedback loops on type-2 MFs, the accuracy of other learning methods such as gradient-based methods are lowered considerably.

Furthermore, the accuracies of extended Kalman filter and the proposed SMC-based learning method are similar. As previously discussed, the adaptation laws obtained in the proposed SMC-based learning method have explicit forms which do not have any derivative computations of the output of RIT2FWNN concerning trainable parameters and manipulation of some high-order matrices. This is the main reason why the computation time for extended Kalman filter and gradient-based methods is higher than SMC-based methods (see Table 2). Additionally, further results are provided to demonstrate the benefits of the proposed model with its type-1 counterpart. As can be seen, the proposed type-2 model achieves smaller test and train RMSE than that by the type-1.

Table 2 The RMSE values of different methods in Example 1

Fig. 2

a Plant output of example 1 and the RIT2FWNN system. b RMSE values during the online identification procedure. c Adaptation of the learning rate. d Adaptation of parameter q

Remark 2

As the simulation results show, the proposed model have better RMSE results than others. However it is more complicated in network structure. The best advantages of the proposed RIT2FWNN with respect to other such as [12], is the rate of convergence. Most controllers in real-world application are based on model and it is needed to be achieved faster. Hence, the degree of freedom in the proposed model is increased to obtain a faster convergence speed. Furthermore, several experiments have been done on the speed of convergence of different models. The average arising times are approximately 29 and 38 s for the proposed and [12] respectively, which confirm the favorable convergence behavior of the proposed model versus time.

Example 2

As the second example, we will verify the effectiveness of the proposed method to synchronize two different uncertain fractional-order Duffing-Holmes chaotic time-delay systems [1]. The master and slave systems dynamics are given as follows, respectively:

$$ \left\{ {\begin{array}{*{20}l} {D^{\alpha } x_{1} (t) = } & {2.5x_{2} (t)} \\ {D^{\alpha } x_{2} (t) = } & - \left( {\frac{1}{{2.5}}x_{1} (t)} \right)^{3} - \frac{1}{{2.5}}x_{1} (t) - 0.1x_{2} (t) \hfill \\ + 0.01x_{1} (t - 0.001) + 0.01x_{1} (t)^{2} (t - 0.001) \hfill \\ + 0.01x_{2} (t - 0.001) + 25\cos (1.29t). \\ \end{array} } \right. $$

(44)

$$ \left\{ {\begin{array}{*{20}c} {D^{\alpha } y_{1} (t) = } & {2.2y_{2} (t)} \\ {D^{\alpha } y_{2} (t) = } & - \left( {\frac{1}{{2.0}}y_{1} (t)} \right)^{3} - \frac{1}{{1.8}}y_{1} (t) - 0.1y_{2} (t) \hfill \\ + 0.01y_{1} (t - 0.001) + 0.01y_{1} (t)^{2} (t - 0.001) \hfill \\ + 0.01y_{2} (t - 0.001) + 25\cos (1.29t) + \omega (t) + u(t). \end{array} } \right. $$

(45)

where $\omega (t)=0.7\sin(t)$ is the external bounded disturbance, and u(t) is control input of the slave system. The initial conditions are $x(0)=[x_1(0),x_2(0)]^T=[0,0]$ and $y(0)=[y_1(0),y_2(0)]^T=[1,-1]$. The simulation sample time is 0.001 and the fractional derivative order is considered as $\alpha =0.98$. The control effort of the slave can be obtained as follows:

$$ u=-K^{Te}+D^{\alpha} x_2+u_s$$

(46)

where $K=[900, 30]$. The following cost function is considered to achieve the control signal $u_s$:

$$\begin{aligned}&\min _{u_s(k),\ldots ,u_s(k+10)} J= \sum _{k-t}^{t+10} {\hat{e}(t)^2 + \varDelta u_s(t)^2} \nonumber \\&\hat{e}(t) = \text{RIT2FWNN}[e(t-1),e(t-2),u_s(t-1)] \end{aligned}$$

(47)

Each three inputs of RIT2FWNN are fuzzified with two Gaussian type-2 MFs with a fixed center and uncertain standard deviation. The premise and consequent parameters of RIT2FWNN are tuned based on the proposed online SMC-based learning algorithm.

Figures 3 and 4 show the control trajectory and tracking error, respectively. The trajectories of the states $x_1$, $y_1$ and $x_2$, $y_2$ are depicted in Fig. 5 that demonstrate synchronization is perfectly achieved. The three-dimensional phase portrait, synchronization performance, of the chaotic master and slave systems is shown in Fig. 6. It can be seen that the synchronization performance of the proposed method in the presence of external disturbances and is successfully realized and the control trajectory is also admissible and bounded. The mean square error (MSE) values for the synchronization errors ($e_1$, $e_2$) are given in Table 3. It can be seen that the performances of the proposed method in this paper are significantly better than other approaches; (1) sliding mode technique [16], (2) nonlinear model predictive controller (NMPC) [23]. Additionally, tracking error results in the presence of pulse disturbance are depicted in Fig. 7. As can be seen, the controller is robust against external disturbances.

Fig. 3

Tracking error for Example 2

Fig. 4

Control signal for Example 2

Fig. 5

Trajectories of the states $x_1$, $y_1$ and $x_2$, $y_2$, Example 2

Fig. 6

3D phase portrait, synchronization performance, of the master and slave systems for Example 2

Fig. 7

Tracking error when the pulse disturbance applied for Example 2

Table 3 Comparison the values of MSE for different methods in Example 2

Example 3

In this example, we will apply the proposed method to synchronize two nonidentical fractional-order time-delay chaotic systems. The master system is as follows [31]:

$$ \left\{ {\begin{array}{*{20}l} {D^{\alpha } y_{1} (t) = y_{3} - 3y_{1} (t)y_{2} (t - 0.001) + \omega _{1}^{m} (t)} \hfill \\ {D^{\alpha } y_{2} (t) = 1 - 0.1y_{2} (t) - y_{1}^{2} (t - 0.001) + \omega _{2}^{m} (t)} \hfill \\ {D^{\alpha } y_{3} (t) = - y_{1} (t - 0.001) - y_{3} (t) + \omega _{3}^{m} (t)} \hfill \\ \end{array} } \right.{\text{ }}$$

(48)

The initial conditions are $y(0)=[y_1(0),y_2(0),y_3(0)]^T=[0.1,4,0.5]$ and the simulation sample time is 0.001.The slave system is Liu fractional-order time-delay chaotic system which its dynamics are as follows [31]:

$${\left\{ \begin{array}{ll} D^\alpha x_1(t)=10(x_2(t)-x_1(t))+\omega ^s_1(t)+u_1(t)\\ D^\alpha x_2(t)=40x_1(t-0.001)-x_1(t)x_3(t)+\omega ^s_2(t)+u_2(t)\\ D^\alpha x_3(t)=-2.5x_3(t-0.001)+4x^2_1(t)+\omega ^s_3(t)+u_3(t) \end{array}\right. }$$

(49)

where the fractional derivative order of both slave and master chaotic systems are $\alpha =0.92$. The initial conditions are $[x_1(0),x_2(0),x_3(0)]^T=[0.1,4,0.5]$. The controller design procedure is the same as Example 2. $d^m_k(t)$ and $d^s_k(t),k=1,2,3$ are the external bounded disturbances of slave and master system respectively which are initialized as follows:

$$\begin{aligned} \omega ^m(t)&=(\omega ^m_1(t),\omega ^m_2(t),\omega ^m_3(t))^T \nonumber \\&=(-0.1\cos(10t),0.2\cos(20t),0.1\sin(10t))^T \nonumber \\ \omega ^s(t)&=(\omega ^m_1(t),\omega ^s_2(t),\omega ^s_3(t))^T \nonumber \\&=(0.1\sin(20t),-0.3\sin(10t),-0.5\cos(10t))^T \end{aligned}$$

(50)

The trajectories of the states $x_k$, $y_k$ where $k=1,2,3$ and the control signals are shown in Figs. 8 and 9, respectively. As one can see from the figure, the tracking performance is good even in the presence of disturbances and unknown functions of dynamics of the system. The designed controller can synchronize effectively two nonidentical fractional-order time-delay chaotic systems. From Fig. 10, it can be observed that the tracking errors $e_1(t)$, $e_2(t)$ and $e_3(t)$ converge both to small intervals around zero. Table 4 indicates that the obtained MSE results are comparable with the results in [31]. Figure 11 shows the tacking error results in the presence of pulse disturbances. It is shown that the developed controller preserves the robustness properties against external disturbances.

Fig. 8

Trajectories of the states $x_k$, $y_k$ for $k=1,2,3$ for Example 3

Fig. 9

Control signals for Example 3

Fig. 10

Tracking error for Example 3

Fig. 11

Tracking error when the pulse disturbance applied for Example 3

Table 4 Comparison the values of MSE for different methods in Example 3

6 Conclusion and Future Work

In this paper, a novel robust model RIT2FWNN with fully SMC-based learning algorithm is proposed to design a model-based predictive controller to deal with synchronization between two different fractional-order time-delay chaotic systems with subject to uncertainty and external additive disturbances. This synchronization is effectively obtained which demonstrate the superior performance of the proposed methodology. The model is tested against identification of a nonlinear and time-varying dynamic system. Since the output of these system depends on different step delayed outputs and inputs, the task of identification of such systems is difficult. The simulation results indicate that the proposed approach is quite useful in modeling unknown function of dynamic systems, having not only favorable tracking performance but also produce strong robustness and faster convergence speed. The Lyapunov stability theorem is applied to derive the parameter update rule of the model to guarantee all parameters uniformly ultimately bounded.

The proposed RIT2FWNN owns some advantages:

• 1. The proposed SMC-based learning strategy efficiently updates the parameters of RIT2FWNN to cope with online problems which face uncertainty and external disturbances. Additionally, the adaptive learning rate can get fast convergence for the systems.

• 2. The parameters adjustments can guarantee the convergence of RIT2FWNN that can be maintained in experimental results and theoretical analysis.

• 3. Utilizing wavelet function and considering recurrent part in the structure along side with the proposed learning method make the performance of the proposed model better with respect to other learning methods under uncertain conditions in the presence of disturbances.

• 4. High Synchronization accuracy which implies that the proposed model is a suitable choice. Hence, it is applied to MPC applications.

However, the proposed RIT2FWNN network has disadvantages such as fixed structure which makes it complex spatially for systems with higher numbers of inputs.

As future work, there are many challenging issues remaining to investigate, including the choice of higher order sliding mode control in the process of training, employing self-structuring methods to achieve optimized construction of RIT2FWNN network.

Appendix: Proof of Theorem 1

The time derivative of (16) is calculated as follows:

$$\begin{aligned}&\dot{\tilde{\underline{w}}}_{r}=\frac{\dot{\underline{w}}_{r}\sum _{r=1}^{N}\underline{w}_{r} -\sum _{r=1}^{N}\dot{\underline{w}}_{r}\underline{w}_{r}}{\left( \sum _{r=1}^{N}\underline{w}_{r}\right) ^2} \ =\frac{\dot{\underline{w}}_{r}-\tilde{\underline{w}}_{r}\sum _{r=1}^{N}\dot{\underline{w}}_{r}}{\sum _{r=1}^{N}\underline{w}_{r}} \nonumber \\&\dot{\tilde{\overline{w}}}_{r}=\frac{\dot{\overline{w}}_{r}\sum _{r=1}^{N}\overline{w}_{r} -\sum _{r=1}^{N}\dot{\overline{w}}_{r}\overline{w}_{r}}{\left( \sum _{r=1}^{N}\overline{w}_{r}\right) ^2} \ =\frac{\dot{\overline{w}}_{r}-\tilde{\overline{w}}_{r}\sum _{r=1}^{N}\dot{\overline{w}}_{r}}{\sum _{r=1}^{N}\overline{w}_{r}} \end{aligned}$$

(51)

considering the following equations for $\dot{\underline{w}}_{r}$ and $\dot{\overline{w}}_{r}$:

$$\begin{aligned} \dot{\underline{w}}_{r}=\underline{J}_r \underline{w}_r ; \ \ \dot{\overline{w}}_{r} =\overline{J}_r \overline{w}_r \end{aligned}$$

(52)

thus the Eq. (51) changes as follows:

$$\begin{aligned} \dot{\tilde{\overline{w}}}_{r}&= -\tilde{\overline{w}}_{r} \overline{J}_r + \tilde{\overline{w}}_{r} \sum _{r=1}^{N}\tilde{\overline{w}}_{r}\overline{J}_r;\ \dot{\tilde{\underline{w}}}_{r}\nonumber \\&=-\tilde{\underline{w}}_{r} \underline{J}_r + \tilde{\underline{w}}_{r} \sum _{r=1}^{N}\tilde{\underline{w}}_{r}\underline{J}_r \end{aligned}$$

(53)

Furthermore, the time derivative of upper and lower of type-2 MFs are calculated as (54):

$$\begin{aligned} \dot{\underline{\mu }}_{ik}(x_i)&=-\left( \frac{\left( x_i+\xi _{ik}-c_{ik}\right) (\dot{x}_i+\dot{\xi }_{ik}-\dot{c}_{ik})}{ \underline{\sigma }_{ik}^2} \right. \nonumber \\&\quad -\left. \frac{\dot{\underline{\sigma }}_{ik}\left( x_i+\xi _{ik}-c_{ik}\right) ^2}{\underline{\sigma }_{ik}^3}\right) \nonumber \\ \dot{\overline{\mu }}_{ik}(x_i)&=-\left( \frac{\left( x_i+\xi _{ik}-c_{ik}\right) (\dot{x}_i+\dot{\xi }_{ik}-\dot{c}_{ik}}{ \overline{\sigma }_{ik}^2}\right. \nonumber \\&\quad -\left. \frac{\dot{\overline{\sigma }}_{ik}\left( x_i+\xi _{ik}-c_{ik}\right) ^2}{\overline{\sigma }_{ik}^3}\right) \end{aligned}$$

(54)

and the time derivative of the recurrent parameter is as follows:

$$\begin{aligned} \dot{\xi }_{ik}= \frac{\dot{\underline{\theta }}_{ik} (\underline{\mu }_{ik}(t-1)-\xi _{ik}) + \dot{\overline{\theta }}_{ik} (\overline{\mu }_{ik}(t-1)-\xi _{ik})}{(\underline{\theta }_{ik}+\overline{\theta }_{ik})} \end{aligned}$$

(55)

considering $\dot{\underline{\mu }}_{ik}(x_i)=-\underline{A}_{ik} \dot{\underline{A}}_{ik}$ where $\underline{A}_{ik}$ and $\dot{\underline{A}}_{ik}$ are as follows:

$$\begin{aligned} \underline{A}_{ik}&=\frac{x_i}{\underline{\sigma }_{ik}} - \frac{c_{ik}}{\underline{\sigma }_{ik}}+ \frac{\underline{\theta }_{ik} \underline{\mu }_{ik}(t-1) + \overline{\theta }_{ik} \overline{\mu }_{ik}(t-1)}{\underline{\sigma }_{ik}(\underline{\theta }_{ik}+\overline{\theta }_{ik})} \nonumber \\ \dot{\underline{A}}_{ik}&=\frac{\dot{x}_i}{\underline{\sigma }_{ik}} - \frac{\dot{c}_{ik}}{\underline{\sigma }_{ik}} - \dot{\underline{\sigma }}_{ik} \left( \frac{x_i-c_{ik}+\xi _{ik} }{\underline{\sigma }_{ik}^2}\right) \nonumber \\&\quad +\frac{\dot{\underline{\theta }}_{ik}(\underline{\mu }_{ik}(t-1) -\xi _{ik})}{\underline{\sigma }_{ik}(\underline{\theta }_{ik} +\overline{\theta }_{ik})} +\frac{\dot{\overline{\theta }}_{ik}\left( \overline{\mu }_{ik}(t-1) -\xi _{ik}\right) }{\underline{\sigma }_{ik}(\underline{\theta }_{ik} +\overline{\theta }_{ik})} \end{aligned}$$

(56)

By using Maclaurin series expansion:

$$\begin{aligned}\frac{1}{\underline{\sigma }_{ik}}&=\frac{1}{\frac{\underline{\sigma }_{ik}+\overline{\sigma }_{ik}}{2}+ \frac{\underline{\sigma }_{ik}-\overline{\sigma }_{ik}}{2}}\nonumber \\& =\frac{2}{\overline{\sigma }_{ik}+\underline{\sigma }_{ik}} \left( 1 \underbrace{-\frac{\underline{\sigma }_{ik}-\overline{\sigma }_{ik}}{\overline{\sigma }_{ik}+\underline{\sigma }_{ik}} +\left( \frac{\overline{\sigma }_{ik}-\underline{\sigma }_{ik}}{\underline{\sigma }_{ik}+\overline{\sigma }_{ik}}\right) ^2 +H.O.T }_{\underline{D}_{ik}}\right) \nonumber \\ \frac{1}{\overline{\sigma }_{ik}} & =\frac{1}{\frac{\overline{\sigma }_{ik}+\underline{\sigma }_{ik}}{2}+ \frac{\overline{\sigma }_{ik}-\underline{\sigma }_{ik}}{2}}\nonumber \\ & =\frac{2}{\underline{\sigma }_{ik}+\overline{\sigma }_{ik}} \left( 1 \underbrace{-\frac{\overline{\sigma }_{ik}-\underline{\sigma }_{ik}}{\underline{\sigma }_{ik}+\overline{\sigma }_{ik}} +\left( \frac{\underline{\sigma }_{ik}-\overline{\sigma }_{ik}}{\overline{\sigma }_{ik}+\underline{\sigma }_{ik}}\right) ^2 +H.O.T }_{\overline{D}_{ik}} \right) \end{aligned}$$

(57)

$\underline{D}_{ik}$ and $\overline{D}_{ik}$ are limited as follows:

$$\begin{aligned} \left( 1+\underline{D}_{ik}\right) ^2+1<B_D, \ \left( 1+\overline{D}_{ik}\right) ^2+1<B_D \end{aligned}$$

(58)

thus the $\overline{J}_r$ and $\underline{J}_r$ in (53) are as follows:

$$\begin{aligned} \overline{J}_r= -\sum _{i=1}^I \overline{A}_{ik} \dot{\overline{A}}_{ik} \ ; \ \ \ \ \underline{J}_r=-\sum _{i=1}^I \underline{A}_{ik} \dot{\underline{A}}_{ik} \end{aligned}$$

(59)

by substituting (19)–(23) in the above equation:

$$\begin{aligned} \overline{J}_r = \underline{J}_r = I \alpha \text{sgn}(e) \end{aligned}$$

(60)

In order to check the stability condition, the following Lyapunov function is considered:

$$\begin{aligned} V=\frac{1}{2}e^2 +\frac{1}{2\gamma }\left( \alpha -\alpha ^*\right) ^2 \end{aligned}$$

(61)

The stability condition is met when the time derivative of V is negative definite ($\dot{V}<0$). So,

$$\begin{aligned} \dot{V}=\dot{e}e+\frac{1}{\gamma }\dot{\alpha }\left( \alpha -\alpha ^*\right) =e\left( \dot{y_N}-\dot{y}\right) +\frac{1}{\gamma }\dot{\alpha }\left( \alpha - \alpha ^*\right) \end{aligned}$$

(62)

by differentiating (17)

$$\begin{aligned} \dot{y}_N &=\dot{q} \sum _{r=1}^{N} f_{r}\underline{\tilde{w}}_{r}+q\sum _{r=1}^{N} \left( \dot{f}_{r}\underline{\tilde{w}}_{r}+f_{r}\dot{\tilde{\underline{w}}}_{r}\right) \nonumber \\ & \quad - \dot{q} \sum _{r=1}^{N} f_{r}\tilde{\overline{w}}_{r} +\left( 1-q\right) \sum _{r=1}^{N} \left( \dot{f}_{r}\tilde{\overline{w}}_{r}+f_{r}\dot{\tilde{\overline{w}}}_{r}\right) \end{aligned}$$

(63)

by substituting (53):

$$\begin{aligned} \dot{y}_N & =\dot{q} \sum _{r=1}^{N} f_{r}\underline{\tilde{w}}_{r} \nonumber \\ & \quad +q\sum _{r=1}^{N} \left( \dot{f}_{r}\underline{\tilde{w}}_{r}+f_{r}(-\tilde{\underline{w}}_{r} \underline{J}_r + \tilde{\underline{w}}_{r} \sum _{r=1}^{N}\tilde{\underline{w}}_{r}\underline{J}_r)\right) \nonumber \\ & \quad -\dot{q} \sum _{r=1}^{N} f_{r}\tilde{\overline{w}}_{r} \nonumber \\ & \quad +\left( 1-q\right) \sum _{r=1}^{N} \left( \dot{f}_{r}\tilde{\overline{w}}_{r}+f_{r}\left( -\tilde{\overline{w}}_{r} \overline{J}_r + \tilde{\overline{w}}_{r} \sum _{r=1}^{N}\tilde{\overline{w}}_{r}\overline{J}_r\right) \right) \end{aligned}$$

(64)

by considering (60):

$$\begin{aligned}\dot{y}_N & =\dot{q} \sum _{r=1}^{N} f_{r}\underline{\tilde{w}}_{r}\nonumber \\&\quad +q\sum _{r=1}^{N} \left( \dot{f}_{r}\underline{\tilde{w}}_{r}-I \alpha \text{sgn}(e) \ f_{r}\left( \tilde{\underline{w}}_{r}-\tilde{\underline{w}}_{r}\sum _{r=1}^{N}\tilde{\underline{w}}_{r}\right) \right) \nonumber \\&\quad -\dot{q} \sum _{r=1}^{N} f_{r}\tilde{\overline{w}}_{r} \nonumber \\&\quad +\left( 1-q\right) \sum _{r=1}^{N} \left( \dot{f}_{r}\tilde{\overline{w}}_{r}-I \alpha \text{sgn}(e) \ f_{r} \left( \tilde{\overline{w}}_{r}-\tilde{\overline{w}}_{r}\sum _{r=1}^{N}\tilde{\overline{w}}_{r}\right) \right) \end{aligned}$$

(65)

since $\sum _{r=1}^{N} \tilde{\overline{w}}_{r}=1$ and $\sum _{r=1}^{N} \tilde{\underline{w}}_{r}=1$ Eq. (65) can be summarized and then by substituting $\dot{q}$ according to (27),

$$\begin{aligned} \dot{y}_N &= -\frac{1}{F(\tilde{\underline{W}}-\tilde{\overline{W}})^T} \alpha \text{sgn}(e) \sum _{r=1}^{N} f_{r} \left( \tilde{\underline{w}}_{r}-\tilde{\overline{w}}_{r}\right) \nonumber \\ & \quad +\sum _{r=1}^{N} \dot{f}_{r} \left( q\tilde{\underline{w}}_{r}+ (1-q)\tilde{\overline{w}}_{r}\right) \nonumber \\ & = - \alpha \text{sgn}(e) + \sum _{r=1}^{N} \dot{f}_{r}(q\underline{\tilde{w}}_{r} + (1-q)\tilde{\overline{w}}_{r}) \end{aligned}$$

(66)

and the time derivative of ${f}_{r}$ in (10) is calculated as:

$$\begin{aligned} \dot{f}_{r}&= \sum _{i=1}^{I} \dot{\rho }_{ri} \varPsi _{ri}(z)\nonumber \\&\quad +\sum _{i=1}^{I} \rho _{ri} \left( -\frac{1}{2} \dot{a}_{ri} a_{ri}^{-1} |a_{ri}|^{-\frac{1}{2}} (1-z_{ri}^2) e^{-\frac{z_{ri}^2}{2}} \right) \nonumber \\&\quad + \rho _{ri} \left( |a_{ri}|^{-\frac{1}{2}}\left[ -2\dot{z}_{ri}z_{ri} e^{-\frac{z_{ri}^2}{2}} - \dot{z}_{ri}z_{ri} e^{-\frac{z_{ri}^2}{2}} (1-z_{ri}^2) \right] \right) \end{aligned}$$

(67)

$$\begin{aligned} \dot{f}_{r}&= \sum _{i=1}^{I} \dot{\rho }_{ri} \varPsi _{ri}(z) + \sum _{i=1}^{I} \rho _{ri} (-\frac{1}{2} \dot{a}_{ri} a_{ri}^{-1}) \varPsi _{ri}(z) \nonumber \\&\quad - \sum _{i=1}^{I} \rho _{ri} \dot{z}_{ri}z_{ri} \left[ 2 \frac{\varPsi _{ri}(z)}{1-z_{ri}^2} + \varPsi _{ri}(z) \right] \nonumber \\&= \sum _{i=1}^{I} \dot{\rho }_{ri} \varPsi _{ri}(z) + \sum _{i=1}^{I} \rho _{ri} \varPsi _{ri}(z) \nonumber \\&\quad \left( -\frac{1}{2} \dot{a}_{ri} a_{ri}^{-1} - \dot{z}_{ri}z_{ri}\left( \frac{2}{1-z_{ri}^2} +1\right) \right) \nonumber \\&= \sum _{i=1}^{I} \dot{\rho }_{ri} \varPsi _{ri}(z) + \sum _{i=1}^{I} \rho _{ri} \varPsi _{ri}(z) \nonumber \\&\quad \left( -\frac{1}{2} \dot{a}_{ri} a_{ri}^{-1} - \dot{z}_{ri}z_{ri} \left( \frac{3-z_{ri}^2}{1-z_{ri}^2}\right) \right) \nonumber \\&= \sum _{i=1}^{I} \dot{\rho }_{ri} \varPsi _{ri}(z) + \sum _{i=1}^{I} \rho _{ri}\varPsi _{ri}(z) \left( -\frac{1}{2} \dot{a}_{ri} a_{ri}^{-1} \right. \nonumber \\&\quad -\left. \left( \frac{\dot{x}_{i} - \dot{b}_{ri}}{a_{ri}} - \dot{a}_{ri} \frac{x_i-b_{ri}}{a_{ri}^2}\right) z_{ri} \left( \frac{3-z_{ri}^2}{1-z_{ri}^2}\right) \right) \end{aligned}$$

(68)

$$\begin{aligned} \dot{f}_{r} &= \sum _{i=1}^{I} \dot{\rho }_{ri} \varPsi _{ri}(z) + \sum _{i=1}^{I} \rho _{ri} \varPsi _{ri}(z) \nonumber \\&\quad \left( \dot{a}_{ri} \left( -\frac{1}{2} a_{ri}^{-1} +\frac{x_i-b_{ri}}{a_{ri}^2} \frac{3-z_{ri}^2}{1-z_{ri}^2}z_{ri} \right) \right) \nonumber \\&\quad -\sum _{i=1}^{I} \rho _{ri} \varPsi _{ri}(z) \left( \frac{\dot{x}_i}{a_{ri}} \frac{3-z_{ri}^2}{1-z_{ri}^2} z_{ri} + \frac{\dot{b}_{ri}}{a_{ri}} z_{ri} \left( \frac{3-z_{ri}^2}{1-z_{ri}^2}\right) \right) \end{aligned}$$

(69)

so $\dot{y}_N$ in (66) changes as follows:

$$\begin{aligned} \dot{y}_N&= - \alpha \text{sgn}(e) + \sum _{r=1}^{N} \sum _{i=1}^{I} \dot{\rho }_{ri} \varPsi _{ri}(z) \nonumber \\&\quad + \sum _{i=1}^{I} \rho _{ri}\varPsi _{ri}(z) \left( \dot{a}_{ri} \left( -\frac{1}{2} a_{ri}^{-1} +\frac{x_i-b_{ri}}{a_{ri}^2} \frac{3-z_{ri}^2}{1-z_{ri}^2}z_{ri} \right) \right. \nonumber \\&\quad -\left. \frac{\dot{x}_i}{a_{ri}} \frac{3-z_{ri}^2}{1-z_{ri}^2} z_{ri} + \frac{\dot{b}_{ri}}{a_{ri}} z_{ri} \left( \frac{3-z_{ri}^2}{1-z_{ri}^2}\right) \right) \nonumber \\&\quad \left( q\underline{\tilde{w}}_{r} + (1-q)\tilde{\overline{w}}_{r}\right) \end{aligned}$$

(70)

substituting $\dot{y}_N$ (70) and then $\dot{a}_{ri}$, $\dot{b}_{ri}$ and $\dot{\rho }_{ri}$ according to (24) to (26) into the time derivative of Lyapunov function (62):

$$\begin{aligned} \dot{V}&= -|e|(3IN+1)\alpha +e \left[ \sum _{r=1}^{N}\left[ \sum _{i=1}^{I} \rho _{ri} \left( -\varPsi _{ri}(z) \frac{\dot{x}_i}{a_{ri}} \right. \right. \right. \nonumber \\&\quad \left. \left. \left. \frac{3-z_{ri}^2}{1-z_{ri}^2} z_{ri}\right) \left( q\underline{\tilde{w}}_{r} + (1-q)\tilde{\overline{w}}_{r}\right) \right] -\dot{y} \right] \nonumber \\&\quad + \frac{1}{\gamma }\dot{\alpha }\left( \alpha -\alpha ^{*} \right) \nonumber \\ \dot{V}&< -|e|(3IN+1)\alpha +|e| \left[ \sum _{r=1}^{N}\left[ \sum _{i=1}^{I} B_{\rho } \right. \right. \nonumber \\&\quad \left. \left( -B_{\psi } \frac{B_{\dot{x}}}{a_{ri}} \left| \frac{3-z_{ri}^2}{1-z_{ri}^2} \right| |z_{ri}|\right) (q\underline{\tilde{w}}_{r} + (1-q)\tilde{\overline{w}}_{r}) \right] \nonumber \\&\quad \left. -B_{\dot{y}} \right] + \frac{1}{\gamma }\dot{\alpha }\left( \alpha -\alpha ^{*} \right) \nonumber \\&< -|e|(3IN+1)\alpha +|e| \left( N I B_{\rho } B_{\psi } B_{\dot{x}} B_{a} - B_{\dot{y}} \right) \nonumber \\&\quad +\frac{1}{\gamma }\dot{\alpha }\left( \alpha -\alpha ^{*} \right) \end{aligned}$$

(71)

where, $\alpha ^{*} \ge \frac{( N I B_{\rho } B_{\psi } B_{\dot{x}} B_{a} -B_{\dot{y}})}{(3NI+1)}$ which is regarded as an unknown parameter and is determined during the tuning of learning rate. Thus,

$$\begin{aligned} \dot{V}&\le -|e|(3IN+1) \alpha +|e| \left( N I B_{\rho } B_{\psi } B_{\dot{x}} B_{a} - B_{\dot{y}} \right) \nonumber \\&\quad + |e|(3IN+1) \alpha ^* -|e|(3IN+1) \alpha ^* + \frac{1}{\gamma }\dot{\alpha }\left( \alpha -\alpha ^{*} \right) \nonumber \\&\le |e| \left( N I B_{\rho } B_{\psi } B_{\dot{x}} B_{a} -B_{\dot{y}} \right) - |e|(3IN+1)\alpha ^{*}\nonumber \\&\quad -(\alpha -\alpha ^{*}) \left( (3IN+1)|e| - \frac{1}{\gamma }\dot{\alpha } \right) \end{aligned}$$

(72)

the adaptive learning rate $(\alpha )$ changes as follows:

$$\begin{aligned} \dot{\alpha } =(3IN+1) \gamma |e|-\nu \gamma \alpha \end{aligned}$$

(73)

in which $\nu$ has small real value. The time derivative of Lyapunov function (72) is changed as follow:

$$\begin{aligned} \dot{V}&\le |e| \left[ N I B_{\rho } B_{\psi } B_{\dot{x}} B_{a} -B_{\dot{y}} \right] \nonumber \\&\quad - |e|(3IN+1) \alpha ^{*}-(\alpha -\alpha ^{*}) \nu \alpha \nonumber \\&\le |e| \left[ N I B_{\rho } B_{\psi } B_{\dot{x}} B_{a} -B_{\dot{y}} \right] \nonumber \\&\quad - |e|(3IN+1) \alpha ^{*} - \nu \left( \alpha - \frac{\alpha ^*}{2}\right) ^2 + \frac{\nu \alpha ^{*2}}{4} \end{aligned}$$

(74)

since $\alpha ^{*} \ge \frac{( N I B_{\rho } B_{\psi } B_{\dot{x}} B_{a} -B_{\dot{y}})}{(3NI+1)}$

$$\begin{aligned} |e| \left( N I B_{\rho } B_{\psi } B_{\dot{x}} B_{a} -B_{\dot{y}} \right) -|e|(3IN+1) \left( \frac{\alpha ^*}{2}\right) \le 0 \end{aligned}$$

(75)

consequently,

$$\begin{aligned} \dot{V} \le - \left( \frac{\alpha ^*}{2}\right) (3IN+1) |e| + \frac{\nu \alpha ^{*2}}{4} \end{aligned}$$

(76)

In this case in order to have a negative definite time derivative of the Lyapunov function, it is required that the following condition holds.

$$\begin{aligned} |e| \le \frac{\alpha ^* \nu }{2(3IN+1)} \end{aligned}$$

(77)

Hence, it is concluded that error converges to a small neighborhood of zero, in which and stays there. Furthermore, the radius of this neighborhood can be made as small as desired using appropriate values for $\alpha ^*$ and $\nu$. This concludes the proof.