Characterisation of B type hydraulic jump by experimental simulation and numerical modeling using MacCormack technique

Abstract

A hydraulic jump occurs when the supercritical flow transforms into subcritical nature along with the dissipation of energy. It occurs on a variety of horizontal and inclined channels. In this study, two types of jumps were classified, namely the B types that occur partially in the sloping and partially in the horizontal level of plane sections and the plane types that are typical hydraulic jumps occurring on beds with continuous slopes or horizontal beds. Froude numbers at inlet ranged from 2 to 6 for the study and tests were performed at four different angles for B-type jumps. The profiles of the jumps and streamwise flow velocities at different sections of the jumps were determined. From these data, the nature of the rate of decay of stream wise velocity across the jumps was established for both B and plane jumps. To validate the experimental results, numerical simulation was done for both B and plane jumps using the de-Saint Venant hyperbolic equations as governing equations and an explicit scheme MacCormack technique for the second-order accuracy of time and space. A source code was written in Fortran language using the G-Fortran compiler to numerically determine post-jump profiles. Using the appropriate initial boundary conditions, accurate simulated profiles of the jumps were obtained by it. The numerically simulated jump profiles were compared with experimentally obtained jump profiles in current and previous research studies and were found to be consistent. Based on the accuracy achieved, a combined empirical relation was proposed to determine jump profiles that operate both plane and B jumps.

Introduction

The phenomenon hydraulic jump is the flow transition from supercritical to subcritical positions with an increase in depth of water and dissipation of energy. Hydraulic jumps have several applications which include the dissipation of energy at the spillway-reservoir junction to avoid downstream scour, prevent flooding, mixing of chemicals in water, and its aeration in the city’s water supplies, and also to remove air packs from the water supply. In this regard, we need to determine certain characteristics and conditions governing the jump, such as the jump length, jump profile, and jump location, the amount of dissipated energy for designing hydraulic structures. Significance depends on the decay rate of maximum instantaneous velocity along with the flow as it shifts from supercritical to subcritical nature.

In the early days, extensive exploratory research was conducted and several empirical relations were established to institute the theory of plane jump. The first experimental study was conducted by Bidone (1818). Thereafter extensive laboratory research was done to determine the plane jump characteristics throughout the last century (Belanger 1828; Ellms 1932; Bakhmetef and Matzke 1936; Kindsvater 1944; Rouse 1950; Silvester 1964; Rajaratnam 1968; Garg and Sharma 1971; Leutheusser and Kartha 1972; Sarma and Newnham 1973; Andersen 1978; Peterka 1984; Hager 1985; Li 1995; Molls and Chaudhry 1995; Gunal and Narayanan 1996; Gotoh et al. 2005; Dey and Sarkar 2006; Chakraborty et al. 2014; Das et al. 2014; Palermo and Pagliara 2018; Arjenaki and Sanayei 2020).

An in-depth study of jumps on inclined channels was carried out where the conditions of B-type and D-type jumps were evaluated (Ohtsu and Yasuda 1991). Also, two-dimensional velocity fields were observed with a B jump at 30° sloping (Kawagoshi and Hager 1990). The work on oblique jumps was further progressed (Adam et al. 1993) by introducing sequent-depth proportion (H) (Beirami and Chamani 2006). Using previous experimental data, the accuracy of existing empirical relationships was assessed for what was used to measure the H value of the B jumps (Shokrian and Shafai Bejestan 2013). Analysis of magnitude and partial self-regulation was used and proposed an effective correlation of the successive depth of hydraulic jumps over horizontal smooth and rough beds (Carollo et al. 2009). The B jumps experiments were performed at 8.5, 17.5, and 30 degrees (Carollo et al. 2011). An effort has been made to verify all aspects (especially the turbulent features) of the pre-jump and post-jump regions of jumps (Chakraborty et al. 2014). Subsequent jump experiments were conducted using a 72.68° slopping, with sidewall, trapezoidal channel (Cherhabil and Debabeche 2016). Other experimental studies focused solely on developing equations empirically to determine the H ratio independent of the jump length (Carollo et al. 2011; Bejestan and Shokrian 2014).

But with the advent of modern digital computers and advanced computer conversion techniques, computational fluid dynamics methods are now being applied to numerically simulate the jump profile and characteristics by solving the governing equations of flow numerically. To numerically determine jump locations, the jump profiles were computed, and the jumps are formed at locations where the key specific forces on both pre-jump and post-jump sides are alike (Chow 1959). A finite-difference approach was used for numerically solving the de-Saint Venant’s partial-differential equations (Basco 1983; MacCowan 1985; Chaudhry 1993; Roohi et al. 2020) and obtaining the flow profile (Abbot et al. 1969).

The strip-integral technique was employed for computing the jump lengths, jump profiles, and developing pressures near the bed (McCorquodale and Khalifa 1983). Subsequently, a finite-element method was applied for computing the jump lengths (Katopodes 1984; Chippada et al. 1994). Three distinct explicit techniques, namely MacCormack, Lambda, and Gabutti, were used to numerically simulate open-channel unsteady shocks or bores (Fennema and Chaudhry 1990). Computational methods were proposed for the solution of 2-D equations applicable for shallow water in supercritical steady flow (Jimenez and Chaudhry 1988). Boussinesq equations were compiled for simulating the profile of hydraulic jump on horizontal beds using the MacCormack technique and two-four schemes (Gharangik and Chaudhry 1991). Subsequently, several types of research were conducted for numerical simulations on plane hydraulic jumps (Terrence 1994; Javan and Eghbalzadeh 2013; Mortazavi et al. 2016; Valero et al. 2019; Hafnaoui and Debabeche 2020; Mirzaei and Tootoonchi 2020). The MacCormack process was recently used to determine hydraulic jump profiles at slopes 0°, 1.25°, and 2.5° (Nandi et al. 2020).

It is clear from the literature that nearly no other studies regarding the simulation of the hydraulic jumps were conducted other than Gharangik and Chaudhry (1991) and Nandi et al. (2020) in which simulations were performed with plane hydraulic jumps on horizontal level beds and very low sloping beds (0°–2.5°).

This paper aims to study the decay rate of stream wise flow velocity for hydraulic jumps inclined beds (B type) with much higher sloping angles ranging from 8.5° to 25.7° and simultaneously in plane beds. It then compares the experimental profiles obtained of both oblique B types and plane jumps with their numerically simulated profiles obtained in current and previous studies. Simultaneously, numerical simulations have been done by applying the de-Saint Venant’s quasi-linear hyperbolic equations as governing equations and using an explicit technique called the MacCormack technique with an accuracy of the second order for time and space. A source code of the simulation is written in the Fortran language using the GNU-Fortran or GFortran compiler in code blocks ide (integrated development environment). Using the appropriate initial boundary conditions, simulated profiles of the B and plane jumps were obtained by it. The numerically simulated jump profiles were compared with experimentally obtained jump profiles of current and previous research studies. It is considered whether they agree well or not. Finally, a new correlation was proposed between the jump length, pre-jump supercritical depth, post-jump subcritical depth, bottom slope, and inlet Froude number.

Theory

The phenomenon of unsteady flow like hydraulic jump forming in sloping channels are frequently modeled as a 1-D flow that is expressed by quasi-linear-type equations of hyperbolic nature with partial differences, acknowledged as popularly de-Saint Venant hyperbolic Eqs. (1, 2). The 1-D de-Saint Venant partial-differential-type hyperbolic equations are:

$$ {\text{Continuity}}:\,\frac{\partial h}{{\partial t}} + u\frac{\partial h}{{\partial x}} + h\frac{\partial u}{{\partial x}} = 0 $$

(1)

$$ {\text{Momentum}}:\,u\frac{\partial h}{{\partial t}} + t\frac{\partial u}{{\partial t}} + \frac{\partial }{\partial x}\left( {\frac{1}{2}gh^{2} + hu^{2} } \right) = gh\left( {S - S_{e} } \right) $$

(2)

where h symbolises channel transition flow-depth (instantaneous), t symbolises operating time, u stands for instantaneous velocity towards flow that is x-direction, x is distance changing towards the parallel of channel bottom (taken positive towards downstream direction), g is gravity induced acceleration, S_e is the slope of grade line of energy and S is bed slope. Equation (3) of Manning is applied to determine friction slope S_e.

$$ S_{e} = \frac{{M_{n}^{2} u\left| u \right|}}{{C_{f}^{2} R^{\frac{4}{3}} }} $$

(3)

where M_n is coefficient for roughness identified by Manning, 2R is hydraulic diameter, C_f is correction factor; in SI units C_f = 1; and in English units C_f = 1.49. In the conservation and vector form, the equations can be written as in Eq. (4).

$$ \frac{{\partial \Upsilon_{1} }}{\partial t} + \frac{{\partial \Upsilon_{2} }}{\partial x} = B $$

(4)

in which $\Upsilon_{1} = \left[ {\begin{array}{*{20}c} h \\ {uh} \\ \end{array} } \right]\,\Upsilon_{2} = \left[ {\begin{array}{*{20}c} {uh} \\ {hu^{2} + \frac{1}{2}gh^{2} } \\ \end{array} } \right]\,B = \left[ {\begin{array}{*{20}c} 0 \\ {gh(S - S_{e} )} \\ \end{array} } \right]$.

Here, $\Upsilon_{1}$ is the function of u, h; $\Upsilon_{2}$, and B are the functions of $\Upsilon_{1}$. The product of the transition depth h, and transition velocity u symbolizes the x-direction flow.

Numerical simulation

For solving the 1-D de-Saint Venant hyperbolic equations, an explicit technique called the MacCormack technique was used. This method was developed by MacCormack (1969) and is a predictor–corrector technique with two steps (Anderson et al. 1984). In predictor steps, forward difference schemes are well used for spatial derivatives (Eq. 5) while in corrector steps, rearward difference schemes are judiciously applied for the same (Eq. 6). Referring to Fig. 1, the finite-difference Eqs. (5, 6) can be expressed as given in the Predictor Step.

$$ \frac{{\partial \Upsilon_{k} }}{\partial t} = \frac{{\Upsilon_{ki}^{*} - \Upsilon_{ki}^{n} }}{\Delta t} $$

(5)

$$ \frac{{\partial \Upsilon_{k} }}{\partial x} = \frac{{\Upsilon_{ki + 1}^{n} - \Upsilon_{ki}^{n} }}{\Delta x} $$

(6)

Fig. 1

Configuration of the finite-difference grid for experiments

where $\Upsilon_{k}$ is a function of u, h; subscript k = 1 or 2; asterisks refer to the predicted value of variables; i is indicating node for x-direction; ∆t is the minimum spacing between two consecutive time steps; n is indicating node for time direction, and ∆x is the minimum spatial gap between two consecutive grids.

With the help of the above finite-difference steps, we can obtain the predicted values of $h_{i}^{*}$ and $u_{i}^{*} h_{i}^{*}$ from Eqs. (7) and (8):

$$ h_{i}^{*} = h_{i}^{n} - \frac{\Delta t}{{\Delta x}}\left( {u_{i + 1}^{n} h_{i + 1}^{n} - u{}_{i}^{n} h_{i}^{n} } \right) $$

(7)

$$ u_{i}^{*} h_{i}^{*} = u_{i}^{n} h_{i}^{n} - \frac{\Delta t}{{\Delta x}}\left[ {\left\{ {\left( {u_{i + 1}^{n} } \right)^{2} h_{i + 1}^{n} + \frac{g}{2}\left( {h_{i + 1}^{n} } \right)^{2} } \right\} - \left\{ {\left( {u_{i}^{n} } \right)^{2} h_{i}^{n} + \frac{g}{2}\left( {h_{i}^{n} } \right)^{2} } \right\}} \right] + \frac{\Delta t}{2}gh_{i}^{n} \left( {S - S_{e} } \right)_{i}^{n} $$

(8)

From the Eqs. (3, 5, 6), given above, Eqs. (9, 10, 11) have been developed.

$$ S_{ei}^{n} = \frac{{M_{n}^{2} \left( {u_{i}^{n} } \right)^{2} }}{{C_{f}^{2} \left( {h_{i}^{n} } \right)^{\frac{4}{3}} }} $$

(9)

Corrector steps are shown by Eqs. (10, 11) for the variables $\Upsilon_{1}$ and $\Upsilon_{2}$.

$$ \frac{{\partial \Upsilon_{k} }}{\partial t} = \frac{{\Upsilon_{ki}^{n + 1} - \Upsilon_{ki}^{*} }}{\Delta t} $$

(10)

$$ \frac{{\partial \Upsilon_{k} }}{\partial x} = \frac{{\Upsilon_{ki}^{*} - \Upsilon_{ki - 1}^{*} }}{\Delta x} $$

(11)

where subscript k = 1 or 2. Based on the above two Eqs. (10 and 11), we can obtain the value of $h_{i}^{**}$ and $u_{i}^{**} h_{i}^{**}$ from Eqs. (12) and (13).

$$ h_{i}^{**} = h_{i}^{*} - \frac{\Delta t}{{\Delta x}}(u_{i}^{*} h_{i}^{*} - u{}_{i - 1}^{*} h_{i - 1}^{*} ) $$

(12)

$$ u_{i}^{**} h_{i}^{**} = \, u_{i}^{*} h_{i}^{*} - \frac{\Delta t}{{\Delta x}}\left[ {\left\{ {\left( {u_{i}^{*} } \right)^{2} h_{i}^{*} + \frac{g}{2}\left( {h_{i}^{*} } \right)^{2} } \right\} - \left\{ {\left( {u_{i - 1}^{*} } \right)^{2} h_{i - 1}^{*} + \frac{g}{2}\left( {h_{i - 1}^{*} } \right)^{2} } \right\}} \right] + \frac{\Delta t}{2}gh_{i}^{*} \left( {S - S_{e} } \right)_{i}^{*} $$

(13)

In the above Eq. (13), $S_{ei}^{n}$ is given by Eq. (14).

$$ S_{ei}^{*} = \frac{{M_{n}^{2} \left( {u_{i}^{*} } \right)^{2} }}{{C_{f}^{2} \left( {h_{i}^{*} } \right)^{\frac{4}{3}} }} $$

(14)

Finally, the values of velocity u_iⁿ⁺¹ and depth h_iⁿ⁺¹ at the next grid level of time n + 1 are obtained from corrected values of the same using Eqs. (15) and (16), respectively.

$$ h_{i}^{n + 1} = \frac{1}{2}\left( {h_{i}^{**} + h_{i}^{n} } \right) $$

(15)

$$ u_{i}^{n + 1} h_{i}^{n + 1} = \frac{1}{2}\left( {u_{i}^{**} h_{i}^{**} + u_{i}^{n} h_{i}^{n} } \right) $$

(16)

It should be noted that the entire flow channel is subdivided into N reaches equal to flow wise grid spacing ∆x. The upstream-most end grids are numbered 1 for each simulation and subsequently, downstream end grids are numbered N + 1. The initial along with boundary conditions are given as follows:

At the initial condition, the flow coming into the whole channel is considered as in a supercritical regime. The initial conditions at different sections of the stream are computed by numerically solving the GVF Eq. (17).

$$ \frac{dh}{{dx}} = \frac{{\left( {S - S_{e} } \right)}}{{1 - \alpha \frac{{u^{2} }}{gh}}} $$

(17)

where the energy correction factor α is conceded unity as the entire flume cross section remains constant. The upstream height h_u and velocity u_u of supercritical water remain unchanged starting from initial conditions. Then, the downstream height h_d is mentioned and the downstream velocity u_d is thereby calculated applying characteristic Eq. (18).

$$ u_{i + 1}^{n + 1} = u_{i}^{n} - \left( {\frac{g}{{u_{w} }}} \right)_{i}^{n} \left( {h_{i + 1}^{n + 1} - h_{i}^{n} } \right) + u_{i}^{n} g\Delta t\left( {S - S_{e} } \right)_{i}^{n} $$

(18)

where the celerity of the wave $u_{w}$ is given as $\sqrt {gh}$ (Gharangik and Chaudhry 1991). The MacCormack technique is found stable if following popular Courant (C), Friedrich, and Lewy (CFL) criterion (Eq. 19) is satisfied.

$$ \Delta t = C\frac{\Delta x}{{{\text{maximum of }}(\left| u \right| + \sqrt {gh} )}} $$

(19)

wherein C is Courant’s number which is set ≤ 1 for using the MacCormack technique. In this study, C = (2/3). To smooth out high-frequency oscillatory movements, artificial viscosity is added by the method shown by Jameson et al. (1981) in Eqs. (20, 21, 22).

$$ \varepsilon_{i}^{n} = \frac{{\left| {\left( h \right)_{{_{i + 1} }}^{n} - 2\left( h \right)_{{_{i} }}^{n} + \left( h \right)_{{_{i - 1} }}^{n} } \right|}}{{\left| {\left( h \right)_{{_{i + 1} }}^{n} } \right| + 2\left| {\left( h \right)_{{_{i} }}^{n} } \right| + \left| {\left( h \right)_{{_{i - 1} }}^{n} } \right|}} $$

(20)

$$ \varepsilon_{{_{{i + \frac{1}{2}}} }}^{n} = \kappa \frac{\Delta x}{{\Delta t}}{\text{max}}\left( {\varepsilon_{{_{i + 1} }}^{n} ,\varepsilon_{{_{i} }}^{n} } \right) $$

(21)

in which the dissipative term or artificial viscosity term κ is employed for regulating the measure of dissipation. Here, the terms ε_iⁿ, ε_i+(1/2)ⁿ, and ε_i+1ⁿ are the round-off errors at the close, open and close grids [i,n], [(i + ½), n], and [i + 1,n], respectively. The target was to smoothen the profiles by minimizing the round-off errors, thereby stabilizing the finite-difference MacCormack technique. In this study, after trial-and-error application, the value of κ is set equal to 3/100. Then, variables for computation like h, u, etc. are then adjusted using Eq. (22).

$$ \Upsilon_{ki}^{n + 1} = \Upsilon_{ki}^{n + 1} + \varepsilon_{{i + \frac{1}{2}}} \left( {\Upsilon_{ki + 1}^{n + 1} - \Upsilon_{ki}^{n + 1} } \right) - \varepsilon_{{i - \frac{1}{2}}} \left( {\Upsilon_{ki}^{n + 1} - \Upsilon_{ki - 1}^{n + 1} } \right)\,{\text{where}}\,k = \, 1 \, or \, 2 $$

(22)

A source code for simulation, shown in Appendix, is written based on Eqs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 in Fortran language using GNU-Fortran or GFortran compiler in code blocks ide (integrated development environment) for numerically determining the locations, profiles, and velocities of the post jump. Using proper initial boundary conditions, simulated profiles of the jumps were obtained accurately by it.

Experimental work

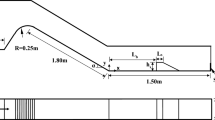
The plane and B-type jump laboratory experiments performed out in a 5.0 m long rectangular sloping facilitated Perspex made flume of 0.355 m wide internally and 0.450 m high (refer to Fig. 2). The discharge to be measured was monitored by a digital-type flow metering device. The sloping flume employed herein is equipped with a tailgate for controlling the desired inflow or pre-jump depth. This tailgate then was adjusted to control the jump location. The depths of water in both the upstream and downstream sections were accurately measured by a Vernier pointed gauge having 0.1 cm precision. There were incessant undulations observed in the flume water level located at the post-jump section of B type and plane jump. The average water depths (half of the maximum plus minimum) at a section downstream of jump were considered as the depth at that particular section. Pitot tubes were used to study the streamwise flow velocity at different sections of the flow especially during transitions and from these data.

Fig. 2

Experimental flume setup for θ = 17.6°

Two different types of flow set-up were arranged: (a) for B-type hydraulic jumps and (b) for plane hydraulic jumps. To set up B-type hydraulic jump, four different slopes were arranged, namely θ = 8.5°, 12.8°, 17.6° (Refer to Fig. 2), and 25.7°. The upstream section of the flume was given the abovementioned slopes using a broad crested weir and a ramp constructed with the perspex sheet and made watertight with silicone sealant. The remaining downstream portion of the flume was kept horizontal. In this way, the hydraulic jumps were partly developed on the oblique platform and partially on the horizontal segment of the flume, thereby forming B-type hydraulic jump (Refer to Fig. 3). In this way, 13 different laboratory experiments for B-type hydraulic jumps were set up having Froude numbers ranging from 2 to 3 (Refer to Fig. 4 and Table 1). The pre-jump Froude number (F_r1) at inlet section for inclined jumps is calculated by the following Eq. (23) of Ohtsu and Yasuda (1991):

$$ F_{r1} = \frac{{u_{u} }}{{\sqrt {gh_{1} \cos \theta } }} $$

(23)

Fig. 3

A 2-D schematic illustration of experimental setup for B-type jumps

Fig. 4

Views of plane jumps and B-type jumps captured during experimentation

Table 1 Details about the experimental conditions

θ = slope of sloping portion of channel; u_u = average velocity at supercritical flow condition and h₁ = supercritical depth normal to bed.

To set up a plane hydraulic jump, three conditions were used. In one case, the bed was kept completely horizontal that is at zero slopes. In the other two cases, the entire flume was given a slope of 2.3° and 3.4°, respectively. In total, six different experiments were set up for plane jumps having Froude numbers varying between 4 and 6.

In the current study, velocity measurements are carried out at regular intervals along the channel with the help of an L type of glass pitot tube. At a section velocity, measurements are approximately taken at the midpoint of the section and a depth of 40 percent of total depth for B-type jumps and a depth of 60% of total depth for plane hydraulic jumps.

Results and discussion

Having obtained the experimental results, we proceeded to analyze them to develop useful trends and relationships. For the velocity characteristics study, we use the measured sectional velocities to develop the nature of the decay curve of streamwise flow velocity during the transition. We again obtained the velocity profiles by performing numerical simulations applying the de-Saint Venant quasi-linear equations as governing equations and using an explicit technique called the MacCormack technique with an accuracy of the second order for time and space. A source code for simulation, shown in Appendix, is written in Fortran language using GNU-Fortran or GFortran compiler in code blocks ide (integrated development environment). Using proper initial boundary conditions, simulated profiles of the jumps were obtained by it. We further compare the experimental and numerical profiles of both oblique and plane hydraulic jumps and see that they are in good agreement. Using dimensional and regression analysis, we obtained an empirical relationship for numerically predicting experimental sequent–depth ratios (H) in the case of B jumps.

The decay rate of flow velocity

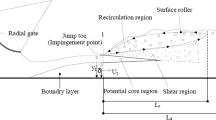
Velocity characteristic studies carried out for B jumps having slopes 17.6° and 25.7° are shown in Figs. 5a–d, 6a–d. Velocity studies are also made for plane hydraulic jumps having slopes equal to 0, 2.3° (throughout), and 3.3° (throughout). In the following graphs, Figs. 5, 6, u/u_u (ratio of velocity measured at each section to initial velocity upstream) are plotted against x/h_u (ratio of horizontal distance along with the flow to supercritical flow depth). The scale of ordinates is intentionally kept much larger than the scale of abscissa to show the decay rate of flow velocity with better representation.

Fig. 5

Velocity decay rate for a θ = 17.6°, F_r1 (Froude number) = 2.3, H (Sequent depth ratio) = 7.61; b θ = 17.6°, F_r1 = 2.3, H = 8.69; c for θ = 25.7°, F_r1 = 2.1, H = 8.4; and d θ = 25.7°, F_r1 = 2.2, H = 6.31

Fig. 6

Velocity decay rate for a θ = 0°, F_r1 = 4.3, H = 6.83; b θ = 3.4° (throughout), F_r1 = 4.8, H = 13.91; c θ = 3.4° (throughout), F_r1 = 6, H = 10.75; and d θ = 2.3° (throughout), F_r1 = 5.3, H = 12.47

As shown in Fig. 5a–d, B-type hydraulic jump carried out at θ = 17.6° and θ = 25.7°, Froude number (F_r1) = 2.3, 2.2, and 2.1 sequent-depth ratio (h_d/h_u = H) = 7.61, 8.69, 8.4 and 6.31. There are also two dashed lines, in graphs, one of which denotes the section at which jump toe is located and another which denotes the section at which the junction between the sloping part of the channel and horizontal part of the channel occurred. In some cases, we see a change in the nature of the curves. For θ = 25.7°; F_r1 = 2.1, H = 8.4; and F_r1 = 2.2, H = 6.31 the jumps occur early compared to the jumps at θ = 17.6°. It confirms bed slope has a significant role in changing the post-jump location. Again for θ = 25.7°, energy dissipation is more and post-jump depths are less compared to the energy dissipation and post-jump depths for θ = 17.6°. It means post-jump velocity increases with the increase of bed slope θ.

For the plane jumps, velocity studies were carried out which shows that plane jumps having horizontal beds, namely zero slopes, have concave decay trends while those having a bed slope all throughout have convex decay trends. In the following graphs (Fig. 6a–d), u/u_u (ratio of velocity measured at each section to initial velocity upstream) is plotted against x/h_u (ratio of horizontal distance along with the flow to supercritical flow depth). There is a dashed line which denotes the section at which jump toe is located. Figure 6 confirms that plane jump lengths also gradually increase with the continuing increase of inlet Froude number F_r1. Here, u/u_u decreases with the increase of x/h_u. Figure 6 also confirms that both F_r1 and θ control the change of x/h_u.

Numerical modeling

The numerical model developed herein is of second-order precision [(∆x)²]. The de-Saint Venant’s hyperbolic equations are then worked out using the MacCormack technique. The minimum grid spacing size for the time step was confined using the stability state (Warming and Hyett 1974) of Courant and the minimum spatial grid-gap as well. Courant (C) value was set 0.65 since most excellent outcomes are achieved when the C value is ~ 2/3. For smoothing the curvature of oscillations of high frequency near B and plane jumps, the dissipation factor κ as in Jameson's approach was then computed using the trial-and-error application when κ is around 3/100.

For the numerical model run, the inflow or pre-jump depth h_u and upstream velocity u_u and only the post jump or outflow depth h_d are identified. The upstream or pre-jump velocity u_u for trial runs was calculated using continuity equation, discharge Q = bh_uu_u, where b is internal flume width. The inflow or pre-jump Froude number F_r1 is found out from Eq. (24).

$$ F_{r1} = {{u_{u} } \mathord{\left/ {\vphantom {{u_{u} } {\sqrt {gh_{u} } }}} \right. \kern-\nulldelimiterspace} {\sqrt {gh_{u} } }} $$

(24)

The type of jump that is B or plane, slope S or tanθ, upstream measured depth h_u, upstream velocity u_u, upstream Froude number F_r1, inflow Reynolds number Re_u and downstream measured depth h_d in non-dimensional form for all different experimental runs are displayed below in Table 1. For all trial runs, Manning coefficient (M_n) was found using the trial-and-error application and fixed at 0.010–0.015 for B-type jumps and 0.014–0.012 for plane jumps. The inlet Reynolds number (Re_u) was maintained ~ 1 × 10⁵ to ~ 1.07 × 10⁵ for the B jump and ~ 1.77 × 10⁵ to ~ 2.46 × 10⁵ for the plane jump.

The spatial grid size ∆x is a very important parameter. More so, as according to the CFL condition, the time step size ∆t is limited and controlled by it. Trials were computed with ∆x values ranging from 0.05 to 0.28. For engineering applications, it is seen that using a judicious value of ∆x, satisfactory simulation and modeling can be obtained. After observations, ∆x value of 0.1 is selected as herein the plane and oblique hydraulic jumps are formed at more than four computational grid points.

Comparison of numerical and experimental jump profiles

When the numerical findings are converged into a steady-state approach the immediate depths at subsequent points of grids are obtained that presents the jump flow profile. The numerical data are compared with the experimentally obtained flow profile. Figure 7a–k presents a comparative observation between experimental results and numerical results for flows at varying inflow or pre-jump Froude number and varying slopes for both B-type and plane hydraulic jumps. Along with these, the real-life experiment pictures are also provided both in plane view and top view. The total depth h_t (= h_e + h) of flow non-dimensionlised by h_u is plotted non-dimensionally in the vertical axis whereas distance x non-dimensionlised by h_u is the distance along the flume, plotted in abscissa where h is an instantaneous depth of water from the sloping ramp and h_e is the elevation of jump toe section from the bed.

Fig. 7

Jump profile for a F_r1 = 2.1 and slope = 8.5°; b F_r1 = 2 and slope = 12.8; c F_r1 = 2.1 and slope = 12.8°; d F = 2.3 and slope = 17.6°; e F_r1 = 2.3 and slope = 17.6°; f F_r1 = 2 and slope = 17.6°; g F_r1 = 2.3 and slope = 17.6°; h F_r1 = 2.3 and slope = 17.6°; i F_r1 = 2 and slope = 17.6°; j F_r1 = 2.1 and slope = 25.7°; k F_r1 = 2 and slope = 25.7°; l F_r1 = 2.2 and slope = 25.7°; m F_r1 = 2.4 and slope = 25.7°; n F_r1 = 5.3 and slope = 2.3° (throughout); o Jump profile for F_r1 = 4 and slope = 0° (throughout); p F_r1 = 4.3 and slope = 0° (throughout) q F_r1 = 4.8 and slope = 3.4° (throughout); r F_r1 = 6 and slope = 0° (throughout); and s F_r1 = 5.3 and slope = 2.3° (throughout)

In the case of the B-type jumps, the inclined bed of flume is plotted in the centre line. The jump profile from experimental data is plotted in dashed lines and that from simulated data in solid lines. For plane hydraulic jumps, the jump profile from experimental data is plotted in dashed lines and that from simulated data in solid lines.

In Fig. 8, experimental and numerical jump lengths (L) are non-dimensionlised by upstream jump height (h_d) for both plane and B jump. Plotted points are shown in the blue circle in Fig. 8. These are almost clustered around the 1:1 line. The overall dimensionless jump length comparison shown in Fig. 8 depicts the divergence of the non-dimensional jump locations determined numerically [L/h_u (simulated)], using the MacCormack technique on the de-Saint Venant’s hyperbolic equations, from the gauged locations [L/h_u (measured)] is within ± 15%.

Fig. 8

Comparison between experimentally obtained and numerically formed non-dimensional jump locations

The experimental and numerically modeled data obtained from current study are judged with the previous results obtained from Nandi et al. (2020) where experiments were conducted for the very lower slopes of 1.25° and 2.5° and F_r1 2.17 to 7.00. It is observed that almost 90% of the data of Nandi et al. (2020) are also falling nicely within the ± 15% range. It further strengthens the aptness of using the MacCormack technique for analyzing sloping channels.

However, the accuracy would be more if bed roughness is taken care of and separate graphs are plotted for both plane jump and B jump. For sloping channels, it has been tested and confirmed that the MacCormack technique gives a better result than the two-four scheme.

Empirical solution for jump length

Either to determine jump length or H value, an empirical type relationship is created between the major parameters which determine the jump locations using dimensional analysis and self-similarity theory. From this empirical equation, the results here obtained are critically compared with computed numerical results.

For dimensional analysis, it is considered that only dependent variable L that is the spacing between the commencement of location of plane and oblique B jumps to the end location of plane and oblique B jumps that is jump length is dependent on the subsequent independent variables: flow density ρ, the pre-jump supercritical depth h_u, the downstream or tail water or post-jump depth h_d at channel end, the upstream or pre-jump velocity u_u, bottom slope S, a parameter G [= (h_t—h_e)/h_d] and the gravity acceleration g for determining the effect of simultaneous variations of head and tailwater levels.

$$ f(L,\rho ,h_{u} ,h_{d} ,u_{u} ,g,S,G) = 0 $$

(25)

Using Buckingham π theorem and dimensional analysis.

$\pi_{1} = L/h_{u}$, $\pi_{2} = h_{d} /h_{u} = H$, $\pi_{3} = u_{u} /\sqrt {gh_{u} }$, $\pi_{4} = S$ and $\pi_{5} = G$. These terms of π are sensibly arranged in non dimensional form given in Eq. (26).

$$ f\left( {\frac{L}{{h_{u} }},\frac{{h_{d} }}{{h_{u} }},\frac{{u_{u} }}{{\sqrt {gh_{u} } }},S,G} \right) = 0 $$

(26)

Finally completing the analysis, the following empirical relation is obtained:

$$ L/h_{u} = \frac{{e^{x} H^{6.6} S^{7.2} G^{34} }}{{F_{r1}^{15.6} }} $$

(27)

where e = exponential, x is a coefficient whose range changes from 39.5 to 47.5 with the change of slope. Equation (27) is used to predict the locations of the hydraulic jumps of B types. The non-dimensional predicted values [L/h_u (empirical) using Eq. 27] were judged with the non-dimensional simulated values [L/h_u (simulated) using MacCormack technique] of B jump to verify the soundness of Eq. (27). Therefore, some of the experimental results collected from previous researches (Peterka 1984; Carollo et al. 2011; Nandi et al. 2020) are compared with the results of the present study. Non-dimensional L/h_u values were determined from the researches Peterka (1984) for slopes 1.25–1.5° and F_r1 3.35–5.9; from Carollo et al. (2011) for slopes 8.5° and 17.5° and F_r1 1.12 to 6.29 and Nandi et al. (2020) for slopes 1.25° and 2.5° and F_r1 2.17 to 7.00. The evaluation between the non-dimensional predicted jump length and observed jump length values corroborates very good conformity with ± 85% accuracy as exemplified in Fig. 9. When data of previous experiments are considered for comparison, then this correlation is found within ± 75% accuracy and this is fair enough. Therefore, Eq. (27) provides good conformity for slopes ranging from 1.25° to 17.5° with F_r1 ranging from 1.12 to 7.00.

Fig. 9

Comparison between the dimensionless numerical (simulated) and empirical results

Though Eq. (27) may not furnish very good results for other experimental outcomes since Eq. (27) is developed using a 19 number of runs, however, this is a part where further effort can be made for establishing a better empirical correlation linking the parameters of sloping hydraulic jump. The performance may be improved further if bed roughness is considered along with smaller space and time grid resolutions and a more accurate Courant number.

Summary and conclusion

In this current study, the plane and B jump experiments were conducted at slope angles ranging from 8.5 to 25.7 degrees. The nature of the streamwise decay of flow velocity was established in B-type jumps at slopes equal to 17.6 and 25.7 degrees. The pre-jump Froude’s numbers ranged from 2 to 3 for the B jump. Plane hydraulic jumps were set up at slopes equal to 0 to 3.4 degrees. Here, the decay rate of streamwise velocity was also established for the pre-jump Froude numbers ranged from 4 to 6.

The 1-D de-Saint Venant’s hyperbolic equations for sloping channels were numerically solved by simulating the B and plane hydraulic jumps. Then, starting with properly computed initial states, the de-Saint Venant’s hyperbolic equations were worked out subjected to right boundary conditions until a stable condition form is obtained. For modeling the simulation, MacCormack’s leading process with precision second-order of time grids and space grids has been newly introduced for B-type hydraulic jump. The source code for the numerical simulation and modeling of jump length, post-jump length, and post-jump velocity, illustrated in Appendix, is newly written in the Fortran language using GNU-Fortran or GFortran compiler. Since higher-order approaches with oscillations of high frequency have been generated near hydraulic jumps, so these fluctuations were flattened by applying artificial viscosity term during the modeling.

The experimentally obtained profiles are compared with the numerically simulated and modeled profiles for both present and previous studies. It appears that typically simulated jump locations are formed upstream of the experimentally obtained jump locations. In the case of type B jumps, satisfactory agreements are reached between the experimentally observed and numerically modeled profiles. In general, an increase in the depth of transition from subcritical state to supercritical state occurs at a faster rate in the simulated profiles. In the case of plane jumps, the numerically modeled profiles show good compatibility with those obtained by testing except in the case of a 3.4 degrees sloping.

Depending on the numerically modeled jump locations, a comprehensive dimensionless empirical equation is determined that relates the location of the jump with its key parameters. This empirical equitation has validated 75–85% of the results of three previous pieces of research on B-type jumps for non-zero slopes ranging from 1.25° to 25.7° along with pre-jump Froude numbers ranging from 2 to 7. The work demonstrates the method of further research on sloping channels using the de-Saint Venant’s hyperbolic quasi-linear equations and selecting the appropriate CFD methods as the MacCormack technique.

Appendix: Source code for simulation

Code availability