Efficiency-Wage Competition: What Happens as the Number of Players Increases?

Abstract

In this paper, I explore the consequences of extending the number of firms within an efficiency-wage competition setting by showing that the shape of the effort function is crucial in determining key features of the economy. Specifically, when workers are endowed with a concave (sigmoid) effort function, the wage behaviour of firms follows a collusive (competitive) pattern and the symmetric Nash equilibrium is unstable (stable). Moreover, when effort is concave (sigmoid), full employment is characterized by a labour exploitation that increases (decreases) together with the number of productive units required to sustain that allocation. These findings may have intriguing implications for the existence of involuntary unemployment as well as for policies aimed at increasing employment.

1 Introduction

Some versions of the efficiency-wage theory grounded on adverse-selection recognize that firms may stand in a situation comparable to monopsony in the labour market, in the sense that employers might be able to set employment as well as their wage offer aiming at maximizing profits (e.g. Solow 1979). As argued by a number of scholars, however, in that theoretical setting a special kind of competition could hold instead among productive firms (cf. Hahn 1987; Summers 1988; van de Klundert 1989; Jellal and Wolff 2003). Specifically, even if the labour market experiences a persistent excess of supply, it can happen that firms will avoid wage cuts not only because this would lower their profitability, but also because lower wages would enhance the productivity of their output competitors. In previous works, such a strategic relationship for the optimal wage behaviour of firms has been dubbed as efficiency-wage competition, i.e., a situation in which the profit-maximizing wage bid of a given productive unit depends on the wage bids put forward by all the other firms operating in the economy (cf. Guerrazzi 2013; Guerrazzi and Sodini 2018).

The existing literature on efficiency-wage competition focuses only on 2-firm—or 2-sector—economies and until now nothing has been said about the consequences triggered by an increase in the number of players. In this paper, I aim at filling that gap by exploring what happens in that theoretical framework as the number of competing firms increases. In detail, drawing on Guerrazzi (2013), I study the optimal wage behaviour of firms when all the productive units find profitable to bid and pay the same wage and there are no labour-supply constraints so that some individuals might actually experience involuntary unemployment. Moreover, I analyse the dynamic behaviour of wages in the neighbourhood of the symmetric Nash equilibrium and I explore the features of the full employment allocation.

The findings of this theoretical exploration reveal that the actual shape of the effort function is crucial in determining key features of the model economy. In this regard, the efficiency-wage literature usually has exploited two distinct analytical formulations for the link between wages and workers’ productivity, i.e., sigmoid and concave effort functions (cf. Stiglitz 1973, 1976; Hahn 1987). As I will show below, the choice of one specific formulation leads to completely different outcomes with respect to the other option. Specifically, when workers are endowed with a concave (sigmoid) effort function, the wage behaviour of firms follows a collusive (competitive) pattern. Moreover, assuming that firms adjust their current wage bid on the basis of the lagged bids put forward by their competitors, the adoption of a concave (sigmoid) effort function implies that the symmetric Nash equilibrium is locally unstable (stable) and the speed of divergence (convergence) is an increasing function of the number of productive units engaged in the efficiency-wage competition process. Furthermore, with a concave (sigmoid) effort function, the full employment of workers that are willing to work at the prevailing wage is characterized by a degree of labour exploitation that increases (decreases) together with the number of firms required to sustain that allocation.

Considering efficiency-wage economies with adverse selection, the theoretical findings outlined above may provide some guidance in assessing what type of effort function is the best alternative for a certain economy. At the same time, these results may have intriguing implications for the existence and persistence of involuntary unemployment and for the implementation of policies aimed at increasing the level of employment.

This paper is arranged as follows. Section 2 reviews some of the related literature. Section 3 introduces the theoretical framework. Section 4 explores how wages, effort, employment and profits prevailing in a symmetric Nash equilibrium depend on the number of competing firms. Section 5 analyses the dynamics of wages in the neighbourhood of the Nash equilibrium. Section 6 addresses the issue of labour exploitation when there is no involuntary unemployment. Finally, Sect. 7 concludes by offering some theoretical and policy implications for fighting unemployment in efficiency-wage economies.

2 Related Literature

This paper aims at building a bridge between the wide literature on efficiency wages and the one on wage competition by analysing the effects driven by an extension of the number of firms operating in the economy. The starting points are the seminal papers by Hahn (1987) and Summers (1988). In the former, we find the first attempt to frame the strategic issues underlying a two-firm efficiency-wage economy à la Solow (1979) in which workers’ effort depends positively (negatively) on the internal (external) wage offer of each producer. In the latter, a very similar theoretical framework is used to explore the fragility of equilibria, i.e., the strong sensitivity of equilibrium (un)employment to changes in the parameters of the model, under the hypothesis that workers’ effort depends on relative wages.

Drawing on similar ideas, van de Klundert (1989) and Jellal and Wolff (2003) develop two distinct models with a dual labour market in which firms operating in the primary sector of the economy set efficiency wages whereas in the secondary sector wages are set competitively. In these frameworks, the interaction between the two sectors is established by an effort function in which the wages prevailing in the primary (secondary) sector enter with a positive (negative) sign.

The theoretical contributions recalled above are mainly interested in demonstrating the possibility of an equilibrium with involuntary unemployment and the persistence of wage differentials across the different sectors of the economy. The strategic implications of the wage setting behaviour of firms as well as the consequences triggered by an increase in the number of players, however, remain completely on the background (cf. Guerrazzi 2013; Guerrazzi and Sodini 2018). Although it did not reach any clear conclusion, these important aspects of the wage setting process have been somehow addressed by the most recent literature on wage competition.

On the one side, Bhasker and To (1999) develop a monopsonistic wage-competition model where optimal wage bids are strategic complements and the symmetric wage-strategy prevailing in the Nash equilibrium is a decreasing function of the number of competing firms, a feature that is acknowledged also by the wage-competition model with heterogenous agents set forth by Hamilton et al. (2000). The intuition behind these results is that in a non-Walrasian labour market employers can easily collude with each other with the aim of getting favourable conditions regarding wages. On the other side, that view is challenged by Fiorillo et al. (2000) who develop an oligopsonistic wage-competition model in which the equilibrium wage increases together with the number of productive units. In this framework, labour market frictions work in favour of employed workers so that when the number of employers increases, the competition process triggered to hire the best available workers put upward pressure on wages.

In this paper, confirming the intuitions put forward by Summers (1988), I show that in an efficiency-wage economy populated by many firms in which internal wage offers enter the production possibilities in a labour-augmenting way whereas external offers do exactly the opposite, optimal wage bids are always strategic complements (cf. Guerrazzi 2013). By contrast, the effects on the equilibrium levels of the wage, employment and profit driven by an increase of the number of firms are strictly related to the path of the wage measured in efficiency units. The analysis developed below reveals that the behaviour of such a critical indicator mirrors the actual cost of labour borne by firms and deeply relies on actual shape of the effort function taken into consideration.

3 Theoretical Framework

I consider an efficiency-wage economy in which there are N—with $N\geqslant 2$—identical firms indexed by i that compete with each other to hire high-quality workers. As in Solow (1979), each firm realizes that there is a positive relation between the wage that it pays and the efficiency of recruited workers so that the screening of the available labour force occurs through increasing wage bids. Assuming asymmetric information between firms and workers, such a positive link can be seen as the reflection of the increasing function between workers’ ability and their acceptance wage usually observed by employers who hire applicants from a labour pool under adverse selection conditions (cf. Weiss 1991).

On the output side, following Guerrazzi and Sodini (2018) and Guerrazzi (2013), I assume that each productive unit—no matters the size of N—is endowed with the following production function:

$$\begin{aligned} Y_{i}=A\left( e_{i}\left( \cdot \right) L_{i}\right) ^{\alpha } \ \ \ \ \ \ \ \ \ \ A>0\text {, }0<\alpha <1 \end{aligned}$$

(1)

where $Y_{i}$ is the output of the i-th firm, A is a measure of its total factor productivity, $e_{i}\left( \cdot \right)$ is the effort provided by the single worker hired by the i-th firm, $L_{i}$ is the number of hired workers, whereas $\alpha$ is the curvature of the production function.¹

In the remainder of the paper, I will assume that the production technology described by Eq. (1) is freely accessible to all the firms that decide to enter the market for goods and total output produced in the economy $(NY_{i})$ is always totally sold. The consequences implied by the existence of constraints in the access to the production technology and the effects of deficiencies in effective demand will be briefly addressed in the final section of the manuscript.

The representative firm hires workers in a spot labour market where workers have homogenous preferences over effort provision. In this regard, let $w_{S}\left( LF\right)$—with $\partial w_{S}/\partial LF>0$—be the (invertible) aggregate Marshallian labour supply, where LF denotes the number of workers that are willing to work in the economy provided that $w_{S}\left( \cdot \right)$ is paid. In other words, when all the competing firms find profitable to pay a wage equal to $\overline{w}$, $LF(\overline{w})$ workers are actually willing to work. Consequently, given the wage prevailing in the economy, whenever $LF\left( \overline{w}\right)$ is higher (lower) than the aggregate demand for labour $\left( NL_{i}\right)$, the labour market experiences an excess supply (demand). By contrast, whenever $LF\left( \overline{w}\right)$ is equal to $NL_{i}$, there is full employment since the $LF(\overline{w})$ workers that are willing to work are actually pro quota employed by the N competing firms. For the sake of simplicity, I will assume that the reservation wage is equal to zero so that $w_{S}\left( 0\right) =0$. That hypothesis makes sure that when firms bid a positive wage even labour supply is positive so that some workers are actually willing to provide their labour services.

According to Eq. (1), the productive input of each worker hired by the representative firm is given by $e_{i}(\cdot )$. Such an expression—usually called effort function—conveys in an explicit and continuous manner the link between the efficiency of the employed workforce and the wages paid by competing firms. As stated in the introduction, a special feature of this paper is that I will take into consideration two distinct well-behaved analytical alternatives that have been widely exploited in the theoretical applications of the efficiency-wage theory. On the one hand, extending the expressions in Hahn (1987) and Guerrazzi (2013), I consider a concave specification given by

$$\begin{aligned} e_{i}=\left( \kappa +w_{i}- {\textstyle \sum \limits _{j\ne i}^{N-1}} w_{j}\right) ^{\beta } \ \ \ \ \ \ \ \ \ \ \kappa >0\text {, }0<\beta <1 \end{aligned}$$

(2)

where $\kappa$ is an independent component of effort, $w_{i}$ is the internal wage paid the i-th firm, $w_{j}$ is the external wage paid by a generic opponent of the i-th firm indexed with $j\ne i$, whereas $\beta$ is the curvature of the effort function.²

Recognizing that energy requirements of employed workers—as measured by consumed calories—are given by an exponential combination of their effort and their body mass, Dalgaard and Strulik (2011) show that a concave effort function can be derived from physiological principles. In addition, as argued by Wu and Ho (2012), an effort function like the one in Eq. (2) implies the existence of a positive firm-specific minimum-wage defined as $w_{i}^{\min }\equiv {\textstyle \sum \nolimits _{j\ne i}^{N-1}} w_{j}-\kappa$ below which effort provision is equal to zero. Obviously, this means that $\kappa < {\textstyle \sum \nolimits _{j\ne i}^{N-1}} w_{j}$. Consequently, in this framework, the parameter $\kappa$ counterweights the sum of external wage opportunities in order to yield the wage-floor above which the individual worker employed by the i-th firm find profitable to providing a positive level of effort. Since I assumed that the reservation wage is equal to zero, it is worth noting that as long as $w_{i}$ is positive but lower than $w_{i}^{\min }$, some workers will be actually willing to offer their labour services by participating to labour market activities. Eq. (2), however, implies that these workers—when employed by the representative firm—will find profitable to shirk instead of providing effort by revealing themselves as unproductive (cf. Shapiro and Stiglitz 1984; Bulow and Summers 1986).

On the other hand, drawing on Stiglitz (1973, 1976), I consider also the sigmoid—or s-shaped—specification of effort. In an efficiency-wage competition setting, a sigmoid effort function can be written as

$$\begin{aligned} e_{i}=\frac{w_{i}^{\gamma }}{ {\textstyle \sum \nolimits _{j\ne i}^{N-1}} w_{j}+w_{i}^{\gamma }} \ \ \ \ \ \ \ \ \ \gamma >1 \end{aligned}$$

(3)

where $\gamma$ is a parameter that measures the steepness of the effort function.³

The sigmoid effort function does not imply the existence of a minimum wage so that with such a specification labour supply goes hand in hand with effort provision. Moreover, when $w_{i}$ is equal to $w_{i}^{\inf }\equiv \left( \left( \gamma -1\right) {\textstyle \sum \nolimits _{j\ne i}^{N-1}} w_{j}\right) ^{1/\gamma }$, the function in Eq. (3) has an inflection point. In geometrical terms, this means that for values of $w_{i}$ between zero and $w_{i}^{\inf }$ the function in Eq. (3) is convex whereas for values of $w_{i}$ higher than $w_{i}^{\inf }$ the function is concave. This is the reason why such an effort function is dubbed as sigmoid. According to Stiglitz (1973), such a characterization can be rationalized on evolutionary terms. Specifically, the interval in which $w_{i}$ is between zero and $w_{i}^{\inf }$ denotes a region of starvation. Within this range, the internal wage offer of the representative firm is so low that additional increments in wage payments increase workers’ effort provision at increasing rates. Afterward, when $w_{i}$ is on the right of $w_{i}^{\inf }$, the wage is sufficiently high that workers are in the position to fully satisfy their primary needs. In the latter case, diminishing returns dominate so that additional wage increments increase effort provision at decreasing rates.

Consistently with Solow (1979), the effort functions in Eqs.  (2) and (3) describe an efficiency-wage economy in which each firm tries to screen its applicants by exploiting its current wage bid. Indeed, despite the different shapes, Eqs. (2) and (3) state that workers’ effort for the i-th firm is an increasing function of its own wage offer. Along the lines of the already mentioned efficiency-wage competition literature, however, I assume that—for each productive unit—attainable effort react to the sum of external wage opportunities. In other words, this means that $e_{i}\left( \cdot \right)$ is assumed to be a decreasing function of the wage offer individualistically put forward by each single opponent. The underlying hypothesis is that an improvement (a deterioration) of external wage opportunities may have a negative (positive) effect on internal morale and working effectiveness (cf. Hahn 1987; Summers 1988; van de Klundert, 1988; Jellal and Wolff 2003; Guerrazzi 2013; Guerrazzi and Sodini 2018). Strictly speaking, when the output competitors of firm i increase their wage offer, the i-th productive unit—unless it increases the wage paid to its employed workforce—is assumed to suffer a productivity drop.

According to Summers (1988), the expressions in Eqs. (2) and (3) should posit that individual effort depends upon the divergence between the internal wage and the average of the wage bids put forward by rival firms. The choice to rely on the sum rather than on the average can be rationalized as follows. First, the existence of cognitive limitations could prevent workers from calculating the average of the wage bids in a precise manner (cf. Choi et al. 2014). Moreover, the simplest option conveyed by Eqs. (2) and (3) is consistent with the literature on labour market coordination failures pioneered by Keynes (1936). This literature stresses that workers may have some concern for relative wages (e.g. Hoover 1995). Consequently, as the wage offer of a rival firm increases (decreases), workers may adjust their work intensity downward (upward) in the attempt to obtain a positive (negative) wage adjustment that preserves the original relative positions. To confirm that, Bulow and Summers (1986) argue that firms are usually extremely concerned with assessing where they stand in the wage distribution and this provide a rationale for the large number of available compensation surveys.⁴

Taking the wage distribution as given, the effort functions described above deliver information not only on how individual work intensity reacts to internal and external wage opportunities, but also on how workers’ productivity is affected by the number of competing firms. Specifically, the expressions in Eqs. (2) and (3) share the feature that in a symmetric wage equilibrium, i.e., when $w_{i}=\overline{w}>0$ for all $i=1,...,N$, effort for the individual firm—say $e\left( \overline{w}\right)$—is a decreasing function of the number of productive units operating in the economy. Technically speaking, in the concave and in the sigmoid case respectively, it is straightforward to derive that

$$\begin{aligned} e\left( \overline{w}\right)= & {} \left( \kappa -\left( N-2\right) \overline{w}\right) ^{\beta } \end{aligned}$$

(4)

$$\begin{aligned} e\left( \overline{w}\right)= & {} \frac{1}{1+\left( N-1\right) \overline{w}^{1-\gamma }} \end{aligned}$$

(5)

The economic rationale for the results in Eqs. (4) and (5) can be given by considering the possible effects on workers’ morale driven by the tightness of labour demand. In other words, the higher (lower) the number of firms in the economy, the higher (lower) the employment opportunities for the single worker. Consequently, everything else being equal, as the number of productive players increases (decreases), the individual effort for each firm will be lower (higher) since workers realize that they might have the chance to be employed (it might be difficult to find a job) in a different productive unit (cf. Kuang and Wang 2017; Masters 2016).

A similar negative relationship between $\overline{e}\left( \cdot \right)$ and N is also acknowledged by Lazear et al. (2016) who put forward the possibility that employers may be actively engaged in sorting workers. Specifically, during an expansion (recession), when the number of productive units tends to increase (decrease), new entering (remaining) firms may find profitable to employ less productive applicants that incumbent employers have avoided to hire (retain highly productive insiders and letting go the least productive). In this way, when the number of firms increases (decreases), the average efficiency of employed workers may actually fall (increase) as actually conveyed by Eqs. (4) and (5).⁵

Having regard to a symmetrical wage strategy, it becomes possible to grasp an important difference between the two effort functions in Eqs. (2) and (3), i.e., the implied differences in effort response to changes in internal and external wage offers. Indeed, with a concave effort function, the effort responses to variations in internal and external wage offers are symmetric. Specifically, Eq. (2) implies that

$$\begin{aligned} \left. \frac{\partial e_{i}}{\partial w_{i}}\right| _{w_{i}=w_{j\ne i}=\overline{w}}=-\left. \frac{\partial e_{i}}{\partial w_{j\ne i} }\right| _{w_{i}=w_{j\ne i}=\overline{w}}=\beta \left( \kappa -\left( N-2\right) \overline{w}\right) ^{\beta -1} \end{aligned}$$

(6)

The result in (6) suggests that a concave effort function may be suitable for workers employed in firms that operate in homogenous industries or for workers that are subject to negligible mobility costs (cf. Gruetter and Lalive 2009).

By contrast, with a sigmoid effort function, the effort responses to changes in internal and external wage offers are asymmetric. Specifically, the effort increase triggered by an increase in the internal wage offer is higher than the corresponding effort reduction—taken in modulus—induced by an increase of one external offer. Indeed, Eq. (3) implies that

$$\begin{aligned} \left. \frac{\partial e_{i}}{\partial w_{i}}\right| _{w_{i}=w_{j\ne i}=\overline{w}}=-\gamma \left( N-1\right) \left. \frac{\partial e_{i} }{\partial w_{j\ne i}}\right| _{w_{i}=w_{j\ne i}=\overline{w}} \end{aligned}$$

(7)

The result in (7) suggests that a sigmoid effort function may be suitable for workers who developed a strong attachment to their job—probably for the good working conditions prevailing in the industries where firms are operating—or for workers who are subject to non-negligible mobility costs (cf. Markey et al. 2012).

Before introducing the strategic apparatus developed in the remaining sections of the paper, it might be important to stress that in the version of the efficiency-wage theory exploited in this work monitoring and shirking problems are not directly addresses (cf. Shapiro and Stiglitz 1984). Strictly speaking, when the wage $\overline{w}$ is paid by all the N competing firms, the implied level of effort $e\left( \overline{w}\right)$ is actually provided by the $NL_{i}$ employed workers out of the $LF(\overline{w})$ that are willing to work. On a principal-agent perspective, this means that from the side of workers the relevant participation constraint is given by labour supply whereas solving Eqs. (2) and (3) with respect to the internal wage yields alternative and ever-binding incentive compatibility constraints according to which firms’ expectations of effort provision are always fulfilled.⁶ Consequently, taking into account the expressions in Eqs. (1)–(3), the problem of the representative firm can be written as

$$\begin{aligned} \begin{array} [c]{c} \underset{e_{i},L_{i}}{\max }\text { }\pi _{i}=A\left( e_{i}L_{i}\right) ^{\alpha }-w_{i}L_{i}\\ \text {s.to}\\ w_{i}=\left\{ \begin{array} [c]{c} w_{i}^{\min }+e_{i}^{^{\frac{1}{\beta }}} \ \ \ \ \ \ \ \ \ \text { when effort is concave}\\ \left( {\textstyle \sum \limits _{j\ne i}^{N-1}} w_{j}\right) ^{\frac{1}{\gamma }}\left( \frac{e_{i}}{1-e_{i}}\right) ^{\frac{1}{\gamma }} \ \ \text { when effort is sigmoid} \end{array} \right. \\ w_{i}\geqslant w_{S}\left( NL_{i}\right) \end{array} \end{aligned}$$

(8)

where $\pi _{i}$ is the profit of the i-th productive unit.

As I argued above, the problem in (8) shows that the representative firm maximizes its profits with respect to $e_{i}$ and $L_{i}$ by taking into account two distinct constraints. The former is the incentive compatibility constraint and depending on the shape of the effort function, it gives the wage that the firm has to pay in order to influence the individual efficiency of employed workers. The latter is the participation constraint and it states that—given the number of firms—the pair $(w_{i}\left( e_{i}\right) ,L_{i})$ chosen by each employer must lead workers to offer the required amount of labour services. Such a constraint is binding in the full employment allocation whereas it holds as inequality when the labour market experiences an excess supply.

Echoing some arguments put forward in the literature on malfeasance and enforcement, the incentive compatibility constraints implied by Eqs. (2) and (3) provide a compensation scheme with two components: one related to outside opportunities and the other related to workers’ performance (cf. Becker and Stigler 1974). Specifically, in the concave case, the incentive compatibility constraint states that the firm has to pay a wage that is given by a mark-up over the minimum wage implied by Eq. (2) whereas the aforementioned mark-up is described by a convex increasing function of effort provision defined in the closed interval $[0,+\infty ]$. Furthermore, in the sigmoid case defined by Eq. (3), the incentive compatibility constraint reveals that the firm has to pay a wage equal to a geometrical average between the sum of external wage bids and a convex increasing function of effort provision defined in the open internal [0, 1).

When the participation constraint is not binding so that workers are out of their labour supply, the solution of the problem in (8) allow us to derive the reaction functions expressed in terms of the internal wage offer for the single firm that holds, respectively, in the concave and in the sigmoid case. As I show in Appendix, in formal terms we have

$$\begin{aligned} w_{i}= & {} \frac{1}{1-\beta }\left( {\textstyle \sum \nolimits _{j\ne i}^{N-1}} w_{j}-\kappa \right) \end{aligned}$$

(9)

$$\begin{aligned} w_{i}= & {} \left( \left( \gamma -1\right) {\textstyle \sum \nolimits _{j\ne i}^{N-1}} w_{j}\right) ^{\frac{1}{\gamma }} \end{aligned}$$

(10)

The two expressions in Eqs. (9) and (10) reveal that—for each firm—optimal wage bids are strategic complements no matter the shape of the effort function. In other words, with a concave or a sigmoid effort function, whenever one of the opponent raises (lowers) its wage bid, it is in the best interest of each competing firm to raise (lower) its bid as well.⁷ According to Summers (1988), this feature is a key aspect of any wage theory in which there is a concern for relative wages.

4 Wages, Effort, Employment and Profits in a Symmetric Nash Equilibrium

In the model economy described in Sect. 2, a symmetric Nash equilibrium can be defined as a situation in which all the competing firms find profitable to bid and pay the same wage so that, alternatively, the expressions in Eqs. (9) and (10) simultaneously holds for all the N productive units. As maintained by Guerrazzi (2013) and Guerrazzi and Sodini (2018), this means that the elasticity of the relevant effort function (incentive compatibility) with respect to the internal wage (effort) is equal to one for all the firms. In other words, in the symmetric Nash equilibrium the Solow condition is valid in a generalized manner throughout the economy (cf. Solow 1979). In this section, I will show that whenever employers are not constrained by labour supply and all the firms have access to the same production technology with no deficiencies in effective demand, the shape of the effort function is very important in assessing how the number of firms operating in the economy influences the equilibrium allocation. The implications of a binding labour supply are instead discussed in Sect. 6.

Without any loss of generality, I start by making the hypothesis that effort has the concave shape outlined in Eq. (2). In that case, assume that $w^{*}$ is the common value of the wage paid by all the competing firms. Consequently, the reaction function in Eq. (9) implies that

$$\begin{aligned} w^{*}=\frac{\left( N-1\right) w^{*}-\kappa }{1-\beta } \end{aligned}$$

(11)

Solving Eq. (11) for $w^{*}$ allows us to write the wage prevailing in a symmetric Nash equilibrium for each individual firm as a function of the number of competing firms and the parameters of the effort function. Formally speaking, Eq. (11) implies that

$$\begin{aligned} w^{*}=\frac{\kappa }{N-2+\beta } \end{aligned}$$

(12)

Since I assumed that N is higher or equal to 2, the symmetric wage-strategy that holds when effort is concave is always characterized by a positive value of the equilibrium wage.

When all the firms find profitable to pay a wage equal to $w^{*}$, Eq. (2) implies that the effort supplied by each employed worker is equal to

$$\begin{aligned} e^{*}=\left( \kappa -\left( N-2\right) w^{*}\right) ^{\beta } \end{aligned}$$

(13)

Plugging the result in Eq. (12) into Eq. (13) leads to

$$\begin{aligned} e^{*}=\left( \frac{\beta \kappa }{N-2+\beta }\right) ^{\beta } \end{aligned}$$

(14)

The results in Eqs. (12) and (14) imply that in a symmetric Nash equilibrium the profit of the representative firm can be written as

$$\begin{aligned} \pi ^{*}=A\left( \left( \frac{\beta \kappa }{N-2+\beta }\right) ^{\beta }L^{*}\right) ^{\alpha }-\frac{\kappa }{N-2+\beta }L^{*} \end{aligned}$$

(15)

where $L^{*}$ is the equilibrium level of employment.

The first-order condition for $L^{*}$ is given by

$$\begin{aligned} \alpha A\left( \left( \frac{\beta \kappa }{N-2+\beta }\right) ^{\beta }L^{*}\right) ^{\alpha -1}\left( \frac{\beta \kappa }{N-2+\beta }\right) ^{\beta }-\frac{\kappa }{N-2+\beta }=0 \end{aligned}$$

(16)

Solving Eq. (16) for $L^{*}$ allows us to find the level of employment prevailing in a symmetric Nash equilibrium. Formally speaking, Eq. (16) implies that

$$\begin{aligned} L^{*}=\left( \alpha \beta ^{\alpha \beta }A\left( \left( \frac{\kappa }{N-2+\beta }\right) ^{-\left( 1-\alpha \beta \right) }\right) \right) ^{\frac{1}{1-\alpha }} \end{aligned}$$

(17)

Moreover, plugging Eq. (17) into Eq. (15), the equilibrium level of profits can be written as

$$\begin{aligned} \pi ^{*}=\left( 1-\alpha \right) \left( \alpha ^{\alpha }\beta ^{\alpha \beta }A\left( \frac{\kappa }{N-2+\beta }\right) ^{-\alpha \left( 1-\beta \right) }\right) ^{\frac{1}{1-\alpha }} \end{aligned}$$

(18)

To sum up the expressions in Eqs. (12), (14), (17) and (18) the wage, the effort, the level of employment and the profit prevailing in a symmetric Nash equilibrium for each individual firm when the effort function is concave are given by the elements of the following array:

$$\begin{aligned} \left( \begin{array} [c]{c} w^{*}\\ e^{*}\\ L^{*}\\ \pi ^{*} \end{array} \right) =\left( \begin{array} [c]{c} \Psi \left( N\right) \\ \left( \beta \Psi \left( N\right) \right) ^{\beta }\\ \left( \alpha \beta ^{\alpha \beta }A\left( \Psi \left( N\right) ^{-\left( 1-\alpha \beta \right) }\right) \right) ^{\frac{1}{1-\alpha }}\\ \left( 1-\alpha \right) \left( \alpha ^{\alpha }\beta ^{\alpha \beta } A\Psi \left( N\right) ^{-\alpha \left( 1-\beta \right) }\right) ^{\frac{1}{1-\alpha }} \end{array} \right) \end{aligned}$$

(19)

where $\Psi \left( N\right) \equiv \kappa {/}\left( N-2+\beta \right)$.

The expressions in (19) clearly show that when the effort function is concave a symmetric Nash equilibrium is characterized by the fact that the wage and worker’s effort (employment and profit) decrease (increase) together with the number of competing firms (cf. Bhasker and To 1999; Hamilton et al. 2000). In this case, interestingly, when N tends to infinity, $L^{*}$ and $\pi ^{*}$ tend to explode whereas labour becomes a free good for firms, i.e., the equilibrium wage tends to zero. Moreover, it is worth noting that with a concave effort function variations in the number of firms lead to a counter-cyclical effort pattern (cf. Guerrazzi 2008). Specifically, when the number of firms increases (decreases), aggregate labour demand increases (decreases) as well. Furthermore, the wage and the effort fall (increase) by leading to a reduction (contraction) of labour supply. The lower (higher) labour supply implies a reduction (rise) of involuntary unemployment.

The economic rationale for the results in (19) can be given as follows. When the effort function is concave, the wage per unit of effort is a decreasing function of the number of firms. Indeed, dividing the RHS of Eq. (12) by the RHS of Eq. (14), we easily derive that $w^{*}/e^{*}$ is equal to $\beta ^{-\beta }\left( \Psi \left( N\right) \right) ^{1-\beta }$. Therefore, as the number of opponents increases, each productive unit is able to buy effective labour at a lower unit cost and this allows the recruitment of a larger number of workers. Moreover, hiring more employees at a lower wage counterbalances the lower effort of workers by leading to higher profits. Consequently, when the effort function is concave, the equilibrium wage behaviour of competing firms follows a collusive pattern. In other words, when the number of productive units increases, the optimal wage behaviour of each firm leads to a generalized reduction of the wage per efficiency units paid by employers and this, in turn, provides a price signal that triggers the reduction of the wage bids put forward individualistically by the N competing firms.

Fixing $\alpha =\beta =0.5$ and $A=\kappa =1$, the patterns of wages, effort, employment and profits prevailing in a symmetric Nash equilibrium for different values of N are plotted in the four panels of Fig. 1.

Fig. 1

Wages, effort, employment and profits in a symmetric Nash equilibrium Concave effort function ($\alpha =\beta =0.5$, $A=\kappa =1$, $N=2,...,20$)

The diagrams in Fig. 1 show that under the suggested calibration the equilibrium wage as well as the equilibrium effort suffer a substantial reduction when the number of firms shifts from two to three. By contrast, the increases in equilibrium employment and equilibrium profits observed as N becomes bigger are quite smooth.

Following the same procedure implemented above, it is possible to show that when the effort function has the sigmoid shape outlined in Eq. (3) the quadruplet $\left( \begin{array} [c]{cccc} w^{*}&e^{*}&L^{*}&\pi ^{*} \end{array} \right)$ is given by

$$\begin{aligned} \left( \begin{array} [c]{c} w^{*}\\ e^{*}\\ L^{*}\\ \pi ^{*} \end{array} \right) =\left( \begin{array} [c]{c} \Omega \left( N\right) \\ \frac{\gamma -1}{\gamma }\\ \left( \frac{\alpha A}{\Omega \left( N\right) }\left( \frac{\gamma -1}{\gamma }\right) ^{1+\alpha }\right) ^{\frac{1}{1-\alpha }}\\ \frac{\left( 1-\alpha \right) \left( \alpha A\right) ^{\frac{1}{1-\alpha }} }{\alpha }\left( \frac{\gamma -1}{\gamma \Omega \left( N\right) }\right) ^{\frac{\alpha }{1-\alpha }} \end{array} \right) \end{aligned}$$

(20)

where $\Omega \left( N\right) \equiv \left( \left( N-1\right) \left( \gamma -1\right) \right) ^{1/\left( \gamma -1\right) }$.

The reaction functions in Eqs.  (9) and (10) revealed that the sign of the strategic relation among optimal wage bids is the same no matter the shape of the effort function. The results in (20), however, signal a regime change with respect to the findings summarized in (19). Specifically, when the effort function is sigmoid, a symmetric Nash equilibrium is characterized by the fact that the wage (employment and profits) increases (decrease) as the number of competing firm increases (cf. Fiorillo et al. 2000). By contrast, the number of productive units in the economy does not influence equilibrium workers’ effort and the implied expression for $e^{*}$ confirms that equilibrium labour effectiveness falls into the interval [0, 1). In addition, recalling that $N\geqslant 2$ and $\gamma >1$, the expression for $\Omega \left( N\right)$ shows that in the sigmoid case labour can never be a free good for firms. Eq. (10) actually reveals that with a sigmoid effort the reaction functions of firms are simultaneously verified even when all the productive units bid a wage equal to zero. Nevertheless, such an allocation is not a Nash equilibrium. Indeed, if all the firms but one offers a wage equal to zero, the productive unit that bids a positive wage obtains a positive effort and achieves positive profits (cf. Guerrazzi and Sodini 2018).

From an economic point of view, the findings in (20) can be rationalized as follows. As opposed to what happens with a concave effort function, in the sigmoid case the wage per unit of effort increases together with the number of firms. Indeed, according to the first and the second element in the array in (20), $w^{*}/e^{*}$ is equal to $\left( \gamma /\left( \gamma -1\right) \right) \Omega \left( N\right)$. Therefore, in this case each firm tries to overbid the others in the attempt to secure better workers for itself. When all the firms behave in this way, however, attainable effort for the single productive unit remains the same because the effort reduction triggered by the larger number of players is exactly counterbalanced by their higher wage offers. Consequently, when the effort function is sigmoid, the optimal wage setting behaviour of rival firms can be dubbed as genuinely competitive. In other words, an increase in the number of players is responsible for an increase of the wage per efficiency units and this, in turn, generates a price signal that leads competing firms to overbid each other in the vain attempt to increase the productive effectiveness of their employees. Obviously, such an overbidding process implies the already mentioned decreasing path of individual profits.

Setting $\gamma =2.5$, $\alpha =0.5$ and $A=1$, the patterns of wages, effort, employment and profits prevailing in a symmetric Nash equilibrium for different values of N are plotted in the four panels of Fig. 2.

Fig. 2

Wages, effort, employment and profits in a symmetric Nash equilibrium Sigmoid effort function ($\gamma =2.5$, $\alpha =0.5$, $A=1$, $N=2,...,20$)

The diagrams in Fig. 2 show that the equilibrium wage smoothly raises when the number of competing firms increases. By contrast, the level of equilibrium employment and equilibrium profits substantially drop when the number of firms shifts from two to three. Such a behaviour mirrors the downward jumps observed in the wage and in the effort as found in the concave case plotted in Fig. 1.

5 Wage Dynamics

Let us assume that the efficiency-wage competition game set forth in Sect. 2 is played as a dynamic Cournot output game in which each firm refines its beliefs about the behaviour of its competitors by observing their actual choices (cf. Theocharis 1960; Varian 1992). In the present context, this means that—in any given time period—each productive unit adjusts its wage bid by observing the wage paid by the other firms and conjecturing that external bids will remain unchanged until the next period (cf. Guerrazzi 2013; Guerrazzi and Sodini 2018). Depending on the shape of the effort function, and recalling the reaction functions in Eqs. (9) and (10), the evolution of wages over time will be alternatively described by

$$\begin{aligned} w_{i,t}=\frac{1}{1-\beta }\left( {\textstyle \sum \nolimits _{j\ne i}^{N-1}} w_{j,t-1}-\kappa \right) \end{aligned}$$

(21)

or

$$\begin{aligned} w_{i,t}=\left( \left( \gamma -1\right) {\textstyle \sum \limits _{j\ne i}^{N-1}} w_{j,t-1}\right) ^{\frac{1}{\gamma }} \end{aligned}$$

(22)

where $i=1,..,N$.

In the first case, i.e., when the effort function has a concave shape, the Jacobian matrix associated the to the linear dynamic system in (21) is given by a $N\times N$ matrix whose elements on the main diagonal are equal to zero whereas all the other elements are equal to $\left( 1-\beta \right) ^{-1}$. Such a coefficient corresponds to the constant value of $\partial w_{i,t}/\partial w_{j,t-1}$ retrieved for all the eligible $j\hbox {s}$. Consequently, the eigenvalues of such a matrix are given by the N elements of the following array:

$$\begin{aligned} \left( \begin{array} [c]{cccc} -\frac{1}{1-\beta }&\cdots&-\frac{1}{1-\beta }&\frac{N-1}{1-\beta } \end{array} \right) \end{aligned}$$

(23)

Since $0<\beta <1$ and $N\geqslant 2$, all the components of (23) are higher than one in modulus. Consequently, when the effort function is concave the symmetric Nash equilibrium is locally asymptotically unstable. In other words, whenever one of the firm bids a wage different from $w^{*}$, the system in (21) tends to explode in finite time.⁸ Moreover, the last element of the array in (23) reveal that the speed of explosion of individual wage bids is higher (lower), the higher (lower) the number of competing firms. Therefore, when the optimal wage behaviour of firms follows a collusive pattern and the efficiency-wage competition process is played as a game of alternate wage bids, an increase in the number of productive units is a further destabilizing feature for the model economy. This result somehow recalls the one on the fragility of equilibria highlighted by Summers (1988) in efficiency-wage economies with many firms concerned with relative wages. In the present context, the instability of the Nash equilibrium can be explained by the linear and more than proportional response of internal wage offers to changes in external bids implied by the reaction function in Eq. (9) implemented in the dynamic system in (21).

In the remaining case, i.e., when the effort function has a sigmoid shape, the Jacobian matrix associated to the non-linear dynamic system in (22) is given by a $N\times N$ matrix whose elements on the main diagonal are equal to zero whereas all the other elements are equal to $\left( \left( N-1\right) \gamma \right) ^{-1}$. Such a coefficient depends and the number of competing firms and corresponds to the analytical expression for $\partial w_{i,t}/\partial w_{j,t-1}$ evaluated for $w_{j,t-1}$ equal to $\Omega \left( N\right)$. Consequently, the eigenvalues of such a matrix are given by the N elements of the following array:

$$\begin{aligned} \left( \begin{array} [c]{cccc} -\frac{1}{\gamma \left( N-1\right) }&\cdots&-\frac{1}{\gamma \left( N-1\right) }&\frac{1}{\gamma } \end{array} \right) \end{aligned}$$

(24)

Given that $\gamma >1$ and $N\geqslant 2$, all the components of (24) are lower than one in modulus. Consequently, when the effort function is sigmoid the symmetric Nash equilibrium is locally asymptotically stable. This means that the wage bids put forward by all the competing firms tend to converge towards $w^{*}$ by steering the convergence of the others endogenous variables. Moreover, the first $N-1$ elements of the array in (24) reveal that the speed of convergence of individual wage bids is higher (lower), the higher (lower) the number of competing firms. Therefore, when the optimal wage behaviour of firms follows a competitive pattern, an increase in the number of productive units operating in the market for goods is a further stabilizing feature for the model economy. In this case, the analogy with fragility result highlighted by Summers (1988) does not apply because the reaction function in Eq. (10) implemented in the dynamic system in (22) implies a smoothed response of internal wage offers to changes in external bids.

6 Full Employment and Labour Exploitation

A straightforward implication of the analytical findings outlined in Sect. 4 is that the aggregate demand for labour prevailing in a symmetric Nash equilibrium $\left( NL^{*}\right)$ increases (decreases) with the number of competing firms when workers are endowed with a concave (sigmoid) effort function.

When labour supply is not binding, i.e., whenever $NL^{*}$ is lower than the aggregate supply of labour that holds when the equilibrium wage is equal to $w^{*}$, the model economy experiences some involuntary unemployment. In that case, none of the N profit-maximizing firms will accept to hire applicants that are willing to work for less than the equilibrium values of the wage offer alternatively conveyed by the first element of the arrays in (19) and (20). It can also happen, however, that labour supply is binding so that $NL^{*}$ coincides with the aggregate supply of labour that holds when the wage is equal to its equilibrium level so that the economy achieves full employment.⁹ In the latter case, taking the participation constraint as binding in the maximization problem formulated in (8), the results in (19) and (20) can be exploited to provide an interesting characterization of the full employment allocation that may prevail as a symmetric Nash equilibrium of the efficiency-wage economy described in Sect. 3.

Without any loss of generality, let us assume that there exists a sufficiently large value of N—say $N_{FE}\geqslant 2$—that guarantees the implementation of a full employment allocation as a symmetric Nash equilibrium, so that $LF\left( w^{*}\right) =N_{FE}L^{*}$, where $LF\left( \cdot \right)$ is the inverse of the aggregate labour supply defined in Sect. 3. In other words, taking into account the results in the first element of (19) and (20) , $N_{FE}$ has to alternatively verify one of the following expressions:

$$\begin{aligned}&\frac{\kappa }{N_{FE}-2+\beta }=w_{S}\left( N_{FE}L^{*}\right) \end{aligned}$$

(25)

$$\begin{aligned}&\left( \left( N_{FE}-1\right) \left( \gamma -1\right) \right) ^{\frac{1}{\gamma -1}}=w_{S}\left( N_{FE}L^{*}\right) \end{aligned}$$

(26)

Whenever Eqs. (25) or (26) hold, the model economy described in Sect. 3 rests in situation of symmetric Nash equilibrium that does not admit the possibility of involuntary unemployment. Indeed, all the workers that are willing to work at $w_{S}\left( N_{FE}L^{*}\right)$ are actually employed by the $N_{FE}$ competing firms so that the participation constraint in problem (8) holds as equality. In that situation, deriving the first-order condition for $L_{i}$ allows us to state that in a symmetric Nash equilibrium with full employment the value of $L^{*}$ in each productive unit has to be consistent with the following expression:

$$\begin{aligned} \Phi \left( L^{*}\right) \Gamma \left( L^{*}\right) =\frac{\partial w_{S}}{\partial LF}N_{FE}L^{*}+w_{S}\left( N_{FE}L^{*}\right) \ \ \ \ \ i=1,...,N_{FE} \end{aligned}$$

(27)

where $\Phi \left( L^{*}\right) \equiv \alpha A\left( e_{i}\left( w_{S}\left( N_{FE}L^{*}\right) \right) L^{*}\right) ^{-\left( 1-\alpha \right) }$ and $\Gamma \left( L^{*}\right) \equiv \left( \partial e_{i}/\partial w_{S}\right) ( \partial w_{S}/\partial LF) N_{FE}L^{*}+e_{i}\left( w_{S}\left( N_{FE}L^{*}\right) \right)$.

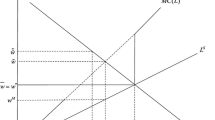
Eq. (27) is the individual labour demand function of the $N_{FE}$ firms that—as a whole—employ all the workers that are willing to work at $w_{S}\left( N_{FE}L^{*}\right)$. Such an expression is qualitatively similar to the corresponding condition that holds in a monopsonistic labour market in which labour is purchased only by one buyer and offered by many sellers (cf. Boal and Ransom 1997). In other words, Eq. (27) states that the marginal product of labour, i.e., the LHS of (27), must be equal to the marginal expenditure for labour, i.e., the RHS of (27). More precisely, on the LHS there is the marginal productivity of labour $\left( \Phi \left( L^{*}\right) \right)$ adjusted in order to consider the positive effect on production driven by a (marginal) wage increase $\left( \Gamma \left( L^{*}\right) \right)$ (cf. Lin 2015; Scapparone 2015). On the RHS there is instead the sum between the full employment wage offer $\left( w_{S}\left( N_{FE}L^{*}\right) \right)$ and a positive component related to fact the each firm realizes that it is operating along the relevant labour supply $\left( \left( \partial w_{S}/\partial LF\right) N_{FE}L^{*}\right)$. A graphical representation of the result conveyed by Eq. (27) is given in Fig. 3.

Fig. 3

Full employment and labour exploitation

The diagram in Fig. 3 shows that—for each value of $L_{i}$—the marginal expenditure for labour $\left( \left( \partial w_{S}/\partial LF\right) N_{FE}L_{i}+w_{S}\left( N_{FE}L_{i}\right) \right)$ is definitely higher than the offering wage $\left( w_{S}\left( N_{FE} L_{i}\right) \right)$. Consequently, when the model economy reaches a symmetric Nash equilibrium in which all the workers that are willing to work at the prevailing wage are actually employed, each competing firm finds itself in the position to pay the labour factor less than its marginal contribution to corporate revenues which are measured by the segment $\overline{OB}$. Analyzing monopsonistic markets, Robinson (1933) called that phenomenon exploitation of labour. By contrast, when the economy reaches a symmetric Nash equilibrium with involuntary unemployment there is no exploitation. In other words, when $NL^{*}<LF\left( w^{*}\right)$ or, equivalently, $w^{*}>w_{S}\left( NL^{*}\right)$, employers are on their labour demand but workers are out of their labour offer so that $\left( \partial w_{S}/\partial LF\right) N_{FE}L^{*}$ is equal to zero. Therefore, in the latter case, employed workers are paid according to their marginal contribution to corporate revenues (cf. Lin 2015; Scapparone 2015).

Recalling that labour supply is upward-sloped so that $\partial w_{S}/\partial LF>0$, the RHS of Eq. (27) reveals that in this setting the labour exploitation is an increasing function of $N_{FE}L^{*}$. Therefore, taking into account the results in the arrays in (19) and (20), it is possible to conclude that when the effort function is concave (sigmoid), the exploitation of labour carried out by each firm is—ceteris paribus—an increasing (decreasing) function of the number of productive units required to sustain the full employment allocation as a symmetric Nash equilibrium.¹⁰ If we think about it, the latter result is far from surprising. Indeed, when the wage behaviour of competing firms follows a collusive (competitive) pattern the exploitation of labour increases as the number of firms increases (decreases).

7 Concluding Remarks

In this paper, drawing on Guerrazzi (2013), I explore the consequences of extending the number of competing firms in an efficiency-wage competition setting by taking into account that workers’ effort can alternatively follow a concave or a sigmoid pattern with respect to the internal wage offer of each player (cf. Stiglitz 1973, 1976; Hahn 1987).

To the best of my knowledge, in the efficiency-wage literature there are no point estimations of the actual shape of effort functions. Therefore, the relation between labour effectiveness provided by workers and the wage paid by firms in the real world remains at least uncertain. Some indirect insights on the wage-effort relation can be derived, however, from contributions on nutritional efficiency-wages and product market deregulation. On the one hand, Powell and Murphy (2014) argue that the nutrition-based efficiency wage theory has been an important framework to explain unemployment persistence in poor countries. On the other hand, Ebell and Haefke (2003) show that in developed countries product market deregulation is usually associated with stronger flows of firms’ entry and increasing wages.

Combining these arguments with the theoretical analysis developed throughout the paper, it seems reasonable to associate the concave (sigmoid) effort specification to developing (developed) countries. In the former case, an efficiency-wage model grounded on the concave effort function in Eq. (2) for which Dalgaard and Strulik (2011) offered a physiological explanation might provide a rationale for the persistence of unemployment observed in poor countries (cf. Leibenstein 1957; Stiglitz 1976; Mirrlees 1976; Bliss and Stern 1978). Moreover, since the antitrust regulation is usually less stringent in these economies so that firms are likely to collude, it may also happen that increases in the number of productive units may actually lead to wage reductions (cf. Cook 2002). In the latter case, on the contrary, an efficiency-wage model in which workers are endowed with the sigmoid function of Eq. (3) where increases in the number of firms go together with increasing wages seems to corroborate the available empirical evidence on wage dynamics triggered by product market deregulation in richer countries (cf. Ebell and Haefke 2009).

The analytical findings resumed above may also have important implications for the theoretical apparatus developed in this paper. First, in an efficiency-wage economy like the one described in Sect. 3 the existence and persistence of involuntary unemployment cannot be attributed to the wage setting behaviour of firms in an unequivocal manner, but it can be seen as the consequence of the presence of a too limited or, alternatively, too higher number of competing firms. Consequently, when the effort function has a concave (sigmoid) specification, policies of deregulation (stricter regulation) of the product market aimed at increasing (reducing) the number of productive units in the economy may be well effective in reducing unemployment even without any intervention on the labour market. Strictly speaking, an increase (a reduction) in the number of firms may be able to generate a reduction of wages that would allow the expansion of the employed labour force and the reduction of labour supply. Obviously, when the effort function is concave (sigmoid) and the wage behaviour of firms is collusive (competitive)—in order to avoid the likely opposition of workers (firms)—the additional profits realized by firms (wage bill gained by new employees) should be used to make side payments to their additional employees (the remaining productive units).

The generality of the policy implications just stated deeply depends on the assumptions according to which firms have no limitation in accessing the production technology and demand constraints on the market for goods are missing. For instance, when the achievement of full employment requires the entering of new firms on the market and the access to the available production technology is somehow restricted—maybe for the existence of legally binding patents—the eradication of involuntary unemployment can actually become quite difficult (cf. Langinier 2004). Moreover, when a reduction of wages is associated to a parallel reduction of the aggregate demand for goods, the number of existing firms cannot be tuned in order to achieve full employment (cf. Setterfield 2010). Furthermore, the analysis developed throughout the paper deeply relies on the hypothesis that among workers and among productive firms there are no heterogeneities and this may put some limits in extending all the conclusions to the real economy (cf. Kirman 1992). For example, a pool of firms with different production functions and/or workers endowed with different effort functions may hinder the straightforward derivation of the monotonic relationships illustrated in Figs. 1 and 2. All the implied extensions are left to further developments.

Appendix: Derivation of the reaction functions

Without any loss of generality, assume that the effort function has a concave shape as conveyed by Eq. (2). In this case, when the participation constraint is not binding and the internal wage offer of each player is substituted for the expression of the relevant incentive compatibility constraint, the problem of the representative firm can be written as

$$\begin{aligned} \underset{e_{i},L_{i}}{\max }\pi _{i}=A\left( e_{i}L_{i}\right) ^{\alpha }-\left( w_{i}^{\min }+e_{i}^{^{\frac{1}{\beta }}}\right) L_{i} \end{aligned}$$

(A1)

Recalling that $w_{i}^{\min }\equiv {\textstyle \sum \nolimits _{j\ne i}^{N-1}} w_{j}-\kappa$, the first-order conditions for $e_{i}$ and $L_{i}$ are respectively given by

$$\begin{aligned}&A\left( e_{i}L_{i}\right) ^{\alpha -1}-\frac{e_{i}^{^{\frac{1-\beta }{\beta }} }}{\beta }=0 \end{aligned}$$

(A2)

$$\begin{aligned}&A\left( e_{i}L_{i}\right) ^{\alpha -1}e_{i}- {\displaystyle \sum \limits _{j\ne i}^{N-1}} w_{j}+\kappa -e_{i}^{^{\frac{1}{\beta }}}=0 \end{aligned}$$

(A3)

Solving (A2) with respect to $A\left( e_{i} L_{i}\right) ^{\alpha -1}$ and plugging the result into (A3) allows us to find the profit-maximizing effort provision as a function of the external wage bids and the parameters of the effort function. Formally speaking, we find that

$$\begin{aligned} e_{i}=\left( \frac{\beta \left( {\textstyle \sum \nolimits _{j\ne i}^{N-1}} w_{j}-\kappa \right) }{1-\beta }\right) ^{\beta } \end{aligned}$$

(A4)

Plugging the expression in (A4) into Eq. (2) and solving for $w_{i}$ returns exactly the reaction function in Eq. (9). A similar procedure can be followed in order to retrieve the reaction function in Eq. (10) that holds in the case of a sigmoid effort function.