Introduction

Robotic science is a modern technology that surpasses the constraints of traditional engineering. A comprehensive understanding of robots and their applications necessitates expertise in electrical engineering, mechanical engineering, system engineering, industrial engineering, computer science, and mathematics. One of the specific robotic systems is UAV. UAVs have become increasingly important in a wide range of fields such as surveillance and reconnaissance, environmental monitoring, gathering information in areas that are difficult to access, locating and assisting individuals in distress, agriculture, irrigation management, infrastructure inspection, film and photography, and numerous commercial applications [1, 2]. In general, it can be said that UAVs have attracted a lot of attention in recent decades. The main advantages of UAVs compared to conventional helicopters are:

  • Flying robots are easier to design and build than helicopters. Also, it does not require a mechanical connection to change the inclination of the blades.

  • Having four smaller rotors than the single rotor of a conventional helicopter allows it to have less kinetic energy and less damage in case of an accidental fall.

  • It has a symmetrical structure, and considering that the movement of UAVs is only dependent on the rotation rate, it makes them maneuverable and requires simpler control systems.

UAVs consist of active control systems with 6 degrees of freedom and four independent controllers. They are devices with four rotors, whose translational and rotational movements are created by changes in the speed of the rotors [3]. To control UAVs, the following three features should be considered:

  • Variable modes with time-delay.

  • Dynamics with uncertainty.

  • Multi-input-multi-output and nonlinear structure.

Studying the stability and control of UAVs concerning nonlinear components and disturbances is a challenging problem. Typically, UAVs can be maneuvered using a remote control system and stabilized with an external controller. Attitude control is employed to maintain the optimal position of UAVs. Various control methods, including linear control, non-linear, adaptive, fuzzy, and neural controllers, have been utilized to control the attitude of UAVs. However, controlling UAVs becomes challenging in the presence of uncertainties [4,5,6].

Literature review

In [7], an adaptive controller is suggested to track the position of the UAV under uncertainty and disturbance. The stability analysis is done using the concept of the Lyapunov scheme. In [8], a control method based on adaptive control and SMC is used to combine the tracking error with the concept of Lyapunov stability. In [9], a tensor transformation model based on SMC is presented. The provided controller is divided into two stages, in the first step, a transformation model is provided, and then, in the second step, the final SMC rule for the time-varying conditions is presented. In [10], a control structure is designed by the feedback linearization approach. The feedback linearization transforms the UAV dynamics into a simple fourth-order linear system, and then SMC is designed. In [11], a hybrid three-axis state control is presented, so that the time-limited SMC is designed to control the three-axis angular rate in the inner loop. Then, a PI based on the linear square regulator is considered to control the rotation angles in the outer ring. In [12], some controllers like fuzzy control, feedback linearization, and SMC have been used for the UAV. In [13], two control methods for the UAV are presented. The first method is designed using PID and the second method is designed on the basis of feedback of nonlinear state and linear matrix inequality. In [14], the dynamic UAV is obtained based on physical laws, then a control method is designed based on the backward design method for the stability of UAV under actuator and sensor errors.

The SMC is known as an effective method for designing a robust controller for high-order systems with uncertainties [15]. The main feature of SMC is less sensitivity to perturbations and changes in system parameters. As a practical example, in [16], an adaptive nonlinear SMC is designed for a robot arm in the presence of uncertainty and disturbance. Also, to demonstrate the effectiveness of the suggested approach, a practical examination is carried out on an inverted pendulum. The paths of the system by the suggested SMC reach to the equilibrium point in a limited time.

The FLSs have good applicability in the control of robotic systems. In some studies, the application of FLSs has been investigated. For instance, a new application of UAVs is introduced in [17] to improve road maintenance on partially erased sidewalk edges. It develops the stabilization and computer vision-based decision-making systems using FLSs. A controller using FLS is implemented in [18] to create a control model in a stable environment, comparing it to conventional control methods. The FLS-based controller approach allows the robot to move easily and efficiently in the test environment, minimizing energy consumption and operating in a flexible scheme. It is shown that the FLS-based controller is faster and more accurate than the traditional methods. An adaptive control scheme using FLSs with Jordan feedback structure is suggested in [19] to address the challenges of operating UAVs in extreme environments. It is shown the FLS strategy can effectively manage system uncertainty and track the reference trajectory with good accuracy, low computational load, and quick convergence rate. The controller’s stability is demonstrated using Lyapunov’s method. In [20], a fractional-order PID using FLSs is studied for stabilizing a UAV considering the nonlinear dynamics. FLSs are used to adjust parameters under disturbances and uncertainties. The multi-objective thermal optimization is employed to determine controller parameters to minimize control energy and tracking errors. A new quadcopter UAV platform is introduced in [21], and a type-2 (T2) FLS-based controller is designed to improve control robustness and manage computation costs for practical control. The designed system is used to control a UAV and is tested using a software-in-the-loop simulator and actual flight experiments. In [22], some controllers and modeling methods are reviewed and compared. In [23], a fuzzy PID is designed for a line following problem. The controller’s gains are chosen online based on changes in position and orientation errors. The results verify that the type-2 FLS-based controller outperforms the convectional fuzzy and PID controllers in stabilization and time-variant trajectory tests.

Recently, type-3 FLSs are widely used for many problems such as: robotic [24, 25], monitoring [26], forecasting [27], electrical vehicles [28, 29], adaptive control systems [30], classification [26], modeling [31], and many others. However, T3-FLS-based control of UAVs has not been studied, well. The literature review shows that:

  • In most controllers, the dynamics of UAVs are considered to be known.

  • In a few studies, FLS-based controllers have been developed, but the robustness analyses are neglected.

  • In a few SMCs, the robustness is studied, but, the dynamic parameters of UAV are considered constant.

  • T3-FLSs based control of UAVs has not been studied, well.

In this paper, a T3-FLS-based controller is developed. The main novelties and contributions are:

  • An adaptive scheme is developed for model identification using the input/output data sets.

  • New adaptation laws are obtained for dynamic parameters.

  • A T3-FLS is developed to compensate for the identification errors.

  • The robustness is analyzed considering the adaptation errors

Fig. 1
figure 1

Schematic of a UAV with four rotors

Full size image

Dynamic modeling

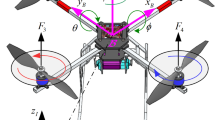
In this research, a UAV with four rotors as shown in Fig. 1 is considered. This UAV consists of a rigid and cross-shaped frame with four propellers. The considered UAV can be moved in certain directions by increasing/reduction of the total propulsion force. If the speed of all four propellers increases or decreases at the same time, vertical movement is created. The rotational movement around the longitudinal axis and the related translational movement are created by increasing and decreasing the speed of propellers one and three in reverse. If the speed of propellers two and four is changed inversely, the rotational movement around the transverse axis and also the translational movement related to it are formed. Finally, the rotational movement around the height axis is made from the torque difference between the two pairs of propellers (1, 3) and (2, 4) [32]. In this research, the following assumptions have been considered:

  • The structure and propellers are rigid and symmetrical.

  • Thrust forces have a proportionality to the square of the rotation speed of the blades.

Based on the above assumptions, the dynamic equations of the aerodynamic forces created by the rotation of the propellers are written as follows based on Newton–Euler equations [33]:

$$\begin{aligned} \left\{ \begin{array}{l} m\ddot{\zeta }= {F_f} + {F_d} + {F_g},\\ J{{\dot{\Phi }}} = - {\Phi ^T}J\Phi + {\rho _f} - {\rho _a} - {\rho _g}, \end{array} \right. \end{aligned}$$
(1)

while m denotes the total mass of the UAV, \(\xi \) is the center of the UAV relative to the inertial frame and a fixed and positive-definite inertial matrix of the UAV is symmetrical to the rigid body. J is defined as follows:

$$\begin{aligned} J = \left[ {\begin{array}{*{20}{c}} {{I_\chi }}&{}0&{}0\\ 0&{}{{I_y}}&{}0\\ 0&{}0&{}{{I_z}} \end{array}} \right] , \end{aligned}$$
(2)

where \({{\textrm{I}}_\chi },\,{{\textrm{I}}_y},\,{{\textrm{I}}_z}\) represent the inertias related to the \(\chi ,\,y,\,z\) axes. \(\Phi \) shows the angular velocities:

$$\begin{aligned} \Phi = \left[ {\begin{array}{*{20}{c}} 1&{}0&{}{ - \sin \Theta }\\ 0&{}{\cos \varphi }&{}{\cos \Theta \sin \varphi }\\ 0&{}{ - \sin \varphi }&{}{\cos \varphi \cos \Theta } \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{{\dot{\varphi }}} }\\ {{{\dot{\Theta }}} }\\ {{{\dot{\Omega }}} } \end{array}} \right] , \end{aligned}$$
(3)

While \(\varphi \), \(\Theta \), and \(\Omega \), denote the angles around the longitudinal, transverse, and height axis, respectively. \({F_f}\) is written as:

$$\begin{aligned} {F_f} = \left[ {\begin{array}{*{20}{c}} {\cos \varphi \cos \Omega \sin \Theta + \sin \varphi \sin \Omega }\\ {\cos \varphi \sin \Theta \sin \Omega - \sin \varphi \cos \Omega }\\ {\cos \varphi \cos \Theta } \end{array}} \right] \sum \limits _{i = 1}^4 {{F_i}} , \end{aligned}$$
(4)

where \({F_i} = {K_p}{w_i}^2\) and \(K_p\) is related to the force and \(w_i\) denotes the angular speed of the rotor. The \(F_d\) represents the result of the forces produced along the axes \(\chi ,y,z\):

$$\begin{aligned} {F_d} = \left[ {\begin{array}{*{20}{c}} { - {K_{fdx}}}&{}0&{}0\\ 0&{}{ - {K_{fdy}}}&{}0\\ 0&{}0&{}{ - {K_{fdz}}} \end{array}} \right] {{\dot{\zeta }}} , \end{aligned}$$
(5)

where \({K_{fdz}},{K_{fdy}},{K_{fdx}}\) are the positive coefficients, respectively. Gravitational force \(F_g\) is shown as follows:

$$\begin{aligned} {F_g} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ { - mg} \end{array}} \right] , \end{aligned}$$
(6)

where \({\rho _f}\) shows the moment of inertia related to the fixed object:

$$\begin{aligned} {\rho _f} = \left[ {\begin{array}{*{20}{c}} {d({F_3} - {F_1})}\\ {d({F_4} - {F_2})}\\ {{C_d}({w_1}^2 - {w_2}^2 + {w_3}^2 - {w_4}^2)} \end{array}} \right] , \end{aligned}$$
(7)

where d denotes the distance between the center and propellers, and \(C_d\) is a coefficient. The torque \({\rho _a}\) is written as:

$$\begin{aligned} {\rho _a} = \left[ {\begin{array}{*{20}{c}} {{K_{fax}}}&{}0&{}0\\ 0&{}{{K_{fay}}}&{}0\\ 0&{}0&{}{{K_{faz}}} \end{array}} \right] {\left\| \Phi \right\| ^2}, \end{aligned}$$
(8)

where \({K_{faz}},{K_{fay}},{K_{fax}}\) are aerodynamic friction coefficients. \({\rho _g}\) means the result of torques created due to the gyroscopic effect:

$$\begin{aligned} {\rho _g} = \sum \limits _{i = 1}^4 {{\Phi ^T}{J_r}\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {{{( - 1)}^{i + 1}}{w_i}} \end{array}} \right] }, \end{aligned}$$
(9)

where \(J_r\) denotes the inertia of rotor. The relationship between the controllers and the velocities is:

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{u_1}}\\ {{u_2}}\\ {{u_3}}\\ {{u_4}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{K_p}}&{}{{K_p}}&{}{{K_p}}&{}{{K_p}}\\ { - {K_p}}&{}0&{}{{K_p}}&{}0\\ 0&{}{ - {K_p}}&{}0&{}{{K_p}}\\ {{C_D}}&{}{ - {C_D}}&{}{{C_D}}&{}{ - {C_D}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{w_1}^2}\\ {{w_2}^2}\\ {{w_3}^2}\\ {{w_4}^2} \end{array}} \right] , \end{aligned}$$
(10)

where \(u_i\), \(i=1,...,4\) are control inputs. The velocities \({w_i}\,\,(i = 1,\,...,\,4)\) can be written as follows:

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{w_1}}\\ {{w_2}}\\ {{w_3}}\\ {{w_4}} \end{array}} \right] = {\left( {{{\left[ {\begin{array}{*{20}{c}} {{K_p}}&{}{{K_p}}&{}{{K_p}}&{}{{K_p}}\\ { - {K_p}}&{}0&{}{{K_p}}&{}0\\ 0&{}{ - {K_p}}&{}0&{}{{K_p}}\\ {{C_D}}&{}{ - {C_D}}&{}{{C_D}}&{}{ - {C_D}} \end{array}} \right] }^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{u_1}}\\ {{u_2}}\\ {{u_3}}\\ {{u_4}} \end{array}} \right] } \right) ^{\frac{1}{2}}}. \end{aligned}$$
(11)

As a result, the dynamic of UAV is determined as:

$$\begin{aligned} \ddot{\chi }{} & {} = \frac{1}{m}\left[ { - {K_{fdx}}{{\dot{\chi }}} + (cos\varphi \sin \Theta \cos \Omega + \sin \varphi \sin \Omega ){u_1}} \right] ,\nonumber \\ \ddot{y}{} & {} = \frac{1}{m}\left[ { - {K_{fdy}}\dot{y} + (cos\varphi \sin \Theta \sin \Omega - \sin \varphi \cos \Omega ){u_1}} \right] ,\nonumber \\ \ddot{z}{} & {} = \frac{1}{m}\left[ { - {K_{fdz}}\dot{z} + (cos\varphi \cos \Theta ){u_1}} \right] - g,\nonumber \\ \ddot{\varphi }{} & {} = \frac{1}{{{I_\chi }}}\left[ {({I_y} - {I_z}){{\dot{\Omega }}} {{\dot{\Theta }}} - {K_{fax}}{{{{\dot{\varphi }}} }^2} - {J_r}{\bar{\Phi }} {{\dot{\Theta }}} + d{u_2}} \right] ,\nonumber \\ \ddot{\Theta }{} & {} = \frac{1}{{{I_y}}}\left[ {({I_z} - {I_\chi }){{\dot{\Omega }}} {{\dot{\varphi }}} - {K_{fay}}{{{{\dot{\Theta }}} }^2} + {J_r}{\bar{\Phi }} {{\dot{\varphi }}} + d{u_3}} \right] ,\nonumber \\ \ddot{\Omega }{} & {} = \frac{1}{{{I_z}}}\left[ {({I_\chi } - {I_y}){{\dot{\varphi }}} {{\dot{\Theta }}} - {K_{faz}}{{{{\dot{\Omega }}} }^2} + {C_D}{u_4}} \right] , \end{aligned}$$
(12)

where \({\bar{\Phi }} = {w_1} - {w_2} + {w_3} - {w_4}\). The considered UAV is fully actuated with four control inputs, which are used to control \(\varphi \), \(\Theta \), \(\Omega \), and z. Assume that \(X = {\left[ {\varphi ,{{\dot{\varphi }}},\Theta ,{{\dot{\Theta }}},\Omega ,{{\dot{\Omega }}},z,\dot{z}} \right] ^T}\) and \(U = {\left[ {{u_2},{u_3},{u_4},{u_1}} \right] ^T}\) denote the state and the controller vectors. The dynamic model considered in (12) based on the state space model is expressed as follows:

$$\begin{aligned} \dot{X} = F({{\upchi }}) + G({{\upchi }})U \end{aligned}$$
(13)

where F and G are written as:

$$\begin{aligned} F({{\upchi }})= & {} \left[ {\begin{array}{c} {{\chi _2}}\\ {{a_1}{\chi _4}{\chi _6} + {a_2}{\chi _2}^2 + {a_3}{\bar{\Phi }} {\chi _4}}\\ {{\chi _4}}\\ {{a_4}{\chi _2}{\chi _6} + {a_5}{\chi _4}^2 + {a_6}{\bar{\Phi }} {\chi _2}}\\ {{\chi _6}}\\ {{a_7}{\chi _2}{\chi _4} + {a_8}{\chi _6}^2}\\ {{\chi _8}}\\ {{a_9}{\chi _8} - g} \end{array}} \right] \end{aligned}$$
(14)
$$\begin{aligned} G({{\upchi }})= & {} \left[ {\begin{array}{cccc} 0&{}0&{}0&{}0\\ {{b_1}}&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ 0&{}{{b_2}}&{}0&{}0\\ 0&{}0&{}0&{}0\\ 0&{}0&{}{{b_3}}&{}0\\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}{\frac{{\cos {\chi _1}\cos {\chi _3}}}{m}} \end{array}} \right] \end{aligned}$$
(15)

where

$$\begin{aligned} \begin{aligned}&{a_1} = \frac{{{I_y} - {I_z}}}{{{I_\chi }}},\,{a_2} = \frac{{ - {K_{fax}}}}{{{I_\chi }}},\,{a_3} = \frac{{ - {J_r}}}{{{I_\chi }}},{a_4} = \frac{{{I_z} - {I_\chi }}}{{{I_y}}}\\&{a_5} = \frac{{ - {K_{fay}}}}{{{I_y}}},\,{a_6} = \frac{{{J_r}}}{{{I_y}}}\,,\,{a_7} = \frac{{{I_\chi } - {I_y}}}{{{I_z}}},\,{a_9} = \frac{{ - {K_{fdz}}}}{m},\\&{b_1} = \frac{d}{{{I_\chi }}},\,{b_2} = \frac{d}{{{I_y}}},\,{b_3} = \frac{{{C_D}}}{{{I_z}}} \end{aligned} \end{aligned}$$
(16)

The following lemma is considered in the analysis.

Lemma 1

Suppose a definite positive function V(t) satisfies:

$$\begin{aligned} \dot{V}(t) \le - \beta V(t) - \alpha {V^\gamma }(t) \end{aligned}$$
(17)

where \(\alpha \)/\(\beta \) are positive, \(0< a < b\), and \(\gamma = \frac{a}{b}\), then V(t) in limited time (18) is converged to zero.

$$\begin{aligned} {t_s} = {t_0} + \frac{1}{{\beta (1 - \gamma )}}\ln \left( \frac{{\beta {V^{1 - \gamma }}({t_0}) + \alpha }}{\alpha }\right) . \end{aligned}$$
(18)
Fig. 2
figure 2

Designed control scheme

Full size image

The designed control scheme is shown in Fig. 2. First, an adaptive model is identified for the plant using the input/output info, and then a SMC is designed. A T3-FLS is used to estimate the disturbances and identification errors.

Type-3 fuzzy systems

Type-2 extensions of traditional type-1 fuzzy systems, which are used in fuzzy logic to model uncertainty and imprecision in decision-making processes. These systems are particularly useful in situations where the uncertainty in the input data is high or where the decision-making process is complex. T2-FLSs allow for the representation of higher levels of uncertainty compared to type-1 FLSs. In a type-2 fuzzy system, each linguistic variable is associated with a fuzzy set that has a membership function that is itself a fuzzy set. This allows for the modeling of uncertainty in both the membership grade and the shape of the membership function. T2-FLSs are useful in situations where the uncertainty in the input data is not well understood or where there is a need to model varying levels of uncertainty.

Fig. 3
figure 3

Schematic of T3-FLS

Full size image

T3-FLSs are an even more advanced extension of type-1 and type-2 FLSs. In a T3-FLS, each linguistic variable is associated with a fuzzy set that has a membership function that is a type-2 fuzzy set. This allows for the representation of even higher levels of uncertainty and complexity in the decision-making process. Type-3 fuzzy systems are particularly useful in situations where the uncertainty in the input data is extremely high or where there is a need to model complex relationships between variables. These systems offer a powerful tool for dealing with uncertainty and imprecision in complex decision-making processes, making them valuable tools for researchers and practitioners in a variety of domains. In this paper, T3-FLSs are used to estimate the disturbances and nonlinearities. The computations are summarized as follows (see Fig. 3): 1) The inputs are the states of plant \(\chi _i,\,i=1,...,n\).

2) The memberships \({{{\bar{q}} }_{{\tilde{\Psi }}_{i\,\,| {{\bar{\lambda } }_k}}^j}}\), , , and for \({{\tilde{\Psi }}_i^j}\) (j-th membership function (MF) for \(\chi _i, \,i=1,2\)) are obtained as (see Fig. 4):

(19)
(20)
(21)
(22)

where represent the upper/lower slices.

Fig. 4
figure 4

Membership functions

Full size image

3) The rule firings \({\bar{\ell }} _{{{{\bar{\lambda }} }_k}}^l\), , , and are written as

(23)
(24)
(25)
(26)

4) The output is given as:

(27)

where,

(28)
(29)

Control

In this section, the control is designed and analyzed. The main results are summarized in Theorem 2. The output vector is \(y = {[\varphi ,\Theta ,\Omega ,z]^T}\), then the errors are defined as follows:

$$\begin{aligned} \begin{aligned}&\,\,\left\{ \begin{array}{l} {e_{{\varphi _1}}} = {y_1} - {\varphi _d}\\ {e_{{\varphi _2}}} = {{\dot{y}}_1} - {{{{\dot{\varphi }}} }_d} \end{array} \right. \,\,\,\,\,\,\,\,\,\,\,\,\,\,\left\{ \begin{array}{l} {e_{{\Theta _1}}} = {y_2} - {\Theta _d}\\ {e_{{\Theta _2}}} = {{\dot{y}}_2} - {{{{\dot{\Theta }}} }_d} \end{array} \right. \\&\,\,\left\{ \begin{array}{l} {e_{{\Omega _1}}} = {y_3} - {\Omega _d}\\ {e_{{\Omega _2}}} = {{\dot{y}}_3} - {{{{\dot{\Omega }}} }_d} \end{array} \right. \,\,\,\,\,\,\,\,\,\,\,\,\left\{ \begin{array}{l} {e_{{z_1}}} = {y_4} - {z_d}\\ {e_{{z_2}}} = {{\dot{y}}_4} - {{\dot{z}}_d} \end{array} \right. \end{aligned} \end{aligned}$$
(30)

where \({y_d} = {[{\varphi _d},{\Theta _d},{\Omega _d},{z_d}]^T}\) is the reference output. The sliding surface is defined as:

$$\begin{aligned} \begin{aligned}&{s_1} = {e_{{\varphi _2}}} + {\alpha ' _1}{e_{{\varphi _1}}} + {k_1}\int \limits _0^t {{s_1}(\tau )} d\tau ,\\&{s_2} = {e_{{\Theta _2}}} + {\alpha ' _2}{e_{{\Theta _1}}}\, + {k_2}\int \limits _0^t {{s_2}(\tau )} d\tau ,\\&{s_3} = {e_{{\Omega _2}}} + {\alpha ' _3}{e_{{\Omega _1}}} + {k_3}\int \limits _0^t {{s_3}(\tau )} d\tau ,\\&{s_4} = {e_{{z_2}}} + {\alpha ' _4}{e_z}_{_1} + {k_4}\int \limits _0^t {{s_4}(\tau )} d\tau , \end{aligned} \end{aligned}$$
(31)

where \({\alpha _l}'\), \(k_l\), \(l=1,...,4\) are positive constants. By taking derivative from (31), we can write:

$$\begin{aligned} \begin{aligned} {{\dot{s}}_1}&= {\dot{e}}_{\varphi _2} + {\alpha ' _1}{{\dot{e}}_{{{\varphi _1}}}} + {k_1}{s_1}\\&= {a_1}{\chi _4}{\chi _6} + {a_2}{\chi _2}^2 + {a_3}{\bar{\Phi }} \chi _4\\&\quad + {b_1}{u_2} - {{\ddot{\varphi }}_d} + {\alpha ' _1}{{\dot{e}}_{{{\varphi _1}}}} + {k_1}{s_1},\\ {{\dot{s}}_2}&= {{\dot{e}}_{{{\Theta _2}}}} + {\alpha ' _2}{{\dot{e}}_{{{\Theta _1}}}} + {k_2}{s_2}\\&= {a_5}{\chi _4}^2 + {\bar{\Phi }} {a_6}{\chi _2} + {b_2}{u_3}+{\chi _2}{a_4}{\chi _6} \\&\quad - {{\ddot{\Theta }}_d} + {\alpha ' _2}{{\dot{e}}_{{{\Theta _1}}}} + {k_2}{s_2},\\ {{\dot{s}}_3}&= {{\dot{e}}_{{{\Omega _2}}}} + {\alpha ' _3}{{\dot{e}}_{{{\Omega _1}}}} + {k_3}{s_3}\\&= {a_7}{\chi _2}{\chi _4} + {a_8}{\chi _6}^2 + {b_3}{u_4} - {{\ddot{\Omega }}_d} + {\alpha ' _3}{{\dot{e}}_{{{\Omega _1}}}} + {k_3}{s_3},\\ {{\dot{s}}_4}&= {{\dot{e}}_{{{z_2}}}} + {\alpha ' _4}{{\dot{e}}_{{{z_1}}}} + {k_4}{s_4}\\&= {a_9}{\chi _8} - g + \frac{{\cos {\chi _1}\cos {\chi _3}}}{m}{u_1} - {{\ddot{z}}_d} + {\alpha ' _4}{{\dot{e}}_{{{z_1}}}} + {k_4}{s_4}. \end{aligned} \end{aligned}$$
(32)

Theorem 2

Considering the dynamic model as (13), sliding surfaces as (31), controllers (33), and adaptation laws (36)–(40), the robot in a limited time is reached to the target position.

The controllers are given as:

$$\begin{aligned} \begin{aligned}&{u_2} = - {f_2}\left( {\chi ,{w_2}} \right) - {{{\hat{\varsigma }} }_1}{\chi _4}{\chi _6} - {{{\hat{\varsigma }} }_2}{\chi _2}^2 - {{{\hat{\varsigma }} }_3}{\bar{\Phi }} {\chi _4} + {{{\hat{h}}}_1}{\kappa _1}\,,\\&{u_3} = - {f_3}\left( {\chi ,{w_3}} \right) - {{{\hat{\varsigma }} }_4}{\chi _2}{\chi _6} - {{{\hat{\varsigma }} }_5}{\chi _4}^2 - {{{\hat{\varsigma }} }_6}{\bar{\Phi }} {\chi _2} + {{{\hat{h}}}_2}{\kappa _2},\\&{u_4} = - {f_4}\left( {\chi ,{w_4}} \right) - {{{\hat{\varsigma }} }_7}{\chi _2}{\chi _4} - {{{\hat{\varsigma }} }_8}{\chi _6}^2 + {{{\hat{h}}}_3}{\kappa _3}\,,\\&{u_1} = - {f_1}\left( {\chi ,{w_1}} \right) + \frac{1}{{{{{{\textrm{cosx}}} }_1}{{{{\textrm{cosx}}} }_3}}}[ - {{{\hat{\varsigma }} }_9}{\chi _8} + {\hat{m}}{\kappa _4}]\,, \end{aligned} \end{aligned}$$
(33)

where \({{\hat{\varsigma }} _i}\,\,(i = 1,\,...\,,\,9)\), \({{\hat{h}}_j}\,\,(j = 1,\,2\,,\,3)\) and \({\hat{m}}\) are the estimation of:

$$\begin{aligned} \begin{aligned}&{\varsigma _1} = \frac{{{a_1}}}{{{b_1}}},{\varsigma _2} = \frac{{{a_2}}}{{{b_1}}},{\varsigma _3} = \frac{{{a_3}}}{{{b_1}}},{\varsigma _4} = \frac{{{a_4}}}{{{b_2}}},{\varsigma _5} = \frac{{{a_5}}}{{{b_2}}}\\&{\varsigma _6} = \frac{{{a_6}}}{{{b_2}}},{\varsigma _7} = \frac{{{a_7}}}{{{b_3}}},{\varsigma _8} = \frac{{{a_8}}}{{{b_3}}},{\varsigma _9} = m{a_9},{h_1} = \frac{1}{{{b_1}}}\\&{h_2} = \frac{1}{{{b_2}}},{h_3} = \frac{1}{{{b_3}}} \end{aligned} \end{aligned}$$
(34)

\({\kappa _r}\,\,(r = 1,...,\,4)\) are written as:

$$\begin{aligned} \begin{aligned}&{\kappa _1} = - {\alpha ' _1}{{\dot{e}}_{{{\varphi _1}}}} - {k_1}{s_1}+{{\ddot{\varphi }}_d},\\&{\kappa _2} = - {\alpha ' _2}{{\dot{e}}_{{{\Theta _1}}}} - {k_2}{s_2}+{{\ddot{\Theta }}_d},\\&{\kappa _3} = {{\ddot{\Omega }}_d} - {\alpha ' _3}{{\dot{e}}_{{{\Omega _1}}}} - {k_3}{s_3},\\&{\kappa _4} = g - {\alpha ' _4}{{\dot{e}}_{{{z_1}}}} - {k_4}{s_4}+ {{\ddot{z}}_d} \end{aligned} \end{aligned}$$
(35)

The adaptation laws are written as:

$$\begin{aligned}{} & {} \left\{ \begin{array}{l} {{\dot{{\hat{\varsigma }}} }_1} = {\alpha _1}{\textrm{sgn}} \big (\frac{{\partial {s_1}}}{{\partial {u_2}}}\big ){\chi _4}{\chi _6}{s_1}^\vartheta \\ {{\dot{{\hat{\varsigma }}} }_2} = {\alpha _1}{\textrm{sgn}} \big (\frac{{\partial {s_1}}}{{\partial {u_2}}}\big ){\chi _2}^2{s_1}^\vartheta \\ {{\dot{{\hat{\varsigma }}} }_3} = {\alpha _1}{\textrm{sgn}} \big (\frac{{\partial {s_1}}}{{\partial {u_2}}}\big ){\bar{\Phi }} {\chi _4}{s_1}^\vartheta \\ {{\dot{{\hat{h}}}}_1} = - {\beta _1}{\textrm{sgn}} \big (\frac{{\partial {s_1}}}{{\partial {u_2}}}\big ){\kappa _1}{s_1} \end{array} \right. \end{aligned}$$
(36)
$$\begin{aligned}{} & {} \left\{ \begin{array}{l} {{\dot{{\hat{\varsigma }}} }_4} = {\alpha _2}{\textrm{sgn}} \big (\frac{{\partial {s_2}}}{{\partial {u_3}}}\big ){\chi _2}{\chi _6}{s_2}^\vartheta \\ {{\dot{{\hat{\varsigma }}} }_5} = {\alpha _2}{\textrm{sgn}} \big (\frac{{\partial {s_2}}}{{\partial {u_3}}}\big ){\chi _4}^2{s_2}^\vartheta \\ {{\dot{{\hat{\varsigma }}} }_6} = {\alpha _2}{\textrm{sgn}} \big (\frac{{\partial {s_2}}}{{\partial {u_3}}}\big ){\bar{\Phi }} {\chi _2}{s_2}^\vartheta \\ {{\dot{{\hat{h}}}}_2} = - {\beta _2}{\textrm{sgn}} \big (\frac{{\partial {s_2}}}{{\partial {u_3}}}\big ){\kappa _2}{s_2} \end{array} \right. \end{aligned}$$
(37)
$$\begin{aligned}{} & {} \left\{ \begin{array}{l} {{\dot{{\hat{\varsigma }}} }_7} = {\alpha _3}{\textrm{sgn}} \big (\frac{{\partial {s_3}}}{{\partial {u_4}}}\big ){\chi _2}{\chi _4}{s_3}^\vartheta \\ {{\dot{{\hat{\varsigma }}} }_8} = {\alpha _3}{\textrm{sgn}} \big (\frac{{\partial {s_3}}}{{\partial {u_4}}}\big ){\chi _6}^2{s_3}^\vartheta \\ {{\dot{{\hat{h}}}}_3} = - {\beta _3}{\textrm{sgn}} \big (\frac{{\partial {s_3}}}{{\partial {u_4}}}\big ){\kappa _3}{s_3} \end{array} \right. \end{aligned}$$
(38)
$$\begin{aligned}{} & {} \left\{ \begin{array}{l} {{\dot{{\hat{\varsigma }}} }_9} = {\alpha _4}{\textrm{sgn}} \big (\frac{{\partial {s_4}}}{{\partial {u_1}}}\big ){\chi _8}cos{\chi _1}cos{\chi _3}{s_4}^\vartheta \\ \dot{{\hat{m}}} = - {\beta _4}{\textrm{sgn}} \big (\frac{{\partial {s_4}}}{{\partial {u_1}}}\big ){\kappa _4}cos{\chi _1}cos{\chi _3}{s_4} \end{array} \right. \end{aligned}$$
(39)
$$\begin{aligned}{} & {} {{\dot{w}}_i} = {\textrm{sgn}} \left( \frac{{\partial {s_i}}}{{\partial {u_2}}}\right) {s_i}{\xi _i} \end{aligned}$$
(40)

Proof

Consider the \(V_1\) as:

$$\begin{aligned} {V_1} = \frac{1}{2}{s_1}^2 \end{aligned}$$
(41)

Time derivative of \(V_1\) yields:

$$\begin{aligned} \begin{aligned} \frac{{{\text {d}}{V_1}}}{{{\text {d}}t}}&= \frac{{\partial {V_1}}}{{\partial {s_1}}}\frac{{\partial {s_1}}}{{\partial {u_2}}}\frac{{\partial {u_2}}}{{\partial {{{\hat{\varsigma }} }_1}}}\frac{{\partial {{\hat{\varsigma } }_1}}}{{\partial t}} + \frac{{\partial {V_1}}}{{\partial {s_1}}}\frac{{\partial {s_1}}}{{\partial {u_2}}}\frac{{\partial {u_2}}}{{\partial {{{\hat{\varsigma }} }_2}}}\frac{{\partial {{\hat{\varsigma } }_2}}}{{\partial t}}\\&\quad + \,\frac{{\partial {V_1}}}{{\partial {s_1}}}\frac{{\partial {s_1}}}{{\partial {u_2}}}\frac{{\partial {u_2}}}{{\partial {{\hat{\varsigma } }_3}}}\frac{{\partial {{{\hat{\varsigma }} }_3}}}{{\partial t}} + \frac{{\partial {V_1}}}{{\partial {s_1}}}\frac{{\partial {s_1}}}{{\partial {u_2}}}\frac{{\partial {u_2}}}{{\partial {{{\hat{h}}}_1}}}\frac{{\partial {{{\hat{h}}}_1}}}{{\partial t}}\\&\quad + \frac{{\partial {V_1}}}{{\partial {s_1}}}\frac{{\partial {s_1}}}{{\partial {u_2}}}\frac{{\partial {u_2}}}{{\partial {w_2}}}\frac{{\partial {w_2}}}{{\partial t}} \end{aligned}\nonumber \\ \end{aligned}$$
(42)

From the adaptation laws (36)–(40), we have:

$$\begin{aligned} \begin{aligned} \frac{{{\text {d}}{V_1}}}{{{\text {d}}t}}&= {s_1}\frac{{\partial {s_1}}}{{\partial {u_2}}}( - {\chi _4}{\chi _6}){\alpha _1}{\textrm{sgn}}\left( \frac{{\partial {s_1}}}{{\partial {u_2}}}\right) {\chi _4}{\chi _6}{s_1}^\vartheta \\&\quad + \,{s_1}\frac{{\partial {s_1}}}{{\partial {u_2}}}( - {\chi _2}^2){\alpha _1}{\textrm{sgn}}\left( \frac{{\partial {s_1}}}{{\partial {u_2}}}\right) {\chi _2}^2{s_1}^\vartheta \\&\quad + {s_1}\frac{{\partial {s_1}}}{{\partial {u_2}}}( - {\bar{\Phi }} {\chi _4}){\alpha _1}{\textrm{sgn}}\left( \frac{{\partial {s_1}}}{{\partial {u_2}}}\right) {\bar{\Phi }} {\chi _4}{s_1}^\vartheta \\&\quad + {s_1}\frac{{\partial {s_1}}}{{\partial {u_2}}}{\kappa _1}( - {\beta _1}){\textrm{sgn}}\left( \frac{{\partial {s_1}}}{{\partial {u_2}}}\right) {\kappa _1}{s_1}\\&\quad - {s_1}\frac{{\partial {s_1}}}{{\partial {u_2}}}\left( {\xi _1^T} \right) {\textrm{sgn}}\left( \frac{{\partial {s_1}}}{{\partial {u_2}}}\right) {s_1}{\xi _1} \end{aligned} \end{aligned}$$
(43)

From the fact that \({\textrm{sgn}} (\frac{{\partial {s_1}}}{{\partial {u_2}}}) = \left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| /\frac{{\partial {s_1}}}{{\partial {u_2}}}\), we can write:

$$\begin{aligned} \begin{aligned} \frac{{{\text {d}}{V_1}}}{{{\text {d}}t}}&= - {\alpha _1}\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| {({\chi _4}{\chi _6})^2}{s_1}^{\vartheta + 1} - {\alpha _1}\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| {\chi _2}^4{s_1}^{\vartheta + 1}\\&\quad - {\alpha _1}\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| {({\bar{\Phi }} {\chi _4})^2}{s_1}^{\vartheta + 1} - {\beta _1}{({\kappa _1})^2}\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| {s_1}^2\\&\quad - {\alpha _1}\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| \,{s_1}^2\xi _1^T{\xi _1} \end{aligned} \end{aligned}$$
(44)

The equation (44) is simplified as:

$$\begin{aligned} \begin{aligned} \frac{{{\text {d}}{V_1}}}{{{\text {d}}t}}&= - {\alpha _1}({({\chi _4}{\chi _6})^2} + {\chi _2}^4 + {({\bar{\Phi }} {\chi _4})^2})\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| {s_1}^{\vartheta + 1}\\&\quad - {\beta _1}{({\kappa _1})^2}\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| {s_1}^2\,\, - {\alpha _1}\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| \,{s_1}^2\xi _1^T{\xi _1} \end{aligned} \end{aligned}$$
(45)

From (45), we have:

$$\begin{aligned} \begin{aligned} \frac{{\partial {V_1}}}{{\partial t}}&= - ({({\chi _4}{\chi _6})^2} + {\chi _2}^4 + {({\bar{\Phi }} {\chi _4})^2}){2^{\frac{{\vartheta + 1}}{2}}}\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| {\alpha _1}{V_1}^{\frac{{\vartheta + 1}}{2}}\\&\quad - 2{\alpha _1}\xi _1^T{\xi _1}\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| {V_1} - 2{\beta _1}{({\kappa _1})^2}\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| {V_1} \end{aligned} \end{aligned}$$
(46)

By defining \(\gamma = \frac{{\vartheta + 1}}{2}\), it is concluded that:

$$\begin{aligned} \begin{aligned} \frac{{{\text {d}}{V_1}}}{{{\text {d}}t}}&= - ({\chi _2}^4 +{({\chi _4}{\chi _6})^2} + {({\chi _4}{\bar{\Phi }} )^2}){2^\gamma }\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| {\alpha _1}{V_1}^\gamma \\&\quad - 2\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| {V_1}{{\kappa _1}^2}{\beta _1}\,\, - 2{\alpha _1}\xi _1^T{\xi _1}\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| {V_1} \end{aligned} \end{aligned}$$
(47)

There are \(\mu _1\) and \(\mu _2\) such that:

$$\begin{aligned} {\dot{V}_1} \le - {\mu _1}{V_1}^\gamma - {\mu _2}{V_1} \end{aligned}$$
(48)

where

$$\begin{aligned} \begin{aligned}&{\mu _1} \le {2^\gamma }{\alpha _1}\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| \left[ {{{\left( {{\chi _4}{\chi _6}} \right) }^2} + {{({\bar{\Phi }} {\chi _4})}^2} + {\chi _2}^4} \right] \\&{\mu _2} \le 2{\kappa _1}^2{\beta _1}\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| \end{aligned} \end{aligned}$$
(49)
Table 1 Control effects of different controllers under different structural conditions
Full size table

From Lemma 1, the convergence time is computed as follows. First, the both side of (48) is divided by \({V_1}^\gamma \):

$$\begin{aligned} {V_1}^{ - \gamma }{\dot{V}_1} \le - {\mu _1} - {\mu _2}{V_1}^{1 - \gamma } \end{aligned}$$
(50)

Some computations result in:

$$\begin{aligned} {\text {d}}t \le - \frac{{{V_1}^{ - \gamma }}}{{{\mu _1} + {\mu _2}{V_1}^{1 - \gamma }}}\,{\text {d}}{V_1} \end{aligned}$$
(51)

Now, by taking integral from (51) at range [\(t_0-t_{s_1}\)], we have:

$$\begin{aligned} {t_{{s_1}}} - {t_0} \le \frac{1}{{{\mu _2}(1 - \gamma )}}\ln \left( \frac{{{\mu _1} + {\mu _2}{V_1}{{({t_0})}^{1 - \gamma }}}}{{{\mu _1}}}\right) \end{aligned}$$
(52)

Then, \(t_{s_1}\) is obtained as:

$$\begin{aligned} {t_{{s_1}}} = {t_0} + \frac{1}{{{\mu _2}(1 - \gamma )}}\ln \left( \frac{{{\mu _2}{V_1}^{1 - \gamma }({t_0}) + {\mu _1}}}{{{\mu _1}}}\right) \end{aligned}$$
(53)

The proof is completed. The other controllers are obtained in the same scheme, just the computations of \({\dot{{\hat{\varsigma }}} _9}\) and \(\dot{{\hat{m}}}\) are different. Consider \({V_4}\) as:

$$\begin{aligned} {V_4} = \frac{1}{2}{s_4}^2 \end{aligned}$$
(54)

By taking time-derivative, we have:

$$\begin{aligned} \begin{aligned} \frac{{{\text {d}}{V_4}}}{{{\text {d}}t}}&= \frac{{\partial {V_4}}}{{\partial {s_4}}}\frac{{\partial {s_4}}}{{\partial {u_1}}}\frac{{\partial {u_1}}}{{\partial {{{\hat{\varsigma }} }_9}}}\frac{{\partial {{\hat{\varsigma } }_9}}}{{\partial t}} + \frac{{\partial {V_4}}}{{\partial {s_4}}}\frac{{\partial {s_4}}}{{\partial {u_1}}}\frac{{\partial {u_1}}}{{\partial {\hat{m}}}}\frac{{\partial {\hat{m}}}}{{\partial t}}\\&\quad + \frac{{\partial {V_4}}}{{\partial {s_4}}}\frac{{\partial {s_4}}}{{\partial {u_1}}}\frac{{\partial {u_1}}}{{\partial {w_4}}}\frac{{\partial {w_4}}}{{\partial t}} \end{aligned} \end{aligned}$$
(55)

Substitution the adaptation laws of \(\dot{w}_4\), \({\dot{\hat{\varsigma }} _9}\) and \(\dot{{\hat{m}}}\), yields:

$$\begin{aligned} \begin{aligned} \frac{{{\text {d}}{V_4}}}{{{\text {d}}t}}&= - {s_4}\frac{{\partial {s_4}}}{{\partial {u_1}}}\frac{1}{{{\textrm{cos}}{{{\upchi }}_1}{\textrm{cos}}{{{\upchi }}_3}}}{\alpha _4}{\textrm{sgn}}\left( \frac{{\partial {s_4}}}{{\partial {u_1}}}\right) {\chi _8}^2cos{\chi _1}cos{\chi _3}{s_4}^\vartheta \\&\quad - {s_4}\frac{{\partial {s_4}}}{{\partial {u_1}}}\frac{1}{{{\textrm{cos}}{{{\upchi }}_1}{\textrm{cos}}{{{\upchi }}_3}}}{\beta _4}{\textrm{sgn}}\left( \frac{{\partial {s_4}}}{{\partial {u_1}}}\right) {\kappa _4}^2cos{\chi _1}cos{\chi _3}{s_4}\\&\quad - {s_4}\frac{{\partial {s_4}}}{{\partial {u_1}}}\frac{1}{{{\textrm{cos}}{{{\upchi }}_1}{\textrm{cos}}{{{\upchi }}_3}}}{\beta _4}{\textrm{sgn}}\left( \frac{{\partial {s_4}}}{{\partial {u_1}}}\right) \xi _4^T\xi _4^Tcos{\chi _1}cos{\chi _3}{s_4} \end{aligned} \end{aligned}$$
(56)

By simplification and considering \({\textrm{sgn}} (\frac{{\partial {s_4}}}{{\partial {u_1}}}) = \left| {\frac{{\partial {s_4}}}{{\partial {u_1}}}} \right| /\frac{{\partial {s_4}}}{{\partial {u_1}}}\), we have:

$$\begin{aligned} \begin{aligned} \frac{{{\text {d}}{V_4}}}{{{\text {d}}t}}&=- {\alpha _4}\left| {\frac{{\partial {s_4}}}{{\partial {u_1}}}} \right| {\chi _8}^2{s_4}^{\vartheta + 1} - {\beta _4}\left| {\frac{{\partial {s_4}}}{{\partial {u_1}}}} \right| \,{\kappa _4}^2{s_4}^2 \\&\quad - \left| {\frac{{\partial {s_4}}}{{\partial {u_1}}}} \right| \xi _4^T\xi _4^T{s_4}^2 \end{aligned} \end{aligned}$$
(57)
Fig. 5
figure 5

Output signals

Full size image
Fig. 6
figure 6

Control signals

Full size image
Fig. 7
figure 7

Sliding surface

Full size image
Fig. 8
figure 8

Adaptation trajectories

Full size image
Fig. 9
figure 9

Adaptation trajectories

Full size image

Considering \(\gamma = \frac{{\vartheta + 1}}{2}\), there are \(\gamma _7\) and \(\gamma _8\) such that:

$$\begin{aligned} {\dot{V}_4} \le - {\mu _7}{V_4}^\gamma - {\mu _8}{V_4} \end{aligned}$$
(58)

where

$$\begin{aligned} \begin{aligned}&{\mu _7} \le {2^\gamma }{\alpha _4}{\chi _8}^2\left| {\frac{{\partial {s_4}}}{{\partial {u_1}}}} \right| \\&{\mu _8} \le 2{\beta _4}{\kappa _4}^2\left| {\frac{{\partial {s_4}}}{{\partial {u_1}}}} \right| \end{aligned} \end{aligned}$$
(59)

\(\square \)

Remark 1

The suggested controller can be developed considering mismatched uncertain disturbances [34], hybrid models [35], and new disturbance rejection methods [36].

Simulation

The initial condition is considered as \({\chi _i}{\mathrm{(0)}} = 0{\mathrm{.10}}\,\,{\mathrm{(}}\forall \,{\textrm{i}} = 1,\,...\,,\,8{\mathrm{)}}\). The initial condition of adaptation rules are considered as: \({{\hat{\varsigma }} _i}{\mathrm{(0)}} = 0{\mathrm{.10}}\,\,\,(\forall \,{\textrm{i}} = 1,\,...\,{\textrm{,}}\,{\mathrm{9)}}\), \({{\hat{h}}_1}{\mathrm{(0) = 0}}{\mathrm{.10}}\), \({{\hat{h}}_2}{\mathrm{(0) = 0}}{\mathrm{.20}}\), \({{\hat{h}}_3}{\mathrm{(0) = 0}}{\mathrm{.30}}\) and \({\hat{m}}{\mathrm{(0) = 0}}{\mathrm{.65}}\). The designing parameters are considered as: \({\alpha '_1} = {\alpha '_2} = 2\), \({\alpha '_3} = {\alpha '_4} = 2\), \({k_1} = {k_2} = 10\), \({k_3} = {k_4} = 5\), \({\alpha _i} = 0.05\,\,\,(\forall i = 1,\,\,...,\,\,4)\), \({\beta _i} = 0.05\,\,\,(\forall i = 1,\,\,...\,,\,\,4)\), \(\vartheta = \frac{3}{7}\). The reference parameters are considered as: \({\varphi _d} = \frac{\pi }{3}\), \({\Theta _d} = \frac{\pi }{6}\), \({\Omega _d} = \frac{\pi }{2}\), and \({z_d} = 3\). It should be noted that the suggested controller is adaptive, and there is no such big restriction on choosing the control parameters. (Table 1) The trajectories of states are shown in Fig. 5. The results show that \([{\chi _1},{\chi _3},{\chi _5},{\chi _7}] = [\varphi ,\Theta ,\Omega ,z]\) follow the reference values \([{\varphi _d},{\Theta _d},{\Omega _d},{z_d}]\). The stabilization of other states is done in a limited time. The simulations show that by the use of the suggested method, the transient responses are faster and smoother. From (53) the time period is computed as follows. Suppose \({t_0} = 0\) and \(\gamma = \frac{{\vartheta + 1}}{2} = \frac{{3/7 + 1}}{2} = 0.71\). From (48), \(\mu _1\) and \(\mu _2\) are computed as:

$$\begin{aligned} \begin{aligned}&{\mu _1} \le {2^\gamma }{\alpha _1}\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| \left[ {{{\left( {{\chi _4}{\chi _6}} \right) }^2} + {{({\bar{\Phi }} {\chi _4})}^2} + {\chi _2}^4} \right] = 0.00002425,\\&{\mu _2} \le 2{\kappa _1}^2{\beta _1}\left| {\frac{{\partial {s_1}}}{{\partial {u_2}}}} \right| = 30.97 \end{aligned} \end{aligned}$$
(60)

By replacing \(\mu _1\) and \(\mu _2\) in (53), the time period is computed as \({t_{{s_1}}} = 2.6\). The others are computed in same way and we have \({t_{{s_2}}} = 2.72\), \({t_{{s_3}}} \simeq 4.21\), \({t_{{s_4}}} = 5.19\).

The control signals are shown in Fig. 6. The signals are smooth with suitable magnitude and fluctuation. The sliding surface is given in Fig. 7. This figure shows that the sliding surface works well and it converges to zero in a short time. The sliding surface converges to zero faster than conventional methods. The sliding signals demonstrate finite-time convergence. The convergence of free parameters is given in Figs. 8 and 9. We see that unknown parameters are converged in a finite time. The trajectories of adapted parameters are smooth and fast. According to simulations, it can be approved that the suggested control is effective for time-limited tracking of the UAVs. To better demonstrate the applicability of the suggested controller, the results are compared with a similar T2-FLS-based controller [21]. In [21], a T2-FLS controller is designed for UAVs, and its accuracy is compared with PID. The designed system is tested using a software-in-the-loop simulator and actual flight experiments. The compared mean square errors (MSEs) are given in Table 2. The values of MSE show that the suggested T3-FLS based controller has better results.

Conclusion

In this paper, the adaptation laws for the dynamic model are derived through the stability analysis, and adaptation error is compensated by an adaptive T3-FLS. The suggested T3-FLS is trained to improve the stability and eliminate the effect of adaptation error of parameters and disturbances. The designed scheme is applied to a case-study UAV with unknown dynamics perturbed by disturbances. The core concept involves incorporating the fundamental dynamics of UAVs and devising adaptation laws to improve modeling precision. Additionally, an optimized T3-FLS with SMC is implemented to eradicate adaptation errors and guarantee robustness. The simulations show the efficacy of the proposed method in achieving rapid and smooth transient responses, as well as the stabilization of various states within a constrained timeframe. The sliding surface demonstrates exceptional performance, swiftly converging to zero and surpassing traditional methods. Moreover, the adaptation of unknown parameters exhibits finite-time convergence, characterized by smooth and expeditious trajectories. Ultimately, the simulation outcomes affirm the effectiveness of the developed control approach for time-constrained tracking and stability of UAVs, thereby contributing to advancements in the field of control systems and robotics.

Table 2 MSE comparison
Full size table