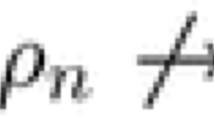1 Introduction and Main Results

Let D be a domain in the complex plane \({\mathbb {C}}\). A family \({\mathcal {F}}\) of meromorphic functions on D is said to be normal if from every sequence \(\{f_n\}\) in \({\mathcal {F}},\) we can extract a subsequence \(\{f_{n_k}\}\) which converges locally uniformly to f in D with respect to the spherical metric, where f is either a meromorphic function or identically equal to infinity in D. A family \({\mathcal {F}}\) is said to be normal at \(z_0\in D\) if it is normal in some neighborhood of \(z_0\); thus, \({\mathcal {F}}\) is normal in D if and only if it is normal at each point \(z\in D\). (see [14]).

Let f and g be two meromorphic functions in D and let \(a\in {\mathbb {C}}\). We shall denote by E(f, a) the set of zeros of \(f-a\) (ignoring multiplicities). We say that f and g share the value a if \(E(f,a)=E(g,a)\). Further, if \(E(f,a)\subset E(g,a)\), we say that f and g share the value a partially (see [18]).

According to Bloch’s principle [14], any condition which reduces a meromorphic function in \({\mathbb {C}}\) to a constant is likely to force a family of meromorphic functions in a domain D to be normal. Although this principle as well as its converse does not hold in general (see, for example [2, 13]), still it serves as a guiding principle for obtaining normality criteria corresponding to Picard-type theorems and vice versa (see [1]).

In 1959, Hayman [5] proved that if f is a meromorphic function in the complex plane, \(a \in {\mathbb {C}}{\setminus } \{0\}\) and the differential polynomial \(f^{'}-af^n, \ n\ge 5\), does not assume a finite complex value in \({\mathbb {C}}\), then f is constant. This result is not true for \(n=3,4\) as shown by Mues [10]. In view of Bloch’s principle, Hayman [6] in 1967 conjectured that there exists a normality criterion corresponding to this Picard-type theorem. Over the next few decades, the following normality criterion was established thereby proving the Hayman’s conjecture.

Theorem 1.1

Let \({\mathcal {F}}\) be a family of meromorphic (holomorphic) functions in a domain D, \(n\in {\mathbb {N}}\) and a, b be two finite complex numbers such that \(n\ge 3 \ (n\ge 2)\) and \(a\ne 0\). If for each \(f\in {\mathcal {F}}\), \(f^{'}-af^n\ne b\), then \({\mathcal {F}}\) is normal in D.

The proof of Theorem 1.1 for meromorphic functions is due to S. Li [8], X. Li [9] and Langley [7] for \(n\ge 5\), Pang [11] for \(n=4\), Chen and Fang [3] and Zalcman [17] for \(n=3\) independently and the proof of Theorem 1.1 for holomorphic functions is due to Drasin [4] for \(n\ge 3\) and Ye [16] for \(n=2\).

In 2008, Zhang [19] considered the idea of shared values and proved the following.

Theorem 1.2

Let \({\mathcal {F}}\) be a family of meromorphic (holomorphic) functions in D, \(n\in {\mathbb {N}}\) and a, b be two finite complex numbers such that \(n\ge 4 \ (n\ge 2)\) and \(a\ne 0\). If for each pair of functions f and g in \({\mathcal {F}}\), \(f^{'}-af^n\) and \(g^{'}-ag^n\) share the value b, then \({\mathcal {F}}\) is normal in D.

In this paper, we consider the related problems concerning two families of meromorphic functions and prove the following theorem:

Theorem 1.3

Let \({\mathcal {F}}\) and \({\mathcal {G}}\) be two families of holomorphic functions on a domain D, and \(a,\ b,\ c\) be three complex numbers such that \(a\ne 0\) and \(b\ne c\). Suppose that \({\mathcal {G}}\) is normal in D such that no sequence in \({\mathcal {G}}\) converges locally uniformly to infinity in D. If \(n\ge 2\) and for each function \(f\in {\mathcal {F}}\), there exists \(g\in {\mathcal {G}}\) such that \(f^{'}-af^{n}\) and \(g^{'}-ag^{n}\) partially share the values b and c, then \({\mathcal {F}}\) is normal in D.

In the following example, we show that the condition ‘partial sharing of two values b and c’ in Theorem 1.3 cannot be reduced to one.

Example 1.4

Consider the two families \({\mathcal {F}}:=\left\{ f_j(z)=e^{jz}:j\in {\mathbb {N}}\right\} \) and \({\mathcal {G}}:=\left\{ 1\right\} \) of holomorphic functions on \({\mathbb {D}}\). Note that \(g_j^{'}-g_j^2\equiv -1\). Therefore, \(f_j^{'}-f_j^2= -1\Rightarrow g_j^{'}-g_j^2=-1\). But \({\mathcal {F}}\) fails to be normal at \(z=0\).

We demonstrate in the subsequent example that Theorem 1.3 fails to be true when \(n=1\). Therefore, the condition \(n=2\) is the best possible for Theorem 1.3.

Example 1.5

Consider the two families \({\mathcal {F}}:=\left\{ f_j(z)=jz:j\in {\mathbb {N}}\right\} \) and \({\mathcal {G}}:=\left\{ -1\right\} \) of holomorphic functions on \({\mathbb {D}}\). Then, clearly, \(f_j^{'}(z)-f_j(z)=j(1-z)\ne 0\), and for each \(f_j\in {\mathcal {F}}\), there exists \(g_j\in {\mathcal {G}}\) such that \(f_j^{'}(z)-f_j(z)=1\Rightarrow g_j^{'}(z)-g_j(z)=1\). But \({\mathcal {F}}\) fails to be normal at \(z=0\).

The following example illustrates that Theorem 1.3 is not valid for the family of meromorphic functions when \(n=2\).

Example 1.6

Consider the two families

$$\begin{aligned} {\mathcal {F}}:=\left\{ f_j(z)=\frac{jz}{1+jz^2}:j\in {\mathbb {N}}\right\} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {G}}:=\left\{ 1\right\} \end{aligned}$$

of meromorphic functions on \({\mathbb {D}}\). Take \(a=-1\). Then, clearly, \(f_j^{'}(z)-af_j^2(z)=\frac{j}{(1+jz^2)^2}\ne 0\) and for each \(f_j\in {\mathcal {F}}\), there exists \(g_j\in {\mathcal {G}}\) such that \(f_j^{'}(z)-af_j^2(z)=1\Rightarrow g_j^{'}(z)-ag_j^2(z)=1\). But \({\mathcal {F}}\) is not normal at \(z=0\) since \(f_j(0)=0\) and for \(z\ne 0,\) \(f_j(z)\rightarrow 1/z\) as \(n\rightarrow \infty \).

However, Theorem 1.3 can be extended to families of meromorphic functions provided that \(n\ge 3\).

Theorem 1.7

Let \({\mathcal {F}}\) and \({\mathcal {G}}\) be two families of meromorphic functions on a domain D, and \(a,\ b,\ c\) be three finite complex numbers such that \(a\ne 0\) and \(b\ne c\). Suppose that \({\mathcal {G}}\) is normal in D such that no sequence in \({\mathcal {G}}\) converges locally uniformly to infinity in D. If \(n\ge 3\) and for each function \(f\in {\mathcal {F}}\), there exists \(g\in {\mathcal {G}}\) such that \(f^{'}-af^{n}\) and \(g^{'}-ag^{n}\) partially share the values b and c, then \({\mathcal {F}}\) is normal in D.

In the following example, we show that the condition ‘partial sharing of two values b and c’ in Theorem 1.7 cannot be reduced to one.

Example 1.8

Consider the two families

$$\begin{aligned} {\mathcal {F}}:=\left\{ f_j(z)=\frac{1}{jz}:j\in {\mathbb {N}}\right\} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {G}}:=\left\{ \frac{1}{z+\frac{1}{j^2}-1}:j\in {\mathbb {N}}\right\} \end{aligned}$$

of meromorphic functions on \({\mathbb {D}}\). Then for each \(f_j\in {\mathcal {F}},\) there exists \(g_j\in {\mathcal {G}}\) such that \(f_j^{'}-f_j^3=0\Rightarrow g_j^{'}-g_j^3=0\). Also, \(g_j(z)\rightarrow g(z)=\frac{1}{z-1}\not \equiv \infty \). But \({\mathcal {F}}\) fails to be normal at \(z=0\).

For \(n=2\), we have the following weak version of the Theorem 1.7.

Theorem 1.9

Let \({\mathcal {F}}\) and \({\mathcal {G}}\) be two families of meromorphic functions on a domain D such that each \(f\in {\mathcal {F}}\) has neither simple zeros nor simple poles. Let \(a,\ b\) and c be three finite complex numbers such that \(a\ne 0\) and \(b\ne c\). Suppose that \({\mathcal {G}}\) is normal in D such that no sequence in \({\mathcal {G}}\) converges locally uniformly to infinity in D. If for each function \(f\in {\mathcal {F}}\), there exists \(g\in {\mathcal {G}}\) such that \(f^{'}-af^{2}\) and \(g^{'}-ag^{2}\) partially share the values b and c, then \({\mathcal {F}}\) is normal in D.

Note that Example 1.6 also shows that the condition ‘each \(f\in {\mathcal {F}}\) has neither simple zeros nor simple poles’ in Theorem 1.9 can not be omitted.

2 Lemmas and Proof of the Results

To prove our results, we need the following lemmas.

Lemma 2.1

[12] Let \(\mathcal {F}\) be a family of meromorphic functions on the unit disk \({\mathbb {D}}\) such that all the zeros of \(f\in {\mathcal {F}}\) are of multiplicity at least p and all the poles of \(f\in {\mathcal {F}}\) are of multiplicity at least q. Suppose that \({\mathcal {F}}\) is not normal at \(z_0\in D\). Then, for every \(\alpha \in (-p, q)\), there exist

  1. (a)

    points \(z_n\) in \({\mathbb {D}}:\) \(z_n\rightarrow z_0;\)

  2. (b)

    functions \(f_n\in \mathcal {F};\)

  3. (c)

    positive real numbers \(\rho _n:\rho _n\rightarrow 0\)

such that the re-scaled sequence \(\left\{ g_n(\zeta )=\rho _{n}^{\alpha }f_n(z_n+\rho _n\zeta )\right\} \) converges spherically locally uniformly on \(\mathbb {C}\) to a non-constant meromorphic function g on \({\mathbb {C}}\) of finite order.

Lemma 2.2

[3] Let f be a meromorphic function in \({\mathbb {C}}\), and let n be a positive integer. If \(f^nf^{'}\) does not assume a non-zero finite complex number in \({\mathbb {C}}\), then f is constant.

Lemma 2.3

[15] Let f be a meromorphic function in \({\mathbb {C}}\) and b be a non-zero complex number. If f has neither simple zero nor simple pole and \(f^{'}(z)\ne b\), then f is constant.

Proof of the Theorem 1.3

We may consider D to be an open unit disk \({\mathbb {D}}.\) Suppose that the family \({\mathcal {F}}\) is not normal at \(z_0\in {\mathbb {D}}\). Then by Lemma 2.1, there exist points \(z_j\in {\mathbb {D}}\) with \(z_j\rightarrow z_0\), a sequence of positive numbers \(\rho _j\rightarrow 0\) and a sequence of functions \(f_j\in {\mathcal {F}}\) such that

$$\begin{aligned} F_j(\zeta )=\rho _j^{\frac{1}{n-1}}f_j(z_j+\rho _j\zeta )\rightarrow F(\zeta ) \end{aligned}$$
(2.1)

is locally uniformly on \({\mathbb {C}}\), where F is a non-constant entire function of finite order.

From (2.1), we have

$$\begin{aligned} \displaystyle \rho _j^{\frac{n}{n-1}}\{(f^{'}_j-af^{n}_j)(z_j+\rho _j\zeta )-b\}=(F^{'}_j-aF^{n}_j)(\zeta )-\rho _j^{\frac{n}{n-1}}b\rightarrow F^{'}(\zeta )-a F^{n}(\zeta )\nonumber \\ \end{aligned}$$
(2.2)

and

$$\begin{aligned} \displaystyle \rho _j^{\frac{n}{n-1}}\{(f^{'}_j-af^{n}_j)(z_j+\rho _j\zeta )-c\}=(F^{'}_j-aF^{n}_j)(\zeta )-\rho _j^{\frac{n}{n-1}}c\rightarrow F^{'}(\zeta )-a F^{n}(\zeta )\nonumber \\ \end{aligned}$$
(2.3)

locally uniformly on \({\mathbb {C}}\).

For each \(f_j\in {\mathcal {F}}\), there exists \(g_j\in {\mathcal {G}}\) such that \(f_j^{'}-af_j^n\) and \(g_j^{'}-ag_j^n\) share the values b and c partially in \({\mathbb {D}}\). Since \({\mathcal {G}}\) is normal, there exists a subsequence in \(\{g_j\}\), again denoted by \(\{g_j\}\), that converges uniformly to a holomorphic function \(g(z)\not \equiv \infty \) in some neighborhood of \(z_0\).

Suppose \((F^{'}-aF^{n})\not \equiv 0\) otherwise \(\frac{-1}{n-1}\frac{1}{F^{n-1}}\equiv a\zeta + d\), for some \(d\in {\mathbb {C}}\), which contradicts to the fact that F is an entire function and \(n\ge 2\). Further, suppose that \((F^{'}-aF^{n})(\zeta )\ne 0\), \(\zeta \in {\mathbb {C}}\). Then \(\frac{F^{'}}{F^{n}}\ne a\). By setting \(F=1/\phi \), we have \(\phi ^{n-2}\phi ^{'}\ne -a\). When \(n\ge 3\), \(\phi \) is constant by Lemma 2.2 and when \(n=2\), \(\phi \) is again constant by Hayman’s alternative since \(\phi \ne 0\) and \(\phi ^{'}\ne -a\). In both cases, \(\phi \) is constant. This implies that F is constant, a contradiction. Thus, \((F^{'}-aF^{n})\) has at least one zero.

Now we have two cases:

Case-I. \((g^{'}-ag^{n})(z_0)\ne b\).

Suppose that \((F^{'}-aF^{n})(\zeta _0)= 0\), for some \(\zeta _0\in {\mathbb {C}}\). From (2.2), by Hurwitz’s theorem, there exists a sequence \(\{\zeta _j\}\) with \(\zeta _j\rightarrow \zeta _0\) such that for sufficiently large j

$$\begin{aligned} (F^{'}_j-aF^{n}_j)(\zeta _j)-\rho _j^{\frac{n}{n-1}}b=0, \end{aligned}$$

and thus

$$\begin{aligned} (f^{'}_j-af^{n}_j)(z_j+\rho _j\zeta _j)=b. \end{aligned}$$

By hypothesis, we have \((g^{'}_j-ag^{n}_j)(z_j+\rho _j\zeta _j)=b\) and so \((g^{'}-ag^{n})(z_0)=b\), a contradiction.

Case-II. \((g^{'}-ag^{n})(z_0) = b.\)

By using (2.3) instead of (2.2) in Case-I, we obtain \((g^{'}-ag^{n})(z_0)=c\ (\ne b)\) which is not true. This completes the proof. \(\square \)

Proof of the Theorem 1.7

We may consider D to be an open unit disk \({\mathbb {D}}.\) Suppose that the family \({\mathcal {F}}\) is not normal at \(z_0\in {\mathbb {D}}\). Then there exists a sequence \(\{f_n\}\subset {\mathcal {F}}\) which has no locally convergent subsequence at \(z_0\). Thus, by Lemma 2.1, there exist points \(z_j\in {\mathbb {D}}\) with \(z_j\rightarrow z_0\), a sequence of positive numbers \(\rho _j\rightarrow 0\), and a sequence of functions in \(\{f_j\}\) again denoted by \(\{f_j\}\) such that

$$\begin{aligned} F_j(\zeta )=\rho _j^{\frac{1}{n-1}}f_j(z_j+\rho _j\zeta )\rightarrow F(\zeta ) \end{aligned}$$
(2.4)

locally uniformly on \({\mathbb {C}}\) with respect to spherical metric, where F is a non-constant meromorphic function on \({\mathbb {C}}\) of finite order.

From (2.4), we have

$$\begin{aligned} \left( F^{'}_j-aF^{n}_j\right) (\zeta )-\rho _j^{\frac{n}{n-1}}b=\rho _j^{\frac{n}{n-1}}\{(f^{'}_j-af^{n}_j)(z_j+\rho _j\zeta )-b\}\rightarrow F^{'}(\zeta )-a F^{n}(\zeta )\nonumber \\ \end{aligned}$$
(2.5)

and

$$\begin{aligned} \left( F^{'}_j-aF^{n}_j\right) (\zeta )-\rho _j^{\frac{n}{n-1}}c=\rho _j^{\frac{n}{n-1}}\{(f^{'}_j-af^{n}_j)(z_j+\rho _j\zeta )-c\}\rightarrow F^{'}(\zeta )-a F^{n}(\zeta )\nonumber \\ \end{aligned}$$
(2.6)

spherically locally uniformly on \({\mathbb {C}}\) except possibly at the poles of F.

For each \(f_j\in {\mathcal {F}}\), there exists \(g_j\in {\mathcal {G}}\) such that \(f_j^{'}-af_j^n\) and \(g_j^{'}-ag_j^n\) partially share the values b and c in \({\mathbb {D}}\). Since \({\mathcal {G}}\) is normal, there exists a subsequence in \(\{g_j\}\), again denoted by \(\{g_j\}\), that converges uniformly to a meromorphic function \(g(z)\not \equiv \infty \) in some neighborhood of \(z_0\).

Claim. \((F^{'}-aF^{n})(\zeta _0)=0\), for some \(\zeta _0\in {\mathbb {C}}\).

Suppose that \((F^{'}-aF^{n})(\zeta )\ne 0\). Then \(\frac{F^{'}}{F^{n}}\ne a\). By setting \(F=1/\phi \), \(\phi ^{n-2}\phi ^{'}\ne -a\). By Lemma 2.2, \(\phi \) and so F is constant, a contradiction. This proves the claim.

Now we have three cases:

Case-I. \((g^{'}-ag^{n})(z_0)\ne b,\infty \).

By Claim, \((F^{'}-aF^{n})(\zeta _0)= 0\), for some \(\zeta _0\in {\mathbb {C}}\). Since \((F^{'}-aF^{n})\not \equiv 0\), otherwise \(\frac{-1}{n-1}\frac{1}{F^{n-1}}\equiv a\zeta + d\), for some \(d\in {\mathbb {C}}\), which contradicts to the fact that F is a non-constant meromorphic function and \(n\ge 3\), by (2.5), there exists a sequence \(\{\zeta _j\}\) with \(\zeta _j\rightarrow \zeta _0\) such that for sufficiently large j, \((f^{'}_j-af^{n}_j)(z_j+\rho _j\zeta _j)=b.\) By assumption, we have \((g^{'}_j-ag^{n}_j)(z_j+\rho _j\zeta _j)=b\) and so \((g^{'}-ag^{n})(z_0)=b\), a contradiction.

Case-II. \((g^{'}-ag^{n})(z_0) = b.\)

Using (2.6) instead of (2.5) in Case-I, we obtain \((g^{'}-ag^{n})(z_0)=c\ (\ne b)\), which is not true.

Case-III. \((g^{'}-ag^{n})(z_0) = \infty .\)

Then, clearly, \(g(z_0)=\infty \). Suppose that \(z_0\) is a pole of g with multiplicity \(k\ge 1\). Then, for sufficiently large j, \(g_j\) has exactly \(l\le k\) distinct poles \(z_j^1,\ldots , z_j^l\) in \(D(z_0,r)\) with multiplicities \(\alpha _1,\ldots ,\alpha _l\) respectively such that \(z_j^i\rightarrow z_0\ (i=1,\ldots , l)\) and \(\sum _{i=1}^{l}\alpha _i=k\). Renumbering if possible, we may assume that the number l and multiplicities \(\alpha _i, i=1,\ldots , l\) are independent of j. Now set

$$\begin{aligned} H_j(z):=g_j(z)\prod _{i=1}^{l}(z-z_j^i)^{\alpha _i}. \end{aligned}$$

Then the functions \(H_n\) are holomorphic in \(D(z_0,r)\) and \(H_n\rightarrow H\) on \(D(z_0,r/2)\setminus \{z_0\}\), where \(H(z)=g(z)(z-z_0)^k\) is holomorphic on \(D(z_0,r)\). Note that \(H(z_0)\ne 0, \infty .\) Hence by maximum principle, \(H_n\rightarrow H\) on \(D(z_0,r/2)\).

We have

$$\begin{aligned} g_j^{'}(z)&=\left( H_{j}(z)\prod _{i=1}^l(z-z_{j}^{i})^{-\alpha _{i}}\right) ^{'}\nonumber \\&=H_j^{'}(z)\prod _{i=1}^l(z-z_j^{i})^{-\alpha _i}-H_j(z)\sum _{i=1}^l\alpha _i(z-z_j^{i})^{-\alpha _{i}-1}\prod _{s\ne i}(z-z_j^{s})^{-\alpha _s}\nonumber \\&=\prod _{i=1}^{l}(z-z_j^{i})^{-\alpha _i-1}\left( H_j^{'}\prod _{i=1}^l(z-z_j^{i})-H_j(z)\sum _{i=1}^l\alpha _i\prod _{s\ne i}(z-z_j^{s})\right) . \end{aligned}$$
(2.7)

Then

$$\begin{aligned} g_j^{'}(z)-ag_j^n(z)-b&=K_j(z)\prod _{i=1}^l (z-z_{j}^{i})^{-\alpha _i-1}, \end{aligned}$$
(2.8)

where

$$\begin{aligned} K_j(z) =&H_j^{'}\prod _{i=1}^l(z-z_j^{i})-H_j(z)\sum _{i=1}^l\alpha _i\prod _{s\ne i}(z-z_j^{s})\nonumber \\&-aH_j^n(z)\prod _{i=1}^l (z-z_{j}^i)^{-\alpha _i(n-1)+1}-b\prod _{i=1}^{l}(z-z_j^{i})^{\alpha _i+1}. \end{aligned}$$
(2.9)

Since \(H(z_0)\ne 0,\infty \), we have

$$\begin{aligned} K_j(z)&\rightarrow H^{'}(z)(z-z_0)^l-H(z) k(z-z_0)^{l-1}-\frac{aH^n(z)}{(z-z_0)^{k(n-1)-l}}-b(z-z_0)^{k+l}\nonumber \\&=\frac{1}{(z-z_0)^{k(n-1)-l}}\left\{ H^{'}(z)(z-z_0)^{k(n-1)}-kH(z)(z-z_0)^{k(n-1)-1}\right. \nonumber \\&\quad \left. -aH^n(z)-b(z-z_0)^{nk}\right\} \end{aligned}$$
(2.10)

and

$$\begin{aligned}&\left( H^{'}(z)(z-z_0)^{k(n-1)}-kH(z)(z-z_0)^{k(n-1)-1}-aH^n(z)-b(z-z_0)^{nk}\right) _{z=z_0}\nonumber \\&\quad =-aH^n(z_0)\ne 0. \end{aligned}$$
(2.11)

Therefore, \(K_j(z)\) and so \(g_j^{'}(z)-ag_j^n(z)-b\) has no zeros in some neighborhood of \(z_0\). By assumption, we find that \(f_j^{'}(z)-af_j^n(z)-b\) has no zero in some neighborhood of \(z_0\). By Theorem 1.1, the sequence \(\{f_j\}\) is normal at \(z_0\), a contradiction. \(\square \)

Proof of the Theorem 1.9

Following the proof of Theorem 1.7, we only need to prove that \(F^{'}-aF^{2}\not \equiv 0\) and \(F^{'}-aF^{2}\) has at least one zero. Suppose that \(F^{'}-aF^{2}\equiv 0\). Then \((\frac{1}{F})^{'}\equiv a\) which implies that \(\frac{1}{F}\equiv a\zeta + d\), for some \(d\in {\mathbb {C}}\), which contradicts the fact that F has no simple pole. Next, suppose that \(F^{'}-aF^{2}\ne 0\). Then \(\frac{F^{'}}{F^{2}}\ne a\). We set \(F=1/\phi \), \(\phi ^{'}\ne -a\). By Lemma 2.3, \(\phi \) and so F is a constant, a contradiction. \(\square \)