Self-Similar Groups and Holomorphic Dynamics: Renormalization, Integrability, and Spectrum

Abstract

In this paper, we explore the spectral measures of the Laplacian on Schreier graphs for several self-similar groups (the Grigorchuk, Lamplighter, and Hanoi groups) from the dynamical and algebro-geometric viewpoints. For these graphs, classical Schur renormalization transformations act on appropriate spectral parameters as rational maps in two variables. We show that the spectra in question can be interpreted as asymptotic distributions of slices by a line of iterated pullbacks of certain algebraic curves under the corresponding rational maps (leading us to a notion of a spectral current). We follow up with a dynamical criterion for discreteness of the spectrum. In case of atomic spectrum, the precise rate of convergence of finite-scale approximands to the limiting spectral measure is given. For the three groups under consideration, the corresponding rational maps happen to be fibered over polynomials in one variable. We reveal the algebro-geometric nature of this integrability phenomenon.

1 Introduction

Spectral theory of the Laplacian is a classical area of Mathematical Physics, with deep connections to Geometry, Probability, Dynamics, Geometric Group Theory, and Number Theory. From the point of view of Quantum Mechanics, it describes the observable energy spectrum of a free particle moving in the space under consideration. In this interpretation, the dichotomy between atomic and continuous spectrum roughly corresponds to the difference between insulating and conducting states of matter (see [24] and Sect. 2.5 for more about this).

In a series of works by Bartholdi, Grigorchuk, Nekrashevich, Sunić, Zuk, and others [4, 30, 50,51,52,53, 59, 60, 62] over the past 20 years, the spectral problem for Cayley, and more generally Schreier graphs has been explored for discrete self-similar groups. Homogeneity and self-similarity of the corresponding spaces leads to invariance of the spectrum under Schur Renormalization transformations, which sometimes happen to be rational maps in two variables. This allowed the authors to describe the spectrum of the corresponding Schreier graphs in three remarkable cases: the Grigorchuk ${\mathcal {G}}$, Lamplighter ${\mathcal {L}}$, and Hanoi ${\mathcal {H}}$ group. In particular, the spectrum turned out to be absolutely continuous in the former case and discrete in the latter two.

In this paper, we bring ideas from Holomorphic Dynamics and Algebraic Geometry to give a new insight into the above spectral phenomena. Namely, we take a close look at the dynamics of the corresponding renormalization transformations and relate the spectral results to the equidistribution theory for dynamical pullbacks of holomorphic curves. We also analyze the nature of integrability of these transformations (that happen to be fibered over one-dimensional maps). In particular, we give a general algebro-geometric criterion for integrability (in the spirit of Diller and Favre [26]) that can be applied to each of the groups in question. This allows us to put all the previous results in a general framework.

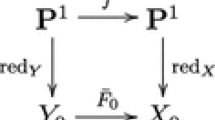
To set up the renormalization scheme (for the above three self-similar groups), one needs to introduce an extra spectral parameter and the corresponding two-parameter pencil of operators. In the nth scale this pencil is reduced to a pencil of matrices of size $d^n$ (where $d=2$ for the groups ${\mathcal {G}}$ , ${\mathcal {L}}$ and $d=3$ for ${\mathcal {H}}$ corresponding to the branching number of the regular tree on which the groups acts). Letting $P_n \in {\mathbb {C}}[{\lambda },\mu ]$ be the characteristic polynomial of that matrix pencil, one obtains the following spectral relation between two consecutive scales:

$$\begin{aligned} P_{n+1} = Q^{d^{n}} \cdot ( P_{n} \circ R ), \end{aligned}$$

(1.1)

where $Q\in {\mathbb {C}}[{\lambda }, \mu ]$, $P_ 0$ is linear, and $R:{\mathbb {C}}^2 \dashrightarrow {\mathbb {C}}^2$ is the renormalization rational map. For the groups ${\mathcal {G}}$, ${\mathcal {H}}$ and ${\mathcal {L}}$, the transformation R is given by the following explicit expressions, respectively:

$$\begin{aligned} R_{{\mathcal {G}}} (\lambda , \mu )&:= \left( \frac{2{\lambda }^2}{4-\mu ^2}, \ \mu + \frac{\mu {\lambda }^2}{4-\mu ^2} \right) ,\\ R_{{\mathcal {L}}}(\lambda ,\mu )&:= \left( - \dfrac{\lambda ^2 - \mu ^2 -2 }{\mu - \lambda } , -\dfrac{2}{\mu - \lambda } \right) ,\\ R_{{\mathcal {H}}}(\lambda ,\mu )&:= \left( \lambda + \dfrac{2\mu ^2 (-\lambda ^2 + \lambda + \mu ^2)}{ (\lambda -1 -\mu )(\lambda ^2 -1 + \mu -\mu ^2 )} ,\right. \\ {}&\qquad \left. \dfrac{\mu ^2 ({\lambda }-1+\mu )}{({\lambda }-1 -\mu )({\lambda }^2 -1 + \mu -\mu ^2 )} \right) . \end{aligned}$$

It shows a clear connection between the spectral algebraic curves $\Gamma _n = \{ P_n = 0\}$ and iterated pullbacks of the initial line $\Gamma _0$ by the rational map R. We obtain the spectral current T of a pencil of operators as the limit in the sense of currents

$$\begin{aligned} T = \lim _{n\rightarrow +\infty } \dfrac{1}{d^n} [P_n=0], \end{aligned}$$

(1.2)

when it exists. This current is supported on an algebraic curve lamination related to the Julia set of R in the Hanoi case and Grigorshuk cases, and to the non-wandering set in the Lamplighter case.¹

The desired spectral measure ${\omega }$ for the Laplacian is the slice of this current by an appropriate line $\{ \lambda = \textrm{const}\}$ and is called the density of states, or is referred in [56, 59] as the KNS spectral measure (after Kesten, Von Neumann and Serre).

The density of states for the groups ${\mathcal {G}}$, ${\mathcal {H}}$ and ${\mathcal {L}}$ (naturally acting on the corresponding regular trees) were described in the papers [4, 51] and [54] respectively. In this paper, we will interprete these results from the outlined dynamical viewpoint, and, for the latter two groups, give the rate of convergence ${\omega }_n\rightarrow {\omega }$, where ${\omega }_n$ is the counting measure for the corresponding eigenvalues in n-th scale.

Theorem A

The following properties hold.

• (i) The density of states ${\omega }$ associated with ${\mathcal {G}}$ is absolutely continuous with respect to the Lebesgue measure (with an explicit density) supported on the union of two intervals. This measure is the pushforward by $\mu \mapsto (\mu +1)/4$ of the slice of the Green current of the renormalization map $R_{\mathcal G}$ by the appropriate line. Its support is the image by the above affine transformation of the slice of the Julia set of $R_{\mathcal G}$ (see Sect. 5.2 and Theorem 5.11).

• (ii) The density of states associated with the group ${\mathcal {L}}$ is atomic, and

  $$\begin{aligned} \omega _n - \omega \sim n/2^{n-1}\, m \end{aligned}$$

  where m is the Lebesgue measure on the interval. This interval (equal to the support of $\omega$) is the slice of the “neutral cylinder” (see Sect. 3.6.2) of the renormalization transformation $R_{\mathcal L}$.

• (iii) The density of states associated with the group ${\mathcal {H}}$ is atomic as well, and

  $$\begin{aligned} {\omega }_n - {\omega }\sim \dfrac{25}{6} \cdot \dfrac{2^n}{3^{n}} \, m \end{aligned}$$

  where m is a Bernoulli measure on a Cantor set K. This Cantor set is the slice of the Julia set (see Sect. 7.2) of the renormalization transformation $R_{\mathcal H}$ by the appropriate line. Moreover, the support of the density of states for ${\mathcal H}$ consists of a countable set of eigenvalues accumulating on K.

Remark 1.1

It turns out that the Hanoi group can be realized as the iterated monodromy group of the rational function $z^2 + 16 /27 z$ whose Julia set is homeomorphic to the Sierpinski gasket [51]. A similar notion of density of states was defined for various fractal sets in [70, 86]. It has been intensely studied for the Sierpinski gasket [38, 69, 79, 87] and other fractals [17, 83, 84]. It would be interesting to explore if there is a direct connection between assertion (iii) and these results.

Remark 1.2

The Julia set for the map $R_{\mathcal G}$ (and for closely related map $R_{\mathcal D}$ for the infinite dihedral group) was independently studied by Goldberg and Yang [41] (see the discussion in Sect.  3.4 for more details).

What makes these results quite easy from the dynamical viewpoint is the “integrability” of the corresponding renormalization transformations. The respective integrals were explicitly given in [4, 51, 54] and communicated to us privately by Vorobets [88]. They lead to the following simple dynamical models:

Theorem B

• (i) There exists two forward invariant domain $U_1, U_2$ whose union is the complement of 4 lines and a conic of ${\mathbb {C}}^2$ such that the restriction of $R_{\mathcal {G}}$ on each $U_i$ is conjugate via a biholomorphic map to the following direct product:

  $$\begin{aligned} (\lambda ,\mu ) \mapsto (\lambda , \mu ^2). \end{aligned}$$

  In this model, the Julia set of $R_ {\mathcal G}$ is equal to the direct product ${\mathbb {C}}\times {\mathbb {T}}$. The original Julia set of $R_{\mathcal G}$ is foliated by complex conics parametrized by an interval.

• (ii) [54] The Lamplighter map $R_{{\mathcal {L}}} :{\mathbb {C}}^2 \dashrightarrow {\mathbb {C}}^2$ is conjugate via an invertible rational map on ${\mathbb {C}}^2$ to the following (rational) skew product:

  $$\begin{aligned} (\lambda , \mu ) \in {\mathbb {C}}^2 \mapsto \left( \lambda , \dfrac{ \lambda \mu - 4}{\mu }\right) \in {\mathbb {C}}^2. \end{aligned}$$

  In this model, the recurrent part of the dynamics is supported by the fixed points locus and the elliptic cylinder.

• (iii) The Hanoi map $R_{{\mathcal {H}}} :{\mathbb {C}}^2 \dashrightarrow {\mathbb {C}}^2$ is conjugate via an invertible rational map on ${\mathbb {C}}^2$ to the following (rational) skew product:

  $$\begin{aligned} (\lambda ,\mu ) \in {\mathbb {C}}^2 \mapsto \left( {\lambda }^2 - {\lambda }- 3 , \dfrac{({\lambda }-1)({\lambda }+2)}{{\lambda }+3} \mu \right) \in {\mathbb {C}}^2. \end{aligned}$$

  In this model, the Julia set of $R_{\mathcal H}$ is equal to the product of the Julia set of ${\lambda }^2-{\lambda }-3$ (which is a hyperbolic Cantor set) times ${\mathbb {C}}$.

Remark 1.3

In [55], the authors asked whether the spectrum is also atomic in the case of the Basilica group, which is the iterated monodromy group for the Julia set of $z^2-1$ [78, §3.9.2]. Though the corresponding renormalization is not integrable, our criterion for atomicity (formulated in Theorem D below) is still applicable due to the fact that the dynamical degree (calculated by Eric Bedford) turns out to be non-integer in this case. We will discuss it in a forthcoming paper ([9] this problem was independently studied in [17]).

Our main focus in this paper is to analyze the nature of this integrability phenomenon, i.e., to identify from general principles invariant fibrations for the maps under consideration. Note with this respect, that though meromorphic surface maps preserving fibrations are classified (see [21, 26, 34]) and certain criteria are known to rule out the existence of an invariant fibration [11, 67], there is no general method of identifying an invariant fibration for a given non-invertible rational surface map.

We provide two ways to identify the above fibrations:

• Either by considering some explicit invariant pencils of conics passing through special points of the maps $R =R_{{\mathcal {G}}}, R_{{\mathcal {L}}}, R_{{\mathcal {H}}}$, namely certain points of indeterminacy and certain fixed/prefixed points;

• Or else, by means of a systematic algebro-geometric approach.

In the latter approach, inspired by [18, 26, 40], we develop an algebraic criterion to detect presence of an invariant (rational) fibration and give a method to calculate an explicit semi-conjugacy. Let us explain briefly the ideas behind our criterion. To construct an explicit semi-conjugacy, one has to find a rational map $\pi :{\mathbb {C}}^2 \rightarrow {\mathbb {C}}$ which semi-conjugates R to a one dimensional map. To this end we apply some ideas from the Minimal Model Program which provides a setting in which one can contract a rational curve to a point. A natural condition, due to Mori (see e.g [71]), is to ask that those curves intersect negatively the first Chern class of the canonical bundle in our space. When this happens, we obtain a map $\pi :{\mathbb {C}}^2 \rightarrow {\mathbb {C}}^k$ where k is either 0, 1 or 2. We then add an additional condition on the contracted curves so that the Riemann–Roch–Hirzebruch formula rules out the cases $k= 0,2$.

To state our next result, we interpret the contracted curves as the [zero and polar loci] of particular holomorphic sections of a holomorphic line bundle whose first Chern class is cohomologically equivalent to the integration along these sections and compute the intersection of classes as a cup-product in the deRham cohomology of ${\mathbb {P}}^2$.

Theorem C

Let $R :{\mathbb {P}}^2 \dashrightarrow {\mathbb {P}}^2$ be a dominant rational map.² Suppose that there exists a surface X obtained from ${\mathbb {P}}^2$ by a finite sequence of blow-ups of ${\mathbb {P}}^2$, an integer $k \geqslant 1$, and a line bundle L on X whose first Chern class $c_1(L) \in H^2(X,{\mathbb {Z}})$ satisfies the following conditions.

• (i) $c_1(L) \cdot c_1(L) = 0$ in $H^4(X,{\mathbb {Z}}) \simeq {\mathbb {Z}}$.

• (ii) For any curve C on X, the intersection $[C] \cdot c_1(L) \in H^{4}(X,{\mathbb {Z}})$ is non-negative where [C] denotes the cohomology class in $H^2(X,{\mathbb {Z}})$ induced by C.

• (iii) $c_1(L) \cdot K_X < 0$ in $H^{4}(X,{\mathbb {Z}})$ where $K_X$ is the first Chern class of the canonical bundle on X.

• (iv) The pullback of the line bundle $R^* L$ by R is isomorphic to the line bundle $L^{\otimes k}$.

  Then the rational map R is rationally semi-conjugate to a degree k rational map on a curve.

Now let us outline some ideas of the proofs.

Theorem C produces a particular semi-conjugacy whose fibers are rational curves. Our proof follows closely the (non-dynamical) construction of a contraction morphism on a ruled surface [71, Theorem 1.28 (2)]. We then show that our criterion applies to the three maps, $R_{{\mathcal {G}}}, R_{{\mathcal {L}}}, R_{{\mathcal {H}}}$, under consideration.

Once Theorem B is proved, then one proves successively the two assertions of Theorem A.

For the first assertion, we let $R = R_{{\mathcal {G}}}$, $d=2$, $P_0= 2 - \lambda - \mu$, and we interpret the density of states $\omega _{{\mathcal {G}}}$ in Theorem A associated with the group ${\mathcal {G}}$ as the limiting measure given by:

$$\begin{aligned} \omega _{\mathcal {G}} = \lim _{n\rightarrow +\infty } \dfrac{1}{2^n} R_{{\mathcal {G}}}^{-n} \{ P_0 =0 \} \cap \{\lambda = -1 \}, \end{aligned}$$

where the intersection $R_G^{-n} \{ P_0 =0 \} \cap \{\lambda = -1 \}$ is the counting measure on the line $\lambda =-1$. The above formula shows that the convergence to the density of states is related to the behavior of the iterated preimage of the curve $\{P_0=0\}$ by $R_{{\mathcal {G}}}^n$ which is a classical equidistribution problem in the two-dimensional holomorphic dynamics [7, 15, 28, 33, 82].

A typical result of this theory asserts that iterated pullbacks of a generic algebraic curve converge to a canonical equivariant current called the Green current (see Sect. 3.3 for a more detailed discussion). Our goal is to justify this assertion in our three special cases. Since in each case the pullback $R_{{\mathcal {G}}}^{-n} \{ P_0 =0 \}$ coincides with the spectrum of the spectral operator pencil on level n, we come up with the interpretation of the Green current as the spectral current for our pencil (and thus, for the corresponding group action).

Let us now dwell on each of our groups, one by one. As $R_{{\mathcal {G}}}$ is conjugate to a simple model ${\text {id}}\times z^2$ on two domains whose union is a Zariski open set of ${\mathbb {C}}^2$, it is easy to show directly that the sequence of curves

$$\begin{aligned} \dfrac{1}{2^n} R_{{\mathcal {G}}}^{-n}\{ P_0 = 0\} \end{aligned}$$

converges towards the Green current of $R_{{\mathcal {G}}}$, while their slices converge to the corresponding transverse measure. (For more general results of this kind see [19, 32].) We recover directly the so-called “joint spectrum” of a particular pencil [41] by looking at the support of the Green current and our approach using currents gives a quantitative way to measure this set. In this case, one finds that the spectral current $T_{{\mathcal {G}}}$ is a current representable by integration or the geometric current in Sullivan’s terminology (see e.g [77, §4.3B]) supported on the union of hyperbolas:

$$\begin{aligned} T_{{\mathcal {G}}}:= \int _{-1}^{1} [4-\mu ^2+{\lambda }^2 - 4\theta \, {\lambda }=0] \ \dfrac{{\text {d}}\theta }{2\pi \sqrt{1 - \theta ^2}} , \end{aligned}$$

(1.3)

where $[4-\mu ^2+{\lambda }^2 - 4\theta \, {\lambda }=0]$ denotes the current of integration on the corresponding hyperbola.

For the Lamplighter and Hanoi group, their spectral currents $T_{\mathcal {L}}$ and $T_{{\mathcal {H}}}$ are both supported on a countable union of curves (instead of a continuum) and one obtains an asymptotic expansion:

$$\begin{aligned} T_{\mathcal {L}}= & {} T_{n, {\mathcal {L}}} - \dfrac{n}{2^{n-1}} \int _{-2}^{2} [\lambda + \mu = \eta ] \ \dfrac{ 2{\text {d}}\eta }{\sqrt{4 - \eta ^2}} + o \left( \dfrac{n}{2^n} \right) ,\\ T_{\mathcal {H}}= & {} T_{n , {\mathcal {H}}} - \dfrac{25 \cdot 2^{n-1}}{6 \cdot 3^n} \int _{{\mathcal {J}}(p)} [\lambda ^2 - 1 - \lambda \mu - 2 \mu ^2 = \eta \mu ] \ {\text {d}}m_p(\eta ) + o \left( \dfrac{2^n}{3^n} \right) , \end{aligned}$$

where $T_{n,{\mathcal {L}}}, T_{n , {\mathcal {H}}}$ are some currents supported on $2^n$ and $3^n$ curves respectively and $m_p$ is the measure of maximal entropy associated to the polynomial $p = z^2 - z -3$.

The proof of the second and third statement of Theorem A is also of dynamical nature. The fact that the spectrum is atomic follows from a discrepancy between the branching degree d of the regular tree T under consideration and the first dynamical degree of the renormalization transformation $R_{{\mathcal {L}}}, R_{{\mathcal {H}}}, R_{{\mathcal {B}}}$, respectively.

The first dynamical degree $\lambda _1(R)$ is defined formally as:

$$\begin{aligned} \lambda _1(R) :=\limsup _{n\rightarrow +\infty } (\deg R^n)^{1/n}, \end{aligned}$$

(where $\deg R^n$ denotes the algebraic degree of $R^n$) and measures the growth of the degree of the iterated preimages of generic algebraic curves.

For the Lamplighter group, $\lambda _1(R_{{\mathcal {L}}}) = 1$ whereas $d=2$, and for the Hanoi group, $\lambda _1(R_{{\mathcal {H}}}) = 2$ whereas $d=3$. To understand the spectral measure, we expand the inductive formula (1.1) into:

$$\begin{aligned} P_n = \left( \prod _{i=0}^{n} Q^{d^{n-1-i}} \circ R^i \right) P_0 \circ R^n. \end{aligned}$$

Observe that there are two different contributions for the growth of the degree of $P_n$, one from the power of d and the other from the iteration of R. We then show that when $\lambda _1(R) < d$, then the function $1/d^n\log |P_n|$ converges to a non-constant function which is equal to $-\infty$ on countably many curves making the density of states atomic.

Theorem D

Take a dominant rational transformation $R:{\mathbb {C}}^2 \dashrightarrow {\mathbb {C}}^2$ and take some polynomials $P_n \in {\mathbb {C}}[{\lambda }, \mu ]$ of degree $d^n$ in the variable $\mu$ satisfying:

$$\begin{aligned} P_{n+1} = Q^{d^{n-k}} \cdot ( P_n \circ R ), \end{aligned}$$

for all integer n, where Q is a fixed polynomial and where $k=0,1,2$. If $\lambda _1(R) < d$, then for any $\lambda _0 \in {\mathbb {C}}$ for which the line $\{\lambda = \lambda _0 \}$ is not contained in any of the curves $\{Q\circ R^n =0\}, \{ P_0\circ R^n =0 \}$ for all n, any weak *-limit point of the sequence of probability measures $1/d^n [P_n(\lambda _0, \cdot ) =0]$ is atomic.

This second statement and its proof are reminiscent of the Dichotomy Theorem by Sabot [83, Theorem 4.1], who observed a similar phenomenon for different rational maps arising from the study of the spectrum of the Laplacian for a class of self-similar sets. In our setting, Theorem D applies to the Lamplighter and Hanoi group and shows that the density of states associated to these two groups is atomic.

Remark 1.4

This project originated at a conference in Saas-Fee in March 2016 as a discussion (nicknamed “Saas-Fee nightmares”) of the dynamical interpretation of the density of states for ${\mathcal {G}}$. It was obtained shortly afterwards and was announced at a conference in the Fields Institute in May 2019. The Lamplighter and Hanoi groups were studied later; the corresponding results were announced at a Luminy meeting in January 2020.

2 Background on Spectra of Graphs and Groups

2.1 General Spectral Theory

The study of spectral properties of operators on groups and graphs is very interesting and important. There are hundreds (if not thousand) of articles on spectra of finite graphs (including such topics as expanders and Ramanujan graphs) and many books on that subject.

By spectrum of a graph $\Gamma =(V,E)$, one means the spectrum of the Laplace operator L. In the case where $\Gamma$ is a d-regular graph, then $L = I - M$ where $M = A/d$ and where A is the adjacency operator (or matrix) on the vertices of $\Gamma$. The operator M is called the Markov operator and corresponds to a simple random walk with uniform transition probability 1/d along each edge of $\Gamma$. One can also consider a more general concept of weighted Markov or Laplace operators when a weight $w :E \rightarrow {\mathbb {R}}^+$ is given. The weighted Laplacians are also used in various situations.

By spectrum of a group G with a system of generators S, one means the spectrum of the Cayley graph $\Gamma (G,S)$.

If G is finite then one may try to use the information about irreducible unitary representations of G to understand the spectrum (although this approach is often not easy to implement). In the case of Cayley graphs or their generalization, Schreier graphs, one chooses the weight $w :S \cup S^{-1} \rightarrow {\mathbb {R}}^+$ so that it is symmetric $w(s) = w(s^{-1}) \ \forall s\in S$. The symmetry of the weight is needed to keep the weighted Laplacian $L_w$ self-adjoint.

The case of infinite graphs or groups is much harder and little is known about their spectral properties. However, a big progress was achieved for self-similar groups and their associated Schreier graphs. We give here some background in this setting.

Let M be a Markov operator on d-regular connected infinite graph $\Gamma = (V,E)$. It is a self-adjoint operator of norm bounded by 1, so its spectrum is contained in the interval $[-1, 1]$. By the spectral theorem for bounded self-adjoint operators, there exists a projection valued measure P defined on Borel subsets of ${\mathbb {R}}$ which plays the role of the diagonalization basis of M (see for instance [80, Chapter VII]). To each vertex $v \in V$, one associates the probability measure defined by:

$$\begin{aligned} \mu _v (B)= \langle \delta _v , P(B) \delta _v \rangle , \end{aligned}$$

where $\delta _v$ is the delta function at the vertex v and where $B \subset {\mathbb {R}}$ is any Borel subset. The moments of this measure,

$$\begin{aligned} \int _{{\mathbb {R}}} \lambda ^n {\text {d}}\mu _v(\lambda )= < M^n \delta _v, \delta _v> \end{aligned}$$

coincide with the probabilities of returns to v for the random walk induced by M. It was proved by Kesten [68, Lemma 2.1] that the support of $\mu _v$ coincides with the spectrum of M when $\Gamma$ is a Cayley Graph.

These spectral measures are often hard to determine, so they were computed in the rare cases: finitely generated free abelian and non-abelian groups are among those [68]. For example, the spectral measure associated to the free abelian group ${\mathbb {Z}}^n$ is absolutely continuous with analytic density and has support in the interval $[-1,1]$. Its density is the pushforward of the Haar measure on the torus ${\mathbb {R}}^n/{\mathbb {Z}}^n$ by the map $(\theta _1, \ldots , \theta _n) \mapsto (1/n) \sum _{i=1}^n \cos (\theta _i)$. Kesten showed that the free group generated by h elements admits a spectral measure which is absolutely continuous, has analytic density and is supported in $[- \sqrt{2h-1}/h , \sqrt{2h-1}/h]$. Moreover, the density of this spectral measure is given by:

$$\begin{aligned} \dfrac{\sqrt{2 h -1 -x^2h^2}}{1- x^2} {\text {d}}x. \end{aligned}$$

2.2 Self-Similar Groups

The idea of self-similarity came to group theory at the beginning of 1980s in the relation to the Burnside problem on periodic group and Milnor’s question on existence of groups of intermediate growth [44,45,46]. The first examples of self-similar groups were presented in dynamical terms, namely as groups acting on the interval [0, 1] or on the square $[0,1] \times [0,1]$ by Lebesgue measure preserving transformations. Later on, along with the development of the algebraic background of the theory of self-similar groups, stimulating relations to various themes in dynamical systems, statistical mechanics, and mathematical physics (including symbolic and holomorphic dynamics, random Schrödinger operator, invariant random subgroups, etc.) were revealed [5, 31, 47, 48, 57, 61, 62].

Initially used for resolving various difficult problems in Algebra and Functional Analysis (e.g., non-elementary amenability), they were found later to be naturally connected to some well-known and popular games like the Chinese puzzle or Hanoi Towers game. Moreover, they can be seen from the analysis of Gray code, automatically generated sequences (like for instance Thue–Morse sequence), Julia sets of one dimensional polynomials (like the Basilica Julia set [55]), higher dimensional holomorphic dynamics, etc. As we have already mentioned above, the latter connection comes from the non-cyclic renormalization relating various scales of the group.

A self-similar group naturally acts on a regular rooted d-regular tree and this action respects the self-similar structure of the tree. Namely, for each element $g \in G$ and a vertex $v \in V(T)$, the restriction $g_v$ of g on the subtree $T_v$ rooted at v can be identified with an element of G (using the canonical identification of $T_v$ with T). There are modifications of this definition that lead to the classes of self-replicating (or recurrent) groups, branch groups, etc. An account of the theory of self-similar group can be found in the surveys [5, 59, 81] and in Nekrashevych’s book [78].

There are two main ways to describe the action of self-similar groups on such tree: either via wreath recursion or via Mealy automata.

Fix $d \geqslant 2$ an integer and let $T= T_d$ be the d-regular rooted tree whose vertices are in bijection with finite words (strings) over an alphabet of cardinality d (a standard choice for A is $\{ 1 , \ldots , d \}$). The ordering on each level is given by the lexicographic order (see Fig. 1 below).

Fig. 1

Picture of a 2 regular rooted tree

The boundary of the tree, denoted $\partial T$ consists of geodesic paths joining the root with infinity. It can naturally be identified with the set $\{ 1 , \ldots , d \}^{{\mathbb {N}}}$, endowed with the product topology and the resulting topological space is homeomorphic to a Cantor set.

The group of automorphism ${\text {Aut}}(T)$ of the (rooted) tree T consists of bijection of the set of vertices of T which fix the root and preserve adjacency relations. For any vertex v of T, let $T_v$ be the d-regular subtree of T whose root is v. There is a canonical isomorphism between $T_v$ and T which is induced by a power of the left shift ${\tau }$ on the symbolic space ${\Sigma }_d^+= \{ 1 , \ldots , d \}^{{\mathbb {N}}}$.

Every automorphism $g \in {\text {Aut}}(T)$ can be described by the following data: an element of the symmetric group $\sigma \in {{\,\textrm{Sym}\,}}(d)$ which corresponds to the restriction of g on the first level of the tree, and a d-tuple $(g_1, \ldots , g_d )$ of elements of ${\text {Aut}}(T)$ called sections at the vertices of the first level which encodes how g acts on each rooted subtree $T_1, \ldots , T_d$ with a root at level 1 using the canonical identification of $T_1, \ldots , T_d$ with T. More precisely, for any word $w \in {\Sigma }_d^+$, $g_i (w ) ={\tau }\circ g ( \overline{i w} )$, where $\overline{i w}$ is the concatenation of the number i with the word w.

Using this description, we obtain an isomorphism:

$$\begin{aligned} \psi : {\text {Aut}}(T) \rightarrow {\text {Aut}}(T)^d \rtimes {{\,\textrm{Sym}\,}}(d), \end{aligned}$$

where the sign $\rtimes$ stands for the semi-direct product of groups and where ${{\,\textrm{Sym}\,}}(d)$ acts on the direct product ${\text {Aut}}(T)^d$ by permuting the factors.

Now, let G be a subgroup acting faithfully on T by automorphisms. We can view G as a subgroup of ${\text {Aut}}(T)$ and consider the restriction of $\psi$ to G. When ${\text {Im}}(\psi _{|G})< G^d \rtimes {{\,\textrm{Sym}\,}}(d)$, we say that the group G is a self-similar group.

Another way to express this is as follows: A subgroup $G \leqslant {\text {Aut}}(T)$ is self-similar if its sections $g_1, \ldots , g_d$ belong to G.

The relation $\psi (g) = (g_1, \ldots , g_d)\, \sigma$ is called the wreath recursion and is usually denoted:

$$\begin{aligned} g = (g_1, \ldots , g_d)\, \sigma . \end{aligned}$$

Example 2.1

Take $A = \{ 1 , \ldots , d\}$ and the wreath recursion given by:

$$\begin{aligned} a = (1 , \ldots , 1 , a)\, \sigma , \end{aligned}$$

where $\sigma$ is a cyclic permutation of A. The subgroup generated by a is an infinite cyclic group which is an algebraic realization of the odometer group (called also the adding machine).

For the next examples, we take $A= \{ 0,1\}$ and denote by $e, \sigma$ the identity and the standard involution in ${{\,\textrm{Sym}\,}}(2)$ respectively.

Example 2.2

Consider the wreath recursion,

$$\begin{aligned} a = (1,1)\, \sigma ,\quad b = (a , b)\, e. \end{aligned}$$

The subgroup $\langle a, b \rangle$ is isomorphic to $D_\infty$, the infinite dihedral group (see [57]).

We now present successively the three self-similar groups of interest in this paper.

Definition 2.3

Consider the wreath recursions

$$\begin{aligned} a = (1,1)\, \sigma ,\quad b = (a, c)\, e,\quad c= (a, d)\, e , \quad d = (1, b)\, e. \end{aligned}$$

The subgroup ${\mathcal {G}} = \langle a,b,c,d \rangle$ is the first Grigorchuk group [4, Section 4.1].

Definition 2.4

Consider the wreath recursions

$$\begin{aligned} a = (b, a)\, \sigma , \quad b = (b,a ) \, e . \end{aligned}$$

The subgroup $\langle a , b \rangle$ is the Lamplighter group [54, Section 5], it is the wreath product ${\mathbb {Z}}_2 \wr {\mathbb {Z}}$ and is isomorphic to the semidirect product

$$\begin{aligned} \left( \underset{{\mathbb {Z}}}{\oplus } \ {\mathbb {Z}}_2 \right) \rtimes {\mathbb {Z}}, \end{aligned}$$

where a generator a of ${\mathbb {Z}}$ acts on $\displaystyle {\underset{{\mathbb {Z}}}{\oplus } \, {\mathbb {Z}}_2 }$ as the shift map.

Definition 2.5

Consider $A = \{ 0, 1, 2 \}$ and the wreath recursions

$$\begin{aligned} a= (1,1,a) \, \alpha ,\quad b= (1, b, 1)\, \beta ,\quad c= (c, 1 ,1)\, \gamma , \end{aligned}$$

where $\alpha = (01), \beta = (0 2), \gamma = (12)$ are the three involutions in ${{\,\textrm{Sym}\,}}(3)$. The subgroup ${\mathcal {H}} =\langle a, b, c \rangle$ is called the Hanoi tower group and is associated to the Hanoi towers game on 3 pegs [51].

The groups in the above examples are not only self-similar groups but they are groups with finite self-similar set of generators [59].

2.3 Spectra of Self-Similar Groups and Density of States

We have explained in the previous section how a self-similar group acts on a d-regular rooted tree T. Moreover, given a group $G \leqslant {\text {Aut}}(T)$ with a finite generating set S, one associates a sequence of finite graph $\Gamma _n = (V_n , E_n)$ where $n=1,2, \ldots$, $|V_n| = d^n$, and an uncountable family of graphs $\{\Gamma _\xi = (V_\xi , E_\xi )\}_{\xi \in \partial T }$ where $V_\xi$ is the G-orbit of the point $\xi$.

The vertices of the graphs $\Gamma _n$ and $\Gamma _\xi$ are level n vertices of T and points in the G-orbit of $\xi$, respectively, and the edges are pairs of vertices of the form $(v, s\cdot v)$ where $s \in S$. Usually, all graphs $\Gamma _\xi$ are infinite (for instance when the G action on T is transitive on each level) and they are natural limits of the graphs $\Gamma _n$. Namely,

$$\begin{aligned} (\Gamma _\xi , \xi ) = \lim _{n} (\Gamma _n , v_n), \end{aligned}$$

where $v_n$ is the vertex of level n on the geodesic path representing $\xi$, and $(\Gamma _\xi , \xi )$, $(\Gamma _n , v_n)$ are the corresponding pointed graphs . The convergence above is taken in the usual way: for all $R > 0$, the balls $B_{V_n}(R)$ of radius R in $(\Gamma _n, v_n)$ converge to $B_\xi (R)$. This leads to the idea of approximating ${{\,\textrm{sp}\,}}(\Gamma _\xi )$ with ${{\,\textrm{sp}\,}}(\Gamma _n)$.

For the groups ${\mathcal {G}}$ and ${\mathcal {H}}$, certain Schreier graphs are shown below.

Fig. 2

Above picture of the binary tree with the action of ${\mathcal {G}}$ on the level 1, 2, 3 vertices, below the first three Schreier graphs associated to ${\mathcal {G}}$

Fig. 3

Third Schreier graph associated to the Hanoi group

The first observation is made in [53]: let us take a point $\xi$ on the boundary of the tree, $v_n$ a vertex of level n which belongs to the geodesic $\xi$, and fix a Markov operator M on $l^2(G\xi )$ which induces a Markov operator on $l^2(G v_n) = l^2(\Gamma _n)$. If $\mu _n$ is the spectral measure associated with the operator $M_n$ and with the delta function on the vertex $v_n$, then

$$\begin{aligned} \lim _{n\rightarrow +\infty } \mu _n = \mu _\xi , \end{aligned}$$

where $\mu _\xi$ is a spectral measure of a Markov operator on $\Gamma _\xi$ determined by the delta function $\delta _\xi \in l^2(G\xi )$.

Since each graph $\Gamma _{n+1}$ covers $\Gamma _n$ and is covered by $\Gamma _\xi$, the spectrum set increases ${{\,\textrm{sp}\,}}(\Gamma _n) \subset {{\,\textrm{sp}\,}}(\Gamma _{n+1})$, and an easy argument [4] shows that

$$\begin{aligned} {{\,\textrm{sp}\,}}(\Gamma _\xi ) \subset \overline{ \bigcup _{n=1}^{\infty } {{\,\textrm{sp}\,}}(\Gamma _n) }. \end{aligned}$$

Moreover, [4, Theorem 3.6] states that if the graph $\Gamma _\xi$ is amenable then

$$\begin{aligned} {{\,\textrm{sp}\,}}(\Gamma _\xi ) = \overline{ \bigcup _{n=1}^{\infty } {{\,\textrm{sp}\,}}(\Gamma _n) }. \end{aligned}$$

(2.1)

Recall that a graph $\Gamma _\xi$ is amenable if its Cheeger constant is 0, or equivalently $||M||=1$ (see [23]). If a group G is amenable then $\Gamma _\xi$ is amenable for all $\xi \in \partial T$.

The three groups studied in this paper, the Grigorchuk group, the Lamplighter, and the Hanoi group, are all amenable, so (2.1) applies to their Scheier graphs.

To a finite graph $\Gamma$, one can associate the counting measure $\eta$ given by:

$$\begin{aligned} \eta := \dfrac{1}{|V| } \sum _{\lambda _i \in {{\,\textrm{sp}\,}}(M)} \delta _{\lambda _i}, \end{aligned}$$

where $\lambda _i$ are the eigenvalues of the matrix M counted with multiplicities.

If $\eta _n$ is the counting measure associated to $\Gamma _n$, we define $\eta$ as the weak limit of measures $\eta = \lim _n \eta _n$. This measure is called the density of states (or KNS spectral measure where the initials stand for Kesten, Von-Neumann, Serre). If $\rho$ is the uniform Bernoulli measure on $\partial T \sim \{0,1 ,\ldots , d-1\}^{\mathbb {N}}$ and $\mu _\xi$ as before is the spectral measure associated to $\Gamma _\xi$ with respect to the vertex $\xi \in \partial T$, then by [49], one has

$$\begin{aligned} \eta = \int _{\partial T} \mu _\xi {\text {d}}\rho (\xi ), \end{aligned}$$

i.e the density of states is an average of the spectral measures $\mu _\xi$.

To obtain the spectrum associated to the Cayley graph of a group G, an additional property is needed. Recall that the action of G is essentially free with respect to the Bernoulli measure $\rho$ on $\partial T$ if $\forall g \in G {\setminus } \{1\}$, $\rho ({\textrm{Fix}}(g))=0$ where ${\textrm{Fix}}(g)$ denotes the set of fixed points of $\partial T$. Equivalently, when G is countable, this condition is equivalent to the property that the $G-$stabilizer of almost any point $\xi \in \partial T$ is trivial.

Under this assumption, $\eta$ coincides with the spectral measure associated with $\delta _1 \in l^2(G)$. Thus, the computation of the density of states leads to the spectrum of the Cayley graph of a group.

2.4 Schur Renormalization Transformations

In this section, we will define some operators on finite matrices called Schur complements. These operators will allow us to deduce inductively the spectrum of the Markov operator on the Schreier graphs as one passes from one scale to another.

Take a finite dimensional vector space H which can be decomposed as the sum of two non-zero subspaces $H = H_1 \oplus H_2$. If M is an endomorphism of H, then M can be expressed as a block-matrix according to this decomposition:

$$\begin{aligned} M := \left( \begin{array}{ll} A &{} B \\ C&{} D \end{array} \right) , \end{aligned}$$

(2.2)

where A, D are endomorphisms of $H_1$ and $H_2$ respectively, C, D are linear transformations from $H_1 \rightarrow H_2$ and $H_2 \rightarrow H_1$ respectively.

Definition 2.6

• (i) Assume that D is invertible, then the first Schur complement, denoted $S_1(M)$, is the endomorphism:

  $$\begin{aligned} S_1(M) := A - BD^{-1} C. \end{aligned}$$

• (ii) Assume that A is invertible, then the second Schur complement, denoted $S_2(M)$, is the endomorphism

  $$\begin{aligned} D - C A^{-1} B. \end{aligned}$$

The Schur complements are useful in our setting because they relate the invertibility of the Markov matrices in various scales, via the following classical result.

Theorem 2.7

(see e.g [50, Theorem 5.1]) Suppose that D is invertible. Then M is invertible if and only if $S_1(M)$ is invertible. Similarly, if A is invertible then M is invertible if and only if $S_2(M)$ is invertible.

In particular, we will exploit the relation between the determinant of M and the Schur complement.

Proposition 2.8

Suppose that D is invertible, then

$$\begin{aligned} \det (M) = \det (D) \det (S_1(M)). \end{aligned}$$

Let us explain how the Schur complement arises in our study. We start with a sequence of vector spaces $H_n$ of dimension $d^n$ together with an identification:

$$\begin{aligned} H_{n+1} = H_n \oplus \cdots \oplus H_n, \end{aligned}$$

for all n, where the direct sum is taken d times. More precisely, $H_n$ will be the (Hilbert) space $l^2(V_n)$ where $V_n$ are the vertices of level n of the rooted tree $T_d$ and each component in the decomposition of $H_{n+1}$ corresponds to the space of functions on the leaves of the subtree.

For all the self-similar group G treated in this paper, we will choose some generators $s_1, \ldots , s_k$, which are identified as operators on $H_n$ and we will consider a pencil of operators (on $H_n$):

$$\begin{aligned} M_n(z_1 ,\ldots , z_k) := z_1 (s_1 + s_1^{-1}) + \cdots + z_k (s_k + s_k^{-1}) \end{aligned}$$

where $z= (z_1, \ldots , z_k) \in {\mathbb {C}}^k$ and where $s_i$ denotes the restriction of $s_i$ to $H_n$.

The self-similarity of the action on the tree and Proposition 2.8 will lead to a relation of the form:

$$\begin{aligned} \det M_{n+1}(z) = Q(z)^{d^{n-p}} \det (M_n(F(z))), \end{aligned}$$

where $p=0,1,2$, $F : {\mathbb {C}}^k \rightarrow {\mathbb {C}}^k$ is a rational map and Q is a polynomial function on ${\mathbb {C}}^k$. The map F is called the renormalization map associated with the spectral problem under consideration.

Under these conditions, we can now introduce the main notion of our paper. When it exists, we say that the limit of currents:

$$\begin{aligned} \lim _{n\rightarrow +\infty } \dfrac{1}{d^n} [\det M_n =0] , \end{aligned}$$

is the spectral current associated to the group G, where $[M_n=0]$ denotes the current of integration on the zeros of the polynomial $\det (M_n)$ (see Appendix 9.1).

Although we do not work directly in the case where the dimension of H is infinite but let us yet explain how the renormalization map can be defined in this situation as well. Assume again that we have a pencil M(z) where $z\in {\mathbb {C}}^k$ of bounded linear operators on an infinite dimensional Hilbert space H. We define the joint spectrum, denoted ${{\,\textrm{jsp}\,}}(M(z))$, as the subset:

$$\begin{aligned} {{\,\textrm{jsp}\,}}(M(z)) = \{ z\in {\mathbb {C}}^k | M(z) \text { is not invertible} \}. \end{aligned}$$

Let us consider $\varphi : H \rightarrow H\oplus \cdots \oplus H$ (called d-similarity) where the direct sum is taken d-times, a map $F : {\mathbb {C}}^k \rightarrow {\mathbb {C}}^k$ and a rational function $A : z \in {\mathbb {C}}^k \mapsto {\mathcal {B}}(H)$ with values in the space of bounded operators on H such that for some $i\leqslant d$, one has:

$$\begin{aligned} S_i (M(z)) = A(z) M(F(z)), \end{aligned}$$

on a Zariski-open set of values of z. In this case, the map F is a renormalization map associated with the problem of finding the joint spectrum ${{\,\textrm{jsp}\,}}(M(z))$. If we understand ${{\,\textrm{jsp}\,}}(A(z))$ then the spectral problem for ${{\,\textrm{jsp}\,}}(M(z))$ gets reduced to a dynamical problem for F.

Observe that the support of the spectral current measures the locus of points in ${\mathbb {C}}^k$ where the restriction of the operator M(z) on finite dimensional subspaces is not invertible. We thus expect the support of the spectral current, when it exists, to be equal to the joint spectrum of M(z) when the group G is amenable.

2.4.1 Schur Transformations for the Grigorchuk Group

The self-similarity of the group ${\mathcal {G}}$ determines a morphism of algebra $\varphi : {\mathbb {C}}[{\mathcal {G}}] \rightarrow {\mathbb {M}}_2({\mathbb {C}}[{\mathcal {G}}])$, where ${\mathbb {M}}_2({\mathbb {C}}[{\mathcal {G}}])$ denotes the space of matrices with coefficient in the non-commutative group algebra ${\mathbb {C}}[{\mathcal {G}}]$.

We consider the pencil $M(\lambda , \mu ) = - \lambda a + b + c + d - 1 - \mu \in {\mathbb {C}}[\lambda ,\mu ][{\mathcal {G}}]$ .

Denote by t the element $(b+ c + d -1) /2$. Then t and a are involutions and the recursion matrix associated to M is precisely the matrix $\varphi (M(\lambda ,\mu ))$ given by:

$$\begin{aligned} \varphi \circ M (\lambda , \mu ) :=\left( \begin{array}{ll} 2a - \mu &{} -\lambda \\ -\lambda &{} 2t - \mu \end{array} \right) . \end{aligned}$$

Since a and t are involutions, one sees directly that the element $2a - \mu$ and $2 t - \mu$ are invertible in ${\mathbb {C}}[G]$. The two Schur complements are given by :

$$\begin{aligned} S_1 \varphi \circ M (\lambda , \mu )= & {} M (F(\lambda ,\mu )),\\ S_2 \varphi \circ M(\lambda ,\mu )= & {} M (G(\lambda , \mu )), \end{aligned}$$

where F, G are the rational maps given by the formulas:

$$\begin{aligned} F({\lambda }, \mu )&= \left( \frac{2{\lambda }^2}{4-\mu ^2}, \ \mu + \frac{\mu {\lambda }^2}{4-\mu ^2} \right) .\\ G : (\lambda , \mu )&\mapsto \left( 2\dfrac{ 4 - \mu ^2}{\lambda ^2} ,\ - \mu \left( 1 + \dfrac{4-\mu ^2}{\lambda ^2}\right) \right) . \end{aligned}$$

2.4.2 Schur Transformations for the Lamplighter Group

The recursion for the Lamplighter group ${\mathcal {L}}$, induces an algebra morphism $\varphi : {\mathbb {C}}[{\mathcal {L}}] \rightarrow {\mathbb {M}}_2({\mathbb {C}}[{\mathcal {L}}])$ as well.

Consider the following pencil of operators:

$$\begin{aligned} M(\lambda , \mu ) := a+ a^{-1} + b + b^{-1} - \lambda {\text {id}}- \mu \sigma , \end{aligned}$$

where $\sigma = b^{-1} a$ is the involution which exchanges the two subtrees $T_1$ and $T_2$ introduced in Sect. 2.2. The recursion matrix associated to M takes the form:

$$\begin{aligned} \varphi \circ M (\lambda , \mu ) := \left( \begin{array}{ll} a + a^{-1} - \lambda &{} a + b^{-1} - \mu \\ b + a^{-1} - \mu &{} b + b^{-1} - \lambda \end{array}\right) . \end{aligned}$$

(2.3)

Consider the rational map F given by:

$$\begin{aligned} F(\lambda , \mu )= \left( \dfrac{\lambda ^2 -\mu ^2 -2}{\mu - \lambda } , \dfrac{2}{\lambda - \mu } \right) . \end{aligned}$$

(2.4)

The two Schur complements turn out to be the same, and are related to F as follows:

Proposition 2.9

We have:

$$\begin{aligned} S_1(\varphi \circ M(\lambda ,\mu )) = S_2(\varphi \circ M(\lambda , \mu )) = M \circ F(\lambda , \mu ). \end{aligned}$$

(2.5)

Proof

The first Schur complement yields:

$$\begin{aligned} S_1 (\varphi \circ M) (\lambda , \mu ) = a + a^{-1} - \lambda {\text {id}}- \dfrac{1}{2(\mu - \lambda )}(b^{-1} - a^{-1} + \lambda - \mu ) (b - a + \lambda - \mu ). \end{aligned}$$

Using the fact that $b^{-1}a = \sigma$, we obtain that $S_1(\varphi \circ M(\lambda ,\mu )) = M(F(\lambda , \mu ))$. Similarly, the second Schur complements gives:

$$\begin{aligned} S_2 (\varphi \circ M)(\lambda ,\mu ) = b+ b^{-1} - \lambda {\text {id}}- \dfrac{1}{2(\mu -\lambda )}(a^{-1} - b^{-1} + \lambda - \mu ) (a-b +\lambda -\mu ). \end{aligned}$$

We then conclude that $S_2 \varphi \circ M(\lambda ,\mu ) = S_1 \varphi \circ M(\lambda ,\mu )$, as required. $\square$

2.4.3 Schur Transformations for the Hanoi Group

Consider the Hanoi group ${\mathcal {H}}$ and we consider the pencil of operator

$$\begin{aligned} M(\lambda , \mu ) := a + b + c - {\lambda }+ (\mu -1)A \in {\mathbb {C}}[{\mathcal {H}}], \end{aligned}$$

where A is the operator given by the matrix:

$$\begin{aligned} A := \left( \begin{array}{lll} 0 &{} 1 &{} 1 \\ 1&{} 0 &{} 1 \\ 1&{} 1 &{}0 \end{array} \right) . \end{aligned}$$

The recursion matrix associated to M on two levels takes the form:

$$\begin{aligned} \varphi (M(\lambda ,\mu )):= \left( \begin{array}{lll|lll|lll} c - {\lambda }&{} 0 &{} 0 &{} \mu &{} 0 &{} 0 &{} \mu &{} 0 &{} 0 \\ 0&{} -{\lambda }&{} 1 &{} 0 &{} \mu &{} 0 &{} 0 &{} \mu &{} 0 \\ 0&{} 1 &{} -{\lambda }&{} 0 &{} 0 &{} \mu &{} 0 &{} 0 &{} \mu \\ \hline \mu &{}0&{} 0 &{} -{\lambda }&{} 0&{} 1 &{} \mu &{} 0 &{} 0\\ 0&{} \mu &{} 0 &{} 0 &{}b-{\lambda }&{} 0&{} 0 &{} \mu &{} 0\\ 0 &{}0 &{}\mu &{} 1&{} 0&{} -{\lambda }&{} 0 &{} 0 &{} \mu \\ \hline \mu &{}0&{} 0 &{} \mu &{} 0 &{} 0 &{} -{\lambda }&{} 1&{} 0 \\ 0&{} \mu &{} 0 &{} 0 &{} \mu &{} 0 &{} 1 &{}-{\lambda }&{} 0\\ 0 &{}0 &{}\mu &{} 0 &{} 0 &{} \mu &{} 0 &{}0 &{}a-{\lambda }\\ \end{array} \right) \end{aligned}$$

The computation of the Schur complement with respect to an appropriate corner was carried out by Grigorchuk and Sunić.

Proposition 2.10

[51, Proposition 3.1] One has the following recursive formula:

$$\begin{aligned} \det M_n (\lambda ,\mu ) = ({\lambda }^2 - (1 + \mu )^2 )^{3^{n-2}} ({\lambda }^2 - 1 + \mu - \mu ^2 )^{2 \cdot 3^{n-2}} \det M_{n-1}(F(\lambda ,\mu )), \end{aligned}$$

where F is the rational transformation

$$\begin{aligned} F : (\lambda ,\mu ) \mapsto \left( {\lambda }+ \dfrac{2\mu ^2 (-{\lambda }^2 + {\lambda }+ \mu ^2)}{ ({\lambda }-1 -\mu )({\lambda }^2 -1 + \mu -\mu ^2 )} , \ \dfrac{\mu ^2 ({\lambda }-1+\mu )}{({\lambda }-1 -\mu )({\lambda }^2 -1 + \mu -\mu ^2 )} \right) \end{aligned}$$

2.5 More Comments

As we have already mentioned in the Introduction, spectral theory of Laplacian has a profound physical meaning, with atomic vs continuous dichotomy corresponding to isolating vs conducting states of the matter (see e.g Rage theorem in [20, p.97]). A thorough mathematical theory of this dichotomy has been recently developed in the context of discrete one-dimensional Schrödinger operators with almost periodic coefficients (see [2]). And recently an intimate connection was revealed between the spectral theory of self-similar groups and the spectral theory of random Schrödinger operators (see [42, 62]).

We have also indicated relation to many other areas of mathematics. As an illustration, let us mention that the spectral theory of the Lamplighter group led to counterexamples to Atiyah’s conjectures [1] on rationality of $L^2$-Betti numbers of compact manifolds. Namely, the atom 1/3 of the spectral measure at 0 calculated in [54] was translated in [58] into the value 7/3 for the third $L^2$-Betti number of a certain 7-dimensional manifold.

However, we are not aware of a direct characterization of the spectral dichotomy in the group-theoretic terms. Let us emphasize with this respect that in fact, we study the spectrum of the action of G on a Schreier graph. Only in the case of the Lamplighter group (out of the three examples we consider) it coincides with the spectrum of the regular action on the Cayley graph. Moreover, it does depend on the choice of generators of the group. In fact, with another natural choice of generators, the spectrum of the Lamplighter group becomes singular continuous [42]. Still, there is some property of the spectral measure, related to the asymptotical behavior of the resolvent at the origin, which does not depend on generators, and thus produces an invariant of the group or its action, called the Novikov–Shubin invariant [12].

As the Schur renormalization is concerned, it can be considered for arbitrary self-similar groups as a transformation of a $C^*$-operator algebra. However, it is rarely a rational function as the inversion involved in the definition of the Schur complement is generally expressed as an infinite power series. So, the three examples we deal in this paper are quite special (not to mention that they turn out to be integrable).

Note with this respect that there is a different viewpoint on the Schur complement as a renormalization of random walks. It was introduced by Bartholdi and Virag [6], and Kaimanovich [66] (as a tool to prove amenability of the Basilica groups), and was related to the Schur complement in [50]. This viewpoint can give a more efficient approach to spectral problems for general self-similar groups.

3 Background in Holomorphic Dynamics

3.1 Equidistribution of Preimages in Dimension One

3.1.1 General Result

Let f be a polynomial, it extends to a holomorphic map on the Riemann sphere ${\hat{{\mathbb {C}}}}$. The filled Julia set ${\mathcal {K}}(f)$ of f is the set of non-escaping points in ${\mathbb {C}}$, the Julia set ${\mathcal {J}}(f)$ is the boundary of that domain and the Fatou set F(f) is the normality locus of f.

Theorem 3.1

[16, 37, 74, 75] Let $f:{\hat{\mathbb {C}}}\rightarrow {\hat{\mathbb {C}}}$ be a rational function of degree $d\ge 2$. Then for all $z\in {\hat{\mathbb {C}}}$ except at most two points, we have:

$$\begin{aligned} \frac{1}{d^n} \sum _{\zeta \in f^{-n} z } {\delta }_\zeta \rightarrow {\omega }, \end{aligned}$$

where ${\omega }$ is the measure of maximal entropy for f. In the polynomial case, ${\omega }$ coincides with the harmonic measure on the Julia set ${{\mathcal {J}}}(f)$.

3.1.2 Squaring Map

The doubling or squaring map is the map $f_0:z \mapsto z^2$. It has two superattracting fixed points on ${\mathbb {P}}^1$ corresponding to the origin and the point at infinity and its Julia set is the unit circle ${\mathbb {T}}$ in ${\mathbb {C}}$. The measure of maximal entropy is the Lebesgue measure on the circle.

3.1.3 Chebyshev Map

The Chebyshev (or Ulam-Neumann) quadratic map ${t}$ appears in several normalizations:

$$\begin{aligned} {t}:z\mapsto 2z^2 -1, \quad {\textrm{or}}\quad z\mapsto z^2-2, \quad {\textrm{or}}\quad z\mapsto 4z(1-z), \end{aligned}$$

(3.1)

all of which are conjugate by appropriate affine changes of variable. Its special place in dynamics becomes clear from the first expression, as it satisfies the functional equation

$$\begin{aligned} \cos 2 \theta = {t}(\cos \theta ) , \end{aligned}$$

telling us that $\cos$ semi-conjugates the doubling map $\theta \mapsto 2 \theta$ to ${t}$. In the coordinate $\zeta = e(\theta )\equiv e^{2\pi i \theta }$, it can be written as

$$\begin{aligned} {\textrm{Zh}}(\zeta ^2) = {t}({\textrm{Zh}}(\zeta )), \quad {\textrm{where}}\ {\textrm{Zh}}(z) = \frac{1}{2} \left( z+\frac{1}{z} \right) \end{aligned}$$

is the Zhukovsky function. Thus, ${\textrm{Zh}}$ semi-conjugates the quadratic map $f_0:z\mapsto z^2$ to the Chebyshev map ${t}$. The Julia set ${{\mathcal {J}}}(f_0)$ is the unit circle ${\mathbb {T}}$, while the Julia set ${{\mathcal {J}}}({t})$ is the interval ${\mathbb {I}}= [-1, 1]$. Naturally, they are related by the Zhukovsky function: ${\textrm{Zh}}({\mathbb {T}}) = {\mathbb {I}}$.

Let

$$\begin{aligned} {\text {d}}m = \frac{1}{2\pi } {\text {d}}\theta \end{aligned}$$

be the normalized Lebesgue measure on ${\mathbb {T}}$. It is the measure of maximal entropy for $f_0$, which gives the asymptotic distribution for the iterated preimages of all points $z\in {\mathbb {C}}^*\equiv {\mathbb {C}}\smallsetminus \{0\}$. (All these are well-known elementary statements.) Let us push this measure forward to ${\mathbb {I}}$:

$$\begin{aligned} {\text {d}}{\omega }:= {\textrm{Zh}}_* ( {\text {d}}m ) = \frac{1}{\pi }\frac{{\text {d}}x}{\sqrt{1-x^2}} . \end{aligned}$$

(3.2)

We see that ${\omega }$ is the measure of maximal entropy for ${t}$, which gives the asymptotic distribution for the iterated preimages of all points $\zeta \in {\mathbb {C}}$.

3.1.4 Cantor Case

Consider the polynomial map $p :z \mapsto z^2 - z -3$. This map is called hyperbolic (see [76, Section 14]) since it is conjugate to $u\mapsto u^2 - 15/4$ where $u = z-1/2$ and the critical point escapes to the attracting fixed point at infinity. The Julia set of this map in the u coordinates is a Cantor set contained in the union of intervals $[-5/2, -\sqrt{5}/2] \cup [\sqrt{5}/2 , 5/2]$. Translating back to the z coordinates, the Julia set of p is a Cantor set contained in the union $[-2, (-\sqrt{5}+1)/2] \cup [(\sqrt{5}+1)/2,2]$. The measure of maximal entropy is the Haar measure on this Cantor set.

So, Theorem 3.1 is straightforward in the three particular cases singled out above. Incidentally, these are the only cases relevant for this paper.

3.2 Algebraic, Topological and Dynamical Degrees, and Algebraic Stability

Take a rational map $F :{\mathbb {P}}^2 \dashrightarrow {\mathbb {P}}^2$ (see Appendix 9.4 for the definition of a rational map on any surface). The map F is determined by three homogeneous polynomials $P_0, P_1, P_2 \in {\mathbb {C}}[x,y,z]$ with no common factors and with the same degree d, which we denote by $\deg (F)$. The integer $d =\deg (F)$ is called the (algebraic) degree of the rational map F. whereas its topological degree is the number of preimages counted with multiplicity of a generic point.

A rational map $F :{\mathbb {P}}^2({\mathbb {C}})\rightarrow {\mathbb {P}}^2({\mathbb {C}})$ is called dominant if its image is not contained in any algebraic curve.

More generally, consider a surface X obtained from ${\mathbb {P}}^2$ by finitely many blow-ups, it is called a rational variety. A given rational map $F :{\mathbb {P}}^2 \dashrightarrow {\mathbb {P}}^2$ lifts to a rational map $F_X$ on X (see Appendix 9.4) and $F_X$ is said to be algebraically stable on X if there is no algebraic curve C whose proper transform under some iterate $F_X^n$ is a point of indeterminacy. When F is algebraically stable on ${\mathbb {P}}^2$, the sequence of degrees is multiplicative (see [36]):

$$\begin{aligned} \deg F^n = (\deg F )^n\quad {\mathrm {for\ all}} \quad n=1,2,\dots , \end{aligned}$$

and if $F_X$ is algebraically stable, then its induced action on the Dolbeaut cohomology $H^{1,1}(X)$ (see Appendix 9.5) satisfies the relation $(F_X^n)^* = (F_X^*)^n$ for all integer n. Note that the sequence $\deg (F^n)$ is submultiplicative:

$$\begin{aligned} \deg (F^{n+m}) \leqslant \deg (F^n) \deg (F^m). \end{aligned}$$

By Fekete’s lemma [35], the first dynamical degree of F, denoted $\lambda _1(F)$ and defined by the formula:

$$\begin{aligned} \lambda _1(F) = \lim _{n\rightarrow +\infty } \deg (F^n)^{1/n}, \end{aligned}$$

is a well defined real number satisfying $\lambda _1(F) \leqslant d$. When the map $F_X$ becomes algebraically stable on a surface X, one can compute the dynamical degree using the following statement.

Proposition 3.2

Let $F:{\mathbb {P}}^2 \dashrightarrow {\mathbb {P}}^2$ and suppose that there exists a rational surface X on which the lift $F_X$ of F is algebraically stable. Then one has:

$$\begin{aligned} \lambda _1(F) = \rho (F_X^*), \end{aligned}$$

where $\rho (F_X^*)$ denotes the spectral radius of the pullback action $F_X^*$ on $H^{1,1}(X)$.

The rational surface X satisfying the conditions of the above Proposition is called an algebraically stable model for the map F. For arbitrary maps, the dynamical degree can be difficult to compute, however there are methods to determine this degree in more rigid situations. To do so, we state the general properties satisfied by these numbers.

Theorem 3.3

([27, 22, Theorem 1], [29, Theorem 1.1]) The following properties are satisfied:

• (i) The dynamical degree is a birational invariant, i.e for any birational map $\varphi :{\mathbb {P}}^2 \dashrightarrow {\mathbb {P}}^2$, one has $\lambda _1(\varphi ^{-1} \circ F \circ \varphi ) = \lambda _1(F)$.

• (ii) If F is a skew-product $F = (x,y) \mapsto (P(x), Q_x(y))$ where P is a rational map of degree p on ${\mathbb {P}}^1$ and $Q_x$ is a rational family of rational maps³ of ${\mathbb {P}}^1$ of degree q, then the dynamical degree of F is given by the formula:

  $$\begin{aligned} \lambda _1(F) = {{\text {max}}}(p,q). \end{aligned}$$

  Moreover, the topological degree of F is equal to the product pq.

3.3 Existence of the Green Currents

Let now $F:{\mathbb {P}}^2({\mathbb {C}})\dashrightarrow {\mathbb {P}}^2({\mathbb {C}})$ be a rational map of the projective space (with points of indeterminacy allowed). Then instead of taking iterated preimages of points as we did in the one-dimensional case, one should consider iterated pullback of holomorphic curves. Let [C] stand for the current of integration over a holomorphic curve C. Then the desirable result would assert that for a typical C, the normalized currents $[(F^n)^* (C) ]$ converge to some current $\Omega$ called Green. There is an extensive literature on this subject [7, 14, 28, 33, 82]. Below we will quote a few sample results of this kind.

Theorem 3.4

[63, Theorem 2.2] Let $F: {\mathbb {P}}^2({\mathbb {C}}) \dashrightarrow {\mathbb {P}}^2({\mathbb {C}})$ be a dominant rational map and let X be a rational surface satisfying the following properties:

• (i) The lift $F_X$ of F to X is algebraically stable.

• (ii) One has $\lambda _1(F) > 1$.

• (iii) There exists a constant $C>0$ such that $\deg (F^n) \leqslant C \lambda _1(F)^n$ for all n.

• (iv) There exits a $\lambda _1(F)$ invariant class $\alpha \in H^{1,1}(X)$ by $F_X^*$ which is represented by a closed smooth semi-positive form.

Then there exists a unique (up to scaling) closed positive (1, 1)-current ${\Omega }$ on X representing $\alpha$ such that

$$\begin{aligned} F_X^*({\Omega }) = \lambda _1(F) {\Omega }. \end{aligned}$$

The current is called the Green current of the rational map F.

This theorem was proved by Fornaess–Sibony [36, 85] in the particular case where $X={\mathbb {P}}^k({\mathbb {C}})$ (in which case conditions (iii) and (iv) are satisfied automatically). However, our maps F (albeit, elementary) do not fit into this framework as they are not algebraically stable on ${\mathbb {P}}^k({\mathbb {C}})$.

However, below we will show that each of them admits an algebraically stable model (condition (i)), and two of them (Grigorchuk and Hanoi) satisfy condition (ii). For these two maps we will provide an explicit geometric description of the Green current (without appealing to Theorem 3.4).

In fact, these two maps do fit into the framework of Guedj’s Theorem. Indeed, conditions (iii) and (iv) of the theorem follow easily from the integrability of F. For instance, if a map F is semi-conjugate to a degree $\lambda _1$ one-dimensional map via a projection $\varphi : X \rightarrow C$ to a smooth projective curve, the invariant cohomology class for F can be represented by the $\varphi$-pullback of a Kähler form on C (providing us with (iv)).

Let us note that though the Lamplighter map does not fit into the above frame (as $\lambda _1=1$), it still admits an analogue of the Green current that will be explicitly described.

In conclusion, let us summarize properties of our three maps:

Group	Grigorchuk group	Lamplighter group	Hanoi group
Branching number for the tree	2	2	3
Algebraic degree	3	2	4
Dynamical degree	$\lambda _1(R_{{\mathcal {G}}})=2$	$\lambda _1(R_{{\mathcal {L}}}) = 1$	$\lambda _1(R_{{\mathcal {H}}})=2$
Topological degree	$d_t(R_{{\mathcal {G}}})=2$	$d_t(R_{{\mathcal {L}}})=1$	$d_t(R_{{\mathcal {H}}}) =2$
Algebraic stability on ${\mathbb {P}}^2({\mathbb {C}})$	No	No	No
Algebraically stable model	Yes (Sect. 5.1)	Yes (Sect. 6.1)	Yes (Sect. 7.1)
Integrability	Yes	Yes	Yes

3.4 Fatou, Julia Sets of Rational Maps in Higher Dimension

Given a rational map $F : {\mathbb {P}}^2({\mathbb {C}}) \dashrightarrow {\mathbb {P}}^2({\mathbb {C}})$, the Fatou set ${{\mathcal {F}}}(F)$ is defined as in the one-dimensional situation: $z\in {{\mathcal {F}}}(F)$ if there is a neighborhood $U\ni z$ such that the iterates $(F^n)_{n=0}^\infty$ are well defined (i.e., they do not hit the indeterminacy points) and form an equicontinuous family on U (so, the orbits near z are Lyapunov stable).⁴ There are two version of the big Julia set:

• A As the support of the Green current ${\mathcal {J}}(F) = {\text {supp}}{\Omega }$.

• B As the complement of the Fatou set, $\tilde{{\mathcal {J}}}(F) = {\mathbb {P}}^2 {\setminus } {\mathcal {F}}(F)$.

For holomorphic map of ${\mathbb {P}}^2$, $\tilde{{\mathcal {J}}}(F)={\mathcal {J}}(F)$ but for rational maps, there could be a difference between these two sets (see [85, Corollary 1.6.7]).

When F is the renormalization map associated to the Grigorchuk group (see Sect. 2.4.1), the discrepancy between Julia sets $\tilde{{\mathcal {J}}}(F) {\setminus } {\mathcal {J}}(F)$ can be made very explicit. From the explicit expression of $\Omega$ in (1.3), the set ${\mathcal {J}}(F)$ is the union:

$$\begin{aligned} {\mathcal {J}}(F) =\bigcup _{-1 \le \theta \le 1} \{ [\lambda , \mu , w] \ | \ 4 w^2 - \mu ^2 + \lambda ^2 - 4 \theta \lambda w =0 \} \subset {\mathbb {P}}^2({\mathbb {C}}) \end{aligned}$$

whereas the precise description of $\tilde{{\mathcal {J}}}(F)$ was obtained by Goldberg–Yang [41]:

$$\begin{aligned} \tilde{{\mathcal {J}}}(F) = \overline{\bigcup _{n \geqslant 0 } I(F^n)} \cup {\mathcal {J}}(F), \end{aligned}$$

where $I(F^n)$ are the indeterminacy points of $F^n$ on ${\mathbb {P}}^2({\mathbb {C}})$. For general maps, the extended indeterminacy set $\overline{\bigcup _{n \geqslant 0 } I(F^n)}$ can be very large, but in our situation, we will see that F is integrable and preserves a fibration by conics (given by the map $\phi$ in (5.5) where $\phi \circ F = \phi$). Since the indeterminacy set I(F) is contained in finitely many fibers of this fibration, this set is contained in a union of finitely many conics in ${\mathbb {P}}^2$.

Remark 3.5

In many cases, one can also define a “small” Julia set inside the big one as the support of the measure of maximal entropy (see e.g [7, 10, 85]). However, it is not canonically defined in the cases of interest for us since $\lambda _1(F) = d_{t}(F)$.

3.5 General Equidistribution Results

As we have mentioned above, we are interested in a result of the following type:

Desired Equidistribution Statement

Let ${{\mathfrak {R}}}$ be a certain class of dominant maps of degree $d \ge 2$. Then for any $F \in {{\mathfrak {R}}}$ and a typical algebraic curve $C\subset {\mathbb {P}}^2({\mathbb {C}})$, we have:

• (i)
  $$\begin{aligned} \frac{ [ (F^n)^* C ] }{ d^n \cdot \deg C } \rightarrow {\Omega }. \end{aligned}$$

• (ii) For any holomorphic curve S, the restriction ${\Omega } \, |\,S\equiv {\omega }_S$ is a well defined measure ${\omega }_S$.

• (iii) Letting $\nu _n$ be the probability measure uniformly distributed over $(F^n)^* C \cap S$, we have $\nu _n \rightarrow {\omega }_S$.

Assertion (i) was obtained in the following situations:

• ${{\mathfrak {R}}}$ is the space of non-elementary polynomial automorphisms of ${\mathbb {C}}^2$, C is an arbitrary affine algebraic curve (Bedford and Smillie [7];

• ${{\mathfrak {R}}}$ is the space of proper polynomial maps⁵ of ${\mathbb {C}}^2$, C is a typical (in a capacity sense) affine algebraic curve (Russakovskii and Shiffman [82]);

• ${{\mathfrak {R}}}$ is the space of holomorphic endomorphisms of ${\mathbb {P}}^2({\mathbb {C}})$, C is an algebraic curve which is not contained in the “exceptional subvariety” (Favre and Jonsson [33]);

• ${{\mathfrak {R}}}$ is a space of dominant rational endomorphisms of ${\mathbb {P}}^2({\mathbb {C}})$ (subject of certain technical assumptions); C is an algebraic curve which does not pass through “maximally degenerate” periodic points (Bleher, Lyubich and Roeder [15]).

The validity of assertion (ii) is a consequence of Bedford-Taylor’s intersection theory of (1, 1) currents when the current $\Omega$ has bounded potential or when certain transversality conditions are met (see Appendix 9.1).

Assertion (iii) does not follow immediately from (i). The reason is that the intersection of currents is not continuous with respect to the weak topology. However, this fact is known in particular situations listed below.

• In the study of bifurcation of a holomorphic family of rational maps, Dujardin [32, Theorem 2.11.] obtained these assertions when C is a horizontal curve and when S is the graph of a marked family of critical points.

• The sliced equidistribution was obtained by Chio–Roeder [19, Theorem C] when $F = (\lambda , z) \mapsto (\lambda , f_\lambda (z))$ where $f_\lambda$ is a family of rational maps of the same degree whose coefficients depend algebraically on $\lambda$.

• In [13], Berteloot and Dinh showed that the so-called bifurcation measure associated to the quadratic family $z^2 + c$ can be realized as the slice of the Julia set of a particular tangent map.

3.5.1 Transport of the Equidistribution by Conjugation

Fix two open subsets U, V of ${\mathbb {P}}^2$ and two dominant rational maps F, G on on ${\mathbb {P}}^2$ which preserve U and V respectively and take a biholomorphism $\varphi :U \rightarrow V$ such that $\varphi \circ F = G \circ \varphi$.

The following assertions show that the equidistribution property is invariant under analytic conjugacies.

Lemma 3.6

Take an irreducible algebraic curve C in V. Suppose that the following assertions holds:

• (i) G is algebraically stable on ${\mathbb {P}}^2$.

• (ii) The sequence of currents

  $$\begin{aligned} \dfrac{1}{ \lambda _1(G)^n} (G^n)^* [C] \end{aligned}$$

  converges to the Green current $\Omega _G$ of G.

Then the limit

$$\begin{aligned} \dfrac{1}{\lambda _1(F)^n} (F^n)^* \varphi ^* [C\cap V] \end{aligned}$$

also exists and is equal to the restriction of $\varphi ^* \Omega _G$ to U.

Lemma 3.7

Fix $C_1, C_2$ two irreducible algebraic curves on ${\mathbb {P}}^2$. Suppose that the following properties hold.

• (i) The map G is algebraically stable on ${\mathbb {P}}^2$.

• (ii) The curve $\varphi (C_1 \cap U)$ satisfies the condition of Lemma 3.6.

• (iii) The sequence of measures given by the intersection of currents

  $$\begin{aligned} \dfrac{1}{\lambda _1(G)^n} [\varphi (C_2 \cap U)] \wedge (G^n)^* [\varphi (C_1 \cap U)] \end{aligned}$$

  converges to a multiple of the measure $[\varphi (C_2 \cap U)] \wedge \Omega _G$, where $\Omega _G$ is the Green current of G.

Then the sequence of measures:

$$\begin{aligned} \dfrac{1}{\lambda _1(F)^n} [C_2 \cap U] \wedge (F^n)^* [C_1 \cap U] \end{aligned}$$

converges to a multiple of the measure $[C_2 \cap U] \wedge \varphi ^* \Omega _G$.

3.6 Three Particular Direct Products

Although the existence of the Green current associated to two of our maps follows from general results, the equidistribution of the preimages of curves toward this current and the precise description of the Green current will hold because our maps have a very specific form.

3.6.1 Direct Product ${\text {id}}\times f$ Related to the Grigorchuk Group

Let us consider a map

$$\begin{aligned} F:{\mathbb {C}}^2\rightarrow {\mathbb {C}}^2, \quad F= ( {\text {id}}\times f),\quad (\eta , \theta ) \mapsto (\eta , f(\theta ) ) \end{aligned}$$

where f is a polynomial in one variable of degree $d\ge 2$. It extends to ${\mathbb {P}}^1 \times {\mathbb {P}}^1$ as a holomorphic map. Its filled Julia set ${{\mathcal {K}} }(F)$ (i.e the set of non-escaping points) in ${\mathbb {C}}^2$ is equal to the product ${\mathbb {C}}\times {{\mathcal {K}} }(f)$.

The Green function $G_F$ for F depends only on the second coordinate and is equal to the one-dimensional Green function $G_f (\theta )$ for the polynomial f. Indeed, on the basin of infinity, ${\mathbb {C}}^2\smallsetminus {{\mathcal {K}} }(F)$, we have

$$\begin{aligned} G_F (\eta , \theta ) = \lim \frac{1}{d^n} \log \Vert F^n (\eta , \theta ) \Vert = \lim \frac{1}{d^n} \log | f^n ( \theta ) | = G_f(\theta ), \end{aligned}$$

while on ${{\mathcal {K}} }(F)$ both functions vanish.

The Julia set ${{\mathcal {J}}}(F)= {\mathbb {C}}\times {{\mathcal {J}}}(f)$ is naturally laminated by the horizontal complex lines $L_\theta = {\mathbb {C}}\times \{ \theta \}$, $\theta \in {{\mathcal {J}}}(f)$. The Green current

$$\begin{aligned} {\Omega }&= \frac{i}{2} \partial {\bar{\partial }}G = {\Delta }G_f \, {\text {d}}\theta \wedge {\text {d}} {\bar{\theta }} = {\omega }\, {\text {d}}\theta \wedge {\text {d}} {\bar{\theta }} ,\\&= \int _{{\mathbb {T}}} [L_\theta ] {\text {d}}\omega (\theta ) \end{aligned}$$

is a horizontal laminar current whose transverse measure is equal to the harmonic measure ${\omega }$ for f. Thus, for a non-horizontal holomorphic curve $S\subset {\mathbb {C}}^2$, the restriction ${\Omega } \, |\,S$ is identified with the measure ${\omega }_S := (p_2 \, |\,S) ^* ({\omega })$, where $p_2:{\mathbb {C}}^2\rightarrow {\mathbb {C}}$ is the projection to the $\theta$-axis.

Given two holomorphic curves, C and S, which do not have common irreducible components, we let $[C\cap S ]$ be the counting measure on $C\cap S$, it is equal to the intersection of currents $[C ] \wedge [S]$.

Recall that the points $0, \infty$ are fixed points of the squaring map $z\mapsto z^2$. We thus say that the lines ${\mathbb {P}}^1 \times \{ 0\}$, ${\mathbb {P}}^1 \times \{ \infty \}$ are the exceptional lines for the map ${\text {id}}\times f_0$ where $f_0$ is the squaring map.

Lemma 3.8

Suppose that $F = {\text {id}}\times f_0$ where $f_0$ is the squaring map $z \mapsto z^2$. Let C and S be two irreducible algebraic curves such that C is neither a vertical line nor a horizontal exceptional line while S is not horizontal and such that the points of $C\cap S$ are not on the exceptional lines. Then

$$\begin{aligned} \frac{1}{2^n} \, [ (F^n)^* C \cap S ] \rightarrow (\deg C) \cdot (\deg S)\cdot \omega _S. \end{aligned}$$

(3.3)

Remark 3.9

Observe that the equidistribution of the preimages of C by F does not directly imply the convergence of their intersection with S to the above measure. The main issue is that the product of currents is not continuous with respect to the weak topology on currents. However, here we exploit the basic dynamical properties of the squaring map.

Proof

Denote by $p_1,p_2$ the projection of ${\mathbb {C}}\times {\mathbb {C}}\equiv {\mathbb {C}}_1\times {\mathbb {C}}_2$ onto the first and second factor, ${\mathbb {C}}_1\equiv {\mathbb {C}}\times \{0\}$ and ${\mathbb {C}}_2\equiv \{0\}\times {\mathbb {C}}$, respectively. For $\eta \in {\mathbb {C}}_1$, we let $L_\eta := {\textbf{p}}_1^{-1} (\eta )$ be the fiber line over $\eta$, and let ${\mathbb {T}}_\eta \subset L_\eta$ be the unit circle inside.

Let $B\subset {\mathbb {C}}_1$ be the set of projections of the branch points of $\pi _1: C\rightarrow {\mathbb {C}}_1$. Let

$$\begin{aligned} C^* := C\smallsetminus ( {\textbf{p}}_1^{-1} (B) \cup {\textbf{p}}_2^{-1} (0)). \end{aligned}$$

Note that the points of intersection of the horizontal line ${\mathbb {C}}_1 \times \{0 \}$ with the curve C are fixed points of F, we choose a base point $\eta _{\varvec{\circ }}\in {\mathbb {C}}_1 \smallsetminus (B\cup (C\cap {\mathbb {C}}_1) )$ so that the corresponding vertical line $L_{\eta _{\varvec{\circ }}}$ avoids $C\cap {\mathbb {C}}_1$ and the branch points of ${\textbf{p}}_1 |\, C$.

Let $C \cap L_{\eta _{\varvec{\circ }}} = \{ \eta _{\varvec{\circ }}\} \times Q_{\varvec{\circ }}$; it consists of $\delta := \deg C$ points of transverse intersections. Then let

$$\begin{aligned} Q^n_{\varvec{\circ }}:= F^{-n} (Q) = F^{-n} (C) \cap L_{\eta _{\varvec{\circ }}} = \{\eta _{\varvec{\circ }}\} \times f_0^{-n} (Q_{\varvec{\circ }}) ; \end{aligned}$$

it consists of $\delta d^n$ transverse intersection points. The uniform measures $\mu ^n_{\varvec{\circ }}$ on these sets converge to the Lebesgue measure ${\omega }_{\varvec{\circ }}$ on ${\mathbb {T}}_{\varvec{\circ }}\equiv {\mathbb {T}}_{\eta _{\varvec{\circ }}}$.

Let $T:= S\cap {\textbf{p}}_2^{-1} ({\mathbb {T}})$, and let $T^*$ be obtained from T by puncturing out branch point of $p_1|\, S$ and $p_2|\, S$, and points of $T\cap p_1^{-1} ( B)$. Take a point $s\in T^*$, and select a simply connected neighborhood $U\supset \{\eta _0, p_1(s) \}$ in the horizontal axis ${\mathbb {C}}_1$ whose closure does not contain points of B and C. Then C is decomposed over U in $\delta$ univalent branches $C_i\subset {\mathbb {C}}^2$ (i.e., graphs of holomorphic functions $\psi _i: U\rightarrow {\mathbb {C}}$). Taking preimages of these branches by $F^n$, we obtain ${\delta }\, 2^n$ univalent branches $C_{ij}^n\subset {\mathbb {C}}^2$ over U parametrized by holomorphic functions $\psi _{i,j}^n : U \rightarrow {\mathbb {C}}$ such that:

• (i) They are pairwise disjoint, so they induce a holomorphic motion $h_\eta$ of the set $X_{\varvec{\circ }}:=\bigcup Q^n_{\varvec{\circ }}$ over U (see e.g., [73, §17]).

• (ii) Their slopes go to 0 exponentially fast (since the fibered map F is vertically expanding away from the exceptional lines).

By the $\lambda$-Lemma (see e.g., [73, §17.2]), $h_\eta$ extends to a holomorphic motion of the closure $\overline{ X_{\varvec{\circ }}}= X_{\varvec{\circ }}\cup {\mathbb {T}}_{\varvec{\circ }}$ (for which we will keep the same notation). By (ii), the limiting functions for $\psi ^n_{ij}$ are constants, so $h_\eta |\, {\mathbb {T}}_{{\varvec{\circ }}} = {\text {id}}$.

Take now a relative neighborhood $W\subset S$ of s that projects univalently to ${\mathbb {C}}_2$ by $p_2$, and let $W_{\varvec{\circ }}:= (p_2|\, L_{\eta _{\varvec{\circ }}})^{-1} (p_2(W))$. Then our holomorphic motion induces a homeomorphic holonomy map $\gamma : W_0\rightarrow W$.

Let ${\omega }:= \gamma _* ({\omega }_{\varvec{\circ }})$, $\mu ^n:= \gamma _* \mu ^n_{\varvec{\circ }}$. Take a continuous test function u on S supported on W, and let $u_{\varvec{\circ }}$ be its pullback to $W_0$. Since the measures $\mu ^n_{\varvec{\circ }}$ converge to ${\omega }_{\varvec{\circ }}$,

$$\begin{aligned} \int u_{\varvec{\circ }}\, {\text {d}}\mu ^n_{\varvec{\circ }}\rightarrow \int u_{\varvec{\circ }}\, {\text {d}}{\omega }_{\varvec{\circ }}. \end{aligned}$$

Pushing this forward by $\gamma$ to W, we obtain:

$$\begin{aligned} \int u\, {\text {d}}\mu ^n \rightarrow \int u\, {\text {d}}{\omega }. \end{aligned}$$

It follows that any limiting measure $\nu$ on S for the sequence $(\mu ^n)$, being restricted to $T^*$, coincides with ${\omega }$. In particular, $\nu |\, T^*$ is a probability measure, implying that $\nu (T\setminus T^*) =0$. Hence $\nu = {\omega }$, and the conclusion follows. $\square$

3.6.2 Twist Map on the Elliptic Cylinder Related to the Lamplighter Group

Consider a product map $F :{\mathbb {C}}^2 \rightarrow {\mathbb {C}}^2$ given by:

$$\begin{aligned} (\eta , z ) \mapsto (\eta , M_\eta (z)), \end{aligned}$$

where $M_\eta \in {\textrm{GL}} _2({\mathbb {C}})$ defines a Möbius transformation with polynomial coefficients in ${\mathbb {R}}[\eta ]$ such that the trace ${\text {tr}}(M_\eta )$ is a non-constant polynomial in $\eta$ of some degree d. Denote by $E \subset {\mathbb {C}}$ the locus of parameter $\eta$ such that the transformation $M_\eta$ is neutral (i.e parabolic or elliptic). Observe that $E = \{ \eta \ | \ {\text {tr}}(M_\eta ) \in [-2,2]\}$ is a finite union of at most d intervals. For each $\eta \in E$, $M_\eta$ is conjugate to a rotation by $\rho (\eta )$ and the corresponding conjugation maps the real line to the unit circle. As a result, the set of non-wandering points for F is the union $E\times {\mathbb {C}}$ with the conic of fixed points. Consider the parabolic locus ${\mathcal {P}}$ for the family $(M_\eta )$. To describe the spectral current whose support is on this set, we need to consider the conjugation $\varphi :({\mathbb {C}}\smallsetminus {\mathcal {P}}) \times {\mathbb {C}}\rightarrow ({\mathbb {C}}\smallsetminus {\mathcal {P}}) \times {\mathbb {C}}^*$ such that the restriction to the non-parabolic locus is of the form

$$\begin{aligned} \varphi \circ F \circ \varphi ^{-1} :(\eta , u) \mapsto (\eta , e^{i\rho (\eta )} u ). \end{aligned}$$

Note that $\rho$ is a well-defined function determined by the equation $2\cos (\rho (\eta )) = {\text {tr}}(M_\eta )$, it is thus a non constant analytic function. Letting $\tilde{F} = \varphi \circ F \circ \varphi ^{-1}$ be the conjugate of F by $\varphi$, we obtain the following.

Proposition 3.10

Take two real lines L and C which are neither on a vertical nor horizontal in ${\mathbb {R}}^2$, consider their complexifications $C_{\mathbb {C}}, L_{\mathbb {C}}$ in ${\mathbb {C}}^2$, let $\tilde{C}_{{\mathbb {C}}}$, $\tilde{L}_{\mathbb {C}}$ be their image by $\varphi$, and let $l :{\mathbb {C}}\rightarrow {\mathbb {C}}$ be a rational function whose graph in ${\mathbb {C}}^2$ is equal to $\tilde{L}_{\mathbb {C}}$. Then the following properties hold.

• (i) The sequence of currents

  $$\begin{aligned} \dfrac{1}{n} (\tilde{F}^{n})^*[\tilde{C}_{\mathbb {C}}] \end{aligned}$$

  converges to a current supported on $E\times {\mathbb {C}}^*$, laminated by vertical punctured complex lines with transverse measure $\rho ^* {\text {d}}\theta$ where ${\text {d}}\theta$ is the Lebesgue measure on the circle.

• (ii) The sequence of counting measures

  $$\begin{aligned} \dfrac{1}{n}\tilde{F}^{-n}(\tilde{C}_{\mathbb {C}}) \cap \tilde{L}_{{\mathbb {C}}} \end{aligned}$$

  converges to the measure $l_*\rho ^* {\text {d}}\theta$ on $\tilde{L}_{\mathbb {C}}$.⁶

Remark 3.11

In the case of the Lamplighter group, the associated map F is:

$$\begin{aligned} (\eta , z) \mapsto \left( \eta , \dfrac{\eta z -4}{z}\right) , \end{aligned}$$

and the line $L_{\mathbb {C}}$ we consider is of equation $\eta = z$.

Proof

Let us prove assertion (i). Observe that on the loxodromic locus, the restriction of the above current converges exponentially fast to zero. Indeed, on the loxodromic locus, we can suppose that ${\text {Im}}\rho (\eta ) > 0$ and the forms $(\tilde{F}^n)^* {\text {d}}u, (\tilde{F}^n)^* {\text {d}}{\bar{u}}$ are given by:

$$\begin{aligned} (\tilde{F}^n)^* {\text {d}}u= & {} e^{in {\text {Re}}\rho (\eta )- n {\text {Im}}\rho (\eta )} \left( {\text {d}}u + i n u {\text {d}}\rho \right) ,\\ (\tilde{F}^n)^* {\text {d}}{\bar{u}}= & {} e^{-in {\text {Re}}\rho (\eta ) - n {\text {Im}}\rho (\eta )} \left( {\text {d}}{\bar{u}} - i n {\text {d}}{\bar{\rho }} \right) . \end{aligned}$$

Since these forms converge exponentially fast to zero in the loxodromic locus and since C is not a horizontal line, we obtain that the current $(\tilde{F}^n)^* [\tilde{C}_{\mathbb {C}}]$ converge exponentially fast to zero on that locus.

Let us now consider the current on the elliptic locus. When $\eta \in E$, $\rho (\eta )$ is real and the restriction of $\rho$ to E is a real analytic function. Observe also that the lines C, L are real lines, hence the images $\varphi (C \cap E \times {\mathbb {R}}), \varphi (L \cap E\times {\mathbb {R}})$ are contained in $E \times {\mathbb {T}}$.

Suppose that the curve $\varphi (C)$ is parametrized by $\eta \mapsto g(\eta ) \in {\mathbb {T}}$. By restricting $\rho$ to a smaller subset, we can suppose that $\rho$ is injective on E and let us consider the map $\rho ^{-1}$. The pullback of the line C is then parametrized by:

$$\begin{aligned} \eta \mapsto g(\eta ) - n \rho (\eta ) \in {\mathbb {R}}/2\pi {\mathbb {Z}}. \end{aligned}$$

Reparametrizing by $\omega = \rho (\eta )$, we obtain:

$$\begin{aligned} \omega \in {\mathbb {T}}\mapsto g(\rho ^{-1}(\omega ) ) - n \omega \in {\mathbb {T}}. \end{aligned}$$

Geometrically, the above map is the graph of $\omega \mapsto - n\omega \in {\mathbb {T}}$ which is transported vertically by $g (\rho ^{-1})$. The graphs $\omega \mapsto - n \omega$ equidistribute towards the real laminar current

$$\begin{aligned} \int _{\mathbb {T}}[\{ \omega \} \times {\mathbb {T}}] \ {\text {d}}\theta (\omega ), \end{aligned}$$

so we deduce that the real currents $(1/n)[F^{-n}(\varphi (C))]$ converge to the current

$$\begin{aligned} \int _E [\{\eta \} \times {\mathbb {T}}] \ \rho ^* {\text {d}}\theta \end{aligned}$$

In particular, the currents associated $(1/n)(F^{n})^* [\tilde{C}_{{\mathbb {C}}}]$ converge to the laminar current

$$\begin{aligned} \int _E [\{\eta \} \times {\mathbb {C}}] \ \rho ^* {\text {d}}\theta , \end{aligned}$$

as required.

Let us prove assertion (ii). Let us also observe that the map $\rho :E \rightarrow {\mathbb {T}}\simeq {\mathbb {R}}/2\pi {\mathbb {Z}}$ is surjective. By restricting to a smaller subset, we can suppose furthermore that $\rho :E \rightarrow {\mathbb {T}}$ is bijective. Let us show that $F^{-n}(C) \cap L$ contains n points counted with multiplicity. Let us consider the real curves $\tilde{L} =\varphi (L)$, $\tilde{C} = \varphi (C)$. These two curves $\tilde{L}, \tilde{C}$ are the graphs in $E\times {\mathbb {T}}$ of two analytic functions $l, g :E\rightarrow {\mathbb {T}}$. Using an appropriate parametrization, one can always suppose that l is locally constant function equal to $0 \in {\mathbb {R}}/2\pi {\mathbb {Z}}$. Now the intersection $\tilde{L} \cap \tilde{F}^{-n}( \tilde{C})$ is locally given by:

$$\begin{aligned} \tilde{L} \cap \tilde{F}^{-n}( \tilde{C}):= \{ (\eta ,0) \in E \times {\mathbb {R}}/2\pi {\mathbb {Z}}\ | \ g(\eta ) -n \rho (\eta ) =0 \in {\mathbb {R}}/2\pi {\mathbb {Z}}\}. \end{aligned}$$

Reparametrizing by $\omega = \rho (\eta )$, we consider the set

$$\begin{aligned} \{ g(\rho ^{-1}(\omega )) - n \omega =0 \}. \end{aligned}$$

Let us chop the circle ${\mathbb {T}}$ into n subintervals $[\omega _1 , \omega _2], \ldots , [\omega _n , \omega _{n+1}]$ so that $n\omega _i = 0 \in {\mathbb {R}}/2\pi {\mathbb {Z}}$ and such that the restriction of $\omega \mapsto n \omega$ on each of these subintervals is injective. Now the graph of $g \circ \rho ^{-1}$ intersects the graph of $\omega \mapsto n\omega$ exactly once in each of these subintervals. As a result, the intersection $\tilde{L}\cap \tilde{F}^{-n}(\tilde{C})$ contains n points and we have

$$\begin{aligned} \dfrac{1}{n}\tilde{L}\cap \tilde{F}^{-n}(\tilde{C}) = \dfrac{1}{n}\tilde{L}_{\mathbb {C}}\cap \tilde{F}^{-n}(\tilde{C}_{\mathbb {C}}), \end{aligned}$$

since the measures $\tilde{L}_{\mathbb {C}}\cap \tilde{F}^{-n}(\tilde{C}_{\mathbb {C}})$ have mass n. Moreover, going back to the $\eta$ coordinates, we obtain that the sequence of measures:

$$\begin{aligned} \dfrac{1}{n}(\tilde{L}\cap \tilde{F}^{-n}(\tilde{C})) \end{aligned}$$

converges to the measure $l_* \rho ^* {\text {d}}\theta$. $\square$

3.6.3 Skew Product Over the Cantor Dynamics Related to the Hanoi Group

Let us consider a map $F :{\mathbb {C}}^2 \rightarrow {\mathbb {C}}^2$ of the form

$$\begin{aligned} F = (\eta , \theta ) \mapsto (p(\eta ), \lambda (\eta ) \theta ), \end{aligned}$$

where $p (\eta ) = \eta ^2 - \eta -3$ is a hyperbolic polynomial of degree 2 and

$$\begin{aligned} \lambda (\eta ) = (\eta -1) (\eta + 2)/(\eta +3) , \end{aligned}$$

is a rational function on $\eta$.

Recall from Sect. 3.1.4 that p is conjugate to the map $u \mapsto u^2 - 15/4$ with a Cantor Julia set lying on the real line. The Julia set of F is laminated by a Cantor set of vertical complex lines $\{ \eta \} \times {\mathbb {C}}$ where $\eta \in {\mathcal {J}}(p)$.

The Green current of F

$$\begin{aligned} \Omega = \Delta G_p {\text {d}}\eta \wedge {\text {d}}{\bar{\eta }} =\omega {\text {d}}\eta \wedge {\text {d}}{\bar{\eta }} \end{aligned}$$

is a vertical laminar current whose transverse measure is equal to the measure of maximal entropy $\omega$ for the polynomial p.

Proposition 3.12

Fix $\eta _0 \in {\mathbb {R}}$. Let L a real line which is neither vertical nor horizontal and let $L_{\mathbb {C}}$ be its complexification. Then the following properties hold.

• (i) The sequence of currents

  $$\begin{aligned} \dfrac{1}{2^n} F^{-n}(\{\eta _0 \}\times {\mathbb {C}}) \end{aligned}$$

  converges to the Green current of F.

• (ii) The sequence of counting measures

  $$\begin{aligned} \dfrac{1}{2^n} F^{-n}(\{\eta _0 \}\times {\mathbb {C}}) \cap L_{\mathbb {C}}= \dfrac{1}{2^n} (F^n)^* [\{\eta _0 \}\times {\mathbb {C}}] \wedge L_{\mathbb {C}}\end{aligned}$$

  converges to the measure $\Omega \wedge L_{\mathbb {C}}$ which is the transport under holonomy of the measure of maximal entropy on ${\mathcal {J}}(p)$ to the line L.

Proof

Assertion (i) follows directly from the equidistribution of the preimages of $\eta _0$ towards the equilibrium measure $\omega$ on the Julia set of p. The second assertion then follows from the fact that $L_{\mathbb {C}}$ is transverse to all the fibers $\{\eta \} \times {\mathbb {C}}$. Indeed, let us denote by $\mu _n$ the counting measure

$$\begin{aligned} \mu _n := \dfrac{1}{2^n} F^{-n} (\{\eta _0 \} \times {\mathbb {C}}) \cap L_{\mathbb {C}}. \end{aligned}$$

(3.4)

Observe that the restriction of F on the horizontal axis is given by $(\eta ,0) \mapsto (p(\eta ), 0)$.

The preimage $F^{-n} (\{ \eta _0\} \times {\mathbb {C}})$ is a union of $2^n$ vertical fibers counted with multiplicity and each of the $2^n$ point in the intersection of $F^{-n} (\{\eta _0\} \times {\mathbb {C}})$ with the horizontal axis can moved to a point on $F^{-n}(\{\eta _0 \} \times {\mathbb {C}}) \cap L_{\mathbb {C}}$ via the holonomy along the vertical foliation. Since the sequence of counting measures

$$\begin{aligned} \dfrac{1}{2^n} F^{-n} ( \{\eta _0 \} \times {\mathbb {C}}) \cap ({\mathbb {C}}\times \{0 \}) \end{aligned}$$

converge to the measure of maximal entropy of p on the horizontal axis, we deduce that $\mu _n$ converges to the transport of this measure to $L_{\mathbb {C}}$ along the vertical foliation. $\square$

In conclusion, let us relate this current to the Green current of the map $R_{\mathcal {H}}$. We will see (e.g in §7.1) that the map $R_{{\mathcal {H}}}$ becomes algebraically stable on a blow-up X of ${\mathbb {P}}^2$ at 4 points. Using Guedj’s theorem, the lift $\tilde{R}_{{\mathcal {H}}}$ to X admits a Green current on X that we denote $T_R$. Moreover, the map $\tilde{R}_{{\mathcal {H}}}$ is birationally conjugate to F via a map $\varphi :X \rightarrow {\mathbb {P}}^2$. We claim that $\varphi ^* \Omega = T_R$.

The cohomology class of any fiber $\{\eta =c \}$ in ${\mathbb {P}}^2$ is invariant by $F^*$ and multiplied by 2. Let us consider the projection $\pi :{\mathbb {P}}^2 \rightarrow {\mathbb {P}}^1$ induced by the first projection $(\eta , \theta ) \mapsto \eta$. In general the map $\pi \circ \varphi$ is rational and dominant but in our case, it is holomorphic. Indeed, the map $\pi \circ \varphi$ can be described geometrically as follows. To any point x on X, we find the unique conic $C_x$ of ${\mathbb {P}}^2$ passing through the four points $[\pm 1:0 : 1], [-1:1:0], [2:1:0]$ and going through x. The value of $\eta =\pi \circ \varphi (x)$ can be determined geometrically as the slope of the tangent line to $C_x$ at the point [1 : 0 : 1]. As the coefficients of the equation of the conic $C_x$ are holomorphic functions in x and since taking the slope at a certain point is also holomorphic, we conclude that $\pi \circ \varphi$ is holomorphic. Let us consider the Fubini-Study form $\omega$ on ${\mathbb {P}}^1$ and let $\alpha$ be the pullback $(\pi \circ \varphi )^* \omega$. The form $\alpha$ is a smooth closed and positive current on X, and its class is in the same class as the Green current $T_R$:

$$\begin{aligned} \{T_R\} = \{{\alpha } \}. \end{aligned}$$

Moreover, using the semi-conjugation, we have:

$$\begin{aligned} R_{\mathcal {H}}^* \varphi ^* \Omega = 2 \varphi ^* \Omega . \end{aligned}$$

(3.5)

Using Guedj’s result, the current $T_R$ has minimal singularities among all the invariant current whose class is equal to $\{T_R \}$. By definition, this means that if S is any closed positive invariant current in the same cohomology class as $T_R$, then

$$\begin{aligned} G_S \leqslant G_R + C, \end{aligned}$$

where C is a constant and $G_R, G_S$ are the local potential $T_R = \alpha + dd^c G_R, S = \alpha + dd^c G_S$. We then say that S is more singular than $T_R$, and we say that $T_R$ and S have the same singularity type if S is more singular than $T_R$ and $T_R$ is more singular than S.

In our situation, if $\Omega = {\alpha } + dd^c G_\Omega$, there exists a constant C such that:

$$\begin{aligned} G_\Omega \leqslant G_R+ C. \end{aligned}$$

Moreover, the potential $G_\Omega$ is continuous as it is the pullback of the Green current of a polynomial endomorphism by $\pi \circ \varphi$. Since $G_R$ is bounded above, we get:

$$\begin{aligned} G_R \leqslant G_\Omega + C. \end{aligned}$$

We conclude that $G_R$ and $G_\Omega$ have the same singularity type. Let us consider the difference $u = G_R - \varphi ^* G_F$, it is a bounded function and the invariance gives:

$$\begin{aligned} T_R&= \dfrac{1}{2^n} (\tilde{R}_{{\mathcal {H}}}^n)^* T_R\\&= \dfrac{1}{2^n} (\tilde{R}_{{\mathcal {H}}}^n)^* ( \varphi ^* \Omega + dd^c u )\\&= \varphi ^* \Omega + \dfrac{1}{2^n} dd^c u \circ \tilde{R}_{{\mathcal {H}}}^n. \end{aligned}$$

Taking the limit as $n\rightarrow +\infty$, we deduce that $(1/2^n)u \circ \tilde{R}_{{\mathcal {H}}}^n$ converges to zero in $L^\infty (X)$, hence in $L^1(X)$. Overall, this shows that $T_R = \varphi ^* \Omega$.

4 Atomic Density of States

In some cases, the density of states (defined in Sect. 2.3) is atomic. We explain this phenomenon by a discrepancy between the dynamical degree of the renormalization map and the growth of the number of vertices of the sequence of Schreier graphs that appear in the renormalization. This phenomenon already appeared in the work of Sabot (see [84, Theorem 4.14]) who used it to study the spectrum of the Laplacian arising from fractal sets. In our situation, the renormalization transformation is related to the spectrum in a slightly different way but the resulting statement is similar. We thus state our result.

Theorem 4.1

Consider a sequence of polynomial $P_n \in {\mathbb {C}}[x,y]$ of degree $d^n$ where $d>1$ is an integer and a rational map $F :{\mathbb {C}}^2 \rightarrow {\mathbb {C}}^2$ whose dynamical degree $\lambda _1(F)$ satisfies the condition $\lambda _1(F) < d$ and such that:

$$\begin{aligned} P_{n}(x,y) = Q^{ d^{n-p}} \cdot P_{n-1} (F (x,y)), \end{aligned}$$

where $p=0,1,2$, Q is a polynomial in ${\mathbb {C}}[x,y]$. Then the sequence of currents:

$$\begin{aligned} \dfrac{1}{d^n} [P_n=0] \end{aligned}$$

converges to a limiting current supported on countably many curves and its intersection with a generic curve yields an atomic measure. More precisely, generic means we require that this curve does not coincide with any of the curves $\{ P \circ F^n =0\}, \{ Q \circ F^n =0\}$ for all $n\ge 0$)

Proof

Taking the logarithm in the formula defining $P_n$, we have:

$$\begin{aligned} \dfrac{1}{d^n}\log |P_n| = d^{-p}\log |Q| + \dfrac{1}{d^n} \log |P_{n-1}(F(x,y))|. \end{aligned}$$

Applying the above formula inductively, we obtain:

$$\begin{aligned} \dfrac{1}{d^n}\log |P_n| = \sum _{j=0}^{n-1} \dfrac{1}{d^{j+p}}\log |Q(F^j(x,y))| + \dfrac{1}{d^n} \log |P_{0}(F^n(x,y))|. \end{aligned}$$

Consider the current:

$$\begin{aligned} \sum _{j=0}^n \dfrac{1}{d^{j+p}} [Q \circ F^j =0] + \dfrac{1}{d^n} [P_0 \circ F^n =0] . \end{aligned}$$

(4.1)

Since the dynamical degree of F satisfies the condition $\lambda _1(F)< d$, so the currents $[Q_i \circ F^j=0]/ d^j$ have mass bounded by $C_{\varepsilon }(\lambda _1(F)+\epsilon )^j/d^j$ for any $\epsilon > 0$. This shows that the above currents converge to a current supported on countably many curves, so the current $[P_n=0]/ d^n$ converges to a current satisfying the same properties. The slice of the series by the generic curve C amounts to a series of atomic measures whose partial sums have bounded weight equal to $\deg (C)$ times the mass of the current (4.1) . It follows that this sliced series converges to an atomic measure. $\square$

5 Two Rational Maps Associated with the Grigorchuk Group

We recall from Sect. 2.4.1 that the two maps are:

$$\begin{aligned} F({\lambda }, \mu )&= \left( \frac{2{\lambda }^2}{4-\mu ^2}, \ \mu + \frac{\mu {\lambda }^2}{4-\mu ^2} \right) .\nonumber \\ G :(\lambda , \mu )&\mapsto \left( 2\dfrac{ 4 - \mu ^2}{\lambda ^2} , - \mu \left( 1 + \dfrac{4-\mu ^2}{\lambda ^2}\right) \right) . \end{aligned}$$

(5.1)

In homogeneous coordinates, these maps have the form:

$$\begin{aligned}{} & {} F = [\lambda : \mu : w] \mapsto [2 \lambda ^2 w : \mu (4 w^2 - \mu ^2) + \mu \lambda ^2: w(4w^2 - \mu ^2)], \end{aligned}$$

(5.2)

$$\begin{aligned}{} & {} G :[\lambda : \mu : w] \mapsto [2 (4 w^2 - \mu ^2)w : - \mu (\lambda ^2 + 4w^2 - \mu ^2): \lambda ^2 w ]. \end{aligned}$$

(5.3)

We shall set in this section $P_0, P_1, P_2$ the three polynomials defining F:

$$\begin{aligned} P_0= & {} 2 \lambda ^2 w ,\\ P_1= & {} \mu (4 w^2 - \mu ^2) + \mu \lambda ^2,\\ P_2= & {} w(4w^2 - \mu ^2). \end{aligned}$$

In fact $G = H \circ F$ where H is the particular involution:

$$\begin{aligned} {[}\lambda : \mu : w ] \mapsto [4w : -2 \mu : \lambda ]. \end{aligned}$$

(5.4)

We list the elementary properties satisfied by F, G.

• F and G have topological degree 2.

• F and G have algebraic degree 3.

• Both F and G have five indeterminacy points in total, the points $[0: \pm 2 :1]$ in ${\mathbb {C}}^2$, and three more at infinity, the horizontal pole [1 : 0 : 0] and two diagonal points $[\pm 1: 1 :0]$.

5.1 Integrability of the Two Renormalization Maps

We first investigate the properties of the map on ${\mathbb {P}}^2$ and describe our method to recover two invariant fibrations for F through the analysis of the dynamics of its indeterminacy points and curves.

Consider $\pi :{\mathbb {C}}^2 \dashrightarrow {\mathbb {C}}^2$ the rational map given by:

$$\begin{aligned} \pi :(\lambda , \mu ) \mapsto \left( \eta := \phi ({\lambda },\mu ) , \theta := \psi (\lambda ,\mu ) \right) , \end{aligned}$$

where

$$\begin{aligned} \phi ({\lambda },\mu )= \frac{4-{\lambda }^2+\mu ^2}{4\mu }, \end{aligned}$$

(5.5)

and

$$\begin{aligned} \psi (\lambda ,\mu )= \frac{4-\mu ^2+{\lambda }^2}{4{\lambda }} . \end{aligned}$$

(5.6)

For generic values of $\eta$, the level set $\{\phi = \eta \}$ defines a smooth conic in ${\mathbb {P}}^2$, but at $\eta = \pm 1$, these conics degenerate to a union of two lines. We denote these degenerate lines by

$$\begin{aligned} \{\phi = \pm 1 \} = D_{\pm ,1} \cup D_{\pm ,2}, \end{aligned}$$

where $D_{\pm ,i}$ are given by the equations:

$$\begin{aligned} D_{+,1}= & {} \{ 2 + \lambda - \mu =0 \} , D_{+,2} = \{ 2 + \lambda + \mu =0 \}\\ D_{-,1}= & {} \{ -2 + \lambda - \mu =0 \} , D_{-,2} = \{ 2 + \lambda + \mu =0 \}. \end{aligned}$$

Let us also consider the smooth conic $D_0$ of equation $\{ \phi =0\}$.

Theorem 5.1

The following properties are satisfied.

• (i) The rational map F is semi-conjugate via $\pi$ to ${\text {id}}\times t$ where t is the Chebyshev map (i.e $({\text {id}}\times t) \circ \pi = \pi \circ F$).

• (ii) There exists two F-invariant domain $U_1, U_2 \subset {\mathbb {C}}^2$ such that $U_1 \cup U_2 = {\mathbb {C}}^2 {\setminus } (D_0 \cup (\cup _i D_{\pm , i}))$ and the restriction of F on each of these domain is analytically conjugate to the map $(\eta , z) \mapsto (\eta , z^2)$. Moreover, we can choose the analytic conjugation $\varphi$ on $U_i$ so that:

  $$\begin{aligned} \psi \circ \varphi ^{-1} (\eta , z) = \dfrac{1}{2}\left( z + \dfrac{1}{z}\right) , \end{aligned}$$

  where $\psi : {\mathbb {C}}^2 \rightarrow {\mathbb {C}}$ is the function defined above.

Assertion (ii) in the above statement can be summarized in the diagram below.

Remark 5.2

The second map G was studied in detail by M. and Y. Vorobets and a more complicated conjugation has been determined [88].

The above theorem, for example the first assertion can be checked via a direct calculation however we provide a proof to explain where the formulas come from. To that end, we first study the dynamical properties of the map F in Lemma 5.3, Proposition 5.4, Proposition 5.5. Using these, we then obtain in Proposition 5.6 the existence of two invariant pencils for F. Finally we study in more detail these two pencils by rational curves to determine in Lemma 5.8 an explicit conjugation for the map F.

Let us study the orbit of contracted curves for both maps (i.e curves whose image by F and G is collapsed to a point). Observe that since $F = H \circ G$, the contracted curves for F and G are the same. As a result, one finds that the jacobian of F is of the form:

$$\begin{aligned} J(F) = -12 \lambda (\mu - 2 w) w (\mu + 2 w) (\lambda ^2 - \mu ^2 + 4 w^2). \end{aligned}$$

Observe that the vertical line $\{\lambda =0\}$ is a curve of fixed point for F and is mapped by G to the line at infinity.

Denote by $C_1$ the curve $\{ \lambda ^2 - \mu ^2 + 4 w^2 =0\}$. We obtain:

Lemma 5.3

The curve $C_1$ is collapsed by F to $[-2:0:1]$ which is then mapped by F to the fixed point [2 : 0 : 1] for F.

Proof

Recall that we have denoted by $P_0 = 2 \lambda ^2 w$, $P_1 = \mu (4 w^2 - \mu ^2 + \lambda ^2)$ and $P_2= w(4 w^2 - \mu ^2)$ the homogeneous polynomials defining F. Observe that $\lambda ^2 - \mu ^2 + 4 w^2$ divides the polynomial $P_1$, we have also

$$\begin{aligned} P_0(\lambda , \pm \sqrt{4w^2 + \lambda ^2}, w)= & {} 2 \lambda ^2 w,\\ P_2(\lambda , \pm \sqrt{4w^2 + \lambda ^2}, w)= & {} - w \lambda ^2. \end{aligned}$$

In particular, this proves that the curve $C_1$ is contracted to the point $[-2:0:1]$. Now F maps $[-2:0:1])$ to the point [2 : 0 : 1], which is then fixed by F, as required. $\square$

We summarize the dynamics of all the contracted curves.

Proposition 5.4

The following properties hold.

• (i) The map F collapses the curves $\{\mu = \pm 2 w\}$ to the indeterminacy points $[\pm 1: 1 :0]$ respectively.

• (ii) The map G collapses the curves $\{\mu = \pm 2 w\}$ to the indeterminacy points $[0: \pm 2: 1]$ respectively.

• (iii) The orbit of $C_1$ for both F and G is finite and does not contain any indeterminacy points.

• (iv) The line $\{\lambda =0\}$ is a curve a fixed points for F and is mapped by G the the line at infinity.

• (v) The line at infinity (with the indeterminacy points removed) is collapsed by F and G to the vertical pole $q_v = [0:1:0]$ which is a fixed point for both maps.

Proof

Assertions (i),(ii) , (iv) and (v) follow from the expression (5.2), (5.3) of F and G. Assertion (iii) follows from the previous lemma together with the fact that $G = H \circ F$ and that the points $[-2:0:1], [2:0:1]$ are both fixed by H. $\square$

We now look at the dynamical behavior of F near indeterminate points. Denote by X the blow-up of ${\mathbb {P}}^2$ at the four points $[\pm 1: 1: 0]$ and $[0: \pm 2: 1]$ and by $\pi :X \rightarrow {\mathbb {P}}^2$ the associated (regular) map (see Appendix 9.7). Denote by $E_1, E_2, E_3, E_4$ the exceptional divisors over the points $[-1:1:0], [1:1:0]$, $[0:-2:1]$ and [0 : 2 : 1] respectively. We consider the lifts $\tilde{F},\tilde{G}$ of F and G to X.

Fig. 4

Blow-up of ${\mathbb {P}}^2$ at the four points $[\pm 1 : 1 :0]$, $[0: \pm 2 : 1 ]$

In the proposition below, we refer to Appendix 9.7 for the notion of strict transform.

Proposition 5.5

The following assertions hold.

• (i) The involution H induces an automorphism of X, it exchanges $E_1$ with $E_4$ and $E_2$ with $E_3$.

• (ii) $\tilde{F}$ has one indeterminacy point on $E_3$ and $E_4$, the two exceptional divisors $E_3$ and $E_4$ are fixed by $\tilde{F}$ and the restriction to these divisors has topological degree 2.

• (iii) The image of the indeterminacy points of $\tilde{F}$ on $E_3$ and $E_4$ are the strict transform of the lines $\{ \lambda + \mu + 2 w=0 \}$ and $\{\lambda - \mu - 2 w=0 \}$, respectively.

• (iv) $\tilde{F}$ is regular on $E_1,E_2$ and maps these two divisors to the strict transform of the line $\{ \lambda = -2 w \}$ (each with multiplicity one).

• (v) The image of the indeterminacy point [1 : 0 : 0] by $\tilde{F}$ is the strict transform of the line at infinity.

• (vi) Both $\tilde{F}$ and $\tilde{G}$ are algebraically stable on X.

Proof of Proposition 5.5

Recall that we have denoted by $P_0 = 2 \lambda ^2 w$, $P_1 = \mu (4 w^2 - \mu ^2 + \lambda ^2)$ and $P_2= w(4 w^2 - \mu ^2)$ the homogeneous polynomials defining F.

Observe that (i), (ii) and (iv) imply (vi). Observe that assertion (i), (iv) and (v) are direct computations. We leave assertion (i) and (iv) to the reader and prove assertion (v).

Let us blow-up the point [1 : 0 : 0], we choose some local coordinates $(e = \mu /{\lambda }, l = w/\mu )$ such that the the exceptional divisor over [1 : 0 : 0] has local equation $e=0$. In these blow-up coordinates, the map F composed with the blow-down is given by:

$$\begin{aligned} (e, l) \mapsto [1: e : l e]\in {\mathbb {P}}^2 \mapsto [P_0(1, e , le) : P_1(1,e,le) : P_2(1,e, le)] \in {\mathbb {P}}^2, \end{aligned}$$

and we obtain:

$$\begin{aligned} (e,l) \mapsto [2 l: 1 - e^2 + 4 e^2 l^2: e^2 l (-1 + 2 l) (1 + 2 l) ]. \end{aligned}$$

In particular, the image of the exceptional divisor $e=0$ by this map is parametrized by $l \mapsto [2l: 1 :0]$ and assertion (v) holds.

Let us prove (ii) and (iii) for the exceptional divisor $E_3$, we fix some local coordinates near $E_3$. Take $(e = \lambda / w , l = (\mu /w +2)/(\lambda /w))$ so that $E_3 = \{e=0 \}$, we write $F \circ \pi$ in these coordinates:

$$\begin{aligned} F \circ \pi :(e , l) \mapsto [P_0(e , -2 + l e, 1): P_1(e , -2 + le , 1): P_2(e, -2 + le , 1)]. \end{aligned}$$

We obtain:

$$\begin{aligned} F \circ \pi :(e , l) \mapsto [2 e: -(-2 + e l) (-e - 4 l + e l^2): -l (-4 + e l)]. \end{aligned}$$

In particular, the restriction to $E_3$ is of the form:

$$\begin{aligned} F \circ \pi :(e=0 , l) \mapsto [0: -2l: l] = [0:2:1], \end{aligned}$$

when $l \ne 0$. As a result $F \circ \pi$ contracts $E_3$ to the point $[0:-2:1]$. We can thus compute the lift $\tilde{F}$ in these coordinates as $\tilde{F}$ maps $E_3$ to $E_3$, which is obtained from the following expression.

$$\begin{aligned} \tilde{F} :(e, l) \mapsto \left( e' = \dfrac{P_0(e , -2 + l e, 1)}{P_2(e, -2 + le , 1)} , \ l' = \dfrac{2 + P_1(e , -2 + l e, 1)/ P_2(e , -2 + l e, 1)}{P_0(e , -2 + l e, 1)/ P_2(e , -2 + l e, 1)} \right) . \end{aligned}$$

We thus obtain:

$$\begin{aligned} \tilde{F} :(e, l) \mapsto \left( e'= -\dfrac{2e}{l (-4 + e l)}, \ l'=\dfrac{ -2 + e l + 4 l^2 - e l^3}{2}\right) . \end{aligned}$$

The above formula proves that $l=e=0$ is an indeterminacy point of $\tilde{F}$. Blowing-up this point (e.g writing $e = e_1, l= l_1 e_1$ in $F\circ \pi$) gives the image of the indeterminacy point by $\tilde{F}$, and the computation is direct. The restriction to $E_3$ also yields:

$$\begin{aligned} \tilde{F} :(e=0, l ) \mapsto \left( 0 , -1 + 2 l^2 \right) . \end{aligned}$$

This proves that $E_3$ is mapped to itself with multiplicity 2 by $\tilde{F}$ (i.e the restriction of $\tilde{F}$ to $E_3$ has topological degree 2), we have thus proven assertion (ii) and (iii) for the exceptional divisor $E_3$. Similar computation holds for the determination of the image of $E_4$. $\square$

We now use the dynamical features of F above to find two invariant fibrations.

Let $D_1$ be the pencil of conic in ${\mathbb {P}}^2({\mathbb {C}})$ passing through all four points

$[\pm 1:1:0], [0: \pm 2 :1]$, and let $D_2$ be the pencil of conics in ${\mathbb {P}}^2({\mathbb {C}})$ passing through all four points $[\pm 1: 1 :0] , [\pm 2: 0:1]$. We will now show that both pencils are invariant under F. A general algebraic-geometric view of this phenomenon will be given in Sect. 8.2.

Proposition 5.6

The two pencils $D_1,D_2$ are invariant under F.

Proof

Observe that the vertical line $\{ \lambda =0 \}$ is a line of fixed points, which is transversely super-attracting. So the image of any conic passing through $[0, \pm 2, 1]$ also passes through those points (see Proposition 5.5 (iii)). Take a conic C in the pencil $D_1$. Since the horizontal lines $\{\mu = \pm 2 w\}$ do not belong to the pencil $D_1$, Bezout’s theorem proves that C intersects each of those lines at 2 points. Since these lines are collapsed to $[\pm 1: 1: 0]$ by assertion (i) of Proposition 5.4, this proves that the image of C by F passes through the two points $[\pm 1: 1: 0]$. We have shown that for any conic in the pencil $D_1$, its image by F passes through all four points $[\pm 1:1:0] , [0:\pm 2: 1]$. Let us now argue that the image of any conic in the pencil $D_1$ by F is also a conic, i.e is also a curve of degree 2. Since the curve C passes through all four points $[\pm 1:1:0]$ and $[0:\pm 2: 1]$, we can calculate (using Proposition 9.12 (v)) the class of C in $H^{1,1}(X)$:

$$\begin{aligned} C = 2 \tilde{L}_\infty +E_1 + E_2 -E_3 - E_4 \in H^{1,1}(X), \end{aligned}$$

where $\tilde{L}_\infty$ is the strict transform of the line at infinity by the blow-up at the four points $[\pm 1: 1: 0], [0: \pm 2: 1]$. By Proposition 5.5.(iv), the divisors $E_1$ and $E_2$ are mapped by $\tilde{F}$ to a line in X, the exceptional divisors $E_3,E_4$ are fixed by $\tilde{F}$, their indeterminacy point are mapped to a line and the image of the indeterminacy point [1 : 0 : 0] is the line at infinity. This implies that the image of C by F, denoted $F_* C$ is given by:

$$\begin{aligned} F_* C= & {} 2 F_* \tilde{L}_\infty + F_* E_1 + F_* E_2 - F_* E_3 - F_*E_4 \\= & {} (2 +1 + 1 -1 -1) L_\infty \in H^{1,1}({\mathbb {P}}^2). \end{aligned}$$

In conclusion, F maps a conic in $D_1$ to a conic passing through the same four points, so the pencil $D_1$ is preserved by F.

Let us now prove that the pencil $D_2$ is also invariant. The same argument proves that any conic in $D_2$ has an image of degree 2 which passes through the points $[\pm 1, 1, 0]$. Take a conic C in the pencil $D_2$. Since the conic $C_1:=\{\lambda ^2 - \mu ^2 + 4w^2 =0 \}$ does not belong to the pencil $D_2$, Bezout’s theorem proves that C intersects $C_1$ at four points. By Lemma 5.3, the curve $C_1$ is collapsed by F to $[-2:0:1]$, so the image F(C) passes through that point. Moreover, the point [2 : 0 : 1] is a fixed point for F, so the image F(C) also passes through that point. Overall, we have shown that any conic in the pencil $D_2$ is mapped by F to a conic passing through all four points $[\pm 1: 1: 0], [\pm 2: 0:1]$, hence F preserves the pencil $D_2$, as required. $\square$

We obtain an explicit characterization of the two pencils $D_1$ and $D_2$.

Corollary 5.7

The pencil $D_1$ and $D_2$ are parametrized respectively by two rational maps $\phi :{\mathbb {P}}^2 \dashrightarrow {\mathbb {P}}^1$ and $\psi :{\mathbb {P}}^2 \dashrightarrow {\mathbb {P}}^1$ defined by the formulas (5.6) and (5.5). Moreover, $\phi \circ F = \phi , \psi \circ F = t \circ \psi$ where t is the Chebyshev map,

To go further, we need to parametrize holomorphically the fibers of the map $\phi$ to find an appropriate conjugate for F. Recall that the point [2 : 0 : 1] is fixed by F and that the point $[-2:0:1]$ is mapped by F to that point. These two points correspond to the repelling fixed point and its preimage for the Chebyshev map $2 z^2 -1$.

Choose two simply connected domains $V_1,V_2$ of ${\mathbb {C}}{\setminus } \{ \pm 1, 0 \}$ such that $V_1\cup V_2 = {\mathbb {C}}\setminus \{ - 1, 0\}$. Let us take the preimage $U_i \subset {\mathbb {C}}^2$ of $V_i$ by the map $(\lambda ,\mu ) \mapsto \phi ^2(\lambda , \mu ) -1$. By definition, each domain $U_i$ is contained to ${\mathbb {C}}^2 {\setminus } (D_0 \cup \cup _i D_{\pm , i})$ and we have the equality $U_1 \cup U_2 = {\mathbb {C}}^2 {\setminus } (D_0 \cup \cup _i D_{\pm , i})$. On each of these domains $U_i$, the square root $\sqrt{\eta ^2 -1}= \sqrt{\phi ^2 -1}$ is well-defined.

For each $i=1,2$ and any point $p \in U_i \cap \phi ^{-1}(\eta )$, we take $\varphi _\eta (p) \in {\mathbb {P}}^1$ to be the slope of the line joining p and the point $(2,0) \in {\mathbb {C}}^2$. We normalize in such a way that the tangent line to the hyperbola $\phi ^{-1}(\eta )$ at [2 : 0 : 1] is mapped to $[1:1]\in {\mathbb {P}}^1$, such that the point $[0:2\eta + 2\sqrt{ \eta ^2 -1}:1]$ is mapped to $[0:1] \in {\mathbb {P}}^1$ and the point $[0:2\eta - 2\sqrt{ \eta ^2 -1}:1]$ is mapped to the point at infinity $[1:0] \in {\mathbb {P}}^1$.

Lemma 5.8

The following properties hold.

• (i) For each $i =1,2$ and for any $\eta \in {\mathbb {C}}{\setminus } \{ \pm 1, 0 \}$, the map $\varphi _\eta :U_i \cap \phi ^{-1}(\eta ) \rightarrow {\mathbb {C}}$ is an analytic function of the form:

  $$\begin{aligned} \varphi _\eta :(\lambda , \mu ) \in {\mathbb {C}}^2 \cap \phi ^{-1}(\eta ) \mapsto \dfrac{ 2 - \lambda - \eta \mu - \mu \sqrt{ \eta ^2-1} }{ -2 + \lambda + \eta \mu - \mu \sqrt{ \eta ^2-1}}. \end{aligned}$$

• (ii) For each $i =1,2$ and for any $\eta \in {\mathbb {C}}{\setminus } \{ \pm 1 ,0\}$, the inverse $\varphi _\eta ^{-1}:{\mathbb {C}}\rightarrow U_i \cap \phi ^{-1}(\eta )$ of $\varphi _\eta$ is given by:

  $$\begin{aligned} z \mapsto \left( \lambda =-\dfrac{4 (-1 + \eta ^2) z}{ 1 + z^2 + \eta \sqrt{-1 + \eta ^2} (-1 + z^2) - \eta ^2 (1 + z^2))} , \right. \\ \left. \mu = \dfrac{2 \sqrt{-1 + \eta ^2} (-1 + z) (1 + z)}{1 + z^2 + \eta \sqrt{-1 + \eta ^2} (-1 + z^2) - \eta ^2 (1 + z^2)} \right) . \end{aligned}$$

• (iii) For generic $z \in {\mathbb {C}}$ and for all $\eta \in {\mathbb {C}}{\setminus } \{ \pm 1,0 \}$, one has:

  $$\begin{aligned} \varphi _\eta \circ F \circ \varphi _{\eta }^{-1} (z) = z^2. \end{aligned}$$

• (iv) For generic $z \in {\mathbb {C}}$ and for all $\eta \in {\mathbb {C}}{\setminus } \{ \pm 1 ,0\}$, one has:

  $$\begin{aligned} \psi \circ \varphi _{\eta }^{-1} (z) = \dfrac{1}{2} \left( z + \dfrac{1}{z} \right) . \end{aligned}$$

Proof

Let us describe how one can obtain assertion (i). Let us denote by l the slope $l:=(\lambda -2)/\mu$. At the two point $[0: 2 \eta + 2 \sqrt{\eta ^2-1}:1], [0: 2 \eta - 2 \sqrt{\eta ^2-1}:1]$, the slopes $l_+, l_-$ are given by:

$$\begin{aligned} l_+ := - \eta + \sqrt{\eta ^2 -1}\ ; \ l_-:= -\eta - \sqrt{\eta ^2 -1}. \end{aligned}$$

One checks that the slope l of the hyperbola at the point [2 : 0 : 1] is $-\eta$. Since the Mobius transformation $z \mapsto (z - l_-)/(-z + l_+)$ which maps the triplet $(l_+, l_-, -\eta )$ to the triplet $(0,\infty , 1)$ on ${\mathbb {P}}^1$, we obtain $\varphi _\eta$ by applying this Mobius transformation to $l=(\lambda -2) / \mu$:

$$\begin{aligned} \varphi _\eta (\lambda ,\mu ) := \dfrac{\left( \dfrac{\lambda -2}{\mu } \right) + \eta + \sqrt{\eta ^2 -1}}{- \left( \dfrac{\lambda -2}{\mu } \right) -\eta + \sqrt{\eta ^2 -1} }. \end{aligned}$$

For assertion (ii), one determines the inverse is obtained by first solving the system of equation

$$\begin{aligned} \left\{ \begin{array}{ll} 4 - \lambda ^2 + \mu ^2 = 4 \mu \eta ,\\ \lambda -2 = l \mu . \end{array} \right. \end{aligned}$$

This determines $\lambda , \mu$ as a function of l and then one precompose by the Mobius transformation $z \mapsto (l_+ z + l_-)/(z+1)$ which maps the triplet $(0,\infty , 1)$ to $(l_+,l_-, -\eta )$. The last two assertions (iii) and (iv) also follows from direct computations. $\square$

Recall that the map F leaves each fiber $\phi ^{-1}(\eta )$ invariant, so that one has the following commutative diagram for each $i=1,2$:

Proof of Theorem 5.1

Consider the analytic map $\varphi$ given by

$$\begin{aligned} \varphi (\lambda , \mu ) := \left( \eta := \phi (\lambda ,\mu ) , z:= \varphi _{\phi (\lambda ,\mu )}(\lambda , \mu ) \right) . \end{aligned}$$

Using assertion (iii), (iv) of the previous lemma, we deduce that F and $(\eta , z ) \mapsto (\eta , z^2)$ are conjugate on each $U_i$ via $\varphi$ and that $\psi \circ \varphi _\eta ^{-1}(z) = 1/2 (z+1/z)$, as required. $\square$

5.2 Structure of the Map F

Recall from the last section that we have found a map $\pi :{\mathbb {C}}^2 \dashrightarrow {\mathbb {C}}^2$ such that $\pi \circ F = {t}\circ \pi$, where ${t}$ is the Chebyshev map (3.1) where $\pi$ is defined by $\pi (\lambda , \mu ) = (\eta , \theta )$ with

$$\begin{aligned} \eta = \phi ({\lambda }, \mu ) = \frac{4-{\lambda }^2+\mu ^2}{4\mu } \ , \quad \theta = \psi ({\lambda }, \mu ) = \frac{4-\mu ^2+{\lambda }^2}{4{\lambda }} \ . \end{aligned}$$

This is a rational map of algebraic degree 3, of topological degree 2 with the following features:

• It is equivariant with respect to the reflections $({\lambda }, \mu ) \mapsto (\mu , {\lambda })$ and $(\eta , \theta ) \mapsto (\theta , \eta )$.

• It has the following indeterminacy points: two vertices [0 : 2 : 1] and $[0:-2:1]$ on the line $\{\lambda =0\}$, [1 : 0 : 0] and two “diagonal” points at the line $A_\infty$ at infinity: $d_\pm = [1: \pm 1: 0]$;

• The vertical axis $A^{\textrm{ver}}= \{ {\lambda }=0\}$ is collapsed (after puncturing out the indeterminacy points) to the vertical pole $q_v = [0:1:0]$. Symmetrically, the horizontal axis $A^{\textrm{hor}}$ is collapsed to the horizontal pole $q_h = [1:0:0]$.

• The pullback of a vertical line $L^{\textrm{ver}}_\eta$ through $(\eta ,0)$ is a rational algebraic curves (a “vertical hyperbola” )

  $$\begin{aligned} {\hat{L}}^{\textrm{ver}}_\eta = \{ 4-{\lambda }^2+\mu ^2 - 4\eta \, \mu = 0\} \end{aligned}$$

  union the vertical axis $A^{\textrm{ver}}$. Symmetrically, the pullback of a horizontal line $L^{\textrm{hor}}_\theta$ through $(0,\theta )$ is a horizontal hyperbola

  $$\begin{aligned} {\hat{L}}^{\textrm{hor}}_\theta = \{ 4-\mu ^2+{\lambda }^2 - 4\theta \, {\lambda }= 0\} \end{aligned}$$

  union the horizontal axis $A^{\textrm{hor}}$. The projection $\pi$ is a degree two branched covering of each of the hyperbolas onto its image.

• The vertical hyperbolas ${\hat{L}}^{\textrm{ver}}_\eta$ form a pencil through the points $a_\pm = (\pm 2, 0)$, i.e., all of them pass through these points, and form a holomorphic foliation of ${\mathbb {C}}^2 \smallsetminus \{0, a_\pm , b_\pm \}$. [From the projective point of view, they form a pencil through four points (one should add the diagonal points $d_\pm = [1:\pm 1: 0]$ at infinity) forming a foliation of the same space, ${\mathbb {C}}^2 \smallsetminus \{ 0, a_\pm , b_\pm \}$.] The description of the pencil of horizontal hyperbolas is symmetric (with respect to the reflection $(\eta , \theta )\mapsto (\theta , \eta )$).

• Each real vertical hyperbola ${\hat{L}}_\eta ^{{\textrm{ver}}, {\mathbb {R}}}$ with $|\eta |< 1$ projects under $\pi$ to the interval $\{ \eta \} \times {\mathbb {I}}$ whose endpoints correspond to the points $a_\pm$. For $|\eta |> 1$, the hyperbola ${\hat{L}}_\eta ^{{\textrm{ver}}, {\mathbb {R}}}$ projects to the complement of this interval, $\{\eta \} \times ({\hat{{\mathbb {R}}}}\smallsetminus {\text {int}}{\mathbb {I}})$. The picture for the real horizontal hyperbolas is symmetric.

It follows that $\pi ( {\mathbb{R}\mathbb{P}} ^2)$ is the union of the square $\{ |\eta |\le 1, \ |\theta | \le 1\}$ and four quadrants attached to its vertices.

Fig. 5

Vertical hyperbolas $\hat{L}_\eta ^{{\textrm{ver}}}$ for $-1 \leqslant \eta \leqslant 1$

Fig. 6

Vertical hyperbolas $\hat{L}_\eta ^{{\textrm{ver}}}$ for $|\eta |\geqslant 1$

Now the dynamics of F can be readily understood as the lift by $\pi$ of the Chebyshev dynamics:

• The vertical foliation ${\hat{{\mathcal L}}}^{\textrm{ver}}:= \bigcup _{\eta \in {\mathbb {C}}} {\hat{L}}^{\textrm{ver}}_\eta$ is leafwise invariant, and F restricts to a degree two rational endomorphism on each leaf ${\hat{L}}_\eta ^{\textrm{ver}}$. This endomorphism has two superattracting fixed points, the intersections of ${\hat{L}}_\eta ^{\textrm{ver}}$ with the vertical axis $A^{\textrm{ver}}$. Hence it is conformally conjugate to the squaring map $f_0 :z\mapsto z^2$ of ${\hat{\mathbb {C}}}$. In this coordinate, the projection $\pi :{\hat{L}}_\eta \rightarrow L_\eta$ becomes the canonical semi-conjugacy between $f_0$ and ${t}$.

• The horizontal foliation ${\hat{{\mathcal L}}}^{\textrm{hor}}:= \bigcup _{\theta \in {\mathbb {C}}} \hat{ L_\theta }^{\textrm{hor}}$ is F-invariant, with the leaves transformed by the Chebyshev map:

  $$\begin{aligned} F({\hat{L}}_\theta ) ) = {\hat{L}}_{{t}(\theta ) }. \end{aligned}$$

• Let $W_{\eta \pm }^s$ be the superattracting basins of $F \, |\,{\hat{L}}_\eta ^{\textrm{ver}}$ (with “$+$” corresponding to, say, the fixed point with $|\mu |>2$). Since the orbits in the disks $W_{\eta \pm }^s$ converge to the corresponding fixed points on $A^{\textrm{ver}}$, these disks get interpreted as the global superattracting manifolds of these fixed points.

• The action of F on the real hyperbolas ${\hat{L}}_\eta ^{{\textrm{ver}},{\mathbb {R}}}$ with $|\eta |>1$ is real conjugate to the map $f_0:x\rightarrow x^2$ on ${\mathbb {R}}$. For $|\eta |< 1$ it is real conjugate to the map $\displaystyle {f_0:x\rightarrow \frac{1}{2} \left( x-\frac{1}{x} \right) }$ on ${\mathbb {R}}$ (which is in turn conjugate to $f_0$ on the unit circle ${\mathbb {T}}$).⁷

• The Julia set of F is equal to

  $$\begin{aligned} {{\mathcal {J}}}(F) = \pi ^{-1} ({{\mathcal {J}}}({T})) = \pi ^{-1} ({\mathbb {C}}\times {\mathbb {I}}). \end{aligned}$$

  This is a real-symmetric 3D variety ${\mathcal M}$ that can be described as follows. Let ${\hat{{\mathbb {I}}}}$ be the union of four semi-strips in ${\mathbb {R}}^2$. It is projected by $\psi$ to the interval ${\mathbb {I}}$, and the fibers of this projection are real horizontal hyperbolas. Complexifying these hyperbolas, we obtain ${\hat{{\mathbb {I}}}}$. In this way, ${\mathcal M}$ gets interpreted as the complexification of ${\hat{{\mathbb {I}}}}$ along the horizontal foliation.

• Thus, ${\mathcal M}$ is foliated by (complex) horizontal hyperbolas. This foliation has a global transversal, e.g., an interval ${\mathcal T}_{\lambda }$, ${\lambda }>2$, which is the slice of one of the half-strips of ${\hat{{\mathbb {I}}}}$ by the real vertical line through $({\lambda }, 0)$.

• The transverse measure on ${\mathbb {C}}\times {\mathbb {I}}$ to the horizontal foliation ${\mathcal L}^{\textrm{hor}}$ lifts to a transverse measure on ${\mathcal M}$ to the horizontal foliation ${\hat{{\mathcal L}}}^{\textrm{hor}}$. It is induced by the the 1-form

  $$\begin{aligned} {\hat{{\omega }}} = \pi ^* ({\omega }) = \frac{ {\text {d}}\psi }{\pi \sqrt{1-\psi ^2} } \end{aligned}$$

  restricted to ${\mathcal M}$.

  Explicitly, the Green current is then given by the formula

  $$\begin{aligned} \Omega = \int _{-1}^{1} [4-\mu ^2+{\lambda }^2 - 4\theta \, {\lambda }=0] \ \dfrac{{\text {d}}\theta }{2\pi \sqrt{1 - \theta ^2}}. \end{aligned}$$

Remark 5.9

Note that we normalize by dividing by a factor 2 which corresponds to the degree of the semi-conjugacy, so that $\Omega$ has mass 1.

5.3 The Density of States Via an Equidistribution Result for F

Recall from Sect. 2.4.1 that the sequence of polynomials associated to the density of states follows from the inductive formula:

$$\begin{aligned} P_{n}(\lambda , \mu ) = (4- \mu ^2)^{2^{n-2}} P_{n-1} ( F(\lambda , \mu ) ), \end{aligned}$$

(5.7)

where $P_0 = - \lambda + 2 - \mu$, $P_1 = (-\lambda + 2 - \mu )(\lambda +2 - \mu )$ and $n\geqslant 2$.

The density of states is then deduced from the zeros of the polynomials:

$$\begin{aligned} \omega = \lim _{n\rightarrow +\infty } \dfrac{1}{2^n} \sum _{P_n(-1, \mu )=0} \delta _{(\mu +1)/4}. \end{aligned}$$

Note that one had to apply the transformation $\mu \mapsto (\mu +1)/4$ to get the density of states associated to the Grigorchuk group.

Theorem 5.10

Let C and S be two irreducible algebraic curves in ${\mathbb {C}}^2$ such that C is not a vertical hyperbola while S is not a horizontal hyperbola and the intersection of S with C and the vertical line of fixed points is empty. Then

$$\begin{aligned} \frac{1}{2^n} \, [ (F^n)^* C \cap S ] \rightarrow (\deg C) \cdot (\deg S)\cdot {\hat{{\omega }}}_S, \end{aligned}$$

(5.8)

where ${\hat{{\omega }}}_S$ is the probability measure obtained by restricting the 1-form

$$\begin{aligned} \dfrac{{\text {d}}\psi }{\pi \sqrt{1-\psi ^2}} \end{aligned}$$

to S.

Proof

By Lemma 3.8 applied to the map ${\text {id}}\times f$ where f is the squaring map, we get the convergence of $({\text {id}}\times f^n)^{-1} (C) \cap S$ for any two generic curves C, S. Now since F is locally analytically conjugate to ${\text {id}}\times f$ by assertion (ii) of Theorem 5.1, we conclude that the same property holds for F using Lemma 3.7. $\square$

Consider the affine map $A :\mu \mapsto (\mu +1)/4$. In case of $C= L^{\textrm{hor}}_\theta$, $S={\mathcal T}_{\lambda }$ we obtain the desired equidistribution result.

Theorem 5.11

We have:

• 1. The sequence of currents

  $$\begin{aligned} \dfrac{1}{2^n} [P_n=0] \end{aligned}$$

  converges as $n\rightarrow +\infty$ to the Green current of F.

• 2. The density of states associated with the Grigorchuk group is a multiple of $A_* {\hat{\omega }}_S$ where the measure ${\hat{{\omega }}}_S$ corresponds to the slice of the Green current of F by the line $S:=\{\lambda = 1\}$. Moreover, the support of this measure is a union of two intervals.

Proof

Observe that $P_1 = 4 \mu (\phi -1)$ and that $[P_1 =0] = [\phi -1=0]$. Since $F^* \phi = \phi$ and since $F^* \mu = 4 \lambda \mu \psi / (4 - \mu ^2)$, $F^* \lambda = 2 \lambda ^2/ (4-\mu ^2)$, we obtain using (5.7):

$$\begin{aligned} P_2 = (4-\mu ^2) F^* P_1 = 4 \lambda \mu \psi (\phi -1), \end{aligned}$$

hence

$$\begin{aligned} {{\,\textrm{div}\,}}(P_2) = {{\,\textrm{div}\,}}(4 \lambda \mu \psi (\phi -1)). \end{aligned}$$

Since the term $(4-\mu ^2)$ gets simplified in the previous calculation, we also deduce that:

$$\begin{aligned} {[}P_2 = 0] = F^* [P_1=0]. \end{aligned}$$

By induction, using the fact that $F^* \psi = T \circ \psi$, we get:

$$\begin{aligned} P_n= C_n \mu (\phi -1) \lambda ^{2^{n-1}-1} \prod _{k=1}^{n-1} T^k \circ \psi , \end{aligned}$$

where $C_n \in {\mathbb {C}}^*$ is a constant. The presence of the term $\mu \lambda ^{2^{n-1} -1}$ gives that:

$$\begin{aligned} {[}P_{n} =0] = F^* [P_{n-1} = 0 ]. \end{aligned}$$

Finally we get:

$$\begin{aligned} {[}P_n=0] = (F^n)^* [P_0=0]. \end{aligned}$$

Applying the previous result, we deduce that the sequence of currents $[P_n=0]$ converges to a multiple of the Green current and the sequence of measures $1/2^n[P_n(-1, \cdot ) =0]$ converges to the slice of the Green current by the line $\{\lambda = -1\}$. We finally obtain the density of states by applying the appropriate affine transformation. $\square$

6 The Rational Map Associated with the Lamplighter Group

The map associated to the lamplighter map $F :{\mathbb {C}}^2 \rightarrow {\mathbb {C}}^2$ is defined as:

$$\begin{aligned} F :(\lambda , \mu ) \mapsto \left( - \dfrac{\lambda ^2 - \mu ^2 -2 }{\mu - \lambda } , -\dfrac{2}{\mu - \lambda } \right) . \end{aligned}$$

In homogeneous coordinates, F is of the form:

$$\begin{aligned} F:= [\lambda , \mu , w] \mapsto [-\lambda ^2 + \mu ^2 + 2 w^2 , -2 w^2, (\mu - \lambda ) w], \end{aligned}$$

and it has topological degree 1 and algebraic degree 2.

6.1 Integrability of the Map Associated with the Lamplighter Group

Although the classical identity $\lambda ^2 - \mu ^2 = (\lambda + \mu )(\lambda - \mu )$ implies directly that F preserves a fibration, we also follow our systematic method in this case. The main result of this section is the following proposition.

Proposition 6.1

Take $\varphi :(\lambda , \mu ) \mapsto (\lambda + \mu , \lambda - \mu )$, then the map F is conjugate via $\varphi$ to the map:

$$\begin{aligned} (\alpha , \beta ) \mapsto \left( \alpha , \dfrac{\alpha \beta - 4}{\beta } \right) . \end{aligned}$$

The method of the proof is the same as in the previous section, Sect. 5.1, and allows one to recover the formula for the conjugation $\varphi$.

We consider the blow-up X of ${\mathbb {P}}^2$ at the two points $[\pm 1: 1: 0]$, the lift $\tilde{F}$ of F to X, denote by $\pi :X \rightarrow {\mathbb {P}}^2$ the blow-down map onto ${\mathbb {P}}^2$ and by $E_1$, $E_2$ the two exceptional divisors such that $E_1$ is the exceptional divisor above $[-1:1:0]$, $E_2$ is above [1 : 1 : 0] and $\tilde{L}_\infty$ is the strict transform of the line at infinity.

Fig. 7

Blow-up of ${\mathbb {P}}^2$ at the two points $[\pm 1 : 1 :0]$

Proposition 6.2

The following properties are satisfied.

• (i) F is a birational map, i.e its topological degree is one.

• (ii) F has two indeterminacy points on ${\mathbb {P}}^2$ consisting of the two points $[\pm 1, 1, 0]$ at infinity.

• (iii) The only contracted curves for F are the lines $\{ \lambda = \mu \}$ and the line at infinity.

• (iv) The strict transform of the line at infinity is contracted by F to the fixed point [1, 0, 0], the line $\{\lambda = \mu \}$ is collapsed by F to the indeterminacy point $[-1,1,0]$.

• (v) $\tilde{F}$ is regular near the strict transform of the line at infinity and the image of the line $\{ \lambda =\mu \}$ by $\tilde{F}$ is the exceptional divisor $E_1$.

• (vi) $\tilde{F}$ is regular on $E_1$ and maps $E_1$ to the line $\pi ^{-1}(\{\mu =0\})$.

• (vii) $\tilde{F}$ has one indeterminacy point on $E_2$ and collapses $E_2$ to the point $\pi ^{-1}([1:0:0])$.

• (viii) $\tilde{F}$ maps the indeterminacy point on $E_2$ to the strict transform of the line at infinity.

• (ix) $\tilde{F}$ is algebraically stable on X.

Proof

Let us denote by $P_0 = -\lambda ^2 + \mu ^2 + 2 w^2 , P_1 =-2 w^2, P_2= (\mu - \lambda ) w$ the three homogeneous polynomials defining F.

Assertions (i), (ii), (iv), (v) are direct computations. Observe also that (iv), (v), (vi), (vii) imply that assertion (ix) since no curve is contracted by any iterate of $\tilde{F}$ to an indeterminacy point. Assertion (iii) follows from the fact that the jacobian of the lift of F to ${\mathbb {C}}^3$ is of the form:

$$\begin{aligned} {\text {Jac}}(F) = -8 (\lambda - \mu ) w^2. \end{aligned}$$

Let us prove assertion (vi).

In the coordinate chart $(e = \lambda /\mu +1 , l = (w/\mu )/ (\lambda /\mu +1))$, the map $F\circ \pi$ is given by the expression:

$$\begin{aligned} F \circ \pi :(e, l) \mapsto [P_0(e -1, 1 , le) :P_1(e -1, 1 , le): P_2(e -1, 1 , le) ]. \end{aligned}$$

We obtain:

$$\begin{aligned} F \circ \pi :(e, l) \mapsto [-2 + e - 2 e l^2: -2 e l^2: -(-2 + e) l], \end{aligned}$$

and in the chart $(e= w/\mu , l = (\lambda /\mu +1) / (w/\mu ))$, the map $F \circ \pi$ is given by the expression:

$$\begin{aligned} F \circ \pi :(e, l ) \mapsto [P_0(-1 + le , 1 , e): P_1(-1 + le , 1 , e): P_2(-1 + le , 1 , e)], \end{aligned}$$

which simplifies as follows:

$$\begin{aligned} F\circ \pi :(e, l ) \mapsto [-2 e - 2 l + e l^2: -2 e: 2 - e l]. \end{aligned}$$

In both charts, $F\circ \pi$ is well-defined and $F\circ \pi$ maps regularly $E_1$ to the line $\{\mu =0\}$. Since this line is disjoint from the indeterminacy points $[\pm 1, 1 , 0]$, we deduce that $\tilde{F}$ is regular on $E_1$ and maps $E_1$ to the preimage of the line $\{\mu =0 \}$. We have thus proved (vi).

Let us prove assertion (vii).

Take a first chart $(e = \lambda /\mu -1 , l = (w/\mu )/ (\lambda /\mu -1))$, then $F\circ \pi$ is given by:

$$\begin{aligned} F \circ \pi :(e, l) \mapsto [P_0(1 + e , 1 , l e):P_1(1 + e , 1 , l e):P_2(1 + e , 1 , l e)]. \end{aligned}$$

We obtain:

$$\begin{aligned} F\circ \pi :(e, l) \mapsto [2 + e - 2 e l^2: -2 e l^2: -e l], \end{aligned}$$

(6.1)

and $F\circ \pi$ is regular for near $e=0$ for all $l \in {\mathbb {C}}$. In the other chart $(e= w/\mu , l = (\lambda /\mu -1) / (w/\mu ))$, we have:

$$\begin{aligned} F \circ \pi :(e, l) \mapsto [P_0(1 + l e , 1 , e):P_1(1 + l e , 1 , e): P_2(1 + l e , 1 , e)], \end{aligned}$$

which simplifies as follows:

$$\begin{aligned} F\circ \pi :(e, l) \mapsto [-2 e + 2 l + e l^2: -2 e: -e l], \end{aligned}$$

(6.2)

and the latter expression has a unique indeterminacy at $(e=0, l=0)$. One checks from the last expression that $E_2$ is mapped to [1, 0, 0] by $F\circ \pi$. This finishes the proof of (vii).

Let us prove assertion (viii). We blow up the indeterminacy point $(e=0, l=0)$ on $E_2$ where $(e= w/\mu , l = (\lambda /\mu -1) / (w/\mu ))$. Denote by $\pi '$ the blow-up of this point. Take $e = e_1, l = l_1 e_1$ where $e_1=0$ is the equation for the exceptional divisor, the map $F \circ \pi \circ \pi '$ is given in those coordinates by:

$$\begin{aligned} F \circ \pi \circ \pi ' :(e_1, l_1) \mapsto [P_0(1 + l_1 e_1^2, 1 , e_1): P_1(1 + l_1 e_1^2, 1 , e_1): P_2(1 + l_1 e_1^2, 1 , e_1) ]. \end{aligned}$$

We simplify the above formula and get:

$$\begin{aligned} F \circ \pi \circ \pi ' :(e_1,l_1) \mapsto [-2 + 2 l_1 + e_1^2 l_1^2: -2: -e_1 l_1]. \end{aligned}$$

The above expression is regular near $e_1=0$. Let us look near $l_1=\infty$, take $e = l_2 e_2, l = e_2$, so the map $F \circ \pi \circ \pi '$ is given in those coordinates by:

$$\begin{aligned} F \circ \pi \circ \pi ' :(e_2, l_2)&\mapsto [P_0(1 + l_2 e_2^2 , 1 , e_2 l_2): P_1(1 + l_2 e_2^2 , 1 , e_2 l_2)\\&\quad : P_2(1 + l_2 e_2^2 , 1 , e_2 l_2)]. \end{aligned}$$

We obtain:

$$\begin{aligned} F \circ \pi \circ \pi ' :(e_2, l_2) \mapsto [2 - 2 l_2 + e_2^2 l_2: -2 l_2: -e_2 l_2], \end{aligned}$$

(6.3)

which is also regular near $e_2 =0, l_2 = 0$. In particular, this proves that the map $F\circ \pi \circ \pi '$ is regular on the exceptional divisor above the indeterminacy point of $\tilde{F}$ on $E_2$. The above expression also shows

$$\begin{aligned} F\circ \pi \circ \pi ' :(e_1 =0, l_1) \mapsto [-2 + 2l_1: -2: 0], \end{aligned}$$

so the indeterminacy point of $\tilde{F}$ is mapped to the line at infinity. We have thus proved assertion (viii). $\square$

Consider the pencil D of lines passing through the point at infinity $[-1:1:0]$.

Proposition 6.3

The pencil of lines D is preserved by F.

Proof

Take a line C belonging to the pencil D. We show that the image of C by F is a curve passing through the point $[-1:1:0]$. Observe that the line $\{\lambda = \mu \}$ intersects the line C, and since $\{\lambda = \mu \}$ is collapsed by F to the point $[-1:1:0]$ by assertion (iv) of Proposition 6.2, we deduce that the image of C by F is a curve passing through the point $[-1:1:0]$.

Let us show that the image of C by F is a line or equivalently that the curve $F(C \setminus I(F))$ is of degree 1. Since C is a line passing through the point $[-1:1:0]$, assertion (v) of Proposition 9.12 shows that its strict transform $\tilde{C}$ in X satisfies:

$$\begin{aligned} \tilde{C} = \tilde{L}_\infty + E_2 \in H^{1,1}(X). \end{aligned}$$

We have thus:

$$\begin{aligned} \tilde{F}_* \tilde{C} = \tilde{F}_* \tilde{L}_\infty + \tilde{F}_* E_2. \end{aligned}$$

By assertion (iv) and (v) of Proposition 6.2, the line at infinity is collapsed regularly by $\tilde{F}$ to a point, so we have

$$\begin{aligned} \tilde{F}_* \tilde{L}_\infty = 0 \in H^{1,1}(X). \end{aligned}$$

By assertion (vii) and (viii) of Proposition 6.2, the divisor $E_2$ is collapsed and its indeterminacy point is mapped to $L_\infty$, so we have:

$$\begin{aligned} \tilde{F}_* E_2 = \tilde{L}_\infty \in H^{1,1}(X). \end{aligned}$$

This shows that $\tilde{F}_* \tilde{C} = \tilde{L}_\infty$, hence the line C is mapped to a line by F. $\square$

Observe that the member of the pencil D are lines passing through $[-1:1:0]$, so each of those line is given by an equation of the form:

$$\begin{aligned} \phi (\lambda ,\mu ):= \lambda + \mu = \alpha , \end{aligned}$$

where $\alpha \in {\mathbb {C}}$. One checks that $\phi \circ F = \phi$ so $\phi$ semi-conjugates F to the identity.

We now choose a transverse coordinate on each fiber of $\phi$, let $\psi :{\mathbb {C}}^2 \rightarrow {\mathbb {C}}$ be the map:

$$\begin{aligned} \psi (\lambda , \mu ) = \lambda - \mu , \end{aligned}$$

then the map F is conjugate via $\phi \times \psi$ to the rational map:

$$\begin{aligned} (\alpha , \beta ) \mapsto \left( \alpha , \dfrac{\alpha \beta - 4}{\beta } \right) . \end{aligned}$$

6.2 The Density of States for the Lamplighter Group

Recall from Sect. 2.4.2 that the spectrum of the Schreier graph associated to the lamplighter group is related to a sequence of polynomials $P_n$ defined inductively as follows:

$$\begin{aligned} P_n (\lambda , \mu ) = (\mu - \lambda )^{2^{n-1}} P_{n-1}(F(\lambda ,\mu )), \end{aligned}$$

where $P_0 = 4 - \lambda - \mu$. The spectrum associated to the lamplighter group is the limit of $1/2^n [P_n=0]$ with the line $\{\mu =0\}$. We thus recover the fact that the density of states is atomic, which was first proved by Grigorchuk–Zuk [54, Theorem 3]. Denote by $\omega _n$ the counting measure $1/2^n [P_n=0] \wedge [\mu =0]$ and denote by $\omega$ the limiting measure. Recall that we have defined in Proposition 3.10.(i) a laminar current $T_F$ on the elliptic cylinder.

Theorem 6.4

The following properties are satisfied.

• (i) The sequence of currents $1/2^n [P_n=0]$ converges as n tends to $\infty$ to a current supported on countably many curves.

• (ii) The sequence of measures $1/2^n [P_n =0] \wedge [\mu = 0]$ converges to an atomic measure.

• (iii) The sequence of measures

  $$\begin{aligned} \dfrac{2^n}{n}(\omega - \omega _n) \end{aligned}$$

  converges to the measure $- 2 T_F \wedge \{\mu = 0 \}$.

In particular, assertions (ii) shows that the density of states of the Lamplighter group is atomic.

Proof

By Proposition 6.2, the map F is conjugate to the map:

$$\begin{aligned} G :(\alpha , \beta ) \mapsto \left( \alpha , \dfrac{\alpha \beta - 4}{\beta } \right) . \end{aligned}$$

By assertion (ii) of Theorem 3.3, we have that $\lambda _1(F) = {{\text {max}}}(1,1) = 1 = \lambda _2(F)$ and F is a birational map. Using the change of coordinates, we see that the lines of equations $\mu =0, P_0 =0, \mu - \lambda =0$ are given by the equations $\alpha - \beta = 0$, $\alpha = 4$ and $\beta =0$ respectively. Note that the preimage of the fiber $\{ \alpha =4 \}$ by G is itself, thus it is always distinct from the diagonal $\alpha = \beta$. Let us show that $G^{-n} \{ \beta =0 \}$ is always distinct from the diagonal for all $n\geqslant 0$. Let us observe that the diagonal and $\{\beta =0 \}$ intersect at only $\alpha = \beta =0$. Moreover, when $\alpha$ belongs to the elliptic locus, the map $\beta \mapsto (\alpha \beta -4)/\beta$ is a rotation, and the point $\beta =0$ is never a fixed point of the rotation. In particular, the line $\{\beta =0\}$ restricted to the elliptic locus can be viewed as the graph $\Gamma$ of a non constant section over the circle ${\mathbb {T}}$. Its winding number is exactly 1. Since the restriction of G on each fiber $\alpha = cte$ over the elliptic locus is a rotation, the restriction of curve $G^{-n}\{ \beta =0 \}$ to the elliptic locus is a curve whose winding number is exactly n. In particular, it intersects the diagonal at exactly n distinct points. This shows that $G^{-n} \{\beta =0 \}$ and $\{ \alpha = \beta \}$ are distinct, and we conclude that $F^{-n} \{ \mu = \lambda \}$ and $\{ \mu =0 \}$ have no common components. We have thus shown that the line $\{\mu =0\}$ is generic, hence Theorem 4.1 can be applied and we obtain assertion (i) and (ii).

Let us now prove assertion (iii). Set $\Pi = \{ P_0=0 \}$ and $\Lambda = \{ \mu - \lambda = 0 \}$. Observe that $P_0 = 4 - \lambda - \mu$ so its poles and zeros satisfy the relation:

$$\begin{aligned} {{\,\textrm{div}\,}}(P_0 \circ \pi ) = \pi ^o \Pi + E_1 - \tilde{L}_\infty , \end{aligned}$$

where $\pi ^o \Pi$ denotes the strict transform of the line $\Pi$. Using the inductive relation, the fact that

$$\begin{aligned} {{\,\textrm{div}\,}}((\mu - \lambda )\circ \pi ) = \pi ^o \Lambda + E_2 - \tilde{L}_\infty \end{aligned}$$

and the equality $\tilde{F}^* \tilde{L}_\infty = \tilde{L}_\infty + E_2$, we obtain:

$$\begin{aligned} {{\,\textrm{div}\,}}(P_1 \circ \pi )&= \pi ^o\Lambda + E_2 -\tilde{L}_\infty + \tilde{F}^* (\pi ^o \Pi + E_1 - \tilde{L}_\infty ) \\&= \pi ^o \Lambda - 2\tilde{L}_\infty +\tilde{F}^* (\pi ^o \Pi + E_1) . \end{aligned}$$

Since the strict transform $\pi ^o \Lambda$ is mapped by $\tilde{F}$ to $E_1$ using assertion (v) of Proposition 6.2, we have $\tilde{F}^* E_1 \geqslant \pi ^o \Lambda$ (in the sense of currents). Note that ${\tilde{F}^* E_1 = \tilde{L}_\infty + E_1 \in H^{1,1}(X)}$ by Proposition 8.7 and since the line $\Lambda$ intersects the line at infinity at the point [1 : 1 : 0], its strict transform satisfies $\pi ^o \Lambda = \tilde{L}_\infty + E_1$. In other words, we get the equality of currents $\tilde{F}^* E_1 = \pi ^o \Lambda$.

$$\begin{aligned} {{\,\textrm{div}\,}}(P_1 \circ \pi )&= \pi ^o \Lambda - 2\tilde{L}_\infty +\tilde{F}^* (\pi ^o \Pi + E_1) \\&= 2\pi ^o \Lambda - 2\tilde{L}_\infty +\tilde{F}^* \pi ^o \Pi .\\ {{\,\textrm{div}\,}}(P_2\circ \pi )&= 2 \pi ^o(\Lambda ) - 2 E_2 - 4 \tilde{L}_\infty + 2 \tilde{F}^* \pi ^o(\Lambda ) + (\tilde{F}^2)^* \pi ^o(\Pi ). \end{aligned}$$

We apply the above argument inductively and deduce:

$$\begin{aligned} {{\,\textrm{div}\,}}(P_n \circ \pi )&= \sum _{k=0}^{n-2} 2^{n-1-k} (\tilde{F}^k)^* \pi ^o \Lambda + 2 (\tilde{F}^{n-1})^* \pi ^o \Lambda - 2^n \tilde{L}_\infty \\&\quad + (\tilde{F}^n)^* \pi ^o \Pi \end{aligned}$$

Pushing forward by $\pi$ the previous relation and looking only at the zero locus of $P_n$, we thus obtain that

$$\begin{aligned} \dfrac{1}{2^n} [P_n =0] = \sum _{k=0}^{n-2} \dfrac{1}{2^{1+k}} (F^k)^*\Lambda + \dfrac{1}{2^{n-1}} (F^{n-1})^* \Lambda + \dfrac{1}{2^n} (F^n)^* \Pi . \end{aligned}$$

Setting $T_{{\mathcal {L}}} = \lim _{n\rightarrow +\infty } T_n$ where $T_n = \dfrac{1}{2^n} [P_n =0]$, the difference $T_{{\mathcal {L}}} - T_n$ is of the form:

$$\begin{aligned} T_{{\mathcal {L}}} - T_n = \sum _{k=n}^{+\infty } \dfrac{1}{2^{1+k}} (F^k)^* \Lambda - \dfrac{1}{2^n} (F^n)^* \Pi - \dfrac{1}{2^{n-1}}(F^{n-1})^* \Lambda . \end{aligned}$$

We rescale:

$$\begin{aligned} \dfrac{2^n}{n} (T_{{\mathcal {L}}} - T_n) = \dfrac{2^n}{n} \left( \sum _{k=n}^{+\infty } \dfrac{k}{2^{1+k}} \dfrac{(F^k)^* \Lambda }{k} \right) - \dfrac{1}{n} (F^n)^* \Pi - \dfrac{2}{n} (F^{n-1})^* \Lambda . \end{aligned}$$

By Proposition 3.10, the currents $(1/n) ({F}^n)^*\Lambda$, $(1/n) ({F}^n)^* \Pi$ converge to $T_F$, moreover, we need the following asymptotic expansion:

$$\begin{aligned} \dfrac{1}{n} (F^n)^*\Lambda= & {} T_F + o(1),\\ \dfrac{1}{n} {(F^n)^*\Pi }= & {} T_F + o\left( 1 \right) . \end{aligned}$$

We obtain:

$$\begin{aligned} \dfrac{2^n}{n} (T_{{\mathcal {L}}} - T_n)&= \dfrac{2^n}{n} \left( \sum _{k=n}^{+\infty } \dfrac{k}{2^{1+k}} \left( T_F + o(1) \right) \right) - \left( 1 + \dfrac{2(n-1)}{n} \right) T_F + o\left( 1\right) , \\&= \dfrac{2^n}{n} \left( \sum _{k=n}^{+\infty } \dfrac{k}{2^{1+k}} \right) T_F - \left( 1 + \dfrac{2(n-1)}{n} \right) T_F + o\left( 1\right) ,\\&= \left( \dfrac{2^n }{n} \cdot \dfrac{n+1}{2^n} - \left( 1 + \dfrac{2(n-1)}{n} \right) \right) T_F + o\left( 1 \right) . \\&= -2 T_F + o\left( 1 \right) . \end{aligned}$$

Slicing by $[\mu =0]$ (since we have shown in the first paragraph that $\{\mu =0\}$ is a generic curve), we obtain the convergence:

$$\begin{aligned} \dfrac{2^n}{n} (\omega - \omega _n) = -2 T_F \wedge [\mu =0] + o(1). \end{aligned}$$

We have thus obtained assertion (iii). $\square$

7 The Rational Map Associated with the Hanoi Group

Recall that the renormalization transformation F associated with the Hanoi group was computed given in Proposition 2.10. The map F induces a rational map on ${\mathbb {P}}^2$ given by:

$$\begin{aligned} F := [x,y,z] \mapsto [P_0(x,y,z): P_1(x,y,z): P_2(x,y,z)], \end{aligned}$$

where $P_0, P_1, P_2$ are homogeneous polynomials of degree 4 given by:

$$\begin{aligned} \begin{array}{l} P_0 :=x (x-z - y)(x^2 - z^2 + y z- y^2) + 2 y^2 (-x^2 + xz + y^2), \\ P_1 := y^2z (x-z+y) ,\\ P_2 := (x-z -y)(x^2 - z^2 + yz -y^2)z . \end{array} \end{aligned}$$

The map F has algebraic degree 4, and its topological degree is 2. Note that the computation of the topological degree is not direct and follows from Theorem 7.1.

7.1 Integrability of the Map Associated with the Hanoi Group

The main result of this section is the following theorem.

Theorem 7.1

Take the birational map $\varpi :{\mathbb {C}}^2 \rightarrow {\mathbb {C}}^2$ given by the following formula:

$$\begin{aligned} (x,y) \mapsto \left( \dfrac{x^2 - 1 - x y - 2 y^2}{y} , \ \dfrac{(1 + x - 2 y) (1 + x + y)}{2 y}\right) . \end{aligned}$$

The map F associated with the Hanoi group is conjugate via $\varpi$ to the rational map:

$$\begin{aligned} (x,y) \mapsto \left( x^2 - x -3 , \ \dfrac{(x-1)(x+2)}{x+3} y\right) . \end{aligned}$$

The method of the proof of the above theorem is the same as in the previous sections Sect. 5.1 for the group ${\mathcal {G}}$ and Sect. 6.1 for the group ${\mathcal {L}}$, this allows us to recover the explicit formulas for the conjugation $\varpi$. To determine the map $\varpi$ in the above theorem, we need to explain the dynamical properties of the map F, first in ${\mathbb {P}}^2$ then on an appropriate blow-up of ${\mathbb {P}}^2$.

Lemma 7.2

The map F has five indeterminacy points in ${\mathbb {P}}^2$, the points [1 : 0 : 1], $[-1:0:1]$, $[-1:1:0]$, [1 : 1 : 0] and [2 : 1 : 0].

Proof

We observe that z divides $P_1$ and $P_2$, and that $P_0(x, y ,0)$ factors as:

$$\begin{aligned} P_0 (x,y,0) = (x+y)^2 (x^2 -3xy +2 y^2), \end{aligned}$$

which vanishes when $x=-y=1$ and $x=y=1$ and $x=2, y =1$. This proves that the indeterminacies of F on the line at infinity are the points [1 : 1 : 0], [2, 1, 0], $[-1,1,0]$. Observe that y divides $P_1$ and that $(x-z)(x^2 - z^2)$ divides both $P_0(x,0,z)$ and $P_2(x,0,z)$. This proves that the indeterminacies of F on the line $\{y=0\}$ are [1 : 0 : 1] and $[-1:0:1]$. Let us prove by contradiction that there are no indeterminacy points outside the two lines $\{y=0 \}$ and $\{z=0\}$. Take a point of indeterminacy $[x,y,z] \in {\mathbb {P}}^2\setminus \left( \{y=0 \} \cup \{z=0 \}\right)$ of F. Since $P_2(x,y,z)=0$ and $y,z \in {\mathbb {C}}^*$, this proves that the point (x, y, z) lies on the curve

$$\begin{aligned} x+ y -z =0. \end{aligned}$$

In particular, $z = x+y$ and we compute the polynomial $P_0(x, y , x+y), P_2(x,y,x+y)$:

$$\begin{aligned} \begin{array}{ll} P_0(x, y , x+y) = P_2(x,y, x+y )=2y^2 (x+y)^2. \end{array} \end{aligned}$$

Since $y \ne 0$, this proves that $x+y=0$ but this contradicts the fact that $x+y = z \ne 0$. $\square$

Lemma 7.3

The Jacobian of F is given by the homogeneous polynomial:

$$\begin{aligned} {\text {Jac}}(F)= & {} 4 y (x - y - z) (x + y - z)^2 z (2 x^2 - 2 x y - 4 y^2 - y z - 2 z^2) \\{} & {} (x^2 - y^2 + y z - z^2). \end{aligned}$$

Consider the curves

$$\begin{aligned}{} & {} C_1 := \{x+y -z=0\},\\{} & {} C_2 :=\{-x+ y + z =0 \}, \end{aligned}$$

and

$$\begin{aligned} C_3:= \{ x^2 - y^2 +y z - z^2=0\}. \end{aligned}$$

Proposition 7.4

The following properties are satisfied.

• (i) The only collapsed curves are $C_1, C_2, C_3$ and the line at infinity.

• (ii) The line at infinity is collapsed to the fixed point [1 : 0 : 0].

• (iii) The line $C_1$ is collapsed to the indeterminacy point [1 : 0 : 1].

• (iv) The line $C_2$ is collapsed to the indeterminacy point $[-1:1:0]$.

• (v) The line $C_3$ is collapsed to the indeterminacy point [2 : 1 : 0].

Proof

The above statement follow from direct computations. $\square$

Consider the blow-up X of ${\mathbb {P}}^2$ at the four points $p_1 :=[-1:1:0], p_2:=[2:1:0]$ and $p_3:=[-1:0:1], p_4 := [1:0:1]$ and denote by $\pi :X \rightarrow {\mathbb {P}}^2$ the blow-down morphism. Take the lift $\tilde{F} := \pi ^{-1} \circ F \circ \pi$ of F to X, we look at the dynamics of the collapsed curves. We denote by $E_1, E_2, E_3, E_4$ the four exceptional divisors above $p_1, p_2, p_3$ and $p_4$ respectively, by $L_\infty$ the line at infinity in ${\mathbb {P}}^2$ and by $\tilde{L}_\infty$ its strict transform by $\pi$.

Fig. 8

Blow-up of ${\mathbb {P}}^2$ at the four points $[- 1 : 1 :0]$, [2 : 1 : 0], $[\pm 1 :0 :1]$

To simplify the notation, we shall write by $\tilde{C}_i$ the strict transform of the curves $C_i$ by $\pi$.

Proposition 7.5

The following properties are satisfied.

• (i) The curve $\tilde{C}_1$ is collapsed by $\tilde{F}$ to a point on the exceptional divisor $E_4$ whose orbit by $F_1$ is regular.

• (ii) The line $\tilde{C}_2$ is mapped by $\tilde{F}$ to the exceptional divisor $E_1$.

• (iii) The curve $\tilde{C}_3$ is mapped by $\tilde{F}$ to the exceptional divisor $E_2$.

• (iv) The exceptional divisor $E_1$ is mapped regularly by $F \circ \pi$ to the conic curve parametrized by:

  $$\begin{aligned} l \in {\mathbb {C}}\mapsto [6 - 3 l - l^2: -(-1 + l) l: 2 (2 - l) l] \in {\mathbb {P}}^2, \end{aligned}$$

  where l parametrizes the slopes $z/(x+y)$.

• (v) The exceptional divisor $E_2$ is mapped regularly by $F \circ \pi$ to the line $\{ z = y\} \subset {\mathbb {P}}^2$.

• (vi) The map $\tilde{F}$ fixes $E_3$, it induces a map on $E_3$ with topological degree 2 and it has one indeterminacy point on $E_3$. The image of the indeterminacy point on $E_3$ by $\tilde{F}$ is the line parametrized by:

  $$\begin{aligned} l \mapsto [-22 + 2 l : -8 : 2(3- l)]. \end{aligned}$$

• (vii) The map $\tilde{F}$ fixes $E_4$, it induces a map on $E_4$ with topological degree 2 and has two indeterminacy points on $E_4$. The image of those indeterminacy points are two respective lines, parametrized by:

  $$\begin{aligned} l&\mapsto [-2 - 3 l : 2 : -3 l],\\ l&\mapsto [-17 + 3 l : -4 : -3 (3-l)]. \end{aligned}$$

• (viii) The indeterminacy point on L is mapped to L by $F_1$.

We postpone the proof of this proposition to the end of the section.

Consider the pencil D of conics passing through the four points $[\pm 1 :0: 1]$, $[-1:1:0]$ , [2 : 1 : 0].

Proposition 7.6

The pencil D is invariant by F.

Proof

Take a curve C in the pencil D. We first prove that F(C) passes through all four points $[\pm 1 :0: 1],[-1:1:0] , [2:1:0]$.

Since the line $\{y=0\}$ is a line of fixed point for F, we deduce that the image F(C) passes through $[\pm 1: 0 :1]$. Since the curves $C_2$ and $C_3$ do not pass through the point [2 : 1 : 0], then neither $C_2$ nor $C_3$ belong to the pencil D, hence they intersect C at 2 and 4 points respectively. Since $C_2$ and $C_3$ are mapped by F to the points $[-1:1 : 0]$ and [2 : 1 : 0], we deduce that the image F(C) also passes through these two points. We have thus proved that F(C) is a curve passing through all four points $[\pm 1 : 0:1], [-1:1:0], [2:1:0]$.

We now show that F(C) is a curve of degree 2. Since C is a member of the pencil passing through four points, assertion (v) of Proposition 9.12 shows that its strict transform $\tilde{C}$ by $\pi$ satisfies:

$$\begin{aligned} \tilde{C} = 2 \tilde{L}_\infty + E_1 + E_2 - E_3 - E_4 \in H^{1,1}(X). \end{aligned}$$

Let us compute $(F\circ \pi )_* \tilde{C}$. By Proposition 7.5.(viii) and by Proposition 7.4, the line L is collapsed to a point by $F \circ \pi$ and its indeterminacy point is mapped to L, as a result, we have:

$$\begin{aligned} (F\circ \pi )_* \tilde{L}_\infty = L_\infty \in H^{1,1}({\mathbb {P}}^2). \end{aligned}$$

By Proposition 7.5.(iv), the exceptional divisor $E_1$ is mapped regularly by $F \circ \pi$ to the conic curve parametrized by:

$$\begin{aligned} l \mapsto [6 - 3 l - l^2: -(-1 + l) l: 2 (2 - l) l]. \end{aligned}$$

Since the above curves is of degree 2, we have:

$$\begin{aligned} (F\circ \pi )_* E_1 = 2 L_\infty \in H^{1,1}({\mathbb {P}}^2). \end{aligned}$$

Using assertion (v), (vi), (viii) of Proposition 7.5, we obtain:

$$\begin{aligned} (F\circ \pi )_* E_2 = L_\infty \in H^{1,1}({\mathbb {P}}^2), \end{aligned}$$

since $E_2$ is mapped to a line,

$$\begin{aligned} (F\circ \pi )_* E_3 = L_\infty \in H^{1,1}({\mathbb {P}}^2), \end{aligned}$$

since $E_3$ is collapsed to a point but its indeterminacy point is mapped to a line,

$$\begin{aligned} (F\circ \pi )_* E_4 = 2 L_\infty \in H^{1,1}({\mathbb {P}}^2), \end{aligned}$$

since $E_4$ is collapsed to a point but it has two indeterminacy points which are mapped to lines. Overall, we have:

$$\begin{aligned} (F\circ \pi )_* \tilde{C} = (2 + 2 + 1 -1 -2) L_\infty = 2 L_\infty \in H^{1,1}({\mathbb {P}}^2). \end{aligned}$$

This proves that F maps C to a degree 2 curve, as required. $\square$

Denote by $\psi :{\mathbb {P}}^2 \dashrightarrow {\mathbb {P}}^1$ the map associated with the pencil D.

Corollary 7.7

The map $\psi$ is of the form:

$$\begin{aligned} \psi :[x: y : z] \dashrightarrow [x^2 - z^2 - x y - 2 y^2 :y z]. \end{aligned}$$

Moreover, one has $F \circ \psi = \psi \circ g$ where $g :{\mathbb {P}}^1 \rightarrow {\mathbb {P}}^1$ is the rational map given by the polynomial

$$\begin{aligned} g = x^2 -x -3. \end{aligned}$$

We now pursue our study by finding an appropriate parametrization of the fibers of $\psi$. To do so, let us first observe that any two distinct curves belonging to the pencil D or equivalently any two distinct fiber of $\psi \circ \pi$ intersect the divisors $E_3 , E_4$ at distinct points.

For each $\alpha \in {\mathbb {P}}^1$, let us denote by $s_0(\alpha )$ the intersection of the fiber $(\psi \circ \pi )^{-1}(\alpha )$ with $E_3$ and by $s_\infty (\alpha )$ the intersection of the fiber $(\psi \circ \pi )^{-1}(\alpha )$ with $E_4$. By construction, the two functions

$$\begin{aligned} s_0 , s_\infty :{\mathbb {P}}^1 \dashrightarrow X, \end{aligned}$$

define two marked points on the family of conics $\psi ^{-1}(\alpha )$. Recall that the conics $\psi ^{-1}(\alpha )$ of ${\mathbb {P}}^2$ are rational, we shall consider an explicit rational map from $\psi ^{-1}(\alpha )$ to ${\mathbb {P}}^1$. In this case, for any point p on a conic $\psi ^{-1}(\alpha )$, we associate the line $L_p$ passing through [1 : 0 : 1] and p. Since the set of lines passing through [1 : 0 : 1] is parametrized by ${\mathbb {P}}^1$, we obtain a map from $\psi ^{-1}(\alpha )$ to ${\mathbb {P}}^1$.

More explicitly, for each $\alpha = [\alpha _0 : \alpha _1] \in {\mathbb {P}}^1$, we define the function $\varphi _\alpha :\psi ^{-1}(\alpha ) \dashrightarrow {\mathbb {P}}^1$ induced by the following transformation:

$$\begin{aligned} \varphi _\alpha :(x , y ) \in {\mathbb {C}}^2 \cap \psi ^{-1}(\alpha ) \mapsto \dfrac{x+1 }{y} + \dfrac{\alpha _0/\alpha _1 - 1 }{2} \in {\mathbb {C}}. \end{aligned}$$

In homogeneous coordinates, $\varphi _\alpha$ is of the form:

$$\begin{aligned} {[}x:y :z] \in \psi ^{-1}(\alpha ) \mapsto [2 \alpha _1 x + 2 \alpha _1 z + (\alpha _0 - \alpha _1) y: 2 \alpha _1 y] \in {\mathbb {P}}^1. \end{aligned}$$

In fact, the map $\varphi _\alpha$ is constructed via the above construction and was normalized in such a way that the marked points $s_0(\alpha ) , s_\infty (\alpha )$ are identified to the point [0 : 1] and [1 : 0].

Lemma 7.8

The following properties hold.

• (i) For each $\alpha = [\alpha _0: \alpha _1] \in {\mathbb {P}}^1 \setminus \{[3:1 ] , [1:0] \}$, the map $\varphi _\alpha :\psi ^{-1}(\alpha ) \dashrightarrow {\mathbb {P}}^1$ is invertible and its inverse is given by the formula:

  $$\begin{aligned}{} & {} \varphi _\alpha ^{-1} :[z_0: z_1] \in {\mathbb {P}}^1 \mapsto [4 \alpha _1^2 z_0^2 + 4 \alpha _1^2 z_0 z_1 - \alpha _0^2 z_1^2 + 9 \alpha _1^2 z_1^2: \\{} & {} \quad 8 \alpha _1^2 z_0 z_1: (2 \alpha _1 z_0 - \alpha _0 z_1 - 3 \alpha _1 z_1) (2 \alpha _1 z_0 - \alpha _0 z_1 + 3 \alpha _1 z_1)] \in \psi ^{-1}(\alpha ). \end{aligned}$$

• (ii) For each $\alpha \in {\mathbb {P}}^1 \setminus \{[3:1 ] , [1:0] \}$, the points $s_0 (\alpha ), s_\infty (\alpha )$ are mapped by $\varphi _\alpha \circ \pi$ to the point [0 : 1] and [1 : 0] respectively.

Proof

Assertion (i) follows from solving the system of equation:

$$\begin{aligned} \left\{ \begin{array}{ll} (x^2 - 1 - x y - 2 y^2) /y = \dfrac{\alpha _0}{\alpha _1}, \\ \dfrac{2 \alpha _1 (x + 1 ) + (\alpha _0 - \alpha _1) y}{2 \alpha _1 y} = z_0/z_1, \end{array} \right. \end{aligned}$$

where $[\alpha _0 : \alpha _1], [z_0 : z_1] \in {\mathbb {P}}^1$. Assertion (ii) also follows from the fact that the point [1 : 0 : 1] is mapped by $\varphi _\alpha$ to [1 : 0] and that the tangent line to the conic $\psi ^{-1}(\alpha )$ at the point $[-1:0:1]$ where $\alpha = [\alpha _0 : \alpha _1]$ is given by the equation:

$$\begin{aligned} 2 (\alpha _1 x+ \alpha _1 z) + (\alpha _0 - \alpha _1) y =0. \end{aligned}$$

$\square$

Recall that the fiber $\psi ^{-1}(\alpha )$ is mapped by F to the fiber $\psi ^{-1}(g(\alpha ))$ where g is the polynomial $x^2 - x -3$ so that the following diagram is commutative.

Proposition 7.9

For any $\alpha = [\alpha _0 : \alpha _1] \in {\mathbb {P}}^1$ and set $\beta = \alpha ^2 - \alpha -3$. Then the map $\varphi _\beta \circ F \circ \varphi _\alpha ^{-1} : {\mathbb {P}}^1 \dashrightarrow {\mathbb {P}}^1$ is given by the formula:

$$\begin{aligned} \varphi _\beta \circ F \circ \varphi _\alpha ^{-1} :z \in {\mathbb {P}}^1 \mapsto \dfrac{(\alpha _0 - \alpha _1)(\alpha _0 + 2 \alpha _1)}{\alpha _0 +3 \alpha _1 } z. \end{aligned}$$

Replacing $\alpha = \psi (x,y)$ by its appropriate rational expression in x, y, we deduce a formula for $\varphi _{\psi (x,y)}$ and this yields a map $\varpi :{\mathbb {C}}^2 \rightarrow {\mathbb {C}}^2$ given by:

$$\begin{aligned} (x,y) \mapsto \left( \psi (x,y) = \dfrac{x^2 - 1 - x y - 2 y^2}{y} , \varphi _{\psi (x,y)}= \dfrac{(1 + x - 2 y) (1 + x + y)}{2 y}\right) . \end{aligned}$$

Proof of Theorem 7.1

This follows directly from the fact that $g \circ \psi = \psi \circ F$ and the previous proposition. $\square$

Proof of Proposition 7.5

Assertion (ii) follows from the computation of the restriction to $C_2$ of the function

$$\begin{aligned} \left( P_0/P_1 + 1, \dfrac{P_2/P_1}{P_0/P_1 + 1} \right) . \end{aligned}$$

Similarly, assertion (iii) follows from the computation of the restriction to $C_3$ of the function

$$\begin{aligned} \left( P_0/P_1 -2 , \dfrac{P_2/P_1}{P_0/P_1 -2} \right) . \end{aligned}$$

Assertion (iv) follows from the computation of the restriction to $e=0$ of the following expression:

$$\begin{aligned} (e, l) \mapsto [P_0(-1 + e , 1 , l e): [P_1(-1 + e , 1 , l e) : [P_2(-1 + e , 1 , l e)]. \end{aligned}$$

Similarly, assertion (v) follows from the computation of the restriction to $e=0$ of the following expression:

$$\begin{aligned} (e,l) \mapsto [P_0(2+ e, 1 , le):P_1(2+ e, 1 , le): P_2(2+ e, 1 , le)]. \end{aligned}$$

For assertion (viii), to determine the image of the point [1 : 1 : 0], we restrict to $e=0$ the expression

$$\begin{aligned} (e,l) \mapsto [P_0(1 + e , 1 , le ): P_1(1 + e , 1 , le ) : P_2(1 + e , 1 , le )]. \end{aligned}$$

We now prove successively in detail assertion (vi), (vii), (i).

Let us prove assertion (vi).

In the local coordinates $e= x/z+1 , l = y/(x+z)$, the map $F \circ \pi$ is given by the formula:

$$\begin{aligned} F\circ \pi :(e, l ) \mapsto [P_0(-1 + e , l e , 1):P_1(-1 + e , l e , 1): P_2(-1 + e , l e , 1)], \end{aligned}$$

which simplifies as follows:

$$\begin{aligned} F \circ \pi :(e, l)&\mapsto [-4 + 8 e - 5 e^2 + e^3 + 2 l - 5 e l + 4 e^2 l - e^3 l - 5 e l^2 + 8 e^2 l^2 \\&\quad - 3 e^3 l^2 - e^2 l^3 + e^3 l^3 + 2 e^3 l^4\\&\quad : e l^2 (-2 + e + e l): (2 - e + e l) (2 - e - l + e l^2)]. \end{aligned}$$

In particular, the exceptional divisor $E_3$ given by the local equation $e=0$ is mapped to $p_3$ by $F \circ \pi$, indeed:

$$\begin{aligned} F \circ \pi :(e=0, l) \mapsto [-4 + 2 l: 0: 2 (2 - l)]= [-1:0:1]. \end{aligned}$$

This shows that $\tilde{F}$ maps $E_3$ to either $E_3$ or a point on $E_3$. In the same local coordinates, $\tilde{F}$ is obtained by simplifying the expression:

$$\begin{aligned} \tilde{F} :(e,l)&\mapsto \left( e' := \dfrac{P_0(-1 + e , l e , 1) }{ P_2(-1 + e , l e , 1)} + 1 ,\right. \\&\quad \left. l':=\dfrac{P_1(-1 + e , l e , 1)}{P_0(-1 + e , l e , 1) + P_2(-1 + e , l e , 1)} \right) , \end{aligned}$$

and we get:

$$\begin{aligned}&\tilde{F} :(e, l ) \\&\quad \mapsto \left( e':= \dfrac{e (4 - 4 e + e^2 - 2 l + 3 e l - e^2 l - 4 l^2 + 7 e l^2 - 3 e^2 l^2 + e^2 l^3 + 2 e^2 l^4)}{(2 - e + e l) (2 - e - l + e l^2)},\right. \\&\qquad \left. l':= \dfrac{l^2 (-2 + e + e l)}{4 - 4 e + e^2 - 2 l + 3 e l - e^2 l - 4 l^2 + 7 e l^2 - 3 e^2 l^2 + e^2 l^3 + 2 e^2 l^4} \right) \end{aligned}$$

One sees that the point $(e=0, l=2)$ is the only indeterminate point for $\tilde{F}$ on $E_3$. The restriction to $E_3$ yields:

$$\begin{aligned} \tilde{F} :(e=0, l) \mapsto \left( e'= 0, \ l' = -\dfrac{2 l^2}{4 - 2 l - 4 l^2} \right) , \end{aligned}$$

so the restriction of $\tilde{F}$ to $E_3$ is a self-map of topological degree 2 with one indeterminacy point $(e=0, l=2)$. Let us now compute the image of the indeterminate point $(e=0, l=2)$. Set $e_1= e, l = 2 + l_1 e_1$, we express $F \circ \pi (e_1 , 2 + l_1 e_1)$ :

$$\begin{aligned} (e_1 ,l_1)&\mapsto [-22 + 27 e_1 + 27 e_1^2 + 2 l_1 - 25 e_1 l_1 + 24 e_1^2 l_1 + 63 e_1^3 l_1 \\&\quad -5 e_1^2 l_1^2 + 2 e_1^3 l_1^2 + 51 e_1^4 l_1^2 - e_1^4 l_1^3 + 17 e_1^5 l_1^3 + 2 e_1^6 l_1^4:\\&\qquad (2 + e_1 l_1)^2 (-2 + 3 e_1 + e_1^2 l_1): (2 + e_1 + e_1^2 l_1) (3 - l_1 + 4 e_1 l_1 + e_1^2 l_1^2)]. \end{aligned}$$

Evaluating at $e_1= 0$ yields:

$$\begin{aligned} F \circ \pi (e_1 , 2 + l_1 e_1) :\ (e_1 = 0 , l_1) \mapsto [-22 + 2 l_1: -8: 2 (3 - l_1)]. \end{aligned}$$

In particular, the exceptional divisor $e_1 = 0$ corresponding to the indeterminacy point on $E_3$ is mapped to the line parametrized by:

$$\begin{aligned} l_1 \mapsto [-22 + 2 l_1: -8: 2 (3 - l_1)]. \end{aligned}$$

We have thus proven assertion (vi).

Let us prove assertion (vii). In the local coordinates $e = x/z- 1, l = y/(x-z)$, the map $\tilde{F}$ is of the form:

$$\begin{aligned} \tilde{F} :(e , l)&\mapsto \left( e' = \dfrac{ e (1 + l) (2 + e - 3 l - 2 e l - e l^2 + 2 e l^3)}{(-1 + l) (-2 - e - l + e l^2)}, \right. \\&\quad \left. l'=\dfrac{l^2}{2 + e - 3 l - 2 e l - e l^2 + 2 e l^3} \right) . \end{aligned}$$

The above formula proves that $\tilde{F}$ has two indeterminacy points on $E_4$, the points $(e=0, l =1)$ and $(e=0, l=-2)$. Moreover, the exceptional divisor $E_4$ is fixed and the induced map on $E_4$ is of the form:

$$\begin{aligned} \tilde{F} :(e=0 , l) \mapsto \left( e'=0 , \dfrac{l^2}{2 - 3l} \right) , \end{aligned}$$

which is of topological degree 2. We now compute the image of the two indeterminacy points $(e=0, l =1)$ and $(e=0, l=-2)$. Set $e= e' , l = 1 + e' l'$ so that $e'=0$ denotes the local equation for the exceptional divisor of the blow-up of the point $(e=0, l=1)$, we compute $F \circ \pi (e' ,1+ l' e')$ in these new coordinates:

$$\begin{aligned} (e' , l')&\mapsto [-2 - 3 l' - 7 e' l' + 4 e'^2 l' - e' l'^2 - e'^2 l'^2 + 12 e'^3 l'^2 + e'^3 l'^3 + 9 e'^4 l'^3 + 2 e'^5 l'^4: \\&\quad (1 + e' l')^2 (2 + e' l'): l' (-3 - e' l' + 2 e'^2 l' + e'^3 l'^2)] \in {\mathbb {P}}^2. \end{aligned}$$

In particular, the exceptional divisor $e'=0$ is mapped to the line parametrized by:

$$\begin{aligned} (e' =0, l') \mapsto [-2 - 3 l': 2: -3 l']. \end{aligned}$$

We now determine the image by $\tilde{F}$ of the other indeterminacy point $(e=0, l=-2)$. Set $e= e' , l = -2 + e' l'$, we compute $F \circ \pi (e' , -2 + e' l')$:

$$\begin{aligned} (e' , l')&\mapsto [-17 + 15 e' + 3 l' + 26 e' l' - 41 e'^2 l' - e' l'^2 - 10 e'^2 l'^2 + 39 e'^3 l'^2 + e'^3 l'^3\\&\quad - 15 e'^4 l'^3 + 2 e'^5 l'^4: (-2 + e' l')^2 (-1 + e' l')\\ {}&\quad : (-3 + e' l') (3 - l' - 4 e' l' + e'^2 l'^2)]. \end{aligned}$$

In particular, the exceptional divisor $e'=0$ above $(e=0, l=-2)$ is mapped to the line parametrized by:

$$\begin{aligned} (e'=0, l') \mapsto [-17 + 3 l': -4: -3 (3 - l')]. \end{aligned}$$

We have thus proved assertion (vii).

Let us prove assertion (i).

Take some local coordinates $e= x/z-1 , l= y/ (x-z)$ near the exceptional divisor $E_4$, then the map $\pi ^{-1} \circ F :{\mathbb {P}}^2 \dashrightarrow X$ is of the form:

$$\begin{aligned} \pi ^{-1} \circ F:[x: y : 1] \in {\mathbb {P}}^2 \mapsto (e(x,y), l (x,y)) \in X, \end{aligned}$$

where e(x, y), l(x, y) are two rational functions given by:

$$\begin{aligned} e(x,y)= & {} \dfrac{(-1 + x + y) (1 - x - x^2 + x^3 + y + x y - 2 x^2 y + y^2 - x y^2 + 2 y^3)}{(-1 + x - y) (-1 + x^2 + y - y^2)},\\ l(x,y)= & {} \dfrac{ y^2}{1 - x - x^2 + x^3 + y + x y - 2 x^2 y + y^2 - x y^2 + 2 y^3} . \end{aligned}$$

Since the term $x+ y -1$ divides e(x, y), we conclude that the curve ${C}_1$ is collapsed by $\pi ^{-1} \circ F$ to a point on $E_4$ or the whole curve $E_4$. We compute explicitly $l(x, 1- x) = 1/5$, hence ${C}_1$ is collapsed by $\pi ^{-1}\circ F$ to the point $(e= 0 , l =1/5)$ on X. We now determine the orbit of the point $(e=0, l =1/5)$ by $\tilde{F}$ on $E_4$. In the proof of assertion (viii), we have showed that the induced map on $E_4$ is of the form:

$$\begin{aligned} (e=0 , l) \mapsto \left( e=0, \dfrac{l^2}{2 - 3 l} \right) . \end{aligned}$$

As $l=1/5$ is in the basin of attraction of the fixed point $(e=0, l=0)$, we deduce that the orbit of $(e=0, l=1/5)$ by $\tilde{F}$ avoids the indeterminacy $(e=0, l=1), (e=0, l=-2)$ and converges to the point $(e=0, l=0)$. This proves that the orbit of the line $\tilde{C}_1$ by $\tilde{F}$ is regular and assertion (i) holds. $\square$

7.2 The Density of States for the Hanoi Group

Recall from Sect. 2.4.3 that the spectrum of the Hanoi group is associated to the following families of polynomial $P_n$ defined inductively by the relation:

$$\begin{aligned} P_n(x,y) = \left( x^2 - (1+y)^2 \right) ^{3^{n-2}} \left( x^2 - 1 + y -y^2\right) ^{2 \cdot 3^{n-2}} P_{n-1}(F(x,y)), \end{aligned}$$

where $P_1$ is the polynomial:

$$\begin{aligned} P_1 = - (x-1 -2 y) (x-1 +y)^2. \end{aligned}$$

The density of states is in this case the limit, denoted $\omega$, of the sequence of measures $\omega _n:=1/3^n [P_n =0] \wedge [y=1]$. Denote by $T_F$ the Green current associated to the Hanoi map F.

Theorem 7.10

The following properties are satisfied.

• (i) The sequence of currents $1/3^n [P_n =0]$ converges as n tends to $+\infty$ to a current which is supported on countably many curves.

• (ii) The sequence of measures $1/3^n [P_n = 0] \wedge [y=1]$ converges as n tends to $+\infty$ to an atomic measure.

• (iii) The sequence of measures

  $$\begin{aligned} \dfrac{3^n}{2^n} (\omega - \omega _n) \end{aligned}$$

  converges to the measure $- \dfrac{25}{6}T_F \wedge [y=1]$.

In particular, the density of states associated with the Hanoi group is an atomic measure.

Proof

Applying assertion (ii) of Theorem 3.3, we obtain

$$\begin{aligned} \lambda _1(F) = {{\text {max}}}(2,1)= 2 \end{aligned}$$

since F is conjugate to the map $(x,y) \mapsto \left( x^2 - x - 3, (x-1)(x+2)y/(x+3) \right)$ by Theorem 7.1. Since $\lambda _1(F) < 3$, we have by Theorem 4.1 that the limit of currents:

$$\begin{aligned} T_{{\mathcal {H}}}=\lim _{n\rightarrow +\infty } \dfrac{1}{3^n}[P_n=0] \end{aligned}$$

is supported on countably many curves.

Let us prove assertion (iii). Take the blow-up X of ${\mathbb {P}}^2$ at the four points $[-1:1:0], [2:1:0]$ and $[\pm 1 : 0: 1]$ and we denote by $\pi :X\rightarrow {\mathbb {P}}^2$ the associated blow-down map. We also denote by $E_1, E_2, E_3, E_4$ the exceptional divisors above $[-1:1:0], [2:1:0]$, $[- 1 : 0: 1]$ and [1 : 0 : 1] respectively and by $\tilde{L}_\infty$ the strict transform of the line at infinity by $\pi$.

Let us first observe that the following equalities of cycles hold:

$$\begin{aligned} {{\,\textrm{div}\,}}((x-1 - y) \circ \pi )= & {} \pi ^o [x-1- y =0] + E_4 -\tilde{L}_\infty ,\\ {{\,\textrm{div}\,}}((x+1 + y) \circ \pi )= & {} \pi ^o [x+ 1+ y =0] +E_3 +E_1 - \tilde{L}_\infty ,\\ {{\,\textrm{div}\,}}((x-1 + y-y^2) \circ \pi )= & {} \pi ^o [x- 1+ y - y^2 =0]+ E_4 -2 \tilde{L}_\infty , \end{aligned}$$

where $\pi ^o$ denotes the strict transform by $\pi$. Since $P_1 = - (x-1 -2 y) (x-1 +y)^2$, we obtain the equality of cycles

$$\begin{aligned} {{\,\textrm{div}\,}}(P_1 \circ \pi )&= \pi ^o[x-1 -2 y =0] + E_2 + E_4 \\&\quad + 2 (E_1 + \pi ^o [x-1 + y =0] + E_4) - 3 \tilde{L}_\infty \\&= 2 E_1 + E_2 + 3E_4 + \pi ^o[x-1 -2 y =0]\\ {}&\quad + 2 \pi ^o [x-1 + y =0] - 3 \tilde{L}_\infty . \end{aligned}$$

To simplify the computations, we set:

$$\begin{aligned} L_1&:= \pi ^o [x-1-y =0],\,\, L_2:= \pi ^o [x+1 +y =0],&L_3:= \pi ^o[x-1 -2 y =0] ,\\ L_4&:= \pi ^o [x-1 + y =0] ,\,\, C:= \pi ^o [x- 1+ y - y^2 =0]. \end{aligned}$$

Using the fact that $\tilde{F}^* \tilde{L}_\infty = \tilde{L}_\infty + L_1 + C$ and the inductive relation on the polynomials $P_n$, we get the equality of cycles:

$$\begin{aligned} {{\,\textrm{div}\,}}(P_2 \circ \pi ) =&L_1 + L_2 + 2 C + E_1 +E_3 + 3 E_4 - 6\tilde{L}_\infty \\&+ \tilde{F}^* (2 E_1 + E_2 + 3 E_4 + L_3 + 2 L_4 - 3 \tilde{L}_\infty )\\ =&-2 L_1 + L_2 - C + E_1 + E_3 + 2 E_4 - 9\tilde{L}_\infty \\&+ \tilde{F}^* (2 E_1 + E_2 + 3 E_4 + L_3 + 2 L_4). \end{aligned}$$

Using the above argument inductively, we deduce:

$$\begin{aligned} {{\,\textrm{div}\,}}(P_n \circ \pi )&= \sum _{k=0}^{n-1} 3^{n-2-k} (\tilde{F}^k)^* \left( -2 L_1 + L_2 - C + E_1 + E_3 + 2 E_4 \right) \\&\quad + (\tilde{F}^{n-1})^* (2 E_1 + E_2 + 3 E_4 + L_3 + 2 L_4) - 3^{n} \tilde{L}_\infty . \end{aligned}$$

Taking the current of integration over the zero divisor of $P_n$ and pushing forward by $\pi$, we obtain the equality of currents:

$$\begin{aligned} \dfrac{1}{3^n} [P_n = 0] = \sum _{k=0 }^{n-1} \dfrac{1}{3^{k+2}} (F^k)^*\pi _* L_2 + \dfrac{1}{3^n}(F^{n-1})^* (\pi _*L_3 + 2\pi _* L_4). \end{aligned}$$

Observe that the lines $L_2, L_3 , L_4$ are degenerates fibers of the associated fibers of the fibration map associated to F (it is a fibration by conics passing through the four points $[-1 :1:0], [2:1:0]$ and $[\pm 1:0:1]$). Observe also that the line $\{y=1\}$ is generic as it is transverse to all fibers of the fibration associated to F, we thus conclude by Theorem 4.1 that

$$\begin{aligned} \omega = \lim _{n\rightarrow +\infty } \omega _n =\lim _{n\rightarrow +\infty } \dfrac{1}{3^n}[P_n=0] \wedge [y=1] \end{aligned}$$

is an atomic measure. Let us express the error term as $n \rightarrow +\infty$, the mass of the current $(1/3^n) (F^{n-1})^* (\pi _* L_3 + 2 \pi _* L_4)$ decays exponentially fast with speed $(2/3)^n$, we get:

$$\begin{aligned}&\dfrac{3^{n-1}}{2^n}\left( T_{{\mathcal {H}}} - \dfrac{1}{3^n} [P_n=0] \right) \\&\quad = \dfrac{3^{n-1}}{2^n}\left( \sum _{k=n}^{+\infty } \dfrac{1}{3^{k+2}} (F^k)^* \pi _* L_2 - \dfrac{1}{3^{n-1}} (F^{n-1})^* (\pi _* L_3 + 2 \pi _* L_4) \right) \\&\quad = \dfrac{3^{n-1}}{2^n} \left( \sum _{k=n}^{+\infty } \dfrac{2^k}{3^{k+2}} \dfrac{(F^k)^* \pi _* L_2}{2^k} - \dfrac{1}{3^{n-1}} (F^{n-1})^* (\pi _* L_3 + 2 \pi _* L_4) \right) , \\&\quad = \dfrac{3^{n-1}}{2^n} \left( \sum _{k=n}^{+\infty } \dfrac{2^k}{3^{k+2}} \dfrac{(F^k)^* \pi _* L_2}{2^k} \right) - \dfrac{1}{2} \dfrac{(F^{n-1})^*\left( \pi _* L_3 + 2 \pi _* L_4 \right) }{2^{n-1}} , \end{aligned}$$

By Proposition 3.12, the currents $1/2^n(F^n)^*\pi _* L_2$, $1/2^n(F^n)^* \pi _*L_3$ , $1/2^n(F^n)^* \pi _*L_4$ converge to the current $T_F$, so we have:

$$\begin{aligned} \dfrac{3^{n-1}}{2^n}\left( T_{{\mathcal {H}}} - \dfrac{1}{3^n} [P_n=0] \right)&= \dfrac{3^{n-1}}{2^n} \left( \sum _{k=n}^{+\infty } \dfrac{2^k}{3^{k+2}} ( T_F + o(1)) \right) - \dfrac{1}{2} (3T_F + o(1)) , \\&= \dfrac{1}{9} T_F - \dfrac{3}{2} T_F + o(1),\\&= - \dfrac{25}{18} T_F + o(1), \end{aligned}$$

and their slices by $[y=1]$ converge to $T_F \wedge [y=1]$, this gives:

$$\begin{aligned} \dfrac{3^{n-1}}{2^n}\left( T_{{\mathcal {H}}} - \dfrac{1}{3^n} [P_n=0] \right) \wedge [y=1]&= - \dfrac{25}{18} T_F \wedge [y=1] + o(1). \end{aligned}$$

And we conclude that:

$$\begin{aligned} \lim _{n\rightarrow +\infty }\dfrac{3^n}{2^n} ( \omega - \omega _n) = -\dfrac{25}{6} T_F \wedge [y=1]. \end{aligned}$$

$\square$

Proof of Theorem B

Assertion (i) is the content of Theorem 5.1, assertion (ii) results from Proposition 6.1, and assertion (iii) from Theorem 7.1. $\square$

Proof of Theorem A

Assertion (i) results from Theorem 5.11, assertion (ii) from Theorem 6.4 and assertion (iii) from Theorem 7.10. $\square$

8 Integrability in Algebraic Geometry

8.1 A General Criterion

In this section, we state some criterion to find invariant fibrations for rational surface maps using algebraic methods. Our goal is to present a practical criterion for integrability using the notions described in the appendix (see Sect. 9).

We shall start with the following observation.

Proposition 8.1

Consider a dominant rational map $f :X \dashrightarrow X$ on a projective surface X. If f is semi-conjugate to a degree d map on a projective curve then there exists a birational modification $\tilde{X}$ of X and a nef line bundle L on $\tilde{X}$ satisfying the following conditions:

• (i) One has $(c_1(L) \cdot c_1(L)) = 0$.

• (ii) One has $\tilde{f}^* L = L^{\otimes d}$ where $\tilde{f}$ is the lift of f to $\tilde{X}$.

• (iii) The line bundle L has at least two independent sections.

Proof

Let us suppose that f preserves a fibration over a curve C. Denote by $\varphi :X \dashrightarrow C$ the associated map onto C and denote by $g:C \rightarrow C$ the map semi-conjugating f via $\varphi$. Take the graph $\tilde{X}$ of $\varphi$ in $X\times C$ and denote by $\pi _1, \pi _2$ the projection from $\tilde{X}$ to X and C respectively. We consider the restriction $\tilde{f}$ of the map $f\times g$ in $X\times C$ to $\tilde{X}$. Take the graph $\Gamma$ of $\tilde{f}$ on $\tilde{X}\times \tilde{X}$ and denote by u, v the projections of $\Gamma$ onto the first and second factor respectively. We obtain the following commutative diagram:

(8.1)

Take a point p in C, we consider the divisor $F = \pi _2^* [p]$ in $\tilde{X}$ corresponding to the fiber of $\pi _2$ over p. Since any two general fibers of $\pi _2$ are disjoint, their intersection is zero. As a result, the self-intersection of F satisfies the relation:

$$\begin{aligned} (F \cdot F) =0. \end{aligned}$$

We now compute the pullback of F by $\tilde{f}$. By definition, we have:

$$\begin{aligned} \tilde{f}^* F = u_* v^* F = u_*v^*\pi _2^* [p]. \end{aligned}$$

Using the fact that $\pi _2 \circ v =g \circ \pi _2\circ u$, we get:

$$\begin{aligned} \tilde{f}^* F = u_* v^* F = u_* u^* \pi _2^*g^* [p]. \end{aligned}$$

Since g is of degree d, the preimage of the general point [p] consists of d points counted with multiplicities. As a result, we have $g^* [p] = d [p]$ in $H^{1,1}(C)$, hence the projection formula (Proposition 9.12 (iii)) gives:

$$\begin{aligned} \tilde{f}^* F = d u_* u^* \pi _2^* [p] = d F, \end{aligned}$$

where we have used the fact that u is birational, so its topological degree is one. This proves that the class F is multiplied by d by the action of $\tilde{f}^*$.

Since $(F \cdot F)=0$ and $\tilde{f}^* F = d F$, the two relations also hold for nF where n is an integer. The line bundle $L = {\mathcal {O}}(nF)$ associated to the divisor nF satisfies (i) and (ii). Since the divisor [p] is ample on C, there exists a multiple n such that n[p] is very ample so the line bundle ${\mathcal {O}}_C(n[p])$ has at least two sections by Asymptotic Riemann–Roch’s theorem [72, Example 1.2.19]. Since $L ={\mathcal {O}}(nF)$ is the pullback of this line bundle by $\pi _2$, we deduce that property (iii) holds for a large enough multiple n, as required. $\square$

For the converse statement, we shall need to construct fibrations using a result due to Iitaka (see [72, Theorem 2.1.33]). Precisely, for an integer n, we consider the following rational mapping $\phi : X \dashrightarrow {\mathbb {P}}(H^0(X, n L))$ defined as follows:

$$\begin{aligned} \phi (x) = [ s_0(x): \cdots : s_k(x) ], \end{aligned}$$

where $s_0, \ldots , s_k$ is a basis of holomorphic sections of nL. The map $\phi$ above is the mapping induced by nL.

Theorem 8.2

Let L be a nef line bundle on a surface X and $k>0$ be an integer such that

$$\begin{aligned} 1/C \leqslant \dfrac{h^0(nL)}{n^k} \leqslant C, \end{aligned}$$

for $C>0$ where $h^0(nL)= \dim H^0(X,nL)$. Then for sufficiently large n, the mapping induced by nL, $\phi : X \dashrightarrow {\mathbb {P}}(H^0(X,nL)^*)$ defines a map onto a variety of dimension k.

The integer k in the above theorem is called the Iitaka dimension of L (see e.g [72, Definition 2.1.3]).

In our situation, we will apply the result to a nef line bundle which will satisfy the equation $(c_1(L)^2)=0$. When this happens, the Iitaka map $\phi$ associated to L cannot map to a surface, but will either map to a curve or a to point.

Theorem 8.3

Let $f :{\mathbb {P}}^2 \dashrightarrow {\mathbb {P}}^2$ be a dominant rational map. Suppose that there exists a smooth surface X obtained from ${\mathbb {P}}^2$ by finitely many blow-ups, a line bundle L on X and an integer $d \geqslant 1$ satisfying the following conditions:

• (i) One has $(c_1(L) \cdot c_1(L))=0$.

• (ii) The line bundle L is nef.

• (iii) One has $(K_X \cdot c_1(L)) < 0$ where $K_X$ is the (first) Chern class of the canonical bundle of X.

• (iv) One has $f^* L = L^{\otimes d}$.

Then f is semi-conjugate to a degree d map on a curve.

Remark 8.4

Unfortunately, there is no explicit method for choosing the surface X when the map f is not invertible.

Proof

We shall prove successively the following statements.

Claim 1: The sequence $h^0(X,nL)/n^2$ converges to zero as n tends to infinity.

By Asymptotic-Riemann-Roch theorem (see [72, Example 1.2.36 (ii)]):

$$\begin{aligned} h^0 (nL) = \dfrac{1}{2} n^2 (c_1(L)^2) + O(n). \end{aligned}$$

Since $(c_1(L)^2)=0$, we obtain that $h^0(nL) = O(n)$. As a result, this proves that $h^0(nL)/ n^2$ converges to zero and the claim is proved.

Claim 2: One has $h^0(X,nL) \geqslant \chi (nL)$ for all integer n.

By Serre duality [64, Corollary 7.7], we have $h^2(X, L)= h^0(X, L^{-1} \otimes {\mathcal {O}}(K_X))=0$ since $K_X$ is not effective because X is rational. Indeed, the rationality of X implies that its Kodaira dimension is $-\infty$ so using [3, Theorem 7.2], $\dim H^0(X, K_X)= 0$, hence it cannot be effective. We obtain that:

$$\begin{aligned} \chi (nL)= & {} h^0(X, nL) - h^1(X, nL) + h^2(X,nL) = h^0(X, nL) - h^1(X,nL) \\\leqslant & {} h^0(X,nL), \end{aligned}$$

and the claim is proved.

Claim 3: $\chi (nL) \geqslant \alpha n$ for some $\alpha > 0$.

By Riemann–Roch theorem [3, I Theorem 5.5 (6)] and using the fact that $(c_1(L) \cdot c_1(L))=0$, we have:

$$\begin{aligned} \chi (nL)= & {} \chi ({\mathcal {O}}_X) + \dfrac{1}{2} (n^2(c_1(L) \cdot c_1(L)) - \dfrac{n}{2}(c_1(L) \cdot K_X)) \\= & {} \chi ({\mathcal {O}}_X) - \dfrac{n}{2} (c_1(L) \cdot K_X). \end{aligned}$$

This proves the result as $(c_1(L) \cdot K_X) < 0$.

We now show that the Proposition holds. We consider for n large the map:

$$\begin{aligned} \phi _{nL} :X \dashrightarrow {\mathbb {P}}(H^0(X,nL)^*). \end{aligned}$$

Claim 1 proves that the dimension of the image of $\phi _{nL}$ is not 2. Moreover, Claim 2 and 3 imply that $h^0(X, nL) \geqslant \alpha n$, thus L satisfies the condition of Theorem 8.2 for $k=1$ and $\phi _{nL}$ maps X to a curve C. Finally, the fact that $f^* L = L^{\otimes d}$ proves that $\phi _{nL}$ semi-conjugates f to a degree d map on C. To see this, we first view the zero of a generic section s of L as a generic hyperplane of ${\mathbb {P}}(H^0(X,nL)^*)$ and the zero locus of the section $f^*s$ of $f^* L$ is interpreted as a degree d hypersurface of ${\mathbb {P}}(H^0(X,nL)^*)$. The hyperplane $s=0$ intersect the curve C at $\deg (C)$ points whereas the preimage $f^* s$ intersects C at $\deg (C) \cdot d$ points by Bezout’s theorem. We deduce that the induced map on C has topological degree d. $\square$

8.2 The Integrability Criterion Applied to the Renormalization of the Grigorchuk Group

Recall from Sect. 5.1 that we have defined X to be the blow-up of ${\mathbb {P}}^2$ at the four points $[0: \pm 2 : 1]$ and $[\pm 1 : 1 : 0]$. We denote by $E_1, E_2, E_3 , E_4$ the exceptional divisors above the points $[-1:1:0] ,[1:1:0], [0:-2:1] , [0:2:1]$ respectively and take the strict transform $\tilde{L}_\infty$ of the line at infinity in ${\mathbb {P}}^2$ by the blow-up (see Fig. 4).

We fix a basis of $H^{1,1}(X)$, namely :

$$\begin{aligned} H^{1,1}(X) = {\mathbb {C}}\tilde{L}_\infty \oplus {\mathbb {C}}E_1 \oplus {\mathbb {C}}E_2 \oplus {\mathbb {C}}E_3 \oplus {\mathbb {C}}E_4. \end{aligned}$$

(8.2)

Recall that we have proved in assertion (v) of Proposition 5.5 that the map $\tilde{F}$ is algebraically stable on X.

Corollary 8.5

The pushforward and pullback matrices associated to $\tilde{F}$ and $\tilde{G}$ are of the form:

$$\begin{aligned} \tilde{F}_*= & {} \left( \begin{array}{lllll} 1 &{} 1 &{}1 &{} 1 &{}1 \\ 0 &{} 1 &{} 1 &{} 0&{} 1\\ 0 &{} 1 &{} 1 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 &{}0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 \end{array} \right) , \quad \tilde{F}^* = \left( \begin{array}{lllll} 1 &{} 1 &{} 1 &{} 0&{} 0 \\ 0 &{} 1 &{} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 1 &{} 0 &{} 0 \\ 0 &{} -1&{} 0&{} 1 &{} 0 \\ 0&{} 0 &{} -1 &{} 0 &{} 1 \end{array} \right) ,\\ \tilde{G}_*= & {} \left( \begin{array}{lllll} 1 &{} 1 &{}1 &{} 1 &{}1 \\ 1 &{} 1 &{} 1 &{} 1&{} 2\\ 1 &{} 1 &{} 1 &{} 2 &{} 1\\ -1 &{} 0 &{} 0 &{} 0 &{}-1 \\ -1 &{} 0 &{} 0 &{} -1 &{} 0 \end{array} \right) , \quad \tilde{G}^* = \left( \begin{array}{lllll} 3&{}0&{}0&{}1&{}1 \\ 2&{} 0 &{} 0 &{} 1 &{} 1 \\ 2&{} 0 &{} 0 &{} 1 &{} 1 \\ -2 &{} 0 &{} 1 &{} 0 &{} -1 \\ -2 &{} 1 &{} 0 &{} -1 &{} 0 \end{array} \right) . \end{aligned}$$

Proof

We first compute $\tilde{F}_* \tilde{L}_\infty$, since $\tilde{L}_\infty$ is collapsed to a point and the indeterminacy point [1, 0, 0] is mapped to L by assertion (v) of Proposition 5.5, we deduce that:

$$\begin{aligned} \tilde{F}_* \tilde{L}_\infty = \tilde{L}_\infty . \end{aligned}$$

(8.3)

Moreover, since $E_1$ and $E_2$ are both mapped regularly to the line $\{\lambda = -2w\}$ by assertion (iv) and since assertion (v) of Proposition 9.12 yields the equality $\pi ^o\{ \lambda = -2w \} = \tilde{L}_\infty + E_1 + E_2$ in $H^{1,1}(X)$, we obtain that:

$$\begin{aligned} \tilde{F}_* E_1 = \tilde{F}_* E_2 = \tilde{L}_\infty + E_1 + E_2 \in H^{1,1}(X). \end{aligned}$$

We now compute the image of $E_3$, and the computation for $E_4$ is similar. Using assertion (v) of Proposition 9.12, we obtain the equality $\pi ^o\{ \lambda + \mu + 2 w \} = \tilde{L}_\infty +E_2 -E_3$ in $H^{1,1}(X)$, so assertion (iii) and (iv) of Proposition 5.5 implies that:

$$\begin{aligned} \tilde{F}_* E_3 = \tilde{L}_\infty + E_2 - E_3 + 2 E_3= \tilde{L}_\infty + E_2 + E_3 \in H^{1,1}(X), \end{aligned}$$

and we thus obtain the pushforward action by $\tilde{F}$. The pullback action can be deduced from the matrix of $\tilde{F}_*$ by conjugating the transpose of $\tilde{F}_*$ by the intersection matrix. We thus obtain:

$$\begin{aligned} \tilde{F}^* = I^{-1} \tilde{F}_*^t I = \left( \begin{array}{lllll} 1 &{} 1 &{} 1 &{} 0&{} 0 \\ 0 &{} 1 &{} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 1 &{} 0 &{} 0 \\ 0 &{} -1&{} 0&{} 1 &{} 0 \\ 0&{} 0 &{} -1 &{} 0 &{} 1 \end{array} \right) , \end{aligned}$$

where I is the intersection matrix given by:

$$\begin{aligned} I := \left( \begin{array}{lllll} -1 &{} 1 &{} 1 &{} 0&{} 0 \\ 1 &{} -1 &{} 0 &{} 0 &{} 0 \\ 1 &{} 0 &{}-1 &{} 0 &{} 0 \\ 0 &{} 0&{} 0&{} -1 &{} 0 \\ 0&{} 0 &{} 0 &{} 0 &{} -1 \end{array} \right) . \end{aligned}$$

We finally deduce G from the fact that $G = H \circ F$ and from the fact that H is an automorphism on X whose matrix is given by:

$$\begin{aligned} H_* =\left( \begin{array}{lllll} 1 &{}0 &{} 0 &{} 0&{} 0\\ 1 &{} 0 &{} 0 &{} 0&{} 1\\ 1 &{} 0 &{} 0 &{} 1&{}0\\ -1 &{} 0 &{} 1 &{} 0&{}0\\ -1 &{} 1 &{} 0 &{} 0 &{} 0 \end{array} \right) . \end{aligned}$$

We finally compute the matrices of $\tilde{G}_*$ and $\tilde{G}^*$. $\square$

From the previous result, we see that the line bundle induced by the divisor $D = 2\tilde{L}_\infty + E_1 + E_2 - E_3 - E_4$ is invariant by both $\tilde{F}^*$ and $\tilde{G}^*$ since D is an eigenvector for both matrices associated to the eigenvalue 2. To check that D is nef, we observe that the strict transform C of any irreducible conic in ${\mathbb {P}}^2$ passing through the four points $[0:\pm 2 :1], [\pm 1 :1:0]$ has the same cohomology as D. Since X is a smooth projective surface, any irreducible curve $C'$ distinct from C intersects C non-negatively, we also have $D^2 = C^2 =0$ and this shows that D intersects non-negatively any irreducible curve, hence D is nef.

Recall that by assertion (iv) of Proposition 9.12, the canonical class of X is given by $-3 \tilde{L}_\infty -2 E_1 - 2 E_2 + E_3 + E_4$.

We have summarized the properties satisfied by D:

• 1. $D^2 =0$.

• 2. $(K_X \cdot D) < 0$.

• 3. D is nef.

• 4. $\tilde{F}^*D = \tilde{G}^*D = 2 D$

By Theorem 8.3, the map induced by the linear system |D| denoted $\phi _D :X \dashrightarrow C,$ maps onto an algebraic Riemann surface C. Indeed, we have:

$$\begin{aligned} {{\text {max}}}_{n\in {\mathbb {N}}} \dim \phi _{nD}(X)=1 , \end{aligned}$$

so in particular the dimension $\dim \phi _D(X) \leqslant 1$. Since $\phi _D$ is not a constant map, we thus conclude that $\dim \phi _D(X) =1$, hence it is a curve. Take any holomorphic section s of D and let S be the zero locus $\{s=0\}$. By definition ${{\,\textrm{div}\,}}(s) = [S]$ is linearly equivalent to $2 \tilde{L}_\infty + E_1 + E_2 - E_3 -E_4$. In particular, $\pi (S)$ is a degree 2 curve in ${\mathbb {P}}^2$. Moreover, $(S\cdot E_i)=1$ for $i=1,2,3,4$, hence $\pi (S)$ passes through the four points $[0:\pm 2: 1]$ and $[\pm 1: 1: 0]$. This shows that fibers of $\phi _D$ are mapped by $\pi$ to conics passing through all four points $[0:\pm 2: 1]$ and $[\pm 1: 1: 0]$. Using Theorem 8.3, we deduce the following result.

Proposition 8.6

Both maps F and G preserve the fibration induced by $\phi _D$ and $\lambda _1(F) = \lambda _2(G)=2$ and F is semi-conjugate to $\alpha {\text {id}}\times T$ where $\alpha {\text {id}}$ is the scaling by $\alpha \ne 0$ and where T is the Chebyshev map.

Proof

Since D is stable by pullback by $\tilde{F}$ and $\tilde{G}$, the map $\phi _D$ defines a semi-conjugation. Let us prove that F is semi-conjugate to $\alpha {\text {id}}\times T$. Recall that the divisor $E_3$ is mapped by $\tilde{F}$ to itself and that the restriction of $\tilde{F}$ to $E_3$ (see (5.1)) is of the form:

$$\begin{aligned} (e=0 , l) \in E_3 \mapsto (e=0, 2l^2 -1). \end{aligned}$$

Since the pencil of conic induced by D all pass transversely to $E_3$, we deduce that the induced map on C is the Chebyshev map on ${\mathbb {P}}^1$. Recall that the product formula yields that the relative dynamical degree of F and G is one. Moreover, the fibers of the fibration are rational curves (they are conic curves on ${\mathbb {P}}^2$), and since F fixes the divisors $E_3,E_4$ which are transversal to the pencil of conics, we can identify two points on each fiber of $\phi _D$, for example identify $E_3 \cap \phi _D^{-1}(c_0)$ with $0\in {\mathbb {P}}^1$ and $\phi _D^{-1}(c_0) \cap E_4$ with the point at infinity $\infty \in {\mathbb {P}}^1$. Since F fixes $E_3$ and $E_4$, we deduce that under this identification, F acts on the fiber as a degree one map fixing two points 0 and $\infty$, it is thus semi-conjugate to $\alpha {\text {id}}\times T$. $\square$

We now relate in an explicit way and geometrically the fibration $\phi _D$ with the map $\psi$ given in (5.6). For any point m on the exceptional divisor $E_3$, there exists a unique conic in the linear system passing through m, because our fibers should already pass through the four points $[0,\pm 2, 1]$ and $[\pm 1, 1, 0]$. For any point $[\lambda _0,\mu _0 , w_0]$, the unique conic in the linear system passing through $[\lambda _0,\mu _0 , w_0]$ has equation:

$$\begin{aligned} \lambda _0 w_0 \lambda ^2 - \lambda _0 w_0 \mu ^2 + (-\lambda _0^2 + \mu _0^2 - 4 w_0^2) \lambda w + 4 \lambda _0 w_0 w^2 =0. \end{aligned}$$

(8.4)

The above conic passes through the point $[0,-2,1]$ with a slope:

$$\begin{aligned} \lambda /(\mu + 2) = -\dfrac{\lambda _0^2 - \mu _0^2 + 4 w_0^2}{4 \lambda _0 w_0}. \end{aligned}$$

The map $\phi _D$ is then realized geometrically by the map:

$$\begin{aligned} {[}\lambda : \mu : w] \mapsto -\dfrac{\lambda ^2 - \mu ^2 + 4 w^2}{4 \lambda w} = -\psi (\lambda ,\mu , w) \in E_3, \end{aligned}$$

(8.5)

where $\psi$ is the map defined in (5.6).

8.3 The Integrability Criterion Applied to the Renormalization of the Lamplighter Group

Recall from Sect. 6.1 that we have defined X to be the blow-up of ${\mathbb {P}}^2$ at the two points $[\pm 1 : 1 :0]$. We denote by $\tilde{F}$ the lift of F to X and by $E_1,E_2$ the exceptional divisors above $[-1 :1 :0]$ and [1 : 1 : 0] respectively (see figure 7).

We identify $H^{1,1}(X)$ with ${\mathbb {C}}\tilde{L}_\infty \oplus {\mathbb {C}}E_1 \oplus {\mathbb {C}}E_2$ where $\tilde{L}_\infty$ denotes the strict transform of the line at infinity. Recall that we have proven in assertion (ix) of Proposition 6.2 that $\tilde{F}$ is algebraically stable in X. We thus compute the pullback and pushforward action of $\tilde{F}$ on $H^{1,1}(X)$

Proposition 8.7

The matrices of $\tilde{F}^*$ and $\tilde{F}_*$ are of the form:

$$\begin{aligned} \tilde{F}_* :=\left( \begin{array}{lll} 0 &{}1&{}1\\ 0&{}1&{}0\\ 0&{}0&{}1 \end{array} \right) , \quad \tilde{F}^* := \left( \begin{array}{lll} 1 &{}1&{}0\\ 0&{}1&{}0\\ 1&{}0&{}0 \end{array} \right) . \end{aligned}$$

Proof

We first compute the matrix of $\tilde{F}_*$.

Let us first observe that $\tilde{F}$ is regular on the line $\pi ^{-1}(\{\mu =0\})$ and that this line is mapped to the curve $C_1$ parametrized as follows:

$$\begin{aligned} (\lambda , w) \mapsto [-\lambda ^2 + 2 w^2: -2 w^2 : -w \lambda ]. \end{aligned}$$

Since $[\pi ^{-1}(\mu =0)] = \tilde{L}_\infty + E_1 + E_2$ and since the curve $C_1$ is a degree 2 curve passing through the point $[-1:1:0]$, assertion (v) of Proposition 9.12 shows that $\pi ^o C_1 = 2 \tilde{L}_\infty + E_1 + 2 E_2$ in $H^{1,1}(X)$, and we get:

$$\begin{aligned} \tilde{F}_* (\tilde{L}_\infty + E_1 + E_2) = 2 \tilde{L}_\infty + E_1 + 2 E_2. \end{aligned}$$

(8.6)

Next, we consider the line $\pi ^{o}(\{\lambda = -\mu \})$, since $\tilde{F}$ is regular on $E_1$ by Proposition 6.2 (vi), the image C of this line is parametrized by:

$$\begin{aligned} \lambda \in {\mathbb {C}}^* \mapsto \pi ^{-1}([1:-1: -\lambda ]), \end{aligned}$$

Since assertion (v) of Proposition 9.12 gives $\pi ^{o}(\{\lambda = -\mu \}) =\tilde{L}_\infty + E_2$ and $\pi ^oC= \tilde{L}_\infty + E_2$ in $H^{1,1}(X)$, we deduce:

$$\begin{aligned} \tilde{F}_* (\tilde{L}_\infty + E_2) = \tilde{L}_\infty + E_2. \end{aligned}$$

(8.7)

Finally, we consider the conic curve $Q:=\pi ^{o} \{ \lambda ^2 - 2 \lambda \mu + \mu ^2 - w^2 =0 \}$ which does not intersect $E_2$ at the indeterminacy point of $\tilde{F}$. The image of Q by $\tilde{F}$ is the conic curve $C_2$ parametrized by:

$$\begin{aligned} (\lambda , w) \mapsto [2 - 2 \lambda + w^2 :-2 w^2 : -(\lambda - 1) w]. \end{aligned}$$

(8.8)

Assertion (v) of Proposition 9.12 shows that $\pi ^o C_2 = 2 \tilde{L}_\infty + 2E_1 + 2 E_2$ and $Q= 2 \tilde{L}_\infty + 2 E_1$ in $H^{1,1}(X)$, we obtain:

$$\begin{aligned} \tilde{F}_* (2\tilde{L}_\infty + 2E_1) = 2\tilde{L}_\infty + 2 E_1 + 2 E_2. \end{aligned}$$

(8.9)

Using (8.6), (8.7) and (8.9), we deduce the matrix of $\tilde{F}_*$. We then deduce the pullback matrix $\tilde{F}^*$ using the fact that $\tilde{F}^* = I^{-1} \cdot \tilde{F}_*^t \cdot I$ where I is the intersection matrix given by:

$$\begin{aligned} I := \left( \begin{array}{lll} -1 &{} 1 &{} 1 \\ 1 &{} -1 &{} 0 \\ 1 &{} 0 &{} -1 \end{array} \right) . \end{aligned}$$

$\square$

Recall that by assertion (iv) of Proposition 9.12, the canonical class of X is the divisor $K_X$ satisfying

$$\begin{aligned} K_X = -3 \tilde{L}_\infty - 2 E_1 -2E_2 \in H^{1,1}(X). \end{aligned}$$

From the above proposition, we see that the matrix of $\tilde{F}^*$ admits a Jordan block for the eigenvalue 1. Denote by $D_1 = \tilde{L}_\infty + E_2$, we have:

• (1) $\tilde{F}^* D_1 = D_1$.

• (2) $D_1$ is nef.

• (3) One has $(D_1 \cdot D_1) = 0$.

• (4) One has $(K_X \cdot D_1)= -2 < 0$.

To see that $D_1$ is nef, we take any irreducible algebraic curve C in X, we have $D_1 = \pi ^* L_\infty - E_1$, so $C \cdot D_1 = (C \cdot \pi ^* L_\infty ) - (C\cdot E_1) = (L_\infty \cdot \pi _*(C)) - (C\cdot E_1)$. Two cases appear, either $C= \tilde{L}_\infty$, then $(\tilde{L}_\infty \cdot D_1) = 0 \geqslant 0$, or $\pi (C)$ is a curve which is not contained in $L_\infty$ and it intersects $L_\infty$ with multiplicity $(C\cdot E_1)$ at the point $[-1:1:0]$ and multiplicity m(C) at other points of the line $L_\infty$. In other words we have $m(C) + (C\cdot E_1) = (L_\infty \cdot \pi (C))$, and this shows that $m(C) = (C\cdot D_1) \geqslant 0$. We have shown that $(C\cdot D_1) \geqslant 0$ for any irreducible curve C, hence $D_1$ is nef.

Geometrically, the two divisors $D_1$ defines a pencil, $D_1$ is the pencil of lines in ${\mathbb {P}}^2$ passing through $[-1:1:0]$. Using Theorem 8.3, we deduce that F preserves the fibration induced by $D_1$.

Corollary 8.8

F is semi-conjugate to a linear map on ${\mathbb {P}}^1$ and the action of F on the fiber is also linear.

8.4 The Integrability Criterion Applied to the Renormalization of the Hanoi Group

Recall from Sect. 7.1 that we have defined X to be the blow-up of ${\mathbb {P}}^2$ at the four points $[-1:1:0], [2:1:0], [- 1 : 0 : 1], [1:0:1]$ and that we have set $E_1, E_2 , E_3$ and $E_4$ to be the four exceptional divisors on X (see figure 8).

We identify $H^{1,1}(X)$ with

$$\begin{aligned} H^{1,1}(X) \simeq {\mathbb {C}}\tilde{L}_\infty \oplus {\mathbb {C}}E_1 \oplus {\mathbb {C}}E_2 \oplus {\mathbb {C}}E_3 \oplus {\mathbb {C}}E_4, \end{aligned}$$

where $\tilde{L}_\infty$ is the strict transform of the line at infinity in ${\mathbb {P}}^2$. We denote by $\tilde{F}$ the lift of F to X.

Proposition 8.9

The map $\tilde{F}$ is algebraically stable on X.

Proof

Using Proposition 7.5, we control the orbit of every contracted curve and every exceptional divisor on X, none are contracted to an indeterminacy point of $\tilde{F}$, so $\tilde{F}$ is algebraically stable. $\square$

Corollary 8.10

The pushforward and pullback action of $\tilde{F}$ are given by the matrices:

$$\begin{aligned} \tilde{F}_*= & {} \left( \begin{array}{lllll} 1&{} 2 &{} 1 &{}1 &{} 2 \\ 0 &{} 2 &{} 1 &{} 1 &{} 1 \\ 0 &{} 1 &{} 1 &{} 0 &{} 1 \\ 0&{} 0 &{}0 &{} 1 &{} 0 \\ 0 &{} -1 &{} 0 &{} 0 &{} 0 \end{array} \right) ,\\ \tilde{F}^*= & {} \left( \begin{array}{lllll} 1&{} 1 &{} 2 &{} 0 &{} 1 \\ 0&{} 1 &{} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 2 &{} 0 &{} 1 \\ 0&{} 0 &{} -1 &{} 1 &{} 0 \\ 0 &{} -1 &{} -1 &{} 0 &{} 0 \end{array} \right) . \end{aligned}$$

Proof

We look at the image of $L, E_1, E_2,E_3, E_4$ by $\tilde{F}$.

Since $\tilde{F}$ contracts $\tilde{L}_\infty$ to a point and maps the indeterminacy point on $\tilde{L}_\infty$ to $\tilde{L}_\infty$ by Proposition 7.5.(viii), we have:

$$\begin{aligned} \tilde{F}_* \tilde{L}_\infty = \tilde{L}_\infty . \end{aligned}$$

By Proposition 7.5.(viii), the divisor $E_1$ is mapped regularly by $F\circ \pi$ to the curve parametrized by:

$$\begin{aligned} l \mapsto [6 - 3 l - l^2: -(-1 + l) l: 2 (2 - l) l], \end{aligned}$$

and since this curve is of degree 2 and passes through the point [1 : 0 : 0] , [2 : 1 : 0], [1 : 0 : 1], we deduce using assertion (v) of Proposition 9.12 that:

$$\begin{aligned} \tilde{F}_* E_1 = 2 \tilde{L}_\infty + 2 E_1 + 2 E_2 - E_2 - E_4 = 2 \tilde{L}_\infty + 2 E_1 + E_2 - E_4. \end{aligned}$$

By Proposition 7.5.(v), the exceptional divisor $E_2$ is mapped regularly by $F \circ \pi$ to the line $\{ z = y\} \subset {\mathbb {P}}^2$ and since this line does not pass through any indeterminacy point of F, assertion (v) of Proposition 9.12 gives:

$$\begin{aligned} \tilde{F}_* E_2 = \tilde{L}_\infty + E_1 + E_2. \end{aligned}$$

By Proposition 7.5.(vi), the exceptional divisor $E_3$ is fixed by $\tilde{F}$, the restriction of $\tilde{F}$ to $E_3$ has topological degree 2 and $\tilde{F}$ has one indeterminacy point on $E_3$. The image of the indeterminacy point on $E_3$ by $\tilde{F}$ is the line parametrized by:

$$\begin{aligned} l \mapsto [-22 + 2 l : -8 : 2(3- l)]. \end{aligned}$$

Since this line passes through the points $[2:1:0], [-1:0:1]$, we deduce using assertion (v) of Proposition 9.12 that:

$$\begin{aligned} \tilde{F}_* E_3 = 2E_3 + (\tilde{L}_\infty + E_1 + E_2 - E_2 - E_3) = \tilde{L}_\infty + E_1 +E_3. \end{aligned}$$

By Proposition 7.5.(vii), the exceptional divisor $E_4$ is fixed by $\tilde{F}$ with multiplicity 2 and $\tilde{F}$ has two indeterminacy points on $E_4$. The image of those indeterminacy points are two respective lines, parametrized by:

$$\begin{aligned} l&\mapsto [-2 - 3 l : 2 : -3 l],\\ l&\mapsto [-17 + 3 l : -4 : -3 (3-l)]. \end{aligned}$$

These line pass through the points $[-1:1:0], [1:0:1]$ and through the points [2 : 1 : 0], [1 : 0 : 1] respectively. Thus assertion (v) of Proposition 9.12 gives:

$$\begin{aligned} \tilde{F}_* E_4= & {} 2 E_4 + (\tilde{L}_\infty +E_1 + E_2 - E_1 - E_4) + (\tilde{L}_\infty +E_1 + E_2 - E_2 - E_4) \\= & {} 2 \tilde{L}_\infty + E_1 + E_2 . \end{aligned}$$

Finally, using the expressions image by $\tilde{F}$ of $\tilde{L}_\infty , E_1, E_2, E_3, E_4$, we deduce that the matrix of $\tilde{F}$ is given by:

$$\begin{aligned} \tilde{F}_* = \left( \begin{array}{lllll} 1&{} 2 &{} 1 &{}1 &{} 2 \\ 0 &{} 2 &{} 1 &{} 1 &{} 1 \\ 0 &{} 1 &{} 1 &{} 0 &{} 1 \\ 0&{} 0 &{}0 &{} 1 &{} 0 \\ 0 &{} -1 &{} 0 &{} 0 &{} 0 \end{array} \right) . \end{aligned}$$

We deduce the matrix of the pullback action $\tilde{F}^*$ by conjugating the transpose of the matrix of $\tilde{F}_*$ by the intersection matrix. We get:

$$\begin{aligned} \tilde{F}^* = I^{-1} \tilde{F}_*^t I = \left( \begin{array}{lllll} 1&{} 1 &{} 2 &{} 0 &{} 1 \\ 0&{} 1 &{} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 2 &{} 0 &{} 1 \\ 0&{} 0 &{} -1 &{} 1 &{} 0 \\ 0 &{} -1 &{} -1 &{} 0 &{} 0 \end{array} \right) , \end{aligned}$$

where I is the matrix given by:

$$\begin{aligned} I = \left( \begin{array}{lllll} -1 &{} 1 &{} 1 &{} 0 &{} 0 \\ 1 &{} -1 &{} 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} -1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -1 \end{array} \right) . \end{aligned}$$

$\square$

Recall also that $K_X = -3 \tilde{L}_\infty -2 E_1 - 2 E_2 +E_3 + E_4$. Consider $D = 2 \tilde{L}_\infty + E_1 + E_2 - E_3 - E_4$, the divisor D satisfies the following properties:

• (i) One has $\tilde{F}^* D = 2 D$.

• (ii) One has $(D \cdot D) = 0$ and the divisor D is nef.

• (iii) One has $(K_X \cdot D) < 0$.

The fact that D is nef follows from similar argument as in Sect. 8.2 or from a Perron-Frobenius theorem, since 2 is the spectral radius of the pullback map $\tilde{F}^*$ and that the pullback preserves the cone of nef divisors (see [26, Assertion 2 of Proposition 1.11]).

Geometrically, any element of D corresponds to a conic curve passing through the four points $[-1:1:0],[2:1:0], [\pm 1 : 0:1]$. Using Theorem 8.3, we deduce that F is semi-conjugate to a one dimensional map.

Corollary 8.11

F is semi-conjugate to a degree 2 rational map on a curve.

Appendix: Elements of Complex Geometry

In this appendix, X will be either an irreducible smooth projective surface or an irreducible smooth projective curve, i.e a smooth complex surface or curve which is embedded inside a complex projective space ${\mathbb {P}}^n$ for an integer $n \geqslant 2$. In this particular setting, one can view X as a Kähler manifold, endowed with the topology induced by the balls of ${\mathbb {C}}^{n+1}$, or X can be described as the intersection of the vanishing locus of finitely many homogeneous polynomials in ${\mathbb {C}}^{n+1}$. In the latter viewpoint, X is endowed with the Zariski topology. We refer to [43, p.23] for the definition of the Dolbeaut and deRham cohomology on X.

1.1 Currents and Their Intersection Using Bedford–Taylor’s Method

In this section, X is a smooth projective surface.

A current of bidegree (1, 1) is an element of the dual of smooth (1, 1) forms on X, a current of bidegree (2, 2) is a distribution on X. There are currents of other bidegree but we will not use them in this paper. If T is a (1, 1) current and $\alpha$ is a smooth (1, 1) form on X, we shall denote by $\langle T, \alpha \rangle \in {\mathbb {R}}$ the natural pairing between T and $\alpha$. The deRham differential on smooth forms induces by duality a differential on currents which we also denote by d. We say a (1, 1) current T is closed if $\langle T , d v \rangle$ for any smooth 1-form v on X.

A (1, 1) current T is said to be positive if for any positive function u and for any (1, 0) smooth form $\alpha$ on X, $T \wedge u \alpha \wedge i {\bar{\alpha }}$ is a positive measure on X. Like measures, the support of a (1, 1) current T, denoted ${\text {supp}}(T)$ is the smallest closed subset such that the current is identically zero on $X\setminus {\text {supp}}(T)$.

If T is a closed positive (1, 1) current and $\omega$ is a Kähler form on X, then $T \wedge \omega$ is a positive measure on X and the mass of T is the integral of this measure:

$$\begin{aligned} \int _X T \wedge \omega = \langle T, \omega \rangle . \end{aligned}$$

(9.1)

The main example of currents are the one induced by smooth forms and by plurisubharmonic functions.

Let us describe the first type of currents. Take a smooth (1, 1) form $\alpha$ on X, and define the functional:

$$\begin{aligned} T_\alpha :\beta \mapsto \int _X \alpha \wedge \beta , \end{aligned}$$

where $\beta$ is a smooth (1, 1) form on X. Since $T_\alpha$ is linear and continuous, the functional $T_\alpha$ defines a (1, 1) current.

On the other side of the spectrum, if V is an (complex) analytic curve on X, defined the functional [V] by the formula:

$$\begin{aligned}{}[V]:\beta \mapsto \int _{V^{\text {sm}}} \beta , \end{aligned}$$

where $\beta$ is a smooth (1, 1) form on X and where $V^{\text {sm}}$ denotes the smooth locus of V. When V is an algebraic curve, the functional [V] defines a closed positive (1, 1) current on X, and is referred as the current of integration on V.

The currents induced by plurisubharmonic are in between these two type of (1, 1) currents. A function $\phi :\Omega \subset {\mathbb {C}}^2 \rightarrow {\mathbb {R}}\cup \{ - \infty \}$ on a domain $\Omega$ of ${\mathbb {C}}^2$ is plurisubharmonic if it is upper-semicontinuous and the restriction of $\phi$ on every complex line is subharmonic. We state the main properties satisfied by these functions.

Theorem 9.1

The following assertions hold.

• (i) Plurisubharmonic functions are stable by decreasing limit.

• (ii) If $F :X \rightarrow Y$ is a dominant holomorphic map between two complex surfaces and $\phi$ is a plurisubharmonic function on Y, then the pullback $F^* \phi =\phi \circ F$ is a plurisubharmonic function on X.

Take a plurisubharmonic function $\phi$ on X, then the current T given in local coordinates by

$$\begin{aligned} T := i\partial {\bar{\partial }} \phi =i \sum _{i j} \dfrac{\partial ^2 \phi }{\partial z_i \partial {\bar{z}}_j} {\text {d}}z_i \wedge {\text {d}}{\bar{z}}_j \end{aligned}$$

defines a closed positive (1, 1)-current on X.

An important example is when $V = \{f=0 \}$ is locally the zero locus of a holomorphic function f, then the current of integration on V satisfies the equality:

$$\begin{aligned} {[}V] = i \partial {\bar{\partial }} \log |f|. \end{aligned}$$

We now explain how to intersect two (1, 1) currents to obtain a (2, 2) current (a measure) on X. If $\alpha , \beta$ are two smooth (1, 1) forms on X, then $\alpha \wedge \beta$ defines a signed measure on X, so one can define the intersection $T_\alpha$ with $T_\beta$ by the measure given by $\alpha \wedge \beta$. If V and W are two distinct irreducible complex analytic curves on X, then one can define their intersection as the discrete measure on $V\cap W$ counted with multiplicity. We want to intersect two (1, 1) currents induced by plurisubharmonic functions in such a way that the intersection would coincide with the other ways showed previously. The method in this case is more subtle, but was devised by Bedford–Taylor, then extended by Demailly ([8, 25, Section 4]).

Take two plurisubharmonic functions $\phi , \psi$ on X. One difficulty arises immediately if there are points on X where $\phi$ or $\psi$ are equal to $-\infty$. We thus define the unbounded locus of $\phi$, denoted $L(\phi )$ to be the set of points p for which $\phi$ is unbounded on any neighborhood of p. To define the product $i\partial {\bar{\partial }} \phi \wedge i \partial {\bar{\partial }} \psi$, we shall apply the following result.

Theorem 9.2

[25, Corollary 4.10] Suppose that the intersection $L(\phi ) \cap {\text {supp}}\partial {\bar{\partial }} \psi$ is a countable number of points of X, then the current $\phi i \partial {\bar{\partial }} \psi$ is well-defined and has locally finite mass. Moreover the measure $\partial \bar{\partial }( -\phi \partial \bar{\partial }\psi )$ is a well-defined positive measure and also has locally finite mass.

Theorem 9.3

[25, Proposition 4.6] Consider a plurisubharmonic function $\phi$ on X and a closed positive (1, 1) current T on X. Suppose that the intersection ${\text {supp}}(T) \cap L(\phi )$ is a countable union of points. Then for any compact set K, D in X such that $D \subset K^o$, there exists a neighborhood V of $K \cap L(\phi )$ and a constant $C=C(K,D, \phi )>0$ such that:

$$\begin{aligned} || \phi T||_{ D}\leqslant & {} C ||\phi ||_{ L^{\infty }(K\setminus V)} ||T||_K,\\ || i\partial {\bar{\partial }} (\phi T)||_{ D}\leqslant & {} C ||\phi ||_{ L^{\infty }(K\setminus V)} ||T||_K, \end{aligned}$$

where $|| \cdot ||_L$ denotes the mass of a given current on D.

One key feature of the intersection of currents is the stability by decreasing limit of plurisubharmonic functions.

Theorem 9.4

(See [25, Proposition 4.9]) Let $X = {\mathbb {P}}^1 \times {\mathbb {P}}^1$ or $X = {\mathbb {P}}^2$. Consider $\phi , \psi$ two plurisubharmonic functions such that $L(\phi ) \cap L(\psi )$ is a countable union of points. Then the current:

$$\begin{aligned} - \partial {\bar{\partial }} \phi \wedge \partial {\bar{\partial }} \psi := - \partial {\bar{\partial }} ( \phi \partial {\bar{\partial }} \psi ) \end{aligned}$$

(9.2)

is well defined, and if $\phi _n, \psi _n$ are plurisubharmonic functions decreasing to $\phi$ and $\psi$ respectively, then

$$\begin{aligned} \lim _n -\partial {\bar{\partial }} \phi _n \wedge \partial \bar{\partial }\psi _n = - \partial {\bar{\partial }} \phi \wedge \partial \bar{\partial }\psi . \end{aligned}$$

Remark 9.5

There is a more general version of Theorem 9.4, under the assumption that X is covered by Stein open sets $\Omega$ such that $L(\phi _n) \cap supp (dd^c \psi )$ does not intersect $\partial \Omega$.

As a consequence of the above theorem together with the fact that the pullback of plurisubharmonic functions by holomorphic maps remains plurisubharmonic, we get the following consequence.

Corollary 9.6

In the situation of the previous theorem and when $F :Y \rightarrow X$ is a dominant holomorphic map which does not contract any curve onto $L(\phi )\cap L(\psi )$, then the intersection:

$$\begin{aligned} - \partial {\bar{\partial }} (\phi \circ F) \wedge \partial \bar{\partial }(\psi \circ F), \end{aligned}$$

is a well-defined measure supported in the preimage by F of $L(\phi ) \cap L(\psi )$.

Proof

We deduce the result from the previous theorem, the relations $L(\phi \circ F) = F^{-1}L(\phi ), L(\psi \circ F) = F^{-1} L(\psi )$ and the fact that $L(\phi \circ F) \cap L(\psi \circ F)$ is a countable union of points. $\square$

1.2 Divisors, Line Bundles, and First Chern Class

We shall restrict our discussion to the case where X a smooth projective variety of complex dimension 1 or 2 (a curve or a surface). A divisor D on X is a finite linear combination with integer coefficients $a_i$ of irreducible hypersurfaces $D_i$ in X. We shall denote by:

$$\begin{aligned} D = \sum a_i [D_i]. \end{aligned}$$

If X is a smooth curve, then hypersurfaces are points so a divisor D is a linear combination of points. If X is a complex surface, then a divisor is a linear combination of algebraic curves.

Any divisor D on X induces a cohomology class in the deRham cohomology $H^{2}(X, {\mathbb {C}})$. For each i, the current of integration $[D_i]$ along the smooth locus of $D_i$ yields a d-closed current on X. Since $D_i$ is also a complex manifold, one can also integrate forms of bidegree $(\dim X-1, \dim X-1)$ so the current $[D_i]$ also defines an element of the dual of $H^{\dim X -1 , \dim X -1}(X , {\mathbb {C}})$. Hence $D_i$ induces a class in $H^{1,1}(X,{\mathbb {C}}) \subset H^2(X, {\mathbb {C}})$ by Poincaré duality.

We now explain the connection between line bundles and divisors on curves and surfaces. Given a divisor D on a curve or a surface X, there exists a line bundle $L_D$ which admits a meromorphic section whose divisor of poles and zeros gives D. Conversely, if L is a holomorphic line bundle, then the divisors of poles and zeros of one of its meromorphic section is a divisor on X which by definition represents the first Chern class of L, denoted $c_1(L)$.

1.3 Positivity of Divisors

In this section, we present the various notions of positivity for divisors on a curve or a surface. These notions from algebraic geometry refer to various cones one can consider in the cohomology of an algebraic variety.

Fix a divisor D given by:

$$\begin{aligned} D = \sum a_i D_i, \end{aligned}$$

where $a_i$ are integers and $D_i$ are irreducible hypersurfaces on X.

When all the coefficients $a_i$ are non-negative, one says that D is effective and it is one notion of positivity. The other notions we will use are ampleness and nefness and are related to the intersection product of divisors on surfaces.

Suppose now that X is a surface and take two distinct irreducible curves $D_1$ and $D_2$ on X. If p belongs to the intersection of these two curves, write $f =0 , g=0$ the local equation of $D_1$ and $D_2$ near p and denote by ${\mathcal {O}}_p$ the local ring of holomorphic functions on X near p, then we define the multiplicity of the intersection at p⁸ to be:

$$\begin{aligned} m_p(D_1,D_2):= \dim _{\mathbb {C}}{\mathcal {O}}_p/\langle f,g\rangle \geqslant 0 , \end{aligned}$$

where $\langle f,g\rangle$ denotes the ideal generated by f and g. The intersection of the two divisors $D_1$ and $D_2$, denoted $D_1\cdot D_2$ is by definition the linear combination of points given by:

$$\begin{aligned} D_1 \cdot D_2 = \sum _{p\in D_1 \cap D_2} m_p(D_1, D_2) [p]. \end{aligned}$$

We extend this intersection to linear combination of irreducible curves by linearity and obtain a pairing on divisors. If we sum the contributions of all the multiplicities, we obtain a number called the degree of the intersection, which is denoted $(D_1 \cdot D_2)$:

$$\begin{aligned} (D_1 \cdot D_2) = \sum _{p\in D_1 \cap D_2} m_p(D_1, D_2) \in {\mathbb {Z}}. \end{aligned}$$

We define nefness and ampleness in our setting using Kleiman’s criterion [72, Theorem 1.2.23, Theorem 1.4.9].

A divisor $D= \sum a_i [p_i]$ on a curve X is ample if its degree $\sum a_i$ is positive and it is nef if $\sum a_i$ is non-negative.

A divisor D on a surface X is very ample if the mapping $\phi _D: X \dashrightarrow {\mathbb {P}}(H^0(X, {\mathcal {O}}(D))^*)$ induced by its section is an embedding (see [72, Definition 1.2.1]). A divisor D is ample if for any curve C on X, the intersection $(D\cdot C)$ is positive and it is nef if the intersection $(D\cdot C)$ is non-negative.

Similarly, one says that a line bundle is nef (resp. ample) if it has a meromorphic section whose divisor of poles and zeros is nef (resp. ample).

1.4 Rational Maps

Take two smooth projective surfaces X and Y. Fix two non-empty Zariski open subset U, V of X and Y respectively and take a map $f_U :U \rightarrow V$ given by polynomials in some affine coordinate chart of X, Y. We say that the triple $(U,V,f_U)$ defines a rational map f , and we denote it by $f :X \dashrightarrow Y$. Observe that this definition seems quite loose since one can always restrict $f_U$ to another Zariski open subset contained in U. In any case, the Zariski (or Hausdorff) closure in $X\times Y$ of the graph of $f_U$ does not depend on the choice of the two Zariski open subsets U, V, we call this set the graph of the rational map  f.

When $U=X$, the rational map f is said to be regular.

A rational map $f :X\dashrightarrow Y$ is called birational if the map $f_U :U \rightarrow V$ has an inverse $f^{-1}_V :V \rightarrow U$ defined by polynomials in some affine coordinates. This inverse then induces a rational map $f^{-1}:Y \dashrightarrow X$.

The main advantage of this formulation is that for any rational transformation $f:X \dashrightarrow X$, one can always consider the conjugation $\varphi \circ f \circ \varphi ^{-1}$ where $\varphi :X \dashrightarrow X'$ is a birational map between smooth projective surfaces. Indeed, if $f_U :U \rightarrow V$ is the map associated to f on two Zariski open subsets U, V of X, we choose also two Zariski open subset $U',V'$ of X and a map $\varphi :U' \subset X \rightarrow V' \subset X'$ corresponding to the birational transformation $\varphi$. We consider the map:

$$\begin{aligned} \varphi \circ f_U \circ \varphi ^{-1} :\varphi (U \cap f_U^{-1} (U')) \rightarrow V' , \end{aligned}$$

and this determines a rational map which we denote by $\varphi \circ f \circ \varphi ^{-1}$. In particular, one can lift rational maps on ${\mathbb {P}}^2$ to rational maps on a blow-up of ${\mathbb {P}}^2$.

1.5 Pullback and Pushforward of Divisors

We recall general facts on pullback and pushforward of divisors.

Pushforward by regular maps: Take a regular map $f :X \rightarrow Y$ of smooth surfaces. If C is an irreducible curve in X, the pushforward of the divisor [C] by f, denoted $f_* [C]$ is given by the formula:

$$\begin{aligned} f_* [C] = \left\{ \begin{array}{ll} m [f(C)] \text { if }f(C) \text { is a curve}, \\ 0 \text { if }f(C) \text { is a point}, \end{array} \right. \end{aligned}$$

(9.3)

where $m \in {\mathbb {N}}$ is the topological degree of the restriction of f to C onto its image. We shall refer to m as the multiplicity of the divisor [f(C)]. The pushforward is then defined by extending linearly $f_*$ to the abelian group of divisors on X.

Pullback by regular maps: Take a regular map $f:X\rightarrow Y$ between two smooth projective varieties and take an irreducible hypersurface D on Y. Write a local equation $g=0$ of D near some point $p\in D$, write

$$\begin{aligned} g \circ f = \prod _j g_j^{a_j}, \end{aligned}$$

where $a_j$ are integers and $g_j$ are local holomorphic functions on X vanishing on an irreducible hypersurface $D_j$. Then the pullback of the divisor D by f, denoted $f^* D$ is the divisor given by:

$$\begin{aligned} f^* D := \sum a_i [D_i]. \end{aligned}$$

For a more abstract definition of the pullback, we shall refer to [72].

We now explain the general convention for the pullback and pushforward for rational maps.

Pullback and pushforward for rational maps: Take a rational map $f :X \dashrightarrow Y$ between smooth surfaces, we take the desingularization $\Gamma$ of the graph of f in $X\times Y$ (defined in the previous section) and denote by $\pi _1,\pi _2$ the two projections from $\Gamma$ onto the first and second component respectively. We thus obtain the following commutative diagram:

The pullback and pushforward of a divisor $D_Y$ on Y and of a divisor $D_X$ on X respectively, denoted $f^* D_Y$ and $f_* D_X$ are defined formally as:

$$\begin{aligned} f^* D_Y&:={\pi _1}_* \pi _2^* D_Y,\\ f_* D_X&:= {\pi _2}_*\pi _1^* D_X. \end{aligned}$$

The pullback and pushforward action on divisors induce morphisms in the (1, 1) cohomology:

$$\begin{aligned}{} & {} f_* :H^{1,1}(X) \rightarrow H^{1,1}(Y),\\{} & {} f^* :H^{1,1}(Y) \rightarrow H^{1,1}(X). \end{aligned}$$

One concept we will often use is the notion of strict transform. The strict transform of a curve C in X by f, denoted $f^o(C)$ is by definition the closure

$$\begin{aligned} \overline{f (C\setminus I(f))}, \end{aligned}$$

where I(f) denotes the indeterminacy set of f.

In practice, computing the pullback and pushforward action in cohomology can be done geometrically for classes represented by ample divisors. The method is to choose a representative in good position to simplify the computations. Indeed, if the divisor $D_X$ does not contain any indeterminacy point of f, then its pullback by $\pi _1$ is the preimage of $D_X$ by $\pi _1$ and $f_* D_X$ is the strict transform of $D_X$ by f:

$$\begin{aligned} f_* D_X = [\overline{f(D_X)}]. \end{aligned}$$

When $D_X$ is an ample divisor which passes through an indeterminacy point of f, we can choose another divisor $D'_X$ representing the same class as $D_X$ in $H^{1,1}(X)$ which does not contain any indeterminacy point and determine the strict transform of $D_X'$ by f. However, the difficulty arises when one wants to compute the pullback or the pushforward of a class of a divisor which is not ample, in this case, one needs to compute explicitly the pullback by $\pi _1$ and the pushforward by $\pi _2$ associated with f.

1.6 Canonical Divisor

One divisor of particular interest in the paper is the canonical divisor. We give its definition below. Take a smooth projective curve or a smooth projective surface X and fix $\omega$ a meromorphic 1-form if X is a curve or a meromorphic 2 form if X is a surface. The canonical divisor, denoted $K_X$, is by definition the divisor of poles and zeros of the form $\omega$.

Example 9.7

When $X = {\mathbb {P}}^1$, the form $\omega = dz$ in ${\mathbb {C}}\subset {\mathbb {P}}^1$, and at infinity $\omega$ has a pole of order 2, i.e $\omega$ is of the form $- (1/z'^2)d z'$ where $z' = 1/z$. In particular, we have:

$$\begin{aligned} K_{{\mathbb {P}}^1} = - 2 [\infty ]. \end{aligned}$$

When $X = {\mathbb {P}}^2$, the form $\omega ={\text {d}}x \wedge {\text {d}}y$ in the affine coordinates $[x;y;1] \in {\mathbb {P}}^2$ has a pole of order 3 on the line at infinity. So we have:

$$\begin{aligned} K_{{\mathbb {P}}^2} = - 3 L, \end{aligned}$$

where L is the line at infinity.

1.7 Blowing Up and Down

Let Y be a smooth projective surface and fix a point p in Y. As a set, the blow-up X of Y at the point p is obtained by replacing p with the projective tangent bundle at p:

$$\begin{aligned} X := Y \setminus \{p \}\cup {\mathbb {P}}(T_p Y). \end{aligned}$$

Since p is the smooth point, the tangent space at p is naturally identified to $\{p\} \times {\mathbb {C}}^2$ and since ${\mathbb {P}}({\mathbb {C}}^2) = {\mathbb {P}}^1$, the space X is obtained from Y by adding a ${\mathbb {P}}^1$ corresponding to the tangent directions at p. The subset $E:= {\mathbb {P}}^1 = {\mathbb {P}}(T_p Y)$ is called the exceptional divisor of the blow-up of Y at p. By construction, the spaces $X\setminus E$ and $Y\setminus \{ p \}$ are biholomorphic. The set X has a natural complex structure induced by Y so X is also a smooth projective surface and there is a natural holomorphic map $\pi :X \rightarrow Y$ which collapses E to p and is a biholomorphism from $X\setminus E$ to $Y \setminus \{p\}$. This map $\pi$ is called the blow-down map.

When one works with blow-ups, one common fact is to relate the strict transform with the full preimage by $\pi$. Take a curve C in Y, the strict transform of C is given by:

$$\begin{aligned} \overline{\pi ^{-1}(C \setminus \{p \})}. \end{aligned}$$

One sees that if p belongs to C, then the preimage of $\pi ^{-1}(C)$ is the union of the strict transform of C with the exceptional divisor, whereas $\pi ^{-1}(C)$ is equal to the strict transform of C when the curve C does not pass through p.

Since we will be blowing-up points and compute explicitly the images of exceptional divisors by rational transformations, let us explain how one proceeds in local coordinates. Observe first that blowing up is a local operation as one only modifies the variety near the point p. Let us identify a neighborhood of p as ${\mathbb {C}}^2$ with holomorphic coordinates (x, y) so that p is identified with $(x=0,y=0)$. The set of complex lines passing through (0, 0) are of the form:

$$\begin{aligned} -\lambda x + \mu y =0, \end{aligned}$$

where $[\lambda ; \mu ] \in {\mathbb {P}}^1$. The blow-up X of ${\mathbb {C}}^2$ at (0, 0) is given in coordinates by:

$$\begin{aligned} \{ ((x,y) , [\lambda ; \mu ]) \in {\mathbb {C}}^2 \times {\mathbb {P}}^1 | -\lambda x + \mu y =0 \} \subset {\mathbb {C}}^2 \times {\mathbb {P}}^1. \end{aligned}$$

This is the intrinsic definition of the blow-up, but to write the blow-down map f, one needs to write in the two charts on ${\mathbb {P}}^1$, corresponding to the parametrization of non-horizontal lines and non-vertical lines, we obtain:

$$\begin{aligned} (x,\lambda )\in {\mathbb {C}}^2 \mapsto ((x, \lambda x) , [\lambda ; 1]) \in X \mapsto (x, y= \lambda x) \in Y, \end{aligned}$$

where the exceptional divisor $f^{-1}(0,0)$ has local equation $x=0$ and the second chart is given by:

$$\begin{aligned} (y, \mu ) \in {\mathbb {C}}^2 \mapsto ((\mu y,y) , [1 ; \mu ]) \in X \mapsto (x= \mu y , y ) \in Y, \end{aligned}$$

where $y=0$ is the local equation of the exceptional divisor.

Example 9.8

If C is the curve $P(x,y)=y - x^2=0$, we can compute the local equations of the strict transform $\tilde{C}$ of C on the blow-up of (0, 0). Observe that the tangent line to C at (0, 0) is horizontal. We thus choose the parametrization of non-vertical curves $(x , \lambda ) \mapsto (x, \lambda x), [\lambda , 1]$ on the blow-up: The equations of $f^{-1}( C \setminus \{ (0,0)\})$ are of the form:

$$\begin{aligned} P\circ f:(x, \lambda ) \in {\mathbb {C}}^* \times {\mathbb {C}}\mapsto \lambda x - x^2 = x( \lambda - x). \end{aligned}$$

Since the local equations of E is $x=0$ but $x\ne 0$, we deduce that the local equation of the strict transform is $\lambda - x$. The intersection of $\tilde{C}$ with the exceptional divisor E is transverse at $(x=0,\lambda =0)$, and this comes from the fact that the tangent line to C at (0, 0) is horizontal.

Let us now discuss the cohomology of the blow-up at one point. The cohomology of X can be split into two parts:

$$\begin{aligned} H^{1,1}(X) = \pi ^* H^{1,1}(Y) \oplus {\mathbb {C}}E. \end{aligned}$$

In practice, one decomposes divisors on X as a sum of strict transform of divisors on Y with a multiple of E (see [43, p.475]).

One crucial fact is that the intersection product on X can be deduced from the intersection product on Y together with the fundamental equality (see [43, p. 475]):

$$\begin{aligned} (E \cdot E) = -1. \end{aligned}$$

The intersection of a strict transform of a curve with the exceptional divisor can be deduced geometrically or in coordinates. For the self-intersection of a strict transform of a curve, one uses the following statement.

Proposition 9.9

If Xis the blow-up of Y at a point p. If p is a smooth point on a curve C in Y, then the strict transform $\tilde{C}$ satisfies:

$$\begin{aligned} (\tilde{C} \cdot \tilde{C}) = (C\cdot C) - 1. \end{aligned}$$

Example 9.10

Take a line L in ${\mathbb {P}}^2$ and a point p on L. Let X be the blow-up of ${\mathbb {P}}^2$ at p and denote by $\pi :X \rightarrow {\mathbb {P}}^2$ the blow-down map, E the exceptional divisor $\pi ^{-1}(p)$. Then:

$$\begin{aligned} \pi ^* L = \tilde{L} + E, \end{aligned}$$

where $\tilde{L}$ is the strict transform of the line at infinity by $\pi$. Moreover, we have:

$$\begin{aligned} (\tilde{L}\cdot E) =1 , (E\cdot E) = -1, (\tilde{L} \cdot \tilde{L}) = 0. \end{aligned}$$

Example 9.11

If X is the blow-up of ${\mathbb {P}}^2$ at a point on the line at infinity and $\pi :X \rightarrow {\mathbb {P}}^2$ is the blow-down map, then

$$\begin{aligned} K_X= \pi ^* K_{{\mathbb {P}}^2} + E = - 3 (\tilde{L} + E) + E = - 3 \tilde{L} -2E, \end{aligned}$$

where $\tilde{L}$ is the strict transform of the line at infinity.

We now summarize the formula involving pullback and pushforward of divisors under blow-ups and blow-down and general maps in the following proposition.

Proposition 9.12

Let $f :X \rightarrow Y$ be a regular map of smooth surfaces.

• (i) [39, Proposition 2.3 (c)] Fix D a divisor on Y, $D'$ a divisor on X, one has:

  $$\begin{aligned} (f^* D \cdot D') = (D \cdot f_* D') \end{aligned}$$

• (ii) [72, Remark 1.1.13] Take two divisors $D,D'$ on Y, then one has:

  $$\begin{aligned} (f^* D \cdot f^* D') = d (D \cdot D'), \end{aligned}$$

  where d is the topological degree of f.

• (iii) Take a divisor D on Y. One has $f_* f^* D = d D \in H^{1,1}(Y)$, where d is the topological degree of f.

• (iv) [65, Proposition 2.5.5] Suppose that X is the blow-up at one point of Y and that $\pi$ is the map blowing down the exceptional divisor E to that point, then one has in $H^{1,1}(X)$:

  $$\begin{aligned} K_X = \pi ^* K_Y + E . \end{aligned}$$

• (v) [43, Formula p.475] If X is the blow-up of Y at one point p and $\pi :X \rightarrow Y$ is the blow-down map. Fix an irreducible curve C on Y and consider the local equation $f=0$ defining C near p. The pullback $\pi ^* C$ is equal to:

  $$\begin{aligned} \pi ^* C = \pi ^{o}(C) + {{\,\textrm{ord}\,}}_p(f) E, \end{aligned}$$

  where E is the exceptional divisor above p, $\pi ^o(C)$ is the strict transform of C by $\pi$ and where ${{\,\textrm{ord}\,}}_p(f)$ is the order of vanishing of the function f at the point p.

Proof

We only need to prove (iii), which is a consequence of (i) and (ii). Indeed, take $D,D'$ two divisors on Y, we have using (i):

$$\begin{aligned} (f_* f^* D \cdot D') = (f^* D \cdot f^* D'). \end{aligned}$$

By assertion (ii), we obtain:

$$\begin{aligned} (f_* f^* D \cdot D' ) = d (D \cdot D'), \end{aligned}$$

for all divisors $D'$ on Y. Using the fact the the intersection product is non-degenerate in $H^{1,1}(Y)$, we have proved that $f_* f^* D = d D$. $\square$