Abstract
To discuss the validity of the Kummer–Vandiver conjecture, we consider a generalized problem associated to the conjecture. Let p be an odd prime number and \(\zeta _p\) a primitive p-th root of unity. Using new programs, we compute the Iwasawa invariants of \({\textbf{Q}}(\sqrt{d},\zeta _p)\) in the range \(|d|<200\) and \(200<p <1{,}000{,}000\). From our data, the actual numbers of exceptional cases seem to be near the expected numbers for \(p<1{,}000{,}000\). Moreover, we find a few rare exceptional cases for \(|d|<10\) and \(p>1{,}000{,}000\). We give two partial reasons why it is difficult to find exceptional cases for \(d=1\) including counter-examples to the Kummer–Vandiver conjecture.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let p be an odd prime number and K a finite extension of \({\textbf{Q}}\). \(K_\infty \) denotes the cyclotomic \({\textbf{Z}}_p\)-extension of K. Let \(K_n\) be its n-th layer and \(A_n=A_n(K)\) the p-part of the ideal class group of \(K_n\).
First, let K be the p-cyclotomic field \({\textbf{Q}}(\zeta _p)\), then \(K_n={\textbf{Q}}(\zeta _{p^{n+1}})\). Let \(\omega =\omega _p\) be the Teichmüller character \(({\textbf{Z}}/p {\textbf{Z}})^\times \rightarrow {\textbf{Z}}_p\) such that \(\omega (a)\equiv a \mathrm{\;mod }p\). We identify \(\Delta =\textrm{Gal}(K_\infty /{\textbf{Q}}_\infty )\) with \(({\textbf{Z}}/p {\textbf{Z}})^\times \). Put \( e_{\omega ^k}=\frac{1}{\sharp \Delta } \sum _{\delta \in \Delta } \omega ^k(\delta )\delta ^{-1} \) the idempotent of the group ring \({\textbf{Q}}_p[\Delta ]\). Then we have
where k is an even integer with \(2 \le k \le p-1\). Let \(A_n^+\) (resp. \(A_n^-\)) be the even part (resp. odd part). Let \(r_p\) be the irregularity index, i.e., the number of irregular pairs (p, k). Irregular pairs have been computed by Kummer, Vandiver, D.H. Lehmer, E. Lehmer, Selfridge, Nicol, Pollack, Johnson, Wada, Wagstaff, Tanner, Ernvall, Metsänkylä, Buhler, Crandall, Sompolski, Shokrollahi, Hart, Harvey and Ong. These computations had been connected with verification of Fermat’s last theorem. However, even after the proof was completed by Wiles, they are still interesting because they give us concrete knowledge of the ideal class group of cyclotomic fields. In [1, 2, 5] etc., for any prime number \(p<2^{31}=2{,}147{,}483{,}648\), it has been verified that
The former statement is called the Kummer–Vandiver conjecture. We have a naive explanation of the fact that we have not been able to find any counter-example. If we follow the heuristic argument of [15, pp.158–159], we can expect that the number of exceptions to the Kummer–Vandiver conjecture for \(x_0 \le p \le x_1\) is approximately \((\log \log x_1-\log \log x_0)/2\). Then, \((\log \log 2^{31}-\log \log 37)/2= 0.891756\cdots \) is probably too small to find one counter-example, where 37 is the smallest irregular prime number. Furthermore, the expected number would not be exact, because there are some effects on ideal class groups from an upper bound for the numerator of the Bernoulli number or the K-groups (cf. [10]). If there are another strong effects, the actual number could be much less than the above number. To study the heuristic, we consider the following generalized problem.
Problem 1.1
Let F be an abelian extension of \({\textbf{Q}}\). Let \(N_F(x)\) be the number of prime numbers p such that \(A_0(F(\zeta _p)^+) \ne \{0\}\) for \(p \le x\), where \(F(\zeta _p)^+\) is the maximal real subfield of \(F(\zeta _p)\). Is \(N_F(x)\) bounded as \(x \rightarrow \infty \)? If it is not so, give an approximate function for \(N_F(x)\).
The Kummer–Vandiver conjecture claims that \(N_{{\textbf{Q}}}(x)=0\) for all x, which is much stronger than its boundedness.
In this paper, following [11,12,13,14], we study the above problem when F is \({\textbf{Q}}\) or a quadratic field, because they are easy to be compared. Let \(\chi \) be the Dirichlet character associated to F and \(f_\chi \) its conductor. The main purpose of the paper is to find exceptional cases associated to the \(\chi \omega ^k\)-part to argue about the expected number. We actually computed the Iwasawa invariants of \({\textbf{Q}}(\sqrt{d}, \zeta _p)\) in the range \(|d| <200\) and \(200< p <1{,}000{,}000\) by using new programs, where \(d=d_\chi =\chi (-1) f_\chi \). From our data, the actual number seems to be near the expected number in the range. Moreover, we found a few rare exceptional cases for \(|d|<10\) and \(1{,}000{,}000<p<20{,}000{,}000\).
Our main computations are executed in \(O((f_\chi p)^{1+\epsilon })\) bit operations. See [12, 14] on the relation between these Iwasawa invariants and the higher K-groups of the integer ring of \({\textbf{Q}}(\sqrt{d})\).
2 Iwasawa Invariants of \({\textbf{Q}}(\sqrt{d},\zeta _p)\)
Let \(\chi \) be the trivial character or a quadratic Dirichlet character conductor \(f=f_\chi \) and p an odd prime number such that p does not divide f. Put \(d=d_\chi =\chi (-1)f_\chi \), \(K={\textbf{Q}}(\sqrt{d_\chi },\zeta _{p})\), then \(K_n={\textbf{Q}}(\sqrt{d_\chi },\zeta _{p^{n+1}})\). Let \(A_n\) be the p-part of the ideal class group of \(K_n\).
Put \(\Gamma =\textrm{Gal}(K_\infty /K)\), \(\Delta =\textrm{Gal}(K_\infty /{\textbf{Q}}_\infty )\simeq \textrm{Gal}(K_0/{\textbf{Q}})\) and \(e_{\psi }=\frac{1}{\sharp \Delta } \sum _{\delta \in \Delta } \psi (\delta )\delta ^{-1}\) for a character \(\psi \) of \(\Delta \). We put \(f_0=fp\) and identify \(\Delta \) with a subquotient of \(({\textbf{Z}}/ f_0 {\textbf{Z}})^\times \) in the ordinary way. For a \({\textbf{Z}}_p[\Delta ]\)-module A, \(A^\psi \) denotes \(e_\psi A\). Let \(\lambda _p(\psi )\), \(\mu _p(\psi )\) and \(\nu _p(\psi )\) be the Iwasawa invariants associated to \(A_n^{\psi }\), i.e.,
for sufficiently large n. By Ferrero-Washington’s theorem, we have \(\mu _p(\psi )=0\) for all p and \(\psi \).
Assume that \(\psi \) is even. The Iwasawa polynomial \(g_{\psi }(T) \in {\textbf{Z}}_p[T]\) for the p-adic L-function is defined as follows. Let \(L_p(s,\psi )\) be the p-adic L-function constructed by [8]. By [7, §6], there uniquely exists \(G_{\psi }(T) \in {\textbf{Z}}_p[[T]]\) satisfying \( G_{{\psi }}((1+f_0)^{1-s}-1)=L_p(s,{\psi }) \) for all \(s \in {\textbf{Z}}_p\) if \(\psi \ne \chi ^0\). By [3], p does not divide \(G_{\psi }(T)\). By the p-adic Weierstrass preparation theorem, we can uniquely write \(G_{\psi }(T)=g_{\psi }(T)u_{\psi }(T)\), where \(g_{\psi }(T)\) is a distinguished polynomial of \({\textbf{Z}}_p[T]\) and \(u_{\psi }(T)\) is an invertible element of \({\textbf{Z}}_p[[T]]\). Similarly we can define \(g^*_\psi (T) \in {\textbf{Z}}_p[T]\) from \(G^*_{\psi }(T) \in {\textbf{Z}}_p[[T]]\) satisfying \( G^*_{\psi }((1+f_0)^{s}-1)=L_p(s,{\psi }). \) Put
Put \(f_n=f_0 p^n\) and let \(\gamma \in \Gamma \simeq \textrm{Gal}(\cup _{n \ge 0} {\textbf{Q}}(\zeta _{f_n})/{\textbf{Q}}(\zeta _{f_0})) \) be the generator of \(\Gamma \) such that \(\zeta _{f_n}^{{\tilde{\gamma }}}=\zeta _{f_n}^{1+f_0}\) for all \(n \ge 0\). As usual, we can identify the complete group ring \({\textbf{Z}}_p[[\Gamma ]]\) with the formal power series ring \(\varLambda ={\textbf{Z}}_p[[T]]\) by \(\gamma =1+T\). By this identification, we can consider a \({\textbf{Z}}_p[[\Gamma ]]\)-module as a \(\varLambda \)-module. For a finitely generated torsion \(\varLambda \)-module A, we define the Iwasawa polynomial \(\hbox {char}_\varLambda (A)\) to be the characteristic polynomial of the action T on \(A \otimes {\textbf{Q}}_p\) (cf. [15, §13]). Let \(L_n\) be the maximal unramified abelian extension of \(K_n\) and \(M_n\) the maximal abelian extension of \(K_n\) unramified outside p. By the class field theory, we have \( A_n \simeq \textrm{Gal}(L_n/K_n). \) Set \(L_\infty =\cup _{n\ge 0} L_n\), \(M_\infty =\cup _{n\ge 0} M_n\), \(X_\infty =\textrm{Gal}(L_\infty /K_\infty )\) and \(Y_\infty =\textrm{Gal}(M_\infty /K_\infty )\). By the Iwasawa main conjecture proved by [4, 9], \( \hbox {char}_\varLambda (X_\infty ^{\psi ^{-1}\omega })=g_{\psi }^*(T)\quad \textrm{and }\quad \hbox {char}_\varLambda (Y_\infty ^{\psi })=g_{\psi }(T). \)
In the following, we assume that
with \(2 \le k \le p-2\). Since p does not divide f,
By (C), we have that \(A_n^\psi \simeq X_\infty ^\psi /\omega _n X_\infty ^\psi \) and \(A_n^{\psi ^*} \simeq X_\infty ^{\psi ^*}/\omega _n X_\infty ^{\psi ^*}\), where \(\omega _n=(1+T)^{p^n}-1\) (cf. [6, Lemma 3 and Remark 4]). Moreover, if \(A_0^\psi \) is trivial, we have \(\lambda (\psi )=\nu (\psi )=0\), \( X_\infty ^\psi =\{0\}, \quad Y_\infty ^\psi \simeq \varLambda /(g_\psi (T)) \quad \textrm{and }\quad X_\infty ^{\psi ^*} \simeq \varLambda /(g^*_\psi (T)). \) Put \( a_0=a_0(\psi )=L_p(1,\psi )=G_{\psi }(0)\quad \textrm{and } \quad b_0=b_0(\psi )=L_p(0,\psi )=G_{\psi }^*(0). \) Note that \(v_p(a_0)=v_p(\sharp \textrm{Gal}(M_0/K_0)^\psi )\) and \(v_p(b_0)=v_p(\sharp \textrm{Gal}(L_0/K_0)^{\psi ^*})\).
We call \((p,\chi \omega ^k)\) exceptional pairs when one of the following conditions holds: \([\nu ]:\) \(\nu (\chi \omega ^k)>0\), \([a_0]:\) \(v_p(a_0)>1\), \([b_0]:\) \(v_p(b_0)>1\) or [lmd]: \( {\tilde{\lambda }}(\chi \omega ^k)>1\). In [11,12,13,14], we computed exceptional pairs for \(|d|<200\) and \(p<200{,}000\). By further computation, we obtain the following.
Proposition 2.1
For \(|d|<200\) and \(200{,}000<p<1{,}000{,}000\), all exceptional pairs \((p,\chi \omega ^k)\) are given in Table 1.
To study Problem 1.1 efficiently, we consider the following problem.
Problem 2.1
Let X be a set of primitive Dirichlet characters. Let \(N^{[\nu ]}_{X,x_0}(x)\) be the number of pairs \((p, \chi \omega ^k)\) such that \(\nu (\chi \omega ^k)>0\) for \(\chi \in X\) in the range \(x_0 \le p \le x\). We similarly define \(N^{[a_0]}_{X,x_0}(x)\), \(N^{[b_0]}_{X,x_0}(x)\) and \(N^{[lmd]}_{X,x_0}(x)\). Are they bounded as \(x \rightarrow \infty \)? If they are not so, give approximate functions for them.
In [13], when X is a set of the trivial character or quadratic characters, we give a candidate of approximate functions:
which comes from a heuristic argument similar to that of [15, pp.158–159]. In Fig. 1, we compare actual numbers of exceptional pairs in the range \(f_\chi <200\) and \(200< p \le x\) with the expected number E(x) (\(x_0=200\) and \(\sharp X=123\)). From our data, actual numbers still seem to be near the expected number.
For \(|d|<10\), we obtain the following by further computation.
Proposition 2.2
For \(|d|<10\) and \(10<p<20{,}000{,}000\), all exceptional pairs \((p,\chi \omega ^k)\) are given in Table 2.
Remark 2.1
In [14, Proposition 2], we reported that there is only one exceptional pair \((399181,\chi _{-4} \omega ^{1683})\) in the range \(|d|<10\) and \(200{,}000<p <1{,}000{,}000\), which is included in [lmd] by mistake.
3 A Conjecture on the Number of Exceptional Pairs
We give two partial reasons why it is difficult to find exceptional pairs for \(\chi =\chi ^0\), i.e., \(d=1\). The first partial reason is the fact that the expected number for \(\chi ^0\) is smaller than those for the other characters. Let \(r_{p,\chi }\) be the number of pairs \((p,\chi \omega ^k)\) such that \({\tilde{\lambda }}_p(\chi \omega ^k)>0\). Then we have \(0 \le r_{p,\chi } \le (p-3)/2\). The distribution of the number of p such that \(r_{p,\chi }=r\) for each \(\chi \) in the range \(200<p<20{,}000{,}000\) is similar to that for \(\chi ^0\). However, the distribution for \(\chi \) in the range \(10< p< 200\) is not always similar to that for \(\chi ^0\), which affects expected numbers. For each \(\chi \), put \(E_\chi (x)=\sum _{10 < p \le x, \; p\mathrm{:prime}} \frac{\,r_{p,\chi }\,}{p}\). The following table and figures show differences among \(E_\chi (x)\)s.
In Figs. 2 and 3, we compare \(E_\chi (x)\)s with \(E'(x)={\sum _{37 \le p \le x} \frac{p-3}{2p^2}}\) and \(E''(x)={\sum _{37 \le p \le x} \frac{p-17}{2p^2}}\), where \(E''(x)\) is defined by considering trivialities of \(K_4({\textbf{Z}})\) and numerators of Bernoulli numbers \(B_{2i}\) for \(i=\)1–5 and 7 (see [11, §4.2]).
Table 4 shows the total number \(N_d\) of exceptional pairs in \(200<p<1{,}000{,}000\) for each d, the distribution (\(\%\)) and a Poisson distribution with \(\lambda =4 \sum _{200<p<1{,}000{,}000} \frac{p-3}{2p^2}= 1.8721\cdots \). Since there are 23 d’s with \(N_d=0\) among 123 d’s, it is not very unusual that \(N_1=0\). This is the second partial reason.
From our data and computational results on p-adic L-functions, it is natural to consider the following conjecture.
Conjecture 3.1
Let X be a set of primitive Dirichlet characters. For \(\chi \in X\), let \(n_\chi \) be the order of \(\chi \), \({\mathcal {O}}_{p, \chi }\) the integer ring of \({\textbf{Q}}_p(\zeta _{n_\chi })\), and \({\mathfrak {m}}_{p,\chi }\) the maximal ideal of \({\mathcal {O}}_{p, \chi }\). For a sufficiently large number \(x_0\), an approximate function of \(N^{[\nu ]}_{X, x_0}(x)\), \(N^{[a_0]}_{X, x_0}(x)\), \(N^{[b_0]}_{X, x_0}(x)\) and \(N^{[lmd]}_{X,x_0}(x)\) is given by the sum of
over \(\chi \in X\), where \(p^{f_{p,\chi }}=\sharp ({\mathcal {O}}_{p,\chi }/{\mathfrak {m}}_{p,\chi }) \ge p^2\).
Remark 3.1
By replacing \({\textbf{Z}}_p\) by \({\mathcal {O}}_{p, \chi }\), we can define \(N^{[\nu ]}_{X, x_0}(x)\), ...and \(N^{[lmd]}_{X,x_0}(x)\). If \(\chi \) is not the trivial character nor a quadratic character, then \(\varphi (n_\chi ) \ge 2\) and the expected number is clearly smaller than \(\sum _{x_0 \le p \le x} \frac{p-3}{2p^2}\). This is a reason why we first study characters with \(n_\chi \le 2\).
4 Computations of Arithmetic Elements
To study Iwasawa invariants, we compute the following arithmetic elements (see [12, §5]):
-
(I)
the generalized Bernoulli numbers modulo p, i.e., \(\sum _{k=0}^{p-3} B_{k,\chi }t^k/k! \mathrm{\;mod }p\),
-
(II)
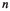 the Iwasawa polynomial \(g_{\chi \omega ^k}(T) \mod p^{n+1}\),
the Iwasawa polynomial \(g_{\chi \omega ^k}(T) \mod p^{n+1}\), -
(III)
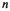 the special cyclotomic unit \((c_n^{\chi \omega ^k})^{Y_n(T)}\) modulo a prime ideal \({\mathfrak {L}}_n\),
the special cyclotomic unit \((c_n^{\chi \omega ^k})^{Y_n(T)}\) modulo a prime ideal \({\mathfrak {L}}_n\), -
(IV)
 the Gauss sum \(g_0(N_{K_n/K_0}{\mathfrak {L}}_n)^{\chi \omega ^{p-k}}\) modulo a prime ideal \({\mathfrak {L}}_0^*\), where \({\mathfrak {L}}_n\) (resp. \({\mathfrak {L}}_n^*\)) is a prime ideal above \(l=1+\kappa f_n\) (resp. \(l^*=1+\kappa ^*(2 f_n l)\)) of \(K_n\).
the Gauss sum \(g_0(N_{K_n/K_0}{\mathfrak {L}}_n)^{\chi \omega ^{p-k}}\) modulo a prime ideal \({\mathfrak {L}}_0^*\), where \({\mathfrak {L}}_n\) (resp. \({\mathfrak {L}}_n^*\)) is a prime ideal above \(l=1+\kappa f_n\) (resp. \(l^*=1+\kappa ^*(2 f_n l)\)) of \(K_n\).
From 2002 to 2007, we used 32-bit programs (bcn.c for even \(\chi \)’s and bcm.c for odd ones) for computations of (I), (II)\(_1\) and (III)\(_0\) in [11,12,13,14]. These programs work when \(f_0\) and \(8 (p-3) \log _{16}(2p^3)\) are smaller than \(2^{31}\). Therefore, for \(f=1\) (resp. 199), they do not work when \(p>15{,}000{,}000\) (resp. 11,000,000). Since 2015, inspired by [2], we have used 64-bit programs (bcn64.c and bcm64.c), which work when p is smaller than 162 million. Further, the program is available to check Greenberg’s conjecture by computing (III)\(_1\). However, since it needs \(O(f_1^{1+\epsilon })\) bit operations, we did not check it for \(p>100{,}000\) except for \((p,k,d)=(157229{,}140434{,}8)\).
Computation of (IV)\(_0\) rigorously proves that the cyclotomic unit \(c_0^{\chi \omega ^k}\) is a p-th power element in \(K_0\), i.e., \(\nu _p(\chi \omega ^k)>0\). From 2002 to 2007, we used 32-bit programs (gauss.c for small \(f_0\)’s and gaussd.c for large ones) for computation of (IV)\(_0\), which work when 2l is smaller that \(2^{31}\). Therefore, for \(f=1\) (resp. 199), they do not work when \(p>11{,}000{,}000/\kappa \) (resp. \(550{,}000/\kappa \)) with \(\kappa =\)2–24. To reduce memory usage, we use HDD and several auxiliary primes \(l_i \approx 1000\) in gaussd.c, which slows down the computation. Since 2020, we have been used 64-bit programs (gauss64.c and gaussd64.c), which work when \(2\,l\) and \(8f_0 \log _{16}(2 {l^*}^2 f_0)\) are smaller than \(2^{63}\). To reduce memory usage, we use HDD and several auxiliary primes \(l_i \approx 100{,}000\) in gaussd64.c.
Computations of (I), (II)\(_1\) and (III)\(_0\) (resp. (IV)\(_0\)) are executed in \(O(f_0^{1+\epsilon })\) (resp. \(O((\kappa f_0)^{1+\epsilon })\)) bit operations. In Table 5, we give the ratios of execution times for (I)–(IV) by a single thread program on a Linux PC, where \(*\) means that we did not compute it for lack of RAM.
For computations of (I) and (IV)\(_0\), we need large RAM for the FFT algorithm. Various methods in [5] will be useful for speed-up and reduction of memory usage in computations of (I), (II)\(_1\) and (III)\(_0\). It will be able to speed up computations of (II)\(_1\) and (III)\(_0\) by parallel computing with GPU.
The above programs and further data have been available in our web page: https://math0.pm.tokushima-u.ac.jp/~hiroki/major/galois1-e.html. These data were obtained by six personal computers for several years. They agree with previous computations by several authors when p is small. Though temporary hardware errors are unusual, they could occur in long-term computation. We computed twice for \(|d|<200\) and \(p<1{,}000{,}000\), and only once for \(|d|<10\) and \(1{,}000{,}000<p<20{,}000{,}000\). As we fixed the data for some temporary hardware errors in the former computation, we are afraid that they occur in the latter computation. However, irregular pairs are double-checked by (I) and (II)\(_1\), and the number of pairs is near the expected number. Therefore these unusual errors would not affect Proposition 2.2.
References
Buhler, J., Crandall, R., Ernvall, R., Metsäankylä, T., Shokrollahi, A.M.: Irregular primes and cyclotomic invariants to \(12\) million. J. Symbol. Comput. 31, 89–96 (2001)
Buhler, J., Harvey, D.: Irregular primes to 163 million. Math. Comp. 80, 2435–2444 (2011)
Ferrero, B., Washington, L.: The Iwasawa invariant \(\mu _p\) vanishes for abelian number fields. Ann. Math. 109, 377–395 (1979)
Greither, C.: Class groups of abelian fields, and the main conjecture. Ann. Inst. Fourier (Grenoble) 42, 449 (1992)
Hart, W., Harvey, D., Ong, W.: Irregular primes to two billion. Math. Comp. 86, 3031–3049 (2017)
Ichimura, H., Sumida, H.: On the Iwasawa invariants of certain real abelian fields II. Internat. J. Math. 7, 721–744 (1996)
Iwasawa, K.: Lectures on \(p\)-adic L-functions. Ann. of Math. Stud., vol. 74, Princeton University Press: Princeton, NJ (1972)
Kubota, T., Leopoldt, H.W.: Eine \(p\)-adische Theorie der Zetawerte, I. Einführung der \(p\)-adischen Dirichletschen \(L\)-Funktionen. J. Reine Angew. Math. 214/215, 328–339 (1964)
Mazur, B., Wiles, A.: Class fields of abelian extensions of \({\textbf{Q} }\). Invent. Math. 76, 179–330 (1984)
Soulé, C.: A bound for the torsion in the \(K\)-theory of algebraic integers. Doc. Math. Extra Vol., 761–788 (2003)
Sumida-Takahashi, H.: Computation of Iwasawa invariants of certain real abelian fields. J. Number Theory 105, 235–250 (2004)
Sumida-Takahashi, H.: The Iwasawa invariants and the higher \(K\)-groups associated to real quadratic fields. Exp. Math. 14, 307–316 (2005)
Sumida-Takahashi, H.: Computation of the \(p\)-part of the ideal class group of certain real abelian fields. Math. Comp. 76, 1059–1071 (2007)
Sumida-Takahashi, H.: Examples of the Iwasawa invariants and the higher \(K\)-groups associated to quadratic fields. J. Math. Univ. Tokushima 41, 33–41 (2007)
Washington, L.: Introduction to Cyclotomic Fields, 2nd edition, Graduate Texts in Mathematics, vol. 83, Springer, New York (1997)
Acknowledgements
The author is grateful to the referee for carefully reading the original manuscript and for valuable comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The author was partially supported by JSPS KAKENHI Grant Number JP17K05176 and JP20H00115.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Sumida-Takahashi, H. A Generalized Problem Associated to the Kummer–Vandiver Conjecture. Arnold Math J. 9, 381–391 (2023). https://doi.org/10.1007/s40598-022-00220-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40598-022-00220-3






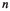 the Iwasawa polynomial
the Iwasawa polynomial 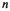 the special cyclotomic unit
the special cyclotomic unit  the Gauss sum
the Gauss sum