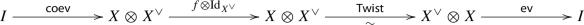Abstract
We show how the formalism of 2-traces can be applied in the setting of derived algebraic geometry to obtain a generalization of the holomorphic Atiyah–Bott formula to the case when an endomorphism is replaced by a correspondence.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let M be a compact manifold, and let f be an endomorphism of M such that the fixed points of f are isolated. The famous Lefschetz fixed point theorem [9, Formula 71.1] expresses the super trace of the map \(H^*(f)\) on cohomology induced by f in terms of some local data at the fixed points of f. In fact, in loc. cit. Lefschetz treated a more general problem: he considered a pair of maps \(g,f:N \rightarrow M\) and gave a cohomological condition for f and g to have a coincidence point. The fixed point theorem above is a special case when \(M=N\) and \(g = {{\,\mathrm{Id}\,}}_M\).
Variations of the Lefschetz fixed point theorem were also found to be very important in algebraic geometry. For example, in the setting of étale cohomology, the Lefschetz fixed point theorems were reestablished by the school of Grothendieck as a part of their program on the proof of Weil conjectures. The variant for coincidence is called Lefschetz–Verdier formula and appeared in [6, Corollaire 4.7]. However, this formula has the drawback that the local terms are in general quite implicit. Deligne made a conjecture that under favorable assumptions the local terms can be made precise, and this conjecture was subsequently proved in [4, 12], and in [13] with the view towards applications to the global functional Langlands correspondence.
Returning to the classical setting of the smooth manifolds, if all fixed points of the endomorphism f are simple, the local terms in the Lefschetz fixed point theorem can also be computed explicitly. Moreover, in this case, the theorem itself admits a vast generalization, which is due to Atiyah and Bott [1, 2]. Specifically, given an elliptic complex E on M and a bundle map \(b:f^{-1}E \rightarrow E\), there is an equality
In [8], we showed how one can use a simple traces machinery in \((\infty , 2)\)-categories to prove an algebro-geometric analogue of the Atiyah–Bott formula (1). In this note, we explain how to adapt our arguments to deduce a version of this theorem for a pair of morphisms, that is, a version of the Lefschetz–Verdier fixed point formula for vector bundles on algebraic varieties (Theorem 1.6), which we will further call the holomorphic Atiyah–Bott formula for correspondence.
Convention
For the rest of this work, we fix an algebraically closed base field k.
To state the holomorphic Atiyah–Bott formula for correspondences we first introduce necessary notations.
Definition 1.1
Let X, Y be a pair of k-schemes. A correspondence is a pair of morphisms \(g,f:Y \rightarrow X\).
Let us now denote by \({{\,\mathrm{Vect}\,}}_k\) the unbounded derived category of cochain complexes over k, and by \({{\,\mathrm{QCoh}\,}}(X)\) the unbounded derived category of quasi-coherent sheaves on X (see conventions below). Recall that for an endomorphism \(f:X \rightarrow X\) a lax-equivariant structure on a sheaf \(E \in {{\,\mathrm{QCoh}\,}}(X)\) is a map \(b :f^* E \rightarrow E\). We first generalize this notion to the case of correspondences.
To do this, let us assume that both X and Y are smooth and proper. Under these assumptions, the pushforward functor \(g_*\) on quasi-coherent sheaves admits a right adjoint \(g^!\), and there is a natural equivalence \(g^!(-) \simeq g^*(-)\otimes \omega _g\), where \(\omega _g := g^!(\mathcal O_X)\) is the relative dualizing complex. This motivates the following
Definition 1.2
Let \(g,f :Y \rightarrow X\) be a correspondence. A lax (g, f)-equivariant structure on \(E \in {{\,\mathrm{QCoh}\,}}(X)\) is a map \(b :f^* E \rightarrow g^! E\) in \({{\,\mathrm{QCoh}\,}}(Y)\).
Recall now the notion of a dualizable object (see Definition 2.1). Similar to the classical Lefschetz number, in the case E is coherent, any lax (g, f)-equivariant structure on E produces an element of k:
Definition 1.3
For a lax (g, f)-equivariant coherent sheaf \((E \in {{\,\mathrm{QCoh}\,}}(X), b: f^*E \rightarrow g^! E)\) on X we define its Lefschetz number \({\mathrm L}(E, b) \in k\) of b as the trace (Definition2.1) in \({{\,\mathrm{Vect}\,}}_k\) of the corresponding endomorphism

on global sections, where the last morphism is obtained from the counit of the adjunction \(g_* \dashv g^!\). Note that the trace makes sense since \(\Gamma (X,E)\) is a dualizable object in \({{\,\mathrm{Vect}\,}}_k\) due to the properness of X.
To state how the Lefschetz number can be described in local terms, for a correspondence as above let us denote by \(Y^{g=f, \text {cl}}\) the classical fixed point scheme, that is, the fiber product

in the category of reduced schemes.
Definition 1.4
Given a correspondence \(g,f:Y \rightarrow X\), we say that g is étale at the fixed points of (g, f) if the morphism g is étale at each \(y\in Y^{g=f,\text {cl}}\).
Remark 1.5
Note that if g is étale at the fixed points, then there is a canonical trivialization \(\omega _{g|Y^{g=f}} \simeq \mathcal O_{Y^{g=f, \text {cl}}}\) in \({{\,\mathrm{QCoh}\,}}(Y^{g=f, \text {cl}})\).
We can now give a description of the local terms of the Atiyah–Bott formula. Let \(g,f:Y \rightarrow X\) be a correspondence such that g is étale at the fixed points, and let \(y \in Y^{g=f, \text {cl}}\) be a fixed point. Note that then:
-
Given a lax (g, f)-equivariant sheaf \((E \in {{\,\mathrm{QCoh}\,}}(X), b: f^*E \rightarrow g^! E)\) on X, we can restrict b to the fiber over y, obtaining an endomorphism
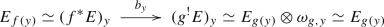
in \({{\,\mathrm{QCoh}\,}}(\{x\}) \simeq {{\,\mathrm{Vect}\,}}_k\), where \(x:=f(y)=g(y)\) and in the last equality we have used the trivialization of \(\omega _{g| Y^{g=f}}\) from Remark 1.5.
-
Since by our assumptions \(d_y g\) is invertible, we obtain an endomorphism
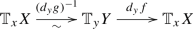
of the tangent space of X at our fixed point.
Finally, we can formulate the main result of this work.
Theorem 1.6
(Holomorphic Atiyah–Bott formula for correspondences) Let X, Y be a pair of smooth proper k-schemes and let \((g,f) :Y \rightarrow X \times X\) be a correspondence such that the graph of Y intersects the diagonal in \(X\times X\) transversally (see Definition 3.1) and g is étale at the fixed points (Definition 1.4). Then for any lax (g, f)-equivariant perfect sheaf \((E \in {{\,\mathrm{QCoh}\,}}(X), b:f^*E \rightarrow g^! E)\) on X there is an equality
Example 1.7
In the case \(Y = X\) and \(g={{\,\mathrm{Id}\,}}_X\), we recover the usual Holomorphic Atiyah–Bott formula [8, Theorem 3.1.2].
One interesting application of Theorem 1.6 is in the context of birational geometry. Namely, given a rational endomorphism \(\phi :X \dashrightarrow X\) of a smooth proper variety X one can take Y to be the closure of the graph of \(\phi \) in \(X\times X\) and \(g,f:Y \rightarrow X\) to be the projections to the first and second factors. Let us illustrate how this works in the simplest nontrivial example.
Example 1.8
Assume that \({{\,\mathrm{char}\,}}k \ne 2\). Let \(X=\mathbb P^2\) and consider the Cremona transformation
By taking the closure of the graph of \(\phi \), we obtain a correspondenc  , where Y is given by
, where Y is given by
The intersection with the diagonal \(x=u, y=v, z=w\) consists of 4 points \((\pm 1: \pm 1: \pm 1)\). Consider \(E=\omega _{\mathbb {P}^2}\). There is a canonical lax-equivariant structure on E given by the pullback on forms \(t:f^*\omega _{\mathbb {P}^2} \rightarrow \omega _Y \simeq g^!\omega _{\mathbb {P}^2}\).
Let us first compute the Lefschetz number of t. Since
It is enough to understand the map on \(H^{2,2}(\mathbb P^2)\), which is the degree of \(\phi \) since \(\mathbb P^2\) is 2-dimensional. Since the Cremona transform is birational, it follows that \(L(t) = 1\).
Now let us compute the right-hand side of the Atiyah–Bott formula. All fixed points lie in the affine chart \(z=1\) with inhomogeneous coordinates (X, Y). The differential of \(\phi \) at a point \(x=(X_0, Y_0)\) is given by the matrix
Since for all fixed points \(X_0^2 = Y_0^2 = 1\), we have
Also in this case the induced map \(f^*\omega _{\mathbb {P}^2,x} \rightarrow g^! \omega _{\mathbb {P}^2,x}\) is just the identity; hence, we find that the right-hand side of the Atiyah–Bott formula is
Conventions.
-
(1)
All categories we work with are assumed to be \((\infty ,1)\)-categories (we refer the reader to [10] for the theory of \((\infty ,1)\)-categories). For an \((\infty ,1)\)-category \(\mathscr {C}\) we will denote by \(\mathscr {C}^{\simeq }\) the underlying \(\infty \)-groupoid of \(\mathscr {C}\) obtained by discarding all the non-invertible morphisms from \(\mathscr {C}\).
-
(2)
For a field k we denote by \({{{\,\mathrm{Vect}\,}}_k}\) the stable symmetric monoidal \((\infty ,1)\)-category of unbounded cochain complexes over k up to quasi-isomorphism with the canonical \((\infty ,1)\)-enhancement.
-
(3)
We will denote by \(\Pr ^{{\mathrm L}}_{\infty }\) the \((\infty ,1)\)-category of presentable \((\infty ,1)\)-categories and continuous functors with a symmetric monoidal structure from [11, Proposition 4.8.1.14.]. Note that \({{\,\mathrm{Vect}\,}}_k\) is a commutative algebra object in \(\Pr ^{{\mathrm L}}_{\infty }\). By [11, Corollary 5.1.2.6.] it follows that the presentable stable \((\infty ,1)\)-category of k-linear presentable \((\infty ,1)\)-categories and k-linear functors \({{\,\mathrm{Cat}\,}}_k:={\text {\textsf {Mod}}}_{{{\,\mathrm{Vect}\,}}_k}(\Pr ^{{\mathrm L}}_{\infty })\) admits a natural symmetric monoidal structure. We will also denote by \(2{{\,\mathrm{Cat}\,}}_k\) the symmetric monoidal \((\infty ,2)\)-category of k-linear presentable \((\infty ,1)\)-categories and continuous k-linear functors, so that the underlying \((\infty ,1)\)-category of \(2{{\,\mathrm{Cat}\,}}_k\) is precisely \({{\,\mathrm{Cat}\,}}_k\).
-
(4)
We will further work in the setting of derived algebraic geometry over some fixed algebraically closed field k, where derived affine schemes are modeled by commutative simplicial k-algebras.Footnote 1 For a derived prestack X we will denote the k-linear symmetric monoidal \((\infty ,1)\)-category of unbounded complexes of quasi-coherent sheaves on X by \({{\,\mathrm{QCoh}\,}}(X) \in {{\,\mathrm{CAlg}\,}}({{\,\mathrm{Cat}\,}}_k)\). Similarly, all the functors between quasi-coherent sheaves are assumed to be derived in an appropriate sense. We refer the reader to [5] for an introduction to the basic concepts of derived algebraic geometry using the functor of points approach.
2 Traces and Morphisms of Traces
We start with the following classical definition.
Definition 2.1
Let \((\mathscr {C}, \otimes , I)\) be a symmetric monoidal \((\infty ,1)\)-category. Then:
-
1.
An object \(X \in \mathscr {C}\) is called dualizable, if there exist an object \(X^{\vee } \in \mathscr {C}\) together with unit
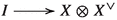 and counit
and counit 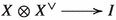 maps satisfying triangle identities.
maps satisfying triangle identities. -
2.
Let
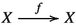 be a morphism in \(\mathscr {C}\) where the object X is dualizable. Then the trace of f denoted by \({\textsf {Tr}}_{\mathscr {C}}(f) \in \ {{\,\mathrm{Hom}\,}}_{\mathscr {C}}(I,I)\) of f is defined as the composite
be a morphism in \(\mathscr {C}\) where the object X is dualizable. Then the trace of f denoted by \({\textsf {Tr}}_{\mathscr {C}}(f) \in \ {{\,\mathrm{Hom}\,}}_{\mathscr {C}}(I,I)\) of f is defined as the composite 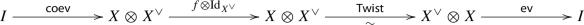
in \(\mathscr {C}\).
Example 2.2
Notice that an object \(V \in {{\,\mathrm{Vect}\,}}_k\) is dualizable if an only if it has finite-dimensional cohomology spaces nonzero only in finitely many degrees. If \(V \in {{\,\mathrm{Vect}\,}}_k\) is dualizable and \(f \in {{\,\mathrm{Hom}\,}}_{{{\,\mathrm{Vect}\,}}_k}(V,V)\) is some morphism, then the trace \({\textsf {Tr}}_{{{\,\mathrm{Vect}\,}}_k}(f) \in {{\,\mathrm{Hom}\,}}_{{{\,\mathrm{Vect}\,}}_k}(k,k) \simeq k\) is the alternating sum of the ranks of the map on the cohomology spaces of V induced by f. In particular, in case \(f={{\,\mathrm{Id}\,}}_V\) we see that \({\textsf {Tr}}_{{{\,\mathrm{Vect}\,}}_k}({{\,\mathrm{Id}\,}}_V)=\mathcal {X}_{{{\,\mathrm{Vect}\,}}_k}(V) \in k\) is simply the Euler characteristic of V.
Remark 2.3
Suppose we are given a dualizable object \(X \in \mathscr {C}\) together with a map  , where \(Y \in \mathscr {C}\) is some object. Similar to the second part of Definition 2.1, one can then consider the composite
, where \(Y \in \mathscr {C}\) is some object. Similar to the second part of Definition 2.1, one can then consider the composite

which we will further call a twisted trace of f.
The notion of trace is extremely useful in the setting of derived algebraic geometry. Namely, note that by [3, Theorem 1.2] for any perfect derived stacks X, Y (see [3, Definition 3.2]) there is a canonical equivalence \({{\,\mathrm{QCoh}\,}}(X) \otimes {{\,\mathrm{QCoh}\,}}(Y) \simeq {{\,\mathrm{QCoh}\,}}(X \times Y)\) obtained from the bicontinuous functor

where

are the projection maps. In particular, the object \({{\,\mathrm{QCoh}\,}}(X) \in {{\,\mathrm{Cat}\,}}_k\) is self-dual, with the unit and counit maps given by

where  is the diagonal map and
is the diagonal map and  is the (derived) global sections functor.
is the (derived) global sections functor.
A convenient way to calculate traces of various endomorphisms of the dualizable object \({{\,\mathrm{QCoh}\,}}(X) \in {{\,\mathrm{Cat}\,}}_k\) is provided by the formalism of kernels. Namely, by [3, Theorem 1.2] there is an equivalence

of \((\infty ,1)\)-categories. The sheaf \(\mathcal K\) is frequently called the kernel of the corresponding functor. Moreover, by [8, Proposition 2.1.6] we have an equivalence
allowing us to instantly calculate trace of an endomorphism of \({{\,\mathrm{QCoh}\,}}(X) \in {{\,\mathrm{Cat}\,}}_k\) in terms of its kernel.
It is now straightforward to see that notion of trace allows us to recover derived fixed points schemes in the setting of derived algebraic geometry:
Definition 2.4
Let  be a correspondence of derived stacks. We then define the derived fixed points stack denoted \(Y^{g=f}\) as the pullback
be a correspondence of derived stacks. We then define the derived fixed points stack denoted \(Y^{g=f}\) as the pullback

of derived stacks.
Proposition 2.5
In the setting of Definition 2.4 for a sheaf \(\mathcal {G} \in {{\,\mathrm{QCoh}\,}}(Y)\) there is a canonical equivalence
in \({{\,\mathrm{Vect}\,}}_k\).
Proof
First, note that the kernel of the functor

is given by the sheaf \((g,f)_* \mathcal {G} \in {{\,\mathrm{QCoh}\,}}(X \times X)\). Indeed, due to projection formula (see [3, Proposition 3.10]) we have
Consequently, using Eq. (3) and projection formula we obtain
as claimed.
Now note that since \({{\,\mathrm{Cat}\,}}_k\) is the underlying \((\infty ,1)\)-category of the \((\infty ,2)\)-category \(2{{\,\mathrm{Cat}\,}}_k\), it is natural to ask whether the 2-morphisms in \(2{{\,\mathrm{Cat}\,}}_k\) provide some additional functoriality on the level of traces. Motivated by this, let us discuss the notion of trace in \((\infty ,2)\)-categories. Let \(\mathscr {E}\) be a symmetric monoidal \((\infty ,2)\)-category (that is, a commutative algebra object in the \((\infty ,1)\)-category of \((\infty ,2)\)-categories, see [5, Chapter V.3, 1.4.1.]). As was shown in [8], in this case, the trace constructions admits additional functoriality:
Proposition 2.6
[8, Proposition 1.2.3] Let \(\mathscr {E}\) be a symmetric monoidal \((\infty ,2)\)-category and suppose we are given a (not necessary commutative) diagram

in \(\mathscr {E}\), where \(\varphi \) is left adjoint to \(\psi \) and

is a 2-morphism in \(\mathscr {E}\). Then there exist a natural morphism

in the \((\infty ,1)\)-category \({{\,\mathrm{Hom}\,}}_{\mathscr {E}}(I,I)\) called a morphism of traces induced by T.
Moreover, given a diagram

in \(\mathscr {E}\), where \(\varphi _1\) is left adjoint to \(\psi _1\), \(\varphi _2\) is left adjoint to \(\psi _2\) and

are 2-morphisms there is an equivalence
where \(\circ _{\textsf {vert}}\) is the vertical composition of 2-morphisms.
We refer the reader to [8, Example 1.2.5] for an explicit description of the \((\infty ,2)\)-categorical trace \({\textsf {Tr}}(\varphi ,T)\).
We now provide several examples in the case \(\mathscr {E}=2{{\,\mathrm{Cat}\,}}_k\):
Example 2.7
[8, Definition 1.2.9] In the case \(\mathscr {E}=2{{\,\mathrm{Cat}\,}}_k\), suppose we are given some dualizable object \(\mathscr {C} \in 2{{\,\mathrm{Cat}\,}}_k\) together with an endofunctor  . Note that there is a canonical equivalence
. Note that there is a canonical equivalence

where \( {{\,\mathrm{Fun}\,}}_{2{{\,\mathrm{Cat}\,}}_k}({{\,\mathrm{Vect}\,}}_k, \mathscr {C})^{\textsf {ladj}} \subseteq {{\,\mathrm{Fun}\,}}_{2{{\,\mathrm{Cat}\,}}_k}({{\,\mathrm{Vect}\,}}_k, \mathscr {C})\) is the full \((\infty ,1)\)-subcategory spanned by those morphisms in \(2{{\,\mathrm{Cat}\,}}_k\) which admit a right adjoint, and \(\mathscr {C}^{\textsf {comp}} \subseteq \mathscr {C}\) is the full \((\infty ,1)\)-subcategory of compact objects (see [5, 7.1.1]).
In particular, given a compact object \(E \in \mathscr {C}^{\textsf {comp}}\) together with a morphism  in \(\mathscr {C}\), we can apply the \((\infty ,2)\)-categorical trace construction to the diagram
in \(\mathscr {C}\), we can apply the \((\infty ,2)\)-categorical trace construction to the diagram

where \(\phi \) is the functor obtained from the compact object \(E \in \mathscr {C}^{\textsf {comp}}\) and T is the 2-morphism obtained from t.
The corresponding element

is called the Chern character of E and is denoted by \({{\,\mathrm{ch}\,}}(E,t) \in {\textsf {Tr}}_{2{{\,\mathrm{Cat}\,}}_k}(F)\).
Example 2.8
(Chern character for vector spaces) In the case \(\mathscr {C}={{\,\mathrm{Vect}\,}}_k\), \(F={{\,\mathrm{Id}\,}}_{{{\,\mathrm{Vect}\,}}_k}\) in the setting of Example 2.7 (in particular, we have \(t \in {{\,\mathrm{Hom}\,}}_{{{\,\mathrm{Vect}\,}}_k}(E,E)\) and \({\textsf {Tr}}_{2{{\,\mathrm{Cat}\,}}_k}(F) \simeq k\)) directly by definition we have an equality \({{\,\mathrm{ch}\,}}(V,t) = {\textsf {Tr}}_{{{\,\mathrm{Vect}\,}}_k}(t)\) of two numbers.
Example 2.9
(Chern character for lax-equivariant sheaf) Let  be a correspondence of perfect derived stacks (see [3, Definition 3.2]), and \(E \in {{\,\mathrm{Perf}\,}}(X)\) be a perfect sheaf (by [3, 3.1] equivalently compact/dualizable object of \({{\,\mathrm{QCoh}\,}}(X)\)) equipped with a map \(t:E \rightarrow f_* (\mathcal {G} \otimes g^*E)\) for some \(\mathcal {G} \in {{\,\mathrm{QCoh}\,}}(Y)\). Then similar to [8, Remark 2.2.4] one checks that the Chern character \({{\,\mathrm{ch}\,}}(E,t)\) of E obtained from the diagram
be a correspondence of perfect derived stacks (see [3, Definition 3.2]), and \(E \in {{\,\mathrm{Perf}\,}}(X)\) be a perfect sheaf (by [3, 3.1] equivalently compact/dualizable object of \({{\,\mathrm{QCoh}\,}}(X)\)) equipped with a map \(t:E \rightarrow f_* (\mathcal {G} \otimes g^*E)\) for some \(\mathcal {G} \in {{\,\mathrm{QCoh}\,}}(Y)\). Then similar to [8, Remark 2.2.4] one checks that the Chern character \({{\,\mathrm{ch}\,}}(E,t)\) of E obtained from the diagram

is equivalent to the twisted trace (see Remark 2.3) of the induced map

in \({{\,\mathrm{QCoh}\,}}(Y^{g=f})\), where \(b:f^*E \rightarrow \mathcal {G} \otimes g^* E\) is the morphism which corresponds to \(t \in {{\,\mathrm{Hom}\,}}_{{{\,\mathrm{QCoh}\,}}(X)}\big (E,f_*(\mathcal {G} \otimes g^* E)\big )\) via the adjunction \(f^* \dashv f_*\).
Example 2.10
The case we are most interested in is when both X and Y are smooth and \(\mathcal G = \omega _g := g^!(\mathcal O_X)\). In this case \(g^*(-)\otimes \omega _g \simeq g^!(-)\), so a morphism of traces corresponding to the lax-equivariant structure from Definition 1.2 under the identification from the previous example corresponds to the twisted trace with the value in \(\Gamma (Y^{g=f}, j^* \omega _g)\).
Remark 2.11
In the setting of Example 2.9, suppose we are given a map

of correspondences (in particular, we automatically get a map \(l :W^{g'=f'} \rightarrow Y^{g=f}\) on derived fixed points). The map \(b :f^* E \rightarrow \mathcal {G} \otimes g^*E\) in \({{\,\mathrm{QCoh}\,}}(Y)\) then gives a map

and hence by adjunction a map \(t' :(u^* E) \rightarrow f'_* (v^* \mathcal {G} \otimes (g')^* (u^*E))\). Moreover, using Example 2.9 we obtain a canonical equivalence
of Chern characters.
Example 2.12
(Todd class) One of the main theorems of [7] is that for a classical smooth scheme X the morphism of traces

induced by the commutative diagram

is given by the multiplication by the classical Todd class, where \({{\,\mathrm{ICoh}\,}}(X)\) here is the \((\infty ,1)\)-category of ind-coherent sheaves and HKR is the Hochschild–Kostant–Rosenberg isomorphism. We refer the reader to [7] for more details.
3 Proof of the Atiyah–Bott Formula
In this section, we show how one can adapt the proof of [8] to the case of correspondences. First we make precise the transversality condition from Theorem 1.6.
Definition 3.1
Let  be a correspondence of algebraic k-varieties. We say that \(Y \rightarrow X\times X\) intersects with the diagonal \(X \rightarrow X \times X\) transversely if the derived fixed point scheme \(Y^{g=f}\) (see Definition 2.4) is discrete. In more classical terms this is equivalent to the following pair of conditions:
be a correspondence of algebraic k-varieties. We say that \(Y \rightarrow X\times X\) intersects with the diagonal \(X \rightarrow X \times X\) transversely if the derived fixed point scheme \(Y^{g=f}\) (see Definition 2.4) is discrete. In more classical terms this is equivalent to the following pair of conditions:
-
The underlying classical scheme \(Y^{g=f, \text {cl}}\) is discrete.
-
The induced map on tangent spaces \(1 - d_y f \circ (d_y g)^{-1}\) is invertible for all \(y \in Y^{g=f, \text {cl}}\).
Proof of Theorem 1.6
The strategy of the proof is similar to [8, Proposition 3.2]. We have a diagram

in \(2{{\,\mathrm{Cat}\,}}_k\), where the 2-morphism \(T_1\) is obtained from the lax (g, f)-equivariant structure on E and the morphism \(T_2\) is given by

By applying the 2-trace formalism Proposition 2.6 to the commutative diagram, we obtain a commutative triangle

in \({{\,\mathrm{Vect}\,}}_k\), that is, an equality
of two numbers. First, we note that using Example 2.8, we have
Second, by Proposition 2.5, we have an equivalence
where \(j:Y^{g=f} \rightarrow Y\) is the natural map. Moreover, by Remark 1.5 we have \(j^*\omega _g \simeq \mathcal O_{Y^{g=f}}\), and hence
where \(e_y:=1 \in \Gamma (\{y\}, \mathcal {O}_y)\). In particular, we can write
Moreover, for \(y\in Y^{g=f}\) by Example 2.9, we obtain

It suffices now to show that the map
sends \(e_y\) to \(1/\det (1-d_y f \circ (d_y g)^{-1})\). Note that \(\int _{Y^{g=f}}\) is independent of E; hence, to compute \(\lambda _y := \int _{Y^{g=f}}(e_y)\), we can apply (4) to the special case \(E:=x_* k\), a skyscraper sheaf at a fixed point \(x=f(y) = g(y)\), with the natural lax (g, f)-equivariant structure given by

In this case, (4) produces an equality

and so we want to see that the trace  is equal to \(\det (1-d_y f \circ (d_y g)^{-1})\). But by smoothness, the cohomology of the derived fiber \(E_x\) can be computed as
is equal to \(\det (1-d_y f \circ (d_y g)^{-1})\). But by smoothness, the cohomology of the derived fiber \(E_x\) can be computed as
and the induced map \(H^*(b_y)\) is precisely \(\Lambda ^*((d_y f \circ (d_y g)^{-1})^\vee )\). The result then follows from the well-known relation between traces and determinants, see [8, Lemma 3.2.5] for more details. \(\square \)
Notes
If characteristic of k is zero this category is equivalent to the \(\infty \)-category of connective commutative dg-algebras.
References
Atiyah, M.F., Bott, R.: A Lefschetz fixed point formula for elliptic complexes I. Ann. Math. 86, 374–407 (1967)
Atiyah, M.F., Bott, R.: A Lefschetz fixed point formula for elliptic complexes II. Appl. Ann. Math. 88, 451–491 (1968)
Ben-Zvi, D., Francis, J., Nadler, D.: Integral transforms and Drinfeld centers in derived algebraic geometry. J. Am. Math. Soc. 23, 909–966 (2010)
Fujiwara, K.: Rigid geometry, Lefschetz–Verdier trace formula and Deligne’s conjecture. Inventiones mathematicae 127, 489–533 (1997)
Gaitsgory, D., Rozenblyum, N.: A Study in Derived Algebraic Geometry, Volume I: Correspondences and Duality Mathematical Surveys and Monographs. American Mathematical Soc., Providence (2017)
Grothendieck, A., Bucur, I., Houzel, C., Illusie, L., Jouanolou, J.-P., Serre, J.-P.: Séminaire de Géométrie Algébrique du Bois Marie. SGA V. Cohomology \(\ell \)-adic et Fonctions \(L\). In: Illusie, L. (ed.) Lecture Notes in Mathematics, vol. 589. Springer, Berlin (1964)
Kondyrev, G., Prikhodko, A.: Equivariant Grothendieck–Riemann–Roch theorem via formal deformation theory. (2019). arXiv:1906.00172
Kondyrev, G., Prikhodko, A.: Categorical proof of Holomorphic Atiyah–Bott formula. J. Inst. Math. Jussieu 19, 1739–1763 (2020)
Lefschetz, S.: Intersections and transformations of complexes and manifolds. Trans. Am. Math. Soc. 28, 1–49 (1926)
Lurie, J.: Higher Topos Theory. Princeton University Press, Princeton (2009)
Lurie, J.: Higher algebra. (2017). eprint: http://www.math.ias.edu/~lurie/papers/HA.pdf
Pink, R.: On the calculation of local terms in the Lefschetz–Verdier trace formula and its application to a conjecture of deligne. Ann. Math. 135, 483–525 (1992)
Varshavsky, Y.: Lefschetz–Verdier trace formula and a generalization of a theorem of Fujiwara. Geom. Funct. Anal. 17, 271–319 (2007)
Acknowledgements
We would like to thank Dennis Gaitsgory for introducing us to the formalism of traces and numerous helpful discussions, and Sergey Galkin for proposing to extend the Atiyah–Bott formula to the case of correspondences. The second author wants to thank Pavel Popov for suggesting Example 1.8. The study has been funded within the framework of the HSE University Basic Research Program.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Kondyrev, G., Prikhodko, A. Holomorphic Atiyah–Bott Formula for Correspondences. Arnold Math J. 8, 497–511 (2022). https://doi.org/10.1007/s40598-022-00206-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40598-022-00206-1





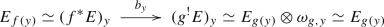
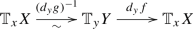
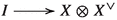 and counit
and counit 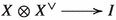 maps satisfying triangle identities.
maps satisfying triangle identities.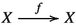 be a morphism in
be a morphism in