Attenuation and dispersion characteristic of Rayleigh waves in a compressed viscoelastic strip: a comparative study

Abstract

The present study develops the dispersion and attenuation characteristics of Rayleigh wave regulations through a pre-stressed Voigt type viscoelastic strip of finite thickness. The displacement expressions of Rayleigh wave in the strip are introduced. The complex frequency equation of the wave motion is thus obtained. We have studied the effects of initial stress, attenuation coefficients and dissipation factor on the phase and damped velocities simultaneously.

1 Introduction

Viscoelasticity means the combination of viscosity and elasticity; it is a special characteristic of materials that display both viscous and elastic behaviour when subjected to distortion. The most determining attribute of the viscoelastic materials is their ability to absorb the high amount of energy produced during volcanic eruptions and earthquakes. Hence, to withstand the tremors during an earthquake, some of the metal alloys possessing viscoelastic property are utilized as dampers in the construction of multi-storey buildings. Therefore, the study of seismic waves through viscoelastic structures has become a matter of interest among several geophysicists and seismologists worldwide [1,2,3]. Recently, Saha et al. [4] investigated the phase velocity variation on the Raylegh wave propagation in a pre-stressed medium.

It is well known that the Earth is a pre-stressed medium. A large quantity of initial stress may generate in the Earth because of several natural and artificial phenomena such as difference in gravity, temperature, weight, manufacturing activities, differential external forces, slow process of creep, hydrostatic tension or compression, presence of overburdened layer, external loading etc. Researchers and seismologists mostly favour the pre-stressed structure to analyse the underground response of seismic surface waves. Some exemplary works on initially stressed media were acknowledged by several authors including [5,6,7,8].

The assumption of Voigt-type viscoelastic surface stratum of the earth resting on an extremely rigid foundation creates a strong basis for the consideration in the study of geomechanical problems. The main aim of this paper is to study the Rayleigh wave propagation through a Voigt-type viscoelastic layer of finite thickness resting over a rigid foundation. A complex frequency equation for the wave propagation obtained using suitable boundary conditions. A comparative observation has been executed through the numerical computations and graphical views concerned to the effects of attenuation coefficient, dissipation factor and initial stress on the phase and damped velocities of the wave.

2 Formulation and assumption of the problem

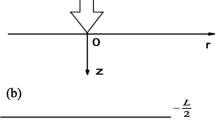
Let us assume a Voigt-viscoelastic layer of finite thickness h under initial stress P resting over a rigid foundation, such that x-axis is parallel to the direction of wave propagation and z-axis is pointing positively in the half-space as shown in Fig. 1.

Fig. 1

Geometry of the problem

3 Solution of the problem

Let $(u,\,v,\,w)$ are displacement component vectors of the viscoelastic strip along x, y and z directions, respectively. Then, by the characteristic of Rayleigh waves, we have

$$ u = u(x;z;t),\,v = 0,\,\,w = w(x;z;t),\,{\text{and}}\,\partial ( \cdot )/\partial y = 0. $$

(1)

In view of (1), non-vanishing equation of motion is governed by (Biot [9])

$$ \begin{aligned} & \frac{{\partial \phi_{11} }}{\partial x} + \frac{{\partial \phi_{13} }}{\partial z} - P\frac{{\partial \omega_{13} }}{\partial z} = \rho \frac{{\partial^{2} u}}{{\partial t^{2} }}, \\ & \frac{{\partial \phi_{13} }}{\partial x} + \frac{{\partial \phi_{33} }}{\partial z} - P\frac{{\partial \omega_{13} }}{\partial x} = \rho \frac{{\partial^{2} w}}{{\partial t^{2} }}, \\ \end{aligned} $$

(2)

where, $\rho$ represents the density of the medium and $\phi_{ij}$ are the stress components.

$$ \phi_{11} = \,(\bar{\lambda } + 2\bar{\mu })\varepsilon_{11} + \bar{\lambda }\varepsilon_{33} ,\quad \phi_{13} = 2\bar{\mu }\varepsilon_{13} ,\quad \phi_{33} = \,(\bar{\lambda } + 2\bar{\mu })\varepsilon_{33} + \bar{\lambda }\varepsilon_{11} . $$

(3)

Here, $\varepsilon_{ij} = \frac{1}{2}\left( {\frac{{\partial w_{i} }}{{\partial x_{j} }} + \frac{{\partial w_{j} }}{{\partial x_{i} }}} \right),$$P = S_{11} - S_{33} ,$$\bar{\lambda } = \left( {\lambda + \lambda_{0} \frac{\partial }{\partial t}} \right)$ and $\overline{\mu } = \left( {\mu + \mu_{0} \frac{\partial }{\partial t}} \right);$$\lambda ,\,\,\mu$ are lame’s constants and $\lambda_{0} ,\,\,\mu_{0}$ are viscosity of viscoelastic medium.

$$ \begin{aligned} & (D_{\lambda } + 2D_{\mu } )\frac{{\partial^{2} u}}{{\partial x^{2} }} + \left( {D_{\lambda } - \frac{P}{2}} \right)\frac{{\partial^{2} u}}{{\partial z^{2} }} + \left( {D_{\lambda } + D_{\mu } + \frac{P}{2}} \right)\frac{{\partial^{2} w}}{\partial x\partial z} = \rho \frac{{\partial^{2} u}}{{\partial t^{2} }}, \\ & \left( {D_{\mu } + \frac{P}{2}} \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} + \left( {D_{\lambda } + 2D_{\mu } } \right)\frac{{\partial^{2} w}}{{\partial z^{2} }} + \left( {D_{\lambda } + D_{\mu } } \right)\frac{{\partial^{2} u}}{\partial x\partial z} = \rho \frac{{\partial^{2} w}}{{\partial t^{2} }}, \\ \end{aligned} $$

(4)

Putting $\left\{ {u,\,w} \right\} = \left\{ {U\left( z \right), \, W\left( z \right)} \right\}{\text{e}}^{i(\eta t - kx)}$ in above equations, where $\eta$ is angular frequency. Then we have

$$ \begin{aligned} & \left[ {\left( {\overline{{D_{\mu } }} - \frac{P}{2}} \right)D^{2} + \eta^{2} \rho - k^{2} \left( {\overline{{D_{\lambda } }} + 2\overline{{D_{\mu } }} } \right)} \right]U - \left[ {ik\left( {\overline{{D_{\lambda } }} + \overline{{D_{\mu } }} + \frac{P}{2}} \right)} \right]DW = 0, \\ & \left[ {\left( {\overline{{D_{\lambda } }} + 2\overline{{D_{\mu } }} } \right)D^{2} + \eta^{2} \rho - k^{2} \left( {\overline{{D_{\mu } }} + \frac{P}{2}} \right)} \right]W - \left[ {ik\left( {\overline{{D_{\lambda } }} + \overline{{D_{\mu } }} } \right)} \right]DU = 0, \\ \end{aligned} $$

(5)

Now substituting $\left\{ {U\left( z \right), \, W\left( z \right)} \right\} = \left\{ {E{\text{e}}^{skz} , \, F{\text{e}}^{skz} } \right\}$ in Eqs. (5), we obtain

$$ \begin{aligned} & \left( {B_{1} s^{2} + B_{2} } \right)E - \left( {isB_{3} } \right)F = 0 \\ & \left( {A_{1} s^{2} + A_{2} } \right)F - \left( {isA_{3} } \right)E = 0, \\ \end{aligned} $$

(6)

where, $B_{1} = \left( {\overline{{D_{\mu } }} - \frac{P}{2}} \right),\,\,$$B_{2} = \frac{{\eta^{2} \rho }}{{k^{2} }} - \left( {\overline{{D_{\lambda } }} + 2\overline{{D_{\mu } }} } \right),\,\,$$B_{3} = \left( {\overline{{D_{\lambda } }} + \overline{{D_{\mu } }} + \frac{P}{2}} \right),\,\,$$A_{1} = \left( {\overline{{D_{\lambda } }} + 2\overline{{D_{\mu } }} } \right),\,\,$$A_{2} = \frac{{\eta^{2} \rho }}{{k^{2} }} - \left( {\overline{{D_{\mu } }} + \frac{P}{2}} \right)$, $A_{3} = \left( {\overline{{D_{\lambda } }} + \overline{{D_{\mu } }} } \right),\,\,\overline{{D_{\mu } }} = \mu \left( {1 + iQ_{1}^{ - 1} } \right),\,\,\overline{{D_{\lambda } }} = \lambda \left( {1 + iQ_{2}^{ - 1} } \right),\,\,\,Q_{1}^{ - 1} = \frac{{\mu_{0} \eta }}{\mu }$ and $Q_{2}^{ - 1} = \frac{{\lambda_{0} \eta }}{\lambda }.$ Here, $Q_{1}^{ - 1}$ and $Q_{2}^{ - 1}$ are dissipation factors of viscoelastic medium [9].

We have a following biquadratic equation for the non-trivial solution of the above two equations

$$ s^{4} + a_{1} s^{2} + a_{2} = 0, $$

(7)

where, $a_{1} = \left( {\frac{{(\rho c^{2} )/(1 + i\delta )^{2} - \overline{{D_{\mu } }} - P/2}}{{\overline{{D_{\lambda } }} + 2\,\overline{{D_{\mu } }} }}} \right) + \left( {\frac{{(\rho c^{2} )/(1 + i\delta )^{2} - \overline{{D_{\lambda } }} - 2\,\overline{{D_{\mu } }} }}{{\,\overline{{D_{\mu } }} - P/2}}} \right) + \left( {\frac{{\overline{{D_{\lambda } }} + \,\overline{{D_{\mu } }} }}{{\overline{{D_{\lambda } }} + 2\,\overline{{D_{\mu } }} }}} \right)\left( {\frac{{\overline{{D_{\lambda } }} + \,\overline{{D_{\mu } }} + P/2}}{{\overline{{D_{\mu } }} - P/2}}} \right)$ and $a_{2} = \left( {\frac{{(\rho c^{2} )/(1 + i\delta )^{2} - \overline{{D_{\mu } }} - P/2}}{{\overline{{D_{\lambda } }} + 2\,\overline{{D_{\mu } }} }}} \right)\left( {\frac{{(\rho c^{2} )/(1 + i\delta )^{2} - \overline{{D_{\lambda } }} - 2\,\overline{{D_{\mu } }} }}{{\,\overline{{D_{\mu } }} - P/2}}} \right)$.

Solution of Eqs. (7) can be obtained as

$$ \begin{aligned} & u = \left( {\sum\limits_{r = 1,2} {E_{i} {\text{e}}^{{ - ks_{r} z}} } + E_{3} {\text{e}}^{{ks_{1} z}} + E_{4} {\text{e}}^{{ks_{2} z}} } \right){\text{e}}^{i(\eta t - kx)} \\ & w = \left( {\sum\limits_{r = 1,2} {F_{r} {\text{e}}^{{ - ks_{r} z}} } + F_{3} {\text{e}}^{{ks_{1} z}} + F_{4} {\text{e}}^{{ks_{2} z}} } \right){\text{e}}^{i(\eta t - kx)} , \\ \end{aligned} $$

(8)

where, $E_{r}$ and $F_{r}$ are arbitrary constants and $s_{r}$ are the roots of bi-quadratic Eq. (7) (for r = 1, 2). But, we have a relation $F_{r} = n_{r} E_{r}$ from (6). Therefore, the appropriate solution can be obtained as

$$ \begin{aligned} & u = \left( {\sum\limits_{r = 1,2} {E_{r} {\text{e}}^{{ - ks_{r} z}} } + E_{3} {\text{e}}^{{ks_{1} z}} + E_{4} {\text{e}}^{{ks_{2} z}} } \right){\text{e}}^{i(\eta t - kx)} \\ & w = \left( {\sum\limits_{r = 1,2} {n_{r} E_{r} {\text{e}}^{{ - ks_{r} z}} } + n_{3} E_{3} {\text{e}}^{{ks_{1} z}} + n_{4} E_{4} {\text{e}}^{{ks_{2} z}} } \right){\text{e}}^{i(\eta t - kx)} , \\ \end{aligned} $$

(9)

where, $n_{r} = \frac{{is_{r} A_{3} }}{{A_{1} s_{r}^{2} + A_{2} }}.$

4 Boundary conditions

• 1. At $z = 0$

  • (a) $\phi_{13} = 0$

  • (b) $\phi_{33} = 0$

• 2. At $z = h$

  • (a) $u = 0$

  • (b) $w = 0$

The above boundary conditions lead to a homogeneous algebraic system of equations with the help of Eq. (9) as

$$ \left( {\begin{array}{*{20}c} {\alpha_{11} } & {\alpha_{12} } & {\alpha_{13} } & {\alpha_{14} } \\ {\alpha_{21} } & {\alpha_{22} } & {\alpha_{23} } & {\alpha_{24} } \\ {\alpha_{31} } & {\alpha_{32} } & {\alpha_{33} } & {\alpha_{34} } \\ {\alpha_{41} } & {\alpha_{42} } & {\alpha_{43} } & {\alpha_{44} } \\ \end{array} \left| {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ {A_{3} } \\ {A_{4} } \\ \end{array} } \right.} \right) = 0, $$

(10)

where, $\alpha_{11} = n_{1} i - s_{1} ,$$\alpha_{12} = n_{2} i - s_{2} ,$$\alpha_{13} = n_{3} i + s_{1} ,$$\alpha_{14} = n_{4} i + s_{2} ,$$\alpha_{21} = \overline{{D_{\lambda } }} n_{1} s_{1} - i\overline{{D_{\mu } }}$$\alpha_{22} = \overline{{D_{\lambda } }} n_{2} s_{2} - i\overline{{D_{\mu } }} ,$$\alpha_{23} = \overline{{ - D_{\lambda } }} n_{3} s_{1} - i\overline{{D_{\mu } }} ,$$\alpha_{24} = \overline{{ - D_{\lambda } }} n_{4} s_{2} - i\overline{{D_{\mu } }} ,$$\alpha_{31} = {\text{e}}^{{s_{1} x(1 + i\delta )}} ,$$\alpha_{32} = {\text{e}}^{{s_{2} x(1 + i\delta )}} ,$$\alpha_{33} = {\text{e}}^{{ - s_{1} x(1 + i\delta )}} ,$$\alpha_{34} = {\text{e}}^{{ - s_{2} x(1 + i\delta )}} ,$$\alpha_{41} = n_{1} {\text{e}}^{{s_{1} x(1 + i\delta )}} ,$$\alpha_{42} = n_{2} {\text{e}}^{{s_{2} x(1 + i\delta )}} ,$$\alpha_{43} = n_{3} {\text{e}}^{{ - s_{1} x(1 + i\delta )}}$ and $\alpha_{44} = n_{4} {\text{e}}^{{ - s_{2} x(1 + i\delta )}} .$

For such a system of simultaneous equations to have a non-trivial solution, it is necessary for the determinant of the coefficient matrix $\left| {\alpha_{ij} } \right|;\,\,(for\,\,i,j = 1,2,3,4)$ to be zero, i.e., $\left| {\alpha_{ij} } \right| = 0,$ and its real part $\text{Re} \left| {\alpha_{ij} } \right| = 0,$ provides dispersion relation associated with phase velocity $\left( {V_{\text{p}} = c/\beta } \right)$, whereas the imaginary part $\text{Im} \left| {\alpha_{ij} } \right| = 0,$ gives damping relation associated with damped velocity $\left( {V_{\text{d}} = c/\beta } \right)$ for the Rayleigh wave. Considering the wave number $k = k_{1} + ik_{2} \,({\text{say}})$ as a complex number, then we have

$$ k = k_{1} (1 + i\delta ), $$

(11)

where, $\delta = \frac{{k_{2} }}{{k_{1} }}$ is dimensionless attenuation coefficient; $k_{1} ,k_{2}$ are real. Therefore, the velocity c of the wave can be evaluated by the relation

$$ \eta = \text{Re} [k]c. $$

(12)

5 Numerical computations and discussions

To execute the comparative study of the effects of dimensionless parameters such as attenuation coefficient $(\delta )$, dissipation factors $(Q_{1}^{ - 1} ,\,\,Q_{2}^{ - 1} )$ and initial stress parameter on the dimensionless phase velocity $\text{(}V_{\text{p}} = c/\beta \text{)}$ and dimensionless damped velocity $\text{(}V_{\text{d}} = c/\beta \text{)}$ with respect to the real wave number $(k_{1} h )$ of the wave, we have taken numerical data $\mu = 32.3\,{\text{GPA}}$$\lambda = 42.9\,{\text{GPA}}$ and $\rho = 2.802\,\,{\text{g/cm}}^{3}$ from Gubbins [10]. Minute observation of all figures concludes that the as the wave number (k₁h) is decreasing phase velocity (V_p) is increasing, whereas damped velocity (V_d) increasing wrt the wave number (k₁h) (Table 1).

Table 1 Fixed values of parameters

Figure 2 describes the effect of attenuation coefficient $\left( \delta \right)$ arising due to the complex wave number on the phase and damped velocities of Rayleigh waves, respectively. It is clear from the figure that phase velocity and damped velocity both are decreasing as the magnitude of attenuation coefficient increasing. The varying effect of attenuation coefficient is more prominent on the damped velocity as compare to the phase velocity.

Fig. 2

Variation of attenuation coefficient $(\delta ) ,$ for a phase velocity $\left( {V_{\text{p}} = c/\beta } \right)$ and b damped velocity $\left( {V_{\text{d}} = c/\beta } \right)$

Figure 3 reveals the effect of dissipation factor $\left( {Q_{1}^{ - 1} } \right)$ (associated with the Lames’ Constant $\mu$ of the strip) on the phase and damped velocities of Rayleigh waves, respectively. The meticulous inspection of delineates that phase velocity of the wave increasing, while the damped velocity is decreasing as the magnitude of $Q_{1}^{ - 1}$ increasing. The varying effect of $Q_{1}^{ - 1}$ is negligible on the phase velocity as compare to the damped velocity.

Fig. 3

Variation of dissipation factor $Q_{1}^{ - 1}$ due to lame’s constants $\lambda$ for a phase velocity $\left( {V_{\text{p}} = c/\beta } \right)$ and b damped velocity $\left( {V_{\text{d}} = c/\beta } \right)$

In Fig. 4, the impacts of dissipation factor $\left( {Q_{2}^{ - 1} } \right)$ (associated with the Lames’ Constant $\lambda$ of the strip) on the phase and damped velocities of Rayleigh waves, respectively. It has been found from the figure that phase velocity and damped velocity both are increasing as the magnitude $Q_{2}^{ - 1}$ increasing. Moreover, the varying effect of $Q_{2}^{ - 1}$ is notable on the damped velocity.

Fig. 4

Variation of dissipation factor $Q_{2}^{ - 1}$ due to lame’s constants $\mu$ for a phase velocity $\left( {V_{\text{p}} = c/\beta } \right)$ and b damped velocity $\left( {V_{\text{d}} = c/\beta } \right)$

The curves plotted in Fig. 5 elucidate the effect of initial stress parameter $\left( \varOmega \right)$ on the phase and damped velocities of Rayleigh waves, respectively. The figure reflects that $\varOmega$ has increasing effect on the phase velocity, whereas it has mixed impact on the damped velocity. The varying effect of $\varOmega$ is very negligible on the phase velocity as compare to the damped velocity (Fig. 5).

Fig. 5

Variation of initial stress parameter $\varOmega = P/2\mu$ for a phase velocity $\left( {V_{\text{p}} = c/\beta } \right)$ and b damped velocity $\left( {V_{\text{d}} = c/\beta } \right)$

6 Conclusion

Within the framework of a pre-stressed Voigt type viscoelastic strip of finite thickness an analytical study has been carried out for the Rayleigh wave propagation. Numerical computation and graphical illustrations have been performed to set forth the analytical findings of parametric effects on the velocity profile of the wave. The important findings emerged in this study are:

• 1. The small variation in the magnitude of parameters makes a significant impact on the damped velocity. On the other hand, it has a low impact on the phase velocity of the wave.

• 2. Both dissipation factors and initial stress have proportional impact on the phase velocity of the wave, whereas attenuation coefficient has inverse impact on the phase velocity.

• 3. The dissipation factor associated with the Lames’ Constant $\lambda$ has proportional impact on the damped velocity, whereas attenuation coefficient and the dissipation factor associated with the Lames’ Constant $\mu$ have inverse impact on the damped velocity. Contrary to all parameters, initial stress has a mixed effect on the damped velocity of the wave.

The present study has possible applications in the geophysical prospecting. It can be useful for the study of seismic waves generated by artificial explosions and can provide valuable information about the selection of proper structural materials in the area of construction work.