Sliding mode control method for three-phase induction motor with magnetic saturation

Abstract

This study applies the sliding mode control technique to control the three-phase induction motor under magnetic saturation. Based on the field-oriented control technique, the proposed sliding mode controller is decoupled into two independent controllers for the stator flux and rotor speed. In addition, the sliding surface and reaching laws are improved to be able to increase the convergence rate and reduce discontinuity phenomena. The simulation and experimental results of the three-phase 1-hp induction motor in magnetic saturation mode will be addressed clearly to show the effectiveness and stability of the proposed control method in ensuring that the motor torque exceeds 5× the rated value.

1 Introduction

The control of a three-phase induction motor (TIM) is always one of the attractive research directions due to its applications in industry today [1,2,3]. In particular, the TIM control in the condition of magnetic saturation is also an important challenge that needs to be solved effectively [4,5,6,7,8,9,10]. As is well known, under the state of magnetic saturation, the TIM can produce higher torque, which is very useful for practical systems that are limited by the rated power/torque of systems [4, 5]. The authors in [6] introduced a direct torque control for a saturated induction motor, which applied a Kalman filter to estimate the speed and flux. This method achieved good tracking control performances for the flux and torque. Accetta et al. in [7] presented a feedback linearization control method for the induction motor in the presence of the magnetic saturation of the iron core. This method can be used when it was satisfied with the selection of a nonlinear function that interpolated the magnetic parameters with the rotor magnetization current and the corresponding magnetic characteristic. By applying the vector-oriented control (VOC) method, the authors in [9] proposed a dual optimization algorithm based on a Luenberger-type interconnected observer to control the TIM system under the magnetic saturation conditions. However, due to complexity of the proposed algorithm [9], the experimental works still need to be studied carefully before it can be deployed. In fact, in order to achieve the best control effects for the TIM with magnetic saturation, the proposed control methods need to be designed with a simple structure, minimizing the computational burden.

In TIM control, the field-oriented control (FOC) method can be a well-known method. It can be considered as an important derivative for development of the decoupling control technique of d-q currents [1], where two independent controllers for flux and speed can be easily exploited in a convenient structure. And by incorporating the VOC technique, the sliding mode control (SMC) methods, with their advantages [11,12,13], can be applied to control the TIM system [14,15,16,17,18,19]. As is known, the SMC techniques always show the merits in ensuring the tracking control and robustness of the control system [11, 12]. However, the SMC also presents a challenge in dealing with the chattering phenomenon under the effect of the sliding switching mechanism [13]. Wai and Liu in [14] also applied SMC-based nonlinear decoupled control to linear induction motor servo-drive, including two SMC controllers for flux and thrust force, and obtained good results. However, the sign(.) functions [16, 18] are applied in the SMC controllers, which can produce the chattering phenomenon if the control gains are not selected appropriately. In order to solve this problem, our previous study in [19] proposed a nonlinear smooth exponential function to replace the sign(.) function. However, by applying a lowpass filter to SMC signals [19], the response rate of the control system can be reduced.

In this study, the FOC and SMC techniques will be used to control the TIM under magnetic saturation. For magnetic saturation, the investigation of the saturated induction motor will be performed first to provide full saturation characteristics. In magnetic saturation mode, the proposed SMC method will be implemented to ensure the tracking control of stator flux and rotor speed. From this base, the SMC controller can control the motor torque more than the rated torque, guaranteeing the tracking motor speed and the stability of the control system. In order to achieve this purpose, the decoupled control-based SMC controller is divided into two independent SMC controllers, one for flux control and the other for speed control. By applying suitable sliding surface and nonlinear smooth function to the proposed control inputs, the response speed, convergence, and discontinuity of the control system will be improved. In addition, the SMC laws is derived from the Lyapunov theorem to ensure the stability of the proposed control system.

The research is structured as follows. Section 2 describes the TIM dynamics model and the investigation of magnetic saturation. In Section 3, the SMC controllers are presented. The simulation and experimental result systems are provided in Section 4. Finally, conclusion is drawn in Section 5.

2 Preliminaries

2.1 System description

The nonlinear model of TIM system with magnetic saturation is standardized by the conventional magnetic circuit model of a pair of rotor and stator [4, 5], as shown in Fig. 1. In which, the nonlinear inductances represent the magnetic saturation in rotor and stator system. Therefore, the model of a pair of rotor and stator is expanded to TIM model with an infinite number of pairs of rotor and stator, in the form of an infinite number of tooth pairs. This model is compatible with the Blondel–Park transformation [5]. Figure 2 describes the equivalent electric circuit of rotor–stator pair. The superscript $t$ indicates an inductance or function according to only a single tooth. The flux linkages, $f_{s}^{t} (.),f_{r}^{t} (.),L_{s}^{t} ,L_{r}^{t} ,L_{l}^{t}$, are the nonlinear parts that will cause saturation of rotor and stator. The scalar function, $f(.)$, presents the relationship between input amplitude and output amplitude, so the relationship between flux and current can be provided as the following form:

$$ \vec{i} = F(\vec{\varphi }) = f(\left\| {\vec{\varphi }} \right\|)\frac{{\vec{\varphi }}}{{\left\| {\vec{\varphi }} \right\|}} $$

(1)

where the $\frac{{\vec{\varphi }}}{{\left\| {\vec{\varphi }} \right\|}}$ term may be considered as an inductance that varies follow the function $\left\| {\vec{\varphi }} \right\|$, so that $\vec{i} = \frac{{\left\| {\vec{\varphi }} \right\|}}{{L(\left\| {\vec{\varphi }} \right\|)}}$. It notes that two modeled nonlinear parts are the $F_{s} (.)$ and $F_{r} (.)$ that present saturation properties in the saturation part of all tooth pairs of the stator and rotor, and they contain only terms of quadratic and higher. Thus, the electrical dynamics of the TIM system, including the saturation of flux with both rotor and stator, can be described as the following system of equations:

$$ \left\{ \begin{gathered} \vec{i}_{s} = F_{s} (\vec{\varphi }_{s} ) + (\frac{1}{{L_{s} }} + \frac{1}{{L_{l} }})\vec{\varphi }_{s} - \frac{1}{{L_{l} }}\vec{\varphi }_{r} \hfill \\ \vec{i}_{r} = F_{r} (\vec{\varphi }_{r} ) + (\frac{1}{{L_{r} }} + \frac{1}{{L_{l} }})\vec{\varphi }_{r} - \frac{1}{{L_{l} }}\vec{\varphi }_{s} \hfill \\ \dot{\vec{\varphi }}_{s} = \vec{u}_{s} - R_{s} \vec{i}_{s} \hfill \\ \dot{\vec{\varphi }}_{r} = \vec{u}_{r} - R_{r} \vec{i}_{r} \hfill \\ \end{gathered} \right. $$

(2)

where over dot (.) indicates the differentiation with respect to time. In addition, based on the symmetric property of electric machine, the resistance matrices, $R_{s}$ and $R_{r}$ can be obtained by multiplying an identity matrix by scalar resistances. And, the subscript $s$ or $r$ on flux linkage $\varphi$ or current $i$ shows the stator and rotor quantities. Moreover, the subscript $s$ also indicates that the flux or current is measured in the stator reference frame (the stationary reference frame). And, the subscript $r$ also indicates that the flux or current is measured in the rotor reference frame (the rotation reference frame).

Fig. 1

Structure of a tooth pair

Fig. 2

Electric circuit model of a tooth pair

By choosing the reference frame associated with the stator flux vector, the angular speed of the coordinate axes is equal to the angular speed of the stator flux vector, and d-axis of the coordinate system coincides with the stator flux vector. Therefore, the following results can be obtained as:

$$ \varphi_{sq} = \varphi_{rq} = 0 $$

(3)

$$ T_{e} = 1.5p(\varphi_{sd} i_{sq} ) $$

(4)

$$ \omega_{r} = \frac{{u_{sq} - R_{s} i_{sq} }}{{\varphi_{sd} }} $$

(5)

And the dynamics equation for stator flux and current can be presented as:

$$ \dot{\varphi }_{sd} = u_{sd} - R_{s} i_{sd} $$

(6)

$$ \begin{aligned} \dot{i}_{{sq}} = & \frac{1}{{L_{l} }}\left[ { - \omega \varphi _{{rd}} + \frac{{\varphi _{{rd}} }}{{\varphi _{{sd}} }}(u_{{sq}} - R_{s} i_{{sq}} )} \right] \\ & - R_{r} \left( {\frac{1}{{L_{r} }} + \frac{1}{{L_{l} }}} \right)i_{{sq}} - R_{r} \frac{{f_{r} (\left\| {\varphi _{r} } \right\|)}}{{\left\| {\varphi _{r} } \right\|}}i_{{sq}} \\ \end{aligned} $$

(7)

2.2 Saturation characteristic

In this section, the saturation characteristics will be investigated through the simulation process to serve as a basis for the design of the proposed method. First, the system parameters of TIM model that are provided in Table 1 as follows:

Table 1 The TIM model parameters

By applying MATLAB/Simulink software, the survey strategy is performed on the TIM system with or without magnetic saturation by an open loop control system, as shown in Fig. 3. And at different operating conditions, in the cases of no load and variable loads (from 0 to 5 Nm), the effects of saturation on the TIM system can be clearly obtained. In Fig. 4, the motor speed increases rapidly when the stator voltage increases from 200 to 600 V. Meanwhile, increasing the torque from 0 N.m to 5 N.m can reduce the motor speed a bit. Therefore, the torque and stator voltage affect the control performance for the motor speed over the entire operating range. For more details, when the load torque or stator voltage increases, the increasing speed becomes slower, and the decreasing speed becomes faster in the case of the same control amplitude.

Fig. 3

Open loop control system

Fig. 4

Effect of stator voltage and torque on motor speed

Next, Table 2 shows the investigated results when $T_{m} = 0$ N.m. When the voltage is increased higher, the stator current in saturated case is larger than in the unsaturated case. In addition, by observing Fig. 5, with saturation parameters in Table 2, at the high voltage levels, the relationships between the voltage and current in saturated case and unsaturated case are distinctly different. In the other hand, in case the rotor is locked, or infinite inertia ($J = \infty$), when the stator voltage varies from 200 to 600 V, then the stator currents in both saturated and unsaturated cases are very close. This shows that when rotor is locked then impact of saturation is negligible.

Table 2 The saturation parameters of motor

Fig. 5

Effect of stator voltage and torque on motor speed

Figures 6 and 7 present the characteristics of stator current and stator flux vector when the load torque varies from 0 to 5 Nm with the stator voltage is 400 V. These results show that the stator current in the saturated case increases faster and larger than the stator current in the unsaturated case, according to the increasing of the load torque. Finally, based on this investigation process, the characteristics of the TIM under the magnetic saturation condition, with the stator current, voltage flux and rotor speed, have been provided clearly. And they show that if a controller is designed to work well in the saturated environment, then it can achieve an optimal performance at higher torque levels.

Fig. 6

The stator current characteristics

Fig. 7

The stator flux characteristic

3 Control algorithms

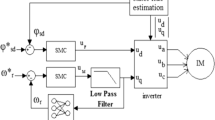
This study will apply the SMC technique to control the TIM under magnetic saturation conditions, such that $\varphi_{sd}^{{}} (t) \to \varphi_{sd}^{*} (t)$ and $\omega_{r} (t) \to \omega_{r}^{*} (t)$ as the time tends to infinite $t \to \infty$, with $\varphi_{sd}^{*} (t),\omega_{r}^{*} (t)$ are the desired stator flux and rotor speed. The proposed control system is shown in Fig. 8.

Fig. 8

The SMC proposed control system

It noted that the results in (6) are completely independent of the magnetic saturation. Meanwhile, the result in (7) is dependent of the nonlinear part, $f_{r} (.)$, which causes the saturation phenomenon. However, the stator current, $i_{sq}$ can be directly measured from the TIM. Therefore, the proposed controller for TIM can be decoupled into two parts as follows. The fist controller uses $u_{sd}$ is the control input for the stator flux $\varphi_{sd}^{{}}$, and the second controller uses $u_{sq}$ is the control input for the stator current. This is basic for the designing the control inputs for the stator flux and rotor speed.

3.1 SMC for the stator flux

The sliding surface for the flux control is applied as the following form:

$$ S_{F} = c_{F} e_{F} + k_{iF} \int\limits_{0}^{t} {e_{F} d\tau } $$

(8)

where $e_{F} = \varphi_{sd}^{*} - \varphi_{sd}$, $c_{F} ,k_{iF}$ are the positive constants. And by differentiating both side of (8) with respect to time, yields:

$$ \dot{S}_{F} = c_{F} \dot{e}_{F} + k_{iF} e_{F} = c_{F} \dot{\varphi }_{sd}^{*} + k_{iF} e_{F} - c_{F} \dot{\varphi }_{sd} $$

(9)

By substituting (6) into (9), we have:

$$ \dot{S}_{F} = c_{F} \dot{\varphi }_{sd}^{*} + k_{iF} e_{F} - c_{F} (u_{sd} - R_{s} i_{sd} ) $$

(10)

From the result in (10), based the SMC technique [20], the proposed control input for the stator flux control is proposed as the following scheme:

$$ \begin{aligned} u_{sd} &= \dot{\varphi }_{sd}^{*} + \frac{{k_{iF} }}{{c_{F} }}e_{F} + R_{s} i_{sd} \\ & \quad + \frac{1}{{c_{F} }}(\varepsilon_{F} Relay(S_{F} ) + k_{F} S_{F} ) \\ \end{aligned} $$

(11)

where $\varepsilon_{F} ,k_{F}$ are the positive constants. In the proposed control input for the control of stator flux, the term $k_{F} S_{F}$ is added to accelerate the convergence of the states of the sliding surface. The term $Relay(S_{F} )$ is like the sign(.) function in the traditional SMC controller, is defined as:

$$ Relay(S_{F} ) = \frac{{S_{F} }}{{\left| {S_{F} } \right| + \delta_{F} }} $$

(12)

where $\delta_{F}$ is a positive constant. As shown in Fig. 9, the $Relay(S_{F} )$ function is clearly a nonlinear smooth function that different with the sign(.). Therefore, this part is added to address the disadvantages of the sign(.) function in the SMC controller, such as chattering phenomena and discontinuity of the control signals.

Fig. 9

The shapes of the Relay (.) and Sign (.) functions

3.2 SMC for the rotor speed

A similar way with the stator flux controller, the sliding surface for the speed control is applied as the following form:

$$ S_{M} = c_{M} e_{M} + k_{iM} \int\limits_{0}^{t} {e_{M} d\tau } $$

(13)

where $e_{M} = \omega_{r}^{*} - \omega_{r}$, $c_{M} ,k_{iM}$ are the positive constants. And by differentiating both side of (13) with respect to time, yields:

$$ \dot{S}_{M} = c_{M} \dot{e}_{M} + k_{iM} e_{M} = c_{M} \dot{e}_{M} + k_{iM} \omega_{r}^{*} - k_{iM} \omega_{r} $$

(14)

By substituting (5) into (14), we have:

$$ \dot{S}_{M} = c_{M} \dot{e}_{M} + k_{iM} \omega_{r}^{*} + \frac{{k_{iM} }}{{\varphi_{sd} }}R_{s} i_{sq} - \frac{{k_{iM} }}{{\varphi_{sd} }}u_{sq} $$

(15)

And, based on the result in (15), by applying the SMC technique [20], the proposed control input for the rotor speed control is proposed as the following scheme:

$$ \begin{aligned} u_{sq} &= \frac{{\varphi_{sd} }}{{k_{iM} }}c_{M} \dot{e}_{M} + \varphi_{sd} \omega_{r}^{*} + R_{s} i_{sq} \\ & \quad + \frac{{\varphi_{sd} }}{{k_{iM} }}(\varepsilon_{M} Relay(S_{M} ) + k_{M} S_{M} ) \\ \end{aligned} $$

(16)

where $\varepsilon_{M} ,k_{M}$ are the positive constants. The parts, $Relay(S_{M} )$ and $k_{M} S_{M}$ are defined and considered to be similar to those of the SMC controller for the stator flux control.

3.3 Stability analysis

Theorem

By considering that the TIM dynamics are at magnetic saturation in Eqs. (1) – (7). If the SMC laws for the stator flux control and rotor speed control are designed as (11) and (16), then the stability of closed-loop control system in (10) and (15) is guaranteed, and sliding surfaces also converge to the stable equilibrium points as time tends to infinite.

Proof (1)

First, by considering the closed-loop control system for the stator flux, the first Lyapunov candidate is addressed as the following form:

$$ V_{F} (S_{F} (t)) = \frac{1}{2}S_{F}^{2} (t) $$

(17)

By differentiating (17) with respect to time, and using the result in (10), the following result can be obtained as:

$$ \dot{V}_{F} = S_{F} (c_{F} \dot{\varphi }_{sd}^{*} + k_{iF} e_{F} - c_{F} (u_{sd} - R_{s} i_{sd} )) $$

(18)

And, by applying the SMC control input in (11) to (18), it yields:

$$ \begin{aligned} \dot{V}_{F} = S_{F} (c_{F} \dot{\varphi }_{sd}^{*} + k_{iF} e_{F} - c_{F} (u_{sd} - R_{s} i_{sd} )) \\= - S_{F} (\varepsilon_{F} Relay(S_{F} ) + k_{F} S_{F} ) \\ = - k_{F} S_{F}^{2} - \varepsilon_{F} \frac{{S_{F}^{2} }}{{\left| {S_{F} } \right| + \delta_{F} }} \\ \le - k_{F} S_{F}^{2} \\ \end{aligned} $$

(19)

From the result in (19), $\dot{V}_{F} \le 0$, it is easy to conclude that the stability of the SMC closed-loop control system for the stator flux control is guaranteed with asymptotic stability, and $S_{F}$ will converge to the stable equilibrium as time tends to infinite [20].

Proof (2)

Next, by considering the closed-loop control system for the rotor speed control, the second Lyapunov candidate can be considered as:

$$ V_{M} (S_{M} (t)) = \frac{1}{2}S_{M}^{2} (t) $$

(20)

By differentiating (20) with respect to time, and using the result in (15), the following result can be obtained as:

$$ \dot{V}_{M} = S_{M} (c_{M} \dot{e}_{M} + k_{iM} \omega_{r}^{*} + \frac{{k_{iM} }}{{\varphi_{sd} }}R_{s} i_{sq} - \frac{{k_{iM} }}{{\varphi_{sd} }}u_{sq} ) $$

(21)

And, by applying the SMC control input in (16) to (21), it yields:

$$ \begin{gathered} \dot{V}_{M} = - S_{M} (\varepsilon_{M} Relay(S_{M} ) + k_{M} S_{M} ) \\ = - k_{M} S_{M}^{2} - \varepsilon_{M} \frac{{S_{M}^{2} }}{{\left| {S_{M} } \right| + \delta_{M} }} \\ \le - k_{M} S_{M}^{2} \\ \end{gathered} $$

(22)

From the result in (22), $\dot{V}_{M} \le 0$, in a similar way to Proof(1), the stability of the SMC closed-loop control system for the rotor speed control is guaranteed the stability of the SMC closed-loop control system for the stator flux control is guaranteed with asymptotic stability, and $S_{M}$ will also converge to the stable equilibrium as time tends to infinite [20].

From the results in the Proof (1) and Proof (2), we can confirm that the theorem has been verified successfully. Thus, the proposed control strategy also has ensured for the stability and the tracking control of the TIM control system.

Remark 1

By substituting the proposed SMC control laws (16) and (11) into Eqs. (5) and (6), respectively, we have the following results as:

$$ \omega_{r} = \frac{1}{{k_{iM} }}c_{M} \dot{e}_{M} + \omega_{r}^{*} + \frac{1}{{k_{iM} }}(\varepsilon_{M} Relay(S_{M} ) + k_{M} S_{M} ) $$

(23)

$$ \dot{\varphi }_{sd} = \dot{\varphi }_{sd}^{*} + \frac{{k_{iF} }}{{c_{F} }}e_{F} + \frac{1}{{c_{F} }}(\varepsilon_{F} Relay(S_{F} ) + k_{F} S_{F} ) $$

(24)

Therefore, the results in (23) and (24) show that, with the proposed SMC laws, the stator flux and rotor speed have not been affected by the stator resistors ($R_{s} ,R_{r}$) when the temperature changes.

Remark 2

The proposed SMC laws also are completely independent to the saturation parameters. In addition, by applying the smooth function $Relay(.)$ to replace traditional sign(.) function, the problems of chattering phenomena and discontinuity can be reduced effectively.

4 Simulation and experimental results

4.1 Simulation results

To address the effectiveness of the proposed method, the simulation model will be implemented as follows. The three-phase cascaded 3-level inverter is applied to control the TIM system, as shown in Fig. 10. The DC link $V_{{{\text{dc}}}} = 200({\text{VDC}})$, the sample time is $T_{s} = 40({\mu s})$, and the dead time is $2.5({\mu s})$, the carrier frequency is $f_{c} = 1250({\text{Hz}})$. The TIM parameters is provided in Table 1. The MATLAB/Simulink software is applied to implement the simulation process as follows.

Fig. 10

The 1-phase structure of the three-phase cascaded 3-level inverter (a) and its output (b)

Figure 11 shows the simulation results with the rated torque is 1 pu. In Fig. 11a, the tracking performance of the stator flux is guaranteed, meanwhile the measured torque has the overshoot points at the times of the speed rapid change. In Fig. 11b, when the desired speed changes then the tracking control for the rotor speed also has good results. It is noted that at lowest speed, 3 rad/s, then the phase A current reaches about 1.5 A.

Fig. 11

Simulation results with $T_{m}^{*} = 1\;{\text{pu}}$

When the torque changes over the rated torque, 5 pu, Fig. 12a shows that the good result can be obtained for tracking control of the stator flux, the measured torque is oscillated around the desired torque. In addition, Fig. 12b shows that the phase A current reaches a value of about 4 A at the lowest speed value of 3 rad/s, the measured speed fluctuates slightly at 3 rad/s, and still follows the desired speed well. This presents that as the torque increases, at the low values of the speed then the current increases, and the SMC controller try to increase the control action to overcome the saturation region of the main flux.

Fig. 12

Simulation results with the torque increases over 5-times rated torque

Figure 13a provides that when the desired torque is 5 pu and $R_{s}$ is increased by 2 times the initial value, the desired flux and measured flux coincide, the measured torque is overshoot at the points of rapidly changing speed. And, Fig. 13b shows that the measured speed still follows the set speed well but fluctuates strongly at the highest value 150 rad/s and the lowest 3 rad/s, the phase A current increases by about 5A at the lowest speed 3 rad/s. At this time, the controller still tries to increase the control action and overcome the saturation region of the main flux.

Fig. 13

Simulation results with $T_{m}^{*} = 5\;{\text{pu}}$ and $R_{s}$ increases 2 times

Finally, Fig. 14a shows that when the desired torque is 0–5 pu and resistors $R_{s} ,R_{r}$ increase 2 times the original value, with the participation of randomly distributed noise d(t) has amplitude of about ± 7 V, then the tracking performance of the flux control still has good results. Figure 14b shows that phase current A reaches a value of about 3A at the lowest speed value of 3 rad/s, as well as the tracking performance for the speed control is also ensured. In general, during the simulation, the proposed control method has shown to be effective in guaranteeing the stability, torque may increase beyond the rated value, the tracking errors achieve acceptable results under the magnetic saturation and various control conditions (resistances, disturbances).

Fig. 14

Simulation results with T^*_m = 5 pu and R_s, R_r increases 2 times with the randomly distributed noise d(t)

4.2 Experimental results

Figure 15 shows the experimental TIM model based on the OPAL-RT system. The OPAL-RT system has delivered eFPGASIM, the industry’s most powerful and intuitive FPGA-based real-time solution. As shown in Fig. 15, the OPAL-RT system includes a monitor part, an OP4510 real-time simulator system, and an OP8660 analog/digital input/output part. The parameters of experimental TIM model are the same as those of the simulation model. The motor speed is measured by the encoder 1024 pulses, and the phase currents are measured by the sensors LEM LF305-S. The saturation parameters are provided in Table 2.

Fig. 15

The OPAL-RT system and experimental TIM model

Figures 16, 17, and 18 show the experimental results with the desired speed is 150 rad/s. Under magnetic saturation, Fig. 16 provides the line voltage V_ab is 358 V with THD is 58.82 5, and the phase currents have average amplitude is 4.6 A with the THD is 20.77%. In Fig. 17, the torque reaches 5 times of the rated torque. The stator flux vector in Fig. 18 shows that the experimental result consists to the simulation result.

Fig. 16

The experimental results with $\omega_{m}^{*} = 150$ rad/s

Fig. 17

The experimental result of torque when $\omega_{m}^{*} = 150$ = 150 rad/s

Fig. 18

The experimental result of flux when $\omega_{m}^{*} = 150$ rad/s

Based on the simulation and experimental results, the proposed SMC method for the TIM system under saturation condition has achieved the advantage features as follows. The simulation results are like the experimental results, such that the measured speed of motor follows the desired speed from low to high, which shows the reasonableness of the proposed algorithm. At changing values of the desired speed, torque, resistance and noise, the tracking control performances are guaranteed. This first shows the stability of the proposed SMC method. In addition, the SMC law is capable of controlling torque exceeding 5 times rated value, the TIM control system remains stable when the resistances of stator and rotor change up to 2 times of initial value in the presence of noises and saturation.

5 Conclusions

This work has applied successfully the proposed SMC control strategy for the TIM system under magnetic saturation in both simulation and experimentation. First, in this study, the characteristics of the saturated TIM are survived to consider the saturation factor of the main flux. Second, based on the FOC technique, the independent SMC controller are proposed to control the stator flux and rotor speed. The SMC controllers are also improved in the capable of reducing the chattering and discontinuity phenomena and increasing the convergence of states. The proposed control system has proven the stability in both theoretical and experimental works in increasing the torque over 5 times the rated value. This proposed method can be considered as a good alternative control method for TIM in realistic applications. And, our upcoming studies are improving this method in the design of adaptive laws for the control gains of the SMC controllers.