Mathematical analysis of wind turbines dynamics under control limits: boundedness, existence, uniqueness, and multi time scale simulations

Abstract

In this study, a mathematical analysis of a wind turbine dynamics is presented. The model represented by control blocks and transfer functions taken from recognized papers and studies, is translated to a system of nonlinear differential algebraic equations. For easier computational and numerical study, we prove the existence of a unique terminal voltage solution, which eliminates the algebraic constraint. Our study provides rigorous proofs of boundedness, existence, and uniqueness for the initial value problem of the system, allowing for the assurance that convergent numerical solutions converge to a unique solution for a given initial condition. This allows scholars to have a free simulator that will aid in dynamical studies of wind turbines without the need for software and Simulink limitations. A safe region within grid parameter space (R and X) is defined, in which existence and uniqueness are guaranteed. We presented time scale analysis and simulations to show that the system can be studied in smaller sizes. Lastly, we introduce cases of two and three time scales.

1 Introduction

The future of humanity lies with renewable energies. There are many reasons that indicate the absolute necessity for the replacement of our energy systems. Some argue this case with economic justifications, while others lean on environmental concerns. Regardless of the reasons behind this need, we require additional understanding of the generation of renewable energies if we are to make this critical change. According to the United States’ Department of Energy [1], wind energy is the fastest growing renewable energy resource being utilized. This rapid expansion demands more scientific research and studies to understand the behavior and dynamics of wind turbine generators (WTGs) if we are to gain the most from this valuable resource. Governments and corporations alike are seeking to understand the challenges and consequences of integrating WTGs within large cities with/without other power systems. As a result of the complexities involved in the implementation of WTGs, research in control systems, power generation, and energy storage of WTGs has increased dramatically over the last decade.

Within the development of emerging technologies, applied mathematics offers the opportunity for increased scientific understanding and accuracy of the phenomena related to the new technology. Due to this, mathematical modeling and analysis needs to be involved in describing and studying WTGs. These mathematical studies provide valuable information in regards to the dynamics of a WTG. In addition, such scientific research provides more accurate results regarding stability, sensitivity, and simulation studies of WTGs.

Type-3 WTGs according to [2] are more efficient in extracting power from the air streams. Coefficients of Performance ($C_p$ curves) are relatively better for type-3 WTGs. Even though many studies focused on optimization of ($C_p$ curves) by developing new designs of WTGs blades such as [3], type-3 as in the studies [3,4,5] is able to provide an extraction efficiency up to 0.4–0.5 of the power available in the air streams. A detailed study about $C_p$ curves can be found in [3].

Due to better control characteristics and options, most agree that Doubly Fed Asynchronous/Induction Generator (DFAG/DFIG) is the future of WTG technologies. Also, it is easier and more practical to connect these type of generators to the grid. A detailed study describing this can be found in the literature review of [6] with citations to many sources in the literature that focus mainly on investigating the applicability of DFAG/DFIG technologies. In separate research, both General Electric [7, 8] and Electric Power Institute [9] suggest the use of DFAG/DFIG. Therefore, we consider Type 3 Doubly Fed Asynchronous/Induction Generator (DFAG/DFIG) in our study. WTGs with DFAG technology can be grouped in three directions of study. The first is studies focused on modeling, as in [10,11,12,13,14,15,16,17]. However [18,19,20], explain the modeling aspect in greater detail. The second direction includes studies focused on small signal stability and faults analysis of practical problems, as in [21, 22]. The third direction of study focuses on the sensitivity, such as [23, 24]. In [24], the authors showed how some of the parameter affected the dynamic behavior of type-3 DFAG. While a larger model with deeper study was analyzed in [23].

In our study, the main citations referenced while building the model are [7, 8, 22, 23]. In [8], the block diagrams cover the basic wind power extraction model and rotor model. Also, discussion about the reference speed, pitch control, and reactive power control in both the cases of power factor and supervisory voltage are provided. In [7], $C_p$ curves are discussed in more detail and two optional control blocks are added (active power and inertia controls). In [22], the model blocks and a simulation for small signal stability are provided. Also, a Simulink model was built and eigenvalues were computed in [22]. The paper [25] summarized some of the important results the General Electric (GE) team presented in [7, 8]. The GE team confirmed in their studies the reliability of using their model to represent WTG models for other companies that manufacture WTGs. Moreover, they have compared their simulations to a lot of scenarios and measured data. Because of the comparability, validation, citations to them, and the possibility of extending GE models to other WTGs, we consider them in our study.

No full time domain analysis or study was found in the literature for the research provided by GE and similar studies. This is despite such studies having been cited as some of the most significant resources towards the building of WTGs models. This is a problem, as it has triggered a cycle in which many scholars focus upon validating and re-validating the model that was based upon engineering experimentation and judgment, not on scientific mathematical analysis. Although the authors in [23] did built a part of the model mathematically for a sensitivity study while activating the pitch control, questions such as whether or how numerical solvers are reliable for simulations and mathematical studies were not addressed. No rigorous proofs or mathematical analysis were identified in the literature to confirm or deny the necessity of the control limits proposed in [7, 8] and many other sources. Also, without the uniqueness of solutions to the initial value problem, we can’t heavily trust simulations using numerical solvers to indicate the full picture of what is occurring within the wind turbine. This hasn’t been discussed or proven in any of the papers that built parts of the model in the form of differential equations, such as [6, 23, 24]. Without any available existence, uniqueness, and boundedness proofs, the mathematical analysis of these models and any resultant contribution is under doubt and subject to questioning. This missing element prevents us from significantly developing an acceptable understanding of the dynamics and stability of WTGs, especially when we integrate them with other power sources that have been more fully studied and analyzed mathematically. We need stronger theoretical analysis to the existent control system as a whole of WTGs to be able to develop new control theory for this emerging technology, and this is the focus of our paper.

In this paper, we layout the model in the form of a differential algebraic system in time domain. We then eliminate the algebraic constraint, allowing for the model to be in the form of a nonlinear system of differential equations (Sect. 2). We then provide a rigorous mathematical analysis by proving boundedness for the WTGs’ state variables, as well as their derivatives; important from a mechanical and electrical point of view. We then prove the existence and uniqueness for the dynamical system. We define a region in R and X space (Safe Region), in which existence and uniqueness are guaranteed (Sect. 3). For a reduced version of the model (low wind speeds), we perform two and three time scale analysis with simulations, which haven’t been previously provided within the literature (Sect. 4). The conclusions of our work is presented at the end.

2 Mathematical model of WTGs

By applying Inverse Laplace Transform to the transfer functions in [7, 8], a model of differential algebraic equations can be built. We did this process in a smaller case in [23, 26, 27] to study limited situations when the pitch control is activated and to study the effect of a Q drop function on the reactive power. Please refer to these references for descriptions about the blocks and groups we have in this paper. After we have the system in differential algebraic equations in Sect. 2.1, then we provide a proof to eliminate the algebraic constraint, which turns the system to differential equations system in Sect. 2.2.

2.1 Differential algebraic form of the system

Group 1: Two-mass rotor.

$$\begin{aligned}&\frac{dw_g}{dt} = \frac{1}{2H_g}\left[ - \frac{P_{elec}}{w_g+w_0}-D_{tg}(w_g-w_t) -K_{tg} \varDelta \theta _m\right] . \nonumber \\\end{aligned}$$

(1)

$$\begin{aligned}&\frac{dw_t}{dt} = \frac{1}{2H}\left[ \frac{P_{mech}}{w_t+w_0}+D_{tg}(w_g-w_t) +K_{tg} \varDelta \theta _m\right] . \nonumber \\\end{aligned}$$

(2)

$$\begin{aligned}&\frac{d(\varDelta \theta _m)}{dt} = w_{base}(w_g-w_t). \end{aligned}$$

(3)

A one-mass model can be used to simplify the two-mass model in group 1. This has been discussed in [7]. This one-mass differential equation was introduced in [24]. The following equation represents the one mass model:

$$\begin{aligned} \frac{dw}{dt} = \frac{1}{H w_{base}}\left[ P_{mech}-P_{elec}\right] . \end{aligned}$$

Whether tow-mass model is used (as in this document) or one-mass model, we have the following relations to be used:

$$\begin{aligned} P_{mech}= & {} \frac{1}{2}C_p(\lambda ,\theta ) \rho A_r v_{wind}^3\\= & {} \frac{1}{2} \left( \sum _{i=0}^{4} \sum _{j=0}^{4} \alpha _{i,j} \theta ^i\lambda ^j\right) \rho A_r v_{wind}^3 \end{aligned}$$

and,

$$\begin{aligned} P_{elec}=V I_{plv}. \end{aligned}$$

Group 2: Pitch control.

$$\begin{aligned} \frac{df_1}{dt}= & {} w_g+w_0-w_{ref}. \end{aligned}$$

(4)

$$\begin{aligned} \frac{df_2}{dt}= & {} P_{inp}-P_{stl}. \end{aligned}$$

(5)

$$\begin{aligned} \frac{d\theta }{dt}= & {} \frac{1}{T_p}\left[ K_{pp}(w_g+w_0-w_{ref})+K_{ip}f_1 \right. \nonumber \\&\left. +\,K_{pc}(P_{inp}-P_{stl})+K_{ic}(f_2-\theta )\right] . \end{aligned}$$

(6)

Group 3: Reference speed.

$$\begin{aligned} \frac{dw_{ref}}{dt} = \frac{1}{60}\left[ -0.75P_{elec}^2+1.59P_{elec}+0.63-w_{ref}\right] .\nonumber \\ \end{aligned}$$

(7)

Group 4: Power order.

$$\begin{aligned} \frac{dP_{inp}}{dt}= & {} \frac{1}{T_{pc}}\left[ (w_g+w_0)(K_{ptrq}\left( w_g+w_0-w_{ref}\right) \right. \nonumber \\&\left. +\,K_{itrq}f_1)-P_{inp}\right] . \end{aligned}$$

(8)

$$\begin{aligned} \frac{dw_{sho}}{dt}= & {} \frac{dP_{inp}}{dt} -\frac{dP_{stl}}{dt} - \frac{1}{T_w}w_{sho}. \end{aligned}$$

(9)

Group 5: Reactive power control (power factor case) and electrical control.

$$\begin{aligned}&\frac{dP_{1elec}}{dt}= \frac{1}{T_{pwr}}\left[ P_{elec}-P_{1elec}\right] . \end{aligned}$$

(10)

$$\begin{aligned}&\frac{dV_{ref}}{dt}= K_{Qi}\left[ Q_{cmd}-Q_{gen}\right] \end{aligned}$$

(11)

where,

$$\begin{aligned} Q_{gen}=\frac{V(E_q-V)}{X_{eq}}. \end{aligned}$$

$Q_{{ cmd}}$ is a part of group 5 and 6 and is given by

$$\begin{aligned} Q_{{ cmd}} = \left\{ \begin{array}{ll} P_{1elec}\cdot \tan ( PFA _{ref}) &{}\quad \text {Power factor case} \\ Q_{ord} &{}\quad \text {Supervisory voltage case} \\ \text {from another model or constant.} \end{array} \right. \end{aligned}$$

Group 6: Reactive power control (supervisory voltage case) and electrical control.

$$\begin{aligned}&\frac{dQ_{drop}}{dt}= \frac{1}{T_{lpqd}}\left[ Q_{ inpt }-Q_{drop}\right] . \end{aligned}$$

(12)

$$\begin{aligned}&\frac{dV_{1reg}}{dt}= \frac{1}{T_r}\left[ V_{reg}-V_{1reg}\right] . \end{aligned}$$

(13)

$$\begin{aligned}&\frac{dQ_{wvl}}{dt}= \frac{1}{T_v}\left[ K_{pv}(V_{ref}-V_{1reg}-V_{qd})-Q_{wvl}\right] . \end{aligned}$$

(14)

$$\begin{aligned}&\frac{dQ_{wvu}}{dt}= K_{iv}\left( V_{ref}-V_{1reg}-V_{qd}\right) . \end{aligned}$$

(15)

$$\begin{aligned}&\frac{dQ_{ord}}{dt}= \frac{1}{T_c}\left( Q_{wvl}+Q_{wvu}-Q_{ord}\right) . \end{aligned}$$

(16)

Equation (11) still holds in this group as well.

Fig. 1

Block diagram of wind turbine model

Group 7: Active power control and inertia control.

$$\begin{aligned}&\frac{dP_{avf}}{dt}= \frac{1}{T_{pav}}\left[ P_{avl}-P_{avf}\right] . \end{aligned}$$

(17)

$$\begin{aligned}&\frac{d({ fltdfwi})}{dt}= \frac{1}{T_{lpwi}}[{ dfdbwi}-{ fltdfwi}]. \end{aligned}$$

(18)

$$\begin{aligned}&\frac{d({ dpwi})}{dt}= \frac{K_{wi}}{T_{lpwi}}[{ dfdbwi}-{ fltdfwi}]- \frac{dpwi}{T_{wowi}}. \end{aligned}$$

(19)

Group 8: DFAG generator/converter.

$$\begin{aligned}&\frac{dE_{qcmd}}{dt}= K_{vi}[V_{ref}-V ]. \end{aligned}$$

(20)

$$\begin{aligned}&\frac{dE_q}{dt}= \frac{1}{0.02}[E_{qcmd}-E_q]. \end{aligned}$$

(21)

$$\begin{aligned}&\frac{dI_{plv}}{dt}= \frac{1}{0.02}\left[ \frac{P_{ord}}{V}-I_{plv}\right] . \end{aligned}$$

(22)

Group 9: The algebraic (network) equation (see [22]):

$$\begin{aligned} 0= & {} (V^2)^2-\left[ 2(P_{elec}R+Q_{gen}X)+E^2\right] V^2\nonumber \\&+\,(R^2+X^2)(P_{elec}^2+Q_{gen}^2). \end{aligned}$$

(23)

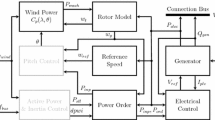
The dynamics of all control blocks and groups of differential equations is summarized in the block diagrams of Fig. 1. The model’s parameter values can be taken from [7, 8, 22]. A summary for the needed parameter values including $C_p$ curves’coefficients is provided in Tables 1 and 2.

Table 1 Parameters values in the model

Table 2 $C_p$ coefficients $\alpha _{i,j}$

2.2 The unique terminal voltage solution

In this section we prove that there exists a unique solution of Eq. (23), such that we have a system that satisfies the steady states within the control limits mentioned in [7] and later summarized in Table 3. From an electrical engineering point of view, what the system normally seeks is current and power flow from the WTG to the grid, which requires $V>E$ ($V>1.0164$), see the value of E in Table 1. In case of disturbances, the faster the system enters this range the better. As mentioned in the control limits by [7] (summarized later in Table 3), there are minimum and maximum allowed values for $E_{qcmd}$ and $\frac{P_{ord}}{V}$ such that $0.5\le E_{qcmd} \le 1.45$ and $\frac{P_{ord}}{V} \le 1.1$. In the steady state, Eqs. (20) and (22) show that $E_q=E_{qcmd}$ and $I_{plv}=\frac{P_{ord}}{V}$. Therefore, in the steady state $0.5\le E_q=E_{qcmd} \le 1.45$ and $I_{plv}=\frac{P_{ord}}{V} \le 1.1$. The following Lemma is to show and identify the unique solution of the terminal voltage that will yield those limits while having $V>1.0164$.

Lemma 2.0

In the steady state, if $0.5\le E_q=E_{qcmd} \le 1.45$ and $I_{plv}=\frac{P_{ord}}{V} \le 1.1$, then there exists a unique solution of (23) such that $V>1.0164$.

Table 3 Control limits to be applied as in [7]

Proof

By setting $Q_{gen}=\frac{V(E_q-V)}{X_{eq}}$ [see Eq. (11)] and $P_{elec}=I_{plv}V$ [see Eq. (3)], Eq. (23) becomes,

$$\begin{aligned} 0= & {} V^4-2(I_{plv}V) RV ^2-2\cdot \frac{V(E_q-V)}{X_{eq}}\cdot XV^2-E^2V^2 \nonumber \\&+\,(R^2+X^2)I^2_{plv}V^2+(R^2+X^2)\cdot \frac{V^2(E_q-V)^2}{X_{eq}}.\nonumber \\ \end{aligned}$$

(24)

Dividing by $V^2$ and algebraic re-arrangement gives

$$\begin{aligned} 0= & {} V^2\left[ 1+\frac{2X}{X_{eq}}+\frac{R^2+X^2}{X_{eq}}\right] \nonumber \\&-\,V\left[ 2I_{plv}R+\frac{2XE_q}{X_{eq}}+\frac{2(R^2+X^2)\cdot E_q}{X_{eq}}\right] \nonumber \\&+\,\left[ \frac{R^2+X^2}{X_{eq}}+(R^2+X^2)\cdot I^2_{plv}-E^2\right] . \end{aligned}$$

(25)

With $A=1+\frac{2X}{X_{eq}}+\frac{R^2+X^2}{X_{eq}},\,B=-\left[ 2I_{plv}R+\right. \left. \frac{2XE_q}{X_{eq}} +\frac{2(R^2+X^2)E_q}{X_{eq}}\right]$ and $C=\frac{R^2+X^2}{X_{eq}}+(R^2+X^2)I^2_{plv}-E^2$, solutions of Eq. (25) are,

$$\begin{aligned} V=\frac{-B \pm \sqrt{B^2 - 4AC}}{2A}. \end{aligned}$$

(26)

With $R,X,X_{eq}>0$, we have $A>0$. If we use the parameter values of $R,\,X$, and $X_{eq}$ given in Table 1 and the upper bounds given in Lemma 2.0 ($E_q<1.45$ and $I_{plv}<1.1$), we get:

$$\begin{aligned} \frac{-B}{2A}=\frac{2I_{plv}R+\frac{2XE_q}{X_{eq}} +\frac{2(R^2+X^2).E_q}{X_{eq}}}{2 \left( 1+\frac{2X}{X_{eq}}+\frac{R^2+X^2}{X_{eq}}\right) }< 0.99. \end{aligned}$$

(27)

This implies that there exists a unique solution for V such that $V>1.0164$ and that solution is:

$$\begin{aligned} V=f(I_{plv},E_q;X;R;E)=\frac{-B + \sqrt{B^2 - 4AC}}{2A} \nonumber \\ \end{aligned}$$

(28)

with A, B, and C from Eq. (25). $\square$

3 Boundedness, existence, and uniqueness proofs

In this section, we start by proving boundedness for the solution of the system of differential equations in Eqs. (1)–(22) with V as in Eq. (28). After that, we prove the right hand sides of the differential equations are uniformly Lipschitz continuous and then existence and uniqueness of initial value problem solutions follows. We then extend our study for existence and uniqueness in the parameter space of X and R.

3.1 Boundedness of the system state variables and their derivatives under control limits

We define the control limits introduced in [7] to be the lower and upper bounds as in Table 3.

Remark 3.0

Boundedness of $\theta ,\,P_{inp},\,V_{ref},\,Q_{wvl},\,Q_{wvu},$ $dpwi,\,E_{qcmd},\,\frac{dP_{inp}}{dt}$, and $\frac{d\theta }{dt}$ follow from Table 3.

The effect of the system’s controls impose other boundedness conditions. One such condition is the non-wind up control limit. This control is to make sure the integrators are not divergent. This is also reasonable from hardware point of view as the integrators can’t accumulate infinite data. As a result of that, all integrators such as $f_1,\,f_2$, and $\varDelta \theta _{m}$ are bounded by non-wind up control limit. Other physical consequences that follow from the controls are the boundedness of variables such as $V_{reg}$ and $Q_{ inpt }$. Those variables are signals that are generated by the operator controls (machine or human). The operator (machine or human) will not generate an infinite physical quantity such as voltage in the case of $V_{reg}$ or power in the case of $Q_{ inpt }$. The boundedness of $\frac{dP_{inp}}{dt}$ (see Table 3) gives the boundedness of $w_g$ since $\frac{dP_{inp}}{dt}=f(w_g)$, and $f(w_g)$ is polynomial [see Eq. (8)]. Physically, $P_{mech}$ as the power extracted from the air streams can’t exceed the Betz limit (approximately 0.59, see section 1.1 for discussion and references) of the available power in the air streams. The fact that the power in the air streams is a finite quantity implies that $P_{mech}$ is bounded. Since $P_{mech}=f(\theta ,w_t,v_{wind})$ is a polynomial of $\theta$ and $w_t$ (see the detail of $P_{mech}$ after Eq. 3), then $w_t$ is bounded as $\theta$ is bounded from Table 3 and $v_{wind}$ is physically finite. $P_{elec}$ has upper and lower thresholds (see page 4.17 in [7]), which impose $P_{elec}$ boundedness and support the boundedness assumption for $w_g$. In the inertia control, dfdbwi is bounded since it is an output of bounded function.

Conclusion to the previous paragraph: Non wind up controls, operator and threshold controls, and physical consequences of the controls give boundedness for the variables $f_1,\,f_2,\,\varDelta \theta _{m},\,V_{reg},\,Q_{ inpt },\,w_g,\,w_t,\,P_{mech},\,P_{elec}$, and dfdbwi. Those boundedness conditions lead to the following conditions.

Conditions 3.0

$f_1,\,f_2,\,\varDelta \theta _{m},\,V_{reg},\,Q_{ inpt },\,w_g,\,w_t,\,$ $P_{mech},\,P_{elec}$, and dfdbwi have real lower and upper bounds such that the following inequalities hold:

$$\begin{aligned}&f_{1min}\le f_1\le f_{1max}, \end{aligned}$$

(29)

$$\begin{aligned}&f_{2min}\le f_2\le f_{2max}, \end{aligned}$$

(30)

$$\begin{aligned}&\varDelta \theta _{mmin}\le \varDelta \theta _{m}\le \varDelta \theta _{mmax}, \end{aligned}$$

(31)

$$\begin{aligned}&V_{regmin}\le V_{reg}\le V_{regmax}, \end{aligned}$$

(32)

$$\begin{aligned}&Q_{inptmin}\le Q_{ inpt }\le Q_{{ inptmax}}, \end{aligned}$$

(33)

$$\begin{aligned}&w_{gmin}\le w_g \le w_{gmax}, \end{aligned}$$

(34)

$$\begin{aligned}&w_{tmin}\le w_t \le w_{tmax}, \end{aligned}$$

(35)

$$\begin{aligned}&P_{mechmin}\le P_{mech}\le P_{mechmax}, \end{aligned}$$

(36)

$$\begin{aligned}&P_{elecmin}\le P_{elec}\le P_{elecmax}, \end{aligned}$$

(37)

$$\begin{aligned}&dfdbwi_{min}\le { dfdbwi}\le { dfdbwi}_{max}. \end{aligned}$$

(38)

Now, we start our proof for the system’s boundedness for both state variables and their derivatives.

Lemma 3.0

Suppose $w_{ref}$ and $\frac{dw_{ref}}{dt}$ are continuous in $t\in [0,\infty )$, then $w_{ref}(t)$ is bounded as well as its derivative.

Proof

Since $P_{elec}$ is bounded [condition (37)], then by the extreme value theorem we let:

$$\begin{aligned} w_{refmin}=\min \left[ \frac{-0.75P^2_{elec}+1.59P_{elec}+0.63}{60}\right] \end{aligned}$$

and,

$$\begin{aligned} w_{refmax}=\max \left[ \frac{-0.75P^2_{elec}+1.59P_{elec}+0.63}{60}\right] . \end{aligned}$$

Then from Eq. (7), we get,

$$\begin{aligned} w_{refmin}-\frac{w_{ref}}{60}\le \frac{dw_{ref}}{dt}\le w_{refmax}-\frac{w_{ref}}{60} \end{aligned}$$

(39)

and then,

$$\begin{aligned} w_{refmin}\le \frac{dw_{ref}}{dt}+\frac{w_{ref}}{60}\le w_{refmax}. \end{aligned}$$

(40)

Multiplying by $e^\frac{t}{60}$ (the integrator factor), then,

$$\begin{aligned} w_{refmin}\cdot e^\frac{t}{60}\le \frac{d\left[ w_{ref}\cdot e^\frac{t}{60}\right] }{dt}\le w_{refmax}\cdot e^\frac{t}{60}. \end{aligned}$$

(41)

Since $w_{ref}$ and $\frac{dw_{ref}}{dt}$ are continuous in t, then the they are Riemann integrable. By applying $\int _{t_0}^{t}(\,)dt$ to the estimate (41), we get:

$$\begin{aligned}&60\cdot w_{refmin}\left( e^\frac{t}{60}-e^\frac{t_0}{60}\right) \le w_{ref}e^\frac{t}{60}\nonumber \\&\quad -\,w_{ref}(t_0)e^\frac{t_0}{60}\le 60\cdot w_{refmax}\left( e^\frac{t}{60}-e^\frac{t_0}{60}\right) . \end{aligned}$$

(42)

By re-arranging the estimate (42), we get:

$$\begin{aligned}&60\cdot w_{refmin}+e^\frac{t_0}{60}(w_{ref}(t_0)-60\cdot W_{refmin})e^\frac{-t}{60} \le \,w_{ref} \nonumber \\&\quad \le 60\cdot w_{refmax}+e^\frac{t_0}{60}\left( w_{ref}(t_0)-60\cdot w_{refmax}\right) e^\frac{-t}{60}.\nonumber \\ \end{aligned}$$

(43)

Then as $t\rightarrow \infty ,\,w_{ref}$ is bounded such that:

$$\begin{aligned} 60\cdot w_{refmin}\le w_{ref} \le 60\cdot w_{refmax}. \end{aligned}$$

(44)

The boundedness for $w_{ref}$ can be shown independent on t by taking the absolute of estimate (43) such that:

$$\begin{aligned} \left| w_{ref}\right|\le & {} \left| 60\cdot w_{refmax}+e^\frac{t_0}{60}(w_{ref}(t_0)-60\cdot w_{refmax})e^\frac{-t}{60}\right| \nonumber \\\le & {} \left| 60\cdot w_{refmax}\right| +\left| e^\frac{t_0}{60}(w_{ref}(t_0)-60\cdot w_{refmax})\right| \,\,\nonumber \\ \end{aligned}$$

(45)

for all t.

From the estimate (40), $\frac{dw_{ref}}{dt}$ can be shown independent on t as well. After re-arrangement and taking the absolute of the estimate (40), we get:

$$\begin{aligned} \left| \frac{dw_{ref}}{dt}\right|\le & {} \left| w_{refmax}-\frac{w_{ref}}{60}\right| \le \left| w_{refmax}\right| +\left| \frac{w_{ref}}{60}\right| \nonumber \\\le & {} \left| w_{refmax}\right| \nonumber \\&+\,\left| \frac{60.w_{refmax}|+|e^\frac{t_0}{60}(w_{ref}(t_0)-60.w_{refmax})}{60}\right| \,\,\nonumber \\ \end{aligned}$$

(46)

for all t.

This proves Lemma 3.0. $\square$

For the many of the remaining differential equations, similar proof steps could be conducted. We find upper bounds and lower bounds from the control limits (Table 3) and/or the Condition 3.0, so we can turn the equations to estimates and then we multiply them by the appropriate integrating factors. After that, boundedness can be shown for the state variables and their derivatives. A summary of these proof results is given below.

Results 3.0

Suppose the state variables $w_{sho},\,P_{1elec},\,Q_{ inpt },\,Q_{ord},\,P_{avl},\,fltdfwi,\,E_{qcmd}$, and $I_{plv}$ as well as their derivatives are continuous in $t\in [0,\infty )$, then those state variables are bounded as well as their derivatives, and the following estimates hold for all t.

$$\begin{aligned}&\left| w_{sho}\right| \le \left| T_wdP_{max}\right| +\left| e^\frac{t_0}{T_w}(w_{sho}(t_0)-T_wdP_{max})\right| , \end{aligned}$$

(47)

$$\begin{aligned}&\left| \frac{dw_{sho}}{dt}\right| \le \left| dP_{max}\right| \nonumber \\&\quad +\,\left| \frac{[T_wdP_{max}+e^\frac{t_0}{T_w}(w_{sho}(t_0)-T_wdP_{max})]}{T_w}\right| , \end{aligned}$$

(48)

$$\begin{aligned}&\left| P_{1elec}\right| \le \left| P_{elecmax}\right| +\left| e^\frac{t_0}{T_{pwr}}(P_{1elec}(t_0)-dP_{max})\right| , \end{aligned}$$

(49)

$$\begin{aligned}&\left| \frac{dP_{1elec}}{dt}\right| \le \left| \frac{P_{elecmax}}{T_{pwr}}\right| \nonumber \\&\quad +\,\left| \frac{[P_{elecmax}+e^\frac{t_0}{T_{pwr}}(P_{1elec}(t_0)-dP_{max})]}{T_{pwr}}\right| , \end{aligned}$$

(50)

$$\begin{aligned}&\left| Q_{drop}\right| \le \left| Q_{{ inptmax}}\right| +\left| e^\frac{t_0}{T_{lpdq}}(Q_{drop}(t_0)-Q_{{ inptmax}})\right| , \end{aligned}$$

(51)

$$\begin{aligned}&\left| \frac{dQ_{drop}}{dt}\right| \le \left| \frac{Q_{{ inptmax}}}{T_{lpdq}}\right| \nonumber \\&\quad +\,\left| \frac{[Q_{{ inptmax}}+e^\frac{t_0}{T_{lpdq}}(Q_{drop}(t_0)-Q_{{ inptmax}})]}{T_{lpdq}}\right| , \end{aligned}$$

(52)

$$\begin{aligned}&\left| V_{1reg}\right| \le \left| V_{regmax}\right| +\left| e^\frac{t_0}{T_r}(V_{1reg}(t_0)-V_{regmax})\right| , \end{aligned}$$

(53)

$$\begin{aligned}&\left| \frac{dV_{1reg}}{dt}\right| \le \left| \frac{V_{regmax}}{T_r}\right| +\left| \frac{[ V_{regmax}+e^\frac{t_0}{T_r}(V_{1reg}(t_0)-V_{regmax})]}{T_r}\right| , \nonumber \\\end{aligned}$$

(54)

$$\begin{aligned}&\left| Q_{ord}\right| \le \left| Q_{max}\right| +\left| e^\frac{t_0}{T_c}(Q_{ord}(t_0)-Q_{max})\right| , \end{aligned}$$

(55)

$$\begin{aligned}&\left| \frac{dQ_{ord}}{dt}\right| \le \left| \frac{Q_{max}}{T_c}\right| +\left| \frac{[ Q_{max}+e^\frac{t_0}{T_c}(Q_{ord}(t_0)-Q_{max})]}{T_c}\right| , \end{aligned}$$

(56)

$$\begin{aligned}&\left| P_{avf}\right| \le 1+\left| e^\frac{t_0}{T_{pav}}(P_{avf}(t_0)-1)\right| , \end{aligned}$$

(57)

$$\begin{aligned}&\left| \frac{dP_{avf}}{dt}\right| \le \frac{1}{T_{pav}}+\left| \frac{[ 1+e^\frac{t_0}{T_{pvl}}(P_{avf}(t_0)-1)]}{T_{pvf}}\right| , \end{aligned}$$

(58)

$$\begin{aligned}&\left| fltdfwi\right| \le \left| dfdwi_{max} \right| +\left| e^\frac{t_0}{T_{lpwi}}(fltdfwi(t_0)-dfdwi_{max})\right| , \nonumber \\\end{aligned}$$

(59)

$$\begin{aligned}&\left| \frac{d(fltdfwi)}{dt}\right| \le \left| \frac{dfdwi_{max}}{T_{lpwi}}\right| \nonumber \\&\quad +\,\left| \frac{[ dfdwi_{max}+e^\frac{t_0}{T_{lpwi}}(fltdfwi(t_0)-dfdwi_{max})]}{T_{lpwi}}\right| , \end{aligned}$$

(60)

$$\begin{aligned}&\left| E_q\right| \le \left| Xl_{Qmax}\right| +\left| e^\frac{t_0}{0.02}(E_q(t_0)-Xl_{Qmax})\right| , \end{aligned}$$

(61)

$$\begin{aligned}&\left| \frac{dE_q}{dt}\right| \le \left| \frac{Xl_{Qmax}}{0.02}\right| +\left| \frac{[ Xl_{Qmax}+e^\frac{t_0}{0.02}(E_q(t_0)-Xl_{Qmax})]}{0\ldots 02}\right| , \end{aligned}$$

(62)

and,

$$\begin{aligned}&\left| I_{plv}\right| \le \left| I_{pmax}\right| +\left| e^\frac{t_0}{0.02}(I_{plv}(t_0)-I_{pmax})\right| , \end{aligned}$$

(63)

$$\begin{aligned}&\left| \frac{dI_{plv}}{dt}\right| \le \left| \frac{I_{pmax}}{0.02}\right| +\left| \frac{[ I_{pmax}+e^\frac{t_0}{0.02}(I_{plv}(t_0)-I_{pmax})]}{0\ldots 02}\right| .\nonumber \\ \end{aligned}$$

(64)

Some of the state variables are bounded but we still need to show the boundedness of their derivatives. The following lemma is to show that. Boundedness of $P_{elec}$ [estimate (37)] and $I_{plv}$ [estimate (63)] imply the boundedness of V ($P_{elec}= VI _{plv}$). $Q_{gen}$ [see Eq. (11)] boundedness follows from the boundedness of V and $E_q$ [estimate (61)]. Looking at Sect. 2.1, after Eq. (11) we find that the two cases of $Q_{cmd}$ are bounded based on the bounds in the estimates (10) and (16).

Conditions 3.1

$V,\,Q_{gen}$, and $Q_{cmd}$ have lower and upper bounds such that the following inequalities hold:

$$\begin{aligned}&V_{mnm}\le V \le V_{mxm} \end{aligned}$$

(65)

$$\begin{aligned}&Q_{mnm}\le Q_{gen} \le Q_{mxm} \end{aligned}$$

(66)

$$\begin{aligned}&Q_{cmdmax}\le Q_{cmd} \le Q_{cmdmin} \end{aligned}$$

(67)

Lemma 3.1

In addition to the continuity conditions stated in Lemma 3.0 and Results 3.0, we suppose $w_g,\,w_t,\,\varDelta \theta _m,\,f_1, f_2,V_{ref},\,Q_{wvl},\,Q_{wvu},\,dpwi$, and $E_{qcmd}$ are continuous in $t\in [0,\infty )$, then $\frac{dw_g}{dt},\,\frac{dw_t}{dt},\frac{d\varDelta \theta _m}{dt},\,\frac{df_1}{dt},\,\frac{df_2}{dt},\,\frac{dV_{ref}}{dt},\,\frac{dQ_{wvl}}{dt},\frac{dQ_{wvu}}{dt},\,\frac{d(dpwi)}{dt}$, and $\frac{dE_{qcmd}}{dt}$ are bounded.

Proof

We multiply Eq. (1) by $2H_g$, Eq. (2) by 2H, and then by adding them,

$$\begin{aligned}&2H_g\frac{dw_g}{dt}+2H\frac{dw_t}{dt}=\frac{-P_{elec}}{w_g+w_0}+\frac{P_{mech}}{w_t+w_0} \end{aligned}$$

(68)

$$\begin{aligned} \left| 2H_g\frac{dw_g}{dt}+2H\frac{dw_t}{dt}\right|= & {} \left| \frac{-P_{elec}}{w_g+w_0}+\frac{P_{mech}}{w_t+w_0}\right| \nonumber \\\le & {} \left| \frac{-P_{elec}}{w_g+w_0}\right| +\left| \frac{P_{mech}}{w_t+w_0}\right| \nonumber \\\le & {} \left| \frac{P_{elecmax}}{w_{tmin}+w_0}\right| +\left| \frac{P_{mechmax}}{w_{gmin}+w_0}\right| .\nonumber \\ \end{aligned}$$

(69)

By taking the absolute value of Eqs. (3)–(4) with the conditions (34)–(35) we get:

$$\begin{aligned} \left| \frac{d\varDelta \theta _{m}}{dt}\right| \le w_{base}\left| w_{gmax}\right| +w_{base}\left| w_{tmax}\right| \end{aligned}$$

(70)

and with $|w_{ref}|$ from the estimate (45) we have,

$$\begin{aligned} \left| \frac{df_1}{dt}\right|\le & {} \left| w_{gmax}\right| +w_0+\left| 60\cdot w_{refmax}\right| \nonumber \\&+\,\left| e^\frac{t_0}{60}\left( w_{ref}(t_0)-60\cdot w_{refmax}\right) \right| . \end{aligned}$$

(71)

By taking the absolute value of Eq. (5) and the bounds in Table 3 we get:

$$\begin{aligned} \left| \frac{df_2}{dt}\right| \le \left| P_{inpmax}\right| +P_{stl}. \end{aligned}$$

(72)

By taking the absolute value of Eq. (20) and from condition (65) and the bounds in Table 3 we get:

$$\begin{aligned} \left| \frac{dE_{qcmd}}{dt}\right| \le \left| \frac{V_{min}}{K_{vi}}\right| +\left| \frac{V_{mxm}}{K_{vi}}\right| . \end{aligned}$$

(73)

By taking the absolute value of Eq. (20) and from conditions (66)–(67) we get:

$$\begin{aligned} \left| \frac{dV_{ref}}{dt}\right| \le \left| K_{Qi}Q_{cmdmax}\right| +\left| K_{Qi}Q_{mxm}\right| \end{aligned}$$

(74)

By taking the absolute value of Eqs. (14)–(15) and the bounds in Table 3 we get:

$$\begin{aligned} \left| \frac{dQ_{wvl}}{dt}\right| \le \left| \frac{K_{pv}}{T_v}V_{ermx}\right| +\left| \frac{K_{pv}}{T_v}Q_{max}\right| \end{aligned}$$

(75)

and,

$$\begin{aligned} \left| \frac{dQ_{wvu}}{dt}\right|\le & {} \left| K_{iv}V_{ermx}\right| . \end{aligned}$$

(76)

By taking the absolute value of Eq. (19) and with the bounds in Table 3 and condition (38) we get:

$$\begin{aligned} \left| \frac{d(dpwi)}{dt}\right|\le & {} \left| \frac{K_{wi}}{T_{lpwi}}dfdbwi_{max}\right| +\left| \frac{K_{wi}}{T_{lpwi}}fltdfwi\right| \nonumber \\&+\,\left| \frac{P_{maxwi}}{T_{wowi}}\right| \end{aligned}$$

(77)

and by using the bound pf $|{ fltdfwi}|$ from the estimate (18), we rewrite the estimate (77) to be,

$$\begin{aligned} \left| \frac{d({ dpwi})}{dt}\right|\le & {} 2\left| \frac{K_{wi}}{T_{lpwi}}{} { dfdbwi}_{max}\right| \nonumber \\&+\,\left| \frac{K_{wi}}{T_{lpwi}}e^\frac{t_0}{T_{lpwi}}({ fltdfwi}(t_0)-{ dfdwi}_{max})\right| \nonumber \\&+\,\left| \frac{P_{maxwi}}{T_{wowi}}\right| . \end{aligned}$$

(78)

This proves Lemma 3.1. $\square$

Theorem 3.0

Under the control limits in Table 3 and Conditions 3.0 and 3.1, the differential equations system in Eqs. (1)–(22) with V as in Eq. (28) have bounded state variables and derivatives independent on time t.

The proof of Theorem 3.0 follows from Lemma 3.0 and 3.1 and Conditions 3.0 and 3.1.

3.2 Existence and uniqueness under control limits

We start our analysis by proving the existence and uniqueness of the solution under the control limits. After that we discuss some conditions in which existence and uniqueness can still be proven.

Throughout this section we use the following notations:

• Let i be an index such that $i\in \{1,2,\ldots ,22\}$.

• Let $y\in \mathbb {R}^{22}$ represent the state variables by order of the system in Eqs. (1)–(22) defined for $t\in [0,\infty )$. Then $y_i$ represents the ith component of y. For every i we have:

  $$\begin{aligned} y_i{:}\,t\mapsto \mathbb {R}. \end{aligned}$$

  (79)

• Let f(t, y) represents the right hand sides of the derivatives in Eqs. (1)–(22). Then $f_i$ represents the ith component of f(t, y). For every i we have:

  $$\begin{aligned} f_i{:}\,\mathbb {R}^+\times \mathbb {R}^{22}\mapsto \mathbb {R}. \end{aligned}$$

  (80)

• Let $Y\in \mathbb {R}^{22}$ be the vector of the upper bounds of y (see Theorem 4.0 for boundedness proofs of y) such that for all $i,\,\left| y_i\right| \le Y_i$.

• Let $\left| \left| \cdot \right| \right|$ be the $\ell ^1$ norm.

Before we proceed to existence and uniqueness proofs, we study first the terminal voltage solution in Eq. (28). As mentioned in condition (65), $V\in \mathbb {R}$ and bounded for the given parameters in Table 1. The problem is that the parameters R and X are out of the system’s control as they are parameters of the grid and we want to understand their effect on V. From Eq. (28), we see that there exist no real solutions for the steady states or for the system if $B^2-4AC<0$. Therefore, we study the behavior of $B^2-4AC$, and where it can have negative values and therefore, we have no real solution for the system. The following Lemma shows that the function $B^2-4AC$ has no local minimum or maximum in the given rectangular domain.

Lemma 3.2

With $\min (y_{21})>0,\,\min (y_{22})>0$, and $R,X,E,X_{eq}>0$, the function $g(y_{21},y_{22})=B^2-4AC$ has no local minimum or maximum in the interior of $[\min (y_{21}),\max (y_{21})]\times [\min (y_{22}),\max (y_{22})]$.

Proof

The proof is by contradiction. $\square$

Suppose there exists a point $(y^*_{21},y^*_{22})$ in the interior of $[\min (y_{21}),\max (y_{21})]\times [\min (y_{22}),\max (y_{22})]$ that is a local maximum or minimum, then

$$\begin{aligned} \left. \frac{\partial g(y_{21},y_{22})}{\partial y_{21}} \right| _{(y^*_{21},y^*_{22})}=0 \end{aligned}$$

This implies that,

$$\begin{aligned} 0= & {} 2\left[ 2y^*_{22}R+\frac{2Xy^*_{21}}{X_{eq}}+\frac{2R^2y^*_{21}+2X^2y^*_{21}}{X_{eq}}\right] \nonumber \\&\quad \left[ \frac{2X+2R^2+2X^2}{X_{eq}}\right] \nonumber \\= & {} 2y^*_{22}R+\frac{2Xy^*_{21}}{X_{eq}}+\frac{2R^2y^*_{21}+2X^2y^*_{21}}{X_{eq}} \nonumber \\&>2\min (y_{22})R+\frac{2X\min (y_{21})}{X_{eq}}\nonumber \\&+\,\frac{2R^2\min (y_{21})+2X^2\min (y_{21})}{X_{eq}} \nonumber \\&>0. \end{aligned}$$

(81)

Thus, there cannot be a local minimum or maximum.

Corollary 3.2

For the given parameter values in Table 1, control limits in Table 3, and Conditions 4.0 and 4.1, there exists a positive minimum of $g(y_{21},y_{22})=B^2-4AC$ for the given rectangular domain in Lemma 4.2. We let $g_{min}=\min (g(y_{21},y_{22}))$.

Lemma 3.3

For all $f_i$ a vector component of f(t, y), we have $\left| \left| \nabla f_i\right| \right|$ is bounded.

Proof

We apply the partial derivatives for all $f_i$, the right hand side of Eqs. (1)–(22) and find the bound for $\left| \left| \nabla f_i\right| \right| =\sum _{j=1}^{22} \left| \frac{\partial f_i}{\partial y_j}\right|$ for any given t and y. We start by partial derivatives for $V=f(y_{21},y_{22})$ in Eq. (28):

$$\begin{aligned}&\frac{\partial V}{\partial y_{21}}=\frac{2X+2R^2+2X^2}{2AX_{eq}}\nonumber \\&\quad +\,\frac{-2\left[ 2y_{22}R+\frac{2Xy_{21}+2R^2y_{21}+2X^2y_{21}}{X_{eq}}\right] \left( \frac{2X+2R^2+2X^2}{X_{eq}}\right) }{4A\sqrt{B^2-4AC}},\nonumber \\ \end{aligned}$$

(82)

$$\begin{aligned}&\left| \frac{\partial V}{\partial y_{21}}\right| \le \frac{2X+2R^2+2X^2}{2AX_{eq}}\nonumber \\&\quad +\,\left( \frac{4X+4R^2+4X^2}{2AX_{eq}}\right) \left| \frac{Y_{22}R+\frac{Y_{21}(2X+2R^2+2X^2)}{X_{eq}}}{\sqrt{g_{min}}}\right| .\nonumber \\ \end{aligned}$$

(83)

Similarly it can be shown that,

$$\begin{aligned} \left| \frac{\partial V}{\partial y_{22}}\right|\le & {} \frac{X+R^2+X^2}{AX_{eq}}+R\left| \frac{Y_{22}R+\frac{Y_{21}(2X+2R^2+2X^2)}{X_{eq}}}{2A\sqrt{g_{min}}}\right| \nonumber \\&+\,\left| \frac{2(R^2+X^2)Y_{22}}{\sqrt{g_{min}}}\right| . \end{aligned}$$

(84)

Since $\left| \frac{\partial V}{\partial y_{21}}\right|$ and $\left| \frac{\partial V}{\partial y_{22}}\right|$ are bounded as in the estimates (83)–(84), then there are lower and upper bounds for them such that:

$$\begin{aligned} V_{min1}\le & {} \left| \frac{\partial V}{\partial y_{21}}\right| \le V_{max1}, \end{aligned}$$

(85)

$$\begin{aligned} V_{min2}\le & {} \left| \frac{\partial V}{\partial y_{22}}\right| \le V_{max2}. \end{aligned}$$

(86)

From the conditions (85)–(86), and (65) we get:

$$\begin{aligned} \left| \left| \nabla f_1\right| \right|\le & {} \left| \frac{P_{elecmax}}{2H_g(w_{gmin}+w_0)^2}\right| +\frac{D_{tg}+K_{tg}}{2H_g}\nonumber \\&+\,\left| \frac{(V_{max1}+V_{max2})Y_{22}+V_{mxm}}{2H_g(w_{gmin}+x_0)}\right| . \end{aligned}$$

(87)

Before working on $\left| \left| \nabla f_2\right| \right|$, we will find the bound of $\left| \frac{\partial P_{mech} }{\partial y_2}\right|$. We find that:

$$\begin{aligned} \left| \frac{\partial P_{mech} }{\partial y_2}\right|= & {} \left| \frac{1}{2}\frac{\partial C_p \left( \frac{y_2+w_0}{v_{wind}},y_6\right) }{\partial y_2}\rho A_r v_{wind}^3\right| \nonumber \\= & {} \left| \frac{1}{2}\rho A_r v_{wind}^3\frac{\partial \sum _{i=0}^{4} \sum _{j=0}^{4} \alpha _{i,j} y^i_6 \left( \frac{y_2+w_0}{v_{wind}}\right) ^j}{\partial y_2}\right| \nonumber \\= & {} \left| \frac{1}{2}\rho A_r v_{wind}^3 \sum _{i=0}^{4} \sum _{j=1}^{4} \alpha _{i,j} y^i_6 (\frac{y_2+w_0}{v_{wind}})^{j-1}\frac{j}{v_{wind}}\right| \nonumber \\\le & {} \left| \frac{1}{2}\rho A_r v_{wind}^2\sum _{i=0}^{4} \sum _{j=1}^{4} j \alpha _{i,j} Y^i_6 \left( \frac{Y_2+w_0}{v_{wind}}\right) ^{j-1}\right| .\nonumber \\ \end{aligned}$$

(88)

Similarly, we can find an upper bound for $\left| \frac{\partial P_{mech} }{\partial y_6}\right|$. There are upper bounds for $\left| \frac{\partial P_{mech} }{\partial y_2}\right|$ and $\left| \frac{\partial P_{mech} }{\partial y_6}\right|$ such that:

$$\begin{aligned} \left| \frac{\partial P_{mech} }{\partial y_2}\right|\le & {} P_{mechmax1}, \end{aligned}$$

(89)

$$\begin{aligned} \left| \frac{\partial P_{mech} }{\partial y_6}\right|\le & {} P_{mechmax2}. \end{aligned}$$

(90)

From conditions (89)–(90), (36), and (35) we get:

$$\begin{aligned} \left| \left| \nabla f_2\right| \right|\le & {} \left| \frac{P_{mechmax1}}{2H(w_{tmin}+w_0)}\right| +\left| \frac{P_{mechmax}}{2H(w_{tmin}+w_0)^2}\right| \nonumber \\&+\,\left| \frac{D_{tg}+K_{tg}}{2H}\right| \nonumber \\&+\,\left| \frac{P_{mechmax2}}{2H(w_{tmin}+w_0)}\right| . \end{aligned}$$

(91)

For $\left| \left| \nabla f_3\right| \right| ,\,\left| \left| \nabla f_4\right| \right| ,\,\left| \left| \nabla f_5\right| \right|$, and $\left| \left| \nabla f_6\right| \right|$ the bounds are as following:

$$\begin{aligned} \left| \left| \nabla f_3\right| \right|\le & {} \left| 2w_{wbase}\right| , \end{aligned}$$

(92)

$$\begin{aligned} \left| \left| \nabla f_4\right| \right|\le & {} 2, \end{aligned}$$

(93)

$$\begin{aligned} \left| \left| \nabla f_5\right| \right|\le & {} 1. \end{aligned}$$

(94)

The bound for $\left| \left| \nabla f_6\right| \right|$ is given by

$$\begin{aligned} \left| \left| \nabla f_6\right| \right| \le \left| \frac{2K_{pp}+K_{ip}+K_{pc}+K_{ic}+1}{T_p}\right| . \end{aligned}$$

(95)

From conditions (65), (85) and (90) the bound of $\left| \left| \nabla f_6\right| \right|$ is given by

$$\begin{aligned}&\left| \left| \nabla f_7\right| \right| \nonumber \\&\!\quad \le \left| \frac{1.5V^2_{mxm}Y_{22}+1.5V_{mxm}V_{max2}Y^2_{22}+1.59V_{mxm}+1.59V_{max2}Y_{22}}{60}\right| \nonumber \\&\quad \quad +\,\left| \frac{1.5V_{mxm}V_{max1}Y^2_{22}+1.59V_{max1}Y_{22}}{60}\right| +\frac{1}{60}. \end{aligned}$$

(96)

The bound of $\left| \left| \nabla f_6\right| \right|$ is given by

$$\begin{aligned} \left| \left| \nabla f_8\right| \right|\le & {} \left| \frac{3K_{ptrq}(Y_1+w_0)}{T{pc}}\right| +\left| \frac{K_{ptrq}(Y_1+w_0+Y_7)}{T{pc}}\right| \nonumber \\&+\,\left| \frac{K_{itrq}(Y_4+1)+1}{T{pc}}\right| . \end{aligned}$$

(97)

The bounds of $\left| \left| \nabla f_9\right| \right|$ comes from the bound in the estimate Eq. (97) [see Eq. (9)]. Then the bound of $\left| \left| \nabla f_9\right| \right|$ is given by

$$\begin{aligned} \left| \left| \nabla f_9\right| \right| \le \left| \left| \nabla f_8\right| \right| +\frac{1}{T_w}. \end{aligned}$$

(98)

Then the bound of $\left| \left| \nabla f_{10}\right| \right|$ is given by

$$\begin{aligned} \left| \left| \nabla f_{10}\right| \right| \le \left| \frac{V_{mxm}+V_{max2}Y_{22}+V_{max1}Y_{21}}{T{pwr}}\right| +\left| \frac{1}{T_{pwr}}\right| . \nonumber \\ \end{aligned}$$

(99)

In case $Q_{cmd}=y_{10}\tan ({ PFA}_{ref})$, then $\frac{\partial Q_{cmd}}{\partial y_{10}}=\tan ({ PFA}_{ref})$. In case $Q_{cmd}=y_{16}$, then $\frac{\partial Q_{cmd}}{\partial y_{16}}=1$. With conditions (65), (85) and (90), Then the bound of $\left| \left| \nabla f_{11}\right| \right|$ is given by

$$\begin{aligned}&\left| \left| \nabla f_{11}\right| \right| \le K_{Qi}\cdot \max \{\tan ({ PFA}_{ref}),1\}+K_{Qi} \left| \frac{2V_{mxm}Y_{21}}{X_{eq}}\right| \nonumber \\&\quad \quad +\,K_{Qi}\left| \frac{V_{mxm}+V_{max1}Y_{21}}{X_{eq}}\right| +K_{Qi}\left| \frac{2V_{mxm}V_{max2}}{X_{eq}}\right| .\nonumber \\ \end{aligned}$$

(100)

Then the bound of $\left| \left| \nabla f_{12}\right| \right|$ is given by

$$\begin{aligned} \left| \left| \nabla f_{12}\right| \right| \le \left| \frac{1}{T_{lpqd}}\right| . \end{aligned}$$

(101)

With $V_{qd}=K_{qd}Q_{drop}$, the bounds of $\left| \left| \nabla f_{13}\right| \right| \ldots \left| \left| \nabla f_{19}\right| \right|$ are given by

$$\begin{aligned} \left| \left| \nabla f_{13}\right| \right|\le & {} \left| \frac{1}{T_r}\right| , \end{aligned}$$

(102)

$$\begin{aligned} \left| \left| \nabla f_{14}\right| \right|\le & {} \left| \frac{K_{pv}(2+K_{qd})+1}{T_v}\right| , \end{aligned}$$

(103)

$$\begin{aligned} \, \left| \left| \nabla f_{15}\right| \right|\le & {} \left| K_{iv}(2+K_{qd})\right| , \end{aligned}$$

(104)

$$\begin{aligned} \left| \left| \nabla f_{16}\right| \right|\le & {} \left| \frac{3}{T_c}\right| , \end{aligned}$$

(105)

$$\begin{aligned} \left| \left| \nabla f_{17}\right| \right|\le & {} \left| \frac{1}{T_{pav}}\right| , \end{aligned}$$

(106)

$$\begin{aligned} \left| \left| \nabla f_{18}\right| \right|\le & {} \left| \frac{1}{T_{lpwi}}\right| , \end{aligned}$$

(107)

$$\begin{aligned} \left| \left| \nabla f_{19}\right| \right|\le & {} \left| \frac{K_{wi}}{T_{lpwi}}+\frac{1}{T_{wowi}}\right| . \end{aligned}$$

(108)

From conditions (89)–(90), the bound of $\left| \left| \nabla f_{20}\right| \right|$ is given by,

$$\begin{aligned} \left| \left| \nabla f_{20}\right| \right| \le \left| K_{vi}+K_{vi}V_{max1}+K_{vi}V_{max2}\right| . \end{aligned}$$

(109)

The bound of $\left| \left| \nabla f_{21}\right| \right|$ is given by,

$$\begin{aligned} \left| \left| \nabla f_{21}\right| \right| \le 100. \end{aligned}$$

(110)

From conditions (65), (85) and (90) the bound of $\left| \left| \nabla f_{22}\right| \right|$ is given by,

$$\begin{aligned} \left| \left| \nabla f_{22}\right| \right|\le & {} \left| \frac{1}{0.02V_{mnm}}\right| + \left| \frac{Y_8}{0.02V_{min1}}\right| \nonumber \\&+\,\left| \frac{Y_8}{0.02V_{min2}}\right| +50. \end{aligned}$$

(111)

Estimates (87)–(111) establishes our result and prove Lemma 3.3. $\square$

Lemma 3.4

The function f(t, y) is uniformly Lipschitz continuous in y.

Proof

Based on the proof of Lemma 4.3, we let FF be a vector in $\mathbb {R}^{22}$, such that for all i, we have $\left| \left| \nabla f_i\right| \right| \le { FF}_i$ and we let the largest component of FF be ${ FF}_{max}$. Since t is a defined parameter such that the map (80) holds true. Then, by the mean value theorem of several variables, for any given $y_j,\,y_k$ and $j,k \in \{1,2\ldots 22\}$, we have:

$$\begin{aligned} \left| \left| f_i(t,y_j)-f_i(t,y_k) \right| \right| \le { FF}_i \left| \left| y_j-y_k \right| \right| . \end{aligned}$$

(112)

Now, we can show that:

$$\begin{aligned} \left| \left| f(t,y_j)-f(t,y_k) \right| \right|\le & {} \sum _{i=1}^{22} \left| \left| f_i(t,y_j)-f_i(t,y_k) \right| \right| \nonumber \\\le & {} \sum _{i=1}^{22} { FF}_i \left| \left| y_j-y_k \right| \right| \nonumber \\\le & {} 22\cdot { FF}_{max}\left| \left| y_j-y_k \right| \right| . \end{aligned}$$

(113)

Since $22\cdot { FF}_{max}$ is independent on t, then f(t, y) is uniformly Lipschitz continuous in y and this shows the proof for Lemma 3.4. $\square$

Theorem 3.1

For the initial value problem $\frac{dy}{dt}=f(t,y), y(t_0)=y_0$, there exists $\epsilon >0$ such that there is a unique solution for the given initial value problem on $[t_0-\epsilon ,t_0+\epsilon ]$.

Remark 3.2

Proof of Theorem 3.1 follows from Picard–Lindelof Theorem as in chapter 13, sections 1 and 2 of the analysis reference [28], supported by the continuity assumption of f(t, y) in t, and both Theorem 3.0 and Lemma 3.4.

3.3 General study of existence and uniqueness versus grid parameters

The results of existence and uniqueness proofs depend on the behavioral analysis of the function $g(y_{21},y_{22})=B^2-4AC$ that we have in Lemma 4.2, as we showed that this function has a minimum only on the borders of a given rectangle domain. By checking the borders of the rectangle domain with fixed R, X in Table 1, we have $g(y_{21},y_{22})>0$, which enables us to prove the existence and uniqueness of real solutions. Since R, X represent the impedance of the grid, it is reasonable to assume that a change or drop can happen in their values. This raises the question of whether we can still prove existence and uniqueness with different R, X and have a safe region in the space of R, X, such that, existence and uniqueness are still guaranteed.

Fig. 2

Safe region in which $0\le -\frac{R^2+X^2}{X_{eq}}-(R^2+X^2)Y^2_{22}+E^2$

We want to have $V=\frac{-B + \sqrt{B^2 - 4AC}}{2A}$ with $0\le B^2-4AC$ as in Eq. (28). This will lead us to find a region within R, X space such that the following estimate holds,

$$\begin{aligned} 0\le & {} \left[ 2y_{22}R+\frac{2Xy_{21}}{X_{eq}} +\frac{2(R^2+X^2)y_{21}}{X_{eq}}\right] ^2 \nonumber \\&-\,4\left( 1+\frac{2X}{X_{eq}}+\frac{R^2+X^2}{X_{eq}}\right) \nonumber \\&\quad \left( \frac{R^2+X^2}{X_{eq}}+(R^2+X^2)y^2_{22}-E^2\right) . \end{aligned}$$

(114)

We found that if we compute the number $Y_{22}$, then we can find a region $0\le -\frac{R^2+X^2}{X_{eq}}-(R^2+X^2)Y^2_{22}+E^2$ in the first quadrant of R, X in which the estimate (114) holds, and therefore existence and uniqueness for the initial value problem for any give R, X in that area. The following Lemma is to show that.

Lemma 3.5

With $R,X\ge 0,\,X_{eq}$ and E as in Table 1, $0<y_{22}\le Y_{22}$, and $0< y_{21}$, then if

$$\begin{aligned} 0\le -\frac{R^2+X^2}{X_{eq}}-(R^2+X^2)\cdot Y^2_{22}+E^2, \end{aligned}$$

(115)

the inequality (114) holds.

Proof

The following estimate follows from the given condition $y_{22}\le Y_{22}$,

$$\begin{aligned}&\left( \frac{R^2+X^2}{X_{eq}}+(R^2+X^2)y^2_{22}-E^2\right) \nonumber \\&\quad \le \left( \frac{R^2+X^2}{X_{eq}}+(R^2+X^2)Y^2_{22}-E^2\right) . \end{aligned}$$

(116)

We multiply the inequality (116) by the negative quantity $-4\left( 1+\frac{2X}{X_{eq}}+\frac{R^2+X^2}{X_{eq}}\right)$, then we get:

$$\begin{aligned}&-4\left( 1+\frac{2X}{X_{eq}}+\frac{R^2+X^2}{X_{eq}}\right) \nonumber \\&\quad \left( \frac{R^2+X^2}{X_{eq}}+(R^2+X^2).y^2_{22}-E^2\right) \ge \nonumber \\&\quad -\,4\left( 1+\frac{2X}{X_{eq}}+\frac{R^2+X^2}{X_{eq}}\right) \nonumber \\&\quad \left( \frac{R^2+X^2}{X_{eq}}+(R^2+X^2).Y^2_{22}-E^2\right) . \end{aligned}$$

(117)

Then, if $0\le -\frac{R^2+X^2}{X_{eq}}-(R^2+X^2)Y^2_{22}+E^2$, we have:

$$\begin{aligned} 0\le & {} -4\left( 1+\frac{2X}{X_{eq}}+\frac{R^2+X^2}{X_{eq}}\right) \nonumber \\&\quad \left( \frac{R^2+X^2}{X_{eq}}+(R^2+X^2).Y^2_{22}-E^2\right) \nonumber \\\le & {} \left[ 2y_{22}R+\frac{2Xy_{21}}{X_{eq}} +\frac{2(R^2+X^2).y_{21}}{X_{eq}}\right] ^2 \nonumber \\&\quad -\,4\left( 1+\frac{2X}{X_{eq}}+\frac{R^2+X^2}{X_{eq}}\right) \nonumber \\&\quad \left( \frac{R^2+X^2}{X_{eq}}+(R^2+X^2).y^2_{22}-E^2\right) . \end{aligned}$$

(118)

This proves Lemma 3.5. $\square$

One can now clearly see that we can find a value for $Y_{22}$, followed by a safe region in which the estimate (118) holds. From our boundedness analysis previously discussed, as shown in estimate (63), we see that,

$$\begin{aligned} 0 \le y_{22}= & {} I_{plv} \le I_{pmax}\nonumber \\&+\,e^\frac{t_0}{0.02}(I_{plv}(t_0)-I_{pmax})e^\frac{-t}{0.02}=Y_{22} \end{aligned}$$

(119)

Looking at Eq. 22 $\left( \frac{dI_{plv}}{dt}= \frac{1}{0.02}\left[ \frac{P_{ord}}{V}-I_{plv}\right] \, \text {with} \, y_{22}=I_{plv}\right)$, we see that in the steady state $y_{22}=\frac{P_{ord}}{V}$. From the control limits (Table 3), we see that $\frac{P_{ord}}{V}$ is bounded above by $I_{pmax}$. If we assume that $y_{22}(0)\le I_{pmax}$ we then can find a number for $Y_{22}$ and therefore a graphical result for Lemma 4.5.

Proposition 3.5

If $I_{plv}(t_0) \le I_{pmax}$ then we have $Y_{22}=I_{pmax}=1.1$.

Proof

If $I_{plv}(t_0) \le I_{pmax}$, then from the estimate (119), we have:

$$\begin{aligned} y_{22}=I_{plv} \le I_{pmax}=Y_{22}. \end{aligned}$$

(120)

Now we can define our safe region and find it graphically. $\square$

Definition 3.5

With $y_{22}(0)\le 1.1$ and $Y_{22}=1.1$, the safe region is the region in R, X space bounded by $R=0,\,X=0$, and $\frac{R^2+X^2}{X_{eq}}-(R^2+X^2)Y^2_{22}+E^2=0$ such that the solution for the initial value problem exists bounded and unique for all R, X. The safe region is graphically found in Fig. 2.

4 Time scale analysis with simulations

In [26, section 2.C], there is a discussion and explanation about the model’s activated and deactivated controls based on the range of wind speed. The same discussion shows that for low wind speeds, in specific the range $3<v_{wind}<8.2$ (see figure 8 in [26]), the pitch control is set to zero to maximize the power extraction. As a result, Eqs. (5)–(6) are eliminated in this range. In [27, section 2], we see in the block description, that the reactive power control can be either in the power factor case [Group 5, Eqs. (10)–(11)] or supervisory voltage case [Group 6, Eqs. (12)–(16) in addition to (11)]. Therefore, if we consider the system for lower wind speeds ($3<v_{wind}<8.2$) and in power factor case, then as explained above, as in [26, 27], the system reduces to Eqs. (1)–(4), (7)–(8), (10)–(11), and (20)–(22). Multi time scale analysis is often possible when there are some variables that act fast in comparison to some other variables. We see that, at least locally, variables correspond to eigenvalues [diagonal components of the matrix D in Eq. (121)] with significant differences in magnitude. As noticed $\lambda _{1-4}$ are significantly larger in magnitude than the other eigenvalues. Also, the opposite holds true for $\lambda _{11}$, as it is significantly smaller in magnitude compared to the other eigenvalues.

Another factor that encourages a multi time scale study, is that, for the given range of wind speeds, eigenvalues are not sensitive to wind speed as mentioned in [23]. So locally we can linearize around the steady state and diagonalize in such a way that we have eleven variables that correspond one to one with the eigenvalues. Locally then, we can divide the system into smaller systems within different time scales. After that, we can test how far from the steady state the new systems can approximate the main system, and therefore approximate the nonlinear dynamics.

We start with fixing $v_{wind}=5$ m/s and the parameters as in Table 1. We compute the Jacobian matrix (A), at the steady state for the differential equations system that we have now, which is consistent of 11 nonlinear differential equations. We eliminate the algebraic equation using Eq. (28), and compute the matrices $P,P^{-1}$ and D such that,

$$\begin{aligned} P^{-1} A P = D \,,\, A = PDP ^{-1} \end{aligned}$$

(121)

where,

$$\begin{aligned} D= \left[ \begin{array}{cccccccccccc} -51.61 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -48.66 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -20 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -16.47 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -1.42+12.03i &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -1.42-12.03i &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.68+2.13i &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.68-2.13i &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.19-0.19i &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.19-0.19i &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.014\\ \end{array}\right] \end{aligned}$$

Now, let i, j be indices for the rows and columns of the matrix P respectively.

we construct a matrix

$$\begin{aligned} PP= \left[ \begin{array}{cccccccccccc} \phi _1&\quad \!\! \phi _2&\quad \!\! \phi _3&\quad \!\! \phi _4&\quad \!\! \phi _5&\quad \!\! \phi _6&\quad \!\! \phi _7&\quad \!\! \phi _8&\quad \!\! \phi _9&\quad \!\! \phi _{10}&\quad \!\! \phi _{11} \end{array}\right] \end{aligned}$$

such that $\phi _k=P_{i=1\ldots 11,j=k}$ for $k=1,2,3,4,11$. Those columns are the eigenvectors associated with the real eigenvalues $\lambda _{1,2,3,4,11}$. However, $\phi _5=Real[P_{i=1\ldots 11,j=5}],\,\phi _6=Imag[P_{i=1\ldots 11,j=5}],\,\phi _7=Real[P_{i=1\ldots 11,j=7}],\phi _8=Imag[P_{i=1\ldots 11,j=7}],\,\phi _9=Real[P_{i=1\ldots 11,j=9}]$, and $\phi _{10}=Imag[P_{i=1\ldots 11,j=9}]$.

We can see now that

$$\begin{aligned} PP ^{-1} \cdot A \cdot PP = DD \,,\, A = PP \cdot DD \cdot PP^{-1} \end{aligned}$$

(122)

where

$$\begin{aligned} DD = \left[ \begin{array}{cccccccccccc} -51.61 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -48.66 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -20 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -16.47 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -1.42 &{}\quad 12.03 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -12.03 &{}\quad -1.42 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.68 &{}\quad 2.13 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -2.13 &{}\quad -0.68 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.19 &{}\quad 0.19 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.19 &{}\quad -0.19 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.014 \end{array}\right] . \end{aligned}$$

The target for us now, is to diagonalize and have a set of new variables that have full one to one correspondence to the eigenvalues and the eigenvectors respectively.

Let the new variables be $V_i \,, \, i=1\ldots 11$ such that,

$$\begin{aligned} \mathbf {V}= & {} [V_1 \, V_2\, V_3\, V_4\, V_5\, V_6\, V_7\, V_8\, V_9\, V_{10}\, V_{11}]^T=PP^{-1}\mathbf {y^*} \nonumber \\= & {} PP^{-1}[w_{ref}\,f_1\,w_g\,w_t\,\varDelta \theta _m \,P_{inp}\,P_{1elec}\,V_{ref}\,\nonumber \\&E_{qcmd}\,E_q\,I_{plv}]^T. \end{aligned}$$

(123)

The transformation between the new set of variables and the old ones is given by,

$$\begin{aligned} \mathbf {V}=PP^{-1}\cdot \mathbf {y^*} \,, \, \mathbf {y^*}=PP\cdot \mathbf {V}. \end{aligned}$$

(124)

We already have the system $\frac{d\mathbf {y^*}}{dt}=f(\mathbf {y^*})$ and we want to construct $\frac{d\mathbf {V}}{dt}=f(\mathbf {V})$. We start with the terminal voltage in Eq. (28). We let the terminal voltage in terms of the new variables be $V_{new}$ and derived as following,

$$\begin{aligned} V= & {} V^*\left( E_q=y^*_{10},I_{plv}=y^*_{11}\right) \nonumber \\= & {} V^*\left( PP _{i=10,j=1\ldots 11}\cdot \mathbf {V}, PP _{i=11,j=1\ldots 11}\cdot \mathbf {V}\right) \nonumber \\= & {} V_{new}(\mathbf {V}). \end{aligned}$$

(125)

Since we have $\frac{dy^*_k}{dt}=\frac{d}{dt}\left[ PP _{i=k,j=1\ldots 11}\cdot \mathbf {V}\right]$, for all k $=1\ldots 11$, then $\frac{dy^*_k}{dt}$ can be rewritten,

$$\begin{aligned} \frac{dy^*_k}{dt}=\sum _{n=1}^{n=11} PP _{i=k,j=n} \frac{dV_n}{dt} \,\, \text {for all k}=1\ldots 11. \end{aligned}$$

(126)

For the vector function $f(\mathbf {y^*})$, every vector component $f_k(\mathbf {y^*})=f_k(PP\cdot \mathbf {V})$. Simply, in the right hand side of the differential equations, we substitute,

$$\begin{aligned} y^*_k= & {} PP _{i=k,j=1\ldots 11}\nonumber \\&\cdot \mathbf {V}=\sum _{n=1}^{n=11} PP _{i=k,j=n} V_n \,\, \text {for all k}=1\ldots 11. \end{aligned}$$

(127)

Now we combine Eqs. (125)–(127), then we get:

$$\begin{aligned} \sum _{n=1}^{n=11} PP _{i=k,j=n} \frac{dV_n}{dt}=f_k( PP \cdot \mathbf {V}) \,\, \text {for all k}=1\ldots 11. \nonumber \\ \end{aligned}$$

(128)

For every given k, we have an equation out of Eq. (128). After solving this system of 11 equations, we get,

$$\begin{aligned}&\frac{dV_k}{dt}=\sum _{n=1}^{n=11} Ca_{i=k,j=n}V_n+Ca_{i=k,j=12}+\,\frac{\sum _{n=1}^{n=11} Cl_{i=k,j=n}V_n+Cl_{i=k,j=12}}{V_{new}} \nonumber \\&\quad \qquad \quad +\,\left( \sum _{n=1}^{n=11} Cb_{i=k,j=n}V_n+Cc_{i=k,j=12}\right) \left( \sum _{n=1}^{n=11} Cc_{i=k,j=n}V_n+Cc_{i=k,j=12}\right) \nonumber \\&\quad \quad \qquad +\,V_{new}\left( \sum _{n=1}^{n=11} Cd_{i=k,j=n}V_n+Cd_{i=k,j=12}\right. \left. +\,\frac{\sum _{n=1}^{n=11} Ce_{i=k,j=n}V_n+Ce_{i=k,j=12}}{\sum _{n=1}^{n=11} Cf_{i=k,j=n}V_n+Cf_{i=k,j=12}} \right) \nonumber \\&\quad \quad \qquad +\,\frac{\left[ \sum _{n=1}^{n=11} Cg_{i=k,j=n}V_n+Cg_{i=k,j=12}+\left( \sum _{n=1}^{n=11} Ch_{i=k,j=n}V_n+Ch_{i=k,j=12}\right) ^2\right] }{\sum _{n=1}^{n=11} Ck_{i=k,j=n}V_n+Ck_{i=k,j=12}} \nonumber \\&\quad \quad \qquad +\,\frac{\left[ \left( \sum _{n=1}^{n=11} Ci_{i=k,j=n}V_n+Ci_{i=k,j=12}\right) ^3+\left( \sum _{n=1}^{n=11} Cj_{i=k,j=n}V_n+Cj_{i=k,j=12}\right) ^4 \right] }{\sum _{n=1}^{n=11} Ck_{i=k,j=n}V_n+Ck_{i=k,j=12}} \nonumber \\&\quad \quad \qquad +\,V_{new}^2\left( \sum _{n=1}^{n=11} Cm_{i=k,j=n}V_n+Cm_{i=k,j=12}\right) ^2\,\,\quad \text {for all k}=1\ldots 11.\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \end{aligned}$$

(129)

As noticed, we stored the resulting values of the computations in the arrays $Ca,\,Cb,\,Cc,\,Cd,\,Ce,\,Cf,\,Cg,\,Ci,\,Cj, Ck,\,Cl$, and Cm where they have a size of 11 rows and 12 columns. The row k corresponds to the coefficients of $V_{1\ldots 11}$ and the constant term respectively on the right hand side of the differential equation $\frac{dV_k}{dt}$ in the system. The vector of the steady state, of the original system $x_{states}$, relates to the vector of the steady state of the new system $V_{state}$ as follows,

$$\begin{aligned} \mathbf {V}_{state}= PP ^{-1}\cdot \mathbf {x}_{state}, \,\mathbf {x}_{state}= PP \cdot \mathbf {V}_{state}. \end{aligned}$$

(130)

The same holds for the vectors of initial conditions in the original and new systems respectively $\mathbf {x}_{initial}$ and $\mathbf {V}_{initial}$,

$$\begin{aligned} \mathbf {V}_{initial}= PP ^{-1}\cdot \mathbf {x}_{initial}, \,\mathbf {x}_{initial}= PP \cdot \mathbf {V}_{initial}. \end{aligned}$$

(131)

For $v_{wind}=5$ and parameters in Table 1, we derived the new system as in Eq. (129). We computed $\mathbf {V}_{state}$ both by the transformation in Eq. (130) and numerical solving of the system by setting the derivatives to zero. As a first validation, we found them matching. Table 4 shows the result.

Table 4 Steady state in both original and new systems at $v_{wind}=5$

A second validation, will be by linearizing the new system and then substituting the variables by the new steady state in the Jacobian matrix. The eigenvalues are typical to the original system and Eq. (121) holds for D Such that,

$$\begin{aligned} P_{new}^{-1}\cdot A_{new}\cdot P_{new} = D,\, A_{new} = P_{new}\cdot D\cdot P_{new}^{-1} \end{aligned}$$

(132)

where

$$\begin{aligned} P_{new}= \left[ \begin{array}{cccccccccccc} -1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.7071 &{}\quad -0.7071 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad - 0.7071i &{}\quad 0.7071i &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad - 0.7071i &{}\quad 0.7071i &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0.7071 &{}\quad 0.7071 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad - 0.7071i &{}\quad 0.7071i &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0.7071 &{}\quad 0.7071 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -1 \end{array}\right] , \end{aligned}$$

Fig. 3

Capture of $V_2$ solution. Full system (solid), fast solution (dashed), and slow solution (doted)

and $A_{new}= DD$ [see Eq. (122)].

4.1 Two time scales for any wind speed

We ran a simulation for the 11 by 11 system in Eq. (129). Then, we constructed two time scale systems to approximate the solutions of the full system. Since locally $V_{1\ldots 4}$ correspond to very large negative eigenvalues $\lambda _{1\ldots 4}$ respectively, then we treat them as fast variables. Conversely, $V_{5\ldots 11}$ correspond to $\lambda _{5\ldots 11}$ which are slow variables. While the dynamics of the fast variables $V_{1\ldots 4}$ are taking place in the fast time scale, the derivatives of the slow variables, with respect to the fast time scale, are approximately zero, which means that they stay constant as their initial conditions in the fast time scale. After the fast variables reach their steady state in the fast time scale, the slow variables start their dynamics in the slow time scale and the derivatives of the fast variables become algebraic equations coupled with the slow system.

From the physical system, we have the initial conditions $\mathbf {x}_{initial}$ and we calculate the corresponding $\mathbf {V}_{initial}$ from Eq. (131). We let $t_f$ and $t_s$ represent the fast and slow time scales respectively, then we have the following two systems which approximate the behavior of the system in Eq. (129):

$$\begin{aligned} \frac{dV_k}{dt_f}= & {} f(t_f,V_{1\ldots 4}) \, \, \text {for all}\,\text {k}=1\ldots 4 \, \, \text {(system of 4 DEs)} \nonumber \\ V_k= & {} f(t_f)=\text {constant} \nonumber \\ {}= & {} \text {initial condition} \, \, \text {for all}\,\text {k}=5\ldots 11 \end{aligned}$$

(133)

and,

$$\begin{aligned} \frac{dV_k}{dt_s}= & {} 0=f(t_s,V_{1\ldots 11}) \, \, \text {for all}\,\text {k}=1\ldots 4 \nonumber \\ \frac{dV_k}{dt_s}= & {} f(t_f,V_{5\ldots 11}) \, \, \text {for all}\,\text {k}=5\ldots 11 \nonumber \\&\quad \text {(system of 7 DEs and 4 algabraic equations)}. \nonumber \\ \end{aligned}$$

(134)

We ran simulations when the initial conditions are very close to the steady states and, as expected, the results are as expected. That wasn’t surprising, as the approximation is more accurate the closer the initial conditions are to the steady state. However, we wanted to test the nonlinear dynamics, as the initial conditions are far enough from the steady state. We ran a simulation for $\mathbf {x}_{initial}= \mathbf {x}_{state}+\mathbf {0.5}$ and captured the results. Those initial conditions represent some of the most nonlinear dynamics that can happen, as $\mathbf {x}_{state}+\mathbf {0.5}$ exceed the control limits for most of the state variables. The simulations gave promising results. As a sample for the Two time scale simulations, Figs. 3, 4 and 5 show $V_2$ full simulation with and without two time scale approximation. We found the approximation is good even for these extreme initial conditions, which exceeded the control limits for some of the state variables.

Fig. 4

Focused figure for the transient slow solution of $V_2$. Full system (solid), fast solution (dashed), and slow solution (doted)

Fig. 5

Focused figure for the fast solution of $V_2$. Full system (solid) and fast solution (dashed)

Fig. 6

$V_8$ in full system (solid), fast is not apparent, medium (dashed), and slow (underneath the both the fast and medium)

Fig. 7

Focused figures for the $V_8$ solution behavior to capture the slow solution (solid). The fast is dashed. a Focused figure for the transient slow solution. Full system (solid) and medium (dashed), b focused figure for the fast solution

4.2 Three time scales for any wind speed

By looking at the magnitudes of the eigenvalues, we notice that we can group them not only in two scales, but in three as well. The order of $\lambda _{11}$ is, by far, the smallest and still significantly smaller than $\lambda _{5\ldots 10}$. As a result, we ran another simulation for the system by approximating the solution behavior by three time scales smaller systems. $t_f$ is still the fast time scale, in which $V_{1\ldots 4}$ (the fast variables) dynamics take place, while $t_m$ is a medium time scale in which $V_{5\ldots 10}$ are the medium variables for which their dynamics take place in $t_m$. $t_s$ represents the slow time scale in which $V_{11}$ dynamics take place in this time scale. We tested the system for initial conditions that are close enough to the steady state and the results were as expected, however, we prefer to present results of nonlinear behavior. We ran the simulation with the same initial conditions as in the previous subsection. Figures 6 and 7b show $V_8$ full simulation with and without three time scale approximation.

$$\begin{aligned} \frac{dV_k}{dt_f}= & {} f(t_f,V_{1\ldots 4}) \, \, \text {for all}\,\text {k}=1\ldots 4 \, \, \text {(system of 4 DEs)} \nonumber \\ V_k= & {} f(t_f)=\text {constant}\nonumber \\= & {} \text {initial condition} \, \, \text {for all}\,\text {k}=5\ldots 11 \end{aligned}$$

(135)

and,

$$\begin{aligned} \frac{dV_k}{dt_f}= & {} 0=f(t_s,V_{1\ldots 11}) \, \, \text {for all}\,\text {k}=1\ldots 4 \nonumber \\ \frac{dV_k}{dt_m}= & {} f(t_m,V_{5\ldots 10}) \, \, \text {for all}\,\text {k}=5\ldots 10 \nonumber \\ V_k= & {} f(t_m)=\text {constant}=\text {initial condition} \, \, \text {for}\,k=11 \nonumber \\&\text {(system of 6 DEs and 4 algabraic equations)} \end{aligned}$$

(136)

and,

$$\begin{aligned} \frac{dV_k}{dt_s}= & {} 0=f(t_s,V_{1\ldots 11}) \, \, \text {for all}\,\text {k}=1\ldots 10 \nonumber \\ \frac{dV_k}{dt_s}= & {} f(t_f,V_{5\ldots 11}) \, \, \text {for}\,\text {k}=11 \nonumber \\&\text {(one DE and 10 algabraic equations)}. \end{aligned}$$

(137)

5 Conclusions

The mathematical model suggested by recognized papers and studies to represent wind turbines dynamics has now been translated to a system of nonlinear algebraic equations. Proof of the uniqueness to the terminal voltage has been represented, which generates a system of nonlinear differential equations. Under control limits, the system’s state variables and derivatives have been rigorously proven to be bounded. Under a defined ‘Safe Region’ in R and X space, we proved the existence and uniqueness for a given initial value problem. These proofs add assurances to implement the system by numerical solvers, guaranteeing that convergence of numerical solvers and simulators is a convergence to the unique solution of the given initial value problem. For a reduced version of the system, we have shown and performed two and three time scale analysis. This should open a whole new door for the dynamical study of wind turbines nonlinear dynamics. Since the literature had not previously provided any of the proposed mathematical analysis or time scale simulations, we assert that this paper is a base theoretical study for this emerging nonlinear dynamical system.