Ankle torque estimation based on disturbance observers for robotic rehabilitation

Abstract

Designing safe and tailored strategies for robotic therapy requires the knowledge of patient joint torques, allowing control strategies to adjust the torque level provided by the robotic device according to the patient’s performance. Given the impracticability of measuring human joint torques directly, many works in the area have used estimation techniques that require complex calibration and signal processing or introduce uncertainty in their system modeling. This paper evaluates three disturbance observer techniques for estimating ankle joint torque as an alternative solution. Based on the generalized momentum and Kalman filter methodologies, the approaches were implemented on a robotic device for ankle rehabilitation. They were evaluated on six healthy voluntary users for sitting position movements. The techniques demonstrated effectiveness in estimating human joint torque across three distinct human–robot interaction modes, with performance evaluation through normalized root-mean-square error (NRMSE) metrics. Statistical analysis, including ANOVA, Kruskal–Wallis, and Dunn’s post hoc tests, was employed to assess approach performance and impact effects under different configuration settings. These analyses highlighted significant differences in performance among the techniques, enhancing the understanding of the estimation approaches and highlighting their potential integration into robotic rehabilitation settings.

1 Introduction

In physical therapy, understanding patient joint torques is essential for muscle strength assessment and evaluation of neuromuscular impairment [1]. In clinical and research settings, the isometric and isokinetic dynamometers are commonly used devices for muscle strength assessment. They can measure the human joint torques while providing isometric or concentric resistance training of the limbs at constant angular joint velocity [2]. Nevertheless, these dynamometers do not consider issues associated with gravitational torques [3] that need to be compensated as well as passive torques introduced by the viscoelastic properties of the limbs [4]. A broader explanation of the above issue can be found in [5, 6].

Knowledge of human joint torques is also essential for other robotic rehabilitation devices, such as exoskeletons and platforms, to guarantee safe physical human–robot interaction [7, 8] and to achieve adaptive robot assistance according to the patient’s participation during the therapy session [9]. Nevertheless, in practice, human joint torques cannot be measured directly. Hence, the estimation of such torques turns out to be an ongoing challenge in the field of assistance and rehabilitation robotics. It is worth noting that this study specifically focuses on dealing with torque rather than Joint Contact Forces (JCF), given the direct significance of rotational forces in the field of robotic rehabilitation [10,11,12]. While JCF encompasses a broader spectrum of musculoskeletal forces, torque, specifically refers to the rotational forces that are central to the physical interaction between the patient and the robotic device. The distinction between these terms has been underscored in notable works in the biomechanics literature [13,14,15].

The most relevant works in the literature have estimated human joint torques either by inverse dynamics [16,17,18] or by electromyography (EMG) [19,20,21]. Despite the benefits of using inverse dynamics, body segment inertial parameters are estimated from pre-existing anthropometric data, introducing uncertainty in the system modeling. In addition, kinematic data contain significant measurement errors due to inaccurate localization and misalignment of markers during motion capture [22]. Regarding electromyography, electrode fixation is time-consuming, it requires calibration measurement, and signal processing can be complicated.

An alternative approach for robotic rehabilitation is to assume human dynamic behavior as the main source of disturbance inputs of the robotic system [23,24,25,26,27], that is, to treat the human joint torques as disturbances to be estimated. In robotic control system design, disturbance observer (DOB) [28] has been a useful technique for estimating unmeasurable load torques. It was initially designed for robotic industrial applications to compensate for the effect of destabilizing perturbations produced by the unknown external environment, unmodeled dynamics, or even uncertainties in the modeling [29, 30] and more recently in [31]. Based on the assumption that human joint torques can be considered as disturbance inputs, disturbance observers have been used to estimate upper-limb joint torques in robotic rehabilitation scenarios [32,33,34]. One of the benefits of using DOB for human torque estimation is that it only requires the measurement of joint angles, velocities, and robotic signals (current, voltage, and motor torque). Another well-adopted technique from robotic applications to estimate external torques is the generalized momentum observer (GMO) [35, 36]. It is a DOB-based approach that predicts the changes of momentum at the robot when contact with the environment occurs. Compared with the inverse dynamic approaches, the GMO does not need the computation of inverse inertia matrices. Also, it avoids the calculation of acceleration that introduces noise and delays [37].

The Kalman filter (KF) is another technique used for torque estimation in robotic scenarios [38, 39]. It provides an optimal estimate even in the presence of noise measurements. As a disturbance observer, the process model of the Kalman filter is augmented considering a disturbance model [40]. The Kalman filter can also be combined with the generalized momentum to estimate unknown external forces/torques in robotic scenarios [41]. DOB-based approaches for joint torque estimation in upper-limb robotic rehabilitation systems were found in [32, 33, 42]. On the other hand, there is a lack of research studies for lower limb in robotic rehabilitation systems. Some works for knee joint were reported in [43,44,45]. Nevertheless, most of these works assessed torque estimation performance by comparing it with EMG signals.

As an effort to develop techniques for estimating the human torque in lower-limb robotic scenarios, in this paper, we present the implementation of three DOB-based approaches for ankle torque estimation using the Anklebot robot [46]. The approaches are the generalized momentum observer, the Kalman filter augmented with a disturbance model, and the Kalman filter combined with the generalized momentum. To the best of our knowledge, in robotic rehabilitation, none of those mentioned techniques was found to be implemented for ankle torque estimation. The remainder of this paper is organized as follows. Section 2 describes the methods. Section 3 presents the implementation of the estimation approaches on voluntary users. Finally, Sect. 4 presents the discussion and conclusions.

2 Methods

2.1 Experimental setup

The approaches were implemented on the Anklebot [46], a robot device oriented for the research of ankle rehabilitation. The Anklebot is a backdrivable robot with low intrinsic mechanical impedance, designed to be used in therapeutic assistance training to help people who have suffered from brain damage by restoring the range of motion and strength of the ankle. It operates through a control strategy that regulates the dynamic relationship between actuator torque and the desired joint angle trajectory. This relationship is governed by the control law:

$$\begin{aligned} \tau _{r} = K_\textrm{v}(\theta _\textrm{ref} -\theta ) + B_\textrm{v}{\dot{\theta }}, \end{aligned}$$

(1)

where $\theta _\textrm{ref}$ and $\theta$ are the ankle’s reference trajectory and actual angular position in the dorsi- and plantar-flexion directions, respectively. ${\dot{\theta }}$ represents the angular velocity. $K_\textrm{v}$ and $B_\textrm{v}$ are control gains representing virtual stiffness and damping, respectively. In this work, the Anklebot is operated only in the dorsi-/plantar-flexion direction. To provide a method for verification of the estimates, a customized ankle–foot orthosis (AFO) was assembled, and it is equipped with on its back a miniature load cell that measures tension and compression forces within a range of 0–5 KgF (50 N). During the experiments, the users wear the AFO to measure the ankle torque for movements in the sagittal plane. The torque provided by the load cell on the AFO is equivalent to measuring the ankle joint torque if considered a simple hinge joint.

Fig. 1

Experimental setup. a Configuration of the experiments with a user wearing the Anklebot. b Diagram showing during the customized AFO equipped with the load cell

Experiments were conducted with six voluntary users regarding the physical activity they may perform in a training session with this robot (Fig. 1a). The experimental protocol was approved by the Ethics Committee of the Federal University of São Carlos (Number 26054813.1.0000.5504). The users have given informed consent to the investigations. The experiments follow the control diagram described in Fig. 2. Since compensation or rejection of disturbance is out of scope, the torque estimation approaches are programmed on the Anklebot robot so that they are executed simultaneously without affecting the control system.

Fig. 2

Schematic for the proposed torque estimation approaches. The generalized momentum observer (GMO), the augmented Kalman filter (KF), and the Kalman filter based on momentum dynamics (KF-M) approaches are implemented simultaneously and are not fed back into the robotic control system

2.2 Physical human–robot interaction configurations during experiments

Depending on the physical activity, the representation of human joint mechanical impedance as spring–damper lumped systems had been treated either as being constant [47,48,49] or variable [50, 51]. When using the Anklebot for sitting position training, the translational movement of the thigh and knee is restricted by securing the knee brace to a perforated metal sheet attached to the chair. Consequently, the ankle does not bear any load nor contacts the ground, leading to minimal variation in ankle joint impedance parameters, which can thus be regarded as constant. With this premise, the methodology accounted for three operation modes reflecting different types of physical human–robot interaction during Anklebot training sessions:

Passive mode In this mode, participants allowed their ankles to remain relaxed, not resisting the robot’s guidance. This condition is characterized by low mechanical impedance, resulting in ankle torques that are anticipated to be comparable to the load cell measurements.

Resistive mode Participants actively resisted the robot’s movements, which increases their mechanical impedance compared to the passive mode. If the participant maintained a neutral ankle position, load cell torque readings would be minimized, effectively counteracting the robot’s efforts.

Cooperative mode This mode required participants to follow a predefined trajectory with reduced control gains, decreasing the robot’s torque assistance and requiring a greater effort from the user. The ankle mechanical impedance in this mode is averaged between those of the passive and resistive modes.

During all interaction modes, participants received online visual feedback on a screen, displaying both the reference trajectory and their current ankle position, facilitated by a graphical interface.

2.2.1 Description of the types of experiments for the assessment of the techniques

Ankle torque and trajectory in robotic-assisted training typically exhibit patterned behaviors, which can be effectively modeled using sinusoidal functions. For this study, we defined two distinct reference trajectories for the robotic control system to simulate during evaluations: a simple sine wave and a more complex gait-shaped trajectory. The mathematical model generating such signals is given by the following sum of sines function [52, 53]:

$$\begin{aligned} \theta _\textrm{ref} (t) = \sum _{n = 1}^{n_{d}} a_{n} \sin (\omega _{n} t + \phi _{n}), \hspace{0.5cm} t > 0 \end{aligned}$$

(2)

where $n_{d}$ represents the number of sine functions making up the signal, the function is set as $n = 1$, for the pure sine and, $n = 3$, for the gait-shaped trajectory. For each n-th element, the terms $a_{n}$, $\omega _{n}$, and $\phi _{n}$ stand for the amplitude, frequency, and phase, respectively. The frequency is expressed in rad/s, that is, $\omega _{n} = 2 \pi f_{n}$, where $f_{n}$ is the frequency in Hertz. Table 1 shows the parameters used in all experiments. Experiment 1 uses a single set of parameters with n = 1 for the basic sine wave, while Experiments 2 and 3 use three sets of parameters (n = 1, 2, 3) to define the gait-shaped trajectory.

Table 1 Parameter identification for the sinusoidal trajectories

Experiment 1: simple flexion–extension movements. The initial type of experiment commanded the Anklebot to track a simple sinusoidal reference ($\theta _\textrm{ref}$) with specified amplitude and frequency settings for 60 s. For safety, the virtual stiffness and damping of the impedance controller were set as $K_\textrm{v}$= 30 N m/rad and $B_\textrm{v}$ = 5 N m s/rad, respectively. These settings were selected based on knowledge of Anklebot impedance responses and supported by the previous studies [27, 54], ensuring that the torque generated by the robot remains within a safe range that is neither too forceful to cause harm nor too weak to be ineffective. Throughout the trial, participants were instructed to alter their dynamic behavior every 20 s, beginning with a passive mode, transitioning to a resistive mode, and finishing with a cooperative mode.

Experiments 2 and 3: Gait pattern trajectory with passive and resistive modes. The passive and resistive modes were also evaluated independently for the gait-shaped trajectory. In these experiments, the robot was commanded to track the reference signal described in Eq. 2 using a $n_\textrm{d} = 3$ sine function. Before each test, the users were asked to walk during a short trial, and ankle motion was collected and processed using the fast Fourier transform algorithm (FFT) to estimate the amplitude and frequency parameters that describe their corresponding gait–sinusoidal trajectory.

The impedance controller gains were set to $K_\textrm{v}$= 60 N m/rad and $B_\textrm{v}$ = 5 N m s/rad for the passive mode, and $K_\textrm{v}$= 30 N m/rad and $B_\textrm{v}$ = 5 N m s/rad for the resistive mode.

2.3 Dynamic model

Consider the following dynamic model for the ankle/Anklebot system:

$$\begin{aligned} I_\textrm{h,r} \ddot{\theta } + B_\textrm{h,r} {\dot{\theta }} + K_\textrm{h,r} \theta + G (\theta ) + \tau _{f} ({\dot{\theta }}) = \tau _\textrm{h} + \tau _{r}, \end{aligned}$$

(3)

with $\theta \in {\mathbb {R}}^1$, that is, the system is a 1 degree of freedom (DoF). According to [46], ankle kinematics is obtained using simple geometry and typical anthropometric data for each volunteer. The disturbance observers are formulated from Eq. 3. $\tau _\textrm{h}$ is the human ankle torque, and the scalar parameters I, B, and K represent torsional inertia, damping, and stiffness, respectively. The subscripts h and r refer to the combination of the human ankle and robot joint dynamics, i.e., $I_\textrm{h,r} = I_\textrm{h} +I_\textrm{r}$, $B_\textrm{h,r} =B_\textrm{h} +B_\textrm{r}$ and $K_\textrm{h,r} =K_\textrm{h} +K_\textrm{r}$.

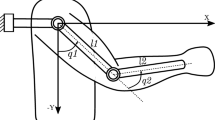
The gravitational torque is modeled as $G (\theta ) = m \hspace{0.05cm} x_\textrm{cm} \hspace{0.05cm} g \hspace{0.05cm} \cos (\theta )$, where m is the mass combination of the ankle and the foot, g is the acceleration due to gravity, and $x_\textrm{cm}$ is the center of mass of the foot (see Fig. 1b). For each user, the equivalent of equivalent mass (m) and center of mass $x_\textrm{cm}$ were computed according to [13]. These values were averaged to 1.507 kg and 0.05 cm, respectively, which were adopted as the nominal model parameters. This averaging process aimed to provide a representative baseline that, while not capturing every anatomical difference of users, offers an approximation suitable for our analysis of gravitational torque.

The model also includes the nonlinear function, $\tau _f({\dot{\theta }})$, to describe the robot friction torque based on [55, 56]. This function is compound by the static, $\tau _\textrm{s}$, Coulomb, $\tau _\textrm{c}$, and viscous friction, $\tau _\textrm{v}$, parameters and is given by

$$\begin{aligned} \tau _{f}({\dot{\theta }}) = \left\{ \begin{array}{ll} \qquad \tau _{s}, &{} \quad \text {if } {\dot{\theta }} \le \delta \hspace{0.05cm} \text {and} \hspace{0.05cm} |\tau _{r} |< \tau _\textrm{s},\\ \quad \tau _\textrm{c}\hspace{0.1cm} sgn({\dot{\theta }}), &{} \quad \text {if } {\dot{\theta }} \le \delta \hspace{0.05cm} \text {and} \hspace{0.05cm} |\tau _{r} |\ge \tau _\textrm{s},\\ \tau _\textrm{c} \hspace{0.1cm} sgn({\dot{\theta }}) + \tau _\textrm{v} \hspace{0.1cm} {\dot{\theta }}, &{} \quad \text {otherwise}, \end{array}\right. \end{aligned}$$

(4)

where the parameter $\delta$ represents boundary lubrication of the actuator velocity. To identify the parameters associated with Eq. 4, an experimental procedure based on [57] was reproduced here. To this, the Anklebot was configured to operate in an open-loop mode and to track a ramp torque reference:

Fig. 3

Friction parameter characterization. Plots: angular velocity (top-left), angle robot (top-right), the torque applied (bottom-left), and the correlation between robot torque and angular velocity (bottom-right) resulting

$$\begin{aligned} \tau _{r}(t) = h \hspace{0.1cm} t, \hspace{0.25cm} 0 < t > t_{(\theta \max )}, \end{aligned}$$

(5)

where t denotes the time, and $h>$ 0 is the ramp slope. The applied robot torque was programmed to finish when reaching an upper-limit angle, $\theta _{\max }$ = 0.5236 rad (30 degrees).

The static friction, $\tau _\textrm{s}$, was approximated to 3.88 Nm, and it was obtained by observing the torque at the time instant when the stationary position $\theta >0$ and relative motion, ${{\dot{\theta }}} > 0$, are overcome. By projecting a regression line over the angular velocity (top-left in Fig. 3), the slope a, the intersection b/a with the time axis, and the projection b are obtained to compute the viscous and Coulomb parameters as $\tau _\textrm{v} = \frac{h}{a}$ = 0.61 N m s/rad and $\tau _\textrm{c} = \frac{b}{a} h$ = 3.76 Nm, respectively. The boundary lubrication velocity, $\delta = 0.05$ rad/s, was obtained by observing the angular velocity when static friction occurs (see bottom-right plot in Fig. 3).

2.3.1 Model Parameter Identification

In this section, it is presented the identification of the human–robot impedance parameters ($I_\textrm{h,r}$, $I_\textrm{h,r}$, and $I_\textrm{h,r}$ in Eq. 3) for each of the voluntary users. These parameters were identified for the passive and resistive modes. An experimental procedure based on [58] was carried out for each of the voluntary users. The Anklebot was commanded to hold a $0^{\circ }$ reference while a random torque perturbation, $\tau _{rand}$, in dorsi-/plantar-flexion direction was applied during 60 s. For both the passive and resistive tests, the impedance controller was programmed with $K_\textrm{v} = 5$ N m/rad and $B_\textrm{v} = 0$ N m s/rad. The perturbation signal was set with ± 7.7 N.m of amplitude and 100 Hz of bandwidth. The gravitational and friction torques were compensated in these experiments. From Eq. 3, the closed-loop transfer function between the random torque perturbation input and the resulting angular displacement is defined as follows:

$$\begin{aligned} Y_{CL_\textrm{h,r}}(s) = \frac{1}{I_\textrm{h,r} s^2 + (B_\textrm{h,r} + B_\textrm{v}) s + (K_\textrm{h,r} + K_\textrm{v})}. \end{aligned}$$

(6)

Figure 4 shows the frequency response of $Y^{-1}(s)$ for the user 1 for the corresponding passive (left) and resistive (right) modes. They were obtained by using MATLAB’s tfestimate function that estimates the spectral density of the signals. Linear second-order models were adjusted heuristically (red lines in magnitude and phase plots) to fit with the frequency function responses (blue lines). The parameters fitted of such theoretical models represent those of Eq. (6), and the results for all the users in passive and resistive modes are shown in Table 2. The impedance parameters for the cooperative mode were assumed to be the mean value between the passive and resistive modes.

Fig. 4

Frequency response estimation of $Y^{-1}(s)$ to obtain the ankle-robot impedance parameters for user 1. a passive mode. b Resistive mode

Table 2 Rendered human–robot impedance parameters for passive and resistive modes

2.4 Torque Estimation Approaches

This section presents the proposed estimation techniques, they consider the ankle joint torque as the disturbance to be estimated.

2.4.1 Generalized momentum observer

The idea of this approach is to observe the momentum when physical interaction between the robot and its environment occurs. The momentum of the ankle/Anklebot system is defined by $p = I_\textrm{h,r} {\dot{\theta }}$, by assuming that the inertia parameter does not change over time, the momentum time derivative can be computed as $\dot{{p}} = I_\textrm{h,r} \ddot{\theta }$. Thus, the dynamic Eq. 3 can be expressed in terms of the generalized momentum as:

$$\begin{aligned} \dot{{p}} = \tau _\textrm{r} - B_\textrm{h,r} {\dot{\theta }} - K_\textrm{h,r} \theta - \tau _{f}({\dot{\theta }})- G(\theta ) + \tau _\textrm{h}. \end{aligned}$$

(7)

The dynamics of the momentum observer is given by

$$\begin{aligned} \dot{\hat{p}} = \tau _\textrm{r} - B_\textrm{h,r} {\dot{\theta }} - K_\textrm{h,r} \theta - \tau _{f}({\dot{\theta }})- G(\theta ) + K_I e, \end{aligned}$$

(8)

where $\hat{p}$ is a predictor of the momentum dynamics, $K_I$ is a positive gain, and $e = p - \hat{p}$ is the prediction error of the momentum. By defining a residual term as $r = K_Ie$, and by combining it with (7) and (8), we obtain

$$\begin{aligned} {\dot{r}} = K_I({\dot{p}} - \dot{\hat{p}}) = K_I\tau _\textrm{h} - K_I\textrm{r}. \end{aligned}$$

(9)

Applying the Laplace transformation to Eq. (9), we obtain,

$$\begin{aligned} r(s) = \frac{K_I}{s + K_I} \tau _\textrm{h} (s). \end{aligned}$$

(10)

thus, the residual term, r, is the result of applying the disturbance torque through a first-order low-pass filter, namely, r is a smoothed estimate version of $\tau _\textrm{h}$, i.e., $r = \hat{\tau }_\textrm{h}$, $K_I$ represents the cut-off frequency. The adjustment of $K_I$ implies a compromise between the amplitude and phase of the filtered signal r, i.e., the higher the gain, the larger the amplitude, and conversely, the lower the gain, the larger the phase shift. For the subsequent implementation of this approach, $K_I$ was adjusted as 4.

2.4.2 Kalman filter augmented with sinusoidal disturbance models

This Kalman filter formulation uses a state-space representation of the system dynamics described in Eq. 3 augmented with a dynamic disturbance model representing the ankle torque similar to the joint angle trajectory, it was assumed that the ankle torque can also be represented as a sinusoidal temporal series. Then, simple extension and gait trajectories can be achieved by defining the orders $n_\textrm{d}$ = 1 and $n_\textrm{d}$ = 3, respectively, of the time-series equation. The augmented state-space system considering the dynamics of Eq. 3 and the sinusoidal disturbance model is given by

$$\begin{aligned} \underbrace{\left[ \begin{array}{l} \ddot{\theta } \\ {\dot{\theta }} \\ {\dot{x}}_{d_{(2n_\textrm{d} \times 1)}} \end{array} \right] }_{{\dot{x}}} =&\underbrace{ \left[ \begin{array}{lllll} -\frac{B_\textrm{h,r}}{ I_\textrm{h,r}} &{} - \frac{K_\textrm{h,r}}{ I_\textrm{h,r}} &{} 0_{(1 \times (2n_\textrm{d}-1))} &{} -\frac{1}{I_\textrm{h,r}} \\ 1 &{} 0 &{} 0_{(1 \times (2n_\textrm{d}-1))} &{} 0\\ 0_{(2n_\textrm{d} \times 1)} &{} 0_{(2n_\textrm{d} \times 1)} &{} A_{d_{(n_\textrm{d} \times n_\textrm{d})}} &{} &{} \end{array} \right] }_{A_\textrm{c}} \underbrace{ \left[ \begin{array}{l} {\dot{\theta }} \\ \theta \\ x_{d_{(2n_\textrm{d} \times 1) }} \end{array}\right] }_{x} \nonumber \\&+ \underbrace{\left[ \begin{array}{l} \frac{1}{I_\textrm{h,r}} \\ 0_{((2n_\textrm{d}+1) \times 1)}\end{array} \right] }_{B_\textrm{c}} \underbrace{(\tau _{r}-\tau _{f}({\dot{\theta }}) - G(\theta ) )}_{u}, \end{aligned}$$

(11)

$$\begin{aligned} y&=\underbrace{\left[ \begin{array}{ll} I_{(2 \times 2)}&{} 0_{(2n_\textrm{d} \times 2)} \\ 0_{(2 \times 2n_\textrm{d})} &{} 0_{(2n_\textrm{d} \times 2n_\textrm{d})} \end{array} \right] }_{H} \underbrace{\left[ \begin{array}{l} {\dot{\theta }} \\ \theta \\ x_{d_{(2n_\textrm{d} \times 1) }} \end{array}\right] }_{x}. \end{aligned}$$

(12)

here $A_\textrm{d}$ represents the sinusoidal time-series dynamics expressed into the state-space domain. The formulations for simple extension and gait trajectories, employing equation orders of $n_\textrm{d} = 1$ and $n_\textrm{d} = 3$, respectively, are elaborated in Appendix A. It is worth noting that the formulations in the appendix only depend on the frequencies to define the matrices. The terms $A_\textrm{c}$ and $B_\textrm{c}$ stand for the augmented continuous state transition and input matrices, respectively, H is the measurement gain matrix, x and u are the augmented state and input vectors, respectively. Since the standard Kalman filter was proposed for linear systems, the gravitational and friction torques were included in the input, u, instead of the state transition matrix, $A_\textrm{c}$. Once the state-space formulation of the Kalman filter is defined, it is implemented according to the standard discrete-time algorithm [59]. The covariance matrices for the process and measurement noise were adjusted as $Q = 0.1 I_{4}$ and $R = 0.001 I_{4}$ for the $n_\textrm{d}$= 1 case, and $Q = 0.1 I_{10}$ and $R = 0.001 I_{10}$ for the $n_\textrm{d}$= 3 case.

2.4.3 Combined Kalman filter and generalized momentum approach

This combined approach was based on the one proposed in [31] to estimate the external forces of a 7-DoF manipulator. The idea of this formulation is to combine the robot generalized momentum with a disturbance model given by the following first-order model:

$$\begin{aligned} \dot{\tau _\textrm{d}} = A_{d} \tau _\textrm{d} + w_\textrm{d}, \end{aligned}$$

(13)

where $A_\textrm{d}$ determines the dynamics assumed for the disturbance, $\omega _\textrm{d} \sim N(0,Q_{d})$ are modeling inaccuracies represented as zero-mean normally distributed random variables. By defining the state vector $x = [p^T \hspace{0.25cm} \tau _\textrm{d}^T]^T$ and introducing the abbreviation $\bar{\tau } = \tau _\textrm{r} - B_\textrm{h,r} {\dot{\theta }} - K_\textrm{h,r} \theta - G(\theta )- \tau _{f}({\dot{\theta }})$, Eqs. (13) and (7) can be rearranged to form the augmented system.

$$\begin{aligned} \underbrace{ \left[ \begin{array}{c} {\dot{p}} \\ \dot{\tau _\textrm{d}} \end{array} \right] }_{{\dot{x}}} = \underbrace{ \begin{bmatrix} 0 &{} -1 \\ 0 &{} A_\textrm{d} \end{bmatrix} }_{A_\textrm{c}} \underbrace{ \left[ \begin{array}{c} p \\ \tau _\textrm{d} \end{array} \right] }_{x} + \underbrace{ \left[ \begin{array}{c} 1 \\ 0 \end{array} \right] }_{B_\textrm{c}} \underbrace{\bar{\tau }}_u + w. \end{aligned}$$

(14)

The vector $w = [w_p^T \hspace{0.25cm} w_\textrm{d}^T]^T$ includes the disturbance noise and not modeled input noises, $w_p$. By assuming a measurement noise at the generalized momentum, $v \sim N(0,R)$, represented as zero-mean normally distributed random variables, the output equation is given by:

$$\begin{aligned} p = \underbrace{[1 \hspace{0.25cm} 0]}_{H} \underbrace{ \left[ \begin{array}{c} p \\ \tau _{d} \end{array} \right] }_{x} + v. \end{aligned}$$

(15)

The implementation of this formulation is also carried out according to the discrete-time algorithm of the Kalman filter. The covariance matrices for the process and measurement noise were adjusted as $Q =1\textrm{e}{-4}*I_{2}$ and $R = 1\textrm{e}{-5}*I_{2}$, respectively. Finally, the discretization of $A_\textrm{c}$ and $B_\textrm{c}$ for both Kalman filter formulations was made by using $A_k = I + A_\textrm{c} T_\textrm{s}$ and $B_k = T_\textrm{s} B_\textrm{c}$, for a time sample of $T_\textrm{s}$ = 0.5 ms.

3 Results

This section presents the results of the implementation of the approaches for estimating the ankle torque in the experiments described in Sect. 2.2.1. These experiments aimed to assess the estimation results in different configurations of trajectory type and HRI operation mode. Each of the six volunteer users conducted the three experiment types. To quantify the performance of the approaches during each experiment and to facilitate comparison among the different configurations, which may present different scales, the normalized root-mean-square error (NRMSE) was computed using the following expressions:

$$\begin{aligned} \text {RMSE} = \sqrt{\frac{\sum _{i=1}^n (y_i - \hat{y})^2}{n}}, \hspace{0.5cm} \text {NRMSE} = \frac{\text {RMSE}}{y_{\max } - y_{\min }} \end{aligned}$$

(16)

where y represents the reference for each experiment obtained from the load cell torque $(\tau _{lc})$, and $\hat{y}$ stands for the estimated torque of each approach $(\hat{\tau }_{\textrm{h}_{KF}}, \hat{\tau }_{\textrm{h}_{GMO}}, \hat{\tau }_{\textrm{h}_{KFM}})$.

3.1 Torque estimation results of Experiment 1

This section presents the results of Experiment 1, including the torque estimation performance of each approach under the passive, resistive, and cooperative dynamic modes. Figure 5 displays the temporal responses for user 1, demonstrating concordance with the expected behavior detailed in Sect. 2.2.

Fig. 5

Temporal responses of Experiment 1 for the user 1. Estimation approaches are KF (red), GMO (green), and KF-M (purple)

Figure 6 summarizes the NRMSE values calculated across all participants during Experiment 1. The lower subplots show the distribution of errors, including its median, interquartile range, and outliers. Each colored outlier at the boxplots corresponds to each user as indicated by the bar plot legends in Figs. 6 and 9. As shown in Fig. 6, the three methodologies exhibited low NRMSE values, with median values below 0.5 N.m in passive mode, indicating high accuracy, with all KF errors below 0.3 Nm, and GMO and KF-M errors below 66.6% and 50%, respectively, falling below 0.3 N.m. Looking at the interquartile ranges, it can be deduced that all the approaches presented a lower spread and variability in their cooperative mode than the others.

Fig. 6

Performance assessment for Experiment 1. The RMSE of the three approaches during the different dynamic behaviors was computed for each user

3.2 Torque estimation results of Experiments 2 and 3

This section presents the torque estimation results for Experiments 2 and 3. Figures 7 and 8 show the temporal responses for user 1 tests for each of the experiments.

Fig. 7

Temporal responses of Experiment 2 for user 1 in passive mode. a Angular references. b Robot torque. c Estimated torques

Fig. 8

Temporal responses of Experiment 3 for user 1 in resistive mode. a Angular references. b Robot torque. c Estimated torques

The NRMSE was also computed in these two experiments and is described in Fig. 9. For Experiment 2 (Fig. 9a), which uses the gait trajectory in passive mode, the Kalman filter (KF) demonstrated higher precision with the lowest median RMSE and compactest interquartile range, indicating consistent performance among all users. All the median NRMSE approaches were proximal, with the KF presenting the lowest value of 0.38 N.m.

Fig. 9

Performance assessment of torque estimation using the gait-based trajectory experiments. a Experiment 2: passive and b Experiment 3: resistive

In contrast, GMO showed slightly higher variability, as indicated by a wider interquartile range compared to KF, though it still maintains competitive performance, especially compared to KF-M, which yielded the highest variability and median NRMSE. For Experiment 3 (Fig. 9b), which explored the gait trajectory in resistive mode, both KF and GMO displayed better performance than KF-M, with GMO slightly surpassing KF in terms of lower median RMSE and a narrower interquartile range.

3.3 Statistical analysis

In this section, it is developed a statistical analysis to assess the performance differences among the approaches using the complete dataset from the three types of experiments.

3.3.1 Analysis of Variance

Before analyses, distribution normality tests were performed to validate the assumptions necessary for ANOVA. After removing outliers and rearranging the dataset for each variance analysis, the Shapiro–Wilk tests were performed, indicating that the data could be considered normally distributed for this analysis. Initially, a repeated measures ANOVA analysis was conducted to determine the influence of the interaction mode (factor) changes on the torque estimation accuracy of the three approaches. For this analysis, the dataset was filtered to include only those tests from Experiment 1 that featured a simple sine trajectory with the three operation modes, passive, resistive, and cooperative. The test was employed to define the null hypothesis, H0: There are no differences in the normalized root-mean-square error (NRMSE) across the operation modes for each approach, against the alternative hypothesis, H1: At least one operation mode significantly affects the NRMSE for at least one of the approaches. A significance level set at 0.05 was defined for the test.

The results from the repeated measures ANOVA showed that the main effect of operation mode on the NRMSE was statistically significant (F = 20.135, p-value < 0.0001), indicating that operation mode significantly affects the estimation accuracy. In contrast, the interaction effect between the estimation approaches and operation modes did not reach statistical significance (F = 2.3032, p-value 0.0815F), suggesting that the impact of operation mode is generally consistent across the different approaches. This implies that while operation mode itself has an impact on NRMSE, the type of estimation approach does not significantly alter this effect.

Following the repeated measures ANOVA evaluation, a broader analysis was conducted using the two-way ANOVA to explore the interaction effects between operation mode and trajectory type on the estimation error across different approaches in all experiments. To ensure data balance, analyses excluded the cooperative mode, resulting in two levels each for operation mode (passive and resistive) and trajectory (simple sine and gait). The treatment groups were thus defined: passive–sine, passive–gait, resistive–sine, and resistive–gait. The hypotheses posited were: Null Hypothesis H0: There is no interaction effect between operation mode and trajectory on the NRMSE for each estimation approach, and no main effects of either operation mode or trajectory alone; Alternative Hypothesis H0: There are potential interaction effects and/or main effects of operation mode, trajectory, or both on the NRMSE. The significance level was set at 0.05.

Table 3 presents the two-way ANOVA results. Similar to the one-way ANOVA, the analysis indicated significant effects of operation mode on all variables (p < 0.01), with notably strong influences observed for KF (F = 32.24, $p<$ 0.0001). The trajectory also significantly affected outcomes, particularly for KF (F = 26.25, p = 0.0001) and GMO (F = 11.96, p = 0.0025). The interaction between operation mode and trajectory was not significant for GMO and KF-M, suggesting consistent effects of operation mode across different trajectories.

Table 3 Two-way ANOVA results for KF, GMO, and KF-M

Although all three approaches (KF, GMO, and KF-M) yielded p-values above the conventional threshold of 0.05, the KF approach exhibited a notably lower p-value (0.0958), suggesting a dynamic influence between operation mode and trajectory changes. Figure 10 shows an interaction plot for the KF errors of the dataset. The figure evidences greater variability in errors under resistive conditions compared to passive, indicating a heightened sensitivity of KF to trajectory variations. Although the interaction effect was not statistically significant at the 0.05 level, this outcome suggests impactful performance differences for this approach.

Fig. 10

Interaction plot for KF: operation mode and trajectory factors

3.3.2 Statistical Comparison of Approaches

To determine the superiority of one approach over another, the Kruskal–Wallis test was implemented. This is a non-parametric method used here to assess if there are statistically significant differences between the measures of independent groups, in this case, the medians of KF, GMO, and KF-M approaches. The hypotheses were formulated as follows: H0: The median NRMSE for all approaches is equal. H1: At least one of the approaches has a median NRMSE that is different from the others. This test combines and sorts the data from all groups to assign ranks. The Chi-square statistic H, which measures the variance among the group ranks compared to the overall rank variance, is computed using the formula:

$$\begin{aligned} H = \left( \frac{12}{N(N+1)} \sum _{i=1}^{k} \frac{R_i^2}{n_i}\right) - 3(N+1) \end{aligned}$$

(17)

where $N = 90$ (the total number of observations from the three experiments), $k = 3$ (the number of groups), $R_i$ is the sum of ranks in the i-th group, and $n_i$ is the number of observations in the i-th group. The test revealed significant differences in the NRMSE distributions among the approaches, with a Chi-square statistic of 12.13 and a p-value of 0.0023, leading to the rejection of the null hypothesis. Given the significant results, a post hoc analysis was conducted using Dunn’s non-parametric multiple comparison test to further investigate the differences between pairs of approaches.

Table 4 Dunn’s test results for pairwise comparisons among approaches

The Dunn’s test made pairwise comparisons between the approaches, focusing on differences in median NRMSE. Table 4 presents both the sum and mean ranks of each group along with the outcomes of these comparisons. Significant differences were observed between KF-M and both KF and GMO, as indicated by the Q-values exceeding the critical values, leading to the rejection of the null hypothesis in these cases. Conversely, no significant difference was found between KF and GMO, suggesting similar performance levels.

4 Discussion and conclusions

In this paper, three approaches for ankle joint torque estimation based on the well-known disturbance observer technique were implemented on the Anklebot robot. They were the generalized momentum observer, a Kalman filter augmented with a sinusoidal disturbance model, and a Kalman filter based on the generalized momentum. The formulation of these approaches included identification in the frequency domain of inertial, damping, and stiffness parameters for all the voluntary users. Although the Anklebot is specified as a backdrivable robot, a frictional force was observed that opposes the movement of the linear actuators during its operation; thus, the dynamic model also included the identification of the robot friction torque. The torque due to gravitational effects was also considered in the model. Using a customized AFO allowed us to measure the ankle torque if considered a simple hinge joint and compare it with the estimation approaches. The choice to employ a customized ankle–foot orthosis (AFO) equipped with a load cell was intended to quantify rotational forces exerted by the ankle joint, conceptualized as a simple hinge joint.

This choice of the load cell over EMG measurement systems aligns with the emphasis of this research on dealing with torque rather than joint contact forces (JCF), as torque measurements provide a direct and objective assessment of the rotational exogenous dynamics viewed by the robotic device. Unlike EMG measurement systems which are used to compute the moments or torque based on muscle activation patterns, load cells offer a direct measure of the torque applied or resisted by the robotic joint.

This choice of the load cell over EMG measurement systems aligns with the emphasis of this research on dealing with torque rather than joint contact forces (JCF). As torque measurements provide a direct and objective assessment of the rotational exogenous dynamics viewed by the robotic device, they offer a reliable alternative to EMG systems, which compute torques based on muscle activation patterns and are influenced by a variety of physiological and methodological factors. Unlike EMG systems that can introduce complexities in calibration and signal interpretation, load cells provide a straightforward measure of the torque applied or resisted by the robotic joint, ensuring greater accuracy and reproducibility of results.

Given the distinct methodologies employed in torque estimation—from traditional EMG and inverse kinematics (IK) to our load cell-based approach—it becomes imperative to further explore how these methods compare under varying clinical and research settings. Future studies should, therefore, focus on conducting a comprehensive comparative analysis between these classical methods and our disturbance observer techniques. This would not only validate the strengths and limitations of each approach but also highlight potential synergies and improvements for robotic therapy applications.

In an ideal scenario, the robot and ankle torques would be the same if they were sharing the same movement; nevertheless, in practice, misalignment on the joints might prompt loss in the transmission of the assistive robot torques on the user’s joints and generate residual undesired torques. Therefore, using the AFO’s load cell turns out helpful in quantifying the real interaction occurring in experiments. Using sinusoidal desired trajectories and the above-mentioned dynamic behavior modes are supported by the knowledge of the different types of strategies applied for the robotic training in sitting position [60] and gait assistance [9, 61].

For overall experiments, the passive mode of KF, regardless of the type of trajectories, resulted in lower medians and tighter variability ranges. The KF showed the lowest median NRMSEs with values of 0.1792 N.m and 0.384 N.m for sine (Fig. 6a) and gait (Fig. 9a) trajectories, respectively, surpassing those achieved by GMO and KF-M. Regarding the tests performed with the configuration of the resistive mode, all the approaches degraded their performances, facing a mismatch problem concerning the disturbance estimation. The existence of non-modeled residual torques due to misalignment may affect either the load cell measurement or the robot torque. This directly influenced the estimations. Nevertheless, the GMO advantaged the other approaches in resistive mode regardless of type trajectory. In simple sine, its median was minimally lower than KF (Fig. 6b), and in gait, its median and variability were notably the lowest (Fig. 9b). The KF-M showed higher medians and greater variability across in almost all experiments when compared to KF and GMO.

For Experiment 1, simple sine experiments outperformed gait trajectory experiments for all approaches, with both KF and GMO producing comparable lower metrics. The results showed that the passive and cooperative modes performed lower error values than the resistive modes. The medians calculated using the cooperative mode were similar to those of the passive mode but with the benefit of showing less variability. This indicates more consistency in the estimates. However, the lack of cooperative mode testing for the gait trajectory makes it difficult to make a conclusive comparison with the other modes.

For Experiment 2, in the cases, where the gait trajectory was not perfectly tracked, the ankle torque could not match exactly this periodic signal. As a consequence, compared with the simple sine case, the approaches presented hither NRMSE values which can be interpreted as less effective torque estimation. Nevertheless, the GMO approach was lower than KF in the gait trajectory, especially in the resistive mode. One probable explanation could be that the GMO approach can perform better in more complex dynamics where physical collisions are involved without requiring a detailed mathematical model, as opposed to using a precise nominal disturbance model that, unless precisely modeled, may not accurately describe the torque, leading to less effective estimations in the gait experiments.

The time lag observed in almost all results of KF-M was much larger compared to the other approaches. Since RMSE is highly sensitive to both the magnitude and timing of the prediction errors, the performance metrics calculated for KF-M were more affected by this time lag. Through cross-correlation analysis between the KF-M’s estimated torque and the reference torque from the load cell, we identified a consistent time lag of nearly 1 s across most users in the pure sine trajectory tests. For instance, this can be graphically evidenced by looking at the KF-M estimated torque for Experiment 1 of user 1 as shown in Fig. 5. This delay, evident in the time response figures where the KF-M signal precedes the reference, corresponds to a 90-degree phase shift relative to the expected trajectory. Such a phase shift could imply that the angular velocity component within the generalized momentum formulation critically affects the estimated torque by this method. Implementing a time lag compensation technique could solve the gap in KF-M performance.

Regarding the statistical analysis, two distinct ANOVA analyses were employed to evaluate the effects of operation modes and trajectories on torque estimation accuracy. A repeated measures ANOVA was first applied specifically on data of Experiment 1, which used a simple sine trajectory, to isolate the effects of operation mode across the three approaches within a consistent experimental setup. This test focused on intra-subject variability. Subsequently, a two-way ANOVA expanded on this analysis by incorporating data from multiple experiments, focusing on interactive effects between operation modes and trajectory types. The two-way ANOVA test was implemented using a lumped dataset of Experiments 1, 2, and 3 to investigate the combined effects of changing both operation modes and the type of trajectory. Based on the two-way ANOVA, it can be said that these factors individually influence the NRMSE results. Particularly, the KF demonstrated more sensitivity to the combined interaction effects. However, the interaction between operation mode and trajectory did not significantly affect the performance of GMO and KF-M, suggesting that these models could perform consistently across varying scenarios without requiring specific adjustments. It is worth mentioning that the cooperative mode was excluded from the two-way ANOVA analysis due to its absence in Experiments 2 and 3, ensuring a balanced and consistent dataset between the factors analyzed. Hence, this limited the generalizability of the results to only non-cooperative operational settings. Future studies should consider including a comprehensive evaluation of all operational modes across experiments to broaden the applicability of the findings. The Kruskal–Wallis test further confirmed the significant differences in the median NRMSEs among the approaches, with post hoc Dunn’s test identifying KF-M as having higher error rates compared to KF and GMO. This suggests that while KF-M may not always offer the best reliability, KF and GMO could be preferred for their consistent performance.

While the disturbance observer techniques developed in this study effectively estimated ankle joint torques, they, like inverse kinematics (IK) and electromyography (EMG), rely on nominal parameters, including anthropometric data. This reliance introduces a degree of uncertainty in the modeling. Comparative analyses between these classical methods and our observer-based techniques could help to validate the effectiveness of our approaches across different settings. Such studies could also explore the potential for integrating DO techniques with classical methods to develop more robust and adaptable estimation systems.

Since the operation of the Anklebot was delimited for sitting position movements, the mechanical impedance parameters of the human ankle torque (inertia, damping, and stiffness) were assumed to be constant over time. If the experiments had been done on a treadmill, joint mechanical impedance modulation during the gait cycle must have been considered [50, 51]. The experiments on this work were carried out with voluntary healthy users, which allowed the implementation of the method found in [51] for ankle joint mechanical impedance identification literature [51]. With all this in mind, the results obtained here are yet to be considered a generalization of the human ankle torque estimation issue. This work continues the research developed in [54] in which the same approaches were implemented for a mock-up ankle device. We intend to extend the results obtained here to a broader control group as well as evaluation on a treadmill scenario where ground reaction torques and strong human–robot interaction forces are generated on the human and robot joints. Moreover, robust observers and robotic feedback control for compensation purposes will be studied for implementation.

Appendices

Appendix

Computation of the sinusoidal parameters

• State-space matrices for sinusoidal disturbance models

Equation 18 is used for the $n_\textrm{d}$ = 1 case, and Eq. 19 for the $n_\textrm{d}$ = 3 case.

$$\begin{aligned} \underbrace{\left[ \begin{array}{c} \ddot{\tau _\textrm{d}}\\ \dot{\tau _\textrm{d}} \end{array} \right] }_{{\dot{x}}_{d_{(2 n_\textrm{d} \times 1)}}} = \underbrace{\begin{bmatrix} 0 &{} -\omega ^2_1 \\ 1 &{} 0 \end{bmatrix} }_{A_{d_{(2 n_\textrm{d} \times 2 n_\textrm{d} )}}} \underbrace{\left[ \begin{array}{c} \dot{\tau _\textrm{d}} \\ \tau _\textrm{d} \end{array}\right] }_{x_{d_{(2 n_\textrm{d} \times 1)}}} \end{aligned}$$

(18)

$$\begin{aligned} \underbrace{ \left[ \begin{array}{c} {\mathop {\tau _\textrm{d}}\limits ^{{\varvec{\cdot }}~{\varvec{\cdot }}~{\varvec{\cdot }}~{\varvec{\cdot }}~{\varvec{\cdot }}~{\varvec{\cdot }}}} \\ {\mathop {\tau _\textrm{d}}\limits ^{{\varvec{\cdot }}~{\varvec{\cdot }}~{\varvec{\cdot }}~{\varvec{\cdot }}~{\varvec{\cdot }}}} \\ {\mathop {\tau _\textrm{d}}\limits ^{{\varvec{\cdot }}~{\varvec{\cdot }}~{\varvec{\cdot }}~{\varvec{\cdot }}}} \\ {\mathop {\tau _\textrm{d}}\limits ^{{\varvec{\cdot }}~{\varvec{\cdot }}~{\varvec{\cdot }}}} \\ \ddot{\tau _\textrm{d}} \\ \dot{\tau _\textrm{d}} \end{array} \right] }_{{\dot{x}}_{d_{(2 n_\textrm{d} \times 1)}}} = \underbrace{ \begin{bmatrix} 0 &{} -D_1 &{} 0 &{} -D_2 &{} 0 &{} -D_3 \\ 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \end{bmatrix} }_{A_{d_{(2 n_\textrm{d} \times 2 n_\textrm{d} )}}} \underbrace{ \left[ \begin{array}{c} {\mathop {\tau _\textrm{d}}\limits ^{{\varvec{\cdot }}~{\varvec{\cdot }}~{\varvec{\cdot }}~{\varvec{\cdot }}~{\varvec{\cdot }}}} \\ {\mathop {\tau _\textrm{d}}\limits ^{{\varvec{\cdot }}~{\varvec{\cdot }}~{\varvec{\cdot }}~{\varvec{\cdot }}}} \\ {\mathop {\tau _\textrm{d}}\limits ^{{\varvec{\cdot }}~{\varvec{\cdot }}~{\varvec{\cdot }}}} \\ \ddot{\tau _\textrm{d}} \\ \dot{\tau _\textrm{d}} \\ \tau _\textrm{d} \end{array}\right] }_{x_{d_{(2 n_\textrm{d} \times 1)}}} \end{aligned}$$

(19)

where the parameters $D_1$, $D_2$, and $D_3$ are computed as follows:

$$\begin{aligned} D_1 =&\hspace{0.1cm} (\omega _1^2 + \omega _2^2 + \omega _3^2) \nonumber \\ D_2 =&\hspace{0.1cm} (\omega _1^2\omega _2^2 + \omega _1^2\omega _3^2 + \omega _2^2\omega _3^2) \nonumber \\ D_3 =&\hspace{0.1cm} (\omega _1^2 \hspace{0.1cm} \omega _2^2 \hspace{0.1cm} \omega _3^2 ) \end{aligned}$$

(20)