Evaluation of numerical techniques for modeling flutter phenomenon into two geometries: the 1:4.9 rectangle and the Great Belt East Bridge in scale 1:7

Abstract

The flutter phenomenon must be carefully evaluated, as it can lead structures to collapse. This study presents a methodology based on computational fluid dynamics to obtain the flutter derivatives and the critical flutter velocity, through forced vibrations in bodies immersed in a fluid medium. Two approaches were analyzed. In the first (8COEF), torsion and flexural movements were imposed. In the second, simulations were carried out in torsion mode, and through linear equations (LE), the complete set of eight coefficients was obtained. While the first can be seen as the most robust, as all coefficients are obtained from computer simulations, the second is less computationally expensive. The study was applied to a 1:4.9 rectangle and to the cross-section of the Great Belt East Bridge (GBEB). The simulations were submitted to turbulent flow with Reynolds number equal to 10$^{5}$, using k–$\omega$ SST and k–$\omega$ SSTLM turbulence models. For the static case, simulations were performed to obtain the average values of the aerodynamic coefficients. OpenFOAM^® was used to solve the Navier–Stokes equations for an incompressible fluid. The critical flutter velocity for the GBEB was estimated using the 8COEF and the LE approaches. It was noticed that the results estimated with the LE were effective and with a good approximation with those of the 8COEF but at a lower computational cost. All results were validated with numerical and experimental studies available in the literature. Finally, this research stands out in presenting an assertive and pragmatic CFD methodology to obtain critical flutter velocity on structures.

1 Introduction

The mitigation of aeroelastic phenomena in structural engineering has been a subject of research in numerous works. Slender and flexible structures, such as large-span bridges, tend to be more sensitive to wind action, directly influencing the project from its conception.

Aerodynamic and aeroelastic analyses must be carefully performed. For this, there is computational fluid dynamics (CFD), constantly evolving and increasingly used by researchers to obtain reliable results via numerical methods.

In this context, this study’s main objective is to use CFD for the aerodynamic and aeroelastic study of two profiles of interest to structural engineering: a rectangle with an aspect ratio (width/height ratio) 1:4.9 and the Great Belt East Bridge (GBEB), the latter in 1:7 scale.

As specific objectives, there are, first, aerodynamic studies with structures at rest and Reynolds number ($R_{e}$) of $10^5$. k–$\omega$ SST turbulence models, proposed by Menter et al. [1], and k–$\omega$ SSTLM, proposed by Menter et al. [2], were employed. This study defines the simulations’ numerical parameters and evaluates the turbulence models’ performance.

Subsequently, the same geometries are evaluated under forced, torsional and vertical oscillation using the methodology proposed by Le Maître et al. [3] to obtain flutter coefficients or flutter derivatives. In the simulations, the k–$\omega$ SST and k–$\omega$ SSTLM turbulence models were also used since the structures were submitted to the same number value of $R_{e}$, that is 10$^{5}$.

Two approaches to obtaining the complete sets of flutter derivatives are proposed in the literature and employed in this research. The first follows the original proposal of Le Maître et al. [3], where forced vibrations are applied in bending and torsion modes. The flutter derivatives are then correlated with the harmonic components of the lift force and aerodynamic moment signals. This approach is called 8COEF, as eight aeroelastic coefficients are obtained from the CFD simulations for each study situation.

In the second approach, proposed by Matsumoto [4], simulations are performed in torsion mode only, and the coefficients related to the flexural modes are linear combinations of those obtained in the simulated mode (torsion). Matsumoto [4] assumes a linear relationship between pressure and angle of attack and does not consider the contribution of viscosity to aerodynamic forces. The validation of the dependency relationship between the coefficients is done through experiments on rectangular profiles. The results obtained for the second approach are called LE. The purpose of LE is to reduce the computational cost of simulations.

Using the results obtained by 8COEF and by LE, the critical flutter velocity for the GBEB was evaluated. Finally, the results obtained by validating them with the literature were compared. It was verified that the proposed methodologies offer consonant results with the experimental and numerical data reported in the literature.

Consequently, some of the contributions of this research are:

• The evaluation of the performance of the k–$\omega$ SST [1] and k–$\omega$ SSTLM [2] turbulence models for the case studies. These are models designed to monitor adverse pressure gradients in the boundary layer and the transition between laminar and turbulent regimes in this region. The evaluation of these models in the cases studied was not observed in the bibliographic review.

• When modeling flows using discrete techniques, special care must be taken regarding the treatment of the term associated with transport, which introduces nonlinearity in the solution schemes. This research presents an extensive study, yet not observed in the literature, on using CFD techniques to treat the convective term for the GBEB example. The performances of the upwind (first-order and bounded), quadratic upstream interpolation for convective kinematics—QUICK [5] (second-order, unbounded), linear upwind (second-order, unbounded), and limited linear [6] (first-/second-order, unbounded) techniques were investigated.

• The evaluation of two approaches, the 8COEF and the LE, to obtain the critical flutter velocity for the bridge profile is also a differential of this research. While the first can be seen as the most robust, all coefficients are obtained from computer simulations, the second is less computationally expensive. Many authors [4, 7] use the LE approach without, however, making a qualitative comparison with the complete 8COEF approach. In this research, a comparative analysis was performed between these methods, and it was observed that the LE approach, for the analyzed case of the GBEB, is assertive in obtaining the critical flutter velocity, at a lower computational cost.

• The proposed methodology is simple and feasible since a two-dimensional linear self-excited aeroelastic analysis is performed. Furthermore, it contributes to certifying that the approximation LE can be effective and is a fast assessment of bridge flutter performance by the imposition of forced vibrations in torsion mode.

• Regarding treating temporal signals of torsion and/or flexural flutter derivatives, a numerical routine was implemented by adjusting the dispersion of data from simulations via curve fitting by applying the least-square method (LSM). This avoids the use of decomposition of the signals at different frequencies and the Fourier transform, facilitating the interpretation of the obtained results.

This text is structured as follows: This section presents the relevance of the theme, the objectives, and the main contributions of this research. Afterward, Sect. 2 is dedicated to a bibliographical review of several studies available in the literature and how their work contributed to the topic in question. Section 3 discusses the theory of the fundamental basis of fluid dynamics and turbulence models. In Sect. 4, we consider aspects of the solution, modeling, and methodology of the approaches employed in the research. Section 5 deals with the characterization of the problem, the object of study, and the initial modeling conditions necessary for the simulations. Section 6 is dedicated to the research results and bringing a brief methodology about critical velocity. Finally, Sect. 7 highlights the conclusion and directions for future studies.

2 Literature review

In recent decades, researchers have been engaged in studying the aeroelastic phenomena resulting from the action of the wind on large structures through numerical and experimental methods, seeking to guarantee the stability of these structures and prevent eventual accidents.

The research by Scanlan and Tomko [8] sought to associate the vibration phenomena of the Tacoma Narrows Bridge with the behavior of the NACA 0012 airfoil and proposed an analytical method of free oscillation to measure the vibration coefficients of the bridge (flutter derivatives), similar to those of the airfoil. The airfoil results validated the experimental method, and the study ended up being extended to other bridge geometries, attesting to the effectiveness of the proposed methodology.

Larsen [9] presented wind tunnel test results for three models of the GBEB structure. He studied the structure in geometric scale 1:80 to establish flutter performance and obtain mean coefficients $C_{\text {d}}$, $C_{\text {l}}$, and $C_{\text {m}}$. In the 1:200 scale tests, the structure was tested under laminar and turbulent conditions and under winds deviating from the GBEB axis to analyze the structure’s behavior associated with the different wind directions. On a scale of 1:300, the experiment allowed a faithful simulation of the atmospheric boundary layer at the bridge construction site.

Matsumoto [4], in his experimental study, analyzed the aerodynamic damping in rectangular sections under a laminar flow regime, which still characterizes the aerodynamic instability of torsional flutter or coupled flutter. It also discussed the flutter derivatives obtained from the measurement of unstable pressure under forced oscillation. The contribution of his study was the proposal to estimate the flutter derivatives for bending through LE, one of the most favorable contributions in current numerical studies to minimize the computational cost.

Scanlan et al. [10] investigated the interrelations and the approximate equivalences (or dependencies) among the flutter derivatives of a low-velocity airfoil, which are analytically described. They obtained, experimentally, the flutter derivatives of three different bridge deck sections. The main finding of this research is that the approximate equivalences of flutter derivatives suggested by airfoil theory are seen to be contradicted mainly by experimental results, even in the case of a streamlined bridge deck such as Tsurumi.

The study by Larsen and Walther [11, 12] was based on the analysis of 2D incompressible viscous flows in five generic cross-sections of bridge decks, which were investigated using the meshless discrete vortex method and the code DVMFLOW^®. “The DVMFLOW^® code is a computational method designed to simulate two-dimensional, viscous flows that introduce the no-slip boundary condition to calculate surface vorticity, which, in turn, helps determine the strengths of vortexes introduced into the flow field. To handle viscous diffusion, the code utilizes a random-walk algorithm.” The analysis provided average values of the coefficients $C_{\text {d}}$, $C_{\text {l}}$ and $C_{\text {m}}$ and St for fixed sections and flutter derivatives for sections that were subjected to oscillatory crosswinds forced.

Le Maîte et al. [3] presented two methodologies, based on the resolution of the incompressible Navier–Stokes equations and a stream function-vorticity formulation, for calculating the aerodynamics coefficients associated with the motion-related force functions proposed by Scanlan and Tomko [8]. These are based on forced motion, employed in this research, and spring-mounted airfoil experiments.

Huang et al. [13] proposed a domain decomposition method, based on the FLUENT^® code and RNG k–$\varepsilon$ Reynolds-averaged Navier–Stokes (RANS) turbulence model, to obtain the GBEB flutter derivatives. They discretized the computational domain into rigid, dynamic, and static boundary layer mesh regions by controlling the height of mesh cells close to the object and employing the default wall function. The simulated results showed good agreement with the theoretical and experimental resolutions. This study proved the effectiveness of the computational method in obtaining the coefficients.

Bai et al. [14] solved the fluid–structure interaction (FSI) through a self-developed code, combined with CFX^® and proposed an improved CFD method, based on interactive block coupling, which can be easily used for modeling 2D and 3D. To obtain the flutter derivatives, they performed a 3D viscous incompressible turbulent flow simulation applied to the 3D analysis of the bridge deck, with a detached-eddy simulation (DES) turbulence model. DES is a transformation of a RANS model, in which the model switches into a large eddy simulation (LES) turbulence model in sharply refined regions. The flutter derivatives and the coefficients $C_{\text {d}}$, $C_{\text {l}}$ and $C_{\text {m}}$ obtained were then compared to the wind tunnel test results, demonstrating the prediction that the 3D simulations outperform the precision 2D simulations.

Jurado et al. [15] developed analytical aeroelasticity methods, which tried to solve deck movement equations, and involved classic aeroelasticity concepts that had already been applied to aeronautical engineering. Their main idea was a hybrid approach consisting of two phases: the first was to test a reduced deck section model in an aerodynamic wind tunnel, and the second was a computational stage to process the data obtained in the first phase, using the same linear approach from Le Maître et al. [3].

The research by authors Miranda et al. [16] numerically analyzed the capability of the k–$\omega$ and k–$\omega$ SST turbulence models. A RANS approach considering a 2D incompressible flow was considered to verify this approach’s accuracy and limits of applicability. Therefore, the convergence of the results of the simulations carried out through the FLUENT^® code, subjected to turbulent flow with $R_{e}$ 1.4 $\times$ 10$^{5}$ of the flutter derivatives in structures of elongated rectangular sections with different proportions, ranging from 1:5 to 1:20. The authors concluded that the k–$\omega$ SST formulation proved to be more accurate than the k–$\omega$. Furthermore, k–$\omega$ SST is more simplified configuration management due to its insensitivity to turbulence-related input parameters than k–$\omega$.

Farsani et al. [17] presented the development of index functions (IFs) for the 2D cross-section of the GBEB. They implemented two approaches: In the time domain, the IFs are determined by imposing a change of angle of attack. In the frequency domain, the IFs are the derivatives of the flutter derivatives. To determine the aerodynamic response of the GBEB due to a pitching change in the angle of attack and to calculate the flutter derivatives of sinusoidal oscillations, they used the code DVMFLOW^®. The authors concluded that the research proposal could be applied in developing reduced-order models (ROM) of aerodynamic loads suitable for investigating FSI.

Nieto et al. [7] addressed the numerical method with 2D URANS modeling, applying the k–$\omega$ SST turbulence model and the LE approximation, proposed by Matsumoto [4] and improved by Tubino [18]. The simulation of the static coefficients $C_{\text {d}}$, $C_{\text {l}}$ and $C_{\text {m}}$ and of flutter was carried out in OpenFOAM^®, in two geometries: the 1:4.9 rectangle and the GBEB cross-section. The analytical relation method was used to halve the number of simulations and thus reduce the computational cost for calculating the coefficients. The conclusion was that the methodology presented good results, with precision similar to those obtained by other authors.

Bakis et al. [19] addressed the issue of suppressing aeroelastic instabilities using trailing-edge and leading-edge controllable flaps. They combined a mathematical formulation for capturing the essential aeroelastic characteristics of suspension bridges, using a reduced-size structural model, with the classical results from potential flow theory and Theodorsen circulation function to input aerodynamic forces. Using feedback as well as a rational approximation of the circulatory term, they implemented the transformation of the wing-aileron-tab to the flap-deck-flap configuration.

The classic iterative process is based on a heuristic approach, including wind tunnel testing. The dependence of experimental aeroelastic studies on the cross-section of the bridge deck requires a high demand for resources. Therefore, to overcome this process, Cid Montoya et al. [20] proposed to apply a numerical strategy in the design of the GBEB deck: a surrogate model of the aerodynamic response of the deck and some changes from its original shape allowed through simulations in OpenFOAM^®. With this proposal, the flutter derivatives were approximated through an almost stationary formulation, allowing the calculation of the critical velocity. These combined structural and aeroelastic optimization approaches contributed to the knowledge of improving GBEB performance.

Zamiri and Sabbagh-Yazdi [21] proposed a 2D numerical methodology that admits the variable angle of attack of the wind in the FSI, associated with rotations of the fixed cross-section of the GBEB, in the computational domain. In contrast, the flow approach’s gradual slope and the attack angle are applied to the far-field boundaries of the initial mesh. The coefficients $C_{\text {d}}$, $C_{\text {l}}$, $C_{\text {m}}$ and flutter were obtained using the FLUENT^® code. The accuracy of the strategy in obtaining the coefficients was demonstrated by comparing the results with data from the literature.

Costa et al. [22] compared the k–$\varepsilon$ and k–$\omega$ SST, and LES Smagorinsky turbulence models applied in 2D numerical simulations with the CFX^® of the GBEB model. Coefficients $C_{\text {d}}$, $C_{\text {l}}$, $C_{\text {m}}$, and St were studied, in addition to the flutter derivatives, to estimate the critical velocity. Thus, the results with the k–$\omega$ SST were considered acceptable when compared with the literature. However, the numbers obtained through the flutter results with the LES were more accurate. The authors suggested that the rearrangement of the mesh after the oscillations of the board affects the simulation results. Therefore, it should be considered when selecting a turbulence model.

Since then, numerical approaches for analyzing large-span bridge structures, such as the one proposed here, can provide an efficient alternative to wind tunnel tests; in this way, aerodynamic analyses seek a better aeroelastic and structural performance that can be applied. Although numerical studies do not replace experimental ones, researchers have increasingly used this approach with the constant evolution of computational tools.

One of the numerous advantages of CFD is that it allows aerodynamic and mathematical parameters, among others, to be modeled and adjusted for subsequent test execution in different virtual scenarios, simulating real scenarios. Thus, with a set of results, it is possible to verify which presents low performance and find the ideal scenario more easily. From there, prototypes are built, only of the models that performed well in the CFD simulations, for tests in a wind tunnel, for example.

3 Theoretical basis

3.1 Governing equations of fluid dynamics

In this research, the incompressible, viscous and Newtonian flow was assumed. The equations that model it are represented by the Navier–Stokes equations that express a physical–mathematical model, based on the conservation of mass and momentum, expressed in the Eqs. 1 and 2, respectively:

$$\begin{aligned}{} & {} \nabla \vec {v}=0 \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \rho \frac{\partial \vec {v}}{\partial t}+\rho \nabla \vec {v}\vec {v}=-\nabla p+\nabla \bar{\bar{\tau }}+\rho \vec {g}+\vec {F} \end{aligned}$$

(2)

In Eqs. 1 and 2, $\rho$ is the density of the fluid; p is the pressure; $\vec {v}$ is the velocity field; $\bar{\bar{\tau }} = \mu \left[ \left( \nabla \vec {v}+\nabla \vec {v}^{T} \right) \right]$ is the stress tensor; $\mu$ is viscosity; $\rho \vec {g}$ and $\vec {F}$ are gravitational and external forces, respectively.

3.2 Turbulence models

This section briefly describes the k–$\omega$ SST two-equation model and the k–$\omega$ SSTLM four-equation model, which were adopted in this research.

3.2.1 k–$\omega$ SST

Menter [1] proposed this model based on the combination of the k–$\varepsilon$ and k–$\omega$ models for modeling turbulent flows, allowing the models to act at different points, but simultaneously, that is, in regions close to the wall use k–$\omega$ and regions far from the wall use k–$\varepsilon$. Therefore, it is possible to model turbulent regions with adverse pressure gradients, and in the vicinity of the boundary layer, [23, 24].

The k–$\omega$ SST is composed of the transport equations (k) of the turbulent kinetic energy and its dissipation rate ($\omega$), described in 3 and 4.

$$\begin{aligned}{} & {} \frac{\partial k}{\partial t}+U_{j}\frac{\partial k}{\partial x_{j}}=\widetilde{P}_{k}-\beta ^{*}k\omega +\frac{\partial }{\partial x_{j}}\left[ \left( \mu +\sigma _{k}\mu _{t} \right) \frac{\partial k}{\partial x_{j}} \right] \end{aligned}$$

(3)

$$\begin{aligned}{} & {} \frac{\partial \omega }{\partial t}+U_{j}\frac{\partial \omega }{\partial x_{j}}=\frac{\gamma }{\mu _{t}} \widetilde{P}_{k}-\beta \omega ^{2}+\frac{\partial }{\partial x_{j}}\left[ \left( \mu +\sigma _{\omega }\mu _{t} \right) \frac{\partial \omega }{\partial x_{j}}\right] +2\left( 1-F_{1} \right) \sigma _{\omega 2}\frac{1}{\omega }\frac{\partial k}{\partial x_{i}}\frac{\partial \omega }{\partial x_{i}} \end{aligned}$$

(4)

Thus,

$$\begin{aligned} P_{k}=\mu _{t}\frac{\partial U_{i}}{\partial x_{i}}\left( \frac{\partial U_{i}}{\partial x_{j}}+\frac{\partial U_{j}}{\partial x_{i}} \right) \rightarrow \widetilde{P}_{k}=\min \left( P_{k},10\cdot \beta ^{*}k \omega \right) \end{aligned}$$

(5)

In the equations above, $U_{j}$ represents velocity components, $\mu$ is the molecular dynamic viscosity, $P_{k}$ is a production term in Eq. 3, and $\beta$, $\beta ^{*}$, $\sigma _{k}$, and $\sigma _{\omega }$ are empirical constants of the turbulence models. The term $F_{1}$ is a blending function, defined as:

$$\begin{aligned} F_{1}=\tanh \left\{ \left\{ \min \left[ \max \left( \frac{\sqrt{k}}{\beta ^{*}\omega y},\frac{500\nu }{y^{2}\omega } \right) ,\frac{4\sigma _{\omega 2}k}{\text {CD}_{k\omega }y^{2}} \right] \right\} ^{4} \right\} \end{aligned}$$

(6)

where $F_{1}=0$ in the free flow region, the k–$\varepsilon$ model characteristics are used, whereas in the viscous sub-layer, with $F_{1}=1$, properties of the k–$\omega$ model are employed.

Also, y is the distance from the wall to the first mesh point, $\sigma _{\omega 2}$ is a constant, and $\text {CD}_{k\omega }$ is the cross-diffusion term, which is expressed as:

$$\begin{aligned} \text {CD}_{k\omega }=\max \left( 2\sigma _{\omega 2}\frac{1}{\omega }\frac{\partial k}{\partial x_{i}}\frac{\partial \omega }{\partial x_{i}}, 10^{-10}\right) \end{aligned}$$

(7)

The turbulent viscosity of vortexes is defined as:

$$\begin{aligned} \mu _{t}=\frac{a_{1}k}{\max (a_{1}\omega ,S F_{2})} \end{aligned}$$

(8)

with the mean rate of flow deformation,

$$\begin{aligned} S=\sqrt{2S_{ij}S_{ij}} \end{aligned}$$

(9)

, and it is given by:

$$\begin{aligned} k=\frac{3}{2}\left( I U_{\infty } \right) ^{2} \end{aligned}$$

(10)

where I is the turbulence intensity and $U_{\infty }$ is the reference velocity.

The specific turbulent dissipation rate is given by:

$$\begin{aligned} \omega =\frac{k^{0.5}}{C_{\mu }^{0.25}L} \end{aligned}$$

(11)

where $C_{\mu }$ is a constant with a value of 0.09, and L is a reference length scale.

The term $F_{2}$ is also a blending function for turbulent viscosity defined as:

$$\begin{aligned} F_{2}=\tanh \left[ \left[ \max \left( \frac{2\sqrt{k}}{\beta ^{*}\omega y},\frac{500\nu }{y^{2}\omega } \right) \right] ^{2} \right] \end{aligned}$$

(12)

The values of $\sigma _{k}$, $\sigma _{\omega }$, $\beta$, and $\gamma$ are combined using:

$$\begin{aligned} \phi =F_{1}\phi _{1}+\left( 1-F_{1} \right) \phi _{2} \end{aligned}$$

(13)

The model constants are described in Table 1. This model has some updates in its formulation that can be verified in the research by Menter et al. [25] with more details.

Table 1 Constants from the k–$\omega$ SST turbulence model

3.2.2 k–$\omega$ SSTLM

Menter et al. [2] proposed that the k–$\omega$ SSTLM model or $\gamma$-$R_{e \theta }$ , as it is also known, is a transition model based on correlations. The model makes use of the transport equations for the intermittency ($\gamma$) and moment-thickness transition of the Reynolds Number ($R_{e \theta }$), respectively, described in 14 and 15, in addition to Eqs. 3 and 4 that are presented in 3.2.1.

$$\begin{aligned}{} & {} \frac{\partial \gamma }{\partial t} +\frac{\partial U_{j}\gamma }{\partial x_{j}}=P_{\gamma }-E_{\gamma }+\frac{\partial }{\partial x_{j}}\left[ \left( \mu +\frac{\mu _{t}}{\sigma _{f}} \right) \frac{\partial \gamma }{\partial x_{j}}\right] \end{aligned}$$

(14)

$$\begin{aligned}{} & {} \frac{\partial \widetilde{R}_{e \theta t}}{\partial t}+\frac{\partial U_{j}\widetilde{R}_{e \theta t}}{\partial x_{j}}=P_{\theta t}+\frac{\partial }{\partial x_{j}}\left[ \sigma _{\theta t}\left( \mu +\mu _{t} \right) \frac{\partial \widetilde{R}_{e \theta t}}{\partial x_{j}} \right] \end{aligned}$$

(15)

The production term ($P_{\gamma }$) and the destruction term ($E_{\gamma }$), introduced by Langtry [26], are defined in Eqs. 16 and 17, respectively.

$$\begin{aligned}{} & {} P_{\gamma }=F_{\text {length}}c_{a1}S\left[ \gamma F_{\text {onset}} \right] ^{0.5}\left( 1-c_{e1}\gamma \right) \end{aligned}$$

(16)

$$\begin{aligned}{} & {} E_{\gamma }=c_{a2}\Omega \gamma F_{\text {turb}} \left( c_{e2}\gamma -1\right) \end{aligned}$$

(17)

In Eqs. 16 and 17, $F_{\text {onset}}$ and $F_{\text {turb}}$ are triggering functions that activate intermittency production and deactivate relaminarization, respectively. $c_{a1}$, $c_{a2}$, $c_{e1}$, and $c_{e2}$ are constants of the model. $\Omega$ represents the magnitude of vortexes. $F_{\text {length}}$ and $R_{e \theta c}$, the latter embedded in $F_{\text {onset}}$, are empirical correlations expressed as functions of $\widetilde{R}_{e \theta t}$.

The production term ($P_{\theta t}$) is designed to force the transported scalar $\widetilde{R}{e \theta t}$ to match the local value of $R{e \theta t}$ calculated from an off-wall correlation. It is defined in Eq. 18 as follows:

$$\begin{aligned}{} & {} P_{\theta t}=c_{\theta t}\frac{1}{\tau }\left( R_{e \theta t}-\widetilde{R}{e \theta t} \right) \left( 1-F{\theta t} \right) \end{aligned}$$

(18)

$$\begin{aligned}{} & {} \tau =\frac{500\mu }{U^{2}} \end{aligned}$$

(19)

where $c_{\theta t}$ is the model constant, $\tau$ is a time scale, and $F_{\theta t}$ is a blending function that ensures that within the boundary layer, the production term is turned off and that the transported scalar $R_{e \theta t}$ corresponds to the value of the correlation $R_{e \theta t}=f\left( \lambda _{\theta },T_{u} \right)$ in the free stream, defined in Eq. 20:

$$\begin{aligned} R_{e \theta t}=\left\{ \begin{array}{ll} \left( 1173-589.428T_{u}+\frac{0.2196}{T_{u^{2}}} \right) F\left( \lambda _{\theta } \right) , &{} \quad T_{u} \ge 1.3 \%; \\ 331.5\left( T_{u}-0.5658 \right) ^{-0.671}F\left( \lambda _{\theta } \right) , &{}\quad T_{u} > 1.3 \% \end{array} \right. \end{aligned}$$

(20)

with

$$\begin{aligned} T_{u}=100\frac{\sqrt{2/3 k}}{U_{\infty }} \end{aligned}$$

(21)

In Eq. 10, the value of k is described. The complete formulation can be verified in Menter et al. [2].

4 Solution methods for obtaining flutter derivatives

4.1 Numerical formulation

The static aerodynamic coefficients $C_{\text {d}}$, $C_{\text {l}}$ and $C_{\text {m}}$ depend on the geometric characteristics of the structure, the angle of attack of the wind, and also on the $R_{e}$ that expresses the relation between the inertial forces and the viscous forces of the flow described in Eq. 22.

$$\begin{aligned} R_{e}=\frac{DU}{\nu }=\frac{\rho DU}{\mu } \end{aligned}$$

(22)

where D is the characteristic dimension of the structure, U is the average velocity, $\nu$ is the kinematic viscosity, $\rho$ is the fluid density and $\mu$ is the dynamic viscosity.

When a fluid flows over a structure, a resultant force and a moment arise about a given axis. These results, when decomposed in the wind direction and perpendicular to the wind, and in their dimensionless form, correspond to the coefficients of drag force $C_{\text {d}}$, lift $C_{\text {l}}$ and moment $C_{\text {m}}$.

Figure 1 illustrates the force components resulting from the fluid–structure interaction, treated in 2D, and decomposed in the same direction as the fluid.

Fig. 1

Aerodynamic forces on the cross-section of the GBEB deck

In Eqs. 23, the aerodynamic coefficients are defined.

$$\begin{aligned} C_{\text {d}}=\frac{F_{\text {d}}}{\frac{1}{2}\rho U^{2}B};{} & {} C_{\text {l}}=\frac{F_{\text {l}}}{\frac{1}{2}\rho U^{2}B};{} & {} C_{\text {m}}=\frac{M}{\frac{1}{2}\rho U^{2} B^{2}} \end{aligned}$$

(23)

where $F_{\text {d}}$ and $F_{\text {l}}$ are the drag and lift forces, M is the average moment, $\rho$ is the fluid density, and B is the characteristic width of the structure.

The relationship between the vortex shedding frequency $f_{v}$, the flow velocity U, and the characteristic height of the structure H defines the Strouhal number, St, expressed by Eq. 24.

$$\begin{aligned} \text {St}=\frac{f_{v}H}{U} \end{aligned}$$

(24)

The flutter aeroelastic phenomenon is characterized by an unstable oscillation guided by the flow and comprised of two degrees of freedom, rotation, and vertical translation [27]. The structure’s equation of motion can be seen in 25 and 26.

$$\begin{aligned}{} & {} m\ddot{h}+S_\alpha \ddot{\alpha }+c_h\dot{h}+k_hh=L \end{aligned}$$

(25)

$$\begin{aligned}{} & {} S_\alpha \ddot{h}+I_\alpha \ddot{\alpha }+c_\alpha \dot{\alpha }+k_\alpha \alpha =M \end{aligned}$$

(26)

where m is the mass per unit length, $S_\alpha = ma$ is the inertial coupling between twisting motions and vertical displacement, and $\alpha$ the distance between the elastic center of torsion and the center of mass, $I_\alpha$ is the mass moment of inertia, $k_h$, $k_\alpha$ are the stiffnesses, the mechanical damping coefficients are $c_h$ and $c_\alpha$. L and M are the aeroelastic forces. In the case of symmetrical profiles, the center of mass lies in the vertical plane of the centerline, and in this case, $\alpha =0$ [27].

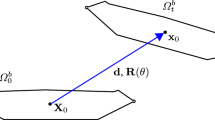
In Fig. 2, the modeling of the problem can be verified.

Fig. 2

Modeling problem on the cross-section of the GBEB deck

Various forms for the linear expression for L and M have been employed [27]. This research employs the analytical formulation proposed by Scalan and Tomko [8] and Le Maître [3], in which L and M are expressed in terms of the flutter derivatives $H_{i}^{*}$ and $A_{i}^{*}$ ($i=1,..,4$).

$$\begin{aligned}{} & {} L=\frac{1}{2}{\rho U^{2}B}\left[ K H_{1}^{*}\frac{\dot{h}}{U}+KH_{2}^{*}\frac{B\dot{\alpha }}{U} +K^2H_{3}^{*}\alpha +K^2H_{4}^{*}\frac{h}{B}\right] \end{aligned}$$

(27)

$$\begin{aligned}{} & {} M=\frac{1}{2}{\rho U^{2}B^2}\left[ K A_{1}^{*}\frac{\dot{h}}{U} + K A_{2}^{*}\frac{B\dot{\alpha }}{U}+ K^2A_{3}^{*}\alpha +K^2 A_{4}^{*}\frac{h}{B}\right] \end{aligned}$$

(28)

so K is the reduced frequency defined as:

$$\begin{aligned} K = \frac{B\omega }{U} \end{aligned}$$

(29)

B is the deck width, $\omega$ the circular frequency of oscillation, h is the heave displacement, $\alpha$ is the torsional rotation $\dot{h}$ and $\dot{\alpha }$ are the time derivatives.

The Strouhal number (St) in Eq. 24 is a dimensionless parameter that relates the frequency of vortex shedding or unsteady flow phenomena to the flow velocity and a characteristic length scale. The reduced frequency K in equation 29 helps determine the level of aeroelastic coupling between the aerodynamic loads and structural response.

Another significant parameter is the reduced velocity ($U_{r}$), as the flutter derivatives are often expressed as a function of this velocity, defined in Eq. 30.

$$\begin{aligned} U_{r}=\frac{U}{f B} \end{aligned}$$

(30)

where f is the frequency (in Hz) imposed on the structure.

In this research, the flutter derivatives are obtained through the methodology proposed by Le Maître et al. [3]. For different values of K, forced sinusoidal vibrations in h or alpha are imposed on the structure. The lift force (L) and moment (M) responses are decomposed, and the sinusoidal and cosine contributions are associated with the respective parcels in 27 and 28. Note that the coefficients $H_{1}^{*}$, $H_{4}^{*}$, $A_{1}^{*}$ and $A_{4}^{*}$ have relationship with the vertical movement h, while the others compose the torsional vibration $\alpha$.

In the solution of Eqs. 27 and 28, Eqs. 31 and 32, which are sinusoidal functions, are used to analyze displacements of flexural and torsion movements.

$$\begin{aligned}{} & {} h(t)=h_{0}\sin (\omega t) \rightarrow \dot{h}(t)= h_{0} \omega \cos (\omega t) \end{aligned}$$

(31)

$$\begin{aligned}{} & {} \alpha (t)=\alpha _{0}\sin (\omega t) \rightarrow \dot{\alpha }(t)= \alpha _{0} \omega \cos (\omega t) \end{aligned}$$

(32)

where $h_{0}$ and $\alpha _{0}$ are the amplitudes of the oscillations.

4.2 L and M signal processing: least-square method (LSM)

We obtain the flutter derivatives by extracting the scattered points in the time domain $C_\text {l}$ and $C_\text {m}$ and adjusting them by the least-square method (LSM). Equation 33 represents any harmonic signal x(t), with its amplitude $\rho _{\text {amp}}$ (see Eq. 34), its oscillation frequency $\bar{\omega }$, and its phase angle $\theta$ (see Eq. 35).

$$\begin{aligned} x(t)=\rho _{\text {amp}}\cos (\bar{\omega } t + \theta ) \end{aligned}$$

(33)

The amplitude $\rho _{\text {amp}}$ and the phase angle $\theta$ are given by:

$$\begin{aligned}{} & {} \rho _{\text {amp}}= \sqrt{A^2 + B^2} \end{aligned}$$

(34)

$$\begin{aligned} \theta = \tan ^{-1}\left( \frac{-B}{A} \right) \end{aligned}$$

(35)

Analogously, the variable dependent on the response of the coefficients as a function of time is represented by x(t); the frequency of movement associated with each reduced velocity, per $\bar{\omega }$, and A and B are numerical constants. The following form (see Eq. 36) represents the curve fitting made from the coefficients responses, approximating the solution of Eq. 33.

$$\begin{aligned} \sum _{k=0}^{m}a_m g_m (t) \end{aligned}$$

(36)

where the term that minimizes the sum of squares of the residuals is $a_m$; the function to be adjusted is $g_m(t)$, and the constants A and B of terms $\rho _{\text {amp}}$ and $\theta$ of Eq. 33 are $a_o$ and $a_1$, respectively.

4.3 Dimensionless coefficients of flutter (8COEF) and linear equations (LE)

After some manipulations, the expressions 37–40 for the torsion movement and 41–44 for the bending movement are obtained for the identification of the dimensionless flutter derivatives.

$$\begin{aligned} H_{2}^{*}= & {} \frac{a(C_{\text {l}})}{2K B^{2} \alpha _{0} \omega } \end{aligned}$$

(37)

$$\begin{aligned} H_{3}^{*}= & {} \frac{b(C_{\text {l}})}{2B K^{2} \alpha _{0}} \end{aligned}$$

(38)

$$\begin{aligned} A_{2}^{*}= & {} \frac{a(C_{\text {m}})}{2K B^{3} \alpha _{0} \omega } \end{aligned}$$

(39)

$$\begin{aligned} A_{3}^{*}= & {} \frac{b(C_{\text {m}})}{2K^{2} B^{2} \alpha _{0}} \end{aligned}$$

(40)

$$\begin{aligned} H_{1}^{*}= & {} \frac{a(C_{\text {l}})}{2K B h_{0} \omega } \end{aligned}$$

(41)

$$\begin{aligned} H_{4}^{*}= & {} \frac{b(C_{\text {l}})}{2K^{2} h_{0}} \end{aligned}$$

(42)

$$\begin{aligned} A_{1}^{*}= & {} \frac{a(C_{\text {m}})}{2K B^{2} h_{0} \omega } \end{aligned}$$

(43)

$$\begin{aligned} A_{4}^{*}= & {} \frac{b(C_{\text {m}})}{2K^{2} B h_{0}} \end{aligned}$$

(44)

where $a(C_\text {l} \text { or } C_\text {m})$ are the cosine amplitude, and $b(C_\text {l} \text { or } C_\text {m})$ are the sine amplitude.

A second approach, proposed by Matsumoto [4], proposes to calculate the flexural coefficients $H_{1}^{*}$, $H_{4}^{*}$, $A_{1}^{*}$ and $A_{4}^{*}$, from the torsion coefficients $H_{2}^{*}$, $H_{3}^{*}$, $A_{2}^{*}$ and $A_{3}^{*}$. The hypothesis adopted by the referred author relies on the assumption that unsteady pressure is proportional to the magnitude of the relative angle of attack. Matsumoto [4] validates this hypothesis through experiments on rectangular sections. These relationships are presented in Eqs. 45–48.

$$\begin{aligned} H_{1}^{*}= & {} K H_{3}^{*} \end{aligned}$$

(45)

$$\begin{aligned} H_{4}^{*}= & {} -K H_{2}^{*} \end{aligned}$$

(46)

$$\begin{aligned} A_{1}^{*}= & {} K A_{3}^{*} \end{aligned}$$

(47)

$$\begin{aligned} A_{4}^{*}= & {} -K A_{2}^{*} \end{aligned}$$

(48)

4.4 Methodology

The methodology consists of three steps: pre-processing, processing, and post-processing.

In the pre-processing step, the geometry, the object of study, is initially chosen. Next, the choice of the mesh generator program is made (Gmsh^® was chosen). Then, the computational domain and mesh type are defined. Here, triangular elements discretized in finite volume method (FVM) were chosen.

Next, boundary conditions (Sect. 5) and the characteristics of the fluid to be simulated are defined (in this case, incompressible, Newtonian, and viscous fluid). These characteristics are governed by the Navier–Stokes equations (Sect. 3.1), which will be solved during the simulation. For this purpose, a solver is used. In this case, PIMPLE is employed. Finally, the turbulence models to be used are chosen.

In the processing step, the simulation of the static case is performed using a simulator (OpenFOAM^® was chosen), with the chosen turbulence models. Then, the numerical schemes to be used in the simulation are selected to obtain the static coefficients $C_{\text {d}}$, $C_{\text {l}}$, and $C_{\text {m}}$, as well as $S_{t}$ (Sect. 4.1). If the results are accurate, the simulation proceeds to the flutter analysis; otherwise, the process returns to the pre-processing step, reviewing each step.

In the processing step, for the flutter simulation, certain characteristics are imposed, such as forced vibration for bending and torsion motions (Sect. 4.1), the type of mesh movement (ALE was chosen), and the use of the two turbulence models employed in the static case.

In the post-processing step, numerical treatment using the least-squares method (Sect. 4.2) is performed, yielding two results: $a(C_\text {l} \text { or } C_\text {m})$, which represent the cosine amplitude, and $b(C_\text {l} \text { or } C_\text {m})$, which represent the sine amplitude. These results are then used in the flutter equations (Sect. 4.1) to obtain the 8 flutter derivatives for bending and torsion motions through the 8COEF method (Sect. 4.3) and the LE method (Sect. 4.3). If convergence is achieved, the critical velocity ($U_{c}$) is calculated (Sect. 6.4). Otherwise, the numerical treatment via the least-square method is repeated.

The methodology adopted in this research is schematically presented in Fig. 3.

Fig. 3

CFD numerical process description

5 Geometries and computational modeling

This research considered two different geometries as case studies: rectangle ($B = 4.9$ and $H = 1$) and GBEB ($B = 7$ and $H = 1$).

For simulations, under a turbulent regime with $R_{e}$ 10$^{5}$, 2D RANS was used applying the turbulence models k–$\omega$ SST and k–$\omega$ SSTLM with turbulence intensity I = 1%. The boundary conditions of the turbulence modeling were estimated with Eqs. 49 [2, 28], considering $C_{\mu }$ = 0.09 and L = 1. The angle of attack of the wind was $\alpha$ = 0$^\circ$. These parameters are the same as adopted in the literature [7, 11, 13, 14, 16, 17, 20], which allows the comparison and validation of the methodology.

$$\begin{aligned} k = \frac{3}{2}(UI)^2 \quad \omega =\frac{k^{0.5}}{C_{\mu }^{0.25}L} \quad Re_{\theta }=\frac{331.5}{(I-0.5658)^{0.671}} \end{aligned}$$

(49)

5.1 Rectangle

The 2D computational domain and the boundary conditions used for this problem are illustrated in Fig. 4, with the following definitions:

• inlet: is the flow inlet boundary, with:

  • $u = U$ is the velocity component of $\vec {v}$ in the horizontal direction;

  • $v=0$ is the velocity component $\vec {v}$ in the vertical direction;

  • $\frac{\partial p}{\partial n}=0$ is a Neumann boundary condition, which means that the gradient of the respective quantity (p) is zero in the direction perpendicular to the boundary.

  • $d=0$ is a variable of the mesh movement, which assumes a null value in this boundary.

• top and bottom: are the upper and lower borders, where:

  • $u = U$ is the velocity component of $\vec {v}$ in the horizontal direction;

  • $v=0$ is the velocity component of $\vec {v}$ in the vertical direction;

  • $d=0$ is the mesh displacement, which assumes a null value in this boundary.

• outlet: is the outflow, where

  • $\frac{\partial \vec {v}}{\partial n}=0$ is a Neumann boundary condition, which means that the gradient of the respective quantity ($\vec {u}$) is zero in the direction perpendicular to the boundary.

  • $p=0$ and $d=0$ are the pressure and mesh displacement values in this border.

• the rectangle represents the geometry of the profile, with:

  • $u=v=0$ are the velocity components of $\vec {v}$ in the horizontal and vertical direction, respectively (this boundary condition is also known as no-slip boundary condition).

  • $d=d_0 \sin (\omega t)$: is the imposed vertical or torsional movements.

Fig. 4

Computational domain for the 1:4.9 rectangle

The numerical schemes adopted in the simulations reported here are: the discretization made in the finite volume method (FVM), where the values of the cell centers to the centers of the faces were made using a linear scheme, pressure–velocity coupling by the PIMPLE scheme, a combination of the SIMPLE (Semi-implicit Method for Pressure Linked Equation) [29], and PISO (Pressure Implicit with Splitting of Operators) [30] schemes. For the gradient and divergent terms, the Gauss linear and linear upwind [6] schemes were used, respectively.

5.2 GBEB

The analyzed model is the GBEB cross-section, whose cross-sectional model is represented in the proportion 1:7. Although a reduced-scale model was used, Fig. 5 shows some actual geometric characteristics of the structure.

Fig. 5

Project drawings—adaptation [31]

Therefore, the 2D computational domain modeling and the boundary conditions used for this problem are illustrated in Fig. 6. The same definitions of the nomenclature and the boundary conditions presented in Sect. 5.1 remain applicable for this obstacle.

Fig. 6

Computational domain for the GBEB

The discretization was also done in FVM. The gradient terms were discretized using the linear Gauss scheme. For the divergence terms, the Gauss scheme was also selected, adopting four schemes: upwind [32], QUICK (Quadratic Upstream Interpolation for Convective Kinematics) [5], limited linear [33] and linear upwind [6].

6 Results and discussion

6.1 Mesh convergence test for the static case

6.1.1 Rectangle

Five unstructured meshes named M1 40566/40046; M2 57372/56734; M3 71412/70696; M4 125418/123834; and M5 173006/171346 with different node/element characteristics were proposed. The simulations were performed with the k–$\omega$ SST turbulence model, and, in addition, a comparison with the k–$\omega$ SSTLM is shown.

Figure 7 shows the evolution of the average values of $C_{\text {d}}$, RMS $C_{\text {l}}'$, and St for the meshes analyzed together with the validation of the research by Nieto et al. [7]. These authors use CFD with k–$\omega$ SST turbulence model, in block-structured meshes with approximately 150000 cells, and a Gauss scheme with a linear upwind and limited linear interpolation scheme for the divergence terms.

Fig. 7

$C_{\text {d}}$ $\blacklozenge$; RMS $C_{\text {l}}'$ $\star$; St $\bullet$; $C_{\text {d}}$ $\square$ CFD Nieto et al. [7]; $C_{\text {l}}$ $\triangle$ CFD Nieto et al. [7]; St $\vartriangleleft$ CFD Nieto et al. [7]

The simulations performed with the turbulence models generally had a good agreement. Note that the results of St were very close to that of Nieto et al. [7]. Finally, the results were corroborated by the validation, which attested to the effectiveness of the simulations with the turbulence models.

The choice of the mesh in the flutter study was established through the analysis of the static case, investigating the convergence of the aerodynamic coefficients and the Strouhal number. In this way, the M2 mesh was chosen to follow in the flutter simulations, as it is more agile than the others. In Fig. 8, the mesh M2 is illustrated.

Fig. 8

Representation of the M2 mesh

6.1.2 GBEB

Four unstructured meshes were proposed: M1 88798/259134; M2 100100/287512; M3 118756/342212; and M4 130404/376406 with different node/element characteristics. The meshes are in increasing order of refinement, with M1 being the least refined and M4 being the most refined.

The development of simulations aims at determining the average values of $C_{\text {d}}$, $C_{\text {l}}$, $C_{\text {m}}$, in addition to St together with divergent schemes of a turbulent flow, in fixed section, to establish a comparison between the schemes as well as defining the appropriate mesh parameters for subsequent simulations.

The simulations were carried out with the k–$\omega$ SST and k–$\omega$ SSTLM turbulence model with the numerical schemes: Gauss upwind, QUICK, linear upwind, and limited linear, in which an analysis of the schemes was performed. The complete analysis of the results referring to the k–$\omega$ SST can be verified in Araújo et al. [34]. In addition, Figs. 9, 10, 11 and 12 show the evolutions of $C_{\text {d}}$, $C_{\text {l}}$, $C_{\text {m}}$, in addition to $S_ {t}$ for the different schemes and the comparison of the two turbulence models.

The results were validated with CFD studies by Nieto et al. [7], Larsen and Walther [11], Farsani et al. [17], and Cid Montoya et al. [20]. The studies from Larsen and Walther [11] and Farsani et al. [17] were based on the meshless discrete vortex method implemented in the DVMFLOW code [11, 12]. The CFD k–$\omega$ SST turbulence model from Nieto et al. [7] and Cid Montoya et al. [20] employs 2D block-structured meshes with approximately 260000 cells and a Gauss scheme with a linear upwind and limited linear interpolation scheme for the divergence terms.

It can be seen in the graphs in Fig. 9 that the results obtained for the upwind scheme were satisfactory. Some agreed well with the validation, even with reasonable proximity to the literature, emphasizing the meshes M1 and M2.

Fig. 9

Upwind scheme—a $C_{\text {d}}$ $\blacksquare$; $C_{\text {l}}$ $\blacktriangle$; $C_{\text {m}}$ $\blacklozenge$; $C_{\text {d}}$ $\square$ CFD Nieto et al. [7]; $C_{\text {l}}$ $\triangle$ CFD Nieto et al. [7]; $C_{\text {m}}$ $\Diamond$ CFD Nieto et al. [7]—b St $\blacktriangle$; St $\square$ CFD Nieto et al. [7]; St $\Diamond$ CFD Farsani et al. [17]; St $\vartriangleleft$ CFD Larsen e Walther [11]

Figure 10 shows the results obtained from QUICK scheme. A better performance is observed than the previous one, emphasizing the meshes M1, M2, and M4 that had results very close to those of the literature, corroborating the effectiveness of the adopted scheme with the reference results.

Fig. 10

QUICK scheme—a $C_{\text {d}}$ $\blacksquare$; $C_{\text {l}}$ $\blacktriangle$; $C_{\text {m}}$ $\blacklozenge$; $C_{\text {d}}$ $\square$ CFD Nieto et al. [7]; $C_{\text {l}}$ $\triangle$ CFD Nieto et al. [7]; $C_{\text {m}}$ $\Diamond$ CFD Nieto et al. [7]—b St $\blacktriangle$; St $\square$ CFD Nieto et al. [7]; St $\Diamond$ CFD Farsani et al. [17]; St $\vartriangleleft$ CFD Larsen e Walther [11]

Figures 11 and 12 present the results obtained with linear upwind and limited linear schemes, respectively. Although some similarities with the upwind scheme results, these schemes performed better since they are a higher order with flow limiter and were also adopted by the references [7, 20]. Another point to be observed is the results from meshes M1 and M2, which reached a good approximation with the results of the references.

Fig. 11

Linear upwind scheme—a $C_{\text {d}}$ $\blacksquare$; $C_{\text {l}}$ $\blacktriangle$; $C_{\text {m}}$ $\blacklozenge$; $C_{\text {d}}$ $\square$ CFD Cid Montoya et al. [20]; $C_{\text {l}}$ $\triangle$ CFD Cid Montoya et al. [20]; $C_{\text {m}}$ $\Diamond$ CFD Nieto et al. [7]—b St $\blacktriangle$; St $\triangledown$ CFD Cid Montoya et al. [20]; St $\Diamond$ CFD Farsani et al. [17]; St $\vartriangleleft$ CFD Larsen e Walther [11]

Fig. 12

Limited linear scheme—a $C_{\text {d}}$ $\blacksquare$; $C_{\text {l}}$ $\blacktriangle$; $C_{\text {m}}$ $\blacklozenge$; $C_{\text {d}}$ $\square$ CFD Nieto et al. [7]; $C_{\text {l}}$ $\triangle$ CFD Nieto et al. [7]; $C_{\text {m}}$ $\Diamond$ CFD Nieto et al. [7]—b St $\blacktriangle$; St $\square$ CFD Nieto et al. [7]; St $\Diamond$ CFD Farsani et al. [17]; St $\vartriangleleft$ CFD Larsen e Walther [11]

Simulations with k–$\omega$ SST, in general, and in comparison with k–$\omega$ SSTLM, showed better agreement, although some results with k–$\omega$ SSTLM showed promising results and some even close to those of the references. Based on the analysis of the results, the M1 mesh was chosen to continue in the flutter simulations, as it is more agile than the others and presents results that agree well with the references, especially with the QUICK scheme. The choice of the QUICK scheme is justified by the fact that it is a second-order accurate scheme and is designed to improve accuracy, especially in regions of steep gradients [5, 35]. In Fig. 13, mesh M1 is illustrated.

Fig. 13

Representation of the M1 mesh

6.2 Flutter derivatives for the rectangle

The flutter derivatives for the torsional movement were obtained numerically via 8COEF. Forced oscillation simulations considering an initial amplitude $\alpha _{0}$ = 0.0125 rad, the reduced velocities $U_{r}$ = 2, 4, 6, 8, 10, 12, 15, 20, 22 and 25 using the model of turbulence k–$\omega$ SST. Results were validated with CFD searches by Nieto et al. [7] and Miranda et al. [16], in addition to Matsumoto’s experimental studies (EXP) [4].

6.2.1 Torsion coefficients

The values for the coefficients found in Fig. 14, for $H^{*}_{2}$ , showed some divergences when compared to the reference values of Nieto et al. [7], despite the setting’s similarity and Matsumoto [4], mainly from high reduced velocities $U_{r}$ = 20, 22 and 25. On the other hand, the results were close to those of Miranda et al. [16]. This last reference also addressed a numerical method with a k–$\omega$ SST but with a second-order upwind scheme. This fact can, probably, justify the best correspondence with the presented results.

Despite the discrepancies observed for high values of reduced velocities, the results presented for now certify the methodology used in this research. In real cases of flexible structures, characterized by natural frequencies lower than 1 Hz, these high values of $U_r$ correspond to extremely high velocities that may not be compatible with the real scenario of the structure.

It is noteworthy that in Matsumoto [4] research, the rectangle was excited in an amplitude $\alpha _{0}$ = 0.0349 rad, while in Miranda et al. [16] $\alpha _{0}$ = 0.0523 rad was used.

Still, in this analysis of Fig. 14, in the results of $A^{*}_{2}$, one can notice an excellent agreement between the results when compared with the references.

Fig. 14

8COEF k–$\omega$ SST $\bullet$; $\Diamond$ CFD Nieto et al. [7]; $\triangle$ CFD Miranda et al. [16]; $\square$ EXP Matsumoto [4]

In Fig. 15, the results of $H^{*}_{3}$ and $A^{*}_{3}$ are presented. Note that the results of the two coefficients are close to the references.

Fig. 15

8COEF k–$\omega$ SST $\bullet$; $\Diamond$ CFD Nieto et al. [7]; $\triangle$ CFD Miranda et al. [16]; $\square$ EXP Matsumoto [4]

It is important to emphasize that for the highest velocities, the results had a slight divergence in all cases compared to the experimental values. In practice, this does not affect the quality of the results, which the baseline results corroborated to attest to the effectiveness of the 8COEF approach.

6.2.2 Flexural coefficients

To identify the flutter derivatives via 8COEF and LE of Matsumoto [4], forced oscillation simulations were carried out at reduced velocities $U_{r}$ = 4, 8, and 10 with a k–$\omega$ SST turbulence model.

Initially, the results were obtained, via 8COEF, proposing an initial amplitude $h_{0}/H$ = 0.0125, the same proposed by Le Maître et al. [3] in the NACA 0012 airfoil simulation. Then, these results were compared with those obtained via LE. The comparison between the two methods was validated with research by Nieto et al. [7], Matsumoto [4], who used the LE approach, and the research by Miranda et al. [16], which simulates the eight flutter derivatives. The results are shown in Figs. 16 and 17.

Fig. 16

8COEF k–$\omega$ SST $\bullet$; LE k–$\omega$ SST $\blacksquare$; $\Diamond$ LE Nieto et al. [7]; $\triangle$ LE Matsumoto [4]; $\vartriangleleft$ CFD Miranda et al. [16]

Fig. 17

8COEF k–$\omega$ SST $\bullet$; LE k–$\omega$ SST $\blacksquare$; $\Diamond$ LE Nieto et al. [7]; $\triangle$ LE Matsumoto [4]; $\vartriangleleft$ CFD Miranda et al. [16]

The results are consistent with those in the literature and close to the respective schemes in the literature.

The percentage differences between the 8COEF and LE results, taking the 8COEF results as a reference and representative values of the responses for the two turbulence models, are presented in Table 2.

Table 2 Comparative between flutter derivatives for rectangle

In the results of Table 2, it appears that the comparison of the percentage difference between the 8COEF and LE approaches decreased as $U_{r}$ increased, and this proves that the LE approach is effective in the estimation of the flutter derivatives for the case of the rectangular profile. The greatest difference found for $U_{r}$ = 4 can be explained by the values of $A_{4}^{*}$ closer to 0. The use of LE allows obtaining coefficients dependent on vertical vibration since the magnitude value of the offset $h_{0}$ is not required. Its effectiveness was proven in this research compared with the results obtained by 8COEF.

6.3 Flutter derivatives for the GBEB

To identify the flutter derivatives, simulations of forced oscillation were carried out, proposing an initial amplitude $\alpha _{0}$ = 0.0175 rad, being the same proposed by Nieto et al. [7] in the GBEB simulation, at reduced velocities $U_{r}$ = 2, 4, 6, 8, 10 and 12, as in Larsen and Walther [11].

6.3.1 Torsion coefficients

The results of $H^{*}_{2}$, $A^{*}_{2}$, $H^{*}_{3}$ and $A^{*}_{3}$ for the k–$\omega$ SST and k–$\omega$ SSTLM models are compared with studies that applied the CFD methodology of the 2D k–$\omega$ SST from Nieto et al. [7], DVMFLOW from Larsen and Walther [11] and 3D CFD DES (detached-eddy simulation) from Bai et al. [14].

Figure 18a, b shows the values of $H^{*}_{2}$ and $A^{*}_{2}$, respectively. For the results of $H^{*}_{2}$, there was a divergence in the simulated results with the k–$\omega$ SST turbulence model at $U_{r}$ = 8, 10, and 12, which did not occur with k–$\omega$ SSTLM.

Regarding the results of $A^{*}_{2}$, an excellent agreement between the results in the two turbulence models can be noticed.

Fig. 18

8COEF k–$\omega$ SST $\bullet$; 8COEF k–$\omega$ SSTLM $\blacklozenge$; $\square$ CFD Nieto et al. [7]; $\triangle$ CFD Larsen e Walther [11]; $\vartriangleleft$ CFD Bai et al. [14]

Figure 19a, b shows the results of $H^{*}_{3}$ and $A^{*}_{3}$, respectively. For the results of $H^{*}_{3}$, one can see almost a coincidence of the simulated results in the two turbulence models with those of the references. Concerning the results of $A^{*}_{3}$, one can note the consistency of the results of the models among themselves, showing exponential growth similar to that of the references, although proportionally lower, mainly from $U_{r}$ = 6.

Fig. 19

8COEF k–$\omega$ SST $\bullet$; 8COEF k–$\omega$ SSTLM $\blacklozenge$; $\square$ CFD Nieto et al. [7]; $\triangle$ CFD Larsen e Walther [11]; $\vartriangleleft$ CFD Bai et al. [14]

In the first set of GBEB results, it is possible to notice that the turbulence models considered in the research had similar performances, except for the coefficient $H^{*}_{2}$. For this coefficient, the k–$\omega$ SSTLM model had a better performance when compared to the k–$\omega$ SST.

It should be noted that the coefficient $H^{*}_{2}$ is the portion associated with the aerodynamic damping of the torsional degree of freedom of Eq. 27. In the classic flutter phenomenon, the aerodynamic damping (the part with $H^{*}_{2}$), when combined with the structural damping, results in zero or negative damping, characterizing the divergent oscillations of the phenomenon.

In general, the results are very close to the results of Nieto et al. [7] and those of Bai et al. [14]. The proximity to the former is due to the good correlation between the simulation parameters. Bai et al. [14] conducted three-dimensional simulations with a detached-eddy simulation (DES) turbulence model. Note that the results obtained from the two-dimensional simulations of the present research are close to the three-dimensional simulations by Bai et al. [14].

6.3.2 Flexural coefficients

The flutter derivatives of the flexural movement are obtained by 8COEF and LE proposed by Matsumoto [4]. In Figs. 20 and 21, the results for $H^{*}_{1}$, $A^{*}_{1}$, $H^{*} _{4}$ and $A^{*}_{4}$ are compared with CFD studies by Huang et al. [13], Larsen and Walther [11] and Bai et al. [14].

The values of the results for 8COEF and by LE for the coefficients $H^{*}_{1}$ and $A^{*}_{1}$ are shown in Fig. 20. In the results of $H^{*}_{1}$, there was an unexpected divergence in $U_{r}$ = 12 for 8COEF k–$\omega$ SST, which was not repeated in the other results. Regarding the results of $A^{*}_{1}$, a good agreement between the results in both approaches and with the literature can be noted.

The references used for comparisons adopt the forced vibration approach in torsion and bending modes to obtain the complete set of flutter derivatives, an approach similar to 8COEF in the present work. Briefly, the main characteristics of these references are

• Larsen and Walther [11]: a meshless discrete vortex method and the DVMFLOW code.

• Bai et al. [14]: 3D DES CFD model.

• Huang et al. [13]: 2D RNG k–$\varepsilon$ CFD simulations, with SIMPLE pressure linked equation solver, a second-order upwind scheme for the divergence terms, with 26300 cells.

The values of the results for 8COEF and by LE for the coefficients $H^{*}_{1}$ and $A^{*}_{1}$ are shown in Fig. 20. In the results of $H^{*}_{1}$, there was an unexpected divergence in $U_{r}$ = 12 for 8COEF k–$\omega$ SST, which was not repeated in the other results. Regarding the results of $A^{*}_{1}$, a good agreement between the results in both approaches and with the literature can be noted.

Fig. 20

8COEF k–$\omega$ SST $\bullet$; LE k–$\omega$ SST $\star$; 8COEF k–$\omega$ SSTLM $\blacksquare$; LE k–$\omega$ SSTLM $\blacklozenge$; $\square$ CFD Huang et al. [13]; $\triangle$ CFD Larsen e Walther [11]; $\vartriangleleft$ CFD Bai et al. [14]

The results for $H^{*}_{4}$ and $A^{*}_{4}$ are shown in Fig. 21. The similarity of behavior in the results is observed, but with more pronounced differences for higher values of reduced velocities as in $U_{r}$ = 8, 10, and 12, mainly for the 8COEF values. In addition, it is observed in the graph of $A^{*}_{4}$ that the solution by LE distances itself from the values of the 8COEF and the references, unlike the results presented in the graph of $H^{*}_{ 4}$, these with better agreement.

Fig. 21

8COEF k–$\omega$ SST $\bullet$; LE k–$\omega$ SST $\star$; 8COEF k–$\omega$ SSTLM $\blacksquare$; LE k–$\omega$ SSTLM $\blacklozenge$; $\square$ CFD Huang et al. [13]; $\triangle$ CFD Larsen e Walther [11]

The percentage differences between the 8COEF and LE results, taking the 8COEF results as a reference and representative values of the responses for the two turbulence models, are presented in Table 3.

Table 3 Comparative between flutter derivatives for GBEB

About the results of Table 3, the percentage difference was reasonably dispersed, behaving similarly between the $U_{r}$. In the case of an aerodynamic structure, the results of the flutter derivatives for bending were also quite dispersed, as can be seen in 6.3.2, mainly in the results of $H_{4}^{*}$ and $A_{4}^{*}$.

However, it should be noted that the high values presented in Table 3 are related to almost zero values in the respective graphs of the coefficients, mainly for the coefficients $H_4^*$ and $A_4^*$. These coefficients, as can be seen in Eqs. 27 and 28, are associated with the flexural stiffness portions h (elastic forces). In the classic flutter mechanism, characterized by the coupling of flexural and torsion modes, there is a loss of stability associated with aerodynamic damping, predominant torsional movement. It is understood, therefore, that these results do not compromise the global analysis of the structure regarding the phenomenon studied here.

Scanlan et al. [10] applied the same interrelations among flutter derivatives in three streamlined bridges, the Kap Shui Mun Bridge in Hong Kong, the Golden Gate Bridge in the USA, and the Tsurumi Bridge in Japan. They pointed out that, in almost all analyses, “none of the suggested equivalences of Eqs. 45 to 48 appear to hold”, especially the relation for $H_4^*$ 46.

It is also noteworthy that according to Šarki$\acute{c}$ et al. [36], this divergence in results may be associated with the fact that flutter derivatives simulated in a CFD environment are not resolved with good consistency for very high reduced velocities.

In addition to these facts, it is emphasized, again, that high values of $U_r$ are associated, in flexible structures, with very strong winds that are not representative of their real scenario. For the GBEB case, for example, whose natural frequencies are presented in Appendix 1 [11], the value of $U_r$ = 15 corresponds to a real strong wind velocity of around 300 km/h.

6.4 Critical flutter velocity estimate for the GBEB

Assuming that there is a solution to the flutter problem, considering that the harmonic motion is predominant during the critical velocity, evaluating it is simple. The flutter derivatives $H_i^*$ and $A_i^*$, as functions of the reduced frequency K, and the assembly of the harmonic motions with the equations 27 and 28 provides a system in amplitude movement of h and $\alpha$.

The procedures for obtaining the critical flutter velocity are [8]:

• 1. A value of K is chosen, and the values of $H_i^*$ and $A_i^*$ corresponding to that value are extracted from plots of $H_i^*$ and $A_i^*$ as a function of the reduced velocity.

• 2. It is then assumed that h and $\alpha$ have solutions proportional to $e^{i\omega t}$ which are inserted into Eqs. 25, 26, 27, and 28. These substitutions generate a system of equations in h and $\alpha$.

• 3. As a condition of stability, the determinant of the coefficients of the amplitudes h and $\alpha$ is set equal to zero, which results in a complex equation at the unknown vibration frequency $\omega$, which must be solved [27, 37]. This constitutes in fact a complex quartic equation in the unknown flutter frequency $\omega$, requiring a solution.

• 4. The solution obtained will, in general, be on the form $\omega =\omega _1+ i \omega _2$, with $\omega _2 \ne 0$, and will therefore represent either a decaying ($\omega _2 >0$) or a divergent ($\omega _2 < 0$) oscillation.

• 5. A new value of K is then chosen, and the procedure is repeated until the solution is purely (or very nearly) real, that is, until $\omega _2=0$, so that $\omega =\omega _1$. To that solution, there corresponds the flutter condition at real frequency $\omega _1$.

• 6. The intersection point’s coordinates between the imaginary and real solutions are utilized for computing the critical flutter velocity.

• 7. Therefore, the critical velocity is calculated using Eq. 50:

  $$\begin{aligned} U_{c}=\frac{B X \omega _h}{K} \end{aligned}$$

  (50)

  where X is the critical flutter velocity frequency rate (Eq. 51),

  $$\begin{aligned} X=\frac{\omega }{\omega _h} \end{aligned}$$

  (51)

  where B is the width of the cross-section and $\omega _{h}$ is the natural frequency of vertical vibration.

The results of the flutter derivatives arranged in the section 6.3 were used to calculate the critical velocity. Responses are validated with experimental studies, and CFD by Larsen [9], by Bakis et al. [19], and by Jurado et al. [15].

Table 4 describes some of the structural properties of the GBEB [9, 22].

Table 4 GBEB structural properties used in the critical velocity calculation

The critical flutter velocity was obtained with the result sets of the 8COEF and LE approaches and k–$\omega$ SST and k–$\omega$ SST LM turbulence models.

Figure 22a shows the X and 1/K curves obtained with the flutter derivatives from k–$\omega$ SST turbulence model simulations and 8COEF approach. Figure 22b shows the X and 1/K curves obtained with the flutter derivatives from k–$\omega$ SSTLM turbulence model simulations and 8COEF approach. Figure 23a shows curves X and 1/K for LE results and k–$\omega$ SST model. Figure 23b shows curves X and 1/K for LE results and k–$\omega$ SSTLM turbulence model.

The critical flutter velocity was obtained with the result sets of the four cases:

• 1. turbulence model k–$\omega$ SST with LE approach.

• 2. turbulence model k–$\omega$ SST with 8COEF approach.

• 3. turbulence model k–$\omega$ SSTLM with LE approach

• 4. turbulence model k–$\omega$ SSTLM with 8COEF approach.

The first model, k $\omega$ SST with LE approach, can be seen as the one with the lowest computational cost since it requires the solution of two additional differential equations referring to the turbulence model and the simulations in torsion mode only. The last model, on the other hand, is the most robust, but with a longer processing time. This employs a turbulence model for laminar–turbulent transition flow with four differential equations, in addition to requiring simulations in torsion and bending mode.

These figures are intended to share with readers the intermediate steps to obtain the critical flutter velocity for each adopted model. Through these, it is possible to notice that there is little discrepancy between the values of the intersection point, used to calculate the critical velocities presented in Table 5

Fig. 22

Real part 1 $\Diamond$; real part 2 $\circ$; imaginary part $\square$; intersection $\blacksquare$

Fig. 23

Real part 1 $\Diamond$; real part 2 $\circ$; imaginary part $\square$; intersection $\blacksquare$

Table 5 presents a summary of these results, a comparison between the two methods used in the calculations of this study, and a comparison with the results in the literature.

Table 5 Flutter critical velocity estimate for the GBEB

In this study, the same vibration modes found in Larsen’s research [9] were used, and they can be seen in Appendix 1.

The list of vibration modes utilized by the authors is also provided in Appendix 1.

It is noted that the results of the methodology used in the present research, in the two approaches, 8COEF and LE, correlate well with the literature results. In particular, the comparison with the values provided by Larsen [9] from his experiments in a wind tunnel for sectional (2D) and complete (3D) models shows that the model currently being investigated presents satisfactory results. Comparison with the analytical multi-modal formulation by Bakis et al. [19] and Jurado et al. [15] also shows that the values obtained in this research are lower and more conservative.

As for the models used in the research, it can be noted that the 8COEF and LE had similar results. There is a good approximation in estimating the critical flutter velocity for the LE approximation compared to the 8COEF full simulation approach, despite the dispersed results for the flutter derivatives via the LE of Sect. 6.3.2. As for the computational cost criterion, the LE approach and the SST turbulence model have the lowest cost.

Larsen [9] highlights in his research the importance of developing models and methodologies, which can be used in the conceptual phase of the structural project to guarantee integrity throughout the useful life of the structure. It can be seen, therefore, that more conservative flutter critical velocity values are an exciting premise for the conceptual design. In addition, compared to the others, the model employed requires an effective cost of installations and computational costs lower than those of the other authors.

7 Final remarks and future works

This research presented a methodology in two-dimensional CFD for aerodynamic and aeroelastic studies of a rectangular section of proportion 1:4.9 and a cross-section of the GBEB in proportion 1:7. Simulations were performed for turbulent flow with $R_{e}$ 10$^{5}$. To this end, to monitor the effects in the boundary layer, the 2D RANS k–$\omega$ SST turbulence models by Menter et al. [25], and k–$\omega$ SSTLM from Menter et al. [2] were employed.

The aerodynamic analyses allowed the validation of the numerical model and the choice of mesh for the subsequent aeroelastic analyses. The aeroelastic model is based on the work of Le Maître et al. [3] and employs the methodology of forced vibrations associated with a model that linearizes the relationships between aerodynamic forces and the structural model. In this aeroelastic model, the aerodynamic force portions are represented by aeroelastic coefficients ($H_{i}^{*}$ and $A_{i}^{*}$). Subsequently, these values were used to estimate the critical flutter velocity.

Obtaining the coefficients, as mentioned earlier, for different values of reduced velocity was one of the main objectives of the research. This work highlights the evaluation of two approaches to obtain the complete flutter derivatives. In the first, 8COEF, all coefficients were obtained from computational simulations, with forced and independent vibrations in vertical and torsional bending modes. The second approach, called LE, employs linear relations to obtain the flexural coefficients from the coefficients obtained for the torsion mode.

In a comparative analysis of the coefficients, the turbulence models showed good consistency with the reference values, attesting that both the turbulence models and the 2D RANS approach accurately captured these coefficients. For the two studied turbulence models, comparing the numerically obtained flutter derivatives with the experimental ones and others from the literature resulted in good results. Also, the proposed LSM was efficient for extracting the flutter derivatives.

Based on the results obtained in the calculation of the flutter derivatives, the estimation of the critical flutter velocity for the GBEB was carried out. Comparing the critical velocity, it is noted that the LE linearization was considered adequate, with results even close to the 8COEF methodology and those in the literature. Finally, to minimize the computational cost, applying the LE approach and the k–$\omega$ SST model is justified.

This research brings a new vision of using CFD-based techniques in obtaining numerical and LE results, as it demonstrates the adequacy of computational results using an efficient 2D approach. Furthermore, it is also an essential step in applying numerical optimization techniques. Therefore, a fully computational approach for analyzing static and flutter derivatives, such as the one reported here, is necessary for applying numerical optimization techniques, such as reducing computational demands.

As an extension of this research, it is suggested to carry out the simulations, including the accessories of the GBEB structure (guardrail and median); employ the 3D LES (large eddy simulation) approach in the simulations; investigate the influence of Reynolds Number on aeroelastic parameters and structural behavior, and extend it to 3D models of other streamlined bridge structures. Such an approach requires greater computational demands.

Appendix A Vibration modes from Table 5

See Table 6.

Table 6 Vibration modes