1 Introduction

Ball bearings, the widely used supporting component, are the weakest link in a precision spindle system, which directly affects the service reliability and operational stability of the mechanical system. In the actual service process, the bearing is fixed on the shaft through an interference fit, and the constant pressure preload method and the fix-position preload method are applied to provide the appropriate preload force. However, the spindle shaft encounters some problems during the manufacturing process such as cutting vibration and thermal deformation, which lead to the shaft deflection and the bearing angular ring misalignment. As a result, the assembly states of the shaft-bearing and the contact properties within the bearing are both changed, even weakening the bearing capacity and service life.

Since the application of Hertz contact theory to the static analysis of the ball bearing [1], many scholars have conducted theoretical and experimental studies on bearing dynamic properties using the constant pressure preload method. Palmgren [2] proposed a simplified mechanical model of the angular contact ball bearing, and further analyzed the load distribution within the bearing under the combined loads. He pointed out that the maximum load acting on the rolling elements directly affected the bearing fatigue life, which was an important factor in determining the bearing stability. Jones [3] firstly introduced the centrifugal force and gyroscopic moment into the bearing mechanical model, and the 3-DOF quasi-static model was established to investigate the effect of operation conditions on bearing dynamic properties. Cao et al. [4] derived the stiffness matrix of the 5-DOF quasi-static model, and explored a general modeling method that couples the shaft, angular contact ball bearing, and bearing housing. They also compared the numerical results with experimental data, and investigated the influence of preload and rotation speed on bearing capacity on that basis. Cheng et al. [5] proposed a modified quasi-static model with local defects to explore the load distribution and the stiffness variations. They pointed out that the stiffness and load distribution interacted with each other, and further jointly affected the dynamic properties of the bearing-rotor system. Truong et al. [6, 7] proposed an improved bearing stiffness calculation model considering thermal effects. The heat generation was calculated using the finite element method, and the results were then input into the bearing quasi-static model to calculate the stiffness matrix. Though they investigated the effect of rotation speed on bearing stiffness, the complex combined loads were not considered.

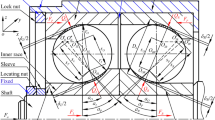
In the above analysis, the researchers focused mainly on the bearing service performance under the constant pressure preload method. However, the fix-position preload method is also an indispensable preload mechanism to improve bearing dynamic properties. As shown in Fig. 1, the compression spring is applied on the outer ring to achieve the constant pressure preload method, while the fix-position preload method is achieved by the constraints of relative position between the inner and outer ring. In recent research, fewer references have analyzed the fix-position preload method. Cao et al. [8] investigated the effect of different preload mechanisms on the spindle shaft dynamic properties, while the variation of bearing stiffness under different conditions was not considered in detail. Wang et al. [9] comparatively discussed the variation of bearing dynamic properties under different preload mechanisms, and studied the influence of preload force and rotation speed on bearing fatigue life. Their studies showed that, compared with the constant pressure preload method, the fix-position preload could enhance the service performance, whereas the fatigue life was reduced. Lin and Jiang [10] proposed the quasi-static model of the duplex angular contact ball bearing considering different preload mechanisms, and derived the interaction and relative position among bearing components using spatial coordinate transformations. They also constructed the stiffness matrix, and analyzed the effects of bearing configurations and preload mechanisms on the angular stiffness and the cross-coupling stiffness. Zhang et al. [11] derived the stiffness matrix of the ball bearing, and investigated the effects of different preload mechanisms on bearing stiffness under combined loads. They also compared the numerical results with the experimental data to verify the calculation accuracy. Dong et al. [12] set up a test-bed system to evaluate the effect of thermal characteristics on the bearing stiffness. They proposed an optimal initial preload method with respect to rotation speed to maximize the thermal stiffness.

Fig. 1
figure 1

Different preload mechanisms: a fix-position preload; b constant pressure preload

Full size image

As seen from the recent studies, most numerical and experimental methods are used to investigate the variation of bearing dynamic properties in ideal conditions, and the influence of angular ring misalignment caused by shaft deflection and assembly errors is ignored. Therefore, Zhang et al. [13] further proposed an improved quasi-static model of the ball bearing based on the vector solution method to investigate the influence of angular ring misalignment on bearing stiffness and contact fatigue life under different load conditions. They pointed out that the angular ring misalignment played a significant role in load distribution within bearing, and it could not be ignored in theoretical research. Xu et al. [14] constructed a quasi-static model of the duplex angular contact ball bearing in terms of the vector and matrix methods to investigate the effect of angular ring misalignment on bearing capacity and load distribution. It can be concluded that the angular ring misalignment directly affects the bearing capacity and service performance, which is the key issue to improve the operation accuracy and prolong the service life of the mechanical system. However, those researchers pay more attention to the effects of angular ring misalignment on bearing dynamic properties in the constant pressure preload method, which cannot consider the influence of bearing deformations and different preload mechanisms.

To further investigate the effects of deformations and angular ring misalignment on bearing dynamic properties, this paper proposes a comprehensive model of the ball bearing. Firstly, the geometrical interactions between assembly state and bearing deformations are derived. The principles of the two types of preload mechanisms are then analyzed. An efficient calculation method based on the finite difference method is adopted to analyze the bearing stiffness. Finally, the effects of initial interference value, shaft rotation speed, and angular ring misalignment on bearing dynamic properties are investigated.

2 Theoretical analysis

2.1 Bearing deformations and structural parameter modifications

The interference fit is applied to connect the bearing inner ring to the shaft in the actual service process, and there is assembly stress at the joint surface between the shaft and inner ring due to the presence of the initial interference value. Especially in high-speed operation conditions, the influence of centrifugal stress gradually emerges with the increase in shaft rotation speed, which results in the change of the assembly state. The bearing structural parameters eventually alter caused by the combined effects of assembly and centrifugal stress.

Figure 2 denotes the schematic diagram of the assembly state for the bearing-rotor system. In this figure, Ba denotes the width of the bearing inner ring, and it indicates its axial direction. Similarly, Dr represents the inner diameter of the bearing, which is along the radial direction for the inner ring.

Fig. 2
figure 2

Schematic diagram of the assembly state for the bearing-rotor system

Full size image

It can be seen from Fig. 2 that the axial dimension Ba for the bearing inner ring is much smaller than its radial dimension Dr, and it can be regarded as a hollow disc. According to the elasticity theory, the axisymmetric plane stress theory is applied to resolve the bearing deformation [15]. Thus, combining the equilibrium equation, geometric equations, and elastic constitutive equations for the hollow disc, one can get the following equation:

$$\frac{{d^{2} u}}{{dr^{2} }} + \frac{1}{r}\frac{du}{{dr}} - \frac{u}{{r^{2} }} = - \frac{{1 - \mu^{2} }}{E}\rho \omega^{2} r$$
(1)

where ρ and ω are the material density and the shaft rotation speed, respectively; E and μ are the material elastic modulus and the Poisson’s ratio, respectively [16].

Solving Eq. (1) by the integral method, one can get the equations of radial displacement and stress:

$$u = S_{1} r + \frac{{S_{2} }}{r} - \frac{1}{8E}\left[ {\rho \omega^{2} r^{3} \left( {1 - \mu^{2} } \right)} \right]$$
(2)
$$\sigma_{r} = E\left[ {\frac{{S_{1} }}{1 - \mu } - \frac{{S_{2} }}{{r^{2} \left( {1 + \mu } \right)}}} \right] - \frac{{\rho \omega^{2} r^{2} }}{8}\left( {3 + \mu } \right)$$
(3)

where S1 and S2 are constants generated by twice integrating Eq. (1).

Assuming that P1 is the assembly pressure between the inner ring and the shaft, the boundary conditions of the inner ring can be obtained:

$$\left\{ \begin{gathered} r = r_{2} ,\sigma_{r} = - P_{1} \hfill \\ r = r_{3} ,\sigma_{r} = 0 \hfill \\ \end{gathered} \right.$$
(4)

where r2 is the radius of the joint surface for the shaft-inner ring; r3 is the outer radius for the inner ring [17, 18].

Combining Eqs. (3) and (4), one can obtain:

$$\left\{ \begin{gathered} S_{1} = \frac{{r_{2}^{2} \left( {1 - \mu } \right)}}{{\left( {r_{3}^{2} - r_{2}^{2} } \right)}}\left[ {EP_{1} + \frac{{E\rho \omega^{2} \left( {3 + \mu } \right)}}{{8r_{2}^{2} }}\left( {r_{3}^{4} - r_{2}^{4} } \right)} \right] \hfill \\ S_{2} = \frac{{r_{2}^{2} r_{3}^{2} \left( {1 + \mu } \right)}}{{\left( {r_{3}^{2} - r_{2}^{2} } \right)}}\left[ {EP_{1} + \frac{{E\rho \omega^{2} \left( {3 + \mu } \right)}}{8}\left( {r_{3}^{2} - r_{2}^{2} } \right)} \right] \hfill \\ \end{gathered} \right.$$
(5)

Substituting Eqs. (2)–(5), one can derive the inner ring radial deformations at r = r2 and r3:

$$u_{{r_{2} }} = S_{1} r_{2} + \frac{{S_{2} }}{{r_{2} }} - \frac{1}{8E}\left[ {\rho \omega^{2} r_{2}^{3} \left( {1 - \mu^{2} } \right)} \right]$$
(6)
$$u_{{r_{3} }} = S_{1} r_{3} + \frac{{S_{2} }}{{r_{3} }} - \frac{1}{8E}\left[ {\rho \omega^{2} r_{3}^{3} \left( {1 - \mu^{2} } \right)} \right]$$
(7)

Analogously, the axial dimension of the shaft is much larger than its cross section, and the shaft can be regarded as a beam of equal cross section generally. According to the elasticity theory, the radial deformation and stress can be obtained:

$$s = S_{3} r + \frac{{S_{4} }}{r} - \frac{{\rho \omega^{2} r^{3} }}{{8E\left( {1 - \mu } \right)}}\left( {1 - 2\mu } \right)\left( {1 + \mu } \right)$$
(8)
$$\tilde{\sigma }_{r} = \frac{1}{1 + \mu }\left( {\frac{{ES_{3} }}{1 - 2\mu } - \frac{{ES_{4} }}{{r^{2} }}} \right) - \frac{1}{{8\left( {1 - \mu } \right)}}\left[ {\rho \omega^{2} r^{2} \left( {3 - 2\mu } \right)} \right]$$
(9)

The boundary conditions of the shaft can be given as:

$$\left\{ \begin{gathered} r = r_{2} ,\sigma_{r} = - P_{1} \hfill \\ r = r_{1} ,\sigma_{r} = 0 \hfill \\ \end{gathered} \right.$$
(10)

where r1 is the inner radius for the shaft.

Substituting Eqs. Eq. (9)–(10), one can get:

$$\left\{ \begin{gathered} S_{3} = \frac{{r_{2}^{2} \left( {1 - 2\mu } \right)\left( {1 + \mu } \right)}}{{\left( {r_{2}^{2} - r_{1}^{2} } \right)}}\left[ { - EP_{1} + \frac{{E\rho \omega^{2} \left( {3 - 2\mu } \right)}}{{8r_{2}^{2} \left( {1 - \mu } \right)}}\left( {r_{2}^{4} - r_{1}^{4} } \right)} \right] \hfill \\ S_{4} = \frac{{r_{1}^{2} r_{2}^{2} \left( {1 + \mu } \right)}}{{\left( {r_{2}^{2} - r_{1}^{2} } \right)}}\left[ { - EP_{1} + \frac{{E\rho \omega^{2} \left( {3 - 2\mu } \right)}}{{8\left( {1 - \mu } \right)}}\left( {r_{2}^{2} - r_{1}^{2} } \right)} \right] \hfill \\ \end{gathered} \right.$$
(11)

Combining Eqs. (11) and (8), one can obtain the shaft radial deformation at r = r2:

$$s_{{r_{2} }} = S_{3} r_{2} + \frac{{S_{4} }}{{r_{2} }} - \frac{{\rho \omega^{2} r_{2}^{3} }}{{8E\left( {1 - \mu } \right)}}\left( {1 - 2\mu } \right)\left( {1 + \mu } \right)$$
(12)

Assuming that δini is the initial interference value, one can get the following equation:

$$\delta_{ini} = 2\left( {u_{{r_{2} }} - s_{{r_{2} }} } \right)$$
(13)

Combining Eqs. (6)–(13), the inner ring radial deformations at r = r3 can be solved, which is adopted to modify the bearing structural parameters.

2.2 Quasi-static model of the ball bearing considering angular ring misalignment

Angular ring misalignment is generally induced by installation errors, deflection, and thermal deformations, which will change the relative positions among bearing components and further affect the bearing service performance. To reveal the effect of angular ring misalignment on bearing dynamic properties, it is assumed that the bearing outer ring is fixed and the inner ring rotates with the shaft. The angular ring misalignment θ can be defined as:

$$\theta = \left[ {\theta_{y} ,\theta_{z} } \right]$$
(14)

where θy and θz are the angular ring misalignment around the Y-axis and Z-axis of the inner ring, respectively.

Figure 3 illustrates the conditions of geometric and deformation compatibility within the bearing. It can be seen that with the increase in rotation speed, the ball center is no longer collinear with the inner and outer raceway groove curvature center. Meanwhile, due to the action of centrifugal force, the ball center and inner raceway groove curvature center gradually reach their equilibrium positions. In addition, the inner ring displacement vector \({\varvec{d}} = \left\{ {\delta_{X} ,\delta_{Y} ,\delta_{Z} } \right\}\) with respect to the outer ring is subjected to the operation load vector \({\varvec{F}} = \left\{ {F_{X} ,F_{Y} ,F_{Z} } \right\}\), where FX, FY, and FZ are the operation load components along the X, Y, and Z-axis, respectively; δX, δY, and δZ are the inner ring displacements along X, Y, and Z-axis, respectively.

Fig. 3
figure 3

Geometry and mechanical relations for the ball bearing: a coordinate systems and force analysis; b relative positions of the ball center and the raceway groove curvature center

Full size image

According to the Pythagorean theorem, the geometric equilibrium equations can be obtained:

$$\left( {A_{1j} - X_{1j} } \right)^{2} + \left( {A_{2j} - X_{2j} } \right)^{2} = \Delta_{ij}^{2}$$
(15)
$$X_{1j}^{2} + X_{2j}^{2} = \Delta_{oj}^{2}$$
(16)

with

$$\left\{ \begin{gathered} A_{1j} = (r_{i} + r_{0} - 0.5D)\sin \alpha_{0} + u_{i} \hfill \\ A_{2j} = (r_{i} + r_{0} - 0.5D)\cos \alpha_{0} + v_{i} \hfill \\ \end{gathered} \right.$$
(17)
$$\left\{ \begin{gathered} \Delta_{oj} = \left( {r_{o} - 0.5D} \right) + \delta_{oj} \hfill \\ \Delta_{ij} = \left( {r_{i} - 0.5D} \right) + \delta_{ij} \hfill \\ \end{gathered} \right.$$
(18)
$$\left[ {\begin{array}{*{20}c} {u_{i} } \\ {v_{i} } \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}c} 1 & 0 & 0 & {R_{i} \sin \varphi_{j} } & { - R_{i} \cos \varphi_{j} } \\ 0 & {\sin \varphi_{j} } & {\cos \varphi_{j} } & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\delta_{X} } & {\delta_{Y} } & {\delta_{Z} } & {\theta_{Y} } & {\theta_{Z} } \\ \end{array} } \right]^{{\text{T}}}$$
(19)

where A1j and A2j are the axial and vertical displacement between the inner and outer raceway groove curvature center after operation, respectively; X1j and X2j are the axial and vertical displacement between the ball center and the outer raceway groove curvature center, respectively; Δij and Δoj are the distance between the ball center and the inner raceway groove curvature center, and the distance between the ball center and the outer raceway groove curvature center, respectively; D is the ball diameter; δij and δoj are the contact deformation of the ball-inner and the ball-outer raceway, respectively; ui and vi are axial and vertical displacement of the inner raceway groove curvature center before and after operation, respectively; ri and ro are the inner and outer raceway groove curvature radius, respectively; αij and αoj are the contact angles of the ball-inner and the ball-outer raceway, respectively; φj is the angular position of the balls, \(\varphi_{j} = {{2\pi \left( {j - 1} \right)} \mathord{\left/ {\vphantom {{2\pi \left( {j - 1} \right)} Z}} \right. \kern-0pt} Z}\) [19]; Z is the ball number; α0 is the initial contact angle, and it can be obtained based on the bearing deformation:

$$\alpha_{0} {\text{ = arccos}}\left( {1 - \frac{{d_{o} - (d_{i} + 2u_{r3} ) - 2D}}{{2\left( {r_{i} + r_{o} - D} \right)}}} \right)$$
(20)

where di and do are the inner and outer raceway contact diameter, respectively.

Furthermore, the contact angles of the ball-inner and the ball-outer raceway can be given as:

$$\left\{ \begin{gathered} \sin \alpha_{oj} = \frac{{X_{1j} }}{{\left( {r_{o} - 0.5} \right) + \delta_{oj} }} \, \cos \alpha_{oj} = \frac{{X_{2j} }}{{\left( {r_{o} - 0.5} \right) + \delta_{oj} }} \hfill \\ \sin \alpha_{ij} = \frac{{A_{1j} - X_{1j} }}{{\left( {r_{i} - 0.5} \right) + \delta_{ij} }} \, \cos \alpha_{ij} = \frac{{A_{2j} - X_{2j} }}{{\left( {r_{i} - 0.5} \right) + \delta_{ij} }} \hfill \\ \end{gathered} \right.$$
(21)

According to the force analysis of the ball and the raceway as shown in Fig. 3, the mechanical equilibrium equations can be derived as follows:

$$\left[ {\begin{array}{*{20}c} {\sin \alpha_{ij} } & { - \sin \alpha_{oj} } \\ {\cos \alpha_{ij} } & { - \cos \alpha_{oj} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {Q_{ij} } \\ {Q_{oj} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} { - \cos \alpha_{ij} } & {\cos \alpha_{oj} } \\ {\sin \alpha_{ij} } & { - \sin \alpha_{oj} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {F_{ij} } \\ {F_{oj} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ {F_{cj} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right]$$
(22)

where Qij and Qoj are the contact loads of the ball-inner and the ball-outer raceway, respectively; Fcj is the centrifugal force; Fij and Foj are the friction force of the ball-inner and the ball-outer raceway, respectively [20].

The contact loads of the ball-raceway can be defined as:

$$\left\{ \begin{gathered} Q_{ij} = K_{ij} \delta_{ij}^{1.5} \hfill \\ Q_{oj} = K_{oj} \delta_{oj}^{1.5} \hfill \\ \end{gathered} \right.$$
(23)

where Kij and Koj are the contact stiffness of the ball-inner and the ball-outer raceway, respectively [21, 22].

The friction force of the ball-raceway can be derived as:

$$\left\{ \begin{gathered} F_{ij} = \lambda_{ij} M_{j} /D \hfill \\ F_{oj} = \lambda_{oj} M_{j} /D \hfill \\ \end{gathered} \right.$$
(24)

where Mj is the gyroscopic moment; λij and λoj are the raceway control parameters, respectively, and it can be selected according to Ref. [23, 24].

The centrifugal force and gyroscopic moment can be obtained:

$$\left\{ \begin{gathered} F_{cj} = \frac{1}{2}md_{m} \omega_{i}^{2} \left( {\frac{{\omega_{mj} }}{{\omega_{i} }}} \right)^{2} \hfill \\ M_{j} = J\left( {\frac{{\omega_{rj} }}{{\omega_{i} }}} \right)\left( {\frac{{\omega_{mj} }}{{\omega_{i} }}} \right)\omega_{i}^{2} \sin \beta_{j} \hfill \\ \end{gathered} \right.$$
(25)

where m and J are the mass and the inertia of moment for the ball, respectively; ωrj and ωmj are the orbital speed and the rotation speed for the ball, respectively; ωi is the shaft rotation speed; βj is the ball pitch angle defined by the raceway control theory [23, 25].

The global equilibrium equations of the inner ring can be derived as follows:

$$\left[ {\begin{array}{*{20}c} {F_{x} } \\ {F_{y} } \\ {F_{z} } \\ \end{array} } \right] = \sum\limits_{j = 1}^{Z} {\left\{ {\left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & {\sin \varphi_{j} } \\ 0 & {\cos \varphi_{j} } \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {Q_{ij} \sin \alpha_{ij} - F_{ij} \cos \alpha_{ij} } \\ {Q_{ij} \cos \alpha_{ij} + F_{ij} \sin \alpha_{ij} } \\ \end{array} } \right]} \right\}}$$
(26)

To reveal the influence of angular ring misalignment, the moment loads acting on the inner ring can be calculated by the angular ring misalignment:

$$\left[ {\begin{array}{*{20}c} {M_{Y} } \\ {M_{Z} } \\ \end{array} } \right]{ = }\sum\limits_{j = 1}^{Z} {\left\{ {\left[ {\begin{array}{*{20}c} {R_{ii} \cos \varphi_{j} } & 0 \\ 0 & {R_{ii} \sin \varphi_{j} } \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {Q_{ij} \sin \alpha_{ij} - F_{ij} \cos \alpha_{ij} } \\ {Q_{ij} \sin \alpha_{ij} - F_{ij} \cos \alpha_{{_{ij} }} } \\ \end{array} } \right]} \right\}}$$
(27)

where Rii is the locus circle radius of the inner raceway groove curvature center [26].

Combined with the geometric equilibrium equations Eqs. (15) and (16), the mechanical equilibrium equation of the ball Eq. (22), and the mechanical equilibrium equation of the inner ring Eq. (26), the improved quasi-static model is then established, and the Newton–Raphson method is further applied to investigate the bearing dynamic properties.

2.3 Bearing preload mechanism analysis

Generally, there is an internal clearance inside the bearing when the bearing is in a free state, which is used to ensure the proper installation and debugging of bearing components. Therefore, in the actual service process, the clearance is eliminated by the external constraints (the fix-position and constant pressure preload methods) to improve the bearing dynamic properties.

As shown in Fig. 4, under the static conditions, the axial displacement of the inner ring is generated by the preload, and the total displacement is (δp/x + 0.5Pe). The axial displacement can be divided into two phases. In the first phase (see Fig. 4c), the axial displacement 0.5Pe is used to eliminate the bearing axial clearance, which generates the initial contact angle. In the second phase (see Fig. 4d), the axial displacement δp/x is induced by the contact deformations of the ball-raceway, which determines the actual preload force acting on the inner ring. For the bearing with constant pressure preload method, the preload force basically keeps constant, while the axial displacement δx is changed due to the combined effects of centrifugal force and gyroscopic moment. In contrast, the total axial displacement (δp + 0.5Pe) with the fix-position preload method keeps constant, which is caused by the constrained relative position of the inner and outer raceway groove curvature center. Therefore, the actual preload force changes with the bearing axial clearance.

Fig. 4
figure 4

Schematic diagram of the preload process applied to the ball bearing: a initial free state; b total axial displacement; c first phase; d second phase

Full size image

The bearing axial clearance can be defined as:

$$P_{e} = 2\left( {r_{i} + r_{o} - D} \right)\sin \alpha_{0}$$
(28)

According to Sects. 2.1 and 2.2, the initial contact angle α0 is modified by the assembly and centrifugal stress. Meanwhile, the angular ring misalignment also leads to the variation of axial displacement δp for the inner ring, which further changes the bearing dynamic properties.

3 Bearing stiffness calculation

Bearing stiffness denotes the ability to resist deformations after operations, and it expresses the strong nonlinear characteristics in the service process.

The bearing calculation method can be divided into two methods. The first method is to solve the contact stiffness of the ball-raceway in every direction, then the contact stiffness can be accumulated to obtain the bearing stiffness components along the specific direction [27]. Furthermore, the second method is to obtain the bearing stiffness components through an analytical method, which is mainly to derive the partial derivative form of the external load vector \({\varvec{F}}_{0} = \left\{ {F_{X} ,F_{Y} ,F_{Z} ,M_{Y} ,M_{Z} } \right\}\) with respect to the inner ring displacement vector \({\varvec{d}}_{0} = \left\{ {\delta_{X} ,\delta_{Y} ,\delta_{Z} ,\theta_{Y} ,\theta_{Z} } \right\}\) [28]. In general, the first method can reflect the bearing capacity under specific operation conditions, while there are larger numerical errors in high-speed conditions. At the same time, in terms of investigating the effect of angular ring misalignment on bearing stiffness, it is difficult to derive the transformation equations from contact stiffness to bearing angular stiffness. Thus, the second method is used to obtain the bearing stiffness.

The bearing stiffness matrix can be derived as follows:

$$\left[ {\mathbf{K}} \right] = \left[ {\begin{array}{*{20}c} {K_{x} } & {K_{xy} } & {K_{xz} } & {K_{x\theta y} } & {K_{x\theta z} } \\ {K_{yx} } & {K_{y} } & {K_{yz} } & {K_{y\theta y} } & {K_{y\theta z} } \\ {K_{zx} } & {K_{zy} } & {K_{z} } & {K_{z\theta y} } & {K_{z\theta z} } \\ {K_{\theta yx} } & {K_{\theta yy} } & {K_{\theta yz} } & {K_{\theta y} } & {K_{\theta y\theta z} } \\ {K_{\theta zx} } & {K_{\theta zy} } & {K_{\theta zz} } & {K_{\theta z\theta y} } & {K_{\theta z} } \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}c} {\frac{{\partial F_{X} }}{{\partial \delta_{X} }}} & {\frac{{\partial F_{X} }}{{\partial \delta_{Y} }}} & {\frac{{\partial F_{X} }}{{\partial \delta_{Z} }}} & {\frac{{\partial F_{X} }}{{\partial \theta_{Y} }}} & {\frac{{\partial F_{X} }}{{\partial \theta_{Z} }}} \\ {\frac{{\partial F_{Y} }}{{\partial \delta_{X} }}} & {\frac{{\partial F_{Y} }}{{\partial \delta_{Y} }}} & {\frac{{\partial F_{Y} }}{{\partial \delta_{Z} }}} & {\frac{{\partial F_{Y} }}{{\partial \theta_{Y} }}} & {\frac{{\partial F_{Y} }}{{\partial \theta_{Z} }}} \\ {\frac{{\partial F_{Z} }}{{\partial \delta_{X} }}} & {\frac{{\partial F_{Z} }}{{\partial \delta_{Y} }}} & {\frac{{\partial F_{Z} }}{{\partial \delta_{Z} }}} & {\frac{{\partial F_{Z} }}{{\partial \theta_{Y} }}} & {\frac{{\partial F_{Z} }}{{\partial \theta_{Z} }}} \\ {\frac{{\partial M_{Y} }}{{\partial \delta_{X} }}} & {\frac{{\partial M_{Y} }}{{\partial \delta_{Y} }}} & {\frac{{\partial M_{Y} }}{{\partial \delta_{Z} }}} & {\frac{{\partial M_{Y} }}{{\partial \theta_{Y} }}} & {\frac{{\partial M_{Y} }}{{\partial \theta_{Z} }}} \\ {\frac{{\partial M_{Z} }}{{\partial \delta_{X} }}} & {\frac{{\partial M_{Z} }}{{\partial \delta_{Y} }}} & {\frac{{\partial M_{Z} }}{{\partial \delta_{Z} }}} & {\frac{{\partial M_{Z} }}{{\partial \theta_{Y} }}} & {\frac{{\partial M_{Z} }}{{\partial \theta_{Z} }}} \\ \end{array} } \right]$$
(29)

where the elements on the main diagonal Kx, Ky, and Kz are the bearing stiffness components along the X-axis, Y-axis, and Z-axis, respectively. Kθy and Kθz are the angular stiffness around the Y-axis and Z-axis, respectively. For the partial derivatives \(\partial {\varvec{F}}_{0} /\partial {\varvec{d}}_{0}\) of the external loads and the inner ring displacements, the explicit solution is usually used to calculate the bearing stiffness [29]. The calculation method is complicated and requires a large number of partial derivative calculations. The other method to obtain the bearing stiffness is the tangent method, which approximates \(\partial {\varvec{F}}_{0} /\partial {\varvec{d}}_{0}\) by \(\Delta {\varvec{F}}_{0} /\Delta {\varvec{d}}_{0}\). So the step size of the external loads and the displacements impacts the numerical accuracy, which must be determined by large numerical experiments.

This paper presents an improved bearing stiffness calculation method based on the finite difference method, which is used to investigate the bearing stiffness. The calculation equations can be derived as follows:

$${\mathbf{K}} = \frac{{{\varvec{F}}_{0} \left( {{\varvec{d}}_{0} + \Theta {\varvec{d}}_{0} } \right) - {\varvec{F}}_{0} \left( {{\varvec{d}}_{0} - \Theta {\varvec{d}}_{0} } \right)}}{{2\Theta {\varvec{d}}_{0} }}$$
(30)

where d0 is the inner raceway displacement vector under the specific working conditions; \(\Theta {\varvec{d}}_{0} { = }\left\{ {\Theta \delta_{X} ,\Theta \delta_{Y} ,\Theta \delta_{Z} ,\Theta \delta_{\theta Y} ,\Theta \delta_{\theta Z} } \right\}\) is the small disturbance vector with respect to d0. Furthermore, in the solution procedure for the quasi-static model, the general calculation process is to solve the calculation results under the specific working conditions. Similarly, the results of the quasi-static model can be used to obtain the actual working conditions, since the governing equations of the model satisfy the conditions of a unique solution. Thus, \({\varvec{F}}_{0} \left( {{\varvec{d}}_{0} + \Theta {\varvec{d}}_{0} } \right)\) and \({\varvec{F}}_{0} \left( {{\varvec{d}}_{0} - \Theta {\varvec{d}}_{0} } \right)\) can be solved based on the inverse calculation process.

The calculation method proposed in this paper directly constructs the relationships between global iterative variables and the external loads, and the complicated partial derivatives can be ignored. At the same time, this method optimizes the selection method for the step size of the displacements and the loads, which eliminates the need to conduct lots of numerical experiments. Based on the numerical analysis in this paper, when the small displacement disturbance is less than a minimum (which is set as 10–7 in this paper), the numerical results have great accuracy and reliability.

4 Model solution and validation

Figure 5 illustrates the calculation flowchart under the different preload mechanisms. Firstly, the influence of centrifugal and assembly stress is considered in the quasi-static model, and it can be used to modify the bearing structural parameters and obtain the actual preload state. Then the appropriate boundary conditions are selected through preload mechanisms. For the constant pressure preload method, the force boundary conditions are used to keep the preload force constant. In contrast, the fix-position preload method applies the displacement boundary conditions to keep the total axial displacements (δp + 0.5Pe) constant. Secondly, the improved quasi-static model is solved by the raceway control theory to reveal the contact properties of the ball-raceway. Finally, the numerical results of the quasi-static model are input into the stiffness matrix to investigate the bearing capacity.

Fig. 5
figure 5

Calculation flowchart under different preload mechanisms

Full size image

To evaluate the validity of the numerical model in this paper, the calculation results are compared with the experimental data. The tested bearing structural parameters can be found in Ref. [11, 30, 31], which is listed in Table 1. Then Fig. 6 illustrates a comparison of bearing stiffness solved by different methods.

Table 1 Tested bearing structural parameters [11, 30, 31]
Full size table
Fig. 6
figure 6

Comparison of the calculation results with the experimental data: a axial stiffness; b radial stiffness

Full size image

In Fig. 6, when the shaft rotation speed is set as 1 kr/min and the initial interference value is taken as 2 μm, the calculation results are almost consistent with the experimental data, and the axial and radial stiffness increase with the increment of preload. Meanwhile, the variation of bearing stiffness in the constant pressure preload method is basically the same as that of the fix-position preload method, which may be attributed to the combined effect of a small rotation speed and a low initial interference value.

We also compare the axial stiffness solved by the present method with the numerical results in previous research [13], as shown in Fig. 7. The axial load is set as 300 N, and the simulated bearing structural parameters are presented in Table 2. It can be found that there is an obvious stiffness softening phenomenon, and the axial stiffness decreases with the increase in rotation speed. Additionally, the results obtained by the present method are similar to those reported in Ref. [13].

Fig. 7
figure 7

Comparison of the axial stiffness with Ref. [13]: a axial stiffness solved by the present method; b numerical results in Ref [13]

Full size image
Table 2 Simulated bearing structural parameters [13]
Full size table

In general, according to the above comparative analysis, the reliability of the calculation results in this paper can be proven.

5 Result and discussion

Based on the above theoretical analysis, the effects of initial interference, shaft rotation speed and ring misalignment on bearing deformations and stiffness are investigated. The type of ball bearing is 7008C, and its structural parameters are listed in Table 3. The axial preload force is set as 590 N, which is the heavily preloaded state.

Table 3 Bearing structural parameters
Full size table

5.1 Bearing deformation analysis

The bearing inner ring and the shaft are generally assembled by an interference fit, and the contact deformation characteristics of the joint surface are one of the major factors affecting the interaction among bearing components.

The inner ring deformation ur2 is larger than the shaft deformation sr2 at the joint surface between the inner ring and the shaft, as shown in Fig. 8a, b. According to the deformation coordination conditions, the increment of initial interference value leads to the increase in the deformation ur2, while the deformation sr2 also increases, but negative deformation occurs. Meanwhile, the influence of centrifugal effect gradually emerges with the increased rotation speed. For example, when the initial interference value is set as 6 μm and the shaft rotation speed is taken as 30 kr/min, the assembly pressure at the joint surface decreases to zero, while there is the looseness between the inner ring and the shaft (as seen in Fig. 8c). It is worth noting that there is a relationship between the interference and the loosing speed, and the increment of initial interference value can effectively improve the critical loosing speed. So the inner ring deformations are affected by the combined effects of centrifugal and assembly stress. It can be concluded from Fig. 8d that the deformation ur3 increases with the increment of rotation speed and initial interference value, which leads to the decreased bearing internal clearance. However, when the rotation speed is greater than the critical loosing speed, the centrifugal stress plays a major role in the bearing deformations. As the rotation speed increases continuously, the deformations will increase sharply, which results in the change of actual bearing preload state.

Fig. 8
figure 8

Effects of shaft rotation speed and initial interference value on bearing deformations: a bearing deformation ur2; b shaft deformation sr2; c assembly pressure P1; d bearing deformation ur3

Full size image

Figure 9a illustrates the effect of initial interference value on bearing inner ring axial displacement in a static state. It can be found that the increase in initial interference value can lead to the increase in inner ring axial displacement in both preload mechanisms, while the axial displacement δp of the fix-position preload method is larger than that of the constant pressure preload method δx. Combined with Fig. 8, the increase in initial interference value can increase the deformation ur3, which results in the increment of inner raceway contact diameter and the decrement of initial contact angle (see Fig. 9b). For the bearing applied by the fix-position preload method, the total axial displacement of inner ring (δp + 0.5Pe) keeps constant, and the decrease in bearing axial clearance Pe leads to the increase in axial displacement δp, which finally increases the actual preload force Fx_real applied to the inner ring (see Fig. 9b). In contrast, the constant pressure preload method keeps the preload force unchanged. The initial contact angle decreases with the increase in initial interference value, which results in the change of load distribution within the bearing and the increase in inner ring axial displacement δx.

Fig. 9
figure 9

Effect of initial interference value on bearing structure and assembly state: a axial displacement of inner ring; b actual preload force and initial contact angle

Full size image

Figure 10a, b illustrate the effect of shaft rotation speed on bearing inner ring axial displacement under different preload mechanisms. It can be found that the inner ring axial displacement is affected by the centrifugal and assembly stress when the shaft rotation speed is less than the critical loosing speed (in this part, the initial interference value is set as 6 μm, and the shaft rotation speed is taken as 30 kr/min). For the bearing applied with the fix-position preload method, the axial displacement δp increases with the increase in rotation speed, which leads to the increase in actual preload force (see Fig. 10c). In contrast, the variation of axial displacement δx with respect to the rotation speed in the constant pressure preload method is opposite to that of the fix-position preload method δp, and the reduction is much smaller than that without considering deformations. As the rotation speed is greater than the critical rotation speed, the inner ring is loosened from the shaft, and the centrifugal stress is the main factor affecting the bearing deformations. In the meantime, the actual preload force Fx_real applied to the inner ring and the axial displacement δp sharply increase under the fix-position preload method, while the axial displacement δx in the constant pressure preload method gradually increases, which is the opposite of that without considering deformations. Similarly, the initial contact angle decreases with the increase in rotation speed, whereas the initial contact angle stays constant when the bearing deformations are ignored.

Fig. 10
figure 10

Effect of shaft rotation speed on inner ring displacement, actual preload force, and initial contact angle: a axial displacement of the fix-position preload method; b axial displacement of the constant pressure preload method; c actual preload force; d initial contact angle

Full size image

As seen from the above analysis, the initial interference value and shaft rotation speed have an influence on the bearing actual preload state through the change of bearing deformations and internal clearance. In Fig. 11, for the constant pressure preload method, the axial displacement δx increases with the increase in angular ring misalignment. Meanwhile, the angular ring misalignment directly affects the total axial displacement of inner ring (δp + 0.5Pe) under the fix-position preload method, and the axial displacement δp decreases with the increase in angular ring misalignment, while the actual preload force applied to the inner ring reduces. Combined with Fig. 3, it can be concluded that the angular ring misalignment induces the change of relative position for the inner and outer raceway groove curvature center, which leads to the fluctuation of load distribution within the bearing. Furthermore, the contact properties and load distribution caused by the angular ring misalignment can weaken the bearing capacity to some extent.

Fig. 11
figure 11

Effect of angular ring misalignment on bearing assembly state: a axial displacement of the inner ring in the constant pressure preload method; b axial displacement of the inner ring in the fix-position preload method; c total axial displacement of the inner ring in the fix-position preload method; d actual preload force in the fix-position preload method

Full size image

To further reveal the effects of initial interference value, shaft rotation speed, and angular ring misalignment on bearing capacity, the variation of bearing dynamic properties under different factors is investigated below. Meanwhile, we select the θy to evaluate the influencing mechanism of angular ring misalignment.

5.2 Discussion of bearing dynamic properties

5.2.1 Contact loads

Figure 12 illustrates the effects of shaft rotation speed and initial interference value on contact loads of the ball-raceway.

Fig. 12
figure 12

Effects of shaft rotation speed and initial interference value on contact loads of the ball-raceway: a contact loads of the ball-inner raceway in the constant pressure preload method; b contact loads of the ball-inner raceway in the fix-position preload method; c contact loads of the ball-outer raceway in the constant pressure preload method; d contact loads of the ball-outer raceway in the fix-position preload method

Full size image

It can be found that the axial displacement for the bearing inner ring increase with the increase in initial interference value, which leads to the increase in contact loads. In addition, the contact loads in fix-position preload method are larger than those in constant pressure preload method. Similarly, the increased shaft rotation speed can promote the centrifugal effect, and the contact loads on the outer raceway is larger than those on the inner raceway. Furthermore, the critical loosing speed is correspondent with the initial interference value, and the centrifugal stress is the main factor to affect the actual assembly state when the rotation speed is larger than the critical speed.

The reason is that the increase in rotation speed can increase the bearing deformation ur3 and decrease the bearing internal clearance, which leads to the increase in actual preload force and the contact load of the ball-raceway. For the bearing with the constant pressure preload method, the balls tend to “leave” the inner raceway, and the contact loads of the ball-outer raceway increase. Furthermore, the shaft rotation speed leads to the change of axial displacement for the inner ring, which affects the load distribution. When the rotation speed is less than the critical loosing speed, the contact loads of the ball-inner raceway decrease with the increase in speed. In contrast, the contact loads of the ball-inner raceway gradually increase when the inner ring is loosened from shaft.

As shown in Fig. 13, the angular ring misalignment induces the fluctuation of load distribution, which may lead to early fatigue failure. Meanwhile, the fluctuation of contact loads with the fix-position preload method is larger than that with the constant pressure preload method. It can be concluded that the angular ring misalignment can change the relative position of the inner and outer raceway groove curvature center, and the inner ring will incline. With the increase in angular ring misalignment, the contact loads near 0 and 180º angular position increase, and those near 90º and 270º angular position decrease. In addition, the angular ring misalignment can decrease the axial displacement of the inner ring, and the reduction of the fix-position preload method is less than that of the constant pressure preload method. Thus, the fix-position preload method is more sensitive to the angular ring misalignment, which leads to the larger fluctuation of contact loads.

Fig. 13
figure 13

Effect of angular ring misalignment on contact loads of the ball-raceway: a constant pressure preload method; b fix-position preload method

Full size image

5.2.2 Contact angles

Figure 14 illustrates the effects of shaft rotation speed and initial interference value on contact angles of the ball-raceway.

Fig. 14
figure 14

Effects of shaft rotation speed and initial interference value on contact angles of the ball-raceway: a contact angles of the ball-inner raceway in the constant pressure preload method; b contact angles of the ball-inner raceway in the fix-position preload method; c contact angles of the ball-outer raceway in the constant pressure preload method; d contact angles of the ball-outer raceway in the fix-position preload method

Full size image

In Fig. 14, the increase in rotation speed increases the contact angles of the ball-inner raceway and decreases the contact angles of the ball-outer raceway. This is because the balls are suppressed on the outer raceway due to the influence of centrifugal stress, which is consistent with the variation of the contact loads. Meanwhile, the initial interference value can increase the contact angles when the bearing is preloaded using the fix-position method. In contrast, for the constant pressure preload method, the variation of the contact angles for the ball-inner raceway increases with the increase in initial interference value, while the variation of the contact angles for the ball-outer raceway is the opposite of that on the inner raceway.

Figure 15 illustrates the effect of angular ring misalignment on contact angles. It can be concluded that the variation of the contact angles with respect to the angular ring misalignment in different preload mechanisms is the same, and the contact angles of the fix-position preload method are slightly larger than those of the constant pressure preload method. Furthermore, with the increase in angular ring misalignment, the contact angles near the 180º angular position increase, and those near the 0 angular position decrease. Thus, it is necessary to eliminate the angular ring misalignment in the actual service process.

Fig. 15
figure 15

Effect of angular ring misalignment on contact angles of the ball-raceway: a constant pressure preload method; b fix-position preload method

Full size image

5.2.3 Bearing stiffness

Figure 16 illustrates the effects of initial interference value and angular ring misalignment on bearing stiffness. It can be concluded that the preload mechanisms have a significant effect on the bearing capacity, and the bearing stiffness of the fix-position preload method is larger than that of the constant pressure preload method.

Fig. 16
figure 16figure 16

Effects of initial interference value and angular ring misalignment on bearing stiffness, where the shaft rotation speed is taken as 10 kr/min

Full size image

For the bearing applied with the constant preload method, with the increase in initial interference value, the contact loads of the ball-raceway increase, while the contact angles decrease. The variation of the contact angles leads to the decrease in contact loads along the axial direction, whereas the contact loads along the radial direction increase, which finally induces the decrease in axial stiffness and the increase in radial stiffness. The bearing angular stiffness mainly reflects the slewing support properties, and the increase in radial stiffness leads to the decrease in angular stiffness in the corresponding direction. Analogously, for the bearing applied with the fix-position preload method, the actual preload force increases with the increase in initial interference value, which leads to the increase in bearing stiffness.

The angular ring misalignment plays a significant role in the bearing capacity. The load distribution inside the bearing can fluctuate due to the angular ring misalignment, which leads to the decrease in radial stiffness along the angular misalignment direction and the increase in the perpendicular direction. Meanwhile, the angular ring misalignment results in the increase in angular stiffness along the angular ring misalignment direction and the decrease in the perpendicular direction. Furthermore, the axial stiffness is less sensitive to the angular ring misalignment.

Figure 17 denotes the variation of bearing stiffness affected by the shaft rotation speed and angular ring misalignment.

Fig. 17
figure 17figure 17

Effects of shaft rotation speed and angular ring misalignment on bearing assembly state, where the initial interference value is taken as 6 μm

Full size image

It can be found that the increase in rotation speed leads to the characteristics of the “stiffness softening” in the constant pressure preload method, which greatly weakens the bearing capacity. In contrast, the total axial displacement of the inner ring for the fix-position preload method keeps constant. The bearing stiffness decreases slightly with the increase in rotation speed when the speed is less than the critical rotation speed, whereas the bearing stiffness increases when the speed is larger than the critical rotation speed. In addition, the variation of the bearing stiffness in the two preload mechanisms is basically consistent with that of the axial displacement for the inner ring.

The angular ring misalignment has an influence on bearing stiffness through the change of load distribution within the bearing. The reason is that the increase in angular ring misalignment leads to the increase in contact loads near the 0 and 180° angular position, while the contact loads near the 90° and 270° angular position decrease. Thus, the angular stiffness along the angular ring misalignment increases, whereas the angular stiffness in the perpendicular direction decreases.

Bearings with the fix-position preload method have great support performance, which can improve the stability of the bearing-rotor system. However, it cannot be suitable for the operation conditions required long fatigue life. So the preload mechanisms and assembly state must be designed based on the actual service conditions. Furthermore, though the angular ring misalignment increases the bearing capacity in the specific directions to some extent, it weakens the service performance of the mechanical system.

6 Conclusions

This paper proposes a comprehensive model of the ball bearing considering deformations and angular ring misalignment. Then the effects of initial interference value, shaft rotation speed, and angular ring misalignment on bearing dynamic properties are discussed. The main conclusions can be drawn as follows:

  1. (1)

    The shaft and the bearing inner ring are connected through an interference fit, and the assembly states are jointly affected by the centrifugal and assembly stress; The bearing deformations increase with the increment of the initial interference value and the shaft rotation speed, which leads to decreased bearing internal clearance, thereby improving the load distribution within the bearing;

  2. (2)

    Compared with the constant pressure preload method, the fix-position preload method has great stiffness, and it can overcome the stiffness softening in high-speed conditions; The numerical values of the contact loads with the fix-position preload method are larger than those with the constant pressure preload, whereas the bearing fatigue life is mitigated to some extent;

  3. (3)

    Angular ring misalignment leads to the variation of interaction and relative position among bearing components, which induces the fluctuation of load distribution and further causes the early fatigue failure; Although the angular ring misalignment enhances the bearing capacity in the specific directions, it generally reduces the service performance of mechanic system.

In future research, the influence of angular ring misalignment and different preload mechanisms on the bearing dynamic behavior will be investigated, and the comprehensive model proposed in this paper can be applied to optimize the bearing structural parameters.