Keywords

19.1 Introduction

Rolling bearing is an important supporting component of rotating machinery, widely used in aerospace, precision machine tools, transportation and other fields. Its dynamic performance directly affects the operation stability and service reliability of the whole machine equipment. It is of great engineering significance to carry out the research on the dynamic properties of bearings.

Since Stribeck [1] constructs a static analyse model of ball bearing based on hertz contact theory, more and more scholars do a large number of theoretical analysis and experiment research. Jones [2] introduces the centrifugal force and gyro moment into the force balance equation of ball, and the quasi-static model of ball bearing is constructed considering the deformation of axle and structural support. Gupta [3] establishes a dynamic model based on the spatial coordinate transformation relationship of bearing components, and verifies the accuracy through experiments. They also develop the software Adore to analysis how the lubrication properties and working condition affect the dynamic performance of ball bearing [4]. Zivkovic et al. [5] combines the quasi-static model and finite element model of spindle system to investigate the effect of rotating speed on bearing stiffness, but the research method is only used in mainshaft bearing. Cao and Altintas [6] carry out the dynamic model for bearing working at machine tool, and analyze the changing rule of bearing stiffness under high speed to research on the effects of stiffness on the vibration performance of spindle system. Ye and Wang [7] used the newton–raphson method and runge–kutta method to solve the force balanced equations and dynamical equations respectively, and research on the effect of working condition on the skidding behavior of cage and the instability of ball bearing. Fang et al. [8] adopt the coordinate transformation method to derive the relationship between the azimuth angle and deformation of ball, and study the effects of preload on bearing stiffness. However, this model is analyzed by static method, which deviates greatly from the engineering application. Zhang et al. [9] consider the influence of misalignment of ring on dynamic characteristics of rotor-bearing system, and study on the effects of working condition and installation errors on bearing stiffness. In the above research, it mainly focuses on the influence of working condition on the dynamic properties of ball bearing. However, there are few studies to research the effects of bearing structural parameters. At the same time, the solution method adopted in above papers is complex, and they also have the problem of weak convergence.

In this paper, the relationships of interaction and relative motion between bearing components is deeply analyzed and the quasi-static model of ball bearing is established combining the Jones-Harris model and raceway control theory. Meanwhile, an improved solution method for the quasi-static model is proposed to investigate the working condition and structural parameters on dynamic properties. This research could provide the theoretical fundamental for life prediction and stiffness analysis.

19.2 Quasi-Static Model

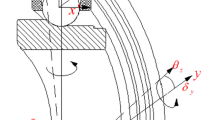
In order to investigate the dynamic properties of ball bearing under the combined axial, radial, and moment loads, the bearing coordinate system is established as shown in Fig. 19.1a. Assuming the outer raceway is fixed, and the inner raceway has a displacement \(d = \left\{ {\delta_a ,\delta_r ,\theta } \right\}\) when the applied loads on inner raceway consists of axial loads Fa, radial loads Fr, moment loads M.

Fig. 19.1
figure 1

Coordinate system and position angle of ball bearing

Full size image

In Fig. 19.1, Dout, Din, Dm are the outer raceway contact diameter, the inner raceway contact diameter, and the pitch diameter of bearing, respectively. α0 is the initial contact angle, ψj is the position angle of the jth ball, and the △ψ is the angle difference between the jth ball and (j + 1)th ball.

The relative positions of the jth ball center with the inner and outer raceway groove curvature centers is shown in Fig. 19.2. It can be seen that the ball center is initially collinear with the groove curvature center. With the increase of speed, the centrifugal force has a significant influence on dynamic properties of bearing, the outer-raceway contact angles and the inner-raceway contact angles are not equal to initial contact angle.

Fig. 19.2
figure 2

Relative positions of the jth ball center with the inner and outer raceway groove curvature centers

Full size image

According to Fig. 19.2, the Pythagorean theorem gives two geometric equations:

$$\left( {A_{1j} - X_{1j} } \right)^2 + \left( {A_{2j} - X_{2j} } \right)^2 = \Delta_{ij}^2$$
(19.1)
$$X_{1j}^2 + X_{2j}^2 = \Delta_{oj}^2$$
(19.2)

where

$$A_{1j} = BD\sin \alpha_0 + \delta_{\text{a}} + R_i \theta \cos \psi_j$$
(19.3)
$$A_{2j} = BD\cos \alpha_0 + \delta_r \cos \psi_j$$
(19.4)
$$\Delta_{ij} = \left( {f_i - 0.5} \right)D + \delta_{ij}$$
(19.5)
$$\Delta_{oj} = \left( {f_o - 0.5} \right)D + \delta_{oj}$$
(19.6)
$$BD = (f_i + f_0 - 0.5)D$$
(19.7)

where A1j, A2j are the axial and radial distance between inner raceway curvature centre and fixed outer raceway curvature centre, respectively. X1j, X2j are the axial and radial distance between ball centre and outer raceway curvature centre, respectively. △ij, △oj are the distance between the centre of ball and inner and outer raceway curvature centre, respectively. Ri, δij, δoj are the radius of locus of inner raceway curvature centre and the normal contact deformations of the j th ball at the inner and outer raceway contacts, respectively. fi, fo are inner-raceway and outer-raceway groove curvature radius coefficient, respectively.

In Fig. 19.2, αij and αoj respectively denote the inner-raceway and outer-raceway contact angles for j th ball. The sine and cosine expressions for the two angles are

$$\left\{ \begin{gathered} \sin \alpha_{oj} = \frac{{X_{1j} }}{{\left( {f_o - 0.5} \right)D + \delta_{oj} }} \, \cos \alpha_{oj} = \frac{{X_{2j} }}{{\left( {f_o - 0.5} \right)D + \delta_{oj} }} \hfill \\ \sin \alpha_{ij} = \frac{{A_{1j} - X_{1j} }}{{\left( {f_i - 0.5} \right)D + \delta_{ij} }} \, \cos \alpha_{ij} = \frac{{A_{2j} - X_{2j} }}{{\left( {f_i - 0.5} \right)D + \delta_{ij} }} \hfill \\ \end{gathered} \right.$$
(19.8)

The forces acting on the jth ball are shown in Fig. 19.3. The equilibrium equations are derived as:

$$Q_{ij} \sin \alpha_{ij} - Q_{oj} \sin \alpha_{oj} - \lambda_{ij} \frac{M_j }{D}\cos \alpha_{ij} + \lambda_{oj} \frac{M_j }{D}\cos \alpha_{oj} = 0$$
(19.9)
$$Q_{ij} \cos \alpha_{ij} - Q_{oj} \cos \alpha_{oj} + \lambda_{ij} \frac{M_j }{D}\sin \alpha_{ij} - \lambda_{oj} \frac{M_j }{D}\sin \alpha_{oj} + F_{cj} = 0$$
(19.10)
Fig. 19.3
figure 3

Forces acting on the jth ball

Full size image

where

$$M_j = J\left( {\frac{\omega_r }{{\omega_n }}} \right)_j \left( {\frac{\omega_m }{{\omega_n }}} \right)_j \omega_n^2 \sin \beta_j$$
(19.11)
$$F_{cj} = \frac{1}{2}md_m \omega_n^2 \left( {\frac{\omega_m }{{\omega_n }}} \right)_j^2$$
(19.12)

where Qij, Qoj are the contact loads at the inner and outer raceway contacts, respectively. Fcj, Mj are the centrifugal force and gyroscopic torque, respectively. \(\omega_r\), \(\omega_m\), \(\omega_n\) are the speed of ball about its own axis, orbital speed of ball, and inner ring revolution speed, respectively. βj is the pitch angles of the ball. In addition, according to outer-raceway control theory, the constant coefficients are set \(\lambda_{ij} = 0\), \(\lambda_{oj} = 2\).

On the basis of local ball analysis, the global equilibrium equations of inner ring can be written as:

$$F_a - \sum_{j = 1}^Z {\left( {Q_{ij} \sin \alpha_{ij} - \lambda_{ij} \frac{M_j }{D}\cos \alpha_{ij} } \right)} = 0$$
(19.13)
$$F_r - \sum_{j = 1}^Z {\left( {Q_{ij} \cos \alpha_{ij} - \lambda_{ij} \frac{M_j }{D}\sin \alpha_{ij} } \right)\cos \psi_j } = 0$$
(19.14)
$$M - R_i \sum_{j = 1}^Z {\left( {Q_{ij} \sin \alpha_{ij} - \lambda_{ij} \frac{M_j }{D}\cos \alpha_{ij} } \right)\cos \psi_j } = 0$$
(19.15)

Combining the equilibrium equations of ball and inner ring, the quasi-dynamic model would be established, and the newton–raphson method is applied to solve the problem.

In the traditional calculation, the calculation of static model is usually taken as the initial value of the quasi-static method, but the selection of X1j, X2j, δij, δoj has strong randomness.

In order to improve the convergence efficiency of the algorithm, the influence of random values on the convergence of the algorithm is overcome according to the geometric relation of local variables in the quasi-static model.

The local variables can be written as:

$$X_{1j} = \left[ {\left( {f_o - 0.5} \right)D + \delta_{oj} } \right]\sin \alpha_{oj}$$
(19.16)
$$X_{2j} = \left[ {\left( {f_o - 0.5} \right)D + \delta_{oj} } \right]\cos \alpha_{oj}$$
(19.17)

where αoj can be replaced by α0.

According to the Hertz contact theory, the normal contact deformations can be written as:

$$\delta _{ij(oj)} = \left( {\frac{{4.5\Gamma _{ij(oj)}^3 \Sigma \rho _{ij(oj)} }}{{\pi ^2 k_{ij(oj)}^2 E^{_{ij(oj)}^{^{\prime} 2} } \Sigma _{ij(oj)} }}} \right)^{1/3} Q_{ij(oj)}^{2/3}$$
(19.18)

where \(\Gamma\), \(\Sigma\) are the first and second kinds of elliptical intergration, \(k\) is the elliptical ratio, \(E^{\prime}\) is the equivalent Elastic modulus, \(\Sigma \rho\) is the function of principal curvature.

19.3 Results and Discussion

Based on the present model, the angular contact ball bearing B218 under different working conditions and structural parameters is investigated. The basic structure and material parameters of bearing are shown in Table 19.1.

Table 19.1 Basic structure and material parameters of B218
Full size table

19.3.1 The Effect of Working Condition on Dynamic Properties

Figure 19.4 shows the results of contact angles and contact loads under different bearing rotating speed and axial load on dynamic properties. It can be concluded that the increase of rotating speed leads to the increment of the difference for contact angles between ball and outer raceway and inner raceway. The influence of centrifugal effect gradually emerges with the increase of rotating speed, and the ball-outer raceway contact loads is always greater than the force at inner raceway. The axial load could compress the ball, and the contact load between ball and raceway increases when the axial loads increases. The calculation results in present model are also similar with those in Ref. [10] under the condition of \(F_a = 2000 \, N\). It could prove the correctness of the present model to a certain extent.

Fig. 19.4
figure 4

Effects of rotating speed and axial loads on dynamic properties of ball bearing

Full size image

Figure 19.5 investigates the effects of radial loads on contact angles and contact loads under the condition of \(F_a = 8000\;N\), \(n = 10,000\;{\text{rpm}}\). The increment of radial loads would lead to the increase of the fluctuation of internal load, so does the maximum contact force. The radial load leads to the increasing of contact load of ball, and the fluctuation of the load distribution also increase. Excessive radial loads could induce the early failure of ball bearing.

Fig. 19.5
figure 5

Effects of radial loads on dynamic properties of ball bearing

Full size image

19.3.2 The Effects of Structural Parameters on Dynamic Properties

In order to research the effects of structural parameters on dynamic properties, the working condition would be set \(F_a = 10,000\;N\), \(F_r = 0\), \(n = 10,000\;{\text{rpm}}\).

Figure 19.6 shows the influence of number of ball on contact angles and contact loads. As can be seen from picture, increasing the number of ball would increase the contact angle of inner raceway, and decrease the outer raceway contact angle. As the number of balls increases, the contact force of the rolling elements is improved to a certain extent. Meanwhile, the contact force of the single rolling element decreases, which induce the changing of contact angle. The number of ball could improve the contact load on each ball and internal load distribution to a certain extent.

Fig. 19.6
figure 6

Effects of number of ball on dynamic properties of ball bearing

Full size image

Figure 19.7 gives the contact angles and contact loads at different groove curvature radius coefficient, where it can be seen that with the increase of radius coefficient, contact angles decrease and contact loads increase. This factor acts by affecting the elliptical contact area between the ball and the raceway, and larger groove curvature radius coefficient tends to shorten the contact fatigue life of the ball bearing.

Fig. 19.7
figure 7

Effects of groove curvature radius coefficient on dynamic properties of ball bearing

Full size image

19.4 Conclusions

This paper presents an improved solution method for the quasi-static model to investigate the effects of working condition and structural parameters on dynamic properties of ball bearing. The results show that centrifugal force plays an significant role in dynamic properties. The increase of rotating speed could enhance the centrifugal effect, which increase the contact angles at ball-outer raceway, and decrease the contact angles at ball-inner raceway. Increasing the axial loads would compress the ball, which leads to the increase of contact loads. Meanwhile, the increased radial force leads to the increase of internal load fluctuation, it is the main reason of early fatigue failure of bearings. The number of ball could improve the internal load distribution, while increasing the groove curvature radius coefficient would the decrease of contact fatigue life of ball bearing.