Introductory application of a natural neighbour meshless elastic formulation to double-lap adhesive joints

Abstract

Nowadays, adhesive bonding is an essential joining technique in top-end sectors, such as aircraft, automotive, and construction industries. Due to their advantages over traditional joining methods, adhesive joints research has been under huge developments in recent years, being the development of accurate and efficient numerical techniques a leading challenge in adhesive joint design. Although the finite element method (FEM) is an established discretisation technique, meshless methods emerged as alternative discretisation methods to evaluate adhesive joints. Nonetheless, meshless techniques still require deeper research in adhesive joint simulations, where strength prediction is hindered by intricate stress states and material behaviour. This paper aims to evaluate the natural neighbours radial point interpolation method (NNRPIM) in the linear analysis of adhesive joints. The capability of the method was addressed by comparing it with analytical models, the FEM and experimental data. As the applications of meshless methods to analyse adhesive joints are scarce, this work evaluates the behaviour of double-lap joints (DLJ) considering distinct overlap lengths and adhesive materials. DLJ has a different behaviour than single-lap joints, which are more commonly analysed. Thus, this work provides a preliminary linear analysis, which could be the basis for further analyses of adhesive joints combining the NNRPIM with elastic–plastic, hyper-elastic, and large deformations formulations. Although it is remarked that elastic formulations underpredict joint strength, the NNRPIM shows similar results to the FEM, which supports the extension of the NNRPIM to more representative mathematical formulations and complex joint designs.

1 Introduction

Adhesive bonding allows the joining of similar and dissimilar materials. In addition, the stress concentrations in the joint are smaller in those bonded than in those joined by other methods like fasteners or welding; furthermore, bonded joints are often lighter than their counterparts. Because of these advantages, bonded joints have an important role in modern manufacture [1].

Different joint configurations exist, which depend on the relative alignment of the substrates. Joints bonding parallel substrates are the most studied, being the single-lap joint (SLJ) amongst these and extensively analysed because of its geometric simplicity. However, its geometry also causes eccentric loading, which results in lower joint strength (${P}_{\rm max}$). On the contrary, the double-lap joint (DLJ) has three substrates where the centre substrate is opposite to the top and bottom ones, and so, the eccentric loading is highly reduced [1], making it suitable for structural applications [2]. Moreover, the joints’ behaviour is highly sensitive to different design variables, such as adherend and adhesive properties (namely ductility), overlap length, adherend thickness, adhesive thickness, curing process of the adhesive and surface preparation [3]. The adhesive layer must be thin (0.1 mm ≤ ${t}_{a}$  ≤ 1 mm) to achieve the best ${P}_{\rm max}$ [4]. In lap joints, the overlap is also related to ${P}_{\rm max}$ [5, 6], being ${P}_{\rm max}$ almost proportional to ${L}_{O}$, but this also depends on the adhesive type [7].

Stress distributions in the adhesive layer can be obtained analytically and numerically. The former method provides a relative fast approximation of the stresses, mainly for elastic material models. Although there are analytical models suitable for elastic–plastic adhesives and substrates, their application is less straightforward. An extensive review of the most important analytical formulations has been performed by da Silva et al. [8, 9]. Analytical formulations are often chosen for performing parametric studies because the solution time is minimum. For example, Her and Chan [2] proposed an analytical formulation based on the sandwich model for the DLJ; the analytical model was validated using a numerical model, i.e. finite element method (FEM) through commercial software, a good agreement was found in the solutions. Then, it was used to perform a parametric study about the variables influencing ${P}_{\rm max}$. On the other hand, the numerical analyses permit to consider more variety of material behaviours for adhesives and substrates and therefore are more present in the literature. Regardless of the approach, analytical or numerical, stress distributions are obtained. Then, ${P}_{\rm max}$ can be determined using continuum mechanics criteria, like those described by Crocombe [10]. Unfortunately, the choice of failure criteria depends on the joint type and the materials involved, as stated by Hart-Smith [11]. In consequence, those used in the literature can only be used as a starting point.

Turning back to the numerical techniques mentioned above, the FEM has been proven as a reliable and accurate method to determine stresses and strains in adhesive joints [7, 12]. Furthermore, the capabilities of the method are increased by means of cohesive zone modeling (CZM) [7, 12], and more recently, by the eXtended finite element method (XFEM) [12]. Despite this, the FEM’s solution and accuracy rely on a structured element mesh, which on occasions can be distorted, compromising the accuracy. This problem is often addressed by highly refining the mesh around the points where high-stress gradients are expected. However, this is mostly performed manually and requires a large amount of time [13, 14]. As a consequence, meshless methods have been on development, which accuracy does not rely on a predefined element mesh; these methods are described by Chen [14]. Those meshless methods based on Radial Point Interpolators, like the radial point interpolation method (RPIM) [15] and the natural neighbour radial Point interpolation method (NNRPIM) [16] possess comparable accuracy to the FEM [17], being the NNRPIM a truly meshless method since it does not need a predefined background integration mesh. In addition, the shape functions of these RPI-based meshless methods possess the Kronecker’s delta property, which is also present in the FEM’s shape functions. Consequently, the imposition of boundary conditions is similar. In addition, the numerical routines developed for the FEM can be easily expanded to meshless methods [13].

Although meshless methods are a promising alternative to analyse adhesive joints, their application to this subject is scarce, as reviewed by Ramalho [18]. One of the first works applied to bonded joints was that of Tsai et al. [19], whose analysis proposal consisted of the combination between CZM and the symmetric smoothed particle hydrodynamics meshless method (SSPH). The double-cantilever beam (DCB) was the joint geometry, under mode I, mode II and mixed-mode, enabling the experimental/meshless comparison and validation. The meshless strength predictions, using continuum mechanics criteria, were acceptable for both mode I and prevalent mode I loadings. Mubashar and Ashcroft [20] compared the smoothed particle hydrodynamics (SPH) method against CZM, both using the Abaqus® (Dassault Systèmes, Inc.) embedded formulations. However, the SPH stresses revealed non-negligible oscillations and peel stresses overshooting the real joint behaviour, contrarily to shear stresses, which were below the expected. Nonetheless, and despite the produced noise in the load–displacement curves, the failure load was offset to around 9%, leading to reasonably good results. Ramalho et al. [21] used the radial point interpolation method (RPIM) together with the critical longitudinal strain (CLS) criterion, continuum-mechanics based, for strength prediction of SLJ with aluminium adherends and under tensile loads, via stress and strain distributions analysis. The maximum load predictions were accurate for adhesives that ranged from brittle to ductile. However, the CLS parameters were found to vary between different overlap lengths. The method was considered a good choice, and it only required an additional interface node layer to limit the influence domains of the integration points that linger near the material interfaces. The maximum error between all tested conditions was 17%, regarded as acceptable in view of using continuum mechanics criteria. From the aforementioned cases, it can be observed that meshless applications to adhesive joints had been focussed on SLJ and DCB joints. However, these studies usually focus on unique geometries and one adhesive material, while do not address geometric variations nor ductile adhesives. Furthermore, although linear-elastic analyses are often overlooked, they are a suitable tool for small strains and conservative design of joints.

As reviewed, applications of meshless methods to analyse adhesively bonded joints are scarce. Given the meshless methods’ theoretical assets to model the intricate behaviours of adhesively bonded joints, their extension to such applications is currently a research necessity. Regarding the NNRPIM, its application to adhesive joint modeling is still in the first stages of development. In this work, the NNRPIM is originally extended to DLJ adhesive joints modeling, which presents a different behaviour to SLJ, the most commonly analysed joint configuration. Therefore, a linear-elastic formulation is employed to validate the NNRPIM methodology, quantify the impact of considering linear-elastic assumptions, and investigate the suitability of continuum mechanics criteria based on linear-elastic assumptions. The suitability of the method for numerical stress analysis and joint strength prediction was discussed by comparing it with known analytical linear-elastic models, the FEM and experimental data for joints bonded with different overlap lengths and adhesive materials (ranging from brittle to ductile). A linear-elastic NNRPIM analysis of adhesively bonded DLJ is discussed, hence providing the foundation for further complex DLJ modeling combining the NNRPIM with elastic–plastic, hyper-elastic, and large deformations formulations.

2 Experimental work

2.1 Joint geometry

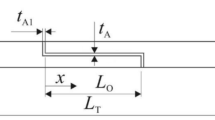
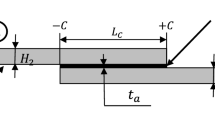
The selected bonded joint configuration is the DLJ, whose geometry and relevant parameters are presented in Fig. 1. The necessary dimensions to fully define the joint are (in mm): adherend thickness t₁ = 3, adhesive thickness t_a = 0.2, L₀ = 12.5, 25, 37.5, and 50 mm, and total joint length between grips L_T = 180 mm. Five specimens were fabricated and tested for each DLJ set, composed of adhesive/L_O combination, giving sixty specimens overall. As shown in Fig. 1, all adherends have the same t_P. This creates an unbalanced joint as using the inner adherend with twice t_P of the outer adherends produces an area-balanced joint [22].

Fig. 1

DLJ geometry, dimensions, and symmetry conditions for the numerical analysis

2.2 Materials

The adherends were cut to size from a plate of aluminium alloy, AW6082 T651, which tensile strength properties were characterised, in previous work [23], by following the specifications of the ASTM-E8M-04 standard [24]. Data analysis led to the reported properties: longitudinal elastic modulus (E) = 70.07 ± 0.83 GPa, yield strength (σ_y) = 261.67 ± 7.65 MPa, failure strength (σ_f) = 324 ± 0.16 MPa and strain at failure (ε_f) = 21.70 ± 4.24%. Bonded joints were fabricated with three adhesives, from brittle to ductile; the selected adhesives were the Araldite® AV138 (strong and brittle epoxy), Araldite® 2015 (less strong but medium ductile epoxy), and the Sikaforce® 7888 (strong and ductile polyurethane). The experimental stress–strain (σ-ε) curves of these adhesives are presented in Fig. 2.

Fig. 2

Representative σ-ε curves of the three adhesives considered

Tensile mechanical properties (E, σ_y, σ_f, and ε_f) were obtained experimentally from bulk tests. The specimen fabrication and testing were done following the standard NF T 76–142. Shear properties (shear modulus—G, shear yield stress—τ_y, shear strength—τ_f, and shear failure strain—γ_f) were obtained using Thick Adherend Shear Tests (TAST), for which fabrication and testing protocols followed the 11,003–2:1999 ISO standard, with emphasis to specimen curing in a rigid mould to ensure the proper adherends’ longitudinal alignment, and usage of DIN C45E steel adherends to minimise adherend-induced deformations affecting the obtained results. Table 1 provides the relevant data for the three adhesives and relevant yield and failure criteria parameters, which are defined in subsequent sections.

Table 1 Properties of the adhesives Araldite® AV138, Araldite® 2015, and SikaForce® 7888 [23]

2.3 Fabrication and testing

The fabrication of the joint specimens was initiated by cutting the aluminium plate to the required length and width (w = 25 mm) to produce the adherends. The adherends were then subjected to proper surface preparation by mechanical methods (grit blasting), followed by acetone degreasing, with emphasis to the blasted surfaces, preventing adhesive contamination and promoting cohesive failures in the adhesive layer, which are essential for the correct joint analysis [25]. The adhesive was poured into the bonding surfaces by different methods (either automatic gun application or manual mixing and application with a spatula). Assembly and adhesive curing were aided with a steel jig to align the adherends and provide the correct t_a. Actually, t_a value was enforced by positioning the outer adherends with calibrated metallic blocks [26]. Longitudinal stops provided the correct L₀ and L_T. Joint alignment during testing was secured by glueing tabs (25 mm × 25 mm × 3 mm) at the joint edges. The specimens were left in the jig for one week at room temperature to cure. After removal from the jig, the excess of adhesive from the specimens was removed by milling as Fig. 3a illustrates. The specimens were tested in a Shimadzu AG–X 100 testing machine (Fig. 3b shows a specimen prior to testing). The load cell was 100 kN, and the testing speed was 1 mm/min. It was assured that at least four valid tests for each joint configuration were made available.

Fig. 3

Milling the excess of adhesive (a), and a DLJ specimen fixed in the testing machine (b)

3 Methods

3.1 Failure criteria

A wide range of failure criteria is available to predict joint strength. The global yielding (GY) criteria, originally introduced by Crocombe [27], is a limit state criterion that can be derived from the Hart-Smith model [28], assuming several simplifications [29] of the original complex formulation. It is considered that the adhesive fully yields before joint failure, which allows defining the maximum load as:

$${P}_{\rm max}={\tau }_{f}\bullet {L}_{0}\bullet w,$$

(1)

being ${\tau }_{f}$ the adhesive ultimate shear strength, ${L}_{0}$ the overlap length, and $w$ the width of the DLJ. The joint strength is also limited by the adherends’ tensile strength, being the maximum load supported by the adherends given by:

$${P}_{\rm max}={\sigma }_{f}\bullet {t}_{1}\bullet w,$$

(2)

where ${\sigma }_{f}$ is the adherend failure stress and ${t}_{1}$ the adherend thickness. Therefore, joint strength is either restricted by adhesive or substrate failure.

Maximum stress or maximum strain value criteria are an intuitive yet valid approach to predict joint strength. These variables are evaluated along the adhesive’s layer mid-thickness; then, when a point along that line reaches the material’s failure value, the joint is considered to have reached its maximum strength (${P}_{\rm max}$). The review by Quispe Rodríguez [29] provides a wide range of failure criteria for adhesively bonded joints. Due to its simplicity and easy implementation within the linear-elastic formulation, in this work, the NNRPIM is combined with several continuum mechanics criteria. The maximum peel stress criterion states that failure occurs when the maximum peel stress at the adhesive layer reaches the materials’ failure stress,

$${\sigma }_{y}^{max}={\sigma }_{f.}$$

(3)

Similarly, the maximum shear stress criterion is defined as:

$${\tau }_{xy}^{max}=\frac{{\sigma }_{1}-{\sigma }_{2}}{2}={\tau }_{f,}$$

(4)

and the maximum principal stress criterion as

$${\sigma }_{1}^{max}={\sigma }_{f,}$$

(5)

being ${\sigma }_{1}$ and ${\sigma }_{2}$ the principal stresses, ${\sigma }_{f}$ the adhesive tensile strength, and ${\tau }_{f}$ the adhesive shear strength. In addition, analogous strain criteria were also evaluated, even though less discussed due to the limited applicability to linear-elastic conditions.

3.2 Volkersen’s closed-form model for DLJ

Volkersen’s analytical elastic model [30] is usually implemented in SLJ design, even though it does not account for the bending moment caused by load eccentricity in SLJ; thus, suitable to analyse DLJs. The DLJ geometry minimises the bending deformation present in SLJ. Also, considering the symmetry conditions shown in Fig. 1, the Volkersen model can be easily extended to DLJ. It is assumed that the adhesive only deforms in shear, while the adherends maintain the stress level below its elastic limit. Solving the differential equation proposed by Volkersen yields to:

$$\tau =\frac{P}{b{L}_{0}}\bullet \frac{w}{2}\bullet \frac{\mathrm{cosh}\left(wX\right)}{\mathrm{sinh}\left(\frac{w}{2}\right)}+\left(\frac{{t}_{1}-{t}_{2}}{{t}_{1}+{t}_{2}}\right)\bullet \frac{w}{2}\bullet \frac{\mathrm{sinh}\left(wX\right)}{\mathrm{cosh}\left(\frac{w}{2}\right)} ,$$

(6)

being $\tau$ the shear stress in the adhesive, $P$ the applied load, $b$ the joint width, ${L}_{0}$ the overlap length, ${t}_{1}$ the top adherend’s thickness, ${t}_{2}$ the bottom adherend’s thickness, and $X=\frac{x}{{L}_{0}}$ with $-0.5\le X\le 0.5$. The characteristic shear-lag distance, $w$, [29] is given by:

$$w=\sqrt{\frac{G{l}^{2}}{E{t}_{1}{t}_{a}}\bullet \left(1+\frac{{t}_{1}}{{t}_{2}}\right) },$$

(7)

being $G$ the adhesive shear modulus, $E$ the adherend elastic modulus, and ${t}_{a}$ the adhesive thickness. Since the Volkersen method assumes a pure shear deformation of the adhesive, a shear-based criterion must be considered.

3.3 The natural neighbour radial point interpolation method

Nowadays, the Volkersen analytical model (and other closed-form methods) provides benchmark solutions to simple adhesive lap joints. In complex practical adhesive joint applications, analytical models are rarely applicable, being generally used to validate numerical methods in simple geometry joints. Numerical methods are capable to simulate complex joints subjected to arbitrary load cases. Although several discretisation techniques are available to predict DLJ strength, this work presents the application of an accurate meshless technique, the NNRPIM, to numerically simulate DLJ. Additionally, a four-node Lagrangian FEM formulation is used for comparison.

Contrarily to the FEM, the NNRPIM does not require a predetermined connectivity or element mesh to establish and integrate the partial differential equilibrium equations. Rather, an integration mesh uniquely dependent on the nodal spatial information is constructed, resorting to the Voronoï diagram of the field nodes discretising the problem domain. First, considering a set of nodes ${\varvec{N}}=\left\{\begin{array}{cccc}{{\varvec{x}}}_{1}& {{\varvec{x}}}_{2}& \cdots & {{\varvec{x}}}_{N}\end{array}\right\}\in {\mathbb{R}}^{2}$ (Fig. 4a), the Voronoï diagram of ${\varvec{N}}$ is constructed (Fig. 4b). Afterward, a Delaunay triangulation is constructed by connecting each interest node to its natural neighbours as illustrated in Fig. 4c. This procedure allows dividing the Voronoï cell of an interest node ${{\varvec{x}}}_{I}$ in $n$ sub cells, being $n$ the number of natural neighbours of ${{\varvec{x}}}_{I}$. The constructed subcells can then be used to perform the Gauss–Legendre integration. It is reported in the literature that a single integration point per sub-cell is sufficient to numerically integrate the NNRPIM shape functions in elastostatic problems [16]. Therefore, the integration scheme shown in Fig. 4d is considered in this work. The Voronoï diagram is also used to obtain the nodal connectivity directly from the nodal discretisation, being the influence-cell (or influence-domain) of an interest point ${{\varvec{x}}}_{I}$ defined by its natural neighbours (Fig. 4b).

Fig. 4

NNRPIM integration scheme considering a regular nodal discretization

The NNRPIM uses the radial point interpolators (RPI) to locally approximate the field variables, i.e. $u$. Thus, the interpolation function $u\left({{\varvec{x}}}_{I}\right)$ is defined by the combination of a radial basis function (RBF), ${\varvec{R}}\left({{\varvec{x}}}_{I}\right)$, and a polynomial basis function (PBF), ${\varvec{P}}\left({{\varvec{x}}}_{I}\right)$:

$$u\left({{\varvec{x}}}_{I}\right)=\sum_{i=1}^{n}{R}_{i}\left({{\varvec{x}}}_{I}\right){a}_{i}\left({{\varvec{x}}}_{I}\right)+\sum_{j=1}^{m}{P}_{j}\left({{\varvec{x}}}_{I}\right){b}_{j}\left({{\varvec{x}}}_{I}\right),$$

(8)

being $n$ the number of nodes in the influence domain of ${{\varvec{x}}}_{I}$ and $m$ the number of monomials in the PBF. Although several RBF are available in literature, this work considers the multiquadrics (MQ-RBF) [31],

$${R}_{ij}={\left({d}_{ij}^{2}+{c}^{2}\right)}^{p},$$

(9)

where the Euclidean distance, ${d}_{ij}$, is the only variable in the RBF; $c$ and $p$ are shape parameters of the RBF whose choice must minimise the interpolation error, as described by Wang and Liu [32]. Hence, these parameters had to be optimised to achieve such function. For the present NNRPIM formulation, such parameters were previously determined and optimised by solving several 2D tests [16], being $c=0.0001$ and $p=0.9999$ the optimal parameters used in this work. The coefficients ${a}_{i}\left({{\varvec{x}}}_{I}\right)$ and ${b}_{j}\left({{\varvec{x}}}_{I}\right)$, in Eq. (8), are determined by establishing the following equation for each node inside the influence domain of ${{\varvec{x}}}_{I}$:

$$\left\{\begin{array}{cc}{\varvec{R}}& {\varvec{P}}\end{array}\right\}\left\{\begin{array}{c}{\varvec{a}}\\ {\varvec{b}}\end{array}\right\}={{\varvec{u}}}_{s} ,$$

(10)

being ${{\varvec{u}}}_{s}$ the vector of the corresponding nodal values. To obtain a set of $n+m$ equations with $n+m$ unknowns, an extra set of equations, ${{\varvec{P}}}^{{\varvec{T}}}{\varvec{a}}=0$, is added to the system [33], which yields:

$$ \underbrace {{\left\{ {\begin{array}{*{20}c} \user2{R} & \user2{P} \\ {\user2{P}^{\user2{T}} } & 0 \\ \end{array} } \right\}}}_{\user2{M}}\left\{ {\begin{array}{*{20}c} \user2{a} \\ \user2{b} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\user2{u}_{\user2{s}} } \\ 0 \\ \end{array} } \right\}\user2{~}. $$

(11)

Solving Eq. (11) permits to define the interpolation function as:

$${\varvec{u}}\left({{\varvec{x}}}_{I}\right)=\left\{\begin{array}{cc}{\varvec{r}}{\left({{\varvec{x}}}_{I}\right)}^{T}& {\varvec{p}}{\left({{\varvec{x}}}_{I}\right)}^{T}\end{array}\right\}{{\varvec{M}}}^{-1}\left\{\begin{array}{c}{{\varvec{u}}}_{{\varvec{s}}}\\ 0\end{array}\right\}=\left\{\begin{array}{cc}\boldsymbol{\varphi }{\left({{\varvec{x}}}_{I}\right)}^{T}&{\varvec{\psi}}{\left({{\varvec{x}}}_{I}\right)}^{T}\end{array}\right\}\left\{\begin{array}{c}{{\varvec{u}}}_{{\varvec{s}}}\\ 0\end{array}\right\}\boldsymbol{ },$$

(12)

where ${\varvec{\psi}}{\left({{\varvec{x}}}_{I}\right)}^{T}$ is a by-product of Eq. (12) that is negligible [16]; thus,$u\left({{\varvec{x}}}_{I}\right)=\boldsymbol{\varphi }\left({{\varvec{x}}}_{I}\right){{\varvec{u}}}_{{\varvec{s}}}$. In addition, the shape functions’ spatial partial derivatives can then be easily computed as detailed by Belinha [16].

The procedure to obtain the final set of discrete equations, which is established in the Galerkin weak form, is analogous to the FEM. The equilibrium equations are given by $\nabla{\varvec{\sigma}}+{\varvec{b}}=0$, with ${\varvec{\sigma}}{\varvec{n}}=\overline{{\varvec{t}} }$ on the natural boundary ${\Gamma }_{t}$, and ${\varvec{u}}=\overline{{\varvec{u}} }$ on the essential boundary ${\Gamma }_{u}$, being ${\varvec{\sigma}}$ the Cauchy stress tensor, ${\varvec{b}}$ the body force per unit volume vector, ${\varvec{n}}$ the unit outward vector normal to ${\Gamma }_{t}$, $\overline{{\varvec{t}} }$ the traction force on ${\Gamma }_{t}$, and $\overline{{\varvec{u}} }$ the prescribed displacement on ${\Gamma }_{u}$. The Galerkin weak form for the present linear-static problem is defined as:

$$\delta L=\underset{\Omega }{\overset{}{\int }}\delta {{\varvec{\varepsilon}}}^{T}{\varvec{\sigma}}d\Omega -\underset{\Omega }{\overset{}{\int }}\delta {{\varvec{u}}}^{T}{\varvec{\sigma}}{\varvec{b}}d\Omega -\underset{{\Gamma }_{\mathrm{t}}}{\overset{}{\int }}\delta {{\varvec{u}}}^{T}{\varvec{t}}d\Gamma =0 .$$

(13)

Manipulation of Eq. (13) allows to establish a system of equations in the form [16]:

$${\varvec{K}}{\varvec{u}}={{\varvec{f}}}_{{\varvec{b}}}+{{\varvec{f}}}_{{\varvec{t}}} ,$$

(14)

where the global stiffness matrix ${\varvec{K}}$ and the natural force ${{\varvec{f}}}_{{\varvec{t}}}$ vector are defined as:

$${\varvec{K}}=\underset{\Omega }{\overset{}{\int }}{{\varvec{B}}}^{T}{\varvec{c}}{\varvec{B}}d\Omega =\sum_{i=1}^{{n}_{g}}{{\varvec{B}}\left({{\varvec{x}}}_{I}\right)}^{T}{\varvec{c}}\left({{\varvec{x}}}_{{\varvec{I}}}\right){\varvec{B}}\left({{\varvec{x}}}_{I}\right)\bullet {w}_{I}\left({{\varvec{x}}}_{I}\right) ,$$

(15)

$${{\varvec{f}}}_{{\varvec{t}}}=\underset{{\Gamma }_{t}}{\overset{}{\int }}{{\varvec{H}}}^{T}\overline{{\varvec{t}}}d{\Gamma }_{t}=\sum_{i=1}^{{n}_{g}}{{\varvec{H}}\left({{\varvec{x}}}_{I}\right)}^{T}\overline{{\varvec{t}}}\bullet {w }_{I}^{t}\left({{\varvec{x}}}_{I}\right) ,$$

(16)

being ${\varvec{B}}$ the deformability matrix containing the shape functions’ partial derivatives, ${\varvec{c}}$ the material constitutive matrix for plane strain conditions, ${\varvec{H}}$ the shape function interpolation matrix, ${n}_{g}$ the total number of Gauss points, and ${w}_{I}$ the weight of integration point ${{\varvec{x}}}_{I}$. The method is fully described in Reference [16]. The NNRPIM and FEM were programmed in MATLAB (The MathWorks Inc. USA) using custom-written routines, easing comparison between methods.

3.4 Preliminary convergence analysis

A preliminary convergence analysis is first presented to evaluate the nodal density effect on the specimens force/displacement and stress at the adhesive layer. For that, nine nodal discretisations (m1 to m9) of increasing nodes, as Fig. 5 presents, were built. The nodal meshes were created using a custom-written MATLAB script. Notice that the nodal mesh is refined near the adhesive layer to capture high-stress gradients occurring in such zone, without compromising the computational cost of the analysis. At this stage, only models with ${L}_{0}=\mathrm{12,5} \mathrm{mm}$ are considered. Next, numerical analyses assuming plane strain conditions were carried out using the NNRPIM and the FEM, the two numerical methods used in this work.

Fig. 5

Nodal discretisations and interest points

In the FEM case, four-node quadrilateral elements were used, considering $2\times 2$ Gauss points per element in the numerical integration (Fig. 6b), whilst the NNRPIM uses the integration scheme described in Sect. 3.3, which results in the integration point discretisation type presented in Fig. 6c. For an equal number of nodes, the NNRPIM requires a higher integration point density than the FEM, which allows more information regarding the stress/strain fields; however, the higher number of integration points leads to a slightly higher computational cost as discussed next.

Fig. 6

Nodal discretisation for ${L}_{0}=12.5 \mathrm{mm}$ (a), FEM discretisation (b) and NNRPIM discretization (c)

A displacement was imposed at the right end adherend as Fig. 1 indicates. Hence, the applied reaction force at that boundary is evaluated and plotted in Fig. 7a for each nodal discretisation. It can be observed that, from the 4000 nodes mark, the applied force converges to a defined value for both the FEM and NNRPIM.

Fig. 7

Convergence analysis: reaction force at the right boundary (a), stresses (b) and strains (c) at the interest point

Strains and stresses were evaluated at the adhesive layer left mid-point (interest point in Fig. 5). In that region, a high-stress concentration occurs, hence strain and stress at interest points are obtained by extrapolating the strain and stress values calculated at the surrounding integration points to the interest node. In this manner, the stress singularity is smoothed, and mesh-independent solutions can be achieved as Fig. 7b, c show. Both strain and stresses at the interest point converge to well-defined values for discretisations with more than 6000 nodes.

In the present preliminary study, the NNRPIM computational time is compared with the FEM. Figure 8 shows the computational time of the FEM and NNRPIM techniques for each nodal discretisation considered (m1 to m9). The total computational cost is divided in the pre-processing phase (Fig. 8a) and linear-elastic analysis (Fig. 8b). Nodal/element meshes were created separately from the structural analysis module, and the respective cost is not included in the computational time here presented. In the FEM, integration mesh and nodal connectivity are naturally determined in the mesh generation. Regarding the NNRPIM, the pre-processing phase includes the construction of the Voronoï diagram, integration mesh, influence domains and shape functions, which compared to the FEM (Fig. 8a) requires a significant computational effort in a pre-processing phase. Nevertheless, this process is automated by the method, and so, no user intervention is necessary, while the pre-processing in the FEM is usually dependent on user inputs [13]. Concerning the structural analysis module, Fig. 8b shows that the NNRPIM and FEM require similar computational time. Meshless methods are usually costlier than the FEM due to the complex shape functions and integration schemes, which are determined in the pre-processing phase. In the linear analysis module, the computational cost is mostly dependent on mesh refinement. If first-degree influence cells are considered in the NNRPIM formulation, a reduced nodal connectivity (around 8 nodes in influence domains) is obtained, and a computational cost similar to the FEM can be achieved.

Fig. 8

Computational time for the pre-processing (a), and linear analysis (b) modules (axis in logarithmic scale)

Taking into account the preliminary results presented, the following numerical analyses are performed considering the nodal discretisation m6 (see Fig. 5). Four distinct ${L}_{0}$ are studied in this work. Thus, a discretised model was built for each DLJ model. The m6 nodal mesh was built with ${L}_{0}=\mathrm{12,5} \mathrm{mm}$. For higher ${L}_{0}$, the m6 nodal density is maintained by increasing the number of nodes in the adhesive layer. Hence, it is expected that the joint with ${L}_{0}=50 \mathrm{mm}$ is discretised with more field nodes than the model with ${L}_{0}=12.5 \mathrm{mm}$. Models with ${L}_{0}=12.5$, ${L}_{0}=25.0$, ${L}_{0}=37.5$, and ${L}_{0}=50.0 \mathrm{mm}$ were discretised with 6058, 9322, 12,586, and 15,850 nodes, respectively.

4 Results

4.1 Experimental evaluation

The experimental results are discussed in this section. Regarding the brittle AV138 adhesive, most joints resulted in pure cohesive failure, nonetheless, in some experiments failure occurred near the adhesive interface. Figure 9a shows the cohesive failure near the interface of an AV138 bonded joint with ${L}_{0}=12.5 \mathrm{mm}$. In DLJ bonded with the 2015, no failures occurred near the interface. All specimens with ${L}_{0}=12.5 \mathrm{mm}$ resulted in a cohesive failure. For ${L}_{0}=25$ and ${L}_{0}=37.5 \mathrm{mm}$, some specimens showed cohesive failure, while others failed at the substrate. Due to the high ductility of the 2015 adhesive, all DLJ with ${L}_{0}=50 \mathrm{mm}$ failed at the substrate. For the 7888, similar results to those of the 2015 were obtained, except that for ${L}_{0}=50 \mathrm{mm}$, cohesive failure occurred in some specimens. Figure 9b, c show a cohesive failure of a 2015 and 7888 DLJ, respectively.

Fig. 9

Failure modes: AV138 cohesive failure near the interface for ${L}_{0}=12.5 \mathrm{mm}$ (a), 2015 cohesive failure (b), and 7888 cohesive failure for ${L}_{0}=50 \mathrm{mm}$ (c)

In AV138 DLJ, no plastic deformation developed prior to failure, as Fig. 10a shows. For overlaps up to ${L}_{0}=50 \mathrm{mm}$, the same linear behaviour was verified. In 2015 and 7888 adhesive joints, a linear-elastic behaviour up to failure occurred for the specimens with ${L}_{0}=12.5 \mathrm{mm}$ (Fig. 10a). For DLJ with ${L}_{0}>12.5 \mathrm{mm}$, clear plastic deformation occurred in the specimens bonded with the 2015 and 7888. Figure 10a shows the obtained $P-\delta$ curve for a DLJ with ${L}_{0}=50 \mathrm{mm}$ bonded with the 2015. It is noticeable that the high ductility of the 2015 allows the adherends to undergo plastic deformation, which led such DLJ to fail by the adherend.

Fig. 10

Experimental data: $P-\delta$ curves for of a representative specimen bonded considering different adhesives and overlap lengths (a) and maximum load for the three adhesives considered (b)

Figure 10b shows the maximum experimental loads obtained for each DLJ configuration combining the adhesives used and ${L}_{0}$. Although the AV138 has the highest ultimate strength, its brittle behaviour causes the respective DLJ to have low maximum loads compared with the 2015 and 7888 ductile adhesives. The 7888 combines high strength and ductility. Hence, it is expected that joints using this adhesive support higher loads compared to the remaining adhesives (Fig. 10b). It is also noticeable that the failure load does not increase linearly with the ${L}_{0}$ but converges to a defined failure load.

4.2 Numerical stress distribution

The FEM and NNRPIM stress field solutions are now presented. First, the stress distribution at the adhesive mid-thickness is evaluated. Stress values are obtained at the integration points and then extrapolated to the field nodes. This procedure permits to smooth the strain and stress fields and define mesh-independent stress values in the mid-adhesive layer (see Sect. 3.4). Additionally, by considering stresses at the mid-adhesive layer to evaluate adhesively bonded joints, which is a standard procedure in the literature, the known singularity problem leading to mesh dependent stress values at the interface corners is circumvented. Nevertheless, a mesh sensitivity analysis is still recommended to obtain the most efficient nodal distribution for the analysed case. Figure 11 shows the obtained numerical peel stress distribution, normalised to the average shear stress, ${\sigma }_{y}/{\tau }_{xy}^{avg}$, at the mid-adhesive plane for each adhesive studied. The ${\tau }_{xy}^{avg}$ at the adhesive layer mid-line was calculated by averaging the shear stress values of the nodes in the mid-line [34]. Similarly, the normalised shear stress distribution, ${\tau }_{xy}/{\tau }_{xy}^{avg}$, using the NNRPIM and the FEM is presented in Fig. 12. First, it can be noticed that contrarily to SLJ, the stress distribution in the considered DLJ is more complex and not symmetric within the overlap region. Thus, maximum stress values are obtained at one of the adhesive layer edges. As ${L}_{0}$ is increased, the adhesive becomes less stressed (in both peel and shear) at the centre region ($x/{L}_{0}=0.5$) of the adhesive. This conclusion is in accordance with the extensively reported fact that joint strength is not increased linearly with the overlap length [35]. Comparing the three adhesives studied, the brittle AV138 adhesive presents the higher stresses at $x=0$, since it has the highest stiffness of all studied adhesives (Table 1). The 2015 and 7888 have similar elastic properties, and thus present similar stress peaks and distributions along the mid-adhesive thickness. Although small oscillations between the NNRPIM and the FEM are observed at the adhesive boundaries (more significant for ${L}_{0}=12.5 \mathrm{mm}$), Figs. 11 and 12 demonstrate that the NNRPIM and FEM provide analogous solutions in all linear-elastic analyses.

Fig. 11

Peel stress distribution: AV138 (a), 2015 (b) and 7888 (c)

Fig. 12

Shear stress distribution: AV138 (a), 2015 (b) and 7888 (c)

Figure 13 compares the FEM and NNRPIM normalised stress field solutions within the full adhesive layer, rather than just assessing mid-thickness values. Due to the similar stress distributions between the adhesives considered, only the contour plots for the 2015 are presented. Each contour plot in Fig. 13 represents the full adhesive layer not to scale. Regarding the peel stress distribution, the NNRPIM and FEM solutions are closely related for every ${L}_{0}$ considered. The influence of ${L}_{0}$ on the peel stress distribution is visible in the respective contour plots. For higher ${L}_{0}$, the peak stresses region (left) becomes narrower, and the centre region of the adhesive becomes less stressed. The same remarks can be extended to the shear stress distribution; although the NNRPIM and FEM calculate analogous peak shear stress values, shear stress distributions present some variations. Considering the shear stress distributions in Fig. 13, the NNRPIM provides a distinct distribution than the FEM, with curved stress isolines within the adhesive layer. This is justified by the higher integration point density in the NNRPIM, which permits to capture stress variations that the FEM discretisation may not be sensible to.

Fig. 13

Peel and shear stress distribution in the adhesive layer (not to scale)

4.3 Strength prediction

Regarding the GY criteria and the Volkersen analytical model, predicted DLJ failure load can be directly obtained by substituting the adhesive shear ultimate stress ${\tau }_{f}$ in the governing equations. In the FEM and NNRPIM methodology, a stress field not necessarily equivalent to the DLJ failure state is obtained. Considering the obtained numerical stress field, a resultant reaction force is obtained (Fig. 1). Then, to obtain the DLJ strength prediction using the NNRPIM or FEM, the maximum stress obtained numerically is extrapolated to the adhesive failure stress. The maximum stress is evaluated at the mid adhesive layer rather than the full domain, as in the analytical solutions, to smooth the singularity and mesh dependent values at the interface corners. Hence, for the maximum shear stress criterion, DLJ failure load is calculated as:

$${P}_{\rm max}=\frac{{\tau }_{xy}^{max}}{{\tau }_{xy}^{nnrpim}}\bullet R{F}^{nnrpim} ,$$

(17)

being ${\tau }_{xy}^{max}$ the adhesive shear strength, ${\tau }_{xy}^{nnrpim}$ the maximum stress at the adhesive layer obtained using the NNRPIM, and $R{F}^{nnrpim}$ the corresponding reaction force applied in the DLJ. It must be noted that, since DLJ symmetry conditions are considered, the reaction force obtained using the numerical model is doubled to compare the numerical results with the experimental data. The same methodology is easily extended to the failure criteria considered in this work and presented in Sect. 3.1.

It is reported in adhesive joints’ literature that linear elastic formulations underpredict experimental joint strength due to the plastic behaviour of the adhesive joint prior to failure [23, 36]. Nonetheless, numerical elastostatic analyses provide the basic methodology to more complex strength prediction models considering elastoplastic or hyper-elastic formulations. The strength prediction results considering stress-based criteria are shown in Fig. 14. The GY criterion is the technique that best approximates the experimental DLJ performance. Regarding the AV138 adhesive (Fig. 14a), the GY criterion overpredicts joint strength. Actually, the GY criterion considers a fully plasticised adhesive at failure. Due to the brittleness of the AV138, experimental failure occurs without plasticisation, which causes the GY criterion to overpredict joint strength. Therefore, the GY criterion is more suitable for high-ductility adhesive joints, in which substrate failure may even occur prior to adhesive failure. Considering the ductile 2015 and 7888 (Fig. 14b-c), the GY closely predicts joint strength. The GY criterion efficiently predicts the strength of simple geometry joints such as SLJ or DLJ. However, it is not applicable to complex practical applications.

Fig. 14

Joint strength prediction: AV138 (a), 2015 (b) and 7888 (c)

Regarding the linear models used in this work, Fig. 14 shows that such formulations underpredict the experimental joint strength. The best approximation occurs in the case of the AV138 adhesive (Fig. 14a), in which the use of elastic models may be less impactful due to the adhesive brittleness. In this analysis, the Volkersen analytical model, and the NNRPIM and FEM methods provide similar DLJ failure loads for every ${L}_{0}$. If ductile adhesives are considered, linear elastic formulations significantly underpredict joint strength, which justifies the implementation of more complex formulations, such as elastoplastic, hyper-elastic, or large deformations to closely predict experimental DLJ failure loads. It can be concluded from Fig. 14 that NNRPIM solutions are in accordance with the vastly experimented FEM, which allows to confidently extend the NNRPIM meshless technique and its inherent advantages over the FEM to more demanding adhesive joint formulations.

Joint strengths determined through strain-based failure criteria are also presented due to their ease of implementation. The literature suggests that strain-based criteria are suitable to predict the strength of adhesive joint bonded with ductile adhesives such as the 2015 and 7888. However, the results presented in this work permit to conclude that stress-based criteria are more adequate when considering linear-elastic material behaviour, even though the numerical analysis significantly underpredict joint strength.

The full numerical analysis work results can be consulted in Table 2. For every adhesive material and overlap length, the predicted maximum load using the NNRPIM and FEM combined with stress- and strain-based criteria is presented. From Table 2, several remarks can be withdrawn. Regarding stress-based criteria, the lowest percentual errors occur when the brittle AV138 adhesive is considered. For this adhesive, the linear-elastic model is better suited for the smallest ${L}_{0}$, where the present NNRPIM formulation underpredicts the experimental load by 18%. For the ductile 2015 and 7888 adhesives, the lowest errors still occur for the smallest ${L}_{0}$, although errors of approximately 30% are observed. Strain criteria results are also presented in Table 2. The magnitude of ${\varepsilon }_{f}$ for the 7888 completely hinders the application of strain criteria under elastic material behaviour, being the predictions in such analyses indisputable. For the AV138, the lowest errors occur when the maximum principal criterion is used (${\varepsilon }_{1}^{max}$), allowing to underpredict experimental strength by approximately 10% for ${L}_{0}=\mathrm{12,5} \mathrm{mm}$ and by approximately 30% for ${L}_{0}>\mathrm{12,5} \mathrm{mm}$. A noticeable remark in Table 2 is that the same ${\varepsilon }_{1}^{max}$ criterion closely predicts the strength of 2015 bonded joints with ${L}_{0}>\mathrm{12,5} \mathrm{mm}$.

Table 2 Numerical maximum loads and errors relative to experimental data

Figure 15 shows the numerical linear-elastic curves along with the experimental data from Fig. 10a. For interpretation purposes, only results considering DLJ with ${L}_{0}=\mathrm{12,5} \mathrm{mm}$ and ${L}_{0}=50 \mathrm{mm}$ and bonded with the AV138 and 2015 adhesive are presented. In the left close-up, one can see that the DLJ with ${L}_{0}=50 \mathrm{mm}$ are stiffer than the DLJ with ${L}_{0}=12.5 \mathrm{mm}$. But, as noticeable in the main centre plot, the change in stiffness is negligible, and ${L}_{0}$ mostly influences the joint strength. Comparing the numerical curves with experimental data, it can be observed that the linear-elastic analyses approximate reasonably well the experimental curves for small displacements ($\delta <\mathrm{0,5} \mathrm{mm}$). However, over this $\delta$ the adhesive joint exhibits highly nonlinear material behaviour, and the linear-elastic approximation is inaccurate. The discrepancy in stiffness (curves’ slope) between the experimental and numerical curves may occur due to the boundary conditions imposed in the numerical model (Fig. 5) that cannot be fully replicated in practical experiments. Furthermore, experimental testing is affected by external factors (e.g. grip slippage) as described by Chowdhury et al. [37], thus resulting in experimental curves softer than the rigid numerical analyses ones.

Fig. 15

Experimental and numerical force displacement curves for the AV138 and 2015 adhesive joints

In this work, the NNRPIM and the FEM are used in parallel for comparison and validation purposes. It was found in Sect. 4.2 that similar stress distributions at the mid adhesive layer were obtained for both numerical methods. Such similar stress distribution further leads to the close strength prediction between the NNRPIM and FEM for each joint geometry and adhesive material, as shown in Fig. 14 and Table 2. It can be concluded that the numerical underpredictions are related to the employed failure criteria, which are derived from the solid mechanics linear-elastic formulation. The combination of the NNRPIM with more complex material modeling and failure criteria is then required to predict the experimental strength of DLJ adhesive joints. The present application validates the NNRPIM against the FEM for a converged regular discretisation, which is suitable for both the FEM and NNRPIM modeling. However, the NNRPIM assets permit higher flexibility in the domain discretisation, i.e. discretisation refinement can be easily optimised without the concern of regular or well-conditioned (undistorted) elements. This is the main advantage of the NNRPIM, since its unique dependency on an arbitrary nodal discretisation permits to establish the discrete system of equations without the need for a predefined (nodal independent) integration mesh. Moreover, the flexibility of the natural neighbours concept to establish the influence domain of each integration point permits straightforward modeling of the material discontinuity at the adherend/adhesive interfaces. Such assets can then be explored to predict the intricate stress distribution in complex adhesively bonded joints. Considering that meshless methods and the NNRPIM in particular possess high convergence rates [16], as discussed in Sect. 4.2, the accurate and smooth stress fields can be obtained for arbitrary nodal distributions and less dense discretisations than FEM models [16]. The extension of the NNRPIM to more complex adhesive joint applications is then fundamental.

5 Conclusions

This work presents an experimental and numerical assessment of adhesively bonded DLJ using the AV138, 2015, and 7888 adhesives. To numerically evaluate the DLJ stress distribution, joint strength and force–displacement approximation, a truly meshless technique was applied, the NNRPIM. Despite the inherent advantages of the NNRPIM to model material discontinuities, its application to adhesively bonded joints is still under development. Although the NNRPIM was previously used to analyse SLJ, this work presents an original extension of the NNRPIM to DLJ, which presents a less studied geometry than SLJ. Thus, an introductory linear-static evaluation was carried out to present the NNRPIM and compare it to the FEM.

It was found that the NNRPIM and FEM provide analogous results in the linear-elastic analysis of DLJ, which validates the presented NNRPIM and supports its extension to more demanding formulations. Regarding the experimental joint strength, the GY criterion closely predicted the strength of DLJ bonded with ductile adhesives. Differently, the presented linear NNRPIM and FEM formulations underpredicted the DLJ strength. Therefore, plasticity, large deformations or crack propagation algorithms must be considered to efficiently simulate the experimental behaviour. Within the present NNRPIM linear-elastic formulation, it was found that stress-based criteria are more adequate than strain-based criteria, being the closest predictions obtained for the DLJ bonded with the brittle AV138 considering the maximum peel stress criterion. If complex material modeling is considered, strain criteria may be appropriate, especially for ductile adhesives.

Comparing NNRPIM to FEM, it was found in a preliminary convergence analysis that the NNRPIM presents a much higher computational cost. However, such cost is mainly due to the pre-processing phase. During the processing phase, both formulations present similar computational costs. Much of this cost is a consequence of the natural neighbour procedure and also of the higher number of integration points. However, with more integration points, it is possible to attain more information regarding the stress/strain fields. Moreover, the literature [16] shows that the NNRPIM converges faster than the FEM. Thus, NNRPIM requires a less dense discretisation than FEM. Thus, taking into account all these factors, for nonlinear analyses (such as elastoplastic or hyper-elastic analyses), in which the processing phase represents the bulk of the computational time, using the NNRPIM instead of the FEM will be an asset.