1 Introduction

The use of the piezoelectric materials, as well as FG-CNT structures in various fields in energy storage, molecular electronics, thermal materials, electrical conductivity, air and water filtration, conductive adhesive, and biomedical, is expanding. The piezoelectric material is a special type of dielectric material which simultaneously comprises two branches of elasticity and electricity.

Due to the complexity of the dynamic behavior of the piezoelectric materials as well as FG-CNT when the structures are subjected to low-velocity impact, there is an interest to study these materials. Various scientific articles have been investigated in the field of low-velocity impact. Cestino et al. [1] studied buckling behavior and stress analysis of a circular plate after low-velocity impact, experimentally, and numerically. In this investigation, the tensile load, impact energy, and residual stress were calculated. There was a good agreement between the results. Bikakis [2] studied dynamic response analysis of Glare plates subjected to low-velocity impact, theoretically. In this research, the results to determine the contact force were compared to those obtained by experimental tests. Yellur et al. [3] studied the thermoplastic analysis of a rectangular sandwich plate with honeycomb core subjected to low-velocity impact, experimentally. In this study, the contact fore, energy observation, and stress distribution were calculated in terms of time. Saleh et al. [4] studied a three-dimensional study of the low-velocity impact on a rectangular plate. In this study, the contact force was calculated as a function of the plate’s deformation. Kareem and Majeed [5] studied the transient dynamic analysis of a spherical shell subjected to the low-velocity impact, experimentally, and numerically. The equations of motion were obtained by using HSDT and Hamilton's principle. The results of the numerical solution to calculate the contact force and deflection were compared to those obtained by experimental tests. Gao et al. [6] studied the low-velocity impact on a sandwich plate with a honeycomb core. In this paper, the effect of honeycomb shape on energy observation was calculated, theoretically. Mohmmed et al. [7] studied the stress analysis of a rectangular sandwich plate with a foam core subjected to the low-velocity impact, experimentally, and numerically. In this investigation, the maximum contact force and stress distribution of the plate were calculated. Mao et al. [8] studied the nonlinear dynamic response of the FG spherical shell subjected to low-velocity impact. In this research, the equations of motion were derived by using Giannakopoulos's 2D contact model, first-order shear deformation theory (FSDT), and Hamilton's principle. Lei and Tong [9] studied stress analysis of a simply supported FG-CNT cylindrical shell subjected to the low-velocity impact, theoretically. In this research, the classic shell theory was used and the impact load was considered as the Fourier series. In addition, the effects of temperature, length, and thickness of the shell on the impact force and deflection of the shell were calculated.

Khodadadi et al. [10] studied the failure analysis of an aluminum-rubber sandwich plate subjected to the impact of a hemispherical impactor. In this paper, the numerical results obtained by LS-DYNA were compared to those obtained by experimental tests. Sy et al. [11] studied the low-velocity impact behavior of a flax-epoxy laminate plate, experimentally. The results of experimental tests to determine contact forces were compared with those obtained by LS-DYNA. Erklig and Dogan [12] studied stress analysis of a rectangular hybrid nano-composite plate subjected to the low-velocity impact, experimentally. In this investigation, the effects of the ply-angle orientation, and thickness of the plate as well as the energy of the impact on the stress components, impact force, and deflection of the plate were calculated. Yao et al. [13] studied the failure analysis of a circular composite plate subjected to low-velocity impact. In this study, by using Abaqus software and experimental tests, the impact force and energy observation were calculated. Guo et al. [14] studied dynamic analysis of a bolted joint in a rectangular composite plate subjected to low-velocity impact. In this investigation, Abaqus software was used and the effect of impact location on the stress distribution was calculated. Meo et al. [15] studied the dynamic response of the rectangular sandwich plate with honeycomb core subjected to the low-velocity impact experimentally. In this investigation, the contact force was calculated in terms of the energy observation. Sun et al. [16] studied the dynamic response of a circular sandwich plate subjected to low-velocity impact, experimentally. In this paper, the contact force and energy observation were calculated in terms of the plate's displacement. Gunes and Sahin [17] studied the effect of surface crack on the dynamic response of a rectangular hybrid laminated composite plate subjected to the low-velocity impact, experimentally. In this study, the effects of the geometry of the plate and the energy of the impact on the impact force and deflection of the plate were studied.

He et al. [18] studied failure analysis of a clamped circular sandwich plate with X-frame core subjected to low-velocity impact. In this research, by using Abaqus software as well as experimental tests, the contact force, and energy observation in terms of time were calculated. Dai et al. [19] studied dynamic analysis of a rectangular sandwich plate with honeycomb core subjected to low-velocity impact, experimentally. In this research, the effect of impact energy on the contact force, impact duration, and deformation of the plate was investigated. Yuan et al. [20] studied dynamic analysis of a carbon fiber composite plate subjected to low-velocity impact, experimentally. In this research, the effect of the ply-angle laminate on the contact force was calculated. He et al. [21] studied the low-velocity impact of a rectangular sandwich plate with a honeycomb core, numerically, and experimentally. In this investigation, the effects of the thickness of honeycomb as well as the impact velocity were studied to determine the contact force and the energy observation in terms of time. Sohel et al. [22] studied dynamic analysis of a column subjected to impact loads. In this investigation, the numerical solution based on a finite element analysis was done and the results were compared to those obtained by experimental tests. Moreover, deflection of the column was calculated in terms of time and initial velocity. Sadeghpour et al. [23] studied the stress analysis of a curved sandwich beam with a foam core subjected to the low-velocity impact, theoretically. In this study, the maximum deflection of the beam, the variation of projective velocity, and the contact force were calculated in terms of time. Fan et al. [24] studied the dynamic analysis of a laminated beam with FG-CNT layers rested on the viscoelastic foundation subjected to low-velocity impact. In this investigation, the maximum contact force as well as the maximum deflection of beam were compared to those obtained by the previous study. Xu et al. [25] studied experimental and numerical investigations on a rectangular composite plate with shape memory alloy layers subjected to low-velocity impact. In this research, experimental tests and finite element method were used to determine the contact force. Nasrin and Ibrahim [26] studied the dynamic analysis of a beam with an initial crack subjected to low-velocity impact, numerically, and experimentally. In this investigation, the beam deflection as well as the failure analysis of the beam were calculated. Manohar et al. [27] carried out some experimental tests to study the dynamic analysis of a composite plate. In this study, the drop test was carried out and the collision energy and deflection of the plate were calculated.

Various studies have been carried out in the field of LT. In most studies, it has been assumed that the out-of-plate or out-of-shell displacement is an independent function of the vertical component of the coordinate system defined along with thickness of the plate or shell. Hosseini and Kolahchi [28] used LT along with third-order shear deformation theory (TSDT) to study the dynamic analysis of a cylindrical FG-CNT shell subjected to the earthquake load. Cong et al. [29] studied LT along with TSDT to determine the nonlinear dynamic response of a curved sandwich shell subjected to blast pressure. Raissi [30, 31] studied LT along with HSDT to determine the stress distribution in the cylindrical and spherical sandwich shells with piezoelectric face sheets and FG-CNT core subjected to blast pressure. Romera et al. [32] studied LT along with FSDT to determine the stress distribution in a rectangular composite plate subjected to a tensile load. Malikan and Nguyen [33] studied buckling analysis of a rectangular piezo-magneto-electric nano-plate subjected to a hygro-thermal environment and external voltage. In this investigation, LT along with FSDT was used. Van et al. [34] studied LT along with FSDT to determine the stress distribution in a three-layer sandwich plate rested on the viscoelastic foundation subjected to a moving mass.

The main topic that will be examined in the present study is the effect of the low-velocity impact on the stress components in a sector of the spherical sandwich shell. The spherical sandwich shell is made in such a way that there are two piezoelectric layers in the face sheets, and it also has an FG-CNT core. Layerwise theory, Hamilton’s principle, the classical non-adhesive elastic contact theory, and Hunter's relationship are used to determine the equations of motion. Raissi [30, 31] studied the stress distribution in a sector of the spherical and cylindrical sandwich shells with piezoelectric face sheets and FG-CNT core subjected to blast pressure. The difference between the current paper with those carried out in Refs. [30, 31] is that in the current investigation, the issue of the low-velocity impact will be studied but in Refs. [30, 31], the blast phenomena in the sector of the spherical and cylindrical sandwich shells with piezoelectric face sheets and FG-CNT core had been investigated. In addition, Raissi et al. [35] studied LT along with FSDT to study the stress distribution in a five-layer sandwich plate subjected to static pressure. It can be seen that the present study is completely different from the paper mentioned in Ref. [35]. Neves et al. [36, 37] used LT along with sinusoidal and hyperbolic sinusoidal shear deformation theories to calculate the free vibration analysis of the FG plate. In these investigations, the transverse displacement was considered as a quadratic in the thickness direction.

It is noteworthy that the innovation of the present study is in three issues. Definition of the problem of the effect of the low-velocity impact on a sector of the sandwich spherical shell with two piezoelectric face sheets and one FG-CNT core is the first innovation. In addition, the physical model of the impact of the spherical ball with the spherical sandwich shell is approximated as a mathematical model based on the classical non-adhesive elastic contact theory and Hunter's relationship. So far, there has been no research in this regard.

According to the mention references, there is a variety of LT along with higher-order shear deformation theory on the subject of impact, but few papers [36, 37] have examined the vertical displacement of the shell as a quadratic function along the thickness direction. The reason for this is the enormous intensity of the volume of the equations and how to solve them. In addition, the complex behavior of FG-CNT as well as the extraordinary piezoelectric behavior will further complicate the problem. The use of layerwise theory along with higher-order shear deformation theory in the problem of low-velocity impact is the second innovation. Furthermore, it is assumed that the out-of-shell displacement in the face sheets and core of the sandwich shell is assumed to be a second-order polynomial function of the thickness of the layers. This means that the normal strain changes in the form of a linear function along with the thickness of the layer.

Finally, the third innovation that consists of two prior innovations, the simultaneous solving of the dynamic equations will be defined as a function in terms of time. It is noteworthy that according to the classical non-adhesive elastic contact theory, the normal contact pressure distribution is defined as a relationship in terms of time, as well as a function of distance from the center of the contact location. Therefore, the normal contact pressure is defined as the combination of a sinusoidal function in terms of time as well as a radical function in terms of distance from the center of the contact location. Hamilton's principle and Maxwell's static equation are used to obtain the equations of motion.

Therefore, the present investigation tries to present a new theoretical solution based on layerwise theory along with higher-order shear deformation theory and Hamilton’s principle to study the dynamic behavior of the three-layer spherical sandwich sector with piezoelectric face sheets and FG-CNT core subjected to the low-velocity impact.

2 The geometry and material properties of the sandwich shell

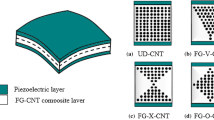
Figure 1 shows a simply supported spherical sandwich shell with two piezoelectric face sheets and one FG-CNT core. The sandwich shell is subjected to the low-velocity impact of the spherical ball that hits on its top face sheet. It is assumed that no separation will have occurred between the layers.

Fig. 1
figure 1

The simply supported sector of the spherical sandwich shell with FG-CNT core and piezoelectric face sheets subjected to low-velocity impact

Full size image

The variation in modulus of elasticity, Poisson’s ratio, and density of the FG-CNT core along its thickness are defined by Eqs. (A1)–(A11) presented in “Appendix A”. The stress analysis is performed for the five FG-CNT samples as FG-UV, FG-▽, FG-△, FG-O, and FG-X. Moreover, Fig. 2 shows the shape of the five samples of FG-CNT defined in the current study for the core of the sandwich sector. As mentioned in Eqs. (A1)–(A11), the direction of the functionally graded nano-carbon layers is defined so that they are located in the circular direction of the spherical shell (ξ1 direction).

Fig. 2
figure 2

The shape of the FG-CNT samples in the matrix

Full size image

3 Derivation of governing equations

Based on HSDT, the displacement components in the thickness direction for each layer change according to the higher-order shear deformation theory. The displacement components in the sandwich plate are given in Eqs. (B1)–(B9) presented in “Appendix B”.

For a simply supported spherical sandwich shell, the displacement components and curvatures (u0, v0, w0, \(\psi _{i}^{{\left( k \right)}}\), \(\alpha _{i}^{{\left( k \right)}}\), \(\beta _{j}^{{\left( k \right)}}\) and \(\lambda _{j}^{{\left( k \right)}}\) (i = 1, 2, 3; j = 1, 2 and k = 1, 2, 3)) can be introduced by Eqs. (C1)–(C13) presented in “Appendix C.”

Based on linear elasticity, the strain components in the kth layer can be written in terms of displacements, as shown in Eq. (1). According to Fig. 1, r(k) defined in Eq. (1) represents the radius of the middle layer of the bottom face sheet, the core, and the top face sheet for values of k from one to three, respectively. Substituting for displacement components from Eqs. (B1)–(B9) presented in “Appendix B,” the strain vector in each layer can be written in terms of u0, v0, w0, \(\psi _{i}^{{\left( k \right)}}\), \(\alpha _{i}^{{\left( k \right)}}\), \(\beta _{j}^{{\left( k \right)}}\), and \(\lambda _{j}^{{\left( k \right)}}\) (i = 1, 2, 3; j = 1, 2 and k = 1, 2, 3).

$$ \left\{ \begin{array}{l} \varepsilon _{1}^{{\left( k \right)}} = \frac{1}{{r^{{(k)}} \sin \xi _{2}^{{\left( k \right)}} }}\frac{{\partial u_{1}^{{\left( k \right)}} }}{{\partial \xi _{1}^{{\left( k \right)}} }} + \frac{1}{{r^{{(k)}} }}u_{3}^{{\left( k \right)}} + \frac{1}{{r^{{(k)}} }}u_{2}^{{\left( k \right)}} \cot \xi _{2}^{{\left( k \right)}} ;\, \hfill \\ \varepsilon _{2}^{{\left( k \right)}} = \frac{1}{{r^{{(k)}} }}\frac{{\partial u_{2}^{{\left( k \right)}} }}{{\partial \xi _{2}^{{\left( k \right)}} }} + \frac{1}{{r^{{(k)}} }}u_{3}^{{\left( k \right)}} ; \hfill \\ \varepsilon _{3}^{{\left( k \right)}} = \frac{{\partial u_{3}^{{\left( k \right)}} }}{{\partial \xi ^{{(k)}} }}; \hfill \\ \gamma _{{23}}^{{\left( k \right)}} = \frac{{\partial u_{2}^{{\left( k \right)}} }}{{\partial \xi ^{{(k)}} }} + \frac{1}{{r^{{(k)}} }}\frac{{\partial u_{3}^{{\left( k \right)}} }}{{\partial \xi _{2}^{{\left( k \right)}} }} - \frac{1}{{r^{{(k)}} }}u_{2}^{{\left( k \right)}} ;\, \hfill \\ \gamma _{{13}}^{{\left( k \right)}} = \frac{1}{{r^{{(k)}} \sin \xi _{2}^{{\left( k \right)}} }}\frac{{\partial u_{3}^{{\left( k \right)}} }}{{\partial \xi _{1}^{{\left( k \right)}} }} + \frac{{\partial u_{1}^{{\left( k \right)}} }}{{\partial \xi ^{{(k)}} }} - \frac{1}{{r^{{(k)}} }}u_{1}^{{\left( k \right)}} ;\, \hfill \\ \gamma _{{12}}^{{\left( k \right)}} = \frac{1}{{r^{{(k)}} \sin \xi _{2}^{{\left( k \right)}} }}\frac{{\partial u_{2}^{{\left( k \right)}} }}{{\partial \xi _{1}^{{\left( k \right)}} }} + \frac{1}{{r^{{(k)}} }}\frac{{\partial u_{1}^{{\left( k \right)}} }}{{\partial \xi _{2}^{{\left( k \right)}} }} - \frac{1}{{r^{{(k)}} }}u_{1}^{{\left( k \right)}} \cot \xi _{2}^{{\left( k \right)}} ; \hfill \\ \end{array} \right. $$
(1)

Based on Hooke’s principle, the stress–strain relation in FG-CNT core and piezoelectric face sheets can be written as Eqs. (D1) and (D2) (k = 1 and 3) presented in “Appendix D,” respectively. Moreover, the electric displacement relations for piezoelectric face sheets can be written as Eq. (D3). In this study, the electric potential (Φ(k)) for the first and third layers of the sandwich shell is assumed as Eq. (2). The reason for choosing this value of the electric potential is that the voltage in the middle layer of the piezoelectric face sheets (\(\xi ^{{\left( 1 \right)}} = 0\) or \(\xi ^{{\left( 3 \right)}} = 0\)) is not considered zero and at the same time it is considered zero in the innermost and outermost layers (\(\xi ^{{\left( i \right)}} = - h_{i} /2\) or \(\xi ^{{\left( i \right)}} = h_{i} /2\), i = 1 or 3). In addition, it is essential to choose the electrical potential that satisfied the Maxwell equation. Moreover, this value of the electric potential distribution was used for the electrical potential in Refs. [30, 31]. Furthermore, a similar distribution of the electric potential was presented in Refs. [38, 39].

$$ \Phi ^{{\left( k \right)}} \left( {\xi _{1} ,\xi _{2} ,\xi ^{{\left( k \right)}} ,t} \right) = \left\{ {\begin{array}{ll} {\varphi ^{{\left( 3 \right)}} \left( {\xi _{1} ,\xi _{2} ,t} \right)\cos \left( {\frac{{\pi \xi ^{{\left( 3 \right)}} }}{{h_{3} }}} \right)} & {{\text{Top}}\,{\text{piezoelectric}}\,{\text{layer}}} \\ {\varphi ^{{\left( 1 \right)}} \left( {\xi _{1} ,\xi _{2} ,t} \right)\cos \left( {\frac{{\pi \xi ^{{\left( 1 \right)}} }}{{h_{1} }}} \right)} & {{\text{Bottom}}\,{\text{piezoelectric}}\,{\text{layer}}} \\ \end{array} ;\,\,{\text{where}}:\,\,\,k = 1\,\,\,{\text{or}}\,\,3.} \right.$$
(2)

It is noteworthy that the electrical fields of the piezoelectric layers affect the resin of the core [40,41,42,43]. According to Refs. [40,41,42,43], it can be observed that by applying a certain value of the electrical voltage to the resin, there is a possibility of mechanical failure in the resin. In the current study, the effect of the electrical fields on the mechanical behavior of the resin used in the core has been neglected.

In order to generate the equations of motion, Hamilton's principle is used as Eq. (3). In this equation, δK, δU, and δW are virtual kinetic energy, virtual strain energy, and virtual work due to the external forces, respectively.

$$ \int_{0}^{T} {\delta L{\text{d}}t} = \int_{0}^{T} {\left[ {\delta K - \left( {\delta U - \delta W} \right)} \right]} {\text{d}}t = 0 $$
(3)

Equation (4) shows how to calculate the virtual kinetic energy. Equation (E1) presented in “Appendix E” can be derived for the virtual kinetic energy by simplifying Eq. (4) and classifying component by component,

$$ \delta K = \int_{V} {\sum_{{k = 1}}^{3} {\rho ^{{\left( k \right)}} \left( {\dot{u}_{1}^{{\left( k \right)}} \delta \dot{u}_{1}^{{\left( k \right)}} + \dot{u}_{2}^{{\left( k \right)}} \delta \dot{u}_{2}^{{\left( k \right)}} + \dot{u}_{3}^{{\left( k \right)}} \delta \dot{u}_{3}^{{\left( k \right)}} } \right)} } {\text{d}}V $$
(4)

Equation (5) shows how to calculate the virtual strain energy. By simplifying Eq. (5) and classifying component by component, Eq. (E2) presented in “Appendix E” can be calculated for the virtual strain energy.

$$ \delta U = \int_{V} {\sigma _{{ij}} \varepsilon _{{ij}} {\text{d}}V} $$
(5)

In order to calculate the virtual work, it is necessary to determine the normal contact pressure distribution resulting from the collision of the spherical ball when it hits the top face sheet in terms of time. According to Fig. 1, the spherical ball hits the top face sheets of the sector with initial velocity V0. According to the classical non-adhesive elastic contact theory, the radius of the contact area and the applied force can be defined as Eqs. (6a) and (6b), respectively.

$$ a = \sqrt {R_{{{\text{eff}}}} d} $$
(6a)
$$ F = Kd^{{\frac{3}{2}}}\quad {\text{where}}\,\,\,K = \frac{4}{3}E_{{{\text{eff}}}} R_{{{\text{eff}}}}^{{\frac{1}{2}}} $$
(6b)

In addition, the effective radius and the effective elastic modulus can be defined as Eqs. (6c) and (6d), respectively.

$$ R_{{{\text{eff}}}} = \frac{{\left( {R + \frac{h}{2}} \right)R_{0} }}{{R + R_{0} + \frac{h}{2}}} $$
(6c)
$$ E_{{{\text{eff}}}} = \left( {\frac{{1 - \nu _{{12}}^{{\left( 3 \right)^{2} }} }}{{E_{{11}}^{{\left( 3 \right)}} }} + \frac{{1 - \nu _{0}^{2} }}{{E_{0} }}} \right)^{{ - 1}} $$
(6d)

Due to the initial velocity of the spherical ball (V0), the maximum contact depth, the maximum radius of the contact area, the maximum contact force, the maximum normal contact pressure, and the impact time duration are calculated as Eqs. (7a)–(7e), respectively.

$$ d_{{\max }} = \left( {\frac{5}{4}\frac{{V_{0}^{2} }}{{K^{\prime}K}}} \right)^{{\frac{2}{5}}} \quad{\text{where}}\,\,\,K^{\prime} = \frac{1}{{M_{0} }} $$
(7a)
$$ a_{{\max }} = \sqrt {R_{{{\text{eff}}}} d_{{\max }} } $$
(7b)
$$ F_{{\max }} = Kd_{{\max }}^{{\frac{3}{2}}} $$
(7c)
$$ P_{0} = \frac{{3F_{{\max }} }}{{2\pi a_{{\max }}^{2} }} $$
(7d)
$$ t_{{\max }} = \frac{4}{5}\sqrt \pi \frac{{\Gamma \left( {\frac{2}{5}} \right)}}{{\Gamma \left( {\frac{9}{{10}}} \right)}}\frac{{d_{{\max }} }}{{V_{0} }} $$
(7e)

According to Hunter's relationship, the maximum force can be approximated in terms of time as Eq. (8a). The maximum normal contact pressure distribution in terms of time and distance of the center of impact line (see Fig. 1) due to Hunter's relationship can be defined as Eq. (8b).

$$ F = F_{{\max }} \sin \left( {\frac{{\pi t}}{{t_{{\max }} }}} \right) $$
(8a)
$$ P = P_{0} \sin \left( {\frac{{\pi t}}{{t_{{\max }} }}} \right)\sqrt {1 - \frac{{r^{2} }}{{a_{{\max }}^{2} }}} $$
(8b)

Based on the contact pressure presented in Eq. (8b), the virtual work can be derived by Eq. (9). By inserting Eqs. (E1), (E3) and (9) into Eq. (3) and classifying relations, the seventeen equations can be obtained from  (10a)–(10q).

$$ \delta W = \int_{0}^{{2\pi }} {\int_{0}^{{a_{{\max }} }} {P\left( t \right)} } \delta u_{3}^{{\left( 3 \right)}} r{\text{d}}r{\text{d}}\xi _{1} \Rightarrow $$
$$ \delta W = \frac{{2\pi }}{3}P_{0} a_{{\max }}^{2} \sin \left( {\frac{{\pi t}}{{t_{{\max }} }}} \right)\delta u_{3}^{{\left( 3 \right)}} $$
(9)
$$ \begin{array}{l} \delta u_{0} : \sum\limits_{{k = 1}}^{3} {\left( {\frac{1}{{r^{{(k)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial N_{{11}}^{{\left( k \right)}} }}{{\partial \xi _{1} }} - N_{{13}}^{{\left( k \right)}} + \frac{{\partial N_{{12}}^{{\left( k \right)}} }}{{\partial \xi _{2} }} - N_{{12}}^{{\left( k \right)}} \cot \xi _{2} } \right]} \right)} \hfill \\ \quad= \left\{ \begin{subarray}{l} \left( {I_{0}^{{\left( 1 \right)}} + I_{0}^{{\left( 2 \right)}} + I_{0}^{{\left( 3 \right)}} } \right)\ddot{u}_{0} + \left( { - \frac{{h_{1} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\psi }_{1}^{{\left( 1 \right)}} + \left( { - \frac{{h_{2} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 2 \right)}} - \frac{4}{{3h_{2}^{2} }}I_{3}^{{\left( 2 \right)}} + \frac{{h_{2} }}{3}I_{0}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{1}^{{\left( 2 \right)}} + \left( {\frac{{h_{3} }}{3}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{1}^{{\left( 3 \right)}} \\ - \left( {\frac{{h_{1}^{2} }}{8}I_{0}^{{\left( 1 \right)}} + \frac{1}{2}I_{2}^{{\left( 1 \right)}} } \right)\ddot{\alpha }_{1}^{{\left( 1 \right)}} - \left( {\frac{{h_{2}^{2} }}{8}I_{0}^{{\left( 1 \right)}} + \frac{1}{2}I_{2}^{{\left( 2 \right)}} + \frac{{h_{2}^{2} }}{8}I_{0}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{1}^{{\left( 2 \right)}} - \left( {\frac{{h_{3}^{2} }}{8}I_{0}^{{\left( 3 \right)}} + \frac{1}{2}I_{2}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{1}^{{\left( 3 \right)}} + \left( {\frac{{h_{1}^{3} }}{{24}}I_{0}^{{\left( 1 \right)}} - \frac{1}{3}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\lambda }_{1}^{{\left( 1 \right)}} \\ + \left( {\frac{{h_{2}^{3} }}{{24}}I_{0}^{{\left( 1 \right)}} - \frac{1}{3}I_{3}^{{\left( 2 \right)}} - \frac{{h_{2}^{3} }}{{24}}I_{0}^{{\left( 3 \right)}} } \right)\ddot{\lambda }_{1}^{{\left( 2 \right)}} - \left( {\frac{{h_{3}^{3} }}{{24}}I_{0}^{{\left( 3 \right)}} + \frac{1}{3}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\lambda }_{1}^{{\left( 3 \right)}} - \frac{8}{{3h_{1}^{2} }}I_{0}^{{\left( 1 \right)}} \ddot{\beta }_{1}^{{\left( 1 \right)}} - \frac{4}{{3h_{2}^{2} }}\left( {I_{0}^{{\left( 1 \right)}} + I_{0}^{{\left( 2 \right)}} + I_{0}^{{\left( 3 \right)}} } \right)\ddot{\beta }_{1}^{{\left( 2 \right)}} - \frac{8}{{3h_{3}^{2} }}I_{0}^{{\left( 3 \right)}} \ddot{\beta }_{1}^{{\left( 3 \right)}} \end{subarray} \right\} \hfill \\ \end{array} $$
(10a)
$$ \begin{array}{l} \delta \psi _{1}^{{\left( 1 \right)}} : \left( \begin{subarray}{l} - \frac{{h_{1} }}{{3r^{{(1)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial N_{{11}}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial N_{{12}}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }}} \right] - \frac{1}{{r^{{(1)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial M_{{11}}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial M_{{12}}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} - \frac{4}{{3h_{1}^{2} }}\left( {\frac{1}{{\sin \xi _{2} }}\frac{{\partial q_{{11}}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial q_{{12}}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }}} \right)} \right] \\ + \left[ {\left( {1 + \frac{{h_{1} }}{{3r^{{(1)}} }}} \right)N_{{13}}^{{\left( 1 \right)}} + \frac{{h_{1} }}{{3r^{{(1)}} }}N_{{12}}^{{\left( 1 \right)}} \cot \xi _{2} - \frac{4}{{h_{1}^{2} }}P_{{13}}^{{\left( 1 \right)}} } \right] + \frac{1}{{r^{{(1)}} }}\left[ {M_{{13}}^{{\left( 1 \right)}} + M_{{12}}^{{\left( 1 \right)}} \cot \xi _{2} - \frac{4}{{3h_{1}^{2} }}\left( {q_{{13}}^{{\left( 1 \right)}} + q_{{12}}^{{\left( 1 \right)}} \cot \xi _{2} } \right)} \right] \end{subarray} \right) \hfill \\ \quad = \left\{ \begin{subarray}{l} \left( { - \frac{{h_{1} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 1 \right)}} } \right)\ddot{u}_{0} + \left( {\frac{{h_{1}^{2} }}{9}I_{0}^{{\left( 1 \right)}} - \frac{{2h_{1} }}{3}I_{1}^{{\left( 1 \right)}} + I_{2}^{{\left( 1 \right)}} + \frac{8}{{9h_{1} }}I_{3}^{{\left( 1 \right)}} - \frac{8}{{3h_{1}^{2} }}I_{4}^{{\left( 1 \right)}} + \frac{{16}}{{9h_{1}^{4} }}I_{6}^{{\left( 1 \right)}} } \right)\ddot{\psi }_{1}^{{\left( 1 \right)}} - \frac{{h_{2} }}{3}\left( { - \frac{{h_{1} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\psi }_{1}^{{\left( 2 \right)}} \\ + \left( {\frac{{h_{1}^{3} }}{{24}}I_{0}^{{\left( 1 \right)}} - \frac{{h_{1}^{2} }}{8}I_{1}^{{\left( 1 \right)}} + \frac{{h_{1} }}{6}I_{2}^{{\left( 1 \right)}} - \frac{1}{3}I_{3}^{{\left( 1 \right)}} + \frac{2}{{3h_{1}^{2} }}I_{5}^{{\left( 1 \right)}} } \right)\ddot{\alpha }_{1}^{{\left( 1 \right)}} - \frac{{h_{2}^{2} }}{8}\left( { - \frac{{h_{1} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\alpha }_{1}^{{\left( 2 \right)}} - \frac{1}{3}\left( {\frac{{h_{1}^{4} }}{{24}}I_{0}^{{\left( 1 \right)}} - \frac{{h_{1}^{3} }}{8}I_{1}^{{\left( 1 \right)}} - \frac{{h_{1} }}{6}I_{3}^{{\left( 1 \right)}} + I_{4}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{6}^{{\left( 1 \right)}} } \right)\ddot{\lambda }_{1}^{{\left( 1 \right)}} \\ + \frac{{h_{2}^{3} }}{{24}}\left( { - \frac{{h_{1} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\lambda }_{1}^{{\left( 2 \right)}} - \frac{8}{{3h_{1}^{2} }}\left( { - \frac{{h_{1} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\beta }_{1}^{{\left( 1 \right)}} - \frac{4}{{3h_{2}^{2} }}\left( { - \frac{{h_{1} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\beta }_{1}^{{\left( 2 \right)}} \end{subarray} \right\} \hfill \\ \end{array} $$
(10b)
$$ \begin{array}{l} \delta \psi _{1}^{{\left( 2 \right)}} : \left( \begin{subarray}{l} \frac{{h_{2} }}{{3\sin \xi _{2} }}\left[ {\frac{1}{{r^{{(1)}} }}\frac{{\partial N_{{11}}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} - \frac{1}{{r^{{(3)}} }}\frac{{\partial N_{{11}}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }}} \right] + \frac{{h_{2} }}{3}\left[ {\frac{1}{{r^{{(1)}} }}\frac{{\partial N_{{12}}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} - \frac{1}{{r^{{(3)}} }}\frac{{\partial N_{{12}}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }}} \right] - \frac{1}{{r^{{(2)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial M_{{11}}^{{\left( 2 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial M_{{12}}^{{\left( 2 \right)}} }}{{\partial \xi _{2} }} - \frac{4}{{3h_{2}^{2} }}\left( {\frac{1}{{\sin \xi _{2} }}\frac{{\partial q_{{11}}^{{\left( 2 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial q_{{12}}^{{\left( 2 \right)}} }}{{\partial \xi _{2} }}} \right)} \right] \\ + \left[ {N_{{13}}^{{\left( 2 \right)}} - \frac{4}{{h_{2}^{2} }}P_{{13}}^{{\left( 2 \right)}} } \right] + \frac{1}{{r^{{(2)}} }}\left[ {M_{{13}}^{{\left( 2 \right)}} + M_{{12}}^{{\left( 2 \right)}} \cot \xi _{2} - \frac{4}{{3h_{2}^{2} }}\left( {q_{{13}}^{{\left( 2 \right)}} + q_{{12}}^{{\left( 2 \right)}} \cot \xi _{2} } \right)} \right] + \frac{{h_{2} }}{3}\left[ { - \frac{{N_{{13}}^{{\left( 1 \right)}} }}{{r^{{(1)}} }} - \frac{{N_{{12}}^{{\left( 1 \right)}} }}{{r^{{(1)}} }}\cot \xi _{2} + \frac{{N_{{13}}^{{\left( 3 \right)}} }}{{r^{{(3)}} }} + \frac{{N_{{12}}^{{\left( 3 \right)}} }}{{r^{{(3)}} }}\cot \xi _{2} } \right] \end{subarray} \right) \hfill \\ \quad= \left\{ \begin{array}{l} \left( { - \frac{{h_{2} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 2 \right)}} - \frac{4}{{3h_{2}^{2} }}I_{3}^{{\left( 2 \right)}} + \frac{{h_{2} }}{3}I_{0}^{{\left( 3 \right)}} } \right)\ddot{u}_{0} + \frac{{h_{2} }}{3}\left( {\frac{{h_{1} }}{3}I_{0}^{{\left( 1 \right)}} - I_{1}^{{\left( 1 \right)}} + \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\psi }_{1}^{{\left( 1 \right)}} \hfill \\ + \left( {\frac{{h_{2}^{2} }}{9}\left( {I_{0}^{{\left( 1 \right)}} + I_{0}^{{\left( 3 \right)}} } \right) + I_{2}^{{\left( 2 \right)}} - \frac{8}{{3h_{2}^{2} }}I_{4}^{{\left( 2 \right)}} + \frac{{16}}{{9h_{2}^{4} }}I_{6}^{{\left( 2 \right)}} } \right)\ddot{\psi }_{1}^{{\left( 2 \right)}} + \frac{{h_{2} }}{3}\left( {\frac{{h_{3} }}{3}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{1}^{{\left( 3 \right)}} \hfill \\ + \frac{{h_{2} }}{3}\left( {\frac{{h_{1}^{2} }}{8}I_{0}^{{\left( 1 \right)}} + \frac{1}{2}I_{2}^{{\left( 1 \right)}} } \right)\ddot{\alpha }_{1}^{{\left( 1 \right)}} + \left( {\frac{{h_{2}^{3} }}{{24}}\left( {I_{0}^{{\left( 1 \right)}} - I_{0}^{{\left( 3 \right)}} } \right) - \frac{1}{2}I_{3}^{{\left( 2 \right)}} + \frac{2}{{3h_{2}^{2} }}I_{5}^{{\left( 2 \right)}} } \right)\ddot{\alpha }_{1}^{{\left( 2 \right)}} - \frac{{h_{2} }}{3}\left( {\frac{{h_{3}^{2} }}{8}I_{0}^{{\left( 3 \right)}} + \frac{1}{2}I_{2}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{1}^{{\left( 3 \right)}} \hfill \\ - \frac{{h_{2} }}{3}\left( {\frac{{h_{1}^{3} }}{{24}}I_{0}^{{\left( 1 \right)}} - \frac{1}{3}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\lambda }_{1}^{{\left( 1 \right)}} - \left( {\frac{{h_{2}^{4} }}{{72}}\left( {I_{0}^{{\left( 1 \right)}} + I_{0}^{{\left( 3 \right)}} } \right) + \frac{1}{3}I_{4}^{{\left( 2 \right)}} - \frac{4}{{9h_{2}^{2} }}I_{6}^{{\left( 2 \right)}} } \right)\ddot{\lambda }_{1}^{{\left( 2 \right)}} - \frac{{h_{2} }}{3}\left( {\frac{{h_{3}^{3} }}{{24}}I_{0}^{{\left( 3 \right)}} + \frac{1}{3}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\lambda }_{1}^{{\left( 3 \right)}} \hfill \\ + \frac{{8h_{2} }}{{9h_{1}^{2} }}I_{0}^{{\left( 1 \right)}} \ddot{\beta }_{1}^{{\left( 1 \right)}} + \frac{4}{{3h_{2}^{2} }}\left( {\frac{{h_{2} }}{3}\left( {I_{0}^{{\left( 1 \right)}} - I_{0}^{{\left( 3 \right)}} } \right) - I_{1}^{{\left( 2 \right)}} + \frac{4}{{3h_{2}^{2} }}I_{3}^{{\left( 2 \right)}} } \right)\ddot{\beta }_{1}^{{\left( 2 \right)}} - \frac{{8h_{2} }}{{9h_{3}^{2} }}I_{0}^{{\left( 3 \right)}} \ddot{\beta }_{1}^{{\left( 3 \right)}} \hfill \\ \end{array} \right\} \hfill \\ \end{array} $$
(10c)
$$ \begin{array}{l} \delta \psi _{1}^{{\left( 3 \right)}} : \left( \begin{subarray}{l} \frac{{h_{3} }}{{3r^{{(3)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial N_{{11}}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial N_{{12}}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }}} \right] - \frac{1}{{r^{{(3)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial M_{{11}}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial M_{{12}}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} - \frac{4}{{3h_{3}^{2} }}\left( {\frac{1}{{\sin \xi _{2} }}\frac{{\partial q_{{11}}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial q_{{12}}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }}} \right)} \right] \\ + \left[ {\left( {1 - \frac{{h_{3} }}{{3r^{{(3)}} }}} \right)N_{{13}}^{{\left( 3 \right)}} - \frac{{h_{3} }}{{3r^{{(3)}} }}N_{{12}}^{{\left( 3 \right)}} \cot \xi _{2} - \frac{4}{{h_{3}^{2} }}P_{{13}}^{{\left( 3 \right)}} } \right] + \frac{1}{{r^{{(3)}} }}\left[ {M_{{13}}^{{\left( 3 \right)}} + M_{{12}}^{{\left( 3 \right)}} \cot \xi _{2} - \frac{4}{{3h_{3}^{2} }}\left( {q_{{13}}^{{\left( 3 \right)}} + q_{{12}}^{{\left( 3 \right)}} \cot \xi _{2} } \right)} \right] \end{subarray} \right) \hfill \\ \quad = \left\{ \begin{subarray}{l} \left( {\frac{{h_{3} }}{3}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}I_{3}^{{\left( 3 \right)}} } \right)\ddot{u}_{0} + \frac{{h_{2} }}{3}\left( {\frac{{h_{3} }}{3}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{1}^{{\left( 2 \right)}} + \left( {\frac{{h_{3}^{2} }}{9}I_{0}^{{\left( 3 \right)}} + \frac{{2h_{3} }}{3}I_{1}^{{\left( 3 \right)}} + I_{2}^{{\left( 3 \right)}} - \frac{8}{{9h_{3} }}I_{3}^{{\left( 3 \right)}} - \frac{8}{{3h_{3}^{2} }}I_{4}^{{\left( 3 \right)}} + \frac{{16}}{{9h_{3}^{4} }}I_{6}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{1}^{{\left( 3 \right)}} \\ - \frac{{h_{2}^{2} }}{8}\left( {\frac{{h_{3} }}{3}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{1}^{{\left( 2 \right)}} - \left( {\frac{{h_{3}^{3} }}{{24}}I_{0}^{{\left( 3 \right)}} + \frac{{h_{3} }}{6}I_{2}^{{\left( 3 \right)}} + \frac{{h_{3}^{2} }}{8}I_{1}^{{\left( 3 \right)}} + \frac{1}{3}I_{3}^{{\left( 3 \right)}} + \frac{2}{{3h_{3}^{2} }}I_{5}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{1}^{{\left( 3 \right)}} - \frac{{h_{2}^{3} }}{{24}}\left( {\frac{{h_{3} }}{3}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\lambda }_{1}^{{\left( 2 \right)}} \\ - \frac{1}{3}\left( {\frac{{h_{3}^{4} }}{{24}}I_{0}^{{\left( 3 \right)}} + \frac{{h_{3}^{3} }}{8}I_{1}^{{\left( 3 \right)}} + \frac{{h_{3} }}{6}I_{3}^{{\left( 3 \right)}} + I_{4}^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}I_{6}^{{\left( 3 \right)}} } \right)\ddot{\lambda }_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{2}^{2} }}\left( {\frac{{h_{3} }}{3}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\beta }_{1}^{{\left( 2 \right)}} - \frac{8}{{3h_{3}^{2} }}\left( {\frac{{h_{3} }}{3}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\beta }_{1}^{{\left( 3 \right)}} \end{subarray} \right\} \hfill \\ \end{array} $$
(10d)
$$ \begin{array}{l} \delta v_{0} : \sum\limits_{{k = 1}}^{3} {\left( {\frac{1}{{r^{{(k)}} }}\left[ {N_{{11}}^{{(k)}} \cot \xi _{2} + \frac{{\partial N_{{22}}^{{\left( k \right)}} }}{{\partial \xi _{2} }} + \frac{1}{{\sin \xi _{2} }}\frac{{\partial N_{{12}}^{{\left( k \right)}} }}{{\partial \xi _{1} }} - N_{{23}}^{{(k)}} } \right]} \right)} \hfill \\ \quad= \left\{ \begin{subarray}{l} \left( {I_{0}^{{\left( 1 \right)}} + I_{0}^{{\left( 2 \right)}} + I_{0}^{{\left( 3 \right)}} } \right)\ddot{v}_{0} + \left( { - \frac{{h_{1} }}{3} + I_{1}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\psi }_{2}^{{\left( 1 \right)}} + \left( { - \frac{{h_{2} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 2 \right)}} - \frac{4}{{3h_{2}^{2} }}I_{3}^{{\left( 2 \right)}} + \frac{{h_{2} }}{3}I_{0}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{2}^{{\left( 2 \right)}} + \left( {\frac{{h_{3} }}{3}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{2}^{{\left( 3 \right)}} \\ - \left( {\frac{{h_{1}^{2} }}{8}I_{0}^{{\left( 1 \right)}} + \frac{1}{2}I_{2}^{{\left( 1 \right)}} } \right)\ddot{\alpha }_{2}^{{\left( 1 \right)}} - \left( {\frac{{h_{2}^{2} }}{8}I_{0}^{{\left( 1 \right)}} + \frac{1}{2}I_{2}^{{\left( 2 \right)}} + \frac{{h_{2}^{2} }}{8}I_{0}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{2}^{{\left( 2 \right)}} - \left( {\frac{{h_{3}^{2} }}{8}I_{0}^{{\left( 3 \right)}} + \frac{1}{2}I_{2}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{2}^{{\left( 3 \right)}} + \left( {\frac{{h_{1}^{3} }}{{24}}I_{0}^{{\left( 1 \right)}} - \frac{1}{3}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\lambda }_{2}^{{\left( 1 \right)}} + \left( {\frac{{h_{2}^{3} }}{{24}}I_{0}^{{\left( 1 \right)}} - \frac{1}{3}I_{3}^{{\left( 2 \right)}} - \frac{{h_{2}^{3} }}{{24}}I_{0}^{{\left( 3 \right)}} } \right)\ddot{\lambda }_{2}^{{\left( 2 \right)}} \\ - \left( {\frac{{h_{3}^{3} }}{{24}}I_{0}^{{\left( 3 \right)}} + \frac{1}{3}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\lambda }_{2}^{{\left( 3 \right)}} - \frac{8}{{3h_{1}^{2} }}I_{0}^{{\left( 1 \right)}} \ddot{\beta }_{2}^{{\left( 1 \right)}} - \frac{4}{{3h_{2}^{2} }}\left( {I_{0}^{{\left( 1 \right)}} + I_{0}^{{\left( 2 \right)}} + I_{0}^{{\left( 3 \right)}} } \right)\ddot{\beta }_{2}^{{\left( 2 \right)}} - \frac{8}{{3h_{3}^{2} }}I_{0}^{{\left( 3 \right)}} \ddot{\beta }_{2}^{{\left( 3 \right)}} \end{subarray} \right\} \hfill \\ \end{array} $$
(10e)
$$ \begin{array}{l} \delta \psi _{2}^{{\left( 1 \right)}} : \left( \begin{subarray}{l} - \frac{{h_{1} }}{{3r^{{(1)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial N_{{12}}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial N_{{22}}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }}} \right] - \frac{1}{{r^{{(1)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial M_{{12}}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial M_{{22}}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} - \frac{4}{{3h_{1}^{2} }}\left( {\frac{1}{{\sin \xi _{2} }}\frac{{\partial q_{{12}}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial q_{{22}}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }}} \right)} \right] \\ - \frac{{h_{1} }}{{3r^{{(1)}} }}N_{{11}}^{{(1)}} \cot \xi _{2} + \left( {1 + \frac{{h_{1} }}{{3r^{{(1)}} }}} \right)N_{{23}}^{{\left( 1 \right)}} - \frac{4}{{h_{1}^{2} }}P_{{23}}^{{\left( 1 \right)}} - \frac{1}{{r^{{(1)}} }}\left[ {M_{{11}}^{{(1)}} \cot \xi _{2} - M_{{23}}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}\left( {q_{{11}}^{{(1)}} \cot \xi _{2} - q_{{23}}^{{\left( 1 \right)}} } \right)} \right] \end{subarray} \right) \hfill \\ \quad = \left\{ \begin{subarray}{l} \left( { - \frac{{h_{1} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 1 \right)}} } \right)\ddot{v}_{0} + \left( {\frac{{h_{1}^{2} }}{9}I_{0}^{{\left( 1 \right)}} - \frac{{2h_{1} }}{3}I_{1}^{{\left( 1 \right)}} + I_{2}^{{\left( 1 \right)}} + \frac{8}{{9h_{1} }}I_{3}^{{\left( 1 \right)}} - \frac{8}{{3h_{1}^{2} }}I_{4}^{{\left( 1 \right)}} + \frac{{16}}{{9h_{1}^{4} }}I_{6}^{{\left( 1 \right)}} } \right)\ddot{\psi }_{2}^{{\left( 1 \right)}} - \frac{{h_{2} }}{3}\left( { - \frac{{h_{1} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\psi }_{2}^{{\left( 2 \right)}} \\ + \left( {\frac{{h_{1}^{3} }}{{24}}I_{0}^{{\left( 1 \right)}} - \frac{{h_{1}^{2} }}{8}I_{1}^{{\left( 1 \right)}} + \frac{{h_{1} }}{6}I_{2}^{{\left( 1 \right)}} - \frac{1}{3}I_{3}^{{\left( 1 \right)}} + \frac{2}{{3h_{1}^{2} }}I_{5}^{{\left( 1 \right)}} } \right)\ddot{\alpha }_{2}^{{\left( 1 \right)}} - \frac{{h_{2}^{2} }}{8}\left( { - \frac{{h_{1} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\alpha }_{2}^{{\left( 2 \right)}} + \frac{1}{3}\left( { - \frac{{h_{1}^{4} }}{{24}}I_{0}^{{\left( 1 \right)}} + \frac{{h_{1}^{3} }}{8}I_{1}^{{\left( 1 \right)}} + \frac{{h_{1} }}{6}I_{3}^{{\left( 1 \right)}} - I_{4}^{{\left( 1 \right)}} + \frac{4}{{3h_{1}^{2} }}I_{6}^{{\left( 1 \right)}} } \right)\ddot{\lambda }_{2}^{{\left( 1 \right)}} \\ + \frac{{h_{2}^{3} }}{{24}}\left( { - \frac{{h_{1} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\lambda }_{2}^{{\left( 2 \right)}} - \frac{8}{{3h_{1}^{2} }}\left( { - \frac{{h_{1} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\beta }_{2}^{{\left( 1 \right)}} - \frac{4}{{3h_{2}^{2} }}\left( { - \frac{{h_{1} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\beta }_{2}^{{\left( 2 \right)}} \end{subarray} \right\} \hfill \\ \end{array} $$
(10f)
$$ \begin{array}{l} \delta \psi _{2}^{{\left( 2 \right)}} : \left( \begin{subarray}{l} \frac{{h_{2} }}{{3\sin \xi _{2} }}\left[ {\frac{1}{{r^{{(1)}} }}\frac{{\partial N_{{12}}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} - \frac{1}{{r^{{(3)}} }}\frac{{\partial N_{{12}}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }}} \right] + \frac{{h_{2} }}{3}\left[ {\frac{1}{{r^{{(1)}} }}\frac{{\partial N_{{22}}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} - \frac{1}{{r^{{(3)}} }}\frac{{\partial N_{{22}}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }}} \right] - \frac{1}{{r^{{(2)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial M_{{12}}^{{\left( 2 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial M_{{22}}^{{\left( 2 \right)}} }}{{\partial \xi _{2} }} - \frac{4}{{3h_{2}^{2} }}\left( {\frac{1}{{\sin \xi _{2} }}\frac{{\partial q_{{12}}^{{\left( 2 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial q_{{22}}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }}} \right)} \right] \\ - \frac{1}{{r^{{(2)}} }}\left[ {M_{{11}}^{{\left( 2 \right)}} \cot \xi _{2} + M_{{23}}^{{\left( 2 \right)}} - \frac{4}{{3h_{2}^{2} }}\left( {q_{{11}}^{{\left( 2 \right)}} \cot \xi _{2} + q_{{23}}^{{\left( 2 \right)}} } \right)} \right] + \left[ {N_{{23}}^{{\left( 2 \right)}} - \frac{4}{{h_{2}^{2} }}P_{{23}}^{{\left( 2 \right)}} } \right] + \frac{{h_{2} }}{3}\left[ {\frac{{N_{{11}}^{{\left( 1 \right)}} }}{{r^{{(1)}} }}\cot \xi _{2} - \frac{{N_{{23}}^{{\left( 1 \right)}} }}{{r^{{(1)}} }} - \frac{{N_{{11}}^{{\left( 3 \right)}} }}{{r^{{(3)}} }}\cot \xi _{2} + \frac{{N_{{23}}^{{\left( 3 \right)}} }}{{r^{{(3)}} }}} \right] \end{subarray} \right) \hfill \\ \quad = \left\{ \begin{array}{l} \left( { - \frac{{h_{2} }}{3}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 2 \right)}} - \frac{4}{{3h_{2}^{2} }}I_{3}^{{\left( 2 \right)}} + \frac{{h_{2} }}{3}I_{0}^{{\left( 3 \right)}} } \right)\ddot{v}_{0} + \frac{{h_{2} }}{3}\left( {\frac{{h_{1} }}{3}I_{0}^{{\left( 1 \right)}} - I_{1}^{{\left( 1 \right)}} + \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\psi }_{2}^{{\left( 1 \right)}} \hfill \\ + \left( {\frac{{h_{2}^{2} }}{9}\left( {I_{0}^{{\left( 1 \right)}} + I_{0}^{{\left( 3 \right)}} } \right) + I_{2}^{{\left( 2 \right)}} - \frac{8}{{3h_{2}^{2} }}I_{4}^{{\left( 2 \right)}} + \frac{{16}}{{9h_{2}^{4} }}I_{6}^{{\left( 2 \right)}} } \right)\ddot{\psi }_{2}^{{\left( 2 \right)}} + \frac{{h_{2} }}{3}\left( {\frac{{h_{3} }}{3}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{1}^{2} }}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{2}^{{\left( 3 \right)}} \hfill \\ + \frac{{h_{2} }}{3}\left( {\frac{{h_{1}^{2} }}{8}I_{0}^{{\left( 1 \right)}} + \frac{1}{2}I_{2}^{{\left( 1 \right)}} } \right)\ddot{\alpha }_{2}^{{\left( 1 \right)}} + \left( {\frac{{h_{2}^{3} }}{{24}}\left( {I_{0}^{{\left( 1 \right)}} - I_{0}^{{\left( 3 \right)}} } \right) - \frac{1}{2}I_{3}^{{\left( 2 \right)}} + \frac{2}{{3h_{2}^{2} }}I_{5}^{{\left( 2 \right)}} } \right)\ddot{\alpha }_{2}^{{\left( 2 \right)}} - \frac{{h_{2} }}{3}\left( {\frac{{h_{3}^{2} }}{8}I_{0}^{{\left( 3 \right)}} + \frac{1}{2}I_{2}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{2}^{{\left( 3 \right)}} \hfill \\ - \frac{{h_{2} }}{3}\left( {\frac{{h_{1}^{3} }}{{24}}I_{0}^{{\left( 1 \right)}} - \frac{1}{3}I_{3}^{{\left( 1 \right)}} } \right)\ddot{\lambda }_{2}^{{\left( 1 \right)}} - \left( {\frac{{h_{2}^{4} }}{{72}}\left( {I_{0}^{{\left( 1 \right)}} + I_{0}^{{\left( 3 \right)}} } \right) + \frac{1}{3}I_{4}^{{\left( 2 \right)}} - \frac{4}{{9h_{2}^{2} }}I_{6}^{{\left( 2 \right)}} } \right)\ddot{\lambda }_{2}^{{\left( 2 \right)}} - \frac{{h_{2} }}{3}\left( {\frac{{h_{3}^{3} }}{{24}}I_{0}^{{\left( 3 \right)}} + \frac{1}{3}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\lambda }_{2}^{{\left( 3 \right)}} \hfill \\ + \frac{{8h_{2} }}{{9h_{1}^{2} }}I_{0}^{{\left( 1 \right)}} \ddot{\beta }_{2}^{{\left( 1 \right)}} + \frac{4}{{3h_{2}^{2} }}\left( {\frac{{h_{2} }}{3}\left( {I_{0}^{{\left( 1 \right)}} - I_{0}^{{\left( 3 \right)}} } \right) - I_{1}^{{\left( 2 \right)}} + \frac{4}{{3h_{2}^{2} }}I_{3}^{{\left( 2 \right)}} } \right)\ddot{\beta }_{2}^{{\left( 2 \right)}} - \frac{{8h_{2} }}{{9h_{3}^{2} }}I_{0}^{{\left( 3 \right)}} \ddot{\beta }_{2}^{{\left( 3 \right)}} \hfill \\ \end{array} \right\} \hfill \\ \end{array} $$
(10g)
$$ \begin{array}{l} \delta \psi _{2}^{{\left( 3 \right)}} : \left( \begin{subarray}{l} \frac{{h_{3} }}{{3r^{{(3)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial N_{{12}}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial N_{{22}}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }}} \right] - \frac{1}{{r^{{(3)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial M_{{12}}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial M_{{22}}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} - \frac{4}{{3h_{3}^{2} }}\left( {\frac{1}{{\sin \xi _{2} }}\frac{{\partial q_{{12}}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial q_{{22}}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }}} \right)} \right] \\ + \frac{{h_{3} }}{{3r^{{(3)}} }}N_{{11}}^{{\left( 3 \right)}} \cot \xi _{2} + \left( {1 - \frac{{h_{3} }}{{3r^{{(3)}} }}} \right)N_{{23}}^{{\left( 3 \right)}} - \frac{4}{{h_{3}^{2} }}P_{{23}}^{{\left( 3 \right)}} - \frac{1}{{r^{{(3)}} }}\left[ {M_{{11}}^{{\left( 3 \right)}} \cot \xi _{2} - M_{{23}}^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}\left( {q_{{11}}^{{\left( 3 \right)}} \cot \xi _{2} - q_{{23}}^{{\left( 3 \right)}} } \right)} \right] \end{subarray} \right) \hfill \\ \quad = \left\{ \begin{subarray}{l} \left( {\frac{{h_{3} }}{3}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}I_{3}^{{\left( 3 \right)}} } \right)\ddot{v}_{0} + \frac{{h_{2} }}{3}\left( {\frac{{h_{3} }}{3}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{2}^{{\left( 2 \right)}} + \left( {\frac{{h_{3}^{2} }}{9}I_{0}^{{\left( 3 \right)}} + \frac{{2h_{3} }}{3}I_{1}^{{\left( 3 \right)}} + I_{2}^{{\left( 3 \right)}} - \frac{8}{{9h_{3} }}I_{3}^{{\left( 3 \right)}} - \frac{8}{{3h_{3}^{2} }}I_{4}^{{\left( 3 \right)}} + \frac{{16}}{{9h_{3}^{4} }}I_{6}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{2}^{{\left( 3 \right)}} \\ - \frac{{h_{2}^{2} }}{8}\left( {\frac{{h_{3} }}{3}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{2}^{{\left( 2 \right)}} - \left( {\frac{{h_{3}^{3} }}{{24}}I_{0}^{{\left( 3 \right)}} + \frac{{h_{3}^{2} }}{8}I_{1}^{{\left( 3 \right)}} + \frac{{h_{3} }}{6}I_{2}^{{\left( 3 \right)}} + \frac{1}{3}I_{3}^{{\left( 3 \right)}} - \frac{2}{{3h_{3}^{2} }}I_{5}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{2}^{{\left( 3 \right)}} - \frac{{h_{2}^{3} }}{{24}}\left( {\frac{{h_{3} }}{3}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\lambda }_{2}^{{\left( 2 \right)}} \\ - \frac{1}{3}\left( {\frac{{h_{3}^{4} }}{{24}}I_{0}^{{\left( 3 \right)}} + \frac{{h_{3}^{3} }}{8}I_{1}^{{\left( 3 \right)}} + \frac{{h_{3} }}{6}I_{3}^{{\left( 3 \right)}} + I_{4}^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}I_{6}^{{\left( 3 \right)}} } \right)\ddot{\lambda }_{2}^{{\left( 3 \right)}} - \frac{4}{{3h_{2}^{2} }}\left( {\frac{{h_{3} }}{3}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\beta }_{2}^{{\left( 2 \right)}} - \frac{8}{{3h_{3}^{2} }}\left( {\frac{{h_{3} }}{3}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}I_{3}^{{\left( 3 \right)}} } \right)\ddot{\beta }_{2}^{{\left( 3 \right)}} \end{subarray} \right\} \hfill \\ \end{array} $$
(10h)
$$ \begin{array}{l} \delta w_{0} : \sum\limits_{{k = 1}}^{3} {\left( {\frac{1}{{r^{{(k)}} }}\left[ {N_{{11}}^{{\left( k \right)}} + N_{{22}}^{{\left( k \right)}} + \frac{{\partial N_{{23}}^{{\left( k \right)}} }}{{\partial \xi _{2} }} + \frac{1}{{\sin \xi _{2} }}\frac{{\partial N_{{13}}^{{\left( k \right)}} }}{{\partial \xi _{1} }}} \right]} \right)} \hfill \\ \quad = \left\{ \begin{subarray}{l} \left( {I_{0}^{{\left( 1 \right)}} + I_{0}^{{\left( 2 \right)}} + I_{0}^{{\left( 3 \right)}} } \right)\ddot{w}_{0} + \left( { - \frac{{h_{1} }}{2}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 1 \right)}} + \left( { - \frac{{h_{2} }}{2}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 2 \right)}} + \frac{{h_{2} }}{2}I_{0}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 2 \right)}} \\ + \left( {\frac{{h_{3} }}{2}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 3 \right)}} + \left( {\frac{{h_{1}^{2} }}{4}I_{0}^{{\left( 1 \right)}} + I_{2}^{{\left( 1 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 1 \right)}} + \left( {\frac{{h_{2}^{2} }}{4}I_{0}^{{\left( 1 \right)}} + I_{2}^{{\left( 2 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 2 \right)}} + \left( {\frac{{h_{3}^{2} }}{4}I_{0}^{{\left( 3 \right)}} + I_{2}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 3 \right)}} \end{subarray} \right\} + \frac{{2\pi }}{3}P_{0} a_{{\max }}^{2} \sin \left( {\frac{{\pi t}}{{t_{{\max }} }}} \right) \hfill \\ \end{array} $$
(10i)
$$ \begin{array}{l} \delta \psi _{3}^{{\left( 1 \right)}} :\left( { - \frac{{h_{1} }}{{2r^{{(1)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial N_{{13}}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial N_{{23}}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} + N_{{11}}^{{\left( 1 \right)}} + N_{{22}}^{{\left( 1 \right)}} } \right] - \frac{1}{{r^{{(1)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial M_{{13}}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial M_{{23}}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} + M_{{11}}^{{\left( 1 \right)}} + M_{{22}}^{{\left( 1 \right)}} } \right] + N_{{33}}^{{\left( 1 \right)}} } \right) \hfill \\ \quad = \left\{ \begin{subarray}{l} \left( { - \frac{{h_{1} }}{2}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} } \right)\ddot{w}_{0} + \left( {\frac{{h_{1}^{2} }}{4}I_{0}^{{\left( 1 \right)}} - h_{1} I_{1}^{{\left( 1 \right)}} + I_{2}^{{\left( 1 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 1 \right)}} - \frac{{h_{2} }}{2}\left( { - \frac{{h_{1} }}{2}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 2 \right)}} \\ + \left( { - \frac{{h_{1}^{3} }}{8}I_{0}^{{\left( 1 \right)}} + \frac{{h_{1}^{2} }}{4}I_{1}^{{\left( 1 \right)}} - \frac{{h_{1} }}{2}I_{2}^{{\left( 1 \right)}} + I_{3}^{{\left( 1 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 1 \right)}} + \frac{{h_{2}^{2} }}{4}\left( { - \frac{{h_{1} }}{2}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 2 \right)}} \end{subarray} \right\} \hfill \\ \end{array} $$
(10j)
$$ \begin{array}{l} \delta \psi _{3}^{{\left( 2 \right)}} :\left( \begin{subarray}{l} \frac{{h_{2} }}{2}\left[ {\frac{1}{{r^{{(1)}} }}\left( {\frac{1}{{\sin \xi _{2} }}\frac{{\partial N_{{13}}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial N_{{23}}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }}} \right) - \frac{1}{{r^{{(3)}} }}\left( {\frac{1}{{\sin \xi _{2} }}\frac{{\partial N_{{13}}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial N_{{23}}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }}} \right)} \right] - \frac{1}{{r^{{(2)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial M_{{13}}^{{\left( 2 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial M_{{23}}^{{\left( 2 \right)}} }}{{\partial \xi _{2} }}} \right] \\ + \frac{{h_{2} }}{2}\left[ {\frac{{N_{{11}}^{{\left( 1 \right)}} }}{{r^{{(1)}} }} + \frac{{N_{{22}}^{{\left( 1 \right)}} }}{{r^{{(1)}} }} - \frac{{N_{{11}}^{{\left( 3 \right)}} }}{{r^{{(3)}} }} - \frac{{N_{{22}}^{{\left( 3 \right)}} }}{{r^{{(3)}} }}} \right] - \frac{1}{{r^{{(2)}} }}\left[ {M_{{11}}^{{\left( 2 \right)}} + M_{{22}}^{{\left( 2 \right)}} } \right] + N_{{33}}^{{\left( 2 \right)}} \end{subarray} \right) \hfill \\ \quad = \left\{ \begin{subarray}{l} \left( { - \frac{{h_{2} }}{2}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 2 \right)}} + \frac{{h_{2} }}{2}I_{0}^{{\left( 3 \right)}} } \right)\ddot{w}_{0} + \frac{{h_{2} }}{2}\left( {\frac{{h_{1} }}{2}I_{0}^{{\left( 1 \right)}} - I_{1}^{{\left( 1 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 1 \right)}} \\ + \left( {\frac{{h_{2}^{2} }}{4}\left( {I_{0}^{{\left( 1 \right)}} + I_{0}^{{\left( 3 \right)}} } \right) + I_{2}^{{\left( 2 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 2 \right)}} + \frac{{h_{2} }}{2}\left( {\frac{{h_{3} }}{2}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 3 \right)}} - \frac{{h_{2} }}{2}\left( {\frac{{h_{1}^{2} }}{4}I_{0}^{{\left( 1 \right)}} + I_{2}^{{\left( 1 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 1 \right)}} \\ + \left( {\frac{{h_{2}^{3} }}{8}\left( { - I_{0}^{{\left( 1 \right)}} + I_{0}^{{\left( 3 \right)}} } \right) + I_{3}^{{\left( 2 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 2 \right)}} + \frac{{h_{2} }}{2}\left( {\frac{{h_{3}^{2} }}{4}I_{0}^{{\left( 3 \right)}} + I_{2}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 3 \right)}} \end{subarray} \right\}+ \frac{{\pi h_{2} }}{3}P_{0} a_{{\max }}^{2} \sin \left( {\frac{{\pi t}}{{t_{{\max }} }}} \right) \hfill \\ \end{array} $$
(10k)
$$ \begin{array}{l} \delta \psi _{3}^{{\left( 3 \right)}} : \left( {\frac{{h_{3} }}{{2r^{{(3)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial N_{{13}}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial N_{{23}}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} + N_{{11}}^{{\left( 3 \right)}} + N_{{22}}^{{\left( 3 \right)}} } \right] - \frac{1}{{r^{{(3)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial M_{{13}}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial M_{{23}}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} + M_{{11}}^{{\left( 3 \right)}} + M_{{22}}^{{\left( 3 \right)}} } \right] + N_{{33}}^{{\left( 3 \right)}} } \right) \hfill \\ \quad = \left\{ \begin{subarray}{l} \left( {\frac{{h_{3} }}{2}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} } \right)\ddot{w}_{0} + \frac{{h_{2} }}{2}\left( {\frac{{h_{3} }}{2}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 2 \right)}} + \left( {\frac{{h_{3}^{2} }}{4}I_{0}^{{\left( 3 \right)}} + h_{3} I_{1}^{{\left( 3 \right)}} + I_{2}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 3 \right)}} \\ + \frac{{h_{2}^{2} }}{4}\left( {\frac{{h_{3} }}{2}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 2 \right)}} + \left( {\frac{{h_{3}^{3} }}{8}I_{0}^{{\left( 3 \right)}} + \frac{{h_{3}^{2} }}{4}I_{1}^{{\left( 3 \right)}} + \frac{{h_{3} }}{2}I_{2}^{{\left( 3 \right)}} + I_{3}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 3 \right)}} \end{subarray} \right\} + \frac{{2\pi h_{3} }}{3}P_{0} a_{{\max }}^{2} \sin \left( {\frac{{\pi t}}{{t_{{\max }} }}} \right) \hfill \\ \end{array} $$
(10l)
$$ \begin{array}{l} \delta \alpha _{3}^{{\left( 1 \right)}} :\left( {\frac{{h_{1}^{2} }}{{4r^{{(1)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial N_{{13}}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial N_{{23}}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} + N_{{11}}^{{\left( 1 \right)}} + N_{{22}}^{{\left( 1 \right)}} } \right] + \frac{1}{{r^{{(1)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial P_{{13}}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial P_{{23}}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} + P_{{11}}^{{\left( 1 \right)}} + P_{{22}}^{{\left( 1 \right)}} } \right] - 2M_{{33}}^{{\left( 1 \right)}} } \right) \hfill \\ \quad = \left\{ \begin{subarray}{l} \left( {\frac{{h_{1}^{2} }}{4}I_{0}^{{\left( 1 \right)}} + I_{2}^{{\left( 1 \right)}} } \right)\ddot{w}_{0} + \left( { - \frac{{h_{1}^{3} }}{8}I_{0}^{{\left( 1 \right)}} + \frac{{h_{1}^{2} }}{4}I_{1}^{{\left( 1 \right)}} - \frac{{h_{1} }}{2}I_{2}^{{\left( 1 \right)}} + I_{3}^{{\left( 1 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 1 \right)}} - \frac{{h_{2} }}{2}\left( {\frac{{h_{1}^{2} }}{4}I_{0}^{{\left( 1 \right)}} + I_{2}^{{\left( 1 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 2 \right)}} \\ + \left( {\frac{{h_{1}^{4} }}{{16}}I_{0}^{{\left( 1 \right)}} + \frac{{h_{1}^{2} }}{2}I_{2}^{{\left( 1 \right)}} + I_{4}^{{\left( 1 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 1 \right)}} + \frac{{h_{2}^{2} }}{4}\left( {\frac{{h_{1}^{2} }}{4}I_{0}^{{\left( 1 \right)}} + I_{2}^{{\left( 1 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 2 \right)}} \end{subarray} \right\} \hfill \\ \end{array} $$
(10m)
$$ \begin{array}{l} \delta \alpha _{3}^{{\left( 2 \right)}} : \left( {\frac{1}{{r^{{(2)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial P_{{13}}^{{\left( 2 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial P_{{23}}^{{\left( 2 \right)}} }}{{\partial \xi _{2} }} + P_{{11}}^{{\left( 2 \right)}} + P_{{22}}^{{\left( 2 \right)}} } \right] - \frac{{h_{2}^{2} }}{4}\left[ \begin{subarray}{l} \frac{1}{{r^{{(1)}} }}\left( {\frac{1}{{\sin \xi _{2} }}\frac{{\partial N_{{13}}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial N_{{23}}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} + N_{{11}}^{{\left( 1 \right)}} + N_{{22}}^{{\left( 1 \right)}} } \right) + \\ \frac{1}{{r^{{(3)}} }}\left( {\frac{1}{{\sin \xi _{2} }}\frac{{\partial N_{{13}}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial N_{{23}}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} + N_{{11}}^{{\left( 3 \right)}} + N_{{22}}^{{\left( 3 \right)}} } \right) \end{subarray} \right] - 2M_{{33}}^{{\left( 2 \right)}} } \right) \hfill \\ \quad = \left\{ \begin{subarray}{l} \left( {\frac{{h_{2}^{2} }}{4}\left( {I_{0}^{{\left( 1 \right)}} + I_{0}^{{\left( 3 \right)}} } \right) + I_{2}^{{\left( 2 \right)}} } \right)\ddot{w}_{0} + \frac{{h_{2}^{2} }}{4}\left( { - \frac{{h_{1} }}{2}I_{0}^{{\left( 1 \right)}} + I_{1}^{{\left( 1 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 1 \right)}} + \left( {\frac{{h_{2}^{3} }}{8}\left( { - I_{0}^{{\left( 1 \right)}} + I_{0}^{{\left( 3 \right)}} } \right) + I_{3}^{{\left( 2 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 2 \right)}} \\ + \frac{{h_{2}^{2} }}{4}\left( {\frac{{h_{3} }}{2}I_{0}^{{\left( 3 \right)}} + I_{1}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 3 \right)}} + \frac{{h_{2}^{2} }}{4}\left( {\frac{{h_{1}^{2} }}{4}I_{0}^{{\left( 1 \right)}} + I_{2}^{{\left( 1 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 1 \right)}} + \left( {\frac{{h_{2}^{2} }}{4}\left( {I_{0}^{{\left( 1 \right)}} + I_{0}^{{\left( 3 \right)}} } \right) + I_{4}^{{\left( 2 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 2 \right)}} \\ + \frac{{h_{2}^{2} }}{4}\left( {\frac{{h_{3}^{2} }}{4}I_{0}^{{\left( 3 \right)}} + I_{2}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 3 \right)}} \end{subarray} \right\} + \frac{{\pi h_{2}^{2} }}{6}P_{0} a_{{\max }}^{2} \sin \left( {\frac{{\pi t}}{{t_{{\max }} }}} \right) \hfill \\ \end{array} $$
(10n)
$$ \begin{array}{l} \delta \alpha _{3}^{{\left( 3 \right)}} :\left( {\frac{{h_{3}^{2} }}{{4r^{{(3)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial N_{{13}}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial N_{{23}}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} + N_{{11}}^{{\left( 3 \right)}} + N_{{22}}^{{\left( 3 \right)}} } \right] + \frac{1}{{r^{{(3)}} }}\left[ {\frac{1}{{\sin \xi _{2} }}\frac{{\partial P_{{13}}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial P_{{23}}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} + P_{{11}}^{{\left( 3 \right)}} + P_{{22}}^{{\left( 3 \right)}} } \right] - 2M_{{33}}^{{\left( 3 \right)}} } \right) \hfill \\ \quad = \left\{ \begin{subarray}{l} \left( {\frac{{h_{3}^{2} }}{4}I_{0}^{{\left( 3 \right)}} + I_{2}^{{\left( 3 \right)}} } \right)\ddot{w}_{0} + \frac{{h_{2} }}{2}\left( {\frac{{h_{3}^{2} }}{4}I_{0}^{{\left( 3 \right)}} + I_{2}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 2 \right)}} + \left( {\frac{{h_{3}^{3} }}{8}I_{0}^{{\left( 3 \right)}} + \frac{{h_{3} }}{2}I_{2}^{{\left( 3 \right)}} + \frac{{h_{3}^{2} }}{4}I_{1}^{{\left( 3 \right)}} + I_{3}^{{\left( 3 \right)}} } \right)\ddot{\psi }_{3}^{{\left( 3 \right)}} \\ + \frac{{h_{2}^{2} }}{4}\left( {\frac{{h_{3}^{2} }}{4}I_{0}^{{\left( 3 \right)}} + I_{2}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 2 \right)}} + \left( {\frac{{h_{3}^{4} }}{{16}}I_{0}^{{\left( 3 \right)}} + \frac{{h_{3}^{2} }}{4}I_{2}^{{\left( 3 \right)}} + \frac{{h_{3}^{2} }}{4}I_{2}^{{\left( 3 \right)}} + I_{4}^{{\left( 3 \right)}} } \right)\ddot{\alpha }_{3}^{{\left( 3 \right)}} \end{subarray} \right\} + \frac{{\pi h_{3}^{2} }}{3}P_{0} a_{{\max }}^{2} \sin \left( {\frac{{\pi t}}{{t_{{\max }} }}} \right) \hfill \\ \end{array} $$
(10o)
$$ \delta \varphi ^{{\left( 1 \right)}} : \frac{1}{{\sin \xi _{2} }}\frac{{\partial \Gamma _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial \Gamma _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} - \Gamma _{3}^{{\left( 1 \right)}} = 0 $$
(10p)
$$ \delta \varphi ^{{\left( 3 \right)}} : \frac{1}{{\sin \xi _{2} }}\frac{{\partial \Gamma _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} + \frac{{\partial \Gamma _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} - \Gamma _{3}^{{\left( 3 \right)}} = 0 $$
(10q)

In order to satisfy Maxwell’s static equation, Eqs. (11a) and (11b) need to be true for the first and third piezoelectric face sheets of the spherical sandwich shell, respectively.

$$ \vec{\nabla } \cdot \vec{D}^{{\left( 1 \right)}} = 0 \Rightarrow \frac{1}{{r^{{\left( 1 \right)}} \sin \xi _{2} }}\frac{{\partial D_{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} + \frac{1}{{r^{{\left( 1 \right)}} \sin \xi _{2} }}\frac{{\partial \left( {D_{2}^{{\left( 1 \right)}} \sin \xi _{2} } \right)}}{{\partial \xi _{2} }} + \frac{{\partial D_{3}^{{\left( 1 \right)}} }}{{\partial \xi }} + \frac{{2D_{3}^{{\left( 1 \right)}} }}{{r^{{\left( 1 \right)}} }} = 0 $$
(11a)
$$ \vec{\nabla } \cdot \vec{D}^{{\left( 3 \right)}} =\, 0 \Rightarrow \frac{1}{{r^{{\left( 3 \right)}} \sin \xi _{2} }}\frac{{\partial D_{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} + \frac{1}{{r^{{\left( 3 \right)}} \sin \xi _{2} }}\frac{{\partial \left( {D_{2}^{{\left( 3 \right)}} \sin \xi _{2} } \right)}}{{\partial \xi _{2} }} + \frac{{\partial D_{3}^{{\left( 3 \right)}} }}{{\partial \xi }} + \frac{{2D_{3}^{{\left( 3 \right)}} }}{{r^{{\left( 3 \right)}} }} = 0 $$
(11b)

By inserting Eqs. (C1)–(C13) and (D3) into Eqs. (11) and classifying relations, Eqs. (12) can be written. In order to solve the low-velocity impact problem in the spherical sandwich shell, it is necessary that the nineteen Eqs. (10) and (12) are solved together.

$$ \left[ \begin{subarray}{l} \frac{{e_{5} }}{{r^{{\left( 1 \right)}} \sin \xi _{2} }}\left[ \begin{subarray}{l} \frac{1}{{r^{{(1)}} \sin \xi _{2}^{{\left( 1 \right)}} }}\left[ \begin{subarray}{l} \frac{{\partial ^{2} w_{0} }}{{\partial \xi _{1}^{2} }} - \frac{{h_{2} }}{2}\frac{{\partial ^{2} \psi _{3}^{{\left( 2 \right)}} }}{{\partial \xi _{1}^{2} }} + \frac{{h_{2}^{2} }}{4}\frac{{\partial ^{2} \alpha _{3}^{{\left( 2 \right)}} }}{{\partial \xi _{1}^{2} }} \\ - \frac{{h_{1} }}{2}\frac{{\partial ^{2} \psi _{3}^{{\left( 1 \right)}} }}{{\partial \xi _{1}^{2} }} + \frac{{h_{1}^{2} }}{4}\frac{{\partial ^{2} \alpha _{3}^{{\left( 1 \right)}} }}{{\partial \xi _{1}^{2} }} \\ + \xi ^{{\left( 1 \right)}} \frac{{\partial ^{2} \psi _{3}^{{\left( 1 \right)}} }}{{\partial \xi _{1}^{2} }} + \xi ^{{\left( 1 \right)^{2} }} \frac{{\partial ^{2} \alpha _{3}^{{\left( 1 \right)}} }}{{\partial \xi _{1}^{2} }} \end{subarray} \right] + \left[ {\left[ {1 - \frac{4}{{h_{1}^{2} }}\xi ^{{\left( 1 \right)^{2} }} } \right]\frac{{\partial \psi _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} - \xi ^{{\left( 1 \right)}} \frac{{\partial \alpha _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} - \xi ^{{\left( 1 \right)^{2} }} \frac{{\partial \lambda _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }}} \right] \\ - \frac{1}{{r^{{(1)}} }}\left[ \begin{gathered} \frac{{\partial u_{0} }}{{\partial \xi _{1} }} - \frac{{h_{2} }}{3}\frac{{\partial \psi _{1}^{{\left( 2 \right)}} }}{{\partial \xi _{1} }} - \frac{{h_{2}^{2} }}{8}\frac{{\partial \alpha _{1}^{{\left( 2 \right)}} }}{{\partial \xi _{1} }} \hfill \\ - \frac{4}{{3h_{2}^{2} }}\frac{{\partial \beta _{1}^{{\left( 2 \right)}} }}{{\partial \xi _{1} }} + \frac{{h_{2}^{3} }}{{24}}\frac{{\partial \lambda _{1}^{{\left( 2 \right)}} }}{{\partial \xi _{1} }} - \hfill \\ \frac{{h_{1} }}{3}\frac{{\partial \psi _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} - \frac{{h_{1}^{2} }}{8}\frac{{\partial \alpha _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} - \frac{4}{{3h_{1}^{2} }}\frac{{\partial \beta _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} + \frac{{h_{1}^{3} }}{{24}}\frac{{\partial \lambda _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} + \left[ {\xi ^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}\xi ^{{\left( 1 \right)^{3} }} } \right]\frac{{\partial \psi _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} - \frac{1}{2}\xi ^{{\left( 1 \right)^{2} }} \frac{{\partial \alpha _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} \hfill \\ - \frac{4}{{3h_{1}^{2} }}\frac{{\partial \beta _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} - \frac{1}{3}\xi ^{{\left( 1 \right)^{3} }} \frac{{\partial \lambda _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1} }} \hfill \\ \end{gathered} \right] \end{subarray} \right] + \frac{{e_{4} }}{{r^{{\left( 1 \right)}} }}\left[ \begin{subarray}{l} \left[ {\left[ {1 - \frac{4}{{h_{1}^{2} }}\xi ^{{\left( 1 \right)^{2} }} } \right]\frac{{\partial \psi _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} - \xi ^{{\left( 1 \right)}} \frac{{\partial \alpha _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} - \xi ^{{\left( 1 \right)^{2} }} \frac{{\partial \lambda _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }}} \right] + \frac{1}{{r^{{(1)}} }}\left[ \begin{subarray}{l} \frac{{\partial ^{2} w_{0} }}{{\partial \xi _{2}^{2} }} - \frac{{h_{2} }}{2}\frac{{\partial ^{2} \psi _{3}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{2} }} + \frac{{h_{2}^{2} }}{4}\frac{{\partial ^{2} \alpha _{3}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{2} }} - \frac{{h_{1} }}{2}\frac{{\partial ^{2} \psi _{3}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{2} }} \\ + \frac{{h_{1}^{2} }}{4}\frac{{\partial ^{2} \alpha _{3}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{2} }} + \xi ^{{\left( 1 \right)}} \frac{{\partial ^{2} \psi _{3}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{2} }} + \xi ^{{\left( 1 \right)^{2} }} \frac{{\partial ^{2} \alpha _{3}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{2} }} \end{subarray} \right] \\ - \frac{1}{{r^{{(1)}} }}\left[ \begin{subarray}{l} \frac{{\partial v_{0} }}{{\partial \xi _{2} }} - \frac{{h_{2} }}{3}\frac{{\partial \psi _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2} }} - \frac{{h_{2}^{2} }}{8}\frac{{\partial \alpha _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2} }} - \frac{4}{{3h_{2}^{2} }}\frac{{\partial \beta _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2} }} \\ + \frac{{h_{2}^{3} }}{{24}}\frac{{\partial \lambda _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2} }} - \frac{{h_{1} }}{3}\frac{{\partial \psi _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} - \frac{{h_{1}^{2} }}{8}\frac{{\partial \alpha _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} - \frac{4}{{3h_{1}^{2} }}\frac{{\partial \beta _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} + \frac{{h_{1}^{3} }}{{24}}\frac{{\partial \lambda _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} + \left[ {\xi ^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}\xi ^{{\left( 1 \right)^{3} }} } \right]\frac{{\partial \psi _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} \\ - \frac{1}{2}\xi ^{{\left( 1 \right)^{2} }} \frac{{\partial \alpha _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} - \frac{4}{{3h_{1}^{2} }}\frac{{\partial \beta _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} - \frac{1}{3}\xi ^{{\left( 1 \right)^{3} }} \frac{{\partial \lambda _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2} }} \end{subarray} \right] \\ + \cot \xi _{2} \left[ \begin{subarray}{l} \frac{1}{{r^{{(1)}} }}\left[ \begin{subarray}{l} \frac{{\partial v_{0} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} - \frac{{h_{2} }}{3}\frac{{\partial \psi _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} - \frac{{h_{2}^{2} }}{8}\frac{{\partial \alpha _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} - \frac{4}{{3h_{2}^{2} }}\frac{{\partial \beta _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} + \frac{{h_{2}^{3} }}{{24}}\frac{{\partial \lambda _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} - \frac{{h_{1} }}{3}\frac{{\partial \psi _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} - \frac{{h_{1}^{2} }}{8}\frac{{\partial \alpha _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} \\ - \frac{4}{{3h_{1}^{2} }}\frac{{\partial \beta _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} + \frac{{h_{1}^{3} }}{{24}}\frac{{\partial \lambda _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} + \left[ {\xi ^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}\xi ^{{\left( 1 \right)^{3} }} } \right]\frac{{\partial \psi _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} - \frac{1}{2}\xi ^{{\left( 1 \right)^{2} }} \frac{{\partial \alpha _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} - \frac{4}{{3h_{1}^{2} }}\frac{{\partial \beta _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} - \frac{1}{3}\xi ^{{\left( 1 \right)^{3} }} \frac{{\partial \lambda _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} \end{subarray} \right] + \\ \frac{1}{{r^{{(1)}} }}\left[ {w_{0} - \frac{{h_{2} }}{2}\psi _{3}^{{\left( 2 \right)}} + \frac{{h_{2}^{2} }}{4}\alpha _{3}^{{\left( 2 \right)}} - \frac{{h_{1} }}{2}\psi _{3}^{{\left( 1 \right)}} + \frac{{h_{1}^{2} }}{4}\alpha _{3}^{{\left( 1 \right)}} + \xi ^{{\left( 1 \right)}} \psi _{3}^{{\left( 1 \right)}} + \xi ^{{\left( 1 \right)^{2} }} \alpha _{3}^{{\left( 1 \right)}} } \right] \end{subarray} \right] \end{subarray} \right] + e_{1} \left[ \begin{subarray}{l} \frac{1}{{r^{{(1)}} \sin \xi _{2}^{{\left( 1 \right)}} }}\left[ \begin{subarray}{l} \left[ {1 - \frac{4}{{h_{1}^{2} }}\xi ^{{\left( 1 \right)^{2} }} } \right]\frac{{\partial \psi _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1}^{{\left( 1 \right)}} }} - \\ \xi ^{{\left( 1 \right)}} \frac{{\partial \alpha _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1}^{{\left( 1 \right)}} }} - \xi ^{{\left( 1 \right)^{2} }} \frac{{\partial \lambda _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1}^{{\left( 1 \right)}} }} \end{subarray} \right] \\ + \frac{1}{{r^{{(1)}} }}\left[ {\psi _{3}^{{\left( 1 \right)}} + \xi ^{{\left( 1 \right)}} \alpha _{3}^{{\left( 1 \right)}} } \right] \\ \frac{1}{{r^{{(1)}} }}\left[ \begin{subarray}{l} \left[ {1 - \frac{4}{{h_{1}^{2} }}\xi ^{{\left( 1 \right)^{2} }} } \right]\psi _{2}^{{\left( 1 \right)}} - \xi ^{{\left( 1 \right)}} \alpha _{2}^{{\left( 1 \right)}} \\ - \xi ^{{\left( 1 \right)^{2} }} \lambda _{2}^{{\left( 1 \right)}} \end{subarray} \right]\cot \xi _{2}^{{\left( k \right)}} \end{subarray} \right] \\ + e_{2} \left[ {\frac{1}{{r^{{(1)}} }}\left[ \begin{subarray}{l} \left[ {1 - \frac{4}{{h_{1}^{2} }}\xi ^{{\left( 1 \right)^{2} }} } \right]\frac{{\partial \psi _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} \\ - \xi ^{{\left( 1 \right)}} \frac{{\partial \alpha _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} - \xi ^{{\left( 1 \right)^{2} }} \frac{{\partial \lambda _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} \end{subarray} \right] + \frac{1}{{r^{{(1)}} }}\left[ {\psi _{3}^{{\left( 1 \right)}} + \xi ^{{\left( 1 \right)}} \alpha _{3}^{{\left( 1 \right)}} } \right]} \right] + 2\alpha _{3}^{{\left( 1 \right)}} e_{3} + \frac{2}{{r^{{\left( 1 \right)}} }}\left[ \begin{subarray}{l} e_{1} \left[ \begin{subarray}{l} \frac{1}{{r^{{(1)}} \sin \xi _{2}^{{\left( 1 \right)}} }}\left[ \begin{subarray}{l} \frac{{\partial u_{0} }}{{\partial \xi _{1}^{{\left( 1 \right)}} }} - \frac{{h_{2} }}{3}\frac{{\partial \psi _{1}^{{\left( 2 \right)}} }}{{\partial \xi _{1}^{{\left( 1 \right)}} }} - \frac{{h_{2}^{2} }}{8}\frac{{\partial \alpha _{1}^{{\left( 2 \right)}} }}{{\partial \xi _{1}^{{\left( 1 \right)}} }} - \frac{4}{{3h_{2}^{2} }}\frac{{\partial \beta _{1}^{{\left( 2 \right)}} }}{{\partial \xi _{1}^{{\left( 1 \right)}} }} + \frac{{h_{2}^{3} }}{{24}}\frac{{\partial \lambda _{1}^{{\left( 2 \right)}} }}{{\partial \xi _{1}^{{\left( 1 \right)}} }} - \frac{{h_{1} }}{3}\frac{{\partial \psi _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1}^{{\left( 1 \right)}} }} - \frac{{h_{1}^{2} }}{8}\frac{{\partial \alpha _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1}^{{\left( 1 \right)}} }} \\ - \frac{4}{{3h_{1}^{2} }}\frac{{\partial \beta _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1}^{{\left( 1 \right)}} }} + \frac{{h_{1}^{3} }}{{24}}\frac{{\partial \lambda _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1}^{{\left( 1 \right)}} }} + \left[ {\xi ^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}\xi ^{{\left( 1 \right)^{3} }} } \right]\frac{{\partial \psi _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1}^{{\left( 1 \right)}} }} - \frac{1}{2}\xi ^{{\left( 1 \right)^{2} }} \frac{{\partial \alpha _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1}^{{\left( 1 \right)}} }} - \frac{4}{{3h_{1}^{2} }}\frac{{\partial \beta _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1}^{{\left( 1 \right)}} }} - \frac{1}{3}\xi ^{{\left( 1 \right)^{3} }} \frac{{\partial \lambda _{1}^{{\left( 1 \right)}} }}{{\partial \xi _{1}^{{\left( 1 \right)}} }} \end{subarray} \right] + \\ \frac{1}{{r^{{(1)}} }}\left[ {w_{0} - \frac{{h_{2} }}{2}\psi _{3}^{{\left( 2 \right)}} + \frac{{h_{2}^{2} }}{4}\alpha _{3}^{{\left( 2 \right)}} - \frac{{h_{1} }}{2}\psi _{3}^{{\left( 1 \right)}} + \frac{{h_{1}^{2} }}{4}\alpha _{3}^{{\left( 1 \right)}} + \xi ^{{\left( 1 \right)}} \psi _{3}^{{\left( 1 \right)}} + \xi ^{{\left( 1 \right)^{2} }} \alpha _{3}^{{\left( 1 \right)}} } \right] + \\ \frac{1}{{r^{{(1)}} }}\left[ \begin{subarray}{l} v_{0} - \frac{{h_{2} }}{3}\psi _{2}^{{\left( 2 \right)}} - \frac{{h_{2}^{2} }}{8}\alpha _{2}^{{\left( 2 \right)}} - \frac{4}{{3h_{2}^{2} }}\beta _{2}^{{\left( 2 \right)}} + \frac{{h_{2}^{3} }}{{24}}\lambda _{2}^{{\left( 2 \right)}} - \frac{{h_{1} }}{3}\psi _{2}^{{\left( 1 \right)}} - \frac{{h_{1}^{2} }}{8}\alpha _{2}^{{\left( 1 \right)}} \\ - \frac{4}{{3h_{1}^{2} }}\beta _{2}^{{\left( 1 \right)}} + \frac{{h_{1}^{3} }}{{24}}\lambda _{2}^{{\left( 1 \right)}} + \left[ {\xi ^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}\xi ^{{\left( 1 \right)^{3} }} } \right]\psi _{2}^{{\left( 1 \right)}} - \frac{1}{2}\xi ^{{\left( 1 \right)^{2} }} \alpha _{2}^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}\beta _{2}^{{\left( 1 \right)}} - \frac{1}{3}\xi ^{{\left( 1 \right)^{3} }} \lambda _{2}^{{\left( 1 \right)}} \end{subarray} \right]\cot \xi _{2}^{{\left( k \right)}} \end{subarray} \right] \\ + e_{2} \left[ \begin{subarray}{l} \frac{1}{{r^{{(1)}} }}\left[ \begin{subarray}{l} \frac{{\partial v_{0} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} - \frac{{h_{2} }}{3}\frac{{\partial \psi _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} - \frac{{h_{2}^{2} }}{8}\frac{{\partial \alpha _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} - \frac{4}{{3h_{2}^{2} }}\frac{{\partial \beta _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} + \frac{{h_{2}^{3} }}{{24}}\frac{{\partial \lambda _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} - \frac{{h_{1} }}{3}\frac{{\partial \psi _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} - \frac{{h_{1}^{2} }}{8}\frac{{\partial \alpha _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} \\ - \frac{4}{{3h_{1}^{2} }}\frac{{\partial \beta _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} + \frac{{h_{1}^{3} }}{{24}}\frac{{\partial \lambda _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} + \left[ {\xi ^{{\left( 1 \right)}} - \frac{4}{{3h_{1}^{2} }}\xi ^{{\left( 1 \right)^{3} }} } \right]\frac{{\partial \psi _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} - \frac{1}{2}\xi ^{{\left( 1 \right)^{2} }} \frac{{\partial \alpha _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} \\ - \frac{4}{{3h_{1}^{2} }}\frac{{\partial \beta _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} - \frac{1}{3}\xi ^{{\left( 1 \right)^{3} }} \frac{{\partial \lambda _{2}^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{{\left( 1 \right)}} }} \end{subarray} \right] + \\ \frac{1}{{r^{{(1)}} }}\left[ {w_{0} - \frac{{h_{2} }}{2}\psi _{3}^{{\left( 2 \right)}} + \frac{{h_{2}^{2} }}{4}\alpha _{3}^{{\left( 2 \right)}} - \frac{{h_{1} }}{2}\psi _{3}^{{\left( 1 \right)}} + \frac{{h_{1}^{2} }}{4}\alpha _{3}^{{\left( 1 \right)}} + \xi ^{{\left( 1 \right)}} \psi _{3}^{{\left( 1 \right)}} + \xi ^{{\left( 1 \right)^{2} }} \alpha _{3}^{{\left( 1 \right)}} } \right] \end{subarray} \right] + e_{3} \left( {\psi _{3}^{{\left( 1 \right)}} + 2\xi ^{{\left( 1 \right)}} \alpha _{3}^{{\left( 1 \right)}} } \right) \end{subarray} \right] + \cos \left( {\frac{{\pi \xi ^{{\left( 1 \right)}} }}{{h_{1} }}} \right)\left[ { - \mu _{1} \frac{1}{{r^{{\left( 1 \right)^{2} }} \sin ^{2} \xi _{2} }}\frac{{\partial ^{2} \varphi ^{{\left( 1 \right)}} }}{{\partial \xi _{1}^{2} }} - \mu _{2} \frac{1}{{r^{{\left( 1 \right)^{2} }} }}\left( {\frac{{\partial \varphi ^{{\left( 1 \right)}} }}{{\partial \xi _{2} }}\cot \xi _{2} + \frac{{\partial ^{2} \varphi ^{{\left( 1 \right)}} }}{{\partial \xi _{2}^{2} }}} \right) + \frac{{\pi ^{2} \mu _{3} }}{{h_{1}^{2} }}\varphi ^{{\left( 1 \right)}} } \right] + \frac{{2\pi \mu _{3} }}{{h_{1} r^{{\left( 1 \right)}} }}\varphi ^{{\left( 1 \right)}} \sin \left( {\frac{{\pi \xi ^{{\left( 1 \right)}} }}{{h_{1} }}} \right) \end{subarray} \right] = 0 $$
(12a)
$$ \left[ \begin{subarray}{l} \frac{{e_{5} }}{{r^{{\left( 3 \right)}} \sin \xi _{2} }}\left[ \begin{subarray}{l} \frac{1}{{r^{{(3)}} \sin \xi _{2}^{{\left( 3 \right)}} }}\left[ \begin{subarray}{l} \frac{{\partial ^{2} w_{0} }}{{\partial \xi _{1}^{2} }} + \frac{{h_{2} }}{2}\frac{{\partial ^{2} \psi _{3}^{{\left( 2 \right)}} }}{{\partial \xi _{1}^{2} }} + \frac{{h_{2}^{2} }}{4}\frac{{\partial ^{2} \alpha _{3}^{{\left( 2 \right)}} }}{{\partial \xi _{1}^{2} }} \\ + \frac{{h_{3} }}{2}\frac{{\partial ^{2} \psi _{3}^{{\left( 3 \right)}} }}{{\partial \xi _{1}^{2} }} + \frac{{h_{3}^{2} }}{4}\frac{{\partial ^{2} \alpha _{3}^{{\left( 3 \right)}} }}{{\partial \xi _{1}^{2} }} \\ + \xi ^{{\left( 3 \right)}} \frac{{\partial ^{2} \psi _{3}^{{\left( 3 \right)}} }}{{\partial \xi _{1}^{2} }} + \xi ^{{\left( 3 \right)^{2} }} \frac{{\partial ^{2} \alpha _{3}^{{\left( 3 \right)}} }}{{\partial \xi _{1}^{2} }} \end{subarray} \right] + \left[ {\left[ {1 - \frac{4}{{h_{3}^{2} }}\xi ^{{\left( 3 \right)^{2} }} } \right]\frac{{\partial \psi _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} - \xi ^{{\left( 3 \right)}} \frac{{\partial \alpha _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} - \xi ^{{\left( 3 \right)^{2} }} \frac{{\partial \lambda _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }}} \right] \\ - \frac{1}{{r^{{(3)}} }}\left[ \begin{gathered} \frac{{\partial u_{0} }}{{\partial \xi _{1} }} + \frac{{h_{2} }}{3}\frac{{\partial \psi _{1}^{{\left( 2 \right)}} }}{{\partial \xi _{1} }} - \frac{{h_{2}^{2} }}{8}\frac{{\partial \alpha _{1}^{{\left( 2 \right)}} }}{{\partial \xi _{1} }} - \frac{4}{{3h_{2}^{2} }}\frac{{\partial \beta _{1}^{{\left( 2 \right)}} }}{{\partial \xi _{1} }} \hfill \\ - \frac{{h_{2}^{3} }}{{24}}\frac{{\partial \lambda _{1}^{{\left( 2 \right)}} }}{{\partial \xi _{1} }} + \frac{{h_{3} }}{3}\frac{{\partial \psi _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} - \frac{{h_{3}^{2} }}{8}\frac{{\partial \alpha _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} \hfill \\ - \frac{4}{{3h_{3}^{2} }}\frac{{\partial \beta _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} - \frac{{h_{3}^{3} }}{{24}}\frac{{\partial \lambda _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} + \left[ {\xi ^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}\xi ^{{\left( 3 \right)^{3} }} } \right]\frac{{\partial \psi _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} - \frac{1}{2}\xi ^{{\left( 3 \right)^{2} }} \frac{{\partial \alpha _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} \hfill \\ - \frac{4}{{3h_{3}^{2} }}\frac{{\partial \beta _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} - \frac{1}{3}\xi ^{{\left( 3 \right)^{3} }} \frac{{\partial \lambda _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1} }} \hfill \\ \end{gathered} \right] \end{subarray} \right] + \frac{{e_{4} }}{{r^{{\left( 3 \right)}} }}\left[ \begin{subarray}{l} \left[ {\left[ {1 - \frac{4}{{h_{3}^{2} }}\xi ^{{\left( 3 \right)^{2} }} } \right]\frac{{\partial \psi _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} - \xi ^{{\left( 3 \right)}} \frac{{\partial \alpha _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} - \xi ^{{\left( 3 \right)^{2} }} \frac{{\partial \lambda _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }}} \right] + \frac{1}{{r^{{(3)}} }}\left[ \begin{subarray}{l} \frac{{\partial ^{2} w_{0} }}{{\partial \xi _{2}^{2} }} + \frac{{h_{2} }}{2}\frac{{\partial ^{2} \psi _{3}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{2} }} + \frac{{h_{2}^{2} }}{4}\frac{{\partial ^{2} \alpha _{3}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{2} }} + \frac{{h_{3} }}{2}\frac{{\partial ^{2} \psi _{3}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{2} }} \\ + \frac{{h_{3}^{2} }}{4}\frac{{\partial ^{2} \alpha _{3}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{2} }} + \xi ^{{\left( 3 \right)}} \frac{{\partial ^{2} \psi _{3}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{2} }} + \xi ^{{\left( 3 \right)^{2} }} \frac{{\partial ^{2} \alpha _{3}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{2} }} \end{subarray} \right] \\ - \frac{1}{{r^{{(3)}} }}\left[ \begin{subarray}{l} \frac{{\partial v_{0} }}{{\partial \xi _{2} }} + \frac{{h_{2} }}{3}\frac{{\partial \psi _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2} }} - \frac{{h_{2}^{2} }}{8}\frac{{\partial \alpha _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2} }} - \frac{4}{{3h_{2}^{2} }}\frac{{\partial \beta _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2} }} \\ - \frac{{h_{2}^{3} }}{{24}}\frac{{\partial \lambda _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2} }} + \frac{{h_{3} }}{3}\frac{{\partial \psi _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} - \frac{{h_{3}^{2} }}{8}\frac{{\partial \alpha _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} - \frac{4}{{3h_{3}^{2} }}\frac{{\partial \beta _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} - \frac{{h_{3}^{3} }}{{24}}\frac{{\partial \lambda _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} + \left[ {\xi ^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}\xi ^{{\left( 3 \right)^{3} }} } \right]\frac{{\partial \psi _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} \\ - \frac{1}{2}\xi ^{{\left( 3 \right)^{2} }} \frac{{\partial \alpha _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} - \frac{4}{{3h_{3}^{2} }}\frac{{\partial \beta _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} - \frac{1}{3}\xi ^{{\left( 3 \right)^{3} }} \frac{{\partial \lambda _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2} }} \end{subarray} \right] \\ + \cot \xi _{2} \left[ \begin{subarray}{l} \frac{1}{{r^{{(3)}} }}\left[ \begin{subarray}{l} \frac{{\partial v_{0} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} + \frac{{h_{2} }}{3}\frac{{\partial \psi _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} - \frac{{h_{2}^{2} }}{8}\frac{{\partial \alpha _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} - \frac{4}{{3h_{2}^{2} }}\frac{{\partial \beta _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} - \frac{{h_{2}^{3} }}{{24}}\frac{{\partial \lambda _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} + \frac{{h_{3} }}{3}\frac{{\partial \psi _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} - \frac{{h_{3}^{2} }}{8}\frac{{\partial \alpha _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} \\ - \frac{4}{{3h_{3}^{2} }}\frac{{\partial \beta _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} - \frac{{h_{3}^{3} }}{{24}}\frac{{\partial \lambda _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} + \left[ {\xi ^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}\xi ^{{\left( 3 \right)^{3} }} } \right]\frac{{\partial \psi _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} - \frac{1}{2}\xi ^{{\left( 3 \right)^{2} }} \frac{{\partial \alpha _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} - \frac{4}{{3h_{3}^{2} }}\frac{{\partial \beta _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} - \frac{1}{3}\xi ^{{\left( 3 \right)^{3} }} \frac{{\partial \lambda _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} \end{subarray} \right] + \\ \frac{1}{{r^{{(3)}} }}\left[ {w_{0} + \frac{{h_{2} }}{2}\psi _{3}^{{\left( 2 \right)}} + \frac{{h_{2}^{2} }}{4}\alpha _{3}^{{\left( 2 \right)}} + \frac{{h_{3} }}{2}\psi _{3}^{{\left( 3 \right)}} + \frac{{h_{3}^{2} }}{4}\alpha _{3}^{{\left( 3 \right)}} + \xi ^{{\left( 3 \right)}} \psi _{3}^{{\left( 3 \right)}} + \xi ^{{\left( 3 \right)^{2} }} \alpha _{3}^{{\left( 3 \right)}} } \right] \end{subarray} \right] \end{subarray} \right] + e_{1} \left[ \begin{subarray}{l} \frac{1}{{r^{{(3)}} \sin \xi _{2}^{{\left( 3 \right)}} }}\left[ \begin{subarray}{l} \left[ {1 - \frac{4}{{h_{3}^{2} }}\xi ^{{\left( 3 \right)^{2} }} } \right]\frac{{\partial \psi _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1}^{{\left( 3 \right)}} }} \\ - \xi ^{{\left( 3 \right)}} \frac{{\partial \alpha _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1}^{{\left( 3 \right)}} }} - \xi ^{{\left( 3 \right)^{2} }} \frac{{\partial \lambda _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1}^{{\left( 3 \right)}} }} \end{subarray} \right] + \\ \frac{1}{{r^{{(3)}} }}\left[ {\psi _{3}^{{\left( 3 \right)}} + 2\xi ^{{\left( 3 \right)}} \alpha _{3}^{{\left( 3 \right)}} } \right] + \\ \frac{1}{{r^{{(3)}} }}\left[ \begin{subarray}{l} \left[ {1 - \frac{4}{{h_{3}^{2} }}\xi ^{{\left( 3 \right)^{2} }} } \right]\psi _{2}^{{\left( 3 \right)}} - \xi ^{{\left( 3 \right)}} \alpha _{2}^{{\left( 3 \right)}} \\ - \xi ^{{\left( 3 \right)^{2} }} \lambda _{2}^{{\left( 3 \right)}} \end{subarray} \right]\cot \xi _{2}^{{\left( 3 \right)}} \end{subarray} \right] \\ + e_{2} \left[ {\frac{1}{{r^{{(3)}} }}\left[ \begin{subarray}{l} \left[ {1 - \frac{4}{{h_{3}^{2} }}\xi ^{{\left( 3 \right)^{2} }} } \right]\frac{{\partial \psi _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} \\ - \xi ^{{\left( 3 \right)}} \frac{{\partial \alpha _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} - \xi ^{{\left( 3 \right)^{2} }} \frac{{\partial \lambda _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} \end{subarray} \right] + \frac{1}{{r^{{(3)}} }}\left[ {\psi _{3}^{{\left( 3 \right)}} + 2\xi ^{{\left( 3 \right)}} \alpha _{3}^{{\left( 3 \right)}} } \right]} \right] + 2\alpha _{3}^{{\left( 3 \right)}} e_{3} + \frac{2}{{r^{{\left( 3 \right)}} }}\left[ \begin{subarray}{l} e_{1} \left[ \begin{subarray}{l} \frac{1}{{r^{{(3)}} \sin \xi _{2}^{{\left( 3 \right)}} }}\left[ \begin{subarray}{l} \frac{\partial }{{\partial \xi _{1}^{{\left( 3 \right)}} }}\frac{{\partial u_{0} }}{{\partial \xi _{1}^{{\left( 3 \right)}} }} + \frac{{h_{2} }}{3}\frac{{\partial \psi _{1}^{{\left( 2 \right)}} }}{{\partial \xi _{1}^{{\left( 3 \right)}} }} - \frac{{h_{2}^{2} }}{8}\frac{{\partial \alpha _{1}^{{\left( 2 \right)}} }}{{\partial \xi _{1}^{{\left( 3 \right)}} }} - \frac{4}{{3h_{2}^{2} }}\frac{{\partial \beta _{1}^{{\left( 2 \right)}} }}{{\partial \xi _{1}^{{\left( 3 \right)}} }} - \frac{{h_{2}^{3} }}{{24}}\frac{{\partial \lambda _{1}^{{\left( 2 \right)}} }}{{\partial \xi _{1}^{{\left( 3 \right)}} }} + \frac{{h_{3} }}{3}\frac{{\partial \psi _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1}^{{\left( 3 \right)}} }} - \frac{{h_{3}^{2} }}{8}\frac{{\partial \alpha _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1}^{{\left( 3 \right)}} }} \\ - \frac{4}{{3h_{3}^{2} }}\frac{{\partial \beta _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1}^{{\left( 3 \right)}} }} - \frac{{h_{3}^{3} }}{{24}}\frac{{\partial \lambda _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1}^{{\left( 3 \right)}} }} + \left[ {\xi ^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}\xi ^{{\left( 3 \right)^{3} }} } \right]\frac{{\partial \psi _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1}^{{\left( 3 \right)}} }} - \frac{1}{2}\xi ^{{\left( 3 \right)^{2} }} \frac{{\partial \alpha _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1}^{{\left( 3 \right)}} }} - \frac{4}{{3h_{3}^{2} }}\frac{{\partial \beta _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1}^{{\left( 3 \right)}} }} - \frac{1}{3}\xi ^{{\left( 3 \right)^{3} }} \frac{{\partial \lambda _{1}^{{\left( 3 \right)}} }}{{\partial \xi _{1}^{{\left( 3 \right)}} }} \end{subarray} \right] + \\ \frac{1}{{r^{{(3)}} }}\left[ {w_{0} + \frac{{h_{2} }}{2}\psi _{3}^{{\left( 2 \right)}} + \frac{{h_{2}^{2} }}{4}\alpha _{3}^{{\left( 2 \right)}} + \frac{{h_{3} }}{2}\psi _{3}^{{\left( 3 \right)}} + \frac{{h_{3}^{2} }}{4}\alpha _{3}^{{\left( 3 \right)}} + \xi ^{{\left( 3 \right)}} \psi _{3}^{{\left( 3 \right)}} + \xi ^{{\left( 3 \right)^{2} }} \alpha _{3}^{{\left( 3 \right)}} } \right] + \\ \frac{1}{{r^{{(3)}} }}\left[ \begin{subarray}{l} v_{0} + \frac{{h_{2} }}{3}\psi _{2}^{{\left( 2 \right)}} - \frac{{h_{2}^{2} }}{8}\alpha _{2}^{{\left( 2 \right)}} - \frac{4}{{3h_{2}^{2} }}\beta _{2}^{{\left( 2 \right)}} - \frac{{h_{2}^{3} }}{{24}}\lambda _{2}^{{\left( 2 \right)}} + \frac{{h_{3} }}{3}\psi _{2}^{{\left( 3 \right)}} - \frac{{h_{3}^{2} }}{8}\alpha _{2}^{{\left( 3 \right)}} \\ - \frac{4}{{3h_{3}^{2} }}\beta _{2}^{{\left( 3 \right)}} - \frac{{h_{3}^{3} }}{{24}}\lambda _{2}^{{\left( 3 \right)}} + \left[ {\xi ^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}\xi ^{{\left( 3 \right)^{3} }} } \right]\psi _{2}^{{\left( 3 \right)}} - \frac{1}{2}\xi ^{{\left( 3 \right)^{2} }} \alpha _{2}^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}\beta _{2}^{{\left( 3 \right)}} - \frac{1}{3}\xi ^{{\left( 3 \right)^{3} }} \lambda _{2}^{{\left( 3 \right)}} \end{subarray} \right]\cot \xi _{2}^{{\left( k \right)}} \end{subarray} \right] \\ + e_{2} \left[ \begin{subarray}{l} \frac{1}{{r^{{(3)}} }}\left[ \begin{subarray}{l} \frac{{\partial v_{0} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} + \frac{{h_{2} }}{3}\frac{{\partial \psi _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} - \frac{{h_{2}^{2} }}{8}\frac{{\partial \alpha _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} - \frac{4}{{3h_{2}^{2} }}\frac{{\partial \beta _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} - \frac{{h_{2}^{3} }}{{24}}\frac{{\partial \lambda _{2}^{{\left( 2 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} + \frac{{h_{3} }}{3}\frac{{\partial \psi _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} - \frac{{h_{3}^{2} }}{8}\frac{{\partial \alpha _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} \\ - \frac{4}{{3h_{3}^{2} }}\frac{{\partial \beta _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} - \frac{{h_{3}^{3} }}{{24}}\frac{{\partial \lambda _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} + \left[ {\xi ^{{\left( 3 \right)}} - \frac{4}{{3h_{3}^{2} }}\xi ^{{\left( 3 \right)^{3} }} } \right]\frac{{\partial \psi _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} - \frac{1}{2}\xi ^{{\left( 3 \right)^{2} }} \frac{{\partial \alpha _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} \\ - \frac{4}{{3h_{3}^{2} }}\frac{{\partial \beta _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} - \frac{1}{3}\xi ^{{\left( 3 \right)^{3} }} \frac{{\partial \lambda _{2}^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{{\left( 3 \right)}} }} \end{subarray} \right] + \\ \frac{1}{{r^{{(3)}} }}\left[ {w_{0} + \frac{{h_{2} }}{2}\psi _{3}^{{\left( 2 \right)}} + \frac{{h_{2}^{2} }}{4}\alpha _{3}^{{\left( 2 \right)}} + \frac{{h_{3} }}{2}\psi _{3}^{{\left( 3 \right)}} + \frac{{h_{3}^{2} }}{4}\alpha _{3}^{{\left( 3 \right)}} + \xi ^{{\left( 3 \right)}} \psi _{3}^{{\left( 3 \right)}} + \xi ^{{\left( 3 \right)^{2} }} \alpha _{3}^{{\left( 3 \right)}} } \right] \end{subarray} \right] + e_{3} \left( {\psi _{3}^{{\left( 3 \right)}} + 2\xi ^{{\left( 3 \right)}} \alpha _{3}^{{\left( 3 \right)}} } \right) \end{subarray} \right] + \cos \left( {\frac{{\pi \xi ^{{\left( 3 \right)}} }}{{h_{1} }}} \right)\left[ { - \mu _{1} \frac{1}{{r^{{\left( 3 \right)^{2} }} \sin ^{2} \xi _{2} }}\frac{{\partial ^{2} \varphi ^{{\left( 3 \right)}} }}{{\partial \xi _{1}^{2} }} - \mu _{2} \frac{1}{{r^{{\left( 3 \right)^{2} }} }}\left( {\frac{{\partial \varphi ^{{\left( 3 \right)}} }}{{\partial \xi _{2} }}\cot \xi _{2} + \frac{{\partial ^{2} \varphi ^{{\left( 3 \right)}} }}{{\partial \xi _{2}^{2} }}} \right) + \frac{{\pi ^{2} \mu _{3} }}{{h_{1}^{2} }}\varphi ^{{\left( 3 \right)}} } \right] + \frac{{2\pi \mu _{3} }}{{h_{1} r^{{\left( 3 \right)}} }}\varphi ^{{\left( 3 \right)}} \sin \left( {\frac{{\pi \xi ^{{\left( 3 \right)}} }}{{h_{1} }}} \right) \end{subarray} \right] = 0 $$
(12b)

4 Validation of the theoretical solution with experimental tests

In order to validate the layerwise theory along with higher-order shear deformation theory, the results of the current theory are compared to those obtained by the experimental tests carried out by other researchers for a rectangular composite plate subjected to the low-velocity impact.

In Ref. [44], an experimental test was carried out for the rectangular composite plate as shown in Fig. 3. According to Fig. 3, the clamped rectangular composite with the carbon-fibers laminates and the ply-angle orientation [0/-45/45/90]s is subjected to the low-velocity impact of a steel hemispherical projectile with an initial velocity of 4 m/s. The composite laminate made of the epoxy vinyl ester matrix (Derakane 470-30-S) reinforced with a level of 30% carbon fiber volumetric ratio. The mechanical properties of the carbon-fiber laminate are presented in Table 1. In addition, the total thickness, length, and width dimensions of the rectangular composite plate are 2.5 mm, 125 mm, and 75 mm, respectively.

Fig. 3
figure 3

The rectangular composite laminated plate with ply-angle [0/-45/45/90]s subjected to the low-velocity impact of a hemispherical projectile with an initial velocity of 4 m/s

Full size image
Table 1 The mechanical properties of the composite carbon fiber/epoxy laminated plate [44]
Full size table

By using LT along with HSDT, the results of Fig. 4 for the displacement variation in terms of time at the point of impact were derived. According to Fig. 4, the results of the experimental tests were compared to those obtained by theoretical solution. It can be seen that the results of LT have good agreement with a difference of less than 7% with the results of the experimental tests.

Fig. 4
figure 4

The variation of displacement in terms of time in the composite plate subjected to a hemispherical projectile with an initial velocity of 4 m/s

Full size image

5 Numerical results and discussion for the spherical sandwich sector

According to Fig. 1, the spherical sandwich shell is exposed to the low-velocity impact of a spherical ball that moves at the initial velocity of V0 = 50 m/s. Furthermore, the normal contact pressure distribution function is considered in terms of time, according to Eq. (8b) and assuming V0 = 50 m/s. By solving the nineteen equations [Eqs. (10) and (12)], the stress components can be calculated in terms of time in the sector.

The spherical coordinates of two points, as well as the six paths that are highlighted in Fig. 1, are presented in the spherical coordinate system shown in Tables 2 and 3, respectively. The mechanical properties of the three layers of the spherical sandwich shell and spherical ball are presented in Table 4.

Table 2 The geometrical location of two points defined in Fig. 1 on the spherical coordinate system
Full size table
Table 3 The location and direction of the six paths defined in Fig. 1, based on its first and end-points in the spherical coordinate system
Full size table
Table 4 Mechanical properties of the sandwich shell [30]
Full size table

Figure 5 shows the stress distribution in terms of time in points 1 and 2 for the five samples as FG-UV, FG-▽, FG-△, FG-O, and FG-X. Figure 5a–c shows the variation of the radial stress \(\left( {\sigma _{\xi } } \right)\), the circumferential stress \(\left( {\sigma _{{\xi _{1} }} } \right)\), and the meridian stress \(\left( {\sigma _{{\xi _{2} }} } \right)\) in terms of time at point 1, respectively. Whereas, Fig. 5d shows the variation of the shear stress \(\left( {\tau _{{_{{\xi \xi _{2} }} }} } \right)\) in terms of time at point 2. The shear stress is shown only at point 2 due to the fact that the maximum shear stress at this point causes on the top face sheet.

Fig. 5
figure 5

The variation of the stress components in terms of time, a \(\sigma _{\xi }\) at point 1, b \(\sigma _{{\xi _{1} }}\) at point 1, c \(\sigma _{{\xi _{2} }}\) at point 1, d \(\tau _{{\xi \xi _{2} }}\) at point 2, for \(h/R = 0.1,h_{1} /h = 0.1,R = 5\,{\text{mm}}\) and \(\chi _{0} = 30^{ \circ }\)

Full size image

According to Fig. 5, it is observed that, the mechanical properties of the core have more effect on the stress components in the top face sheets. Moreover, it can be seen that the sector with FG-UV and FG-O has the minimum and maximum stress distribution in point 1. This means that when the nanotubes are located in the center of the core relative to when they are made uniform leads to an increase in the stress distribution in the top face sheet. According to Fig. 5d, it can be seen that this nanotube arrangement has the opposite effect on shear stress.

Figure 6 shows the stress distribution in the outermost layer of the top piezoelectric face sheet (path 1) at t = tmax/2, where the maximum stresses are observed in the sandwich shell. As shown in Fig. 6a–c, the maximum radial, circumferential, and meridian stresses are observed at the angle ξ2 = 0° in the outermost layer of the top face sheet. According to Fig. 6d, the maximum shear stress occurs at the maximum radius of the contact area (r = amax or ξ2 = amax/(R + h/2)). According to Fig. 6a–c, it can be seen that the radial, circumferential, and meridian stresses are maximum in the sample FG-O as well as being minimum in the sample FG-UV. According to Fig. 6d, it can be seen that the shear stress has the maximum and minimum value in the samples FG-UV and FG-O, respectively.

Fig. 6
figure 6

The variation of the stress components in terms of \(\xi _{2}\) on path 1, a \(\sigma _{\xi }\), b \(\sigma _{{\xi _{1} }}\), c \(\sigma _{{\xi _{2} }}\), d \(\tau _{{\xi \xi _{2} }}\), for \(h/R = 0.1,h_{1} /h = 0.1,R = 5\,{\text{mm}}\) and \(\chi _{0} = 30^{ \circ }\)

Full size image

Figure 7 shows the stress distribution in the innermost layer of the top piezoelectric face sheet (path 2) at t = tmax/2, where the maximum stresses are observed in the sandwich shell. As shown in Fig. 7, the maximum radial, circumferential and meridian stresses are generated at the angle ξ2 = 0 in the innermost layer of the top face sheet. In addition, the maximum shear stress occurs at the maximum radius of the contact area (r = amax or ξ2 = amax/(R + h/2)). According to Fig. 4a, b, it can be seen that the radial and circumferential stresses are maximum in the sample FG-▽ as well as being minimum in the sample FG-UV. This means that when the nanotubes are located in the top layer of the core relative to when they are made uniform leads to an increase in the radial and circumferential stresses in the innermost layer of the top face sheet.

Fig. 7
figure 7

The variation of the stress components in the top piezoelectric layer in terms of \(\xi _{2}\) on path 2, a \(\sigma _{\xi }\), b \(\sigma _{{\xi _{1} }}\), c \(\sigma _{{\xi _{2} }}\), d \(\tau _{{\xi \xi _{2} }}\), for \(h/R = 0.1,h_{1} /h = 0.1,R = 5\,{\text{mm}}\) and \(\chi _{0} = 30^{ \circ }\)

Full size image

In addition, according to Fig. 7c, d, the meridian and shear stresses are maximum in the sample FG-△ as well as being minimum in the sample FG-▽. This means that when the nanotubes are located in the bottom and top layers of the core, the maximum and minimum in both the meridian and shear stresses in the innermost layer of the top face sheet are generated, respectively.

Figure 8 shows the stress distribution in the outermost layer of the core (path 2) at t = tmax/2. As shown in Fig. 8, the maximum radial, circumferential, and shear stresses are generated at the angle ξ2 = amax/(R + h/2). In addition, the maximum meridian stress occurs at the angle ξ2 = 0. According to Fig. 8a, it can be seen that the radial stress has the maximum and minimum value in the samples FG-O and FG-UV, respectively. This means that when the nanotubes are located in the center of the core relative to when they are made uniform leads to an increase in the radial stress in the core.

Fig. 8
figure 8

The variation of the stress components in FG-CNT core in terms of \(\xi _{2}\) on path 2, a \(\sigma _{\xi }\), b \(\sigma _{{\xi _{1} }}\), c \(\sigma _{{\xi _{2} }}\), d \(\tau _{{\xi \xi _{2} }}\), for \(h/R = 0.1,h_{1} /h = 0.1,\,R = 5\,{\text{mm}}\) and \(\chi _{0} = 30^{ \circ }\)

Full size image

According to Fig. 8b, d, it can be seen that the circumferential and shear stresses are maximum in the sample FG-△ as well as being minimum in the sample FG-▽. This means that when the nanotubes are located in the bottom and top layers of the core, the maximum and minimum in both the circumferential and shear stresses in the core are generated, respectively.

According to Fig. 8c, it can be seen that the meridian stress has the maximum and minimum value in the samples FG-△ and FG-UV, respectively. This means that when the nanotubes are located in the bottom layer of the core relative to when they are made uniform leads to an increase in the meridian stress in the core.

Figure 9 shows the maximum radial, circumferential, and shear stresses on path 5, as well as the maximum meridian stress on path 3 at the core at t = tmax/2. According to Fig. 9a, it can be seen that the radial stress has the maximum and minimum value in the samples FG-O and FG-UV, respectively. According to Fig. 9b, it can be seen that the circumferential stress has the maximum and minimum value in the samples FG-△ and FG-UV, respectively. According to Fig. 9c, it can be seen that the meridian stress has the maximum and minimum value in the samples FG-▽ and FG-UV, respectively. According to Fig. 9d, it can be seen that the shear stress has the maximum and minimum value in the samples FG-△ and FG-▽, respectively.

Fig. 9
figure 9

The variation of the stress components in terms of \(\xi ^{{\left( 2 \right)}} /h_{2}\), a \(\sigma _{\xi }\) on path 5, b \(\sigma _{{\xi _{1} }}\) on path 5, c \(\sigma _{{\xi _{2} }}\) on path 3, d \(\tau _{{\xi \xi _{2} }}\) on path 5, for \(h/R = 0.1,h_{1} /h = 0.1,\,R = 5\,{\text{mm}}\) and \(\chi _{0} = 30^{ \circ }\)

Full size image

Figure 10 shows the maximum radial, circumferential, and meridian stresses on path 4, as well as the maximum shear stress on path 6 at the top piezoelectric face sheet at t = tmax/2. According to Fig. 10, it can be seen that the maximum stress components in the sample FG-O are generated compared to the other four models of FG-CNT core. In addition, it can be seen that the minimum stress components in the sample FG-UV are generated compared to the other four models of FG-CNT core. This means that the top face sheet experiences more stress distribution when the nanotubes are located in the center of the core. Whereas, the top face sheet experiences minimal stress distribution when the nanotubes are made uniform in the core.

Fig. 10
figure 10

The variation of the stress components in terms of \(\xi ^{{\left( 3 \right)}} /h_{1}\), a \(\sigma _{\xi }\) on path 4, b \(\sigma _{{\xi _{1} }}\) on path 4, c \(\sigma _{{\xi _{2} }}\) on path 4, d \(\tau _{{\xi \xi _{2} }}\) on path 6, for \(h/R = 0.1,h_{1} /h = 0.1,\,R = 5\,{\text{mm}}\) and \(\chi _{0} = 30^{ \circ }\)

Full size image

Figure 11 shows the variation of the voltage changes caused by the impact of the spherical elastic ball in the top face sheet layer at the point with spherical coordinate (R + (h − h3)/2, 0, 0). According to the figure, it can be observed that the impact phenomena lead to the production of the voltage in the piezoelectric layer in terms of time. Moreover, the maximum and minimum values of the voltage are generated in the sandwich sector with the samples FG-▽ and FG-X, respectively. Furthermore, it can be seen that for tmax ≤ t, the voltage acts as a damping function in terms of time and eventually becomes zero.

Fig. 11
figure 11

The variation of the voltage changes caused by the impact of the spherical elastic ball in the top face sheet layer at the point with spherical coordinate (R + (h − h3)/2, 0, 0) for \(h/R = 0.1,h_{1} /h = 0.1,\,R = 5\,{\text{mm}}\) and \(\chi _{0} = 30^{ \circ }\)

Full size image

6 Conclusions

In the current study, a new theory solution was introduced in the field of layerwise theory along with higher-order shear deformation theory to calculate the stress distribution in the three-layer spherical sandwich shell subjected to the low-velocity impact. In order to solve the impact problem at the three-layer spherical sandwich shell, the sets of the nineteen nonlinear equations should be solved. The results showed that the sample of the FG-CNT core has more effect on the stress distribution in the top face sheet. In addition, the results showed that the top face sheet experiences more stress distribution when the nanotubes are located in the center of the core. Moreover, the top face sheet experiences minimal stress distribution when the nanotubes are made uniform in the core.

According to the results, it can be observed that although the theoretical calculations of the present study are very complex and heavy, LT was able to efficiently solve the issue of the low-velocity impact in a three-layer spherical sector. Moreover, the advantages of the theory are categorized as follows:

  • Solving the low-velocity impact issue of the three-layer sandwich sector with piezoelectric face sheets and FG-CNT core in less than 15 min with high accuracy.

  • Ability to change the geometric dimensions as well as the mechanical properties of the layers and find relevant results, easily.

Finally, the limitations of the current theoretical based on LT along with HSDT are:

  • The other geometry of the structures

    In complex geometries, due to the high volume of calculation, this method may not work well.

  • When the issue of mechanical failure arises

    Due to the mechanical failure, the geometry of the structure will certainly undergo a large deformed shape. The current study only can be used for small deformation and small strain.

  • The classical non-adhesive elastic contact theory and Hunter's relationship.

Due to the different nature of the high-velocity impact, this theory is not able to accurately estimate the contact pressure in terms of time and other parameters.