1 Introduction

The development of electric vehicles (EVs) is a challenge for the automotive industry to face limited fossil fuel sources and environmental issues [1,2,3], of which a major parcel is generated by vehicles propelled by combustion engines [2, 4, 5]. The main characteristics of EVs are no fuel consumption, little noise and good energy efficiency, which makes the EVs the best alternative to reach zero-pollution mobility in the future [6]. However, this kind of vehicles needs to attempt some characteristic as low energy consumption, a good range and acceptable driving performance to become competitive in the market [7]. To achieve these goals, the biggest limitation is related to the energy storage systems (ESS), which have a great impact on vehicle range, energy consumption, weight and cost of these vehicles [1].

Batteries are considered a vital component due to its influence on vehicle acceleration and autonomy on a single charge [8]. Although, batteries have drawbacks such as low-power density, compared with other energy storage devices, a high cost and a lower lifetime. Several types of researches have been made to overcome some of these limitations. Batteries cost, energy density, and especially lifetime are decisive for the EV market [9]. The combination of batteries with other storage devices could be relevant to obtain better performance [10]. Therefore, hybrid energy storage systems (HESSs) can be developed by combining batteries, ultracapacitors, flywheel and/or hydrogen cell [11, 12].

The most common types of HESS are composed of batteries and ultracapacitors [10], seeking to combine the advantages from different power sources [13]. The high-energy-density of batteries provides vehicle autonomy and supports slow transients. In the meantime, the high-power density of the ultracapacitors can help the batteries to prolong their lifetime, which is susceptible to high-duty fluctuated currents [14] and also can recover energy from the regenerative braking. Moreover, the battery/ultracapacitors HESS enables battery size reduction, decreasing its cost, and also enhancing its power management. In EVs applications, it is not possible for the system to be powered only by ultracapacitors because the energy density is low and the price of an ultracapacitors bank is high [15].

Notwithstanding, the HESS practical performance is significantly influenced by its complex sizing and the power management strategy [16]. The HESS sizing challenge is to find the appropriate combination of ultracapacitor banks and battery cells to minimize costs and mass of the HESS and also maximize the battery’s expected life cycle. Some studies have been done into optimal HESS sizing [17,18,19,20]. In most cases, the optimization constraints are transient power requirements, whereas cost, system efficiency, or fuel economy are usually selected as optimization objectives [21].

In power management control (PMC), rule-based strategies and optimization-based approaches are widely used [22, 23]. The first is normally created according to the engineering experience, heuristics, intuition, or mathematical models [16]. The second approach is classified as real-time and global optimizations. This last is composed for the neural network [24], dynamic programming [25, 26], convex programming [27], and other multi-objective optimization [6, 17, 28].

Most of the papers presented in the literature study the sizing and power management challenges separately [29], however, with this approach, only sub-optimal solutions are obtained [16]. Therefore, it is not possible to obtain the global optimal performance once the design and control problems of a HESS are coupled in practice [30]. In this way, this work will investigate the sizing, and the power management of the HESS, which will be also used as design variables to be optimized.

Regarding the vehicle topology, Shi et al. [31] and Liu et al. [32] highlighted the advantages of distributed electric propelling systems, with multiple actuators, concerning vehicle stability performance. Moreover, Othaganont et al. [7] optimized the drivetrain configurations considering four different EMs distribution; single EM assemble to a final drive system at the frontal wheels; two in-wheel EMs connected directly to the frontal wheels; and the replication of these previously described typologies coupled to both, frontal and rear propelling systems. Holjevac et al. [6] also showed the EMs associated with differential transmission assembled to the frontal and rear axles. Furthermore, Eckert et al. [19] and Li et al. [33] studied improved EMs and HESS configurations for the four in-wheel drive EV. Beyond that, Corrêa et al. [34] and Eckert et al. [20, 35] also studied some of the listed configurations and added two extra alternatives that mixed the in-wheel and differential EMs assembly (Fig. 1), resulting in a better trade-off between battery size and driving range. However, all the mentioned EV configurations were analyzed only when submitted to standard driving cycles as the NEDC, WLTP, FTP-75, HWFET, and US06.

Fig. 1
figure 1

Electric vehicle configuration

Full size image

As mentioned before, previous studies used standard driving cycles that may generate solutions that are not optimal when applied to real driving conditions. On the other hand, the urban driving cycles are more complex, due to the frequent vehicle acceleration followed by deceleration [33], and are directly associated with the vehicle energy economy [36]. Therefore, this paper focuses on reaching an EV optimized for a real urban driving scenario, by simulating an experimentally obtained driving cycle of Campinas [37], one of the most populous cities of São Paulo State - Brazil. In addition, this cycle considers the road altimetry, a very important feature that influences the downhill regenerative braking and the uphill requested EMs traction power, frequently not considered in driving cycle standards.

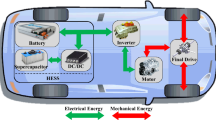
The EV configuration used in this work is powered by an EM connected to a differential transmission system, which drives the rear wheels, and by two in-wheel electric motors (EMs) coupled directly to the front wheels, as shown in Fig. 1. The split of the power demand between the drive systems and the control of the power source which fulfills the EMs is done by the HESS power management control (PMC). The HESS analyzed considers a battery pack associated with an ultracapacitor.

In this way, the main purpose of this work is to optimize the mentioned EV configuration (Fig. 1) drivetrain and HESS size, by means of a bi-criteria optimization problem that minimizes the total mass of the HESS (battery + capacitors) and maximizes the EV driving range, under a real urban driving cycle. Thereby, a genetic algorithm (GA) was used considering the following design variables: battery voltage, battery capacity, ultracapacitors model, ultracapacitors arrangement, EMs torque curves, differential transmission ratio, and the power split (between the HESS battery and capacitors) control parameter. The robust rule-based PMC was applied [35] to find the best efficiency trade-off between the propelling systems while minimizes the HESS discharges.

Finally, the Pareto frontier of non-dominated solutions defines the optimum EV configurations, in which the minimum HESS mass and the maximum drive range configurations were analyzed, in the same way as the solution that presents the best trade-off regarding the optimized criteria.

2 Simulation parameters

The analysis made considers the vehicle longitudinal dynamics modeled by the movement resistance forces, using the equations presented by Gillespie [38], associated with the maximum transmissible traction force [39], initially implemented to conventional vehicles [40, 41], and adapted to be applied on an EV in the current work.

One of the major movement resistance forces, mainly at low speed, is the rolling resistance (\(R_x\)) [N], caused by the tire deformation and adhesion on the contact area. It is a function of the vehicle speed (V) [m/s], mass (M) [kg], gravity acceleration (g) [m/s\(^2\)] and road angle (\(\alpha\)) [rad], described by Eq. (1).

$$\begin{aligned} R_x= 0.01\left( 1+\frac{2.24~V}{100}\right) \,Mg\cos {\alpha } \end{aligned}$$
(1)

Another load is the air resistance, represented by the aerodynamic drag (\(D_\mathrm{A}\)) [N]. It is determined by Eq. (2) and depends on the air density (\(\rho\)) [kg/m\(^3\)], on the vehicle speed (V) [m/s] and on the vehicle geometry (drag coefficient (\(C_D\)) and frontal area (A) [m\(^2\)]).

$$\begin{aligned} D_\mathrm{A}=\frac{1}{2}\rho V^2 C_\mathrm{D}~A \end{aligned}$$
(2)

The total requested torque (\(T_{\mathrm{req}}\)) [Nm] is based on the movement resistance forces (\(R_x\) and \(D_\mathrm{A}\)), on the tire external radius (r) [m] and on the vehicle required acceleration (\(a_{\mathrm{req}}\)) [m/s\(^2\)], as shown in Eq. (3).

$$\begin{aligned} T_{\mathrm{req}} = \left( M(a_{\mathrm{req}}+g \sin {\alpha }) +R_x+D_\mathrm{A}\right) r \end{aligned}$$
(3)

As seen previously in Fig. 1, there are two different propelling systems at the wheels and their inertias need to be considered. Firstly, the inertia of the in-wheel EMs is added to the inertia of the frontal wheels (\(I_{\mathrm{wf}}\)) [kgm\(^2\)], once the EM is directly connected without any transmission system. Secondly, at the rear propelling system, the inertia of the motor is added to the inertia of the differential (\(I_\mathrm{d}\)) [kgm\(^2\)], once it is connected to a differential and its transmission ratio (\(N_\mathrm{d}\)).

For the first case, the requested torque (\(T_{\mathrm{req}}\)) defined by Eq. (3) is divided by the PMC between the propelling systems, frontal and rear. The frontal torque required \(T_{\mathrm{reqF}}\) [Nm] is split to each one of the two EMs (\(T_{\mathrm{EMF}}\)) and the frontal wheels’ inertia with the coupled motors (\(I_{\mathrm{wf}}\)) [kgm\(^2\)] is also considered, as determined by Eq. (4).

$$\begin{aligned} T_{\mathrm{EMF}} = \frac{T_{\mathrm{reqF}}+I_{\mathrm{wf}}\frac{a_{\mathrm{req}}}{r}}{2} \end{aligned}$$
(4)

For the second case, the rear EM torque (\(T_{\mathrm{EMR}}\)) [Nm], as shown in Eq. (5), is defined as a function of the required torque \(T_{\mathrm{reqR}}\) [Nm] and the inertias divided by the efficiency (\(\eta _d\)) and by the differential transmission ratio (\(N_\mathrm{d}\)). The inertia terms in Eq. (5) include the differential with its coupled EM in \(I_\mathrm{d}\) and the two rear wheels inertia \(I_{\mathrm{wr}}\) [kgm\(^2\)].

$$\begin{aligned} T_{\mathrm{EMR}} = \frac{T_{\mathrm{reqR}}+ \left( I_\mathrm{d}N_\mathrm{d}^2+I_{\mathrm{wr}}\right) \frac{a_{\mathrm{req}}}{r}}{N_\mathrm{d} \eta _d} \end{aligned}$$
(5)

However, the motors required torques (\(T_{\mathrm{EMF}}\) and \(T_{\mathrm{EMR}}\)) are limited by the available EMs propelling torques and also by transmissible torque limit on the tire-ground contact [42, 43]. The \(T_{\mathrm{AF}}\) [Nm] and \(T_{\mathrm{AR}}\) [Nm] (maximum EM available torques) are determined by the maximum torque curves according to the motors’ speed, as seen in the electric motors model section. The other limiter is the maximum transmissible torque \(T_{R(\mathrm{max})}\) or \(T_{F(\mathrm{max})}\) defined in Eqs. (6) and (7), as explained by Jazar [39]. Therefore, the PMC has to prevent traction limit excesses in the propel systems requiring less torque than the indicated limits.

$$\begin{aligned} T_{R(\mathrm{max})}= & {} \mu \left( \frac{M g\cos {\alpha }~b + h\sin {\alpha } +Mh~a_\mathrm{x}}{2L}\right) r \end{aligned}$$
(6)
$$\begin{aligned} T_{F(\mathrm{max})}= & {} \mu \left( \frac{M g\cos {\alpha }~c - h\sin {\alpha } -Mh~a_x}{2L}\right) r \end{aligned}$$
(7)

In Eqs. (6 and 7), \(\mu\) is the friction coefficient on the tire-ground contact. Moreover, the vehicle acceleration is considered equal to the required acceleration as an initial approximation (\(a_x = a_{\mathrm{req}}\)). Geometrical parameters were also used, such as the vehicle wheelbase (L) [m], gravity center height (h), [m] and its longitudinal distance between the vehicle rear (c) [m] and frontal (b) [m] axes.

Whether the requested motor torques \(T_{\mathrm{EMF}}\) and/or \(T_{\mathrm{EMR}}\) exceed the mentioned limits, the performance will be bounded by the lower torque value of each driving system. The traction front \(T_\mathrm{F}\) (Nm) and rear \(T_\mathrm{R}\) (Nm) torques to propel the vehicle are shown in Eqs. (8 and 9).

$$\begin{aligned} T_\mathrm{F}= & {} \min \left\{ \begin{array}{ll} 2T_{\mathrm{EMF}}-I_{\mathrm{wf}}\frac{a_x}{r}\\ \\ 2T_{\mathrm{AF}}-I_{\mathrm{wf}}\frac{a_x}{r}\\ \\ T_{\mathrm{F}(\mathrm{max})} \end{array} \right. \end{aligned}$$
(8)
$$\begin{aligned} T_\mathrm{R}= & {} \min \left\{ \begin{array}{ll} T_{\mathrm{EMR}}N_\mathrm{d} \eta _d-\left( I_\mathrm{d}N_\mathrm{d}^2+I_{\mathrm{wr}}\right) \frac{a_\mathrm{x}}{r}\\ \\ T_{\mathrm{AR}}N_\mathrm{d} \eta _d-\left( I_\mathrm{d}N_\mathrm{d}^2+I_{\mathrm{wr}}\right) \frac{a_\mathrm{x}}{r}\\ \\ T_{\mathrm{R}(\mathrm{max})} \end{array} \right. \end{aligned}$$
(9)

According to the second Newton’s law, resultant acceleration is a relation between the sum of the forces and the mass in the movement, in this case, the vehicle mass. Thus, the resultant vehicle acceleration \(a_\mathrm{x}\) [m/s\(^2\)] is defined as indicated by Eq. (10).

$$\begin{aligned} a_\mathrm{x} = \frac{\frac{T_\mathrm{F}+T_\mathrm{R}}{r} -D_\mathrm{A}-R_\mathrm{x}-Mg \sin (\alpha )}{M} \end{aligned}$$
(10)

The maximum transmissible torques presented in Eqs. (6 and 7) change with the resultant acceleration value \(a_x\), featuring an iterative process from Eq. (7, 8, 9 and 10). This process is performed until the \(a_\mathrm{x}\) convergence. Once the real acceleration is known, the vehicle speed V [m/s] is obtained integrating the \(a_\mathrm{x}\) value, finishing the simulation loop. The vehicle parameters used in the simulation are shown in Table 1.

Since the values of traction and acceleration have converged, the effective frontal and rear EMs torques (\(T_{\mathrm{Fef}}\) [Nm] and \(T_{Ref}\) [Nm]) are calculated by Eqs. (11 and 12).

$$\begin{aligned} T_{\mathrm{Fef}} = \frac{T_\mathrm{F}+I_{\mathrm{wf}}\frac{a_\mathrm{x}}{r}}{2} \end{aligned}$$
(11)
$$\begin{aligned} T_{\mathrm{Ref}} = \frac{T_\mathrm{R}+ \left( I_\mathrm{d}N_\mathrm{d}^2+I_{\mathrm{wr}}\right) \frac{a_\mathrm{x}}{r}}{N_\mathrm{d} \eta _d} \end{aligned}$$
(12)

2.1 Electric motors model

The optimization defines the EMs speed and torque values as parameters. Figure 2 presents a generic torque curve and efficiency map, based on the studies of Eckert et al. [19, 20, 35]. This approach is a simplified way to find optimum configurations for the EMs, once a theoretical torque curve is generated and the efficiency map is interpolated according to it. This enables a significant reduction in the computational cost of the model.

Table 1 Simulated vehicle parameters [35, 44]
Full size table
Fig. 2
figure 2

Electric motor efficiency map [19, 35]

Full size image

There are four main points in Fig. 2. The first one is when the EM torque is maximum (\(T_{\mathrm{max}}\)) [Nm] at null speed, representing the startup torque. The second one is the torque constant phase, with the same \(T_{\mathrm{max}}\) value of the previous point, and its respective speed (\(\omega _{\mathrm{Tc}}\)) [rad/s]. Tong [45] shows that the best operating point of the EM happens between \(0.1T_{\mathrm{max}}\) and \(0.3T_{\mathrm{max}}\) at the constant power regime. Therefore, the third point \(T_{\mathrm{Pc}}\) [Nm] is determined as the recommended upper limit (30% \(T_{\mathrm{max}}\)) [8, 20], in Eq. (13). Knowing the EM power is constant, speed values  \(\omega _{\mathrm{Pc}}\) [rad/s] are defined according to Eq. (14).

$$\begin{aligned} T_{\mathrm{Pc}} = 0.3T_{\mathrm{max}} \end{aligned}$$
(13)
$$\begin{aligned} \omega _{\mathrm{Pc}} = \frac{T_{\mathrm{max}}\omega _{\mathrm{Tc}}}{T_{\mathrm{Pc}}} \end{aligned}$$
(14)

The last important point is defined as the zero torque and the EM maximum speed (\(\omega _{\mathrm{max}}\) rad/s) and it is calculated using a linear extrapolation based on the previous points, (\(T_{\mathrm{max}}\), \(\omega _{\mathrm{Tc}}\)) and (\(T_{\mathrm{Pc}}\), \(\omega _{\mathrm{Pc}}\)).

Lastly, based on the interpolation of the points (\(T_{\mathrm{max}}\), \(\omega _{\mathrm{Tc}}\)) and (\(T_{\mathrm{Pc}}\), \(\omega _{\mathrm{Pc}}\)), the curves that determine the available torques (\(T_{\mathrm{AF}}\) and \(T_{\mathrm{AR}}\)) are defined. Once the torque curves are defined, the respective EM efficiency maps (\(\eta _{\mathrm{EMF}}\) and \(\eta _{\mathrm{EMR}}\)) are obtained. Moreover, the EMs inertias are interpolated based on the values presented in Table 1.

After the definitions of motors efficiencies (\(\eta _{\mathrm{EMF}}\) and \(\eta _{\mathrm{EMR}}\)) and their respective inverse efficiencies (\(\eta _{\mathrm{invF}}\) and \(\eta _{\mathrm{invR}}\)), according to Table 2, the total electrical current consumption I [A] of the vehicle is determined as shown in Eq. (15). Beyond efficiencies, it is a function of the HESS voltage \(V_{\mathrm{HESS}}\) (V), of the current EM speed \(\omega _{\mathrm{EM}}\) (rad/s), and of the EM effective torques \(T_{\mathrm{Fef}}\) and \(T_{\mathrm{Ref}}\).

$$\begin{aligned} I = \frac{2T_{\mathrm{Fef}}V}{r~V_{\mathrm{HESS}}~\eta _{\mathrm{EMF}}~\eta _{\mathrm{invF}}} + \frac{T_{\mathrm{Ref}}VN_\mathrm{d}}{r~V_{\mathrm{HESS}}~\eta _{\mathrm{EMR}}~\eta _{\mathrm{invR}}} \end{aligned}$$
(15)
Table 2 Inverter efficiency map [35, 46]
Full size table

Over than providing power during accelerations, the EMs can retrieve part of the kinetic energy during the braking, acting as generators [47] to recharge the HESS ultracapacitors. This braking energy recovery represents an effective approach to increase the EV driving range [48]. In this study, the regenerative braking capacity is bounded to 10% of its maximum torque [19]. Whenever the required torque to brake exceeds this limit, the residual one is supplied by the vehicle’s frictional brake system [49].

2.2 Ultracapacitor and battery models

The PMC divides the current I (A) between the HESS power sources (as seen in Eq. (15)), in this case, a battery pack and an ultracapacitor.

One of the main objectives of this study is to find out the optimum battery size for the EV HESS, therefore, a simplified method is applied to estimate the battery mass \(M_{\mathrm{bat}}\) (kg) as seen in Eq. (16). Once the capacity \(B_\mathrm{c}\) (Ah) and the battery voltage \(V_{\mathrm{bat}}\) [V] will be determined by the optimization algorithm (see Sect. 4), the \(M_{\mathrm{bat}}\) is defined by lithium-ion specific energy \(S_\mathrm{E}\). The battery considered is a lithium-ion model (Simulink™database).

$$\begin{aligned} M_{\mathrm{bat}} = \frac{V_{\mathrm{bat}}B_\mathrm{c}}{S_\mathrm{E}} \end{aligned}$$
(16)

In this paper, it is assumed the state-of-the-art lithium-ion batteries, considering \(S_\mathrm{E}\) = 150 (Wh/kg) specific energy [50, 51]. This \(S_\mathrm{E}\) value was also reported as typical for EV batteries [52, 53]. It is important to highlight that this simplified approach is used only to define the optimum battery capacity \(B_\mathrm{c}\) and voltage \(V_{\mathrm{bat}}\) by simulations. Once the optimum parameters were defined, it is necessary to design or to find out a commercial battery that these required parameters are able to be applied in the real HESS.

Knowing the specific battery power \(P_{\mathrm{max}}\) (300 [W/kg] for lithium-ion batteries), the mass \(M_{\mathrm{bat}}\) and the voltage \(V_{\mathrm{bat}}\) values, the maximum discharge current \(I_{\mathrm{max}}\) (A) of the battery is determined as indicated by Eq. (17).

$$\begin{aligned} I_{\mathrm{max}} = \frac{P_{\mathrm{max}}M_{\mathrm{bat}}}{V_{\mathrm{bat}}} \end{aligned}$$
(17)

Another source is the ultracapacitor \(\mathrm{Cap}\). The ultracapacitors model can be simplified as ideal capacitors \(C_{\mathrm{uc}}\) in series with their respective internal resistances \(R_{\mathrm{uc}}\) where the parallel resistance was neglected as presented by Zhang and Mi [54]. The parameters used for the ultracapacitor simulations are presented in Table 3.

Table 3 Ultracapacitor parameters [19, 20]
Full size table

Capacitors connected in parallel in the HESS present no vantage when compared to those connected in series, as asserted by prior works [19, 55]. Thus, the bank of ultracapacitors considered has only series arrangements and demand \(N_\mathrm{s}\) units, quantified in Eq. (18).

$$\begin{aligned} N_\mathrm{s}= \frac{V_{\mathrm{bat}}}{V_{\mathrm{uc}(n)}} \end{aligned}$$
(18)

Once defined the quantity \(N_\mathrm{s}\), the total mass of the capacitors \(M_{\mathrm{cap}}\) (kg) is worked out by Eq. (19).

$$\begin{aligned} M_{\mathrm{cap}}= N_\mathrm{s}M_{\mathrm{uc}(n)} \end{aligned}$$
(19)

Similar to the work of Ravey et al. [56], the previously calculated masses of the battery \(M_{\mathrm{bat}}\) and the ultracapacitors \(M_{\mathrm{cap}}\) are added to the EV mass without the HESS \(M_{\mathrm{wh}}\) (kg) (seen Table 1) to define the total vehicle mass M as shown in Eq. 20.

$$\begin{aligned} M = M_{\mathrm{wh}} + M_{\mathrm{bat}}+ M_{\mathrm{cap}} \end{aligned}$$
(20)

According to Yang et al. [57] and Prochazka et al. [58], deep discharging and over-charging of the Li-ion cells must be avoided to ensure sufficient lifetime. Therefore, to avoid damages provoked by the whole battery discharge, the power source charge condition \(\mathrm{SoC}\) is limited by the vehicle PMC to 40% [34, 59]. For the same reasons, the capacitors discharge also is limited by the PMC [60].

2.3 Power management control model

The PMC controls the power using a rule-based strategy and considering the EMs/inverters efficiency in its algorithm. It uses a discretization loop to evaluate all possible propelling arrangements among the available drive systems and to distribute the EMs (frontal and rear) requested torque \(T_{\mathrm{req}}\), as shown in Eqs. (4 and 5). It is important to highlight it may exist some cases where the use of only one drive system is better than a combination of both.

This control splits the EV power demand in such a way that the battery supplied continuous power and the supercapacitor quickly compensates the instantaneous demands, acting as power buffers [61,62,63]. With all these features, the PMC keeps the EV working while it generates fewer HESS discharges, which is the best global efficiency among the EMs and its inverters. The PMC algorithm is shown in Fig. 3.

In order to avoid poor acceleration caused by excessive tire slipping, this control also considers the tire ground traction limit, according to Eqs. (7 and 6), which define the maximum applicable torques on the vehicle wheels. In this way, the traction limits will not be exceeded while the propelling systems fulfill the torque request.

Fig. 3
figure 3

Power management control algorithm

Full size image

It is well known that the major advantage of assembling batteries and ultracapacitors in a HESS is transferring the high peak powers response to the ultracapacitors, avoiding the battery high-frequency power fluctuations [64]. Ma et al. [61] highlight that the batteries are more efficient at low and steady power loads, therefore, to make these devices robust to current spikes, it is necessary to excessively increase their storage capacity. Furthermore, Veneri et al. [65] showed that high charging and discharging rates reduce battery efficiency because it is difficult for these devices to recover from rapid power fluctuations, which leads to a lifetime decrease [61]. On the other hand, the ultracapacitors are designed to provide high power and their life cycles are much longer than those presented by batteries [62].

In this paper, the maximum discharge current \(I_{\mathrm{max}}\) of the battery is multiplied by a percentage \(P_\mathrm{I}\) (%) to define the battery current limit, which is defined by the optimization algorithm limit (\(I_{\mathrm{lim}} = P_\mathrm{I}I_{\mathrm{max}}\) [A]). If the required current I (A) defined in Eq. (15) exceeds the battery current limit (\(I>I_{\mathrm{lim}}\)), the ultracapacitors provide the remaining required current. In Eq. (21), it is shown the calculation of the battery \(I_{\mathrm{bat}}\) (A) and ultracapacitors \(I_{\mathrm{cap}}\) (A) currents. This current split strategy was previously implemented by Eckert et al. [19, 20] and Corrêa et al. [55], presenting satisfactory results.

$$\left\{ \begin{gathered} {\text{if}}\;I \le \text{I} _{{{\text{lim}}\,}} \,;\,I_{{{\text{bat}}}} = \,{\text{and}}\,{\text{I}}_{{{\text{cap}}}} = 0 \hfill \\ {\text{if}}\,I\,;\,I_{{\lim }} \,;\,I_{{{\text{bat}}}} = I_{{\lim }} \,{\text{and}}\,{\text{I}}_{{{\text{cap}}}} = I - \text{I} _{{\lim }} \hfill \\ \end{gathered} \right.$$
(21)

Such rule-based power split strategy where the battery provides the average required power and the ultracapacitors fulfill the peak power is presented by Veneri et al. [65]. Moreover, this strategy also considers the possibility of the battery providing the maximum capable discharge power and the ultracapacitors pack providing the remaining required power. Furthermore, when the power demand is very high, the battery can provide the power directly to the motors [63].

Because the discharge limit of the capacitors is higher than the battery limit, the required \(I_{\mathrm{cap}}\) values are not limited. Therefore, the input current resulting from the regenerative braking is fully absorbed by the ultracapacitors, isolating the battery from these power peaks [62,63,64]. In the same way as the battery, the ultracapacitors pack is also limited to avoid its complete discharge, which decreases its life, thus, when the ultracapacitors stage of charge \(\mathrm{SoC}_{\mathrm{UC}}\) (%) is less than 35%, the EV will only be driven by the battery, limited to its \(I_{\mathrm{lim}}\) value. Therefore, the vehicle will exhibit a decrease in acceleration performance due to the reduced torque EMs.

2.4 Driving cycle

Fig. 4
figure 4

Campinas driving cycle [37]

Full size image

In the analysis made in this paper, the simulations were developed with an experimental driving cycle proposed by Oliveira et al. [37]. This cycle allows us to evaluate the EV performance based on the urban driving reality from Campinas city (Fig. 4). Moreover, this cycle was successfully applied in the optimization process of a hybrid vehicle drivetrain [66]. The driving cycle profile, shown in Fig. 4ab, provides the target speed \(V_\mathrm{t}\) (m/s), that is compared to the actual EV speed V (m/s) to define the requested acceleration calculation \(a_{\mathrm{req}}\), as seen in Eq. (22). The \(V_\mathrm{t}\) is the speed one-time step \(\varDelta _t\) (s) ahead of the current simulation time. Furthermore, Fig. 4c provides data to define the road angle \(\alpha\) from the cycle’s altimetry. The real-world driving cycle has a duration of 7500 s and 42 km, normally a reality of Brazilian traffic in some cities.

$$\begin{aligned} a_{\mathrm{req}} = \frac{V_\mathrm{t}-V}{\varDelta _t} \end{aligned}$$
(22)

3 Optimization algorithm

The optimization uses a GA technique to minimize the total mass of the HESS (battery + ultracapacitors), that corresponds to the first optimization criterion \(f_1\), as seen in Eq. (23). The second criterion \(f_2\) (Eq. (24)) is to maximize the EV drive range (\(\mathrm{DR}\)), represented by the traveled distance reached by the EV when the battery reaches the maximum allowed discharge limit (\(\mathrm{SoC}\) = 40%), considering the repetition of the analyzed driving cycle. The optimization algorithm is implemented in MATLAB™.

$$\begin{aligned} f_1 = \min (M_{\mathrm{bat}}+M_{\mathrm{cap}}) \end{aligned}$$
(23)
$$\begin{aligned} f_2 = \max (\mathrm{DR}) \end{aligned}$$
(24)

The GA technique requires the definition of a chromosome \([{\mathbf {X}}]\), which has the optimization parameters used at the EV simulation. Several of these chromosomes and their data make a population database. This algorithm defines the battery voltage \(V_{\mathrm{bat}}\) (V) and capacity \(B_\mathrm{C}\) (Ah), to optimize the criteria presented in Eq. (23) and Eq. (24) (\(f_1\) and \(f_2\)). With this information, the algorithm allows obtaining the battery mass \(M_{\mathrm{bat}}\) using Eq. (16). The GA also decides the ultracapacitor type n that will be used among the available presented in Tab. 3 and the series capacitors number is obtained by Eq. (18).

Another important parameter in the chromosome is the maximum current percentage of the battery \(P_\mathrm{I}\) (%). It is needed to determine the current limit \(I_{\mathrm{lim}}\) of the battery that is used by the power control to split the current between the ultracapacitors and the battery of the HESS. The chromosome \([{\mathbf {X}}]\) with the optimization criteria is shown in Eq. (25).

$$\begin{aligned}{}[{\mathbf {X}}] = [V_{\mathrm{bat}}~B_\mathrm{C}~n~T_{\mathrm{maxF}}~\omega _{\mathrm{TcF}}~T_{\mathrm{maxR}}~\omega _{\mathrm{TcR}}~N_\mathrm{d}~P_\mathrm{I}] \end{aligned}$$
(25)

Subject to: constraints C presented in Eq. (26).

$$C({\mathbf{X}}) = \left\{ {\begin{array}{*{20}c} {100 \le V_{{{\text{bat}}}} \le 400~} & {({\text{V}})} \\ {50 \le B_{{\text{C}}} \le 150} & {({\text{Ah}})} \\ {1 \le n \le 16} & {} \\ {50 \le T_{{{\text{maxF}}}} \le 300} & {{\text{(Nm)}}} \\ {250 \le \omega _{{{\text{TcF}}}} \le 3000} & {{\text{(rpm)}}} \\ {10 \le T_{{{\text{maxR}}}} \le 50} & {{\text{(Nm)}}} \\ {500 \le \omega _{{{\text{TcR}}}} \le 1500} & {{\text{(rpm)}}} \\ {3.5 \le N_{{\text{d}}} \le 7} & {} \\ {5 \le P_{{\text{I}}} \le 95} & {(\% )} \\ \end{array} } \right.$$
(26)

To ensure the EV can execute the proposed driving cycle, the vehicle performance acts as a constraint. Therefore, the simulated solutions need to present a minimum traveled distance of 98% of the standard Campinas driving cycle (42.11 km in its first repetition) or they are removed from the population. Furthermore, it is required the EV performs at least two complete loops of the driving cycle (\(\mathrm{DR} \approx 82.52\) km, considering the minimum acceptable performance) to include its solution in the population.

3.1 Selection, Crossover and Mutation

The Pareto ranking classifies the population using the adaptive-weight approach [67] for fitness values. For the non-dominated solutions, the Pareto frontier receives the first rank \(P = 1\). Based on the dominated solutions only from the first rank solutions, it is determined the second rank \(P = 2\), and so on. For the first Pareto frontier rank (\(P = 1\)), the \(P_\mathrm{R} = 1\), increasing its fitness value. On the other hand, the dominated solutions (\(P \ge 2\)) receive \(P_\mathrm{R} = 0\).

The fitness formulation also considers the optimization criteria. For each optimization criterion j, the maximum \(f_{j_{\mathrm{pop}}^{\mathrm{max}}}\) and minimum \(f_{j_{\mathrm{pop}}^{\mathrm{min}}}\) values are defined. As shown in Eq. (27), \(f_{j_{\mathrm{pop}}^{\mathrm{max}}}\) and \(f_{j_{\mathrm{pop}}^{\mathrm{min}}}\) are used to calculate a weight value \(f_j({\mathbf {X}})\) for each solution.

$$\begin{aligned} Ft({\mathbf {X}}) = \frac{f_{1_{\mathrm{pop}}^{\mathrm{max}}}-f_1({\mathbf {X}})}{f_{1_{\mathrm{pop}}^{\mathrm{max}}}-f_{1_{\mathrm{pop}}^{\mathrm{min}}}} +\frac{f_2({\mathbf {X}})-f_{2_{\mathrm{pop}}^{\mathrm{min}}}}{f_{2_{\mathrm{pop}}^{\mathrm{max}}}-f_{2_{\mathrm{pop}}^{\mathrm{min}}}} +P_R \end{aligned}$$
(27)

The roulette wheel method was chosen for the algorithm selection procedure, aiming to raise the probability of higher fitness \(\mathrm{Ft}(X)\) values in the selected members. As seen in Eq. (28), this probability \(S_\mathrm{P}({\mathbf {X}})\) is defined based on the sum of the fitness values \(\mathrm{Ft}(X)\) of every member (\(1\le ~k~\le ~\mathrm{Ps}\)), where Ps is the size of the population.

$$\begin{aligned} S_\mathrm{P}({\mathbf {X}}) = \frac{\mathrm{Ft}({\mathbf {X}})}{\sum ^{k =\mathrm{Ps}}_{k=1}\mathrm{Ft}(X_k)} \end{aligned}$$
(28)

Based on the \(S_\mathrm{P}({\mathbf {X}})\), the crossover operator chooses five pairs of population members \([{\mathbf {X}}]\) from the database. The new chromosome \([{\mathbf {X}}]\) generated is a random combination, with equal probability among the selected, of the design variables of each selected pair of solutions [68]. A new simulation is made with this new chromosome \([{\mathbf {X}}]\) and the result is included in the population. This crossover procedure is replicated in the optimization until one of the parameters, at least, differs from the selected member, in order to avoid a configuration already simulated.

A simple way of mutation in the case of binary representation is just flipping the chromosomes’ value. The mutation operator modifies some of the parameters from the selected pair of solutions and also from the chromosome generated by the crossover process. In this way, new values are inserted into the population. The mutation operator generates a random value (\(0\ge ~MUT\ge ~1\)) to define whether the selected parameter will or not be mutated. For each parameter, the probability of mutation is 50%.

The constraints [C] in Eq. (26) must be considered by the mutated parameters. If one of the parameters exceeds the limits of the constraints or if no parameters of the chromosome generated present mutation, then this chromosome is disregarded and a new mutation is made until generating a combination that considers the constraints [C]. Table 4 shows the mutation limits.

Table 4 Mutation operator
Full size table

The first population has 100 simulation results that respect the constraint limits. Each one of these was obtained by randomly defined chromosomes. The maximum population size was established as \(P_{\mathrm{lim}} = 500\). When the population oversteps the limit, the last Pareto rank (worst results) is deleted from the population. Whether the non-dominated solutions (\(P=1\)) overstep the population limit, it is redefined as \(P_{\mathrm{lim}} =P_{\mathrm{lim}} +100\).

The convergence criterion is defined by the recurrence of the same Pareto frontier [69] for over 10 generations. Each generation is defined by the offspring of five-pairs of selected chromosomes combined with the crossover and mutation operators.

4 Results

Fig. 5
figure 5

Optimization results

Full size image
Table 5 Non-dominated solution
Full size table

The GA algorithm convergence results in a set of non-dominated solutions (Pareto frontier) presented in Fig. 5. These EV configurations are considered as optimum compromised solutions with a trade-off between the two optimization criteria. Among these results, three were selected to be analyzed in this section. The first one is the \(\min (f_1)\) solution that corresponds to the minimum mass of the HESS system. The second one is the \(\max (f_2)\) that improves the estimated drive range of the EV and the last one is the solution that presents the best trade-off between the optimization criteria, in other words, the solution that has the higher fitness value among the optimum configurations \(\max (\mathrm{Ft})\).

Table 5 presents the design variables and respective results of the three selected configurations: \(\min (f_1)\), \(\max (f_2)\) and \(\max (Ft)\).

Due to the uniformity of the analyzed driving cycle, it is composed basically of urban driving behavior (lowes speed and acceleration) and it only presents a small section of high speed (250 s at \(\approx\) 70 km/h). The optimum EV configurations do not present a large variation as shown in Tab. 6, especially in the drivetrain design variables, that were minimized according to the HESS additional mass.

Table 6 Limit values of the optimum solutions chromosomes
Full size table
Fig. 6
figure 6

HESS state of charge behavior and resultant speed profile according to the optimized EV configurations

Full size image

The optimum HESS configurations converge to the use of the capacitor n = 1 and n = 8. The variation in the battery design variables (\(V_{\mathrm{bat}}\) and \(B_\mathrm{C}\)) associated with the percentage \(P_\mathrm{I}\), that controls the HESS power split, defines the estimated drive range of the EV that vary from 82.75 km (minimum acceptable drive range of 2 cycle loops) up to 188.43 km (largest HESS pack). The EV power system and resulting speed profile for the three selected configurations are presented in Fig. 6.

As presented in Fig. 6, the HESS capacitor state of charge \(\mathrm{SoC}_{\mathrm{UCi}}\) behavior is very similar in the three analyzed cases. Because the optimum capacitors (\(\mathrm{Cap}(1)\), \(\mathrm{Cap}(2)\) and even \(\mathrm{Cap}(7)\)) models do not assemble a high power pack, the \(\mathrm{SoC}_{\mathrm{UCi}}\) drops at the beginning of the cycle until it reaches the maximum allowed discharge of 35%. On the other hand, this low power capacity ultracapacitor pack enables faster recharging during regenerative braking, which is amplified in the downhill sections, as presented in Fig. 7. Also, it shows the \(\mathrm{SoC}_{\mathrm{UCi}}\) of the three analyzed solutions. In other words, a low-power ultracapacitors pack presents a fast discharge while performs a quick recovery, ensuring the system will be able to assist the battery in the current demand peaks. This \(\mathrm{SoC}_{\mathrm{UCi}}\) charging/discharging behavior is repeated during the remaining driving time.

Fig. 7
figure 7

Capacitors \(\mathrm{SoC}_{\mathrm{UCi}}\) during a downhill section of the cycle

Full size image

Besides the HESS system similar behavior of all analyzed solutions, the best trade-off (\(\max {(\mathrm{Ft})}\)) configuration presents a driving range close to the \(\max {(f_2)}\) solution (25.6 km or 13.58%), however, with HESS pack 23.63% lighter (less 98.78 kg). This happens basically because the HESS mass increases the EV total mass M and, consequently, it increases the vehicle power demand, as shown in Eqs. (1 and 3). In other words, even with more power capacity, a bigger HESS also implies a power consumption increase that limits the HESS size. Furthermore, the bigger HESS system implies technical difficulties to assemble all components in the vehicle.

On the other hand, smaller HESS, as the \(\min {(f_1)}\), presents 54.08% less mass as compared to the \(\max {(\mathrm{Ft})}\) configuration, however, the driving range also decreases 49.18%. This specific configuration can be applied in smaller EVs developed for short travels or cities with available charging parks in the EV drive range.

Regarding the EVs drivetrain, it was possible to conclude the resulting configurations are most indicated to urban driving, due to the optimization constraints and mostly because of the chosen driving cycle. The major limitation of this configuration is related to the maximum vehicle speed, once the EMs reach null torque in a specific rotation, that is a direct function of the vehicle longitudinal speed, according to the drive train configuration (in-wheel or differential system).

Equations (29 and 30) show the correlation between the EMs and vehicle speed for the   \(\text{ frontal } V_{{\mathrm{Front}}} (\text{ m }/\text{s})\) and rear \(V_ {\mathrm{Rear}}\) (m/s) driving systems, respectively. The resulting torque curve for the frontal \(T_{\mathrm{Front}}\) [Nm] and rear \(T_{\mathrm{Rear}}\) (Nm) propelling systems are presented by Eqs. (31 and 32).

$$\begin{aligned} V_{\mathrm{Front}}= & {} \frac{\pi r \omega _{\mathrm{EMF}}}{30} \end{aligned}$$
(29)
$$\begin{aligned} V_{\mathrm{Rear}}= & {} \frac{\pi r \omega _{\mathrm{EMR}}}{30 N_\mathrm{d}} \end{aligned}$$
(30)
$$\begin{aligned} T_{\mathrm{Front}}= & {} 2T_{\mathrm{EMF}} \end{aligned}$$
(31)
$$\begin{aligned} T_{\mathrm{Rear}}= & {} T_{\mathrm{EMR}} N_\mathrm{d} \eta _d \end{aligned}$$
(32)
Fig. 8
figure 8

Rear and frontal effective traction torque (at wheels) according to the vehicle speed for the optimum EV configurations

Full size image

The resulting torque curves as a function of the vehicle speed and drivetrain configurations are presented in Fig. 8 and it is possible to observe the rear system reaches null torque up to 60 km/h (\(\min {(f_1)}\) solution) and up to \(\approx\) 92 km/h (\(\min {(f_2)}\) solution). This happens because the differential gear transmission ratio increases the system’s final torque and also allows it to quickly reaches the good efficiency region of the EM (see Fig. 2). This kind of assembling is useful in urban driving, where the vehicle needs to stop several times, especially in jammed traffic conditions as presented between the 1600  and 2300 s (Fig. 4a) and between 5100  and 5600 s (Fig. 4b) of the analyzed cycle.

However, this kind of assembly presents some additional issues. Besides the low-speed limit, this EM needs to be disconnected when it reaches critical speed, possibly by the addition of a clutch system in the powertrain, avoiding possible EM damages caused by high rotation. On the other hand, the rear EM operation at higher rotations could improve the regenerative braking efficiency, but it is necessary to carefully evaluate it due to the EMs operation speed limit.

Once the rear propelling system optimization leads to improve the EV startup and low-speed performance, the frontal in-wheel EMs become responsible to propel the vehicle in the renaming situations, fulfilling the torque demand at low speed and also acting as a single propelling system when the EV reaches the speed of null torque in the rear system.

Finally, the resulting EMs become capable to fulfill the power demand, without significant performance losses, once these configurations were able to complete the desired speed profile. However, the optimization process minimizes the EMs, because smaller EMs reach the high-efficiency regions faster than the larger ones and it results in frontal EMs that reach null torque at \(\approx\) 125 km/h. In this situation, the rear propelling system is already disabled. However, in these high-speed situations, the EV power demand increases especially by the aerodynamic drag action and it can overcome the available traction power, provided only by the frontal in-wheel EMs. Therefore, it may represent an issue, if this vehicle needs to be used in an overtaking and/or highway situation, where high speeds are required.

5 Conclusion

This paper showed a simulation-based approach to the sizing of an EV battery/ultracapacitor pack and drivetrain, using a real driving cycle recorded in Campinas City. A comparative analysis of the EV optimizations was made, considering three different solutions: the maximum drive range, the minimum HESS mass and the best combination between these criteria. The optimization results show that the HESS system presents a similar behavior in all analyzed solutions. Moreover, the optimum EMs converge to a minimum size that reaches the higher efficiency regions faster, without compromising the vehicle acceleration performance.

Furthermore, the results show that HESS technology currently provides the most suitable expansion possibility, given its moderate weight associated with its relatively small volume. The simulations point out the HESS mass could be reduced without decreasing the EV performance. Series battery/ultracapacitor combination offers many benefits, which make it well-suited for light EVs as efficiency and performance enhancement.

However, it is important to highlight that the results reached by this study are theoretical and the optimum configuration parameters need to be evaluated. The battery for a HESS real application should be an adequate commercial model according to the optimum theoretical values, moreover, it is possible to design a battery with a combination of cells to meet the desired voltage and capacity. The optimized EMs also need to be evaluated regarding constructive constraints and the same applies to the differential transmission ratio, that needs to be tuned considering a manufacturable gear teeth combination.

Besides the listed limitations, this paper has shown the HESS is a suitable solution to decrease the electric vehicle overall mass, when submitted to a real urban driving scenario, that considers the road altimetry, without performance losses.

Expansions of this study may include a different real driving cycle considering more highway periods, once the storage system varies depending on different scenarios.