1 Introduction

The monitoring of failures in geared systems has been an important task in the design and maintenance stages of these machine elements. Gear systems are considered: pumps or gear compressors, gear extruders and gearboxes (reduction or multiplication). A failure classified as local involves damage to one or two teeth in a row, such as a chipped or broken tooth. These problems are caused by: flexion fatigue, abrupt overload, advanced stage of contact fatigue or by impact of external body. A failure classified as distributed involves the wear mechanisms and presents itself in a considerable number of teeth.

The contact between two solids at a given frequency and the Hertz pressure (contact pressure) causes a level of vibration [1]. The method of detection by vibration is the most used for the prediction of damages in mechanical elements, such as: gearboxes, bearings, load unbalance, among others [2]. However, the location of the accelerometer installation can cause the impossibility of clearly capturing the signal, or difficulties in distinguishing effects when there are several sources of vibrations. The presence of different oscillatory sources gives rise to complex combinations of frequencies and modulations. The signals generated in the gears are multicomponent originating from transient forces. These forces arise from the interactions between the elastic interfaces in the contact between the work surfaces [1]. The transient signals of the failures can cause inaccuracies in the analysis. It may also be impossible to install the sensor (inaccessible locations, contaminants to the sensor, safety risk to the sensor or installer, among other factors). In [3], it is shown that the elasticity of the sensor mounting interface can affect the transmissibility of the signal by introducing errors in the measured signals.

A strategy that emerged as an alternative to vibrational analysis to detect gear failures, explores the intrinsic capacity of electric motors and generators to act as transducers [4]. A gear failure produces a torsional vibration in the load torque, causing changes in the interaction between the stator and the rotor [5]. These changes affect the stator current and can be detected using the motor current signature analysis (MCSA). The amplitude of the electrical current may change with varying operating conditions such as operating rotation, load, manufacturing material, geometric dimensions, contact reason, among others. In some situations, the failure may not be diagnosed. The use of Park transformation for the evaluation of current signals, in the technique called extended Park vector approach (EPVA), has provided an accurate detection [4]. The EPVA technique considers the three phases of the current, generating a more significant spectrum when compared to MCSA [6]. The impacts of failures in the gearbox on the signature of the motor current were studied theoretically and experimentally in Kar; Mohanty [7,8,9], Henao; Capolino [10,11,12,13,14], Feki; Clerc; Velex [15, 16] and Sena [6, 17].

When there is an increase in the severity of surface wear, an increase in noise is observed in the gear meshing region (GMR). There is also an increase in the magnitude the gear meshing frequency (fGMF) and its sidebands. However, there are no relevant changes in the supply line region (SLR). The transient signs of wear make the spectral analysis uncharacterized. Localized defects, such as pits, splinters and broken teeth, are characterized as changes in the SLR by means of lateral bands of the supply line frequency (fsup). The changes in the SLR in the broken tooth failure are similar to the other failures of the electromechanical set that have an eccentricity effect. An unbalance in the load or misalignment of the coupling causes eccentricity, for example. For the reliable characterization of the broken tooth, the academic community has investigated small changes in the GMR. In this case, evenly spaced backlash appears. The diagnosis using spectral analysis is hampered by the low magnitudes of the backlash.

Recently, some researches have proposed the use of the discrete wavelet transform (DWT) as an alternative to spectral analysis. The wavelet transform provides a time-scale description of a signal. This transformation provides a multi-resolution analysis of the data. Some characteristics that can be extracted from the wavelet decomposition coefficients. The application of predictability measures quantifies the difference between two distributions. Information measures for characterizing signals are: entropy, forecast power and normalized error variance [6]. Entropy is generally understood as a measure of the degree of order or disorder of a signal. After determining the information measures, an algorithm for diagnosis is necessary. Entropy was used in the analysis of defects in gearbox systems by [4, 6, 18,19,20].

The proposal for specialist systems based on artificial intelligence is growing [4]. Recently, artificial neural networks (ANN) were applied for the diagnosis of gearbox failure with vibration signals in [18, 21]. This research used a hybrid classifier based on the support vector machine classifiers (SVM) and ANN for the diagnosis of gear failures. The complexity and time of training can make practical applications of these techniques unfeasible in real production lines. The fuzzy inference can be useful when there are uncertainties in the measurement or when there is non-regularity in the data such as surface wear. In [4, 6], fuzzy systems have been proposed to diagnose gearbox failures.

The cited works do not present a combined diagnosis of broken tooth and wear levels in gearboxes using electrical current signals. The literature review does not make clear the possibility of detecting faults at low rotation. There is no conclusion the differences in broken tooth failures and surface wear in the entropy levels at GMR in current signals. This work seeks a strategy of easy implementation and non-invasive for the automatic diagnosis of the two main failures in gearboxes. For this, this research aims to use wavelet entropy and fuzzy inference to differentiate the broken tooth from superficial wear. Changes caused by failures in EPVA signals can provide stable entropy patterns in specific wavelet details. The strategy can offer advantages over other methods because it reduces the amount of data to be analyzed. Only data from significantly altered frequency bands are evaluated. The effectiveness of the proposed classifier must be assessed under the condition of noise. This work also sought the automatic adjustment of the diagnosis for the low (20 Hz) and high rotation (60 Hz) condition, based on the estimate of the rotation by the method of harmonic slots.

2 Diagnostic strategy proposed

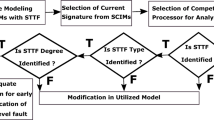
The block diagram in Fig. 1 presents the sequence for implementing the proposed diagnostic strategy.

Fig. 1
figure 1

Source: Author

Block diagram of the diagnostic strategy.

Full size image

Initially, the modulus of the Park vector is calculated from the acquisition of the electric currents of the three phases. In the sequence, the signals of the Park vector module are decomposed by the packet wavelet transform (WPT). The details that characterize the faults are automatically selected by estimating the central frequency of GMR and SLR. The entropy of the selected wavelet details is calculated from the respective relative and total energies. In the present research, the signals were normalized to make them comparable regardless of differences in the amplitude. Normalized entropies were used for better generalization and to ensure that the fuzzy inference results are not influenced by changes in signals due to operating conditions. The results remain unaffected so long as the signal patterns are unchanged. Finally, the fuzzy rules cross the entropies of the two details evaluated, informing the condition of the gearbox.

The investigative process that converged on this strategy was divided into two stages. In the detection stage, it was necessary to configure the wavelet decomposition for an adequate entropy calculation. There is a relationship between the sample rate, the sample size and the machine rotation for the correct detection of failures. The three currents of the stator are acquired with 60,000 points and an acquisition rate of 30 kHz. The entropy values that differentiate the failures in the GMR have been defined. Finally, an analysis of the reliability of the results was carried out. In the diagnostic stage, fuzzy rules are created based on the entropy values in the SLR and GMR. The crossing of information should differentiate the gearbox without fail, with broken tooth and the levels of severity of wear.

2.1 Current signal failure analysis

The GMF frequency set is calculated by Eq. 1. Equation 2 presents the SLR frequency set. Figure 2 presents a typical current signature (spectral analysis) based on Eqs. 1 and 2.

$$f_{\text{Reg\_GMF}} = f_{\text{sup}} \pm m_{\text{bl}} \cdot f_{\text{pin}} \pm n_{\text{bl}} \cdot f_{\text{cor}} \pm q_{\text{bl}} \cdot f_{\text{GMF}}$$
(1)
$$ f_{{{\text{Reg\_sup}}}} = f_{{{\text{sup}}}} \pm m_{{{\text{bl}}}} \cdot f_{{{\text{pin}}}} \pm n_{{{\text{bl}}}} \cdot f_{{{\text{cor}}}} $$
(2)

where fsup is the frequency of the motor's electrical supply in Hz; mbl, nbl and qbl are the harmonic orders (m, n and q = 1, 2, 3,); fpin is the rotation of the gear coupled to the motor in Hz; fcor is the rotation of the gear moved in Hz and fGMF is the gear meshing frequency. GMF is obtained by the rotational of a given gear multiplied by its number of teeth (Z), that is, fGMF = Zpin fpin = Zcor fcor.

Fig. 2
figure 2

Source: Author

Typical current spectrum of a gearbox.

Full size image

In the technique called extended Park vector approach (EPVA), the analysis of the Park vector module is performed in the stator reference. The advantage of the method is that the characteristic components of the defect appear demodulated and highlighted [6]. An odq (Park) transformation represents each original three-phase armature by a two-phase dq armature, plus an isolated coil of index o. The transformation eliminates the mutual magnetic coupling between the phase coils. This makes the flow concatenated on one axis independent of the other. In general, information in the zero sequence stream (iso) is not used. Equations 3 and 4 present the dq currents obtained from this transformation in a conservative form. In a conservative form, the two-phase machine has the same mechanical power, combined and the same speed as the three-phase machine.

$$ i_{{{\text{sd}}}}^{s} = \sqrt {{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}} i_{{{\text{s1}}}}^{s} - {1 \mathord{\left/ {\vphantom {1 {\sqrt 6 }}} \right. \kern-\nulldelimiterspace} {\sqrt 6 }}i_{{{\text{s2}}}}^{s} - {1 \mathord{\left/ {\vphantom {1 {\sqrt 6 }}} \right. \kern-\nulldelimiterspace} {\sqrt 6 }}i_{{{\text{s3}}}}^{s} $$
(3)
$$ i_{{{\text{sq}}}}^{s} = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-\nulldelimiterspace} {\sqrt 2 }}i_{{{\text{s2}}}}^{s} - {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-\nulldelimiterspace} {\sqrt 2 }}i_{{{\text{s3}}}}^{s} $$
(4)

In expressions, the variables \(i_{{{\text{s1}}}}^{s} ,i_{{{\text{s2}}}}^{s} \,\,e\,\,\,i_{{{\text{s3}}}}^{s}\) are the three-phase currents; \(i_{{{\text{sd}}}}^{s} \,e\,\,i_{{{\text{sq}}}}^{s}\) are the currents of the biphasic machine (dq). The Park vector module will be given by:

$$ {\text{EPVA}} = \sqrt {(i_{{{\text{sd}}}}^{s} )^{2} + (i_{{{\text{sq}}}}^{s} )^{2} } $$
(5)

The technique requires the measurement of the three currents of the induction motor only when it is also supplied with neutral. For the other cases, it is possible to measure only two of the currents and the third is estimated.

2.2 Transformed wavelet packet (WPT)

In wavelet theory, the base functions that constitute the representation and reconstruction processes, called wavelet daughters, ψm,n(t). These functions are obtained through translations and expansions of a single prototype wavelet, ψ(t) or ψ1.0(t), known as the mother Wavelet [4]. The mother wavelet is scaled by the scaling factor, m, and displaced by the translation factor, n, in all possible translations over time to scan the signal under analysis. This process gives rise to the daughter wavelets (dyadic and orthonormal), according to Eq. 6.

$$ \psi_{m,n} (t) = 2^{{{{ - m} \mathord{\left/ {\vphantom {{ - m} 2}} \right. \kern-\nulldelimiterspace} 2}}} \psi (2^{ - m} t - n) $$
(6)

When wavelets are used to transform a discrete signal, s(t), the result will be a series of coefficients called decomposition coefficients in wavelets. These coefficients correspond to the discrete wavelet transform (DWT), according to Eq. 7.

$$ {\text{DWT}}\,_{(m,n)} \, = 2^{{{{ - m} \mathord{\left/ {\vphantom {{ - m} 2}} \right. \kern-\nulldelimiterspace} 2}}} \sum\limits_{t}^{{}} {s(t)} \,\psi (2^{ - m} t - n) $$
(7)

The DWT provides a non-redundant representation of the signal, and its values constitute the coefficients of a wavelet series. These wavelet coefficients provide complete information in a simple way and a direct estimate of local energies at different scales. In addition, the information can be organized in a hierarchical schema of aligned subspaces, called multiresolution analysis. In this analysis, a signal can be broken down into two components: approximation and detail. The wavelet function is related to a high-pass filter, which produces the coefficients of details of the wavelet decomposition. An additional function is related to the low-pass filter, called the scaling function, being associated with the approximation coefficients.

In the decomposition of wavelet packet (WPT), the detail coefficients are divided into coefficients of approximation and details. In this way, the decomposition of the signal presents a shape of a binary tree, called the wavelet packet tree [6]. The calculation of the WPT coefficients in Eq. 8 is the sequence resulting from the internal product of an s(t) signal with the wavelet packet functions.

$$ \lambda_{m,f} \,(n) = 2^{{{{ - m} \mathord{\left/ {\vphantom {{ - m} 2}} \right. \kern-\nulldelimiterspace} 2}}} \sum\limits_{n} {\,s(t)\,w_{f} (2^{ - m} t - n)} ,\,\,f \ge 0 $$
(8)

where λm,f (n) are the expansion coefficients of s(t) in the wavelet packet functions; wmnf (t) are the basic wavelet packet functions and f is the frequency index.

The translated, expanded and normalized wavelet packet functions are obtained by Eq. 9.

$$ w_{{{\text{mnf}}}} \,(t) = 2^{{{{ - m} \mathord{\left/ {\vphantom {{ - m} 2}} \right. \kern-\nulldelimiterspace} 2}}} w_{f} (2^{ - m} t - n) $$
(9)

From the conjugated pair of quadrature filters, the library of wavelet packet functions is built with a recursive algorithm. The wf (t) are defined, considering the fixed scale [6], according to Eqs. 10 and 11.

$$ w_{2f} (t) = \sqrt 2 \sum\limits_{{n \in {\rm Z}}} {h_{n} } \,w_{f} (2t - n) = Hw_{f} $$
(10)
$$ w_{2f + 1} (t) = \sqrt 2 \sum\limits_{{n \in {\rm Z}}} {g_{n} } \,w_{f} (2t - n) = Gw_{f} $$
(11)

The initial function for f = 0, w0, is the scaling function itself. For f = 1, w1, the wavelet function is ψ1 of the DWT. The decomposition of wavelet packet can be implemented by applying the filters in the sequence of coefficients in Eqs. 12 and 13, satisfying the recursive relationship [6].

$$ \lambda_{m + 1,2f}^{{}} \,[n] = \sum\limits_{{k \in {\rm Z}}} {h[k - 2n]} \lambda_{m,f} [k] $$
(12)
$$ \lambda_{m + 1,2f + 1}^{{}} [n] = \sum\limits_{{k \in {\rm Z}}} {g[k - 2n} ]\lambda_{m,f} [k] $$
(13)

The WPT based on the quantification of the energy of the original signal in specific frequency bands allows the extraction and obtaining of information in a compact form. Therefore, this transform becomes very useful for the analysis and processing of signals applied to the diagnosis of failures.

This transform makes it possible to retain signal information in the frequency band where the frequencies of a fault occur. So it is possible to discard the bands that contain noise and less important information. For this, some criteria for selecting the optimal coefficients are used. The most used the criterion based on the quantification of the energy contained in the signal [4]. Figure 3 presents a decomposition of the WPT type into eight levels and a sampling rate of 30 kHz.

Fig. 3
figure 3

Source: Author

WPT decomposition used for sample processing.

Full size image

The concept of entropy has been widely used as a measure of a system's disorder. Shannon's entropy measures the dispersion or randomness of energy within a process. The energy concentration is related to low entropy values. Entropy-based methods allow the comparison of system properties in numerical terms. This occurs through a distribution of probabilities, since entropy can be used as a measure of dispersion [4]. The wavelet spectrum of energy on the m scale is defined by Eq. 14.

$$ E_{mnf} = \left| {\lambda_{m,f} (n)\,} \right|^{2} $$
(14)

Therefore, the wavelet energy spectrum for a given time window on the m scale, can be calculated according to Eq. 15.

$$ E_{m} = \sum\limits_{n} {E_{mnf} } $$
(15)

The total energy of the signal can then be expressed by Eq. 16.

$$ E = \sum\limits_{m} {E_{m} } $$
(16)

The normalized energy value (relative energy), which corresponds to the energy of each wavelet packet, is given by Eq. 17.

$$ p_{m} = \frac{{E_{m} }}{E} $$
(17)

Being pm the energy distribution of the signal. It is worth mentioning that Σm pm = 1.

The total entropy of Eq. 19 is defined as the sum of the entropy computed over the entire extension of the frequencies of Eq. 18, in nats, called Wavelet Packet Entropy (WPE).

$$ {\text{WPE}}_{m} = - p_{m} \ln (p_{m} ) $$
(18)
$$ {\text{WPE}}_{{{\text{tot}}}} = \sum\limits_{m} {{\text{WPE}}_{m} } $$
(19)

According to [6], this method allows the extraction and obtaining of compact information, being able to quantify the energy values, relating them the frequency of a fault.

Depending on the phenomenon to be studied, there will be a need for scale harmonization through the normalization of the entropy values (WPEm)N. A widely used method consists of linearly normalizing the data between [0, 1] by means of the maximum (WPEmmax) and minimum (WPEmmin) values according to Eq. 20.

$$ ({\text{WPE}}_{m} )_{N} = \frac{{{\text{WPE}}_{m} - {\text{WPE}}_{m\,\min } }}{{{\text{WPE}}_{m\,\max } - {\text{WPE}}_{m\,\min } }} $$
(20)

3 Experimental results of the detection stage

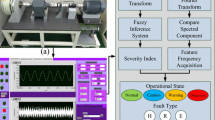
The experimental setup presents in Fig. 4a consists of a Siemens™ three-phase Induction Motor of 2 hp (1.5 kW), 8.6 Nm, 4 poles, 3.64 A/380 V. The motor can be driven with a WEG™ CFW08 vector control frequency inverter (2 hp/220 V) or direct start (380 V/60 Hz).

Fig. 4
figure 4

Source: Author

Proposed experimental setup: a main components, b damaged gear.

Full size image

The gearbox present in Fig. 4b is made up of spur cylindrical gears of module 3 and a gear ratio of 2:1. The drive gear has 23 teeth, tooth height of 675 mm and pressure angle of 20°. The motor drives the gearbox which is coupled to a mechanical brake by means of a toothed belt. To obtain surface wear, the load imposed on the electric motor was approximately 60% of the nominal. This is an orientation suggested by [22]. After the formation of the fault, the system was activated in the other loads.

The frequency inverter does not follow the motor's nominal characteristics. Thus, chosen loads were obtained through sensitivity tests. The same loads were adopted for convenience for the broken tooth tests. A load cell measures the load applied by the mechanical brake to the electric motor.

The currents are obtained from linear sensors of Hall Effect type ACS712ELC-30 A that has a sensitivity of 66 mV/A. The data acquisition (DAQ) used was the NI USB-6211 model from National Instruments™. The module has 16-bit converters with a sample rate of up to 250 ks/s. From the signals obtained by DAQ, the failure analysis is performed using a LabView™ code.

All samples were decomposed by WPT as presents in Fig. 3. In the 60 Hz rotation (supply line and frequency inverter), the wavelet details λ7.0 and λ7.5 were used. The λ7.0 wavelet detail is the SLR, and the λ7.5 detail is the GMR. For the 20 Hz rotation, the λ8.0 wavelet detail is the SLR and the λ8.3 detail is the GMR.

3.1 Experimental tests of broken tooth

The failure of a broken tooth was obtained by cutting a tooth at its base. Were broken two gears (driving wheel), to observe the repeatability of the results. For each failed gear, five samples of each operating condition were obtained. Figure 5 presents the transmission system with a broken tooth failure. Figure 6 presents a schematic of the procedure used to detect failure.

Fig. 5
figure 5

Source: Author

Experimental tests of broken teeth in the detection stage.

Full size image
Fig. 6
figure 6

Source: Author

Test base for broken tooth: a gear without failure, b gear with broken tooth.

Full size image

Figure 7 presents the percentage changes in the entropy of each wavelet packet detail (first fifty) with broken tooth failure. In Fig. 7, it is possible to verify that the literature references on the location of the characteristic frequencies of the broken tooth present significant changes in the distribution of the set of entropies.

Fig. 7
figure 7

Source: Author

Percentage changes in wavelet entropy due to broken tooth failure.

Full size image

Figure 8 presents the wavelet entropy values for each sample in the broken tooth tests. The graphs present the changes in the SLR and GMR due to the presence of the fault.

Fig. 8
figure 8

Source: Author

Entropies normalized to conditions without failure and broken tooth at each rotation.

Full size image

The entropy calculations applied to the wavelet decompositions of EPVA signals presented good homogeneity according to the classification proposed by [23]. A low dispersion (CV ≤ 15%) expressed by the Pearson variation coefficients (CV) for detecting broken teeth is observed. Table 1 presents a statistical summary of entropies for the broken tooth. In the SLR, the condition of broken tooth showed significant changes in entropy in relation to the state without failure. In the GMR, the backlash effect caused by the broken tooth presented a small increase in entropy. Changes in the two wavelet details differentiate the broken tooth from the other failures in the electromechanical set.

Table 1 Statistical summary of entropies to conditions without failure and broken tooth.
Full size table

3.2 Experimental tests of surface wear formation

The surface wear stages were obtained naturally in approximately 20 h. Five samples were acquired for each severity level in each damaged gear (two gears) operating without lubrication. The testing time was limited due to the noise level affecting the acquisition system. The measurement intervals were chosen due to the significance of the changes in the tooth profiles observed by visual inspection. Only soft wear did not show relevant changes in relation to the condition without failure.

Figure 9 presents the severity levels observed in the visual inspection in the superficial wear tests, adopting the terms: smooth, moderate, severe and excessive, suggested by [22]. Figure 10 presents a schematic of the procedure performed in the wear formation tests.

Fig. 9
figure 9

Source: Author

Surface wear levels observed in the tests: a without failure, b smooth wear, c moderate wear, d severe wear and e excessive wear.

Full size image
Fig. 10
figure 10

Source: Author

Test base for the formation of surface wear.

Full size image

Figure 11 presents the wavelet entropy values for each sample in the surface wear tests. The graphs present the changes in the SLR and GMR due to the presence of the fault.

Fig. 11
figure 11

Source: Author

Entropies normalized to conditions without failure and levels of surface wear at each rotation.

Full size image

Table 2 presents a statistical summary of entropies for the surface wear. The entropy calculation presented a low dispersion for most samples when defining the levels of severity of surface wear. These values confirm the increase in entropy with increased wear. The condition of excessive wear presented medium dispersion due to the high level of vibration. The greatest dispersion was observed in the rotation of 60 Hz with the frequency inverter. These samples had a Pearson coefficient of variation of 29.01%. Excessive wear measurement harms the data acquisition system by limiting the analysis.

Table 2 Statistical summary of entropies to conditions without failure and surface wear.
Full size table

There are differences between the entropy values in the GMR comparing the two failures. Broken tooth failure values are below moderate wear values. Transient signs of surface wear also alter the SLR with values below the broken tooth failure. These results prove the possibility of a combined diagnosis of the two failures. Inaccuracies in the visual inspection to choose the measurement intervals caused differences between the tests of the first and second gear. Even with differences, the entropy calculation provided a reliable analysis.

4 Experimental results of the fuzzy diagnosis

The proposed fuzzy inference system has two inputs for the 60 Hz rotation called SLR-H and GMR-H, referring to the entropies of the SLR and GMR. Figure 12 presents the membership functions of the SLR-H and GMR-H input variables, with their respective linguistic terms (GI, GII, GIII, GIV and GV). The membership functions were based on the averages and standard deviations from Tables 1 and 2 (stage detection). The distributions were adjusted to define fuzzy sets.

Fig. 12
figure 12

Source: Author

Pertinence functions and their respective linguistic terms: a SLR-H input variable and b GMR-H input variable.

Full size image

In the 20 Hz rotation, the inputs are called SLR-L and GMR-L, also related to the entropies of the SLR and GMR, respectively. Figure 13 presents the membership functions of the SLR-L and GMR-L input variables. The membership functions were also based on the statistical distributions defined in Tables 1 and 2. The same linguistic terms were used for 60 Hz.

Fig. 13
figure 13

Source: Author

Pertinence functions and their respective linguistic terms: a SLR-L input variable and b GMR-L input variable.

Full size image

For the proposed system, the variable DIH was defined for the diagnosis of failures with a rotation of 60 Hz, and DIL for the rotation of 20 Hz. The linguistic terms adopted for the two variables were: WF (Without failure), BT (Broken Tooth), MW (Moderate Wear), SW (Severe Wear), EW (Excessive Wear) and IN (Inconsistency of the result). Therefore, there are 25 rules for the implication of the DIH output, and 15 rules for DIL. Table 3 presents the rule base for the diagnosis in high rotation and Table 4 in low rotation.

Table 3 Rules base for diagnosis in high rotation (60 Hz).
Full size table
Table 4 Rules base for diagnosis at low rotation (20 Hz).
Full size table

The following parameters were used for the inference system: and operator (Zadeh), then operator (minimum), aggregation operator (maximum) and defuzzification method (area center method). The output membership functions were based on the entropies of the tables presented in the detection, however, adjustments were necessary. The configuration of the output pertinence functions allowed a dimensionless scale (from 0 to 1) to output the defuzzification, denouncing the condition of the gears. Figure 14 presents the pertinence functions of the output variables, DIH and DIL, with their respective linguistic terms.

Fig. 14
figure 14

Source: Author

Pertinence functions of the output variables, DIH and DIL, and their respective linguistic terms.

Full size image

4.1 Broken tooth diagnosis

In the diagnosis stage, a new gear was installed. Three samples were obtained without fail and then three samples with broken tooth. The samples were obtained at 1 h intervals. Figure 15 presents the behavior of the input wavelet entropies with the diagnosis of the conditions without failure and broken tooth.

Fig. 15
figure 15

Source: Author

Diagnosis of broken tooth: a supply line, b with inverter at 60 Hz, c with inverter at 20 Hz.

Full size image

In the diagnostic stage, the entropy values confirmed the analysis performed in the detection. The failure caused a small change in GMR. This change was enough to characterize the backlash effect caused by the broken tooth.

4.2 Diagnosis of surface wear levels

A new set of gears was installed for the diagnostic stage. The results of the diagnosis with the levels of wear were obtained in a similar way to the procedure adopted in the detection stage. The measurement interval was 30 min during 20 h of operation of the set. It was possible to observe the growth of the failure during the measured time. This growth in entropy was associated with visual inspection of the severity of the failure. In Fig. 16, wavelet entropies are plotted as a function of wear development time.

Fig. 16
figure 16

Source: Author

Diagnosis of the formation of surface wear: a supply line, b with inverter at 60 Hz, c with inverter at 20 Hz.

Full size image

With 8 h of operation, it was possible to observe the first signs of moderate wear. After 13:30 h the first signs of severe wear. Excessive wear occurred after 17:30 h of operation. The results are in accordance with the values observed in the detection stage.

5 Conclusions

According to the analysis of the experimental results, some significant conclusions were reached:

  • The proposed strategy allows the combined diagnosis of broken teeth and wear levels in gearboxes. It is possible to differentiate the broken tooth failures from the other failures of the electromechanical set through the joint analysis of entropy in the SLR and GMR. In this research, it was possible to differentiate the broken tooth from the superficial wear in the GMR through different levels of entropy. When the backlash effects of the broken tooth are visible, there is a small change in entropy in the GMR. The noise caused by surface wear in the GMR has higher entropy levels than the backlash.

  • The detection stage proved that it is possible to analyze failures in low rotation.

  • The entropy of the wavelet details of the EPVA signals provided a low dispersion of most samples (maximum CV of 14.31%). The transient signs of excessive wear cause problems in data acquisition and greater dispersions in entropy (maximum CV of 29.01%).

  • Entropy is a measure of information that can be analyzed using basic statistics such as the coefficient of variation (CV). In the strategy, the mean and standard deviation of the samples were used to define the pertinence functions of the fuzzy inference. This process is easier compared to training and machine learning strategies.

  • The advantage of this strategy was to reduce the amount of data to be analyzed, since only the significantly altered frequency bands are evaluated. This is an important feature in a future implementation of the strategy through an embedded system.

  • The fuzzy inference presented a coherent behavior of the severity of wear in relation to visual inspections, enabling a reliable diagnosis.

  • It has been demonstrated that the fuzzy inference is capable of correctly classifying the gear condition even in case of noise.

As limitations, the decomposition of the package wavelet must be sized according to the acquisition rate, the sample size, the gear rotation, the loading conditions and the effects of the failures. Detail entropy will be assertive and statistically reliable if these parameters are correctly adjusted. This adjustment can be laborious. The results produced in this work can be considered satisfactory. However, some improvements are suggested in order to make this strategy generalist: to extend the study to different sizes of induction motors, as well as to different gears varying dimensions and material; extend the study to other speeds and load conditions.