1 Introduction

The components of a mechanism are considered as links connected by a joint, constituting a mechanical combination for a specific purpose. During movement of the mechanism, especially at high speeds, numerous factors such as the relative movement between components of the mechanism, dynamic loads, material deformation, as well as manufacturing errors can cause clearance in the joints of the mechanism. Therefore, it is not possible to entirely eliminate joint clearance from a mechanism. Given the precise performance expected of a mechanism, observations have shown that clearance is one of the most important causes of vibration, noise and imbalance while it also causes errors in transmission of the movement of the mechanism such as traversed path and positioning. In recent years, researchers have made attempts to perceive the behavior of mechanisms having joint clearance. In this respect, Kolhatkar and Yajnik [37] calculated the maximum output deviation owing to the jumping of joints due to their clearance in generating a mechanism function. Dubowski and Freudenstein [15] also formulated a dynamical model of a mechanism with joint clearance and then investigated its dynamic response. Earles and Wu [16] presented a model with the assumption of constant contact for clearance. In this model, the clearance was replaced with a massless virtual link assuming that two links were constantly in contact with each other. The given model has been widely used by numerous researchers [56]. In this regard, Grant et al. [32] similarly examined the effects of this model by considering the joint clearance between input link and output link in a four-bar mechanism and evaluated conditions or contacts between the pin and bearing. Bengisu et al. [10] also proposed a dimensionless parameter to detect separation of two members in a joint with clearance. They further used this parameter to investigate the behavior of a four-bar mechanism with some joint clearances both theoretically and experimentally. Moreover, Haines et al. [34] experimentally evaluated the dynamic behavior of joint clearance with respect to changes in its size. Lankarani et al.[38] presented a model for contact forces in joint clearance of a mechanism wherein such forces were obtained based on Hertz’s law [35], and the friction forces at joints were gained on the basis of Coulomb’s law. Bai and Zhao [8, 9] also took the advantage of methods developed by Lankarani and Nickravesh to analyze four-bar and slider-crank mechanisms with joint clearance. Olayei and Ghazavi [43] also utilized this model to analyze slider-crank mechanism with joint clearance and then reduced strokes at it via a control method. In this line, Schwab et al. [45] compared different models of clearance with rigid and elastic links. Tian et al. [50] also investigated dynamics of spatial mechanisms with clearance at spherical joints in both lubrication and dry contact modes. Using a massless link model [16], Erkaya and Uzmay [25] dynamically analyzed slider-crank mechanisms with two joint clearances and compared theoretical and experimental results with each other. In another study, Erkaya[17] addressed vibrational characteristics of a mechanism with joint clearance and neural networks. In another work, Ting et al.[51] investigated the joint clearance’s effect on a four-bar mechanism in terms of position deviation along with orientation of members using a virtual massless link model. Tsai and Lai [52] also proposed an appropriate method for analyzing the transmission angle with joint clearance and then analyzed four-bar transmission angles with joint clearance as an example. Innocenti et al. [36] further evaluated the effects of joint clearance using the principle of virtual work in spatial mechanisms. Besides, Venanzi and Parenti-Castelli [55] proposed a new method to express the effects of joint clearance on the deviation and rotation of members of spatial mechanisms. This technique was also based on virtual work, in which the joint size was considered to be negligible.

It should be noted that joint clearance increases the impact forces in mechanism joints and consequently results in vibrational forces and moments or dynamic imbalance in a mechanism as a well-known issue in mechanical engineering since dynamic loads cause noise, attenuation and fatigue in machines. Any reduction in the amount of shaking force and torque also enhances durability and efficiency of a mechanism. Researchers [1,2,3,4, 11, 12, 26,27,28, 30, 40, 48, 57] have thus performed extensive studies on improving dynamic balancing and eliminating shaking forces and shaking moment. However, these studies have often been done without considering clearance in joints, so that there is almost no research directly aimed at optimal design of mechanisms by focusing on mechanism balancing with regard to joint clearance. In the above-mentioned studies, the effects of clearance have been investigated in one or more joints in kinematics and dynamics of mechanisms, and designs performed considering clearance and with the help of optimization methods are few.

Optimization, especially multi-objective, is regarded as one of the important issues in engineering [58]. In multi-objective optimization problems [13], several different objective functions are defined in order to minimize or maximize them simultaneously. These objective functions are often at odds with one another implying that improvement of one of them leads to deterioration of the other objective functions. Therefore, there is no optimal solution that fits all of the objective functions. Rather, there are a set of optimal solutions, known as Pareto optimal solutions or Pareto fronts[5], considered as the main difference in the general nature of single-objective problems with multi-objective ones. The Pareto theory or the set of optimal solutions in the space of objective functions in multi-objective problems is based on the sets of solutions neither one of which is superior to the others. In other words, change in the vector of design variables in the front cannot improve all objective functions simultaneously, because it results in deterioration of at least one objective function. It should be noted that these non-superior solutions are arranged in different layers formed based on the order of the Pareto front, so they include the most important ones. In this respect, Salehpur et al. [44] used the Pareto fronts in most of their works on multi-objective optimization. Felezi et al. [29] also utilized a genetic algorithm to optimize the multi-objective four-bar mechanism of a rice transplant machine to travel the path required to be planted by a machine fork. In addition, Erkaya et al. [18] investigated the dynamic behavior of a four-bar mechanism with joint clearance. To this end, they used an objective function based on shaking forces and shaking moment. They also proposed neural network genetic algorithms via a combined single-objective optimization method to design a four-bar mechanism to minimize the additional effects of joint clearance on shaking forces and shaking moment under relevant constraints. In fact, they tried to bring shaking forces and moment of the mechanism from clearance to non-clearance state. Considering joint clearance, Erkaya and Uzmay [22] determined kinematic parameters of mechanisms with the aim of minimizing path error using genetic algorithm. In another study, they also optimized the transmission angle of a crank-slider mechanism by genetic algorithm [23] and exploited massless link models in all of their studies to simulate clearance. In this research study, shaking force and moment applied to the mechanism by the frame have been significantly reduced by using an optimization method. Moreover, transmission quality has been improved significantly through defining another objective function. Considering joint clearance, Daniali et al. [14] proposed an algorithm for kinematic and dynamic optimization of the mechanisms. Their research involved two optimization processes. The first one is kinematic optimization with the aim of mitigating path error with kinematic design variables, and second one is optimization of the mechanism that is achieved by another optimization process to minimize a single-objective with dynamic design variables such as linear and angular acceleration of links, joint forces and input torque. The problem was that the clearance angles would change, and this could cause the path error function to lose optimal state obtained in the first step during dynamic optimization due to changes in the dynamic parameters such as mass and moment of inertia. In addition, variations in kinematic parameters also affect dynamic properties of the mechanism and there is no need for separating design variables to meet the requirements of kinematic and dynamic optimization. Moreover, Varedi [54] addressed optimized dynamic synthesis of a slider-crank mechanism with focus on minimizing joint forces as single-objective optimization.

Erkaya [20] showed the effect of joint clearance and its magnitude on vibration response of a spatial mechanism by both computational and experimental approaches. Erkaya [21] investigated in a six degree of freedom robotic system for more accuracy. Li et al. [39] investigated the effects of different locations for joint clearances of a slider-crank mechanism with rigid and flexible components on dynamic behavior of the mechanism. Sun et al. [47] improved the kinematic accuracy of a constrained mechanical system with joint clearance using a robust multi-objective optimization approach. Erkaya [19] optimized the trajectory of a walking mechanism with joint clearance by using the ANFIS approach. Hai-Yang et al. [33] used a parameter optimization method for planar joint clearance model and applied the optimization results for dynamic simulation reciprocating compressor. More references with complete and detail review of analytical, experimental and numerical approaches on joint clearance can be found in [49].

What is of interest in this study and differentiates it from other works is the optimal design of a slider-crank mechanism with joint clearance and multi-objectively improvement of dynamic balance and transmission quality in dynamic and kinematic domains. The design variables were thus selected in accordance with reference [23], and the results were compared with the same reference as the only optimal design of slider-crank mechanisms in the presence of sliding performed in order to improve the transmission angle of mechanisms. Other studies were either simply dynamic with no emphasis on kinematic objective functions[6, 7, 24, 53] or kinematic with no focus on dynamic balance of mechanisms[22, 23] or they performed optimization without the presence of clearance [1,2,3,4, 11, 12, 26,27,28, 30, 40, 48, 57], and all of them were in the form single-objective optimization except [27, 28]. Therefore, the present study fills the gap in this area. To this end, the results are presented as Pareto front, which can give the designer some sub-optimal points. This diagram is a good tool for selecting a mechanism with the desired specifications and according to the importance of each of the objective functions. Comparing the results with those of previous works also demonstrates the superiority of this study. The rest of the study is organized as follows: Sect. 1 presents kinematic and dynamic analysis of slider-crank mechanism with joint clearance; the joint clearance simulation method is presented in Sect. 2; Sect. 3 presents the definition of the optimization problem, and results and discussions are finally presented in Sect. 4.

1.1 Kinematic and dynamic analysis of slider-crank mechanism with joint clearance

To model the clearance, a massless virtual link with a length equal to the extent of clearance obtained from the journal and bearing radius was used. The model employed in this regard is shown in Fig. 1. The link begins from the center of the base link pin and ends at the center of the socket connected to the next link.

Fig. 1
figure 1

Joint clearance model with massless virtual link[24]

Full size image

Clearance is the difference between the radius of the bearing and the journal, indicated by r as shown in Fig. 1.

Joint clearance can be simulated with one and two degree of freedom models. For each of these models, many studies have been done by researchers in planar mechanisms (often crank-slider and four-bar mechanisms), which are discussed in detail in the introduction. In this paper, the massless virtual link model or permanent contact between the bearing and the journal is selected to model joint clearance. However, the fact that the pin and bearing are separated at some moments and they are in touch with each at other moments cannot be denied in this case.

When constant contact between the journal and bearing at each joint is assumed, clearance can be modeled as a vector equivalent to a massless virtual link with a length equal to the length of joint clearance. In this case, analysis of a mechanism with joint clearance becomes analysis of a mechanism with ideal joints (without clearance) and more members. As Fig. 1 shows, the amount of clearance is equal to the difference between the radius of the journal and the bearing. According to this assumption and also neglecting friction, the direction of the clearance vector is always in the direction of the common vertical of two surfaces at point of contact. In this model, each joint clearance adds an uncontrolled degree of freedom to the mechanism and the unknown variable is the angular vector of joint clearance. For example, if clearance in one joint is considered, then a four-bar mechanism with one degree of freedom will convert to a five-bar mechanism with two degrees of freedom, and this complicates kinematic and dynamic analysis of the mechanism. Erkaya used a virtual massless link with continuous contact to model joint clearance in 4-bar and slider-crank mechanisms in [22] and [23] and verified the model with a mechanical simulation system that simulates joint clearance with a damper-spring model, and the results confirmed each other with high accuracy. Moreover, this model was used in the previous study with which the results of this research are compared. Given that using the same model in two studies leads to a more accurate comparison of results, use of virtual massless link model in this research is justified.

The angular position of a slider-crank mechanism with clearance, one at the crank-pin and the other at the slider-pin, are obtained. The mechanism in question includes input link, connecting rod, and slider link or piston, as well as virtual links related to the clearance. The x-axis is the horizontal axis and the y-axis shows the vertical one, and each link has its own center of mass and structural angle. r1 and r2 also indicate the length of the massless virtual links related to the clearance; θ2 and θ3 represent the angles of crank and connecting rod to the horizontal axis, and \(\gamma_{2}\) and \(\gamma_{3}\) show the angles of the virtual massless links for joint clearance. Moreover, \(\alpha_{2}\) and \(\alpha_{3}\) refer to structural angles that determine the center of mass of each link. \(k_{2}\) and \(k_{3}\) similarly stand for coefficients of \(l_{2}\) and \(l_{3}\) to determine the length of structural links. Each virtual link assumed as a clearance also adds a degree of freedom to the mechanism. The examined mechanism has three degrees of freedom along \(\gamma_{2}\), \(\gamma_{3}\), and \(\theta_{2}\) given that there are two clearances. It is clear that the slider does not have angular position.

Figure 2 illustrates a slider-crank mechanism that clearly shows its joint clearances, and Fig. 3 depicts the status of a slider-crank mechanism in vector form. Mechanism components are considered rigid and friction is ignored in this research.

Fig. 2
figure 2

An overview of a slider-crank mechanism

Full size image
Fig. 3
figure 3

Vector representation of crank-slider mechanism with two joint clearances [25]

Full size image

Considering the geometry of the mechanism, Eqs. 1–3 represent the center of mass position of the mechanism links.

$$\left[ {\begin{array}{*{20}c} {x_{{G_{2} }} } \\ {y_{{G_{2} }} } \\ \end{array} } \right] = k_{2} R\left[ {\begin{array}{*{20}c} {\cos \left( {\theta_{2} + \alpha_{2} } \right)} \\ {\sin \left( {\theta_{2} + \alpha_{2} } \right)} \\ \end{array} } \right]$$
(1)
$$\left[ {\begin{array}{*{20}c} {x_{{G_{3} }} } \\ {y_{{G_{3} }} } \\ \end{array} } \right] = R\left[ {\begin{array}{*{20}c} {\cos \left( {\theta_{2} } \right)} \\ {\sin \left( {\theta_{2} } \right)} \\ \end{array} } \right] + r_{2} \left[ {\begin{array}{*{20}c} {\cos \left( {\gamma_{2} } \right)} \\ {\sin \left( {\gamma_{2} } \right)} \\ \end{array} } \right] + k_{3} L\left[ {\begin{array}{*{20}c} {\cos \left( {\theta_{3} + \alpha_{3} } \right)} \\ {\sin \left( {\theta_{3} + \alpha_{3} } \right)} \\ \end{array} } \right]$$
(2)
$$\left[ {\begin{array}{*{20}c} {x_{{G_{4} }} } \\ {y_{{G_{4} }} } \\ \end{array} } \right] = R\left[ {\begin{array}{*{20}c} {\cos \left( {\theta_{2} } \right)} \\ {\sin \left( {\theta_{2} } \right)} \\ \end{array} } \right] + r_{2} \left[ {\begin{array}{*{20}c} {\cos \left( {\gamma_{2} } \right)} \\ {\sin \left( {\gamma_{2} } \right)} \\ \end{array} } \right] + L\left[ {\begin{array}{*{20}c} {\cos \left( {\theta_{3} } \right)} \\ {\sin \left( {\theta_{3} } \right)} \\ \end{array} } \right] + r_{3} \left[ {\begin{array}{*{20}c} { - \cos \left( {\gamma_{3} } \right)} \\ { - \sin \left( {\gamma_{3} } \right)} \\ \end{array} } \right]$$
(3)

Given that \(y_{{G_{4} }}\) is always equal to zero, the angle \(\theta_{3}\) is obtained.

$$R\sin \left( {\theta_{2} } \right) + r_{2} \sin \left( {\gamma_{2} } \right) + L\sin \left( {\theta_{3} } \right) - r_{3} \sin \left( {\gamma_{3} } \right) = 0$$
(4)
$$\theta_{3}^{c} = \sin^{ - 1} \left[ { - \frac{{L_{2} \sin \theta_{2} + r_{2} \sin \gamma_{2} + r_{3} \sin \left( {\pi + \gamma_{3} } \right)}}{{L_{3} }}} \right]$$
(5)
$$\mu^{c} = \cos^{ - 1} \left[ {\frac{{L_{2} \sin \theta_{2} + r_{2} \sin \gamma_{2} + r_{3} \sin \left( {\pi + \gamma_{3} } \right)}}{{L_{3} }}} \right]$$
(6)

Equation 6 stands for the transmission angle of the mechanism.

R refers to crank length \(l_{2}\) and L refers to crank and piston connecting rod \(l_{3}\).

Equation 4 is derived in terms of \(\theta_{2}\), \(\gamma_{2}\), and \(\gamma_{3}\), and the equations are written as a matrix equation as shown in Eq. 7:

$$\left[ {\begin{array}{*{20}c} {\frac{{\partial \theta_{3} }}{{\partial \theta_{2} }}} \\ {\frac{{\partial \theta_{3} }}{{\partial \gamma_{2} }}} \\ {\frac{{\partial \theta_{3} }}{{\partial \gamma_{3} }}} \\ \end{array} } \right] = \frac{1}{{\cos \left( {\theta_{3} } \right)}}\left[ {\begin{array}{*{20}c} {\frac{ - R}{L}\cos \left( {\theta_{2} } \right)} \\ {\frac{{ - r_{2} }}{L}\cos \left( {\gamma_{2} } \right)} \\ {\frac{{r_{3} }}{L}\cos \left( {\gamma_{3} } \right)} \\ \end{array} } \right]$$
(7)

Also, by taking the derivative of Eq. 4 twice with respect to \(\theta_{2}\), \(\gamma_{2}\), and \(\gamma_{3}\) and sorting the obtained equations in the form of a matrix equation, Eq. 8 is derived as the second derivative of the angle:

$$\left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} \theta_{3} }}{{\partial \theta_{2}^{2} }}} \\ {\frac{{\partial^{2} \theta_{3} }}{{\partial \theta_{2} \partial \gamma_{2} }}} \\ {\frac{{\partial^{2} \theta_{3} }}{{\partial \theta_{2} \partial \gamma_{3} }}} \\ {\frac{{\partial^{2} \theta_{3} }}{{\partial \gamma_{2}^{2} }}} \\ {\frac{{\partial^{2} \theta_{3} }}{{\partial \gamma_{3}^{2} }}} \\ {\frac{{\partial^{2} \theta_{3} }}{{\partial \gamma_{2} \partial \gamma_{3} }}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} \frac{R}{L} & {\left( {\frac{{\partial \theta_{3} }}{{\partial \theta_{2} }}} \right)^{2} } & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\frac{{\partial \theta_{3} }}{{\partial \theta_{2} }}\frac{{\partial \theta_{3} }}{{\partial \gamma_{2} }}} & 0 & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\frac{{\partial \theta_{3} }}{{\partial \theta_{2} }}\frac{{\partial \theta_{3} }}{{\partial \gamma_{3} }}} & 0 & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\left( {\frac{{\partial \theta_{3} }}{{\partial \gamma_{2} }}} \right)^{2} } & 0 & {\begin{array}{*{20}c} {\frac{{r_{2} }}{L}} & 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\left( {\frac{{\partial \theta_{3} }}{{\partial \gamma_{3} }}} \right)^{2} } & 0 & {\begin{array}{*{20}c} 0 & { - \frac{{r_{3} }}{L}} \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\frac{{\partial \theta_{3} }}{{\partial \gamma_{2} }}\frac{{\partial \theta_{3} }}{{\partial \gamma_{3} }}} & 0 & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {\sin \left( {\theta_{2} } \right)} \\ {\sin \left( {\theta_{3} } \right)} \\ {\sin \left( {\gamma_{2} } \right)} \\ {\sin \left( {\gamma_{3} } \right)} \\ \end{array} } \right]$$
(8)

The angular velocity and angular acceleration equations of the connecting link are also obtained according to Eqs. 9 and 10. Equations 7 and 8 are used to obtain the angular velocity and angular acceleration of the connecting link.

$$\dot{\theta }_{3} = \dot{\theta }_{2} \frac{{\partial \theta_{3} }}{{\partial \theta_{2} }} + \dot{\gamma }_{2} \frac{{\partial \theta_{3} }}{{\partial \gamma_{2} }} + \dot{\gamma }_{3} \frac{{\partial \theta_{3} }}{{\partial \gamma_{3} }}$$
(9)
$$\begin{aligned} \ddot{\theta }_{3} = & \ddot{\theta }_{2} \frac{{\partial \theta_{3} }}{{\partial \theta_{2} }} + \dot{\theta }_{2}^{2} \frac{{\partial^{2} \theta_{3} }}{{\partial \theta_{2}^{2} }} + 2\dot{\theta }_{2} \dot{\gamma }_{2} \frac{{\partial^{2} \theta_{3} }}{{\partial \theta_{2} \partial \gamma_{2} }} + 2\dot{\theta }_{2} \dot{\gamma }_{3} \frac{{\partial^{2} \theta_{3} }}{{\partial \theta_{2} \partial \gamma_{3} }} \\ & \quad + \ddot{\gamma }_{2} \frac{{\partial \theta_{3} }}{{\partial \gamma_{2} }} + \ddot{\gamma }_{3} \frac{{\partial \theta_{3} }}{{\partial \gamma_{3} }} + \dot{\gamma }_{2}^{2} \frac{{\partial^{2} \theta_{3} }}{{\partial \gamma_{2}^{2} }} \\ & \quad + \dot{\gamma }_{3}^{2} \frac{{\partial^{2} \theta_{3} }}{{\partial \gamma_{3}^{2} }} + 2\dot{\gamma }_{2} \dot{\gamma }_{3} \frac{{\partial^{2} \theta_{3} }}{{\partial \gamma_{2} \partial \gamma_{3} }} \\ \end{aligned}$$
(10)

\(K_{2}\) and \(K_{3}\) are also used to determine the mass centers. From the first- and second-time derivatives of the center of mass position, the velocity and acceleration of each link are obtained using Eqs. 11 and 12.

$$\left[ {\begin{array}{*{20}c} {\dot{x}_{{G_{i} }}^{c} } \\ {\dot{y}_{{G_{i} }}^{c} } \\ \end{array} } \right] = \dot{\theta }_{2} \left[ {\begin{array}{*{20}c} {\frac{{\partial x_{{G_{i} }}^{c} }}{{\partial \theta_{2} }}} \\ {\frac{{\partial y_{{G_{i} }}^{c} }}{{\partial \theta_{2} }}} \\ \end{array} } \right] + \mathop \sum \limits_{j = 2}^{3} \dot{\gamma }_{j} \left[ {\begin{array}{*{20}c} {\frac{{\partial x_{{G_{i} }}^{c} }}{{\partial \gamma_{2} }}} \\ {\frac{{\partial y_{{G_{i} }}^{c} }}{{\partial \gamma_{2} }}} \\ \end{array} } \right]$$
(11)
$$\begin{aligned} \left[ {\begin{array}{*{20}c} {\ddot{x}_{{G_{i} }}^{c} } \\ {\ddot{y}_{{G_{i} }}^{c} } \\ \end{array} } \right] = & \ddot{\theta }_{2} \left[ {\begin{array}{*{20}c} {\frac{{\partial x_{{G_{i} }}^{c} }}{{\partial \theta_{2} }}} \\ {\frac{{\partial y_{{G_{i} }}^{c} }}{{\partial \theta_{2} }}} \\ \end{array} } \right] + \dot{\theta }_{2}^{2} \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} x_{{G_{i} }}^{c} }}{{\partial \theta_{2}^{2} }}} \\ {\frac{{\partial^{2} y_{{G_{i} }}^{c} }}{{\partial \theta_{2}^{2} }}} \\ \end{array} } \right] + 2\dot{\theta }_{2} \mathop \sum \limits_{j = 2}^{3} \dot{\gamma }_{j} \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} x_{{G_{i} }}^{c} }}{{\partial \theta_{2} \partial \gamma_{2} }}} \\ {\frac{{\partial y_{{G_{i} }}^{c} }}{{\partial \theta_{2} \partial \gamma_{2} }}} \\ \end{array} } \right] + \mathop \sum \limits_{j = 2}^{3} \ddot{\gamma }_{j} \left[ {\begin{array}{*{20}c} {\frac{{\partial x_{{G_{i} }}^{c} }}{{\partial \gamma_{j} }}} \\ {\frac{{\partial y_{{G_{i} }}^{c} }}{{\partial \gamma_{j} }}} \\ \end{array} } \right] + \\ & \quad \mathop \sum \limits_{j = 2}^{3} \dot{\gamma }_{2}^{2} \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} x_{{G_{i} }}^{c} }}{{\partial \gamma_{2}^{2} }}} \\ {\frac{{\partial^{2} y_{{G_{i} }}^{c} }}{{\partial \gamma_{2}^{2} }}} \\ \end{array} } \right] + \mathop \sum \limits_{j = 2}^{3} \mathop \sum \limits_{j = 2}^{3} \dot{\gamma }_{j} \dot{\gamma }_{k} \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} x_{{G_{i} }}^{c} }}{{\partial \gamma_{j} \partial \gamma_{k} }}} \\ {\frac{{\partial^{2} y_{{G_{i} }}^{c} }}{{\partial \gamma_{j} \partial \gamma_{k} }}} \\ \end{array} } \right]\left( {k \ne j} \right) \\ \end{aligned}$$
(12)

Dynamic analysis of the mechanism involves expression of joint forces and output torque of the mechanism in terms of position of the input link. Assuming that the input link speed remains constant, analysis of the joint forces of the mechanism is done by using the inertial effect of each link as well as the superposition principle. The contact between the bearing and journal is also assumed to be permanent. Equations 13–15 are written according to Fig. 4, showing a free diagram of a slider-crank mechanism using Newton’s second law and Euler equations:

$$F_{{i\left( {i + 1} \right)_{x} }} + F_{{\left( {i + 2} \right)\left( {i + 1} \right)_{x} }} + \left( { - m_{{\left( {i + 1} \right)}} \ddot{x}_{{G_{i + 1} }} } \right) = 0$$
(13)
$$F_{{i\left( {i + 1} \right)_{y} }} + F_{{\left( {i + 2} \right)\left( {i + 1} \right)_{y} }} + \left( { - m_{{\left( {i + 1} \right)}} \ddot{y}_{{G_{i + 1} }} - m_{{\left( {i + 1} \right)}} g} \right) = 0$$
(14)
$$\sum M_{{G_{{\left( {i + 1} \right)}} }} - I_{{G_{{\left( {i + 1} \right)}} }} \ddot{\theta }_{{\left( {i + 1} \right)}} = 0$$
(15)
Fig. 4
figure 4

Force representation of crank-slider mechanism [27]

Full size image

\(F_{{i\left( {i + 1} \right)_{x} }}\) and \(F_{{i\left( {i + 1} \right)_{y} }}\) represent the joint force applied to link \(\left( {i + 1} \right)\) of link \(i\) in two x and y directions. Moreover, shaking forces and moments that flow from the frame to the piston and the crank link are shown in Eqs. 16–18.

$$\sum F_{{sh_{x} }} = \sum F_{{41_{x} }} + \sum F_{{21_{x} }}$$
(16)
$$\sum F_{{sh_{y} }} = \sum F_{{41_{y} }} + \sum F_{{21_{y} }}$$
(17)
$$M_{sh} = x_{G4} i \otimes \sum F_{{41}_{{y}}} i$$
(18)

\(\sum F_{41}\) and \(\sum F_{21}\) represent the forces resulting in the slider-frame and crank-frame joints; respectively. Also, j shows the number of joint clearances.

1.2 Force and torque equations

Horizontal and vertical forces at the place of crank-frame joint resulting from input torque and inertia effect of the second, third and fourth links are obtained separately according to Eqs. 19–26 by means of Fig. 4 showing forces and torque applied to the mechanism as follows [24]:

$$F_{21x}^{I} = \frac{{T_{in} \cos \gamma_{2} }}{{l_{2} \sin \left( {\theta_{2} - \gamma_{2} } \right)}}$$
(19)
$$F_{21y}^{I} = \frac{{T_{in} \sin \gamma_{2} }}{{l_{2} \sin \left( {\theta_{2} - \gamma_{2} } \right)}}$$
(20)
$$F_{21x}^{II} = \frac{{\left[ { - \left( {m_{2} \ddot{x}_{{G_{2} }} } \right)K_{2} L_{2} \sin \left( {\theta_{2} + \alpha_{2} } \right) + K_{2} L_{2} \cos \left( {\theta_{2} + \alpha_{2} } \right)\left[ {m_{2} \ddot{y}_{{G_{2} }} + m_{2} g} \right]} \right]\cos \gamma_{2} }}{{l_{2} \sin \left( {\theta_{2} - \gamma_{2} } \right)}} - \left( {m_{2} \ddot{x}_{{G_{2} }} } \right)$$
(21)
$$\begin{aligned} F_{21y}^{II} = & \frac{{\left[ { - \left( {m_{2} \ddot{x}_{{G_{2} }} } \right)K_{2} L_{2} \sin \left( {\theta_{2} + \alpha_{2} } \right) + K_{2} L_{2} \cos \left( {\theta_{2} + \alpha_{2} } \right)\left[ {m_{2} \ddot{y}_{{G_{2} }} + m_{2} g} \right] + \left( {I_{{G_{2} }} \ddot{\theta }_{2} } \right)} \right]\sin \gamma_{2} }}{{l_{2} \sin \left( {\theta_{2} - \gamma_{2} } \right)}} - \left( {m_{2} \ddot{y}_{{G_{2} }} } \right) \\ & \quad - \left( {m_{2} g} \right) \\ \end{aligned}$$
(22)
$$\begin{aligned} F_{21x}^{III} = & - \frac{{\left( {m_{3} \ddot{x}_{{G_{3} }} } \right)\left[ {\overline{{G_{3} B}} \sin \left( {\theta_{3} + \alpha_{3} + \Psi } \right) + \left( {r_{3} } \right)\sin \gamma_{3} } \right]\cos \gamma_{2} }}{{K_{3} L_{3} \sin (\gamma_{2} - \theta_{3} - \alpha_{3} ) + \overline{{G_{3} B}} \sin \left( {\theta_{3} + \alpha_{3} + \Psi - \gamma_{2} } \right) + \left( {r_{3} } \right)\sin (\gamma_{3} - \gamma_{2} )}} \\ & \quad + \frac{{\left[ {m_{3} \ddot{y}_{{G_{3} }} + m_{3} g} \right]\left[ {\overline{{G_{3} B}} \cos \left( {\theta_{3} + \alpha_{3} + \Psi } \right) + \left( {r_{3} } \right)\cos \gamma_{3} } \right]\cos \gamma_{2} }}{{K_{3} L_{3} \sin (\gamma_{2} - \theta_{3} - \alpha_{3} ) + \overline{{G_{3} B}} \sin \left( {\theta_{3} + \alpha_{3} + \Psi - \gamma_{2} } \right) + \left( {r_{3} } \right)\sin (\gamma_{3} - \gamma_{2} )}} \\ & \quad + \frac{{\left( {I_{{G_{3} }} \ddot{\theta }_{3} } \right)\cos \gamma_{2} }}{{K_{3} L_{3} \sin (\gamma_{2} - \theta_{3} - \alpha_{3} ) + \overline{{G_{3} B}} \sin \left( {\theta_{3} + \alpha_{3} + \Psi - \gamma_{2} } \right) + \left( {r_{3} } \right)\sin (\gamma_{3} - \gamma_{2} )}} \\ \end{aligned}$$
(23)
$$\begin{aligned} F_{21y}^{III} = & - \frac{{\left( {m_{3} \ddot{x}_{{G_{3} }} } \right)\left[ {\overline{{G_{3} B}} \sin \left( {\theta_{3} + \alpha_{3} + \Psi } \right) + \left( {r_{3} } \right)\sin \gamma_{3} } \right]\sin \gamma_{2} }}{{K_{3} L_{3} \sin (\gamma_{2} - \theta_{3} - \alpha_{3} ) + \overline{{G_{3} B}} \sin \left( {\theta_{3} + \alpha_{3} + \Psi - \gamma_{2} } \right) + \left( {r_{3} } \right)\sin (\gamma_{3} - \gamma_{2} )}} \\ & \quad + \frac{{\left[ {m_{3} \ddot{y}_{{G_{3} }} + m_{3} g} \right]\left[ {\overline{{G_{3} B}} \cos \left( {\theta_{3} + \alpha_{3} + \Psi } \right) + \left( {r_{3} } \right)\cos \gamma_{3} } \right]\sin \gamma_{2} }}{{K_{3} L_{3} \sin (\gamma_{2} - \theta_{3} - \alpha_{3} ) + \overline{{G_{3} B}} \sin \left( {\theta_{3} + \alpha_{3} + \Psi - \gamma_{2} } \right) + \left( {r_{3} } \right)\sin (\gamma_{3} - \gamma_{2} )}} \\ & \quad + \frac{{\left( {I_{{G_{3} }} \ddot{\theta }_{3} } \right)\sin \gamma_{2} }}{{K_{3} L_{3} \sin (\gamma_{2} - \theta_{3} - \alpha_{3} ) + \overline{{G_{3} B}} \sin \left( {\theta_{3} + \alpha_{3} + \Psi - \gamma_{2} } \right) + \left( {r_{3} } \right)\sin (\gamma_{3} - \gamma_{2} )}} \\ \end{aligned}$$
(24)
$$F_{21x}^{IV} = 0$$
(25)
$$F_{21y}^{IV} = 0$$
(26)

The shaking forces acting on the mechanism are the result of input torque and inertial effect of links 2, 3 and 4. In fact, the principle of superposition has been used to obtain \(F_{21x}\), \(F_{21y}\), \(F_{41x}\) and \(F_{41y}\). For example \(F_{21}^{I}\) is obtained by considering the mass of the links to be zero and only considering the effect of input torque and then decomposing in the x and y directions.

In other words, the part of \(F_{21}^{I}\) that is obtained from input torque results and its components are called \(F_{21x }^{I}\) and \(F_{21y}^{I}\). It should be noted that input torque is obtained by solving the Lagrange equation in direction \(\theta_{2}\). \(F_{21x}^{II}\) represents the part of the shaking force \(F_{21}\) in the x direction which is the result of inertial effect of link 2. That is, the mass of all mechanism links except link number 2 are assumed to be zero. Previously, the effect of input torque was also calculated, and it is considered equal to zero in this section. Then the dynamic equations are written and \(F_{21x}^{II}\) and \(F_{21y}^{II}\) are obtained.

This concept also applies to links 3 and 4 from which the relations \(F_{21x}^{III}\) and \(F_{21x}^{IV}\) are obtained.

Because of the neglecting of friction in this study, \(F_{41x}\) is equal to zero.The components of the horizontal and vertical forces of the slider-frame as functions of input torque and the inertia effect of the links 2, 3 and 4 are obtained as shown in Eqs. 27–34 with the same assumption and were showed in Eqs. 19–26:

$$F_{41y}^{I} = - \frac{{T_{in} \sin \gamma_{3} }}{{l_{2} \sin \left( {\theta_{2} - \gamma_{2} } \right)}}$$
(27)
$$F_{41y}^{II} = \frac{{\left[ { - \left( {m_{2} \ddot{x}_{{G_{2} }} } \right)K_{2} L_{2} \sin \left( {\theta_{2} + \alpha_{2} } \right) + K_{2} L_{2} \cos \left( {\theta_{2} + \alpha_{2} } \right)\left[ {m_{2} \ddot{y}_{{G_{2} }} + m_{2} g} \right] + \left( {I_{{G_{2} }} \ddot{\theta }_{2} } \right)} \right]\sin \gamma_{3} }}{{l_{2} \sin \left( {\theta_{2} - \gamma_{2} } \right)}}$$
(28)
$$\begin{aligned} F_{41y}^{III} = & \frac{{\left( {m_{3} \ddot{x}_{{G_{3} }} } \right)\left[ {\overline{{G_{3} B}} \sin \left( {\theta_{3} + \alpha_{3} + \Psi } \right) + \left( {r_{3} } \right)\sin \gamma_{3} } \right]\sin \gamma_{2} }}{{K_{3} L_{3} \sin (\gamma_{2} - \theta_{3} - \alpha_{3} ) + \overline{{G_{3} B}} \sin \left( {\theta_{3} + \alpha_{3} + \Psi - \gamma_{2} } \right) + \left( {r_{3} } \right)\sin (\gamma_{3} - \gamma_{2} )}} \\ & \quad - \frac{{\left[ {m_{3} \ddot{y}_{{G_{3} }} + m_{3} g} \right]\left[ {\overline{{G_{3} B}} \cos \left( {\theta_{3} + \alpha_{3} + \Psi } \right) + \left( {r_{3} } \right)\cos \gamma_{3} } \right]\sin \gamma_{2} }}{{K_{3} L_{3} \sin (\gamma_{2} - \theta_{3} - \alpha_{3} ) + \overline{{G_{3} B}} \sin \left( {\theta_{3} + \alpha_{3} + \Psi - \gamma_{2} } \right) + \left( {r_{3} } \right)\sin (\gamma_{3} - \gamma_{2} )}} \\ & \quad - \frac{{\left( {I_{{G_{3} }} \ddot{\theta }_{3} } \right)\sin \gamma_{2} }}{{K_{3} L_{3} \sin (\gamma_{2} - \theta_{3} - \alpha_{3} ) + \overline{{G_{3} B}} \sin \left( {\theta_{3} + \alpha_{3} + \Psi - \gamma_{2} } \right) + \left( {r_{3} } \right)\sin (\gamma_{3} - \gamma_{2} )}} \\ & \quad - m_{3} \ddot{y}_{{G_{3} }} - m_{3} g \\ \end{aligned}$$
(29)
$$F_{41y}^{IV} = - m_{4} g$$
(30)

The horizontal and vertical forces on the crank-frame and slider-frame are obtained as follows:

$$\sum F_{21x} = F_{21x}^{I} + F_{21x}^{II} + F_{21x}^{III} + F_{21x}^{IV}$$
(31)
$$\sum F_{21y} = F_{21y}^{I} + F_{21y}^{II} + F_{21y}^{III} + F_{21y}^{IV}$$
(32)
$$\sum F_{41x} = F_{41x}^{I} + F_{41x}^{II} + F_{41x}^{III} + F_{41x}^{IV}$$
(33)
$$\sum F_{41y} = F_{41y}^{I} + F_{41y}^{II} + F_{41y}^{III} + F_{41y}^{IV}$$
(34)

As Eqs. 32–35 show, the relations \(F_{41x}\) and \(F_{41y}\) can be obtained with the same assumptions as shown in Eqs. 19–30.

This method has already been used in the reference [24] to obtain the shaking forces and shaking moment of a four-bar mechanism.

It is noteworthy that the input torque is achieved by writing the Lagrangian equation with respect to \(\theta_{2}\) and replacing the corresponding equations of \(K\), \(U\) and \(D_{c}\) which represent kinetic, potential and wasted energy, respectively [41].

$$\frac{{{\text{d}}\left( {\frac{\partial T}{{\partial \dot{\theta }_{2} }}} \right)}}{{{\text{d}}t}} - \frac{\partial T}{{\partial \theta_{2} }} + \frac{\partial U}{{\partial \theta_{2} }} + \left( {\frac{{\partial D_{c} }}{{\partial \dot{\theta }_{2} }}} \right) = T_{in}$$
(35)
$$K = \frac{1}{2}\mathop \sum \limits_{i = 2}^{4} I_{i} \left( {\theta_{i}^{c} } \right)^{2} + \frac{1}{2}\mathop \sum \limits_{i = 2}^{4} m_{i} \left[ {\left( {x_{{G_{i} }}^{c} } \right)^{2} + \left( {y_{{G_{i} }}^{c} } \right)^{2} } \right]$$
(36)
$$U = \mathop \sum \limits_{i = 2}^{4} m_{i} gy_{{G_{i} }}^{c}$$
(37)
$$D_{c} = \frac{1}{2}\mathop \sum \limits_{i = 2}^{4} C_{{\theta_{i} }} (\theta_{i}^{c} )^{2} + \frac{1}{2}C_{{\gamma_{2} }} \dot{\gamma }_{2}^{2} + \frac{1}{2}C_{{\gamma_{3} }} \dot{\gamma }_{3}^{2}$$
(38)
$$\mathop \sum \limits_{i = 2}^{4} \left[ {I_{i} \ddot{\theta }_{i}^{c} \frac{{\partial \left( {\theta_{i}^{c} } \right)}}{{\partial \theta_{2} }} + m_{i} \left( {\ddot{x}_{{G_{i} }}^{c} \frac{{\partial (x_{{G_{i} }}^{c} )}}{{\partial \theta_{2} }} + \ddot{y}_{{G_{i} }}^{c} \frac{{\partial (y_{{G_{i} }}^{c} )}}{{\partial \theta_{2} }}} \right) + gm_{i} \frac{{\partial (y_{{G_{i} }}^{c} )}}{{\partial \theta_{2} }} + C_{{\theta_{i} }} \dot{\theta }_{i}^{c} \frac{{\partial (\theta_{i}^{c} )}}{{\partial \theta_{2} }}} \right] + C_{{\gamma_{2} }} \dot{\theta }_{2} = T_{in}$$
(39)

1.3 Joint clearance simulation method

According to Eqs. 1–40, the values of \(\gamma_{2}\) and \(\gamma_{3}\) virtual angles for each input angle \(\theta_{2}\) must be specified to determine velocity and acceleration as well as other kinematic parameters and obtain vibrational forces and torques of slider-crank mechanism with joint clearance. These values can be obtained by solving the Lagrangian equation governing the examined mechanism according to Eqs. 40 and 41.

$$a = \mathop \sum \limits_{i = 2}^{4} \left[ {I_{i} \ddot{\theta }_{i}^{c} \frac{{\partial \left( {\theta_{i}^{c} } \right)}}{{\partial \gamma_{2} }} + m_{i} \left( {\ddot{x}_{{G_{i} }}^{c} \frac{{\partial \left( {x_{{G_{i} }}^{c} } \right)}}{{\partial \gamma_{2} }} + \ddot{y}_{{G_{i} }}^{c} \frac{{\partial \left( {y_{{G_{i} }}^{c} } \right)}}{{\partial \gamma_{2} }}} \right) + gm_{i} \frac{{\partial \left( {y_{{G_{i} }}^{c} } \right)}}{{\partial \gamma_{2} }} + C_{{\theta_{i} }} \dot{\theta }_{i}^{c} \frac{{\partial \left( {\theta_{i}^{c} } \right)}}{{\partial \gamma_{2} }}} \right] + C_{{\gamma_{2} }} \dot{\gamma }_{2} = 0$$
(40)
$$b = \mathop \sum \limits_{i = 2}^{4} \left[ {I_{i} \ddot{\theta }_{i}^{c} \frac{{\partial \left( {\theta_{i}^{c} } \right)}}{{\partial \gamma_{3} }} + m_{i} \left( {\ddot{x}_{{G_{i} }}^{c} \frac{{\partial \left( {x_{{G_{i} }}^{c} } \right)}}{{\partial \gamma_{3} }} + \ddot{y}_{{G_{i} }}^{c} \frac{{\partial \left( {y_{{G_{i} }}^{c} } \right)}}{{\partial \gamma_{3} }}} \right) + gm_{i} \frac{{\partial \left( {\theta_{i}^{c} } \right)}}{{\partial \gamma_{3} }} + C_{{\theta_{i} }} \dot{\theta }_{i}^{c} \frac{{\partial \left( {\theta_{i}^{c} } \right)}}{{\partial \gamma_{3} }}} \right] + C_{{\gamma_{3} }} \dot{\gamma }_{3} = 0$$
(41)

To solve Eqs. 40 and 41, they can be transformed into Eq. 42, as follows:

$$\left| a \right| + \left| b \right| = 0$$
(42)

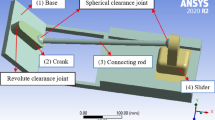
Equation 42 shows six unknown variables \(\left[ {\gamma_{2} ,\dot{\gamma }_{2} ,\ddot{\gamma }_{2} } \right]\) and \(\left[ {\gamma_{3} ,\dot{\gamma }_{3} ,\ddot{\gamma }_{3} } \right]\) at each \(\theta_{2}\) angle. This equation is nonlinear, and it cannot be solved with high precision using conventional numerical methods due to the existence of nonlinear terms that make it complicated. To minimize Eq. 42, genetic algorithm is used. The design variables are also the same \(\left[ {\gamma_{2} ,\dot{\gamma }_{2} ,\ddot{\gamma }_{2} ,\gamma_{3} ,\dot{\gamma }_{3} ,\ddot{\gamma }_{3} } \right]\). Moreover, the components of the genetic algorithm are selected according to Table 1 and optimization is performed for each input \(\theta_{2}\) angle from 0 to 360 degrees with one degree segmentation. The design variables of the optimization are also used to obtain the objective functions of the optimization problem in this research study as discussed in the next section. In Fig. 5, simulation diagrams of clearance angles and their derivatives in one rotation of the crank link for an optimized mechanism are also plotted for the optimization problem at hand. To verify the accuracy of the computations performed in this research for simulating clearance angles and their derivatives, an optimal selected mechanism (A), modeled in ANSYS18 Software and as shown in Fig. 5, the results obtained in this work are nearly in accordance with those obtained by ANSYS. Goldberg [31] reported that population size of 30 to 200 are a common choice of many GA researchers. In general, the initial population is randomly generated and can be of any size, from a few individuals to thousands [5]. Optimization process or number of iterations goes on until termination conditions are met.

Table 1 Genetic algorithm components in simulation of joint clearance angles and their derivatives
Full size table
Fig. 5
figure 5

Diagram of clearance angles and their derivatives in terms of \(\theta_{2}\) for point A(Suggested by this work) in a full rotation of crank link

Full size image

There may be many reasons to end a GA usually called termination condition. The first termination condition is finding a very good solution. Or it may be the case that the algorithm does not stop to converge, such as the case when in the last N interactions, the fitness function does not increase more than a predefined threshold. Other reasons for termination are constraints such as available time and money.

Crossover helps exploit and enhance convergence [6]. Most empirical results and theoretical studies suggest a relatively higher probability pc for crossover in the range of 0.6 to 0.95, while mutation probability pm is typically very low, around 0.001 to 0.05. These values correspond to a high level of mixing and exploitation.

Three sets of values were considered for crossover and mutation in this study: 1 − (0.95 and 0.1)[29], 2 − (0.8 and 0.2)[23], 3 − (0.95 and 0.005). The third category showed the highest compliance with the simulation software, and it was therefore selected for the optimization parameters.

The elimination criticism is a criteria for more efficiency of the algorithm, and its general value is given in Table 1 [42].

2 Multi-Objective optimization

2.1 Definition of optimization

A full balancing of a mechanism can be achieved by eliminating shaking forces and shaking moment. Eliminating each of these parameters also leads to an increase in the other one [18]. Therefore, it is not possible to completely eliminate them due to their conflict with each other. On the other hand, presence of clearance in a joints increases shaking force and shaking moment of a mechanism and consequently leads to unbalancing. The transmission angle can further determine the motion quality in a mechanism which is taken into account as an important criterion in the design of mechanisms and the best possible choice for it is to be maximized. The closer the transmission angle to 90 degrees is, the better will the outcome be. This value also helps designers choose the best mechanism with the most effective transmission force. Accordingly, a mechanism whose transmission angle is far from 90 degrees has poor performance quality, and its low transmission angle at high speeds can cause inertia and noise. Therefore, improving the dynamic performance of a mechanism for better equilibrium along with better transmission quality is defined as a bi-objective optimization problem. Two objective functions are thus defined for this problem. One is represented as the sum of vertical and horizontal components of shaking forces and shaking moment, and the other is the deviation of transmission angle from 90 degrees, indicated by Eqs. 43 and 44.

The values of shaking forces and shaking moment obtained from Eqs. 19–39 are only for one value of the angular position of the input link \(\theta_{2}\), because the values of shaking force and shaking moment and for a full rotation of driving link as the input link are required in order to investigate the balancing of a mechanism. Hence, a full rotation cycle of the input link which is \(360^{^\circ }\) (2π radians) is divided into s points that is assumed to be 360 in this study. Therefore, for these 360 points for each angle of the input link, first \(\left[ {\gamma_{2} ,\dot{\gamma }_{2} ,\ddot{\gamma }_{2} ,\gamma_{3} ,\dot{\gamma }_{3} ,\ddot{\gamma }_{3} } \right]\) are calculated by minimizing the Lagrangian equations, and then, they are employed to calculate the values of shaking force and shaking moment as well as transmission angle. As a result, the values of the objective functions for each point are obtained and then summing them in a full rotation leads to the value of the final objective functions in the form of Eqs. 43 and 44:

$$f_{1} \left( x \right) = \mathop \sum \limits_{1}^{s} \left( {F_{21x} + F_{21y} + F_{41y} + M_{sh} } \right)$$
(43)
$$f_{2} \left( x \right) = \mathop \sum \limits_{1}^{s} \left( {\frac{\pi }{2} - \mu } \right)$$
(44)

where \(f_{1} \left( x \right)\) and \(f_{2} \left( x \right)\) are called balancing the objective function and the transmission angle objective function, respectively.

All components are considered equally in the balancing function because equal importance for the components of shaking forces and shaking moment has been considered in optimization problem.

Erkaya [18] showed that the balancing objective function should include shaking forces and shaking moment that have different dimensions. He showed that if researchers do not consider both shaking moment and shaking forces in the balancing function, the obtained decreasing ratio will be worse than the case of considering them both in one objective function. Therefore, the proposed objective function structure is appropriate for the balancing function.

It should be noted that the friction between the slider and the ground is neglected and the objective function is shown in Eq. 45:

$$Min f\left( x \right) = \left\{ {f_{1} \left( x \right),f_{2} \left( x \right) } \right\}$$
(45)

which must be minimized according to a set of constraints including the upper and lower limits of the vector design variables that are necessary to create a working mechanism. The design variables are defined as follows:

(46)

\(\alpha_{i}\) as \(\alpha_{1}\) and \(\alpha_{2}\) constitute structural angles of the moving links. \(k_{2}\) and \(k_{3}\) are coefficients between zero and one used to determine the structural side or the center of mass, and \(l_{2 } {\text{ and }}l_{3}\) are the lengths of the crank and coupler links. The upper and lower limits of the design variables are adopted according to the mechanism workspace, geometry of links, as well as depth, thickness and length of each moving link of the main mechanisms. The geometrical and mass parameters of the primary mechanism are presented in Table 2. Moreover, the angular velocity of the input link is assumed to be 600 rpm.

Table 2 Mass and geometrical parameters of the primary mechanism
Full size table

To solve this optimization problem, a multi-objective genetic algorithm adopted from reference [29] is used.

The crossover and mutation parameters of this study have been set to 0.8 and 0.2 just like the previous study [23]. The results are shown as Pareto fronts. Given that the optimization is a multi-objective problem and there is no method to minimize or maximize the objective functions simultaneously, solving multi-objective optimization problems leads to a set of non-superior optimal solutions compared with each other in which the sum of all dominant solutions of the optimal Pareto set and the associated objective functions are called Pareto fronts. Figure 6 shows an optimal Pareto front with two objective functions. The general process of solving the optimization problem is as follows:

  1. I.

    Start

  2. II.

    Obtain clearance angles and their derivatives for each \(\theta_{2}\) angle

  3. III.

    Obtain location, velocity and acceleration of the center of mass of the links

  4. IV.

    Enter into the optimization process

Fig. 6
figure 6

Optimum Pareto front of a multi-objective optimization problem [46]

Full size image

The overall process of solving the mentioned optimization problem in this section has been shown as a flowchart in Fig. 7.

Fig. 7
figure 7

The overall process of solving the optimization problem of the present research

Full size image

3 Results and discussion

The modified bi-objective genetic algorithm [29] is used to optimize the two proposed functions; i.e., transmission angle and balancing function \(\left( {f_{1} \left( x \right),f_{2} \left( x \right)} \right)\) for a clearance value of 1 mm. The various parts of the selected genetic algorithm are presented in Table 1 for calculating direction of clearances. The Pareto chart as the outcome of this optimization is illustrated in Fig. 8. Each point in the Pareto diagram represents a mechanism that can be selected as an answer to the problem according to the design criteria. Although none of the points in the Pareto diagram are superior to the others, points A and B will be examined as the suggested ones. Point A represents the mechanism with the least value for the balancing function. This point is the trade off point resulting from optimization. To obtain the trade off point, all values of the non-superior points of the objective functions are also mapped at a range of 0 to 1. The optimal design point from the point of view of all objective functions, called A, is the point that has the smallest sum of the mapped objective functions.

Fig. 8
figure 8

Pareto front of balancing objective function and transmission angle function with more zoom in Pareto particles

Full size image

A brief review of the proposed Pareto front shows that improvement in the value of one objective function leads to deterioration of the other one. Therefore, choosing any point relative to other points of the Pareto front can bring about a decrease in one objective function and an increase in the other ones, or even a rise in both functions. In other words, it can cause the point to be located on a worse area of the Pareto front. In a minimization problem, the worse space in the Pareto front is located in the upper/right region and the better space is located in the lower/left one, and point B is chosen based on this criterion. Points C, D and E are the optimal points introduced by reference [23] as shown on the Pareto front and point F is the main mechanism in a non-optimal state. As a natural result of optimization, shaking force and shaking moment of the selected optimal mechanisms of this study are much lower than that of the original mechanism and the mechanisms suggested by the optimization results of ref [23].

Figure 4 gives the crank-frame and follower-frame joint forces which are the subcomponents of shaking force after the optimization. There is a certain decrease of the force values. The X component of the crank-frame joint force of point A decreased by 78.045, 84.62, 76.51 and 72.72 relative to points C, D, E and F, respectively. These ratios for point B are 77.125, 83.98, 75.53 and 71.57. The Y component of the crank-frame joint force of point A decreased by 72.53, 76.54, 69.51 and 70.22 relative to points C, D, E and F, respectively. These ratios are 70.9, 75.14, 67.70 and 68.45 for point B. For the case of follower-frame only in Y-direction, the component of shaking force exists due to neglecting friction. The decrease ratio for point A in Y direction is respectively 83.95, 85.61, 80 and 83.18 relative to points C, D, E and F. These ratios are 83.27, 85, 79.16 and 82.47 for point B. The decrease ratio for shaking moment of points A relative to mechanisms C, D, E and F is, respectively, 78.85, 80.66, 75.09 and 77.94, respectively. This ratio is 77.84, 79.73, 73.9 and 76.89 for point B relative to points C, D, E and F. These effects reduce noise and vibrations and increase kinematic and dynamic efficiencies of the mechanism.

Erkaya [18] showed that the objective function of balancing should comprise of both shaking force and shaking moment while their dimensions do not match; Erkaya showed if researchers do not consider both shaking moment and shaking forces in the balancing function, the obtained reduced ratio will be worse than the case when they are considered together in an objective function. So the proposed structure of objective function is appropriate for the balancing function.

The values of the design variables of these mechanisms and their objective functions are presented in Table 3. The components of shaking forces and shaking moments of each optimized and non-optimized points are given in Table 4 for more clarification. Decreasing ratios of the subcomponents of balancing function of mechanisms A and B those suggested by this work relative to mechanisms C, D, E and F those suggested by [23] are given in Table 5 for more clarification. Moreover, the percent improvements in the objective functions of the optimum mechanisms selected in this research study compared with the ones introduced by reference [23] and its non-optimal main mechanism are listed in Table 6 and 7, which clearly shows the outperformance of the proposed method in the present study over previously published research. The Pareto front in Fig. 8 also reveals that the rest of the design points obtained from the optimization of the optimal reference mechanisms and the main mechanism are superior in terms of both the balancing objective function and the transmission angle except for one point. Figure 9 shows the diagram of the sum of shaking forces and shaking moment in terms of input link angle \(\left( {\theta_{2} } \right)\). This diagram is plotted for points A and B, which are the optimum selected points of this study, as well as points C, D, E and F as the optimum reference points of the reference and those of the main mechanism. The diagram also shows that the sum of the vibrational force and torque in this study has reduced significantly compared with that in the previous research study. It also indicates that the diagram of the balancing objective function is intensely rising in certain angles of \(\theta_{2}\) like 22° and 170°, which means that shaking forces and torques hit the mechanism like a sudden stroke. In mechanisms A and B, this sudden stroke has reduced and damped to a large extent, leading to a significant improvement in the dynamical balancing of the mechanism.

Table 3 Values of design variables and objective functions of selected optimal mechanisms suggested by this work (A,B), optimal mechanisms suggested by reference[23] mechanisms (C,D and E) and main mechanism (F)[23]
Full size table
Table 4 The components of shaking forces and shaking moments of points A, B, C, D, E and F (optimized and non-optimized mechanisms)
Full size table
Table 5 Decreasing ratios the subcomponents of balancing function of mechanisms A and B (suggested by this work) relative to mechanisms C, D, E and F (suggested by [23])
Full size table
Table 6 Percent improvement in objective functions of mechanism A (suggested by this work) relative to optimal reference [23] mechanisms and main mechanism[23]
Full size table
Table 7 Percent improvement in objective functions of mechanism B (suggested by this work) relative to optimal reference [23] mechanisms and main mechanism [23]
Full size table
Fig. 9
figure 9

Balancing function diagram in a full rotation of crank link for points A, B, C, D, E and F(suggested by this work and ref[23])

Full size image

Moreover, the transmission angle that is the objective function of the other optimization problem investigated in this study is recognized in the mechanism model as a criterion for its kinematic performance. In reference[23], only the difference between the transmission angles of the mechanism in both assumptions of clearance existence and non-existence is minimized. Improvements are also visible in transfer angle function in Tables 6 and 7. The decrease ratio for transmission angle function of point A relative to points C, D, E and F are 17.68, 17.67, 17.66 and 17.88, respectively. This ratio is 18.2, 18.19, 18.18 and 18.4, respectively, for point B. This result improves the kinematic quality and force transmission efficiency and mechanical performance. Therefore, mechanical working condition becomes better.

However, in this study, in addition to minimizing shaking forces and shaking moment applied to the mechanism, its transmission angle is optimized with the assumption of having clearance, and in fact it approaches \(90^{^\circ }\), which is the ideal mode of transmission angle in the slider-crank mechanism. Significant improvement in terms of this objective function can be seen in the Pareto front of Fig. 8 and Tables 6 and 7. In addition, the diagram of the transmission angle function in terms of the input link or crank in a full rotation of the crank link is plotted in Figs. 10 and 11 for the optimal points A and B compared with the best introduced reference point, confirming the outperformance of the present study over previously reported research studies in terms of transmission angle. Although the optimization proposed by reference [23] leads to improvement in transmission angle approaching a non-clearance mechanism as shown in Table 3, it leads to deterioration of the mechanism in terms of balancing. The method used in this study eliminates this design defect, presents mechanisms and simultaneously provides designers with high transmission quality and desirable dynamical balancing.

Fig. 10
figure 10

Diagram of transmission angle function in terms of crank link angle in its complete circulation for optimal point A (this work) compared with that of reference[23]

Full size image
Fig. 11
figure 11

Diagram of transmission angle function in terms of crank link angle in its complete circulation for optimal point B (this work) compared with that of reference [23]

Full size image

4 Conclusion

In this research study, balancing and transmission angle of a planar slider-crank mechanism is improved through solving a bi-objective optimization problem with regard to clearance in crank and piston joints. The joint clearance is considered as a conventional model of massless link, and the contact between the bearing and journal is taken into account by assuming a continuous model. The length of clearance for each joint has been considered to be 1 mm. The Lagrangian equation minimization method is also used to simulate clearance angles and their derivatives. In accordance with the numerical results of clearance angles of this method compared with simulation of a mechanical system, the continuous contact assumption is used for modeling joint clearance in this study. To state the optimization problem, the kinematic equations of the mechanism were at first extracted using Newton’s second law and Euler equations. Then, equations of shaking forces and shaking moment applied to the mechanism were extracted considering the inertial effect of each link and using the superposition principle.

The two objective functions defined were the sum of the forces and moments applied to the mechanism and the transmission angle of the ideal angle 90° at one rotation of the input link for bi-objective optimization in order to simultaneously improve dynamic and kinematic efficiency of the mechanism.

The objective function of balancing should comprise of both shaking force and shaking moment while their dimensions do not match as shown in previous studies. Mechanism design variables also included the length and the position of the center of mass of the moving links of the mechanism other than the piston. Input or crank link speeds were also set at 600 rpm. The optimization process is performed using bi-objective genetic algorithm. The crossover and mutation parameters of this study have been set to be 0.8 and 0.2 like the previous study. The bi-objective optimization results were a number of optimal points of the design that were presented in a Pareto chart due to the dual purpose of the optimization problem whereby designers can select one point as the optimal design point depending on their needs. To select the best point of the Pareto chart, a point called trade off point is considered as the best solution to the problem through mapping the objective functions. Bi-objective functions were thus defined: one as the sum of the shaking forces and shaking moment applied to the mechanism and the other one as deviation of the transmission angle from its ideal angle, i.e., \(90^{^\circ }\) at one full rotation of the input link. At this point, an average decrease of 78.6% in the balancing objective function and an average decline of 17.72% in the transmission angle objective function were observed compared with previous studies wherein optimization is simply performed to improve transmission angle. After the optimization process, the shaking force for mechanism A (the mechanism selected for this study) with the joint clearance of 1 mm decreases by 77.97% and 77.69% in x and y directions, respectively. The shaking moment decreases by 78.45% for the selected optimal mechanism for this study. These results can be seen as a measure of success of optimization strategy. This can be easily adapted to different mechanisms having joints with clearance.

To gain a better understanding, the results of the objective function diagram of the selected optimal points from the optimization results are plotted and compared with a previous reference for a full rotation of the crank or input link. The results confirmed that the present study outperforms previous works. The balancing diagram also shows that the sum of the vibrational force and torque in this study has reduced significantly compared with that in the previous research study. It also indicates that the balancing objective function is rising intensely near certain angles of \(\theta_{2}\) like 22° and 170°, which means that shaking forces and torques hit the mechanism like a sudden stroke. This sudden stroke has been damped and reduced to a large extent, leading to a significant improvement in the dynamic balancing of the mechanism in the mechanisms suggested in this work. The joint clearance also causes noise and destructive vibrations and ultimately reduces the durability of the mechanism. Therefore, the use of an optimized mechanism in terms of dynamical balancing and transmission quality with joint clearance, as an inevitable issue, may decrease or eliminate many of the factors reducing useful performance of the mechanism like dynamic and kinematic quality and force transmission, and ultimately increase its efficiency. It is suggested to use this method to optimize other planar or spatial mechanisms and even robots.