An efficient three-node triangular Mindlin–Reissner flat shell element

Abstract

Shell elements are extensively used by engineers for modeling the behavior of shell structures. Among common shell elements, triangular shell elements are not influenced by element warping. This paper proposes a new three-node triangular flat shell element with six degrees of freedom per each node, named TMRFS. The element is formed by assemblage of new bending and membrane elements. The bending element is formulated based on the hybrid displacement function element method and Mindlin–Reissner plate theory. In this element, an assumed displacement function is employed as the trial function. The membrane component is an unsymmetric triangular membrane element with drilling vertex rotations. The membrane element employs two different types of displacement fields as the test and trial functions. The test function is a displacement field which is the same as one used in well-known Allman triangular element. Meanwhile, instead of displacement field, the analytical stress field is considered as the trial function. Numerical tests show that the accuracy of the proposed flat shell element is reasonable in comparison with some popular triangular elements and its performance is insensitive to geometry, load and boundary conditions. Moreover, the proposed element preserves the advantages of its formulation including free of membrane locking, shear locking and stiffness matrix singularity problems.

1 Introduction

Finite element method is an efficient approach for numerical analysis of shell structures. Over last decades, a number of studies have been done to develop an efficient shell element with simple formulation [1,2,3]. There are three types of shell element that can be employed in shell analysis: (1) flat shell element which is formed by superposition of membrane and plate bending elements; (2) degenerated shell element which is formulated based on solid-shell theory; and (3) curved shell element which is defined based on classical shell theory. Among these elements, the flat shell element avoids complicated forms of shell equations that can be used easily by engineers. It should be noted, curved shell element is more capable in curved geometry modeling, but using the classical shell theory leads to complex formulation of this element that is not attractive for engineers. Triangular and quadrilateral flat shell elements are conventional in finite element analysis of shell structures. The remarkable advantage of triangular elements is that they are not influenced by element warping. This study is focused with the development of an efficient triangular flat shell element.

During recent decades, significant studies have been done on Mindlin–Reissner plate bending elements. The main drawback of these elements is the over stiffness problem in thin plate caused by shear locking. To meet this challenge, different methods have been introduced, such as the hybrid-mixed variational method [4], using shear strain interpolation obtained by Timoshenko’s beam functions [5], the smoothed finite element method [6], the combined hybrid method [7], the discrete shear gap method [8], the enhanced assumed strain method [9], polygonal finite element method [10], and node-variable plate theory [11]. Beside the shear locking problem, the performance of bending element should be insensitive to geometry (sometimes problem geometry leads to irregular mesh pattern) and the error of estimated solution must be lower. In 1988, Zienkiewicz and Lefebvre [12] proposed a new triangular plate bending element through independent interpolations for displacements and shear forces. Using assumed shear strain fields and Mindlin–Reissner plate theory, Katili [13] presented a new discrete Kirchhoff–Mindlin element. By employing the Timoshenko’s beam functions and refined nonconforming element method, Wanji and Cheung [14] introduced a new triangular Mindlin–Reissner plate bending element. Using the cell-based strain smoothing technique and discrete shear gap method, Nguyen-Thoi et al. [8] presented a three-node triangular plate bending element. Although these bending elements had better accuracy than the other ones, their performance was sensitive to problem geometry. To overcome this challenge in plane element, Cen et al. [15, 16] presented the hybrid stress-function element method which was based on the minimum complementary energy. The resulting element performance was acceptable even for complex geometry. The trial function in hybrid stress-function element method was a stress field that satisfied the element governing equations. Using this concept, an extended hybrid-Trefftz method was proposed by Jirousek et al. [17, 18]. The hybrid-Trefftz method which was developed by Jirousek and Leon [19] is a convenient approach to introduce lower-order bending elements with simple formulation such as, four- and eight-node quadrilateral plate bending elements [20, 21]. However, most of the hybrid-Trefftz bending elements possess spurious zero modes. As a solution, using Mindlin–Reissner plate theory Cen et al. [22] presented the hybrid displacement function element method which was formulated based on the extended hybrid-Trefftz stress element method. In this method an assumed displacement function was employed as variational functional of complementary energy and the displacements along each element edge were determined by the Timoshenko’s beam theory. Afterward, Shang et al. [23] investigated the performance of the hybrid displacement function element method on the edge effect of Mindlin–Reissner plate caused by specific boundary conditions. Furthermore, using generalized conforming theory they improved this method [24] for orthotropic Mindlin–Reissner plate. For free vibration analysis of Mindlin–Reissner plate, Huang et al. [25] proposed a triangular bending element by employing hybrid displacement function element method. The results of these studies proved the efficiency of the hybrid displacement function element method.

As for membrane element over the past decades, a number of studies have carried out on introducing high performance membrane element which can provide acceptable accuracy in complex geometry, such as the hybrid-EAS method [9], the spline element method [26], the quadrilateral area coordinate method [27], the overlapping element method [28] and so on. In 1956, Turner et al. [29] developed the constant strain triangle (CST) element which was the first triangular membrane element that extensively used in finite element analysis. Another widely used triangular membrane element is the linear strain triangle (LST) element introduced by Veubeke [30]. The major drawback of these elements is lack of drilling degrees of freedom. Drilling degrees of freedom in membrane element enhance the displacement field order without increasing element nodes. Moreover, membrane element with drilling rotations avoids stiffness matrix singularity problem in flat shell element. Allman [31] introduced the first triangular membrane element with drilling degrees of freedom. In this element the drilling rotations were obtained through an interpolation along each element edge. Since then, several studies have been carried out on membrane element with drilling rotations specifically Allman-type ones, namely Choo et al. [32] proposed a new triangular membrane element with drilling degrees of freedom through the hybrid-Trefftz method and Allman-type drilling rotations. Huang et al. [33] proposed a modified Allman’s triangular membrane element with drilling vertex rotations. Using hybrid variational principle and analytical solution Rezaiee-Pajand and Karkon [34] presented an efficient hybrid stress membrane element with Allman-type drilling rotations. However, the performance of these elements is not reasonable. The unsymmetric finite element method is a promising approach to introduce membrane element with insensitivity to problem geometry. In addition, the unsymmetric membrane element is free of membrane locking and has explicit stiffness matrix in Cartesian coordinates. In this method two different types of displacement fields are used as the test function and trial function. In 2003, Rajendran and Liew [35] developed the first unsymmetric membrane element using the test and trial functions in isoparametric set and metric set, respectively. Although the obtained results proved its performance, this element suffers from rotational frame dependence and the completeness condition that caused by metric-based trial function. To eliminate these defects, Cen et al. [36] proposed an improved unsymmetric finite element method by employing the analytical trial function method. Using this improved method, Cen et al. [37, 38] introduced two quadrilateral membrane elements for geometrically linear and nonlinear analysis of structures. The trial functions of these elements were based on the displacement approximations in Cartesian coordinates that satisfy elements governing equations. In 2018 Shang and Ouyang [39] proposed a new version of unsymmetric finite element method by using stress field as the trial function. Through this way and Allman-type drilling rotations, they introduced the first unsymmetric quadrilateral element with drilling degrees of freedom.

Great efforts have been made on triangular flat shell elements with drilling vertex rotations to propose an element with acceptable performance; nevertheless, more studies are still needed. Providas and Kattis [40] proposed a triangular flat shell element by using a constant strain triangular element with drilling rotations. In this flat shell element the added rotation stiffness had minimum contribution to the element strain energy. Moreover, the drilling rotations were obtained through an independent approximation of rotation field. By employing the Timoshenko’s beam function and quasi-conforming technique, Wang and Hu [41] presented two triangular flat shell elements with different string net functions that can maintain their accuracies even in complex geometry. Zengjie and Wanji [42] introduced flat triangular shell elements which were formed by combining refined triangular discrete Mindlin plate element and either the constant strain membrane element with drilling rotations and linear strain membrane element. The obtained results illustrated the poor performance of the proposed elements. Zhang et al. [43] presented a triangular flat shell element using the refined nonconforming method-based bending element and ANDES-based membrane element with drilling vertex rotations and then evaluated its performance by experimental test. In a similar study Shin and Lee [44] developed a triangular flat shell element in which the free parameters were included in the membrane component formulation. Although the obtained numerical results proved the accuracy of the proposed shell element, its performance was highly sensitive to the free parameters and defining the free parameters was the main challenge in this element.

This study presents a novel three-node triangular flat shell element with 6 degrees of freedom per each node (three translational and three rotational degrees of freedom) named TMRFS. The proposed shell element is obtained by combining newly introduced membrane and plate bending elements. The membrane component is an unsymmetric three-node triangular element with drilling vertex rotations formulated based on the unsymmetric finite element method. The element’s test function coincides with well-known Allman [31] triangular membrane element. The element’s trial function is defined based on the stress polynomial approximations derived from the Airy stress function in Cartesian coordinates, same as the one used for the hybrid stress-function elements [15, 16]. The presence of drilling degrees of freedom in membrane component can avoid the stiffness matrix singularity that appears when all elements are coplanar. The bending component is a three-node triangular Mindlin–Reissner bending element which is formulated based on the hybrid displacement function element method [22]. In this method, the variational functional of complementary energy is an assumed displacement field and the Timoshenko’s beam functions are used to define the displacements along each element edge. To assess the proposed triangular flat shell element, some classic benchmark examples are employed and their results are compared with some popular triangular elements. The obtained results prove that the proposed TMRFS element passes all patch tests, avoids locking problems and provides acceptable accuracy in complex geometry.

2 Formulation

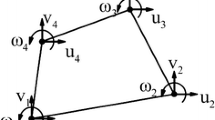
As discussed earlier, a flat shell element is obtained by assemblage of membrane and plate bending elements. For the proposed TMRFS element, the membrane part is a new three-node unsymmetric triangular membrane element with two translations (u_i and v_i) and one drilling vertex rotation $(\theta_{zi} )$ per each element node. The bending part is a new triangular hybrid displacement function bending element with one translation $(w_{i} )$ and two bending rotations $(\theta_{{xi_{{}} }}\,{\text{and}}\,^{{}} \theta_{yi} )$. Accordingly, the degrees of freedom for each node of the proposed flat shell element can be expressed as follows

$$\textbf{d}_{i}^{\text{T}} = \left\{ {\begin{array}{*{20}c} {u_{i} } & {v_{i} } & {w_{i} } & {\theta_{xi} } & {\theta_{yi} } & {\theta_{zi} } \\ \end{array} } \right\},\quad (i = 1\,\sim\,3).$$

(1)

For the proposed TMRFS flat shell element, the element equation can be written as follows

$${\mathbf{K}}_{\text{s}} {\mathbf{d}} = {\mathbf{f}}_{\text{s}}$$

(2)

where ${\mathbf{d}}$ is the nodal displacements, ${\mathbf{f}}$ is the element load vector and ${\mathbf{K}}_{\text{s}}$ is the stiffness matrix of the TMRFS flat shell element which is formed by combining the membrane stiffness and bending stiffness matrices, as follows

$$\textbf{K}_{\text{s}} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{\text{m}} } & 0 \\ 0 & {{\mathbf{K}}_{\text{p}} } \\ \end{array} } \right],$$

(3)

where ${\mathbf{K}}_{\text{m}}$ is the membrane stiffness matrix and ${\mathbf{K}}_{\text{p}}$ is the plate bending stiffness matrix. Above equations illustrate element stiffness matrix, load vector and displacement vector in global coordinate systems. If the local axes for the proposed element are not parallel to the global ones, the axes transformation should be applied. The matrix form of axes transformation can be written as follows

$${\varvec{\uplambda}} = \left[ {\begin{array}{*{20}c} {l_{1} } & {m_{1} } & {n_{1} } \\ {l_{2} } & {m_{2} } & {n_{2} } \\ {l_{3} } & {m_{3} } & {n_{3} } \\ \end{array} } \right]$$

(4)

in which $l_{i} , \, m_{i} {\text{ and }}n_{i}$ are the cosines of angles between global and local axes, Ref. [45] provides more details about the evaluation procedure of these matrix elements. The global form of stiffness matrix, load vector and displacement vector can be defined by employing the axes transformation matrix, as follows:

$${\mathbf{K}} = {\mathbf{T}}^{\text{T}} {\mathbf{K}}_{\text{loc}} {\mathbf{T}},$$

(5)

$${\mathbf{d}} = {\mathbf{T}}^{\text{T}} {\mathbf{d}}_{\text{loc}} {\mathbf{T}},$$

(6)

$${\mathbf{f}} = {\mathbf{T}}^{\text{T}} {\mathbf{f}}_{\text{loc}} {\mathbf{T}},$$

(7)

where

$${\mathbf{T}} = \left[ {\begin{array}{*{20}c} {\varvec{\uplambda}} & {} & {} & \cdots & {} & 0 \\ {} & {\varvec{\uplambda}} & {} & {} & {} & {} \\ {} & {} & {\varvec{\uplambda}} & {} & {} & \vdots \\ \vdots & {} & {} & {\varvec{\uplambda}} & {} & {} \\ {} & {} & {} & {} & {\varvec{\uplambda}} & {} \\ 0 & {} & \cdots & {} & {} & {\varvec{\uplambda}} \\ \end{array} } \right]_{18 \times 18}$$

(8)

in which ${\mathbf{K}}_{\text{loc}} , \, {\mathbf{d}}_{\text{loc}} {\text{ and }}{\mathbf{f}}_{\text{loc}}$ are the stiffness matrix, displacement vector and load vector in local coordinate systems, respectively.

2.1 The bending component

The bending component of the proposed flat shell element is a novel three-node triangular bending element formulated based on the hybrid displacement function element method [22] and Mindlin–Reissner plate theory. In hybrid displacement function element method, an assumed displacement function F is employed as the variational functional of complementary energy. Then, the resultant forces that satisfy the equilibrium equations are obtained using the assumed displacement function and the nodal displacements are defined along each element edge through the Timoshenko’s beam theory. Finally, the stiffness matrix of bending element can be computed by employing the minimum complementary energy principle. Figure 1 shows the proposed Mindlin–Reissner plate element that its mid-surface is defined on (x, y) plane and z axis is along the element thickness.

Fig. 1

Triangular Mindlin–Reissner plate bending element

In the Mindlin–Reissner plate theory, the displacements at any point can be expressed as follows

$$u = - z\theta_{x} ,\,v = - z\theta_{y} ,\,w = w(x,y),\quad \left( { - \, \frac{h}{2} \le \, z \le \frac{h}{2}} \right),$$

(9)

in which h is the plate thickness. The governing equations of the Mindlin–Reissner plate theory are the equilibrium equations and strain–displacement equations. For a uniformly distributed load q, the equilibrium equations can be written as follows

$$\begin{aligned} & \frac{{\partial M_{x} }}{\partial x} + \frac{{\partial M_{xy} }}{\partial y} - Q_{x} = 0, \\ & \frac{{\partial M_{xy} }}{\partial x} + \frac{{\partial M_{y} }}{\partial y} - Q_{y} = 0, \\ & \frac{{\partial Q_{x} }}{\partial x} + \frac{{\partial Q_{y} }}{\partial y} + q = 0, \\ \end{aligned}$$

(10)

in which $M_{x}$ and $M_{y}$ are the bending moments, $M_{xy}$ is the twisting moment, $Q_{x}$ and $Q_{y}$ are the shear forces, as shown in Fig. 1. For linear plate, by employing the approximation of small displacements, the strain–displacement equations can be expressed as

$$\begin{aligned} & \kappa_{x} = - \frac{{\partial \theta_{x} }}{\partial x},\,\kappa_{y} = - \frac{{\partial \theta_{y} }}{\partial y},\,\,\kappa_{xy} = - \, \left( {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \right), \\ & \gamma_{x} = \frac{\partial w}{\partial x} - \theta_{x} ,\,\gamma_{y} = \frac{\partial w}{\partial y} - \theta_{y} , \\ \end{aligned}$$

(11)

where $\gamma_{x}$ and $\gamma_{y}$ are the shear strains and $\kappa_{x} ,_{{}} \kappa_{y}$ and $\kappa_{xy}$ are the curvatures. The elasticity matrix $\textbf{D}_{\text{p}}$ for the proposed bending element is given by

$$\textbf{D}_{\text{p}} = \left[ {\begin{array}{*{20}c} D & {\upsilon D} & 0 & 0 & 0 \\ {\upsilon D} & D & 0 & 0 & 0 \\ 0 & 0 & {\tfrac{1 - \upsilon }{2}D} & 0 & 0 \\ 0 & 0 & 0 & C & 0 \\ 0 & 0 & 0 & 0 & C \\ \end{array} } \right],$$

(12)

with

$$D = \frac{{Eh^{3} }}{{12(1 - \upsilon^{2} )}},^{{}} C = \frac{5}{6}_{{}} Gh,$$

(13)

in which $\upsilon$ is the Poisson’s ratio, E is the Young’s modulus and G is the shear modulus. Matrix ${\mathbf{D}}_{\text{p}}$ is computed by the following equation:

$${\mathbf{D}}_{\text{p}} = \int_{{ - {\raise0.5ex\hbox{$\scriptstyle h$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}}^{{{\raise0.5ex\hbox{$\scriptstyle h$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}} { \, z^{2} {\mathbf{C}}_{\text{H}} {\text{d}}z} ,$$

(14)

where ${\mathbf{C}}_{\text{H}}$ is the material matrix (Hook’s matrix) in plane stress condition. Accordingly, the constitutive relations can be defined as

$$\textbf{R = D}_{\text{p}} \textbf{E} ,$$

(15)

where R and E are defined as follows

$$\begin{aligned} & \textbf{R} = [\begin{array}{*{20}c} {M_{x} } & {M_{y} } & {M_{xy} } & {Q_{x} } & {Q_{y} } \\ \end{array} ]^{\text{T}} , \\ & \textbf{E} = [\begin{array}{*{20}c} {\kappa_{x} } & {\kappa_{y} } & {\kappa_{xy} } & {\gamma_{x} } & {\gamma_{y} } \\ \end{array} ]^{\text{T}} . \\ \end{aligned}$$

(16)

Based on the hybrid displacement function element method, the deflection and rotations of bending element can be obtained by a displacement function F, as follows

$$w = F -_{{}} \left( {\frac{{h^{2} }}{5(1 - \upsilon )}} \right)_{{}} \nabla^{2} F,_{{}} \theta_{x} = \frac{\partial F}{\partial x},_{{}} \theta_{y} = \frac{\partial F}{\partial y},$$

(17)

in which the displacement function F should satisfy the following equation:

$$D\nabla^{2} \nabla^{2} F = q.$$

(18)

Substitution of Eq. (17) into Eq. (11) yields

$$\begin{aligned} & \kappa_{x} = - \frac{{\partial^{2} F}}{{\partial x^{2} }},\quad \kappa_{y} = - \frac{{\partial^{2} F}}{{\partial y^{2} }},\quad \kappa_{xy} = - 2\frac{{\partial^{2} F}}{\partial x\partial y}, \\ & \gamma_{x} = - \frac{D}{C}\left( {\frac{{\partial \nabla^{2} F}}{\partial x}} \right),\,\,\gamma_{y} = - \frac{D}{C}\left( {\frac{{\partial \nabla^{2} F}}{\partial y}} \right). \\ \end{aligned}$$

(19)

By substituting Eq. (17) in Eq. (15), the resultant forces are determined in terms of displacement function F, as follows

$$\begin{aligned} & M_{x} = - D\left( {\frac{{\partial^{2} F}}{{\partial x^{2} }} + \upsilon \frac{{\partial^{2} F}}{{\partial y^{2} }}} \right), \\ & M_{y} = - D\left( {\frac{{\partial^{2} F}}{{\partial y^{2} }} + \upsilon \frac{{\partial^{2} F}}{{\partial x^{2} }}} \right), \\ & M_{xy} = - D(1 - \upsilon ) \, \left( {\frac{{\partial^{2} F}}{\partial x\partial y}} \right), \\ & Q_{x} = - D\left( {\frac{{\partial \nabla^{2} F}}{\partial x}} \right), \\ & Q_{y} = - D\left( {\frac{{\partial \nabla^{2} F}}{\partial y}} \right). \\ \end{aligned}$$

(20)

The displacement function F is the solution of Eq. (18) that can be divided into homogeneous $(F^{\text{h}} )$ and particular $(F^{\text{p}} )$ parts, as follows

$$F = F^{\text{h}} + F^{\text{p}} ,$$

(21)

in which $F^{\text{h}}$ is the solution of homogeneous biharmonic equation $\nabla^{2} \nabla^{2} F = 0$ that can be assumed as

$$F^{\text{h}} = \hat{\textbf{S}}\beta ,$$

(22)

With

$$\begin{aligned} & \hat{\textbf{S}} = \left[ {\begin{array}{*{20}c} {F_{1} } & {F_{2} } & \ldots & {F_{11} } \\ \end{array} } \right], \\ & {\beta } = \left[ {\begin{array}{*{20}c} {\beta_{1} } & {\beta_{2} } & \ldots & {\beta_{11} } \\ \end{array} } \right]^{\text{T}} , \\ \end{aligned}$$

(23)

where $\beta_{i}$(i = 1 ~ 11) are undetermined coefficients and $F_{i}$(i = 1 ~ 11) are the polynomial approximations for homogeneous part of displacement function. These polynomial approximations should be selected at least from the second-order terms and possess completeness of selected order in Cartesian coordinates; the details of the derivation of these polynomial approximations can be found in Ref. [46].

Cen et al. [16] assessed the performance of hybrid stress-function elements that in their trial functions different number of polynomial approximations were used. In a similar way, for the proposed bending element the first seven (third-order), eleven (forth-order) and fifteen (fifth-order) polynomials are considered. For each of them the element performance is evaluated by numerical problems. The obtained results show all cases have acceptable performance; moreover, the bending element with the first eleven polynomials (forth-order completeness) provides better performance when combined with the considered membrane element than the other cases. The main difference between the proposed bending element and the one presented by Huang et al. [25] is the order of considered polynomial approximations in the trial function. These polynomials are illustrated in Table 1.

Table 1 The first eleven polynomial approximations for the homogenous part and their resultant forces

Then, the resultant forces of homogenous solutions can be defined by using Eq. (20) as follows

$$\textbf{R}^{\text{h}} = \left\{ {\begin{array}{*{20}c} {M_{x}^{\text{h}} } \\ {M_{y}^{\text{h}} } \\ {M_{xy}^{\text{h}} } \\ {Q_{x}^{\text{h}} } \\ {Q_{y}^{\text{h}} } \\ \end{array} } \right\} = \hat{\textbf{S}}\beta = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {M_{x1}^{\text{h}} } & {M_{x2}^{\text{h}} } & \ldots & {M_{x11}^{\text{h}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {M_{y1}^{\text{h}} } & {M_{y2}^{\text{h}} } & \ldots & {M_{y11}^{\text{h}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {M_{xy1}^{\text{h}} } & {M_{xy2}^{\text{h}} } & \ldots & {M_{xy11}^{\text{h}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {Q_{x1}^{\text{h}} \begin{array}{*{20}c} {} \\ \end{array} } & {Q_{x2}^{\text{h}} \begin{array}{*{20}c} {} \\ \end{array} } & \ldots & {Q_{x11}^{\text{h}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {Q_{y1}^{\text{h}} \begin{array}{*{20}c} {} \\ \end{array} } & {Q_{y2}^{\text{h}} \begin{array}{*{20}c} {} \\ \end{array} } & \ldots & {Q_{y11}^{\text{h}} } \\ \end{array} } \\ \end{array} } \right]_{{}} \left\{ {\begin{array}{*{20}c} {\beta_{1} } \\ {\beta_{2} } \\ \vdots \\ \vdots \\ {\begin{array}{*{20}c} \vdots \\ {\beta_{11} } \\ \end{array} } \\ \end{array} } \right\},$$

(24)

in which $M_{x}^{\text{h}} ,\,M_{y}^{\text{h}} ,\,M_{xy}^{\text{h}} ,\,Q_{x}^{\text{h}} \,{\text{and}}\,Q_{y}^{\text{h}}$ are defined in Table 1. The particular part of displacement function $F^{\text{p}}$ can be defined from Eq. (18). For instance, if the applied load q is a uniformly distributed force, the particular part of displacement function can be written as follows

$$F^{\text{p}} = \frac{q}{48D}(x^{4} + y^{4} ).$$

(25)

Accordingly, the particular solutions of resultant forces can be obtained by using Eq. (20) as follows

$$\textbf{R}^{\text{p}} = \left\{ {\begin{array}{*{20}c} {M_{x}^{\text{p}} } \\ {M_{y}^{\text{p}} } \\ {M_{xy}^{\text{p}} } \\ {Q_{x}^{\text{p}} } \\ {Q_{y}^{\text{p}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\tfrac{ - q}{4}(x^{2} + \upsilon y^{2} )} \\ {\tfrac{ - q}{4}(\upsilon x^{2} + y^{2} )} \\ 0 \\ {\tfrac{ - q}{2}x} \\ {\tfrac{ - q}{2}y} \\ \end{array} } \right\}.$$

(26)

Now the stiffness matrix of bending element can be determined using the defined displacement function F. For a Mindlin–Reissner plate bending element, the complementary energy functional [47] can be written as

$$\prod_{c} = \iint_{A} {\left( {\tfrac{1}{2}\textbf{R}^{\text{T}} \textbf{D}_{\text{p}}^{ - 1} \textbf{R}} \right){\text{d}}A} + \int_{S} {(\bar{\textbf{R}\bar{d}}){\text{d}}s} ,$$

(27)

in which R is the total resultant force vector that is equal to the sum of the homogenous and particular parts of resultant forces $(\textbf{R} = \textbf{R}^{\text{h}} + \textbf{R}^{\text{p}} ) ,$$\bar{\textbf{R}}$ denotes the value of total resultant force vector along the element edges, and $\bar{\textbf{d}}$ is the value of deflections and rotations along the element boundaries which can be expressed as follows

$$\bar{\textbf{d}} = \bar{\textbf{N}}_{\text{p}} \textbf{q}_{\text{p}} ,$$

(28)

where $\textbf{q}_{\text{p}}$ is the displacement vector of bending element and $\bar{\textbf{N}}_{\text{p}}$ is an interpolation function matrix that should be defined for each element edge separately by employing the Timoshenko’s beam function. The evaluation procedure of matrix ${\bar{\mathbf{N}}}_{\text{p}}$ is detailed in “Appendix”. Then, using the total resultant forces and Eq. (24) the complementary energy functional can be expressed as

$$\begin{aligned} \varPi_{c} & = \iint_{A} {\tfrac{1}{2}(\hat{\textbf{S}}\beta + \textbf{R}^{\text{p}} )^{\text{T}} \textbf{D}_{\text{p}}^{ - 1} (\hat{\textbf{S}}\beta + \textbf{R}^{\text{p}} ){\text{d}}A} + \int_{S} {(\hat{\textbf{S}}\beta + \textbf{R}^{\text{p}} )\bar{\textbf{N}}{q}_{\text{p}} {\text{d}}s} \\ & = \tfrac{1}{2}({\beta }^{\text{T}} \textbf{M}\beta + {\beta }^{\text{T}} \textbf{M}^{\text{p}} + (\textbf{M}^{\text{p}} )^{\text{T}} {\beta } + \textbf{T}) + {{\beta}^{\text{T}} \textbf{H}q}_{\text{p}} + \textbf{Vq}_{\text{p}} , \\ \end{aligned}$$

(29)

in which

$$\begin{aligned} & \textbf{M} = \iint_{A} {\hat{\textbf{S}}^{\text{T}} \textbf{D}_{\text{p}}^{ - 1} \hat{\textbf{S}}{\text{d}}A},\,\textbf{M}^{\text{p}} = \iint_{A} {\hat{\textbf{S}}^{\text{T}} \textbf{D}_{\text{p}}^{ - 1} \textbf{R}^{\text{p}} {\text{d}}A},\,\textbf{T} = \iint_{A} {(\textbf{R}^{\text{p}} )^{\text{T}} \textbf{D}_{\text{p}}^{ - 1} \textbf{R}^{\text{p}} {\text{d}}A}, \\ & \textbf{H} = \int_{S} {\hat{\textbf{S}}^{\text{T}} \bar{\textbf{N}}_{\text{p}} {\text{d}}s,\,} \textbf{V} = \int_{S} {(\textbf{R}^{\text{p}} )^{\text{T}} \bar{\textbf{N}}_{\text{p}} {\text{d}}s.} \\ \end{aligned}$$

(30)

Using the stationary condition of complementary energy, the undetermined coefficient vector can be defined as

$${\beta } = - \textbf{M}^{ - 1} (\textbf{M}^{\text{p}} + \textbf{Hq}_{\text{p}} ).$$

(31)

Accordingly, by using Eqs. (31), (29) can be rewritten as follows

$$\varPi_{c} = - \,\frac{1}{2}{\mathbf{q}}_{\text{m}}^{\text{T}} {\mathbf{H}}^{\text{T}} {\mathbf{M}}^{ - 1} {\mathbf{Hq}}_{\text{m}} - \frac{1}{2}({\mathbf{M}}^{\text{p}} )^{\text{T}} {\mathbf{M}}^{ - 1} {\mathbf{M}}^{\text{p}} + \frac{1}{2}{\mathbf{T}} - ({\mathbf{M}}^{\text{p}} )^{\text{T}} {\mathbf{M}}^{ - 1} {\mathbf{Hq}}_{\text{m}} + {\mathbf{Vq}}_{\text{m}} ,$$

(32)

Finally, by employing the principal of minimum energy, the stiffness matrix $\textbf{K}_{\text{p}}$ and nodal load vector $\textbf{P}_{\text{p}}$ for the proposed bending element can be defined as follows

$$\begin{aligned} & \textbf{K}_{\text{p}} = \textbf{H}^{\text{T}} \textbf{M}^{ - 1} \textbf{H}, \\ & \textbf{P}_{\text{p}} = \,\textbf{V}^{\text{T}} - \textbf{H}^{\text{T}} \textbf{M}^{ - 1} \textbf{M}^{\text{p}} . \\ \end{aligned}$$

(33)

2.2 The membrane component

The membrane component of TMRFS element is a new three-node triangular membrane element with drilling degrees of freedom. The membrane element is formulated in the framework of unsymmetric finite element method developed by Shang and Ouyang [39]. The element’s test function is a conventional displacement field which was used in well-known Allman [31] triangular membrane element. The trial function of the proposed membrane element is a stress field which is defined based on the polynomial approximations in Cartesian coordinates. These polynomials satisfy the Airy stress-function similar to the one used in hybrid stress-function elements [15, 16]. Then, to define the relationship between the trial function and nodal degrees of freedom the quasi-conforming technique [48, 49] is employed. Finally, the membrane stiffness matrix can be derived using the virtual work principle. Figure 2 shows the proposed unsymmetric membrane element with drilling vertex rotations.

Fig. 2

Triangular unsymmetric membrane element with drilling vertex rotations

Based on the unsymmetric finite element method for the proposed membrane element, two different types of displacement fields are used as the test and trial functions. The test function coincides with the displacement field of Allman [31] triangular membrane element, in which the drilling degrees of freedom were defined by using displacement interpolation along each element boundary, as follows

$${\bar{\mathbf{u}}} = {\bar{\mathbf{N}}}_{\text{m}} {\mathbf{q}}_{\text{m}} ,$$

(34)

with

$${\bar{\mathbf{N}}}_{\text{m}} = \left[ {\begin{array}{*{20}c} \ldots & {\begin{array}{*{20}c} {\xi_{i} } & 0 & {\frac{1}{2}(b_{k} \xi_{i} \xi_{j} - \, b_{j} \xi_{k} \xi_{i} )} \\ 0 & {\xi_{i} } & {\frac{1}{2}(c_{k} \xi_{i} \xi_{j} - \, c_{j} \xi_{k} \xi_{i} )} \\ \end{array} } & \ldots \\ \end{array} } \right],\quad (i = 1\sim3),$$

(35)

and $b_{i} , \, c_{i}$ are defined as

$$\begin{aligned} b_{i} = y_{i} - y_{k} , \hfill \\ c_{i} = x_{k} - x_{j} , \hfill \\ \end{aligned}$$

(36)

in which ${\mathbf{q}}_{{\mathbf{m}}}$ is the membrane element displacement vector, $\xi_{i}$ are the triangular area coordinates, i = (1,2,3), j = mod(i/3) + 1 and k = mod((i + 1)/3) + 2. Thus, the corresponding strain matrix ${\bar{\mathbf{\varepsilon }}}$ is deduced by the considered test function ${\bar{\mathbf{u}}}$ as follows

$${\bar{\mathbf{\varepsilon }}} = {\bar{\mathbf{B}}\mathbf{q}}_{\text{m}} ,$$

(37)

With

$${\bar{\mathbf{B}}} = \frac{1}{2A}\left[ {\begin{array}{*{20}c} \, & {b_{i} } & 0 & {\frac{1}{2}b_{i} (b_{k} \xi_{j} - b_{j} \xi_{k} )} & \, \\ \ldots & 0 & {c_{i} } & {\frac{1}{2}c_{i} (c_{k} \xi_{j} - c_{j} \xi_{k} )} & \ldots \\ {\,\,} & {c_{i} } & {b_{i} } & {\frac{1}{2}(\xi_{j} (b_{k} c_{i} + b_{i} c_{k} ) - \xi_{k} (b_{i} c_{j} + b_{j} c_{i} ))} & \, \\ \end{array} } \right],\quad (i = 1\,\sim\,3),$$

(38)

where A is the area of the membrane element. As described above instead of using displacements, the element’s trial function can be independently assumed in unsymmetric finite element method. For the proposed membrane element, the trial function is a stress field which can be defined as

$${\hat{\mathbf{u}}} = {\hat{\mathbf{\sigma }}} = {\hat{\mathbf{T}}\mathbf{q}}_{\text{m}} ,$$

(39)

where

$${\hat{\mathbf{\sigma }}} = {\mathbf{L\alpha }},$$

(40)

in which ${\varvec{\upalpha}}$ is the undetermined coefficient vector and L is the stress matrix which is defined based on the analytical approximations of Airy stress function in Cartesian coordinates, as follows

$${\mathbf{L}} = \left[ {\begin{array}{*{20}c} {} & {\sigma_{xi} } & {} \\ \cdots & {\sigma_{yi} } & \cdots \\ {} & {\tau_{xyi} } & {} \\ \end{array} } \right],(i = 1\sim11),$$

(41)

In matrix L, each column is one set of analytical stress approximations of plane problem [15, 16] $(\sigma_{x} ,^{{}} \sigma_{y}^{{}} {\text{and}}_{{}} \tau_{xy} ).$ These analytical stresses are determined using the polynomial approximations that satisfy the Airy stress function. As should be noted, these solutions must be selected at least from second-order completeness. Similar to proposed bending element, for the membrane component the first seven (third-order), eleven (forth-order) and fifteen (fifth-order) polynomials are evaluated, the obtained results prove that the first eleven polynomials lead to appropriate performance of proposed TMRFS shell element in analysis of shell structures. These polynomial approximations $(p_{i} )$ and the resultant analytical stresses are listed in Table 2.

Table 2 The first eleven polynomial approximations and resultant stresses

Now the main challenge is the relationship between the nodal displacement vector ${\mathbf{q}}_{\text{m}}$ and trial function ${\hat{\mathbf{u}}}$ because there are eleven undetermined coefficients, whereas only nine nodal displacements are available. Accordingly, to define this relationship the quasi-conforming technique [48, 49] which is based on the weighted residual method is employed, as follows

$$\iiint_{V} {{\mathbf{L}}^{\text{T}} ({\bar{\mathbf{\varepsilon }}} - {\hat{\mathbf{\varepsilon }}}){\text{d}}V = 0} ,$$

(42)

where ${\hat{\mathbf{\varepsilon }}}$ is the strain related to trial function that can be obtained through the following equation

$${\hat{\mathbf{\varepsilon }}} = {\mathbf{D}}_{\text{m}}^{ - 1} {\hat{\mathbf{\sigma }}} = {\mathbf{D}}_{\text{m}}^{ - 1} {\mathbf{L\alpha }} ,$$

(43)

in which ${\mathbf{D}}_{\text{m}}$ is the elasticity matrix of membrane element which is deduced from the material matrix (Hook’s matrix) in plane stress condition, as follows

$${\mathbf{D}}_{\text{m}} = \frac{E}{{1 - \upsilon^{2} }}\left[ {\begin{array}{*{20}c} 1 & \upsilon & 0 \\ \upsilon & 1 & 0 \\ 0 & 0 & {\tfrac{1 - \upsilon }{2}} \\ \end{array} } \right],$$

(44)

Accordingly, Eq. (42) can be rewritten as follows

$$\begin{aligned} & \iiint_{V} {{\mathbf{L}}^{\text{T}} ({\bar{\mathbf{B}}\mathbf{q}}_{\text{m}} - {\mathbf{D}}_{\text{m}}^{{^{ - 1} }} {\mathbf{L\alpha }}){\text{d}}V} \\ & = \iiint_{V} {({\mathbf{L}}^{\text{T}} {\bar{\mathbf{B}}\mathbf{q}}_{\text{m}} - {\mathbf{L}}^{\text{T}} {\mathbf{D}}_{\text{m}}^{{^{ - 1} }} {\mathbf{L\alpha }}){\text{d}}V} \\ & = \iiint_{V} {({\mathbf{Xq}}_{\text{m}} - {\mathbf{Z\alpha }}){\text{d}}V} = 0. \\ \end{aligned}$$

(45)

By solving Eq. (45), the relation between the nodal displacement vector ${\mathbf{q}}_{\text{m}}$ and undetermined coefficient vector ${\varvec{\upalpha}}$ can be defined as follows

$${\varvec{\upalpha}} = {\mathbf{Z}}^{ - 1} {\mathbf{Xq}}_{\text{m}} ,$$

(46)

with

$$\begin{aligned} & {\mathbf{Z}} = \iiint_{V} {{\mathbf{L}}^{\text{T}} {\mathbf{D}}_{\text{m}}^{ - 1} {\mathbf{L}}{\text{d}}V}, \\ & {\mathbf{X}} = \iiint_{V} {{\mathbf{L}}^{\text{T}} {\bar{\mathbf{B}}}{\text{d}}V}. \\ \end{aligned}$$

(47)

Accordingly, by substituting Eq. (46) into Eq. (39), matrix ${\hat{\mathbf{T}}}$ can be expressed as follows

$${\hat{\mathbf{T}}} = {\mathbf{LZ}}^{ - 1} {\mathbf{X}} .$$

(48)

By defining the test and trial functions, the membrane stiffness matrix can be determined using the virtual work principle [35, 39] as follows

$$\iiint_{V} {\delta {\bar{\mathbf{\varepsilon }}}^{\text{T}} {\hat{\mathbf{u}}}{\text{d}}V} - \iiint_{V} {\delta {\bar{\mathbf{u}}}^{\text{T}} {\mathbf{J}}{\text{d}}V - \int_{\varvec{\varGamma}} {\delta {\bar{\mathbf{u}}}^{\text{T}} {\mathbf{I}}{\text{d}}\varGamma } = 0},$$

(49)

where J is the body force and I is the surface force; by using Eqs. (37), (43) and (46), Eq. (43) can be rewritten as follows

$$\begin{aligned} & \iiint_{V} {\delta {\bar{\mathbf{\varepsilon }}}^{\text{T}} {\mathbf{D}}_{\text{m}} {\hat{\mathbf{\varepsilon }}}{\text{d}}V} - \iiint_{V} {\delta {\bar{\mathbf{u}}}^{\text{T}} {\mathbf{J}}{\text{d}}V - \int_{\varvec{\varGamma}} {\delta {\bar{\mathbf{u}}}^{\text{T}} {\mathbf{I}}{\text{d}}\varGamma } } \\ & = \iiint_{V} {\delta ({\bar{\mathbf{B}}\mathbf{q}}_{\text{m}} )^{\text{T}} {\mathbf{LZ}}^{ - 1} {\mathbf{Xq}}_{\text{m}} {\text{d}}V} - \iiint_{V} {\delta ({\bar{\mathbf{N}}}_{\text{m}} {\mathbf{q}}_{\text{m}} )^{\text{T}} {\mathbf{J}}{\text{d}}V} - \int_{\varvec{\varGamma}} {\delta ({\bar{\mathbf{N}}}_{\text{m}} {\mathbf{q}}_{\text{m}} )^{\text{T}} {\mathbf{I}}{\text{d}}\varGamma } \\ & = (\delta {\mathbf{q}}_{\text{m}} )^{\text{T}} \iiint_{V} {{\bar{\mathbf{B}}}^{\text{T}} {\mathbf{LZ}}^{ - 1} {\mathbf{Xq}}_{\text{m}} {\text{d}}V} - \iiint_{V} {({\bar{\mathbf{N}}}_{\text{m}} )^{\text{T}} {\mathbf{J}}{\text{d}}V} - \int_{\varvec{\varGamma}} {({\bar{\mathbf{N}}}_{\text{m}} )^{\text{T}} {\mathbf{I}}{\text{d}}\varGamma } \\ & = (\delta {\mathbf{q}}_{\text{m}} )^{\text{T}} ({\mathbf{K}}_{\text{m}} {\mathbf{q}}_{\text{m}} - {\mathbf{P}}_{\text{m}} ) = 0 ,\\ \end{aligned}$$

(50)

with

$$\begin{aligned} & {\mathbf{K}}_{\text{m}} = \iiint_{V} {{\bar{\mathbf{B}}}^{\text{T}} {\mathbf{LZ}}^{ - 1} {\mathbf{Xq}}_{\text{m}} {\text{d}}V}, \\ & {\mathbf{P}}_{\text{m}} = \iiint_{V} {({\bar{\mathbf{N}}}_{\text{m}} )^{\text{T}} {\mathbf{J}}{\text{d}}V} + \int_{\varvec{\varGamma}} {({\bar{\mathbf{N}}}_{\text{m}} )^{\text{T}} {\mathbf{I}}{\text{d}}\varGamma } . \\ \end{aligned}$$

(51)

By solving Eq. (50) the following finite element equation can be defined

$${\mathbf{K}}_{\text{m}} {\mathbf{q}}_{\text{m}} = {\mathbf{P}}_{\text{m}} ,$$

(52)

in which ${\mathbf{K}}_{\text{m}}$ is the membrane stiffness matrix and ${\mathbf{P}}_{\text{m}}$ is the load vector of membrane element.

3 Numerical examples

In order to analyze and evaluate the validity of the proposed TMRFS flat shell element, some numerical standard problems are employed, including patch tests, cantilever beam, Cook’s beam, clamped square plate, Razzaque’s skew plate, Scordelis–Lo roof, pinched cylinder, hemispherical shell and hyperbolic paraboloid shell problems. In each case, 4-point Gaussian integration scheme is employed to compute the stiffness matrix and load vector of the proposed shell element. Moreover, to show the superiority of the proposed element the obtained results are compared with the ones from following popular triangular elements:

• Allman: a triangular membrane element with drilling vertex rotations [31] combined with the DKTM [13] plate bending element.

• Cook: a stabilized three-node triangular flat shell element proposed by Cook [50].

• Providas and Kattis: three-node triangular flat shell element with drilling stiffness presented by Providas and Kattis [40].

• ANDES: three-node triangular flat shell element with optimal membrane element based on the ANDES formulation proposed by Felippa [51].

• QCS31: three-node triangular flat shell element formulated based on the quasi-conforming technique presented by Wang and Hu [41].

• Shin and Lee: three-node triangular flat shell element using strain smoothing technique introduced by Shin and Lee [44].

• MITC3 +: three-node triangular shell element based on the mixed interpolation of tensorial component proposed by Lee et al. [52].

• T3: three-node triangular bending element with full integration presented by Hughes and Taylor [53].

• T3-R: three-node triangular bending element with reduced integration proposed by Pugh and Zienkiewicz [54].

• DKT: three-node triangular bending element based on the discrete Kirchhoff theory proposed by Batoz et al. [55].

• RDKTM: a refined three-node triangular bending element based on the Mindlin-Reissner plate theory introduced by Wanji and Cheung [14].

3.1 Patch tests

Membrane and bending patch tests are well-known problems for evaluating the convergence and numerical implementation of the proposed TMRFS shell element. The membrane patch test is a numerical constant stress problem with five elements, Fig. 3a.

Fig. 3

Geometry and material definition of patch tests. a Membrane patch test. b bending patch test

The membrane patch test is performed by enforcing the following analytical displacements

$$u = 10^{ - 3} (x + y/2),_{{}} v = 10^{ - 3} (y + x/2)$$

(53)

For the boundary nodes, these displacements are considered as the boundary conditions. Accordingly, the corresponding stresses for the inner nodes should be equal to the following values

$$\sigma_{x} = \sigma_{y} = 1333.333,_{{}} \tau_{xy} = 400.0$$

(54)

The obtained results in Table 3 prove that the proposed element gives the exact solution for membrane patch test.

Table 3 Numerical results for membrane patch test

For bending patch test, a numerical constant moment problem with five elements is employed, Fig. 3b. The analytical displacements corresponding to constant moment patch test are as follows

$$w = \frac{1}{2}(x^{2} + xy + y^{2} ),_{{}} \theta_{x} = \frac{1}{2}(y + 2x),_{{}} \theta_{y} = \frac{1}{2}(2y + x),$$

(55)

According to the considered analytical displacements, the moment values are

$$M_{x} = M_{y} = - 0.011111,_{{}} M_{xy} = - 0.00333,_{{}} Q_{x} = Q_{y} = 0$$

(56)

Table 4 presents the values of the moments for inner nodes by enforcing the analytical displacements as the boundary conditions at boundary nodes. The obtained results depict that the proposed shell element passes the bending patch test.

Table 4 Numerical results for bending patch test

3.2 Cantilever beam problem

A clamped beam, as shown in Fig. 4, is loaded by a shear force at free edge. This is a stringent test to assess the membrane behavior of the proposed TNRFS shell element.

Fig. 4

Cantilever beam problem $(E = 3 \times 10^{4} , \, \upsilon = 0.25, \, h = 1, \, W = 12, \, L = 48{\text{ and }}P = 40)$

The normalized vertical deflection at the free end of cantilever beam (point A) for all of the considered elements is presented in Table 5. The results are obtained through $N \times 4N$(N = 1, 2, 4 and 8) element meshes and normalized by the corresponding analytical reference value 0.3558 [46]. The obtained results prove that the accuracy and convergence of the proposed TMRFS flat shell element are reasonable.

Table 5 The normalized results of cantilever beam problem

3.3 Cook’s beam problem

Figure 5 shows a clamped trapezoidal beam loaded by a distributed shear force at free end. This is a standard test to evaluate the membrane behavior of the proposed shell element in a problem with irregular mesh pattern.

Fig. 5

Cook’s beam problem $(E = 1, \, h = 1, \, W = 44, \, L = 16, \, I = 48, \, P = 1{\text{ and }}\upsilon = 1/3)$

Table 6 presents the normalized displacement at point C for the proposed TMRFS element and the other ones. The results are computed using $N \times N$(N = 2, 4, 8 and 16) element meshes and normalized by the reference value 23.95 [56].

Table 6 The normalized results of Cook’s beam problem

The obtained results show that the proposed flat shell element is effective in this test. Although the element introduced by Shin and Lee is more accurate, by considering the results of other problems the performance of the proposed element is satisfactory.

3.4 Clamped square plate problem

Clamped square plate is a suitable test to evaluate the bending behavior of the proposed element in dealing with the presence of shear locking. Figure 6 illustrates a square plate under uniform distributed load (P) which is bounded by clamped boundary conditions. Owing to symmetry, one-quarter of the plate is analyzed. For the considered region the boundary conditions are: $u = \theta_{y} = \theta_{z} = 0$ along AB, $v = \theta_{x} = \theta_{z} = 0$ along AD and $u = \, v = \, w = \theta_{x} = \theta_{y} = \theta_{z} = 0$ along BC and DC.

Fig. 6

Square plate problem $(E = 1.092 \times 10^{3} , \, h = 0.01, \, L = 1, \, P = 1{\text{ and }}\upsilon = 0.3)$

Table 7 shows the transverse deflection at the center of the plate (point A) for all of the considered elements. The results are obtained using different element meshes and normalized by the analytical reference value 0.1265 [57]. The obtained results show that the performance of the proposed element is competitive among the considered shell elements.

Table 7 The normalized results of clamped square plate problem

3.5 Razzaque’s skew plate problem

Figure 7 shows a plate with skew angle of 60° under a uniformly distributed unit load bounded by simply supported boundary conditions at two opposite edges while the other two opposite edges are free. This is a severe test to assess the bending behavior of the proposed element in a problem with irregular mesh pattern. For the considered plate, the boundary conditions are: $u = \, v = \, w = 0$ along AB and DC edges.

Fig. 7

Razzaque’s skew plate problem $(E = 1.092 \times 10^{5} , \, h = 0.1, \, L = 100,{\text{ and }}\upsilon = 0.3)$

For all the considered shell elements, Table 8 presents vertical deflection at center of the skew plate (point E). The results are computed using various element meshes and normalized by the reference value 0.7945 [58]. The results in Table 8 illustrate that the accuracy and convergence of the proposed TMRFS element are appropriate when compared with other elements. Element T3 has the worst accuracy (for $12 \times 12$ elements the reported value is 0.0006) and convergence among the considered elements.

Table 8 The normalized results of Razzaque’s skew plate problem

3.6 Scordelis–Lo roof problem

Figure 8 shows a roof structure that is supported by clamped boundary conditions and loaded by its self-weight. This is a benchmark test to evaluate the element performance in combined membrane-bending behavior. Utilizing symmetry, one-quarter of the roof is analyzed. For ABCD region the boundary conditions are: $u = \, w = \theta_{y} = 0$ along AD, $v = \theta_{x} = \theta_{z} = 0$ along BC and $u = \theta_{y} = \theta_{z} = 0$ along AB.

Fig. 8

Scordelis–Lo roof problem $(E = 4.32 \times 10^{8} , \, h = 0.25, \, L = 50,{\text{ density }}\rho = 360, \, g = 1, \, R = 25{\text{ and }}\upsilon = 0.0)$

For all the considered shell elements, the normalized displacement at point C is provided in Table 9. The results are obtained using different element meshes and normalized by the reference value 0.3024 [59]. The obtained results prove that the proposed TMRFS shell element is more accurate than the other ones and rapidly converges to the corresponding reference solution.

Table 9 The normalized results of Scordelis–Lo roof problem

3.7 Hemispherical shell problem

Figure 9 shows a hemispherical shell with a hole that is subjected to two opposite pairs of point loads along two perpendicular directions. This is a severe test to assess the proposed shell element in dealing with the effect of membrane locking, inextensible bending modes and rigid body motion of shell element. Taking advantage of symmetry, one-quarter of the hemispherical is modeled with the following boundary conditions: $u = \theta_{y} = \theta_{z} = 0$ along BC, $v = \theta_{x} = \theta_{z} = 0$ along AD and $w = 0$ at point A.

Fig. 9

Hemispherical shell problem $(E = 6.825 \times 10^{7} , \, h = 0.04, \, P = 2, \, R = 10{\text{ and }}\upsilon = 0.3)$

Table 10 presents the normalized displacement along the applied load at point A. The results are presented for various element meshes and normalized by the reference value 0.093 [60]. The results of Table 10 show, although the proposed element converges slowly to the reference solution, it has acceptable performance.

Table 10 The normalized results of hemispherical shell problem

3.8 Pinched cylinder problem

This is a benchmark test to investigate the ability of the proposed TMRF element in handling both complex membrane and inextensible bending state of stresses. As shown in Fig. 10, a cylinder is bounded by rigid diaphragm at both ends and subjected to a pair of opposite point loads at the middle of the cylinder. Due to symmetry, one-eighth of the cylinder is examined with the following boundary conditions: $w = \theta_{x} = \theta_{y} = 0$ along DC, $v = \theta_{x} = \theta_{z} = 0$ along BC, $u = \, w = \theta_{y} = 0$ along AD and $u = \theta_{y} = \theta_{z} = 0$ along AB.

Fig. 10

Pinched cylinder problem $(E = 3 \times 10^{6} , \, h = 3, \, R = 300,{\text{ L = 600, }}P = 1{\text{ and }}\upsilon = 0.3)$

For the proposed TMRFS shell element and the other considered ones, Table 11 presents the vertical displacement at point B. All the results for various element meshes are normalized by the reference value $1.8248 \times 10^{ - 5}$ [61]. The obtained results show that the performance of the proposed element is reasonable and does not differ significantly among the considered shell element.

Table 11 The normalized results of pinched cylinder problem

3.9 Hyperbolic paraboloid shell problem

Figure 11 shows a hyperbolic paraboloid shell which is subjected to its self-weight and bounded by clamped boundary conditions at one edge. This is a suitable test to evaluate the locking behavior of proposed shell element in bending dominated problem. Owing to symmetry, one-half of the structure is modeled and analyzed. The boundary conditions are: $u = \, v = \, w = \theta_{x} = \theta_{y} = \theta_{z} = 0$ along AD and $u = \theta_{y} = \theta_{z} = 0$ along DC.

Fig. 11

Hyperbolic paraboloid shell problem $(E = 2 \times 10^{11} , \, h = 0.001, \, L = 1,{\text{ density }}\rho = 360, \, g = 1{\text{ and }}\upsilon = 0.3)$

For all the shell elements, Table 12 shows the vertical displacement at point C. For various element meshes, the obtained results are normalized by reference value $2.8780 \times 10^{ - 4}$ [62]. The results illustrate that the proposed shell element converges slowly to the reference value with better accuracy

Table 12 The normalized results of hyperbolic paraboloid shell problem

4 Conclusion

One of the shell elements which is used by engineers in finite element analysis of shell structures is flat shell element because of the formulation simplicity, computation effectiveness and flexibility in applications. This paper presents a three-node triangular flat shell element which is obtained by combining novel membrane and plate bending elements, without using mid-side node and fictitious degrees of freedom that meet the back trend toward the simplicity of formulation. The bending component is a new triangular Mindlin–Reissner plate bending element formulated based on the hybrid displacement function element method. In this method the element’s trial function is expressed as an assumed displacement function and the displacements along the element edges are defined using Timoshenko’s beam theory. The membrane component of the proposed flat shell element is a new triangular element which is formulated based on the unsymmetric finite element method. The test function is a displacement field used in the well-known Allman triangular membrane element. The trial function is a stress field determined using the analytical approximations of Airy stress function in Cartesian coordinates. Based on the parent formulation, the proposed element is free of shear locking and membrane locking problems. Furthermore, the presence of drilling degrees of freedom avoids singularity problem of stiffness matrix. In order to investigate the ability of the proposed triangular flat shell element called TMRFS, several classic benchmark problems are employed. The numerical results demonstrate that the proposed shell element provides high precision results among the considered triangular element in literature and its performance is less sensitive to geometry, load and boundary conditions. Furthermore, the proposed TMRFS element performs well in problems with both membrane and bending behaviors. Therefore, it is being effective for complicated problems, in which the both categories exist or change to each other simultaneously.

Appendix

Matrix ${\bar{\mathbf{N}}}_{\text{p}}$ can be defined through the Timoshenko’s beam functions and a linear function. Timoshenko’s beam functions are employed to determine the deflection $(w )$ and tangential rotation $(\theta_{s} )$ and the linear function is employed to determine normal rotation $(\theta_{n} )$, as follows

$$\begin{aligned} & w = \,(L_{1} + \upsilon L_{1} L_{2} (L_{1} - L_{2} ))w_{i} + \frac{{l_{ij} }}{2}(L_{1} L_{2} + \upsilon L_{1} L_{2} (L_{1} - L_{2} ))\theta_{si} \\ & \quad + (L_{2} + \upsilon L_{1} L_{2} (L_{2} - L_{1} ))w_{j} + \frac{{l_{ij} }}{2}( - L_{1} L_{2} + \upsilon L_{1} L_{2} (L_{1} - L_{2} ))\theta_{sj} \\ & \theta_{s} = \, - (6L_{1} L_{2} /l_{ij} )\mu w_{i} + L_{1} (1 - 3\mu L_{2} )\theta_{si} + (6L_{1} L_{2} /l_{ij} )\mu w_{j} \\ & \quad + L_{2} (1 - 3\mu L_{1} )\theta_{sj} \\ & \theta_{n} = (1 - s)\theta_{ni} + s\theta_{nj} \\ \end{aligned}$$

(57)

with

$$\mu { = }\frac{{5(1 - \upsilon )l_{ij}^{2} }}{{5(1 - \upsilon )l_{ij}^{2} + 12h^{2} }},$$

(58)

in which $l_{ij}$ is the length of edge ij, s is the coordinate along the edge ij, $L_{1} = 1 - s/l_{ij} \,{\text{and}}\,L_{2} = s/l_{ij} .$ It should be noted, $\theta_{n}$ and $\theta_{s}$ are the rotations in the local coordinates that should be transformed to global coordinates. The relationship between $(\theta_{n} ,\theta_{s} )$ and $(\theta_{x} ,\theta_{y} )$ can be defined as follows

$$\left\{ {\begin{array}{*{20}c} {\theta_{n} } \\ {\theta_{s} } \\ \end{array} } \right\} = \frac{1}{{l_{ij} }}\left[ {\begin{array}{*{20}c} {y_{j} - y_{i} } & {x_{i} - x_{j} } \\ {x_{j} - x_{i} } & {y_{j} - y_{i} } \\ \end{array} } \right]_{{}} \left\{ {\begin{array}{*{20}c} {\theta_{x} } \\ {\theta_{y} } \\ \end{array} } \right\}$$

(59)

where $\left( {x_{i} ,y_{i} } \right)$ and $(x_{j} ,y_{j} )$ are, respectively, the Cartesian coordinates of nodes i and j located on the edge ij. As was mentioned, matrix ${\bar{\mathbf{N}}}_{\text{p}}$ is an interpolation function that must be defined along each element edge, as follows

$$\begin{aligned} \bullet \,\,\,{\text{Along}}\,{\text{edge}}\,12:\,{\bar{\mathbf{N}}}_{\text{p}} = [{\mathbf{N}}^{\text{k}} {\mathbf{N}}^{\text{f}} {\mathbf{N}}^{\text{h}} ] \hfill \\ \bullet \,\,\,{\text{Along}}\,{\text{edge}}\,23:\,{\bar{\mathbf{N}}}_{\text{p}} = [{\mathbf{N}}^{\text{h}} {\mathbf{N}}^{\text{k}} {\mathbf{N}}^{\text{f}} ] \hfill \\ \bullet \,\,\,{\text{Along}}\,{\text{edge}}\,31:\,{\bar{\mathbf{N}}}_{\text{p}} = [{\mathbf{N}}^{\text{h}} {\mathbf{N}}^{\text{k}} {\mathbf{N}}^{\text{f}} ] \hfill \\ \end{aligned}$$

(60)

In which ${\mathbf{N}}^{\text{h}}$ is a $5 \times 3$ matrix with zero components and the components of ${\mathbf{N}}^{\text{k}}$ and ${\mathbf{N}}^{\text{f}}$ are as follows

$$\begin{aligned} & N_{11}^{k} = \, - \,6{\kern 1pt} \:\frac{{L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \mu {\kern 1pt} \:x_{ij} {\kern 1pt} \:y_{ij} }}{{l_{ij}^{3} }},\,N_{21}^{k} = 6{\kern 1pt} \:\frac{{L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu {\kern 1pt} \:x_{ij} {\kern 1pt} \:y_{ij} }}{{l_{ij}^{3} }},\,N_{31}^{k} = 6{\kern 1pt} \:\frac{{L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu {\kern 1pt} \:\left( {x_{ij}^{2} - y_{ij}^{2} } \right)}}{{l_{ij}^{3} }} \\ & N_{41}^{k} = - y_{ij} {\kern 1pt} \:\left( {\frac{s}{{l_{ij} }} + L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu {\kern 1pt} \:\left( {2{\kern 1pt} \:\frac{s}{{l_{ij} }} - 1} \right) - 1} \right)l_{ij}^{ - 1} ,\,N_{51}^{k} = x_{ij} {\kern 1pt} \:\left( {\frac{s}{{l_{ij} }} + L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu {\kern 1pt} \:\left( {2{\kern 1pt} \:\frac{s}{{l_{ij} }} - 1} \right) - 1} \right)l_{ij}^{ - 1} \\ & N_{12}^{k} = y_{ij}^{3} \left( {\frac{s}{{l_{ij} }} - 1} \right)l_{ij}^{ - 3} + x_{ij}^{2} y_{ij} {\kern 1pt} \:\left( {\frac{s}{{l_{ij} }} + 3{\kern 1pt} \:L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu - 1} \right)l_{ij}^{ - 3} ,\,N_{22}^{k} = - 3{\kern 1pt} \:\frac{{L_{1} {\kern 1pt} \:L_{{2{\kern 1pt} }} \:\mu {\kern 1pt} \:x_{ij}^{2} y_{ij} }}{{l_{ij}^{3} }} \\ & N_{32}^{k} = - x_{ij} {\kern 1pt} \:\left( {\frac{{x_{ij}^{2} }}{{l_{ij}^{2} }} - \frac{{y_{ij}^{2} }}{{l_{ij}^{2} }}} \right)\left( {\frac{s}{{l_{ij} }} + 3{\kern 1pt} \:L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu - 1} \right)l_{ij}^{ - 1} - 2{\kern 1pt} \:x_{ij} {\kern 1pt} \:y_{ij}^{2} \left( {\frac{s}{{l_{ij} }} - 1} \right)l_{ij}^{ - 3} \\ & N_{42}^{k} = - {\kern 1pt} \:\frac{{L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:x_{ij} {\kern 1pt} \:y_{ij} {\kern 1pt} \:\left( {\mu {\kern 1pt} \:l_{ij} - 2{\kern 1pt} \:\mu {\kern 1pt} \:s + l_{ij} } \right)}}{{2l_{ij}^{2} }},\,N_{52}^{k} = {\kern 1pt} \:\frac{{L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:x_{ij}^{2} \left( {\mu {\kern 1pt} \:l_{ij} - 2{\kern 1pt} \:\mu {\kern 1pt} \:s + l_{ij} } \right)}}{{2l_{ij}^{2} }} \\ & N_{13}^{k} = 3{\kern 1pt} \:\frac{{L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu {\kern 1pt} \:x_{ij} {\kern 1pt} \:y_{ij}^{2} }}{{l_{ij}^{3} }},\,N_{23}^{k} = - x_{ij}^{3} \left( {\frac{s}{{l_{ij} }} - 1} \right)l_{ij}^{ - 3} - x_{ij} {\kern 1pt} \:y_{ij}^{2} \left( {\frac{s}{{l_{ij} }} + 3{\kern 1pt} \:L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu - 1} \right)l_{ij}^{ - 3} \\ & N_{33}^{k} = 2{\kern 1pt} \:x_{ij}^{2} y_{ij} {\kern 1pt} \:\left( {\frac{s}{{l_{ij} }} - 1} \right)l_{ij}^{ - 3} - y_{ij} {\kern 1pt} \:\left( {\frac{{x_{ij}^{2} }}{{l_{ij}^{2} }} - \frac{{y_{ij}^{2} }}{{l_{ij}^{2} }}} \right)\left( {\frac{s}{{l_{ij} }} + 3{\kern 1pt} \:L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu - 1} \right)l_{ij}^{ - 1} \\ & N_{43}^{k} = - {\kern 1pt} \:\frac{{L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:y_{ij}^{2} \left( {\mu {\kern 1pt} \:lij - 2{\kern 1pt} \:\mu {\kern 1pt} \:s + l_{ij} } \right)}}{{2l_{ij}^{2} }},\,N_{53}^{k} = \frac{{L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:x_{ij} {\kern 1pt} \:y_{ij} {\kern 1pt} \:\left( {\mu {\kern 1pt} \:l_{ij} - 2{\kern 1pt} \:\mu {\kern 1pt} \:s + l_{ij} } \right)}}{{2l_{ij}^{2} }} \\ & N_{11}^{f} = 6{\kern 1pt} \:\frac{{L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu {\kern 1pt} \:x_{ij} {\kern 1pt} \:y_{ij} }}{{l_{ij}^{3} }},\,N_{21}^{f} = - 6{\kern 1pt} \:\frac{{L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu {\kern 1pt} \:x_{ij} {\kern 1pt} \:y_{ij} }}{{l_{ij}^{3} }},\,N_{31}^{f} = - 6{\kern 1pt} \:\frac{{L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu {\kern 1pt} \:\left( {x_{ij}^{2} - y_{ij}^{2} } \right)}}{{l_{ij}^{3} }} \\ & N_{41}^{f} = y_{ij} {\kern 1pt} \:\left( {\frac{s}{{l_{ij} }} + L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu {\kern 1pt} \:\left( {2{\kern 1pt} \:\frac{s}{{l_{ij} }} - 1} \right)} \right)l_{ij}^{ - 1} ,\,N_{51}^{f} = - x_{ij} {\kern 1pt} \:\left( {\frac{s}{{l_{ij} }} + L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu {\kern 1pt} \:\left( {2{\kern 1pt} \:\frac{s}{{l_{ij} }} - 1} \right)} \right)l_{ij}^{ - 1} \\ & N_{12}^{f} = \frac{{ - y_{ij} {\kern 1pt} \:\left( { - 3{\kern 1pt} \:L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu {\kern 1pt} \:l_{ij} {\kern 1pt} \:x_{ij}^{2} + sx_{ij}^{2} + sy_{ij}^{2} } \right)}}{{l_{ij}^{4} }},\,N_{22}^{f} = - 3{\kern 1pt} \:\frac{{L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu {\kern 1pt} \:x_{ij}^{2} y_{ij} }}{{l_{ij}^{3} }} \\ & N_{32}^{f} = x_{ij} {\kern 1pt} \:\left( {\frac{s}{{l_{ij} }} - 3{\kern 1pt} \:L_{{1{\kern 1pt} }} \:L_{2} {\kern 1pt} \:\mu } \right)\left( {\frac{{x_{ij}^{2} }}{{l_{ij}^{2} }} - \frac{{y_{ij}^{2} }}{{l_{ij}^{2} }}} \right)l_{ij}^{ - 1} + 2{\kern 1pt} \:\frac{{sx_{ij} {\kern 1pt} \:y_{ij}^{2} }}{{l_{ij}^{4} }} \\ & N_{42}^{f} = {\kern 1pt} \:\frac{{L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:x_{ij} {\kern 1pt} \:y_{ij} {\kern 1pt} \:\left( { - \mu {\kern 1pt} \:l_{ij} + 2{\kern 1pt} \:\mu {\kern 1pt} \:s + l_{ij} } \right)}}{{2l_{ij}^{2} }},\,N_{52}^{f} = {\kern 1pt} \:\frac{{ - L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:x_{ij}^{2} \left( { - \mu {\kern 1pt} \:l_{ij} + 2{\kern 1pt} \:\mu {\kern 1pt} \:s + l_{ij} } \right)}}{{2l_{ij}^{2} }} \\ & N_{13}^{f} = 3{\kern 1pt} \:\frac{{L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu {\kern 1pt} \:x_{ij} {\kern 1pt} \:y_{ij}^{2} }}{{l_{ij}^{3} }},\,N_{23}^{f} = \frac{{x_{ij} {\kern 1pt} \:\left( { - 3{\kern 1pt} \:L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu {\kern 1pt} \:l_{ij} {\kern 1pt} \:y_{ij}^{2} + sx_{ij}^{2} + sy_{ij}^{2} } \right)}}{{l_{ij}^{4} }} \\ & N_{33}^{f} = y_{ij} {\kern 1pt} \:\left( {\frac{s}{{l_{ij} }} - 3{\kern 1pt} \:L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:\mu } \right)\left( {\frac{{x_{ij}^{2} }}{{l_{ij}^{2} }} - \frac{{y_{ij}^{2} }}{{l_{ij}^{2} }}} \right)l_{ij}^{ - 1} - 2{\kern 1pt} \:\frac{{sx_{ij}^{2} y_{ij} }}{{l_{ij}^{4} }} \\ & N_{43}^{f} = {\kern 1pt} \:\frac{{L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:y_{ij}^{2} \left( { - \mu {\kern 1pt} \:l_{ij} + 2{\kern 1pt} \:\mu {\kern 1pt} \:s + l_{ij} } \right)}}{{2l_{ij}^{2} }},\,N_{53}^{f} = \frac{{ - L_{1} {\kern 1pt} \:L_{2} {\kern 1pt} \:x_{ij} {\kern 1pt} \:y_{ij} {\kern 1pt} \:\left( { - \mu {\kern 1pt} \:l_{ij} + 2{\kern 1pt} \:\mu {\kern 1pt} \:s + l_{ij} } \right)}}{{2l_{ij}^{2} }} \\ \end{aligned}$$

(61)