Entropy generation and regression analysis on stagnation point flow of Casson nanofluid with Arrhenius activation energy

Abstract

This article presents the study of two-dimensional hydromagnetic stagnation point flow of Casson nanofluid over a stretching sheet in a non-Darcy porous medium with binary chemical reaction stimulated by Arrhenius activation energy. The energy equation is obtained by considering the production of heat due to Joule and viscous dissipations, heat generation/absorption and thermal radiation of the liquid. The flow model is developed and presented in the form of a system of nonlinear partial differential equations together with appropriate boundary conditions. The particle flux at the sheet is taken to be zero. The leading PDEs are transformed into dimensionless coupled ordinary differential equations (ODEs) by the usual procedure of transformation. The obtained ODEs are solved using optimal homotopy analysis method, and the effects of underlying parameters on the fluid velocity, temperature, concentration, entropy generation and Bejan number are demonstrated with the help of graphs. Also, the numerical values of skin friction coefficient, Nusselt number and Sherwood number are presented in tabular form. Linear as well as quadratic regression analysis for quantities of physical interest has also been carried out. Entropy generation is perceived to rise on increasing diffusive variable and Brinkman number, whereas Brownian diffusion has an adverse effect on it. Skin friction coefficient is reduced on increasing Casson fluid parameter and activation energy.

1 Introduction

It is an established fact that the transfer of heat from one mechanical system to other takes place in a huge number of technological processes. Such processes involve the fluid movement and fluid cooling/heating. Thus, the better cooling methods are required for such processes. The nanofluid, whose thermal conductivity is much better than other heat transfer fluids such as engine oil, water and ethylene glycol, seems to be the fluid which provides better cooling and hence can be used to improve the heat transfer rate, owing to its exceptional characteristics. Nanofluids are colloidal suspension of particles with nanoscale dimensions in a regular fluid, known as base fluid. Furthermore, the flows of electrically conducting nanofluid under the influence of a strong magnetic field have been observed in various engineering and industrial setups and have diverse usage in biomedical techniques, viz. gastric medications, wound treatment, elimination of tumors, sterilized devices, asthma treatment, etc. Thus, owing to such important applications of nanofluid flows, a lot of studies have been carried out. Heris et al. [1] investigated the laminar flow of nanofluid with Al$_2$O$_3$ as nanoparticles in a circular tube experimentally and exhibited that the coefficient of convective heat transfer of pure water was improved by 41% with only 3% volume fraction of Al$_2$O$_3$-nanoparticle. Turkyilmazoglu [2] analyzed the flow of four different kinds of nanofluids, viz. Cu-nanofluid, Ag-nanofluid, TiO$_2$-nanofluid and CuO-nanofluid, where the whole flow domain is permeated by magnetic field, and found the analytical solution for mass transport in nanofluids. Sandeep and Reddy [3] discussed MHD Cu-nanofluid flow near a cone and a wedge, and they observed that increasing the volume fraction of nanoparticles results in increased temperature. Some of the recent research works in this context are done by Tripathi et al. [4], Kumar et al. [5], Munyalo and Xuelai [6], Hamid et al. [7].

Entropy is that part of thermal energy of a thermodynamic system which is unavailable for conversion into mechanical work. As per the second law of thermodynamics:, for a reversible thermodynamic process, the total entropy of the system remains unchanged. However, if the system is undergoing an irreversible process, there is an increase in the net entropy of the system. Fluid flows consisting of various species over a heated surface go through some irreversible processes such as chemical reaction, diffusion, friction between the layers of fluid due to viscosity, thermal resistance, etc. Thus, there is an increase in net entropy of the system. In order for better effectiveness of some of the industrial equipment and components such as electrochemicals, microchannels, reactors, air separators, fuel cells and helical coils, the entropy production needs to be minimized. Bejan [8] was the first one to analyze the entropy generation in an irreversible process and introduce the entropy generation rate for heat transfer flows. Nouri et al. [9] scrutinized the flow of nanofluid in the presence of a spherical heat source and estimated the entropy generation for such flows. Following the earlier research works on entropy generation, Rashidi et al. [10] tried to understand the effects of magnetic field on the entropy generation for the flow past a rotating disk. Reddy et al. [11] established a mathematical model to understand unsteady natural convection flow of Casson fluid over a vertical cylinder under the effect of magnetic field. They noted that Casson fluid parameter is one of the reasons for the increase in the entropy heat generation. Adesanya and Makinde [12] obtained the analytical expressions for the flow of a couple-stressed fluid in a channel, considering the entropy generation. Their observation suggests that in the region of channel flow, the rise in couple stress parameter results in lower entropy generation as compared to the entropy generation near the walls. Seth et al. [13] carried out the research work concerning the MHD flow of nanofluids with colloidal suspension of carbon nanotubes past a stretching sheet. They concluded that a rise in Brinkmann number causes the improvement in thermal energy irreversibility. Mahian et al. [14] reviewed the flows of nanofluids and entropy generation for various geometries with a different set of conditions at the boundary. Hayat et al. [15] presented a study to analyze the effectiveness of entropy generation in peristaltic flow of Jeffrey fluid in a curved channel which is completely filled with porous materials.

It has been observed that the dispersion of species by virtue of chemical reaction in heat and mass transfer flows has significant application in various industrial/scientific processes such as water and air pollution processes, flow in a desert cooler and food processing. However, for chemical reaction to take place among species, an essential amount of energy must be supplied to the atoms or molecules. This minimum energy is known as Arrhenius activation energy, first proposed by Svante Arrhenius in 1889. There are some research works on fluid flows concerning chemical reaction with activation energy. Bestman [16] considered the free convection flow over a plane surface with the consideration of binary reaction stimulated by providing activation energy. Ramzan et al. [17] developed a mathematical model to illustrate micropolar nanofluid flow with chemical reaction under the consideration of activation energy. Awad et al. [18] discussed the unsteady flow past a stretching surface, considering chemical reaction under the action of activation energy in a rotating frame. They realized that an increase in the activation energy results into increased concentration boundary layer. Khan et al. [19] investigated 2-D cross flow of nanofluids with nonlinear thermal radiation past a stretching surface considering the effect of chemical reaction between species, triggered by activation energy. They observed that increase in activation energy is responsible for slowing down the rate of mass transfer. Mustafa et al. [20] considered the buoyancy-driven flow of nanofluids along a vertical surface, taking chemical reaction with activation energy into account. Their study revealed that heat flux near the vertical surface decreases with the rise in rate of chemical reaction. Shafique et al. [21] considered the three-dimensional (3-D) flow of Maxwell fluid, incorporating the mutual influences of activation energy with binary chemical reaction over a stretchable surface in a rotating frame.

So far as the research studies on hydromagnetic stagnation point flow of Casson nanofluid over a horizontal stretching surface in a porous medium are concerned, only a few research studies have been reported. However, no one has ever considered such flows through a non-Darcy porous medium by considering Darcy–Forchheimer model for flows in porous medium. In this article, we have also considered the influences of Joule dissipation and thermal radiation. In addition, we have also considered this flow problem with chemical reaction stimulated by activation energy. A brief discussion of entropy generation and the effect of various relevant flow parameters on the entropy generation rate is also presented. The obtained coupled highly nonlinear ODEs are solved by using series solution by OHAM [22,23,24,25,26]

2 Modeling of the flow

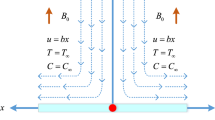
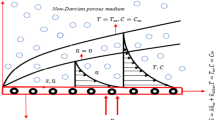
Consider the MHD stagnation point flow of an electrically conducting, thermally radiating Casson nanoliquid in a Darcy–Forchheimer environment, considering the influence of viscous and Joule dissipations. The flow domain is permeated by an unvarying magnetic field of intensity $B_0$. It is assumed that magnetic field induced by fluid flow is insignificant in comparison with applied one due to consideration of small Reynolds number. The mutually perpendicular Cartesian system (x, y, z) is chosen to represent the geometry where the stretching sheet lies in the x-direction. Two opposite forces of equal magnitude are employed for stretching the sheet, so that the point O with coordinate (0, 0, 0) is unmoved, as depicted in Fig. 1. The net flux of nanoparticles at the surface is considered zero. The temperature at the sheet is considered to be $T_w$, temperature of nanoliquid in free stream is assumed ${T_\infty },$ and concentration of nanoparticles is ${C_\infty }$. It is also assumed that a binary chemical reaction among the species takes place with a constant rate $k_r$. Furthermore, the effect of Joule heating is also considered.

Fig. 1

Schematic diagram of the problem

The governing equations for the stagnation point flow of Casson nanoliquid in a Darcy–Forchheimer environment under above assumptions in a compact form are given as:

$$\nabla .V = 0,$$

(1)

$$\rho \left( {V.\nabla } \right) V = - \nabla p + \nabla .\tau + (J \times B) + \rho \,f,$$

(2)

$$\begin{aligned}&{\left( {\rho c} \right) _f}\left( {V.\nabla T} \right) = k{\nabla ^2}T + {\left( {\rho {c_p}} \right) _s}\nonumber \\&\quad \left[ {\frac{{{D_T}}}{{{T_\infty }}}\left( {\nabla T.\,\,\nabla T} \right) + {D_B}\left( {\nabla T.\nabla C} \right) } \right] + \mu {\left( {\nabla V} \right) ^2} + J.E + \phi ,\end{aligned}$$

(3)

$$\begin{aligned}&\left( {V.\nabla C} \right) = {D_B}{\nabla ^2}C + \frac{{{D_T}}}{{{T_\infty }}}{\nabla ^2}T \nonumber \\&\quad - k_r^2{\left( {\frac{T}{{{T_\infty }}}} \right) ^m}\left( {C - {C_\infty }} \right) \exp \left( {\frac{{ - {E_a}}}{{KT}}} \right) . \end{aligned}$$

(4)

In the above Eqs. (1)–(4), $V = ( {u, v, 0} )$ denotes the velocity vector, p stands for pressure, $\tau$ is viscous stress tensor, $B = \left( {0,\,{B_0},\,0} \right)$ represents the strength of the magnetic field, $J = {\sigma ^*}\left( {V \times B} \right)$ is the current density in which ${\sigma ^*}$ indicates the electrical conductivity of the fluid, f accounts for other body force vectors, T is the fluid temperature, E is the electric field, and $\phi$ accounts for other heat sources to be considered in the flow problem.

The rheological equation of state for Casson fluid model is

$${\tau _{jk}} = \left\{ \begin{array}{l} 2({{P_y}/\sqrt{2\pi }+\mu _\beta }){e_{jk}},\,\,\,\,\,\pi > {\pi _c}, \\ 2({{P_y}/\sqrt{2{\pi _c}}+\mu _\beta }){e_{jk}},\,\,\,\,\pi < {\pi _c} \\ \end{array} \right.$$

(5)

where $\mu _{B}$ denotes plastic dynamic viscosity of Casson fluid, $P_{y}$ stands for yield stress of fluid $\pi =e_{jk}$, $e_{jk}$ represents the (j, k)th component of rate of deformation, and ($\pi$, $\pi _{c}$) are product of component of deformation rate with itself and critical value of this product, respectively.

2.1 Effect of Lorentz force in the momentum equation

The effect of magnetic field is represented in the momentum equation by $\frac{{\left( {J \times B} \right) }}{\rho }.$ Therefore, we can simplify the term as

$$\begin{aligned} \frac{{\left( {J \times B} \right) }}{\rho } &= \frac{{{\sigma ^ * }}}{\rho }\left[ {\left( {V \times B} \right) \times B} \right] = \frac{{{\sigma ^ * }}}{\rho }\left( {\begin{array}{*{20}{c}} i&{}j&{}k\\ u&{}v&{}0\\ 0&{}{{B_0}}&{}0 \end{array}} \right) \\ &\quad\times B = \frac{{{\sigma ^ * }}}{\rho }\left[ {i.(0) - j.(0) + k.(u{B_0})} \right] \times B\\ & = \frac{{{\sigma ^ * }}}{\rho }\left[ {k.(u{B_0})} \right] \times \left[ {0,\,{B_0},\,0} \right] = \frac{{{\sigma ^ * }}}{\rho }\left( {\begin{array}{*{20}{c}} i&{}j&{}k\\ 0&{}0&{}{u{B_0}}\\ 0&{}{{B_0}}&{}0 \end{array}} \right) \\ & = \frac{{{\sigma ^ * }}}{\rho }\left[ {i.( - uB_0^2) + 0 + 0} \right] = - \frac{{{\sigma ^ * }uB_0^2}}{\rho }. \end{aligned}$$

2.2 Appearance of Brownian diffusion and thermophoresis

To understand the appearance of Brownian diffusion and thermophoresis terms in energy and nanoparticle transport equation, we need to understand the mechanism by which the nanoparticles can develop a slip velocity with respect to the base fluid. As per Whitmore and Meisen [27] and Xuan and Roetzel [28], there are in total seven possible slip mechanisms, which are inertia, Brownian diffusion, thermophoresis, diffusiophoresis, magnus effect, fluid drainage and gravity settling. However, in the cases where turbulent effects are not important, i.e., in laminar flows, only Brownian diffusion and thermophoresis effect are important, whereas other slip mechanisms have very small to no contribution in the slipping of nanoparticles [29]. Thus, we discuss these two slip mechanisms in detail

2.2.1 Brownian diffusion

The random motion of nanoparticles within the base fluid is called Brownian motion and results from continuous collisions between the nanoparticles and the molecules of the base fluid. Brownian motion is described by the Brownian diffusion coefficient, $D_B$ which is given by the Einstein–Stokes equation [29]

$${D_B} = \frac{{{k_B}T}}{{3\,\pi \,\mu \,{d_p}}},$$

(6)

where $k_B$ is Boltzmann constant, $\mu$ is viscosity and $d_p$ indicates nanoparticle diameter. The nanoparticle mass flux due to Brownian diffusion, ${j_{p,\,B}},$ can be evaluated as: ${j_{p,\,B}} = - {\rho _p}\,{D_B}\,\nabla \phi ,$ where $\rho _p$ is density of nanoparticles and $\phi$ is nanoparticle volume fraction.

2.2.2 Thermophoresis

The diffusion of particles under the influence of temperature gradient is called thermophoresis. The thermophoretic velocity $V_T$ is given as

$${V_T} = - \beta \frac{\mu }{\rho }.\,\frac{{\nabla T}}{T}.$$

(7)

2.3 Nanoparticles concentration

The conservation equation for the nanoparticles in the absence of chemical reactions is:

$$V.\nabla C = - \frac{1}{{{\rho _p}}}\nabla .{j_p}$$

(8)

In the above equation, $j_p$ is the diffusion mass flux for the nanoparticles $(kg/{m^2}s)$ which represents the nanoparticle flux relative to the nanofluid velocity V. If the external forces are insignificant, $j_p$ can be written as the sum of only two diffusion terms, i.e., Brownian diffusion and thermophoresis

$${j_p} = {j_{p,\,\,B}} + \,{j_{p,\,\,T}} = - \rho {D_B}\nabla C - {\rho _p}{D_T}\frac{{\nabla T}}{T}.$$

(9)

The ${D_B} = \frac{{{k_B}T}}{{3\,\pi \,\mu \,{d_p}}}$ and ${D_T} = \beta \frac{\mu }{\rho }C$ are the diffusion coefficients. Substituting the value of $j_p$ in (8), we have

$$V.\nabla C = \nabla .\left[ {{D_B}\nabla C + {D_T}\frac{{\nabla T}}{T}} \right].$$

(10)

Equation (10) states that the nanoparticles can move homogeneously with the fluid (second term of the left-hand side), but they also possess a slip velocity relative to the fluid (right-hand side), which is due to Brownian diffusion and thermophoresis.

2.4 Energy equation

The energy equation for the nanofluid can be written as

$$\rho c\left( {V.\nabla T} \right) = - \nabla .q + {h_p}\nabla .{j_p},$$

(11)

where q is the energy flux relative to the nanofluid velocity V. $h_p$ is the specific enthalpy of the nanoparticle material J / kg,  and q can be calculated as the sum of the conduction heat flux and the heat flux due to nanoparticle diffusion.

$$q = - k\nabla T + {h_p}{j_p},$$

(12)

Substituting Eq. (12) in Eq. (11) and recognizing that $\nabla .\left( {{h_p}{j_p}} \right) = {j_p}.\nabla {h_p} + {h_p}\nabla .{j_p},$ one gets

$$\rho c\left( {V.\nabla T} \right) = \nabla .k\nabla T - {c_p}{j_p}.\nabla T,$$

(13)

where $\nabla {h_p}$ has been set equal to ${c_p}\nabla T.$ Note that if ${j_p}$ is zero, Eq. (13) becomes the familiar energy equation for a pure fluid. Substituting the value of $j_p$ in (13), the final form of the energy equation for the nanofluid is found

$$\rho c\left( {V.\nabla T} \right) = \nabla .k\nabla T + {\rho _p}{c_p}\left[ {{D_{{B}}}\nabla C .\nabla T + {D_T}\frac{{\nabla T.\nabla T}}{T}} \right].$$

(14)

Equation (14) states that heat can be transported in a nanofluid by convection (second term on the left-hand side), by conduction (first term on the right-hand side) and also by virtue of nanoparticle diffusion (second and third terms on the right-hand side). It is important to emphasize that $\rho c$ is the heat capacity of the nanofluid and thus already accounts for the sensible heat of the nanoparticles as they move homogeneously with the fluid. Therefore, the last two terms on the right-hand side truly account for the additional contribution associated with the nanoparticle motion relative to the fluid.

Now after considering the standard boundary layer approximations, the governing equation in scalar form for the problem under consideration can be written as:

$$\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} = 0,$$

(15)

$$\left. \begin{array}{l} u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} = \upsilon \left( {1 + \frac{1}{\beta }} \right) \frac{{{\partial ^2}u}}{{\partial {y^2}}} + {u_e}\frac{{d{u_e}}}{{dx}} + \frac{{B_0^2{\sigma ^*}}}{\rho }\left( {{u_e} - u} \right) + \frac{\upsilon }{k}\left( {{u_e} - u} \right) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, - {F_r}\left( {{u^2} - u_e^2} \right) + g\left( {{\beta _T}\left( {T - {T_\infty }} \right) + {\beta _C}\left( {C - {C_\infty }} \right) } \right) \end{array} \right\},$$

(16)

$$\left. \begin{array}{l} u\frac{{\partial T}}{{\partial x}} + v\frac{{\partial T}}{{\partial y}} = \alpha \frac{{{\partial ^2}T}}{{\partial {y^2}}}\, + \delta \left( {\frac{{{D_T}}}{{{T_\infty }}}{{\left( {\frac{{\partial T}}{{\partial y}}} \right) }^2} + {D_B}\frac{{\partial T}}{{\partial y}}\frac{{\partial C}}{{\partial y}}} \right) + \frac{{B_0^2{\sigma ^*}}}{{{{\left( {\rho c} \right) }_f}}}{u^2}\\ \,\,\,\,\,\,\,\,\,\, + \frac{{{Q_0}\left( {T - {T_\infty }} \right) }}{{{{\left( {\rho c} \right) }_f}}} - \frac{1}{{{{\left( {\rho c} \right) }_f}}}\frac{{\partial {q_r}}}{{\partial y}} + \frac{\mu }{{{{\left( {\rho c} \right) }_f}}}\left( {1 + \frac{1}{\beta }} \right) {\left( {\frac{{\partial u}}{{\partial y}}} \right) ^2} \end{array} \right\},$$

(17)

$$\begin{aligned}&\,\,\,\,\,u\frac{{\partial C}}{{\partial x}} + v\frac{{\partial C}}{{\partial y}} = {D_B}\frac{{{\partial ^2}C}}{{\partial {y^2}}} + \frac{{{D_T}}}{{{T_\infty }}}\frac{{{\partial ^2}T}}{{\partial {y^2}}} - k_r^2\nonumber \\&\quad \left( {C - {C_\infty }} \right) {\left( {\frac{T}{{{T_\infty }}}} \right) ^m}\exp \left( {\frac{{ - {E_a}}}{{\mathrm{K}T}}} \right) . \end{aligned}$$

(18)

The conditions at the boundary are given as

$$u = {u_w} = cx,\,v = 0,\,T = {T_w},\,{D_B}\frac{{\partial C}}{{\partial y}} + \frac{{{D_T}}}{{{T_\infty }}}\frac{{\partial T}}{{\partial y}} = 0\,\,\,\,\,\,\,\,\,at\,y = 0,$$

(19)

$$u = {u_e} = ax,\,T = {T_\infty },C = {C_\infty } \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,as\,y \rightarrow \infty,$$

(20)

Using Rosseland approximation, for the thermal radiation, the radiative heat flux $q_r$ is expressed as

$${q_r} = - \frac{{4{\sigma_1 }}}{{3{k^ * }}}\frac{{\partial {T^4}}}{{\partial y}} = - \frac{{16{\sigma_1 }}}{{3{k^ * }}}{T^3}\frac{{\partial T}}{{\partial y}}.$$

(21)

where $\beta$ is Casson fluid parameter, $\nu$ is kinematic coefficient of viscosity, $\rho$ is fluid density, $u_e$ is free stream velocity, $F_r=\frac{C_b}{xk^{1/2}}$ is non-uniform inertia coefficient, $Q_0$ symbolizes the coefficient of heat generation/absorption, $C_b$ is drag coefficient, k is permeability of porous medium, $\beta _T$ is coefficient of thermal expansion, $q_r$ is radiative heat flux, g is gravitational acceleration, T is fluid temperature, $T_\infty$ is ambient temperature, $\beta _c$ is coefficient of concentration expansion, $\alpha$ is thermal conductivity, C is concentration, $C_\infty$ is ambient concentration, $\mu$ is fluid viscosity, $\delta =(({\rho c_p})_p/({\rho c_p})_{f})$, $D_T$ is coefficient of thermophoresis diffusion, $D_B$ is Brownian diffusion coefficient, m is fitted rate constant, $k_r$ is reaction rate, $E_a$ is activation energy, K is Boltzmann constant, $u_w$ is stretching velocity, $k^ *$ is mean absorption coefficient and $\sigma_1$ is Stefan–Boltzmann constant.

The flow phenomena which are characterized in mathematical form can be handled in an easier way by transforming the nonlinear PDEs (15) to (18) into nonlinear ODEs. This job is done with the use of following similarity transformations:

$$\begin{aligned} \eta&= \sqrt{\frac{c}{\nu }} y,\,\,u = cxf'\left( \eta \right) ,\,\,v = - \sqrt{c\nu } f\left( \eta \right) ,\,\,\nonumber \\&\theta \left( \eta \right) = \frac{{T - {T_\infty }}}{{{T_f} - {T_\infty }}},\,\,\phi \left( \eta \right) = \frac{{C - {C_\infty }}}{{{C_f} - {C_\infty }}}.\,\, \end{aligned}$$

(22)

Making use of (22), governing Eqs. (16)–(18) are converted into the following system of ODEs:

$$\begin{aligned}&\left( {1 + \frac{1}{\beta }} \right) f''' + {A^2} + M\left( {A - f'} \right) - {f'^2} + ff'' \nonumber \\&\quad + {\lambda _1}\theta + {\lambda _2}\phi - {\lambda _3}f' - F{f'^2}, \end{aligned}$$

(23)

$$\begin{aligned}&\frac{{\left( {1 + R} \right) }}{{\Pr }}\theta '' + Nb\theta '\phi ' + Nt{\theta '^2} + f\theta ' + EcM{f'^2}\nonumber \\&\quad + Ec{f''^2}+\gamma \theta = 0, \end{aligned}$$

(24)

$$\begin{aligned}&\frac{1}{{Sc}}\phi '' + f\phi ' + \frac{{Nt}}{{ScNb}}\theta '' \nonumber \\&\quad + {\sigma }{\left( {1 + \theta {\theta _w}} \right) ^m}\phi \exp \left( {\frac{{ - E}}{{1 + \theta {\theta _w}}}} \right) = 0. \end{aligned}$$

(25)

The transformed conditions at boundary are as follows:

$$f' = 1,\,\,\theta = 1,\,\,f = 0,\,\,Nt\theta ' + Nb\phi ' = 0\,\,\,\,\,\,\,\,\,at\,\,\eta = 0,$$

(26)

$$f' = A,\,\,\theta = 0,\,\,\phi = 0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,as\,\,\eta \rightarrow \infty,$$

(27)

where $M = \frac{{\sigma ^* B_0^2}}{{\rho c}}$ is magnetic parameter, $A = \frac{a}{c}\,$ indicates ratio parameter, ${\lambda _1} = \frac{{Gr}}{{{\mathop {{\mathrm{Re}}}\nolimits } _x^2}}$ is thermal buoyancy parameter, ${\lambda _2} = \frac{{G{r^ * }}}{{{\mathop {{\mathrm{Re}}}\nolimits } _x^2}}$ is concentration buoyancy parameter, ${\lambda _3} = \frac{\nu }{k}$ represents the porosity parameter, $F = \frac{{{C_b}}}{{{k^{1/2}}}}$ denotes inertia coefficient parameter, $Gr = \frac{{g{\beta _T}\left( {{T_f} - {T_\infty }} \right) {x^3}}}{{{\nu ^2}}}$ is Grashof number due to temperature, $G{r^ * } = \frac{{g{\beta _C}\left( {{C_f} - {C_\infty }} \right) {x^3}}}{{{\nu ^2}}}$ is Grashof number due to concentration, $R = \frac{{16{\sigma_1 }T_\infty ^3}}{{3k{k^ * }}}$ is radiative parameter, $\Pr = \frac{\nu }{\alpha }$ is Prandtl number, $Nb = \delta \frac{{{D_B}\left( {{C_f} - {C_\infty }} \right) }}{\nu }$ is Brownian motion variable, $Nt = \delta \frac{{{D_T}\left( {{T_f} - {T_\infty }} \right) }}{{{T_\infty }\nu }}$ is thermophoresis parameter, $Ec = \frac{{{c^2}{x^2}}}{{{c_f}\left( {{T_f} - {T_\infty }} \right) }}$ is Eckert number, $Sc = \frac{\nu }{{{D_B}}}$ is Schmidt number, ${\theta _w} = \frac{{\left( {{T_f} - {T_\infty }} \right) }}{{{T_\infty }}}$ is temperature difference, ${\sigma } = \frac{{k_r^2}}{c}$ is chemical reaction parameter, $E = \frac{{{E_a}}}{{\mathrm{K}{T_\infty }}}$ is activation energy and $\gamma = \frac{{{Q_0}}}{{c{{\left( {\rho {c_p}} \right) }_f}}}$ signifies heat generation/absorption parameter.

3 Quantities of physical interest

The physical quantities of interest, viz. skin friction coefficient ${C_f}$, Nusselt Number (rate of heat transfer) $N{u_x}$ and Sherwood Number (rate of mass transfer) $S{h_x}$, are defined as

$$\begin{aligned} {C_f}&= \frac{1}{{\rho u_w^2}}\left( {{\mu _B} + \frac{{{P_y}}}{{\sqrt{2\pi } }}} \right) {\left. {\frac{{\partial u}}{{\partial y}}} \right| _{y = 0}},\,\,N{u_x} = \frac{{{q_w}x}}{{k\left( {{T_f} - {T_\infty }} \right) }},\,\nonumber \\ S{h_x}&=\frac{{{J_w}x}}{{{D_B}\left( {{C_f} - {C_\infty }} \right) }}. \end{aligned}$$

(28)

These physical quantities in non-dimensional form are given as follows:

$$\begin{aligned} {C_f}{\mathop {{\mathrm{Re}}}\nolimits } _x^{1/2}&= \left( {1 + \frac{1}{\beta }} \right) f''\left( 0 \right) ,\,\,\,N{u_x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 1/2} \nonumber \\&= - \left( {1 + R} \right) \theta '\left( 0 \right) ,\,\,\,S{h_x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 1/2} = - \phi '\left( 0 \right) , \end{aligned}$$

(29)

where ${q_w} = - k{\left. {\frac{{\partial T}}{{\partial y}}} \right| _{y = 0}}$, ${J_w} = - {D_B}{\left. {\frac{{\partial C}}{{\partial y}}} \right| _{y = 0}}$ and ${{\mathop {\mathrm{Re}}\nolimits } _x} = \frac{{{u_w}x}}{\nu }$ are heat flux, mass flux and local Reynolds number, respectively.

4 Solution methodology

In order to find solutions of ODEs (23)–(25) along with the boundary conditions (26) and (27), optimal homotopy analysis method (OHAM) is used. Here, we have chosen the appropriate initial approximations $\left( {{f_0}\left( \eta \right) ,\,{\theta _0}\left( \eta \right) ,\,{\phi _0}\left( \eta \right) \,} \right)$ and auxiliary linear operator $\left( {{L_f},{L_\theta },{L_\phi }} \right)$ as:

$${f_0} = A\eta + \left( {1 - A} \right) \left( {1 - {e^{ - \eta }}} \right) , \,\,{\theta _0} = {e^{ - \eta }} \,\,and \,\,{\phi _0} =- \frac{{Nt}}{{Nb}}{e^{ - \eta }}.$$

(30)

$${L_f} = \frac{{{\partial ^3}f}}{{\partial {\eta ^3}}} - \frac{{\partial f}}{{\partial \eta }},\,\,{L_\theta } = \frac{{{\partial ^2}\theta }}{{\partial {\eta ^2}}} - \theta \, and \,\, {L_\phi } = \frac{{{\partial ^2}\phi }}{{\partial {\eta ^2}}} - \phi .$$

(31)

with the property

$$\begin{array}{l} {L_f}\left( {{C_0} + {C_1}{e^{ - \eta }} + {C_2}{e^{ - \eta }}} \right) = 0,\\ {L_\theta }\left\{ {{C_3} + {C_4}{e^{ - \eta }}} \right\} = 0,\\ {L_\phi }\left\{ {{C_5} + {C_6}{e^{ - \eta }}} \right\} = 0, \end{array}$$

(32)

in which ${C_i},\,\,i = 0\,\,to\,\,6$ express the arbitrary constants. The zeroth- and mth-order deformation problems in the presence of linear operators can be easily established for the current problem.

4.1 Optimal convergence control parameters

It is observed that the Taylor series solutions of $f,\,\,\theta \,\,\mathrm{{and}}\,\phi$ contain nonzero convergence control parameters ${h_f},\,\,{h_\theta }\,\,\mathrm{{and}}\,\,{h_\phi }$ in the homotopy solutions which regulate both convergence rate and convergence region. To find the optimal values of ${h_f},\,\,{h_\theta }\,\,\mathrm{{and}}\,\,{h_\phi }$ , the idea of minimization of average squared residual errors has been used, which is given as

$$E_m^f = \frac{1}{{k + 1}}{\sum \limits _{j = 0}^k {\left[ {{N_f}{{\left( {\sum \limits _{i = 0}^m {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}}_i}\left( \eta \right) ,\,} \sum \limits _{i = 0}^m {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }}_i}\left( \eta \right) ,\,} \sum \limits _{i = 0}^m {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }} _i}\left( \eta \right) \,} \right) }_{\eta = j\delta \eta }}} \right] } ^2}d\eta,$$

(33)

$$E_m^\theta = \frac{1}{{k + 1}}{\sum \limits _{j = 0}^k {\left[ {{N_g}{{\left( {\sum \limits _{i = 0}^m {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}} _i}\left( \eta \right) ,\,} \sum \limits _{i = 0}^m {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta }} _i}\left( \eta \right) ,\,} \sum \limits _{i = 0}^m {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } } _i}\left( \eta \right) \, \right) }_{\eta = j\delta \eta }}} \right] } ^2}d\eta,$$

(34)

$$E_m^\phi = \frac{1}{{k + 1}}{\sum \limits _{j = 0}^k {\left[ {{N_\theta }{{\left( {\sum \limits _{i = 0}^m {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}} _i}\left( \eta \right) ,\,} \sum \limits _{i = 0}^m {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } } _i}\left( \eta \right) ,\, \sum \limits _{i = 0}^m {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } } _i}\left( \eta \right) \, \right) }_{\eta = j\delta \eta }}} \right] } ^2}d\eta,$$

(35)

Following Liao [22, 23], we have

$$E_m^t = E_m^f + E_m^\theta + E_m^\phi.$$

(36)

Table 1 Optimal values of convergence control parameters versus different orders of approximation and total average squared residual error

Table 2 Individual average squared residual errors using optimal values of auxiliary parameters for $m=6$

where $E_m^t$ stands for total squared residual error defined by Eq. (36). The total average squared residual error is minimized by using BVPh2.0 routine of Mathematica. Optimal values of convergence control parameters and least values of the total average squared residual error versus different orders of approximation are displayed in Table 1. Table 2 presents individual average squared residual error at various orders of approximations together with CPU time.

5 Analysis for entropy generation

Investigation of entropy generation is very important to understand the irreversibility of thermal energy of a system. The expression for the entropy generation for the Casson nanofluid flow in the dimensional form is written as

$$\begin{aligned} {S_G}&= \frac{k}{{T_\infty ^2}}{\left( {\frac{{\partial T}}{{\partial y}}} \right) ^2}\left( {1 + \frac{{16{\sigma ^*}T_\infty ^3}}{{3k{k^*}}}} \right) + \left( {1 + \frac{1}{\beta }} \right) \frac{\mu }{{{T_\infty }}}{\left( {\frac{{\partial u}}{{\partial y}}} \right) ^2}\nonumber \\&\quad+ \frac{{RD}}{{{C_\infty }}}{\left( {\frac{{\partial C}}{{\partial y}}} \right) ^2} + \frac{{\sigma B_0^2{u^2}}}{{{T_\infty }}} + \frac{{RD}}{{{T_\infty }}}\left( {\frac{{\partial T}}{{\partial x}}\frac{{\partial C}}{{\partial x}} + \frac{{\partial C}}{{\partial y}}\frac{{\partial T}}{{\partial y}}} \right) . \end{aligned}$$

(37)

Using (22), dimensional Eq. (37) gets converted into following dimensionless form:

$$\begin{aligned} {N_g}&s= \left( {1 + R} \right) {\alpha _1}{\theta '^2} + \left( {1 + \frac{1}{\beta }} \right) Br{f''^2} + BrM{f'^2} \nonumber \\&\quad+ L\left( {\frac{{{\alpha _2}}}{{{\alpha _1}}}{{\phi '}^2} + \phi '\theta '} \right) . \end{aligned}$$

(38)

In the above expression (38), $Br = \frac{{\mu {c^2}{x^2}}}{{k\Delta T}}$ is Brinkman number, ${N_G} = \frac{{{S_G}{T_\infty }\upsilon }}{{ck\Delta T}}$ represents entropy generation rate, ${\alpha _1} = \frac{{\left( {{T_f} - {T_\infty }} \right) }}{{{T_\infty }}}$ is temperature ratio variable, $L = \frac{{RD\left( {{C_f} - {C_\infty }} \right) }}{k}$ is diffusive variable and ${\alpha _2} = \frac{{\left( {{C_f} - {C_\infty }} \right) }}{{{C_\infty }}}$ is concentration ratio variable.

The evaluation of Bejan Number (which is basically a ratio of entropy generation by virtue of heat transfer irreversibility to the total entropy generation) is one of the main tasks in order to study the irreversibility of heat transport, and value of this number ranges from 0 to 1. The dimensionless form of the Bejan number is defined as

$$Be = \frac{{\left( {1 + R} \right) {\theta '^2}{\alpha _1}}}{{\left( {1 + R} \right) {\theta '^2}{\alpha _1} + Br\left( {1 + \frac{1}{\beta }} \right) {{f''}^2} + BrM{{f'}^2} + L\phi '\theta ' + \frac{{{\alpha _2}}}{{{\alpha _1}}}L{{\phi '}^2}}}.$$

(39)

From the above expression, it can be said that when Bejan number varies from 0 to 0.5, fluid friction irreversibility dominates, whereas if it varies from 0.5 to 1 then irreversibility due to heat transfer dominates. Be = 0.5 represents the case when heat transfer and fluid friction irreversibility contribute equally to the entropy generation.

6 Regression analysis

In this section, the linear and quadratic regression analysis is performed which is nothing but a type of a statistical technique to estimate the skin friction coefficient and the reduced Nusselt number. More precisely, regression analysis plays an important role in understanding how the specific value of a dependent variable differs due to variation in one independent variable while the other independent variables are kept fixed. The linear model for estimated regression for the skin friction coefficient is defined as:

$${C_f}_{\,est} = {C_f}{\mathop {{\mathrm{Re}}}\nolimits } _x^{1/2} + {R_1}A + {R_2}{\lambda _1} + {R_3}{\lambda _2} + {R_4}F,$$

(40)

where ${R_1},\,\,{R_2},\,\,{R_3}$ and ${R_4}$ are the coefficients of the linear regression corresponding to $A,\,\,{\lambda _1},\,\,{\lambda _2}$ and F, respectively. For different values of magnetic parameter M, the regression coefficients and the estimated skin friction coefficient along with the maximum relative absolute error ${\varepsilon _{cf}}$ are calculated in Table 3. The expression for the maximum relative absolute error ${\varepsilon _{cf}}$ is given as

$${\varepsilon _{cf}} = \left| {\frac{{{C_f}_{\,est} - {C_f}{\mathop {{\mathrm{Re}}}\nolimits } _x^{1/2}}}{{{C_f}{\mathop {{\mathrm{Re}}}\nolimits } _x^{1/2}}}} \right|.$$

(41)

In the case for particular values of magnetic parameter M (suppose $M=1.2$), the values of ${C_f}{\mathop {{\mathrm{Re}}}\nolimits } _x^{1/2}$ are estimated for 100 sets of values of $A,\,\,{\lambda _1},\,\,{\lambda _2}$ and F which are randomly generated from the interval [0.01, 0.5], and we achieve a linear regression on the results. This gives the following correlation:

$${C_f}_{\,est} = 0.7049 + 0.0701A - 0.0081{\lambda _1} - 0.0436{\lambda _2} - 0.0654F,$$

(42)

where maximum relative error is around $1.9\%$. This shows that an increase in the coefficients of the stretching parameter A and concentration buoyancy parameter ${\lambda _2}$, as per Eq. (40), leads to a decrement in the value of ${C_f}{\mathop {{\mathrm{Re}}}\nolimits } _x^{1/2},$ whereas with the increment in the value of thermal buoyancy parameter ${\lambda _1}$ and Forchheimer parameter F, the value of ${C_f}{\mathop {{\mathrm{Re}}}\nolimits } _x^{1/2}$ is getting increased. For other values of M, this exercise is repeated and presented in Table 3. Finally, we also notice from this table that linear regression estimate is more accurate for smaller value of parameter M

Table 3 Numerical computations for linear regression coefficients and error bound for ${C_f}{\mathop {{\mathrm{Re}}}\nolimits } _x^{1/2}$

For a lot of practical problems, the simple linear regression formula can be used to get an estimate of physical quantities up to some degree of accuracy. But if the focus is on getting more accurate results as compared to the linear regression, the quadratic regression analysis is performed. Therefore, a quadratic regression estimation has also been carried out for reduced Nusselt number Nur ($N{u_x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 1/2}$ is referred to as the reduced Nusselt number) which is presented in Table 4. The model for the estimated quadratic regression for reduced Nusselt number is given as:

$$\begin{aligned} \begin{array}{l} Nu{r_{\,est}} = Nur + S_1Nb+S_2Nt+S_3Ec +S_4N{b^2} +S_5N{t^2}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, +S_6E{c^2} + S_7NtNb + S_8EcNb + S_9EcNt, \end{array} \end{aligned}$$

(43)

where ${S_r}\,\left( {r = 1\,\,\,to\,\,9} \right)$ is the coefficient of quadratic regression corresponding to Nb, Nt and Ec. The expression for the maximum relative absolute error ${\varepsilon _{Nu}}$ is given as

$${\varepsilon _{Nu}} = \left| {\frac{{Nu{r_{\,\,\,est}} - Nur}}{{Nur}}} \right| .$$

(44)

The regression analysis has been achieved by considering different values of radiation parameter R. For a specific value of R (e.g., R= 0.6), the values of reduced Nusselt number (Nur) are calculated for 100 sets of values of the parameters Nb, Nt and Ec which are chosen arbitrarily from [0.1, 1.0]. This leads to correlation in the following form:

$$\begin{aligned} Nu{r_{\,est}}&= Nur + 0.0489Nb - 0.0640Nt - 2.3159Ec \nonumber \\&- 0.0130N{b^2} + 0.0114N{t^2}\nonumber \\&- 0.0390E{c^2} + 0.0010NtNb - 0.1317EcNb + 0.0814EcNt, \end{aligned}$$

(45)

with a maximum relative error about 0.25%.

Table 4 Numerical computations for quadratic regression coefficients and error bound for Nur

7 Results and discussion

In this section, the influence of various physical parameters, namely ratio parameter A, Casson parameter $\beta$, thermal buoyancy parameter $\lambda _1$, Forchheimer parameter F, concentration buoyancy parameter $\lambda _2$, Brownian motion parameter Nb, radiation parameter R, thermophoresis parameter Nt, Eckert number Ec, heat generation/absorption parameter $\gamma$, chemical reaction parameter $\sigma$, activation energy E, Brinkman number Br, diffusive variable L, temperature ratio variable $\alpha _1$ and concentration ratio variable $\alpha _2,$ on velocity $f'\left( \eta \right)$, temperature $\theta \left( \eta \right)$, concentration $\phi \left( \eta \right)$, entropy generation Ng, Bejan number Be, skin friction coefficient $\left( {{C_f}{\mathop {{\mathrm{Re}}}\nolimits } _x^{1/2}} \right)$, rate of heat transfer $\left( {N{u_x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 1/2}} \right)$ and rate of mass transfer $\left( {S{h_x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 1/2}} \right)$ is discussed and displayed graphically and in the tabular form.

7.1 Velocity profiles

The behavior of $f'\left( \eta \right)$ against different values of the parameters $A,\,\beta ,\,{\lambda _1},\,{\lambda _2}\,\,and\,\,F$ is shown in Figs. 2, 3, 4, 5 and 6. Figure 2 illustrates the effect of parameter A on velocity, and it is seen from this figure that $f'\left( \eta \right)$ increases with the rise in the value of parameter A. Since A is the ratio of free stream velocity to stretching velocity and when A is increased, it means retarding force reduces and therefore fluid velocity increases. Figure 3 represents that increment in the value of Casson parameter $\beta$ causes fluid velocity to decrease. Since the parameter $\beta$ is directly proportional to the plastic dynamic viscosity, increasing the values of $\beta$ means enhancing the dynamic viscosity of the fluid which provides greater resistance to the fluid flow; hence, a reduction in the fluid velocity is observed on increasing $\beta$. The behaviors of fluid velocity $f'\left( \eta \right)$ against thermal buoyancy parameter ${\lambda _1}$ and concentration buoyancy parameter ${\lambda _2}$ are demonstrated in Figs. 4 and 5, respectively. It is noticed from these two figures that there is an acceleration in fluid velocity $f'\left( \eta \right)$ when there is an increment in the parameters ${\lambda _1}$ and ${\lambda _2}$. We see that parameters ${\lambda _1}$ and ${\lambda _2}$ are directly proportional to Gr and $Gr^*,$ respectively. Now, since Gr signifies the ratio of thermal buoyancy force to viscous force and $Gr^*$ signifies the ratio of solutal buoyancy force to viscous force, an increase in either of Gr or $Gr^*$ will result in the enhancement of buoyancy force, which will ultimately increase the fluid velocity. Figure 6 is plotted to see the effect of inertia parameter F on $f'\left( \eta \right)$. It is observed from this figure that $f'\left( \eta \right)$ is getting reduced on increasing F. Since the inertia parameter also known as Forchheimer parameter F is the ratio of inertial liquid–solid interaction to viscous resistance, an increase in the value of inertia parameter F means a stronger inertial liquid–solid interaction which suggests a greater resistance to the fluid flow and therefore fluid velocity is getting decreased with increasing F.

Fig. 2

Graph of $f'\left( \eta \right)$ against A

Fig. 3

Graph of $f'\left( \eta \right)$ against $\beta$

Fig. 4

Graph of $f'\left( \eta \right)$ against $\lambda _1$

Fig. 5

Graph of $f'\left( \eta \right)$ against $\lambda _2$

Fig. 6

Graph of $f'\left( \eta \right)$ against F

7.2 Temperature profiles

Figures 7, 8, 9, 10, 11, 12 and 13 present the influence of parameters $\,M,\,Ec,\,\,Nt,\,\,Nb,\,\,R\,\,\mathrm{{and}}\,\,\gamma$ on fluid temperature $\theta \left( \eta \right)$. The effect of parameter M on $\theta \left( \eta \right)$ is shown in Fig. 7. It is seen from this figure that $\theta \left( \eta \right)$ is getting increased with increasing M. Since externally applied magnetic field is responsible for increase in dissipation of energy generated by Lorentz force, an increment in magnetic parameter results in increased fluid temperature. In Fig. 8, behavior of fluid temperature for increasing values of Eckert number Ec is shown. As per this figure, temperature of the fluid is increasing with rising value of Ec. Since Ec presents the ratio of kinetic energy and enthalpy, consequently, an increase in Ec means the dissipative heat is stored in the liquid via frictional heating, which increases the fluid temperature $\theta \left( \eta \right)$. Figures 9 and 10 are plotted to understand the behavior of fluid temperature against the parameters Nt and Nb, respectively. Figure 9 shows that $\theta \left( \eta \right)$ gets increased with the increment in the values of Nt. Thermophoresis is a phenomenon where small particles diffuse under the effect of temperature gradient. An increase in the value of thermophoretic parameter sets the nanoparticle in motion, and thus on the hotter side, the momentum of nanoparticles rises. Due to the rise in the momentum, nanoparticles transfer their kinetic energy in the direction of cooler side, and thus, region gets warmed up quickly; i.e., temperature of fluid is increased. Furthermore, Fig. 10 also suggests that the nanofluid temperature $\theta$ rises with increasing value of Nb. The temperature is behaving this way because of the fact that Brownian motion is the chaotic motion of nanoscale particles in the regular fluid. Consequently, for larger value of Nb, the intensity of this chaotic motion leads to increment in the kinetic energy of the nanoscale particles and hence temperature of the fluid is increasing. In Fig. 11, temperature distribution is shown for various values of radiation parameter R and it is noticed that $\theta \left( \eta \right)$ is getting increased with increasing R. This is due to the reason that the fluid absorbs more heat when the value of R is enhanced, due to which temperature of nanofluid is increased. Figures 12 and 13 represent the effect of $\gamma$ on $\theta \left( \eta \right)$. From these two figures, it is observed that fluid temperature rises when heat generation variable is increased $\left( {\gamma > 0} \right)$. Since comparatively more heat is generated in the system for increasing values of $\left( {\gamma > 0} \right)$ , there is an increment in the fluid temperature while the temperature falls with an increase in heat absorption variable $\left( {\gamma < 0} \right)$.

Fig. 7

Graph of $\theta \left( \eta \right)$ against M

Fig. 8

Graph of $\theta \left( \eta \right)$ against Ec

Fig. 9

Graph of $\theta \left( \eta \right)$ against Nt

Fig. 10

Graph of $\theta \left( \eta \right)$ against Nb

Fig. 11

Graph of $\theta \left( \eta \right)$ against R

Fig. 12

Graph of $\theta \left( \eta \right)$ against $\gamma <0$

Fig. 13

Graph of $\theta \left( \eta \right)$ against $\gamma >0$

7.3 Concentration profiles

To understand the behavior of $\phi \left( \eta \right)$ against the variations in the parameters: $Nt,\,Nb,\,E$ and $\sigma$, the graphs of $\phi \left( \eta \right)$ are presented in Figs. 14, 15, 16 and 17. Figures 14 and 15 are sketched to show the behavior of $\phi \left( \eta \right)$ when Nt and Nb are varied. Here, $\phi \left( \eta \right)$ is getting enhanced with increasing Nt while an opposite effect is noticed with increasing Nb. Physically, because of the thermophoretic force, there is a migration of nanoscale particles from hotter region, due to which $\phi \left( \eta \right)$ is increased. Further, the Brownian diffusion rate is proportional to Nb and so there is a reduction in $\phi \left( \eta \right)$ when Nb is increased. Figure 16 is presented to visualize the behavior of concentration profile $\phi \left( \eta \right)$ against the variation in activation energy parameter E. It is perceived from this figure that $\phi \left( \eta \right)$ decreases with increasing value of E. This occurrence can be justified with the fact that higher activation energy E tends to increase the modified Arrhenius function ${\left( {\frac{T}{{{T_\infty }}}} \right) ^m}\exp \left( {\frac{{ - {E_a}}}{{\mathrm{K}T}}} \right) ,$ which ultimately stimulates the chemical reaction. This results in the consumption of species with a better rate, and consequently the concentration is decreased. In Fig. 17, the relationship between $\phi \left( \eta \right)$ and chemical reaction parameter $\sigma$ is presented. From this figure, it is observed that increasing the value of $\sigma$ causes $\phi \left( \eta \right)$ to increase. That is, consumption of reactive species is improved for higher $\sigma$.

Fig. 14

Graph of $\phi \left( \eta \right)$ against Nt

Fig. 15

Graph of $\phi \left( \eta \right)$ against Nb

Fig. 16

Graph of $\phi \left( \eta \right)$ against E

Fig. 17

Graph of $\phi \left( \eta \right)$ against $\sigma$

7.4 Entropy generation and Bejan number

Figures 18, 19, 20, 21, 22, 23, 24, 25, 26 and 27 are portrayed to display the behavior of parameters $\beta ,\,Br,\,L,\,{\alpha _1}\,and\,{\alpha _2}$ on entropy generation $Ng\left( \eta \right)$ and Bejan number Be. Figures 18 and 19 are plotted to analyzed the effect of $\beta$ on $Ng\left( \eta \right)$ and Be . It is apparent from Fig. 18 that $Ng\left( \eta \right)$ decreases for larger values of $\beta$. Since an increase in the value of $\beta$ causes faster shearing of the liquid along the surface, the entropy generation is reducing. From Fig. 19, it is found that Bejan number Be increases with increasing $\beta$. Since the rate of entropy generation decreases when Casson parameter increases, Bejan number increases. The variation in $Ng\left( \eta \right)$ and Be against the Brinkman number Br is been plotted in Figs. 20 and 21, respectively. It is inferred from Fig. 20 that $Ng\left( \eta \right)$ is getting increased with increasing value of Br. Since Br presents the ratio of release of heat by viscous heating to heat transfer by molecular conduction. Therefore, more heat is generated in the system for increasing values of Br, and therefore, there is a rise in the disorderliness of the entire system, which subsequently increases the entropy of the system. Moreover, as per Fig. 21, we see that the Bejan number Be is getting reduced with increasing values of Br. Figures 22 and 23 depict the influence of diffusive variable L on $Ng\left( \eta \right)$ and Be, respectively. Both the figures show that $Ng\left( \eta \right)$ and Be both are getting increased with increasing value of L. For larger values of L, diffusivity in the fluid particle is enhanced, which results in the increase in disorderliness. Therefore, with a rise in the value of diffusive variable, there is an increment in the entropy generation. Figure 23 depicts that Be is increasing when L is increased. Figures 24 and 25 are portrayed to display the behavior of $Ng\left( \eta \right)$ and Be against the variation in the temperature ratio parameter $\alpha _1$ on $Ng\left( \eta \right)$ and Be, respectively. The higher the difference in temperature, the more will be disorderliness in the system. It results in a rise of entropy generation. For larger values of $\alpha _1$, the thermal irreversibilities dominate over the fluid friction and viscous diffusion irreversibilities. Therefore, Bejan number Be is increased. Influence of $\alpha _2$ on $Ng\left( \eta \right)$ and Be is shown in Figs. 26 and 27, respectively. It is evident from these two figures that both $Ng\left( \eta \right)$ and Be get enhanced for larger values of concentration ratio variable $\alpha _2$.

Fig. 18

Graph of Be against $\beta$

Fig. 19

Graph of Ng against $\beta$

Fig. 20

Graph of Ng against Br

Fig. 21

Graph of Be against Br

Fig. 22

Graph of Ng against L

Fig. 23

Graph of Be against L

Fig. 24

Graph of Ng against $\alpha _1$

Fig. 25

Graph of Be against $\alpha _1$

Fig. 26

Graph of Ng against $\alpha _2$

Fig. 27

Graph of Be against $\alpha _2$

7.5 Quantities of physical interest

Tables 5, 6 and 7 are prepared to discuss the changes in skin friction coefficient, rate of heat transfer and rate of mass transfer against the parameters $\beta ,\,M,\,F,\,A,\,{\lambda _1},\,{\lambda _2},\,{\lambda _3},\,E,\,Ec,\,Nt,\,Nb,\,\gamma ,\,Sc,\,\sigma \,and\,{\theta _w}$. From Table 5, it is observed that the skin friction coefficient is enhanced for the larger values of the parameters $\beta ,\,F,\,{\lambda _3},\,and\,E$ while completely opposite trend is seen for parameters $M,\,A,\,{\lambda _1}\,and\,{\lambda _2}$. Rate of heat transfer gets enhanced with rising values of the flow parameters $Ec,\,Nt,\,Nb\,and\,\gamma ,$ whereas this physical quantity is getting reduced with the progress of E. Rate of mass transfer is getting lowered with the increment in the value of the parameters $Sc,\,Nb\,and\,E$ while opposite pattern is perceived for $Nt,\,\sigma \,and\,{\theta _w}$.

Table 5 Variation in skin friction coefficient

Table 6 Variation in Nusselt number

Table 7 Variation in Sherwood number

8 Conclusions

Our aim in carrying out this research work is to investigate the features of entropy generation on two-dimensional hydromagnetic stagnation point flow of Casson nanofluid with binary chemical reaction stimulated by activation energy. Noteworthy outcomes of the current study are summarized as follows:

• 1. Fluid velocity is getting accelerated with increasing either of thermal buoyancy parameter, ratio parameter or concentration buoyancy parameter while increase in Forchheimer parameter tends to decelerate the fluid velocity because of a stronger inertial liquid–solid interaction which provides a greater resistance to the flow.

• 2. As a result of passive control of nanoparticles at the stretching surface, the non-dimensional concentration of nanoparticles has a negative value at the surface. A negative value of non-dimensional concentration of nanoparticles means that concentration of nanoparticles on the surface of sheet is lesser than the value of concentration outside the boundary layer i.e., lower than that in free stream.

• 3. Entropy generation is perceived to rise with increasing diffusive variable, Brinkman number and concentration ratio variable, whereas the Brownian diffusion parameter has an adverse effect on this physical quantity.

• 4. Rate of heat transfer decreases with increase in activation energy while reverse trend is seen for Brownian motion parameter and thermophoresis parameter. Rate of mass transfer gets improved with rise in the values of chemical reaction parameter, whereas Brownian motion parameter and activation energy have an adverse effect on this physical quantity.