Entropy generation on double diffusive MHD Casson nanofluid flow with convective heat transfer and activation energy

Abstract

The viscous and Joule dissipation effects on stagnation point flow of thermally radiating Casson nanoliquid over a convectively heated stretching sheet under hydromagnetic assumptions are discussed. The influence of heat absorption on heat transfer and chemical reaction prompted by activation energy on mass transfer is also considered. The appropriate transformations are implemented for converting the governing partial differential equations into a set of coupled ordinary differential equations. BVP4C routine of MATLAB has been used to solve the coupled nonlinear ODEs. The way fluid velocity, concentration, temperature, Bejan number and entropy generation behave subject to change in the flow parameters, has been discussed through graphs, whereas the important physical quantities such as skin friction coefficient, Nusselt number and Sherwood number are analyzed on the basis of numerical values presented in tables. On the obtained numerical data of Nusselt number, linear and quadratic regression analyses have been performed. It is concluded that for larger values of thermal and concentration buoyancy parameters, fluid velocity tends to decrease inside the boundary layer region. It is also found that plastic dynamic viscosity of Casson nanoliquid tends to reduce the rate of entropy generation.

1 Introduction

In the recent past, nanofluids, which are liquids containing colloidal suspension of nanoparticles, are found to have significantly greater thermal conductivity than expected from the effective medium theories. A small fraction of nanoparticles, when diffused homogeneously in the base fluid, can result in remarkable enhancement in the thermal properties of fluids. This makes nanofluids very attractive as heat transfer fluids in many applications. Thus, the nanofluid technology is proving to be worthy of an investigation in order to alleviate the heat consumption. Choi [1] is believed to be the first person who popularized the term nanofluid in his pioneering work. A concrete study of convective transport of nanofluid is done by Buongiorno [2]. Nanofluids can be used as coolants in the electronics and automobile industries. The use of nanofluids for heat transfer in solar heat exchangers was shown by Farshad et al. [3].

The researchers at MIT, Kim et al. [4] carried out a research study to consider the feasibility of nanofluids in nuclear applications by enhancing the performance of any water-cooled nuclear system that is heat removal limited. Possible applications include pressurized water reactor (PWR) primary coolant, standby safety systems, accelerator targets and plasma divertors. In a pressurized water reactor nuclear power plant system, the limiting process of the heat generation is critical heat flux between the fuel rods and the water, when vapor bubbles that end up covering the surface of the fuel rods conduct very little heat as opposed to liquid water [5]. Using nanofluids instead of water, the fuel rods become coated with nanoparticles such as alumina, which actually pushes newly formed bubbles away, preventing the formation of a layer of vapor around the rod and subsequently increasing the critical heat flux significantly. Some of the investigations in this context are due to Gorla et al. [6], Reddy et al. [7], Chamkha et al. [8] and Reddy et al. [9].

The magnetohydrodynamic flows over plane surfaces are observed in a lot of scientific and industrial processes. Furthermore, the flow of liquid metals under the effect of magnetic field has several applications such as the continuous casting of steel and the crystal growth, in the manufacture of microstructures in three dimensions, etc. Keeping in mind the significance of such an analysis, Takhar et al. [10] discussed the magnetohydrodynamic flow of viscous fluid over a moving plate, taking Hall effect into account. Magyari and Chamkha [11] investigated the laminar thermo-solutal boundary layer flow of electrically conducting fluid under hydromagnetic assumptions. Some important studies on MHD flows have been carried out by Seth et al. [12], Chamkha [13, 14], Takhar et al. [15], Chamkha and Khaled [16], Al-Mudhaf and Chamkha [17] and Kumar et al. [18].

The phenomena of fluid flows induced by stretching/moving surfaces have been observed in many practical situations such as manufacturing of plastic sheets, wrapping and shrinking of the boundary layers along material handling conveyers, extrusion of sheet, cooling of metallic sheets, polymer sheets and filaments, etc. Influenced by the wide occurrence of fluid motion over stretching surfaces, Elbashbeshy and Bazid [19] in their research article, scrutinized the two-dimensional flow in the vicinity of stretching surface. Nazar et al. [20] used the Keller-box technique to analyze the 2-D stagnation point flow induced by a stretching sheet. Reddy and Chamkha [21] carried out a study dealing with the nanofluid flow over a stretching sheet within the porous medium.

It has been observed that few non-Newtonian liquids act like elastic solid, i.e., they cease to flow, until the application of a threshold shear stress, known as yield stress. Casson fluid falls into the category of such fluids. Therefore, only when the intensity of applied shear stress exceeds the yield stress, Casson fluid starts flowing. In view of significance of Casson fluid, Damseh et al. [22] inspected the influence of chemical reaction and heat generation/absorption on the flow of micropolar fluid due to a stretching surface. Raju and Sandeep [23] scrutinized the unsteady flow of Casson nanofluid with CoFe$_2$O$_4$ as nanoparticles, flowing over a cone in a rotating medium. Ullah et al. [24] scrutinized the two-dimensional hydromagnetic flow of Casson fluid past an elongating surface, at which the velocity slip was allowed to take place. Some of the other important research works on the flow of non-Newtonian fluid under various conditions are due to research works carried out in the literature [25,26,27,28,29,30,31].

As per the second law of thermodynamics, entropy generation is connected with thermodynamical irreversibility. As per this law, the total entropy of the system tends to increase during an irreversible process. When a viscous fluid with dissolved solute flows over a heated sheet, it undergoes some irreversible processes such as thermal radiation, occurrence of friction within fluid layers, and chemical reaction. Therefore, total entropy of the system is bound to increase. To enhance the efficiency of some technological systems such as fuel cells, helical coils, air-separators electro-chemicals, microchannels, etc., entropy generation needs to be minimized. Bejan [32] was the first person who analyzed the production of entropy and irreversibility and introduced the rate of entropy generation. Rashidi et al. [33] presented an entropy generation analysis on 2-D nanofluid flow past a permeable rotating disc where the flow domain is permeated by an invariable magnetic field. Ellahi et al. [34] used the homotopy analysis method (HAM) to study the entropy generation analysis on the hydromagnetic flow of power law fluid between two horizontal parallel plates. Kumar et al. [35] presented a theoretical study dealing with the entropy generation as well as regression analysis for the stagnation point flow of Casson nanofluid over a linearly stretching sheet in the magnetic field environment. They concluded that rate of entropy generation increases on increasing Brinkman number, while the increase in Brownian diffusion tends to slow down the entropy generation. Some of the studies in this context are due to Rashidi et al. [36], Zeeshan et al. [37], Khan et al. [38] etc.

The species dispersion by means of chemical reaction has been observed in various industrial processes such as air and water pollution processes, food processing, and recovery of thermal oil. Catalysts are resources which accelerate the rate of reactions by enabling another pathway for the making and/or breaking of chemical bonds. The crucial part in this alternative arrangement is a lower activation energy than that needed for the non-catalyzed reaction. The activation energy is that minimum energy which must be supplied to the molecules to react chemically, and this term activation energy was suggested by Svante Arrhenius, a Swedish Engineer in 1889. A lot of basic and applied researches have been carried out by industrial companies and university research laboratories to find out how the activation energy can be lowered and vice versa, i.e., to find out the effect of activation energy on the concentration of reacting species. Also, there are various biological applications that include magnetic nanofluid such as hyperthermia treatment, and targeted drug delivery. Based on specific applications, there are distinct chemical reaction and syntheses developed for different types of magnetic nanofluids, which can change the properties of nanofluids depending on the particular application. In light of these applications, Mustafa et al. [39] investigated the mixed convective nanofluid flow induced by a stretching surface, considering the binary chemical reaction stimulated by activation energy. They concluded that the species concentration of dissolved solute is getting increased as the activation energy is increased. Khan et al. [40] studied the influence of chemical reaction stimulated by activation energy, on stagnation point cross flow of nanofluid under hydromagnetic assumptions. Hamid et al. [41] in their article, presented the analysis on the hydromagnetic flow of Williamson nanofluid, where the fluid flow was induced by horizontal circular stretching cylinder, with the consideration of chemical reaction along with the activation energy. Dhlamini et al. [42] incorporated the spectral quasilinearization technique to discuss the chemical reaction effects under the influence of activation energy on transient one-dimensional nanofluid flow over a flat plate.

The current research work is carried out to analyze the consequences of convective heating, viscous and Joule dissipation effects on two-dimensional hydromagnetic stagnation point flow of Casson nanofluid over a stretching sheet, considering the effect of chemical reaction under the influence of activation energy, which has not been explored by researchers in the past. In addition, we have also considered the fluid to be thermally radiating. If the activation energy can be lowered, it may be possible to lower the working pressure and/or temperature at which the chemical process takes place and thus we can save fuel which is one of the most important expenses in a large-scale chemical process. Thus analysis of non-Newtonian nanofluid flow considering chemical reaction stimulated by activation energy is one of the prominent research fields for industries dealing with large-scale chemical reaction. Entropy generation for the flow problem is also discussed.

2 Formulation of the problem

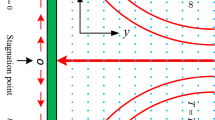
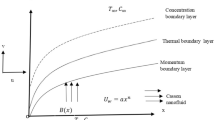
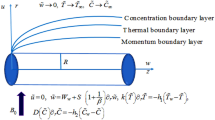
Consider the two-dimensional hydromagnetic mixed convective stagnation point flow of a binary Casson nanoliquid with dissolved solutes and suspended nanoparticles, over a horizontal stretching sheet. The liquid is considered electrically conducting and a magnetic field of fixed magnitude $B_0$ is permeating through the flow region. Considering the flow situation for small magnetic Reynolds number, the effect of induced magnetic field has been neglected. The Cartesian system (x, y, z) is chosen to represent the flow configuration as shown in Fig. 1. The vertical sheet is lying on the $x-$axis and is being stretched by applying identical forces given by $u= cx$ ($c>0$) at the ends of sheet. The fluid flow is confined in the region $y\ge 0$ where y-axis is taken in the direction perpendicular to the stretching sheet. At the surface of the sheet, convective heating is considered with heat transfer coefficient $h_1$. Moreover, free stream temperature is denoted by $T_{\infty }$ and the concentration in the ambient fluid is taken as $C_{\infty }$. It is also assumed that a binary chemical reaction among the species takes place with a constant rate $K_{\mathrm{a}}$, which is stimulated by Arrhenius activation energy.

The rheological equation of Casson fluid [43] is given as:

$$\begin{aligned} \tau _{ij} = \left\{ \begin{array}{l} 2\left( {{\mu _{\mathrm{B}}} + \frac{{{\tau _y}}}{{\sqrt{2\Pi } }}} \right) {\varepsilon _{ij}},\,\,\,\,\,\,\Pi > {\Pi _{\mathrm{c}}}\\ 2\left( {{\mu _{\mathrm{B}}} + \frac{{{\tau _y}}}{{\sqrt{2{\Pi _{\mathrm{c}}}} }}} \right) {\varepsilon _{ij}},\,\,\,\,\Pi < {\Pi _{\mathrm{c}}} \end{array} \right. \end{aligned}$$

(1)

In the above expression, ${\mu _{\mathrm{B}}}$ represents the plastic dynamic viscosity of the Casson fluid, ${\varepsilon _{ij}}$ and ${\tau _{ij}}$ are (i, j)th component of deformation rate and stress tensor, respectively, $\Pi$ is the product of the component of deformation rate with itself, $\Pi _{\mathrm{c}}$ is a critical value of this product, and ${\tau _{y}}$ indicates the yield stress of fluid.

Fig. 1

Geometry of the problem

The governing equations [44, 45] for the stagnation point flow of Casson nanoliquid under above-mentioned assumptions are given as:

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, \end{aligned}$$

(2)

$$\begin{aligned}&\left. {\begin{array}{*{20}{l}} {u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} = \upsilon \left( {1 + \frac{1}{\beta }} \right) \frac{{{\partial ^2}u}}{{\partial {y^2}}} + {u_e}\frac{{\mathrm{d}{u_e}}}{{\mathrm{d}x}} + \frac{{{\sigma ^*}}}{\rho }B_0^2\left( {{u_e} - u} \right) }\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+ g\left( {{\beta _{\mathrm{T}}}\left( {T - {T_\infty }} \right) + {\beta _C}\left( {C - {C_\infty }} \right) } \right) \end{array}} \right\} \end{aligned}$$

(3)

$$\begin{aligned}&\left. \begin{array}{l} u\frac{{\partial T}}{{\partial x}} + v\frac{{\partial T}}{{\partial y}} = \alpha \frac{{{\partial ^2}T}}{{\partial {y^2}}} + \frac{\mu }{{{{\left( {\rho {c_p}} \right) }_f}}}\left( {1 + \frac{1}{\beta }} \right) {\left( {\frac{{\partial u}}{{\partial y}}} \right) ^2} + \frac{{16{\sigma ^*}T_\infty ^3}}{{3{k^*}{{\left( {\rho {c_p}} \right) }_f}}}\frac{{{\partial ^2}T}}{{\partial {y^2}}} + \frac{{\sigma B_0^2}}{{{{\left( {\rho {c_p}} \right) }_f}}}{(u-u_e)^2}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{{Q_0}}}{{{{\left( {\rho {c_p}} \right) }_f}}}\left( {T - {T_\infty }} \right) + \tau \left( {{D_{\mathrm{B}}}\frac{{\partial C}}{{\partial y}}\frac{{\partial T}}{{\partial y}} + \frac{{{D_{\mathrm{T}}}}}{{{T_\infty }}}{{\left( {\frac{{\partial T}}{{\partial y}}} \right) }^2}} \right) , \end{array} \right\} \end{aligned}$$

(4)

$$\begin{aligned}&u\frac{{\partial C}}{{\partial x}} + v\frac{{\partial C}}{{\partial y}} = {D_{\mathrm{B}}}\frac{{{\partial ^2}C}}{{\partial {y^2}}} + \frac{{{D_{\mathrm{T}}}}}{{{T_\infty }}}\frac{{{\partial ^2}T}}{{\partial {y^2}}} - k_{\mathrm{r}}^2{\left( {\frac{T}{{{T_\infty }}}} \right) ^m}\exp \left( {\frac{{ - {E_{\mathrm{a}}}}}{{{K^*}T}}} \right) \left( {C - {C_\infty }} \right) . \end{aligned}$$

(5)

The conditions at the boundary are given as

$$\begin{aligned} \begin{array}{l} u = {u_w} = cx,\quad \,v = 0,\quad \, - {k_1}\frac{{\partial T}}{{\partial y}} = {h_1}\left( {{T_f} - T} \right) ,\quad \, - {k_2}\frac{{\partial C}}{{\partial y}} = {h_2}\left( {{C_f} - C} \right) \,\,\,{\mathrm{at}}\,\,\,\,y = 0,\\ u = {u_e} = bx,\quad \,T = {T_\infty },\quad C = {C_\infty }\,\,\,{\mathrm{as}}\,\,y \rightarrow \infty , \end{array} \end{aligned}$$

(6)

where $\rho$ is the fluid density, $\sigma ^*$ represents the electrical conductivity, $\upsilon$ stands for the kinematic viscosity, $\beta$ is the Casson fluid parameter, ${u_e}$ is the free stream velocity, $B_0$ denotes the magnetic field strength, $\alpha$ is the thermal diffusivity, g is the gravitational acceleration, $\alpha = \frac{k}{{{{\left( {\rho c_p^{}} \right) }_f}}}$ is the thermal diffusivity, T specifies the temperature, $T_{\infty }$ represents the ambient temperature, $\beta _{\mathrm{T}}$ indicates the coefficient of thermal expansion, $\beta _C$ stands for the concentration expansion coefficient, $\left( {{h_1},\,{h_2}} \right)$ are heat and mass transfer coefficients, respectively, C is the species concentration, $C_{\infty }$ is the ambient species concentration, $\tau = \frac{{{{\left( {\rho {c_p}} \right) }_s}}}{{{{\left( {\rho {c_p}} \right) }_f}}}$ denotes ratio between the effective nanoparticle material heat capacity and the base fluid heat capacity, $\mu$ denotes the dynamic fluid viscosity, $K^*$ indicates the Boltzmann constant, $D_{\mathrm{B}}$ is the Brownian diffusion coefficient, $D_{\mathrm{T}}$ is the thermophoresis diffusion coefficient, $E_{\mathrm{a}}$ represents the activation energy, m is the fitted rate constant, $k_{\mathrm{r}}$ symbolizes the reaction rate and $u_w$ implies the stretching velocity.

The flow phenomenon which is characterized in mathematical form can be handled in an easier way by transforming the nonlinear PDEs (2)–(5) into nonlinear ODEs. This job is done by using the following similarity transformations:

$$\begin{aligned}&\eta = \sqrt{\frac{c}{\upsilon }} y,\quad \,u = cxf'\left( \eta \right) ,\quad v = - \sqrt{c\nu } f\left( \eta \right) ,\,\,\nonumber \\&\theta \left( \eta \right) = \frac{{T - {T_\infty }}}{{{T_f} - {T_\infty }}} \quad \text{and} \quad \phi \left( \eta \right) = \frac{{C - {C_\infty }}}{{{C_f} - {C_\infty }}}. \end{aligned}$$

(7)

By employing (7), the governing fluid flow Eqs. (3)–(5) are metamorphosed into the following system of coupled nonlinear ODEs:

$$\begin{aligned}&\left( {1 + \frac{1}{\beta }} \right) f''' + M\left( {A - f'} \right) - {f^{\prime 2}} + ff'' + A^2+ {\lambda _1}\theta + {\lambda _2}\phi = 0, \end{aligned}$$

(8)

$$\begin{aligned}&\frac{{\left( {1 + R} \right) }}{{\Pr }}\theta '' + \text{Nb}\theta '\phi ' + \text{Nt}{\theta ^{\prime 2}} + f\theta ' + Q\theta + EcM{f^{\prime 2}}\nonumber \\&\quad + \left( {1 + \frac{1}{\beta }} \right) \text{Ec}{f^{\prime \prime 2}} = 0, \end{aligned}$$

(9)

$$\begin{aligned}&\frac{1}{{\text{Sc}}}\phi '' + f\phi ' + \frac{{\text{Nt}}}{{ScNb}}\theta '' - \sigma {\left( {1 + \theta {\theta _w}} \right) ^m}\exp \left( {\frac{{ - E}}{{1 + \theta {\theta _w}}}} \right) \phi = 0. \end{aligned}$$

(10)

The transformed conditions at the boundary are as follows:

$$\begin{aligned} \left. \begin{array}{l} f'\left( 0 \right) = 1,\,\,f'\left( \infty \right) = A,\,\,f\left( 0 \right) = 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\ \,\theta '\left( 0 \right) = - \text{Bi}_{1}\left( {1 - \theta \left( 0 \right) } \right) ,\,\,\,\,\theta \left( \infty \right) = 0,\,\,\,\,\,\,\,\\ \phi '\left( 0 \right) = - \text{Bi}_{2}\left( {1 - \phi \left( 0 \right) } \right) = 0,\;\;\phi \left( \infty \right) = 0, \end{array} \right\} \end{aligned}$$

(11)

where $A = \frac{b}{c}$ stands for the stretching parameter,$\,\,{\lambda _1} = \frac{{\mathrm{Gr}}}{{{\mathop {{\mathrm{Re}}}\nolimits } _x^2}}$ represents the thermal buoyancy parameter, $\text{Gr} = \frac{{g{\beta _{\mathrm{T}}}{x^3}\left( {{T_f} - {T_\infty }} \right) }}{{{\upsilon ^2}}}$ indicates the thermal Grashof number, ${\lambda _2} = \frac{{G{r^ * }}}{{{\mathop {{\mathrm{Re}}}\nolimits } _x^2}}$ denotes the concentration buoyancy parameter, $G{r^ * } = \frac{{g{\beta _C}{x^3}\left( {{C_f} - {C_\infty }} \right) }}{{{\upsilon ^2}}}$ is the solutal Grashof number, ${{\mathop {{\mathrm{Re}}}\nolimits } _x} = \frac{{{u_e}x}}{\nu }$ is the local Reynolds number, $\,M = \frac{{{\sigma ^*}B_0^2}}{{\rho c}}$ denotes the magnetic parameter, $\nu = \frac{\mu }{\rho }$ is the kinematic diffusivity, k is the thermal conductivity, $\mathrm{Bi}_{1} = \frac{{{h_1}}}{{{k_1}}}\sqrt{\frac{\nu }{c}}$ is the thermal Biot number, $\text{Bi}_{2} = \frac{{{h_2}}}{{{k_2}}}\sqrt{\frac{\nu }{c}}$ is the solutal Biot number, $\Pr = \frac{\nu }{\alpha }$ is the Prandtl number, $R = \frac{{16{\sigma ^ * }T_\infty ^3}}{{3k{k^ * }}}$ is radiative parameter, $\text{Nt} = \frac{{{D_{\mathrm{T}}}\tau \left( {{T_f} - {T_\infty }} \right) }}{{\upsilon {T_\infty }}}$ indicates the thermophoresis parameter, $\text{Nb} = \frac{{{D_{\mathrm{B}}}\tau \left( {{C_f} - {C_\infty }} \right) }}{\upsilon }$ represents the Brownian motion variable, $Q = {{{{Q_0}}/ {\left( {\rho {c_p}} \right) }}_f}c$ is the heat generation parameter, $\text{Ec} = \frac{{u_e^2}}{{{c_f}\left( {{T_f} - {T_\infty }} \right) }}$ represents the Eckert number, $\sigma$ is the chemical reaction parameter, ${\theta _w} = \frac{{\left( {{T_f} - {T_\infty }} \right) }}{{{T_\infty }}}$ denotes the temperature difference, $\text{Sc} = \frac{\nu }{{{D_{\mathrm{B}}}}}$ stands for the Schmidt number and $E = \frac{{{E_{\mathrm{a}}}}}{{{K^*}{T_\infty }}}$ specifies the non-dimensional activation energy.

3 Quantities of physical interest

From practical and engineering point of view, the quantity of physical interest, viz. skin friction coefficient, Nusselt Number and Sherwood Number, are presented as follows:

$$\begin{aligned} {C_f}= {} \frac{1}{{\rho u_w^2}}\left( {{\mu _{\mathrm{B}}} + \frac{{{P_y}}}{{\sqrt{2\pi } }}} \right) {\left. {\frac{{\partial u}}{{\partial y}}} \right| _{y = 0}}, \end{aligned}$$

(12)

$$\begin{aligned} \text{Nu}_{x}= {} \frac{{{q_w}x}}{{k\left( {{T_f} - {T_\infty }} \right) }}, \end{aligned}$$

(13)

$$\begin{aligned} \text{Sh}_{x}= {} \frac{{{J_w}x}}{{{D_{\mathrm{B}}}\left( {{C_f} - {C_\infty }} \right) }}, \end{aligned}$$

(14)

where ${q_w} = - \left( {k + \frac{{16{\sigma _1}T_\infty ^3}}{{3{k^*}{{\left( {\rho {c_p}} \right) }_f}}}} \right) {\left. {\frac{{\partial T}}{{\partial y}}} \right| _{y = 0}}$ and ${J_w} = - {D_{\mathrm{B}}}{\left. {\frac{{\partial C}}{{\partial y}}} \right| _{y = 0}}$ are heat and mass fluxes, respectively.

Equations (12) to (14) in the non-dimensional form are given as follows:

$$\begin{aligned} {C_f}{\mathop {{\mathrm{Re}}}\nolimits } _x^{1/2} = \left( {1 + \frac{1}{\beta }} \right) f''\left( 0 \right) ,\,\, \text{Nu}_{x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 1/2} = - \left( {1 + R} \right) \theta '\left( 0 \right) ,\,\, \text{Sh}_{x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 1/2} = - \phi '\left( 0 \right) , \end{aligned}$$

(15)

where ${{\mathop {{\mathrm{Re}}}\nolimits } _x} = \frac{{{u_w}x}}{\nu }$ is the local Reynolds number.

4 Entropy generation analysis

Expression of the entropy generation [46] for the non-Newtonian fluid (Casson nanofluid) in the dimensional form is given as

$$\begin{aligned} \left. \begin{array}{l} {S_G} = \underbrace{\frac{k}{{T_\infty ^2}}{{\left( {\frac{{\partial T}}{{\partial y}}} \right) }^2}\left( {1 + \frac{{16{\sigma ^*}T_\infty ^3}}{{3k{k^*}}}} \right) }_{{\mathrm{thermal}}\,\,{\mathrm{irreversibility}}} + \underbrace{\frac{{{\sigma ^*}B_0^2}}{{{T_\infty }}}{(u_e-u)^2}}_{\begin{array}{c} \scriptstyle {\mathrm{Joule \,\, heating }}\\ \scriptstyle {\mathrm{irreversibility}} \end{array}} + \underbrace{\frac{{RD}}{{{T_\infty }}}\left( {\frac{{\partial T}}{{\partial x}}\frac{{\partial C}}{{\partial x}} + \frac{{\partial C}}{{\partial y}}\frac{{\partial T}}{{\partial y}}} \right) + \frac{{RD}}{{{C_\infty }}}{{\left( {\frac{{\partial C}}{{\partial y}}} \right) }^2}}_{{\mathrm{concentration\,\,irreversibility}}}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \,\underbrace{\left( {1 + \frac{1}{\beta }} \right) \frac{\mu }{{{T_\infty }}}{{\left( {\frac{{\partial u}}{{\partial y}}} \right) }^2}}_{{\mathrm{fluid\,\, friction\,\, irreversibility}}}. \end{array} \right\} \end{aligned}$$

(16)

The above expression shows that there are mainly four sources of entropy generation. The first source (1st term in RHS) is the thermal irreversibility due to thermal radiation and heat transfer, while the second term is the irreversibility due to interaction of magnetic field with moving fluid (Joule heating), third and fourth terms present irreversibilities due to diffusion of species and viscous dissipation respectively.

Using (7), dimensional equation (16) gets converted into following dimensionless form:

$$\begin{aligned} {N_g} = {\alpha _1}\left( {1 + R} \right) {\theta ^{\prime 2}} + \text{Br}\left( {1 + \frac{1}{\beta }} \right) {f^{\prime \prime 2}} + \text{Br}M{f^{\prime 2}} + L\left( {\frac{{{\alpha _2}}}{{{\alpha _1}}}{{\phi }^{\prime 2}} + \phi '\theta '} \right) , \end{aligned}$$

(17)

where ${N_G} = \frac{{{S_G}{T_\infty }\upsilon }}{{ak\Delta T}}$ represents the entropy generation rate, $\,\,{\alpha _1} = \frac{{\left( {{T_f} - {T_\infty }} \right) }}{{{T_\infty }}}$ is the dimensionless temperature ratio variable, $\text{Br} = \frac{{\mu {a^2}{x^2}}}{{k\Delta T}}$ is the Brinkman number, $L = \frac{{RD\left( {{C_f} - {C_\infty }} \right) }}{k}$ is the diffusive variable and ${\alpha _2} = \frac{{\left( {{C_f} - {C_\infty }} \right) }}{{{C_\infty }}}$ is the dimensionless concentration ratio variable.

Further, to get an understanding of relative importance of entropy generation caused by heat transfer irreversibility, Bejan number is defined which is given as

$$\begin{aligned} \text{Be} = \frac{{{\mathrm{Entropy}}\,{\mathrm{generation}}\,{\mathrm{due}}\,{\mathrm{to}}\,{\mathrm{heat}} \,{\mathrm{and}}\,{\mathrm{mass}}\,{\mathrm{transfer}}}}{{{\mathrm{Total}}\,{\mathrm{entropy}}\, {\mathrm{generation}}}} \end{aligned}$$

(18)

In mathematical terms, it is given by:

$$\begin{aligned} \text{Be} = \frac{{{\alpha _1}\left( {1 + R} \right) {{\theta }^{\prime 2}}}}{{{\alpha _1}\left( {1 + R} \right) {{\theta }^{\prime 2}} + \text{Br}\left( {1 + \frac{1}{\beta }} \right) {{f}^{\prime \prime 2}} + \text{Br}M{{f}^{\prime 2}} + L\left( {\phi '\theta ' + \frac{{{\alpha _2}}}{{{\alpha _1}}}{{\phi }^{\prime 2}}} \right) }} \end{aligned}$$

(19)

5 Regression analysis

In this section, the linear and quadratic regression analyses (Kuznetsov and Nield [47]) are performed to estimate the average effect of different flow parameters on Nusselt number. More precisely, it is a mathematical measure, expressing an average of relationship between two or more variables in terms of the original units of the data. The linear and quadratic regressions for the reduced Nusselt number Nur ($\text{Nu}_{x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 1/2}$ is referred to as the reduced Nusselt number), which incorporates the impact of magnetic parameter M and Prandtl number $\Pr$, are defined as:

$$\begin{aligned} \text{Nur}_{\mathrm{est}} = \text{Nur} + {E_1}M + {E_2}\Pr , \end{aligned}$$

(20)

and

$$\begin{aligned} \text{Nur}_{\mathrm{est}} = \text{Nur} + {E_3}M + {E_4}\Pr + {E_5}{M^2} + {E_6}{\Pr ^2} + {E_7}M\Pr , \end{aligned}$$

(21)

In Eqs. (20) and (21), $\left( {{E_1},\,{E_2}} \right)$ and $\left( {{E_3},\,{E_4},{E_5},\,{E_6},\,{E_7}} \right)$ are the coefficients of the linear and quadratic regressions corresponding to M and $\Pr$, respectively. For different values of Eckert number Ec, the regression coefficients and the estimated reduced Nusselt number Nur along with the maximum relative absolute error ${\varepsilon _{\mathrm{Nu}}}$ are calculated and are presented in Table 1.

The expression for the maximum relative absolute error is defined as

$$\begin{aligned} {\varepsilon _{\mathrm{Nu}}} = \left| {\frac{{Nu{r_{\,\,est}} - \text{Nur}}}{{\text{Nur}}}} \right| \end{aligned}$$

(22)

For a specific value of Ec (e.g., $\text{Ec}=0.6$ ), the reduced Nusselt number (Nur) is estimated for 100 sets of values of the parameters M and $\Pr$, chosen arbitrarily from the interval [0.1, 1.0]. On this data, linear and quadratic regression analyses are performed. The following are the correlations for linear and quadratic regressions, respectively:

$$\begin{aligned}\text{Nur}_{\mathrm{est}} = 0.3715851 - 0.1084790M\begin{array}{*{20}{l}} { - 0.0023155} \end{array}\Pr , \end{aligned}$$

(23)

$$\begin{aligned}&\left. \begin{array}{l} \text{Nur}_{\mathrm{est}} = 0.342778 - 0.0181415M + 0.0928443\Pr \\ + 0.0120526{M^2} + 0.0102882{\Pr ^2} - 0.3206821M\Pr , \end{array} \right\} \end{aligned}$$

(24)

with maximum relative absolute error of about $3.3\%$ (in linear regression) and $0.15\%$ (in quadratic regression). It can be observed from Tables 1 and 2 that strengthening the magnetic parameter M leads to reduction in Nur for both linear and quadratic cases, while $\Pr$ has positive influence on the reduced Nusselt number. We can see from these tables that linear as well as quadratic regression estimates are more accurate for smaller value of Eckert number.

Table 1 Coefficients of linear regression in $\text{Nu}_{\mathrm{est}}$ with respective maximum error for Nur

Table 2 Coefficients of quadratic regression in $\text{Nu}_{\mathrm{est}}$ with respective maximum error for Nur

6 Solution methodology

In order to find out the numerical solution of coupled ODEs (8) to (10) with the boundary conditions (11), the bvp4c routine of MATLAB is employed. This method is based on a relaxation method which makes use of polynomial interpolation on a systematically defined grid. This method has an accuracy of fourth order. In this routine, the numerical solutions are attained by transforming the boundary value problem into system of first order differential equations (DEs). To do this, we introduce the following substitutions:

$$\begin{aligned} {g_1} = f,\,\,{g_2} = f',\,\,{g_3} = f'',\,\,g{g_1} = f''',\,\,{g_4} = \theta ,\,\,{g_5} = \theta ',\,\,g{g_2} = \theta '',\,\,{g_6} = \phi ,\,\,{g_7} = \phi ',\,\,g{g_3} = \phi ''. \end{aligned}$$

(25)

By incorporating the above-mentioned substitutions, Eqs. (8)–(10) along with the boundary conditions (11) are converted into following forms:

$$\begin{aligned} g{g_1}= {} - \left( {1+\frac{1}{{\beta }}} \right) \left( {M\left( {A - {g_2}} \right) - g_2^2 + {g_1}{g_3} + {A^2} + {\lambda _1}{g_4} + {\lambda _2}{g_6}} \right) , \end{aligned}$$

(26)

$$\begin{aligned} g{g_2}&= {} - \left( {\frac{{\Pr }}{{1 + R}}} \right) \left( \text{Nb}{g_5}{g_7} + Ntg_5^2 + {g_1}{g_5} + Q{g_4} \right. \nonumber \\&\quad +\left. EcMg_2^2 + \left( {1+\frac{1}{{\beta }}} \right) Ecg_3^2\right) , \end{aligned}$$

(27)

$$\begin{aligned} g{g_3}= {} - \text{Sc}\left( {{g_1}{g_7} + \frac{{\text{Nt}}}{{ScNb}}g{g_2} - \sigma {{\left( {1 + {g_4}{\theta _w}} \right) }^m}\exp \left[ {\frac{{ - E}}{{1 + {g_4}{\theta _w}}}} \right] {g_6}} \right) . \end{aligned}$$

(28)

with

$$\begin{aligned} \left. \begin{array}{l} {g_2}\left( 0 \right) = 1,\,\,{g_2}\left( \infty \right) = A,\,\,{g_1}\left( 0 \right) = 0,{g_5}\left( 0 \right) = - \text{Bi}_{1}\left( {1 - {g_4}\left( 0 \right) } \right) ,\,\, \\ {g_4}\left( \infty \right) = 0,\,\,{g_7}\left( 0 \right) = - \text{Bi}_{2}\left( {1 - {g_6}\left( 0 \right) } \right) ,\,\,{g_6}\left( \infty \right) = 0. \\ \end{array} \right\} \end{aligned}$$

(29)

In order to make the numerical computations feasible, a range of values of the similarity variable is considered. For $\eta = 20$, the velocity, thermal and concentration distributions are converging to their corresponding values in the free stream region. Therefore, the maximum value of $\eta$ is taken as 20 for entire numerical computations.

7 Validation of result

Table 3 is prepared to validate the results achieved in the present study. We have compared our result of $-\theta '\left( 0 \right)$ and $-\phi '\left( 0 \right)$ for thermal Biot number $\text{Bi}_{1}$ with that of Ibrahim and Makinde [48]. For this purpose, the values of other relevant flow parameters have been set as $A = 0.4,\,\text{Nt} = 0.1,\,\text{Nb} = 0.1,\,M = 1, \Pr =7, \lambda _1=0, \lambda _2=0, R=0, Q=0, \text{Ec}=0$ and $\sigma =0$. An excellent agreement is perceived between the numerical values of $-\theta '\left( 0 \right)$ and $-\phi '\left( 0 \right)$ of our problem with those obtained by Ibrahim and Makinde [48], as evident from Table 3. Therefore, the bvp4c technique used in this research article is good enough to carry out the subsequent analysis of the problem.

Table 3 Comparison of $-\theta '\left( 0 \right)$ and $-\phi '\left( 0 \right)$ for different value of thermal Biot number $\text{Bi}_{1}$ when $A = 0.4,\,\text{Nt} = 0.1,\,\text{Nb} = 0.1,\,M = 1$

8 Result and discussion

In this section, the influence of various parameters like: ratio parameter A, Casson parameter $\beta ,$ thermal and concentration buoyancy parameter $\left( {\lambda _1, \lambda _2} \right) ,$ heat generation parameter Q,  thermal Biot number $\text{Bi}_1$, solutal Biot number $\text{Bi}_2$, Eckert number $\text{Ec},$ magnetic parameter M,  thermophoresis parameter $\text{Nt} ,$ Brownian motion parameter $\text{Nb},$ chemical reaction parameter $\sigma ,$ radiation parameter R,  diffusive variable L,  activation energy E,  diffusive variable L,  temperature ratio variable $\alpha _1,$ concentration ratio variable $\alpha _2$, and diffusive variable L on velocity $f'\left( \eta \right) ,$ temperature $\theta \left( \eta \right) ,$ concentration $\phi \left( \eta \right) ,$ entropy generation number Ng, Bejan number Be, skin friction coefficient $\left( {{C_f}{\mathop {{\mathrm{Re}}}\nolimits } _x^{0.5}} \right) ,$ rate of heat transfer $\left( {\text{Nu}_{x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 0.5}} \right)$ and rate of mass transfer $\left( {\text{Sh}_{x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 0.5}} \right)$, are discussed and displayed graphically and in the tabular form. The default values of the involved parameters in the governing equations are $A = 0.3,\,\beta = 0.2,\,{\lambda _1} = \,{\lambda _2} = 0.5,\,M = 0.5,\,\text{Ec} = 0.2, \text{Bi}_{1} = 0.1,\,\text{Bi}_{2} = 0.2,\,Q = 0.5,\,\text{Nt} = ,\,\text{Nb} = 0.1,\,R = 0.2,\,E = 2.0,\,\,m = 0.1,\,{\theta _w} = 0.2,\sigma = 0.1,\,\text{Br} = 0.4,\,{\alpha _1} = 1.1,\,{\alpha _2} = 1.3$ and $L = 0.6$, until otherwise specified particularly.

8.1 Velocity

The behavior of fluid velocity $f'\left( \eta \right)$ against the parameters $A,\, \beta ,\, \lambda _1,\, \lambda _2$ and M is plotted in Figs. 2, 3, 4 and 5. Figure 2 illustrates the influence of ratio parameter A on $f'\left( \eta \right)$. We observe the appearance of two distinct boundary layers near the sheet, depending on the value of A being greater or lesser than 1. Since A is ratio of free stream velocity to stretching velocity, therefore $A < 1$ means stretching velocity is more than free stream velocity and the value of $A > 1$ suggests that free stream velocity is dominant over stretching velocity. The effects of this parameter on fluid velocity have been explained by Kumar et al. [35]. It is witnessed from Fig. 3 that the velocity of the fluid is inversely affected by the Casson parameter $\beta$, i.e., fluid velocity diminishes with an increment in the Casson parameter as observed and explained by Kumar et al. [35]. The effects of $\lambda _1$ and $\lambda _2$ on the velocity of fluid $f(\eta )$ are shown in Figs. 4 and 5, respectively. With increasing values of both $\lambda _1$ and $\lambda _2$ from 2 to 10, there is a noticeable acceleration in fluid velocity $f(\eta )$. Such an effect on the velocity profile can be understood by the fact that the thermal and concentration buoyancy parameters $(\lambda _1, \lambda _2)$ have the direct relation to thermal Grashof number Gr and solutal Grashof number Gc, respectively. Since Gr suggests the ratio of thermal buoyancy force to viscous force and Gc suggests the ratio of solutal buoyancy force to viscous force; therefore, higher thermal or solutal Grashof numbers produce stronger buoyancy forces, which will ultimately increase the fluid velocity.

Fig. 2

Velocity profiles for different values of A

Fig. 3

Velocity profiles for different values of $\beta$

Fig. 4

Velocity profiles for different values of $\lambda _1$

Fig. 5

Velocity profiles for different values of $\lambda _2$

8.2 Temperature

Figures 6, 7, 8, 9, 10, 11 and 12 show the behavior of fluid temperature $\theta (\eta )$ under the effect of parameters $\text{Ec},\, \text{Bi}_1,\,M,\, Q,\, \text{Nt},\, \text{Nb}$ and R. The effects of Magnetic parameter M, thermophoresis parameter $N_{\mathrm{t}}$ and Brownian diffusion parameter $N_{\mathrm{b}}$ are shown in Figs. 8, 10 and 11 respectively. These results have also been obtained by Kumar et al. [35], and the reason for such behavior of fluid temperature has been explained by Kumar et al. [35]. In Fig. 6, behavior of $\theta (\eta )$ for different values of Ec is presented. As per this figure, $\theta (\eta )$ is increasing on increasing Ec. Since Ec suggests the relationship between kinetic energy and enthalpy, an increase in the value of Ec means the dissipative heat is stored in the liquid through frictional heating, and hence fluid temperature gets increased. Figure 7 is drawn to scrutinize the influence of $\text{Bi}_1$ on $\theta (\eta )$. It is seen that temperature rises with the increase in $\text{Bi}_1$. Since $\text{Bi}_1$ is proportional to heat transfer coefficient, therefore higher temperature is expected on increasing $\text{Bi}_1$. The impact of heat generation parameter Q on the fluid temperature $\theta (\eta )$ is presented in Fig. 9. The value $Q>0$ corresponds to the heat generation, and as expected, the temperature of the fluid is improved by an increase in the heat generation parameter Q. This happens because comparatively more heat is produced in the whole system for increasing values of this parameter $Q (>)0$. Figure 12 exhibits the change in the temperature distribution $\theta (\eta )$ for different values of radiation parameter R. As per this figure, increase in the values of radiation parameter tends to enhance the temperature profile within the thermal boundary layer. Physically speaking, fluid absorbs more and more heat when radiation parameter R is increased, due to this reason temperature of the fluid gets increased.

Fig. 6

Temperature distribution for different values of Ec

Fig. 7

Temperature distribution for different values of $\text{Bi}_1$

Fig. 8

Temperature distribution for different values of M

Fig. 9

Temperature distribution for different values of $Q>0$

Fig. 10

Temperature distribution for different values of Nt

Fig. 11

Temperature distribution for different values of Nb

Fig. 12

Temperature distribution for different values of R

8.3 Concentration

Figures 13, 14, 15 and 16 are drawn to understand the behavior of $\phi (\eta )$ against different values of the parameters $E,\,\, \text{Nt},\, \text{Nb}$ and $\text{Bi}_2$. The variation in the concentration profile $\phi (\eta )$ with an increase in the activation energy parameter E is demonstrated in Fig. 13. It is observed that concentration profile $\phi (\eta )$ gets diminished with an increase in the value of activation energy parameter E. This is due to the change in the function ${\left( {\frac{T}{{{T_\infty }}}} \right) ^m}{e^{-\left[ {\frac{{{E_{\mathrm{a}}}}}{{{K^*}T}}} \right] }}$, i.e., lower activation energy increases the modified Arrhenius function which ultimately promotes the destructive kind of chemical reaction. The chemical reaction among species lead to consumption of species and hence $\phi (\eta )$ diminishes on increasing E. Figures 14 and 15 are sketched to show the nature of concentration profile against the parameters Nt and Nb, respectively. It is witnessed from this figure that concentration profile $\phi (\eta )$ rises as the parameter Nt is increased, while a completely opposite effect is observed on increasing Nb, i.e., $\phi (\eta )$ is getting reduced on increasing the values of Brownian diffusion parameter. Since an increase in Nt means increase in thermophoretic force, which result in the movement of nanoscale particles from hot to cool region, due to which an increment in the concentration profile $\phi (\eta )$ is observed. Further, since the Brownian diffusion rate is proportional to Nb, consequently, a downfall in the concentration profile $\phi (\eta )$ is noticed when the parameter Nb is increased. Figure 16 shows the effect of $\text{Bi}_2$ on $\phi (\eta )$. It is noticed from this figure that boundary layer thickness and concentration distribution $\phi (\eta )$ is increased for larger values of $\text{Bi}_2$. Since the rate of mass transfer increases for higher $\text{Bi}_2$ and this yields higher concentration in the boundary layer region.

Fig. 13

Concentration profiles for different values of E

Fig. 14

Concentration profiles for different values of Nt

Fig. 15

Concentration profiles for different values of Nb

Fig. 16

Concentration profiles for different values of $\text{Bi}_2$

8.4 Entropy generation and Bejan number

This section presents the analysis of entropy generation Ng and Bejan number Be, which are plotted in Figs. 17, 18, 19, 20, 21 and 22. The effects of Casson parameter $\beta$ on Ng and Be are presented in Figs. 17 and 18, respectively. We observe from this figure that Ng is decreasing on increasing $\beta$. Since increasing values of $\beta$ causes faster shearing of the liquid along the surface, consequently entropy generation decreases when $\beta$ is increased. It is clear from Fig. 18 that Bejan number rises on increasing $\beta$. This is because the rate with which entropy is generated, decreases when $\beta$ is increased. Figures 19 and 20 are sketched to show the nature of Ng and Be against Brinkman number Br. From Fig. 19, it is seen that Ng gets enhanced as the Brinkman number Br is increased. Since the ratio of heat released by the fractional heating to heat transfer by molecular conduction is referred to as the Brinkman number Br. Hence, comparatively more heat is produced in the entire system for larger Br and consequently, there is an increase in the disorderliness of the whole system. It is also noted that Brinkman number Br tends to reduce the Bejan number when its values are increased (see Fig. 20). Figures 21 and 22 show the influence of magnetic parameter M on Ng and Be. Figure 21 shows that Ng increases with growing value of M. Since increasing M means intensifying the magnetic field which acts in a direction opposite to the motion of fluid. This provides a drag to the flow and therefore, additional disturbance in the system. Thus intensifying magnetic field results in the increment of entropy generation. On the other hand, Be is getting reduced for higher values of M because irreversibility close to the surface due to the fluid friction dominates over the irreversibility due to heat transfer (see Fig. 22).

Fig. 17

Variation of entropy generation for different values of $\beta$

Fig. 18

Variation of Bejan number for different values of $\beta$

Fig. 19

Variation of entropy generation for different values of Br

Fig. 20

Variation of Bejan number for different values of Br

Fig. 21

Variation of entropy generation for different values of M

Fig. 22

Variation of Bejan number for different values of M

8.5 Quantity of physical interest

The change in the bahavior of skin friction coefficient $\left( {{C_f}{\mathop {{\mathrm{Re}}}\nolimits } _x^{1/2}} \right) ,$ Nusselt number $\left( {\text{Nu}_{x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 1/2}} \right)$ and Sherwood number $\left( {\text{Sh}_{x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 1/2}} \right)$ are computed for various flow parameters and are presented in Tables 4, 5 and 6, respectively. Table 4 is prepared to see the impact of parameters $\beta ,\, M,\, \lambda _1$ and $\lambda _2$ on skin friction coefficient $\left( {{C_f}{\mathop {{\mathrm{Re}}}\nolimits } _x^{1/2}} \right)$. From this table it is found that $\left( {{C_f}{\mathop {{\mathrm{Re}}}\nolimits } _x^{1/2}} \right)$ increases on increasing the values of parameters $\beta$ and M, while a completely different behavior is observed when $\lambda _1$ and $\lambda _2$ are increased. Table 5 is prepared to demonstrate the influence of parameters $E_c,\, R,\, \text{Bi}_1$ and E on Nusselt number $\left( {\text{Nu}_{x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 1/2}} \right)$. As per Table 5, $\left( {\text{Nu}_{x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 1/2}} \right)$ is getting reduced with an increase in the value of Eckert number and activation energy parameter, while increase in the radiation parameter and thermal Biot number leads to a rise in Nusselt number. The nature of Sherwood number $\left( {\text{Sh}_{x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 1/2}} \right)$ under the variation of $\text{Nt},\, \text{Nb},\, \sigma ,\, \text{Bi}_2$ and E is elucidated in Table 6. One can conclude from this table that $\left( {\text{Sh}_{x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 1/2}} \right)$ gets reduced with strengthening of $\text{Nt},\, \text{Nb},\, \text{Bi}_2$ and E, while increase in $\sigma$ leads to an enhancement in $\left( {\text{Sh}_{x}{\mathop {{\mathrm{Re}}}\nolimits } _x^{ - 1/2}} \right)$.

Table 4 Variation in skin friction coefficient

Table 5 Variation in Nusselt number

Table 6 Variation in Sherwood number

9 Conclusions

The following points are the main findings for the present analysis

• Velocity of the fluid is perceived to rise on increasing magnetic parameter or plastic dynamic viscosity, i.e., on increasing Casson parameter, whereas fluid is getting accelerated on increasing any of ratio parameter, concentration buoyancy parameter or thermal buoyancy parameter.

• The temperature of liquid is increased when Biot number, magnetic parameter, Eckert number, heat generation parameter, thermophoretic parameter and radiation parameters are increased.

• Species concentration decreases for larger values of solutal Biot number, while it increases on increasing activation energy parameter.

• Rate of heat transfer is increasing function of radiation parameter and thermal Biot number.

• Rate of mass transfer gets enhanced with the increase in the values of chemical reaction parameter, whereas Brownian motion parameter and activation energy have an adverse effect on this physical quantity.

• Entropy generation gets reduced for bigger values of Casson parameter, whereas there is an increase in the net entropy when the values of thermal Biot number, Brinkman parameter and magnetic parameter are increased.

• Bejan number enhances when temperature ratio variable is increased, and it gets reduced for larger values of Brinkman number and magnetic parameter.