1 Introduction

Slug flow is a distinct gas/liquid two-phase flow regime which occurs in vertical pipes for moderate values of gas and liquid superficial velocities. The early researches on slug flows started more than 60 years ago [1,2,3]. The continuous rise of isolated long gas bubbles (called Taylor bubbles) is the main feature of slug flows, and these Taylor bubbles are separated from the pipe wall by a liquid falling film. Moreover, the space between each two consecutive Taylor bubbles is occupied by a liquid slug which itself may contain smaller gas bubbles. In a particular case, for a shear thinning slug flow, apparent viscosity of the liquid phase varies along the flow path and this non-Newtonian rheological behavior affects the overall hydrodynamics of the two-phase flow most prominently the structure of the wake region formed behind the trailing edge of Taylor bubbles [4]. The flow pattern map of two-phase non-Newtonian liquid–gas flows in vertical pipes presented by Dziubinski et al. [5] confirms the occurrence of the shear thinning slug flow for liquid/gas superficial velocities ranging from 0.1 to 1 m/s.

Slug flows are encountered in a wide variety of industrial application including artificially assisted transport of reservoir fluids, gas-lift chemical reactors, volatile organic compounds (VOC) removal for producing high-quality polymer products [6], and slug flow through microchannels [7,8,9]. Due to shear thinning rheological behavior of various industrial fluids, the shear thinning slug flows have attracted a significant interest from the research community. In a pioneering work, Otten and Fayed [10] conducted a series of experiments for measuring the two-phase pressure drop of the shear thinning slug flows. It was reported that frictional drag reduces as the shear thinning behavior of the liquid phase intensifies. Void fraction and gas hold-up for shear thinning slug flows were measured by Rosehart et al. [11] and Terasaka and Tsuge [12].

In another experimental investigation, Niranjan et al. [13] examined the motion of a long CO2 bubble in shear thinning carboxymethyl cellulose (CMC) solutions. They proposed a well-designed correlation for the bubble rise velocity accounting for non-Newtonian behavior of the CMC solution using an effective viscosity calculated at the effective shear rate of \( \dot{\gamma }_{\text{eff}} = 2U_{\text{TB}} /D \) where UTB is the bubble rising velocity and D is the pipe diameter. The use of a proper effective shear rate was further justified by Carew et al. [14] who measured the rising velocity of a long bubble in shear thinning liquids. It was shown that the severity of fluid flow around gas bubbles in vertical slug flows causes a Newtonian plateau for the liquid rheological behavior to emerge where the corresponding apparent viscosity could be best correlated by the local shear rate at the bubble nose (i.e., effective shear rate). Moreover, they confirmed that the effect of shear thinning behavior is more significant for smaller tubes.

Sousa et al. [6] experimentally visualized the flow of multiple CMC solutions with different concentrations around Taylor bubbles using the well-known PIV technique. For the very high concentration CMC solutions which possess strong non-Newtonian rheological behavior, a lacrimal shape for the Taylor bubble trailing edge was observed due to the so-called negative wake generated by the intense viscoelastic effect [15, 16]. As the solution became less viscous, a concave trailing edge was observed and eventually at high enough Reynolds numbers the trailing edge of Taylor bubble became unstable and a 3D asymmetric flow field emerges. The stabilizing effect of viscosity for the shape of Taylor bubble trailing edge was also reported for the polyanionic cellulose (PAC) aquatic solutions [17].

Sousa et al. [4] later conducted a similar experimental study concerning the rise of Taylor bubble in polyacrylamide (PAA) solutions (another shear thinning and viscoelastic liquid). A correlation was derived for the shape of Taylor bubble nose, and it was concluded that the flow field around the bubble nose was not strongly affected by the shear thinning behavior of PAA. However, a notably long liquid recirculation zone was observed at the wake of gas bubbles. This work was extended by Sousa et al. [18] to examine the interaction of two consecutive Taylor bubbles rising in a non-Newtonian shear thinning liquid. It was suggested that the effect of liquid rheology on the bubble interaction become notable when the viscosity of the solution is relatively high and strong viscoelastic effects are present in the flow domain. Zhao et al. [19] proposed empirical correlations for the slug velocity and length inside an aqueous poly (2-hydroxyethylmethacrylate) cryogel slug flow in a microchannel.

As an important step toward theoretical modeling of non-Newtonian slug flows, Picchi et al. [20] proposed a one-dimensional mechanistic model for the shear thinning slug flow in inclined pipelines. They modified the classical formulation of Newtonian slug flows to account for the variation of fluid viscosity. Moreover, a comprehensive experimental study was also undertaken on the slug flow characteristics including the slug length and frequency, and a reliable data set was collected on the pressure drop in non-Newtonian liquid–gas two-phase flows.

More recently, computational fluid dynamics (CFD) has been utilized as a reliable tool for studying Newtonian slug flows. In the majority of these numerical studies, Taylor bubble rising through a quiescent or moving liquid column has been considered as an important model problem for slug flows. Taha and Cui [21] performed axisymmetric and 3D simulations of Taylor bubbles rising in Newtonian liquids. The bubble rise velocity was predicted accurately using volume of fluid method, and behind the Taylor bubble, the transition from a closed axisymmetric to a closed un-axisymmetric wake and from a closed un-axisymmetric wake to an open wake was recognized as the bubble rise velocity was increased. Kashid et al. [22] simulated the Newtonian slug flow in a microstructured reactor. The effect of co-current Newtonian liquid flow on a rising Taylor bubble was investigated by Quan [23]. A comprehensive survey on the characteristic of Newtonian Taylor rising bubbles, including bubble shape, liquid film thickness and velocity profile, bubble rise velocity, wall shear stress, and wake structure, is provided by Araújo et al. [24]. The effects of Reynolds number, capillary number, and channel aspect ratio on the mixing and recirculation for a slug flow in a microchannel were analyzed numerically by Abadie et al. [25].

In the case of Taylor bubble rising in a non-Newtonian liquid, numerical studies are rare to be found. Ratkovich et al. [26] simulated the turbulent sodium CMC/air slug flow in a vertical tube using the power-law model. Araújo et al. [27] were the first who demonstrated the capability of VOF method coupled with the Carreau–Yasuda viscosity function in estimating the main flow characteristics of shear thinning liquid/gas slug flows. A series of axisymmetric numerical simulation was performed and the effect of liquid viscosity variation on the bubble rise velocity and the wake dimension was investigated.

In the present work, we are intended to numerically simulate the rise of a single Taylor bubble in a quiescent vertical column of a shear thinning liquid whose rheological behavior is modeled by Carreau–Yasuda constitutive equation. Use will be made of the volume of fluid method and mainly, we are aimed at,

  1. i.

    Extending the comparison between VOF numerical result for shear thinning Taylor bubble rising with the available experimental data for different concentrations in order to delineate the capabilities and limitations of such a standard CFD scheme in studying non-Newtonian slug flows.

  2. ii.

    Examining the effect of various material constants of Carreau–Yasuda rheological model on the Taylor bubble shape and the shear stress exerted by the pipe wall on the liquid falling film. This will further clarify the extent in which non-Newtonian rheological behavior affects the two-phase slug flows.

  3. iii.

    Advancing the numerical simulation of shear thinning slug flows toward larger bubble velocities (where an asymmetric flow pattern exists) using proper 3D simulations.

2 Mathematical formulation

2.1 Problem description

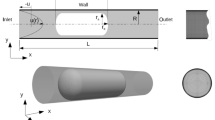
In the present work, the rise of a single Taylor bubble in a vertical tube filled with a shear thinning liquid is numerically simulated. As the physical domain of the problem, a vertical pipe with the diameter of (D = 0.032 m) and the length of (L = 11D) is considered. The length of pipe is chosen large enough so that the motion of a single Taylor bubble was not affected by the liquid inflow and outflow boundary conditions. Moreover, to control the computational cost, the problem is solved within a moving frame of reference attached to the bubble nose. In the moving frame of reference, the boundary conditions and the initial bubble shape is depicted in Fig. 1. As the initial shape of the gas bubble, a hemisphere attached to a vertical cylinder with the same diameter is used and the initial length of Taylor bubble is set at (3D). 2D axisymmetric and 3D simulations are performed to track the motion and deformation of a Taylor bubble rising through a non-Newtonian liquid and ultimately resolve the liquid flow field around the bubble nose and trailing edge.

Fig. 1
figure 1

The computational domain with relevant boundary conditions. (Z and Z* are measured from the bubble nose and the bubble tail respectively)

Full size image

2.2 Governing equations

To model the rise of a long gas bubble in a shear thinning liquid, a one-fluid formulation is adapted here in which a single set of governing equations is solved for both liquid and gaseous phases as follows [28, 29],

$$ \frac{\partial \rho }{\partial t} + \nabla \cdot \left( {\rho {\mathbf{u}}} \right) = 0 $$
(1a)
$$ \frac{{\partial \left( {\rho {\mathbf{u}}} \right)}}{\partial t} + \nabla \cdot \left( {\rho {\mathbf{u}} \otimes {\mathbf{u}}} \right) = - \nabla P + \nabla \cdot \left[ {\mu \left( {\nabla {\mathbf{u}} + \nabla {\mathbf{u}}^{t} } \right)} \right] + \rho {\mathbf{g + f}}_{\text{I}} $$
(1b)

where (ρ, u, t and P) are density, velocity vector, time, and fluid pressure, respectively. Moreover, (fI) is the source term accounting for the surface tension at the gas/liquid interface and μ is the apparent viscosity of the mixture and (g) is the gravitational vector. In the context of volume of fluid method (VOF), the effective properties of the two-phase gas/liquid mixture are calculated using the gas volume fraction (α) as [28],

$$ \rho = \alpha \rho_{g} + \left( {1 - \alpha } \right)\rho_{l} $$
(2a)
$$ \mu = \alpha \mu_{g} + \left( {1 - \alpha } \right)\mu_{l} $$
(2b)

and subscripts ‘g’ and ‘l’ denote the gas and liquid phases, respectively. Moreover, the temporal evolution of gas volume fraction is governed by a first order advection equation as it is given in Eq. 3 [29]:

$$ \frac{\partial \alpha }{\partial t} + {\mathbf{u}} \cdot \nabla \alpha = 0. $$
(3)

To model the surface tension force, the continuous surface force method (CSF) is employed and the corresponding source term in the momentum conservation law of Eq. 1b is approximated as [30] (\( \kappa \) is the local curvature and \( \sigma \) is the surface tension coefficient),

$$ {\mathbf{f}}_{I} = - \sigma \kappa \left( {\nabla \alpha } \right) $$
(4)

Finally, to account for the non-Newtonian behavior of the liquid phase, use is made of the Carreau–Yasuda viscosity function [31] as follows:

$$ \frac{{\mu_{l} - \mu_{\infty } }}{{\mu_{0} - \mu_{\infty } }} = \left[ {1 + \left( {\lambda \dot{\gamma }} \right)^{a} } \right]^{{\frac{n - 1}{a}}} $$
(5)

where \( \left( {\mu_{0} ,\mu_{\infty } } \right) \) are the zero-shear rate and infinity shear rate viscosities which are the maximum and minimum values of the viscosity function. (\( \dot{\gamma } \)) is the shear rate and n is the power-law index which controls the slop of viscosity decline from its maximum value of (\( \mu_{0} \)) to its minimum value of (\( \mu_{\infty } \)). Additionally, (a) and (λ) are two coefficients which bring more flexibility to the viscosity function. The Carreau–Yasuda viscosity function depicts two Newtonian plateaus at very low and very high shear rates with the corresponding viscosities of \( \left( {\mu_{0} ,\mu_{\infty } } \right) \) and a power-law shear thinning region with the slop of (n − 1) between these two plateaus. The curvature of viscosity function transition from Newtonian plateaus to the power-law region is determined by the coefficient (a) and the coefficient (λ) sets the value of threshold shear rate at which transition to shear thinning behavior occurs. The values of these material properties are given in Table 1.

Table 1 The physical parameters of the problem
Full size table

2.3 Non-dimensional numbers

In shear thinning slug flows, the rising velocity of gas bubbles (\( U_{\text{TB}} \)) and the final shape of Taylor bubbles are determined by the interaction of the gravity, buoyancy, viscous drag and inertia forces. Therefore, the relevant non-dimensional numbers for this two-phase flow are Eotvos number (Eo), Morton number (M), viscosity ratio number (S), and power-law index (n) which are defined as:

$$ \begin{array}{*{20}l} {Eo = \frac{{g\left( {\rho_{l} - \rho_{g} } \right)D^{2} }}{\sigma }} \hfill & {M = \frac{{g\mu_{\infty } \left( {\rho_{l} - \rho_{g} } \right)}}{{\rho_{l}^{2} \sigma^{3} }}} \hfill \\ {Fr = \frac{{U_{TB} }}{{\sqrt {gD} }}} \hfill & {S = \frac{{\mu_{\infty } }}{{\mu_{0} }}} \hfill \\ \end{array} $$
(6)

where the viscosity ratio number represents the extent of viscosity variation in liquid phase and (n) regulates the intensity of viscosity reduction for the non-Newtonian Carreau fluid. Eotvos number is the ratio of buoyancy to the surface tension force and the normalized velocity is represented by the Froude number. In the following sections, the numerical results will be presented using aforementioned non-dimensional numbers.

3 Numerical method

Axisymmetric and 3D simulations were performed on rectangular and quadrilateral uniform structured grids depicted in Fig. 2 for the 3D case. A detailed mesh size study was undertaken, and it was concluded that using a mesh size of 52 × 1144 in radial and axial directions for axisymmetric simulations and a uniform mesh with 816,533 volume elements for the 3D simulations provide accurate and mesh independent numerical results. In order to initialize the numerical simulation, the translational velocity of the moving reference frame (V) is approximated by the available correlation for the Taylor bubble velocity (\( U_{\text{TB}} \)) in Newtonian slug flow as [32],

$$ \begin{aligned} Fr & = \frac{{U_{TB} }}{{\sqrt {gD} }} = 0.345\left( {1 - e^{{\frac{{ - 0.01N_{f} }}{0.345}}} } \right)\left( {1 - e^{{\frac{3.37 - Eo}{m}}} } \right); \\ m & = \left\{ {\begin{array}{*{20}l} {25} \hfill & {N_{f} < 18} \hfill \\ {69N_{f}^{ - 0.365} } \hfill & {18 < N_{f} < 250} \hfill \\ {10} \hfill & {250 < N_{f} } \hfill \\ \end{array} ;} \right.\quad N_{f} = \left( {\frac{{Eo^{3} }}{M}} \right)^{0.25} \\ \end{aligned} $$
(7)
Fig. 2
figure 2

Numerical mesh for the 3D simulations

Full size image

The velocity of the moving frame is updated at each time step according to Eq. 8 in which (\( {\mathbf{x}}^{n} \)) is the position vector of the bubble nose at the nth time step.

$$ {\mathbf{V}}^{n + 1} = {\mathbf{V}}^{n} + \left( {\frac{{{\mathbf{x}}^{n + 1} - {\mathbf{x}}^{n} }}{\Delta t}} \right) $$
(8)

Moreover, to accelerate the convergence of the problem, the liquid film thickness (\( \delta \)) is also initialized according to the available correlations for the Newtonian slug flows as follows [33],

$$ \delta = \left[ {\frac{{3\mu_{0} }}{{2\rho g\left( {\frac{D}{2} - \delta } \right)}}U_{TB} \left( {\frac{D}{2} - \delta } \right)^{2} } \right]^{1/3} $$
(9)

The governing equations are discretized using the finite volume method. The convective fluxes are approximated using the second-order upwind scheme and the central differencing is utilized for the diffusive fluxes. The pressure–velocity coupling is handled using the well-known SIMPLE pressure correction method. A constant surface tension is also applied at the gas/liquid interface. To capture the bubble shape, use is made of the linear geometrical reconstruction algorithm of Young’s [34]. All the simulation is performed with the Courant number of 0.25 and the convergence criterion for all the flow variables are set at 10−6.

3.1 CFD code verification

In order to ensure our readers about the accuracy and reliability of the CFD code used in the present work, a comparison is drawn between the numerical result and the available experimental data for the rise of a single Taylor bubble in a stagnant vertical column of a Newtonian liquid. In Fig. 3, the computed liquid velocity profiles in three regions (which are relevant to the slug flow hydrodynamics), including above the bubble nose, within the falling film and in the bubble wake, are depicted and compared to the corresponding experimental data presented in Refs. [35, 36] for the case of (Eo = 187.03 and M = 0.00431).

Fig. 3
figure 3

Comparison between present computations and experimental data of Nogueira et al. [35, 36] for Newtonian liquid phase velocity profile at: a Bubble nose, b developed falling film, c bubble wake (Eo = 187.03, M = 0.00431)

Full size image

As it can be seen, a favorable agreement exists between the numerical result and the experimentally measured data for the liquid velocity. Moreover, the bubble rise velocity is estimated at 0.2311 m/s by the numerical code which deviates less than 3% from the corresponding experimental value of 0.2259 m/s and this further corroborates the accuracy of our numerical code. Being done with the validation of our numerical code, we now proceed with the presentation of numerical results for Taylor bubble rising in shear thinning liquids.

4 Result and discussion

In this section, we are going to present the numerical results of a single Taylor bubble rising in a shear thinning liquid. At first, the rise of a Taylor bubble through a stagnant vertical column of CMC aquatic solutions with different concentrations is investigated and the numerical results are compared to the available experimental data of flow visualization by PIV technique [6] in order to determine the strengths and weaknesses of the present coupled VOF/non-Newtonian formulation in predicting various feature of such a non-Newtonian two-phase flow. Subsequently, we will focus on investigating the effect of viscosity ratio number and power-law index on the Taylor bubble shape and wall shear stress during the rise of a Taylor bubble and we are intended to quantify the extent in which non-Newtonian rheological behavior of liquid phase affects the shear thinning slug flows.

For a viscoelastic fluid like CMC solutions, Deborah number is defined as \( De = \frac{{\lambda_{\text{relax}} }}{{t_{p} }} \); where \( (\lambda_{\text{relax}} ) \) is the relaxation time which is defined as an intrinsic timescale of the material necessary for the adaptation of the fluid microstructure to an externally imposed shear stress/deformation and (tp) is the time scale of observation (or the flow time scale (tp= D/UTB). From the definition of Deborah number, it can be deduced that the higher the Deborah number is, the more intense viscoelastic effects are present within the flow field and in contrast if the Deborah number is small enough for a particular flow, the viscoelastic effects can be neglected all together.

Experimental measurements of Sousa et al. [6] revealed that for the Taylor bubble rising in CMC solutions, De number will be less than 10−3 if the CMC concentration remains below 0.6 wt%. Therefore, in this case (for the low to moderate CMC concentrations) the viscoelastic response of the CMC solution to the bubble rising is extremely small, and as a result, the inelastic Carreau viscosity function can be used to accurately represent the rheological behavior of such CMC solutions. On the contrary, for the CMC concentrations ranging from 0.8 to 1 wt%, the Deborah number is of order of 10−1 and therefore non-negligible viscoelastic effects are present around the rising Taylor bubble. For these high concentration CMC solutions, the use of a complex nonlinear viscoelastic model (e.g., Giesekus model or White–Metzner model) is mandatory to fully capture the corresponding rheological behavior and the use of the inelastic Carreau model for highly concentrated CMC solutions is prone to a certain level of error. Adapting a nonlinear viscoelastic model is well beyond the scope of the present study. However, in the subsequent section, by comparing the experimental data with the numerical solutions obtained by the Carreau–Yasuda viscosity curve fitted to CMC rheograms for the range of 0.8–1 wt%, the level of approximation in the use of this inelastic model for simulating the Taylor bubble rising will be investigated comprehensively.

4.1 Taylor bubble rising in CMC solutions

An aquatic CMC solution is a shear thinning fluid which also exhibits strong viscoelastic behavior provided that the concentration of CMC would be high enough. Moreover, increasing the concentration of CMC increases the solution viscosity and intensifies its non-Newtonian shear thinning and viscoelastic rheological behavior. As it was mentioned earlier, Sousa et al. [6] conducted a comprehensive experimental study and flow visualization on the rise of Taylor bubbles in stagnant CMC solutions with CMC concentrations ranging from 0.1 to 1 wt%. The shear viscosity of CMC solutions could be perfectly correlated by the Carreau–Yasuda viscosity function [6]. Therefore, we simulated the Taylor bubble rising through CMC solutions with different concentrations using the specifications of Sousa’s experimental study in order to demonstrate the strength of our numerical approach for investigating non-Newtonian slug flows.

In Fig. 4a, the shape of bubble nose predicted by the numerical code is illustrated against the experimental data. As it can be seen, for various values of CMC concentrations, the bubble nose keeps its semi-spheroidal shape; however, the mean curvature of the bubble nose and the maximum bubble radius decreases as the CMC concentration increases. The agreement between the experimental and numerical data is satisfactory especially when the CMC concentration is lower than 0.8 wt% above which a strong viscoelastic effect is present in the flow field that could not be modeled by the inelastic Carreau–Yasuda constitutive equation.

Fig. 4
figure 4

The comparison between present computations and experimental data of Sousa et al. [6]: a Bubble nose profile, b vertical component of the liquid velocity along Z = 0 for the 1.0 wt% CMC solution, c axial liquid velocity along the line of Z* = 0.2D

Full size image

Additionally, around the bubble nose, the liquid phase is first propelled upward and then pushed away from the pipe centerline by the bubble ascending motion. As a result, large positive axial velocities (in upward direction) are observed around the pipe axis; on the other hand, in the vicinity of pipe wall the sign of axial velocity changes due to the formation of a liquid falling film which surrounds the Taylor bubble. The volume of fluid method is well capable of predicting the aforementioned velocity field around the bubble nose as it is depicted in Fig. 4b. Moreover, due to fierce velocity gradient around the Taylor bubble nose, intense viscosity variation occurs in this region which affects the liquid velocity field around the bubble nose and the excellent agreement between numerical and experimental values of liquid velocity for the 1.0 wt% CMC solution (possessing the strongest non-Newtonian viscosity variation in the present study) confirms that the Carreau–Yasuda viscosity model could perfectly capture the non-Newtonian shear thinning rheological behavior of CMC solutions around the Taylor bubble nose in the slug flows.

According to Fig. 4c, the liquid velocity decreases with increasing the CMC concentration. It could be explained mentioning that the viscosity of CMC solution elevates as the CMC concentration increases and this reduces the liquid velocity throughout the flow domain. Subsequently, the liquid film jet is dissipated strongly immediately after the trailing edge of the Taylor bubble, and as it is shown in Fig. 5, no distinct wake is observed behind the Taylor bubble in 1 wt% CMC solution and the relative streamlines moves away from the bubble so that no liquid transport occurs for this high concentration CMC solution. The transition from a closed wake to a no-wake flow pattern is realized by the numerical solution accurately as it was reported by experimental visualizations (see Fig. 5).

Fig. 5
figure 5

Numerical streamlines in the wake of a Taylor bubble rising in 0.4 wt% and 1 wt% CMC solutions in a reference frame moving with the bubble

Full size image

Another important feature of slug flows is the shape of Taylor bubble trailing edge and the structure of liquid flow field immediately behind this trailing edge. For the rise of a single Taylor bubble in CMC solutions, three different patterns are reported for the shape of bubble trailing edge [6], including an unstable and asymmetric shape for low CMC concentrations (below 0.3 wt%), a symmetric concave shape for moderate CMC concentrations (0.4 –0.6 wt%) and a symmetric convex teardrop shape for high CMC concentrations (above 0.8 wt%). As a result, 2D axisymmteric simulations are only valid for the moderate to high CMC concentrations where the trialing edge instability does not prevail.

In Fig. 6, the numerically predicted shape of Taylor bubble tail in CMC solutions is compared to the corresponding real image of the bubble for axisymmetric cases. As it can be seen, the numerical simulation could successfully capture the concave shape of bubble trailing edge for the 0.4 and 0.6 wt% CMC solutions. The major deviation between numerical and experimental data is observed for the 0.8 wt% CMC solution where a flat bottom is predicted by the numerical solution for the Taylor bubble instead of the teardrop shape captured in the experimental visualization by Sousa et al. [6]. This discrepancy between numerical and experimental data could be easily justified noting that the convex bottom shape of the bubble is formed due to extra-normal forces experienced by liquid elements in highly viscoelastic 0.8 wt% CMC solution which forces the bubble to contract in its trailing edge. These viscoelastic effects are absent from our theoretical formulation of the problem (by using inelastic Carreau–Yasuda model), and as a result, our numerical code could not predict the convex bottom shape of the Taylor bubble in high concentrations of CMC solutions. To remedy this problem, a nonlinear viscoelastic model needs to be utilized for accurate representation of aquatic CMC solution rheological behavior.

Fig. 6
figure 6

Present numerical data and experimental photographs (Sousa et al. [6]) of bubble trailing edge shape for different concentrations of CMC solution (Dashed lines represent the numerical bubble profiles superimposed on the experimental images) (The permission for the reuse of the pictures is granted by Elsevier under license number 4473650674680)

Full size image

As it was mentioned earlier, for the rise of long gas bubbles in low concentration CMC solutions where the liquid viscosity is relatively low, an asymmetric liquid flow pattern was observed by Sousa et al. [4] immediately behind the bubble. Therefore, to simulate theses high-velocity bubble rising problems, the use of a 2D-axisymmetric geometry is not acceptable and 3D simulations are mandatory. In the present work, 3D simulations are performed for the Taylor bubble rising in 0.1 and 0.3 wt% CMC solutions for which experimental measurements are available. To evaluate the performance of such numerical simulation, in Fig. 7, the obtained velocity profile around the bubble nose is compared to the corresponding experimental data for 0.1 wt% CMC solution and as it can be seen, the deviation of numerical results from experimental measurements is extremely small. Moreover, our 3D simulations are able to predict the bubble rise velocity for 0.1 and 0.3 wt% CMC solutions with the maximum deviation of around 2%.

Fig. 7
figure 7

Comparison between 3D numerical results and the experimental data of Sousa et al. [6] for vertical component of the liquid velocity along Z = 0 for the 0.1 wt% CMC solution

Full size image

Temporal evolution of the Taylor bubble shape is illustrated in Figs. 8 and 9 for 0.1 and 0.3 wt% CMC solutions. As it can be seen, bubble trailing edge oscillates strongly due to the very high-velocity jet detaching from the bubble tail as the liquid leaves the annulus between Taylor bubble and the pipe wall. Moreover, small gas bubbles shed form the Taylor bubble as a result of strong instabilities of Taylor bubble tail. The small bubbles travel upward accompanying the main gas bubble and the bubble shedding intensifies with the reduction of CMC concentration as it is illustrated in Figs. 8 and 9. This trend can be easily justified knowing that the liquid velocity surrounding the Taylor bubble grows notably as CMC concentration and subsequently liquid viscosity reduces.

Fig. 8
figure 8

Temporal evolution of Taylor bubble shape in 0.1 wt% CMC solution

Full size image
Fig. 9
figure 9

Temporal evolution of Taylor bubble shape in 0.3 wt% CMC solution

Full size image

As it is outlined in this section, the non-Newtonian rheological behavior of liquid phase strongly affects the hydrodynamic features of slug flows, including the shape of Taylor bubbles, the liquid velocity profile and the liquid flow pattern near the bubble tail, and the numerical methodology employed in the present study could favorably realize these features and their alteration due to non-Newtonian liquid rheology. This effect stems from two sources: first the extent of viscosity variation represented by the viscosity ratio number (S) and secondly the rate of viscosity variation with the shear rate uniquely controlled by the power-law index (n) in Carreau–Yasuda viscosity function. To clarify the influence of these two key parameters on shear thinning slug flows, a detailed numerical inquiry is conducted in two following sections where the main focus will be placed on the effect of non-Newtonian liquid rheology on the shape of Taylor bubbles and the wall shear stress applied to the liquid film.

4.2 The effect of power-law index (n)

As it is shown in Fig. 10a, when power-law index (n) decreases in Carreau–Yasuda viscosity function, the slop of viscosity decline grows, and as a result, more intense viscosity variation is experienced by the modeled shear thinning fluid. Therefore, for a fixed value of shear rate, the apparent viscosity decreases by any reduction in the value of (n) and additionally limiting infinity shear rate (\( \mu_{\infty } \)) is reached at lower shear rates. Thus, it is expected that the effect of power-law index on a shear thinning slug flow is significant and we devote the present section to investigate this effect. To that end, we fix the other relevant non-dimensional number at (\( Eo = 62.43,\;M = 2.41 \times 10^{ - 12} ,\;S = 0.0045 \) which are adapted from the CMC solution with 0.4% wt) and we will study the effect of (n).

Fig. 10
figure 10

The effect of power-law index (n) on: a the Carreau–Yasuda viscosity function, b bubble nose profile, c bubble maximum radius

Full size image

In Fig. 10b, the shape of Taylor bubble nose is depicted for four different power-law indexes. As it can be seen, as the power-law index decreases, the frontal radius (the mean curvature radius of the bubble nose) of the bubble increases. Moreover, the maximum radius of the bubble (\( R_{ \hbox{max} } \)) is a linear function of (n) as it is shown in Fig. 10c. However, the overall shape of the bubble front remains the same for various values of the power-law index. The radial expansion of a Taylor bubble rising in a non-Newtonian liquid when the shear thinning behavior of the liquid phase intensifies is also evident in Figs. 11a, b, where the bubble shape is presented for two different values of (n).

Fig. 11
figure 11

The liquid velocity vectors and bubble shape for: a n = 0.4 and b n = 0.9, The effect of power-law index (n) on c the velocity profile of liquid phase at the bubble nose, d the fully developed liquid velocity profile across the falling film

Full size image

Moreover, the liquid velocity at the bubble front is not affected notably by the strength of non-Newtonian rheological behavior of the liquid phase as it is illustrated in Fig. 11c in which the liquid velocity profiles at the bubble nose are given for different values of (n). As the power-law index is lowered, the liquid viscosity decreases accordingly and subsequently the liquid axial velocity increases. The elevation of liquid velocity throughout the falling film (which can be seen in Fig. 11d where the fully developed liquid film velocity profiles are given for various power-law indexes) increases the fluid discharge rate out of the annular gap formed between the gas bubble and the pipe wall, and this trend reduces the thickness of the falling film which surrounds the gas bubble. As a result, the gas bubble grows in the radial direction and contracts in the axial direction to preserve the continuity of the gas bubble mass. (Please, see Fig. 11a, b.)

Another important feature of slug flows is the wall shear stress exerted on the falling film which plays a major rule in the pressure loss associated with this particular gas/liquid flow pattern. Therefore, in Fig. 12a, the variation of wall shear stress in axial direction is depicted. As it can be seen, the variation of wall shear stress is a strong function of the film thickness. Around the bubble nose where the falling film starts to form, a sharp increase in the value of wall shear stress is detectable. The wall shear stress continues to grow in the axial direction as the liquid film moves further away from the bubble nose and the film becomes thinner. Ultimately, the film thickness reaches its maximum value and after that a fully developed region emerges for which the wall shear stress remains essentially constant. However, the distance from the bubble nose upon which the shear stress reaches its peak increases with the reduction of (n). Around the gas bubble trailing edge by the propulsion of the liquid film out of the space between the pipe wall and the Taylor bubble, a sharp decrease in the wall shear rate is observed.

Fig. 12
figure 12

a the axial profile of wall shear stress for different power-law indexes, b the liquid velocity profile along the line (Z* = 0.2D) for different power-law indexes

Full size image

According to Fig. 12a, for the value of (n) as low as 0.4, it seems that no constant plateau is reached in the wall shear stress profile due to fierce viscosity variation and the falling flow continues to develop along the entire length of the Taylor bubble. For this case, the film thickness continuously declines and this increases the shear rate at the pipe wall, and as a result, the wall shear stress grows until the bubble bottom is reached. This descending behavior substitutes the constant plateau observed in the shear stress profile for higher power-law indexes. Moreover, the effect of the liquid phase rheology on the value of wall shear stress is crucial. The wall shear stress is an increasing function of (n) and for lower power-law indexes the skin friction on the falling film is smaller. Therefore, in comparison with the Newtonian slug flow, shear thinning slug flows are subjected to lower pressure losses, a deduction which is perfectly corroborated by the experimental measurements by Otten, Fayed [10].

The liquid flow pattern behind the bubble tail is also expected to be affected by the power-law index. This stems from the fact that the velocity of liquid jet near the bubble trailing edge is a strong function of the intensity of non-Newtonian shear thinning behavior or equivalently power-law index (n). As it is shown in Fig. 12b, as the power-law index increases, the fluid velocity reduces near the gas bubble tail. This reduction in liquid velocity weakens the possibility of wake formation behind the bubble tail. This assumption is confirmed in Fig. 13 in which the liquid streamlines are illustrated around the Taylor bubble. According to this figure, for the case of (n = 0.4) a strong recirculation zone is formed behind the bubble and a long wake appears in the flow domain which is a prominent feature in studying the interaction of consecutive Taylor bubbles in a real slug flow.

Fig. 13
figure 13

Liquid streamlines in a moving frame of reference attached to the bubble for: a n = 0.4, b n = 0.6, c n = 0.8, d n = 0.9

Full size image

However, as the power-law index increases and the liquid apparent viscosity elevates, the liquid expands immediately after leaving the falling film. This phenomenon weakens the liquid recirculation adjacent to the bubble tail, and as a result, the length of wake (\( L_{{\text{wake}}} \)) decreases significantly. To quantify this observation, in Table 2, the length of bubble wake is presented for different values of (n). According to the table, more than 80% reduction in wake length occurs when the power-law index is raised from 0.4 to 0.8. As it can be seen in Fig. 13 and Table 2, the wake region completely vanishes for (n = 0.9). It is also of interest to examine the shape of Taylor bubble trailing edge and its evolution with the severity of shear thinning behavior. The task is undertaken in Fig. 13 as well, where the bubble profile is illustrated for different values of (n) ranging from 0.4 to 0.9. As it can be seen, a pronounced concave shape is reported for lower power-law indexes and as (n) grows the bubble bottom flattens significantly. Finally, in Fig. 14, the (non-dimensional) bubble rise velocity is illustrated vs. the power-law index (n). As it can be seen, the bubble rise velocity increases as the liquid becomes more shear thinning.

Table 2 Bubble velocity and length of the bubble wake for different values of n
Full size table
Fig. 14
figure 14

The Froude number (non-dimensional bubble rise velocity) as a function of the power-law index

Full size image

4.3 The effect of viscosity ratio number (S)

According to its definition, viscosity ratio number (S) determines the extent of apparent viscosity variation for a shear thinning liquid. As (S) is increased, the fluid viscosity for a particular shear rate tends toward the infinity shear rate viscosity (i.e., the minimum fluid viscosity), and as a result, the shear thinning liquid becomes less viscous. Therefore, it is expected that the relevant features of a non-Newtonian slug flow strongly depend on the value of viscosity ratio number and thus we devote the present section of our manuscript to fully examine the effect of (S) on the Taylor bubble rising problem. To that end, we fixed (Eo and M) numbers at 62.43 and 2.41 × 10−12, respectively, and simulated the rise of a single Taylor bubble in four different shear thinning liquids with four different values of (S) and the identical power-law index of 0.68.

The effect of (S) on the liquid velocity field around the Taylor bubble is investigated in Fig. 15. With the increase in viscosity ratio number, the liquid viscosity decreases and this promotes the liquid transport through the flow domain. The effect of (S) on the velocity profile is most notable in the falling film and within the bubble wake, and, in contrast, around the bubble nose, the effect of (S) is less significant. The increase in liquid film velocity with (S) supports the formation of a wake region behind the Taylor bubble. As it is depicted in Fig. 16, for smaller values of (S), no wake is observed in the liquid flow field. However, a strong wake region attached to the bubble tail emerges as (S) is elevated and the length of bubble wake is an increasing function of (S). (See Table 3.)

Fig. 15
figure 15

Liquid velocity profiles for 3 different values of “S” at: a bubble nose, b falling film, c bubble tail

Full size image
Fig. 16
figure 16

Streamlines for a S = 0.0125, b S = 0.01, c S = 0.003, d S = 0.002

Full size image
Table 3 The bubble velocity and length of the bubble wake for different values of S
Full size table

The shape of bubble nose and tail is illustrated in Fig. 17 for different values of (S). For all the cases considered, the bubble tail profile is concave, and, additionally, the radius of curvature at the bubble trailing edge is an increasing function of (S). The same trend is observed for the frontal bubble radius (see Fig. 17a). The effect of (S) on the wall shear stress is presented in Fig. 18. Naturally, the shear stress exerted on the liquid film from the pipe wall reduces with (S) as the fluid becomes less viscous and its resistance against flowing diminishes. Once again, the constant plateau of wall shear stress profile completely vanishes as viscosity ratio number increases. Finally, the liquid frictional drag reduction with (S) promotes the rise of gas bubbles and subsequently the bubble rise velocity increases as (S) increases. (See Fig. 19.)

Fig. 17
figure 17

The effect of (S) on bubble shape for: a bubble nose profile, b bubble tail profile

Full size image
Fig. 18
figure 18

The axial profile of wall shear stress for different values of “S”

Full size image
Fig. 19
figure 19

The Bubble rise velocity as a function of the viscosity ratio number

Full size image

5 Conclusion

Numerical simulations were performed in the present study to track the rise of long gas bubbles through non-Newtonian shear thinning Carreau–Yasuda fluids. The volume of fluid (VOF) method was adapted here and a finite volume based two-phase flow solver was developed. To verify the accuracy and reliability of the numerical code, the code was employed to simulate the rise of a single Taylor bubble in shear thinning CMC solutions for which an extensive experimental database had been previously published. It was shown that,

  1. 1.

    The ellipsoidal shape of Taylor bubble nose is accurately predicted by the VOF method.

  2. 2.

    The numerical simulation is able to favorably capture axial velocity profiles of the non-Newtonian liquid throughout the flow domain including: around the bubble nose, at the falling film and within the bubble wake.

  3. 3.

    As for the shape of bubble bottom, in the range of 0.4–0.8 wt% CMC concentration a good agreement exists between the experimental visualization and the concave shape predicted by the numerical code. However, for high concentration CMC solutions (> 0.8 wt%), a flat bottom is resulted from the numerical simulation which does not match the teardrop shape of the Taylor bubble observed in the experiment. The discrepancy stems from the inability of Carreau–Yasuda model to model the strong viscoelastic effects of high concentration CMC solutions.

  4. 4.

    The occurrence of a closed axisymmetric wake behind the bubble tail is realized in numerical solution in a perfect accordance with the experimental data for CMC concentrations ranging from 0.4 to 0.8 wt%.

  5. 5.

    The transition from a closed wake to no-wake flow pattern is predicted by the numerical simulation as the concentration of CMC increases to 1 wt%.

  6. 6.

    For 0.1 and 0.3 wt% CMC solutions, the occurrence of an asymmetric flow pattern is successfully realized by 3D numerical simulations. For these two cases, severe oscillations are observed at the bubble tail profile and bubble shedding is reported. Moreover, no closed wake is detectable behind the Taylor bubble.

As the next step, the effect of two prominent Carreau–Yasuda model constants (i.e., the power-law index and the viscosity ratio number) on the rise of a long gas bubble was investigated comprehensively in the present study. The power-law index (n) governs the rate of viscosity reduction of the liquid phase and it was revealed that with any reduction in the value of (n):

  1. 1.

    The frontal radius of the Taylor bubble and its maximum radius grows (the bubble expands in radial direction and the liquid film thickness reduces).

  2. 2.

    The full development of the liquid film (which surrounds the long gas bubble) is postponed and for a low enough n (n < 0.4), the development of the liquid falling film never ceases along the gas bubble.

  3. 3.

    The frictional drag between liquid falling film and the pipe wall reduces and subsequently the bubble rising velocity increases.

  4. 4.

    The length of bubble wake increases and a more pronounced concave profile is observed for the bubble trailing edge.

As the final part of this study, the effect of viscosity ratio number (S) was thoroughly addressed. This non-dimensional number determines the range of shear viscosity exhibited by the non-Newtonian liquid, and as a result, it influences the increase in Taylor bubbles. It was deduced that the length of bubble wake and the bubble rising velocity are increasing functions of (S). The wall shear stress decreases with (S) and the deformation of bubble tail becomes more notable.