Three-dimensional unsteady flow of Maxwell fluid with homogeneous–heterogeneous reactions and Cattaneo–Christov heat flux

Abstract

This article addresses the unsteady three-dimensional flow of Maxwell fluid. Flow is induced by a bidirectional stretching surface. Fluid fills the porous space. Thermal relaxation time is examined using Cattaneo–Christov heat flux. Homogeneous–heterogeneous reactions are also considered. Suitable transformations are used to convert partial differential equations into nonlinear ordinary differential equations. Convergent series solutions are obtained. Effects of appropriate parameters on the velocity, temperature and concentration fields are examined. It is found that increasing value of Deborah number decreases the fluid flow. Larger values of strength of homogeneous reaction parameter decrease the concentration distribution. Also temperature is decreasing function of thermal relaxation time. Present problem is of great interest in biomedical, industrial and engineering applications like food processing, clay coatings, hydrometallurgical industry, fog formation and dispersion.

1 Introduction

At present researchers and engineers are giving special attention to the study of non-Newtonian fluid. These fluids have various applications in polymer solutions, paints, certain oils, food items, salt solutions, clay coatings, cosmetic products, etc. Non-Newtonian fluids are divided into three categories as the differential, the rate and the integral types. Rate-type fluids describe the behavior of relaxation time and retardation time. Maxwell fluid is simplest subclass of rate-type fluid. Maxwell fluid describes the characteristics of relaxation time. Sui et al. [1] studied slip flow of Maxwell nanofluid with Cattaneo–Christov double-diffusion induced by a stretching sheet. Helical flows of Maxwell fluid between coaxial cylinders have been discussed by Jamil and Fetecau [2]. Wang and Tan [3] studied stability analysis of soret-driven double-diffusive convection of Maxwell fluid in a porous medium. Abbasbandy et al. [4] analyzed Falkner–Skan flow of MHD Maxwell fluid. Three-dimensional boundary layer flow of Maxwell fluid is studied by Awais et al. [5]. Stretched flow of Maxwell fluid with heat source/sink is studied by Ramesh and Gireesha [6]. Ramesh et al. [7] examined three-dimensional flow of Maxwell fluid with suspended nanoparticles past a porous stretching surface with thermal radiation. Stagnation point flow of Maxwell fluid toward a permeable surface in the presence of nanoparticles has been discussed by Ramesh et al. [8]. Mukhopadhyay [9] analyzed time-dependent Maxwell fluid flow induced by a stretching surface with heat source/sink. Three-dimensional flow of Maxwell fluid with chemical reaction has been discussed by Hayat et al. [10].

In biomedical, engineering and industrial applications, heat transfer is very important phenomenon. Fourier [11] was the first one who described the heat transfer mechanism. The main flaw in Fourier’s model is that initial disturbance is immediately observed by the medium under consideration. In reality this could not be possible, so it is called “paradox of heat conduction”. Cattaneo [12] introduced a modification of Fourier’s model in which heat flux relaxation time appeared when the temperature gradient is applied. Further modification of the Maxwell–Cattaneo’s model is carried out by Christov [13]. He incorporated a Lie derivative in terms of constant time derivative for the heat flux. Ciarletta and Straughan [14] present particular and systemic constancy questions with Cattaneo–Christov heat flux model. Han et al. [15] studied coupled flow and heat transfer of viscoelastic fluid. Tibullo and Zampoli [16] examined particular result for the incompressible heat conducting Cattaneo–Christov model. Analogous heat convection problems in a Darcy’s porous medium have been investigated by Straughan [17]. Ramesh et al. [18] studied analysis of heat transfer phenomenon in magnetohydrodynamic Casson fluid flow through Cattaneo–Christov heat flux. Hayat et al. [19] examined influence of chemical reaction and Cattaneo–Christov heat flux in MHD Oldroyd-B fluid flow. Liu et al. [20] studied anomalous convection diffusion and wave coupling transport of cells on comb frame with fractional Cattaneo–Christov flux.

Homogeneous–heterogeneous reactions are involved in many chemically reacting systems, for example, in combustion, catalysis and biochemical systems. Homogeneous and heterogeneous reactions are correlated in very complex manner. In the presence of a catalyst, some of the reactions proceed very slowly or not at all. Some common applications of chemical reactions are in ceramics and polymer production, food processing, hydrometallurgical industry, fog formation and dispersion and many others. Merkin [21] examined the fluid flow under the influence of homogeneous–heterogeneous reactions. He studied the homogeneous reaction with the help of cubic catalysis and the heterogeneous reaction with a first-order procedure. Chaudhary and Merkin [22] studied viscous fluid flow with chemical reaction. Stagnation point flow toward a surface with homogeneous–heterogeneous reactions has been examined by Bachok et al. [23]. Kameswaran et al. [24] studied nanofluid flow past a permeable stretching sheet with homogeneous heterogeneous reactions. Flow of viscoelastic fluid toward a surface subject to homogeneous–heterogeneous reactions has been investigated by Khan and Pop [25]. MHD flow of nanofluid under the influence of homogeneous–heterogeneous reactions has been studied by Hayat et al. [26]. Effect of homogeneous heterogeneous reactions and Newtonian heating in the Stagnation point flow of nanotubes has been analyzed by Hayat et al. [27]. Influence of homogeneous–heterogeneous reactions in flow of Powell–Eyring fluid has been investigated by Hayat et al. [28].

This article explores unsteady three-dimensional flow of Maxwell fluid. Flow is induced by a stretching sheet with heat transfer through Cattaneo–Christov heat flux model. Effect of homogeneous–heterogeneous reactions is also taken into consideration. Convergent series solutions are obtained by homotopy analysis method (HAM) [29,30,31,32,33,34,35]. The behaviors of different parameters on the physical quantities have been examined graphically.

2 Problem formulation

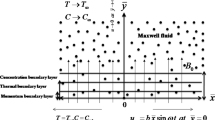
Consider the unsteady three-dimensional flow of Maxwell fluid induced by a stretching sheet at $z=0$. Sheet is stretched with velocities $u_{w}(x)=cx/(1-\alpha t)$ and $v_{w}(y) = {\text {d}}y/(1-\alpha t)$ along the x- and y-directions, respectively. An incompressible fluid fills the porous space. Heat transfer analysis is carried out by considering Cattaneo–Christov heat flux model. Here $T_{w}$ is constant temperature of the sheet, whereas $T_{\infty }$ is the temperature away from the sheet such that $T_{w}>T_{\infty }$ (see Fig 1).

Fig. 1

Geometry of the problem

Homogeneous–heterogenous reactions of two chemical species A and B are also taken into account. Homogeneous reactions at cubic autocatalysis can be demonstrated as:

$$\begin{aligned} A+2B\rightarrow 3B,\quad {\text {rate}}=k_{c}ab^{2}, \end{aligned}$$

(1)

and the heterogenous reaction in first-order isothermal is

$$\begin{aligned} A\rightarrow B,\quad {\text {rate}}=k_{s}a. \end{aligned}$$

(2)

Here $k_{c}$ and $k_{s}$ are the rate constants and a and b are the concentrations of the species A and B. The governing boundary layer flow equations are as follows:

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w }{\partial z}=0, \end{aligned}$$

(3)

$$\begin{aligned}&\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}\nonumber \\&\quad =\nu \frac{\partial ^{2}u}{ \partial z^{2}}-\lambda \left( \frac{\partial ^{2}u}{\partial t^{2}}+2u\frac{ \partial ^{2}u}{\partial x\partial t}+2v\frac{\partial ^{2}u}{\partial y\partial t}+2w\frac{\partial ^{2}u}{\partial z\partial t}+u^{2}\frac{ \partial ^{2}u}{\partial x^{2}}+v^{2}\frac{\partial ^{2}u}{\partial y^{2}} \right. \nonumber \\&\quad \quad \left. +\,w^{2}\frac{\partial ^{2}u}{\partial z^{2}}+2uv\frac{\partial ^{2}u }{\partial x\partial y}+2vw\frac{\partial ^{2}u}{\partial y\partial z}+2uw \frac{\partial ^{2}u}{\partial x\partial z}\right) -\frac{\nu }{{\hat{k}}}u, \end{aligned}$$

(4)

$$\begin{aligned}&\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}\nonumber \\&\quad =\nu \frac{\partial ^{2}v}{ \partial z^{2}}-\lambda \left( \frac{\partial ^{2}v}{\partial t^{2}}+2u\frac{ \partial ^{2}v}{\partial x\partial t}+2v\frac{\partial ^{2}v}{\partial y\partial t}+2w\frac{\partial ^{2}v}{\partial z\partial t}+u^{2}\frac{ \partial ^{2}v}{\partial x^{2}}+v^{2}\frac{\partial ^{2}v}{\partial y^{2}} \right. \nonumber \\&\quad \quad \left. +\,w^{2}\frac{\partial ^{2}v}{\partial z^{2}}+2uv\frac{\partial ^{2}v }{\partial x\partial y}+2vw\frac{\partial ^{2}v}{\partial y\partial z}+2uw \frac{\partial ^{2}v}{\partial x\partial z}\right) -\frac{\nu }{{\hat{k}}}v, \end{aligned}$$

(5)

$$\begin{aligned} \rho C_{p}\left( \frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x} +v\frac{\partial T}{\partial y}+w\frac{\partial T}{\partial z}\right) & = - {\mathbf {\nabla }}.{\mathbf {q}}, \end{aligned}$$

(6)

$$\begin{aligned} \frac{\partial a}{\partial t}+u\frac{\partial a}{\partial x}+v\frac{\partial a}{\partial y}+w\frac{\partial a}{\partial z} & = D_{A}\frac{\partial ^{2}a}{ \partial z^{2}}-k_{c}ab^{2}, \end{aligned}$$

(7)

$$\begin{aligned} \frac{\partial b}{\partial t}+u\frac{\partial b}{\partial x}+v\frac{\partial b}{\partial y}+w\frac{\partial b}{\partial z} & = D_{B}\frac{\partial ^{2}b}{ \partial y^{2}}+k_{c}ab^{2}. \end{aligned}$$

(8)

Corresponding boundary conditions are

$$\begin{aligned} u & = u_{w}=\frac{cx}{1-\alpha t}{\text { , }}\quad v=v_{w}=\frac{{\text {d}}y}{1-\alpha t}{\text { , }}\quad w{\text { =}}0,\quad {\text { }}T={\text { }}T_{w}, \quad {\text { }}D_{A}\frac{\partial a}{ \partial z}=k_{s}a,\quad {\text { }}D_{B}\frac{\partial b}{\partial z}=-k_{s}a{\text { at }}z=0, \nonumber \\ u\rightarrow & 0,\quad {\text { }}v\rightarrow 0,\quad {\text { }}T\rightarrow T_{\infty },\quad {\text { }}a\rightarrow a_{0},\quad {\text { }}b\rightarrow 0\;{\text {as}}\;z\rightarrow \infty , \end{aligned}$$

(9)

where the velocity components u , v and w are in the x-, y- and z-directions, respectively, $\mu$ the dynamic viscosity, $\rho$ the density, $\lambda$ the retardation time, ${\hat{k}}$ the permeability, $C_{p}$ the specific heat, T the temperature, $\nu =\frac{\mu }{\rho }$ the kinematic viscosity of fluid, $a_{0}$ the positive dimensional constant, $D_{A}$ and $D_{B}$ the diffusion species coefficients of A and B and ${\mathbf {q}}$ the specific heat flux which satisfies [17]:

$$\begin{aligned} {\mathbf {q}}+\lambda _{1}\left( \frac{\partial {\mathbf {q}}}{\partial t}+{\mathbf { V}}.{\mathbf {\nabla q-q.\nabla V}}+({\mathbf {\nabla .V)q}}\right) =-k{\mathbf { \nabla }}T, \end{aligned}$$

(10)

where k the fluid thermal conductivity and $\lambda _{1}$ is heat flux relaxation time. Here $\lambda _{1}=0$ corresponds to classical Fourier’s law. As we know that fluid is incompressible so Eq. (10) becomes

$$\begin{aligned} {\mathbf {q}}+\lambda _{1}\left( \frac{\partial {\mathbf {q}}}{\partial t}+{\mathbf { V}}.{\mathbf {\nabla q-q.\nabla V}}\right) =-k{\mathbf {\nabla }}T. \end{aligned}$$

(11)

Eliminating ${\mathbf {q}}$ from Eqs. (6) and (11), we get

$$\begin{aligned}&\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{ \partial T}{\partial y}+w\frac{\partial T}{\partial z}+\lambda _{1}\left( \frac{\partial ^{2}T}{\partial t^{2}}+2u\frac{\partial ^{2}T}{\partial x\partial t}+2v\frac{\partial ^{2}T}{\partial y\partial t}+2w\frac{\partial ^{2}T}{\partial z\partial t}+\frac{\partial u}{\partial t}\frac{\partial T}{ \partial x}\right. \nonumber \\&\left. +\,\frac{\partial v}{\partial t}\frac{\partial T}{\partial y}+\frac{ \partial w}{\partial t}\frac{\partial T}{\partial z}+u^{2}\frac{\partial ^{2}T}{\partial x^{2}}+v^{2}\frac{\partial ^{2}T}{\partial y^{2}}+w^{2}\frac{ \partial ^{2}T}{\partial z^{2}}+u\frac{\partial u}{\partial x}\frac{\partial T}{\partial x}+u\frac{\partial v}{\partial x}\frac{\partial T}{\partial y}+u \frac{\partial w}{\partial x}\frac{\partial T}{\partial z}\right. \nonumber \\&\left. +\,v\frac{\partial u}{\partial y}\frac{\partial T}{\partial x}+v\frac{ \partial v}{\partial y}\frac{\partial T}{\partial y}+v\frac{\partial w}{ \partial z}\frac{\partial T}{\partial z}+w\frac{\partial u}{\partial z}\frac{ \partial T}{\partial x}+w\frac{\partial v}{\partial z}\frac{\partial T}{ \partial y}+w\frac{\partial w}{\partial z}\frac{\partial T}{\partial z}+2uv \frac{\partial ^{2}T}{\partial x\partial y}\right. \nonumber \\&\left. +\,2vw\frac{\partial ^{2}T}{\partial y\partial z}+2uw\frac{\partial ^{2}T}{\partial x\partial z}\right) =\frac{k}{\rho C_{p}}\left( \frac{ \partial ^{2}T}{\partial x^{2}}+\frac{\partial ^{2}T}{\partial y^{2}}+\frac{ \partial ^{2}T}{\partial z^{2}}\right) . \end{aligned}$$

(12)

Using transformations

$$\begin{aligned} u & = \frac{cx}{1-\alpha t}r^{\prime }(\xi ),\quad {\text { }}v=\frac{cy}{1-\alpha t} s^{\prime }(\xi ),\quad {\text { }}w=\sqrt{\frac{c\nu }{1-\alpha t}[r(\xi )+s(\xi )] }, \nonumber \\ {\text { }}\theta (\xi ) & = \frac{T-T_{\infty }}{T_{w}-T_{\infty }},\quad {\text { }} \xi =\sqrt{\frac{c}{\nu (1-\alpha t)}}z,\quad {\text { }}a=a_{0}\phi (\xi ),\quad {\text { }}b=a_{0}h(\xi ). \end{aligned}$$

(13)

The continuity equation is satisfied accordingly and Eqs. (4), (5), (7–9) and (12) give:

$$\begin{aligned}&r^{\prime \prime \prime }-r^{\prime 2}+(r+s)r^{\prime \prime }-A_{1}r^{\prime }-\beta _{1}(r^{\prime \prime \prime }(r+s)^{2}-2r^{\prime }r^{\prime \prime }(r+s)-2A_{1}r^{\prime \prime }(r+s)+2A_{1}^{2}r^{\prime }+2A_{1}r^{\prime 2})-k_{1}r^{\prime }=0, \end{aligned}$$

(14)

$$\begin{aligned}&s^{\prime \prime \prime }-s^{\prime 2}+(r+s)s^{\prime \prime }-A_{1}s^{\prime }-\beta _{1}(s^{\prime \prime \prime }(r+s)^{2}-2s^{\prime }s^{\prime \prime }(r+s)-2A_{1}s^{\prime \prime }(r+s)+2A_{1}^{2}s^{\prime }+2A_{1}s^{\prime 2})-k_{1}s^{\prime }=0, \end{aligned}$$

(15)

$$\begin{aligned}&\frac{1}{Pr}\theta ^{\prime \prime }+(r+s)\theta ^{\prime }-\frac{1}{2} \xi A_{1}\theta ^{\prime }-\gamma \left[ (r+s)^{2}\theta ^{\prime \prime }-A_{1}\xi (r+s)\theta ^{\prime \prime }+\frac{1}{4}A_{1}^{2}\xi ^{2}\theta ^{\prime \prime }\right. \nonumber \\&\quad \quad \left. +\,(r+s)(r^{\prime }+s^{\prime })\theta ^{\prime }-\frac{1}{2} A_{1}\xi (r^{\prime }+s^{\prime })\theta ^{\prime }-\frac{3}{2} A_{1}(r+s)\theta ^{\prime }+\frac{3}{4}A_{1}^{2}\xi \theta ^{\prime }\right] =0, \end{aligned}$$

(16)

$$\begin{aligned}&\frac{1}{Sc}\phi ^{\prime \prime }+(r+s)\phi ^{\prime }-\frac{1}{2}A_{1}\xi \phi ^{\prime }-K\phi h^{2}=0, \end{aligned}$$

(17)

$$\begin{aligned}&\frac{\delta }{Sc}h^{\prime \prime }+(r+s)h^{\prime }-\frac{1}{2}A_{1}\xi h^{\prime }+K\phi h^{2}=0, \end{aligned}$$

(18)

$$\begin{aligned}&r^{\prime }(\xi ) =1,\quad {\text { }}r(\xi )=0,\quad s^{\prime }(\xi )=\beta _{2}{\text {,}}\quad s(\xi )=0,\quad \theta (\xi )=1{\text { at }}\xi =0,\nonumber \\&\phi ^{\prime }(\xi ) = K_{1}\phi (\xi ),\quad \delta h^{\prime }(\xi )=-K_{1}\phi (\xi ){\text { at }}\xi =0,\nonumber \\&r^{\prime }(\xi ) \rightarrow 0,\quad \ s^{\prime }(\xi )\rightarrow 0{\text {,}}\quad \theta (\xi )\rightarrow 0,\quad {\text { }}\phi (\xi )\rightarrow 1,\quad h(\xi )\rightarrow 0\;{\text {as}}\;\xi \rightarrow \infty . \end{aligned}$$

(19)

Here prime denotes derivative with respect to $\xi$, $\beta _{1}=\frac{ \lambda c}{1-\alpha t}$ is the Deborah number, $k_{1}=\nu (1-\alpha t)/{\hat{k}}c$ is the porosity parameter, $A_{1}=\frac{\alpha }{c}$ is the unsteady parameter,$Pr =\nu \rho C_{p}/k$ is the Prandtl number, $\gamma =\lambda _{1}c/(1-\alpha t)$ is the non-dimensional thermal relaxation parameter, $Sc=\nu /D_{A}$ is the Schmidt number, $K=k_{c}a_{0}^{2}(1-\alpha t)/c$ is the measure of the strength of the homogeneous reaction, $K_{1}=k_{s}\sqrt{ \nu (1-\alpha t)}/D_{A}\sqrt{c}$ is the measure of the strength of the heterogeneous reaction, $\beta _{2}=d/c$ is the ratio of stretching rates and $\delta =D_{B}/D_{A}$ is the ratio of the diffusion coefficient.

Chemical species A and B having diffusion coefficients are assumed to be of approximate size. Further assuming that diffusion coefficients $D_{A}$ and $D_{B}$ are identical, i.e., $\delta =1$ [25]. Hence we have from Eq. (19)

$$\begin{aligned} \phi (\xi )+h(\xi )=1. \end{aligned}$$

(20)

Thus Eqs. (17) and (18) become

$$\begin{aligned} \frac{1}{Sc}\phi ^{\prime \prime }+(r+s)\phi ^{\prime }-\frac{1}{2}A_{1}\xi \phi ^{\prime }-K\phi (1-\phi )^{2}=0, \end{aligned}$$

(21)

subject to the boundary conditions

$$\begin{aligned} \phi ^{\prime }(0)=K_{1}\phi (0),\quad {\text { }}\phi (\infty )\rightarrow 1. \end{aligned}$$

(22)

Skin friction coefficients along the x- and y-directions are defined as follows:

$$\begin{aligned} C_{{\text {f}}x}=\frac{\tau _{{\text {w}}x}}{\rho u_{w}^{2}},\quad {\text {}}C_{{\text {f}}y}=\frac{\tau _{{\text {w}}y}}{ \rho v_{w}^{2}}, \end{aligned}$$

(23)

where the surface shear stresses $\tau _{{\text {w}}x}$ and $\tau _{wy}$ along the x- and y- directions are given by

$$\begin{aligned} \tau _{{\text {w}}x}=\left. \mu \frac{\partial u}{\partial z}\right| _{z=0},\quad {\text { }}\tau _{{\text {w}}y}=\left. \mu \frac{\partial v}{\partial z}\right| _{z=0}. \end{aligned}$$

(24)

Dimensionless skin friction coefficients are

$$\begin{aligned} C_{{\text {f}}x}({Re}_{x})^{1/2}=(1+\beta _{1})f^{\prime \prime }(0),\quad {\text { }} C_{{\text {f}}y}({Re}_{y})^{1/2}=(1+\beta _{1})g^{\prime \prime }(0), \end{aligned}$$

(25)

where $({Re}_{x})^{1/2}=x\sqrt{c/\nu }$ and $({Re}_{y})^{1/2}=y \sqrt{c/\nu }$ denote the local Reynolds number.

3 HAM solutions

The initial guesses and auxiliary operators are taken as follows:

$$\begin{aligned} r_{0}(\xi ) & = 1-e^{-\xi },\quad s_{0}(\xi )=1-e^{-\xi },\quad {\text { }}\theta _{0}(\xi )=e^{-\xi },\quad {\text { }}\phi _{0}(\xi )=1-\frac{1}{2}e^{-K_{1}\xi }, \end{aligned}$$

(26)

$$\begin{aligned} {\mathcal {L}}_{1} & = r^{\prime \prime \prime }-r^{\prime },\quad {\mathcal {L}} _{2}=s^{\prime \prime \prime }-s^{\prime },\quad {\text { }}{\mathcal {L}}_{3}=\theta ^{\prime \prime }-\theta ,\quad {\text { }}{\mathcal {L}}_{4}=\phi ^{\prime \prime }-\phi , \end{aligned}$$

(27)

with

$$\begin{aligned} {\mathcal {L}}_{1}(c_{1}+c_{2}e^{\xi }+c_{3}e^{-\xi }) & = 0,\quad {\text { }}{\mathcal {L}} _{2}(c_{4}+c_{5}e^{\xi }+c_{6}e^{-\xi })=0,\quad {\text { }} \nonumber \\ {\mathcal {L}}_{3}(c_{7}e^{\xi }+c_{8}e^{-\xi }) & = 0,\quad {\text { }}{\mathcal {L}} _{4}(c_{9}e^{\xi }+c_{10}e^{-\xi })=0, \end{aligned}$$

(28)

in which $c_{1}-c_{10}$ are the constants.

Zeroth-order deformation equations are:

$$\begin{aligned} (1-p){\mathcal {L}}_{1}\left[ {\hat{r}}(\xi ,p)-r_{0}(\xi )\right] & = p\hbar _{r} {\mathcal {N}}_{1}[{\hat{r}}(\xi ,p),{\hat{s}}(\xi ,p)], \end{aligned}$$

(29)

$$\begin{aligned} (1-p){\mathcal {L}}_{2}\left[ {\hat{s}}(\xi ,p)-s_{0}(\xi )\right] & = p\hbar _{s} {\mathcal {N}}_{2}[{\hat{r}}(\xi ,p),{\hat{s}}(\xi ,p)], \end{aligned}$$

(30)

$$\begin{aligned} (1-p){\mathcal {L}}_{3}\left[ {\hat{\theta }}(\xi ,p)-\theta _{0}(\xi )\right] & = p\hbar _{\theta }{\mathcal {N}}_{3}[{\hat{\theta }}(\xi ,p),{\hat{r}}(\xi ,p),\hat{s }(\xi ,p)], \end{aligned}$$

(31)

$$\begin{aligned} (1-p){\mathcal {L}}_{4}\left[ {\hat{\phi }}(\xi ,p)-\phi _{0}(\xi )\right] & = p\hbar _{\phi }{\mathcal {N}}_{4}[{\hat{\phi }}(\xi ,p),{\hat{r}}(\xi ,p),{\hat{s}}(\xi ,p)], \end{aligned}$$

(32)

where $p\in [0,1]$ is the embedding parameter, ${\mathcal {N}}_{1},$ ${\mathcal {N}}_{2},$ ${\mathcal {N}}_{3}$ and ${\mathcal {N}}_{4}$ are the nonlinear operators and $\hbar _{r}$, $\hbar _{s}$, $\hbar _{\theta }$ and $\hbar _{\phi }$ are the nonzero auxiliary parameters. The nonlinear operators are

$$\begin{aligned} {\mathcal {N}}_{1}\left[ {\hat{r}}(\xi ,p),{\hat{s}}(\xi ,p)\right] & = \frac{ \partial ^{3}{\hat{r}}(\xi ,p)}{\partial \xi ^{3}}-\left( \frac{\partial \hat{r }(\xi ,p)}{\partial \xi }\right) ^{2}+({\hat{r}}(\xi ,p)+{\hat{s}}(\xi ,p))\frac{ \partial ^{2}{\hat{r}}(\xi ,p)}{\partial \xi ^{2}}-A_{1}\frac{\partial {\hat{r}} (\xi ,p)}{\partial \xi } \nonumber \\&-\,\beta _{1}\left( \left( {\hat{r}}(\xi ,p)+{\hat{s}}(\xi ,p)\right) ^{2}\frac{ \partial ^{3}{\hat{r}}(\xi ,p)}{\partial \xi ^{3}}-2({\hat{r}}(\xi ,p)+{\hat{s}} (\xi ,p))\frac{\partial {\hat{r}}(\xi ,p)}{\partial \xi }\frac{\partial ^{2} {\hat{r}}(\xi ,p)}{\partial \xi ^{2}}\right. \nonumber \\&\left. -\,2A_{1}\frac{\partial ^{2}{\hat{r}}(\xi ,p)}{\partial \xi ^{2}}(\hat{r }(\xi ,p)+{\hat{s}}(\xi ,p))+2A_{1}^{2}\frac{\partial {\hat{r}}(\xi ,p)}{ \partial v}+2A_{1}\left( \frac{\partial {\hat{r}}(\xi ,p)}{\partial \xi } \right) ^{2}\right) \nonumber \\&-\,k_{1}\frac{\partial {\hat{r}}(\xi ,p)}{\partial \xi }, \end{aligned}$$

(33)

$$\begin{aligned} {\mathcal {N}}_{2}\left[ {\hat{r}}(\xi ,p),{\hat{s}}(\xi ,p)\right] & = \frac{ \partial ^{3}{\hat{s}}(\xi ,p)}{\partial \xi ^{3}}-\left( \frac{\partial \hat{s }(\xi ,p)}{\partial \xi }\right) ^{2}+({\hat{r}}(\xi ,p)+{\hat{s}}(\xi ,p))\frac{ \partial ^{2}{\hat{s}}(\xi ,p)}{\partial \xi ^{2}}-A_{1}\frac{\partial {\hat{s}} (\xi ,p)}{\partial \xi } \nonumber \\&-\,\beta _{1}\left( \left( {\hat{r}}(\xi ,p)+{\hat{s}}(\xi ,p)\right) ^{2}\frac{ \partial ^{3}{\hat{s}}(\xi ,p)}{\partial \xi ^{3}}-2({\hat{r}}(\xi ,p)+{\hat{s}} (\xi ,p))\frac{\partial {\hat{s}}(\xi ,p)}{\partial \xi }\frac{\partial ^{2} {\hat{s}}(\xi ,p)}{\partial \xi ^{2}}\right. \nonumber \\&\left. -\,2A_{1}\frac{\partial ^{2}{\hat{s}}(\xi ,p)}{\partial \xi ^{2}}(\hat{r }(\xi ,p)+{\hat{s}}(\xi ,p))+2A_{1}^{2}\frac{\partial {\hat{s}}(\xi ,p)}{ \partial \xi }+2A_{1}\left( \frac{\partial {\hat{s}}(\xi ,p)}{\partial \xi } \right) ^{2}\right) \nonumber \\&-\,k_{1}\frac{\partial {\hat{s}}(\xi ,p)}{\partial \xi }, \end{aligned}$$

(34)

$$\begin{aligned} {\mathcal {N}}_{3}\left[ {\hat{\theta }}(\xi ,p),{\hat{r}}(\xi ,p),{\hat{s}}(\xi ,p) \right] & = \frac{1}{Pr }\frac{\partial ^{2}{\hat{\theta }}(\xi ,p)}{\partial \xi ^{2}}+({\hat{r}}(\xi ,p)+{\hat{s}}(\xi ,p))\frac{\partial {\hat{\theta }}(\xi ,p)}{\partial \xi }-\frac{1}{2}\eta A_{1}\frac{\partial {\hat{\theta }}(\xi ,p) }{\partial \xi } \nonumber \\&-\,\gamma \left( ({\hat{r}}(\xi ,p)+{\hat{s}}(\xi ,p))^{2}\frac{\partial ^{2} {\hat{\theta }}(\xi ,p)}{\partial \xi ^{2}}-A_{1}\xi ({\hat{r}}(\xi ,p)+{\hat{s}} (\xi ,p))\right. \nonumber \\&\left. \frac{\partial ^{2}{\hat{\theta }}(\xi ,p)}{\partial \xi ^{2}}+\frac{1 }{4}A_{1}^{2}\xi ^{2}\frac{\partial ^{2}{\hat{\theta }}(\xi ,p)}{\partial \xi ^{2}}+({\hat{r}}(\xi ,p)+{\hat{s}}(\xi ,p))\left( \frac{\partial {\hat{r}}(\xi ,p) }{\partial \xi }\right. \right. \nonumber \\&\left. \left. +\,\frac{\partial {\hat{s}}(\xi ,p)}{\partial \xi }\right) \frac{ \partial {\hat{\theta }}(\xi ,p)}{\partial \xi }-\frac{1}{2}A_{1}\xi \left( \frac{\partial {\hat{r}}(\xi ,p)}{\partial \xi }+\frac{\partial {\hat{s}}(\xi ,p) }{\partial \xi }\right) \frac{\partial {\hat{\theta }}(\xi ,p)}{\partial \xi } \right. \nonumber \\&\left. -\,\frac{3}{2}A_{1}({\hat{r}}(\xi ,p)+{\hat{s}}(\xi ,p))\frac{\partial {\hat{\theta }}(\xi ,p)}{\partial \xi }+\frac{3}{4}A_{1}^{2}\xi \frac{\partial {\hat{\theta }}(\xi ,p)}{\partial \xi }\right) , \end{aligned}$$

(35)

$$\begin{aligned} {\mathcal {N}}_{4}[{\hat{\phi }}(\xi ,p),{\hat{r}}(\xi ,p),{\hat{s}}(\xi ,p)] & = \frac{ 1}{Sc}\frac{\partial ^{2}{\hat{\phi }}(\xi ,p)}{\partial \xi ^{2}}+({\hat{r}}(\xi ,p)+{\hat{s}}(\xi ,p))\frac{\partial {\hat{\phi }}(\xi ,p)}{\partial \xi }-\frac{1 }{2}A_{1}\xi \frac{\partial {\hat{\phi }}(\xi ,p)}{\partial \xi } \nonumber \\&-\,k{\hat{\phi }}(\xi ,p)-k\left( {\hat{\phi }}(\xi ,p)\right) ^{3}+2k({\hat{\phi }} (\xi ,p))^{2}, \end{aligned}$$

(36)

with boundary conditions

$$\begin{aligned} {\hat{r}}^{\prime }(0,p) & = 1,\quad {\text { }}{\hat{r}}(0,p)=0,\quad {\text { }}{\hat{r}}^{\prime }(\infty ,p)=0, \end{aligned}$$

(37)

$$\begin{aligned} {\hat{s}}^{\prime }(0,p) & = \beta _{2},\quad {\text { }}{\hat{s}}(0,p)=0,\quad {\hat{s}} ^{\prime }(\infty ,p)=0, \end{aligned}$$

(38)

$$\begin{aligned} {\hat{\theta }}(0,p) & = 1,\quad {\text { }}{\hat{\theta }}(\infty ,p)=0, \end{aligned}$$

(39)

$$\begin{aligned} {\hat{\phi }}^{\prime }(0,p) & = K_{1}{\hat{\phi }}(0,p),\quad {\hat{\phi }}(\infty ,p)=1. \end{aligned}$$

(40)

The mth-order deformation equations are

$$\begin{aligned} {\mathcal {L}}_{1}\left[ r_{m}(\xi )-\chi _{m}r_{m-1}(\xi )\right] & = \hbar _{r} {\mathcal {R}}_{r,m}(\xi ), \end{aligned}$$

(41)

$$\begin{aligned} {\mathcal {L}}_{2}\left[ s_{m}(\xi )-\chi _{m}s_{m-1}(\xi )\right] & = \hbar _{s} {\mathcal {R}}_{s,m}(\xi ), \end{aligned}$$

(42)

$$\begin{aligned} {\mathcal {L}}_{3}\left[ \theta _{m}(\xi )-\chi _{m}\theta _{m-1}(\xi )\right] & = \hbar _{\theta }{\mathcal {R}}_{\theta ,m}(\xi ), \end{aligned}$$

(43)

$$\begin{aligned} {\mathcal {L}}_{4}\left[ \phi _{m}(\xi )-\chi _{m}\phi _{m-1}(\xi )\right] & = \hbar _{\phi }{\mathcal {R}}_{\phi ,m}(\xi ), \end{aligned}$$

(44)

with

$$\begin{aligned} \chi _{m} & = \left\{ \begin{array}{c} 0,\quad {\text { }}m\le 1 \\ 1,\quad {\text { }}m>1 \end{array} \right. , \end{aligned}$$

(45)

$$\begin{aligned} {\mathcal {R}}_{r,m}\left( \xi \right) & = r_{m-1}^{\prime \prime \prime }+\sum \limits _{k=0}^{m-1}\left[ r_{m-1-k}r_{k}^{\prime \prime }+s_{m-1-k}r_{k}^{\prime \prime }-r_{m-1-k}^{\prime }r_{k}^{\prime }\right] -A_{1}r_{m-1}^{\prime }-\beta _{1}\left( \mathop {\textstyle \sum }\limits _{l=0}^{m-1}r_{m-1-l}^{\prime \prime \prime }\left( \mathop {\textstyle \sum }\limits _{j=0}^{l}r_{l-j}r_{j}\right. \right. \nonumber \\&\left. +\,\mathop {\textstyle \sum }\limits _{j=0}^{l}s_{l-j}s_{j}+2\mathop {\textstyle \sum }\limits _{j=0}^{l}r_{l-j}s_{j} \right)- \mathop {\textstyle \sum }\limits _{l=0}^{m-1}r_{m-1-l}^{\prime \prime }\left( 2\mathop {\textstyle \sum }\limits _{j=0}^{l}r_{l-j}^{\prime }r_{j}+2\mathop {\textstyle \sum }\limits _{j=0}^{l}r_{l-j}^{\prime }s_{j}\right) +2A_{1}^{2}r_{m-1}^{\prime } \nonumber \\&\left. -\,2A_{1}\sum \limits _{k=0}^{m-1}[r_{m-1-k}^{\prime \prime }r_{k}-r_{m-1-k}^{\prime \prime }s_{k}]+2A_{1}\sum \limits _{k=0}^{m-1}r_{m-1-k}^{\prime }r_{k}^{\prime }\right) -k_{1}r_{m-1}^{\prime }, \end{aligned}$$

(46)

$$\begin{aligned} {\mathcal {R}}_{s,m}\left( \xi \right) & = s_{m-1}^{\prime \prime \prime }+\sum \limits _{k=0}^{m-1}\left[ r_{m-1-k}s_{k}^{\prime \prime }+s_{m-1-k}s_{k}^{\prime \prime }-s_{m-1-k}^{\prime }s_{k}^{\prime }\right] -A_{1}s_{m-1}^{\prime }-\beta _{1}\left( \mathop {\textstyle \sum }\limits _{l=0}^{m-1}s_{m-1-l}^{\prime \prime \prime }\left( \mathop {\textstyle \sum }\limits _{j=0}^{l}r_{l-j}r_{j}\right. \right. \nonumber \\&\left. +\,\mathop {\textstyle \sum }\limits _{j=0}^{l}s_{l-j}s_{j}+2\mathop {\textstyle \sum }\limits _{j=0}^{l}r_{l-j}s_{j}\right)- \mathop {\textstyle \sum }\limits _{l=0}^{m-1}s_{m-1-l}^{\prime \prime }\left( 2\mathop {\textstyle \sum }\limits _{j=0}^{l}r_{l-j}s_{j}^{\prime }+2\mathop {\textstyle \sum }\limits _{j=0}^{l}s_{l-j}s_{j}^{\prime }\right) +2A_{1}^{2}s_{m-1}^{\prime } \nonumber \\&\left. -\,2A_{1}\sum \limits _{k=0}^{m-1}[s_{m-1-k}^{\prime \prime }r_{k}-s_{m-1-k}^{\prime \prime }s_{k}]+2A_{1}\sum \limits _{k=0}^{m-1}s_{m-1-k}^{\prime }s_{k}^{\prime }\right) -k_{1}s_{m-1}^{\prime }, \end{aligned}$$

(47)

$$\begin{aligned} {\mathcal {R}}_{\theta ,m}(\xi ) & = \frac{1}{Pr }\theta _{m-1}^{\prime \prime }-\frac{1}{2} A_{1}\xi \theta _{m-1}^{\prime }+\mathop {\textstyle \sum }\limits _{l=0}^{m-1}\left( \theta _{m-1-l}^{\prime }r_{l}+\theta _{m-1-l}^{\prime }s_{l}\right) -\,\gamma \left[ \theta _{m-1-l}^{\prime \prime }\mathop {\textstyle \sum }\limits _{j=0}^{l}[r_{l-j}r_{j}+s_{l-j}s_{j}+2r_{l-j}s_{j}]+\theta _{m-1-l}^{^{\prime }}\mathop {\textstyle \sum }\limits _{j=0}^{l}[r_{l-j}r_{j}^{\prime }+s_{l-j}s_{j}^{\prime }\right. \nonumber \\&\left. \left. +\,r_{l-j}s_{j}^{\prime }+s_{l-j}r_{j}^{\prime }]-A_{1}\xi \theta _{m-1-l}^{^{\prime \prime }}r_{l}-A_{1}\xi \theta _{m-1-l}^{^{\prime \prime }}s_{l}-\frac{1}{2}A_{1}\xi \theta _{m-1-l}^{\prime }r_{l}\right. \right. \nonumber \\&\left. -\,\frac{1}{2}A_{1}\xi \theta _{m-1-l}^{\prime }s_{l}-\frac{3}{2} A_{1}\theta _{m-1-l}^{\prime }r_{l}-\frac{3}{2}A_{1}\theta _{m-1-l}^{\prime }s_{l}\right] , \end{aligned}$$

(48)

$$\begin{aligned} {\mathcal {R}}_{\phi ,m}(\xi ) & = \frac{1}{Sc}\phi _{m-1}^{\prime \prime }-\frac{1 }{2}A_{1}\xi \phi _{m-1}^{\prime }+\mathop {\textstyle \sum }\limits _{l=0}^{m-1}\left[ \phi _{m-1-l}^{\prime }r_{l}+\phi _{m-1-l}^{\prime }s_{l}-K\phi _{m-1-l}\mathop {\textstyle \sum }\limits _{j=0}^{l}\phi _{l-j}\phi _{j}+2k\phi _{m-1-l}\phi _{l} \right] -K\phi _{m-1} \end{aligned}$$

(49)

and the boundary conditions

$$\begin{aligned} r_{m}^{\prime }(0) & = r_{m}(0)=r_{m}^{\prime }(\infty )=s_{m}^{\prime }(0)=s_{m}(0)=s_{m}^{\prime }(\infty )=0 \nonumber \\ \theta _{m}(0) & = \theta _{m}(\infty )=\phi _{m}^{\prime }(0)-K_{s}\phi _{m}(0)=\phi _{m}(\infty )=0. \end{aligned}$$

(50)

The general solutions $(r_{m},$ $s_{m},$ $\theta _{m},\ \phi _{m})$ comprising the special solutions $(r_{m}^{*},$ $s_{m}^{*},$ $\theta _{m}^{*},$ $\phi _{m}^{*})$ are given by

$$\begin{aligned} r_{m}(\xi ) & = r_{m}^{*}(\xi )+c_{1}+c_{2}e^{\xi }+c_{3}e^{-\xi }, \nonumber \\ s_{m}(\xi ) & = s_{m}^{*}(\xi )+c_{4}+c_{5}e^{\xi }+c_{6}e^{-\xi }, \nonumber \\ \theta _{m}(\xi ) & = \theta _{m}^{*}(\xi )+c_{7}e^{\xi }+c_{8}e^{-\xi }, \nonumber \\ \phi _{m}(\xi ) & = \phi _{m}^{*}(\xi )+c_{9}e^{\xi }+c_{10}e^{-\xi }, \end{aligned}$$

(51)

where the constants $c_{i}$ ($i=1,2,\ldots ,10$) with the boundary conditions (50) are

$$\begin{aligned} c_{2} & = c_{5}=c_{7}=c_{9}=0,\quad {\text { }}c_{3}=\frac{\partial r_{m}^{*}(\xi ) }{\partial \xi }|_{\xi =0},\quad {\text { }}c_{6}=\frac{\partial s_{m}^{*}(\xi )}{ \partial \xi }|_{\xi =0},{\text { }} \nonumber \\ c_{1} & = -c_{3}-r_{m}^{*}(0),\quad {\text { }}c_{4}=-c_{6}-s_{m}^{*}(0),\quad {\text { }}c_{8}=-\theta _{m}^{*}(0),{\text { }} \nonumber \\ c_{10} & = \frac{1}{1+K_{1}}\left( \frac{\partial \phi _{m}^{*}(\xi )}{ \partial \xi }|_{\xi =0}-K_{1}\phi _{m}^{*}(0)\right) . \end{aligned}$$

(52)

4 Convergence analysis

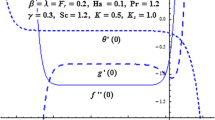
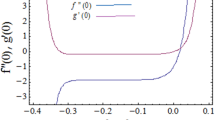
Homotopy analysis method gives us great choice to obtain the convergence of the series solutions. Region of convergence is controlled by auxiliary parameters $\hbar _{r},$ $\hbar _{s},$ $\hbar _{\theta }$ and $\hbar _{\phi }$. The admissible ranges of these parameters are $-\,0.9\le \hbar _{r}\le -\,0.5,$ $-\,1.0\le \hbar _{s}\le -\,0.4,$ $-\,1.4\le \hbar _{\theta }\le -\,0.6$ and $-\,0.8\le \hbar _{\phi }\le -\,0.4$ (Figs. 2, 3, 4, 5).

Fig. 2

$\hbar$-curve for $r^{\prime \prime }(0)$

Fig. 3

$\hbar$-curve for $s^{\prime \prime }(0)$

Fig. 4

$\hbar$-curve for $\theta ^{\prime }(0)$

Fig. 5

$\hbar$-curve for $\phi ^{\prime }(0)$

Table 1 Convergence of series solutions when $A_{1}=0.1,$ $\gamma =1.0,$ $\beta _{1}=0.5,$ $\beta _{2}=0.5,$ $K=0.2,$ $Pr =1.0,$ $Sc=1.4,$ $k_{1}=0.6$ and $K_{1}=0.7$

Table 1 gives the convergence of series solutions of velocities, temperature and concentration distributions.

5 Results and discussion

5.1 Dimensionless velocity profiles

Here we discuss the impact of different embedded parameters on dimensionless velocity profiles $r^{\prime }$ and $s^{\prime }$. Figure 6 depicts the variation of Deborah number $\beta _{1}$ on velocity profiles. As viscous forces are dominant for larger Deborah number which resist the fluid motion, so fluid flows along the x- and y-directions. Figure 7 shows the impact of ratio of stretching rates $\beta _{2}$ on velocity profiles. Increasing values of $\beta _{2}$ shows higher rate of stretching. When we increase the ratio of stretching rates, the velocity along x-direction decreases, while the velocity along y-direction increases. Figure 8 presents the velocity profiles for larger value of porosity parameter $k_{1}.$ Here velocity profiles are decreasing functions of $k_{1}$. As increasing porosity parameter causes a decrease in permeability of fluid which reduces the fluid flow. Impact of unsteady parameter $A_{1}$ on velocity field is shown in Fig. 9. When unsteady parameter $A_{1}$ increases, the stretching constant decreases hence velocity decreases.

Fig. 6

Behavior of $\beta _{1}$ on $r^{\prime }(\xi )$ and $s^{\prime }(\xi )$

Fig. 7

Behavior of $\beta _{2}$ on $r^{\prime }(\xi )$ and $s^{\prime }(\xi )$

Fig. 8

Behavior of $k_{1}$ on $r^{\prime }(\xi )$ and $s^{\prime }(\xi )$

Fig. 9

Behavior of $A_{1}$ on $r^{\prime }(\xi )$ and $s^{\prime }(\xi )$

5.2 Dimensionless temperature profile

Now we discuss the behavior of involved parameters on dimensionless temperature profile $\theta (\xi )$. Impact of thermal relaxation time $\gamma$ on temperature field is illustrated in Fig. 10. Temperature profile decreases for increasing thermal relaxation time. Because particles show non-conducting behavior when thermal relaxation time is increased, i.e., particles need more time to transfer heat so the temperature decreases. Figure 11 shows the variation of Prandtl number Pr on temperature profile. As thermal diffusivity decreases, when the Prandtl number is enhanced; hence, the temperature profile decreases.

Fig. 10

Behavior of $\gamma$ on $\theta \left( \xi \right)$

Fig. 11

Behavior of Pr on $\theta (\xi )$

5.3 Dimensionless concentration profile

Figures 12, 13, 14 and 15 show the behavior of Schmidt number Sc, the measure of strength of the homogeneous reactions K, the measure of strength of the heterogeneous reaction $K$ and the ratio of stretching rates $\beta _{2}$ on concentration profile $\phi (\xi )$. Figure 12 depicts impact of Sc on $\phi (\xi )$. Larger values of Schmidt number correspond to an increase in concentration profile. Ratio of momentum to mass diffusion rate is known as Schmidt number. For higher Schmidt number, the momentum diffusion rate increases and consequently concentration field enhances. Figure  13 shows there is decrease in concentration field when homogeneous reaction parameter K increases. This is because during homogeneous reaction the reactants are consumed. Figure 14 depicts that concentration profile enhances when we increase the heterogeneous reaction parameter $K_{1}$. Figure 15 illustrates the behavior of $\beta _{2}$ on $\phi (\xi ).$ Here larger $\beta _{2}$ enhances the concentration field increases. This is because of decreased stretching rate in x-direction.

Fig. 12

Behavior of Sc on $\phi (\xi )$

Fig. 13

Behavior of K on $\phi (\xi )$

Fig. 14

Behavior of $K_{1}$ on $\phi (\xi )$

Fig. 15

Behavior of $\beta _{2}$ on $\phi (0)$

5.4 Surface concentration

Effects of homogeneous reaction parameter K and heterogeneous reaction parameter $K_{1}$ on surface concentration $\phi (0)$ are shown in the Figs. 16 and 17. From Fig. 16, we observe that $\phi (0)$ decreases when we increase the strength of homogeneous reaction K. Figure 17 shows that surface concentration enhances for larger strength of heterogeneous reaction parameter $K_{1}.$ Figure 18 depicts behavior of homogeneous reaction parameter K via Schmidt number Sc on surface concentration $\phi (0).$ Here $\phi (0)$ decreases when K is increased.

Fig. 16

Behavior of K on $\phi (0)$

Fig. 17

Behavior of $K_{1}$ on $\phi (0)$

Fig. 18

Behavior of K on $\phi (0)$

Table 2 Values of $-f^{\prime \prime }(0)$ for various values of Deborah number $\beta _{1}$ when $A_{1}=k_{1}=0$

Table 2 shows the comparison of the present results with the numerical solution of Mukhopadhyay [9] and Hayat et al. [10] in limiting case. It is found that our solution has good agreement with the limiting numerical solution.

6 Main results

Cattaneo–Christov heat flux model is used to examine time-dependent flow of Maxwell fluid with chemical reaction. Main points are given below:

• Velocity profiles are decreasing functions of Deborah number, porosity parameter and unsteady parameter.

• Temperature is decreasing function of thermal relaxation time and Prandtl number.

• Concentration profile increases for larger Schmidt number and it decreases for when homogeneous reaction parameter increases.

• Impact of strengths of homogeneous and heterogeneous reactions is opposite on wall concentration.

• Present problem has many applications like food processing, clay coatings, hydrometallurgical industry, fog formation and dispersion.