Effect of thickness stretching on the static deformations, natural frequencies, and critical buckling loads of laminated composite and sandwich beams

Abstract

The present study investigates the bending, buckling, and vibration responses of shear deformable laminated composite and sandwich beams using trigonometric shear and normal deformation theory. The most important feature of the present theory is that it includes the effects of transverse shear and normal deformations, i.e., the effect of thickness stretching. Therefore, the theory is also called as a quasi-2D theory. The axial displacement uses sine function in terms of the thickness coordinate to include the effect of transverse shear deformation, and the transverse displacement uses cosine function in terms of the thickness coordinate to include the effect of transverse normal deformation, i.e., the thickness stretching. The present theory satisfies the zero shear stress conditions at top and bottom surfaces of the beam without using shear correction factor. Governing differential equations and associated boundary conditions of the theory are derived by employing the dynamic version of principle of virtual work. Navier-type closed-form solutions are obtained for simply supported boundary conditions. The numerical results are obtained for deflections, stresses, natural frequencies, and critical buckling loads for isotropic, laminated composite, and sandwich beams. Since exact elasticity solutions for laminated composite and sandwich beams are not available in the literature, the results are compared with those obtained by using other higher-order shear deformation theories to demonstrate the accuracy of the proposed theory.

1 Introduction

Laminated composite and sandwich beams are being widely used in many industries due to their attractive properties such as high strength and stiffness-to-weight ratio. The effects of transverse shear deformation and thickness stretching are more pronounced in the thick beams. Therefore, static bending, free vibration, and buckling analysis of laminated composite and sandwich thick beams have received widespread attention in recent years. Analysis of composite beams is difficult by using three-dimensional (3D) elasticity theory due to complex mathematics. Therefore, still 3D elasticity solutions for the bending, buckling, and free vibration analysis of laminated composite and sandwich beams are not available in the literature. This led to the development of approximate beam theories for the analysis of beams. Various beam theories are developed by the researchers for the analysis of laminated composite and sandwich beams. Recently, these theories are reviewed by Sayyad and Ghugal [1].

The effects of shear deformation and thickness stretching are neglected by classical thin beam theory (CBT) developed by Bernoulli–Euler [2, 3]. Timoshenko [4, 5] was the first person who considered the effect of shear deformation in his first order shear deformation theory (FSDT) which is also called as Timoshenko beam theory (TBT). But this theory needs shear correction factor and gives constant shear strain through the thickness. These limitations of CBT and TBT led the foundation for the development of refined beam theories. Several higher-order shear deformation theories (HSDTs) are developed by researchers which consider the effect of transverse shear deformation. These HSDTs are classified as equivalent single-layer theories, layerwise theories, and zigzag theories. The present study deals with the analysis of composite beams using equivalent single-layer theories.

1.1 Motivation of the present study

It can be noted that an initiation of delamination in multilayered composite structures is caused due to interlaminar transverse shear and normal stresses. Therefore, any refinement of classical models is meaningless, in general, unless the effects of interlaminar continuous transverse shear and normal stresses are both taken into account in a multilayered beam theory [6,7,8]. However, no consideration is given to the effect of transverse normal deformation/strain ($\varepsilon_{z} \ne 0$) in higher-order beam theories existing in the literature when these theories are applied to laminated composite and sandwich beams in view of minimizing the number of unknown variables. Therefore, refined theories which consider the effects of transverse normal deformations, i.e., thickness stretching, need more attention. Table 1 shows the review of various beam theories available in the literature.

Table 1 Review of various beam theories with and without normal deformation effect ($\varepsilon_{z}$)

1.2 Novelty of the present theory and major contributions

• 1. From Table 1, it is pointed out that very few theories are available in the literature which consider the effects of transverse normal deformation. Also, most of them are applied for the analysis of plates. It can be noted that the well-known theory of Reddy [11] also neglects the effect of transverse normal deformation. Therefore, the present study focuses on the study of the effects of transverse shear and normal deformations on static deformation, natural frequencies, and critical buckling loads of laminated composite and sandwich beams using trigonometric shear and normal deformation theory.

• 2. The most important feature of the present theory is that it includes the effects of transverse shear and normal deformations, i.e., the effect of thickness stretching. The axial displacement uses sine function in terms of the thickness coordinate to include the effect of transverse shear deformation, and the transverse displacement uses cosine function in terms of the thickness coordinate to include the effect of transverse normal deformation, i.e., thickness stretching.

• 3. The kinematics of the present theory is much richer than those of the other higher-order shear deformation theories, because if the trigonometric term is expanded in power series, the kinematics of higher-order theories is implicitly taken into account to good deal of extent.

• 4. In polynomial-type higher-order shear deformation theories, it needs to be noted that not only every additional power of thickness coordinate in the displacement field introduces an additional unknown variable in those theories, but these variables are also difficult to interpret physically. Thus, the use of the sinusoidal function (non-polynomial type) in terms of thickness coordinate enhances the richness of the theory and also results in reduction in the number of unknown variables as compared to other type of displacement-based higher-order theories without loss of physics of the problem in modeling.

• 5. The present theory satisfies the zero shear stress conditions at top and bottom surfaces of the beam without using problem-dependent shear correction factor.

• 6. The estimation of through-the-thickness distributions of interlaminar transverse shear and normal stresses using equations of equilibrium of the theory of elasticity has not been studied satisfactorily by the various researchers as can be seen from the open literature. Evaluation of these interlaminar stresses in the present study is an important contribution.

• 7. The study of global response of softcore sandwich structures is a challenging problem in physical modeling, especially using simplified (1D or 2D) theories, rather than 3D elasticity. In the present study, deflections, interlaminar stresses, natural frequencies of various modes of vibration and critical buckling loads are obtained for softcore sandwich beams which can be served as benchmark solutions and can be treated as another important contribution of the present study.

In the present study, governing differential equations and associated boundary conditions of the theory are derived by employing the dynamic version of principle of virtual work and the fundamental lemma of calculus of variations. Navier-type closed-form solutions are obtained for simply supported isotropic, laminated composite, and sandwich beams. The results of displacements, stresses, natural frequencies, and critical buckling loads are compared with the theories existing in literature [44,45,46,47,48,49,50,51,52,53,54,55,56,57,58] to demonstrate the accuracy of the proposed theory.

2 Beam under consideration

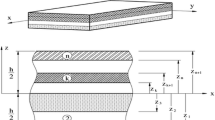
Consider a beam of rectangular cross section (b × h) and span L as shown in Fig. 1. The beam is composed of N number of thin layers perfectly bonded together. The beam is assumed in a Cartesian coordinate system where the x-, y-, and z-axes are taken along the length, the width, and the thickness of the beam, respectively. The z-axis is taken downward positive. The beam is subjected to transverse loading q (x) on the upper surface of the beam in case of bending and subjected to axial compressive forces ($N_{x}^{0}$) in case of buckling. The transverse and axial loads are assumed to be zero for the free vibration analysis.

Fig. 1

Beam geometry, lamina material axes, and laminate reference axes

2.1 Kinematics of the present beam theory

The displacement field of the present trigonometric shear and normal deformation theory is given as:

$$\begin{aligned} & u\left( {x,z,t} \right) = u_{0} \left( {x,t} \right) + u_{\text{b}} \left( {x,z,t} \right) + u_{\text{s}} \left( {x,z,t} \right) \\ & w\left( {x,z,t} \right) = w_{0} \left( {x,t} \right) + w_{\text{s}} \left( {x,z,t} \right) \\ \end{aligned}$$

(1)

where $u_{0}$ is the axial displacement of the neutral axis along x-axis, $u_{\text{b}}$ is the bending component analogous to the Euler–Bernoulli beam theory, and $u_{\text{s}}$ is the shear component assumed to be sinusoidal in nature with respect to thickness coordinate. The transverse displacement w in z direction is assumed to be a function of x and z coordinates. Therefore, the displacement field of the present trigonometric shear and normal deformation beam theory takes the following form.

$$\begin{aligned} & u\left( {x,z,t} \right) = u_{0} - zw_{0,x} + f\left( {\bar{z}} \right)\,\phi \left( {x,t} \right), \\ & w\left( {x,z,t} \right) = w_{0} \left( {x,t} \right) + g\left( {\bar{z}} \right)\,\xi \left( {x,t} \right) \\ \end{aligned}$$

(2)

where $u_{0} ,\,\,w_{0} ,\,\,\phi \,\,{\text{and}}\,\,\xi$ are the four unknown displacement functions of the neutral axis of the beam, while $f\left( {\bar{z}} \right)$ and $g\left( {\bar{z}} \right)$ represent functions determining the distribution of the transverse shear and normal stresses along the thickness of the beam. When transverse displacement w is a function of z coordinate, transverse normal strain $\varepsilon_{z}$ is not equal to zero which represent the thickness stretching effect. The kinematics proposed in Eq. (2) is strongly based on solution of three-dimensional Navier’s equations of elastostatics for thick plate under flexure presented by Cheng [59] which involves transverse shear stress and transverse normal stress. The kinematics of proposed theory is the reduction problem from three-dimensional considerations to one-dimensional one. Hence, the theory represented by Eq. (2) is correct deduction from the three- dimensional elasticity for thick plate.

The nonzero strain components associated with the present displacement field are as follows:

$$\begin{aligned} & \varepsilon_{x} = \varepsilon_{x}^{0} + z\varepsilon_{x}^{1} + f\left( {\bar{z}} \right)\,\varepsilon_{x}^{2} , \\ & \varepsilon_{z} = g'\left( {\bar{z}} \right)\,\xi , \\ & \gamma_{xz} = g\left( {\bar{z}} \right)\gamma_{xz}^{0} + f'\left( {\bar{z}} \right)\phi \\ \end{aligned}$$

(3)

where

$$\begin{aligned} & \varepsilon_{x}^{0} = u_{0,x} ,\quad \varepsilon_{x}^{1} = - w_{0,xx} ,\quad \varepsilon_{x}^{2} = \,\phi_{,x} ,\quad \gamma_{xz}^{0} = \xi_{,x} , \\ & f\left( {\bar{z}} \right) = \left( {h/\pi } \right){ \sin }\left( {\pi \bar{z}} \right)\quad {\text{and}}\quad g\left( {\bar{z}} \right) = \left( {h/\pi } \right){ \cos }\left( {\pi \bar{z}} \right) \\ \end{aligned}$$

(4)

where $\bar{z} = z/h$ and ‘,_x’ represents the derivative with respect to x. Here, $\varepsilon_{z} \ne 0$ shows that the present theory considered the effect of transverse normal deformation, i.e., thickness stretching. Many well-known theories neglect this effect as shown in Table 1.

2.2 Constitutive relations

Since the present theory considered the effects of both transverse shear and normal deformations, a two-dimensional Hooke’s law is used to obtained stress quantities in the beam domain. The laminate is made of several orthotropic layers. The constitutive relations in the kth layer of laminate are given as:

$$\left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{z} } \\ {\tau_{xz} } \\ \end{array} } \right\}^{\left( k \right)} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{13} } & 0 \\ {Q_{13} } & {Q_{33} } & 0 \\ 0 & 0 & {Q_{55} } \\ \end{array} } \right]^{\left( k \right)} \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{z} } \\ {\gamma_{xz} } \\ \end{array} } \right\}^{\left( k \right)}$$

(5)

where $\left\{ \sigma \right\}^{\left( k \right)}$ is the stress vector, $\left\{ \varepsilon \right\}^{\left( k \right)}$ is the strain vector and $\left[ {Q_{ij} } \right]^{\left( k \right)}$ is the transformed rigidity matrix. The elements of transformed rigidity matrix are as follows:

$$Q_{11} = \frac{{E_{1} }}{{1 - \mu_{13} \,\mu_{31} }};\quad Q_{13} = \frac{{\mu_{13} E_{3} }}{{1 - \mu_{13} \,\mu_{31} }};\quad Q_{33} = \frac{{E_{3} }}{{1 - \mu_{13} \,\mu_{31} }};\quad Q_{55} = G_{13}$$

(6)

Here $E_{i} ,G_{ij} ,\mu_{ij} \;\left( {i,j = 1,3} \right)$ are the material properties of lamina and 1, 2, 3 are the lamina fiber (material) axes, and x, y, z are the laminate reference axes (see Fig. 1). The principal material axes of lamina (1, 2, 3) may not coincide with the reference axes of the laminate (x, y, z) in case of angle ply laminates. It is therefore necessary to transform the constitutive relations from lamina fiber axes to laminate reference axes.

2.3 Equations of motion

The equations of motion of the proposed theory are derived using dynamic version of principle of virtual work. The principle of virtual work is applied in the following analytical form:

$$\begin{aligned} & \sum\limits_{k = 1}^{N} b \int_{{h_{k} }}^{{h_{k + 1} }} {\int_{0}^{L} {\left[ {\sigma_{x}^{k} \delta \varepsilon_{x} + \sigma_{z}^{k} \delta \varepsilon_{z} + \tau_{xz}^{k} \delta \gamma_{zx} } \right]} {\text{d}}x{\text{d}}z} - \int_{0}^{L} {q\left( x \right)\delta w{\text{d}}x} \\ & + \;\rho^{\left( k \right)} \sum\limits_{k = 1}^{N} {\int_{{h_{k} }}^{{h_{k + 1} }} {\int_{0}^{L} {\left[ {u_{,tt} \delta u + w_{,tt} \delta w} \right]{\text{d}}x{\text{d}}z} } } - \int_{0}^{L} {N_{x}^{0} w_{,x} \delta w_{0,x} {\text{d}}x} = 0\\ \end{aligned}$$

(7)

where $\rho$ is the mass per unit volume and $\delta$ denotes the variational operator. Substituting expressions for virtual strains and displacements into the Eq. (7) and introducing stress resultants, one can write:

$$\begin{aligned} & \int_{0}^{L} {\left[ {N_{x} \delta u_{0,x} - M_{x}^{\text{c}} \delta w_{0,xx} + M_{x}^{\text{s}} \delta \phi_{,x} + V_{z} \delta \xi + V_{x} \delta \xi_{,x} + V_{x} \delta \phi } \right]{\text{d}}x} - \int_{0}^{L} {q\left( x \right)\delta w{\text{d}}x} \\ & + I_{1} \int_{0}^{L} {\left( {u_{0,tt} \delta u_{0} + w_{0,tt} \delta w_{0} } \right){\text{d}}x} - I_{2} \int_{0}^{L} {\left( {u_{0,tt} \delta w_{0,x} + w_{0,xtt} \delta u_{0} } \right){\text{d}}x} + I_{3} \int_{0}^{L} {\left( {u_{0,tt} \delta \phi + \phi_{,tt} \delta u_{0} } \right){\text{d}}x} \\ & + I_{4} \int_{0}^{L} {w_{0,xtt} \delta w_{0,x} {\text{d}}x} - I_{5} \int_{0}^{L} {\left( {w_{0,xtt} \delta \phi + \phi_{,tt} \delta w_{0,x} } \right){\text{d}}x} + I_{6} \int_{0}^{L} {\left( {w_{0,tt} \delta \xi + \xi_{,tt} \delta w_{0} } \right){\text{d}}x} \\ & + I_{7} \int_{0}^{L} {\phi_{,tt} \delta \phi {\text{d}}x + I_{8} } \int_{0}^{L} {\xi_{,tt} \delta \xi {\text{d}}x - N_{x}^{0} } \int_{0}^{L} {w_{,x} \delta w_{0,x} {\text{d}}x} = 0 \\ \end{aligned}$$

(8)

Integrating the Eq. (8) by parts and setting the coefficients of $\delta u_{0} ,\;\,\delta w_{0} ,\;\,\delta \phi \;{\text{and}}\;\delta \xi$ equal to zero, the following governing equations and boundary conditions are obtained:

$$\begin{aligned} & \delta u_{0} \text{:}{\text{N}}_{\text{x,x}} = I_{1} u_{0,tt} - I_{2} w_{0,xtt} + I_{3} \phi_{,tt} \\ & \delta w\text{:}{\text{M}}_{x,xx}^{\text{c}} + {\text{q}} - N_{x}^{0} w_{0,xx} = I_{2} u_{0,xtt} - I_{4} w_{0,xxtt} + I_{1} w_{0,tt} + I_{5} \phi_{,xtt} + I_{6} \xi_{,tt} \\ & \delta \phi \text{:}{\text{M}}_{\text{x,x}}^{\text{s}} - {\text{V}}_{x} = I_{3} u_{0,tt} - I_{5} w_{0,xtt} + I_{7} \phi_{,tt} \\ & \delta \xi \text{:}{\text{V}}_{x,x} - \frac{\pi }{h}V_{z} = I_{6} w_{0,tt} + I_{8} \xi_{,tt} \\ \end{aligned}$$

(9)

where $N_{x}$ is the axial force resultant, ${\text{M}}_{x}^{\text{c}}$ is the moment resultant analogous to classical beam theory; ${\text{M}}_{\text{x}}^{\text{s}}$ is the refined moment due to transverse shear deformation effect, $V_{x}$ and $V_{z}$ are the shear force resultants due to transverse shear deformation and transverse normal deformation effects, respectively. These force and moment resultants acting on the cross section of the laminate are defined as:

$$\begin{aligned} & N_{x} = \sum\limits_{k = 1}^{N} {\int_{{h_{k} }}^{{h_{k + 1} }} {\sigma_{x}^{k} {\text{d}}z} } = A_{11} u_{0,x} - B_{11} w_{0,xx} + As_{11} \phi_{,x} - \frac{\pi }{h}As_{12} \xi \\ & M_{x}^{\text{c}} = \sum\limits_{k = 1}^{N} {\int_{{h_{k} }}^{{h_{k + 1} }} {\sigma_{x}^{k} z{\text{d}}z} } = B_{11} u_{0,x} - D_{11} w_{0,xx} + Bs_{11} \phi_{,x} - \frac{\pi }{h}Bs_{12} \xi \\ & M_{x}^{\text{s}} = \sum\limits_{k = 1}^{N} {\int_{{h_{k} }}^{{h_{k + 1} }} {\sigma_{x}^{k} f\left( {\bar{z}} \right){\text{d}}z} } = As_{11} u_{0,x} - Bs_{11} w_{0,xx} + Ass_{11} \phi_{,x} - \frac{\pi }{h}Ass_{12} \xi \\ & V_{x} = \sum\limits_{k = 1}^{N} {\int_{{h_{k} }}^{{h_{k + 1} }} {\tau_{xz}^{k} f^{\prime}\left( {\bar{z}} \right){\kern 1pt} {\text{d}}z} } = Acc_{55} \left( {\phi + \frac{h}{\pi }\xi_{,x} } \right) \\ & V_{z} = \sum\limits_{k = 1}^{N} {\int_{{h_{k} }}^{{h_{k + 1} }} {\sigma_{zz}^{k} g^{\prime}\left( {\bar{z}} \right){\kern 1pt} {\text{d}}z} } = - \frac{\pi }{h}\left[ {As_{12} u_{0,x} - Bs_{12} w_{0,xx} + Ass_{12} \phi_{,x} - \frac{\pi }{h}Ass_{22} \xi } \right] \\ & Q_{x} = M_{x,x}^{\text{c}} = B_{11} u_{0,xx} - D_{11} w_{0,xxx} + Bs_{11} \phi_{,xx} - \frac{\pi }{h}Bs_{12} \xi_{,x} \\ \end{aligned}$$

(10)

The boundary conditions at the supports (x = 0 and x = L) of the beam are of the following form:

$${\text{Either}}\;N_{x} = 0\;{\text{or}}\;u_{0} = 0\;{\text{is}}\;{\text{prescribed}}$$

(11)

$${\text{Either}}\;V_{x} = 0\;{\text{or}}\;w = 0\;{\text{is}}\;{\text{prescribed}}$$

(12)

$${\text{Either}}\;M_{x}^{\text{c}} = 0\;{\text{or}}\;w_{,x} = 0\;{\text{is}}\;{\text{prescribed}}$$

(13)

$${\text{Either}}\;M_{x}^{\text{s}} = 0\;{\text{or}}\;\phi = 0\;{\text{is}}\;{\text{prescribed}}$$

(14)

$${\text{Either}}\;V_{z} = 0\;{\text{or}}\;\xi = 0\;{\text{is}}\;{\text{prescribed}}$$

(15)

The governing equations in terms of unknown variables ($u_{0} ,\,w_{0} ,\,\phi \,{\text{and}}\,\xi$) are obtained as follows:

$$- A_{11} u_{0,xx} + B_{11} w_{0,xxx} - As_{11} \phi_{,xx} + As_{13} \frac{\pi }{h}\xi_{,x} + I_{1} u_{0,tt} - I_{2} w_{0,xtt} + I_{3} \phi_{,tt} = 0$$

(16)

$$- B_{11} u_{0,xxx} + D_{11} w_{0,xxxx} - Bs_{11} \phi_{,xxx} + \frac{\pi }{h}Bs_{13} \xi_{,xx} + I_{2} u_{0,xtt} - I_{4} w_{0,xxtt} + I_{1} w_{0,tt} + I_{5} \phi_{,xtt} = q + N_{x}^{0} w_{0,xx}$$

(17)

$$- As_{11} u_{0,xx} + Bs_{11} w_{0,xxx} - Ass_{11} \phi_{,xx} + Acc_{55} \phi + Ass_{13} \frac{\pi }{h}\xi_{,x} + Acc_{55} \frac{h}{\pi }\xi_{,x} + I_{3} u_{0,tt} - I_{5} w_{0,xtt} + I_{7} \phi_{,tt} = 0$$

(18)

$$- \frac{\pi }{h}As_{13} u_{0,x} + \frac{\pi }{h}Bs_{13} w_{0,xx} - \left( {\frac{\pi }{h}Ass_{13} + \frac{h}{\pi }Acc_{55} } \right)\phi_{,x} - \frac{{h^{2} }}{{\pi^{2} }}Acc_{55} \xi_{,xx} + \frac{{\pi^{2} }}{{h^{2} }}Ass_{33} \xi + I_{6} w_{0,tt} \,\, + I_{8} \xi_{,tt} = 0$$

(19)

where the beam stiffness and inertia constants are defined as follows:

$$\begin{aligned} & \left\{ {\begin{array}{*{20}c} {A_{ij} } & {B_{ij} } & {D_{ij} } \\ \end{array} } \right\} = \sum\limits_{k = 1}^{N} {\int\limits_{{h_{k} }}^{{h_{k + 1} }} {Q_{ij}^{\left( k \right)} \left\{ {\begin{array}{*{20}c} 1 & z & {z^{2} } \\ \end{array} } \right\}{\text{d}}z} ,} \quad \left( {i,j = 1,3} \right), \\ & \left\{ {\begin{array}{*{20}c} {As_{ij} } & {Bs_{ij} } \\ \end{array} } \right\} = \sum\limits_{k = 1}^{N} {\int\limits_{{h_{k} }}^{{h_{k + 1} }} {Q_{ij}^{\left( k \right)} f\left( {\bar{z}} \right)\left\{ {\begin{array}{*{20}l} 1 \hfill & z \hfill \\ \end{array} } \right\}{\text{d}}z} ,} \quad \left( {i,j = 1,3} \right), \\ & \left\{ {Ass_{ij} } \right\} = \sum\limits_{k = 1}^{N} {\int\limits_{{h_{k} }}^{{h_{k + 1} }} {Q_{ij}^{\left( k \right)} f^{2} \left( {\bar{z}} \right){\text{d}}z,} } \quad \left( {i,j = 1,3} \right), \\ & \left\{ {Acc_{ij} } \right\} = \sum\limits_{k = 1}^{N} {\int\limits_{{h_{k} }}^{{h_{k + 1} }} {Q_{ij}^{\left( k \right)} \left[ {f'\left( {\bar{z}} \right)} \right]^{2} {\text{d}}z} } \quad \left( {i,j = 5} \right) \\ \end{aligned}$$

(20)

$$\begin{aligned} & I_{1} = \sum\limits_{k = 1}^{N} {\rho^{\left( k \right)} \int_{{h_{k} }}^{{h_{k + 1} }} {{\text{d}}z} } ,\quad I_{2} = \sum\limits_{k = 1}^{N} {\rho^{\left( k \right)} \int_{{h_{k} }}^{{h_{k + 1} }} {z{\text{d}}z} } ,\quad I_{3} = \sum\limits_{k = 1}^{N} {\rho^{\left( k \right)} \int_{{h_{k} }}^{{h_{k + 1} }} {f\left( {\bar{z}} \right){\text{d}}z} } , \\ & I_{4} = \sum\limits_{k = 1}^{N} {\rho^{\left( k \right)} \int_{{h_{k} }}^{{h_{k + 1} }} {z^{2} {\text{d}}z} } ,\quad I_{5} = \sum\limits_{k = 1}^{N} {\rho^{\left( k \right)} \int_{{h_{k} }}^{{h_{k + 1} }} {zf\left( {\bar{z}} \right){\text{d}}z} } ,\quad I_{6} = \sum\limits_{k = 1}^{N} {\rho^{\left( k \right)} \int_{{h_{k} }}^{{h_{k + 1} }} {g\left( {\bar{z}} \right){\text{d}}z} } , \\ & I_{7} = \sum\limits_{k = 1}^{N} {\rho^{\left( k \right)} \int_{{h_{k} }}^{{h_{k + 1} }} {f^{2} \left( {\bar{z}} \right){\text{d}}z} } ,\quad I_{8} = \sum\limits_{k = 1}^{N} {\rho^{\left( k \right)} \int_{{h_{k} }}^{{h_{k + 1} }} {g^{2} \left( {\bar{z}} \right){\text{d}}z} } . \\ \end{aligned}$$

(21)

2.4 Closed-form solution

The solution which satisfies governing differential equations at any point of the beam can be either in the form of a finite or infinite series. The solutions expressed in terms of finite number of terms are called as closed-form solutions. In the present study, Navier’s solution technique is employed to obtain the closed-form solution. Navier’s solution for the simply supported laminated composite and sandwich beam is developed satisfying the following boundary conditions.

$${\text{at}}\;x = 0\,{\text{and}}\,x = L :\;N_{x} = w_{0} = \xi = M_{x}^{\text{c}} = M_{x}^{\text{s}} = 0$$

(22)

The transverse distributed load is expanded using the Fourier sine series as

$$q\left( x \right) = \sum\limits_{m = 1,3,5}^{\infty } {\left\{ {\begin{array}{*{20}l} {q_{0} { \sin }\alpha x} \hfill & {\left( {m = 1} \right)} \hfill & {\text{for sinusoidal loading}} \hfill \\ {\frac{{4q_{0} }}{m\pi }\,{ \sin }\alpha x} \hfill & {\left( {m = 1,3,5 \ldots } \right)} \hfill & {\text{for uniform loading}} \hfill \\ \end{array} } \right.}$$

(23)

where $q_{0}$ is the maximum intensity of the distributed load. Following the Navier’s solution procedure, the trigonometric forms of displacement variables $u_{0} ,\,w_{0} ,\,\phi \,{\text{and}}\,\xi$ that satisfy the boundary conditions exactly are given by:

$$\begin{aligned} & u_{0} \left( {x,t} \right) = \sum\limits_{m = 1}^{\infty } {u_{m} { \cos }\alpha x{\text{e}}^{i\omega t} } ,\quad w\left( {x,t} \right) = \sum\limits_{m = 1}^{\infty } {w_{m} { \sin }\alpha x{\text{e}}^{i\omega t} } , \\ & \phi \left( {x,t} \right) = \sum\limits_{m = 1}^{\infty } {\phi_{m} { \cos }\alpha x{\text{e}}^{i\omega t} } ,\quad \xi \left( {x,t} \right) = \sum\limits_{m = 1}^{\infty } {\xi_{m} { \sin }\alpha x{\text{e}}^{i\omega t} } \\ \end{aligned}$$

(24)

where $\alpha = m\pi \text{/}L$, $i = \sqrt { - 1}$, $\omega$ is the natural frequency and $u_{m} ,\;w_{m} ,\;\phi_{m} \;{\text{and}}\,\xi_{m}$ are the unknown coefficients to be determined. The time-dependent part of Eq. (24) is used only for the free vibration problem; otherwise, it is omitted. The transverse load $q\left( x \right)$ is used only for bending analysis, otherwise discarded for the vibration and buckling analysis. For the buckling analysis of beam, both transverse load and time-dependent terms are omitted. Substituting this form of solution into the governing Eqs. (16)–(19) yields a set of algebraic equations which can be written in matrix form as follows:

Bending analysis of beam:

$$\left[ K \right]\left\{ \Delta \right\} = \left\{ f \right\}\; ( {\text{by setting}}\;N_{x}^{0} \;{\text{and}}\;\omega {\text{ equal to zero)}}$$

(25)

Free vibration analysis of beam:

$$\left( {\left[ K \right] - \omega^{2} \left[ M \right]} \right)\left\{ \Delta \right\} = \left\{ 0 \right\}\; ( {\text{by setting}}\;N_{x}^{0} \;{\text{and}}\;q (x ) {\text{ equal to zero)}}$$

(26)

Buckling analysis of beam:

$$\left( {\left[ K \right] - N_{0} \left[ N \right]} \right)\left\{ \Delta \right\} = \left\{ 0 \right\}\; ( {\text{by setting}}\;\omega = q (x ) {\text{ = 0 and}}\;N_{x}^{0} { = }N_{0} )$$

(27)

where [K] is the stiffness matrix, {f} is the force vector, [M] is the mass matrix, [N] is the geometric matrix due to the axial forces, $\omega$ is the natural frequency and N₀ is the buckling load factor. These matrices are defined as follows:

$$\left[ K \right] = \left[ {\begin{array}{*{20}c} {A_{11} \alpha^{2} } & { - B_{11} \alpha^{3} } & {As_{11} \alpha^{2} } & {\frac{\pi }{h}As_{13} \alpha } \\ { - B_{11} \alpha^{3} } & {D_{11} \alpha^{4} } & { - Bs_{11} \alpha^{3} } & { - \frac{\pi }{h}Bs_{13} \alpha^{2} } \\ {As_{11} \alpha^{2} } & { - Bs_{11} \alpha^{3} } & {\left( {Ass_{11} \alpha^{2} + Acc_{55} } \right)} & {\left( {\frac{\pi }{h}Ass_{13} + \frac{h}{\pi }Acc_{55} } \right)\alpha } \\ {\frac{\pi }{h}As_{13} \alpha } & { - \frac{\pi }{h}Bs_{13} \alpha^{2} } & {\left( {\frac{\pi }{h}Ass_{13} + \frac{h}{\pi }Acc_{55} } \right)\alpha } & {\left( {\frac{{h^{2} }}{{\pi^{2} }}Acc_{55} \alpha^{2} + \frac{{\pi^{2} }}{{h^{2} }}Ass_{33} } \right)} \\ \end{array} } \right]$$

(28)

$$\left\{ \Delta \right\} = \left\{ {\begin{array}{*{20}c} {u_{m} } \\ {w_{m} } \\ {\phi_{m} } \\ {\xi_{m} } \\ \end{array} } \right\}$$

(29)

$$\left\{ f \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ {q_{m} } \\ 0 \\ 0 \\ \end{array} } \right\}$$

(30)

$$\left[ M \right] = \left[ {\begin{array}{*{20}c} {I_{1} } & { - I_{2} \frac{m\pi }{L}} & {I_{3} } & 0 \\ { - I_{2} \frac{m\pi }{L}} & {\left( {I_{4} \frac{{m^{2} \pi^{2} }}{{L^{2} }}{\text{ + I}}_{1} } \right)} & { - I_{5} \frac{m\pi }{L}} & {I_{6} } \\ {I_{3} } & { - I_{5} \frac{m\pi }{L}} & {I_{7} } & 0 \\ 0 & {I_{6} } & 0 & {I_{8} } \\ \end{array} } \right]$$

(31)

$$\left[ N \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & {\alpha^{2} } & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]$$

(32)

3 Numerical results and discussion

In this section, the efficiency of the present theory is proved in predicting the displacements, stresses, natural frequencies, and critical buckling loads of simply supported laminated composite and sandwich beams. The numerical results obtained by using the present theory are compared with those existing in literature. The material properties shown in Table 2 are used in the various illustrated examples. Numerical investigations have been undertaken on bending, free vibration, and buckling analysis of isotropic, laminated composite, and sandwich beams with different material properties and different lamination schemes, namely:

Table 2 Material properties of isotropic, laminated composite, and sandwich beams

• Problem 1: Bending of isotropic beam

• Problem 2: Bending of laminated composite beams.

• Problem 3: Bending of sandwich beams.

• Problem 4: Free vibration of laminated composite beams.

• Problem 5: Free vibration of sandwich beams.

• Problem 6: Buckling of laminated composite and sandwich beams.

3.1 Numerical results

Numerical results for these problems are presented in Tables 3, 4, 5, 6, 7, 8, 9, 10, and 11, and graphically in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12 followed by subsequent discussions. Interlaminar transverse shear and normal stresses cause delamination in multilayered composite structures. The evaluation of transverse shear stresses for the layered beam from the constitutive relations leads to discontinuity at the layer interface. Therefore, in the present study, these stresses are obtained by integrating the 2D elasticity equilibrium equations neglecting the body forces. These equations are as follows:

$$\tau_{xz}^{\left( k \right)} = - \sum\limits_{k = 1}^{N} {\int\limits_{{z_{k} }}^{{z_{k + 1} }} {\frac{{\partial \sigma_{x}^{\left( k \right)} }}{\partial x}{\text{d}}z} } + C_{1} \quad {\text{and}}\quad \sigma_{z}^{\left( k \right)} = - \sum\limits_{k = 1}^{N} {\int\limits_{{z_{k} }}^{{z_{k + 1} }} {\frac{{\partial \tau_{xz}^{\left( k \right)} }}{\partial x}{\text{d}}z} } + C_{2}$$

(33)

Table 3 Comparison of axial displacement, transverse displacement, axial stress, and transverse shear stress for isotropic beam of rectangular cross section

Table 4 Comparison of axial displacement, transverse displacement, axial stress, and transverse shear stress for two-layered (0°/90°) anti-symmetric laminated composite beam

Table 5 Comparison of axial displacement, transverse displacement, axial stress, and transverse shear stress for three-layered (0°/90°/0°) symmetric laminated composite beam

Table 6 Comparison of axial displacement, transverse displacement, axial stress, and transverse shear stress for three-layered (0°/core/0°) symmetric sandwich beam

Table 7 Comparison of non-dimensional vibration frequencies for laminated composite beams

Table 8 Comparison of non-dimensional vibration frequencies for four-layered (0°/90°/90°/0°) laminated beams

Table 9 Comparison of non-dimensional vibration frequencies for three-layered (0°/core/0°) sandwich beams

Table 10 Comparison of non-dimensional critical buckling loads for laminated composite beams

Table 11 Comparison of non-dimensional critical buckling loads for three-layered (0°/core/0°) sandwich beams

Fig. 2

Through-the-thickness variation of non-dimensional axial displacement ($\bar{u}$) at (0, z/h) in (0°/90°) beam under sinusoidal and uniform loadings

Fig. 3

Through-the-thickness variation of non-dimensional bending stress ($\bar{\sigma }_{x}$) at (L/2, z/h) in (0°/90°) beam under sinusoidal and uniform loadings

Fig. 4

Through-the-thickness variation of non-dimensional transverse shear stress ($\bar{\tau }_{xz}$) at (0, z/h) in (0°/90°) beam under sinusoidal and uniform loadings

Fig. 5

Through-the-thickness variation of non-dimensional transverse normal stress ($\bar{\sigma }_{z}$) at (L/2, z/h) in (0°/90°) beam under sinusoidal and uniform loadings

Fig. 6

Through-the-thickness variation of non-dimensional axial displacement ($\bar{u}$) at (0, z/h) in (0°/90°/0°) beam under sinusoidal and uniform loading

Fig. 7

Through-the-thickness variation of non-dimensional bending stress ($\bar{\sigma }_{x}$) at (L/2, z/h) in (0°/90°/0°) beam under sinusoidal and uniform loading

Fig. 8

Through-the-thickness variation of non-dimensional transverse shear stress ($\bar{\tau }_{xz}$) at (0, z/h) in (0°/90°/0°) beam under sinusoidal and uniform loadings

Fig. 9

Through-the-thickness variation of non-dimensional transverse normal stress ($\bar{\sigma }_{z}$) at (L/2, z/h) in (0°/90°/0°) beam under sinusoidal and uniform loadings

Fig. 10

Comparison of through-the-thickness variations of non-dimensional axial displacement ($\bar{u}$) at (0, z/h) in (0°/core/0°) beam under sinusoidal and uniform loadings

Fig. 11

Comparison of through-the-thickness variation of non-dimensional bending stress ($\bar{\sigma }_{x}$) at (L/2, z/h) in (0°/core/0°) beam under sinusoidal and uniform loadings

Fig. 12

Comparison of through-the-thickness variation of non-dimensional transverse shear stress ($\bar{\tau }_{xz}$) at (0, z/h) in (0°/core/0°) beam under sinusoidal and uniform loadings

The interlaminar stresses of kth lamina can be evaluated by layerwise integration of Eq. (33) with respect to the thickness coordinate (z). The C₁ and C₂ can be determined by imposing the continuity and boundary conditions at the appropriate locations. Axial displacement ($u$), transverse displacement ($w$), bending stress ($\sigma_{x}$), transverse shear stress ($\tau_{xz}$), transverse normal stress ($\sigma_{z}$), natural frequencies ($\bar{\omega }$), and critical buckling loads (N_cr) are presented in the following non-dimensional forms available in the literature.

$$\begin{aligned} & \bar{u}\left( {0,\frac{z}{h}} \right) = \frac{{E_{3} u}}{{q_{0} h}},\;\bar{w}\left( {\frac{L}{2},\frac{z}{h}} \right) = \frac{{E_{3} 100h^{3} w}}{{q_{0} L^{4} }},\bar{\sigma }_{x} \left( {\frac{L}{2},\frac{z}{h}} \right) = \frac{{\sigma_{x} }}{{q_{0} }}, \\ & \bar{\tau }_{xz} \left( {0,0} \right) = \frac{{\tau_{xz} }}{{q_{0} }},\;\bar{\sigma }_{z} \left( {\frac{L}{2},\frac{z}{h}} \right) = \frac{{\sigma_{z} }}{{q_{0} }},\bar{\omega } = \frac{\omega L}{h}\sqrt {\left( {\frac{\rho }{{E_{3} }}} \right)_{f} } \,{\text{and}}\;N_{\text{cr}} = \frac{{N_{0} a^{2} }}{{E_{3} h^{3} }} \\ \end{aligned}$$

(34)

where $E_{3}$ is the Young’s modulus of middle layer. Material properties used in the above problems are shown in Table 2.

3.2 Discussion of results

3.2.1 Problem 1: Bending of isotropic beam

Table 3 shows comparison of non-dimensional displacements and stresses of thick isotropic beams subjected to sinusoidal and uniform loadings. The material properties are given in Table 2 (material 1). The numerical results are obtained for various aspect ratios (L/h) and compared with those of Reddy [11], Ghugal and Shimpi [13], Kant et al. [44], TBT [4], and CBT [2, 3]. The results of axial and transverse displacements are exactly matching with the results of exact plane stress elasticity solution given by Kant et al. [44] due to the inclusion of thickness stretching effect in the present theory whereas stresses are in good agreement with other higher-order theories for isotropic beam with aspect ratio 4 in which shear deformation is very significant. For moderately thick beams (L/h = 10–50), the results of displacements and stresses are in excellent agreement with those provided by Kant et al. [44] due to normal deformation effect.

Since the effect of thickness stretching is considered in the present theory, it provides the additional stiffness to the beam, because of which, results predicted by the proposed theory are higher than those predicted by the Euler–Bernoulli theory for low L/h ratios (thick beams) and approaches to thin beam limits (Euler–Bernoulli theory) for high L/h ratios. Higher-order theories which do not include this effect yield a marginal difference in the bending results compared to those of present theory.

3.2.2 Problem 2: Bending of laminated composite beams

Tables 4 and 5 show the non-dimensional displacements and stresses of (0°/90°) and (0°/90°/0°) laminated beams, respectively. In both the lamination schemes, layers are of equal thickness and made up of material 2 (see Table 2). The displacements and stresses are obtained for aspect ratios 4 and 10. The present results are compared with previously published results. The examination of Tables 4 and 5 reveals that the displacements and stresses in two-layered anti-symmetrically laminated beams are higher than those in three-layered symmetrically laminated beams. This is possibly due to presence of bending extension coupling stiffness which is zero in symmetrically laminated beams. Since the present theory considered the effect of transverse normal strain, i.e., thickness stretching, it provides the additional stiffness to the beam, because of which, results predicted by the present theory for (0°/90°/0°) laminated beams (see Table 5) are in excellent agreement with those obtained by Chakrabarti et al. [46] using finite element analysis and plane stress solution given by Kant et al. [44]. Overall observations on Tables 4 and 5 show that the non-dimensional displacements and stresses obtained by using the present theory are in good agreement with those available in the literature. A large discrepancy in the displacements and stresses for laminated thick beam (L/h = 4) can be observed with the use of CBT [2, 3] and TBT [4] due to the neglect of transverse shear and normal deformations. However, for L/h = 10 results obtained using CBT [2, 3] and TBT [4] are in good agreement with each other. The through-the-thickness distribution of displacements and stresses for laminated composite beams under sinusoidal and uniform loading are shown in Figs. 2, 3, 4, 5, 6, 7, 8 and 9. Here, the through-the-thickness distributions of interlaminar transverse shear and normal stresses are obtained using equilibrium equations of theory of elasticity to ascertain stress continuity at layer interface. Figures 5 and 9 show that the value of transverse normal stress at the bottom surface of the beam is zero and equal to magnitude of transverse load at the top surface.

3.2.3 Problem 3: Bending of sandwich beams

Sandwich beam is a special form of laminated composite beam in which the modulus of core material is significantly lower than that of the face sheets. Therefore, study of global response of softcore sandwich structures is a challenging problem in numerical computation, especially using simplified (1D or 2D) theories, rather than 3D elasticity due to severe warping and normal deformation effects. Therefore, equivalent single-layer theories, which include effects of transverse normal strain, i.e., thickness stretching, are more effective for the analysis soft core sandwich beams. In this study, the present theory is applied for the bending of three-layered (0°/core/0°) symmetric sandwich beam. The beam has two face sheets (top and bottom) of thickness 0.1h each and thick soft core of thickness 0.8h. The face sheets are made up of material 2 and core is made up of soft material 3. The material properties are given in Table 2. The comparison of non-dimensional displacements and stresses of the sandwich beam subjected to sinusoidal and uniform loading is given in Table 6. The exact elasticity solution for sandwich beam is not available in the literature. The examination of Table 6 reveals that the results of the present theory are in close agreement with those of plane stress elasticity solution given by Kant et al. [44]. This is the consequence of inclusion of the effect of thickness stretching in the present theory. The results of CBT deviate considerably, compared to those of refined theories due to the neglect of transverse shear and normal deformations. TBT showed similar trend for beams with low aspect ratios due to inclusion of only constant transverse shear strain in the theory. Comparison of through-the-thickness variations of non-dimensional axial displacement, bending stress, and transverse shear stress is shown in Figs. 10, 11, and 12. Considerable deviation in through-the-thickness variations of axial displacement is observed in Fig. 10, which shows that the present theory effectively captures the effect of soft core material compared to theory of Reddy [11] which neglect the effect of transverse normal deformation.

3.2.4 Problem 4: Free vibration of laminated composite beams

The effect of transverse normal deformation is equally important for the dynamic analysis of beams as in static bending of a beam. In this study, free vibration analyses of (0°/90°), (0°/90°/0°) and (0°/90°/90°/0°) laminated beams have been carried out using the present theory. In all the laminated beams, the overall thickness is equally distributed among all the layers. The material properties used are given in Table 2. The (0°/90°) and (0°/90°/0°) laminated beams are made up of material 4, whereas (0°/90°/90°/0°) laminated beam is made up of material 5. The non-dimensional natural frequencies are shown in Tables 7 and 8. From the investigation of Tables 7 and 8, it is observed that the present results are in excellent agreement with those of refined theories available in the literature. Since the frequency of vibration is a global quantity with respect to the neutral axis of the beam, the effect of transverse normal deformation cannot be exhibited explicitly without exact solution, which is not available in literature.

3.2.5 Problem 5: Free vibration of sandwich beams

A three-layered (0°/core/0°) simply supported sandwich beam is analyzed in this problem using the present theory. The core has a thickness of 0.8h, while it is 0.1h each for the two laminated face sheets. The face sheets are made up of material 6, whereas the core is made up of material 7 as given in Table 2. The values of the first four non-dimensional natural frequencies are presented in Table 9 for aspect ratios 5, 10, and 20. The present values of natural frequencies are in good agreement with those reported by Kapuria et al. [56], Chalak et al. [52], and Vidal and Polit [45]. Higher values of frequencies of present theory compared to other refined theories may be attributed to the thickness stretching effect which introduces an additional stiffness in transverse flexural vibration of beam. Since exact solution for this case is not available, the effect of thickness stretching on frequency response cannot be ascertained at present.

3.2.6 Problem 6: Buckling of laminated composite beams

This section presents the buckling behavior of laminated beam due to axial compressive forces. A symmetrically laminated beam is considered for the numerical study. Table 10 shows the comparison of the critical buckling load for (0°/90°/0°) and (0°/90°/90°/0°) laminated beams. The beam is analyzed by considering different modular ratios (E₁/E₂) and different aspect ratios (L/h). The beams are made up of material 4 as shown in Table 2. The results of present theory are compared with those published by Khdeir and Reddy [57], Aydogdu [48], Karama et al. [16] and Vo and Thai [49]. From the examination of Table 10, it is observed that the critical buckling loads for the four-layered symmetric beams are less than those of the three-layered beams. The increase in critical buckling load is observed with increase in aspect ratio as well as the modular ratio. The comparison of results with existing literature indicates that the results of the present theory are in very good agreement with those of other equivalent theories and may be due to inclusion of transverse normal strain effect.

The comparison of the critical buckling load for three-layered (0°/core/0°) sandwich plate is shown in Table 11. The composite face sheets are made up of material 2 and core is of material 3. The thickness of each face sheet is 0.1h and that of the core is 0.8h. For the comparison purpose, results by using HSDT of Reddy [11], TBT of Timoshenko [4], and CBT of Bernoulli–Euler [2, 3] are specially generated. From Table 11, it is observed that the present results are in excellent agreement with those obtained by using HSDT of Reddy. The CBT results are independent of the aspect ratio (a/h), shear deformation being neglected in the theory.

In absence of an exact elasticity solutions for bending, buckling, and vibration of beams, the three-dimensional thick plate’s origin of the sine shear function in one-dimensional analogue of thick plate, i.e., thick beam and the infinity of terms in its polynomial representation allow us to hope that the corresponding beam theory which includes thickness stretching effect will be accurate, without increasing the complexity compared to the TBT.

3.3 Recommendation for other boundary conditions of the beam

All the foregoing solutions are obtained for simply supported boundary conditions of the beam. For the other boundary conditions, the present theory can also be extended.

• 1. For the built-in boundary conditions, finite element method is widely used by various researchers. The present theory is simple and suitable for finite element formulation.

• 2. One can use general solution technique for the other boundary conditions of the beam by decoupling the governing equations from each other and solving them independently.

• 3. One can also use numerical methods such as discrete singular convolution method, Galerkin method, meshless method, radial basis functions, differential quadrature method, Rayleigh–Ritz method, and state-space method for the analysis of laminated composite beams with built-in boundary conditions.

4 Concluding remarks

Present paper deals with the assessment of trigonometric shear and normal deformation theory on bending, free vibration, and buckling analysis of isotropic, laminated composite, and sandwich beams. The present theory considers the effect of transverse shear deformation as well as the transverse normal strain, i.e., thickness stretching. The present theory satisfies the traction free boundary conditions at the top and bottom surfaces of the beam. The theory is variationally consistent and does not require shear correction factor. Navier-type closed-form solutions are obtained for bending, buckling, and vibration of simply supported beams and numerical results are presented. The numerical results for the displacements, stresses, natural frequencies, and critical buckling loads for standard problems of laminated composite and sandwich beams have shown the accuracy of the theory. Therefore, it is finally concluded that the effect of thickness stretching plays an important role while predicting bending, buckling and vibration responses of the laminated composite and sandwich beams. In the absence of an exact elasticity solution, numerical trend indicates that the results of present theory can be served as better reference solutions since the theory is represented by trigonometric functions which are correct from three-dimensional elasticity considerations.