Numerical and experimental evaluation of the dynamic performance of kinematically redundant parallel manipulators

Abstract

Parallel manipulators present high load capacity and rigidity, among other advantages, when compared to the serial manipulators. Due to their kinematic architecture, their parts are lighter. This characteristic may be an asset for designing high dynamic performance manipulators. However, parallel manipulators suffer from singularities in their workspace. This drawback can be circumvented by the use of kinematic redundancies. Due to the presence of these redundancies, the inverse kinematic problem presents an infinite number of solutions. The selection of a single solution among the possible ones is denoted as redundancy resolution. In this manuscript, the impact of several levels of kinematic redundancy on the dynamic performance of a planar parallel manipulator, the 3PRRR, is numerically and experimentally investigated. The kinematic redundancy of this manipulator can be added by the actuation of the active prismatic joints (P). Two redundancy resolution schemes are proposed using a multiobjective optimization problem. Based on the numerical and experimental results, one can conclude that the use of a proper redundancy resolution scheme can considerably reduce the maximum required torque to perform a predefined task.

1 Introduction

Despite their potential attributes, such as high load capacity and better rigidity [1], parallel kinematic machines (PKMs) suffer from some important drawbacks such as the presence of singularities limiting their workspace [2]. The presence of singularities can be reduced by the inclusion of actuation and kinematic redundancies as suggested in Shin et al. [3], Kotlarski et al. [4], Gosselin et al. [5], Huang et al. [6] and Simoni et al. [7], among others. Actuation redundancies can be implemented by the actuation of passive joints or by the inclusion of active kinematic chains. For instance, Shin et al. [3] investigated the use of actuation redundancies for reducing singularities in several PKMs. Kinematic redundancies can be implemented by the introduction of extra active joints in a kinematic chain. Kinematically redundant PKMs are capable of avoiding singularities and obstacles, due to their reconfiguration capabilities. In fact, Kotlarski et al. [4] and Gosselin and Schreiber [5] studied the influence of kinematic redundancy on eliminating the presence of singularities and enlarging the usable workspace of a planar and a spatial PKM, respectively. Huang et al. [6] and Simoni et al. [7] proposed novel reconfigurable parallel mechanisms by including kinematic redundancies. Whilst, Huang et al. [6] proposed to drive a bevel gear system fixed in its base platform to introduce the reconfiguration capabilities, Simoni et al. [7] proposed the introduction of self-aligning degrees-of-freedom that do not interfere in the motion of the moving platform but can furnish interesting characteristics to the manipulator.

The fact that PKMs are usually lighter than serial manipulators can be exploited for designing high dynamic performance manipulators such as the one described in Nabat et al. [8]. Moreover, the inclusion of actuation and kinematic redundancies should be considered during the design of high dynamic performance manipulator due to their aforementioned capabilities. The use of actuation redundancies was exploited by Corbel et al. [9] and by Nadal et al. [10] for designing an ultra-fast PKM. The use of kinematic redundancies was numerically investigated by Fontes et al. [11, Wu et al. [12] and Ruiz et al. 13] for reducing the required torques for the execution of predefined tasks. A numerical comparison between the dynamic performance of planar PKMs with actuation and kinematic redundancies was carried out in Fontes et al. [11]. The non-redundant 3RRR, the redundantly actuated 4RRR and 6RRR, and the kinematically redundant PRRR + 2RRR, 2PRRR + RRR and 3PRRR PKMs were investigated. As commonly used, the letter R corresponds to a revolute joint, the letter P to a prismatic joint, the underline letters to the active joints and the number in front of the letters refers to the number of kinematic chains. To perform this investigation, Fontes and da Silva [11] proposed a pose-dependent metric. Based on this metric and numerical analysis, it was concluded that kinematic redundancies not only promote an enlargement of the usable workspace but also an improvement on the manipulator’s dynamic performance. Since the outcome of this numerical investigation was promising, the use of kinematic redundancies should be further exploited as an alternative to industrial manipulators. For the sake of experimentally evaluating the use of kinematic redundancy, the prototype 3PRRR, depicted in Fig. 1, was built at São Carlos School of Engineering at the University of São Paulo. Up to three levels of kinematic redundancy can be investigated by actuating and/or locking the active prismatic joints. The non-redundant planar 3RRR PKM can be investigated by locking all three prismatic joints. The kinematically redundant planar PRRR + 2RRR, 2PRRR + RRR and 3PRRR PKMs can be investigated by actuating one, two or three prismatic joints, respectively.

Fig. 1

The prototype 3PRRR

The inverse kinematic model of a kinematically redundant PKM presents infinite number of solutions. In other words, a single end-effector’s pose can be achieved by infinite kinematic configurations [14]. The selection of a single kinematic configuration among the several possibilities is denoted as redundancy resolution and can be mathematically formulated as an optimization problem [15]. Several strategies have been proposed for solving this problem for kinematically redundant serial manipulators [14, 15]. These strategies should be revisited and adapted for kinematically redundant parallel manipulators. In general, two strategies are found in the literature to treat this problem: the local and the global approaches. The local approaches take into account kinematic relations that are valid locally such as gradient projection methods and Jacobian-based strategies [14]. Local approaches have been treated in Cha et al. [16] and Boudreau and Nokleby [17] for avoiding singularities during the execution of predefined tasks. The global approaches, also known as tracking problems, attempt to minimize the error between the end-effector’s pose and a reference trajectory. Among others, global approaches have been proposed by formulating an optimization problem that maximizes the precision of a robotic system [18, 19] or that minimizes the required torques for executing predefined tasks in Fontes et al. [11]. In these works [11, 18, 19], two strategies were numerically exploited to plan the motion of the redundant actuators: the prepositioning and ongoing approaches. The positions of the redundant actuators are modified before and during the task execution in the prepositioning and ongoing approaches, respectively. Recently, Santos and da Silva [20] and Hauser [21] exploited local properties for proposing global redundancy resolution schemes based on differential dynamic programming and optimal collision-free inverse kinematics problems, respectively. The reconfiguration capabilities of the 3PRRR prototype, depicted in Fig. 1, have been evaluated experimentally using the redundancy resolution scheme proposed by Kotlarski et al. [20].

Whilst favourable experimental results on the reconfiguration capabilities for avoiding singular regions of kinematically redundant parallel manipulators can be found in the literature [18,19,20], experimental results on the dynamic performance of this kind of machines are seldom. In this way, the main contribution of the present work is the experimental evaluation of the impact of several levels of kinematic redundancies on the dynamic performance of a kinematically redundant PKM, the 3PRRR PKM depicted in Fig. 1. The redundancy resolution is solved via a global optimization problem (tracking problem). Preliminary experimental results using the optimization problem proposed by [19] yielded unsatisfactory performance for several levels of kinematic redundancies. In this way, a multiobjective optimization problem is proposed in an attempt to not only minimize the required torques for executing a predefined task but also to maximize the distance of the manipulator’s end-effector to singular regions. The prepositioning and the ongoing positioning approaches are considered using the proposed multiobjective optimization problem. The experimental assessment of the dynamic performance for a tracking problem is task-dependent. In this way, this optimization problem is exploited for deriving the required inputs for the execution of a predefined task. A numerical non-dependent task assessment of the dynamic performance of kinematically redundant manipulators is proposed in Fontes et al. [11] and is out of the scope of the present manuscript.

The remainder of this paper is organized as follows. Details of the experimental prototype are given in Sect. 2. Section 3 summarizes the kinematic and dynamic models of the manipulators under study. The extended global approaches for redundancy resolution are described in Sect. 4. Numerical and experimental results on the manipulators’ dynamic performance are discussed in Sect. 5. Finally, conclusions are drawn in Sect. 6.

2 Prototype description

In this section, the prototype 3P RRR (see Fig. 1) is described. The actuation of the active prismatic and revolute joints is performed by brushless Maxon EC60 flat motors connected to Maxon GP52C planetary gearheads. The nominal torque of these motors is 0.257 Nm @ 3580 rpm. Since the reduction rate of the gearheads is 3.5:1, the resulting nominal torque is 0.82 Nm @ 1200 rpm. The linear motion is performed by three table systems with ball screw HIWIN KK60-10-C-E-600-A-1-F0-S3. Their stroke range is 600 mm and their lead is 10 mm.

The communication scheme is illustrated in Fig. 2. Each motor is connected to a control board named EPOS. The PC is connected to the first control board, EPOS 1, via USB communication. This control board executes a gateway to implement the communication between the control boards via CAN protocol. These control boards present several control modes. Among them, the most appropriate mode is the interpolated position mode since all actuators must simultaneously perform smooth trajectories. In this mode, the user provides the desired positions and velocities at discrete time steps. In this manuscript, positions and velocities are found via a redundancy resolution scheme. This data is, then, interpolated through splines by the control board and is used as a reference signal to the control strategies. Moreover, in this mode, linear position feedforward and position feedback control strategies are used to guarantee performance and robustness. The control parameters, the feedforward and feedback gains, have been adjusted manually in a human machine interface built in Matlab.

Fig. 2

An illustration of the communication scheme

3 Kinematic and dynamic models

For sake of completeness, this section summarizes the kinematic and dynamic models of the non-redundant 3RRR PKM and the kinematically redundant PRRR + 2RRR, 2PRRR + RRR and 3PRRR PKMs. Details on this derivation can also be found in Fontes et al. [11]. Nevertheless, experimental investigations have demonstrated that sliding friction plays an important role in this prototype and its modeling has been included in this work. The outcome of these models furnishes the terms that are used in the cost functions for describing the redundancy resolution scheme formulated as a multiobjective optimization problem.

3.1 Kinematics

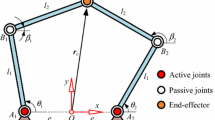
The following description of a single kinematic chain i, illustrated in Fig. 3, is employed to derive comprehensive models for the all manipulators under study. The kinematic models can be found by evaluating the geometrical relations of the manipulators’ links and joints [22]. The base coordinate system $O$-xy is located in the centre of the manipulator’s workspace as illustrated in the upper right corner of the Figs. 3 and 4 and the moving coordinate system $D$-XY is located in the end-effector’s centre as illustrated in the same figures. The position vector of the end-effector’s centre is given by $\mathbf {X}=[x \; y \; \alpha ]^T$ relative to the base coordinate system. Every kinematic chain presents an active revolute joint at $A_i$ (motor) and two passive revolute joints at $B_i$ and $C_i$. Kinematic redundancy is achieved by adding an active prismatic joint which is responsible for the position $\delta _i$ of $A_i$. The prismatic joint’s orientation is given by the angles $\gamma _i$ and $\lambda _i$ according to the base coordinate as illustrated in Fig. 4. In addition, $\theta _i$ is the orientation angle of the link $A_iB_i$, $\beta _{i}$ is the orientation of the link $B_iC_i$, $a_i$ is the shortest distance between the linear guide and the point O, $\alpha +\eta _{i}$ is the angle between the axis Ox and the link $C_iD$ and $h_i$ is the distance between the centre of the end-effector and the point $C_i$. The subscript $i=1 \ldots 3$ according to the kinematic chain.

Fig. 3

An illustration of the kinematic chain i, modified from Fontes et al. [11]

Fig. 4

Geometrical details of the manipulator’s end-effector

Using the geometrical constraint equation $\left\| \overrightarrow{B_iC_i} \right\| = l_{2}$ and the notation suggested by Wu et al. [23], the angles $\theta _i$ can be derived as:

$$\begin{aligned} \theta _i=2a {{\mathrm{\,tan_2}}}\left( \frac{-e_{i1}\pm \ \sqrt{e^2_{i1}+e^2_{i2}-e^2_{i3}}}{e_{i3}-e_{i2}} \right) , \end{aligned}$$

(1)

where $e_{i1}= -2l_{1i} \rho _i$, $e_{i2}= -2l_{1i} \mu _i$, $e_{i3}= {\mu _i}^2 +{\rho _i}^2 + (l_{1i})^2 - (l_{2i})^2$, $\mu _{i}=x-h_i cos(\alpha +\eta _{i}) -a_i cos(\lambda _{i}) - \delta _i cos(\gamma _{i})$ and $\rho _{i}=y - h_i sin(\alpha +\eta _{i}) -a_i sin(\lambda _{i}) - \delta _i sin(\gamma _{i})$.

The position vector of the active joints, ${\boldsymbol{\varTheta }}$, is dependent on the number of redundant actuators, denoted by M. Table 1 summarizes the content of the vector ${\boldsymbol{\varTheta }}$ for the manipulators under study.

The dynamic analysis requires the calculation of the velocities and accelerations of each moving part of the manipulators. The relation between the velocity vector of the manipulator’s end-effector, $\dot{\mathbf {X}}=[\dot{x} \; \dot{y} \; \dot{\alpha }]^T$, and the velocities of the active joints, $\dot{{\boldsymbol{\varTheta }}}$, can be found by taking the time derivative of the geometrical constraint $\left\| \overrightarrow{B_iC_i} \right\| = l_{2}$, as derived in Fontes et al. [11]. This relation can be rewritten in a matrix form:

$$\begin{aligned} \mathbf {A}\dot{\mathbf {X}}=\mathbf {B}\dot{{\boldsymbol{\varTheta }}}, \end{aligned}$$

(2)

where the elements of the Jacobian matrix $\mathbf {A} \in \mathbb {R}^{3 \times 3}$ can be described $a_{i1}=l_2\cos (\beta _i)$, $a_{i2}=l_2\sin (\beta _i)$ and $a_{i3}=-l_2h\sin (\beta _i-\eta _i-\alpha )$ and the terms of the Jacobian matrix $\mathbf {B} \in \mathbb {R}^{3 \times (3+M)}$ varies according to the number of redundant actuators, M (see Table 1). In a general way, the matrix $\mathbf {B}$ can be defined by the augmented matrix $\mathbf {B}=(\mathbf {B}_0|\mathbf {B}_M)$. The elements of the diagonal matrix $\mathbf {B}_0 \in \mathbb {R}^{3 \times 3}$ can be described by $b_{ii}=l_1l_2sin(\beta _i-\theta _i)$. The elements of matrix $\mathbf {B}_M \in \mathbb {R}^{3 \times M}$ are defined by $bM_{ im}=l_2cos(\beta _i-\gamma _i)$ if $i=m$ and $bM_{im}=0$ if $i \ne m$, where $i=1 \ldots 3$ according to kinematic chain and $m=1 \ldots M$ according to the number of redundant actuators. For instance, according to this description, the matrix $\mathbf {B}_M=[bM_{11};bM_{21};bM_{31}]=[l_2cos(\beta _1-\gamma _1);0;0]$ for the kinematically redundant PRRR+2RRR PKM ($M=1$, see Table 1).

Table 1 The position vectors of the active joints of the manipulators understudy

The velocities and accelerations of the end-effector can be calculated by taking the time derivatives of its position vector, $\mathbf {X}$. If the $\mathbf {A}$ is invertible, these quantities are defined by:

$$\begin{aligned} \dot{\mathbf {X}}=\mathbf {J}\dot{{\boldsymbol{\varTheta }}}=\mathbf {A}^{-1}\mathbf {B}\dot{{\boldsymbol{\varTheta }}}\; \text {and} \end{aligned}$$

(3)

$$\begin{aligned} \ddot{\mathbf {X}}=\mathbf {J}\ddot{{\boldsymbol{\varTheta }}}+\dot{\mathbf {J}}\dot{{\boldsymbol{\varTheta }}}, \end{aligned}$$

(4)

where $\mathbf {J} \in \mathbb {R}^{3 \times (3+M)}$ is the Jacobian matrix.

Table 2 Notation and inertia properties of the moving parts

The velocities and accelerations of the other moving parts can be calculated by taking the time derivatives of the position vector of these parts. To do so, each moving body is denoted by j according to the notation introduced in Table 2. In this way, the velocities and accelerations of each moving part j of each kinematic chain i can be defined by:

$$\begin{aligned} \dot{\mathbf {d}}_{ij}=\mathbf {K}_{ij}\dot{{\boldsymbol{\varTheta }}} \; \text {and} \end{aligned}$$

(5)

$$\begin{aligned} \ddot{\mathbf {d}}_{ij}=\mathbf {K}_{ij}\ddot{{\boldsymbol{\varTheta }}}+\dot{\mathbf {K}}_{ij}\dot{{\boldsymbol{\varTheta }}}, \end{aligned}$$

(6)

where $\mathbf {K}_{ij} \in \mathbb {R}^{3 \times (3+M)}$ are also the Jacobian matrices that can be calculated using the same methodology used to define $\mathbf {J}$ (see Eq. 3). This derivation that is fully described in Fontes et al. [11] yields:

$$\begin{aligned} \mathbf {K}_{i0}=\begin{bmatrix} 0&\cdots&\cos (\gamma _i)&\cdots&0\\ 0&\cdots&\sin (\gamma _i)&\cdots&0\\ 0&\cdots&0&\cdots&0 \end{bmatrix} \, \text {and} \end{aligned}$$

(7)

$$\begin{aligned} \mathbf {K}_{i1}=\begin{bmatrix} 0&\cdots&\cos (\gamma _i)&\cdots&0\\ 0&\cdots&\sin (\gamma _i)&\cdots&0\\ 0&\cdots&1&\cdots&0 \end{bmatrix}, \end{aligned}$$

(8)

where the non-zero terms are located in column $i+3$, and

$$\begin{aligned} \mathbf {K}_{i2} =\begin{bmatrix} \mathbf {H}_{i2}\\ \mathbf {G}_{i2} \end{bmatrix}, \end{aligned}$$

(9)

where

$$\begin{aligned} \mathbf {H}_{i2}=\begin{bmatrix} 0&\cdots&l_1(-\sin (\theta _i))&\cdots&\cos (\gamma _i)&\cdots&0\\ 0&\cdots&l_1\cos (\theta _i)&\cdots&\sin (\gamma _i)&\cdots&0 \end{bmatrix} \end{aligned}$$

(10)

where non-zero values are in columns i and $i+3$ and

$$\begin{aligned} \mathbf {G}_{i2} = \bigg [\frac{1}{l_2} [-\sin (\beta _i)&\cos (\beta _i)] \quad [\mathbf {H}_e-h [-\sin (\eta _i+\alpha ) \quad \cos (\eta _i+\alpha )] \mathbf {G}_e -\mathbf {H}_{i2}]\bigg ]. \end{aligned}$$

(11)

Using the aforementioned equations, the kinematics of the non-redundant and redundant manipulators under study can fully be determined.

3.2 Dynamics

The equations of motion of the manipulators under study are derived in this section using the Newton–Euler formulation and the aforementioned kinematics. For this derivation, the inertia data described in Table 2 is used. Moreover, the mass and inertia of the end-effector is $m_e$ and $I_e$.

Using the Newton–Euler formulation, the components of the vector $\mathbf {p}_{ij}$ composed by the combination of forces and moment applied on the body j of the chain i can be described as:

$$\begin{aligned} \mathbf {p}_{ij}=\begin{bmatrix} m_j(\ddot{r}_{x_{ij}}-\ddot{\phi }_{ij}s_j\sin (\phi _{ij})-\dot{\phi }_{ij}^2s_j\cos (\phi _{ij}))\\ m_j(\ddot{r}_{y_{ij}}+\ddot{\phi }_{ij}s_j\cos (\phi _{ij})-\dot{\phi }_{ij}^2s_j\sin (\phi _{ij}))\\ m_js_j(\ddot{r}_{x_{ij}}(-\sin (\phi _{ij}))+\ddot{r}_{y_{ij}}\cos (\phi _{ij}))+I_j\ddot{\phi }_{ij} \end{bmatrix}, \end{aligned}$$

(12)

where $s_j$ is the distance between of the mass centre of the body j and its pivotal point, and the vector $\mathbf {d}_{ij}$ is described in Table 2. Similarly, the components of the vector $\mathbf {p}_{e}$ composed by the forces and moment applied on the end-effector can be described as:

$$\begin{aligned} \mathbf {p}_e=\begin{bmatrix} m_e\ddot{x}\\ m_e\ddot{y}\\ I_e\ddot{\alpha } \end{bmatrix}. \end{aligned}$$

(13)

The relation between the generalized forces $\varvec{\tau _g} \in \mathbb {R}^{(3+M) \times 1}$ applied by the actuators and the forces and moments on the system can be expressed using the principle of virtual work [23]. This strategy yields the following relation:

$$\begin{aligned} \varvec{\tau _g}=\mathbf {J}^T \mathbf {p}_e +\sum _{i=1}^{3}\sum _{j=0 \, \text { or } \, 1}^{2} \mathbf {K}_{ij}^T \mathbf {p}_{ij}, \end{aligned}$$

(14)

where the lower limit is $j=0$ when there is a redundant actuator in the kinematic chain i and $j=1$, otherwise.

The matrices $\mathbf {Z}_{ij}$, $\mathbf {N}_{ij}$ and $\mathbf {Z}_e$ can be used for rewriting Eq. (14) in function of the position vector ${\boldsymbol{\varTheta }}$. These matrices are defined as:

$$\begin{aligned} \mathbf {Z}_{ij}=\begin{bmatrix} m_j&0&-m_j s_{ij}\sin {\phi _{ij}} \\ 0&m_j&m_j s_{ij}\cos {\phi _{ij}} \\ -m_j s_{ij}\sin {\phi _{ij}}&m_j s_{ij}\cos {\phi _{ij}}&I_j \end{bmatrix}, \end{aligned}$$

(15)

$$\begin{aligned} \mathbf {N}_{ij}=\begin{bmatrix} 0&0&-m_j \dot{\phi }_{ij} s_{ij}\cos {\phi _{ij}} \\ 0&0&-m_j \dot{\phi }_{ij} s_{ij}\sin {\phi _{ij}} \\ 0&0&0 \end{bmatrix} \quad \text {and} \end{aligned}$$

(16)

$$\begin{aligned} \mathbf {Z}_{e}=\begin{bmatrix} m_e&0&0 \\ 0&m_e&0 \\ 0&0&I_e \end{bmatrix}. \end{aligned}$$

(17)

In this way, the generalized forces $\varvec{\tau _g}$ can be expressed in a function of the time derivatives of the position vector ${\boldsymbol{\varTheta }}$:

$$\begin{aligned} \varvec{\tau _g}=\mathbf {M} {\ddot{\boldsymbol{\varTheta }}}+\mathbf {V} {\dot{\boldsymbol{\varTheta }}}, \end{aligned}$$

(18)

where

$$\begin{aligned} \mathbf {M}=\mathbf {J}^T \mathbf {Z}_e \mathbf {J} +\sum _{i=1}^{3}\sum _{j=0 \, \text { or } \, 1}^{2} \mathbf {K}_{ij}^T \mathbf {Z}_{ij} \mathbf {K}_{ij} \; \text {and} \end{aligned}$$

(19)

$$\begin{aligned} \mathbf {V}=\mathbf {J}^T \mathbf {Z}_e \dot{\mathbf {J}} +\sum _{i=1}^{3}\sum _{j=0 \, \text { or } \, 1}^{2} \mathbf {K}_{ij}^T \mathbf {Z}_{ij} \dot{\mathbf {K}}_{ij} + \sum _{i=1}^{3}\sum _{j=0 \, \text { or } \, 1}^{2} \mathbf {K}_{ij}^T \mathbf {N}_{ij} \mathbf {K}_{ij}. \end{aligned}$$

(20)

To achieve a good agreement between the experimental and the numerical data, the sliding friction of the linear guides has been also considered in the model. In this way, the torques and forces, $\varvec{\tau }_f=[\tau _{f1} \quad \tau _{f2} \quad \tau _{f3} \quad \tau _{f4} \quad \tau _{f5} \quad \tau _{f6}]^T$, required to perform a task can be calculated according to

$$\begin{aligned} \varvec{\tau }_f=\varvec{\tau }_g+\varvec{\tau }_\mu , \end{aligned}$$

(21)

where $\varvec{\tau }_\mu =[0 \quad 0 \quad 0 \quad \mu \dot{\delta }_1 \quad \mu \dot{\delta }_2 \quad \mu \dot{\delta }_3]^T$ and $\mu$ is the sliding friction factor. Whilst, the first three terms of $\varvec{\tau }_f$ are the torques related to the active revolute joints, the other terms are forces related to the active prismatic joints. A force–torque transformation can be used to the last three terms yielding an input vector containing efforts of the same type. Using this transformation, the input vector containing torques can be described by:

$$\begin{aligned} \varvec{\tau }=\begin{bmatrix} \tau _1&\tau _2&\tau _3&\tau _4&\tau _5&\tau _6 \end{bmatrix}^T, \end{aligned}$$

(22)

where $\tau _i=\tau _{fi}$ for $i=1 \ldots 3$ and $\tau _i= K \tau _{fi}/(2\pi )$ for $i=4 \ldots 6$ and K is the lead of the linear guide.

4 Motion planning via redundancy resolution

Kinematically redundant manipulators present infinite kinematic configurations, ${\boldsymbol{\varTheta }}$, for a constant end-effector’s pose, $\mathbf {X}$. In other words, there are infinite solutions for the inverse kinematic problem. A suitable choice among the possibilities should be made based on the system requirements. In this manuscript, this choice is made via a multiobjective optimization problem.

4.1 Cost function

In this manuscript, redundancy resolution schemes for improving the dynamic performance of a planar kinematically redundant PKM are investigated. An alternative to improve the manipulator’s dynamic performance is to minimize the absolute value of the maximum required torque during the execution of a predefined trajectory of the end-effector (tracking problem). Numerical results using this optimization problem were discussed for several levels of kinematic redundancies in Fontes et al. [11]. In spite of avoiding high torque values, this strategy was unable to deliver a singularity-free motion during the execution of experimental tasks using the 3PRRR prototype. In this way, an extension of this strategy is proposed: a multiobjective optimization. Whilst the first cost function penalizes high torque values, the second one penalizes motion near singular regions. Due to the multiobjective nature of this optimization problem, both cost functions should be normalized [24].

The first cost function, that penalizes the maximum required torque, can be mathematically described by $\left\| \varvec{\tau } \right\| _\infty / \varvec{\tau }_\mathrm{{max}}$. The term $\left\| \varvec{\tau } \right\| _\infty$ indicates the maximum required torque and the term $\varvec{\tau }_\mathrm{{max}}$ is the normalization factor given by a fixed value.

The second cost function, that penalizes motion near singular regions can be related to the Condition Number of the Jacobian matrix $\mathbf {A}$ as proposed in Alba-Gomez et al. [25] and Reveles et al. [26]. In fact, this number can be interpreted as a measurement of the closeness of the end-effector and singular regions. Nevertheless, the Jacobian matrix $\mathbf {A}$ of the manipulators under study is dimensionally heterogeneous. Due to this, the performance indexes derived from this matrix can be misleading [27]. An alternative to treat this issue is to homogenize it using the manipulator’s characteristic length $L_\mathrm{{c}}=\sqrt{2}h$ as proposed in Alba-Gomez et al. [25] and Reveles et al. [26]:

$$\begin{aligned} \mathbf {{A}}' = \begin{bmatrix} a_{11}&a_{12}&a_{13}/L_\mathrm{{c}}\\ a_{21}&a_{22}&a_{23}/L_\mathrm{{c}}\\ a_{31}&a_{32}&a_{33}/L_\mathrm{{c}} \end{bmatrix}. \end{aligned}$$

(23)

As a result, the condition number $\kappa ({\mathbf {A}}')$ of the homogenized Jacobian matrix $\mathbf {{A}}'$ can be calculated by:

$$\begin{aligned} \kappa ({\mathbf {A}}')=\frac{\mathrm{{max}}\ \nu ({\mathbf {A}}')}{\mathrm{{min}}\ \nu ({\mathbf {A}}')}, \end{aligned}$$

(24)

where $\nu ({\mathbf {A}}')$ are the singular values of the matrix ${\mathbf {A}}'$. This value can be defined as the manipulator’s conditioning index which is bounded, $1 \le \kappa ({\mathbf {A}}') \le \infty$ [25]. Ideal isotropic configurations occur where $\kappa ({\mathbf {A}}')=1$ and singularities are found where $\kappa ({\mathbf {A}}')=\infty$. In this way, the second cost function can mathematically be described as $\left\| \kappa ({\mathbf {A}}') \right\| _\infty / \kappa ({\mathbf {A}}')_\mathrm{{max}}$. The term $\left\| \kappa ({\mathbf {A}}') \right\| _\infty$ indicates the maximum reached condition number of the homogenized Jacobian matrix $\mathbf {A}'$ during a task and the term $\kappa ({\mathbf {A}}')_\mathrm{{max}}$ is the normalization factor given by a fixed value.

Mathematically, the decision variables are composed of the position vector of the redundant actuators, $\delta _i(t)$ where $i=1 \ldots M$. These decision variables are bounded by the stroke range of the linear guides, $\delta _\mathrm{{min}}\le \delta _i(t)\le \delta _\mathrm{{max}}$. The optimal position vector of the redundant actuators, $\delta _{i,\mathrm{{opt}}}$, can be found by solving the following optimization problem:

$$\begin{aligned} \delta _{i,\mathrm{{opt}}}(t) = \text {arg} \quad \underset{\delta _i(t)}{\text {min}} \ \Bigg (\frac{\left\| \varvec{\tau } \right\| _\infty }{\varvec{\tau }_\mathrm{{max}}}, \frac{\left\| \kappa ({\mathbf {A}}') \right\| _\infty }{\kappa ({\mathbf {A}}')_\mathrm{{max}}} \Bigg ) \\ \nonumber \text {subject \, to:} \ \delta _\mathrm{{min}}\le \delta _i(t)\le \delta _\mathrm{{max}}. \end{aligned}$$

(25)

The optimization problem described by Eq. (25) can be solved using linear scalarization and by defining weighting factors for each cost function [24]. The values of the weighting factors can be selected according to the system requirements and the designer’s expertise. In this way, a single cost function is used by calculating a weighted sum of the cost functions in the next section.

4.2 Redundancy resolution

Global strategies for redundancy resolution seek the optimal redundant actuators’ inputs for a predefined task. These values are dependent on time and are used for calculating the kinematics and dynamics via the aforementioned inverse models. Kotlarski et al. [19] proposed two strategies to deal with the motion of the redundant actuator as discussed in Sect 1. These strategies have been revisited in Fontes et al. [11] using a different nomenclature: (1) the prepositioning and (2) the ongoing positioning approaches. These strategies are exploited hereafter considering not only extra levels of kinematic redundancies but also different cost functions (Eq. 25).

The prepositioning approach consists of determining the best position vector of redundant actuators, $\delta _i$ where $i=1 \ldots M$, before the execution of the task. Note that the values $\delta _i$ are the same throughout the entire task execution. So, in this case, the optimization problem has just one decision variable for each redundant actuator, $\delta _{\mathrm{{fixed}}_i}$. The optimal values of these variables, $\delta _{\mathrm{{fixed}}_i,opt}$, can be found by the following optimization problem:

$$\begin{aligned} &[\delta _{{{\text{fixed}}_{i} ,{\text{opt}}}} ] = {\text{arg}}\quad \mathop {{\text{min}}}\limits_{{\delta _{{{\text{fixed}}_{i} }} }} \;w_{1} \frac{{\left\| \tau \right\|_{\infty } }}{{\tau _{{{\text{max}}}} }} + w_{2} \frac{{\left\| {\kappa ({\mathbf{A}}^{\prime } )} \right\|_{\infty } }}{{\kappa ({\mathbf{A}}^{\prime } )_{{{\text{max}}}} }} \\ & \quad \quad \quad {\text{subject}}\,{\text{to:}}\,\delta _{{{\text{min}}}} \le \delta _{{{\text{fixed}}_{i} }} \le \delta _{{{\text{max}}}}\end{aligned} .$$

(26)

where $w_1$ and $w_2$ are the weighing factors of the multiobjective optimization problem.

The ongoing positioning approach consists of determining the best motion of the redundant actuators, $\delta _i$ where $i=1 \ldots M$, during the task execution. The mathematical description of this motion can be defined by a polynomial trajectory. Due to this description, only the initial and final positions, $\delta _{0_i}$ and $\delta _{f_i}$, are considered as decision variables in the optimization problem. In this manuscript, a polynomial of degree five is selected to describe the movement of $\delta _i$ from $\delta _{0_i}$ to $\delta _{f_i}$ between the time interval $[t_0,t_f]$ with null initial and final velocities/accelerations according to:

$$\begin{aligned} \delta _i(t) = cc(0)+cc(1)t+cc(2)t^2+cc(3)t^3+cc(4)t^4+cc(5)t^5, \end{aligned}$$

(27)

where t is time in seconds and the coefficients of the polynomial are given by:

$$\begin{aligned} \mathbf {cc}= \mathbf {AA}^{-1}\mathbf {BB}, \end{aligned}$$

(28)

where

$$\begin{aligned} \mathbf {AA} =\begin{bmatrix} 1&t_0&t_0^2&t_0^3&t_0^4&t_0^5 \\ 0&1&2t_0&3t_0^2&4t_0^3&5t_0^4 \\ 0&0&2&6t_0&12t_0^2&20t_0^3 \\ 1&t_f&tf^2&t_f^3&t_f^4&t_f^5 \\ 0&1&2t_f&3t_f^2&4t_f^3&5t_f^4 \\ 0&0&2&t_f^3&12t_f^2&20t_f^3 \end{bmatrix} \; \text{ and } \end{aligned}$$

(29)

$$\begin{aligned} \mathbf {BB} = \begin{bmatrix} \delta _{0_i,\mathrm{{opt}}}&\dot{\delta }_{0_i,\mathrm{{opt}}}&\ddot{\delta }_{0_i,\mathrm{{opt}}}&\delta _{f_i,\mathrm{{opt}}}&\dot{\delta }_{f_i,\mathrm{{opt}}}&\ddot{\delta }_{f_i,\mathrm{{opt}}} \end{bmatrix}^T. \end{aligned}$$

(30)

In this case, the optimization problem has, for each level of kinematic redundancy, two variables, $\delta _{0_i}$ and $\delta _{f_i}$. In this way, the number of variables is 2M, where M is the number of redundant actuators according to Table 1. The optimal values of these variables, $\delta _{0_i,\mathrm{{opt}}}$ and $\delta _{f_i,\mathrm{{opt}}}$ for $i=1 \ldots M$, can be found by solving the following optimization problem:

$$\begin{aligned}{} [{\delta _{0_i,\mathrm{{opt}}},\delta _{f_i,\mathrm{{opt}}}}] &= \text {arg} \quad \underset{[\delta _{0_i},\delta _{f_i}]}{\text {min}} \ w_1\frac{\left\| \varvec{\tau } \right\| _\infty }{\varvec{\tau }_\mathrm{{max}}} + w_2 \frac{\left\| \kappa ({\mathbf {A}}') \right\| _\infty }{\kappa ({\mathbf {A}}')_\mathrm{{max}}} \\ & \nonumber \qquad \text {subject \, to} \\ & \nonumber \quad \delta _{\rm {min}}\le \delta _{0_i}\le \delta _\mathrm{{max}} \nonumber \\ & \quad \delta _{\rm {min}}\le \delta _{f_i}\le \delta _\mathrm{{max}} \nonumber \\ & \quad \delta _{\rm {min}}\le \delta _{i}\le \delta _\mathrm{{max}} \nonumber . \end{aligned}$$

(31)

The optimization problems defined by Eqs. (26) and (31) can be solved using evolutionary or deterministic methods that can solve constrained multivariable non-convex optimization problems [24]. In this work, starting values have been found using genetic algorithm and the optimum values by using sequential quadratic programming [24].

5 Results

Some prototype’s physical properties are given in Table 3. Moreover, the distances $a=0.26$ m and $h=0.06$ m, while the limits of the linear guides are $\delta _\mathrm{{min}} = -\,0.3$ m and $\delta _\mathrm{{max}} = 0.3$ m. These limits are used in the constraints of the optimization problem (Eq. 25). The sliding friction factor is $\mu =1200.00$ Ns/m and the lead of the linear guide $K=0.01$ m. The linear guides’ angular orientations are described in Table 4.

Table 3 Prototype’s physical properties

Table 4 Angular orientations of the linear guides

For sake of comparison, the same task is performed numerically and experimentally by the manipulators under study considering the prepositioning and the ongoing approaches as redundancy resolution methods. The task is a point-to-point trajectory represented by a straight line shown in Fig. 5. The end-effector moves from the position ($-\,0.0208$, 0.1182) m to the position (0.0104, $-\,0.0591$) m with a fixed null angular position during the task execution. The total time is 1 s.

Fig. 5

Task to be executed

Both prepositioning and the ongoing approaches were described by multiobjective problems, defined by Eqs. (26) and (31), respectively. Both optimization problems were solved using the same weighting factors, $w_1=w_2=1$. These values were selected for both cost functions since both criteria are relevant for the application and the objectives were normalized. Finally, the two normalization factors were $\tau _\mathrm{{max}}= 0.400$ Nm and $\kappa _\mathrm{{max}}= 3.000$.

Numerical results such as the optimal cost function value, the maximum condition number and the maximum required torque are shown in Table 5 for different levels of kinematic redundancies and redundancy resolution methods. In this table, the maximum value of the required torque to perform the task experimentally is also described.

Table 5 Numerical and experimental results for the manipulators and redundancy resolution methods under study

According to Table 5, the more complex the redundancy resolution method and higher the number of level of kinematic redundancies, the lower the objective function. By comparing the redundancy resolution methods at the same redundancy level, one can verify that the ongoing positioning approach has obtained lower optimal objective function values than the prepositioning approach for the cases under investigation.

Both numerical and experimental results indicated that the maximum required torque can be reduced by the use of any level of kinematic redundancy and/or redundancy resolution method. Experimentally, one, two and three levels of kinematic redundancies assured at least a 7.2, 24.4 and $30.6\%$ reduction of the maximum required torque, respectively. This demonstrates that the use of two or more kinematic redundant actuators can be beneficial for the manipulator’s dynamic performance. Moreover, both redundancy resolution methods yielded similar maximum required torque values for the same number of kinematic redundancies, numerically and experimentally.

Table 5 also demonstrates the correlation between the manipulators’ conditioning number and the experimental required torques. For instance, the numerical results indicated that the use of the prepositioning approach and a single level of kinematic redundancy (PRRR + 2RRR—prepositioning approach) could yield the lowest value of the maximum required torque, 0.176 Nm. This outcome could not be confirmed by the experimental results. In fact, the experimental data indicated that the lowest value of the maximum required torque had been achieved by the use of the ongoing approach and three levels of redundancies (3PRRR—ongoing approach). One can verify that the condition number of the former is higher than the later combination ($2.286>1.546$). Higher condition number values indicate that there is motion near singular regions. Whilst, this issue had little impact on the numerical assessment of the manipulators’ dynamic performance, it become a major issue on their experimental assessment.

Fig. 6

a Numerical and b experimental torques performed by the motors of the non-redundant manipulator 3RRR

Fig. 7

a Numerical and b experimental torques performed by the motors of the redundant manipulator 3PRRR using the prepositioning approach

Fig. 8

a, b Numerical and c, d experimental torques performed by the motors of the redundant manipulator 3PRRR using the ongoing positioning approach

Figures 6, 7 and 8 show the numerical and experimental required torques for the 3RRR, 3PRRR (prepositioning approach) and 3PRRR (ongoing approach) to perform the task illustrated in Fig. 5, respectively. In fact, Fig. 6 depicts the required torques of the active revolute joints of the 3RRR: Motor 1, Motor 2 and Motor 3. This is also the data depicted in Fig. 7 for the redundant 3PRRR manipulator, since the redundancy resolution method is the preposition approach and the prismatic joints are locked during the task execution. Figure 8 shows the torques of the active revolute and prismatic joints of the redundant 3PRRR manipulator using the ongoing approach as redundancy resolution method. In this figure, the active revolute joints are denoted as Motor 1, Motor 2 and Motor 3 and the active prismatic joints are denoted as Motor 4, Motor 5 and Motor 6.

One can notice by evaluating Figs. 6, 7 and 8, that the numerical kinematic and dynamic models were able to capture the behaviour of the non-redundant and redundant manipulators. Moreover, both redundancy resolution methods were capable of reducing the required torques to perform the task. This important result demonstrates that kinematic redundancy can be an alternative for improving the dynamic performance of PKMs.

6 Conclusions

In this manuscript, numerical and experimental analysis for evaluating the impact of several levels of kinematic redundancy on performance of a planar parallel manipulator were performed. Since the inverse kinematic model of kinematically redundant manipulators present infinite solutions, redundancy resolution methods were exploited. In this manuscript, the definition of the motion of the redundant actuators was done using a multiobjective optimization problem. The cost functions of this problem took into account indexes related to the singularities’ avoidance and the improvement of the manipulator’s dynamic performance. Two approaches were exploited for the proposed redundancy resolution method: (1) the prepositioning and (2) the ongoing positioning approaches.

With respect to the numerical modeling, it could be verified that the numerical models were able to capture the dynamic behaviour of non-redundant and redundant manipulators. These were achieved by the inclusion of the sliding friction term in the dynamic modeling.

In regard to the mathematical description of the redundancy resolution scheme via a multiobjective optimization problem, it could be verified that the inclusion of a term penalizing the proximity to singular regions is the utmost importance. This penalty term exploited the condition number of a homogenized Jacobian matrix. This homogenization step is essential due to the presence of angular and translational DoFs. Due to the presence of this penalization, lower torque values were required in the experimental results.

About the inclusion of several levels of kinematic redundancies, it could be concluded that they have been capable of reducing the required torque for executing the selected task. This outcome was verified for both exploited redundancy resolution schemes. It is important to highlight that both schemes penalized the proximity to singular regions. If this penalty term was not included, the reduction of the required torque for executing the same task could not be achieved experimentally. This demonstrates the importance of selecting a proper reduction resolution scheme.

Regarding the redundancy resolution methods and the selected task, it could be demonstrated that the ongoing approach may yield slightly lower objective function values than the prepositioning approach. Nevertheless, experimental results demonstrated that both approaches required approximately the same amount of torque for executing the selected task for the same number of redundant actuators.

In spite of being task dependent, these important results motivate further investigations on the impact of the inclusion of several levels of kinematic redundancy on the energy consumption of a PKM. The outcome of this investigation demonstrates the potential of kinematic redundancies on improving the dynamic performance of parallel manipulators. This is an alternative that could be considered by the designer for improving industrial manipulators.