1 Introduction

Fatigue analysis of ductile fracture has been the object of great importance, since most metals in engineering application fail according to this mechanism. Fracture behavior of ductile materials is quite different from that of brittle materials. Ductile materials generally exhibit slow stable crack growth accompanied by considerable plastic deformation [1]. The ductile fatigue fracture growth often leads to sudden and catastrophic failure of structures or components. Therefore, fatigue analysis of ductile fracture growth is vital in ensuring the reliability of the structures under cyclic loading.

For the fracture mechanics problems, FEM requires that the mesh should be highly refined and rigorously aligned with the physical discontinuity. Moreover, special elements [2] around the crack tip should be created to handle the singularity. Hence, the strenuous procedure of re-meshing procedure is required as the crack propagates. Adaptive mesh-generation strategies have been proposed and conjugate with the FEM code. For example, Miranda et al. [3] proposed a two-phase methodology for mixed-mode crack growth under variable amplitude, using automatic re-meshing procedure in FE code. Meggiolaro et al. [4, 5] developed an automatic re-meshing algorithm which works both for region without crack and that with one or multiple cracks. Over years, researchers have devoted to develop efficient numerical methods for the cracking modeling, such as the boundary element method [6–8], mesh-free method [9–11], numerical manifold method [12] and extended finite element method (XFEM) [13, 14]. Among those methods, XFEM offers great advantages over others, since it enables the mesh to be independent of the evolving crack geometry; in addition, it avoids adaptive re-meshing and refinement work as the crack propagates. Fries [15] modified the standard XFEM approximation with a ramp function to overcome the shortcoming lying in blending elements, so optimal convergence rate and high accuracy can be achieved; the method is frequently referred to as corrected XFEM. Till now, the XFEM has been applied in various fracture problems including the cohesive crack propagation [16, 17], crack growth with frictional contact [18, 19], elastodynamic crack propagation [20], branched and intersecting crack growth [14], three dimension crack propagation [21] and even heat transfer problem [22].

So far, most of the developments in XFEM have focused mainly on linear elastic material behavior based on linear elastic fracture mechanics theory. The stress at the crack tip is theoretically infinite in the assumption of linear elastic fracture mechanics, where no real material can stand such stress. With regard to brittle material, the analysis within the elastic linear theory is still acceptable because the plastic zone around the crack tip is relatively small. However, for the highly ductile material, the elastic linear theory is not admissible and the difference is significant. In the field of continuum mechanics, FEM has no limitation in solving nonlinear problems. For example, FEM was extended to nonlinear materials and large deformation problems by Zienkiewicz et al. [23]. The application of XFEM to elastic–plastic fracture problem has been studied; however, there are still some limitations, such as the location of the initial crack locus or plastic behavior at the crack tip. For example, Jovicic et al. [24] examined the possibility of applying standard XFEM algorithm without near tip enriching functions in the zone of plasticity. Elguedj et al. [25] extracted elastic–plastic enrichment basis from the well-known Hutchinson–Rice–Rosengren (HRR) fields to represent the singularities in elastic–plastic fracture mechanics. Seabra et al. [26] combined XFEM with Lemaitre ductile damage model to simulate the whole process from crack initiation to crack propagation, but as for the formulation of XFEM only Heaviside enrichment function was incorporated and the accuracy of local stress field might be compromised. Shedbale et al. [27] used nonlinear XFEM to simulate plate in the presence of a major pure mode I crack and other multiple discontinuities. XFEM was also extended by Singh et al. [28] to simulate elastic–plastic crack growth problem with large deformation. In their work, the developed technique was applied to pure mode I crack growth problems, and it was recommended that the work should be further extended to simulate stable crack growth for arbitrary cracks in ductile materials. Therefore, the fatigue analysis for arbitrary cracks in ductile materials is the main work in the current paper. In real fatigue life problems, the crack path is generally arbitrary and forms a mixed-mode problem. With enrichment functions modified, the corrected XFEM can offer the advantages of optimal convergence rate and more accurate asymptotic crack tip stress field, which make the method more suitable for elastic–plastic fracture analysis. Hence, different from the previous nonlinear XFEM simulation, the corrected XFEM formulation was chosen to carry out elastic–plastic fracture analysis.

In the present work, corrected XFEM is extended to simulate mixed-mode crack growth in ductile materials. The Newton–Raphson technique is employed to solve the nonlinear equation. Mixed-mode stress intensity factors (SIFs) are calculated by interaction integral method, and crack growth rate is evaluated by modified Paris law. Two numerical examples are presented in this work. A comparison study with the experimental data and ANSYS simulation is presented to verify this numerical method; then, the proposed methodology is applied to investigate the mixed-mode crack growth problem under constant amplitude cyclic loading.

2 Numerical formulation

2.1 Framework of corrected XFEM

Based on the partition of unity method, standard finite element displacement approximation is locally enriched with enrichment functions to model the discontinuity and the singularity. As for 2D-corrected XFEM, displacement approximation takes the form:

$$\begin{aligned} u^{h} (x) & = \sum\limits_{j \in N} {N_{j} (x)u_{j} } + \sum\limits_{k \in M} {N_{k} (x)[H(x) - H(x_{k} )]a_{k} } \\ \, & \quad + \sum\limits_{l \in I \cup J} {N_{l} (x)\mu (x)\sum\limits_{\alpha = 1}^{4} {\left( {\beta_{\alpha } (x) - \beta_{\alpha } (x_{l} )} \right)b_{l}^{\alpha } } } . \\ \end{aligned}$$
(1)

As marked in Fig. 1, N is the set of all nodes in the mesh; M is the set of nodes belonging to those split elements which intersect the crack; I is the set of nodes belonging to the tip element which contains the crack tip. If a node belongs both to the split element and tip element, then the node belongs to the I set. Those elements, in which parts of nodes belong to subset I, are blending elements. J is the set of those nodes belonging to blending elements, but does not belong to the tip element.

Fig. 1
figure 1

Nodal subsets and element types

Full size image

In Eq. (1), u j is the classical finite element displacement; N j (x), N k (x) and N l (x) are standard FE shape functions. Technically, N k (x) and N l (x) do not have to be the same as N j (x). H(x) is the Heaviside function used to model the discontinuity in displacement, which takes +1 on one side of the crack surface and −1 on the other side. a k is the nodal unknowns added to the M set of nodes. β α(x) (α = 1–4) are four asymptotic crack tip branch functions, used to incorporate the crack tip displacement field into tip elements. \(b_{l}^{\alpha }\) (α = 1–4) are the nodal unknowns added to the I and J set of nodes. Considering the local polar coordinates r and θ centered at the crack tip, these four branch functions can be written as:

$$[\beta_{\alpha } (x),\alpha = 1 - 4] = \left[ {r^{l} \cos \frac{\theta }{2},r^{l} \sin \frac{\theta }{2},r^{l} \cos \frac{\theta }{2}\sin \theta ,r^{l} \sin \frac{\theta }{2}\sin \theta } \right],$$
(2)

where, for linear XFEM, the value of exponent l = 0.5, and for nonlinear XFEM, the value of exponent \(l = 1 /(1 + \bar{n})\), with \(\bar{n}\) being the hardening exponent, which depends on the material.

μ(x) is a ramp function which is defined as

$$\mu (x) = \sum\limits_{l \in I} {N_{l} (x)} .$$
(3)

As shown in Fig. 2, within the tip element, μ(x) = 1, while, in the blending elements, μ(x) varies continuously and reaches zero at the J set of nodes. After the modification, the value of the enrichment functions is the same as those in standard XFEM within the tip element and is zero in elements with some of their nodes in the J set.

Fig. 2
figure 2

The value of ramp function μ(x) over a meshed domain

Full size image

2.2 Mathematical theory of plasticity

The von Mises yield criterion along with isotropic strain hardening is used to determine the stress level at which plastic deformation begins. After the initial yielding, the strain can be assumed to be divisible into elastic and plastic components, and the complete relation between stress increment and strain increment can be written as:

$$\{ {\text{d}}\varepsilon \} = \{ {\text{d}}\varepsilon_{\text{e}} \} + \{ {\text{d}}\varepsilon_{\text{p}} \} ,$$
(4)

where, {dε e} is the elastic strain increment. According to generalized Hooke’s law, {dε e} = [D]−1{dσ}, [D] is the elastic constitutive matrix; {dε p} is the plastic strain increment, which according to flow rule is proportional to the stress gradient of the plastic potential function Q:

$$\{ {\text{d}}\varepsilon_{\text{p}} \} = \lambda \left\{ {\tfrac{\partial Q}{\partial \sigma }} \right\}.$$
(5)

In Eq. (5), λ is a proportional constant termed the plastic multiplier. Equation (5) is known as flow rule, which governs the plastic constitutive relation after yielding. The complete constitutive relation can be rewritten as

$$\{ {\text{d}}\varepsilon \} = [D]^{ - 1} \{ {\text{d}}\sigma \} + \lambda \left\{ {\tfrac{\partial Q}{\partial \sigma }} \right\}.$$
(6)

The von Mises yield function can be written as

$$F(\{ \sigma \} ,\kappa ) = 0,$$
(7)

where κ is the plastic work during plastic deformation for the hardening material.

According to the total derivative method, the following equation can be obtained:

$$\left\{ {\tfrac{\partial F}{\partial \sigma }} \right\}^{T} \{ {\text{d}}\sigma \} + A\lambda = 0.$$
(8)

After mathematical manipulations, the plastic multiplier is calculated as

$$\lambda = \frac{{\left\{ {\tfrac{\partial F}{\partial \sigma }} \right\}^{T} [D]\{ {\text{d}}\varepsilon \} }}{{\left\{ {\tfrac{\partial F}{\partial \sigma }} \right\}^{T} [D]\left\{ {\tfrac{\partial Q}{\partial \sigma }} \right\} - A}},$$
(9)
$$\, A = \tfrac{\partial F}{\partial \kappa }\{ \sigma \}^{T} \left\{ {\tfrac{\partial Q}{\partial \sigma }} \right\}.$$
(10)

According to plastic flow rule of Drucker’s postulate, the yield function and potential function are identical, Q ≡ F, and this form of plastic constitutive relation is called associated flow rule. Hence, the complete relation of stress and strain increments can be rewritten as:

$$\{ {\text{d}}\sigma \} = [D]_{\text{ep}} \{ {\text{d}}\varepsilon \} = ([D] - [D]_{\text{p}} )\{ {\text{d}}\varepsilon \} ,$$
(11)
$$[D]_{\text{p}} = \frac{{[D]\left\{ {\tfrac{\partial Q}{\partial \sigma }} \right\}\left\{ {\tfrac{\partial F}{\partial \sigma }} \right\}^{T} [D]}}{{\left\{ {\tfrac{\partial F}{\partial \sigma }} \right\}^{T} [D]\left\{ {\tfrac{\partial Q}{\partial \sigma }} \right\} - A}},$$
(12)

where A = −H′, and H′ is the hardening function which defines the strain hardening of the material. As mentioned above, in Drucker’s postulate, the yield function and potential function are identical; in this case, the elastic–plastic constitutive matrix [D]ep is symmetric.

2.3 Computation of stress intensity factors

Three main SIF calculation methods including displacement correlation technique, the potential energy release rate method and the equivalent domain integral (EDI) were compared by Miranda et al. [29]. It was concluded that the EDI results in the best SIF prediction. In this paper, a similar and more sophisticated method is employed, in which the J-integral is obtained by calculation of a domain-based interaction integral [30]. In this method, deliberately selected auxiliary fields which satisfy both equilibrium equation and boundary conditions are superimposed onto the actual fields. The interaction integral for auxiliary state and actual state is given as

$$M^{(1,2)} = \int_{{A^{*} }} {\left[ {\sigma_{ij}^{(1)} \frac{{\partial u_{i}^{(2)} }}{{\partial x_{1} }} + \sigma_{ij}^{(2)} \frac{{\partial u_{i}^{(1)} }}{{\partial x_{1} }} - W^{(1,2)} \delta_{1j} } \right]} \frac{{\partial q_{s} }}{{\partial x_{j} }}{\text{d}}A,$$
(13)

where A * is the integral domain which contains the crack tip; q s is a smoothing function; W (1,2) is the interaction strain energy density. The superscripts denote auxiliary and actual stress equilibrium states. The superscripts 1 and 2 represent actual and auxiliary state, respectively.

Then, by intentionally selecting the auxiliary state as \(K_{\rm I}^{(2)} = 1\), \(K_{\coprod }^{(2)} = 0\), and then \(K_{\rm I}^{(2)} = 0\), \(K_{\coprod }^{(2)} = 1\), the mixed SIFs can be obtained through the following equation:

$$M^{(1,2)} = \frac{2}{{E^{\prime}}}\left( {K_{\rm I}^{(1)} K_{\rm I}^{(2)} + K_{\coprod }^{(1)} K_{\coprod }^{(2)} } \right).$$
(14)

2.4 Fatigue crack growth model

In the present work, a modified version of Paris law introduced by Huang et al. [31] is used to predict the crack growth rate, with consideration of the stress ratio effect. The modified Paris model takes the form of

$$\frac{{{\text{d}}a}}{{{\text{d}}N}} = C(M_{\text{R}} \varDelta K_{\text{eq}} )^{m} ,$$
(15)

where a is the crack length, N is the number of loading cycles, and C and m are Paris constants that depend on material properties. ΔK eq is the equivalent SIF range obtained by equivalent SIF \(K_{\text{eq}}^{\hbox{max} }\) and \(K_{\text{eq}}^{\hbox{min} }\) which correspond to the maximum and minimum applied load in a single cycle. M R is the stress ratio correction factor, given as

$$M_{\text{R}} = \left\{ \begin{aligned} & 1 - R)^{\gamma } \quad & 0 \le R < 0.5 \\ & (1.05 - 1.4R + 0.6R^{2} )^{\gamma } \quad & 0.5 \le R < 1 \\ \end{aligned} \right.,$$
(16)

where γ is a constant obtained from experimental data.

The direction of crack propagation is accepted to be a function of the mixed-mode stress intensity factors present at a crack tip. To determine the crack propagation direction, maximum principal stress criteria [32] is used, which assumes that the crack propagates in the direction perpendicular to the maximum principal stress. The direction of crack growth θ c is obtained by making local shear stress zero, which is written as

$$\theta_{\text{c}} = 2\arctan \left[ {\frac{1}{4}\frac{{K_{\text{I}} }}{{K_{\text{II}} }} - {\text{sign}}\left( {K_{\text{II}} } \right)\frac{1}{4}\sqrt {\frac{{K_{\text{I}}^{2} }}{{K_{\text{II}}^{2} }} + 8} } \right].$$
(17)

The equivalent SIF is given as

$$K_{\text{eq}} = \frac{1}{2}\cos \left( {\frac{{\theta_{\text{c}} }}{2}} \right)[K_{\text{I}} (1 + \cos \theta_{\text{c}} ) - 3K_{\text{II}} \sin \theta_{c} ].$$
(18)

3 Discretization and integration

3.1 Discretization

The discrete system of equilibrium equation takes the same form as that of classical FEM. However, the additional DOFs and enrichment functions result in an expansion in global stiffness matrix and force vector. For each element e, the stiffness matrix K e, force vector f h and nodal unknown u h are defined as:

$$K_{ij}^{e} = \left[ {\begin{array}{*{20}c} {K_{ij}^{uu} } &\quad {K_{ij}^{ua} } & \quad {K_{ij}^{ub} } \\ {K_{ij}^{au} } & \quad {K_{ij}^{aa} } & \quad {K_{ij}^{ab} } \\ {K_{ij}^{bu} } & \quad {K_{ij}^{ba} } & \quad {K_{ij}^{bb} } \\ \end{array} } \right],$$
(19)
$$f^{h} = \left\{ {\begin{array}{*{20}c} {f_{i}^{u} } & {f_{i}^{a} } & {f_{i}^{b1} } & {f_{i}^{b2} } & {f_{i}^{b3} } & {f_{i}^{b4} } \\ \end{array} } \right\}^{\text{T}} ,$$
(20)
$$u^{h} = \left\{ {\begin{array}{*{20}c} u & a & {b_{1} } & {b_{2} } & {b_{3} } & {b_{4} } \\ \end{array} } \right\}^{\text{T}} .$$
(21)

The sub-matrices in the Eqs. (19–21) are given as:

$$K_{ij}^{\text{rs}} = \int_{{\varOmega^{\text{e}} }} {(B_{i}^{r} )^{\text{T}} } D_{\text{eq}} (B_{j}^{s} )h{\text{d}}\varOmega ,\quad (r,s = u,a,b),$$
(22)
$$f_{i}^{u} = \int_{{\varOmega^{\text{e}} }} {N_{i} b{\text{d}}\varOmega } + \int_{\varGamma t} {N_{i} \bar{t}{\text{d}}\varGamma } ,$$
(23)
$$f_{i}^{a} = \int_{{\varOmega^{\text{e}} }} {N_{i} (H(x) - H(x_{i} ))b{\text{d}}\varOmega } + \int_{\varGamma t} {N_{i} (H(x) - H(x_{i} ))\bar{t}{\text{d}}\varGamma } ,$$
(24)
$$f_{i}^{b\alpha } = \int_{{\varOmega^{\text{e}} }} {N_{i} (\beta_{\alpha } (x) - \beta_{\alpha } (x_{i} ))b{\text{d}}\varOmega } + \int_{\varGamma t} {N_{i} (\beta_{\alpha } (x) - \beta_{\alpha } (x_{i} ))\bar{t}{\text{d}}\varGamma } ,$$
(25)

where b and \(\bar{t}\) are body force and surface force, respectively. \(B_{i}^{u} ,B_{i}^{a} ,B_{i}^{b}\) are shape function derivatives, defined as:

$$B_{i}^{u} = \left[ {\begin{array}{*{20}l} {N_{i,x} } & 0 \\ 0 & {N_{i,y} } \\ {N_{i,y} } & {N_{i,x} } \\ \end{array} } \right]_{3 \times 8} ,$$
(26)
$$B_{i}^{a} = \left[ {\begin{array}{*{20}l} {[N_{i} (H(x) - H(x_{i} ))]_{,x} } & 0 \\ 0 & {[N_{i} (H(x) - H(x_{i} ))]_{,y} } \\ {[N_{i} (H(x) - H(x_{i} ))]_{,y} } & {[N_{i} (H(x) - H(x_{i} ))]_{,x} } \\ \end{array} } \right],$$
(27)
$$B_{i}^{b} = \left[ {\begin{array}{*{20}c} {B_{i}^{b1} } & {B_{i}^{b2} } & {B_{i}^{b3} } & {B_{i}^{b4} } \\ \end{array} } \right],$$
(28)
$$B_{i}^{b\alpha } = \left[ {\begin{array}{*{20}l} {[N_{i} (\beta_{\alpha } (x) - \beta_{\alpha } (x_{i} ))R]_{,x} } & 0 \\ 0 & {[N_{i} (\beta_{\alpha } (x) - \beta_{\alpha } (x_{i} ))R]_{,y} } \\ {[N_{i} (\beta_{\alpha } (x) - H(x_{i} ))R]_{,y} } & {[N_{i} (\beta_{\alpha } (x) - \beta_{\alpha } (x_{i} ))R]_{,x} } \\ \end{array} } \right]_{3 \times 8} ,\quad (\alpha = 1,2,3,4),$$
(29)

where R is the ramp function, as defined in Eq. (3).

We present in Fig. 3 the XFEM simulation of involving a crack.

Fig. 3
figure 3

Flowchart of XFEM simulation

Full size image

3.2 Numerical integration

As the integrands in split elements and tip elements are non-smooth, standard Gauss quadrature scheme cannot be used for numerical integration. In case of elastic material, the numerical integration of cut elements is generally performed by partitioning them into standard sub-triangles [33].

In case of an elastic–plastic media, the values of stress and strain field are computed at Gauss points. Therefore, we chose to partition the tip element into 12 quadrilaterals, to better capture and display the singularity of the stress field asymptotic crack tip, which is an improvement in the present work. The division of enriched elements and Gauss points distribution is shown in Fig. 4. Within the tip element, the size of the inner four sub-quadrilaterals can be relatively small, which leads to a concentration of Gauss points at crack tip to model the singularity of the stress field.

Fig. 4
figure 4

Division of enriched elements and Gauss points distribution. a Element split into quadrilaterals. b Element split into triangles. c Tip element

Full size image

4 Numerical simulation

Two examples of fatigue crack growth under constant amplitude cyclic loading are presented below. The first example is pure mode I problem, in which comparison is made with a reference FE simulation and experimental data to verify the capacity of the established method. The second is aimed at studying the mixed-mode crack growth. Both examples are treated as plane stress conditions. The specimens are made of 2024-T4 aluminum alloy, and material properties are summarized in Table 1, shown in [34]. In Table 1, the units of C and m are corresponding to the unit of da/dN being mm/cycle, and ΔK being \({\text{MPa}} \times \sqrt m\) [35]. Ramberg–Osgood model covers strain hardening behavior and shows that smooth elastic–plastic transition is used and given as:

$$\varepsilon = \frac{\sigma }{E} + \alpha \frac{\sigma }{E}\left( {\frac{\sigma }{{\sigma_{y} }}} \right)^{{\bar{n} - 1}} .$$
(30)
Table 1 Material properties of the 2024-T4 aluminum alloy
Full size table

The specimens are subjected to constant cyclic loading. In each cycle, the amount of crack growth may be in the order of nanometers. In practice, simulation is conducted at discrete points. At each evaluation point, cyclic loading is applied on the specimen, and SIF is evaluated on the bases of XFEM results. Then, the crack propagates at a small magnitude ∆a, which represents thousands of loading cycles, until its final failure when K Ieq reaches K IC. The usual incremental plasticity theory is used to predict the stress and strain history.

4.1 Crack growth in round compact tension specimen

The experiment of crack growth in round compact tension specimen (RCT) under constant amplitude cyclic loading is selected from the literature [35]. The geometry and boundary condition is shown in Fig. 5. The thickness of the specimen is 3.7 mm, and the initial crack length is \(a_{0} = 5\;{\text{mm}}\). The domain is discretized using 4 node quadrilateral elements, totally 1407 elements and 1515 nodes are generated. Two loading cases are simulated here, i.e., maximum applied load P max = 3 kN, stress ratio R = 0.3 and P max = 2 kN, R = 0.1, respectively.

Fig. 5
figure 5

Geometry and boundary conditions of RCT specimen (unit: mm)

Full size image

As a reference numerical simulation, FEM analysis by commercial software ANSYS is conducted, and quarter point singular elements are generated circumferentially around the crack tip. According to the symmetry, only the upper half of the specimen is taken out for simulation, with the mesh highly refined at the crack tip. Whenever the crack propagates, the mesh is renewed. The meshes used in XFEM and FEM are shown in Fig. 6. The fixed crack growth increment is chosen as ∆a = 6 mm.

Fig. 6
figure 6

Meshing of the RCT specimen. a XFEM; b FEM

Full size image

The stress state at the integration points was checked against a material strength criterion. The plastic zone is displayed by all those integration points entering the yielding and hardening stage. The variation of plastic zone at the crack tip corresponding to maximum and minimum loading is provided in Fig. 7. By the choice of the Gauss points proposed by the current work, the plastic zone size can be better displayed. The stress contour plots obtained by the elastic–plastic XFEM and ANSYS at a = 7.5 mm, are shown in Fig. 8. The stress contour plots show that the results obtained by the present method are in good agreement with those by ANSYS. Because of the discontinuity, those elements which intersect the crack should be traction free. As expected, a tensile stress zero area is shown in the front of the crack tip, and the maximum stress occurs at the crack tip except the loading holes. A compressive stress zone is shown at the right end of the specimen due to the nature of RCT specimen loading.

Fig. 7
figure 7

Variation of plastic zone at the crack tip; a under minimum load; b under maximum load

Full size image
Fig. 8
figure 8

Stress contour plots for the RCT specimen; a σ xx by XFEM; b σ yy by XFEM; c σ xx by ANSYS; d σ yy by ANSYS (unit: MPa)

Full size image

At each stage of crack propagation, the crack growth rate is predicted using modified Paris law. Figure 9 provides the comparison of numerical results and experimental data. It shows that the results obtained by FEM and elastic–plastic XFEM are both in good agreement with the experimental data, while linear XFEM produces a reduced crack growth rate. The higher the applied load, the more significantly the result of linear XFEM deviates from the experimental data. Hence, the effect of plasticity is not negligible, when the applied load is high enough. Although simulation by traditional ANSYS software is more time consuming due to the refinement, the material plasticity and isotropic hardening can be taken into account with ease, and more sophisticated plasticity models are available.

Fig. 9
figure 9

Relationship between crack growth rate and crack length; a P max = 3 kN, R = 0.3; b P max = 2 kN, R = 0.1

Full size image

4.2 Overhanging beam specimen

An overhanging beam depicted in Fig. 10 is taken for mixed-mode analysis. The thickness of the specimen is 10 mm, and the initial crack length is \(a_{0} = 10\;{\text{mm}}\). The beam is subjected to concentrated load P max = 30 kN, the stress ratio is set as \(R = 0.3\), and the crack growth increment is chosen to be ∆a = 3 mm.

Fig. 10
figure 10

Geometry, loading, boundary conditions and meshing (unit: mm)

Full size image

The deformed shape of the overhanging beam in the final stage is depicted in Fig. 11. The crack path at different stages of crack growth is shown in Fig. 12. The whole process of the crack propagation is visualized in the XFEM, which is one of the advantages that XFEM offers. Generally in numerical simulation, the crack path vacillates at first and then gradually become smooth. As expected, the crack path develops roughly at the orientation of principal stress.

Fig. 11
figure 11

Deformed geometry of overhanging beam specimen (scaled by 50)

Full size image
Fig. 12
figure 12

Crack paths at different stages

Full size image

The stress contour plot of the beam is shown in Fig. 13. The elements near the loading points are made much stiffer to avoid local excessive stress and deformation. For overhanging beam, the stress component σ xx plays a dominant role. The maximum tensile stress occurs in front of the crack tip, and tensile stress at the surfaces of the crack is close to zero. The shear stress σ xy at both sides of the crack tip is negative, which is different from the pure mode I case.

Fig. 13
figure 13

Stress contour plots for overhanging beam specimen; a σ xx; b σ xy; c σ yy (unit: MPa)

Full size image

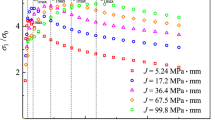
The phase angle \(\phi = \arctan (K_{\text{I}} /K_{\text{II}} )\) that defines the ratio of the stress intensity factor is provided in Fig. 14. This parameter is insensitive to the load value. As the figure shows, the phase angle decreases from 19° and remains stable around 0° finally. As a reference simulation, a different yield strength S y = 240 MPa is used, while all other material properties remain the same. The crack growth rate against crack length is shown in Fig. 15. In case of nonlinear analysis, a lower yield strength leads to a larger plastic zone area and reduced fatigue life. As compared to linear analysis, a reduction of 3.13 and 7.53 % in fatigue life is observed corresponding to the yield strength of 324 and 240 MPa, respectively. It indicates that to ensure the reliability of components or structures of low strength metal, nonlinear analysis should be carried out.

Fig. 14
figure 14

Phase angle variation as crack propagates

Full size image
Fig. 15
figure 15

Relationship between crack growth rate and crack length

Full size image

5 Conclusions

In the present work, the corrected XFEM has been successfully extended to simulate arbitrary crack growth in ductile materials. The elastic–plastic behavior is modeled by von Mises yield criterion and isotropic hardening; incremental plasticity theory along with Newton–Raphson technique is applied to solve the nonlinear problem. A domain-based interaction integral is used to evaluate the SIF values from the XFEM solution, and the crack growth rate is evaluated using modified Paris law at each stage of crack growth. The main contribution of this paper is extending the corrected XFEM for arbitrary cracks in ductile materials. On the basis of simulations, it can be concluded that XFEM can model mixed-mode crack growth in ductile materials with ease, as it enables the mesh to be completely independent of evolving crack geometry.

The crack growth rate obtained by the nonlinear analysis shows a good agreement with the experimental data and traditional ANSYS analysis for the RCT specimen. When the maximum load value increases, the difference between the results of linear and nonlinear analysis is more significant. The fatigue life analysis of overhanging beam shows that mixed-mode crack growth problem can be effectively modeled by nonlinear XFEM. The commercial FEM has the advantage of including various plasticity models. The elastic–plastic XFEM can produce acceptable results with minimal computational costs. It can be seen that, in the case of lower yield strength ductile material, the difference in fatigue life predicted by linear and nonlinear analysis is more significant as compared to higher yield strength ductile materials. The present method is applicable to large-scale yielding under constant amplitude loading. It can also be extended to situations of variable amplitude loading, if retardation effects are taken into account.