1 Introduction

Micro-perforated panel (MPP) is a type of sound absorber with relatively high sound absorption coefficient and wide frequency band [1]. A typical configuration of the MPP sound absorber usually consists of a plate with micro-perforations and a rigid wall behind it. The sound absorption mechanism of the MPP sound absorber depends on its micro-perforation and the resonance phenomenon, which is conceptually similar to Helmholtz resonator [2]. The MPP can be considered a lattice of short narrow tubes distributed on a plate, where the separation distance between the tubes is larger than the diameters of perforations, but small compared to the wavelength of the impinging sound. The propagation of a sound wave in the short tube has been studied by Lord [3] and has been simplified by Crandall [4]. The equation for the sound absorption coefficient of the MPP was first developed by Dah-You [5].

The equation for sound absorption coefficient was shown to reliably predict the sound absorption coefficient of the MPP sound absorber on the assumption that the MPP has high rigidity and thus the vibration of the plate can be neglected [5], where the thickness of the MPP under consideration should be similar or close to the perforation’s diameter [1]. However, this equation does not accurately describe the membrane or limp type MPP, for which the panel suffers from high flexibility and vibration, and for which the vibration effect has to be considered when determining the sound absorption coefficient [6, 7]. The effect of vibration on the sound absorption coefficient of a MPP sound absorber has been treated as a mass reactance and a mechanical loss [8–11], and considered as the imaginary and real parts of the MPP acoustic impedance, respectively. In the equivalent electro-acoustical circuit, the mass reactance is added in parallel to the micro-perforation’s acoustic impedance. This simplified approach ignores the higher order modes of the plate. In real applications, the actual behaviour of a MPP can differ from that of the model. For example, when a MPP of considerable size is mounted or lined on the wall, the MPP will be more flexible and will have more vibration modes compared with small MPP specimen [12] mounted in the impedance tube during testing. In this case, the size of the MPP and the mounting method will affect the vibration of the MPP, as well as the sound absorption coefficient. In the past, owing to plate or cavity resonance, several analyses of sound absorption mechanisms have neglected the bending stiffness of the plate [13–16]. In contrast, Ford and McCormick [17] considered the bending stiffness of a plate for the panel sound absorber sound absorption mechanism, and showed that the stiff panel sound absorber offers more than one sound absorption band. This shows that vibro-acoustic effect can improve the performance of the MPP sound absorber. This fact is augmented by the work of Lee et al. in which these authors used the bending stiffness effect in the analysis of flexible MPP for which the classical plate equation is coupled with the acoustic wave equation. Results of these studies indicated that the panel vibration effect can dissipate more energy and the peak sound absorption coefficient band can be widened by appropriately selecting the design parameters of the MPP sound absorber [18]. The study by Lee et al. is important because it shows how vibro-acoustic effect can be included in the sound absorption coefficient calculation of the MPP by including the modes of the plate.

In its most basic form, the MPP sound absorber consists of a single layer MPP that is backed by a rigid wall, and the gap in between forms the air cavity. The limitation of a single layer MPP sound absorber is its narrow frequency band of sound absorption coefficient. Different designs of MPP sound absorbers, aiming to widen the sound absorption coefficient frequency band, have been proposed and analysed, such as multiple-layered MPP configurations, different perforation diameters, partitioning air cavity, and thick layer MPP [2, 19–23]. For noise frequencies lower than 1,000 Hz, the resonator-type, rather than the porous type, sound absorber is more suitable for attenuating the noise levels [24]. An MPP sound absorber with many perforations not only provides good sound absorption, but also enhances the conductive heat dissipation for a motor or compressor. To achieve the optimal design of the MPP sound absorber, an optimization technique with global maximization searching process should be used, because there is a possibility that several local maxima exist in the space of solutions. Simulated annealing (SA) and genetic algorithms are two techniques that can help overcome such problems [25, 26]. The SA technique has been successfully applied to acoustical problems, such as the optimization of aluminium foam and constrained composite sound absorber [27, 28], as well as to the investigations of noise barriers [29, 30]. Thus far, research on SA-based optimization of multiple-layered MPP sound absorbers has been done by limiting the sound absorption mechanism of the sound absorber to the perforation and air cavity resonance, and by ignoring the effect of plate vibration [31, 32]. The more accurate mathematical models, such as those developed by Ford and McCormick [17], Takahashi and Tanaka [33], and Lee et al. [18] have not been used to search for the optimally designed models of MPP sound absorbers. As the material for the MPP becomes thinner and lighter, the vibration modes within the range of frequencies of interest will increase; this will strongly influence the overall sound absorption performance of the MPP [34]. In the search for the optimally designed MPP sound absorber, it is longer be possible to ignore the vibration effect of the plate that is used for the MPP production. In this work, we demonstrate the effectiveness of the vibro-acoustic model of the MPP by performing the optimization of the sound absorption coefficient for a double-layered MPP sound absorber that is designed to absorb noise from a typical air conditioner with noise frequencies ranging from 200 to 1,000 Hz [35–37]. This work demonstrates the advantages of including the vibro-acoustic effect in the derivation of optimal performance of a double-layered MPP.

The benefit of the selected model for the optimization of MPP is the potential of improving further the performance of double-layered MPP by considering the vibration effect in the tuning of the design parameters. To demonstrate this, the simple rectangular geometries of model will be considered since this shape represents the majority of application of MPP in architectural and mechanical application. The effect of the plate modes and the back air cavity depth are investigated. The model assumes the incident sound wave is plane wave normal to the MPP thus only the perpendicular sound absorption is considered and the approach is not applicable for the oblique sound wave [18, 33, 34].

2 Theoretical derivation

In this section, the mathematical model development for the MPP sound absorber is presented, which considers the vibro-acoustic effect. The vibro-acoustic effect of an MPP absorber is based on the micro-perforation effect and acoustical-structural interaction.

2.1 Micro-perforation effect

As shown in Fig. 1, the four major design parameters in the modelling of MPP sound absorber’s sound absorption coefficient are the perforation diameter d, the plate thickness t, the perforation ratio σ, and the air cavity depth D. In this figure, the MPP sound absorber is formed by a plate with micro-perforations punched on it, and is backed with a rigid wall with air cavity in between. The perforation ratio σ is defined as the ratio of the total perforated area A p to the area of the MPP, A mpp, which depends on the distance between the two perforations and on their spatial arrangement.

Fig. 1
figure 1

Parameters that were used in the modeling of MPP sound absorber’s sound absorption coefficient

Full size image

The sound absorption coefficient of a MPP sound absorber is related to the acoustic impedance of the micro-perforations and the air cavity depth. Figure 2 shows a typical configuration of a MPP sound absorber, and the equivalent electro-acoustical circuit that is used to describe it. By referring to Fig. 2, the equivalent electro-acoustical circuit, the components of the MPP’s acoustic impedance in the complex quantity are analogous to those of electrical impedance; the real part of the MPP’s acoustic impedance represents the acoustic resistance, R, and the imaginary part represents the acoustic reactance, M. A similar analogy is also applied for the backed air cavity. The acoustic impedance of the perforations on the plate can be written as [1]:

$$ z_{0} = z_{\text{OR}} + z_{\text{OI}} = R + jM, $$
(1)

where

$$ R = \frac{32\mu t}{{\rho_{0} cd^{2} }}\left[ {\sqrt {1 + \frac{{x^{2} }}{32}} + x\frac{\sqrt 2 d}{8t}} \right], $$
(2)
$$ M = \frac{\omega t}{c}\left[ {1 + \frac{1}{{\sqrt {3^{2} + {{x^{2} } \mathord{\left/ {\vphantom {{x^{2} } 2}} \right. \kern-0pt} 2}} }} + 0.85\frac{d}{t}} \right]. $$
(3)
Fig. 2
figure 2

A typical configuration of a MPP sound absorber (left) and its equivalent electro-acoustical circuit (right) [1]

Full size image

The acoustic impedance, z 0 , consists of real (z OR) and imaginary (z OI) parts, which represent the acoustic resistance, R, and the acoustic reactance, M, respectively. For Eqs. (2) and (3), the perforation constant is x = d(ρ 0 ω/4μ) 1/2 and it is defined as the ratio of the perforation’s diameter to the thickness of the air at the viscous boundary’s layer in the perforation. Kinematic viscosity constant of the air is μ, the speed of sound is c, and ρ 0 is the density of air.

The acoustic impedance equation in Eq. (1) ignores the vibration effect that is induced by the incoming sound wave. The effect of the MPP’s vibration can be taken into consideration by taking into account the acoustic-structural interaction, as proposed by Lee et al. [18] and Takahashi and Tanaka [33]. In the following section, we derive the MPP vibro-acoustic effect, based on the classical plate equation coupled with acoustic wave in addition to acoustic coupling with the vibrating perforated plates [33].

2.2 Acoustical-structural interaction

Figure 3a shows a rectangular cavity-backed MPP of length a, width b, and depth D. Figure 3b shows the mean particle velocity \( \bar{V} \) in relation to the plate velocity v p and the air particle velocity v 0 averaged over the perforation ratio σ of the MPP. The MPP is vibrating under acoustic loading with the pressure difference between the external pressure, p, and the internal pressure p D at location (x, y, D). In this case, the viscous force at the air–solid interface in the perforation depends on the relative velocity v 0 – v p. The resistance term of the perforation’s acoustic impedance, z 0, is related to the air–solid interaction. The relation between the perforation’s acoustic impedance, the plate’s velocity, and the velocity of air particles was proposed by Takahashi and Tanaka [33], and is given as:

$$ z_{\text{OR}} \left( {v_{0} - v_{\text{p}} } \right) + z_{\text{OI}} v_{\text{p}} = p - p_{D} . $$
(4)
Fig. 3
figure 3

a The flexible MPP backed air cavity, b analytical model of the MPP

Full size image

When the MPP is vibrating, it is subjected to the pressure difference, Δp = p − p D , and the governing equation for the MPP with the vibration effect [12] can be written as:

$$ D_{\text{p}} \nabla^{4} S\left( {x,y,t} \right) + \rho_{\text{p}} \frac{{\partial^{2} S\left( {x,y,t} \right)}}{{\partial t^{2} }} = \left( {p - p_{D} } \right)\exp \left( {j\omega t} \right), $$
(5)

where

$$ \nabla^{4} = \left( {\frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }}} \right)^{2} ;\quad D_{\text{p}} = \frac{{Et^{3} }}{{12\left( {1 - v^{2} } \right)}}. $$

The quantity D p is the plate bending stiffness, E is the Young modulus, v is the Poisson ratio, ρ p is the plate surface density, and S is the plate displacement, which can be expressed as:

$$ S\left( {x,y,t} \right) = S\left( {x,y} \right)\exp \left( {j\omega t} \right) = \sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {A_{mn} X_{m} \left( x \right)Y_{n} \left( y \right)} \exp \left( {j\omega t} \right)} . $$
(6)

In this case, A mn is the modal amplitude of the (m, n) mode, and X m (x) Y n (y) is the (m, n) normal mode shape. The M and N are the numbers of structural modes that are used in the study. For a plate with simply supported boundary condition, the normal mode shape can be written as:

$$ X_{m} \left( x \right) = \sin \left( {\chi_{m} x} \right);\quad Y_{n} \left( y \right) = \sin \left( {\chi_{n} y} \right), $$
(7)

where χ m  = mπ/a and χ n  = nπ/b [12]. At the same time, the velocity of the plate can be expressed in terms of the mode shapes X m (x) Y n (y) at the location (x, y) by differentiating S(x, y)exp(jωt) with respect to time:

$$ v_{\text{p}} \left( {x,y} \right) = \frac{\partial }{\partial t}\left[ {S\left( {x,y} \right)\exp \left( {j\omega t} \right)} \right] = j\omega S\left( {x,y} \right)\exp \left( {j\omega t} \right) = \sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {B_{mn} X_{m} \left( x \right)Y_{n} \left( y \right)} \exp \left( {j\omega t} \right)} , $$
(8)

where B mn  = jωA mn is the modal velocity amplitude for the (m, n) mode.

The amplitude of the sound pressure, p D , at the location (x, y, D) within the air cavity is given as:

$$ p_{D} = \sum\limits_{u = 0}^{U} {\sum\limits_{w = 0}^{W} {\left[ {\frac{{\bar{z}_{0} z_{a}^{uw} }}{{\beta^{uw} \left( {\bar{z}_{0} + z_{a}^{uw} } \right)}}\int\limits_{0}^{a} {\int\limits_{0}^{b} {\left( {v_{\text{p}} + \frac{p}{{\bar{z}_{0} }}} \right)\cos \left( {\frac{u\pi x}{a}} \right)\cos \left( {\frac{w\pi y}{b}} \right){\text{d}}x{\text{d}}y} } } \right] \times } \cos \left( {\frac{u\pi x}{a}} \right)\cos \left( {\frac{w\pi y}{b}} \right)} , $$
(9)

where

$$ z_{a}^{uw} \;=\; j\rho_{0} \omega \frac{{\coth \left( {\mu^{uw} D} \right)}}{{\mu^{uw} }};\quad \mu^{uw} = \sqrt {\left( {\frac{u\pi }{a}} \right)^{2} + \left( {\frac{w\pi }{b}} \right)^{2} + \left( {\frac{\omega }{c}} \right)^{2} } ;\quad \beta^{uw} = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\cos \left( {\frac{u\pi x}{a}} \right)} }^{2} \cos \left( {\frac{w\pi x}{b}} \right)^{2} {\text{d}}x{\text{d}}y. $$

\( \bar{z}_{0} = z_{0} /\sigma \) is the averaged acoustic impedance of the micro-perforations on the plate, and \( z_{a}^{uw} \) is the acoustic impedance of the air cavity for the (u, w) acoustic mode in the x and y directions. The quantities U and W are the numbers of the acoustic modes that are used in the x and y directions. The detailed derivation of Eq. (9) can be found in the work of Lee et al. [18].

The averaged velocities and pressure are obtained from Eq. (4) by integrating over the MPP area, as shown below:

$$ z_{\text{OR}} \left( {\bar{v}_{0} - \bar{v}_{\text{p}} } \right) + z_{\text{OI}} \bar{v}_{\text{p}} = p - \bar{p}_{D} , $$
(10)

where

$$ \Delta \bar{p} = p - \bar{p}_{D} = \frac{{\int\limits_{0}^{a} {\int\limits_{0}^{b} {p - p_{D} {\text{d}}x{\text{d}}y} } }}{ab};\quad \bar{v}_{\text{p}} = \frac{{\int\limits_{0}^{a} {\int\limits_{0}^{b} {v_{p} {\text{d}}x{\text{d}}y} } }}{ab};\quad \bar{v}_{0} = \frac{{\int\limits_{0}^{a} {\int\limits_{0}^{b} {v_{0} {\text{d}}x{\text{d}}y} } }}{ab}. $$

The averaged plate’s velocity, \( \bar{v}_{\text{p}} \), and the averaged particle’s velocity at the location (x, y, D), \( \bar{V} \), are given in Eqs. (11) and (12), respectively, as:

$$ Z\bar{v}_{\text{p}} = p - \bar{p}_{D} , $$
(11)
$$ \bar{V} = \left( {1 - \sigma } \right)\bar{v}_{\text{p}} + \sigma \bar{v}_{0} , $$
(12)

where Z is the impedance of the plate. In Eq. (4), the component p − p D is replaced with \( \Delta \bar{p} \). The averaged velocity and the impedance of the plate [18] are obtained as:

$$ \bar{v}_{\text{p}} = \sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {\frac{{\Delta \bar{p}\varepsilon_{mn} \varepsilon_{mn}^{'} }}{{\eta_{mn} z_{mn} }}} } , $$
(13)
$$ Z = \Delta \bar{p}\left( {\frac{1}{{\bar{v}_{p} }}} \right) = \left[ {\sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {\frac{{\varepsilon_{mn} \varepsilon_{mn}^{'} }}{{\eta_{mn} z_{mn} }}} } } \right]^{ - 1} , $$
(14)

where

$$ \eta_{mn} = \int\limits_{0}^{b} {\int\limits_{0}^{a} {X_{m} \left( x \right)^{2} } } Y_{n} \left( y \right)^{2} {\text{d}}x{\text{d}}y;\quad \varepsilon_{mn} = \int\limits_{0}^{b} {\int\limits_{0}^{a} {X_{m} \left( x \right)Y_{n} \left( y \right){\text{d}}x{\text{d}}y} } ;\quad \varepsilon_{mn}^{\prime} = \frac{{\varepsilon_{mn} }}{ab};\quad z_{mn} = \rho_{p} \frac{{\xi_{mn} \omega_{mn} \omega + j\left( {\omega^{2} - \omega_{mn}^{2} } \right)}}{\omega }, $$

z mn is the modal impedance of the (m, n) mode of the plate, ξ mn is the modal damping ratio, and ω mn is the resonant frequency at the (m, n) mode.

The relationship between the averaged particle velocities in the perforation and the averaged velocity of the plate can be obtained by substituting Eq. (11) into Eq. (10):

$$ z_{\text{OR}} \left( {\bar{v}_{0} - \bar{v}_{\text{p}} } \right) + z_{\text{OI}} \bar{v}_{\text{p}} = Z\bar{v}_{\text{p}} \Rightarrow \bar{v}_{0} = \frac{{\left( {Z + z_{\text{OR}} } \right)}}{{z_{\text{o}} }}\bar{v}_{\text{p}} . $$
(15)

In order to eliminate \( \bar{v}_{0} \), Eq. (15) is substituted into Eq. (12), which gives:

$$ \bar{V} = \frac{{\frac{{z_{\text{OR}} + \left( {1 - \sigma } \right)z_{\text{OI}} }}{\sigma } + Z}}{{\bar{z}_{\text{o}} }}\bar{v}_{p} \approx \frac{{\bar{z}_{\text{o}} + Z}}{{\bar{z}_{\text{o}} }}\bar{v}_{\text{p}} \quad {\text{when}}\;\sigma \ll 1. $$
(16)

The acoustic impedance of the MPP, normalised by the ρ 0 c, is defined as:

$$ Z_{\text{mpp}} = \frac{{p - \bar{p}_{D} }}{{\rho_{0} c\bar{V}}}. $$
(17)

Equations (11) and (16) are substituted into Eq. (17) to result in:

$$ Z_{\text{mpp}} = \frac{{Z\bar{v}_{\text{p}} }}{{\rho_{0} c\frac{{\bar{z}_{\text{o}} + Z}}{{\bar{z}_{\text{o}} }}\bar{v}_{\text{p}} }} \Rightarrow Z_{\text{mpp}} = \frac{{\bar{z}_{\text{o}} Z}}{{\rho_{0} c\left( {\bar{z}_{\text{o}} + Z} \right)}}. $$
(18)

The acoustic impedance for the backed air cavity MPP, Z c [5], is given as below:

$$ Z_{\text{c}} = - j\cot \left( {kD} \right), $$
(19)

where k is the wave number and D is the air cavity depth.

The resulting total acoustic impedance of the MPP sound absorber is the summation of acoustic impedance of the MPP, Z mpp, and the acoustic impedance of the backed air cavity:

$$ Z_{\text{total}} = Z_{\text{mpp}} + Z_{\text{c}} . $$
(20)

The resulting normal-incidence sound absorption coefficient, α, can be calculated as:

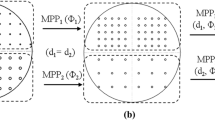
$$ \alpha = \frac{{4\text{Re} \left( {Z_{\text{total}} } \right)}}{{\left( {1 + \text{Re} \left( {Z_{\text{total}} } \right)} \right)^{2} + \left( {\text{Im} \left( {Z_{\text{total}} } \right)} \right)^{2} }}. $$
(21)

Equation (21) gives the sound absorption coefficient for a typical single layer MPP sound absorber. As suggested by some researchers, multiple layer MPP sound absorbers can be used in order to broaden the frequency band of the sound absorption coefficient [5, 10, 21, 38]. In the present study, we used a double-layered MPP sound absorber. Figure 4a shows the sound absorber with two layers of MPPs and two air cavities. For the double-layered MPP configuration, the distance between the two MPP layers is D 1 and the distance between the inner layer MPP and the rigid wall is D 2. This configuration can also be represented by the equivalent electro-acoustical circuit for a double-layered MPP sound absorber, as depicted in Fig. 4b. Figure 4b shows that the impedances of plate 1, Z 1, and plate 2, Z 2, which consider the vibration effect, are added in parallel to the acoustic impedance of perforated plate 1, \( \bar{z}_{\text{o1}} \), and perforated plate 2, \( \bar{z}_{\text{o2}} \), respectively. This gives the resulting acoustic impedance of MPP 1, Zmpp1, and acoustic impedance of MPP 2, Zmpp2. The acoustic impedances of air cavity for MPP 1, Z C1, and MPP 2, Z C2 are maintained.

Fig. 4
figure 4

a A typical configuration of a double-layered MPP sound absorber, b the equivalent electro-acoustical circuit that includes the effect of MPP vibration

Full size image

Based on the equivalent circuit of double-layered MPP sound absorber that is shown in Fig. 4b, the overall acoustic impedance can be calculated as:

$$ Z_{\text{DMPP}} = Z_{\text{mpp1}} + Z_{\text{T2}} , $$
(22)

where \( Z_{\text{T2}} = \frac{{\left( {Z_{\text{mpp2}} + Z_{\text{c2}} } \right)}}{{Z_{\text{c1}} + Z_{\text{c1}} \left( {Z_{\text{mpp2}} + Z_{\text{c2}} } \right)}} ;\quad\) \( Z_{\text{mpp1}} = \frac{{\bar{z}_{\text{o1}} Z_{1} }}{{\rho_{0} c\left( {\bar{z}_{\text{o1}} + Z_{1} } \right)}};\quad\) \( Z_{\text{mpp2}} = \frac{{\bar{z}_{\text{o2}} Z_{2} }}{{\rho_{0} c\left( {\bar{z}_{\text{o2}} + Z_{2} } \right)}};\quad \) \( Z_{\text{c1}} = - j\cot \left( {kD_{1} } \right);\quad \) \( Z_{\text{c2}} = - j\cot \left( {kD_{2} } \right);\quad \) \( \bar{z}_{\text{o1}} = R_{1} + jM_{1};\quad \) \( \bar{z}_{\text{o2}} = R_{2} + jM_{2}. \)

The resulting normal-incidence sound absorption coefficient, α′, can be calculated for a double-layered MPP sound absorber as:

$$ \alpha^{'} = \frac{{4\text{Re} \left( {Z_{\text{DMPP}} } \right)}}{{\left( {1 + \text{Re} \left( {Z_{\text{DMPP}} } \right)} \right)^{2} + \left( {\text{Im} \left( {Z_{\text{DMPP}} } \right)} \right)^{2} }}. $$
(23)

3 Methodology

The SA solver available in the MATLAB was used in the MPP sound absorber optimization. The objective function is maximizing the mean sound absorption coefficient for the prescribed frequency range. When running the SA optimization in the MATLAB, the initial temperature is set (normally start with zero) and a random trial point is generated by the algorithm. Then the algorithm starts with a new point and the objective function is evaluated. The algorithm will determine whether the new point is better or worse than the current point. If the new point is better than the current point, it becomes the next point. However, if the new point is worse than the current point, the algorithm can still make it to the next point referring to the acceptance function [P(T) = exp(ΔF/BT)] in which the ΔF, B, and T are the difference of the objective function, Boltzmann constant, and current temperature, respectively. If the criteria are not achieved, then the iteration is restarted at the starting point until a new point is obtained.

The algorithm will lower the temperature systematically and store the best point found so far. The algorithm keeps looping and only stops to iterate when the average change in the objective function is small relative to the prescribed stopping value. By this, the design parameters of MPP sound absorber which considered in the SA evaluation are optimally tuned. This optimization evaluation was carried out on a computer with Intel® Xeon® Processor W3520 (2.67 GHz) and 12 GB DRAM system.

The vibro-acoustic model for the sound absorption coefficient of the MPP sound absorber, shown in Sect. 2, was implemented in MATLAB programming script. For this optimization study, the thickness of the MPP was taken as 0.574 mm, which corresponds to Gauge 24 of the standard metal sheet gauges. The MPP was rectangular, with length and width of 0.65 and 0.511 m, respectively. This corresponded to a typical size of a wall mounted air conditioner outdoor unit with 0.6 kW compressor. For the initial case study, the MPP’s edge boundary condition was assumed as simply supported with no damping.

In order to validate this approach, a single layer MPP sound absorber was analysed to obtain the optimal sound absorption coefficient for the targeted frequency of 500 Hz. The design parameters of a single layer MPP sound absorber for the SA optimization included the diameter of the perforations, d, the perforation ratio (=distance between the perforations), σ, and the air cavity depth, D. A single layer MPP sound absorber with these design parameters was used to verify the results obtained from the SA optimization algorithm, and the data set was used for the mode shape estimation, which is important in the implementation of Eqs. (6)–(8).

In the initial case study of a single layer MPP sound absorber, nine mode shapes (m, n), of aluminium plate were considered for the optimization. The mode shapes considered were (m, n), where m = 1, 2, 3 and n = 1, 2, 3. The symbol (m, n) denotes the number of nodal lines in x and y directions, respectively. The frequencies and the mode shapes were obtained by using the finite element method software ABAQUS [39], and are shown in Fig. 5. In these figures, the nodes and the antinodes can be clearly seen in the mode shapes of the plate. The frequencies are tabulated in Table 1 and are used in the subsequent optimization process.

Fig. 5
figure 5

Natural frequencies and natural vibration modes of the aluminum plate with thickness 0.574 mm

Full size image
Table 1 Natural frequency of the respected mode shape obtained from the finite element analysis
Full size table

3.1 Optimization of a single layer MPP

For a single layer MPP sound absorber, the diameter of the perforations on the plate should be in sub-millimetre range [1, 5]. For practical purposes, the perforation ratio was set at <1 % for both the single and the double-layered MPPs, and for each the cavity depth was limited to 30 mm. Optimization of design parameters was done in order to obtain the optimal design parameters for a single layer MPP sound absorber to maximise the absorptivity at the centre frequency of 500 Hz. The objective function of the sound absorption coefficient for a single layer MPP sound absorber OBJ1 was:

$$ {\text{Maximise:}}\;{\text{OBJ}}_{ 1} = \alpha \left( {f,d,\sigma ,D} \right) = \frac{{4\text{Re} \left( {Z_{\text{total}} } \right)}}{{\left( {1 + \text{Re} \left( {Z_{\text{total}} } \right)} \right)^{2} + \left( {\text{Im} \left( {Z_{\text{total}} } \right)} \right)^{2} }} $$
(24)
$$ \begin{gathered} f = 500\left( {\text{Hz}} \right);\;0.0001\left( {\text{m}} \right) \le d \le 0.0008\left( {\text{m}} \right); \hfill \\ {\text{Subject to}}{:}\;0.05\left( \% \right) \le \sigma \le 1\left( \% \right);\;0.001\left( {\text{m}} \right) \le D \le 0.03\left( {\text{m}} \right) \hfill \\ \end{gathered} $$

3.2 Optimization of a double-layered MPP

An existing noise spectrum of an air conditioner was previously used in order to demonstrate the practical applicability of the MPP [36]. An additional consideration in the design of the MPP sound absorber is to obtain a wider frequency band for sound absorption, which can be achieved by using a double-layered MPP. When considering the optimization of the double-layered MPP sound absorber, the constraints on the design parameters were similar to the constraints on the single layer MPP sound absorber design parameters. We sought to maximise the averaged sound absorption coefficient \( \bar{\alpha }^{\prime} \) of a double-layered MPP sound absorber for the frequency band, Δf, from 200 to 1,000 Hz. The optimal sound absorption performance of a double-layered MPP absorber was investigated with respect to the five design parameters, namely the vibro-acoustic effect, the configuration, the thickness, the damping ratio, and the edge boundary condition. The objective function of the averaged sound absorption coefficient for the double-layered MPP sound absorber was:

$$ {\text{Maximise}}:\;{\text{OBJ}}_{2} = \bar{\alpha }^{\prime}\left( {\Delta f,d_{1} ,\sigma_{1} ,D_{1} ,d_{2} ,\sigma_{2} ,D_{2} } \right). $$
(25)

The series of constraints for the design parameters of double-layered MPP sound absorber were as follows:

$$ \begin{gathered} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\,\;\;\Delta f = 200\left( {\text{Hz}} \right) - 1000\left( {\text{Hz}} \right);\,0.0001\left( {\text{m}} \right) \le d_{1} \le 0.0008\left( {\text{m}} \right);\;0.05\left( \% \right) \le \sigma_{1} \le 1\left( \% \right); \hfill \\ {\text{Subject to}}:\ 0.001\left( {\text{m}} \right) \le D_{1} \le 0.03\left( {\text{m}} \right);\;0.0001\left( {\text{m}} \right) \le d_{2} \le 0.0008\left( {\text{m}} \right);\;0.05\left( \% \right) \le \sigma_{2} \le 1\left( \% \right); \hfill \\ \;0.001\left( {\text{m}} \right) \le D_{2} \le 0.03\left( {\text{m}} \right). \hfill \\ \end{gathered} $$

4 Results and discussion

In this section, verification is conducted for the model validation of sound absorption coefficient of MPP sound absorber with vibro-acoustic effect by comparing with the published results. This is followed by the mode shape estimation of aluminium plate for the subsequent optimization study. In this optimization study, the double-layered MPP sound absorber is investigated with respect to five design parameters, which are vibro-acoustic effect, the configuration, the thickness, the damping ratio and the edge boundary condition. The respective optimization results and analysis will be presented in the subsequent sections.

4.1 Model verification

In this study, we used the results that were published by Lee and Lee [40] in order to test the validity of the vibro-acoustic model. Design parameters similar to those used in the study of Lee et al. were used in the present model, and the sound absorption coefficient of a single layer MPP sound absorber was calculated and plotted, as shown in Fig. 6.

Fig. 6
figure 6

Sound absorption coefficient of a single layer MPP sound absorber, calculated from the present model, and measured in the studies of Lee and Lee [40]: a = b = 0.32 m, D = 100 mm, σ = 0.15 %, d = 0.5 mm, t = 0.5 mm, ρ p = 3.9 kg/m2, ξ 11 = ξ 31 = ξ 13 = 0.02, ω 31 = 2π × 154 rad/s, ω 51 = 2π × 264 rad/s, and ω 11 = 2π × 275 rad/s

Full size image

As Fig. 6 shows, the curve that describes the modelled sound absorption coefficient closely followed the trend shown by the measured results [40]; this indicates that the modelling results are in a good agreement with the experimental ones. For both curves, the correlation coefficient, R 2, was found to be 0.86, which shows that the modelling of vibro-acoustic effect is plausible. At the same time, for both sets of results, the root mean square error, and the coefficient of the root mean square error, CV, attained relatively low values of 0.082 and 0.152, respectively. This validated vibro-acoustic model of the MPP sound absorber will be used for optimization, as we describe next.

4.2 Mode shape estimation

We used a single layer MPP sound absorber with four design parameters (Fig. 1), in order to correctly capture the influence of the vibro-acoustic effect on the sound absorption coefficient during the optimization process. The objective of the optimization process was to use the SA optimization to maximise the sound absorption coefficient frequency at 500 Hz. The resultant (optimized) sound absorption coefficient is shown in Fig. 7, and optimal design parameters are listed in Table 2. As Fig. 7 shows, the optimal sound absorption coefficient peaked at the target frequency of 500 Hz.

Fig. 7
figure 7

Sound absorption coefficient of a single layer MPP sound absorber. Parameters: (d, t, σ, D) = (0.70347, 0.574 mm, 0.21 %, 25.7 mm)

Full size image
Table 2 Optimized design parameters for a single layer MPP sound absorber (without vibro-acoustic effect)
Full size table

The optimal design parameters, obtained for the single layer MPP sound absorber, were then used to determine the sound absorption coefficient for the scenario that accounts for the vibration effect of the MPP by using, in Eq. (14), the different modes of the aluminium plate. Table 3 lists the modes (labelled from S0 to S6) that were considered in the vibro-acoustic model of the MPP to compute the sound absorption coefficient of the MPP sound absorber.

Table 3 The sets of modes that were used to determine the sound absorption coefficient of the single layer MPP sound absorber
Full size table

Figure 8 shows four sets of modes (S0, S2, S3, and S4) that are included in the computation of sound absorption coefficient. It can be seen that the sound absorption coefficient curves of modes S2, S3, and S4 overlap and are quite similar to each other, but are not similar to S0. This shows that inclusion of modes (1, 1), (1, 2), and (1, 3) in Eq. (14) is sufficient to influence the sound absorption coefficient of the MPP.

Fig. 8
figure 8

Sound absorption coefficient of a single layer MPP sound absorber calculated by including the sets of modes S0, S2, S3, and S4. Parameters: (d, t, σ, D) = (0.70347, 0.574 mm, 0.21 %, 25.7 mm)

Full size image

In Fig. 9, the sound absorption coefficient curves use the individual mode (1, 1) to describe the curve S1, modes (1, 2), (2, 1), (2, 2), (2, 3), and (3, 2) to describe the curve S6, modes (1, 3), (3, 1), and (3, 3) to describe the curve S5, and the curve S0 is used as a reference for the comparison. It can be seen that the sound absorption coefficient curve S6 overlaps the curve S0 when its mode shape or vibration effect consideration is excluded for the calculation of sound absorption coefficient. Based on this observation, it can be concluded that the modes (1, 2), (2, 1), (2, 2), (2, 3), and (3, 2) do not contribute to the sound absorption coefficient performance of the MPP sound absorber. However, the sound absorption coefficient curve of S1 that considers the (1, 1) mode shows that the peak is shifted and becomes more significant when compared with the curves S0 and S6. It can be seen that the mode (1, 1) is the dominant mode that significantly affects the sound absorption coefficient of a MPP sound absorber.

Fig. 9
figure 9

Sound absorption coefficient of a single layer MPP sound absorber calculated by including the sets of mode shapes S0, S1, S5, and S6. Parameters: (d, t, σ, D) = (0.70347, 0.574 mm, 0.21 %, 25.7 mm)

Full size image

This result can be explained by considering the vibration mode shape, as depicted in Fig. 5. From Fig. 5a for the mode (1, 1), it can be seen that the whole plate has a displacement pattern that gives the maximum averaged plate’s velocity [34, 41]. Based on Fig. 5, the plate mode shapes for the even modes of (1, 2), (2, 1), (2, 2), (2, 3), and (3, 2) show the pattern displacement which result in the averaged plate’s velocity to be zero which cannot contribute to the overall sound absorption coefficient. However, vibration mode shapes for the odd modes of (1, 3), (3, 1), and (3, 3) show the displacement pattern where the averaged plate’s velocity is not zero, which allows them to contribute and influence the sound absorption coefficient. This explains why the sound absorption coefficient curve S5 is located between the curves S0 and S6, as is shown in Fig. 9. In this figure, the curve S5 with the vibration mode shapes of (1, 3), (3, 1), and (3, 3) result in the averaged plate’s velocity, which contributed and influenced the sound absorption coefficient of the MPP sound absorber although the effect was not as strong when compared with the dominant mode (1, 1). Indeed, as shown by Lee et al. [18], the m and n of the mode shape (m, n) that denote the nodal lines for directions x and y, respectively, should always be odd numbers in order to contribute significantly to the sound absorption coefficient of a MPP sound absorber when vibro-acoustic model is used.

4.3 Double-layered MPP

In this section, design parameters of a double-layered MPP sound absorber are considered for optimization that aims to maximise the mean sound absorption coefficient for wideband sound absorption, and mean sound absorption coefficient is used to reflect the overall increase in the sound absorption for this design. To simplify the optimization and to allow for direct comparison with single layer MPP, the design constraints of the MPP are similar for the outer and inner layers of the MPP. The sound absorption coefficient curve of the many-layered sound absorber usually exhibits several peaks, and makes it difficult to optimize the sound absorption coefficient at a single target frequency [32, 42]. Thus, the objective function here is to maximise the mean sound absorption coefficient of the double-layered MPP sound absorber around the desired optimized frequency band.

4.3.1 Vibration effect

The optimized design parameters that were obtained by including the vibration effect are tabulated in Table 4. For comparison, these values of design parameters were also used to determine the sound absorption coefficient in the mathematical model that does not account for the vibration effect, and these results are shown in Fig. 10.

Table 4 Optimized design parameters obtained for sound absorption coefficients, with and without MPP vibration effect
Full size table
Fig. 10
figure 10

Sound absorption coefficients obtained with and without vibration effect taken into account

Full size image

Figure 10 shows the sound absorption coefficient of the MPP sound absorber, obtained with and without vibration effect taken into account. When the vibration effect was accounted for, the MPP performance was characterised by a wider band of sound absorption coefficient and improved overall sound absorption coefficient. Improvement could be observed in the frequency range 190–540 Hz (increase of 12.52 %) and for higher frequency range 780–1,600 Hz (increase of 8.88 %). These results show that the vibration effect influences the sound absorption coefficient of a double-layered MPP sound absorber. Similar observation was also made in the study of Takahashi and Tanaka [33], in which the plate vibration was found to produce appreciably increased sound absorption coefficient of the perforated plate’s sound absorber. Therefore, the vibration effect of a MPP should be taken into consideration for the calculation of a MPP’s sound absorption coefficient, in order to better capture the behaviour of a MPP sound absorber.

4.3.2 Configuration of MPP

We compared the effectiveness of a double-layered MPP sound absorber with the effectiveness of a single layered MPP in delivering the wider frequency band of sound absorption coefficient. Tables 5 and 6 list optimized design parameters that were obtained for the single and double-layered MPP sound absorbers, respectively. The sound absorption coefficient curves for single and double-layered MPP sound absorbers are shown in Fig. 11.

Table 5 Optimized design parameters for a single layer MPP sound absorber
Full size table
Table 6 Optimized design parameters for a double-layered MPP sound absorber
Full size table
Fig. 11
figure 11

Sound absorption coefficients of single and double-layered MPP sound absorbers

Full size image

Using the data shown in Fig. 11 it is found that the mean sound absorption coefficient for the single and double-layered MPP sound absorbers with the optimized design parameters are 0.6396 and 0.8268, respectively. It is observed that the sound absorption characteristic of a double-layered MPP sound absorber has a wider band and higher peak value compared with a single layer MPP sound absorber. The sound absorption coefficient performance of a single layer MPP sound absorber is limited, in that it can only provide a peak sound absorption coefficient at the frequency 720 Hz and within a narrow frequency band. On the other hand, a double-layered MPP sound absorber provides a wider frequency band of sound absorption coefficient.

A double-layered MPP sound absorber will typically exhibit two significant peaks of the sound absorption coefficient at the resonant frequency, which is caused by the Helmholtz-type resonance. This phenomenon had also been observed in the studies of Sakagami et al. [21] and Lee and Lee [40], in which the bandwidth of the sound absorption coefficient of the double-layered MPP sound absorber was generally wider than that of the single layer MPP sound absorber due to the two resonance peaks that overlapped each other to produce a broader absorption region. On the other hand, the dip between the two resonance peaks is not obvious, flattened out, and becomes smooth. This happened due to the appropriately tuned combination of design parameters for the double-layered MPP sound absorber that was achieved by the SA optimization. This suggests that a double-layered MPP sound absorber can be optimally tuned for the attenuation of the wide frequency band noise, especially when dealing with the noise that is generated by electrical appliances, which normally drops in intensity for frequencies lower than 1,000 Hz [35].

4.3.3 Thickness of MPP

In this section, we consider the thickness of the MPP as a study parameter. Four different MPP thickness values were considered for the SA optimization: 1.024 mm (Gauge 18), 0.574 mm (Gauge 23), 0.32 mm (Gauge 28), and 0.16 mm (Gauge 34). The natural frequencies for each mode shape and the respective thickness are listed in Table 1. Table 7 lists the optimized design parameters that were obtained for the double-layered MPP sound absorbers with different values of MPP thickness. As is shown in Table 7, the perforation ratio of layer 1, σ 1 , decreases and the perforation ratio of layer 2, σ 2 , increases when the plate becomes thinner. At the same time, the number of iterations for the optimization also increases and more iterations are required for the thinner plate scenario. The sound absorption coefficient curves for different values of MPP thickness are compared in Fig. 12.

Table 7 Optimized design parameters for double-layered MPP sound absorber with MPPs of different thickness
Full size table
Fig. 12
figure 12

Sound absorption coefficients of double-layered MPP sound absorber obtained for MPPs of different thickness

Full size image

Figure 12 shows the sound absorption coefficients obtained for the four different values of MPP’s sheet thickness. For frequencies lower than 430 Hz, there is not much difference between the sound absorption coefficients for MPPs of different thickness. As the MPP sheet becomes thinner, the sound absorption coefficient of a double-layered MPP sound absorber increases for frequencies that are higher than 950 Hz. In the range of frequencies from 950 to 2,000 Hz, the sound absorption coefficient of the MPP gauge 34 increases by 63 % compared with the MPP gauge 18.

The increasing thickness of a MPP and the relatively small perforations induce larger acoustic resistance or reactance, which in turn results in low acoustical performance of a MPP sound absorber. According to Sakagami et al. [43], as the thickness of a MPP increases, the peak sound absorption coefficient shifts to the lower frequency range and its amplitude is greatly reduced. This happens because the acoustic resistance of the panel becomes high due to the increasing thickness of a MPP. When comparing this with the effect of the MPP’s thickness, a similar trend of the sound absorption coefficient curves is observed. For the MPP thickness of 1.024 mm, the peak sound absorption coefficient is shifted toward the lower frequency range and becomes narrow frequency band, while at the same time its intensity is decreased. However, the thinnest MPP (t = 0.16 mm) gives the relatively wide bandwidth of sound absorption coefficient.

4.3.4 Damping

Three levels of damping ratio were considered in the present study: 0, 4, and 8 %. The optimized design parameters, obtained by taking into account the MPP damping ratio, are listed in Table 8. The sound absorption coefficients are compared in Fig. 13.

Table 8 Optimized design parameters for double-layered MPP sound absorber with different damping ratios of MPP
Full size table
Fig. 13
figure 13

Sound absorption coefficients of double-layered MPP sound absorber obtained for MPPs with different damping ratios

Full size image

Comparison of the sound absorption coefficients (Fig. 13) shows that these are not significantly affected when the damping ratio is increased from 0 to 8 %. For frequencies that range from 480 to 1,000 Hz, the sound absorption coefficient improves by 2.18 % when the damping ratio is changed from 0 to 8 %. The damping ratio of 4 % maintains the trend that is similar to that of the non-damped case, and thus is not able to improve the sound absorption coefficient. Based on the results of this study, we conclude that the damping ratio cannot be used to effectively improve the sound absorption coefficient of a double-layered MPP sound absorber.

4.3.5 Boundary condition

In the optimization studies that were performed above, the edge clamping boundary condition of a MPP was assumed as simply supported. Bolted condition is more representative of the real application because the mounting of plates requires the edge to be bolted or riveted. A total of 24 bolted mountings at the four edges of a rectangular MPP sheet were modelled using the ABAQUS FEA software. The mode shape analysis was carried out on the model and the resulting natural frequencies of MPP for bolted boundary condition are tabulated in Table 1. Optimization was carried out for bolted boundary condition and the related optimized design parameters of a double-layered MPP sound absorber are listed in Table 9. Figure 14 shows the sound absorption coefficient curves for the simply supported panel and bolted panel.

Table 9 Optimized design parameters for double-layered MPP sound absorber with different edge clamping boundary conditions
Full size table
Fig. 14
figure 14

Sound absorption coefficients of double-layered MPP sound absorber with different boundary conditions

Full size image

From Fig. 14, it can be seen that the shapes of the sound absorption coefficient curves for simply supported and 24 bolted edge clamping boundary conditions are almost similar. This implies that, for a double-layered MPP sound absorber, the 24 bolted and simply supported boundary conditions provide an almost similar sound absorption coefficient performance. This observation was also reported in the study of Lee and Lee [40] in which the sound absorption coefficient of a MPP sound absorber was not significantly affected by two different boundary conditions: (1) two opposite sides simply supported and two opposite sides clamped (SCSC), and (2) four sides simply supported (SSSS) [40]. In other words, the conventionally bolted mounting of a MPP on the wall with 24 bolted edge clamping boundary condition can be safely modelled as a simply supported boundary condition.

4.4 Effect of relaxing the boundary value

It is also interesting to see whether the results of the optimization have achieved saturation value. This effect can be monitored by relaxing the boundary values of the constraints of the design parameters. In this case the air cavity depth parameter of D 1 and D 2 are further increased to 0.04, 0.05 and 0.06 m. The optimized output, \( \bar{\alpha }^{\prime} \) (mean sound absorption coefficient) and the optimized design parameters for the each value of relaxed boundary condition of the air cavity depths are listed in Table 10.

Table 10 Optimized design parameters for double-layered MPP sound absorber with MPPs of different upper limit constraint of air cavity depth, D 1 and D 2
Full size table

From Table 10 the mean sound absorption coefficient of the MPP sound absorber is improving as the upper limit of boundary constraint is allowed a larger value however there seems to be a saturation of the mean sound absorption coefficient of 0.8990.

5 Conclusion

The proposed vibro-acoustic model for the double-layered MPP is successfully applied by considering the vibration model of the panel. It is the (1, 1) mode which was found to dominate the sound absorption performance. The results for the MPP sound absorber that were generated by the model were found to be in a good agreement with the published results with a strong correlation coefficient of 0.86. When the MPP vibration effect was taken into account during the optimization, there was an 8.88–12.52 % improvement in sound absorption coefficient for frequencies ranging from 200 to 1,000 Hz.

In this study, it was also observed that the double-layered MPP sound absorber yields a wider band sound absorber compared with a single layer MPP sound absorber, with 21.2 % improvement in sound absorption coefficient and preferably thinner panel of t = 0.120 mm. The effects of both damping ratio and the bolted and simply supported boundary conditions were almost negligible.