Unconditionally convergence and superconvergence error analysis of a mass- and energy-conserved finite element method for the Schrödinger–Poisson equation

Abstract

This paper aims to investigate the unconditionally optimal and superconvergent error estimates of a mass- and energy-conserved finite element method for the Schrödinger–Poisson equation. Firstly, a priori error bound of the numerical solutions in $H^1$-norm is obtained by the conserved property. Secondly, the unconditionally optimal error estimates in $L^2$-norm are derived without any timestep restriction in terms of the bound of the numerical solution. Thirdly, the unconditionally superclose error estimates in $H^1$-norm are got by treating the coupled nonlinear term rigorously and skillfully. Furthermore, the unconditionally superconvergent error estimates in $H^1$-norm are acquired by the interpolation post-processing approach. Finally, some numerical results are provided to verify the theoretical analysis.

1 Introduction

In this paper, we consider the following two dimensional Schrödinger–Poisson (SP) equation:

$$\begin{aligned}&\textrm{i}u_t=-\Delta u+\Phi u,\quad (\varvec{x},t)\in \Omega \times (0,T], \end{aligned}$$

(1.1)

$$\begin{aligned}&-\Delta \Phi =\mu |u|^2, \quad (\varvec{x},t)\in \Omega \times (0,T], \end{aligned}$$

(1.2)

$$\begin{aligned}&u(\varvec{x},0)=u_0(\varvec{x}), \quad \varvec{x}\in \Omega , \end{aligned}$$

(1.3)

$$\begin{aligned}&u(\varvec{x},t)=0,\quad \Phi (\varvec{x},t)=0,\quad (\varvec{x},t)\in \partial \Omega \times (0,T], \end{aligned}$$

(1.4)

where $u=u(\varvec{x},t)$ is a complex-valued function with respect to time t and spatial variable $\varvec{x}=(x,y)\in \Omega$, which is a bounded rectangular domain in $\mathbb {R}^2$, $\mu =\pm 1$ is a rescaled physical constant, which signifies the property of the underlying forcing, repulsive if $\mu >0$ and attractive if $\mu <0$ (Yi and Liu 2022). $\textrm{i}=\sqrt{-1}$ denotes the imaginary unit and $T>0$ is the final time.

The SP equation can be employed in many physical applications, including semiconductors (Ringhofer and Soler 2000; Markowich et al. 1990), plasma physics (Shukla and Eliasson 2011) and cosmology (Uhlemann et al. 2014). System (1.1)–(1.4) preserves both the mass and the energy. It is an important and interesting thing to design numerical schemes that satisfy discrete analogues of these laws, as typically this leads to good qualitative behaviour of numerical solutions for longer computational times (Athanassoulisa et al. 2023). There exists a very large literature on numerical methods and analysis for the SP equation. A conservative discontinuous Galerkin scheme was developed in Yi and Liu (2022) for the SP equation and the corresponding optimal $L^2$ error estimates were obtained. With the help of a Crank–Nicolson temporal and finite difference spatial discretization, a predictor–corrector scheme was studied in Ringhofer and Soler (2000). In Auzinger et al. (2017), a rigorous stability and error analysis was presented in terms of the second-order Strang splitting finite element discretization. The convergence rates were established for the periodic SP equation based on a Galerkin approximation in Bohun et al. (1996). An error analysis of Strang-type splitting integrators was discussed in detail for Schrödinger–Poisson and cubic nonlinear Schrödinger equations in Lubich (2008). Moreover, a second order convergence of the Strang splitting method was discussed in Auzinger et al. (2017) for Schrödinger–Poisson equation.

The objective of this work is to develop a structure-preserving fully-discrete Galerkin scheme for the SP equation, which preserves both mass and energy at the discrete level. In particular, for the spatial discretization, we adopt the standard conforming finite element method, while for the temporal discretization, we use the Crank–Nicolson method. The main advantage of the proposed scheme is that it avoids the grid ratio restrictions between temporal step size and spatial step size, while some certain restriction required in the previous literature. More precisely, a priori error bound in $H^1$-norm rather than the $L^{\infty }$-norm is derived according to the mass- and energy conserved properties. Then, by treating the nonlinear and coupled term rigorously and skillfully, the unconditionally optimal error estimates in $L^2$-norm and the superconvergent error estimates in $H^1$-norm are established.

The rest of this paper is organized as follows. In Sect. 2, we introduce some preliminaries and lemmas, which are needed in the error analysis. In Sect. 3, the unconditionally optimal error estimates in $L^2$-norm are presented for the conserved Crank–Nicolson fully-discrete finite element scheme. In Sect. 4, the unconditionally superconvergent error estimates in $L^2$-norm are studied. In Sect. 5, some numerical experiments are carried out to confirm the theoretical analysis.

2 Some preliminaries and lemmas

Let $W^{m,p}(\Omega )$ be the standard Sobolev space (Adams and Fournier 2003) with the norm $\Vert \cdot \Vert _{m,p}$ and semi-norm$|\cdot |_{m,p}$. For any two complex functions $u,~v\in L^2(\Omega )$, we define the $L^2(\Omega )$ inner product by $(u,v)=\int _{\Omega }u(\varvec{x})(v(\varvec{x}))^*d\varvec{x},$ where $v^{*}$ denotes the conjugate of v. Moreover, for any Banach space Y and function $f: [0,T]\rightarrow Y$, define the norm

$$\begin{aligned} \Vert f\Vert _{L^p(Y)}=\left\{ \begin{array}{l} \left( \int _{0}^{T}\Vert f(t)\Vert _{Y}^pdt\right) ^{1/p},\quad 1\le p< \infty ,\\[0.2cm] \textrm{ess}\sup _{t\in [0,T]}\Vert f(t)\Vert _Y,\quad p=\infty . \end{array} \right. \end{aligned}$$

Let $\mathcal {T}_h$ be a uniform rectangular partition of $\Omega$ into rectangles $\{K\}$ and $h=\max _{K\in \mathcal {T}_h}\{\text{ diam } (K)\}$ be the mesh size. For a given element $K\in \mathcal {T}_h$, we define the bilinear finite element space

$$\begin{aligned} V_h=\{v_h\in C(\overline{\Omega });~v_h|_K\in \textrm{span}\{1,x,y,xy\},~v_h|_{\partial \Omega }=0,~~\forall K\in \mathcal {T}_h\}. \end{aligned}$$

Moreover, define $R_h: H_0^1(\Omega )\rightarrow V_h$ to be the Ritz projection operator by

$$\begin{aligned} (\nabla (u-R_hu),\nabla v_h)=0,\quad \forall v_h\in V_h. \end{aligned}$$

(2.1)

Then, by the classical finite element theory (Thomee 2006; Brenner and Scott 2002), there holds for $u\in H^2(\Omega )\cap H_0^1(\Omega )$ that

$$\begin{aligned} \Vert u-R_hu\Vert _0+h\Vert \nabla (u-R_hu)\Vert _0\le Ch^2|u|_2. \end{aligned}$$

(2.2)

The weak formulation of the problem (1.1)–(1.4) reads: find $u:~[0,T]\rightarrow H_0^1(\Omega )$ and $\Phi :~[0,T]\rightarrow H_0^1(\Omega )$, such that

$$\begin{aligned}&\textrm{i}(u_t,v)=(\nabla u,\nabla v)+(\Phi u,v),\quad \forall v\in H_0^1(\Omega ), \end{aligned}$$

(2.3)

$$\begin{aligned}&(\nabla \Phi ,\nabla w)=\mu (|u|^2,w),\quad \forall w\in H_0^1(\Omega ). \end{aligned}$$

(2.4)

In order to present the fully-discrete scheme, let $\{t_n|~t_n=n\tau ;0\le n \le N\}$ be a uniform partition in time with time step $\tau =T/N$ and $f^n=f(\varvec{x},t_n)$. For a sequence of functions $\{f^n\}_{n=0}^N$, we denote

$$\begin{aligned} D_{\tau }f^n=\frac{f^n-f^{n-1}}{\tau },\quad \quad \bar{f}^n=\frac{f^n+f^{n-1}}{2}. \end{aligned}$$

Then, the fully-discrete scheme is: for given $u_h^{n-1}\in V_h$ and $\Phi _h^{n-1}\in V_h$, find $u_h^{n}\in V_h$ and $\Phi _h^{n}\in V_h$, such that

$$\begin{aligned}&\textrm{i}(D_{\tau }u_h^n,v_h)=(\nabla \bar{u}_h^n,\nabla v_h)+(\bar{\Phi }_h^n\bar{u}_h^n,v_h),\quad \forall v_h\in V_h, \end{aligned}$$

(2.5)

$$\begin{aligned}&(\nabla \Phi _h^n,\nabla w_h)=\mu (|u_h^n|^2,w_h),\quad \forall w_h\in V_h, \end{aligned}$$

(2.6)

with the initial approximations $u_h^0$ and $\Phi _h^0$ defined by

$$\begin{aligned} u_h^0=R_hu_0,\quad \text{ and }\quad (\nabla \Phi _h^0,\nabla w_h)=(|u_h^0|^2,w_h),\quad \forall w_h\in V_h. \end{aligned}$$

(2.7)

Lemma 1

The numerical scheme (2.5)–(2.6) has the following mass and energy-conversed properties

$$\begin{aligned} \mathcal {M}^n=\mathcal {M}^0,\quad \quad \mathcal {E}^n =\mathcal {E}^0, \end{aligned}$$

(2.8)

where

$$\begin{aligned} \mathcal {M}^n&=\Vert u_h^n\Vert _0^2=\int _{\Omega }|u_h^n|^2 dxdy,\quad \text{ and }\quad \mathcal {E}^n=\Vert \nabla u_h^n\Vert _0^2+\frac{1}{2\mu }\Vert \nabla \Phi _h^n\Vert _0^2\\&=\int _{\Omega }|\nabla u_h^n|^2+\frac{1}{2\mu }|\nabla \Phi _h^n|^2 dxdy. \end{aligned}$$

Proof

Choosing $v_h=\bar{u}_h^n$ in (2.5) and taking the imaginary parts of the resulting equation give that

$$\begin{aligned} \frac{1}{2\tau }(\Vert u_h^n\Vert _0^2-\Vert u_h^{n-1}\Vert _0^2)=0, \end{aligned}$$

which shows that

$$\begin{aligned} \Vert u_h^n\Vert _0^2=\Vert u_h^{n-1}\Vert _0^2=\cdots =\Vert u_h^0\Vert _0^2. \end{aligned}$$

(2.9)

Clearly, by the definition of $\mathcal {M}^n$, the mass conservation is obtained. Moreover, choosing $v_h=D_{\tau }u_h^n$ in (2.5) and taking the real parts of the resulting equation result in

$$\begin{aligned} \frac{1}{2\tau }(\Vert \nabla u_h^n\Vert _0^2-\Vert \nabla u_h^{n-1}\Vert _0^2)+Re(\bar{\Phi }_h^n\bar{u}_h^n,D_{\tau }u_h^n)=0. \end{aligned}$$

(2.10)

Note that

$$\begin{aligned} (\bar{\Phi }_h^n\bar{u}_h^n,D_{\tau }u_h^n)&=\frac{1}{2\tau }(\bar{\Phi }_h^n(u_h^n+u_h^{n-1}),u_h^n-u_h^{n-1})\nonumber \\&=\frac{1}{2\tau }[(\bar{\Phi }_h^nu_h^n,u_h^n)-(\bar{\Phi }_h^nu_h^n,u_h^{n-1})+(\bar{\Phi }_h^nu_h^{n-1},u_h^n)-(\bar{\Phi }_h^nu_h^{n-1},u_h^{n-1})], \end{aligned}$$

one can get

$$\begin{aligned} Re(\bar{\Phi }_h^n\bar{u}_h^n,D_{\tau }u_h^n)=\frac{1}{2\tau }((\bar{\Phi }_h^nu_h^n,u_h^n)-(\bar{\Phi }_h^nu_h^{n-1},u_h^{n-1}))=\frac{1}{2\tau }(|u_h^n|^2-|u_h^{n-1}|^2,\bar{\Phi }_h^n). \end{aligned}$$

(2.11)

Substituting (2.11) into (2.10) yields that

$$\begin{aligned} (\Vert \nabla u_h^n\Vert _0^2-\Vert \nabla u_h^{n-1}\Vert _0^2)+(|u_h^n|^2-|u_h^{n-1}|^2,\bar{\Phi }_h^n)=0. \end{aligned}$$

(2.12)

On the other hand, from (2.6) at $t=t_n$ and $t=t_{n-1}$, we have

$$\begin{aligned} (\nabla (\Phi _h^n-\Phi _h^{n-1}),\nabla w_h)=\mu (|u_h^n|^2-|u_h^{n-1}|^2,w_h),\quad \forall w_h\in V_h. \end{aligned}$$

(2.13)

Then, choosing $w_h=\bar{\Phi }_h^n$ in (2.13) leads to

$$\begin{aligned} \frac{1}{2}(\Vert \nabla \Phi _h^n\Vert _0^2-\Vert \nabla \Phi _h^{n-1}\Vert _0^2)=\mu (|u_h^n|^2-|u_h^{n-1}|^2,\bar{\Phi }_h^n). \end{aligned}$$

(2.14)

Substituting (2.14) into (2.12) gives that

$$\begin{aligned} \Vert \nabla u_h^n\Vert _0^2+\frac{1}{2\mu }\Vert \nabla \Phi _h^n\Vert _0^2=\Vert \nabla u_h^{n-1}\Vert _0^2+\frac{1}{2\mu }\Vert \nabla \Phi _h^{n-1}\Vert _0^2=\cdots =\Vert \nabla u_h^{0}\Vert _0^2+\frac{1}{2\mu }\Vert \nabla \Phi _h^{0}\Vert _0^2. \end{aligned}$$

Then, by the definition of $\mathcal {E}^n$, we obtain the energy conservation. The proof is complete.

Lemma 2

Suppose that $u_0\in H_0^1(\Omega )$, we have the following a priori error bound

$$\begin{aligned} \Vert u_h^n\Vert _1\le C,\quad n=0,1,\ldots ,N, \end{aligned}$$

(2.15)

where C is a constant independent of n, h and $\tau$.

Proof

From Lemma 1, one can check that

$$\begin{aligned} \Vert \nabla u_h^n\Vert _0^2&= \Vert u_h^0\Vert _0^2+\frac{1}{2\mu }\Vert \nabla \Phi _h^0\Vert _0^2-\frac{1}{2\mu }\Vert \nabla \Phi _h^n\Vert _0^2. \end{aligned}$$

(2.16)

Choosing $w_h=\Phi _h^0$ in (2.6) at $t=t_0$ yields that

$$\begin{aligned} \Vert \nabla \Phi _h^0\Vert _0^2\le C\Vert u_h^0\Vert _{0,4}^2\Vert \nabla \Phi _h^0\Vert _0. \end{aligned}$$

Thus, we have

$$\begin{aligned} \Vert \nabla \Phi _h^0\Vert _0\le C\Vert u_h^0\Vert _1^2\le C. \end{aligned}$$

(2.17)

Moreover, choosing $w_h=\Phi _h^n$ in (2.6) at $t=t_n$ gives that

$$\begin{aligned} \Vert \nabla \Phi _h^n\Vert _0^2&\le C\Vert u_h^n\Vert _0\Vert u_h^n\Vert _{0,4}\Vert \Phi _h^n\Vert _{0,4}=C\Vert u_h^0\Vert _0\Vert u_h^n\Vert _{0,4}\Vert \Phi _h^n\Vert _{0,4} \le C\Vert u_h^n\Vert _0^{\frac{1}{2}}\Vert \nabla u_h^n\Vert _0^{\frac{1}{2}}\Vert \nabla \Phi _h^n\Vert _0, \end{aligned}$$

(2.18)

where we have used (2.9), Sobolev inequality $\Vert \chi \Vert _{0,4}^2\le C\Vert \chi \Vert _0\Vert \nabla \chi \Vert _0$, for $\chi \in H_0^1(\Omega )$, $H^1(\Omega )\hookrightarrow L^4(\Omega )$ and Poincare inequality in the above estimate. From (2.18), it is not difficult to see that

$$\begin{aligned} \Vert \nabla \Phi _h^n\Vert _0^2&\le C\Vert u_h^n\Vert _0\Vert \nabla u_h^n\Vert _0\le C\Vert u_h^n\Vert _0^2+\Vert \nabla u_h^n\Vert _0^2\le C+\Vert \nabla u_h^n\Vert _0^2, \end{aligned}$$

(2.19)

where we have used (2.9) again in the above estimate.

Hence, by (2.16), (2.17) and (2.19), we have

$$\begin{aligned} \Vert \nabla u_h^n\Vert _0^2&\le C+\frac{1}{2}\Vert \nabla \Phi _h^n\Vert _0^2\le C+\frac{1}{2}\Vert \nabla u_h^n\Vert _0^2. \end{aligned}$$

Hence, the desired result (2.15) is obtained by Poincare inequality.

Next, we present the discrete Gronwall inequality, which is an important tool for analyzing time-dependent problems.

Lemma 3

(Gronwall’s inequality Heywood and Rannacher 1990; Riviére 2008) Let $\tau$, B, $C>0$ and let $\{a_n\}$, $\{b_n\}$, $\{c_n\}$ be sequences of nonnegative numbers satisfying

$$\begin{aligned} a_n+\tau \sum _{k=0}^nb_k\le B+C\tau \sum _{k=0}^na_k+\tau \sum _{k=0}^nc_k,\quad n\ge 0. \end{aligned}$$

Then, if $C\tau <1$, there holds

$$\begin{aligned} a_n+\tau \sum _{k=0}^nb_k\le e^{C(n+1)\tau }\left( B+\tau \sum _{k=0}^nc_k\right) ,\quad n\ge 0. \end{aligned}$$

Remark 1

Note that $(n+1)\tau \le 2T$, one can see that the constant in the above Gronwall’s inequality is exponentially dependent on the final time T.

3 Unconditionally optimal error estimate in $L^2$-norm of the fully-discrete scheme

We present the first main result in the following theorem.

Theorem 3.1

Suppose that $(u^n,\Phi ^n)$ and $(u_h^n,\Phi _h^n)$ are the solutions of (2.3)–(2.4) and (2.5)–(2.6) at $t=t_n$, respectively. Moreover, suppose that $u, u_t, u_{tt}\in L^{\infty }(H^2(\Omega ))$, $u_{ttt}\in L^{\infty }(L^2(\Omega ))$, $\Phi \in L^{\infty }(H^2(\Omega ))$, $\Phi _{tt}\in L^{\infty }(L^2(\Omega ))$. Then we have the following unconditionally optimal error estimate

$$\begin{aligned} \Vert u^n-u_h^n\Vert _0+\Vert \Phi ^n-\Phi _h^n\Vert _0\le C(h^2+\tau ^2). \end{aligned}$$

(3.1)

Proof

For the sake of simplicity, we split the errors $u^n-u_h^n$ and $\Phi ^n-\Phi _h^n$ as:

$$\begin{aligned}&u^n-u_h^n=u^n-R_hu^n+R_hu^n-u_h^n:=\xi ^n+\eta ^n,\\&\quad \Phi ^n-\Phi _h^n=\Phi ^n-R_h\Phi ^n+R_h\Phi ^n-\Phi _h^n:=\sigma ^n+\theta ^n. \end{aligned}$$

From (2.3)–(2.4) and (2.5)–(2.6), we have the following error equations:

$$\begin{aligned} \textrm{i}(D_{\tau }\eta ^n,v_h)&=-\textrm{i}(D_{\tau }\xi ^n,v_h)+(\nabla \bar{\xi }^n,\nabla v_h)+(\nabla \bar{\eta }^n,\nabla v_h)+ (\bar{\Phi }^n\bar{u}^n-\bar{\Phi }_h^n\bar{u}_h^n,v_h)\nonumber \\&+\textrm{i}(D_{\tau }u^n-u_t^{n-\frac{1}{2}},v_h)+(\nabla (u^{n-\frac{1}{2}}-\bar{u}^n),\nabla v_h)+(\Phi ^{n-\frac{1}{2}}u^{n-\frac{1}{2}}-\bar{\Phi }^n\bar{u}^n,v_h),\nonumber \\&\quad \forall v_h\in V_h, \end{aligned}$$

(3.2)

$$\begin{aligned} (\nabla \theta ^n,\nabla w_h)&=-(\nabla \sigma ^n,\nabla w_h)+\mu (|u^n|^2-|u_h^n|^2,w_h), \quad \forall w_h\in V_h, \end{aligned}$$

(3.3)

Choosing $v_h=\bar{\eta }^n$ in (3.2) and taking the imaginary parts result in

$$\begin{aligned} \frac{1}{2\tau }(\Vert \eta ^n\Vert _0^2-\Vert \eta ^{n-1}\Vert _0^2)&=-Re(D_{\tau }\xi ^n,\bar{\eta }^n)+Im(\bar{\Phi }^n\bar{u}^n-\bar{\Phi }_h^n\bar{u}_h^n,\bar{\eta }^n) +Re(D_{\tau }u^n-u_t^{n-\frac{1}{2}},\bar{\eta }^n)\nonumber \\&\quad +Im(\nabla (u^{n-\frac{1}{2}}-\bar{u}^n),\nabla \bar{\eta }^n)+Im(\Phi ^{n-\frac{1}{2}}u^{n-\frac{1}{2}}-\bar{\Phi }^n\bar{u}^n,\bar{\eta }^n)=:\sum _{k=1}^5A_k, \end{aligned}$$

(3.4)

where we have used the definition of Ritz projection.

By the Cauchy–Schwarz inequality and (2.2), $A_1$ can be bounded by

$$\begin{aligned} A_1\le \Vert D_{\tau }\xi ^n\Vert _0\Vert \bar{\eta }^n\Vert _0\le Ch^2\Vert \bar{\eta }^n\Vert _0\le Ch^4+C(\Vert \eta ^n\Vert _0^2+\Vert \eta ^{n-1}\Vert _0^2). \end{aligned}$$

(3.5)

In order to estimate $A_2$, we rewrite $\bar{\Phi }^n\bar{u}^n-\bar{\Phi }_h^n\bar{u}_h^n$ as

$$\begin{aligned} \bar{\Phi }^n\bar{u}^n-\bar{\Phi }_h^n\bar{u}_h^n&=\bar{\Phi }^n(\bar{u}^n-\bar{u}_h^n)+(\bar{\Phi }^n-\bar{\Phi }_h^n)\bar{u}_h^n =\bar{\Phi }^n\bar{\xi }^n+\bar{\Phi }^n\bar{\eta }^n+\bar{\sigma }^n\bar{u}_h^n+\bar{\theta }^n\bar{u}_h^n\nonumber \\&=\bar{\Phi }^n\bar{\xi }^n+\bar{\Phi }^n\bar{\eta }^n-\bar{\sigma }^n\bar{\eta }^n+\bar{\sigma }^nR_h\bar{u}^n -\bar{\theta }^n\bar{\eta }^n+\bar{\theta }^nR_h\bar{u}^n:=\sum _{k=1}^6{A_{2}^k}. \end{aligned}$$

(3.6)

One can easily see that

$$\begin{aligned} (A_2^1,\bar{\eta }^n)+(A_2^2,\bar{\eta }^n)+(A_2^4,\bar{\eta }^n)&\le \Vert \bar{\Phi }^n\Vert _{0,\infty }(\Vert \bar{\xi }^n\Vert _0+\Vert \bar{\eta }^n\Vert _0)\Vert \bar{\eta }^n\Vert _0+\Vert \bar{\sigma }\Vert _0\Vert R_h\bar{u}^n\Vert _{0,\infty }\Vert \bar{\eta }^n\Vert _0\nonumber \\&\le Ch^4+C(\Vert \eta ^n\Vert _0^2+\Vert \eta ^{n-1}\Vert _0^2). \end{aligned}$$

(3.7)

By Hölder inequality, we have

$$\begin{aligned} (A_2^3,\bar{\eta }^n)&\le C\Vert \bar{\sigma }^n\Vert _0\Vert \bar{\eta }^n\Vert _{0,4}^2\le C\Vert \bar{\sigma }^n\Vert _0\Vert \bar{\eta }^n\Vert _0\Vert \nabla \bar{\eta }^n\Vert _0\le C\Vert \bar{\sigma }^n\Vert _0\Vert \bar{\eta }^n\Vert _0\nonumber \\&\le Ch^2\Vert \bar{\eta }^n\Vert _0\le Ch^4+C(\Vert \eta ^n\Vert _0^2+\Vert \eta ^{n-1}\Vert _0^2), \end{aligned}$$

(3.8)

where we have used Lemma 2 and the Sobolev inequality. Similarly, we have

$$\begin{aligned} (A_2^5,\bar{\eta }^n)+(A_2^6,\bar{\eta }^n)&\le \Vert \bar{\theta }^n\Vert _0\Vert \bar{\eta }^n\Vert _{0,4}^2+\Vert \bar{\theta }^n\Vert _0\Vert R_h\bar{u}^n\Vert _{0,\infty }\Vert \bar{\eta }^n\Vert _0\nonumber \\&\le C\Vert \bar{\theta }^n\Vert _0\Vert \bar{\eta }^n\Vert _0\Vert \nabla \bar{\eta }^n\Vert _0+C\Vert \bar{\theta }^n\Vert _0\Vert \bar{\eta }^n\Vert _0\nonumber \nonumber \\&\le C\Vert \bar{\theta }^n\Vert _0\Vert \bar{\eta }^n\Vert _0\le C\Vert \bar{\theta }^n\Vert _0^2+C(\Vert \eta ^n\Vert _0^2+\Vert \eta ^{n-1}\Vert _0^2). \end{aligned}$$

(3.9)

Based on the estimates (3.7)–(3.9), $A_2$ can be bounded by

$$\begin{aligned} A_2&\le Ch^4+C\Vert \bar{\theta }^n\Vert _0^2+C(\Vert \eta ^n\Vert _0^2+\Vert \eta ^{n-1}\Vert _0^2). \end{aligned}$$

(3.10)

According to Taylor expansion and integration by parts, we have

$$\begin{aligned} A_3+A_4+A_5&\le C\tau ^2\Vert \bar{\eta }^n\Vert _0\le C\tau ^4+C(\Vert \eta ^n\Vert _0^2+\Vert \eta ^{n-1}\Vert _0^2). \end{aligned}$$

(3.11)

Substituting (3.5), (3.10) and (3.11) into (3.4) yields that

$$\begin{aligned} \frac{1}{2\tau }(\Vert \eta ^n\Vert _0^2-\Vert \eta ^{n-1}\Vert _0^2)&\le C(h^4+\tau ^4)+C\Vert \bar{\theta }^n\Vert _0^2+C(\Vert \eta ^n\Vert _0^2+\Vert \eta ^{n-1}\Vert _0^2)\nonumber \\&\le C(h^4+\tau ^4)+C\Vert \nabla \bar{\theta }^n\Vert _0^2+C(\Vert \eta ^n\Vert _0^2+\Vert \eta ^{n-1}\Vert _0^2). \end{aligned}$$

(3.12)

On the other hand, choosing $w_h=\theta ^n$ in (3.3) leads to

$$\begin{aligned} \Vert \nabla \theta ^n\Vert _0^2=\mu (|u^n|^2-|u_h^n|^2,\theta ^n), \end{aligned}$$

(3.13)

where we have used the definition of Ritz projection. Note that

$$\begin{aligned} |u^n|^2-|u_h^n|^2&=(u^n-u_h^n)(u^n)^{*}+u_h^n(u^n-u_h^n)^{*}=(\xi ^n+\eta ^n)(u^n)^{*}+u_h^n((\xi ^n)^{*}+(\eta ^n)^{*}), \end{aligned}$$

one can check that

$$\begin{aligned} ((\xi ^n+\eta ^n)(u^n)^{*},\theta ^n)&\le C(\Vert \xi ^n\Vert _0+\Vert \eta ^n\Vert _0)\Vert \theta ^n\Vert _0\le C(h^2+\Vert \eta ^n\Vert _0)\Vert \nabla \theta ^n\Vert _0, \end{aligned}$$

(3.14)

and

$$\begin{aligned} (u_h^n((\xi ^n)^{*}+(\eta ^n)^{*}),\theta ^n)&\le \Vert u_h^n\Vert _{0,4}(\Vert \xi ^n\Vert _0+\Vert \eta ^n\Vert _0)\Vert \theta ^n\Vert _{0,4}\nonumber \\&\le C\Vert \nabla u_h^n\Vert _0(h^2+\Vert \eta ^n\Vert _0)\Vert \nabla \theta ^n\Vert _0\nonumber \\&\le C(h^2+\Vert \eta ^n\Vert _0)\Vert \nabla \theta ^n\Vert _0, \end{aligned}$$

(3.15)

where we have used Lemma 2.

Hence, substituting (3.14) and (3.15) into (3.13) results in

$$\begin{aligned} \Vert \nabla \theta ^n\Vert _0^2\le C(h^2+\Vert \eta ^n\Vert _0)\Vert \nabla \theta ^n\Vert _0, \end{aligned}$$

which implies that

$$\begin{aligned} \Vert \nabla \theta ^n\Vert _0\le C(h^2+\Vert \eta ^n\Vert _0). \end{aligned}$$

(3.16)

Clearly, we also have

$$\begin{aligned} \Vert \nabla \theta ^{n-1}\Vert _0\le C(h^2+\Vert \eta ^{n-1}\Vert _0). \end{aligned}$$

(3.17)

Substituting (3.16) and (3.17) into (3.12) gives that

$$\begin{aligned} \frac{1}{2\tau }(\Vert \eta ^n\Vert _0^2-\Vert \eta ^{n-1}\Vert _0^2)&\le C(h^4+\tau ^4)+C(\Vert \eta ^n\Vert _0^2+\Vert \eta ^{n-1}\Vert _0^2). \end{aligned}$$

(3.18)

Multiplying both sides of (3.18) by $2\tau$ and summing up the resulting equation, we have

$$\begin{aligned} \Vert \eta ^n\Vert _0^2&\le C(h^4+\tau ^4)+C\tau \sum _{k=1}^n\Vert \eta ^k\Vert _0^2. \end{aligned}$$

(3.19)

An application of Gronwall inequality, we have

$$\begin{aligned} \Vert \eta ^n\Vert _0\le C(h^2+\tau ^2). \end{aligned}$$

(3.20)

Substituting (3.20) into (3.16) yields that

$$\begin{aligned} \Vert \theta ^n\Vert _0\le C\Vert \nabla \theta ^n\Vert _0\le C(h^2+\tau ^2). \end{aligned}$$

(3.21)

Finally, by triangle inequality, one can check that

$$\begin{aligned} \Vert u^n-u_h^n\Vert _0+\Vert \Phi ^n-\Phi _h^n\Vert _0&\le \Vert u^n-R_hu^n\Vert _0+\Vert R_hu^n-u_h^n\Vert _0+\Vert \Phi ^n\nonumber \\&\quad -R_h\Phi ^n\Vert _0+\Vert R_h\Phi ^n-\Phi _h^n\Vert _0\nonumber \\&\le Ch^2+C(\Vert \eta ^n\Vert _0+\Vert \theta ^n\Vert _0)\le C(h^2+\tau ^2), \end{aligned}$$

which is the desired result. The proof is complete.

4 Unconditionally superconvergent error estimate in $H^1$-norm of the fully-discrete scheme

We present the second main result in the following theorem.

Theorem 4.1

Suppose that $(u^n,\Phi ^n)$ and $(u_h^n,\Phi _h^n)$ are the solutions of (2.3)–(2.4) and (2.5)–(2.6) at $t=t_n$, respectively. Moreover, suppose that $u\in L^{\infty }(H^3(\Omega ))$, $u_t, u_{tt}, u_{ttt}\in L^{\infty }(H^2(\Omega ))$, $u_{tttt}\in L^{\infty }(L^2(\Omega ))$, $\Phi \in L^{\infty }(H^3(\Omega ))$, $\Phi _{tt}\in L^{\infty }(H^2(\Omega ))$, $\Phi _{ttt}\in L^{\infty }(L^2(\Omega ))$. Then we have the following unconditionally superclose error estimate

$$\begin{aligned} \Vert \nabla (I_hu^n-u_h^n)\Vert _0+\Vert \nabla (I_h\Phi ^n-\Phi _h^n)\Vert _0\le C(h^2+\tau ^2), \end{aligned}$$

(4.1)

where the constant C is independent of h, $\tau$ and n, but depends on u, T.

Proof

Letting $v_h=D_{\tau }\eta ^n$ in (3.2) and taking the real parts of the resulting equation give that

$$\begin{aligned}&\frac{1}{2\tau }(\Vert \nabla \eta ^n\Vert _0^2-\Vert \nabla \eta ^{n-1}\Vert _0^2)=Im(D_{\tau }\xi ^n,D_{\tau }\eta ^n)- Re(\bar{\Phi }^n\bar{u}^n-\bar{\Phi }_h^n\bar{u}_h^n,D_{\tau }\eta ^n)\nonumber \\&\quad -Im(D_{\tau }u^n-u_t^{n-\frac{1}{2}},D_{\tau }\eta ^n)-Re(\nabla (u^{n-\frac{1}{2}}-\bar{u}^n),\nabla D_{\tau }\eta ^n)\nonumber \\&\quad -Re(\Phi ^{n-\frac{1}{2}}u^{n-\frac{1}{2}}-\bar{\Phi }^n\bar{u}^n,D_{\tau }\eta ^n). \end{aligned}$$

(4.2)

In terms of Cauchy–Schwarz inequality and (2.2), we have

$$\begin{aligned} Im(D_{\tau }\xi ^n,D_{\tau }\eta ^n)\le \Vert D_{\tau }\xi ^n\Vert _0\Vert D_{\tau }\eta ^n\Vert _0\le Ch^2\Vert D_{\tau }\eta ^n\Vert _0\le Ch^4+C\Vert D_{\tau }\eta ^n\Vert _0^2. \end{aligned}$$

(4.3)

Noticing that

$$\begin{aligned} \bar{\Phi }^n\bar{u}^n-\bar{\Phi }_h^n\bar{u}_h^n&=\bar{\Phi }^n(\bar{u}^n-\bar{u}_h^n)+(\bar{\Phi }^n-\bar{\Phi }_h^n)\bar{u}_h^n\nonumber \\&=\bar{\Phi }^n(\bar{u}^n-\bar{u}_h^n)+(\bar{\Phi }^n-\bar{\Phi }_h^n)(\bar{u}_h^n-R_h\bar{u}^n)+(\bar{\Phi }^n-\bar{\Phi }_h^n)R_h\bar{u}^n, \end{aligned}$$

we have from (3.1) that

$$\begin{aligned}&-Re(\bar{\Phi }^n(\bar{u}^n-\bar{u}_h^n),D_{\tau }\eta ^n)-Re((\bar{\Phi }^n-\bar{\Phi }_h^n)R_h\bar{u}^n,D_{\tau }\eta ^n)\nonumber \\&\quad \le C(\Vert \bar{u}^n-\bar{u}_h^n\Vert _0+\Vert \bar{\Phi }^n-\bar{\Phi }_h^n\Vert _0)\Vert D_{\tau }\eta ^n\Vert _0 \le C(h^2+\tau ^2)\Vert D_{\tau }\eta ^n\Vert _0\nonumber \\&\quad \le C(h^4+\tau ^4)+C\Vert D_{\tau }\eta ^n\Vert _0^2, \end{aligned}$$

(4.4)

and

$$\begin{aligned}&-Re((\bar{\Phi }^n-\bar{\Phi }_h^n)(\bar{u}_h^n-R_h\bar{u}^n),D_{\tau }\eta ^n)\\&\quad =Re(\bar{\sigma }^n\bar{\eta }^n,D_{\tau }\eta ^n)+Re(\bar{\theta }^n\bar{\eta }^n,D_{\tau }\eta ^n)\nonumber \\&\quad \le \Vert \bar{\sigma }^n\Vert _{0,4}\Vert \bar{\eta }^n\Vert _0\Vert D_{\tau }\eta ^n\Vert _{0,4}+ \Vert \bar{\theta }^n\Vert _{0,4}\Vert \bar{\eta }^n\Vert _{0,4}\Vert D_{\tau }\eta ^n\Vert _0\nonumber \\&\quad \le Ch(h^2+\tau ^2)(h^{-1}\Vert D_{\tau }\eta ^n\Vert _0)+C\Vert \nabla \bar{\theta }^n\Vert _0\Vert \nabla \bar{\eta }^n\Vert _0\Vert D_{\tau }\eta ^n\Vert _0\nonumber \\&\quad \le C(h^2+\tau ^2)\Vert D_{\tau }\eta ^n\Vert _0\le C(h^4+\tau ^4)+C\Vert D_{\tau }\eta ^n\Vert _0^2, \end{aligned}$$

where we have used (2.15), (3.1) and (3.21).

Hence, one can check that

$$\begin{aligned} -Re(\bar{\Phi }^n\bar{u}^n-\bar{\Phi }_h^n\bar{u}_h^n,D_{\tau }\eta ^n)\le C(h^4+\tau ^4)+C\Vert D_{\tau }\eta ^n\Vert _0^2. \end{aligned}$$

(4.5)

In addition,by using Taylor expansion and integration by parts, we have

$$\begin{aligned} -Im(D_{\tau }u^n-u_t^{n-\frac{1}{2}},D_{\tau }\eta ^n)&-Re(\nabla (u^{n-\frac{1}{2}}-\bar{u}^n),\nabla D_{\tau }\eta ^n)-Re(\Phi ^{n-\frac{1}{2}}u^{n-\frac{1}{2}}-\bar{\Phi }^n\bar{u}^n,D_{\tau }\eta ^n)\nonumber \\&\le C\tau ^2\Vert D_{\tau }\eta ^n\Vert _0\le C\tau ^4+C\Vert D_{\tau }\eta ^n\Vert _0^2. \end{aligned}$$

(4.6)

Substituting (4.3), (4.5) and (4.6) into (4.2) yields that

$$\begin{aligned} \frac{1}{2\tau }(\Vert \nabla \eta ^n\Vert _0^2-\Vert \nabla \eta ^{n-1}\Vert _0^2)\le C(h^4+\tau ^4)+C\Vert D_{\tau }\eta ^n\Vert _0^2, \end{aligned}$$

which implies that

$$\begin{aligned} \Vert \nabla \eta ^n\Vert _0^2\le C(h^4+\tau ^4)+C\tau \sum _{k=1}^n\Vert D_{\tau }\eta ^k\Vert _0^2. \end{aligned}$$

(4.7)

In what follows, we pay our attention to estimate $\Vert D_{\tau }\eta ^n\Vert _0$. To do this, subtracting the $n-1$-level from the n-level of (3.2), we have

$$\begin{aligned}&\textrm{i}(D_{\tau }\eta ^n-D_{\tau }\eta ^{n-1},v_h)-(\nabla (\bar{\eta }^n-\bar{\eta }^{n-1}),\nabla \ v_h)=-\textrm{i}(D_{\tau }\xi ^n-D_{\tau }\xi ^{n-1},v_h)\nonumber \\&\quad +((\bar{\Phi }^n\bar{u}^n-\bar{\Phi }_h^n\bar{u}_h^n)-(\bar{\Phi }^{n-1}\bar{u}^{n-1}-\bar{\Phi }_h^{n-1}\bar{u}_h^{n-1}),v_h) +\textrm{i}((D_{\tau }u^n-u_t^{n-\frac{1}{2}})\nonumber \\&\quad -(D_{\tau }u^{n-1}-u_t^{n-\frac{3}{2}}),v_h)\nonumber \\&\quad +(\nabla ((u^{n-\frac{1}{2}}-\bar{u}^n)-(u^{n-\frac{3}{2}}-\bar{u}^{n-1})),\nabla v_h)\nonumber \\&\quad +((\Phi ^{n-\frac{1}{2}}u^{n-\frac{1}{2}}-\bar{\Phi }^n\bar{u}^n)- (\Phi ^{n-\frac{3}{2}}u^{n-\frac{3}{2}}-\bar{\Phi }^{n-1}\bar{u}^{n-1}),v_h). \end{aligned}$$

(4.8)

Choosing $v_h=D_{\tau }\bar{\eta }^n=\frac{1}{2}(D_{\tau }\eta ^n+D_{\tau }\eta ^{n-1})$ in (4.8) and taking the imaginary parts of the resulting equation, we have

$$\begin{aligned} \frac{1}{2\tau }(\Vert D_{\tau }\eta ^n\Vert _0^2-\Vert D_{\tau }\eta ^{n-1}\Vert _0^2)&= -Re (D_{\tau }\xi ^n-D_{\tau }\xi ^{n-1},D_{\tau }\bar{\eta }^n)\nonumber \\&\quad +Im((\bar{\Phi }^n\bar{u}^n-\bar{\Phi }_h^n\bar{u}_h^n)-(\bar{\Phi }^{n-1}\bar{u}^{n-1}-\bar{\Phi }_h^{n-1}\bar{u}_h^{n-1}),D_{\tau }\bar{\eta }^n)\nonumber \\&\quad +Im((D_{\tau }u^n-u_t^{n-\frac{1}{2}})-(D_{\tau }u^{n-1}-u_t^{n-\frac{3}{2}}),D_{\tau }\bar{\eta }^n)\nonumber \\&\quad +Im(\nabla ((u^{n-\frac{1}{2}}-\bar{u}^n)-(u^{n-\frac{3}{2}}-\bar{u}^{n-1})),D_{\tau }\bar{\eta }^n)\nonumber \\&\quad +Im ((\Phi ^{n-\frac{1}{2}}u^{n-\frac{1}{2}}-\bar{\Phi }^n\bar{u}^n)- (\Phi ^{n-\frac{3}{2}}u^{n-\frac{3}{2}}-\bar{\Phi }^{n-1}\bar{u}^{n-1}),D_{\tau }\bar{\eta }^n)\nonumber \\&:=\sum _{k=1}^5B_k. \end{aligned}$$

(4.9)

By using Cauchy–Schwarz inequality, Taylor expansion and (2.2), we have

$$\begin{aligned} B_1\le C\tau h^2\Vert D_{\tau }\bar{\eta }^n\Vert _0\le C\tau h^4+C\tau \Vert D_{\tau }\bar{\eta }^n\Vert _0^2. \end{aligned}$$

(4.10)

By using Cauchy–Schwarz inequality, Taylor expansion and integration by parts, we have

$$\begin{aligned} B_3+B_4+B_5\le C\tau ^3\Vert D_{\tau }\bar{\eta }^n\Vert _0\le C\tau \cdot \tau ^4+C\tau \Vert D_{\tau }\bar{\eta }^n\Vert _0^2. \end{aligned}$$

(4.11)

To estimate $B_2$, we rewrite $(\bar{\Phi }^n\bar{u}^n-\bar{\Phi }_h^n\bar{u}_h^n)-(\bar{\Phi }^{n-1}\bar{u}^{n-1}-\bar{\Phi }_h^{n-1}\bar{u}_h^{n-1})$ as

$$\begin{aligned}&(\bar{\Phi }^n\bar{u}^n-\bar{\Phi }_h^n\bar{u}_h^n)-(\bar{\Phi }^{n-1}\bar{u}^{n-1}-\bar{\Phi }_h^{n-1}\bar{u}_h^{n-1})\nonumber \\&\quad =[(\bar{\Phi }^n-\bar{\Phi }^{n-1})\bar{u}^n+\bar{\Phi }^{n-1}(\bar{u}^n-\bar{u}^{n-1})] -[(\bar{\Phi }_h^n-\bar{\Phi }_h^{n-1})\bar{u}_h^n+\bar{\Phi }_h^{n-1}(\bar{u}_h^n-\bar{u}_h^{n-1})]\nonumber \\&\quad =(\bar{\Phi }^n-\bar{\Phi }^{n-1})(\bar{u}^n-\bar{u}_h^n)+[(\bar{\Phi }^n-\bar{\Phi }^{n-1}) -(\bar{\Phi }_h^n-\bar{\Phi }_h^{n-1})]\bar{u}_h^n\nonumber \\&\quad \quad +(\bar{\Phi }^{n-1}-\bar{\Phi }_h^{n-1})(\bar{u}^n-\bar{u}^{n-1})+\bar{\Phi }^{n-1}[(\bar{u}^n-\bar{u}^{n-1})-(\bar{u}_h^n-\bar{u}_h^{n-1})]\nonumber \\&\quad =(\bar{\Phi }^n-\bar{\Phi }^{n-1})(\bar{u}^n-\bar{u}_h^n)+[(\bar{\Phi }^n-\bar{\Phi }^{n-1}) -(\bar{\Phi }_h^n-\bar{\Phi }_h^{n-1})](\bar{u}_h^n-R_h\bar{u}^n)\nonumber \\&\quad \quad +[(\bar{\Phi }^n-\bar{\Phi }^{n-1}) -(\bar{\Phi }_h^n-\bar{\Phi }_h^{n-1})]R_h\bar{u}^n\nonumber \\&\quad \quad +(\bar{\Phi }^{n-1}-\bar{\Phi }_h^{n-1})(\bar{u}^n-\bar{u}^{n-1})+(\bar{\Phi }^{n-1}-R_h\bar{\Phi }^{n-1})[(\bar{u}^n-\bar{u}^{n-1})-(\bar{u}_h^n-\bar{u}_h^{n-1})]\nonumber \\&\quad \quad +R_h\bar{\Phi }^{n-1}[(\bar{u}^n-\bar{u}^{n-1})-(\bar{u}_h^n-\bar{u}_h^{n-1})]:=\sum _{k=1}^6B_2^k. \end{aligned}$$

(4.12)

According to Cauchy–Schwarz inequality, Taylor expansion and (3.1), it follows that

$$\begin{aligned} Im(B_2^1,D_{\tau }\bar{\eta }^n)&=((\bar{\Phi }^n-\bar{\Phi }^{n-1})(\bar{u}^n-\bar{u}_h^n),D_{\tau }\bar{\eta }^n)\le C\tau \Vert \bar{u}^n-\bar{u}_h^n\Vert _0\Vert D_{\tau }\bar{\eta }^n\Vert _0\nonumber \\&\le C\tau (h^4+\tau ^4)+C\tau \Vert D_{\tau }\bar{\eta }^n\Vert _0^2. \end{aligned}$$

(4.13)

For $B_2^2$, we have by (2.15) and (3.20)

$$\begin{aligned}&Im([(\bar{\Phi }^n-\bar{\Phi }^{n-1}) -(\bar{\Phi }_h^n-\bar{\Phi }_h^{n-1})](\bar{u}_h^n-R_h\bar{u}^n),D_{\tau }\bar{\eta }^n) =-\tau ((D_{\tau }\bar{\sigma }^n+D_{\tau }\bar{\theta }^n)\bar{\eta }^n,D_{\tau }\bar{\eta }^n)\nonumber \\&\quad \le \tau \Vert D_{\tau }\bar{\sigma }^n\Vert _{0,4}\Vert \bar{\eta }^n\Vert _0\Vert D_{\tau }\bar{\eta }^n\Vert _{0,4} +\tau \Vert D_{\tau }\bar{\theta }^n\Vert _{0,4}\Vert \bar{\eta }^n\Vert _{0,4}\Vert D_{\tau }\bar{\eta }^n\Vert _0\nonumber \\&\quad \le \tau (Ch)\Vert \bar{\eta }^n\Vert _0(Ch^{-1}\Vert D_{\tau }\bar{\eta }^n\Vert _0)+C\tau \Vert \nabla D_{\tau }\bar{\theta }^n\Vert _0\Vert \nabla \bar{\eta }^n\Vert _0\Vert D_{\tau }\bar{\eta }^n\Vert _0\nonumber \\&\quad \le C\tau (h^2+\tau ^2)+C\tau \Vert \nabla D_{\tau }\bar{\theta }^n\Vert _0\Vert D_{\tau }\bar{\eta }^n\Vert _0 \le C\tau (h^4+\tau ^4)+C\tau \Vert \nabla D_{\tau }\bar{\theta }^n\Vert _0^2+C\tau \Vert D_{\tau }\bar{\eta }^n\Vert _0^2. \end{aligned}$$

(4.14)

For $B_2^3$, there holds

$$\begin{aligned} Im([(\bar{\Phi }^n-\bar{\Phi }^{n-1}) -(\bar{\Phi }_h^n-\bar{\Phi }_h^{n-1})]R_h\bar{u}^n, D_{\tau }\bar{\eta }^n)\le C\tau (\Vert D_{\tau }\bar{\sigma }^n\Vert _0+\Vert D_{\tau }\bar{\theta }^n\Vert _0)\Vert D_{\tau }\bar{\eta }^n\Vert _0\nonumber \\ \le C\tau h^4+C\tau \Vert \nabla D_{\tau }\bar{\theta }^n\Vert _0^2+C\tau \Vert D_{\tau }\bar{\eta }^n\Vert _0^2. \end{aligned}$$

(4.15)

In terms of (3.1), we have for $B_2^4$ that

$$\begin{aligned} Im((\bar{\Phi }^{n-1}-\bar{\Phi }_h^{n-1})(\bar{u}^n-\bar{u}^{n-1}),D_{\tau }\bar{\eta }^n)&\le C\tau \Vert \bar{\Phi }^{n-1}-\bar{\Phi }_h^{n-1}\Vert _0\Vert D_{\tau }\bar{\eta }^n\Vert _0\nonumber \\&\le C\tau (h^2+\tau ^2)\Vert D_{\tau }\eta ^n\Vert _0\nonumber \\&\le C\tau (h^4+\tau ^4)+C\tau \Vert D_{\tau }\bar{\eta }^n\Vert _0^2. \end{aligned}$$

(4.16)

For $B_2^5$, we have

$$\begin{aligned} ((\bar{\Phi }^{n-1}-R_h\bar{\Phi }^{n-1})[(\bar{u}^n-\bar{u}^{n-1})-(\bar{u}_h^n-\bar{u}_h^{n-1})],D_{\tau }\eta ^n) =-\tau (\bar{\theta }^{n-1}(D_{\tau }\bar{\xi }^n+D_{\tau }\bar{\eta }^n),D_{\tau }\bar{\eta }^n). \end{aligned}$$

(4.17)

By using (3.1), one can check that

$$\begin{aligned} -\tau Im(\bar{\theta }^{n-1}D_{\tau }\bar{\xi }^n,D_{\tau }\bar{\eta }^n)&\le \tau \Vert \bar{\theta }^{n-1}\Vert _0\Vert D_{\tau }\bar{\xi }^n\Vert _{0,4}\Vert D_{\tau }\bar{\eta }^n\Vert _{0,4}\nonumber \\&\le \tau \Vert \bar{\theta }^{n-1}\Vert _0(Ch)(Ch^{-1}\Vert D_{\tau }\bar{\eta }^n\Vert _0)\nonumber \\&\le C\tau (h^2+\tau ^2)\Vert D_{\tau }\bar{\eta }^n\Vert _0\le C\tau (h^4+\tau ^4)+C\tau \Vert D_{\tau }\bar{\eta }^n\Vert _0^2. \end{aligned}$$

(4.18)

To estimate the term $-\tau (\bar{\theta }^{n-1}D_{\tau }\bar{\eta }^n,D_{\tau }\bar{\eta }^n)$ appeared on the right hand side of (4.17), we will discuss in two different cases.

Case I $\tau \le h$. In this case, from (3.21), we have

$$\begin{aligned} \Vert \theta ^n\Vert _0\le C(h^2+\tau ^2)\le Ch^2, \end{aligned}$$

which shows that

$$\begin{aligned} \Vert \theta ^n\Vert _{0,\infty }\le Ch^{-1}\Vert \theta ^n\Vert _0\le Ch^{-1}(Ch^2)\le C. \end{aligned}$$

(4.19)

Hence, we conclude that

$$\begin{aligned} -\tau Im(\bar{\theta }^{n-1}D_{\tau }\bar{\eta }^n,D_{\tau }\bar{\eta }^n)&\le \tau \Vert \bar{\theta }^{n-1}\Vert _{0,\infty }\Vert D_{\tau }\bar{\eta }^n\Vert _0\Vert D_{\tau }\bar{\eta }^n\Vert _0\le C\tau \Vert D_{\tau }\bar{\eta }^n\Vert _0^2. \end{aligned}$$

(4.20)

Case II $\tau \ge h$. In this case, from (3.20), we have

$$\begin{aligned} \Vert \eta ^n\Vert _0\le C(h^2+\tau ^2)\le C\tau ^2. \end{aligned}$$

(4.21)

Hence, we conclude that

$$\begin{aligned} -\tau Im(\bar{\theta }^{n-1}D_{\tau }\bar{\eta }^n,D_{\tau }\bar{\eta }^n)&\le \tau \Vert \bar{\theta }^{n-1}\Vert _{0,4}\Vert D_{\tau }\bar{\eta }^n\Vert _{0,4}\Vert D_{\tau }\bar{\eta }^n\Vert _0\le C\tau \Vert \nabla \bar{\theta }^{n-1}\Vert _0\Vert D_{\tau }\bar{\eta }^n\Vert _{0,4}\Vert D_{\tau }\bar{\eta }^n\Vert _0\nonumber \\&\le C\tau \Vert \nabla \bar{\theta }^{n-1}\Vert _0(\tau ^{-1}(\Vert \eta ^n\Vert _{0,4}+\Vert \eta ^{n-2}\Vert _{0,4}))(\tau ^{-1}(\Vert \eta ^n\Vert _0+\Vert \eta ^{n-2}\Vert _0))\nonumber \\&\le C\tau \Vert \nabla \bar{\theta }^{n-1}\Vert _0(\tau ^{-1}(\Vert \nabla \eta ^n\Vert _{0}+\Vert \nabla \eta ^{n-2}\Vert _{0}))(\tau ^{-1}(C\tau ^2))\nonumber \\&\le C\tau \Vert \nabla \bar{\theta }^{n-1}\Vert _0(\Vert \nabla \eta ^n\Vert _{0}+\Vert \nabla \eta ^{n-1}\Vert _{0}+\Vert \nabla \eta ^{n-2}\Vert _{0})\nonumber \\&\le C\tau (h^4+\tau ^4)+C\tau (\Vert \nabla \eta ^n\Vert _{0}^2+\Vert \nabla \eta ^{n-1}\Vert _{0}^2+\Vert \nabla \eta ^{n-2}\Vert _{0}^2), \end{aligned}$$

(4.22)

where we have used (3.21).

Therefore, one can see that

$$\begin{aligned} -\tau Im(\bar{\theta }^{n-1}D_{\tau }\bar{\eta }^n,D_{\tau }\bar{\eta }^n)&\le C\tau (h^4+\tau ^4)+C\tau (\Vert D_{\tau }\eta ^n\Vert _0^2+\Vert D_{\tau }\eta ^{n-1}\Vert _0^2)\nonumber \\&\quad +C\tau (\Vert \nabla \eta ^n\Vert _{0}^2+\Vert \nabla \eta ^{n-1}\Vert _{0}^2+\Vert \nabla \eta ^{n-2}\Vert _{0}^2). \end{aligned}$$

(4.23)

Based on the estimates (4.18) and (4.23), we have

$$\begin{aligned} Im(B_2^5,D_{\tau }\bar{\eta }^n)&\le C\tau (h^4+\tau ^4)+C\tau (\Vert D_{\tau }\eta ^n\Vert _0^2+\Vert D_{\tau }\eta ^{n-1}\Vert _0^2)\nonumber \\&\quad +C\tau (\Vert \nabla \eta ^n\Vert _{0}^2+\Vert \nabla \eta ^{n-1}\Vert _{0}^2+\Vert \nabla \eta ^{n-2}\Vert _{0}^2). \end{aligned}$$

(4.24)

In addition, it follows that for $B_2^6$

$$\begin{aligned} Im(R_h\bar{\Phi }^{n-1}[(\bar{u}^n-\bar{u}^{n-1})-(\bar{u}_h^n-\bar{u}_h^{n-1})],D_{\tau }\bar{\eta }^n)&\le C\tau (\Vert D_{\tau }\bar{\xi }^n\Vert _0+\Vert D_{\tau }\bar{\eta }^n\Vert _0)\Vert D_{\tau }\bar{\eta }^n\Vert _0\nonumber \\&\le C\tau h^4+C\tau \Vert D_{\tau }\bar{\eta }^n\Vert _0^2. \end{aligned}$$

(4.25)

Substituting the estimates $B_2^1\sim B_2^6$ into $B_2$, we have

$$\begin{aligned} B_2 \le C\tau (h^4+\tau ^4)&+C\tau (\Vert D_{\tau }\eta ^n\Vert _0^2+\Vert D_{\tau }\eta ^{n-1}\Vert _0^2)+C\tau \Vert \nabla D_{\tau }\bar{\theta }^n\Vert _0^2\nonumber \\&+C\tau (\Vert \nabla \eta ^n\Vert _{0}^2+\Vert \nabla \eta ^{n-1}\Vert _{0}^2+\Vert \nabla \eta ^{n-2}\Vert _{0}^2). \end{aligned}$$

(4.26)

Substituting the estimates $B_1\sim B_6$ into (4.9) yields

$$\begin{aligned} \frac{1}{2\tau }(\Vert D_{\tau }\eta ^n\Vert _0^2-\Vert D_{\tau }\eta ^{n-1}\Vert _0^2)&\le C\tau (h^4+\tau ^4)+C\tau (\Vert D_{\tau }\eta ^n\Vert _0^2+\Vert D_{\tau }\eta ^{n-1}\Vert _0^2)+C\tau \Vert \nabla D_{\tau }\bar{\theta }^n\Vert _0^2\nonumber \\&+C\tau (\Vert \nabla \eta ^n\Vert _{0}^2+\Vert \nabla \eta ^{n-1}\Vert _{0}^2+\Vert \nabla \eta ^{n-2}\Vert _{0}^2). \end{aligned}$$

Summing up the above inequality from 2 to n gives that

$$\begin{aligned} \Vert D_{\tau }\eta ^n\Vert _0^2\le \Vert D_{\tau }\eta ^1\Vert _0^2+C(h^4+\tau ^4)+C\tau \sum _{k=1}^n\Vert \nabla D_{\tau }\theta ^k\Vert _0^2+C\tau \sum _{k=1}^n\Vert \nabla \eta ^k\Vert _0^2+C\tau \sum _{k=1}^n\Vert D_{\tau }\eta ^k\Vert _0^2. \end{aligned}$$

(4.27)

Next, we focus on the estimate $\Vert \nabla D_{\tau }\theta ^n\Vert _0$. From (3.3), we have

$$\begin{aligned} (\nabla D_{\tau }\theta ^n,\nabla w_h)&=\mu \tau ^{-1}((|u^n|^2-|u_h^n|^2)-(|u^{n-1}|^2-|u_h^{n-1}|^2),w_h), \quad \forall w_h\in V_h. \end{aligned}$$

(4.28)

Choosing $w_h=D_{\tau }\theta ^n$ in (4.28) leads to

$$\begin{aligned} \Vert \nabla D_{\tau }\theta ^n\Vert _0^2&=\mu \tau ^{-1}((|u^n|^2-|u_h^n|^2)-(|u^{n-1}|^2-|u_h^{n-1}|^2),D_{\tau }\theta ^n). \end{aligned}$$

(4.29)

One can check that

$$\begin{aligned} (|u^n|^2-|u_h^n|^2)&-(|u^{n-1}|^2-|u_h^{n-1}|^2)=((u^n-u_h^n)-(u^{n-1}-u_h^{n-1}))(u^n)^{*}\nonumber \\&+(u^{n-1}-u_h^{n-1})(u^n-u^{n-1})^{*}\nonumber \\&+((u_h^n-u_h^{n-1})-R_h(u^n-u^{n-1}))(u^n-u_h^n)^{*}\nonumber \\&+R_h(u^n-u^{n-1})(u^n-u_h^n)^{*}+u_h^{n-1}((u^n-u_h^n)-(u^{n-1}-u_h^{n-1}))^{*}:=\sum _{k=1}^5D_k. \end{aligned}$$

(4.30)

By using Cauchy–schwarz inequality and (2.2), we have

$$\begin{aligned} \mu \tau ^{-1}(D_1,D_{\tau }\theta ^n)&\le C(\Vert D_{\tau }\xi ^n\Vert _0+\Vert D_{\tau }\eta ^n\Vert _0)\Vert D_{\tau }\theta ^n\Vert _0\nonumber \\&\le C(h^2+\Vert D_{\tau }\eta ^n\Vert _0)\Vert \nabla D_{\tau }\theta ^n\Vert _0. \end{aligned}$$

(4.31)

It is not difficult to check that by (3.1)

$$\begin{aligned} \mu \tau ^{-1}(D_2,D_{\tau }\theta ^n)&\le C\tau ^{-1}\Vert u^{n-1}-u_h^{n-1}\Vert _0\Vert u^n-u^{n-1}\Vert _{0,\infty }\Vert D_{\tau }\theta ^n\Vert _0\nonumber \\&\le C(h^2+\tau ^2)\Vert \nabla D_{\tau }\theta ^n\Vert _0. \end{aligned}$$

(4.32)

For $D_3$, we have by (2.15)

$$\begin{aligned} \mu \tau ^{-1}(D_3,D_{\tau }\eta ^n)&=-\mu (D_{\tau }\eta ^n(\xi ^n)^{*},D_{\tau }\theta ^n)-\mu (D_{\tau }\eta ^n(\eta ^n)^{*},D_{\tau }\theta ^n)\nonumber \\&\le C\Vert D_{\tau }\eta ^n\Vert _0\Vert \xi ^n\Vert _{0,4}\Vert D_{\tau }\theta ^n\Vert _{0,4}+C\Vert D_{\tau }\eta ^n\Vert _0\Vert \eta ^n\Vert _{0,4}\Vert D_{\tau }\theta ^n\Vert _{0,4}\nonumber \\&\le C\Vert D_{\tau }\eta ^n\Vert _0\Vert \nabla D_{\tau }\theta ^n\Vert _0. \end{aligned}$$

(4.33)

In addition, by (3.1), we have

$$\begin{aligned} \mu \tau ^{-1}(D_4,D_{\tau }\theta ^n)&\le C\tau ^{-1}\Vert R_h(u^n-u^{n-1})\Vert _{0,\infty }\Vert u^n-u_h^{n}\Vert _0\Vert D_{\tau }\theta ^n\Vert _0\nonumber \\&\le C(h^2+\tau ^2)\Vert \nabla D_{\tau }\theta ^n\Vert _0. \end{aligned}$$

(4.34)

By using (2.15) again, there holds

$$\begin{aligned} \mu \tau ^{-1}(D_5,D_{\tau }\theta ^n)&\le \Vert u_h^n\Vert _{0,4}(\Vert D_{\tau }\xi ^n\Vert _0+\Vert D_{\tau }\eta ^n\Vert _0)\Vert D_{\tau }\theta ^n\Vert _{0,4}\nonumber \\&\le C(h^2+\Vert D_{\tau }\eta ^n\Vert _0)\Vert \nabla D_{\tau }\theta ^n\Vert _0. \end{aligned}$$

(4.35)

Thus, based on the above estimates $D_1\sim D_5$, we conclude that

$$\begin{aligned} \Vert \nabla D_{\tau }\theta ^n\Vert _0&\le C(h^2+\tau ^2+\Vert D_{\tau }\eta ^n\Vert _0). \end{aligned}$$

(4.36)

Substituting (4.36) into (4.27) results in

$$\begin{aligned} \Vert D_{\tau }\eta ^n\Vert _0^2\le \Vert D_{\tau }\eta ^1\Vert _0^2+C(h^4+\tau ^4)+C\tau \sum _{k=1}^n\Vert \nabla \eta ^k\Vert _0^2+C\tau \sum _{k=1}^n\Vert D_{\tau }\eta ^k\Vert _0^2. \end{aligned}$$

(4.37)

Finally, there remains the term $\Vert D_{\tau }\eta ^1\Vert _0$ to estimate. To do this, letting $n=1$ in (3.2),we have

$$\begin{aligned} \textrm{i}\left( \frac{\eta ^1}{\tau },v_h\right) -\left( \nabla \frac{\eta ^1}{2},\nabla v_h\right)&=-\textrm{i}(D_{\tau }\xi ^1,v_h)+(\bar{\Phi }^1\bar{u}^1-\bar{\Phi }_h^1\bar{u}_h^1,v_h)+\textrm{i}(D_{\tau }u^1-u_t^{\frac{1}{2}},v_h)\nonumber \\&\quad +(\nabla (u^{\frac{1}{2}}-\bar{u}^1),\nabla v_h)+(\Phi ^{\frac{1}{2}}u^{\frac{1}{2}}-\bar{\Phi }^1\bar{u}^1,v_h),\quad \forall v_h\in V_h, \end{aligned}$$

(4.38)

where we have used $\eta ^0=0$.

Choosing $v_h=\frac{\eta ^1}{\tau }$ in (4.38) and taking the imaginary parts of the resulting equation give that

$$\begin{aligned} \left\| \frac{\eta ^1}{\tau }\right\| _0^2&=-Re\left( D_{\tau }\xi ^1,\frac{\eta ^1}{\tau }\right) +Im\left( \bar{\Phi }^1\bar{u}^1-\bar{\Phi }_h^1\bar{u}_h^1,\frac{\eta ^1}{\tau }\right) +Re\left( D_{\tau }u^1-u_t^{\frac{1}{2}},\frac{\eta ^1}{\tau }\right) \nonumber \\&\quad +Im\left( \nabla (u^{\frac{1}{2}}-\bar{u}^1),\nabla \frac{\eta ^1}{\tau }\right) +Im\left( \Phi ^{\frac{1}{2}}u^{\frac{1}{2}}-\bar{\Phi }^1\bar{u}^1,\frac{\eta ^1}{\tau }\right) . \end{aligned}$$

(4.39)

By using Cauchy–Schwarz inequality, (2.2), Taylor expansion and integration by parts, we have

$$\begin{aligned} -Re\left( D_{\tau }\xi ^1,\frac{\eta ^1}{\tau }\right) +&Re\left( D_{\tau }u^1-u_t^{\frac{1}{2}},\frac{\eta ^1}{\tau }\right) +Im\left( \nabla (u^{\frac{1}{2}}-\bar{u}^1),\nabla \frac{\eta ^1}{\tau }\right) \nonumber \\&+Im\left( \Phi ^{\frac{1}{2}}u^{\frac{1}{2}}-\bar{\Phi }^1\bar{u}^1,\frac{\eta ^1}{\tau }\right) \nonumber \\&\le C(h^2+\tau ^2)\left\| \frac{\eta ^1}{\tau }\right\| _0. \end{aligned}$$

(4.40)

Noticing that

$$\begin{aligned} \bar{\Phi }^1\bar{u}^1-\bar{\Phi }_h^1\bar{u}_h^1&=(\bar{\Phi }^1-\bar{\Phi }_h^1)\bar{u}^1+(\bar{\Phi }_h^1-R_h\bar{\Phi }^1)(\bar{u}^1-\bar{u}_h^1) +R_h\bar{\Phi }^1(\bar{u}^1-\bar{u}_h^1), \end{aligned}$$

we have by (2.15), (3.1) and (3.21)

$$\begin{aligned} Im\left( \bar{\Phi }^1\bar{u}^1-\bar{\Phi }_h^1\bar{u}_h^1,\frac{\eta ^1}{\tau }\right)&\le C\Vert \bar{\Phi }^1-\bar{\Phi }_h^1\Vert _0\left\| \frac{\eta ^1}{\tau }\right\| _0 +C\Vert \bar{\theta }^1\Vert _0\Vert \bar{\xi }^1\Vert _{0,4}\left\| \frac{\eta ^1}{\tau }\right\| _{0,4}\nonumber \\&+\Vert \bar{\theta }^1\Vert _{0,4}\Vert \eta ^1\Vert _{0,4}\left\| \frac{\eta ^1}{\tau }\right\| _0+C\Vert \bar{u}^1-\bar{u}_h^1\Vert _0\left\| \frac{\eta ^1}{\tau }\right\| _0\nonumber \\&\le C(h^2+\tau ^2)\left\| \frac{\eta ^1}{\tau }\right\| _0+C\Vert \nabla \bar{\theta }^1\Vert _0\left\| \frac{\eta ^1}{\tau }\right\| _0\le C(h^2+\tau ^2)\left\| \frac{\eta ^1}{\tau }\right\| _0. \end{aligned}$$

(4.41)

Substituting (4.40) and (4.41) into (4.39) results in

$$\begin{aligned} \left\| \frac{\eta ^1}{\tau }\right\| _0&\le C(h^2+\tau ^2). \end{aligned}$$

(4.42)

Then, substituting (4.42) into (4.37) gives that

$$\begin{aligned} \Vert D_{\tau }\eta ^n\Vert _0^2\le C(h^4+\tau ^4)+C\tau \sum _{k=1}^n\Vert \nabla \eta ^k\Vert _0^2+C\tau \sum _{k=1}^n\Vert D_{\tau }\eta ^k\Vert _0^2. \end{aligned}$$

(4.43)

Hence, by (4.7) and (4.43), we have

$$\begin{aligned} \Vert \nabla \eta ^n\Vert _0^2+\Vert D_{\tau }\eta ^n\Vert _0^2\le C(h^4+\tau ^4)+C\tau \sum _{k=1}^n(\Vert \nabla \eta ^k\Vert _0^2+\Vert D_{\tau }\eta ^k\Vert _0^2). \end{aligned}$$

(4.44)

An application of Gronwall inequality yields that

$$\begin{aligned} \Vert \nabla \eta ^n\Vert _0+\Vert D_{\tau }\eta ^n\Vert _0\le C(h^2+\tau ^2). \end{aligned}$$

(4.45)

Furthermore, according to triangle inequality and the superclose estimate between $R_hu^n$ and $I_hu^n$ (Shi et al. 2014; Yang 2021), i.e., for $u\in H^3(\Omega )$, there holds

$$\begin{aligned} \Vert \nabla (R_hu-I_hu)\Vert _0\le Ch^2|u|_3, \end{aligned}$$

Hence, we conclude that

$$\begin{aligned} \Vert \nabla (I_hu^n-u_h^n)\Vert _0\le \Vert \nabla (I_hu^n-R_hu^n)\Vert _0+\Vert \nabla (R_hu^n-u_h^n)\Vert _0\le C(h^2+\tau ^2). \end{aligned}$$

(4.46)

Moreover, in terms of (3.21), we also have

$$\begin{aligned} \Vert \nabla (I_h\Phi ^n-\Phi _h^n)\Vert _0\le C(h^2+\tau ^2). \end{aligned}$$

(4.47)

The desired result (4.1) is obtained and the proof is complete.

In what follows, we adopt the interpolation post-processing approach to derive the global superconvergence result. A macroelement $\widetilde{K}$ is constructed with 4 elements $K_j$, $j=1,2,3,4$ (see Fig. 1), the local interpolation operator $I_{2\,h}: C(\widetilde{K})\rightarrow Q_{22}(\widetilde{K})$ is adopted as interpolation post-processing operator (Lin and Lin 2006) with the following interpolation conditions

$$\begin{aligned} I_{2h}u(z_i)=u(z_i),~~i=1,2,\ldots ,9, \end{aligned}$$

where $z_i$, $i=1,2,\ldots ,9$ are the nine vertices of $\widetilde{K}$ and $Q_{22}(\widetilde{K})$ denotes biquadratic polynomial space on $\widetilde{K}$.

Fig. 1

The macroelement $\tilde{K}$

What’s more, one can check that the properties, which have been shown in Lin and Lin (2006), for operator $I_{2h}$ hold:

$$\begin{aligned}&I_{2h}I_hu=I_{2h}u, \end{aligned}$$

(4.48)

$$\begin{aligned}&\Vert u-I_{2h}u\Vert _1\le Ch^2\Vert u\Vert _3,\quad \forall u\in H^3(\Omega ), \end{aligned}$$

(4.49)

$$\begin{aligned}&\Vert I_{2h}v_h\Vert _1\le C\Vert v_h\Vert _1,\quad \forall v_h\in V_h. \end{aligned}$$

(4.50)

Therefore, in terms of (4.46) and (4.48)–(4.50), the global superconvergent error estiamte can be obtained.

Theorem 4.2

Under the conditions of Theorem 4.1, we have for $n=1,2,\ldots ,N$

$$\begin{aligned} \Vert u^n-I_{2h}u_h^n\Vert _1+\Vert \Phi ^n-I_{2h}\Phi _h^n\Vert _1\le C(h^2+\tau ^2). \end{aligned}$$

(4.51)

Proof

From (4.48)–(4.50) and Theorem 4.1, one can see that

$$\begin{aligned} \Vert u^n-I_{2h}u_h^n\Vert _1&\le \Vert u^n-I_{2h}I_hu^n\Vert _1+\Vert I_{2h}I_hu^n-I_{2h}u_h^n\Vert _1\nonumber \\&\le \Vert u^n-I_{2h}u^n\Vert _1+\Vert I_{2h}(I_hu^n-u_h^n)\Vert _1\nonumber \\&\le Ch^2\Vert u^n\Vert _3+C\Vert I_hu^n-u_h^n\Vert _1\nonumber \\&\le C(h^2+\tau ^2). \end{aligned}$$

Similarly, we can derive the superconvergent result for $\Phi ^n$. Hence, we complete the proof.

5 Numerical results

In this section, we present some numerical results to verify the correctness of the theoretical analysis.

Example 1

(Error estimates and order of convergence) We set the domain $\Omega =(0,1)\times (0,1)$ and the final time $T=1$ in the computation. Consider the following SP equation

$$\begin{aligned}&\textrm{i}u_t+\Delta u=\Phi u+f, \quad (x,y)\in \Omega ,\quad 0<t\le T,\\&-\Delta \Phi =|u|^2+g,\quad (x,y)\in \Omega ,\quad 0<t\le T,\\&u|_{\partial \Omega }=\Phi |_{\partial \Omega }=0,\quad (x,y)\in \partial \Omega ,\quad 0<t\le T,\\&u(0)=\sin (\pi x)\sin (\pi y),\quad (x,y)\in \Omega . \end{aligned}$$

Let the functions f and g and the initial and boundary conditions be chosen corresponding to the exact solutions

$$\begin{aligned} u(t,x,y)=\exp (-t)\sin (\pi x)\sin (\pi y),\quad \quad \Phi (t,x,y)=\exp (-t)x(1-x)y(1-y). \end{aligned}$$

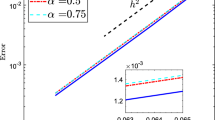
We present the numerical errors of $\Vert u^n-u_h^n\Vert _0$, $\Vert u^n-u_h^n\Vert _1$, $\Vert I_hu^n-u_h^n\Vert _1$, $\Vert u^n-I_{2\,h}u_h^n\Vert _1$ and $\Vert \Phi ^n-\Phi _h^n\Vert _0$, $\Vert \Phi ^n-\Phi _h^n\Vert _1$, $\Vert I_h\Phi ^n-\Phi _h^n\Vert _1$, $\Vert \Phi ^n-I_{2\,h}\Phi _h^n\Vert _1$ at $t=0.2,~1.0$ in Tables 1, 2. Obviously, we can see that the numerical results agree well with the theoretical analysis, i.e., the convergence rates are $O(h^2)$, O(h), $O(h^2)$ and $O(h^2)$, respectively.

Table 1 The numerical errors and convergence orders at $t=0.2$

Table 2 The numerical errors and convergence orders at $t=1.0$

Example 2

(Conservation of discrete mass and energy) We set the domain $\Omega =(0,1)\times (0,1)$ and the final time $T=100$. Consider the following SP equation

$$\begin{aligned}&\textrm{i}u_t+\Delta u=\Phi u, \quad (x,y)\in \Omega ,\quad 0<t\le T=100,\\&-\Delta \Phi =|u|^2,\quad (x,y)\in \Omega ,\quad 0<t\le T=100,\\&u|_{\partial \Omega }=\Phi |_{\partial \Omega }=0,\quad (x,y)\in \partial \Omega ,\quad 0<t\le T=100,\\&u(0)=\sin (\pi x)\sin (\pi y),\quad (x,y)\in \Omega . \end{aligned}$$

The temporal direction is divided with time stepsize $\tau =1$, and the spatial direction is divided with stepsize $h=\frac{\sqrt{2}}{40}$. In Fig. 2, we present some values of the discrete mass and energy for the scheme (2.5)–(2.6) at various time levels $t^n$. It can be seen that the scheme (2.5)–(2.6) preserves the discrete mass and energy, which is consistent with the theoretical analysis.

Fig. 2

The profile of the discrete mass $\mathcal {M}^n$ and energy $\mathcal {E}^n$