A posteriori $L^{\infty }(L^{\infty })$-error estimates for finite-element approximations to parabolic optimal control problems

Abstract

We derive space–time a posteriori error estimates of finite-element method for the linear parabolic optimal control problems in a convex bounded polyhedral domain. The variational discretization is used to approximate the state and co-state variables with the piecewise linear and continuous functions, while the control variable is computed using the implicit relation between the control and co-state variables. The temporal discretization is based on the backward Euler method. The key feature of this approach is not to discretize the control variable but to implicitly utilize the optimality conditions for the discretization of the control variable. Our error analysis relies on the elliptic reconstruction technique introduced by Makridakis and Nochetto (SIAM J Numer Anal, 41:1585–1594, 2003) in conjunction with heat kernel estimates for linear parabolic problem. The use of elliptic reconstruction technique greatly simplifies the analysis by allowing us to take the advantage of existing elliptic maximum norm error estimate and the heat kernel estimate. We derive a posteriori error estimates for the state, co-state, and control variables in the $L^\infty (0,T;\, L^\infty (\varOmega ))$-norm. Numerical experiments are conducted to illustrate the performance of the derived estimators.

1 Introduction

Let $\varOmega$ be a convex bounded polyhedral domain in $\mathbb {R}^d \, (d=2,\,3)$ with Lipschitz boundary $\partial \varOmega$. Set $\varOmega _T=\varOmega \times (0,T]$, $\varGamma _T=\partial \varOmega \times (0,T]$ with $T<\infty$. We consider the following parabolic optimal control problems:

$$\begin{aligned} \min _{u\in U_{ad}} J(u,y)= \min _{u\in U_{ad}}\frac{1}{2}\int _{0}^{T}\left\{ \Vert y-y_{d}\Vert ^{2}+\Vert u\Vert ^{2}\right\} \,\mathrm{d}s, \end{aligned}$$

(1.1)

subject to the state equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle {\frac{\partial y}{\partial t}- \varDelta y=f+u \;\;\text {in}\;\;\varOmega _T,}\\ \displaystyle {y(x,0)=y_{0}(x)\;\; \text {in}\;\; \varOmega ,}\\ \displaystyle {y=0\;\;\;\;\;\;\;\; \text {on}\;\;\varGamma _T,} \end{array}\right. } \end{aligned}$$

(1.2)

and the control constraints

$$\begin{aligned} u_a\le u(x,t)\le u_b\;\;\;\text {a.e.}\;\;\;\text {in}\;\;\varOmega _T, \end{aligned}$$

(1.3)

where $y_0 \in L^\infty (\varOmega )$, $y_d \in L^\infty (0,T;L^\infty (\varOmega ))$ and $f \in L^\infty (0,T;L^\infty (\varOmega ))$. Here, $y=y(x,t)$ and $u=u(x,t)$ denote the state and the control variables, respectively. The set of admissible controls is defined by

$$\begin{aligned} U_{ad}=\left\{ u\in L^\infty \left( 0,T;L^\infty (\varOmega )\right) :\;u_{a}\le u\le u_{b}\; \;a.e. \;\;\text {in}\;\varOmega _T\right\} \end{aligned}$$

with $u_{a},u_{b}\in \mathbb {R}$ fulfill $u_{a}<u_{b}$.

There have been extensive studies in the literature by numerous researchers on the finite-element approximations to optimal control problems. Some of recent progress in this area can be found in Barbu (1984), Becker and Kapp (1997), Becker et al. (1998), Haslinger and Neittaanmaki (1989), Hinze (2005), Lions (1971), Neittaanmaki and Tiba (1994), Pironneau (1984), Tiba (1995), and references quoted therein. In Hinze (2005), Hinze has introduced a variational discretization approach for elliptic optimal control problems. The main feature of this discretization is not to discretize the control variable but to implicitly utilize the optimality conditions and the discretization of the state and co-state variables to compute the control variable. The literature concerning a priori error analysis of finite-element methods for parabolic optimal control problems can be found in Knowles (1982), Nietzel and Vexler (2012), Rösch (2004), Winther (1978), and references therein. Recently, adaptive finite-element methods for approximating solutions to optimal control problems are the most important means to enhance accuracy and efficiency of the finite-element discretization. The adaptive method ensures a higher density of nodes in certain area of the given domain with the help of a posteriori error estimators where the solution is more difficult to approximate. There is a vast literature on a posteriori error estimates for parabolic optimal control problems using different approaches; for instance, see Langer et al. (2016), Liu and Yan (2003), Sun et al. (2013), Tang and Chen (2012a), Tang and Chen (2012b), Tang and Hua (2014),Xiong and Li (2011). While residual type a posteriori error estimates of finite-element methods for parabolic optimal control problems are discussed in Liu and Yan (2003), the authors of Tang and Chen (2012a) have derived a posteriori error bounds in the $L^\infty (0,T;L^2(\varOmega ))$ and $L^2(0,T;H^1(\varOmega ))$ norms with integral constraint. Tang and Chen (2012a) have studied a recovery type a posteriori error estimate for fully discrete variational discretization approximations of parabolic optimal control problems. The same authors have discussed a priori and a posteriori error analysis for parabolic control problems with control constraints using variational discretizations in Tang and Chen (2012b). Subsequently, Tang and Hua (2014) have established upper bounds in $L^\infty (0,T;L^2(\varOmega ))-$norm for the semi-discrete variational discretization approximations of optimal control problems using elliptic reconstruction. Later, Sun et al. (2013) have derived both lower and upper bounds of the errors for parabolic optimal control problems. For functional type a posteriori error estimates for parabolic optimal control problems, one may refer to Langer et al. (2016).

Most of adaptive finite-element methods are design to control only energy norms of solutions. The pointwise error control is also a natural goal when computing free boundaries. Some recent papers of adaptive finite-element method for controlling pointwise errors in elliptic and parabolic problems are contained in Dari et al. (2000), Demlow (2006, 2007), Nochetto (1995), Nochetto et al. (2003, 2005, 2006), Otárola et al. (2019), Boman (2000), Demlow et al. (2009), and Eriksson and Johnson (1995), respectively. For stationary optimal control problems, the authors of Otárola et al. (2019) have introduced an a posteriori error estimator which yields optimal rate of convergence in the maximum norm. Both reliability and efficiency of the estimators are discussed in Otárola et al. (2019). In the present work, we address control of the maximum norm error for the variational discretization approximations of the parabolic optimal control problems (1.1)–(1.3). The state and co-state variables are approximated using the piecewise linear and continuous functions, while the control variable is computed using implicit relation between the control and co-state variables. We derive a posteriori error estimates for the state, co-state, and control variables in the $L^\infty (0,T;\,L^\infty (\varOmega ))$-norm for both the semi-discrete and fully discrete variational discretization approximations. Essential to our error analysis is the elliptic reconstruction techniques and heat kernel estimate for linear parabolic problems. The elliptic reconstruction approach was introduced earlier by Makridakis and Nochetto (2003) in the context of semi-discrete problems for parabolic equations and subsequently extend to fully discrete problems in Lakkis and Makridakis (2006). The role of elliptic reconstruction operator in a posteriori estimates is quite similar to the role played by elliptic projection introduced by Wheeler (1973) for recovering optimal order error estimate in the priori error analysis of finite-element Galerkin approximations to parabolic problems. Compared to Otárola et al. (2019), our proofs employ only basic estimate for the heat kernel and the elliptic reconstruction error. The elliptic reconstruction technique greatly simplifies our analysis by allowing the straightforward combination of heat kernel estimates with existing elliptic maximum norm error estimates. To the best of authors’ knowledge, for the first time, we report the work on $L^\infty (0,T;L^\infty (\varOmega ))$ a posteriori estimates for parabolic optimal control problems.

The paper is organized as follows. Section 2 contains some basic prerequisite materials for future use and optimal control problem. In Sect. 3, we discuss semi-discrete variational discretization approximation for optimal control problem (1.1)–(1.3) and derive a posteriori error estimates for semi-discrete problem. Section 4 is devoted to the fully discrete variational discretization approximations of optimal control problem (1.1)–(1.3) and derive a posteriori error estimates for the fully discrete problem. Numerical results are presented in Sect. 5. Finally, we present some concluding remarks in the last section.

2 Preliminaries

This section introduces notation for working function spaces to be used in the subsequent sections. Furthermore, we recall maximum norm a posteriori error estimates for elliptic problems and some properties of a Green’s function for the heat equation.

We shall adopt the standard notation $W^{m,p}(\varOmega )$ for Sobolev spaces on $\varOmega$ with norm $\Vert \cdot \Vert _{m,p,\varOmega }$ and semi-norm $|\cdot |_{m,p,\varOmega }$. When $p=2$, we denote $W^{m,p}(\varOmega )=H^m(\varOmega )$ with norm $\Vert \cdot \Vert _{m,p,\varOmega }=\Vert \cdot \Vert _{m,\varOmega }$ and semi-norm $|\cdot |_{m,p,\varOmega }=|\cdot |_{m,\varOmega }$. Let $L^r(0,T;W^{m,p}(\varOmega ))$ be the Banach space of all $L^{r}$-integrable functions from [0, T] into $W^{m,p}(\varOmega )$ with norm

$$\begin{aligned} \Vert v\Vert _{L^r(0,T;W^{m,p}(\varOmega ))}=\left( \int _0^T\Vert v\Vert _{m,p,\varOmega }^r\,\mathrm{d}s\right) ^{\frac{1}{r}},\;\;\;\;1\le p<\infty , \end{aligned}$$

and the standard modification for $p=\infty$. We denote

$$\begin{aligned} a(v,w)=\int _{\varOmega }\nabla v\nabla w\,\mathrm{d}x\;\;\;\;\forall v, w\in H^1_0(\varOmega ), \end{aligned}$$

where $H_0^1(\varOmega )=\{v\in H^1(\varOmega ): \;v=0\;\text {on}\;\partial \varOmega \}$. We assume that the bilinear form $a(\cdot ,\cdot )$ is bounded and coercive on $H^1_0(\varOmega )$, i.e., $\exists$ $\alpha _0,\,\alpha _1>0$, such that

$$\begin{aligned} |a(v,w)|\le & {} \alpha _0\Vert v\Vert _1\Vert w\Vert _1,\;\;\;\;\;\forall v,w\in H^1_0(\varOmega ),\\ \end{aligned}$$

and

$$\begin{aligned} a(v,v)\ge & {} \alpha _1\Vert v\Vert _1^2,\;\;\;\;\;\forall v\in H^1_0(\varOmega ). \end{aligned}$$

The weak form of parabolic optimal control problem (1.1)–(1.3) is defined as follows: Find a pair $(y, u)\in L^\infty (0,T;L^\infty (\varOmega ))\cap H^1(0,T;H^{-1}(\varOmega ))\times U_{ad}$, such that

$$\begin{aligned} \min _{u\in U_{ad}} J(u,y)=\min _{u\in U_{ad}} \frac{1}{2}\int _{0}^{T}\left\{ \Vert y-y_{d}\Vert ^{2}+\Vert u\Vert ^{2}\right\} \,\mathrm{d}s, \end{aligned}$$

(2.1)

subject to

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle {\left( \frac{\partial y}{\partial t},v\right) +a(y,v)=(f+u,v),\;\;\;\;\;\forall v\in H^1_0(\varOmega ),}\\ \displaystyle {y(\cdot ,0)= y_{0}(x),\;\;\;\;\;x\in \varOmega .} \end{array}\right. } \end{aligned}$$

(2.2)

Observe that $L^\infty (0,T;L^\infty (\varOmega ))\cap H^1(0,T;H^{-1}(\varOmega ))\subset C^0([0,T]; L^{\infty }(\varOmega ))$.

It is well known Lions (1971) that the convex optimal control problem (2.1)–(2.2) has a unique solution (y, u) if and only if there exists a co-state variable p, such that the triplet (y, p, u) satisfies the following optimality conditions for $t\in [0,T]$:

$$\begin{aligned} \left( \frac{\partial y}{\partial t},v\right) +a(y,v)= & {} (f+u,v),\;\;\;\;\;\forall v\in H^1_0(\varOmega ), \end{aligned}$$

(2.3)

$$\begin{aligned} y(x,0)= & {} y_{0}(x),\;\;\;\;\;x\in \varOmega , \end{aligned}$$

(2.4)

$$\begin{aligned} -\left( \frac{\partial p}{\partial t},v\right) +a(p,v)= & {} (y-y_{d},v),\;\;\;\;\;\forall v\in H^1_0(\varOmega ), \end{aligned}$$

(2.5)

$$\begin{aligned} p(x,T)= & {} 0,\;\;\;\;\;x\in \varOmega , \end{aligned}$$

(2.6)

$$\begin{aligned} \left( u+p,\hat{u}-u\right)\ge & {} 0,\;\;\;\;\;\forall \hat{u}\in U_{ad}. \end{aligned}$$

(2.7)

Let $\varPi _{[u_a,u_b]}$ be a pointwise projection on the admissible set $U_{ad}$, and defined as

$$\begin{aligned} \varPi _{[u_a,u_b]}(\chi (x,t)):=\min \left\{ u_b,\,\max \left\{ u_a,\chi (x,t)\right\} \right\} . \end{aligned}$$

Arguing as in Meyer and Rösch (2004), one can easily express the equivalent form of (2.7) as

$$\begin{aligned} u(x,t)=\varPi _{[u_a,u_b]}(-p(x,t)). \end{aligned}$$

(2.8)

We now introduce the reduced cost functional

$$\begin{aligned} j:L^\infty \left( 0,T;L^\infty (\varOmega )\right)\rightarrow & {} \mathbb {R}\\u\mapsto & {} j(u):=J(u,y(u)), \end{aligned}$$

where y(u) is the solution of (2.2). Hence, the optimal control problem (2.1)–(2.2) can be equivalently reformulated as

$$\begin{aligned} \min _{u\in U_{ad}} j(u). \end{aligned}$$

2.1 Elliptic a posteriori estimates

For $\psi \in L^{\infty }(\varOmega )$, let $\varPhi \in H^1_0(\varOmega )$ be the solution of

$$\begin{aligned} - \varDelta {\varPhi }= & {} \psi \;\;\;\; \text {in} \;\;\; \varOmega ,\\ \varPhi= & {} 0 \;\;\;\; \text {on} \;\;\; \partial {\varOmega }, \end{aligned}$$

where $\varOmega \subset \mathbb {R}^d (d=2,\,3)$ is a convex polyhedral domain. We assume that $\mathcal {T}_h$ is a shape regular simplicial decomposition of $\varOmega$, and define the finite-dimensional space $V_{h}:=\{v_h\in C(\bar{\varOmega }):\;v_h|_{K} \in \mathbb {P}_1,\;\;\forall K\in \mathcal {T}_h\}$, where $\mathbb {P}_1$ is the space of polynomials of degree$\le 1$ on K and set $V_h^0:= V_{h}\cap H^1_0(\varOmega )$. Let $\varPhi _h \in V^0_h$ be the finite-element approximation to $\varPhi$ defined by

$$\begin{aligned} \int _\varOmega \nabla \varPhi _h \nabla v_h\, \mathrm{d}x= \int _\varOmega \psi \, v_h\, \mathrm{d}x, \;\;\;\; \forall \; v_h \in V^0_h. \end{aligned}$$

For $K_1,\;K_2 \in \mathcal {T}_h$, let E be the element side or face, such that $E=K_1 \cap K_2$. We now define the jump residual across an element side E as

$$\begin{aligned} {[}[\nabla \varPhi _h]]_{E}(x):=\lim _{\epsilon \rightarrow 0}\left( \nabla \varPhi _h\left( x+\epsilon \mathbf {n}_{E}\right) -\nabla \varPhi _h\left( x-\epsilon \mathbf {n}_{E}\right) \right) \cdot \mathbf {n}_E, \end{aligned}$$

where $\mathbf {n}_E$ is a unit normal vector to E at the point x. Let $h_K$ be the diameter of the element K. For $1 \le p \le \infty$ and $j\ge 0$, we define the elementwise error indicator as

$$\begin{aligned} \Re _{p,-j}(K)=h_K^{2+j}\left\| \psi +\varDelta \varPhi _h\right\| _{L^p(K)}+h_K^{j+1+\frac{1}{p}} \left\| \left[ [\nabla \varPhi _h]\right] \right\| _{L^p(\partial K)}, \end{aligned}$$

and the global estimator as

$$\begin{aligned} \mathfrak {E}_{p,-j}\left( \varPhi _h, \psi \right) = {\left\{ \begin{array}{ll} \displaystyle {\left[ \sum _{K\in \mathcal {T}_h}\left( \Re _{p,-j}(K)\right) ^p\right] ^{1/p},\;\;\; 1\le p <\infty },\\ \displaystyle {\max _{K\in \mathcal {T}_h} \Re _{\infty ,-j}(K),\qquad \qquad \qquad p = \infty }. \end{array}\right. } \end{aligned}$$

(2.9)

We state an elliptic pointwise error estimate from (Nochetto et al. 2006).

Lemma 2.1

Let $\varOmega$ be a convex bounded polyhedral domain in $\mathbb {R}^d\; (d=2,\, 3),$ and $\bar{h}=\displaystyle {\min _{K\in \mathcal {T}_h} h_K}$. Then, the following a posteriori error estimate:

$$\begin{aligned} \Vert \varPhi - \varPhi _h\Vert _{L^{\infty }(\varOmega )} \le C_{\varOmega } \left( \ln \bar{h}\right) ^2 \mathfrak {E}_{\infty ,0}(\varPhi _h, \psi ), \end{aligned}$$

holds.

To bound some of our fully discrete a posteriori error of finite element of the form $\varPhi _1-\varPhi _2-(\varPhi _{h_1}-\varPhi _{h_2})$, where $\varPhi _{h_1}$ and $\varPhi _{h_2}$ are related to different finite element spaces defined on meshes at adjacent time steps, we recall the following results from Demlow et al. (2009).

Let $V_{h_1}^0$ and $V_{h_2}^0$ be the finite-element spaces associated on different meshes $\mathcal {T}_{h_1}$ and $\mathcal {T}_{h_2}$. Let $\varPhi _{h_1}\in V_{h_1}^0$ and $\varPhi _{h_2}\in V_{h_2}^0$ be the finite-element approximations of $\varPhi _1$ and $\varPhi _2$, respectively, and satisfy

$$\begin{aligned} - \varDelta \varPhi _1= & {} {\psi }_1, \;\;\; x \in \varOmega ,\;\; \text {and}\;\; \varPhi _1=0, \;\;\; x\in \partial \varOmega ,\\&\text {and}\\ - \varDelta \varPhi _2= & {} {\psi }_2, \;\;\; x \in \varOmega ,\;\; \text {and}\;\; \varPhi _2=0, \;\;\; x\in \partial \varOmega . \end{aligned}$$

For $1 \le p \le \infty$ and $j\ge 0$, we define the elementwise error indicator for $\hat{K}\in \mathcal {T}_{h_1}\wedge \mathcal {T}_{h_2}$ by

$$\begin{aligned} \hat{\Re }_{p,-j}\left( \hat{K}\right)&=\hat{h}_{\hat{K}}^{2+j}\left\| {\psi }_1-{\psi }_2+\varDelta \left( \varPhi _{h_1}- \varPhi _{h_2}\right) \right\| _{L^p\left( \hat{K}\right) }+\hat{h}_{\hat{K}}^{j+1+\frac{1}{p}}\Bigg \Vert \\&\quad \left[ \left[ \nabla \left( \varPhi _{h_1}-\varPhi _{h_2}\right) \right] \right] \Bigg \Vert _{L^p\left( \varSigma _{\hat{K}}\right) }, \end{aligned}$$

where $\varSigma _{\hat{K}}=(\varSigma _1 \cup \varSigma _2)\cap \hat{K}\; (\varSigma _1 \; \text {and}\; \varSigma _2$ be the collection of all edges of elements $\mathcal {T}_{h_1}$ and $\mathcal {T}_{h_2}, respectively)$ and the global estimator is defined by

$$\begin{aligned} \hat{\mathfrak {E}}_{p,-j}\left( \varPhi _{h_1}- \varPhi _{h_2}, \psi _1-\psi _2; \mathcal {T}_{h_1}, \mathcal {T}_{h_2}\right) = {\left\{ \begin{array}{ll} \displaystyle {\left[ \sum _{\hat{K}\in \mathcal {T}_{h_1}\wedge \mathcal {T}_{h_2}}\left( \hat{\Re }_{p,-j}\left( \hat{K}\right) \right) ^p\right] ^{1/p},\;\;\; 1\le p <\infty },\\ \displaystyle {\max _{\hat{K}\in \mathcal {T}_{h_1}\wedge \mathcal {T}_{h_2}} \hat{\Re }_{p,-j}\left( \hat{K}\right) ,\;\;\; p = \infty }. \end{array}\right. } \end{aligned}$$

Lemma 2.2

Let $\varOmega \subset \mathbb {R}^d\; (d=2,\,3)$ be a convex bounded polyhedral domain, and let $\mathcal {T}_{h_1}$ and $\mathcal {T}_{h_2}$ be compatible triangulations with $\hat{h}=\displaystyle {\min _{x\in \varOmega }\min \{h_1(x), h_2(x)\}}$, we have

$$\begin{aligned} \left\| \varPhi _1-\varPhi _2-\left( \varPhi _{h_1}-\varPhi _{h_2}\right) \right\| _{L^{\infty }(\varOmega )}\le C_{\varOmega }\left( \ln \hat{h}\right) ^2\hat{\mathfrak {E}}_{\infty ,0}\left( \varPhi _{h_1}- \varPhi _{h_2}, \psi _1-\psi _2; \mathcal {T}_{h_1}, \mathcal {T}_{h_2}\right) , \end{aligned}$$

where $C_{\varOmega }$ depends on the number of refinement steps used to pass from $\mathcal {T}_{h_1}$ to $\mathcal {T}_{h_2}$.

As our analysis depends heavily on the properties of the Green’s function for the heat equations, we cite the necessary results in the following two lemmas. The proof of first lemma can be found in Luskin and Rannacher (1982), and for the second lemma, we refer to Aronson (1968), Demlow et al. (2009).

Lemma 2.3

With $\varPsi \in L^2(0,T;L^2(\varOmega ))$, let $\varPhi \in L^2(0,T;H^2(\varOmega )\cap H^1_0(\varOmega ))\cap H^1(0,T;L^2(\varOmega ))$ be the solution of

$$\begin{aligned} {\varPhi }_t-\varDelta \varPhi= & {} \varPsi \;\; \mathrm{in}\;\;\varOmega _{T}, \end{aligned}$$

(2.10)

$$\begin{aligned} \varPhi (x,0)= & {} \varPhi _0 \;\; \mathrm{in} \;\; \varOmega , \end{aligned}$$

(2.11)

$$\begin{aligned} \varPhi= & {} 0 \;\;\; \mathrm{on} \;\; \varGamma _T. \end{aligned}$$

(2.12)

Moreover, we have the following a priori estimate:

$$\begin{aligned} \Vert \varPhi \Vert _{L^2\left( 0,T;H^2(\varOmega )\right) }\le C_R \left( \Vert \varPsi \Vert _{L^2(0,T;L^2(\varOmega ))}+\Vert \varPhi _0\Vert _{L^2(\varOmega )} \right) ,\end{aligned}$$

where $C_R$ is the regularity constant.

Lemma 2.4

Let $\varOmega \subset \mathbb {R}^d\; (d=2,\; 3)$ be a convex bounded polyhedral domain. Then, there exists a Green’s function $\mathfrak {F}(x,t;w,s)$ for the problem (2.10)–(2.12), i.e., there exists a kernel $\mathfrak {F}$, for $(x,t)\in \varOmega \times (0,T]$, the solution $\varPhi (x,t)$ for (2.10)–(2.12) is given by

$$\begin{aligned} \varPhi (x,t)= & {} \int _{\varOmega }\mathfrak {F}(x,t;w,0)\varPhi _0(w)\,\mathrm{d}w+\int _0^t \int _{\varOmega }\mathfrak {F}(x,t;w,s)\varPsi (w,s)\,\mathrm{d}w\,\mathrm{d}s. \end{aligned}$$

(2.13)

Moreover, $s<t$, $\mathfrak {F}$ satisfies the bound

$$\begin{aligned} \left\| \mathfrak {F}(x,t;\cdot ,s)\right\| _{L^1(\varOmega )}\le 1. \end{aligned}$$

(2.14)

3 Error analysis for semi-discrete control problem

This section is devoted to the spatially discrete optimization problem and derive a posteriori upper bounds for the state, co-state, and control variables in the $L^\infty (0,T;L^\infty (\varOmega ))$-norm.

Let $\mathcal {T}_h$ be a regular triangulation of $\varOmega$, such that $\bar{\varOmega }=\displaystyle \cup _{K \in \mathcal {T}_h} \bar{K}$, and if $K_1, K_2 \in \mathcal {T}_h$ and $K_1 \ne K_2$, then either $K_1 \cap K_2 = \emptyset$ or $K_1 \cap K_2$ share a common edge or a common vertex.

Associated with $\mathcal {T}_h$ is a finite-dimensional subspace $V_h$ of $C(\bar{\varOmega })$, such that $v|_K$ is the polynomial of degree less than or equal to 1, for all $v\in V_h$. Now, we set $V^0_h=V_h\cap H^1_0(\varOmega )$.

The semi-discrete variational discretization approximations of (2.1)–(2.2) are to seek a pair $(y_h, u_h)\in C(0,T;V^0_h)\times U_{ad}$, such that

$$\begin{aligned} \min _{u_h\in U_{ad}} J\left( u_h,y_h\right) = \min _{u_h\in U_{ad}} \frac{1}{2}\int _{0}^{T}\left\{ \Vert y_h-y_{d}\Vert ^{2}+\Vert u_h\Vert ^{2}\right\} \,\mathrm{d}s, \end{aligned}$$

(3.1)

subject to

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle {\left( \frac{\partial y_h}{\partial t},v_h\right) +a\left( y_h,v_h\right) =\left( f+u_h,v_h\right) ,\;\;\;\;\;\forall v_h\in V^0_h,}\\ \displaystyle {y_h(\cdot ,0)= y_{h,0}(x),\;\;\;\;\;x\in \varOmega ,} \end{array}\right. } \end{aligned}$$

(3.2)

where $y_{h,0}\in V^0_h$ is a suitable approximation or projection of $y_0$.

It is well known Lions (1971) that the convex optimal control problem (3.1)–(3.2) has a unique solution $(y_h, u_h)$ if and only if there exists a co-state variable $p_h \in C(0,T;V^0_h)$, such that the triplet $(y_h, p_h, u_h)$ satisfies the following optimality conditions for $t\in [0,T]$:

$$\begin{aligned} \left( \frac{\partial y_h}{\partial t},v_h\right) +a(y_h,v_h)= & {} (f+u_h,v_h),\;\;\;\;\;\forall v_h\in V^0_h, \end{aligned}$$

(3.3)

$$\begin{aligned} y_h(\cdot ,0)= & {} y_{h,0},\end{aligned}$$

(3.4)

$$\begin{aligned} -\left( \frac{\partial p_h}{\partial t},v_h\right) +a(p_h,v_h)= & {} (y_h-y_d,v_h),\;\;\;\;\;\forall v_h\in V^0_h,\end{aligned}$$

(3.5)

$$\begin{aligned} p_h(\cdot ,T)= & {} 0,\end{aligned}$$

(3.6)

$$\begin{aligned} \left( u_h+p_h,\hat{u}_h-u_h\right)\ge & {} 0,\;\;\;\;\;\forall \hat{u}_h\in U_{ad}. \end{aligned}$$

(3.7)

Similar to the continuous case, we can express (3.7) equivalently to

$$\begin{aligned} u_h(x,t)=\varPi _{[u_a,u_b]}\left( -p_h(x,t)\right) . \end{aligned}$$

(3.8)

Equation (3.8) reveals that the control variable $u_h$ is the projection of a finite-element function (approximate co-state variable) onto the admissible space $U_{ad}$.

Discrete elliptic operator: The discrete elliptic operator associated with the bilinear form $a(\cdot ,\cdot )$ and the finite-element space $V^0_h$ is the operator $- \mathcal {A}_h:H_0^1(\varOmega )\rightarrow V^0_h+\mathcal {L}_h f$, such that for $w\in H_0^1(\varOmega )$ and $t\in (0,T]$,

$$\begin{aligned} \left( -\mathcal {A}_h w,v_h\right) =a(w,v_h),\;\;\;\;\;\forall v_h\in V^0_h, \end{aligned}$$

where $\mathcal {L}_h$ be the $L^2$-projection onto the finite-element space $V_{h}$. Therefore, we have the following pointwise form of (3.3) and (3.5):

$$\begin{aligned} -\mathcal {A}_hy_h= & {} \mathcal {L}_hf+u_h-\frac{\partial y_h}{\partial t},\\ -\mathcal {A}_hp_h= & {} y_h-\mathcal {L}_hy_d+\frac{\partial p_h}{\partial t}, \end{aligned}$$

respectively.

To begin with, we first establish some intermediate error estimates for the state and co-state variables in the $L^\infty (0,T;L^{\infty }(\varOmega ))$-norm which will enable us to prove the main results of this section. This is accomplished by introducing elliptic reconstructions for the state and co-state variables. For this, we now introduce some auxiliary problems.

For $\hat{u}\in U_{ad}$, let the pair

$$\begin{aligned} \left( y(\hat{u}),p(\hat{u})\right)&\in L^\infty \left( 0,T;L^\infty (\varOmega )\right) \cap H^1\left( 0,T;H^{-1}(\varOmega )\right) \times L^\infty \left( 0,T;L^\infty (\varOmega )\right) \\&\cap H^1\left( 0,T;H^{-1}(\varOmega )\right) \end{aligned}$$

be the solutions of the following equations:

$$\begin{aligned} \left( \frac{\partial y(\hat{u})}{\partial t},v\right) +a(y(\hat{u}),v)= & {} \left( f+\hat{u},v\right) ,\;\;\;\;\;\forall v\in H^1_0(\varOmega ), \end{aligned}$$

(3.9)

$$\begin{aligned} y(\hat{u})(\cdot ,0)= & {} y_{0}(x),\;\;\;\;\;x\in \varOmega , \end{aligned}$$

(3.10)

$$\begin{aligned} -\left( \frac{\partial p(\hat{u})}{\partial t},v\right) +a\left( p(\hat{u}),v\right)= & {} v\left( y(\hat{u})-y_d,v\right) , \;\;\;\;\;\forall v\in H^1_0(\varOmega ), \end{aligned}$$

(3.11)

$$\begin{aligned} p(\hat{u})(\cdot ,T)= & {} 0,\;\;\;\;\;x\in \varOmega . \end{aligned}$$

(3.12)

Define the errors for the state and co-state variables as follows:

$$\begin{aligned} \hat{e}_y:=y_h-y\left( u_h\right) \;\; \text {and} \;\;\hat{e}_p:=p_h-p\left( u_h\right) . \end{aligned}$$

(3.13)

From (3.3)–(3.6) and (3.9)–(3.12) with $\hat{u}=u_h$, we obtain the following error equations for $v\in H^1_0(\varOmega )$:

$$\begin{aligned} \left( \frac{\partial \hat{e}_{y}}{\partial t},v\right) +a\left( \hat{e}_y,v\right)= & {} -\left( \mathcal {G}_y,v\right) +\left( \nabla y_h, \nabla v\right) , \end{aligned}$$

(3.14)

$$\begin{aligned} -\left( \frac{\partial \hat{e}_{p}}{\partial t},v\right) +a\left( \hat{e}_p,v\right)= & {} -\left( \mathcal {\tilde{G}}_p,v\right) +\left( \nabla p_h, \nabla v\right) +\left( \hat{e}_y,v\right) , \end{aligned}$$

(3.15)

where $\displaystyle {\mathcal {G}_y = f+u_h-\frac{\partial y_h}{\partial t}} \;\;\; \text {and} \;\;\;\displaystyle {\mathcal {\tilde{G}}_p =y_h-y_d+\frac{\partial p_h}{\partial t}.}$

For $t\in (0,T]$, we now define the elliptic reconstructions for the state and co-state variables as follows: for given $y_h,\;p_h$, seek $\tilde{y}\in H^1_0(\varOmega )$ and $\tilde{p}\in H^1_0(\varOmega )$, such that

$$\begin{aligned} a\left( \tilde{y},v\right)= & {} \left( \mathcal {G}_y,v\right) ,\;\;\;\;\;\forall v\in H^1_0(\varOmega ), \end{aligned}$$

(3.16)

$$\begin{aligned} a\left( \tilde{p},v\right)= & {} \left( \mathcal {\tilde{G}}_p,v\right) +\left( \tilde{y}-y_h,v\right) ,\;\;\;\;\;\forall v\in H^1_0(\varOmega ). \end{aligned}$$

(3.17)

Using elliptic reconstructions $\tilde{y}$, $\tilde{p}$, we decompose the errors as

$$\begin{aligned} \hat{e}_y=\left( \tilde{y}-y(u_h)\right) -\left( \tilde{y}-y_h\right) =:\hat{\xi }_y-\hat{\eta }_y, \end{aligned}$$

and

$$\begin{aligned} \hat{e}_p=\left( \tilde{p}-p(u_h)\right) -\left( \tilde{p}-p_h\right) =:\hat{\xi }_p-\hat{\eta }_p. \end{aligned}$$

Using (3.14)–(3.17), we obtain

$$\begin{aligned} \left( \frac{\partial \hat{\xi }_y}{\partial t},v\right) +a(\hat{\xi }_y,v)= & {} \left( \frac{\partial \hat{\eta }_y}{\partial t},v\right) ,\;\;\;\;\;\forall v\in H_0^1(\varOmega ), \end{aligned}$$

(3.18)

$$\begin{aligned} -\left( \frac{\partial \hat{\xi }_p}{\partial t},v\right) +a(\hat{\xi }_p,v)= & {} -\left( \frac{\partial \hat{\eta }_p}{\partial t},v\right) +(\hat{\xi }_y,v),\;\;\;\;\;\forall v\in H_0^1(\varOmega ). \end{aligned}$$

(3.19)

As a consequence of elliptic error estimate in Lemma 2.1, we obtain the following bounds for the elliptic reconstruction errors.

Lemma 3.1

Let $(\tilde{y}, \tilde{p})\in H^1_0(\varOmega )\times H^1_0(\varOmega )$ satisfy (3.16)–(3.17) and let Lemma 2.1 be valid. Then, for each $t\in [0,T]$, the following estimates hold:

$$\begin{aligned} \left\| \hat{\eta }_y(t)\right\| _{L^\infty (\varOmega )}\le & {} C_{\varOmega } \left( \ln \bar{h}\right) ^2 \mathfrak {E}_{\infty , 0}\left( y_h(t), \mathcal {G}_y(t) \right) , \end{aligned}$$

and

$$\begin{aligned} \left\| \hat{\eta }_p(t)\right\| _{L^\infty (\varOmega )}\le & {} C_{\varOmega } \left( \ln \bar{h}\right) ^2 \mathfrak {E}_{\infty , 0}\left( p_h(t), \mathcal {\tilde{G}}_p(t) \right) +\left\| \hat{\eta }_y(t)\right\| _{L^\infty (\varOmega )}. \end{aligned}$$

We next turn our attention to derive the bounds for $\hat{\xi }_y$ and $\hat{\xi }_p$.

Lemma 3.2

Let $\hat{\xi }_y$ and $\hat{\xi }_p$ satisfy (3.18) and (3.19), respectively. Then, for any $t\in [0, T]$, the following estimates hold true:

$$\begin{aligned} \left\| \hat{\xi }_y(t)\right\| _{L^{\infty }(\varOmega )}\le \left\| \hat{\xi }_y(0)\right\| _{L^{\infty }(\varOmega )}+c_1\left( \ln \bar{h}\right) ^2\left\| \mathfrak {E}_{\infty ,0}\left( \frac{\partial y_h}{\partial t},\frac{\partial \mathcal {G}_{y}}{\partial t}\right) \right\| _{L^1[0,T]}, \end{aligned}$$

and

$$\begin{aligned} \left\| \hat{\xi }_p(t)\right\| _{L^{\infty }(\varOmega )}\le c_2\left( \ln \bar{h}\right) ^2\left\| \mathfrak {E}_{\infty ,0}\left( \frac{\partial p_h}{\partial t},\frac{\partial \mathcal {\tilde{G}}_{p}}{\partial t}\right) \right\| _{L^1[0,T]}+\left\| \hat{\xi }_y(t)\right\| _{L^\infty (\varOmega )}, \end{aligned}$$

where $\mathfrak {E}_{\infty ,0}$ is the $L^\infty$-type residual estimator defined in (2.9). The constants $c_1$ and $c_{2}$ are positive and depend on the domain $\varOmega$.

Proof

We know that $\hat{\xi }_y$ satisfies (3.18). For any $(x,t) \in \varOmega \times (0,T]$, use of (2.13) leads to

$$\begin{aligned} \hat{\xi }_y(x,t)= \int _{\varOmega } \mathfrak {F}(x,t;w,0)\,\hat{\xi }_y(w,0)\mathrm{d}w+\int _0^{t}\int _{\varOmega } \mathfrak {F}(x,t;w,s)\,\frac{\partial \hat{\eta }_{y}}{\partial t}(w,s)\mathrm{d}w\,\mathrm{d}s. \end{aligned}$$

An application of the Hölder’s inequality yields

$$\begin{aligned} \left\| \hat{\xi }_y(t)\right\| _{L^{\infty }(\varOmega )}&\le \left\| \mathfrak {F}(x,t;w,0)\right\| _{L^1(\varOmega )}\left\| \hat{\xi }_y(0)\right\| _{L^{\infty }(\varOmega )}\\&\quad +\left\| \mathfrak {F}(x,t;w,s)\right\| _{L^1(\varOmega )}\left\| \frac{\partial \hat{\eta }_{y}}{\partial t}\right\| _{L^1\left( 0,t;L^{\infty }(\varOmega )\right) }. \end{aligned}$$

With an aid of (2.14), we have

$$\begin{aligned} \left\| \hat{\xi }_y(t)\right\| _{L^{\infty }(\varOmega )}\le \left\| \hat{\xi }_y(0)\right\| _{L^{\infty }(\varOmega )} +\left\| \frac{\partial \hat{\eta }_{y}}{\partial t}\right\| _{L^1\left( 0,t;L^{\infty }(\varOmega )\right) }, \end{aligned}$$

which combine with Lemma 2.1 to obtain

$$\begin{aligned} \left\| \hat{\xi }_y(t)\right\| _{L^{\infty }(\varOmega )}\le \left\| \hat{\xi }_y(0)\right\| _{L^{\infty }(\varOmega )}+c_1\left( \ln \bar{h}\right) ^2\left\| \mathfrak {E}_{\infty ,0}\left( \frac{\partial y_{h}}{\partial t},\frac{\partial \mathcal {G}_{y}}{\partial t}\right) \right\| _{L^1[0,t]}, \end{aligned}$$

where the constant $c_1$ depends on $\varOmega$, and this proves the first inequality. The proof of the second inequality can be treated in a similar manner using the fact that $\hat{\xi }_p(T)=0$. This completes the proof of the lemma. $\square$

Let (y, p, u) and $(y_h,p_h,u_h)$ be the solutions of (2.3)–(2.7) and (3.3)–(3.7), respectively. To derive a posteriori error bounds for the state and the co-state variables, we decompose the errors as follows:

$$\begin{aligned} y-y_h=\left( y-y(u_h)\right) +\left( y(u_h)-y_h\right) :=\hat{r}_y-\hat{e}_y, \end{aligned}$$

and

$$\begin{aligned} p-p_h=\left( p-p(u_h)\right) +\left( p(u_h)-p_h\right) :=\hat{r}_p-\hat{e}_p, \end{aligned}$$

where $\hat{r}_y=y-y(u_h)$, $\hat{r}_p=p-p(u_h)$ and $\hat{e}_y$, $\hat{e}_p$ are defined in (3.13). With the help of (2.3), (2.5), (3.9), and (3.11), we derive the following error equations for each $t\in (0, T]$:

$$\begin{aligned} \left( \frac{\partial \hat{r}_{y}}{\partial t},v\right) +a(\hat{r}_y,v)=(u-u_h,v),\;\;\; \forall v\in H^1_0(\varOmega ), \end{aligned}$$

(3.20)

and

$$\begin{aligned} -\left( \frac{\partial \hat{r}_{p}}{\partial t},v\right) +a(\hat{r}_p,v)=(\hat{r}_y,v),\;\;\; \forall v\in H^1_0(\varOmega ). \end{aligned}$$

(3.21)

In the following lemma, we derive the bounds for $\hat{r}_y$ and $\hat{r}_p$.

Lemma 3.3

Let (y, p, u) and $(y(u_h),p(u_h))$ be the solutions of (2.3)–(2.7) and (3.9)–(3.12), respectively, with $\hat{u}=u_h$. Then, the following estimates hold:

$$\begin{aligned} \left\| \hat{r}_y\right\| _{L^{\infty }\left( 0,T;L^{\infty }(\varOmega )\right) }\le C(R)\left\| u-u_h\right\| _{L^2\left( 0,T;L^{2}(\varOmega )\right) }, \end{aligned}$$

and

$$\begin{aligned} \left\| \hat{r}_p\right\| _{L^{\infty }\left( 0,T; L^{\infty }(\varOmega )\right) }\le C(R)\left\| u-u_h\right\| _{L^2\left( 0,T;L^{2}(\varOmega )\right) }, \end{aligned}$$

where C(R) depends on the regularity constant $C_R$.

Proof

Note that, for any $t \in [0,T]$

$$\begin{aligned} \left\| \hat{r}_y(t)\right\| _{L^{\infty }(\varOmega )}\le & {} \left\| \hat{r}_y\right\| _{L^2\left( 0,T;L^{\infty }(\varOmega )\right) }\\\le & {} \left\| \hat{r}_y\right\| _{L^2\left( 0,T;C\left( \bar{\varOmega }\right) \right) }. \end{aligned}$$

Using the embedding result $H^2(\varOmega )\hookrightarrow C(\bar{\varOmega })$ and Lemma 2.3, we obtain

$$\begin{aligned} \left\| \hat{r}_y(t)\right\| _{L^{\infty }(\varOmega )} \le \left\| \hat{r}_y\right\| _{L^2\left( 0,T;H^2(\varOmega )\right) }\le C(R)\Vert u-u_h\Vert _{L^2\left( 0,T;L^2(\varOmega )\right) }, \end{aligned}$$

where we have used the fact $\hat{r}_y(0)=0$, and this proves the first inequality.

Analogously, the second inequality can easily be proved for $\hat{r}_p$ using the fact $\hat{r}_p(T)=0$. This completes the rest of the proof. $\square$

The following lemma presents the a posteriori error estimate for the control variable in the $L^{2}(L^{2})$-norm.

Lemma 3.4

Let (y, p, u) and $(y_h,p_h,u_h)$ be the solutions of (2.3)–(2.7) and (3.3)–(3.7), respectively. Assume that $(u_h+p_h)|_{K}\in H^1(K)$ and there exists a positive constant C, and $\tilde{u}_h\in U_{ad}$, such that

$$\begin{aligned} \left| \int _0^T( u_h+p_h,\tilde{u}_h-u)\,\mathrm{d}s\right| \le C\int _0^T\sum _{K\in \mathcal {T}_h}h_K|u_h+p_h|_{H^1(K)}\Vert u-u_h\Vert _{L^2(K)}\,\mathrm{d}s. \end{aligned}$$

(3.22)

Then, we have

$$\begin{aligned} \Vert u-u_h\Vert _{L^2\left( 0,T;L^2(\varOmega )\right) }\le & {} \tilde{C} \Bigg [\left( \int _0^T\sum _{K\in \mathcal {T}_h}h^2_{K}|u_h +p_h|_{H^1(K)}^2\,\mathrm{ds}\right) ^{1/2}\\&+\Vert p_h-p(u_h)\Vert _{L^{2}(0,T;L^{2}(\varOmega ))}\Bigg ], \end{aligned}$$

where $\tilde{C}=\max \{1,C\}$, and $(y(\hat{u}),p(\hat{u}))$ is solution of the system (3.9)–(3.12) with $\hat{u}=u_h$.

Proof

Note that

$$\begin{aligned} \Vert u-u_h\Vert _{L^2\left( 0,T;L^2(\varOmega )\right) }^2= & {} \int _0^T \left( u-u_h, u-u_h\right) \,\mathrm{d}s\\= & {} \int _0^T \left( u, u-u_h\right) \,\mathrm{d}s- \int _0^T \left( u_h, u-u_h\right) \,\mathrm{d}s. \end{aligned}$$

Apply (2.7), and a simple calculation using (3.7) yields

$$\begin{aligned} \Vert u-u_h\Vert _{L^2\left( 0,T;L^2(\varOmega )\right) }^2\le & {} -\int _0^T \left( p, u-u_h\right) \mathrm{d}s-\int _0^T \left( u_h, u-u_h\right) \mathrm{d}s \nonumber \\= & {} -\int ^T_0\left( u_h+p_h,u-\tilde{u}_h\right) \mathrm{d}s-\int _0^T\left( u_h+p_h,\tilde{u}_h-u_h\right) \,\mathrm{d}s \nonumber \\&+\int _0^T\left( p_h-p(u_h),u-u_h\right) \,\mathrm{d}s+\int _0^T\left( p(u_h)-p,u-u_h\right) \,\mathrm{d}s \nonumber \\\le & {} \int _0^T\left( p_h-p(u_h),u-u_h\right) \,\mathrm{d}s+\int _0^T\left( p(u_h)-p,u-u_h\right) \,\mathrm{d}s \nonumber \\&+\int ^T_0\left( u_h+p_h,\tilde{u}_h-u\right) \mathrm{d}s\nonumber \\=: & {} E_1+E_2+E_3. \end{aligned}$$

(3.23)

To bound $E_1$, we use the Cauchy–Schwarz inequality and the Young’s inequality to have

$$\begin{aligned} E_1\le & {} \int _0^T \left\| p_h-p(u_h)\right\| _{L^2(\varOmega )}\Vert u-u_h\Vert _{L^2(\varOmega )}\,\mathrm{d}s\nonumber \\\le & {} \left\| p_h-p(u_h)\right\| ^2_{L^2\left( 0,T;L^2(\varOmega )\right) }+\frac{1}{4}\Vert u-u_h\Vert _{L^2\left( 0,T;L^2(\varOmega )\right) }^2. \end{aligned}$$

(3.24)

Setting $v=p(u_h)-p$ in (3.20), and integrate the resulting equation from 0 to T. Then, an integration-by-parts formula with $\hat{r}_y(0)=\hat{r}_p(T)=0$ leads to

$$\begin{aligned} \int _0^T\left( \hat{r}_y,\frac{\partial \hat{r}_{p}}{\partial t}\right) \,\mathrm{d}s-\int _0^Ta\left( \hat{r}_y,\hat{r}_p\right) \,\mathrm{d}s= & {} \int _0^T\left( u-u_h, p(u_h)-p\right) \,\mathrm{d}s. \end{aligned}$$

(3.25)

Again, choose $v=y(u_h)-y$ in (3.21) and integrate with respect to time from 0 to T to obtain

$$\begin{aligned} \int _0^T\left( \frac{\partial \hat{r}_{p}}{\partial t},\hat{r}_y\right) \,\mathrm{d}s-\int _0^T a\left( \hat{r}_p,\hat{r}_y\right) \,\mathrm{d}s= & {} \int _0^T\left( y-y(u_h),y(u_h)-y\right) \,\mathrm{d}s. \end{aligned}$$

(3.26)

Use of (3.25) and (3.26) yields

$$\begin{aligned} E_2= & {} \int _0^T \left( u-u_h, p(u_h)-p\right) \,\mathrm{d}s=\int _0^T \left( y-y(u_h), y(u_h)-y\right) \,\mathrm{d}s\nonumber \\= & {} - \int _0^T \left\| y-y(u_h)\right\| ^2_{L^2(\varOmega )}\,\mathrm{d}s\le 0. \end{aligned}$$

(3.27)

Finally, assumption (3.22) and an application of the Young’s inequality lead to the bound of $E_3$,

$$\begin{aligned} E_3\le & {} C \int _0^T \sum _{K\in \mathcal {T}_h} h_K|u_h+p_h|_{H^1(K)}\Vert u-u_h\Vert _{L^2(K)}\,\mathrm{d}s\nonumber \\\le & {} C^2\int _0^T \sum _{K\in \mathcal {T}_h} h^2_K|u_h+p_h|^2_{H^1(K)}\,\mathrm{d}s+\frac{1}{4}\Vert u-u_h\Vert ^2_{L^2\left( 0,T;L^2(\varOmega )\right) }. \end{aligned}$$

(3.28)

Altogether, (3.23), (3.24), (3.27), and (3.28) yield the desired estimates. This completes the proof. $\square$

By collecting Lemmas 3.1–3.4, we finally derive the main results for the state and co-state variables in the $L^{\infty }(L^{\infty })$-norm.

Theorem 3.5

Let (y, p, u) and $(y_h,p_h, u_h)$ be the solutions of (2.3)–(2.7) and (3.3)–(3.7), respectively. Let $f\in L^{\infty }(0,T;L^{\infty }(\varOmega )) \cap W^{1,1}(0,T;L^{\infty }(\varOmega ))$. Then, the following a posteriori error estimates hold for each $t\in (0,T]$,

$$\begin{aligned} \Vert u-u_h\Vert _{L^2(0,T;L^2(\varOmega ))}\le & {} \tilde{C}_{1} \left[ \left( \int _0^T\sum _{K\in \mathcal {T}_h}h^2_{K}|u_h+p_h|_{H^1(K)}^2\,\mathrm{d}s\right) ^{1/2}\right. \\&\left. +\left\| \hat{\xi }_y(0)\right\| _{L^{\infty }(\varOmega )}+\left\| \hat{\eta }_y(t)\right\| _{L^{\infty }(\varOmega )}+\left( \ln \bar{h}\right) ^2\right. \\&\times \left. \left\{ \left\| \mathfrak {E}_{\infty ,0}\left( \frac{\partial y_{h}}{\partial t},\frac{\partial \mathcal {G}_{y}}{\partial t}\right) \right\| _{L^1[0,T]}+\mathfrak {E}_{\infty ,0}{\left( p_h(t),\mathcal {\tilde{G}}_p(t)\right) }\right. \right. \\&\left. \left. +\left\| \mathfrak {E}_{\infty ,0}\left( \frac{\partial p_h}{\partial t}, \frac{\partial \mathcal {\tilde{G}}_p}{\partial t}\right) \right\| _{L^1[0,T]}\right\} \right] , \end{aligned}$$

where $\tilde{C}_{1}$ depends on the domain $\varOmega$ and the constant $\tilde{C}$ as defined in Lemma 3.4,

$$\begin{aligned} \Vert y-y_h\Vert _{L^{\infty }(0,T;L^{\infty }(\varOmega ))}\le & {} \Vert y_0-y_{h,0}\Vert _{L^{\infty }(\varOmega )}+\tilde{c}_1\left( \ln \bar{h}\right) ^2\Bigg [\mathfrak {E}_{\infty ,0}{(y_h(t),\mathcal {G}_y(t))} \\&+\mathfrak {E}_{\infty ,0}{(y_{h,0},\mathcal {G}_y(0))}+\left\| \mathfrak {E}_{\infty ,0}\left( \frac{\partial y_{h}}{\partial t},\frac{\partial \mathcal {G}_{y}}{\partial t}\right) \right\| _{L^1[0,T]}\Bigg ]\\&+\Vert u-u_h\Vert _{L^2(0,T;L^2(\varOmega ))},\\ \Vert p-p_h\Vert _{L^{\infty }(0,T;L^{\infty }(\varOmega ))}\le & {} \Vert y_0-y_{h,0}\Vert _{L^{\infty }(\varOmega )}+ \tilde{c}_2 \left( \ln \bar{h}\right) ^2\Bigg [\mathfrak {E}_{\infty ,0}\left( p_h(t), \mathcal {\tilde{G}}_p(t)\right) \\&+\left\| \mathfrak {E}_{\infty ,0}\left( \frac{\partial p_{h}}{\partial t},\frac{\partial \mathcal {\tilde{G}}_{p}}{\partial t}\right) \right\| _{L^1[0,T]}+\mathfrak {E}_{\infty ,0}{\left( y_{h,0},\mathcal {G}_y(0)\right) }\\&+\mathfrak {E}_{\infty , 0}\left( y_h(t), \mathcal {G}_y(t) \right) \Bigg ]+\Vert u-u_h\Vert _{L^2\left( 0,T;L^2(\varOmega )\right) }, \end{aligned}$$

where the constants $\tilde{c}_1$ and $\tilde{c}_2$ depend on the domain $\varOmega$.

Proof

The first inequality follows from Lemmas 3.1, 3.2, and 3.4.

To prove the second inequality, we decompose the error in the state variable as

$$\begin{aligned} y-y_h=(y-y(u_h))+\left( y(u_h)-\tilde{y}\right) +\left( \tilde{y}-y_h\right) =\hat{r}_y-\left( \hat{\xi }_y-\hat{\eta }_y\right) . \end{aligned}$$

For any $t \in (0,T]$, we have

$$\begin{aligned} \Vert (y-y_h)(t)\Vert _{L^{\infty }(\varOmega )}\le \Vert \hat{r}_y(t)\Vert _{L^{\infty }(\varOmega )}+\left\| \hat{\xi }_y(t)\right\| _{L^{\infty }(\varOmega )}+ \left\| \hat{\eta }_y(t)\right\| _{L^{\infty }(\varOmega )}. \end{aligned}$$

An application of Lemma 3.1 yields

$$\begin{aligned} \left\| \hat{\eta }_y(t)\right\| _{L^{\infty }(\varOmega )}\le c_3\left( \ln \bar{h}\right) ^2\mathfrak {E}_{\infty ,0}{\left( y_h(t),\mathcal {G}_y(t)\right) }. \end{aligned}$$

Using Lemma 3.2, it now follows that:

$$\begin{aligned} \left\| \hat{\xi }_y(t)\right\| _{L^{\infty }(\varOmega )}\le & {} \Vert y_0-y_{h,0}\Vert _{L^{\infty }(\varOmega )}+c_4\left( \ln \bar{h}\right) ^2\mathfrak {E}_{\infty ,0}{\left( y_{h,0},\mathcal {G}_y(0)\right) }\\&+c_1\left( \ln \bar{h}\right) ^2\left\| \mathfrak {E}_{\infty ,0}\left( \frac{\partial y_{h}}{\partial t},\frac{\partial \mathcal {G}_{y}}{\partial t}\right) \right\| _{L^1[0,t]}, \end{aligned}$$

where $c_i,\; i=1,3,4$ depend on $\varOmega$. Altogether, these estimates and Lemma 3.3 lead to the desired result, where $\tilde{c}_1=\max \{c_1, c_3, c_4\}$.

Similarly for the co-state variable, we use the triangle inequality to write

$$\begin{aligned} \Vert (p-p_h)(t)\Vert _{L^{\infty }(\varOmega )} \le \Vert \hat{r}_p(t)\Vert _{L^{\infty }(\varOmega )}+\left\| \hat{\xi }_p(t)\right\| _{L^{\infty }(\varOmega )}+\left\| \hat{\eta }_p(t)\right\| _{L^{\infty }(\varOmega )}. \end{aligned}$$

Again, using Lemmas 3.1–3.3 and a similar argument as above, we conclude that

$$\begin{aligned} \Vert (p_h-p)(t)\Vert _{L^{\infty }(\varOmega )}\le & {} c_5 \left( \ln \bar{h}\right) ^2\mathfrak {E}_{\infty ,0}\left( p_h(t), \mathcal {\tilde{G}}_p(t)\right) \\&+c_2\left( \ln \bar{h}\right) ^2\left\| \mathfrak {E}_{\infty ,0}\left( \frac{\partial p_{h}}{\partial t},\frac{\partial \mathcal {\tilde{G}}_{p}}{\partial t}\right) \right\| _{L^1[0,t]}+\Vert y_0-y_{h,0}\Vert _{L^{\infty }(\varOmega )}\\&+c_4\left( \ln \bar{h}\right) ^2\mathfrak {E}_{\infty ,0}{(y_{h,0},\mathcal {G}_y(0))}+C_{\varOmega } \left( \ln \bar{h}\right) ^2 \mathfrak {E}_{\infty , 0}(y_h(t), \mathcal {G}_y(t))\\&+\Vert u-u_h\Vert _{L^2\left( 0,T;L^2(\varOmega )\right) }, \end{aligned}$$

where the constants $c_i, \; i=2,4,5$ depend on the domain $\varOmega$ and $\tilde{c_2}=\max \{c_2, c_4, c_5, C_\varOmega \}$. This completes the proof. $\square$

Theorem 3.6

Let (y, p, u) and $(y_h,p_h, u_h)$ be the solutions of (2.3)–(2.7) and (3.3)–(3.7), respectively. Assume that all the conditions in Theorem 3.5 are valid. Then, for each $t\in (0,T],$ there exists a positive constant $\tilde{C}_2$, such that the following error estimate:

$$\begin{aligned} \Vert u-u_h\Vert _{L^{\infty }(0,T;L^{\infty }(\varOmega ))}\le & {} \tilde{C}_2\Bigg \{ \Vert y_0-y_{h,0}\Vert _{L^{\infty }(\varOmega )}+ \left( \ln \bar{h}\right) ^2\Bigg [\mathfrak {E}_{\infty ,0}{(y_{h,0},G_y(0))}\\&+\mathfrak {E}_{\infty ,0}{(y_h(t),G_y(t))}+\mathfrak {E}_{\infty ,0}(p_h(t), \mathcal {\tilde{G}}_p(t))\\&+\left\| \mathfrak {E}_{\infty ,0}\left( \frac{\partial y_{h}}{\partial t},\frac{\partial \mathcal {G}_{y}}{\partial t}\right) \right\| _{L^1[0,T]}+\Vert \mathfrak {E}_{\infty ,0}(\frac{\partial p_{h}}{\partial t},\frac{\partial \mathcal {\tilde{G}}_{p}}{\partial t})\Vert _{L^1[0,T]}\Bigg ]\\&+\left( \int _0^T\sum _{K\in \mathcal {T}_h}h^2_{K}|u_h+p_h|_{H^1(K)}^2\,\mathrm{d}s\right) ^{1/2}\Bigg \}, \end{aligned}$$

holds, where the constant $\tilde{C}_2$ depends on the domain $\varOmega$, the regularity constant $C_R$, and the constant $\tilde{C}_1$ as defined in Lemma 3.5.

Proof

From (2.8) and (3.8), we obtain

$$\begin{aligned} \Vert u-u_h\Vert _{L^{\infty }(0,T;L^{\infty }(\varOmega ))}= & {} \Vert \varPi _{[u_a,u_b]}(-p)-\varPi _{[u_a,u_b]}(-p_h)\Vert _{L^{\infty }(0,T;L^{\infty }(\varOmega ))}\\\le & {} \Vert p_h-p\Vert _{L^{\infty }(0,T;L^{\infty }(\varOmega ))}, \end{aligned}$$

where we have used the Lipschitz continuity of $\varPi _{[u_a,u_b]}$ with Lipschitz constant 1. An application of Lemma 3.1 and Theorem 3.5 completes the rest of the proof. $\square$

4 Error analysis for fully discrete control problem

This section describes the fully discrete variational discretization approximations of parabolic optimal control problem (3.1)–(3.2). Let  $0=t_0< t_1<\cdots <t_N=T$, be a partition of [0, T] with $I_n=(t_{n-1},t_n]$ and $k_n:=t_n-t_{n-1}$. Let $\mathcal {T}_n:=\{K\}\,(0\le n\le N)$ be the triangulation of $\bar{\varOmega }$ at the time level $t_n$. We assume that $\mathcal {T}_n$ satisfies the following conditions:

(1) If $K_1,K_2\in \mathcal {T}_n$ and $K_1\ne K_2$, then either $K_1\cap K_2=\emptyset$ or $K_1\cap K_2$ share a common edge or a common vertex.

(2) Two simplicial decompositions $\mathcal {T}_{n-1}$ and $\mathcal {T}_{n}$ of $\overline{\varOmega }$ are said to be compatible if they are derived from the same macro-triangulation $\mathcal {T}=\mathcal {T}_0$ by an admissible refinement procedure which preserves the shape regularity (Brenner and Scott 2008) and assures that for any elements $K\in \mathcal {T}_{n-1}$ and $K'\in \mathcal {T}_{n}$, either $K\cap K'=\emptyset$, $K\subset K'$, or $K'\subset K$. There is a natural partial ordering on a set of compatible triangulations namely $\mathcal {T}_{n-1}\le \mathcal {T}_{n}$ if $\mathcal {T}_n$ is a refinement of $\mathcal {T}_{n-1}$. Then, for a given pair of successive compatible triangulations $\mathcal {T}_{n-1}$ and $\mathcal {T}_n$, we define naturally the finest common coarsening $\hat{\mathcal {T}_{n}}:=\mathcal {T}_n\wedge \mathcal {T}_{n-1}$ with local mesh sizes are given by $\displaystyle {\hat{h}_n:=\max \{h_{n-1},h_n\}}$. These conditions allow us to bound the elliptic errors which lie in two adjacent finite-element spaces, see Lakkis and Makridakis (2006).

We shall also need the following notation for future use. For $0\le n\le N$, let $\mathcal {E}_n:=\{E\}$ be the set of all edges of the triangles $K\in \mathcal {T}_n$ which do not lie on $\partial \varOmega$, and $\varSigma _n:=\cup _{E \in \mathcal {E}_n}E$. Furthermore, we will also use the sets $\hat{\varSigma }_n:=\varSigma _n\cap \varSigma _{n-1}$ and $\check{\varSigma }_n:=\varSigma _n\cup \varSigma _{n-1}$.

For each $n=0,\ldots ,N$, we consider the finite-element spaces $V^n$ corresponding to the triangulation $\mathcal {T}_n$ as follows:

$$\begin{aligned} V^n:= & {} \left\{ \chi \in C\left( \overline{\varOmega }\right) :\;\chi |_{K}\in \mathbb {P}_1(K),\;\;\;\;\forall K\in \mathcal {T}_n\right\} , \end{aligned}$$

where $\mathbb {P}_1(K)$ is the space of polynomials of degree less than or equal to 1 on K. Set $V_0^n=V^n\cap H^1_0(\varOmega )$.

For the purpose of fully discrete approximation, we need the following notation:

$$\begin{aligned} \phi ^n:=\phi (\cdot ,t_n),\;\; \bar{\partial }\phi ^n:=\frac{1}{k_n}(\phi ^n-\phi ^{n-1}) \;\;\text {and} \;\; \mathcal {L}_h^n\left( \bar{\partial } \phi ^n\right) :=\frac{1}{k_n}\left( \phi ^n-\mathcal {L}_h^n\phi ^{n-1}\right) , \end{aligned}$$

where $\mathcal {L}^n_h$ is the $L^2$-projection from $L^2(\varOmega )$ to $V^n$.

Representation of the bilinear form: For a function $v\in V^n_0\,(0\le n\le N)$, the bilinear form a(v, w) can be represented as

$$\begin{aligned} a(v,w)=\sum _{K\in \mathcal {T}_n}<-\mathrm{div}(\nabla v),w>_K+\sum _{E\in \mathcal {E}_n}<J_1[v],w>_E,\;\;\;\;\;\forall w\in H^1_0(\varOmega ), \end{aligned}$$

where $J_1[v]$ denotes the spatial jump of the field $\nabla v$ across an element side $E\in \mathcal {E}_n$ defined as

$$\begin{aligned} J_1[v]|_E(x):=\lim _{\epsilon \rightarrow 0}\left( \nabla v\left( x+\epsilon \mathbf {n}_{E}\right) -\nabla v\left( x-\epsilon \mathbf {n}_{E}\right) \right) \cdot \mathbf {n}_E, \end{aligned}$$

where $\mathbf {n}_E$ is a unit normal vector to E at the point x.

Let $\mathcal {L}^n_h$ and $\mathcal {L}^n_{h,0}$ be the $L^2$-projections onto $V^n$ and $V_0^n$, such that

$$\begin{aligned} \left( \mathcal {L}_h^n \phi ,\psi _n\right) =(\phi , \psi _n)\;\;\;\; \forall \;\psi _n \in V^n \;\;\; \text {and} \;\;\; \left( \mathcal {L}_{h,0}^n \phi ,\psi _n\right) =(\phi , \psi _n)\;\;\;\; \forall \;\psi _n \in V_0^n. \end{aligned}$$

Discrete elliptic operator: The discrete elliptic operator associated with the bilinear form $a(\cdot ,\cdot )$ and the finite element space $V^n_0$ is the operator $\mathcal {A}_h^n:H_0^1(\varOmega )\rightarrow V^n_0+\mathcal {L}^n_h f^n$, such that for $v\in H_0^1(\varOmega )$ and $0\le n\le N$,

$$\begin{aligned} \left( -\mathcal {A}_h^n v,w_h\right) =a\left( v,w_h\right) ,\;\;\;\;\;\forall w_h\in V^n_0. \end{aligned}$$

The fully discrete variational discretization approximations of the problem (2.1)–(2.2) are defined as follows: Find $(y_h^n, u_h^n)\in V^n_0 \times U_{ad}$, for $n\in [1:N]$, such that

$$\begin{aligned} \min _{u_h^n\in U_{ad}}\frac{1}{2}\sum _{n=1}^N\int _{I_n}\left\{ \left\| y_h^n-y_d^n\right\| ^2_{L^2(\varOmega )} +\left\| u_h^n\right\| ^2_{L^2(\varOmega )}\right\} \,\mathrm{d}s, \end{aligned}$$

(4.1)

subject to

$$\begin{aligned} {\left\{ \begin{array}{ll} \left( \bar{\partial }y_h^n,v_h\right) +a\left( y_h^n,v_h\right) =\left( f^n+u_h^n,v_h\right) ,\;\;\;\;\;\forall v_h\in V^n_0,\\ y_h^0=y_{h,0}, \end{array}\right. } \end{aligned}$$

(4.2)

where $y_{h,0}$ is the suitable approximation or projection of $y_0$ in $V_0^0$.

The optimal control problem (4.1)–(4.2) admits a unique solution $(y_h^n, u_h^n)$ if and only if there exists a co-state $p_h^{n-1}\in V^n_0$, such that the following optimality conditions are satisfied: For each $n\in [1:N]$,

$$\begin{aligned} \left( \bar{\partial }y_h^n,v_h\right) +a\left( y_h^n,v_h\right)= & {} \left( f^n+u_h^n,v_h\right) ,\;\;\;\;\;\forall v_h\in V^n_0, \end{aligned}$$

(4.3)

$$\begin{aligned} y_h^0= & {} y_{h,0}, \end{aligned}$$

(4.4)

$$\begin{aligned} -\left( \bar{\partial }p_h^n,v_h\right) +a\left( p_h^{n-1},v_h\right)= & {} \left( y_h^n-y_d^n,v_h\right) ,\;\;\;\;\;\forall v_h\in V^n_0, \end{aligned}$$

(4.5)

$$\begin{aligned} p_h^N= & {} 0, \end{aligned}$$

(4.6)

$$\begin{aligned} \left( u_h^n+p_h^{n-1},\hat{u}_h^n-u_h^n\right)\ge & {} 0,\;\;\;\;\;\forall \hat{u}_h^n\in U_{ad}. \end{aligned}$$

(4.7)

Given a sequence of discrete values $\{y_h^n\}$,  $n=0,1,\ldots ,N$, we associate a continuous function of time defined by the continuous piecewise linear interpolant $Y_h(t)$, $t\in I_n$ as

$$\begin{aligned} Y_h(t):=\frac{(t_n-t)}{k_n}y_h^{n-1}+\frac{\left( t-t_{n-1}\right) }{k_n}y_h^n. \end{aligned}$$

Similarly, we define $P_h(t)$, $t\in I_n$, from the set of values $\{p_h^n\},\;n=0,1,\ldots ,N$ as

$$\begin{aligned} P_h(t):=\frac{(t_n-t)}{k_n}p_h^{n-1}+\frac{(t-t_{n-1})}{k_n}p_h^n, \end{aligned}$$

and

$$\begin{aligned} U_h(t)|_{I_n}:=u_h^n. \end{aligned}$$

Finally, we define $Y^n_{h,t}=\frac{\partial }{\partial t}Y_h|_{I_n}$ and $P^n_{h,t}=\frac{\partial }{\partial t}P_h|_{I_n}$. Furthermore, we note that the values of $Y_h(t)$ and $P_h(t)$ at the nodal point $t=t_n,\, n=1,\,2,\ldots ,N$ are coincided with $y_h^n$ and $p_h^n$, respectively.

The weak form of fully discrete schemes (4.3) and (4.5) can be easily transformed into the pointwise form as

$$\begin{aligned} \frac{y^n_h-\mathcal {L}^n_{h,0}y^{n-1}_h}{k_n}-\mathcal {A}_h^ny^n_h= & {} \mathcal {L}^n_h f^n+U_h,\\ -\frac{p^n_h-\mathcal {L}^n_{h,0}p^{n-1}_h}{k_n} -\mathcal {A}_h^np^{n-1}_h= & {} y^n_h-\mathcal {L}^n_h y_d^n. \end{aligned}$$

This implies that

$$\begin{aligned} Y^n_{h,t}-\mathcal {A}_h^ny^n_h= & {} \mathcal {L}^n_h f^n+U_h+\frac{\mathcal {L}^n_{h,0}y^{n-1}_h-y^{n-1}_h}{k_n},\;\;n\ge 1, \end{aligned}$$

(4.8)

$$\begin{aligned} -P^n_{h,t}-\mathcal {A}_h^np^{n-1}_h= & {} y^n_h-\mathcal {L}^n_h y_d^n-\frac{\mathcal {L}^n_{h,0}p^{n-1}_h-p^{n-1}_h}{k_n}\;\;n\ge 1. \end{aligned}$$

(4.9)

Then, the optimality conditions (4.3)–(4.7) can be stated as follows:

$$\begin{aligned} \left( \bar{\partial }Y_h^n,v_h\right) +a\left( Y_h^n,v_h\right)= & {} \left( f^n+U_h,v_h\right) ,\;\;\;\;\;\forall v_h\in V^n_o, \end{aligned}$$

(4.10)

$$\begin{aligned} Y_h^0= & {} y_{h,0},\end{aligned}$$

(4.11)

$$\begin{aligned} -\left( \bar{\partial }P_h^n,v_h\right) +a\left( P_h^{n-1},v_h\right)= & {} \left( Y_h^n-y_d^n,v_h\right) ,\;\;\;\;\;\forall v_h\in V^n_0,\end{aligned}$$

(4.12)

$$\begin{aligned} P_h^N= & {} 0,\end{aligned}$$

(4.13)

$$\begin{aligned} \left( U_h+P_h^{n-1},\hat{u}_h^n-U_h\right)\ge & {} 0,\;\;\;\;\;\forall \hat{u}_h^n\in U_{ad}. \end{aligned}$$

(4.14)

Analogous to the continuous case, we reformulate the discrete optimal control problem (4.1)–(4.2) as

$$\begin{aligned} \min _{U_h\in U_{ad}}j^n_h(U_h):=J\left( U_h,Y_h(U_h)\right) . \end{aligned}$$

Analogous to the semi-discrete error analysis, we first derive some intermediate error estimates for the state and co-state variables in the $L^\infty (L^{\infty })$-norm. Here, the fully discrete analogues of elliptic reconstructions for the state and co-state variables are treated as intermediate objects in the error analysis.

For the purpose of error analysis, we shall define the errors for the state and co-state variables as follows:

$$\begin{aligned} e_y:=Y_h-y(U_h)\;\; \text {and}\;\;e_p:=P_h-p(U_h). \end{aligned}$$

From (3.9), (3.11), (4.10), and (4.12) with $\hat{u}=U_h$, we have the following error equations for $v\in H^1_0(\varOmega )$:

$$\begin{aligned} \left( \frac{\partial e_{y}}{\partial t},v\right) +a\left( e_y,v\right)&=-{\omega }_y^n(v)+a\left( Y_h-y_h^n,v\right) +\left( f^n-f,v\right) , \end{aligned}$$

(4.15)

$$\begin{aligned} -\left( \frac{\partial e_{p}}{\partial t},v\right) +a\left( e_p,v\right)&={\omega }_p^n(v)+a\left( P_h-p_h^{n-1},v\right) +\left( y^n_h-y(U_h),v\right) +\left( y_d-y_d^n,v\right) , \end{aligned}$$

(4.16)

where

$$\begin{aligned} {\omega }_y^n(v)&:=\left( f^n-\mathcal {L}^n_hf^n, v\right) +\left( \frac{y^{n-1}_h-\mathcal {L}_{h,0}^ny^{n-1}_h}{k_n}, v\right) ,\\ {\omega }_p^n(v)&:=\left( y^n_d-\mathcal {L}_h^ny_d^n,v\right) +\left( \frac{p^{n-1}_h-\mathcal {L}_{h,0}^np^{n-1}_h}{k_n}, v\right) . \end{aligned}$$

We now define the elliptic reconstructions at $t=t_n$, $n\in [1:N]$ as follows: For given $y_h^n,\;p_h^{n-1}$, seek $\tilde{y}_h^n,\; \tilde{p}_h^{n-1}\in H^1_0(\varOmega )$ satisfying

$$\begin{aligned} a\left( \tilde{y}_h^n,v\right)= & {} \left( \mathcal {G}_y^n,v\right) ,\;\; \forall v\in H^1_0(\varOmega ), \end{aligned}$$

(4.17)

and

$$\begin{aligned} a\left( \tilde{p}_h^{n-1},v\right)= & {} \left( \mathcal {\tilde{G}}_p^n,v\right) +\left( \tilde{y}_h^n-y_h^n,v\right) ,\;\;\;\;\;\forall v\in H^1_0(\varOmega ), \end{aligned}$$

(4.18)

where

$$\begin{aligned} \mathcal {G}_y^n= {\left\{ \begin{array}{ll} -\mathcal {A}^0_hy^0_h+f^0-\mathcal {L}^0_hf^0,\;\;\; n=0,\\ f^n+U_h-Y^n_{h,t},\;\;\; \;\;\;\;\;\;\;\;\;n\ge 1, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \mathcal {\tilde{G}}_p^n= {\left\{ \begin{array}{ll} -\mathcal {A}^0_hp^0_h+y_d^0-\mathcal {L}^0_hy_d^0,\;\;\; n=0,\\ y_h^n-y_d^n+P^n_{h,t},\;\;\;\;\;\;\;\;\;\;\; \;n\ge 1. \end{array}\right. } \end{aligned}$$

Using a sequence of discrete values $\{\tilde{y}_h^n\}$ for $n=0,1,\ldots ,N$, we set a continuous function of time defined by piecewise linear interpolant $\tilde{y}(t)$ as

$$\begin{aligned} \tilde{y}(t):=\frac{(t_n-t)}{k_n}\tilde{y}_h^{n-1}+\frac{(t-t_{n-1})}{k_n}\tilde{y}_h^n,\;\;\;\;\;t_{n-1}\le t\le t_n,\;\;n=1,\ldots , N. \end{aligned}$$

Similarly, we define $\tilde{p}(t)$ from the set of values $\{\tilde{p}_h^n\}$, $n=1,\ldots ,N$ as

$$\begin{aligned} \tilde{p}(t):=\frac{(t_n-t)}{k_n}\tilde{p}_h^{n-1}+\frac{(t-t_{n-1})}{k_n}\tilde{p}_h^n,\;\;\;\;\;t_{n-1}\le t\le t_n,\;\;n=1,\ldots , N. \end{aligned}$$

We note that functions $\tilde{y}$ and $\tilde{p}$ satisfy, for each $t\in [0,T]$, the following equations:

$$\begin{aligned} a\left( \tilde{y}-Y_h,v\right)= & {} \omega _y(v),\;\;\;\;\;\forall v\in H_0^1(\varOmega ),\\ a\left( \tilde{p}-P_h,v\right)= & {} -\omega _p(v)+\left( \tilde{y}-Y_h,v\right) ,\;\;\;\;\;\forall v\in H^1_0(\varOmega ). \end{aligned}$$

From (4.8) and (4.9), we obtain

$$\begin{aligned} \mathcal {G}^n_y= & {} f^n+U_h-Y^n_{h,t}=-\mathcal {A}_h^ny^n_h+f^n-\mathcal {L}^n_h f^n-\frac{\mathcal {L}^n_{h,0}y^{n-1}_h-y^{n-1}_h}{k_n},\;\;n\ge \\ \mathcal {\tilde{G}}^n_p= & {} y^n_h-y^n_d+P^n_{h,t}=-\mathcal {A}_h^np^{n-1}_h+\mathcal {L}^n_h y_d^n-y^n_d+\frac{\mathcal {L}^n_{h,0}p^{n-1}_h-p^{n-1}_h}{k_n}\;\;n\ge 1. \end{aligned}$$

Using elliptic reconstruction, we decompose the errors as

$$\begin{aligned} e_y=\left( \tilde{y}-y(U_h)\right) -(\tilde{y}-Y_h)=:\xi _y-\eta _y, \;\;\text {and} \;\; e_p=(\tilde{p}-p(U_h))-(\tilde{p}-P_h)=:\xi _p-\eta _p. \end{aligned}$$

Note that

$$\begin{aligned} \tilde{y}-\tilde{y}_h^n:=-\left( 1-l(t)\right) \left( \tilde{y}_h^n-\tilde{y}_h^{n-1}\right) \;\;\text {and}\;\; \tilde{p}-\tilde{p}_h^{n-1}:=l(t)\left( \tilde{p}_h^n-\tilde{p}_h^{n-1}\right) , \end{aligned}$$

where $l(t)=\frac{t-t_{n-1}}{k_n}$. Using (4.17)–(4.18) in (4.15)–(4.16), we obtain

$$\begin{aligned} \left( \frac{\partial \xi _{y}}{\partial t},v\right) +a(\xi _y,v)= & {} \left( \frac{\partial \eta _{y}}{\partial t},v\right) +\left( f^n-f,v\right) \nonumber \\&+(1-l(t))\left( \mathcal {G}_y^{n-1}-\mathcal {G}_y^n,v\right) ,\;\;\;\forall v\in H_0^1(\varOmega ), \end{aligned}$$

(4.19)

$$\begin{aligned} -\left( \frac{\partial \xi _{p}}{\partial t},v\right) +a\left( \xi _p,v\right)= & {} -\left( \frac{\partial \eta _{p}}{\partial t},v\right) +\left( y_d-y_d^n,v\right) +\left( \tilde{y}_h^n-y(U_h),v\right) \nonumber \\&+l(t)\left( \mathcal {\tilde{G}}_p^{n}-\mathcal {\tilde{G}}_p^{n+1},v\right) ,\;\;\;\forall v\in H_0^1(\varOmega ). \end{aligned}$$

(4.20)

Now, we state the following lemma for elliptic error bounds in $L^{\infty }(L^{\infty })$-norm.

Lemma 4.1

Let $(\tilde{y}_h^n,\tilde{p}_h^{n-1})\in H^1_0(\varOmega )\times H^1_0(\varOmega )$ satisfy (4.17)–(4.18). Then, $0\le n\le N$, we have

$$\begin{aligned} \left\| \tilde{y}_h^n-y_h^n\right\| _{L^\infty (\varOmega )} \le C(\varOmega )\left( \ln \hat{h}_n\right) ^2\mathfrak {E}_{\infty ,0}{\left( y_h^n,\mathcal {G}^n_y\right) } . \end{aligned}$$

Moreover, for $n\in [1:N]$, we have

$$\begin{aligned} \left\| \tilde{p}_h^{n-1}-p_h^{n-1}\right\| _{L^\infty (\varOmega )} \le C(\varOmega )\left( \ln \hat{h}_n\right) ^2 \mathfrak {E}_{\infty ,0}{\left( p_h^{n-1},\mathcal {\tilde{G}}^{n}_p\right) } +\left\| \tilde{y}_h^n-y_h^n\right\| _{L^\infty (\varOmega )}, \end{aligned}$$

where $C(\varOmega )$ is a positive constant depend on $\varOmega$.

In the following lemma, we derive the bounds for $\xi _y$ and $\xi _p$.

Lemma 4.2

Let $\xi _y$ and $\xi _p$ satisfy (4.19) and (4.20), respectively. Then, for any $1\le m \le N$ with $\displaystyle {\hat{h}_m=\min _{1\le n\le m}\min _{K \in \mathcal {T}_n}h_K}$, the following estimates hold:

$$\begin{aligned} \Vert \xi _y(t_m)\Vert _{L^{\infty }(\varOmega )}\le & {} \Vert \xi _y(0)\Vert _{L^{\infty }(\varOmega )}+c_6 \left( \ln \hat{h}_m\right) ^2\sum _{n=1}^mk_n\mathfrak {\hat{E}}_{\infty ,0}\Bigg (\frac{y_h^n-y^{n-1}_h}{k_n}, \mathcal {G}_y^n\nonumber \\&-\mathcal {G}_y^{n-1}; \mathcal {T}_{n-1},\mathcal {T}_n\Bigg )+\sum _{n=1}^m\int _{I_n}\Vert f^n-f\Vert _{L^{\infty }(\varOmega )}\,\mathrm{d}s\nonumber \\&+\frac{k_n}{2}\left\| \mathcal {G}_y^{n-1}-\mathcal {G}_y^n\right\| _{L^{\infty }(\varOmega )}, \end{aligned}$$

(4.21)

and

$$\begin{aligned} \Vert \xi _p(t_m)\Vert _{L^{\infty }(\varOmega )}&\le c_7\left( \ln \hat{h}_m\right) ^2\sum _{n=1}^m k_n \mathfrak {\hat{E}}_{\infty ,0}\left( \frac{p_h^{n-1}-p_h^n}{k_n}, \mathcal {\tilde{G}}_p^{n}-\mathcal {\tilde{G}}_p^{n+1}; \mathcal {T}_{n-1}, \mathcal {T}_n\right) \nonumber \\&\quad +\sum _{n=1}^m\int _{I_n}\left\| y_d-y_d^n\right\| _{L^{\infty }(\varOmega )} +\frac{k_n}{2}\left\| \mathcal {\tilde{G}}_p^{n}-\mathcal {\tilde{G}}_p^{n+1} \right\| _{L^{\infty }(\varOmega )}+\Vert \xi _y(t_m)\Vert _{L^{\infty }(\varOmega )}. \end{aligned}$$

(4.22)

In the above, the constants $c_6$ and $c_7$ are positive and depend on the domain $\varOmega$.

Proof

Note that $\xi _y$ satisfies (4.19), for any $t_m\in [0,T]$, a fix point $x_m\in \varOmega$, and an application of (2.13) leads to

$$\begin{aligned} |\xi _y(x_m,t_m)|\le & {} \int _{\varOmega } \left| \mathfrak {F}(x_m,t_m;w,0)\,\xi _y(w,0)\right| \mathrm{d}w\\&+\int _0^{t_m}\int _{\varOmega } \left| \mathfrak {F}(x_m,t_m;w,s)\,\frac{\partial \eta _y}{\partial t}(w,s)\right| \,\mathrm{d}w\,\mathrm{d}s\\&+\sum _{n=1}^m\int _{I_n}\int _{\varOmega } \left| \mathfrak {F}(x_m,t_m;w,s)\,(f^n-f)\right| \, \mathrm{d}w\,\mathrm{d}s\\&+\sum _{n=1}^m\int _{I_n}\int _{\varOmega } \left| \mathfrak {F}(x_m,t_m;w,s)\,(1-l(s))(\mathcal {G}_y^{n-1}-\mathcal {G}_y^n)\right| \,\mathrm{d}w\,\mathrm{d}s; \end{aligned}$$

using the Hölder’s inequality and (2.14) with $|\xi _y(x_m,t_m)|=\Vert \xi _y(t_m)\Vert _{L^{\infty }(\varOmega )}$(since $x_m$ is fixed), we obtain

$$\begin{aligned} \Vert \xi _y(t_m)\Vert _{L^{\infty }(\varOmega )}\le & {} \Vert \xi _y(0)\Vert _{L^{\infty }(\varOmega )}+\left\| \frac{\partial \eta _y}{\partial t}\right\| _{L^1([0,t_m];L^{\infty }(\varOmega ))}+\sum _{n=1}^m\int _{I_n}\Vert f^n-f\Vert _{L^{\infty }(\varOmega )}\,\mathrm{d}s\\&+\frac{k_n}{2}\left\| \mathcal {G}_y^{n-1}-\mathcal {G}_y^n\right\| _{L^{\infty }(\varOmega )}. \end{aligned}$$

Use of Lemma 2.2 leads to

$$\begin{aligned} \Vert \xi _y(t_m)\Vert _{L^{\infty }(\varOmega )}\le & {} \Vert \xi _y(0)\Vert _{L^{\infty }(\varOmega )}+c_6 \left( \ln \hat{h}_m\right) ^2\sum _{n=1}^mk_n\mathfrak {\hat{E}_{\infty ,0}}\Bigg (\frac{y_h^n-y^{n-1}_h}{k_n}, \mathcal {G}_y^n\\&-\mathcal {G}_y^{n-1}; \mathcal {T}_{n-1},\mathcal {T}_n\Bigg )+\sum _{n=1}^m\int _{I_n}\Vert f^n-f\Vert _{L^{\infty }(\varOmega )}\,\mathrm{d}s\\&+\frac{k_n}{2}\left\| \mathcal {G}_y^{n-1}-\mathcal {G}_y^n\right\| _{L^{\infty }(\varOmega )}, \end{aligned}$$

and this completes the proof of (4.21).

To prove (4.22), we first note that $\xi _p$ satisfies (4.20). For any $t_m\in [0,T]$ and fix point $x_m \in \varOmega$, a similar argument as before leads to

$$\begin{aligned} |\xi _p(x_m,t_m)|\le & {} \int _{\varOmega }\left| \mathfrak {F}(x_m,t_m;w,T)\,\xi _p(w,T)\right| \mathrm{d}w\\&+\int _{t_m}^T\int _{\varOmega } \left| \mathfrak {F}(x_m,t_m;w,s)\,\frac{\partial \eta _p}{\partial t}(w,s)\right| \mathrm{d}w\,\mathrm{d}s\\&+\sum _{n=1}^m\int _{I_n}\int _{\varOmega }\left| \mathfrak {F}(x_m,t_m;w,s)\,\left( y_d-y_d^n\right) \mathrm{d}w\right| \,\mathrm{d}s\\&+\sum _{n=1}^m\int _{I_n}\int _{\varOmega } \left| \mathfrak {F}(x_m,t_m;w,s)\,\left( \tilde{y}_h^n-y(U_h)\right) \right| \mathrm{d}w\,\mathrm{d}s\\&+\sum _{n=1}^m\int _{I_n}\int _{\varOmega } \left| \mathfrak {F}(x_m,t_m;w,s)\,l(s)\left( \mathcal {\tilde{G}}_p^{n} -\mathcal {\tilde{G}}_p^{n+1}\right) \right| \,\mathrm{d}w\,\mathrm{d}s. \end{aligned}$$

An application of the Hölder’s inequality and (2.14) with $|\xi _p(x_m,t_m)|=\Vert \xi _p(t_m)\Vert _{L^{\infty }(\varOmega )}$ yields

$$\begin{aligned} \Vert \xi _p(t_m)\Vert _{L^{\infty }(\varOmega )}\le & {} \Vert \xi _p(T)\Vert _{L^{\infty }(\varOmega )}+\left\| \frac{\partial \eta _p}{\partial t}\right\| _{L^1([t_m,T];L^{\infty }(\varOmega ))}+\sum _{n=1}^m\int _{I_n}\Vert y_d-y_d^n \Vert _{L^{\infty }(\varOmega )}\mathrm{d}s\\&+\sum _{n=1}^m\int _{I_n}\Vert \tilde{y}_h^n-y(U_h)\Vert _{L^{\infty }(\varOmega )}\mathrm{d}s +\frac{k_n}{2}\left\| \mathcal {\tilde{G}}_p^{n}-\mathcal {\tilde{G}}_p^{n+1}\right\| _{L^{\infty }(\varOmega )}. \end{aligned}$$

An application of Lemma 2.2 and $\xi _p(T)=0$ imply

$$\begin{aligned} \Vert \xi _p(t_m)\Vert _{L^{\infty }(\varOmega )}\le & {} c_7\left( \ln \hat{h}_m\right) ^2\sum _{n=1}^m k_n \mathfrak {\hat{E}}_{\infty ,0}\left( \frac{p_h^{n-1}-p_h^n}{k_n}, \mathcal {\tilde{G}}_p^{n}-\mathcal {\tilde{G}}_p^{n+1}; \mathcal {T}_{n-1}, \mathcal {T}_n\right) \\&+\sum _{n=1}^m\int _{I_n}\left\| y_d-y_d^n\right\| _{L^{\infty }(\varOmega )}\mathrm{d}s +\frac{k_n}{2}\left\| \mathcal {\tilde{G}}_p^{n}-\mathcal {\tilde{G}}_p^{n+1} \right\| _{L^{\infty }(\varOmega )}+\Vert \xi _y(t_m)\Vert _{L^\infty (\varOmega )}, \end{aligned}$$

which completes the rest of the proof. $\square$

Let (y, p, u) and $(Y_h, P_h, U_h)$ be the solutions of (2.3)–(2.7) and (4.10)–(4.14), respectively. To derive a posteriori error bounds for the state and co-state variables, we decompose the errors as follows:

$$\begin{aligned} y-Y_h= & {} (y-y(U_h))+(y(U_h)-Y_h)=:r_y-e_y,\\ p-P_h= & {} (p-p(U_h))+(p(U_h)-P_h)=:r_p-e_p. \end{aligned}$$

From (2.3), (2.5), (3.9), and (3.11) with $\hat{u}=U_h$, we derive the following error equations:

$$\begin{aligned} \left( \frac{\partial r_y}{\partial t},v\right) +a(r_y,v)= & {} (u-U_h,v), \;\;\;\;\;\forall v\in H_0^1(\varOmega ), \end{aligned}$$

(4.23)

$$\begin{aligned} -\left( \frac{\partial r_p}{\partial t},v\right) +a(r_p,v)= & {} (r_y,v), \;\;\;\;\;\forall v\in H_0^1(\varOmega ). \end{aligned}$$

(4.24)

The following lemma provides the bounds for $r_y$ and $r_p$.

Lemma 4.3

Let (y, p, u) and $(y(\hat{u}),p(\hat{u}))$ be the solutions of (2.3)–(2.7) and (3.9)–(3.12) with $\hat{u}=U_h$, respectively. Then, for any $1\le m \le N$, we have

$$\begin{aligned} \Vert r_y(t_m)\Vert _{L^{\infty }(\varOmega )}\le \Vert r_y(0)\Vert _{L^{\infty }(\varOmega )}+\Vert u-U_h\Vert _{L^2(0,T;L^{2}(\varOmega ))}, \end{aligned}$$

(4.25)

and

$$\begin{aligned} \Vert r_p(t_m)\Vert _{L^{\infty }(\varOmega )}\le \Vert r_p(T)\Vert _{L^{\infty }(\varOmega )}+\Vert r_y\Vert _{L^2(0,T;L^{2}(\varOmega ))}\le C\Vert u-U_h\Vert _{L^2(0,T;L^{2}(\varOmega ))}. \end{aligned}$$

(4.26)

Proof

Following the lines of argument of Lemma 3.3, the proof of inequalities (4.25) and (4.26) can easily be obtained. The details are thus omitted. $\square$

In the following lemma, we derive the a posteriori error estimate for the control variable in the $L^{2}(L^{2})$-norm.

Lemma 4.4

Let (y, p, u) and $(Y_h,P_h,U_h)$ be the solutions of (2.3)–(2.7) and (4.10)–(4.14), respectively. Assume that $(U_h+P_h^{n-1})|_{K}\in H^1(K)$ and $\tilde{u}_h\in U_{ad}$, and there exists a positive constant C, such that

$$\begin{aligned} \left| \int _0^T\left( U_h+P_h^{n-1},\tilde{u}_h-u\right) \,\mathrm{d}s\right| \le C\int _0^T\sum _{K\in \mathcal {T}_n}h_K\left| U_h+P_h^{n-1}\right| _{H^1(K)}\Vert u-\tilde{U}_h\Vert _{L^2(K)}\,\mathrm{d}s. \end{aligned}$$

Then, we have

$$\begin{aligned} \Vert u-U_h\Vert _{L^2(0,T;L^2(\varOmega ))}\le & {} \tilde{C}_3 \Bigg [\left( \int _0^T\sum _{K\in \mathcal {T}_n}h^2_{K}\left| U_h+P_h^{n-1}\right| _{H^1(K)}^2 \,\mathrm{d}s\right) ^{1/2}\\&+\left\| P_h^{n-1}-p(U_h)\right\| _{L^\infty \left( 0,T;L^\infty (\varOmega )\right) }\Bigg ], \end{aligned}$$

where $\tilde{C}_3=\max \{1,C\}$, and $(y(\hat{u}),p(\hat{u}))$ is defined by the system (3.9)–(3.11) with $\hat{u}=U_h$.

Proof

From (2.7), we have

$$\begin{aligned} (u,u-U_h)\le -(p,u-U_h); \end{aligned}$$

using the above inequality, it follows that

$$\begin{aligned} \Vert u-U_h\Vert _{L^2(0,T;L^2(\varOmega ))}^2= & {} \int _{0}^{T}\left( u-U_h,u-U_h\right) \,\mathrm{d}s\\\le & {} \int _0^T\left\{ -\left( p,u-U_h\right) -\left( U_h,u-U_h\right) \right\} \,\mathrm{d}s\\= & {} -\int _{0}^{T}\left( P_h^{n-1}+U_h,u-\tilde{u}_h\right) \,\mathrm{d}s -\int _{0}^{T}\left( U_h+P_h^{n-1},\tilde{u}_h-U_h\right) \,\mathrm{d}s\\&+\int _{0}^T\left( P_h^{n-1}-p(U_h),u-U_h\right) \,\mathrm{d}s+\int _0^T\left( p(U_h)-p,u-U_h\right) \,\mathrm{d}s. \end{aligned}$$

An use of (4.14) yields

$$\begin{aligned} \Vert u-U_h\Vert _{L^2\left( 0,T;L^2(\varOmega )\right) }^2\le & {} \int _0^T\left( U_h+P_h^{n-1},\tilde{u}_h-u\right) \,\mathrm{d}s +\int _{0}^T\left( P_h^{n-1}-p(U_h),u-U_h\right) \,\mathrm{d}s\\&+\int _0^T\left( p(U_h)-p,u-U_h\right) \,\mathrm{d}s\\=: & {} \hat{E}_1+\hat{E}_2+\hat{E}_3. \end{aligned}$$

Following the idea of Lemma 3.4, it is easy to bound the term $\hat{E}_i,\;i=1,2,3$. Therefore, we omit the details. This completes the proof. $\square$

By collecting Lemmas 4.1–4.4, we finally derive the main results of this paper.

Theorem 4.5

Let (y, p, u) and $(Y_h,P_h, U_h)$ be the solutions of (2.3)–(2.7) and (4.10)–(4.14), respectively. Then, there exists constants $\tilde{c}_3$, $\tilde{c}_4$(depend on $\varOmega$), for each $t\in (0,T],$ and any $1\le m \le N$ with $\displaystyle {\hat{h}_m=\min _{1\le n\le m}\min _{K \in \mathcal {T}_n}h_K}$, the following estimates

$$\begin{aligned} \Vert u-U_h\Vert _{L^2\left( 0,T;L^2(\varOmega )\right) }\le & {} \tilde{C}_4 \Bigg [\left( \int _0^T\sum _{K\in \mathcal {T}_n}h^2_{K}|U_h +P_h^{n-1}|_{H^1(K)}^2\,\mathrm{d}s\right) ^{1/2}\nonumber \\&+\Vert \xi _p\Vert _{L^\infty (0,T;L^\infty (\varOmega ))}+\Vert \eta _p\Vert _{L^\infty \left( 0,T;L^\infty (\varOmega )\right) }\Bigg ], \end{aligned}$$

(4.27)

where the constant $\tilde{C}_4$ depends on the domain $\varOmega$ and the constant $\tilde{C}_3$ as defined in Lemma 4.4,

$$\begin{aligned}&\Vert y-Y_h\Vert _{L^\infty (0,T;L^\infty (\varOmega ))}\le \Vert y_0-y_{h,0}\Vert _{L^{\infty }(\varOmega )}+\tilde{c}_3\left( \ln \hat{h}_m\right) ^2\left[ \mathfrak {E}_{\infty ,0}{\left( y_{h,0},\mathcal {G}^0_y\right) }\right. \nonumber \\&\left. \quad +\mathfrak {E}_{\infty ,0}{\left( y_h^m, \mathcal {G}^m_y\right) }+\sum _{n=1}^mk_n\mathfrak {\hat{E}}_{\infty ,0}\left( \frac{y_h^n-y^{n-1}_h}{k_n}, \mathcal {G}_y^n-\mathcal {G}_y^{n-1}; \mathcal {T}_{n-1},\mathcal {T}_n\right) \right] \nonumber \\&\quad +\sum _{n=1}^m\int _{I_n}\Vert f^n-f\Vert _{L^{\infty }(\varOmega ))}\,\mathrm{d}s +\frac{k_n}{2}\left\| \mathcal {G}_y^{n-1}-\mathcal {G}_y^n\right\| _{L^{\infty }(\varOmega )}+ \Vert u-U_h\Vert _{L^2\left( 0,T;L^2(\varOmega )\right) }, \end{aligned}$$

(4.28)

$$\begin{aligned}&\Vert p-P_h\Vert _{L^\infty (0,T;L^\infty (\varOmega ))}\le \tilde{c}_4 (\ln \hat{h}_m)^2\left[ \mathfrak {E}_{\infty ,0}(p_h^m, \mathcal {\tilde{G}}_p^m)+\sum _{n=1}^m k_n \mathfrak {\hat{E}}_{\infty ,0}(\frac{p_h^{n-1}-p_h^n}{k_n}, \right. \nonumber \\&\left. \quad \mathcal {\tilde{G}}_p^{n}-\mathcal {\tilde{G}}_p^{n+1}; \mathcal {T}_{n-1}, \mathcal {T}_n)+\mathfrak {E}_{\infty ,0}(y_h^m, \mathcal {G}_y^m)\right] +\sum _{n=1}^m\int _{I_n}\Vert y_d-y_d^n\Vert _{L^{\infty }(\varOmega )}\mathrm{d}s\nonumber \\&\qquad +\frac{k_n}{2}\Vert \mathcal {\tilde{G}}_p^{n}-\mathcal {\tilde{G}}_p^{n+1}\Vert _{L^{\infty }(\varOmega )}+\Vert \xi _y\Vert _{L^\infty (0,T;L^{\infty }(\varOmega ))}+\Vert u-U_h\Vert _{L^2(0,T;L^2(\varOmega ))} \end{aligned}$$

(4.29)

hold.

Proof

The first inequality (4.27) follows from Lemma 4.4. Next, to prove error estimate for the state variable, we write

$$\begin{aligned} y-Y_h=\left( y-y(U_h)\right) +\left( y(U_h)-\tilde{y}\right) +\left( \tilde{y}-Y_h\right) =r_y-\left( \xi _y-\eta _y\right) . \end{aligned}$$

For a fix $x_m \in \varOmega$ and $t_m \in (0,T]$, we have

$$\begin{aligned} \Vert (y-Y_h)(t_m)\Vert _{L^{\infty }(\varOmega )}\le \Vert r_y(t_m)\Vert _{L^{\infty }(\varOmega )}+\Vert \xi _y(t_m)\Vert _{L^{\infty }(\varOmega )} +\Vert \eta _y(t_m)\Vert _{L^{\infty }(\varOmega )}. \end{aligned}$$

Using Lemma 4.1, the last term of the right hand side is bounded as

$$\begin{aligned} \Vert \eta _y(t_m)\Vert _{L^{\infty }(\varOmega )}\le c_8\left( \ln \hat{h}_m\right) ^2 \mathfrak {E}_{\infty ,0}{\left( y_h^m,\mathcal {G}^m_y\right) }. \end{aligned}$$

By Lemma 4.2, we have

$$\begin{aligned} \Vert \xi _y(t_m)\Vert _{L^{\infty }(\varOmega )}\le & {} \Vert y_0-y_{h,0}\Vert _{L^{\infty }(\varOmega )}+c_4\left( \ln \hat{h}_m\right) ^2\mathfrak {E}_{\infty ,0}{(y_{h,0},\mathcal {G}^0_y)}\\&+c_6 \left( \ln \hat{h}_m\right) ^2\sum _{n=1}^mk_n\mathfrak {\hat{E}}_{\infty ,0}\left( \frac{y_h^n-y^{n-1}_h}{k_n}, \mathcal {G}_y^n-\mathcal {G}_y^{n-1}; \mathcal {T}_{n-1},\mathcal {T}_n\right) \\&+\sum _{n=1}^m\int _{I_n}\Vert f^n-f\Vert _{L^{\infty }(\varOmega ))}\,\mathrm{d}s +\frac{k_n}{2}\Vert \mathcal {G}_y^{n-1}-\mathcal {G}_y^n\Vert _{L^{\infty }(\varOmega )}. \end{aligned}$$

Since $r_y(0)=0$, apply Lemma 4.3 to obtain

$$\begin{aligned} \Vert r_y(t_m)\Vert _{L^{\infty }(\varOmega )}\le \Vert u-U_h\Vert _{L^2(0,T;L^2(\varOmega ))}, \end{aligned}$$

where $c_i, \; i=4,6,8$ depend on $\varOmega$. Combining these above estimates and setting $\tilde{c}_3=\max \{c_4, c_6, c_8\}$, we accomplish (4.28).

Next, we estimate the error for the co-state variable. By the triangle inequality, for any $t_m \in (0,T]$, we have

$$\begin{aligned} \Vert (p-P_h)(t_m)\Vert _{L^{\infty }(\varOmega )}\le \Vert r_p(t_m)\Vert _{L^{\infty }(\varOmega )}+\Vert \xi _p(t_m)\Vert _{L^{\infty }(\varOmega )} +\Vert \eta _p(t_m)\Vert _{L^{\infty }(\varOmega )}. \end{aligned}$$

We apply Lemmas 4.1–4.3 with $\xi _p(T)=0$ and $r_p(T)=0$ to arrive at

$$\begin{aligned}&\Vert (p-P_h)(t_m)\Vert _{L^{\infty }(\varOmega )}\le \tilde{c}_4 (\ln \hat{h}_m)^2\Bigg [\mathfrak {E}_{\infty ,0}\left( p_h^m, \mathcal {\tilde{G}}_p^m\right) +\sum _{n=1}^m k_n \mathfrak {\hat{E}}_{\infty ,0}\\&\left( \frac{p_h^{n-1}-p_h^n}{k_n}, \mathcal {\tilde{G}}_p^{n}-\mathcal {\tilde{G}}_p^{n+1}; \mathcal {T}_{n-1}, \mathcal {T}_n\right) \\&+\mathfrak {E}_{\infty ,0}\left( y_h^m, \mathcal {G}_y^m\right) \Bigg ]+\sum _{n=1}^m\int _{I_n}\left\| y_d-y_d^n\right\| _{L^{\infty }(\varOmega )}\mathrm{d}s\\&+\frac{k_n}{2}\left\| \mathcal {\tilde{G}}_p^{n}-\mathcal {\tilde{G}}_p^{n+1}\right\| _{L^{\infty }(\varOmega )}+\Vert \xi _y\Vert _{L^\infty \left( 0,T;L^{\infty }(\varOmega )\right) }+\Vert r_y\Vert _{L^\infty \left( 0,T;L^{\infty }(\varOmega )\right) }, \end{aligned}$$

where the constants $c_i|_{i=7,9}$ depend on the domain $\varOmega$. Setting $\tilde{c_4}=\max \{c_7, c_9\}$, we complete the rest of the proof. $\square$

Theorem 4.6

Let (y, p, u) and $(Y_h,P_h, U_h)$ be the solutions of (2.3)–(2.7) and (4.10)–(4.14), respectively. Assume that all the conditions in Theorem 4.5 are valid. For each $t\in (0,T]$, there exists a positive constant $\tilde{C}_5$, such that the following error estimate

$$\begin{aligned}&\Vert u-U_h\Vert _{L^{\infty }(0,T;L^{\infty }(\varOmega ))}\\&\quad \le \tilde{C}_5 \left[ \Vert y_0-y_{h,0}\Vert _{L^{\infty }(\varOmega )}+(\ln \hat{h}_m)^2\left\{ \mathfrak {E}_{\infty ,0}{\big (y_{h,0},\mathcal {G}^0_y\big )}+\mathfrak {E}_{\infty ,0}\big (y_h^m, \mathcal {G}_y^m\big )\right. \right. \\&\qquad \left. \left. +\sum _{n=1}^mk_n\mathfrak {\hat{E}}_{\infty ,0}\left( \frac{y_h^n-y^{n-1}_h}{k_n}, \mathcal {G}_y^n-\mathcal {G}_y^{n-1}; \mathcal {T}_{n-1},\mathcal {T}_n\right) +\mathfrak {E}_{\infty ,0}\big (p_h^m, \mathcal {\tilde{G}}_p^m\big )\right. \right. \\&\qquad \left. \left. +\sum _{n=1}^m k_n \mathfrak {\hat{E}}_{\infty ,0}\left( \frac{p_h^{n-1}-p_h^n}{k_n}, \mathcal {\tilde{G}}_p^{n}-\mathcal {\tilde{G}}_p^{n+1}; \mathcal {T}_{n-1}, \mathcal {T}_n\right) \right\} +\frac{k_n}{2}\Vert \mathcal {G}_y^{n-1} -\mathcal {G}_y^n\Vert _{L^{\infty }(\varOmega )}\right. \\&\qquad \left. +\frac{k_n}{2}\Vert \mathcal {\tilde{G}}_p^{n}-\mathcal {\tilde{G}}_p^{n+1}\Vert _{L^{\infty }(\varOmega )} +\sum _{n=1}^m\int _{I_n}\Vert f^n-f\Vert _{L^{\infty }(\varOmega ))}\,\mathrm{d}s\right. \\&\qquad \left. +\sum _{n=1}^m\int _{I_n}\Vert y_d-y_d^n\Vert _{L^{\infty }(\varOmega )}\mathrm{d}s +\left( \int _0^T\sum _{K\in \mathcal {T}_n}h^2_{K}|U_h+P_h^{n-1}|_{H^1(K)}^2\,\mathrm{d}s\right) ^{1/2} \right] \end{aligned}$$

holds, where the constant $\tilde{C}_5$ depends on the domain $\varOmega$, the regularity constant $C_R$, and the constant $\tilde{C}_4$ as defined in Lemma 4.5.

Proof

Use of pointwise projection of u and $U_h$ leads to

$$\begin{aligned} \Vert u-U_h\Vert _{L^\infty (0,T;L^\infty (\varOmega ))}= & {} \Vert \varPi _{[u_a,u_b]}(-p)-\varPi _{[u_a,u_b]}(-P_h)\Vert _{L^\infty (0,T;L^\infty (\varOmega ))}\\\le & {} \Vert P_h-p\Vert _{L^\infty (0,T;L^\infty (\varOmega ))}. \end{aligned}$$

In the above, we have used the Lipschitz continuity of $\varPi _{[u_a,u_b]}$ with Lipschitz constant 1. Inviting Theorem 4.5, we complete the rest of the proof. $\square$

5 Numerical experiments

This section performs two numerical experiments to illustrate the theoretical results of the previous section. For the purpose of adaptive refinement, we need the following error estimators:

• initial data estimator $(\eta _{1})=\Vert y_0-y_{h,0}\Vert _{L^\infty (\varOmega )}$,

• spatial estimator for the state $(\eta _{2})=(\ln \hat{h}_m)^2\mathfrak {E}_{\infty ,0}(y_h^m,\mathcal {G}^m_y)$,

• temporal error estimator for the state $(\eta _{3})={\sum _{n=1}^m\int _{I_n}}\Vert f^n-f\Vert _{L^{\infty }(\varOmega ))}\,\mathrm{d}s+\frac{k_n}{2}\Vert \mathcal {G}_y^{n-1}-\mathcal {G}_y^n\Vert _{L^{\infty }(\varOmega )}$,

• spatial estimator for the co-state $(\eta _{4})=(\ln \hat{h}_m)^2\mathfrak {E}_{\infty ,0}(p_h^m,\mathcal {\tilde{G}}^m_p)$,

• temporal error estimator for the co-state $(\eta _{5})={\sum _{n=1}^m\int _{I_n}}\Vert y_d-y_d^n\Vert _{L^{\infty }(\varOmega )}\mathrm{d}s+\frac{k_n}{2}\Vert \mathcal {\tilde{G}}_p^{n}-\mathcal {\tilde{G}}_p^{n+1}\Vert _{L^{\infty }(\varOmega )}$

• a control error estimator $(\eta _{6})={\Big (\int _0^T\sum _{K\in \mathcal {T}_n}h^2_{K}|U_h+P_h^{n-1}|_{H^1(K)}^2\,\mathrm{d}s\Big )^{1/2}}$, and

• $L^\infty$-type error estimators

  $$\begin{aligned} \eta _{7}= & {} \left( \ln \hat{h}_m\right) ^2 \sum _{n=1}^mk_n\mathfrak {\hat{E}}_{\infty ,0}\left( \frac{y_h^n-y^{n-1}_h}{k_n}, \mathcal {G}_y^n-\mathcal {G}_y^{n-1}; \mathcal {T}_{n-1},\mathcal {T}_n\right) ,\\ \eta _{8}= & {} \left( \ln \hat{h}_m\right) ^2 \sum _{n=1}^m k_n \mathfrak {\hat{E}}_{\infty ,0}\left( \frac{p_h^{n-1}-p_h^n}{k_n}, \mathcal {\tilde{G}}_p^{n}-\mathcal {\tilde{G}}_p^{n+1}; \mathcal {T}_{n-1}, \mathcal {T}_n\right) . \end{aligned}$$

The effective index of the a posteriori error estimator is defined as $\eta / E$, where the total estimated error ($\eta$) and the total error (E) are given by $\eta (y,p,u):=\sum _{j=1}^8 \eta _j$ and

$$\begin{aligned} E(y,p,u):= \Vert y-Y_h\Vert _{L^\infty (0,T;L^\infty (\varOmega ))}+\Vert p-P_h\Vert _{L^\infty (0,T;L^\infty (\varOmega ))} +\Vert u-U_h\Vert _{L^\infty (0,T;L^\infty (\varOmega ))}, \end{aligned}$$

respectively. The numerical simulation is carried out with the help of the software FreeFem++ Hetch (2012) and all the constants involved in the estimators are taken to be 1. We use the following loop:

$$\begin{aligned} \mathrm{SOLVE} \rightarrow \mathrm{ESTIMATE} \rightarrow \mathrm{MARK} \rightarrow \mathrm{REFINE} \end{aligned}$$

to achieve a refinement from the initializing triangulation.

Space–time adaptive algorithm: Given tolerances $\mathcal {E}_{space}$, $\mathcal {E}_{time}$ and the parameters $\delta _1\in (0,1), \; \delta _2>1$, $\lambda _1 \in (0,1)$, $\lambda _2\in (0, \lambda _1)$. Suppose that $(y^{n-1}_h, p^{n}_h, u^{n-1}_h)$ is computed on the mesh $\mathcal {T}_{n-1}$ at time level $t_{n-1}$ with time step-size $k_{n-1}$ using the variational discretization algorithm (see Tang and Chen 2012b).

Step 1. set    $\mathcal {T}_n:=\mathcal {T}_{n-1},\;\; k_n:=k_{n-1},\;\; t_n:=t_{n-1}+k_{n}$

• compute $(y^n_h, p^{n-1}_h, u^{n}_h)$ on $\mathcal {T}_n$ using data $(y^{n-1}_h, p^{n}_h, u^{n-1}_h)$

• from the discrete problem

• compute the estimators $\eta _j,\; j=1,\ldots , 8$ on $\mathcal {T}_n$

Step 2. while $\big (\sum _{j\in \{3,5\}}\eta _j\big ) > \lambda _1 \cdot \mathcal {E}_\mathrm{time}$ do

• $k_n:=\delta _1 k_{n-1},\;\; t_n:=t_{n-1}+k_{n}$

• compute $(y^{n}_h, p^{n-1}_h, u^{n}_h)$ on $\mathcal {T}_n$ by solving the discrete problem

• compute the estimators $\eta _j,\; j=1,\ldots , 8$ on $\mathcal {T}_n$

   end while

Step 3. while $\big (\sum _{j\in \{1,2,4,6,7,8\}} \eta _j\big ) > \mathcal {E}_\mathrm{space}$ do

• refine mesh $\mathcal {T}_n$ generate a modified mesh (say) $\mathcal {T}_n^{h_n}$

• compute $(y^{n}_h, p^{n-1}_h, u^{n}_h)$ on $\mathcal {T}_n^{h_n}$ by solving the discrete problem

• compute the estimators $\eta _j,\; j=1,\ldots , 8$ on $\mathcal {T}_n^{h_n}$

   while $\big (\sum _{j\in \{3,5\}}\eta _j\big ) > \lambda _1 \cdot \mathcal {E}_{time}$ do

• $k_n^{'}:=\delta _1 k_{n-1},\;\; t_n:=t_{n-1}+k_n^{'}.$

• compute $(y^{n}_h, p^{n-1}_h, u^{n}_h)$ on $\mathcal {T}_{n,k_n^{'}}^{h_n}$ by solving the discrete problem.

• compute the estimators $\eta _j\; j=1,\ldots , 8$ on $\mathcal {T}_{n,k_n^{'}}^{h_n}$

   end while

   end while

Step 4. if $\big (\sum _{j\in \{3,5\}}\eta _j\big ) \le \lambda _2 \cdot \mathcal {E}_\mathrm{time}$ do

   set $k_n^{'}:=\delta _2 k_{n-1},\;\; t_n:=t_{n-1}+k_{n}^{'}$

   end if

The role of Step 2 is to reduce the time step-size to keep the time error estimator below the tolerance $\mathcal {E}_{time}$ while keeping the space mesh unchanged. In Step 3, the refinement procedure is carried out until the time and space error estimators satisfy the desired tolerances. In the last step, if the time error estimator is much less than the prescribe time tolerance $\mathcal {E}_{time}$, then we increase the time step size by multiplying a factor $\delta _2$. For marking and refinement of the elements $K\in \mathcal {T}_n$, we follow the strategy of Morin, Nochetto, and Siebert, see (Morin et al. 2000). For both the test example problems, we choose tolerances for time and space as $\mathcal {E}_{time}=\mathcal {E}_{space}=0.001$.

Example 5.1

We consider the spatial domain $\varOmega =[0, 1]\times [0, 1]$ and the time interval $[0, T]=[0, 1]$. We shall use the following data for the optimal control problem (1.1)–(1.3):

$$\begin{aligned} y(x, t)= & {} {\left\{ \begin{array}{ll} t\sin (2\pi x_1)\sin (2\pi x_2),\;\;\; &{} x_1+x_2\le 1,\\ 2t\sin (2\pi x_1)\sin (2\pi x_2),\;\;\; &{} x_1+x_2> 1, \end{array}\right. }\\ p(x, t)= & {} {\left\{ \begin{array}{ll} (t-1)\sin (2\pi x_1)\sin (2\pi x_2),\;\;\; &{} x_1+x_2\le 1,\\ 2(t-1)\sin (2\pi x_1)\sin (2\pi x_2),\;\;\; &{} x_1+x_2> 1, \end{array}\right. } \end{aligned}$$

with $u_a=-0.125,\;\; \text {and}\;\; u_b=+0.125$.

Note that functions f, $y_d$ and u are easily determined from the control problem (1.1)–(1.3) as

$$\begin{aligned}&f=\frac{\partial {y}}{\partial {t}}-\varDelta y-u, \end{aligned}$$

(5.1)

$$\begin{aligned}&y_d=\frac{\partial {p}}{\partial {t}}+ \varDelta p+y, \end{aligned}$$

(5.2)

$$\begin{aligned}&u=\min \left\{ u_b,\,\max \{u_a,-p\}\right\} . \end{aligned}$$

(5.3)

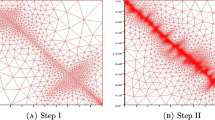
We approximate the time derivative by the backward Euler method. We partition the time interval [0, 1] with the step-size $\varDelta t\approx 5.56\times 10^{-3}$, such that $t_n=n\varDelta t,\; n=1,2,...N$ with the initial mesh $N=T/\varDelta t(=180)$. In the variational discretization, we use piecewise linear and continuous functions for approximations of the state (y) and co-state (p) variables, whereas the control variable (u) is computed using implicit relation between u and p. The variational discretization algorithm is used to solve the fully discrete optimal control problem (4.1)–(4.2). The adaptive meshes are generated via the error estimators $\eta _i,\; i=1,\;2,\;\ldots ,\;8.$ We present some computational results by setting tolerances 0.001 and the time step-size $\varDelta t=5.56 \times 10^{-3}$. In Figs. 2 and 3, the plots of approximate solutions of y and u are depicted on uniform mesh, adaptive mesh step-(I), and adaptive mesh step-(II), respectively, at final time $T=1.0$. Table 1 presents mesh information and errors for the state, co-state, and control variables in the $L^{\infty }(L^\infty )$-norm. This table also reveals that the number of nodes required for adaptive mesh is much less in comparison to the uniform mesh. It is clear from Fig. 1 that the mesh adapts very well in the neighbourhood of the discontinuous line $x_1 + x_2 = 1$. The higher densities of the node points are distributed along the line $x_1 + x_2 = 1$ enable us to save convincing computational work in comparison to uniform mesh. In Table 2, we present the effective index of the total estimators. It is further observed that the total estimated error $(\eta )$ and the total error (E) are decreasing with the increase of number of degrees of freedom (# Dof). The effective index of the a posteriori estimator almost remains constant which exhibits the potential quality of our estimators. The plots for the estimated error verses # Dof, the total error verses # Dof (left), and effective indexes verses # Dof (right) are shown in Fig. 4.

Table 1 Comparison of data on uniform mesh, adaptive mesh step-(I), and adaptive mesh step-(II) for the initial mesh $N=180$

Fig. 1

Uniform mesh, adaptive mesh step-(I), and adaptive mesh step-(II)

Fig. 2

Plots of discrete solution on uniform mesh, adaptive mesh step-(I), and adaptive mesh step-(II), respectively

Fig. 3

Approximate controls corresponding to uniform mesh, adaptive mesh step-(I), and adaptive mesh step-(II), respectively

Table 2 The number of elements, # Dof, total estimated error, and total error and effective index

Fig. 4

Estimated and total errors (left); effective index (right)

The following example considers a three-dimensional data for the control problem (1.1)–(1.3).

Example 5.2

In this example, we consider the domain $\varOmega =[0,1]\times [0,1]\times [0, 1 ]$ with time interval $[0, T]=[0, 1]$ for the control problem (1.1)–(1.3) and use the following data:

$$\begin{aligned}&y(x,t)= t \sin (\pi x_1)\sin (\pi x_2)\sin (\pi x_3),\;\;\;\;(x,t)\in \varOmega _T,\\&p(x,t)=(1-t)\sin (\pi x_1)\sin (\pi x_2)\sin (\pi x_3),\;\;\;\;(x,t)\in \varOmega _T, \end{aligned}$$

with $x=(x_1,x_2,x_3)$, $u_a=-0.075$ and $u_b=0.075$. Note that the functions f, $y_d$ and u are computed from (5.15.2)-(5.3).

Similar to the previous example, we compute errors for the state, co-state, and control variables in the $L^\infty (L^\infty )$-norm. The errors for the state, co-state, and control variables on the uniform mesh as well as on the adaptive mesh are presented in Table 3. We notice that the number of nodes in the adaptive mesh is much less with comparison to the uniform mesh. Table 4 contains the information on the number of elements, # Dof, total estimated error, the total error, and the effective index. It is observed that the total estimated error ($\eta$) and the total error (E) are decreasing with the increase of # Dof. Furthermore, the effective index remains almost constant in the computation. Finally, in Fig. 5, the estimated error, total error verses # Dof (left), and the effective indexes verses # Dof (right) are presented.

Table 3 Comparison of data on uniform mesh, adaptive mesh step-(I), and adaptive mesh step-(II) for the initial mesh $N=30$

Table 4 The number of elements, # Dof, total estimated error, and total error and effective index

Fig. 5

Estimated and total errors (left); effective index (right)

6 Concluding remarks

In this article, we have derived a posteriori error estimates in the $L^\infty (L^\infty )$-norm for variational discretization approximations of the parabolic optimal control problems. We have used the variational discretization approximations where the state and co-state variables are approximated using the piecewise linear and continuous functions, and the control variable is computed using the implicit relation between control and co-state variables (see, (2.8)). The elliptic reconstruction technique in conjunction with Green’s function for the heat kernel are key ingredients in deriving the a posteriori error bounds. Interestingly, the constants involved in Theorems 4.5 and 4.6 are independent of time, but may depend on the domain ($\varOmega$). In fact, some of the constants are stemming from the use of elliptic a posteriori error estimates. The proposed method does not require the discretization of the admissible control set but to implicitly utilize the optimality conditions for the discretization of the control variable. Our theoretical analysis is supported by numerical experiments which reveals that the adaptive scheme is able to save the substantial computational work.