On the unit Burr-XII distribution with the quantile regression modeling and applications

Abstract

In this paper, we modify the Burr-XII distribution through the inverse exponential scheme to obtain a new two-parameter distribution on the unit interval called the unit Burr-XII distribution. The basic statistical properties of the newly defined distribution are studied. Parameters estimation is dealt and different estimation methods are assessed through two simulation studies. A new quantile regression model based on the proposed distribution is introduced. Applications of the proposed distribution and its regression model to real data sets show that the proposed models have better modeling capabilities than competing models.

1 Introduction

Several unit distributions have been used for modelling data for percentage and proportions in many areas such as biological studies, mortality and recovery rates, economics, health, risks, and measurements sciences. No doubt that the beta, Johnson $S_B$ (see Johnson 1949) and Kumaraswamy (see Kumaraswamy 1980) distributions quickly come to the mind, both to model and to obtain inferences based on data sets from the above areas. However, these classical models may be inadequate, which pose many significant problems for accurate data analysis. For this reason, the number of studies on unit modeling increases in the literature. The newly proposed unit distributions have usually been introduced by the transformation of the well-known continuous distributions. The advantage of these unit distributions is to give more flexibility to the basic distribution over the unit interval without adding new parameters. For example, the unit gamma (see Consul and Jain 1971), log-Lindley (see Gómez-Déniz et al. 2014), unit Weibull (see Mazucheli et al. 2018), unit Gompertz (see Mazucheli et al. 2019b), unit Birnbaum-Saunders (see Mazucheli et al. 2018), log-xgamma (see Altun and Hamedani 2018), unit inverse Gaussian (see Ghitany et al. 2019), unit generalized half normal (see Korkmaz 2020b) and log-weighted exponential (see Altun 2021) distributions have been obtained via the negative exponential function transformation of the gamma, Lindley (see Lindley 1958), Weibull, Gompertz, Birnbaum-Saunders, xgamma (see Sen et al. 2016), inverse Gaussian, generalized half normal (see Cooray and Ananda 2008) and log-weighted exponential (see Gupta and Kundu 2009) distributions, respectively. One may refer to Mazucheli et al. (2019a), Altun and Cordeiro (2020), Korkmaz (2020a), Gündüz and Korkmaz (2020), Korkmaz et al. (2021a) and Korkmaz et al. (2021b) for the other unit models which have been obtained with other transformation methods.

On the other hand, Burr (see Burr 1942) has pioneered a system of continuous distributions, which has 12 distributions. This system has been obtained with a differential equation of the form $\mathrm{d}F(x)/\mathrm{d}x = F(x) (1-F(x))g(x)$, where g(x) is a non-negative function and F(x) is the satisfying cumulative distribution function (cdf) to this equation. In this way, the author has generalized the Pearson equation. Among these 12 distributions, the Burr III, Burr XII (BXII) and Burr X distributions are commonly known, and have received much more attention in the literature. The BXII distribution has the following cdf and probability density function (pdf): $\Pi ( z,\alpha ,\beta ) = 1 - \left( 1 + z^\beta \right) ^{ - \alpha }$ and $\pi ( z,\alpha ,\beta ) = \alpha \beta z^{\beta - 1} \left( 1 + z^\beta \right) ^{ - \alpha - 1}$, respectively, where $z>0$ and $\alpha ,\beta >0$ are the shape parameters. Its pdf shapes are unimodal or decreasing. It has found many applications in the literature such as reliability analysis (see Zimmer et al. 1998), portfolio segmentation (see Beirlant et al. 1998), and regression modeling (see Afify et al. 2018; Altun et al. 2018a, b; Cordeiro et al. 2018; Lanjoni et al. 2016; Silva et al. 2008 and Yousof et al. 2019). The Weibull distribution is the limiting distribution of the BXII distribution when $\alpha$ tends to $+\infty$. The inverse BXII distribution is known as the Burr type III distribution. For $\alpha =1$ and $\beta =1$, the BXII model is reduced to the Lomax and log-logistic (Fisk) distributions, respectively. One may see Rodriguez (1977) and Tadikamalla (1980) for its relations to other distributions in detail.

On the other hand, the classic regression models relate the mean response by given certain values of the covariates. If the response variable follows a skew distribution or has outliers, then the classic regression model is not suitable for the inferences based on the relation between the response variable and covariates. Since the mean is affected by these specific situations, the median is a more informative and robust estimate for these situations. As a solution, quantile regression models were proposed by Koenker and Bassett (1978). Mazucheli et al. (2020) have introduced the unit Weibull quantile regression modeling and have compared its performance with the beta regression (see Ferrari and Cribari-Neto 2004) and Kumaraswamy quantile regression (see Mitnik and Baek 2013) modelings.

The scope of this study is to propose a new unit alternative distribution and to introduce its alternative quantile regression modeling to the beta regression (see Ferrari and Cribari-Neto 2004) and Kumaraswamy quantile regression modeling (see Mitnik and Baek 2013) in order to model the percentages and proportions when data has outliers. To obtain a new unit distribution, we use the negative exponential transformation of the BXII distribution. In this way, we will transport its applicability and work-ability to the unit interval. Hence, we will bring into the different pdf and hazard rate function (hrf) properties that the BXII distribution has not on the unit interval.

The paper is organized as follows. The proposed distribution is defined in Sect. 2. Its basic distributional properties are described in Sect. 3. Section 4 is devoted to procedures of the different estimation methods to estimate its unknown parameters. Two different simulation studies are given to see the performance of the different estimates of the model parameters in Sect. 5. The new quantile regression model based on the newly defined distribution is discussed in Sect. 6. Two real data illustrations, which one is related to the univariate data modeling and other is the quantile regression modeling, are illustrated in Sect. 7. Finally, the paper ends in Sect. 8.

2 The new unit distribution and its properties

The new unit distribution is defined as follows: Let Z be a random variable having the BXII distribution with parameters $\alpha$ and $\beta$ and $X =e^{-Z}$. Then, the cdf and pdf of X are presented by

$$\begin{aligned} F( x,\alpha ,\beta ) = \left( {1 + \left( { - \log x} \right) ^\beta } \right) ^{ - \alpha } \end{aligned}$$

(1)

and

$$\begin{aligned} f( x,\alpha ,\beta ) = \alpha \beta x^{ - 1} \left( { - \log x} \right) ^{\beta - 1} \left( {1 + \left( { - \log x} \right) ^\beta } \right) ^{ - \alpha -1 } , \end{aligned}$$

(2)

where $x \in (0,1)$ and $\alpha ,\beta >0$ are the shape parameters. We denote the newly defined distribution as UBXII or $UBXII(\alpha ,\beta )$ when the parameters need to be indicated. The hrf of the $UBXII(\alpha ,\beta )$ distribution is given by

$$\begin{aligned} h( x,\alpha ,\beta ) = \alpha \beta x^{ - 1} \left( { - \log x} \right) ^{\beta - 1} \frac{\left( {1 + \left( { - \log x} \right) ^\beta } \right) ^{ - \alpha -1 }}{1-\left( {1 + \left( { - \log x} \right) ^\beta } \right) ^{ - \alpha } } . \end{aligned}$$

(3)

The analytical behavior of $f( x,\alpha ,\beta )$ and $h( x,\alpha ,\beta )$ is discussed below. When x tends to 0, the following equivalences hold:

$$\begin{aligned} f( x,\alpha ,\beta ) \sim h( x,\alpha ,\beta )\sim \alpha \beta x^{ - 1} \left( { - \log x} \right) ^{-\alpha \beta -1}, \end{aligned}$$

which tends to $+\infty$ for all the values of $\beta >0$ and $\alpha >0$.

When x tends to 1, we have

$$\begin{aligned} f( x,\alpha ,\beta ) \sim \alpha \beta \left( 1-x \right) ^{\beta - 1}, \quad h( x,\alpha ,\beta ) \sim \beta \left( 1-x \right) ^{- 1}. \end{aligned}$$

Therefore, in this case, if $\beta <1$, $f( x,\alpha ,\beta )$ tends to $+\infty$, if $\beta =1$, $f( x,\alpha ,\beta )$ tends to $\alpha$, and if $\beta >1$, $f( x,\alpha ,\beta )$ tends to 0. Moreover, for all the values of $\beta >0$ and $\alpha >0$, $h( x,\alpha ,\beta )$ tends to $+\infty$. The critical points of $f( x,\alpha ,\beta )$ can be determined by solving in a numerical way the following equation with respect to x:

$$\begin{aligned}&\alpha \beta x^{-2} (-\log x)^{\beta - 2} \left( (-\log x)^\beta + 1\right) ^{-\alpha - 2}\\&\quad \left( (-\log x)^{\beta } (\alpha \beta + \log x + 1) - \beta + \log x + 1\right) =0. \end{aligned}$$

If we excluded the bounds 0 and 1, this equation is equivalent to $(-\log x)^{\beta } (\alpha \beta + \log x + 1) - \beta + \log x + 1=0$, which remains of a high complexity from a mathematical point of view. After numerical tests, 0, 1 or 2 critical points into (0, 1) can be found, depending on the values $\alpha$ and $\beta$. For instance, in the simple case where $\beta =1$, there is only one critical point into (0, 1), it is given by $x=e^{-\alpha }$ and is a maximum point.

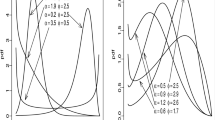
The critical points of $h( x,\alpha ,\beta )$ can be discussed in a similar manner. More elegantly, the possible shapes of $f( x,\alpha ,\beta )$ and $h( x,\alpha ,\beta )$ can be represented graphically. Figure 1 determines the regions of the values of $\alpha$ and $\beta$ where $f(x, \alpha , \beta )$ is U-shaped, increasing, decreasing, inverse N-shaped and unimodal, and $h(x, \alpha , \beta )$ is bathtub and increasing (the other kinds of shapes being excluded). Figure 2 completes the previous analysis by plotting diverse curves of $f(x, \alpha , \beta )$ and $h(x, \alpha , \beta )$ to visualize their possible shapes.

Fig. 1

The possible shapes regions of the pdf (left) and hrf (right)

Fig. 2

The possible shapes of the pdf (left) and hrf (right)

From Figs. 1 and 2 , it is clear that the UBXII distribution enjoys a high level of flexibility, and we can take advantage of it for various statistical applications.

The UBXII distribution is also completely determined by its quantile function (qf) given as the inverse function of $F(x,\alpha , \beta )$. After some development, it is defined by

$$\begin{aligned} Q(u,\alpha , \beta ) = e^{ - \left( {u^{ - 1/\alpha } - 1} \right) ^{1/\beta } }, \end{aligned}$$

(4)

where $u\in (0,1)$. The median of the UBXII distribution is derived by taking $u=0.5$ in the above equation. Similarly, the other quartiles and octiles can be determined. Also, some important qfs can be simply expressed, such as the quantile density and hazard quantile functions obtained as

$$\begin{aligned} q(u,\alpha , \beta )=\frac{1}{\alpha \beta } u^{-1/\alpha -1} \left( {u^{ - 1/\alpha } - 1} \right) ^{1/\beta -1}e^{ - \left( {u^{ - 1/\alpha } - 1} \right) ^{1/\beta } } \end{aligned}$$

and

$$\begin{aligned} \hslash (u,\alpha , \beta )= \frac{\alpha \beta }{1-u} u^{1/\alpha +1} \left( {u^{ - 1/\alpha } - 1} \right) ^{1-1/\beta }e^{ \left( {u^{ - 1/\alpha } - 1} \right) ^{1/\beta } }, \end{aligned}$$

where $u\in (0,1)$, respectively. For the general interpretation of these functions, we refer the reader to Nair and Sankaran (2009).

3 Some properties

This section presents several theoretical results of interest involving the UBXII distribution.

3.1 First-order stochastic dominance

The first-order stochastic dominance is a simple concept allowing to compare distributions through their respective cdfs. We say that a distribution A first-order stochastically dominates another distribution B if their respective cdfs $F_A(x)$ and $F_B(x)$ satisfy the following inequalities: $F_A(x)\le F_B(x)$ for all $x\in {\mathbb {R}}$. This concept is particularly developed in biometrics, reliability, econometrics and actuarial sciences. See, for instance, Shaked and Shanthikumar (2007) and Muller and Stoyan (2002).

We now expose some results on first-order stochastic dominance satisfied by the UBXII distribution. They are contained in the following proposition.

Proposition 1

The two following results hold.

• If $\alpha _1\ge \alpha _2$, then the $UBXII(\alpha _1, \beta )$ distribution first-order stochastically dominates the $UBXII(\alpha _2, \beta )$ distribution.

• The $UBXII(\alpha , \beta )$ distribution is first-order stochastically dominated by the unit Weibull distribution with parameters $\alpha$ and $\beta$ introduced by Mazucheli et al. (2020), and defined by the following cdf:

  $$\begin{aligned} F_{UW}(x, \alpha , \beta )=e^{-\alpha \left( { - \log x} \right) ^\beta }, \end{aligned}$$

  where $x\in (0,1)$.

Proposition 1 shows that the UBXII distribution offers a different alternative to the unit Weibull distribution, in the first-order stochastic sense, and in statistical modelling as well.

3.2 Probability weighted moments with applications

The probability weighted moments of a random variable generalize the ordinary moments, and naturally appear when we deal with the ordinary moments of order statistics. They are also involved in some parametric estimation methods. A detailed description of these moments can be found in Greenwood et al. (1979). In the context of the Burr-XII distribution, we may also refer to Usta (2013).

The following result is about an expression of the probability weighted moments of a random variable having the UBXII distribution.

Proposition 2

Let s and u be two integers, and X be a random variable having the $UBXII(\alpha ,\beta )$ distribution. Then, the $(s,u)^{th}$ probability weighted moment of X can be determined as

$$\begin{aligned} \mu ^{\prime }_{s,u} =E\left[ X^s F(X,\alpha , \beta )^u\right] =\frac{1}{u+1} M_{BXII}(-s, \alpha (u+1), \beta ), \end{aligned}$$

where, in full generality, $M_{BXII}(t,\alpha , \beta )$ denotes the well-known moment generating function (mgf) of the Burr-XII distribution with parameters $\alpha$ and $\beta$ taken at the point t.

An analytical expression of $M_{BXII}(t,\alpha , \beta )$ exists through the use of the Meijer G-function. See, for instance, Paranaíba et al. (2011) and Silva and Cordeiro (2015). It can also be evaluated numerically with an immediate implementation through any mathematical software, such as R, Python, Matlab, etc.

From Proposition 2, we easily derive the $s^{th}$ moment of X by taking $u=0$ which gives $\mu ^{\prime }_{s} =E(X^s)= \mu ^{\prime }_{s,0}$. Also, the mean of X is given by $\mu = \mu ^{\prime }_{1}$, the standard deviation of X is obtained as $\sigma = (\mu ^{\prime }_{2}-\mu ^2)^{1/2}$ and the $s^{th}$ general coefficient of X is specified by

$$\begin{aligned} \Upsilon _s=E\left[ \left( \frac{X-\mu }{\sigma }\right) ^s\right] =\sigma ^{-s} \sum _{k=0}^{s}\left( {\begin{array}{c}s\\ k\end{array}}\right) (-1)^{s-k}\mu ^{s-k}\mu ^{\prime }_{k}. \end{aligned}$$

From this general coefficient, the coefficients of skewness and kurtosis of X are defined by $\Upsilon _3$ and $\Upsilon _4$, respectively. The numerical behavior of these coefficients are shown in Fig. 3.

Fig. 3

The skewness and kurtosis of the UBXII distribution for the parameter values into (0, 5)

From Fig. 3, we see that $\Upsilon _3$ and $\Upsilon _4$ have versatile values with non-monotonic shapes. Also, $\Upsilon _3$ can be close to 0 and large, showing that the UBXII distribution is mainly right-skewed.

3.3 Entropy

The entropy of the UBXII distribution can be evaluated through numerous ways. Here, we propose the Tsallis entropy, revealing a manageable expression through the use of the mgf of the Burr-XII distribution. Generalities on the Tsallis entropy can be found in Amigo et al. (2018). The following result concerns a series expansion of this entropy measure in the context of the UBXII distribution.

Proposition 3

Let $\tau < 1$. Then, the Tsallis entropy of the UBXII distribution exists and it is given as

$$\begin{aligned} T(\tau ,\alpha , \beta )&=\frac{1}{\tau -1} \left[ 1-\int _{0}^{1}f(x,\alpha ,\beta )^{\tau }\mathrm{d}x\right] \\&= \frac{1}{\tau -1} \left[ 1- \alpha ^{\tau }\beta ^{\tau } \int _{0}^{+\infty }e^{(\tau -1)y } y^{\tau (\beta - 1)} \left( {1 + y^\beta } \right) ^{ - \tau ( \alpha +1) } \mathrm{d}y\right] . \end{aligned}$$

For $\tau \in (0,1)$, the following upper bound holds:

$$\begin{aligned} T(\tau ,\alpha , \beta )\le \frac{1}{\tau -1} \left[ 1- \frac{\alpha ^{\tau }\beta ^{\tau }}{(1-\tau )^{\tau (\beta -1)+1}}\Gamma (\tau (\beta -1)+1)\right] , \end{aligned}$$

where $\Gamma (x)$ denotes the standard Euler gamma function.

Proof

The proof is centered around the expression of the integral term. From Equation (2), we get

$$\begin{aligned} \int _{0}^{1}f(x,\alpha ,\beta )^{\tau }\mathrm{d}x= \alpha ^{\tau }\beta ^{\tau } \int _{0}^{1}x^{ - \tau } \left( { - \log x} \right) ^{\tau (\beta - 1)} \left( {1 + \left( { - \log x} \right) ^\beta } \right) ^{ - \tau ( \alpha +1) } \mathrm{d}x. \end{aligned}$$

By performing the change of variables $x=e^{-y}$, we obtain

$$\begin{aligned}&\int _{0}^{1}f(x,\alpha ,\beta )^{\tau }\mathrm{d}x= \alpha ^{\tau }\beta ^{\tau } \int _{0}^{+\infty }e^{(\tau -1)y } y^{\tau (\beta - 1)} \left( {1 + y^\beta } \right) ^{ - \tau ( \alpha +1) } \mathrm{d}y, \end{aligned}$$

which exists if $\tau <1$. Now, for $\tau \in (0,1)$, by using the following inequalities: $\left( {1 + y^\beta } \right) ^{ - \tau ( \alpha +1) }\le 1$ and applying the change of variables $z=(1-\tau )y$, we have

$$\begin{aligned}&\int _{0}^{1}f(x,\alpha ,\beta )^{\tau }\mathrm{d}x\le \alpha ^{\tau }\beta ^{\tau } \int _{0}^{+\infty }e^{-(1-\tau )y } y^{\tau (\beta - 1)} \mathrm{d}y\\&\quad =\frac{\alpha ^{\tau }\beta ^{\tau }}{(1-\tau )^{\tau (\beta - 1)+1}} \int _{0}^{+\infty } z^{\tau (\beta - 1)+1-1}e^{-z } \mathrm{d}z\\&\quad =\frac{\alpha ^{\tau }\beta ^{\tau }}{(1-\tau )^{\tau (\beta - 1)+1}} \Gamma (\tau (\beta - 1)+1). \end{aligned}$$

By substituting this inequality in the definition of $T(\tau ,\alpha , \beta )$ and taking into account that the factor term $(\tau -1)^{-1}$ is negative, we obtain the stated result. $\square$

The integral term in the Tsallis entropy can not be developed. We can however evaluate it numerically, and the Tsallis entropy as well. In a similar way, we can express the Rényi entropy which also depends on the same integral term.

3.4 Stress–strength parameter

In lifetime testing, various resistance measures exist to measure the lifetime of a system. Among them, there is the stress-strength parameter defined by the probability that a component of the system will function satisfactorily if the applied stress is lower than its strength. More details are given in Surles and Padgett (2001)). The following proposition exhibits a simple form for this parameter in the setting of the UBXII distribution.

Proposition 4

Let $X_1$ and $X_2$ be two independent random variables, with $X_1$ having the $UBXII(\alpha _1,\beta )$ distribution and $X_2$ having the $UBXII(\alpha _2,\beta )$ distribution. Then, if we define the stress-strength parameter as $R(\alpha _1, \alpha _2, \beta )=P(X_2 \le X_1)$, then we have

$$\begin{aligned} R(\alpha _1, \alpha _2, \beta )=\frac{\alpha _1}{\alpha _1+\alpha _2}. \end{aligned}$$

The 1/2 value is obtained for $\alpha _1=\alpha _2$. In this case, $X_1$ and $X_2$ are identically distributed. The closed-form expression of $R(\alpha _1, \alpha _2, \beta )$ making it interesting for statistical estimation purposes.

3.5 Order statistics

The modeling of various lifetime systems having some component structures needs the consideration of ordered random variables, called order statistics. The fundamental of this notion can be found in David and Nagaraja (2003). Here, standard distributional properties of the order statistics of the UBXII distribution are presented.

Let $X_1,X_2, \ldots ,X_n$ be a random sample from the UBXII distribution with sample size n, and $X_{(1)}, X_{(2)},\ldots , X_{(n)}$ be their ordered statistics, such that $X_{(1)}\le X_{(2)}\le \ldots , \le X_{(n)}$. For any $j=1,\ldots ,n$, from Equations (1) and (2), the pdf of $X_{(j)}$ is defined as

$$\begin{aligned} f_{X_{(j)}}(x,\alpha , \beta )&=\frac{n!}{(j-1)!(n-j)!}f(x,\alpha , \beta ) F (x,\alpha , \beta ) ^{j-1}[1-F(x,\alpha , \beta ) ]^{n-j}\\&=\frac{n!}{(j-1)!(n-j)!} \alpha \beta x^{ - 1} \left( { - \log x} \right) ^{\beta - 1} \left( {1 + \left( { - \log x} \right) ^\beta } \right) ^{ - \alpha j-1 } \\&\quad \left[ 1-\left( {1 + \left( { - \log x} \right) ^\beta } \right) ^{ - \alpha } \right] ^{n-j}, \end{aligned}$$

where $x\in (0,1)$. In particular, the pdf of the infimum of $X_1,X_2,\ldots ,X_n$, that is $X_{(1)}$, can be expressed as

$$\begin{aligned} f_{X_{(1)}}(x,\alpha , \beta )&=n \alpha \beta x^{ - 1} \left( { - \log x} \right) ^{\beta - 1} \left( {1 + \left( { - \log x} \right) ^\beta } \right) ^{ - \alpha -1 } \\&\quad \left[ 1-\left( {1 + \left( { - \log x} \right) ^\beta } \right) ^{ - \alpha } \right] ^{n-1}, \end{aligned}$$

where $x\in (0,1)$. Also, the pdf of the supremum of $X_1,X_2,\ldots ,X_n$, that is $X_{(n)}$, is

$$\begin{aligned} f_{X_{(n)}}(x,\alpha , \beta )= n \alpha \beta x^{ - 1} \left( { - \log x} \right) ^{\beta - 1} \left( {1 + \left( { - \log x} \right) ^\beta } \right) ^{ - \alpha n-1 }, \end{aligned}$$

where $x\in (0,1)$. We recognize the pdf of the $UBXII(\alpha n, \beta )$ distribution. Therefore, the theory developed in the previous sections for the UBXII distribution can be directly applied for $X_{(n)}$.

The moments of $X_{(j)}$ are discussed in the next proposition.

Proposition 5

Let s be an integer. Then, with the above notations, the $s^{th}$ moment of $X_{(j)}$ can be expressed as a finite linear combination of mgfs of the BXII distribution. More precisely, we have

$$\begin{aligned} \mu ^{*}_{s, (j)} =E(X_{(j)}^s)=\sum _{k=0}^{n-j} a_{(j),k} M_{BXII}(-s, \alpha (k+j), \beta ), \end{aligned}$$

where

$$\begin{aligned} a_{(j),k}=\frac{n!}{(j-1)!(n-j)!}\left( {\begin{array}{c}n-j\\ k\end{array}}\right) (-1)^k \frac{1}{k+j}. \end{aligned}$$

Thanks to Proposition 5, one can express diverse parameters of $X_{(j)}$, such as its mean, variance, standard deviation, central moments, etc. Also, the order statistics of the UBXII distribution will have important roles in the estimation procedures described in the next section.

4 Estimation procedures for the model parameters

In this section, six different estimation methods have been pointed out to estimate the parameters of the UBXII distribution. The details are given below.

4.1 Maximum likelihood estimation

In this subsection, we derive estimations of the parameters $\alpha$ and $\beta$ via the method of the maximum likelihood (ML) estimation. Let $X_{1},X_{2},\dots ,X_{n}$ be a random sample of size n from the $UBXII(\alpha , \beta )$ distribution with observed values $x_{1},x_{2},\dots ,x_{n}$. Let $\varvec{\Upsilon }=\left( \alpha , \beta \right) ^{T}$ be the vector of the model parameters. Then, the log-likelihood function is given by

$$\begin{aligned} \ell (\varvec{\Upsilon })&= n\log \alpha + n\log \beta - \sum \limits _{i = 1}^n {\log x_i } + \left( {\beta - 1} \right) \sum \limits _{i = 1}^n {\log (- \log x_i)} - \left( {\alpha + 1} \right) \nonumber \\&\quad \times \sum \limits _{i = 1}^n {\log \left( {1 + (- \log x_i)^\beta } \right) } . \end{aligned}$$

(5)

Then, the ML estimates (MLEs) of $\alpha$ and $\beta$, say ${\hat{\alpha }}$ and ${\hat{\beta }}$, are obtained by maximizing $\ell (\varvec{\Upsilon })$ with respect to $\varvec{\Upsilon }$. Mathematically, this is equivalent to solve the following non-linear equation with respect to the parameters:

$$\begin{aligned} \frac{\partial }{\partial \alpha }\ell (\varvec{\Upsilon })= \frac{n}{\alpha } - \sum \limits _{i = 1}^n {\log \left( {1 + (- \log x_i)^\beta } \right) } = 0 \end{aligned}$$

(6)

and

$$\begin{aligned} \frac{\partial }{\partial \beta }\ell (\varvec{\Upsilon })&= \frac{n}{\beta } + \sum \limits _{i = 1}^n {\log (- \log x_i)} - \left( {\alpha + 1} \right) \sum \limits _{i = 1}^n {\frac{{\log (- \log x_i)(- \log x_i)^\beta }}{{1 + (- \log x_i)^\beta }}} = 0. \end{aligned}$$

From Equation (6), these solutions are governed by the following relation:

$$\begin{aligned} \alpha = n\left[ {\sum \limits _{i = 1}^n {\log \left( {1 + (- \log x_i)^{\beta } } \right) } } \right] ^{ - 1} . \end{aligned}$$

(7)

Substituting Equation (7) in Equation (5), the profile log-likelihood (PLL) based on the parameter $\beta$ is given by

$$\begin{aligned} \ell \left( \beta \right)&= n\log \left( {n\left[ {\sum \limits _{i = 1}^n {\log \left( {1 + (- \log x_i)^\beta } \right) } } \right] ^{ - 1} } \right) - \sum \limits _{i = 1}^n {\log x_i } + \left( {\beta - 1} \right) \sum \limits _{i = 1}^n {\log (- \log x_i)} \nonumber \\&\quad - n-\sum \limits _{i = 1}^n {\log \left( {1 + (- \log x_i)^\beta } \right) }+ n\log \beta . \end{aligned}$$

(8)

Therefore, the MLE $\hat{\beta }$ is obtained by maximizing Equation (8) based on the parameter $\beta$, which can be obtained through the solving of the following non-linear equation:

$$\begin{aligned} \frac{\partial }{{\partial \beta }}\ell \left( \beta \right)&= \frac{n}{\beta } - n\sum \limits _{i = 1}^n {\frac{{(- \log x_i)^\beta \log (- \log x_i)}}{{1 + (- \log x_i)^\beta }}} \left[ {\sum \limits _{i = 1}^n {\log \left( {1 + (- \log x_i)^\beta } \right) } } \right] ^{ - 1} \nonumber \\&\quad + \sum \limits _{i = 1}^n {\log (- \log x_i)} - \sum \limits _{i = 1}^n {\frac{{(- \log x_i)^\beta \log (- \log x_i)}}{{1 + (- \log x_i)^\beta }}} =0. \end{aligned}$$

Hence, the numerical methods are needed to obtain the MLE $\hat{\beta }$. After the MLE $\hat{\beta }$ is obtained, the $\hat{\alpha }$ is derived from the relation Equation (7).

Under mild regularity conditions, one can use the bivariate normal distribution with the mean $\mu =(\alpha ,\beta )$ and variance-covariance matrix $I^{-1}$, where I denotes the $2\times 2$ Fisher information matrix, to construct confidence intervals or likelihood ratio test on the parameters. The asymptotic variance-covariance matrix of the maximum likelihood estimators of the parameters is given by the inverse of the Fisher information matrix. If the considered pdf is smooth, the related Fisher information matrix is the matrix whose elements are negative of the expected values of the second partial derivatives of the log-likelihood function with respect to the parameters. In applications, the observed information matrix denoted by J, which is the negative of the Hessian matrix of the log-likelihood function with the parameters replaced by their estimates and is a sample-based version of the Fisher information, is usually used instead of I. The components of the observed information matrix can be requested from the authors when it is needed. It is noticed that it is also obtained numerically by computer packages such as R. Then, approximate $100(1-\vartheta )\%$ confidence intervals for $\alpha$ and $\beta$ can be determined by the following bounds: ${\widehat{\alpha }}\pm z_{\vartheta /2} s_{{\hat{\alpha }}}$ and ${\beta }\pm z_{\vartheta /2} s_{{\hat{\beta }}}$, where $z_{\vartheta /2}$ is the upper $(\vartheta /2)^{th}$ percentile of the standard normal distribution, $s_{{\hat{\alpha }}}=\sqrt{J_{\alpha \alpha }^{-1}}$, $s_{{\hat{\beta }}}=\sqrt{J_{\beta \beta }^{-1}}$, and $J_{\epsilon \epsilon }^{-1}$ are diagonal elements of $J^{-1}$ corresponding to $\epsilon =\alpha$ and $\beta$.

4.2 Maximum product spacing estimation

The maximum product spacing (MPS) method has been introduced in Cheng and Amin (1979). It is based on the idea that differences (spacings) between the values of the cdf at consecutive data points should be identically distributed. Let $X_{(1)}, X_{(2)}, \ldots , X_{(n)}$ be the ordered statistics from the UBXII distribution with sample size n, and $x_{(1)}, x_{(2)}, \ldots , x_{(n)}$ be the ordered observed values. Then, we define the MPS function by

$$\begin{aligned} \begin{aligned} MPS(\varvec{\Upsilon })=\frac{1}{n+1}\sum \limits _{i=1}^{n+1}\log \left[ F(x_{(i)},\alpha ,\beta )-F(x_{(i-1)},\alpha ,\beta )\right] . \end{aligned} \end{aligned}$$

(9)

The MPS estimates (MPSEs) can be obtained by maximizing $MPS(\varvec{\Upsilon })$ with respect to $\varvec{\Upsilon }$. They are also given as the simultaneous solutions of the following non-linear equations:

$$\begin{aligned} \frac{\partial MPS(\varvec{\Upsilon })}{\partial \alpha }=\frac{1}{n+1}\sum \limits _{i=1}^{n+1}\left[ \frac{F_{\alpha }^{'}(x_{(i)},\alpha ,\beta )-F_{\alpha }^{'}(x_{(i-1)},\alpha ,\beta )}{F(x_{(i)},\alpha ,\beta )-F(x_{(i-1)},\alpha ,\beta )} \right] =0 \end{aligned}$$

and

$$\begin{aligned} \frac{\partial MPS(\varvec{\Upsilon })}{\partial \beta }=\frac{1}{n+1}\sum \limits _{i=1}^{n+1}\left[ \frac{F_{\beta }^{'}(x_{(i)},\alpha ,\beta )-F_{\beta }^{'}(x_{(i-1)},\alpha ,\beta )}{F(x_{(i)},\alpha ,\beta )-F(x_{(i-1)},\alpha , \beta )} \right] =0, \end{aligned}$$

where

$$\begin{aligned} F_\alpha ^{'} (x,\alpha ,\beta )= - \left( {1 + \left( { - \log x} \right) ^\beta } \right) ^{ - \alpha } \log \left( {1 + \left( { - \log x} \right) ^\beta } \right) \end{aligned}$$

and

$$\begin{aligned} F_\beta ^{'} (x,\alpha ,\beta )= - \alpha \left( {1 + \left( { - \log x} \right) ^\beta } \right) ^{ - \alpha - 1} \left( { - \log x} \right) ^\beta \log \left( { - \log x} \right) \log \left( {1 + \left( { - \log x} \right) ^\beta } \right) . \end{aligned}$$

4.3 Least squares estimation

The least square estimates (LSEs) $\hat{\alpha }_{LSE}$ and $\hat{\beta }_{LSE}$ of $\alpha$ and $\beta$, respectively, are obtained by minimizing the following function:

$$\begin{aligned} LSE(\varvec{\Upsilon })=\sum \limits _{i=1}^{n}\left( F(x_{(i)},\alpha ,\beta )-E\left[ F(X_{(i)}, \alpha , \beta ) \right] \right) ^{2}, \end{aligned}$$

(10)

with respect to $\varvec{\Upsilon }$, where $E\left[ F(X_{(i)}, \alpha , \beta ) \right] =i/(n+1)$ for $i=1,2,\ldots , n$. Then, $\hat{\alpha }_{LSE}$ and $\hat{\beta }_{LSE}$ are solutions of the following equations:

$$\begin{aligned} \frac{\partial LSE(\varvec{\Upsilon })}{\partial \alpha }=2 \sum \limits _{i=1}^{n}F_{\alpha }^{'}(x_{(i)},\alpha ,\beta )\left( F(x_{(i)},\alpha ,\beta )-\frac{i}{n+1}\right) =0 \end{aligned}$$

and

$$\begin{aligned} \frac{\partial LSE(\varvec{\Upsilon })}{\partial \beta }=2 \sum \limits _{i=1}^{n}F_{\beta }^{'}(x_{(i)},\alpha ,\beta )\left( F(x_{(i)}, \alpha ,\beta )-\frac{i}{n+1}\right) =0, \end{aligned}$$

where $F_{\alpha }^{'}(x,\alpha ,\beta )$ and $F_{\beta }^{'}(x,\alpha ,\beta )$ are mentioned before.

4.4 Weighted least squares estimation

Similarly to LSEs, the weighted least square estimates (WLSEs) $\hat{\alpha }_{WLSE}$ and $\hat{\beta }_{WLSE}$ of $\alpha$ and $\beta$, respectively, are obtained by minimizing the following function:

$$\begin{aligned} WLSE(\varvec{\Upsilon })=\sum \limits _{i=1}^{n}\frac{1}{V\left[ F(X_{(i)}, \alpha , \beta )\right] }\left( F(x_{(i)},\alpha ,\beta )-E\left[ F(X_{(i)}, \alpha , \beta ) \right] \right) ^{2}, \end{aligned}$$

(11)

with respect to $\varvec{\Upsilon }$, where $E\left[ F(X_{(i)}, \alpha , \beta ) \right] =i/(n+1)$ and $V\left[ F(X_{(i)}, \alpha , \beta )\right] ={i(n-i+1)}/[(n+2)(n+1)^2]$ for $i=1,2,\ldots , n$. Then, $\hat{\alpha }_{WLSE}$ and $\hat{\beta }_{WLSE}$ are solutions of the following equations:

$$\begin{aligned} \frac{\partial WLSE(\varvec{\Upsilon })}{\partial \alpha }=2 \sum \limits _{i=1}^{n} \frac{(n+2)(n+1)^2}{i(n-i+1)} \left( F(x_{(i)},\alpha ,\beta )-\frac{i}{n+1}\right) F_{\alpha }^{'}(x_{(i)},\alpha ,\beta )=0 \end{aligned}$$

and

$$\begin{aligned} \frac{\partial WLSE(\varvec{\Upsilon })}{\partial \beta }=2 \sum \limits _{i=1}^{n}\frac{(n+2)(n+1)^2}{i(n-i+1)} \left( F(x_{(i)},\alpha ,\beta )-\frac{i}{n+1}\right) F_{\beta }^{'}(x_{(i)},\alpha ,\beta )=0. \end{aligned}$$

4.5 Anderson–Darling estimation

The Anderson–Darling minimum distance estimates (ADEs) $\hat{\alpha }_{AD}$, $\hat{\beta }_{AD}$ of $\alpha$ and $\beta$, respectively, are obtained by minimizing the following function:

$$\begin{aligned} AD\left( \varvec{\Upsilon }\right) = - n - \sum \limits _{i = 1}^n \frac{2i-1}{n}\left[ {\log F(x_{(i)},\alpha ,\beta )+ \log \left\{ {1 - F(x_{( n+1-i)},\alpha ,\beta )} \right\} } \right] , \end{aligned}$$

(12)

with respect to $\varvec{\Upsilon }$. Therefore, $\hat{\alpha }_{AD}$ and $\hat{\beta }_{AD}$ can be obtained as the solutions of the following system of equations:

$$\begin{aligned} \frac{{\partial AD\left( \varvec{\Upsilon } \right) }}{{\partial \alpha }} = - \sum \limits _{i = 1}^n { \frac{2i-1}{n}\left[ {\frac{{F'_\alpha ( x_{(i)} ,\alpha ,\beta )}}{{F(x_{(i)}, \alpha ,\beta )}} - \frac{{F'_\alpha ( x_{( {n + 1 - i})} ,\alpha ,\beta )}}{{1 - F(x_{( n+1-i )}, \alpha ,\beta )}}} \right] }=0 \end{aligned}$$

and

$$\begin{aligned} \frac{{\partial AD\left( \varvec{{\Upsilon }} \right) }}{{\partial \beta }} =- \sum \limits _{i = 1}^n { \frac{2i-1}{n}\left[ {\frac{{F'_\beta ( {x_{(i)}, \alpha ,\beta } )}}{{F(x_{(i)},\alpha ,\beta )}} - \frac{{F'_\beta ( {x_{( {n + 1 - i} )},\alpha ,\beta } )}}{{1 - F( {x_{( n+1-i )}, \alpha , \beta }) }}} \right] }=0. \end{aligned}$$

4.6 The Cramér–von Mises estimation

The Cramér–von Mises minimum distance estimates (CVMEs) $\hat{\alpha }_{CVM}$ and $\hat{\beta }_{CVM}$ of $\alpha$ and $\beta$, respectively, are obtained by minimizing the following function:

$$\begin{aligned} CVM\left( \varvec{\Upsilon }\right) = \frac{1}{12n} + \sum \limits _{i = 1}^n {\left[ {F(x_{(i)},\alpha ,\beta ) - \frac{{2i - 1}}{{2n}}} \right] ^2 }, \end{aligned}$$

(13)

with respect to $\varvec{\Upsilon }$. Therefore, the desired estimates can be obtained as the solutions of the following system of equations:

$$\begin{aligned} \frac{{\partial CVM\left( \varvec{{\Upsilon }} \right) }}{{\partial \alpha }} = 2 \sum \limits _{i = 1}^n { \left( {F(x_{(i)},\alpha ,\beta ) - \frac{{2i - 1}}{{2n}}} \right) F'_\alpha (x_{(i)},\alpha ,\beta ) = 0} \end{aligned}$$

and

$$\begin{aligned} \frac{{\partial CVM\left( \varvec{{\Upsilon }} \right) }}{{\partial \beta }} = 2 \sum \limits _{i = 1}^n { \left( {F( x_{(i)} , \alpha ,\beta ) - \frac{{2i - 1}}{{2n}}} \right) F'_\beta ( x_{(i)} ,\alpha ,\beta ) = 0}. \end{aligned}$$

Since all the equations above contain non-linear functions, it is not possible to obtain explicit forms of all estimates directly. Therefore, they have to be solved by using numerical methods such as the Newton–Raphson and quasi-Newton algorithms. In addition, Equations (5), (9), (10), (11), (12) and (13) can be also optimized directly by using the software such as R (constrOptim, optim and maxLik functions), S-Plus and Mathematica to numerically optimize $\ell (\varvec{\Upsilon } )$ and $MPS\left( \varvec{\Upsilon }\right)$, $LSE\left( \varvec{\Upsilon }\right)$, $WLSE\left( \varvec{\Upsilon }\right)$, $AD\left( \varvec{\Upsilon }\right)$ and $CVM\left( \varvec{\Upsilon }\right)$ functions.

5 Simulations

In this section, we perform two graphical simulation studies to see the performance of the above estimates of the UBXII distribution with respect to varying sample size n. The first step is the generation of $N = 1000$ samples of size $n = 20,25, \ldots ,1000$ from the UBXII distribution based on the actual parameter values. We take them as $\alpha =5$, $\beta =2$ and $\alpha =2$, $\beta =5$ for the first and second simulation studies, respectively. The random numbers generation is obtained by the use of the qf of the model. All the estimations based on the estimation methods have been obtained by employing the constrOptim function in the R program. Further, we calculate the empirical mean, bias and mean square error (MSE) of the estimations for comparisons between estimation methods. For $\epsilon = \alpha$ and $\beta$, the bias and MSE are calculated from all the samples as

$$\begin{aligned} Bias_{\epsilon } (n) = \frac{1}{N}\sum _{i = 1}^N ({\epsilon } - \hat{\epsilon }_i ), \quad MSE_{\epsilon } (n) = \frac{1}{N}\sum _{i = 1}^N ({\epsilon } - \hat{\epsilon }_i )^2 , \end{aligned}$$

respectively. We expect that the empirical means are close to true values when the MSEs and biases are near zero. The results of this simulation study are shown in Figs. 4 and 5.

Figures 4 and 5 show that all estimates are consistent since the MSE and biasedness decrease to zero with increasing sample size as expected. All estimates are asymptotic unbiased also. According to the simulation studies, the amount of the biases and MSEs of the CVM, MLE and MPS methods are bigger than other methods initially for both parameters. However, the performances of all estimation methods come closer to each other while the sample size increases. It can be said that the LSE, WLSE and AD methods may be used to obtain inferences from small samples size. Therefore, all methods can be chosen as alternative results for the newly defined model according to large sample sizes. It is noticed that since the MLE and MPS estimation methods have very important properties such as consistency, efficiency and asymptotic normality, they offer many advantages in terms of inferences. Similar results can be also obtained for different parameter settings.

Fig. 4

The results of on the parameters $\alpha$ (top) and $\beta$ (bottom) for the first simulation study

Fig. 5

The results of the parameters $\alpha$ (top) and $\beta$ (bottom) for the second simulation study

Moreover, we also give a simulation study based on above results of the MLEs for the efficiency of the 95% confidence intervals. We use the coverage length (CL) criteria to see the performance of the MLEs. For $\epsilon =\alpha$ or $\beta$, the estimated CLs are given by

$$\begin{aligned} CL_{\epsilon } (n) = \frac{3.919928}{N}\sum \limits _{i = 1}^N {s_{{\hat{\epsilon }} _i } }, \end{aligned}$$

where $s_{{\hat{\epsilon }}_i}$ is the standard error of the MLE $\epsilon$ at the $i^{th}$ sample (which is evaluated by inverting the observed information matrix).

Figure 6 displays the simulation results for CLs. As seen from Fig. 6, as expected, when the sample size increases the CL decreases for each parameter.

Fig. 6

The estimated ALs for the first (left) and second (right) simulation studies

6 An alternative quantile regression model

The quantile regression has been originally proposed by Koenker and Bassett (1978) as a way to model the conditional quantiles of an outcome variable as a function of explanatory variables without any distributional assumptions on the error term. When the response variable has a skewed distribution or outliers in the measurements, robust estimation results based on the regression model are needed for the model inference. For this reason, the quantile regression is a good robust alternative model to the ordinary LSE model, which estimates the conditional mean of the response variable. In other words, quantile regression can be thought of as an extension of linear regression used when the conditions of linear regression are not met. The quantile regression has also been applied to the analysis of continuous bounded outcomes (see, e.g., Jung 1996; Geraci and Bottai 2007; Liu and Bottai 2009; Bottai et al. 2010). Since the moments of the UBXII distribution are not obtained with a closed-form, its mean is not obtained with a simple term. Although it has no moments with closed-form, its qf given is very manageable. So, we are also motivated with quantile regression modeling thanks to its nice statistical property.

On the other hand, if the support of the response variable is defined on the unit interval, a unit regression model based on the unit distribution can be used for modeling the conditional mean or quantiles of the response variable via independent variables (covariates). No doubt that the beta regression Ferrari and Cribari-Neto (2004) model comes to mind firstly to relate with continuous mean response variables in the standard unit interval with covariates. However, using the beta regression model may not be suitable when the unit response variable has a skewed distribution because the mean is affected by the skewing of the distribution precisely. If the conditional dependent variable is skewed, especially, the median may be more appropriate when compared with the mean Mazucheli et al. (2020).

With the re-parameterizing the probability distribution as a function of the quantile approach, the Kumaraswamy Mitnik and Baek (2013), Bayes et al. (2017) and unit Weibull Mazucheli et al. (2020) quantile regression models have been proposed for modeling the conditional quantiles of the unit response. In light of these references, this Section aims to introduce an alternative quantile regression model considering a parametrization of the UBXII distribution in terms of any quantile. The re-parameterizing process has been applied via a shape parameter as being a quantile of the UBXII distribution. Now, we introduce an alternative quantile regression based on the UBXII distribution.

6.1 The UBXII distribution based on the its quantiles

Since the qf of the UBXII distribution is a very tractable analytic equation, its pdf and cdf can be re-parameterized in terms of its quantiles easily. Firstly, the pdf of the UBXII distribution can be given with a re-parameterization based on its qf given in Equation (4). Let $\mu =Q(u,\alpha , \beta )$ and $\beta = {{\log \left( {u^{ - 1/\alpha } - 1} \right) } / {\log \left( { - \log \mu } \right) }}$. Then, the pdf and cdf of the re-parameterized distribution are given by

$$\begin{aligned} g(y,\alpha ,\mu ) = \frac{{\log \left( {u^{ - 1/\alpha } - 1} \right) ^\alpha }}{{\log \left( { - \log \mu } \right) ^y }}\left( { - \log y} \right) ^{{\textstyle {{\log \left( {u^{ - 1/\alpha } - 1} \right) } \over {\log \left( { - \log \mu } \right) }}} - 1} \left( {1 + \left( { - \log y} \right) ^{{\textstyle {{\log \left( {u^{ - 1/\alpha } - 1} \right) } \over {\log \left( { - \log \mu } \right) }}}} } \right) ^{ - \alpha - 1} \end{aligned}$$

(14)

and

$$\begin{aligned} G(y,\alpha ,\mu ) = \left( {1 + \left( { - \log y} \right) ^{{\textstyle {{\log \left( {u^{ - 1/\alpha } - 1} \right) } \over {\log \left( { - \log \mu } \right) }}}} } \right) ^{ - \alpha }, \end{aligned}$$

(15)

respectively, where $\alpha >0$ is the shape parameter, the parameter $\mu \in (0,1)$ represents the quantile parameter, and u is known. A random variable Y having this pdf is denoted by $Y\sim UBXII( \alpha ,\mu ,u)$. Some possible shapes of the quantile distribution are shown in Fig. 7. We see that the possible pdf shapes the distribution are bathtub shaped, inverse N-shaped and unimodal. It is noticed that we must have either $u> 2^{-\alpha }$ and $\mu > e^{-1}$, either $u < 2^{-\alpha }$ and $\mu < e^{-1}$.

Fig. 7

The pdf shapes of the UBXII quantile distribution

6.2 The UBXII quantile regression model

Now, we focus on the quantile regression model based on the UBXII distribution with pdf in Eq. (14). Let $y_1,y_2,\ldots ,y_n$ such that $y_i$ is an observation of $Y_i\sim UBXII(\alpha ,\mu _i ,u)$ for $i=1,\ldots ,n$, with unknown parameters $\mu _i$ and $\alpha$. Note that the parameter u is known. Then, the new quantile regression model is defined as

$$\begin{aligned} g({\mu _i})= \varvec{\mathrm {x}}_{i}\varvec{ \delta }^T, \end{aligned}$$

where $\varvec{\delta }= {\left( {{\delta _0},{\delta _1},{\delta _2} ,\ldots ,{\delta _p}} \right) ^T}$ and $\varvec{\mathrm {x}}_{i}= {\left( {1,{x_{i1}},{ x_{i2}},{x_{i3}},\ldots ,{x_{ip}}} \right) }$ are the unknown regression parameter vector and known $i^{th}$ vector of the covariates. The function g(x) is the link function which is used to relate the covariates to conditional quantile of the response variable. For instance, when the parameter $u=0.5$, the covariates are linked to the conditional median of the response variable. Since the UBXII distribution is defined on the unit-interval, we use the logit-link function such that

$$\begin{aligned} g({\mu _i})= \mathrm{logit}({\mu _i})= \log \left( {\frac{{\mu _i}}{{1 - {\mu _i}}}} \right) ,\quad i = 1,2 \ldots n. \end{aligned}$$

Alternatively, the probit and log-log link functions can be used for linking to conditional quantiles of the response variable.

6.3 Parameter estimation

We point out the unknown parameters of the UBXII quantile regression model to obtain them via the MLE method. Thus, we consider

$$\begin{aligned} g( {\mu _i} )= \log \left( {\frac{{\mu _i}}{{1 - {\mu _i}}}} \right) = \varvec{\mathrm {x}}_{i}\varvec{\delta }^T. \end{aligned}$$

(16)

From Equation (16), the following relation is obtained

$$\begin{aligned} {\mu _i} = \frac{{\exp \left( \varvec{\mathrm {x}}_{i} \varvec{\delta }^T \right) }}{{1 + \exp \left( \varvec{\mathrm {x}}_{ i}\varvec{\delta }^T \right) }}. \end{aligned}$$

(17)

Let $Y_{1},Y_{2},\dots ,Y_{n}$ be a random sample of size n with $Y_i \sim UBXII (\alpha , \mu _i, u)$ and observed values $y_{1},y_{2},\dots ,y_{n}$, where the $\mu _i$ is given by (17) for $i=1,\ldots ,n$. Then using Equation (14), the associated log-likelihood function is given by

$$\begin{aligned}&\ell \left( \varvec{\Omega }\right) = n\log \alpha + n\log \left[ {\log \left( {u^{ - 1/\alpha } - 1} \right) } \right] - \sum \limits _{i = 1}^n {\log y_i } - \sum \limits _{i = 1}^n {\log \left[ {\log \left( { - \log \mu _i } \right) } \right] } \nonumber \\&\quad - \sum \limits _{i = 1}^n {\left( {{\textstyle {{\log \left( {u^{ - 1/\alpha } - 1} \right) } \over {\log \left( { - \log \mu _i } \right) }}} - 1} \right) \log \left( { - \log y_i } \right) } - \left( {\alpha + 1} \right) \sum \limits _{i = 1}^n {\log \left( {1 + \left( { - \log y_i } \right) ^{{\textstyle {{\log \left( {u^{ - 1/\alpha } - 1} \right) } \over {\log \left( { - \log \mu _i } \right) }}}} } \right) } , \end{aligned}$$

(18)

where $\varvec{\Omega }=\left( \alpha , \varvec{\delta } \right) ^{T}$ is the unknown parameter vector. The MLEs of $\varvec{\Omega }$, say ${\varvec{{\hat{\Omega }} }}=\left( {\hat{\alpha }}, \varvec{{\hat{\delta }} } \right) ^{T}$, is obtained by maximizing $\ell \left( \varvec{\Omega }\right)$ with respect to $\varvec{\Omega }$. Since Equation (18) includes nonlinear function according to model parameters, it can be maximized directly by software such as R, S-Plus, and Mathematica.

It can be noticed that, when $u=0.5$, it is equivalent to model the conditional median. Under mild regularity conditions, the asymptotic distribution of $\left( {{\varvec{{\hat{\Omega }} }} - {\varvec{\Omega }}} \right)$ is multivariate normal $N_{p + 1} \left( 0, I \right)$, where I is the inverse of the expected information matrix. One may use the $(p + 1) \times (p + 1)$ observed information matrix instead of I. The elements of this observed information matrix are evaluated numerically by the software. We use the maxLik function (see Henningsen and Toomet 2011) of R software to maximize Equation (18). This function also gives asymptotic standard errors numerically, which are obtained by the observed information matrix.

6.4 Residual analysis

The residual analysis can be needed to check whether the regression model is suitable. In order to see this, we will point out the randomized quantile residuals (see Dunn and Smyth 1996) and the Cox-Snell residuals (see Cox and Snell 1968).

For $i=1,\ldots ,n$, the $i^{th}$ randomized quantile residual is defined by

$$\begin{aligned} {{\hat{r}}_{i}}=\Phi ^{-1}\left[ G(y_i, \hat{\alpha }, {\hat{\mu }}_i)\right] , \end{aligned}$$

where the $G(y,\alpha , \mu )$ is the cdf of the re-parameterized UBXII distribution given by Equation (15), $\Phi ^{-1}(x)$ is the qf of the standard normal distribution, and ${\hat{\mu }}_i$ is defined by Equation (17) with $\varvec{{\hat{\delta }} }$ instead of $\varvec{\delta }$. If the fitted model successfully deals with the data set, the distribution of the randomized quantile residuals will correspond to the standard normal distribution.

Alternatively, for $i=1,\ldots ,n$, the $i^{th}$ Cox and Snell residual is given by

$$\begin{aligned} {{\hat{e}}_{i}}=-\log \left[ 1-G(y_i, \hat{\alpha }, {\hat{\mu }}_i)\right] . \end{aligned}$$

If the model fits to data accordingly, the distribution of these residuals will distribute the exponential distribution with scale parameter 1.

7 Data analysis

This section provides two real data sets applications for illustrating the modeling ability of the UBXII distribution. The first data set is about univariate real data modeling and the other is about quantile regression modeling. The used data set for both applications consists of some measurements about 239 patients who consented to autologous peripheral blood stem cell (PBSC) transplant after myeloablative doses of chemotherapy between the years 2003 and 2008 at the Edmonton Hematopoietic Stem Cell Lab in Cross Cancer Institute - Alberta Health Services. Autologous PBSC transplants have been widely used for rapid hematologic recovery following myeloablative therapy for various malignant hematological disorders. The data set informs about the patients age, gender, as well as their clinical characteristics such as recovery rates for viable CD34+ cells and chemotherapy receiving of the patients. The data set can be easily found in the simplexreg package, proposed by Zhang et al. (2016), of the R software. We use variable recovery rates of the viable CD34+ cells for univariate data modeling and relate this recovery rate with some covariates in the data set for the second application. The calculations have been obtained by the maxLik (see Henningsen and Toomet 2011) and goftest functions of the R software. The details are the following.

7.1 Univariate modeling for the recovery rates of the viable CD34+ cells data

Here, used data is recovery rates of the viable CD34+ cells of the 239 patients, who consented to autologous PBSC transplant after myeloablative doses of chemotherapy. Some summary statistics and box plot of the data set have been given by Table 1 and Fig. 8. As it can be seen that the data is left skewed and some observations can be considered as outliers.

Table 1 Some summary statistics of the data set

Fig. 8

The box plot of the data set

Based on this data set, we also compare fitting performances of the proposed distribution under the MLE method with well known unit distributions in the literature. These comparing distributions have the following pdfs:

• Beta distribution:

  $$\begin{aligned} f_{Beta}(x,\alpha ,\beta ) = \frac{1}{B(\alpha , \beta )}x^{\alpha -1}\left( {1-x}\right) ^{\beta -1}, \end{aligned}$$

  where $x\in (0,1)$, $\alpha >0$, $\beta >0$ and $B(\alpha ,\beta )$ denotes the classical beta function.

• Johnson $S_{B}$ distribution:

  $$\begin{aligned} f_{S_{B}}(x,\alpha ,\beta ) =\frac{\beta }{{x\left( {1-x} \right) }}\phi \left[ {\beta \log \left( \frac{x}{1-x} \right) +\alpha }\right] \end{aligned}$$

  where $x\in (0,1)$, $\alpha \in {\mathbb {R}}$, $\beta >0$ and $\phi (x)$ denotes the pdf of the standard normal distribution.

• Kumaraswamy (Kw) distribution:

  $$\begin{aligned} f_{Kw}(x,\alpha ,\beta ) =\alpha \beta x^{\alpha -1}\left( { 1-x^{\alpha }}\right) ^{\beta -1}, \end{aligned}$$

  where $x\in (0,1)$, $\alpha >0$ and $\beta >0$.

• Standard two-sided power (STSP) distribution (see van Dorp and Kotz 2002):

  $$\begin{aligned} f_{STSP}(x,\alpha ,\beta ) =\left\{ \begin{array}{l} \beta \displaystyle \left( \frac{x}{\alpha } \right) ^{\beta -1},\quad x\in (0,\alpha ) \\ \beta \displaystyle \left( \frac{1-x}{1-\alpha }\right) ^{\beta -1},\quad x\in (\alpha , 1), \\ \end{array} \right. \end{aligned}$$

  where $\alpha \in (0,1)$ and $\beta >0$.

We use the estimated log-likelihood values $\hat{\ell }$, Akaike information criteria (AIC), Bayesian information criterion (BIC), Kolmogorov–Smirnov (KS), Cramér-von-Mises ($W^{*}$ ) and Anderson–Darling ($A^{*}$) goodness of-fit statistics criteria to determine the optimum model. The optimum model will have the smaller the values of the AIC, BIC, KS, $W^{*}$ and $A^{*}$ statistics and the larger the values of $\hat{\ell }$ and p-value of the goodness-of-statistics.

We give the estimates and the values of goodness-of-fits statistics in Table 2. In particular, Table 2 indicates that the UBXII distribution has the lowest values of AIC and BIC statistics as well as it has the lowest values of $A^{*}$ and $W^{*}$ and K-S statistics with higher p-value. These results show that the UBXII distribution is the best model for the considered data set.

Table 2 MLEs, standard errors (SE) of the estimates (in parentheses), ${\hat{\ell }}$ and goodness-of-fits statistics for the data set (p value is given in $[ \cdot ]$)

Figure 9 presents the estimated pdfs, cdfs, and, the quantile–quantile (QQ) plot of the UBXII model to see how they are the suitability for data set graphically. From this figure, it can be said that the UBXII model has fitted by successfully capturing the skewness and kurtosis of the data set. The QQ plot indicates that the fitting performance of the UBXII distribution is suitable for the data.

Fig. 9

The fitted pdfs (left), cdfs (center) and QQ plot (right) of the UBXII model

Further, to show the likelihood equations have a unique solution, we plot the PLL functions of the parameters $\alpha$ and $\beta$ for the data set in Fig. 10. From this figure, we see that the likelihood equations have a unique solution for the MLEs.

Fig. 10

The plots of the PLL functions for the data set

7.2 Quantile regression modeling for the recovery rates of the viable CD34+ cells data

To see the applicability of the UBXII regression model, this section presents a real application based on the above data set. The aim is to associate these response values (y) with covariates. The response variable y and covariates associated with this response variable are:

• y: recovery rate of CD34+cells;

• $x_1$ (Gender): 0 for female, 1 for male;

• $x_2$ (Chemotherapy): 0 for receiving chemotherapy on a one-day protocol, 1 for a 3-day protocol;

• $x_3$ (Age): adjusted patient’s age, i.e. the current age minus 40.

This data set has been analyzed by Mazucheli et al. (2020). Since the response variable has some observed outliers, the use of the quantile regression will be better for its inferences. Two competitor regression models, which are well-known literature, are considered and compared to the UBXII quantile regression model. They are the beta regression (see Ferrari and Cribari-Neto 2004) and Kumaraswamy quantile regression (see Mitnik and Baek 2013) models. Their pdfs are

$$\begin{aligned} f(y,\alpha , \mu ) = \frac{{\Gamma \left( \alpha \right) }}{{\Gamma \left( {\alpha \mu } \right) \Gamma \left( {\left( {1 - \mu } \right) \alpha } \right) }}y^{\alpha \mu - 1} \left( {1 - y} \right) ^{\left( {1 - \mu } \right) \alpha - 1} ,\quad y\in (0,1), \end{aligned}$$

where $\mu \in (0,1)$ is the mean and $\alpha >0$ and

$$\begin{aligned} f(y,\alpha , \mu ) = \frac{{\alpha \log \left( {0.5} \right) }}{{\log \left( {1 - \mu ^\alpha } \right) }}y^{\alpha - 1} \left( {1 - y^\alpha } \right) ^{\log \left( {0.5} \right) /\left( {\alpha \left( {1 - \mu } \right) - 1} \right) } , \quad y\in (0,1), \end{aligned}$$

where $\mu \in (0,1)$ is the median and $\alpha >0$, for the beta and Kumaraswamy quantile regression models, respectively.

The regression model based on $\mu _i$ is given by

$$\begin{aligned} \mathrm{{logit}}\left( {\mu _i } \right) = \delta _0 + \delta _1 x_{i1} + \delta _2 x_{i2}, + \delta _3 x_{i3}\quad i = 1,2, \ldots ,239. \end{aligned}$$

It is noticed that the quantile parameter u is taken 0.5 for the UBXII and Kumaraswamy quantile regression models. We give the results of the regression analysis in Table 3. From this table, parameter estimations of all models are greater than zero. It means that if there is any relation statistically significant between the recovery rate of CD34+cells and covariates, they will affect the recovery rate of CD34+cells positively. The parameter $\delta _1$ has not been seen statistically significant at usual level for all regression models. So, the gender variable has no effect on the response variable recovery rate. However, the parameters $\delta _2$ and $\delta _3$ have been seen statistically significant at 7% level for the UBXII regression model. Hence, the recovery rate of the old patients is higher than the young patients as well as the recovery rate of the patients who are receiving chemotherapy on a 3-day protocol is higher than those of the patients who are receiving chemotherapy on a one-day protocol.

Further, the UBXII regression model has lower values of the AIC and BIC statistics have an upper log-likelihood value than those of other regression models. So, it can be concluded that the proposed regression model is the best model among application models in terms of better modeling ability than other regression models.

Table 3 The results of fitted regression models with model selection criteria

Figures 11 and 12 display the QQ plots of the randomized quantile residuals and PP plots of the Cox-Snell residuals for all regression models, respectively. These figures indicate that the fitting of the UBXII regression model is better than those of the beta and Kumaraswamy models.

Fig. 11

The QQ plot of the randomized quantile residuals based on the regression application

Fig. 12

The PP plots of the Cox-Snell residuals based on the regression application

Since the distribution behind the randomized quantile residuals are theoretically in adequateness with a standard normal distribution, one may see whether they fit this corresponding distribution. The KS, $A^{*}$ and $W^{*}$ results are given in Table 4. From this table, it is clear that the results based on the UBXII quantile regression model of the randomized quantile residuals are more suitable than those of the beta and Kumaraswamy regression models.

Table 4 The goodness-of-fit results of the randomized quantile residuals for the regression models

8 Conclusion

We define a new unit model, called unit Burr-XII distribution, in order to model percentage, proportion and rate measurements. We investigate general structural properties of the new distribution. The model parameters are estimated by the six different methods. The simulation studies are performed to see the performances of these estimates. The empirical findings indicate that the proposed model provides better fits than the well-known unit probability distributions in the literature for both its univariate data modeling and its regression modeling. It is hoped that the new distribution will attract attention in the other disciplines.