1 Introduction

The bounded distributions are essential for modeling proportions, percentages, especially observed in economic variables such as proportion of income spent, industry market shares, etc. The beta (Ferrari and Cribari-Neto 2004) and simplex (Kieschnick and McCullough 2003) regression models are commonly used approaches for modeling proportions in economics, actuarial, ecology and environmental sciences. Although the beta distribution is widely used in several areas of sciences, it has some shortcomings. One of them is that its cumulative distribution function (cdf) is a special function. These type of special functions increase the computational time and complexity in statistical inference. The Topp–Leone model (Topp and Leone 1955) can be viewed as other widely used unit distribution. It has increased its popularity after the work of Nadarajah and Kotz (2003). One of its most important property is that its cdf has a simple form. The Kumaraswamy distribution (Kumaraswamy 1980) is another distribution defined on the unit interval which has increased its popularity after the article of Cordeiro and de Castro (2011). The unit-Gamma distribution (Grassia 1977) is also a widely used distribution in modeling the bounded data sets. Mazucheli et al. (2018a) studied the parameter estimation of its model parameters based on the bias-corrected maximum likelihood estimation method.

In recent years, several researchers have shown a great interest to define new distributions on bounded supports. Mazucheli et al. (2018b) proposed the unit-Birnbaum-Saunders distribution and demonstrated its performance in modeling the monthly water capacity. Recently, Mazucheli et al. (2019) introduced the unit-Lindley distribution and analyzed the access of people in households with inadequate water supply and sewage in the cities of Brazil using the unit-Lindley and beta regression models. Gómez-Déniz et al. (2014) studied the log-Lindley distribution with application to insurance data. Altun and Hamedani (2018) introduced the log-xgamma distribution and studied its statistical properties. Altun (2019) introduced the log-weighted exponential distributions and its associated regression model. The goal of this paper is to propose a new distribution defined on the unit interval which has tractable statistical properties. It arises from the improved second-degree Lindley (ISDL) distribution (Karuppusamy et al. 2017) and has several advantages over well-known models such as the beta, Kumaraswamy and Topp–Leone distributions. Some of its statistical properties are determined in closed-form, such as probability density function (pdf), ordinary and incomplete moments. More importantly, it can provide better fits than other well-known distributions defined on the unit interval. Moreover, a new regression model based on the proposed distribution is investigated as a useful alternative to the beta regression model.

The rest of the paper is organized as follows. In Sect. 2, we define the new distribution and obtain some of its mathematical properties. In Sect. 3, we estimate the model parameters using five different methods: maximum likelihood, bias-corrected maximum likelihood, moments, least squares and weighted least squares. In Sect. 4, a Monte-Carlo simulation study is conducted to evaluate the finite sample performance of the estimation methods. In Sect. 5, we introduce a new regression model based on the proposed distribution as an alternative to the beta regression model. In Sect. 6, two real data sets are analyzed to prove empirically the flexibility of the new models. Some conclusions are offered in Sect. 7.

2 The unit-ISDL distribution

The Lindley density is

$$\begin{aligned} f({x;\theta }) = \frac{{{\theta ^2}}}{{1 + \theta }}\left( {1 + x} \right) \exp \left( {- \theta x} \right) ,\quad x > 0, \end{aligned}$$

where \(\theta >0\) is the scale parameter. The Lindley distribution is a mixture of the \(\text {Exponential}\left( \theta \right) \) and \(\text {Gamma}\left( 2,\theta \right) \) distributions. Its cdf is

$$\begin{aligned} F({x;\theta }) = 1 - \frac{{\theta + 1 + \theta x}}{{\theta + 1}}\exp \left( { - \theta x} \right) ,\quad x \ge 0. \end{aligned}$$

Most of its statistical properties such as moments, stochastic ordering and entropies were obtained by Ghitany et al. (2008). Recently, Karuppusamy et al. (2017) introduced the ISDL density

$$\begin{aligned} f({x;\lambda }) = \frac{{{\lambda ^3}}}{{{\lambda ^2} + 2\lambda + 2}}{\left( {1 + x} \right) ^2}\exp \left( { - \lambda x} \right) ,\quad x > 0, \end{aligned}$$
(1)

where \(\lambda >0\) is the shape parameter. The cdf corresponding to (1) is

$$\begin{aligned} F\left( {x;\lambda } \right) = 1 - \left[ {1 + \frac{{{\lambda ^2}{x^2} + 2\left( {{\lambda ^2} + \lambda } \right) x}}{{{\lambda ^2} + 2\lambda + 2}}} \right] \exp \left( { - \lambda x} \right) ,\quad x \ge 0. \end{aligned}$$

The ISDL density can be expressed as a mixture of the \(\text {Gamma}(1,\lambda )\), \(\text {Gamma}(2,\lambda )\) and \(\text {Gamma}(3,\lambda )\) densities. So, Eq. (1) can be rewritten as follows

$$\begin{aligned} f( {x;\lambda }) = {p_1}{f_1}( x) + {p_2}{f_2}( x) + {p_3}{f_3}( x), \end{aligned}$$
(2)

where

$$\begin{aligned} {p_1} = \frac{{{\lambda ^2}}}{{{\lambda ^2} + 2\lambda + 2}},\quad {p_2} = \frac{{2\lambda }}{{{\lambda ^2} + 2\lambda + 2}},\quad {p_3} = \frac{2}{{{\lambda ^2} + 2\lambda + 2}}, \end{aligned}$$
(3)

and

$$\begin{aligned} {f_1}( x) = \lambda \exp ( { - \lambda x} ),\quad {f_2}( x) = {\lambda ^2}x\exp ( { - \lambda x} ),\quad {f_3}( x ) = {{{\lambda ^3}{x^2}\exp ( { - \lambda x})} / 2}. \end{aligned}$$
(4)

Substituting (3) and (4) in (2), we find the ISDL density (1). Some statistical properties of the ISDL distribution can be easily obtained from those of the Gamma distribution. Here, we introduce a new distribution on the unit-interval by taking the ISDL distribution as the baseline model.

Proposition 1

Let X be a random variable with pdf (1) and define the random variable \(Y = {X / {( {X + 1})}}\). Then, the pdf of Y is

$$\begin{aligned} f({y;\lambda })=\frac{{{\lambda ^3}{{( {1 - y})}^{ - 2}}}}{{{\lambda ^2} + 2\lambda + 2}}{\left( {1 + \frac{y}{{1 - y}}} \right) ^2}\exp \left( { - \frac{{y\lambda }}{{1 - y}}} \right) ,\quad 0<y < 1, \end{aligned}$$
(5)

where \(\lambda >0\) is the shape parameter. Hereafter, the random variable Y having density (5) is denoted by \(Y\sim \text {unit-ISDL}(\lambda )\).

Note that the density given in (5) could be introduced for a three-component general mixture of Gamma densities using the same transformation. However, it increases the model complexity and its statistical properties cannot be obtained in closed-form. Therefore, particular case of a three-component general mixture of Gamma is used. The cdf corresponding to (5) (for \(0 \le y \le 1\)) is

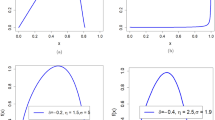
$$\begin{aligned} F({y;\lambda }) = 1 - \left[ {1 + \frac{{{\lambda ^2}{{( {{y / {( {1 - y})}}} )}^2} + 2( {{\lambda ^2} + \lambda } ){y / {( {1 - y}}}}}{{{\lambda ^2} + 2\lambda + 2}}} \right] \exp \left( { - \frac{{y\lambda }}{{1 - y}}} \right) . \end{aligned}$$
(6)

Figure 1 displays some possible unit-ISDL density shapes. It can be a good choice for modeling extremely left or right skewed data sets.

Fig. 1
figure 1

Plots of the unit-ISDL density for some parameter values

Full size image

Random values from \(Y\sim \text {unit-ISDL}(\lambda )\) are generated by solving \(F({y;\lambda })=u\), where \(u\sim uniform(0,1)\). The uniroot function of R software can be used to solve this non-linear equation.

2.1 Moments

The kth ordinary moment of Y takes the form

$$\begin{aligned} E({{Y^k}}) = \int \limits _0^1 {{y^k}}\,\frac{{{\lambda ^3}{{( {1 - y} )}^{ - 2}}}}{{{\lambda ^2} + 2\lambda + 2}}{\left( {1 + \frac{y}{{1 - y}}} \right) ^2}\exp \left( {-\frac{{y\lambda }}{{1 - y}}} \right) dy. \end{aligned}$$

The above integration can not be carried out analytically but only numerically. In particular,

$$\begin{aligned} E(Y) = \frac{{\lambda + 2}}{{{\lambda ^2} + 2\lambda + 2}}\quad \text {and}\quad E(Y^2) = \frac{{ 2}}{{{\lambda ^2} + 2\lambda + 2}}. \end{aligned}$$

The variance of Y follows easily from these results as

$$\begin{aligned} Var(Y) = \frac{2}{{{\lambda ^2} + 2\lambda + 2}} - \frac{{{{( {\lambda + 2} )}^2}}}{{{{( {{\lambda ^2} + 2\lambda + 2} )}^2}}}. \end{aligned}$$

Clearly, the mean and variance of the unit-ISDL distribution decrease when \(\lambda \) increases.

2.2 Incomplete moments

The rth incomplete moment of Y is

$$\begin{aligned} {m_r}(t) = E( {\left. {{Y^r}} \right| y < t}) = \frac{{{\lambda ^3}}}{{{\lambda ^2} + 2\lambda + 2}}\int \limits _0^t {\frac{{{y^r}}}{{{{( {1 - y} )}^2}}}{{\left( {1 + \frac{y}{{1 - y}}} \right) }^2}\exp \left( { - \frac{{\lambda y }}{{1 - y}}} \right) dy}. \end{aligned}$$

The above integration can not be carried out analytically. In particular, for \(r=1\), we have

$$\begin{aligned} {m_1}(t)=\frac{{\lambda } + 2}{{{\lambda }}^2 + 2\, {\lambda } + 2} - \frac{\exp \left( \frac{{\lambda }\, t}{t - 1}\right) ({{\lambda }}^2\, t - {\lambda }\, t^2 + {\lambda } + 2\, t^2 - 4\, t + 2)}{{(t - 1)}^2\, ({{\lambda }}^2 + 2\, {\lambda } + 2)}. \end{aligned}$$

The first incomplete moment can be used to obtain the mean deviations and Lorenz and Bonferroni curves that are fundamental tools for analyzing data in economics and reliability.

2.3 Exponential family

A distribution belongs to the exponential family if it can be expressed as

$$\begin{aligned} f({y ;\lambda })=\exp [{Q( \lambda )T( y ) + D( \lambda ) + S( y)} ]. \end{aligned}$$

It is clear that the unit-ISDL distribution belongs to the exponential family by rewriting (5) as

$$\begin{aligned} f({y;\lambda })= & {} \exp \left[ {- \frac{{y\lambda }}{{1 - y}}} \right] \,\exp \left[ {\ln \left( {\frac{{{\lambda ^3}}}{{{\lambda ^2} + 2\lambda + 2}}} \right) } \right] \\&\exp \left[ {{-2\ln {( {1 - y})}} + 2\ln \left( {1 + \frac{y}{{1 - y}}} \right) } \right] , \end{aligned}$$

where \(Q(\lambda )=\lambda \), \(T(y) = {y / {( {1 - y})}}\),

$$\begin{aligned} S( y) = {-2\ln ( {1 - y} )} + 2\ln \left( {1 + \frac{y}{{1 - y}}} \right) \quad \text {and}\quad D( \lambda ) = \ln \left( {\frac{{{\lambda ^3}}}{{{\lambda ^2} + 2\lambda + 2}}} \right) . \end{aligned}$$

Here, \(T( \mathbf {y}) = \sum \nolimits _{i = 1}^n {{{{y_i}} / {( {1 - {y_i}} )}}} \) is the sufficient statistic for \(\lambda \).

2.4 Comparison of the unit-ISDL and unit-Lindley distributions

The unit-ISDL density has similar shapes of the unit-Lindley density. It is needed to clarify the differences between these two distributions. Therefore, the skewness and kurtosis measures of these two distributions are compared. Moreover, the tail-properties are also discussed. Figure 2 displays the numerical results for the skewness and kurtosis measures of the unit-ISDL and unit-Lindley distributions. The plots in Fig. 2 reveal that the skewness and kurtosis values of the unit-ISDL distribution have wider ranges than those of the unit-Lindley distribution. It is clear that the unit-ISDL distribution is a better choice than the unit-Lindley distribution for modeling left-skewed and leptokurtic data.

Fig. 2
figure 2

Plots of the skewness and kurtosis measures of the unit-ISDL and unit-Lindley distributions

Full size image

Table 1 gives the tail probabilities of the unit-Lindley and unit-ISDL distributions for selected parameter values. These probabilities indicate that the left tail of the unit-ISDL distribution is thinner than that one of the unit-Lindley distribution. Therefore, the new distribution can be preferable than the unit-Lindley for modeling left-skewed and thin-tailed data.

Table 1 The tail probabilities of the unit-Lindley and unit-ISDL distributions for selected parameter values
Full size table

3 Estimation

In this section, we consider the methods of maximum likelihood, moments, least squares and weighted least squares to estimate the unknown parameter of the unit-ISDL distribution.

3.1 Maximum likelihood

Let \(y_{1},\ldots ,y_{n}\) be a random sample from the \(\text {unit-ISDL}\) distribution. The log-likelihood function for \(\lambda \) is

$$\begin{aligned} \ell (\lambda ) \propto 3n\ln ( \lambda ) - n\ln ( {{\lambda ^2} + 2\lambda + 2} ) - \lambda t( \mathbf {y} ), \end{aligned}$$
(7)

where \(t( \mathbf {y} ) = \sum \nolimits _{i = 1}^n {{{{y_i}} / {( {1 - {y_i}} )}}} \). By differentiating (7) with respect to \(\lambda \) gives

$$\begin{aligned} \frac{{\partial \ell }}{{\partial \lambda }} = \frac{{3n}}{\lambda } - \frac{{n( {2\lambda + 2} )}}{{{\lambda ^2} + 2\lambda + 2}} - t\left( \mathbf {y} \right) \end{aligned}$$
(8)

Solving (8) for zero, the maximum likelihood estimate (MLE) of \(\lambda \), say \(\hat{\lambda }\), is

$$\begin{aligned} \hat{\lambda }= & {} \frac{1}{{3z }}\left[ {{{\left( {10{z ^3} + {n^3} + 12z {n^2} + 3\sqrt{6} \sqrt{2{z ^6} + {z ^2}{n^4} + 14{z ^3}{n^3} + 54{z ^4}{n^2} + 16{z ^5}n} + 48{z ^2}n} \right) }^{\frac{1}{3}}}} \right] \\&- \,( {2{z ^2} - {n^2} - 8z n} )\\&\times {\left[ {3z {{\left( {10{z ^3} + {n^3} + 12z {n^2} + 3\sqrt{6} \sqrt{2{z ^6} + {z ^2}{n^4} + 14{z ^3}{n^3} + 54{z ^4}{n^2} + 16{z ^5}n} + 48{z ^2}n} \right) }^{\frac{1}{3}}}} \right] ^{ - 1}}\\&-\, \frac{{2z - n}}{{3z }}, \end{aligned}$$

where \(z=t(\mathbf {y})\). The second-order derivative of (7) with respect to \(\lambda \) is

$$\begin{aligned} \frac{{{\partial ^2}\ell }}{{\partial {\lambda ^2}}} = - \frac{{n( {{\lambda ^4} + 8{\lambda ^3} + 24{\lambda ^2} + 24\lambda + 12} )}}{{{\lambda ^2}{{( {{\lambda ^2} + 2\lambda + 2} )}^2}}}. \end{aligned}$$

Hence, the expected information is

$$\begin{aligned} I(\lambda )= E\left( { - \frac{{{\partial ^2}\ell }}{{\partial {\lambda ^2}}}} \right) = \frac{{n( {{\lambda ^4} + 8{\lambda ^3} + 24{\lambda ^2} + 24\lambda + 12})}}{{{\lambda ^2}{{( {{\lambda ^2} + 2\lambda + 2} )}^2}}}. \end{aligned}$$
(9)

The asymptotic variance of \(\hat{\lambda }\) is easily obtained by inverting (9)

$$\begin{aligned} Var({\hat{\lambda }}) = \frac{{{\lambda ^2}{{( {{\lambda ^2} + 2\lambda + 2} )}^2}}}{{n( {{\lambda ^4} + 8{\lambda ^3} + 24{\lambda ^2} + 24\lambda + 12} )}}. \end{aligned}$$

The equi-tailed \(100(1-p)\%\) confidence interval (CI) for \(\lambda \) is

$$\begin{aligned} \widehat{\lambda } \pm z_{p/2}\sqrt{{Var(\widehat{\lambda })}}, \end{aligned}$$

where \(z_{p/2}\) is the upper p / 2 quantile of the standard normal distribution.

3.2 Bias-corrected maximum likelihood

We adopt a “corrective” approach to reduce the bias of \(\hat{\lambda }\) to order \(O(n^{-2})\) since the MLE is biased to order \(O(n^{-1})\) in finite samples. Following Cox and Snell (1968), when the observations are independent but not necessarily identically distributed, the bias-correction of \(\hat{\lambda }\) can be expressed as

$$\begin{aligned} \mathrm{B}( {\hat{\lambda }})={( {{\kappa ^{11}}} )^2}\left( {\frac{1}{2}{\kappa _{111}} + {\kappa _{11,1}}} \right) + O( {{n^{ - 2}}} ), \end{aligned}$$

where \({\kappa ^{11}} = E{\left( { - \frac{{{\partial ^2}\ell }}{{\partial {\lambda ^2}}}} \right) ^{ - 1}}\), \({\kappa _{111}} = E\left( { - \frac{{{\partial ^3}\ell }}{{\partial {\lambda ^3}}}} \right) \) and \({\kappa _{11,1}} = E\left( { - \frac{{{\partial ^2}\ell }}{{\partial {\lambda ^2}}}\frac{{\partial \ell }}{{\partial \lambda }}} \right) \). These expressions for the unit-ISDL distribution are

$$\begin{aligned}&{\kappa ^{11}} = \frac{{{\lambda ^2}{{( {{\lambda ^2} + 2\lambda + 2})}^2}}}{{n( {{\lambda ^4} + 8{\lambda ^3} + 24{\lambda ^2} + 24\lambda + 12})}}, \\&{\kappa _{111}} = \frac{{6n}}{{{\lambda ^3}}} - n\left[ {\frac{{2{{( {2\lambda + 2})}^3}}}{{{{( {{\lambda ^2} + 2\lambda + 2} )}^3}}} - \frac{{6( {2\lambda + 2})}}{{{{( {{\lambda ^2} + 2\lambda + 2} )}^2}}}} \right] , \end{aligned}$$

and \({\kappa _{11,1}} = 0\).

Thus, the bias-corrected maximum likelihood estimate (BC-MLE) of \(\lambda \) is

$$\begin{aligned} \tilde{\lambda } = \hat{\lambda } - \frac{{{\lambda ^4}/{{( {{\lambda ^2} + 2\lambda + 2} )}^4}}}{{{n^2}{{( {{\lambda ^4} + 8{\lambda ^3} + 24{\lambda ^2} + 24\lambda + 12} )}^2}}}\left[ {\frac{{3n}}{{{\lambda ^3}}} - \frac{n}{2}\left( {\frac{{2{{( {2\lambda + 2})}^3}}}{{{{( {{\lambda ^2} + 2\lambda + 2} )}^3}}} - \frac{{6( {2\lambda + 2} )}}{{{{( {{\lambda ^2} + 2\lambda + 2} )}^2}}}} \right) } \right] . \end{aligned}$$

3.3 Method of moments

The method of moments (MOM) to estimate \(\lambda \) follows by equating the first theoretical moment of the unit-ISDL distribution to the sample mean, namely

$$\begin{aligned} {\hat{\lambda }_{MOM}} = \frac{{\sqrt{ - 4{{\bar{y}}^2} + 4\bar{y} + 1} - 2\bar{y} + 1}}{{2\bar{y}}}, \end{aligned}$$

where \(\bar{y} =\sum _{i = 1}^n y_i \big /n\).

3.4 Least squares

Let \(y_{(1)},\ldots ,y_{(n)}\) denote the ordered sample of size n from the unit-ISDL distribution. The least squares estimator (LSE) of \(\lambda \) is found by minimizing

$$\begin{aligned} {\sum \limits _{i = 1}^n {\left[ {F({{y_{(i)}}};\lambda ) - \frac{i}{{n + 1}}}\right] } ^2}, \end{aligned}$$
(10)

where \(F({{y_{(i)}}};\lambda )\) is the cdf of the unit-ISDL distribution. Inserting (6) in Eq. (10) gives

$$\begin{aligned} {\sum \limits _{i = 1}^n {\left\{ {1 - \left[ {1 + \frac{{{\lambda ^2}{{\left( {{{{y_{\left( i \right) }}} / {\left( {1 - {y_{(i)}}} \right) }}} \right) }^2} + 2( {{\lambda ^2} + \lambda } ){{{y_{(i)}}} / {\left( {1 - {y_{(i)}}} \right) }}}}{{{\lambda ^2} + 2\lambda + 2}}} \right] \exp \left( { - \frac{{{y_{(i)}}\lambda }}{{1 - {y_{(i)}}}}} \right) - \frac{i}{{n + 1}}} \right\} } ^2}. \end{aligned}$$

3.5 Weighted least squares

The weighted least square estimate (WLSE) of \(\lambda \) follows by minimizing

$$\begin{aligned} \sum \limits _{i = 1}^n {\frac{{{{\left( {n + 1} \right) }^2}\left( {n + 2} \right) }}{{i\left( {n - i + 1} \right) }} {{{\left( \begin{array}{l} 1 - \left[ {1 + \frac{{{\lambda ^2}{{\left( {{{{y_{\left( i \right) }}} / {\left( {1 - {y_{\left( i \right) }}} \right) }}} \right) }^2} + 2( {{\lambda ^2} + \lambda } ){{{y_{\left( i \right) }}} / {\left( {1 - {y_{\left( i \right) }}} \right) }}}}{{{\lambda ^2} + 2\lambda + 2}}} \right] \\ \times \exp \left( { - \frac{{{y_{\left( i \right) }}\lambda }}{{1 - {y_{\left( i \right) }}}}} \right) { - \frac{i}{{n + 1}}} \end{array} \right) }^2}}}. \end{aligned}$$

4 The unit-ISDL regression model

The beta regression model is widely used when the response variable is in the interval (0, 1). We define a new regression model as an alternative to the beta regression model by re-parameterizing the new distribution using a convenient systematic component for the mean.

Let \(\lambda =\left( {\sqrt{- 4{\mu ^2} + 4\mu + 1} - 2\mu + 1} \right) {\left( {2\mu } \right) ^{ - 1}}\). Then, the pdf of the re-parametrized unit-ISDL distribution in terms of \(E(Y)=\mu \) takes the form

$$\begin{aligned} \begin{array}{l} f\left( {y;\mu } \right) = \frac{{{{\left[ {\left( {\sqrt{ - 4{\mu ^2} + 4\mu + 1} - 2\mu + 1} \right) {{\left( {2\mu } \right) }^{ - 1}}} \right] }^3}{{\left( {1 - y} \right) }^{ - 2}}}}{{{{\left[ {\left( {\sqrt{ - 4{\mu ^2} + 4\mu + 1} - 2\mu + 1} \right) {{\left( {2\mu } \right) }^{ - 1}}} \right] }^2} + 2\left( {\sqrt{ - 4{\mu ^2} + 4\mu + 1} - 2\mu + 1} \right) {{\left( {2\mu } \right) }^{ - 1}} + 2}}\\ \times {\left( {1 + \frac{y}{{1 - y}}} \right) ^2}\exp \left( { - \frac{{y\left( {\sqrt{ - 4{\mu ^2} + 4\mu + 1} - 2\mu + 1} \right) {{\left( {2\mu } \right) }^{ - 1}}}}{{1 - y}}} \right) ,\quad 0<y <1, \end{array} \end{aligned}$$
(11)

where \(0<\mu <1\). The covariates are linked to the response variable Y in the usual way through the logit-link function

$$\begin{aligned} {\mu _i} = \frac{{\exp \left( {\pmb x_i^T \pmb {\beta } } \right) }}{{1 + \exp \left( {\pmb x_i^T\pmb {\beta } } \right) }},\quad i = 1,\ldots ,n, \end{aligned}$$
(12)

where \(\pmb x_i^T =\left( {{x_{i1}},\ldots ,{x_{ip}}}\right) \) is the vector of covariates and \(\pmb {\beta }={\left( {{\beta _1},\ldots ,{\beta _p}}\right) ^T}\) is the vector of unknown regression coefficients. Other links can be considered in the similar manner.

Inserting (12) in (11), the log-likelihood function can be expressed as

$$\begin{aligned} \begin{array}{l} \ell (\pmb {\beta }) = \displaystyle 3\sum \limits _{i = 1}^n {\ln \left[ {\left( {\sqrt{ - 4\mu _i^2 + 4{\mu _i} + 1} - 2{\mu _i} + 1} \right) {{\left( {2{\mu _i}} \right) }^{ - 1}}} \right] } - 2\sum \limits _{i = 1}^n {\left( {1 - {y_i}} \right) } \\ -\,\displaystyle \sum \limits _{i = 1}^n {\ln \left( \begin{array}{l} {\left[ {\left( {\sqrt{ - 4\mu _i^2 + 4{\mu _i} + 1} - 2{\mu _i} + 1} \right) {{\left( {2{\mu _i}} \right) }^{ - 1}}} \right] ^2}\\ +\, 2\left( {\sqrt{ - 4\mu _i^2 + 4{\mu _i} + 1} - 2{\mu _i} + 1} \right) {\left( {2{\mu _i}} \right) ^{ - 1}} + 2 \end{array} \right) } \\ +\,\displaystyle 2\sum \limits _{i = 1}^n {\ln \left( {1 + \frac{{{y_i}}}{{1 - {y_i}}}} \right) - \sum \limits _{i = 1}^n {\frac{{{y_i}\left( {\sqrt{ - 4\mu _i^2 + 4{\mu _i} + 1} - 2{\mu _i} + 1} \right) {{\left( {2{\mu _i}} \right) }^{ - 1}}}}{{1 - {y_i}}}}}, \end{array} \end{aligned}$$

where \(\mu _i\) is given by (12). Under standard regularity conditions, the asymptotic distribution of \((\widehat{\pmb {\beta }}-\pmb {\beta })\) is multivariate normal \(N_{p}(0,K(\pmb {\beta })^{-1})\), where \(K(\pmb {\beta })\) is the expected information matrix. The asymptotic covariance matrix \(K(\pmb {\beta })^{-1}\) of \(\widehat{\pmb {\beta }}\) can be approximated by the inverse of the \(p\times p\) observed information matrix \(-\ddot{\L }(\pmb {\beta })\), whose elements are evaluated numerically by most statistical packages. The approximate multivariate normal distribution \(N_{p}(0,-\ddot{\L }(\pmb {\beta })^{-1})\) for \(\widehat{\pmb {\beta }}\) can be used in the classical way to construct approximate confidence intervals for the parameters in \(\pmb {\beta }\).

4.1 Residuals analysis

Residual analysis has a critical role in checking the adequacy of the fitted model. In order to analyze departures from the model assumptions, three types of residuals are usually utilized: the residuals introduced by Cox and Snell (1968), the randomized quantile residuals defined by Dunn and Smyth (1996) and Pearson residuals.

4.1.1 Cox and Snell residuals

Cox and Snell (1968) residuals are defined by

$$\begin{aligned} {\hat{e}_i} = - \ln \left[ {1 - F({ {{y_i}}; {{ \pmb {\hat{\beta }} }}})}\right] ,\quad i = 1,\ldots ,n, \end{aligned}$$

where \(F( {{\cdot }})\) is the unit-ISDL cdf. If the fitted model is correct, Cox and Snell’s residuals are approximately distributed as standard exponential distribution.

4.1.2 Randomized quantile residuals

The randomized quantile residuals are defined as

$$\begin{aligned} {\hat{r}_i} = {\Phi ^{ - 1}}\left( {{{\hat{u}}_i}} \right) , \end{aligned}$$

where \({\hat{u}_i} = F({{{y_i}}; {{\pmb {\hat{\beta }}}}})\) and \(\Phi ^{-1}(z)\) is the inverse of the standard normal cdf. If the fitted model is correct, the randomized quantile residuals are distributed as standard normal distribution.

4.1.3 Pearson residuals

The Pearson residual is widely used to detect possible outliers in the data. The Pearson residual is based on the idea of subtracting off the mean and dividing by the standard deviation. For the unit-ISDL regression model, the Pearson residuals can be expressed as

$$\begin{aligned} {r_i} = \frac{{{y_i} - {{\hat{\mu } }_i}}}{{\sqrt{\widehat{{\mathrm{Var}} }\left( {{y_i}} \right) } }}, \end{aligned}$$

where

$$\begin{aligned} {\widehat{{\mathrm{Var}} }\left( {{y_i}} \right) }=\frac{2\, {{\hat{\mu }_\mathrm{i}}}^2\, \left( \sqrt{ - 4\, {{\hat{\mu }_\mathrm{i}}}^2 + 4\, {\hat{\mu }_\mathrm{i}} + 1} - 2\, {\hat{\mu }_\mathrm{i}}\, \sqrt{ - 4\, {{\hat{\mu }_\mathrm{i}}}^2 + 4\, {\hat{\mu }_\mathrm{i}} + 1} + 1\right) }{8\, {\hat{\mu }_\mathrm{i}} + 4\, {\hat{\mu }_\mathrm{i}}\, \sqrt{ - 4\, {{\hat{\mu }_\mathrm{i}}}^2 + 4\, {\hat{\mu }_\mathrm{i}} + 1} + 2\, \sqrt{ - 4\, {{\hat{\mu }_\mathrm{i}}}^2 + 4\, {\hat{\mu }_\mathrm{i}} + 1} + 2}. \end{aligned}$$

The plot of these residuals against the index of the observations should reveal no detectable pattern. If the fitted model is correct, the Pearson residuals lie in the interval \((-\,2,2)\). The residuals outside this range are associated with potential outlier observations.

5 Simulations

In this section, we perform two simulation studies to examine the estimation methods in the proposed models.

5.1 Simulation study for the unit-ISDL distribution

First, we obtain the MLE, BC-MLE, MOM, LSE and WLSE of the unknown parameter \(\lambda \) in the unit-ISDL distribution. We compare the estimation efficiency of these five estimates by means of Monte Carlo simulations. The following simulation procedure is implemented:

  1. 1.

    Set the sample size n and the parameter \(\lambda \);

  2. 2.

    Generate n random observations from the \(\text {unit-ISDL}\left( {\lambda }\right) \) distribution;

  3. 3.

    Use the generated observations in Step 2, estimate \({\lambda }\) by means of the MLE, BC-MLE, MOM, LSE and WLSE methods;

  4. 4.

    Repeat N times the steps 2 and 3;

  5. 5.

    Use \(\hat{\lambda }\) and \(\lambda \) to calculate the mean biases, mean relative estimates (MREs) and mean square errors (MSEs) from the following equations:

    $$\begin{aligned} \begin{array}{l} Bias = \displaystyle \sum \limits _{j = 1}^N {\frac{{{{ { \hat{\lambda } }_{j}}} - { \lambda }}}{N}},\quad MRE = \displaystyle \sum \limits _{j = 1}^N {\frac{{{{{{{{\hat{\lambda } }}}_{j}}} / {{{\lambda }}}}}}{N}}, \quad MSE = \displaystyle \sum \limits _{j = 1}^N {\frac{{{{( {{{{\hat{\lambda } }}_{j}} - {{\lambda }}} )}^2}}}{N}\mathrm{{ }}}. \end{array} \end{aligned}$$

The simulation results are carried out using the R software. We take \({\lambda =0.5}\), \(N=10{,}000\) and \(n=20,25,30,\ldots ,300\). We expect that the MREs are closer to one when the MSEs are near zero. The plots of the estimated mean biases, MSEs and MREs obtained by the MLE, BC-MLE, MOM, LSE and WLSE methods are displayed in Fig. 3. Based on these plots, we note that the mean biases and MSEs of all estimates tend to zero when n increases and, as expected, the MRE values tend to one. Further, they reveal that the BC-MLE method converges to the nominal value of \(\lambda \) faster than the MLE, MOM, LSE and WLSE methods. So, we can conclude that the BC-MLE method can be chosen as more reliable than the MLE, MOM, LSE and WLSE methods for the parameter \(\lambda \) of the new distribution.

Fig. 3
figure 3

Estimated biases, MSEs and MREs for the parameter \(\lambda \) of the unit-ISDL distribution

Full size image

5.2 Simulation study for the unit-ISDL regression

Second, we investigate the performance of the MLEs of the parameters in the unit-ISDL regression model by means of a simulation study. We generate \(N=10,000\) samples of sizes \(n=50,250, 500\) and 1000 from model (12) under the systematic component:

$$\begin{aligned} \mu _i=\frac{\exp \left( \beta _0+ \beta _1x_{i1}+ \beta _2x_{i2}\right) }{1+\exp \left( \beta _0+ \beta _1x_{i1}+ \beta _2x_{i2}\right) }, \end{aligned}$$

where \(x_1\) and \(x_1\) are generated from a uniform U(0, 1) distribution. We take parameter values \(\beta _0=0.5, \beta _1=0.5\) and \( \beta _2=2\), and the response variable \(y_i\) is generated from this systematic component. The precision of the MLEs is based on the averages of the estimates (AEs), mean biases and mean square errors (MSEe). Table 2 gives the simulation results. Based on the figures in this table, we note that the MSEs of the MLEs of the parameters decay toward zero when the sample size increases as expected under first-order asymptotic theory. This fact reveals the consistency property of the MLEs.

Table 2 The AEs, biases and MSEs based on 10,000 simulations for the unit-ISDL regression with parameters: \(\beta _0=0.5\), \(\beta _1=0.5\) and \(\beta _2=2\) for \(n=50, 250, 500\) and 1000
Full size table

6 Empirical studies

6.1 Univariate data modeling

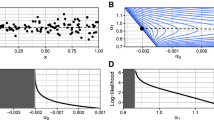
In this section, we compare the unit-ISDL distribution with four alternative distributions by means of a real data set (Nadar et al. 2013). The data refer to the monthly water capacity from the Shasta reservoir in California, USA, taken for the month of February from 1991 to 2010. The information about the hazard shape can be helpful in selecting a suitable model. For this purpose, a device called the total time on test (TTT) plot (Aarset 1987) can be used. The TTT plot is obtained by plotting

$$\begin{aligned} G(r/n)=\left[ {\left( {\sum \limits _{i=1}^{r}{{y_{(i)}}}}\right) +(n-r){ y_{(r)}}}\right] \bigg /\sum \limits _{i=1}^{n}{{y_{(i)},}} \end{aligned}$$

against r / n, where \({{y_{(i)}}}\)\((i=1,\ldots ,n)\) are the order statistics of the sample (for \(r=1,\ldots ,n\)). The TTT plot given in Fig. 4 indicates that the hazard shape of the monthly water capacity data is increasing. As suggested by reviewer, we compare the unit-ISDL distribution with unit-three-component-gamma (unit-3CGamma) distribution. The pdf of 3CGamma distribution is

$$\begin{aligned}&f\left( {x;{\alpha _1},{\alpha _2},{\alpha _3},{\lambda _1},{\lambda _2},{\lambda _3}} \right) = {p_1}\frac{{\lambda _1^{{\alpha _1}}}}{{\Gamma \left( {{\alpha _1}} \right) }}{x^{{\alpha _1} - 1}}\exp \left( { - {\lambda _1}x} \right) \nonumber \\&\quad +\, {p_2}\frac{{\lambda _2^{{\alpha _2}}}}{{\Gamma \left( {{\alpha _2}} \right) }}{x^{{\alpha _2} - 1}}\exp \left( { - {\lambda _2}x} \right) +\, {p_3}\frac{{\lambda _3^{{\alpha _3}}}}{{\Gamma \left( {{\alpha _3}} \right) }}{x^{{\alpha _3} - 1}}\exp \left( { - {\lambda _3}x} \right) \end{aligned}$$
(13)

where

$$\begin{aligned} {p_1} = \frac{{\lambda _1^2}}{{\lambda _1^2 + 2{\lambda _2} + {\lambda _3}}},\quad {p_2} = \frac{{2{\lambda _2}}}{{\lambda _1^2 + 2{\lambda _2} + {\lambda _3}}},\quad {p_3} = \frac{{{\lambda _3}}}{{\lambda _1^2 + 2{\lambda _2} + {\lambda _3}}} \end{aligned}$$
(14)
Fig. 4
figure 4

The TTT plot of the monthly water capacity data

Full size image

Let X be a random variable with pdf (13). Using the transformation \(Y=X/(X+1)\), the pdf of unit-3CGamma distribution \(\left( 0<y<1\right) \) is

$$\begin{aligned} f\left( {y;{\alpha _1},{\alpha _2},{\alpha _3},{\lambda _1},{\lambda _2},{\lambda _3}} \right)= & {} {p_1}\frac{{\lambda _1^{{\alpha _1}}}}{{\Gamma \left( {{\alpha _1}} \right) {{\left( {1 - y} \right) }^{{\alpha _1} + 1}}}}{y^{{\alpha _1} - 1}}\exp \left( { - {\lambda _1}\frac{y}{{1 - y}}} \right) \nonumber \\&+ {p_2}\frac{{\lambda _2^{{\alpha _2}}}}{{\Gamma \left( {{\alpha _2}} \right) {{\left( {1 - y} \right) }^{{\alpha _2} + 1}}}}{y^{{\alpha _2} - 1}}\exp \left( { - {\lambda _2}\frac{y}{{1 - y}}} \right) \nonumber \\&+ {p_3}\frac{{\lambda _3^{{\alpha _3}}}}{{\Gamma \left( {{\alpha _3}} \right) {{\left( {1 - y} \right) }^{{\alpha _3} + 1}}}}{y^{{\alpha _3} - 1}}\exp \left( { - {\lambda _3}\frac{y}{{1 - y}}} \right) \nonumber \\ \end{aligned}$$
(15)

where \(p_1,p_2\) and \(p_3\) are defined in (14). The unit-ISDL distribution is compared with the following five distributions defined on the unit interval (\(0< y < 1\)) as well as unit-3CGamma distribution:

  1. 1.

    Beta distribution

    $$\begin{aligned} f\left( y;\alpha ,\beta \right) = \frac{{\Gamma \left( {\alpha + \beta } \right) }}{{\Gamma \left( \alpha \right) \Gamma \left( \beta \right) }}{y^{\alpha - 1}}{\left( {1 - y} \right) ^{\beta - 1}},\quad \alpha>0,\ \beta > 0; \end{aligned}$$
  2. 2.

    Kumaraswamy distribution

    $$\begin{aligned} f\left( {y;\alpha ,\beta } \right) = \alpha \beta {y^{\alpha - 1}}{\left( {1 - {y^\alpha }} \right) ^{\beta - 1}},\quad \alpha> 0,\ \beta > 0; \end{aligned}$$
  3. 3.

    Topp–Leone distribution

    $$\begin{aligned} f\left( {y;\theta } \right) = \theta ( {2 - 2y} ){\left( {2y - {y^2}} \right) ^{\theta - 1}},\quad \theta > 0; \end{aligned}$$
  4. 4.

    Unit-Lindley distribution

    $$\begin{aligned} f\left( {y;\lambda } \right) = \frac{{{\lambda ^2}}}{{1 + \lambda }}{\left( {1 - y} \right) ^{ - 3}}\exp \left( { - \frac{{\lambda y}}{{1 - y}}} \right) ,\quad \lambda > 0; \end{aligned}$$
  5. 5.

    Unit-Gamma distribution

    $$\begin{aligned} f\left( {y;\alpha ,\phi } \right) = \frac{{{\alpha ^\phi }}}{{\Gamma \left( \phi \right) }}{y^{\alpha - 1}}\,\ln (-y)^{\phi - 1},\quad \alpha> 0,\ \phi > 0. \end{aligned}$$

We use the R software to estimate the model parameters. The estimated parameters of the unit-Gamma distribution are used as initial values of the shape and scale parameters of the unit-3CGamma distribution. The MLEs and corresponding standard errors (SEs), Kolmogorov–Smirnov (K–S) statistic and associated p value, Akaike Information Criteria (AIC), Consistent Akaikes Information Criteria (CAIC), Bayesian Information Criteria (BIC) and Hannan-Quinn Information Criteria (HQIC) for all fitted distributions are reported in Tables 3 and 4. The lower the values of these criteria, the better the fitted model to these data.

Table 3 lists the MLEs of the parameters for the fitted models to the monthly water capacity data, corresponding SEs and K-S test results with its p-values. A seen from K-S test results, all fitted models provides sufficient representation for the current data since all p-values are greater than 0.05. However, the unit-3CGamma distribution has the lowest value of K-S statistics.

Table 3 MLEs and their SEs (on second line) of the fitted models and goodness-of-fit statistics for the monthly water capacity data
Full size table

To decide the best fitted distribution, the model selection criteria, AIC, CAIC, BIC and HQIC, are used and the results are reported in Table 4. The figures in this table reveal that unit-ISDL distribution has the lowest values of the model selection criteria, except AIC value. The unit-3CGamma distribution has the lowest value of AIC. However, there is no big difference between the AIC values of unit-ISDL and unit-3CGamma distributions. More importantly, the unit-ISDL distribution has fewer parameters than unit-3CGamma distribution. When considered the law of parsimony, the proposed distribution can be chosen as the best model for the current data.

Table 4 Model selection criteria of the fitted models for the monthly water capacity data
Full size table

Figure 5 displays the fitted densities to the monthly water capacity histogram and some estimated functions of the unit-ISDL distribution. The right panel of the Fig. 5 reveals that the proposed distribution provides qualified fit to the monthly water capacity data.

Fig. 5
figure 5

The estimated pdfs of the fitted distributions to the monthly water capacity data (left-panel) and some estimated functions for the unit-ISDL distribution (right-panel)

Full size image

6.2 Regression modeling

In this section, we compare the beta, simplex, unit-Lindley and unit-ISDL regression models. The betareg and simplexreg packages of the R software are used to estimate the parameters of the beta and simplex regression models, respectively. For details see https://cran.r-project.org/web/packages/betareg/betareg.pdf and https://cran.r-project.org/web/packages/simplexreg/simplexreg.pdf).

The optim function of the R software is used to obtain the estimated parameters of the unit-Lindley and unit-ISDL regressions.

The aim of the study is to relate the long term interest (LTI) rates of the Organisation for Economic Cooperation and Development (OECD) countries (y) with foreign direct investment. These variables are given in the “Appendix”. The logit link function is used for the fitted regression models. Hence, the systematic component for \(\mu _i\) is

$$\begin{aligned} \text {logit}\left( \mu _i\right) =\beta _0+\beta _1 {FDI}_i. \end{aligned}$$

Table 5 gives the MLEs, their standard errors (SEs) and corresponding p-values for the beta, simplex, unit-Lindley and unit-ISDL regressions fitted to the LTI rates. The parameter \(\psi \) is the dispersion parameter of the beta and simplex regression models. The values in Table 5 reveal that the parameter \(\beta _1\) is statistically significant at 5% level for both regression models. We conclude that the FDI stocks explain the LTI rates. In other words, the LTI rates decrease when the FDI stocks increase.

Table 5 MLEs, SEs and corresponding p-values for the fitted models
Full size table

The minimized \(-\,\hat{\ell }\), AIC and BIC values are adopted to select the best fitted regression. Since the unit-ISDL regression has the lowest values of these statistics, it provides a better fit than the beta and simplex regressions for the current data. Moreover, Fig. 6 displays the randomized quantile residuals for the beta, simplex, unit-Lindley and unit-ISDL regressions. It is clear that the plotted points for the unit-ISDL regression are near to the diagonal line.

Fig. 6
figure 6

The Quantile–Quantile (QQ) plot of the randomized quantile residuals for the beta (top-left), simplex (top-right), unit-Lindley (bottom-left) and unit-ISDL (bottom-right) regression models

Full size image

The plots of the Pearson and Cox–Snell residuals for the unit-ISDL regression are displayed in Fig. 7. They indicate that the Pearson residuals lie between \((-\,2,2)\) and that none of the observations can be considered as possible outliers. The Probability–Probability (PP) plot of the Cox–Snell residuals reveals that the unit-ISDL regression provides an adequate fit to these data.

Fig. 7
figure 7

The Pearson (left) and Cox–Snell residuals (right) plots for the unit-ISDL regression model

Full size image

7 Conclusions

A new one-parameter distribution with bounded support is introduced. Some of its structural properties are obtained. The maximum likelihood, bias-corrected maximum likelihood, moments, least squares and weighted least squares methods are discussed for estimating the unknown parameters of the unit improved second-degree Lindley (unit-ISDL) distribution via simulation study. A new regression model for the unit response variable is introduced and compared with the beta and simples regression models. Empirical findings reveal that the unit-ISDL regression model provides a better fit than the beta, unit-Lindley and simplex regression models when the response variable is close to the boundaries of the unit interval. An extensive study on residual analysis, leverage and outlier detection is planned as a future work of this study. We hope that the results given in this paper will be useful for practitioners in several areas.