1 Introduction

In nature, many physical are modeled with the help of differential equations. Some of these problems are more complex and cannot be modeled by simple differential equations. For these complex and non-local issues, the researchers have developed a new technique which is known as Fractional Differential Equations (FDEs).

FDEs have achieved the attraction of scientists, due to its numerous applications in real-life sciences and engineering problems, such as electrolyte polarization (Deng and Li 2005), electrochemistry of corrosion (Oldham 1983), optics and signal processing (Baskin and Iomin 2013), electro-thermo elasticity (Machado et al. 2011), circuit systems (Hartley et al. 1995), diffusion wave (Bhrawy and Zaky 2015), heat conduction (Povstenko 2009) fluid flow (Kulish and Lage 2002; Mainardi 1997), probability and statistics (Kilbas et al. 2006; Bapna and Mathur 2012), and control theory of dynamical systems (Rossikhin and Shitikova 1997).

The Delay Differential Equations (DDEs) have the numerous properties everywhere, particularly, Fractional Differential Equations (FDEs) with delay argument are interesting topics for its applications in certain processes and systems in engineering and other sciences (Kuang et al. 1993a; b; Smith 2011; Ruan and Wei 2003; Hartung et al. 2006; Shakeri and Dehghan 2008; Yi et al. 2007). For modeling, FDDEs have gained more attention of the mathematicians for modeling as compared to simple ODEs, because a little delay has great impact. FDDEs are used in many areas of mathematics, such as infectious diseases, navigation prediction, population dynamics, circulating blood, the body reaction to carbon dioxide Deng and Li (2005); Oldham (1983); Baskin and Iomin (2013); Machado et al. (2011); Hartley et al. (1995); Bhrawy and Zaky (2015), and some other applications in advance research studies (Hethcote 2000; Arimoto et al. 1984; Podlubny 1998; Obata et al. 2004; Tarasov 2010; Kajiwara et al. 2012; Nelson et al. 2000; Zhu and Zou 2008).

The intensive focus of the researchers is to find the numerical solutions of FDDEs, because there is a no specific algorithm for analytical or exact solution of every FDDEs. Different techniques have been developed for the numerical solutions for these problems. The most common among these methods are Homotopy Perturbation Method (HPM) (Shakeri and Dehghan 2008), New Predictor Corrector Method (NPCM) (Bhalekar and Daftardar-Gejji 2011), Variation Iteration Method (VIM) (Chen and Wang 2010), Legendre Pseudospectral Method (LPSM) (Khader and Hendy 2012), Hermit Wavelet Method (HWM) (Saeed 2014), LMS Method (LMSM) (Engelborghs and Roose 2002), Runge Kutta-Type Methods (RKM) (Wang 2013), Adams–Bashforth–Moulton Algorithm (ABMA) (Wang 2013), Bernoulli Wavelet Method (BWM) (Rahimkhani et al. 2017), Extend Predictor Corrector Method (EPCM) (Moghaddam et al. 2016), Kernal Method (KM) (Xu and Lin 2016), GL Definition (GL) (Wang et al. 2013) , Gegenbauer Wavelet Method (GWM), and Adomian Decomposition Method (ADM) (Saeedi and Mohseni Moghadam 2011) have been used for the numerical and analytical solutions of FDDEs.

Some latest techniques for solving nonlinear and linear fractional partial differential equations are mentioned (Tariq et al. 2018; Rezazadeh et al. Rezazadeh et al. 2018, 2019; Ghanbari et al. 2019; Arqub and Al-Smadi 2018; Arqub and Maayah 2018; Osman et al. 2018; Osman 2017; Abu Arqub and Al-Smadi 2018; Abu Arqub 2018).

In current research work, CWM is extended for the numerical solutions of FDDEs. CWM solutions are calculated at different fractional-order \(\alpha \) which shows that the fractional-order solutions are convergent to integer order solutions. M.H. Heydari et al. have discussed the uniform and stability of the solution obtained by CWM (Heydari et al. 2013). The solutions of the suggested techniques are contrasted with the Kernel Hilbert Space Method (KHSM) approaches (Ghasemi et al. 2015), Haar Wavelet Method (HWM) (Hsiao 1997), Modified Legendre Wavelet Method (MLWM) (Hafshejani et al. 2011), GL Method (GLM) (Wang et al. 2013), and Spline Polynomial (SP) (Ramadan et al. 2006). The comparison shows that CWM has a better level of precision comparison to all other techniques described (Tables 1, 2, 3, 4, 5, 6, 7, 8, 9, 10).

2 Preliminaries’ concepts

In this section, we present some fundamental needed definitions and preliminary ideas linked to fractional calculus, which are used in this current research.

2.1 Caputo operator with fractional derivatives

$$\begin{aligned} D^\nu z(t)= \left\{ \begin{array}{ll} \frac{1}{\varGamma (m-\nu )} \int _{0}^{t} (t-\ell )^{m-\nu -1} \frac{d^m}{d\ell ^m} z(\ell )d\ell , \ \ &{} m-1<\nu <m\\ \frac{d^m}{dt^m}z(t), &{} \ \ m=\nu \end{array}. \right. \end{aligned}$$
(1)
Table 1 CWM, exact result, and absolute error (AE) for \( \alpha =\frac{1}{2}, \) comparison with KHSM of Example 5.1
Full size table
Table 2 CWM absolute error in the dissimilar fractional-order \(\alpha \) of Example 5.1
Full size table
Table 3 Exact, CWM result, and AE compare with HWM of Example 5.2
Full size table
Table 4 CWM AE at distinctly fractional-order \( \alpha \) Example 5.2
Full size table
Table 5 Exact, CWM solutions, and comparison of absolute error with MLWM of Example 5.3
Full size table
Table 6 CWM AE at distinctly fractional-order \( \alpha \) Example 5.3
Full size table
Table 7 Exact, CWM solutions, and comparison of absolute error with HWM and GLM of Example 5.4
Full size table
Table 8 CWM AE at different fractional-order \(\alpha \) of Example 5.4
Full size table
Table 9 Exact, CWM solutions, and absolute error for \( \alpha =0.999, \) comparison with SP of Example 5.5
Full size table
Table 10 CWM AE at dissimilar \( \alpha \) of Example 5.5
Full size table

2.2 Chebyshev wavelet properties

The Chebyshev wavelet develops relatives of components from expansion or conversion of particular function \(\psi (t)\) called mother wavelet. The second kind of Chebyshev polynomial consists of four factors \( \iota , \ell , k, t \), \( as \ \ \psi (t)=\psi (\iota ,\ell ,k,t),\) which is defined in the interval [0,1] as:

$$\begin{aligned} \psi _{\dot{\iota },\ell }(t)= \left[ \begin{array}{l@{\quad }l} 2^{\frac{k}{2}} \widetilde{P_\ell } (2^{k} t-2\dot{\iota }+1), &{} \frac{\dot{\iota }-1}{2^{k-1}}<t< \frac{\dot{\iota }}{2^{k+1}}\\ 0, &{} elsewhere \end{array}, \right. \end{aligned}$$
(2)

where

$$\begin{aligned} \widetilde{P_\ell }(t)= \left[ \begin{array}{l@{\quad }l} (\frac{2}{\pi })^{\frac{1}{2}} P_\ell (t), &{} \ell =0,1,2\cdots ,M-1\\ ({\frac{2}{\pi }})^{\frac{1}{2}}, &{} \ell =0, \end{array} \right. \end{aligned}$$
(3)

and \( P_\ell (t)\) is called Chebyshev polynomial which is calculated as:

$$\begin{aligned} P_{\ell +1} (t)=2tP_\ell (t)-P_{\ell -1} (t), \ \ \ell =1,2,\cdots , \end{aligned}$$
(4)

where

$$\begin{aligned} P_0 (t)=1,\ \ P_1 (t)=2t. \end{aligned}$$

2.3 Lemma 1: Khan et al. (2019)

While the Chebyshev wavelet expansion of a z(t) continuous variable converges evenly, the Chebyshev Wavelet algorithm converges to z(t).

2.4 Lemma 2: Heydari et al. (2014)

A function \(z(t)\in L_2[0,1],\) having defined the second-order derivative, z(t) can be extended in the following convergent series:

$$\begin{aligned} z (t)=\sum _{\dot{\iota }=1}^{\infty } \sum _{\ell =0}^{\infty } \beta _{\dot{\iota },\ell } \psi _{\dot{\iota },\ell } (t). \end{aligned}$$
(5)

3 Chebyshev wavelet approximation

Consider the general fractional-order differential equation:

$$\begin{aligned} \frac{d^{\alpha }z}{dt^{\alpha }} = u(z)+\hbar (t)z\left( \frac{t}{c} -\rho \right) , \ \frac{\dot{\iota }-1}{2}<\alpha <\frac{\dot{\iota }+1}{2}, \end{aligned}$$
(6)

where \( \rho , c > 0\), is constant delay. CWM approximation is defined as:

$$\begin{aligned} z (t)=\sum _{\dot{\iota }=1}^{\infty } \sum _{\ell =0}^{\infty } \beta _{\dot{\iota },\ell } \psi _{\dot{\iota },\ell } (t), \end{aligned}$$
(7)

and \( \psi _{\dot{\iota },\ell }(t) \) is calculated as:

$$\begin{aligned} \psi _{\dot{\iota },\ell }(t)= \left\{ \begin{array}{ll} 2^{\frac{k}{2}} \widetilde{P_\ell } (2^k t-2\dot{\iota }+1), &{} \frac{\dot{\iota }-1}{2^{k-1}}<t< \frac{\dot{\iota }}{2^{k+1}}\\ 0, &{} elsewhere, \end{array}, \right. \end{aligned}$$
(8)

where

$$\begin{aligned} \widetilde{P_\ell }(t)=\left( {\frac{2}{\pi }}\right) ^{\frac{1}{2}}P_\ell (t). \end{aligned}$$
(9)

\( P_\ell (t)\) is defined recursively as:

$$\begin{aligned} P_{\ell +1} (t)=2t P_\ell (t)-P_{\ell -1} (t), \ \ \ell =1,2,\cdots , \end{aligned}$$
(10)

while

$$\begin{aligned} P_0 (t)=1,P_1 (t)=2t. \end{aligned}$$

To reduce the series of CWM approximation for \( \dot{\iota }=1,2,\cdots , 2^{k-1} and \ \ \ell =0,1,\cdots , M-1, \) Eq. (7) become

$$\begin{aligned} z_{\dot{\iota },\ell }(t)=\sum _{\dot{\iota }=1}^{2^{k-1}} \sum _{\ell =0}^{M-1} \beta _{\dot{\iota },\ell } \psi _{\dot{\iota },\ell } (t). \end{aligned}$$
(11)

Using Eq. (11) and caputo derivatives on real delay problems in Eq. (6):

$$\begin{aligned} D^{\alpha }\left( \sum _{\dot{\iota }=1}^{2^{k-1}} \sum _{\ell =0}^{M_1-1} \beta _{\dot{\iota },\ell } \psi _{\dot{\iota },\ell } (t))\right) =u\left( \sum _{\dot{\iota }=1}^{2^{k-1}} \sum _{\ell =0}^{M-1} \beta _{\dot{\iota },\ell } \psi _{\dot{\iota },\ell } (t))\right) +\hbar (t) \left( \sum _{\dot{\iota }=1}^{2^{k-1}} \sum _{\ell =0}^{M-1} \beta _{\dot{\iota },\ell } \psi _{\dot{\iota },\ell } (\frac{t}{c}-\rho )\right) .\nonumber \\ \end{aligned}$$
(12)

Some equations are obtained using initial and boundary conditions in approximation as:

$$\begin{aligned}&\frac{d^\alpha }{dt^\alpha }\left( z_{\dot{\iota },\ell }(0)\right) =\frac{d^\alpha }{dt^\alpha }\left( \sum _{\dot{\iota }=1}^{2^{k-1}} \sum _{\ell =0}^{M-1} \beta _{\dot{\iota },\ell } \psi _{\dot{\iota },\ell } (0)\right) = 0, \ \ 0< \alpha \le 1 \end{aligned}$$
(13)
$$\begin{aligned}&\frac{d^\alpha }{dt^\alpha }\left( z_{\dot{\iota },\ell }(1)\right) =\frac{d^\alpha }{dt^\alpha }\left( \sum _{\dot{\iota }=1}^{2^{k-1}} \sum _{\ell =0}^{M-1} \beta _{\dot{\iota },\ell } \psi _{\dot{\iota },\ell } (1)\right) = 1, \ \ 0< \alpha \le 1. \end{aligned}$$
(14)

Equation (12) has become for distinct value of \(t = t_i\):

$$\begin{aligned} D^{\alpha }\left( \sum _{\dot{\iota }=1}^{2^{k-1}} \sum _{\ell =0}^{M-1} \beta _{\dot{\iota },\ell } \psi _{\dot{\iota },\ell } (t_i))\right) =u\left( \sum _{\dot{\iota }=1}^{2^{k-1}} \sum _{\ell =0}^{M-1} \beta _{\dot{\iota },\ell } \psi _{\dot{\iota },\ell } (t_i))\right) +\hbar (t_i) \left( \sum _{\dot{\iota }=1}^{2^{k-1}} \sum _{\ell =0}^{M-1} \beta _{\dot{\iota },\ell } \psi _{\dot{\iota },\ell } (\frac{t_i}{c}-\rho )\right) ,\nonumber \\ \end{aligned}$$
(15)

where \(t_i \) is calculated as:

$$\begin{aligned} t_i =\frac{\dot{\iota }-0.5}{2^{k-1}M}. \end{aligned}$$
(16)

Thus, Eqs. (13), (14), and (15) make differential equation scheme and determine the unidentified variables \( \beta _{\dot{\iota },\ell } \). I solved the resultant system using maple software, which provide CWM solution for the given problem.

4 Numerical representation

We considered some numerical examples to implement the new algorithm for numerical solution. The fractional delay problems are solved and the results obtained will be compared with the other techniques.

Example 5.1

Consider the linear FDDEs:

$$\begin{aligned} D^{\frac{1}{2}} z(t)-z\left( \frac{t}{2}\right) +z(t)=\hbar (t), \end{aligned}$$
(17)

the initial condition is:

$$\begin{aligned} u(0)=0, \end{aligned}$$

where

$$\begin{aligned} \hbar (t)= \frac{16}{5\varGamma (0.5)} t^{\frac{5}{2}}+\frac{7}{8}t^3, \end{aligned}$$

exact result is

$$\begin{aligned} z(t) =t^3. \end{aligned}$$
Fig. 1
figure 1

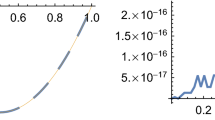
Error plot at distinct fractional-order \(\alpha \), for Example 5.1

Full size image

Foot Note 1:

In Fig 1, the CWM absolute error at different fractional-order \( \alpha \) for Example 5.1 is given. It is cleared that when fractional order approaches to the given fractional order of the problem than the CWM error converges to zero.

Example 5.2

Consider the following linear FDDEs:

$$\begin{aligned} D^{\frac{1}{2}} z(t)=z(t-1)-z(t)+2t-1+\frac{\varGamma (3)}{\varGamma (\frac{2}{5})} t^{\frac{3}{2}}, \ \ t>0, \end{aligned}$$
(18)

subjected to boundary conditions

$$\begin{aligned} z(0)=0,\ \ z(1)=1, \end{aligned}$$

the analytical solution for \( t\ge 0, \) is:

$$\begin{aligned} z(t)=t^2. \end{aligned}$$
Fig. 2
figure 2

Error plot at distinct fractional-order \(\alpha \), for Example 5.2

Full size image

Foot Note 2:

In Fig. 2, the absolute error of the CWM at different fractional-order \(\alpha \) for Example 5.2 is presented. The absolute error has shown that the CWM error is faster converging to zero when \( \alpha \) approaches to given order.

Example 5.3

Consider the following FDDEs:

$$\begin{aligned} D^{\alpha } z(t)=\frac{3}{4}z(t)-z\left( \frac{t}{2}\right) t^2 +2, \ \ 0\le t\le 1, \ \ 1\le \alpha \le 2, \end{aligned}$$
(19)

with the initial conditions

$$\begin{aligned} z(0)=0, \ \ \acute{z}(0)=0, \end{aligned}$$

the exact result of the given equation is:

$$\begin{aligned} z(t)=t^2 . \end{aligned}$$
Fig. 3
figure 3

Error plot at distinct fractional-order \(\alpha \), for Example 5.3

Full size image

Foot Note 3:

In Fig. 3, the absolute error of CWM at different fractional-order \( \alpha \) of Example 5.3 is given. It is clear that when fractional order approaches to integer order than error approaches to zero.

Example 5.4

Consider the following FDDEs:

$$\begin{aligned} D^{\beta } z(t)+z(t)-z(t-\rho )= & {} \frac{2}{\varGamma (3-\beta )}t^{2-\beta }-\frac{1}{\varGamma (2-\beta )}t^{1-\beta }\nonumber \\&+2t\rho -\rho ^2 -\rho , \ \ t>0, \ \ 0< \beta <1, \end{aligned}$$
(20)

The exact solution for \( \beta =0.9, \) and \(\rho = 0.01e^{-t}\) is \( z(t)=t^2-t. \)

Fig. 4
figure 4

Error plot at distinct fractional-order \(\alpha \), for Example 5.4

Full size image

Foot Note 4:

In Fig. 4, the absolute error of CWM at different fractional-order \( \alpha \) for Example 5.4 is presented. It is cleared that when fractional order approaches to integer order than the error approaches to zero.

Example 5.5

Consider the following FDDEs:

$$\begin{aligned} D^{\alpha } z(t)=\frac{3}{4}t^2 +z\left( \frac{t}{2}\right) -z(t)+\frac{2}{\varGamma (3-\alpha )} t^{2-\alpha }, \ \ 0< \alpha \le 1, \end{aligned}$$
(21)

with the initial condition is

$$\begin{aligned} z(0)=0, \end{aligned}$$

the exact result of the given problem as:

$$\begin{aligned} z(t)=t^2 . \end{aligned}$$
Fig. 5
figure 5

Error plot at distinct fractional-order \(\alpha \), for Example 5.5

Full size image

Foot Note 5:

In Fig. 5, the absolute error of CWM at different fractional-order \(\alpha \) for Example 5.2 is presented. The absolute error has shown that CWM solution is faster converging to exact solution for the problem.

5 Conclusion

In this article, we have used a new numerical technique called Chebyshev wavelet Method for the solution of FDDEs. The key benefits of the proposed method are its low-cost computing, small CPU time, and simple to implement. Also the present method has the ability to convert the given problem into system of mathematical equations, which can be solved easily using MAPLE software. Moreover, CWM has the highest accuracy as compared to other numerical methods. In this connection, CWM results are compared with the numerical results of other methods, such as KHSM, HWM, MLWM, GLM, and SP. Based on the above facts, CWM can be easily be extended to other fractional delay or non-delay models in engineering and real-life sciences.